Can machine learning bring cardiovascular risk assessment to the next level? A methodological study using FOURIER trial data

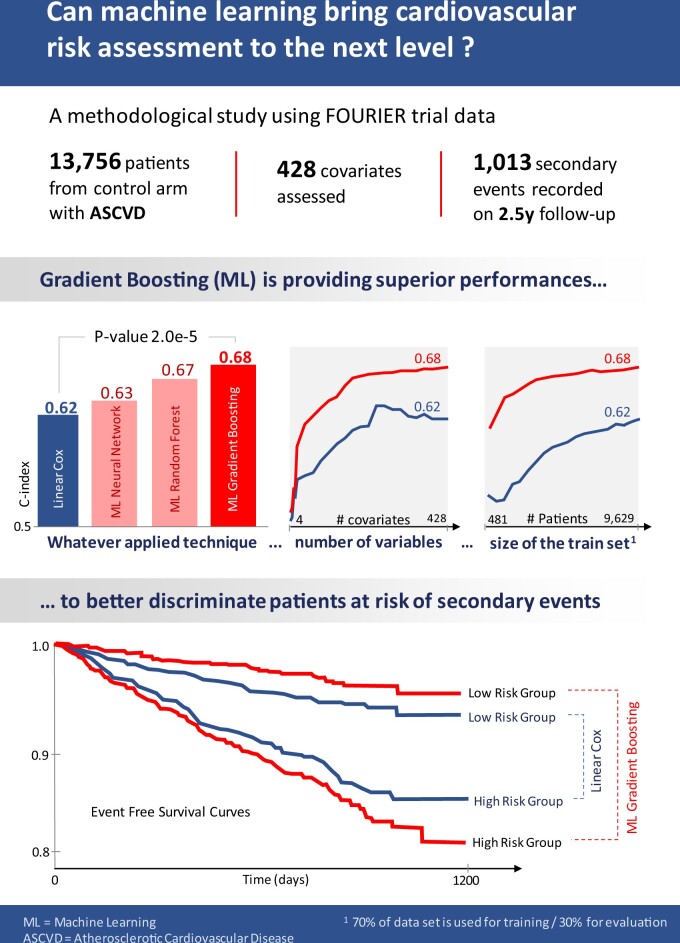
Abstract

Aims

Through this proof of concept, we studied the potential added value of machine learning (ML) methods in building cardiovascular risk scores from structured data and the conditions under which they outperform linear statistical models.

Methods and results

Relying on extensive cardiovascular clinical data from FOURIER, a randomized clinical trial to test for evolocumab efficacy, we compared linear models, neural networks, random forest, and gradient boosting machines for predicting the risk of major adverse cardiovascular events. To study the relative strengths of each method, we extended the comparison to restricted subsets of the full FOURIER dataset, limiting either the number of available patients or the number of their characteristics. When using all the 428 covariates available in the dataset, ML methods significantly (c-index 0.67, P-value 2e−5) outperformed linear models built from the same variables (c-index 0.62), as well as a reference cardiovascular risk score based on only 10 variables (c-index 0.60). We showed that gradient boosting—the best performing model in our setting—requires fewer patients and significantly outperforms linear models when using large numbers of variables. On the other hand, we illustrate how linear models suffer from being trained on too many variables, thus requiring a more careful prior selection. These ML methods proved to consistently improve risk assessment, to be interpretable despite their complexity and to help identify the minimal set of covariates necessary to achieve top performance.

Conclusion

In the field of secondary cardiovascular events prevention, given the increased availability of extensive electronic health records, ML methods could open the door to more powerful tools for patient risk stratification and treatment allocation strategies.

Graphical Abstract

Introduction

Patients with prior symptomatic atherosclerosis cardiovascular disease are known to have a heterogeneous risk of recurrent cardiovascular event¹ and, when treated, are exposed to various degrees of a verse effects.^2–4 A robust stratification of patients could take into account the risk heterogeneity and allow to better balance treatment benefit against the associated side effects or identify patients who would get the greatest benefit from treatment. To this end, several risk scores for primary or secondary prevention have been developed on populations of patients with atherosclerotic cardiovascular diseases (ASCVD): TIMI Risk Score for 2° Prevention (TRS 2°P),⁵ SMART,⁶ REACH,⁷ and SCORE.⁸ While these scores are validated and widely used in daily practice, they only exploit small sets of covariates through linear statistical models.

With electronic health record (EHR) systems being widely deployed in hospitals, the number and availability of patient’s baseline characteristics increased. Cohorts extracted from those EHR are now widely used for research^9–11 and can include different modalities. For instance, the Swedish MI registry, SWEDEHEART, was recently linked to Biobank, offering the possibility to design prognosis models on both genetic and clinical data.¹² Machine learning (ML) methods are well suited to estimate prognosis from those high-dimensional baseline covariates. While classical statistical models assume a linear relationship between the covariates and the outcome, ML methods can fit a wider class of functions, considering potential covariate interactions.

In this article, we studied the benefits of using ML methods to develop secondary cardiovascular risk scores on an extensive base of patients records. To this end, we analysed data from the placebo arm of the FOURIER trial. We compared different ML approaches to the linear Cox proportional hazards model to predict major adverse cardiovascular events (MACE), a composite endpoint comprising cardiovascular death, myocardial infarction, and stroke. The dataset contained a set of covariates larger than what is usually recorded in routine clinical practice. We therefore studied the impact of restricting the covariate dimension on each model’s performance. Additionally, we discussed the benefits and drawbacks of each method in terms of interpretability and ease to deploy.

This work is related to other comparisons of modelling methods for cardiovascular prognosis like Golas et al.,¹³ Li et al.,¹⁴ Desai et al.,¹⁵ Kwon et al.,¹⁶ and VanHouten et al.¹⁷ Compared to these studies, ours focuses on ranking patients by their risk—aiming at properly discriminating patients to identify those the most at risk to experience an event over the follow-up period. This approach provides more methodological information, and empirically assesses the influence of sample size and number of variables for such a task.

Material and methods

Study population and dataset

Our work was conducted on the FOURIER study’s data. FOURIER is a phase III, randomized, double-blind, placebo-controlled trial involving 27 564 patients with ASCVD, either with a history of myocardial infarction, non-haemorrhagic stroke, or symptomatic peripheral artery disease. The trial enrolled patients aged between 40 and 85 years with an LDL-c level ≥70 mg/dL or non-high-density lipoprotein cholesterol ≥100 mg/dL. Patients were on an optimized statin regimen and randomized to evolocumab (140 mg every 2 weeks or 420 mg every month) or matching placebo.

The baseline clinical characteristics of the patients include demographics data, biological measurements, medical history, comorbidities, as well as information about the cardiovascular diagnosis, treatments, and procedures. They were previously described in Table 1 from Sabatine et al.¹⁸ For our study, we focused on the 13 756 patients of the trial control arm who took the placebo, so as not to account for evolocumab treatment effect. Variable selection was kept to a minimum as our comparisons focused on models’ performance on raw data. Among the 527 recorded covariates, we selected 428, removing those that had a constant value or whose Pearson correlation to another covariate was equal to 1.

Table 1.

Performance comparison between best performing models

Model	C-index (CI 95%)	P-value vs. linear	P-value vs. NN	P-value vs. RF
Linear Cox model	0.618 (0.609–0.627)	—	—	—
Neural network	0.634 (0.626–0.642)	7.8e−2	—	—
Random forest	0.674 (0.666–0.681)	1.5e−4	3.2e−3	—
Gradient boosting	0.676 (0.668–0.684)	2.0e−5	1.1e−3	6.1e−1

Based on their performance during the nested cross-validation on the training set, we selected the best performing models and evaluated them on the test set. Comparing the best models of each category to one another, we found that tree-based models significatively improve the C-index. In terms of Net Reclassification Improvement (NRI), the best model (gradient boosting) improved patients’ reclassification by 31.6% (19.0%, 40.7%) compared to the linear Cox model.

Evaluation methodology

As a first step, we randomly divided the placebo arm into a training (70% of the whole dataset: 9629 patients) and testing (the remaining 30%: 4127 patients) datasets, using the stratification criteria defined in the trial. The test set was not used when selecting the models and their hyperparameters. It was only used for the final models’ evaluation, thus guaranteeing that we did not overestimate the local performance. All the metrics that follow were computed on this test set.

In our benchmark, we selected and evaluated the best model and their best hyperparameters on the training set using nested cross-validation. Nested cross-validation, also known as double cross-validation,¹⁹ is a model training and evaluation scheme that consists in repeatedly and independently separating subsets of data used for models’ hyperparameters tuning and performance evaluations. We performed iterations of nested cross validations each. This method helps to prevent overfitting during model selection. The results reported on the training set were averaged over 10 full repetitions of a nested cross-validation, each with five inner loops repeated in five outer loops. The hyperparameter search was performed on the five-fold inner loop of the cross validation. Using this process, we obtained 50 performance evaluations (10 repetitions of 5 outer loops) per considered model.

Each algorithm performance was evaluated for several models resulting from the nested cross-validation and on different subsets of the data for the training metrics. The individual confidence for each of these model’s c-index was computed using the tree-search algorithm from Newson.²⁰ We then aggregated them using Chernozhukov et al.,²¹ which relies on the median of each confidence interval’s lower and upper bounds.

To ensure reproducibility of our simulations, we set an arbitrary seed for the random number generator of both dataset subsampling and model training functions. The preprocessing pipeline was kept minimal and almost identical for all models. We converted all values to numerical ones by one-hot-encoding categorical variables. As the only preprocessing difference between models, since linear models and neural networks do not support missing values and are sensitive to variable’s scale, we imputed missing values using their median and standardized the covariates. More complex imputation methods, like iterative imputation which sequentially imputes variables conditionally on all the others, were evaluated but did not yield any performance improvement. It was therefore decided to keep the preprocessing simple as our reference gradient boosting models natively support missing values and do not require such an imputation by design, while linear and neural network models do.

Evaluation metrics

Performances were assessed using the concordance index²² (c-index), a metric related to the receiver operating characteristic area under the curve (ROC AUC) for survival analysis with censored outcomes. It estimates the probability that, for any comparable pair of patients, the predictor score (i.e. the estimated risk of an event) is greater for the patient with the earlier event. A c-index of 0.5 would be assigned to a random risk score. The closer to 1 the c-index is, the better the model ranks the risks considering the observed event occurrence times. Under no censoring, when all events are observed, c-index’s formula simplifies to the area under the curve (AUC) formula.

On the test set, the c-indexes for the best models were reported. These best models were built by taking the best hyperparameters—those which yielded the best performance on average on the training data during the nested cross-validation—and training the considered model over the whole training dataset. We tested, using a z-score test as in Kang et al.,²³ if the difference of performance between the considered models and the linear model was significant. Additionally, to assess the change in discrimination for the different models, compared to the best linear one, the net reclassification improvement (NRI)²⁴ was calculated. Relying on the continuous NRI from Pencina,²⁵ we quantified the degree to which ML models were making correct change decisions between different risk categories.

As a more detailed visualization of the models’ predictive power, we used time-dependent receiver operating characteristic (ROC) curves. ROC curve analysis can indeed be extended to censored data by considering time-dependent ROC curves which give the sensitivity and specificity compromise at a given horizon in time, as in Kamarudin.²⁶ These curves allow to better assess the true positive rate (sensitivity) and false positive rate (1 − specificity) compromise, if a threshold was to be chosen to make decisions based on the score value.

Lastly regarding the models’ discrimination capacity, to assess the ability of the models to stratify the population into relevant subgroups, we relied on the trained models to divide the population into three different groups of equal sizes. The stratified population Kaplan–Meier curves²⁷ were derived to illustrate the models’ discriminative capacity.

While calibration is not the focus of this study and was not used to select models, we also reported our best model’s calibration for a single time-horizon. We relied on the expected calibration error (ECE) metric from Naeini et al.²⁸ to do so. Across quantiles of predicted probabilities, ECE assesses the mean difference between the predicted event probabilities and the actual proportion of patients who suffered an event.

The TIMI Risk Score for 2° Prevention

The TRS 2°P⁵ a risk score widely used for secondary prevention, was considered as the baseline method to which we compared the other evaluated algorithms. This risk score was developed on a cohort from the TRA 2°P-TIMI 50 trial, independent from the FOURIER trial. It contained 8598 stable patients from the placebo arm who had a previous myocardial infarction (MI) and were followed for a median of 2.5 years. The score relies on 9 predictors: age, diabetes mellitus, hypertension, smoking, peripheral arterial disease, previous stroke, previous coronary bypass grafting, heart failure, and renal dysfunction. The predictors used for the score were identified in different steps. First a set of 150 candidates were chosen based on univariate Z-score, prevalence, and ease of clinical application. Among the candidate variables, 16 baseline ones achieved a significance level of P < 0.10 using a Cox proportional hazards modelling analysis. The 16 characteristics were included in a forward and backward multivariate analysis, leading to the choice of the 9 predictors.

This score was designed for patients who suffered from a previous MI, which is not systematic in the population we considered. Therefore, we used an expanded TRS 2°P by adding a variable to code for a previous MI occurrence to the standard TRS 2°P computation, as has been done previously in analogous situations.²⁹

Machine learning methods

In this work, we compare ML to linear statistical methods.

While there is no well-defined frontier between these methods, in prior articles like Breiman et al.,³⁰ two cultures are defined. On the one hand, the data modelling culture requires prior hypotheses on the (unknown) data generating process and prioritizes models’ interpretability. On the other hand, the algorithmic modelling culture—which would now be designated as ML—can accommodate any underlying data distribution and prioritizes models’ predictive performance. These interpretability and performance objectives are often considered as being in conflict.

As in Desai et al.,¹⁵ we consider ML methods as those which model the relationship between outcome and covariates in a non-linear form, and limit the statistical methods to linear modelling. Machine learning methods can fit a wider class of functions than linear models^31,32 and offer the possibility to work with high dimensional covariates. Therefore, the more covariates are available, the more improvement we expect when relying on ML models. Despite evaluating complex non-linear models, we however do not ignore interpretability. We rely on model agnostic techniques to study which covariates influence our predictions the most and how they do so.

Explored models, hyperparameters, and implementation

In this study, we compared the TRS 2°P and linear models to several ML models for MACE prediction in patients with ASCVD: multilayer perceptron (MLP) neural networks,³³ random forests,³⁴ and gradient boosting machines.³² These models were selected as they proved to yield better results in preliminary explorations and prior similar projects. They were all trained to fit a Cox proportional hazards model of the time-to-event for MACE, maximizing the partial Cox likelihood on the training dataset. In this setting, both the time to observed events and the time to censoring are considered, for patients who did not suffer any MACE by the time of the last potential endpoint ascertainment date. For each model, we explored different regularization methods and hyperparameters in each experimental setting. Cross-validations were implemented using scikit-learn.³⁵

Linear models learn a linear combination of variables to predict the risk, not accounting for any interaction between the patients’ characteristics. They were implemented using elastic-net regularization,³⁶ which mixes L1 (Lasso) and L2 (Ridge) regularizations. Several ratios of L1 and L2 regularizations were explored to better allow these models to select variables and avoid overfitting the training data. These models were trained using scikit-survival.^37–39

The MLP—or fully connected neural network—is the most classical architecture for neural networks. They are networks structured with layers of neurons: the neurons of the first layer each compute a linear combination of the input variables before applying a non-linear activation function, those of the second layer do the same from linear combinations of the first layer outputs… the last layer has only one neuron which computes the risk from the outputs of the previous layer. These models have been proven to be able to approximate any function from their input variables.⁴⁰ We used the ReLU activation function for the hidden layers. We explored several depths, mini-batch sizes, and regularizations. For regularization, batch-normalization proved to be systematically helpful during our initial tests and was used in all the further trainings. We implemented our neural networks using PyTorch.^41,42

Random forest and gradient boosting both model the risk as ensembles of regression trees. Random forests are built by training relatively deep trees in parallel from subsets of the data: each tree is only given access to a subset of the patients and variables when it is trained. Each of these trees are low bias but high variance estimators, meaning that they overfit the subset of the data they were trained on. Yet, the random forest predicts the risk by averaging their predictions, thus limiting the overfitting. Gradient boosting is an opposite approach as it relies on training shallow trees that are high bias but low variance estimators, meaning that they underfit the data they are trained on. Yet, these trees are trained sequentially, each being trained to correct the error of the previous ones to improve the ensemble’s goodness of fit with respect to the training data. For these tree-based models, we tested for several tree depths, learning rates, sampling ratios and variable selection ratios. We also used early stopping to prevent overfitting. These models were trained using XGBoost.⁴³

Model agnostic interpretability

Interpretability encompasses any means of allowing humans to understand what the causes of a model’s predictions are. This interpretability can help domain experts assess the reliability of a model. For our application, the fact that models mostly rely on variables known to be prognostic of MACE can allow cardiologists to validate that the patterns learned by the models indeed make sense. Interpretability can even yield medical insights when less understood patterns are captured, even if good predictors are not necessarily risk factors as correlation does not imply causation. Linear models are trivial to interpret: each variable coefficient indicates how it influences the predictions and these coefficients’ P-values indicate how reliable this influence is.

Machine learning models extract non-linear patterns from the data, leveraging interactions between any number of them. This makes them harder to interpret than linear models and sometimes considered as black boxes. Yet, methods have been developed to extract information about the individual importance of each variable for a considered model. A classical approach for tree-based algorithms consists in using the variables’ gain, as proposed by Breiman.⁴⁴

These methods have recently been criticized for being inconsistent as a variable selection tool, being model specific and not indicating the interaction direction for a variable. We relied on the model agnostic SHAP (SHapley Additive exPlanation) values^45,46 to interpret the trained models. SHAP values estimate how each variable—or group of variables—contributes to a model’s predictions. These values allow ranking the respective prognostic importance of all variables for a given model, as well as illustrate in which way these variables impact predictions.

Subsampling

While more than 400 variables are available in the FOURIER trial, the TRS 2°P only uses 9, making it easier to use in clinical practice. To explore the impact of the data dimension on the performance, we compared the different algorithms on restricted sets of variables.

As a first experiment, we performed a comparison between models on subsets of clinically relevant variables.

We compared all the candidate models by training them on the 9 TRS 2°P variables and an additional one indicating the prior occurrence of a MI, as in Bohula et al.⁴⁷ Whereas the TRS 2°P binarized some variables (e.g. ‘age > 65’), we used the corresponding continuous values when available.

We then selected the following 33 routine clinical variables:

• General: gender, age, smoking status;

• Biology: cholesterol (total), creatinine, left ventricular ejection fraction, glycaemia, HDL-c, haemoglobin, haemoglobin A1c, LDL-c;

• Medical history: coronary artery bypass grafting, MI, peripheral artery disease, stroke;

• Comorbidities: atrial fibrillation, type 2 diabetes, hypertension;

• Medication: angiotensin-converting enzyme inhibitors, aspirin, beta blockers, clopidogrel, enoxaparin sodium, heparin, statin;

• Arteries with stents: left main coronary artery, left anterior descending, left circumflex, right coronary.

These were chosen because they were present in two hospitals’ cardiology EHR datasets from other ongoing studies.⁴⁸

Lastly, to assess the reliability of SHAP values as a model interpretation and variable selection tool, we selected the 25 most important variables defined by the SHAP values of the best-performing gradient boosting model. This number of most important variables was chosen as it proved to be sufficient to almost reach peak performance with most models.

As a second experiment, to further explore the respective approaches we repeated the comparison on random subsets of variables to better explore the impact of data dimension on the linear model—considered as a baseline—and the gradient boosting model—the best performing model in all the settings. For increasing dimensions (from 4 to the 428 dimensions of the original data), we sampled different subsets of variables for all the outer loops of cross-validation (50 different subsets per considered ratio).

We also evaluated the models on increasing sets of the most important variables. Variables were selected by decreasing importance according to the most natural selection method for each model. For linear models, we ranked variables according to their univariate predictive power. This predictive power was assessed using the c-index between each individual variable and the considered outcome. For gradient boosting models, we used the SHAP values from the best performing model to rank them by decreasing importance.

As patient data are widely becoming available in EHR databases, the datasets used to train cardiovascular risk scores are getting larger. We studied the influence of the dataset size, this time in terms of number of patients, on the ability of the two reference models—the linear model as the statistical approach and the gradient boosting model as the ML method—to capture information. To do so, we compared them on sub-cohorts of increasing size, randomly selecting (without replacement) patients in the outer loop of the cross-validation.

Related work

Our work is closely related to several recent studies that have been conducted to compare linear models to ML methods in their ability to accurately predict different cardiovascular outcomes. While previous studies framed the problem as a classification task (30-day readmissions in patients with heart failure,¹³ 1-year death,^14,15 in-hospital mortality after an acute myocardial infarction,¹⁶ and the presence or absence of acute coronary syndrome),¹⁷ we frame the problem as a ranking task.

These studies respectively included 37 baseline characteristics for Kwon et al.,¹⁶ 88 for VanHouten et al.,¹⁷ 59 for Li et al.,¹⁴ 30 (including unstructured text) for Golas et al.,¹³ and 54 for Desai et al.¹⁵ Our study included 428 variables, offering the opportunity to work in a higher dimension setting. To compare with the results obtained in former studies and allow for easier-to-deploy scores, we also repeated experiments on smaller sets of variables.

Results

Comparison to other scores

In all that follows, we only compared our different models to the TRS 2°P score as the other standard scores, that we managed to compute from the available covariates, proved to achieve lower c-indexes. On the test set, these different risk scores’ performances were:

• TRS 2°P: 0.60

• SMART: 0.56

• REACH: 0.56

• SCORE: 0.51

Evaluation on the full dataset

Using the full set of 428 variables, we observed that ML models achieve better performances than linear ones in Figure 1, despite the latter’s regularization. These results are detailed in Table 1, where we computed the P-values of the c-index difference as well as the NRI between the best performing model1 in each category.

Figure 1.

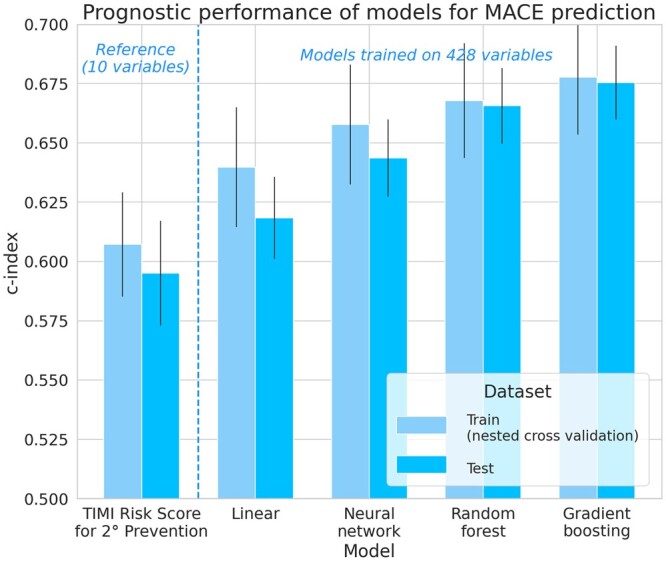
Prognostic performance of models for major adverse cardiovascular events prediction. In this high-dimension setting with 428 variables, tree-based machine learning models (random forests and gradient boosting) proved to yield significantly better results than linear models trained on the same feature space. Since better results were obtained on the training set during the nested cross-validation, in the following, we only report the metrics on the test set, as a fairer and more compact assessment of each model’s performance.

Results of Figure 1 are averages for all models selected during the nested cross validation, whereas the results of Table 1 correspond to the unique best models of each category (according to their performance during the cross-validation) on the test set to allow for testing the c-index differences and computing the NRIs, which ex- plains the slight difference between c-indexes.

The best performing gradient boosting model achieves a c-index of 0.676, whereas the best performing linear model only achieves 0.618.

Even if the best fully connected neural network outperformed the best linear models, these models did not consistently yield better performance, despite exploring several optimization algorithms, testing for several depths and regularization strategies (dropout and batch-norm).

Risk prediction, patient’s stratification, and calibration

Tree-based ensemble algorithms, namely random forests and gradient boosting machines, proved to yield the best performance in our setting. This difference in performance reflects an improved ability to capture more subtle patterns and predict events recurrence. It enables a better compromise between sensitivity (true positive rate) and specificity (true negative rate), which can be illustrated using a time-dependent ROC curve. The time-dependent ROC curves of the best linear and ML models of Figure 2 demonstrate the difference in prognosis performance between these methods for a time-horizon of one year.

Figure 2.

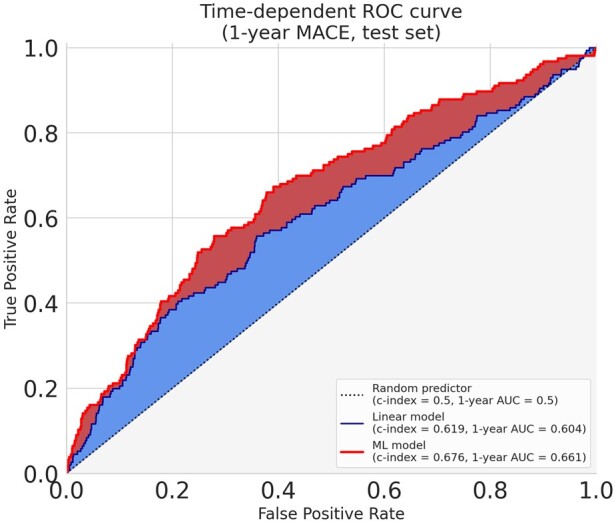
Time-dependent receiving operator curve. The receiving operator curves illustrate the difference between the best linear and the best model (gradient boosting) in properly attributing a higher risk to patients from the test set who suffered a major adverse cardiovascular event less than a year after their enrolment. We chose the duration of 1 year as it is very close to the median of the recurrence time over our training dataset (353 days). This threshold was only used to evaluate the models and build these curves: the models are the ones evaluated in Table 1 which were trained using the whole follow-up. When arbitrarily calibrating both models to predict less than 30% false positives (specificity > 70%), the gradient boosting model achieves an increase in sensitivity of 11% over the linear one (55% vs. 44%).

This allows in turn to better stratify patients based on their risk of MACE during the follow-up, as illustrated in the stratified Kaplan–Meier curves of Figure 3, and prioritize them in refined treatment allocation strategies.

Figure 3.

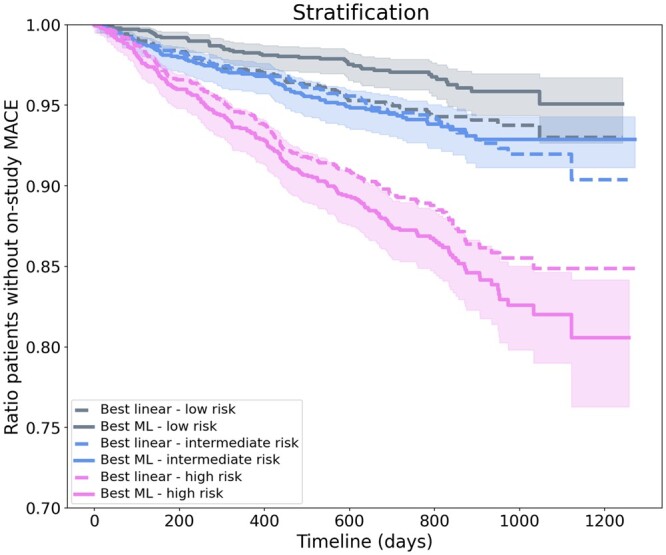
Stratification of patients based on their risks. The stratification Kaplan–Meier curves show the expectation for the first major adverse cardiovascular event occurrence during the study and its confidence interval for each risk group of the best linear and machine learning models. Taking each group of equal size, these curves illustrate how the best machine learning model achieves a much wider separation between the high- and low-risk patients compared to the best linear model.

Considering the same 1-year time-horizon as in Figure 2’s time-dependent ROC curve and 10 bins of predicted scores, we estimated an ECE of 0.01 for our best ML model’s, which is close to a perfect calibration of 0.

Model interpretability

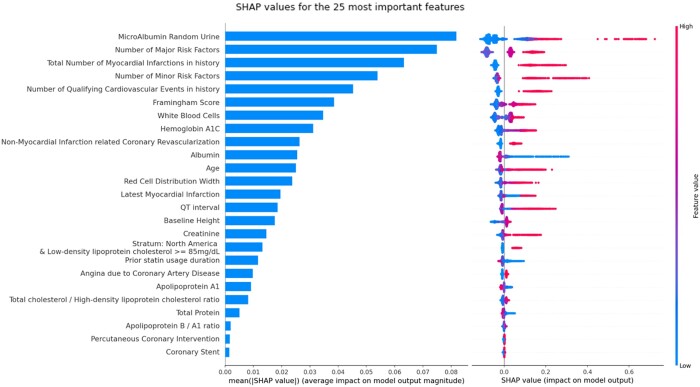
In Figure 4, we displayed the SHAP values for the best performing model. This plot illustrates which 25 variables have the most impact on the model’s predictions. The fact that the model mostly relied on age, cardiovascular history, lipids, renal function, and composite counts of risk factors (including diabetes, smoking status…) to assess the risk is coherent with domain knowledge.

Figure 4.

Best model prognostic features ranking and influence. The SHapley Additive exPlanations values were extracted from the best-performing gradient boosting model on the full set of variables. The left plot illustrates the mean absolute SHapley Additive exPlanations value for each covariate, allowing to select the most important ones for more compact models. The right one provides more detailed information about the direction of these covariates’ influence on the prognosis across the range of values observed for each variable. For example, according to our model on the considered population, it illustrates that having a high value (red point) of microalbumin for random urine tests increases the risk of major adverse cardiovascular events (points on the right).

It also shows how they impact the predictions. For example, our best model learned that high values of microalbumin in the urine increase the risk of MACE. On the other hand, serum albumin has the opposite influence with low values increasing the chance of MACE.

Evaluation on restricted set of covariates

When using the 10 variables in the TRS 2°P, we observed that, on such a low-dimension space, all models performed similarly and achieved c-indexes close to that of TRS 2°P. When using only routine variables, gradient boosting barely outperformed linear models.

Lastly, when using only the 25 most prognostic variables according to the SHAP values from our best performing model (as listed in Figure 4), gradient boosting achieved the same performance as when it was trained on all the 428 FOURIER variables. Other models achieved the high performances, even outperforming similar models trained on all FOURIER variables. This illustrates the ability of ML models to perform automatic variable selection; thus enabling to build more compact risk scores, which are therefore more interpretable, faster to train and easier to deploy.

When randomly sampling variables from the full dataset, linear models’ performance increased up to a point but started decreasing when the dimension was too high due to the increasing number of multicollinearities (ill-conditioned data). On the other hand, the higher the dimension, the more tree models outperformed linear ones. When selecting increasing sets of variables according to their importance, both models once again achieved similar performance if only a few variables are available. Linear models achieve peak performance with relatively few variables (16 ≈ 4% of available covariates) and their performance then decreased as dimension grew. Gradient boosting models’ performance were similar to linear models when the number of variables was relatively low (≤20). They showed a slight but steady improvement when adding more variables, consistently benefiting from bigger feature spaces and outperforming linear models. This illustrates how careful variable selection is required for linear models, whereas gradient boosting can leverage more complex and high-dimension feature spaces without overfitting them.

The results of these benchmarks are reported in Figures 5 and 6.

Figure 5.

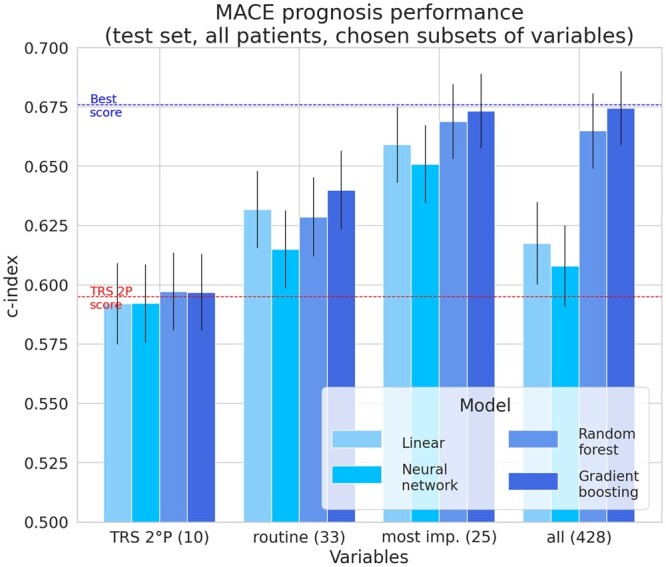
Performances depending on variable selection. For the task of predicting major adverse cardiovascular events, when selecting variables—either based on their use in the TIMI Risk Score for 2° Prevention (TRS 2°P), their availability in routine clinical practice or their importance in our best performing model—compared to using all of them, we observed that tree-based models’ increase in performance was consistent and higher when more variables are available.

Figure 6.

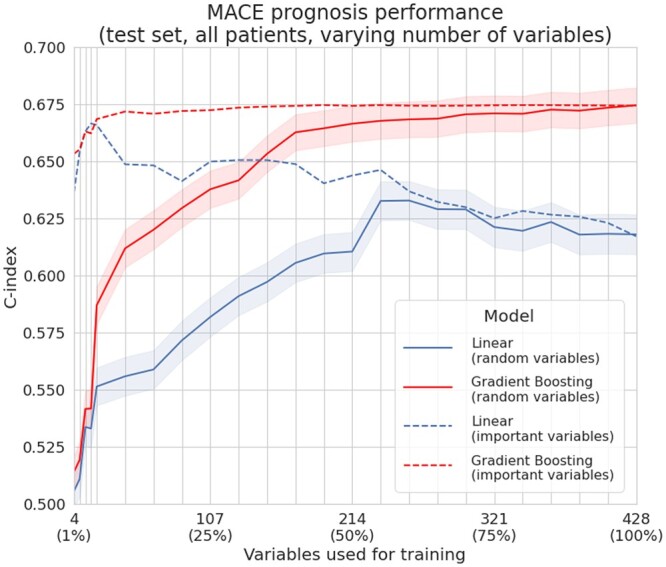
Performances depending on the number of used variables. When randomly sampling variables from the data (right, full lines), even if some of the selected subsets might lack some common prognostic variables and not convey much useful information, we again observed that gradient boosting requires less variables than linear models to achieve similar performance. When selecting variables by order of decreasing importance (right, dashed lines)—using their univariate c-index to the outcome for linear models and their SHAP values for gradient boosting models—both models achieve better performance (compared to random variables sampling) in lower dimension regimes by having access to more prognostic variables. The performance of linear models peaks with few variables,¹⁶ while gradient boosting slightly but consistently improves when more are provided.

Influence of the number of patients

We performed the evaluation from subsets of 481 patients (5% of the training patients selected from the control cohort) to subsets of 9629 patients. Experiments on fewer than 400 patients did not yield comparable results due to the repeated subsampling of the nested cross-validation: many training subsets ended up containing only censored data (no observed MACE) and preventing proper model training.

We observed that gradient boosting models trained with 25% of the data outperformed linear ones trained on the whole dataset. For the compared methods, c-indexes kept increasing when adding patients, showing that they might still improve if more patients were available.

The results from this comparison are reported in Figure 7.

Figure 7.

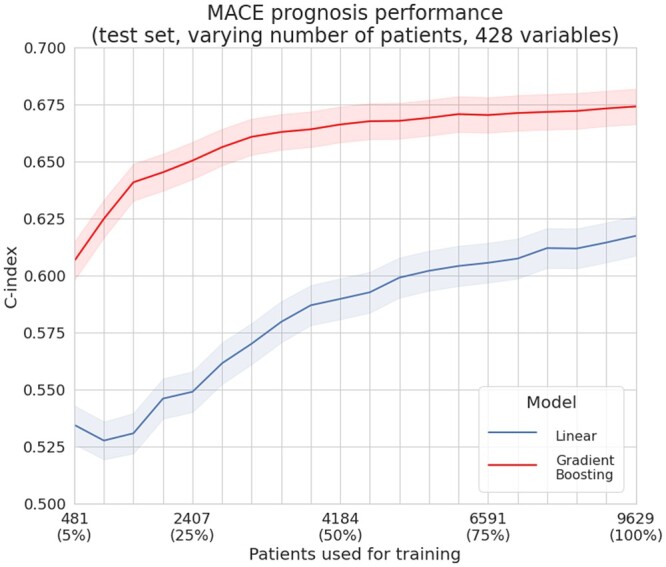
Performances depending on the number of patients available for training. For the task of predicting major adverse cardiovascular events, when restricting the number of patients available for training, gradient boosting always outperformed linear models on our dataset. A gradient boosting algorithm trained on 5% (481 patients) of the training dataset achieves similar performance to a linear model trained on all the dataset (9629 patients).

Discussion

Machine learning can sometimes be perceived as a black box approach dedicated to prediction from unstructured data, like medical imaging or natural language text reports, whereas simpler statistical models can be deemed more relevant for extracting interpretable patterns from structured tabular data. Yet, we showed that ML models can actually help build better risk score models from tabular clinical data and reveal how they leverage predictors to do so. This is especially the case when many patient characteristics are available, which is more and more frequent in routine clinical practice. The increase in prognosis performance is significant, even when fewer patients are available as illustrated in Figure 7. Among ML models, we found that tree-ensemble models and especially gradient boosting proved to yield better results than linear models or neural networks. These results are consistent with previous studies in related fields.^14,15,17,49 Kwon et al.¹⁶ reached slightly better scores with neural networks than with random forests, but did not evaluate gradient boosting.

Gradient boosting therefore appears as a good default approach to this kind of task, given that these models are very expressive—being able to detect complex non-linear patterns—flexible—offering many regularization and optimization hyperparameters—and that they can be trained quickly on limited hardware resources. They proved to perform quite well ‘out of the box’, using the default XGBoost parameters. To further optimize their performance, conducting the hyperparameter search in the inner-loop of a nested cross-validation and training gradient boosting models using early stopping prevented overfitting.

The trained algorithms were composed of thousands of regression trees or, in the case of the deeper neural network we used, hundreds of thousands of numerical weights. Interpretation techniques like SHAP values reveal a summary of how these complex models use the patient characteristics for their risk prediction. Being model-agnostic, they allow to compare what different models learned, contrary to model-specific interpretations like a linear model’s coefficients and their P-values, or the gain of tree-ensembles. They also can help detect and thus prevent overfitting, by permitting to check if the variables a model considers as predictive are indeed relevant from a medical point of view.

On the FOURIER trial data, the difference between statistical linear models and ML models is not as significant when using fewer variables. Using the most prognostic ones, according to a high-dimension ML model, linear models manage to achieve a c-index which is close to the best ML model (Fig 5). Given the similar number of dimensions compared to these studies, these observations are also aligned with the findings of Li et al.,¹⁴ VanHouten et al.,¹⁷ Desai et al.,¹⁵ and Akyea et al.⁴⁹ As gradient boosting proved to achieve the best performance in all settings, even if other approaches reached close c-indexes in some of them, it can be considered a default modelling and/or variable-selection algorithm when analysing a new dataset.

Yet, many hospital EHRs do not record as much data as we used in our best models and some of the above observations might be specific to the studied FOURIER dataset. We therefore do not consider that the models trained for this study would be relevant for any clinical practice use as they are, as they lack external validation and were trained on a population with some selection biases.

Building a global risk score relying on more heterogeneous data from several routine cohorts would be a natural extension of this study. It would require tackling the challenge of training models on separate and only partially overlapping feature spaces—leveraging clinical characteristics which are only available in some hospitals—and patients with more varied selection criteria. This could be achieved by relying on a model training strategy called federated learning.^50,51 Federated learning could enable training such a model without having to gather these EHRs in a single dataset, thus preserving their privacy while learning to account for their patients’ heterogeneity. Additionally, this future work would have to include prospective external validation to ensure its generalization capability. With the support of cardiology experts to select the most relevant variables, such a model could be designed to provide the robustness guarantees for a clinical use, allowing for improved patient prioritization and treatment allocation strategies.

Conclusion

This study illustrated how non-linear ML models can be used to improve cardiovascular risk prediction from EHR data. Across the range of available patients and variables, these models proved to perform at least as well as linear models. Specifically, non-linear machine-learning models did not show to suffer from being provided too many variables, while linear models require a more careful feature selection. Furthermore, we showed how modern interpretation techniques allow to investigate how these models predict the risk, either to validate their relevance or to extract medical insights. Applying similar methods to a more heterogeneous population and variables commonly available in routine clinical practice could open the door to more accurate cardiovascular risk assessment tools.

Data availability

Raw date is owned by a third party: “The data underlying this article were provided by TIMI group by permission.” Regarding the algorithm : The data underlying this article cannot be shared publicly due to copyrights.

Funding

This study was sponsored by Amgen Inc.

Conflict of interest: A.R. and L.R. are current employees at AMGEN. D.D. and A.L.P. are former employees at AMGEN. M.S.S. has received an institutional research grant to the TIMI Study Group at Brigham and Women’s Hospital; consulting—AMGEN; institutional research grant to the TIMI Study Group at Brigham and Women's Hospital—Anthos Therapeutics, AstraZeneca, Bayer, Daiichi-Sankyo, Eisai, Intarcia, IONIS, Medicines Company, MedImmune, Merck, Novartis, Pfizer, Quark Pharmaceuticals; consulting—Althera, Anthos Therapeutics, AstraZeneca, Bristol-Myers Squibb, CVS Caremark, DalCor, Dr. Reddy’s Laboratories, Fibrogen, IFM Therapeutics, Intarcia, MedImmune, Merck, Moderna, Novo Nordisk. In addition, he is a member of the TIMI Study Group, which has also received institutional research grant support through Brigham and Women’s Hospital from: Abbott, Regeneron, Roche, and Zora Biosciences. R.P.G. has received an institutional research grant to the TIMI Study Group and Brigham and Women’s Hospital—AMGEN; institutional research grant to the TIMI Study Group and Brigham and Women’s Hospital—Amgen, Anthos Therapeutics, Daiichi Sankyo; consultant—Amarin, Amgen, CSL Behring, CVS Caremark, Daiichi Sankyo, Esperion, Gilead, Hengrui, Inari, Jannsen, Novartis, Pfizer, PhaseBio Pharmaceuticals, St. Luke’s, Samsung; honoraria for lectures/CME programmes—Amgen, Centrix, Daiichi Sankyo, Dr. Reddy’s Laboratories, Medical Education Resources (MER), Medscape, Merck, Pfizer, SAJA Pharmaceuticals, Servier, Shanghai Medical Telescope, Voxmedia; Chairman of DSMB—CryoLife. R.M., P.T., and M.Z. are current employees of OWKIN which performed the experiments and contributed to the medical writing.