Evaluation of input geological parameters and tunnel strain for strain-softening rock mass based on GSI

Abstract

The regression analysis method is being widely adopted to analyse the tunnel strain, most of which ignore the strain-softening effect of the rock mass and fail to consider the influence of support pressure, initial stress state, and rock mass strength classification in one fitting equation. This study aims to overcome these deficiencies with a regression model used to estimate the tunnel strain. A group of geological strength indexes (GSI) are configured to quantify the input strength parameters and deformation moduli for the rock mass with a quality ranging from poor to excellent. A specific semi-analytical procedure is developed to calculate the tunnel strain around a circular opening, which is validated by comparison with those using existing methods. A nonlinear regression model is then established to analyse the obtained tunnel strain, combining twelve fitting equations to relate the tunnel strain and the factors including the support pressure, GSI, initial stress state, and critical softening parameter. Particularly, three equations are for the estimation of the critical tunnel strain, critical support pressure, and tunnel strain under elastic behaviour, respectively; and the other nine equations are for the tunnel strain with different strain-softening behaviours. The relative significance between the GSI, the initial stress and the support pressure on the tunnel strain is assessed.

Introduction

The tunnel closure should be predicted appropriately as it is utilised to determine the stability of the rock mass and has been adopted in the engineering practices to guide the preliminary support design. Many analytical and numerical methods were proposed to assess the ground reaction curve with different failure criteria, flow rules, and failure behaviours of the rock mass^1–6. The solutions reveal the relationship between the tunnel strain and the support pressure, which are efficacious for determining the support type with a particular geological condition. However, many solutions are often too cumbersome for practical applications due to its complicated derivation, equations, and multiple geological parameters. In this aspect, empirical methods seem to be more accessible to the engineering practisers due to their simplicity. Rock mass rating^7–9, geological strength index¹⁰, and tunnelling quality index Q^11,12 are the commonly utilised systems to guide the tunnel design by adequately quantifying the strength and deformation properties of the rock mass. Based on previous case back-analysis with assumed rock mass behaviours, the empirical methods often fail to account for the input geological parameters for a specific case. Thus, the strain redistribution and support performance cannot always be well-estimated by the empirical methods.

The regression analysis method has been adopted by many researchers to evaluate the tunnel strain as it takes advantage of the accuracy of the numerical tools and the convenience of the empirical schemes^13–21. In the existing studies, great amount of data result was obtained using iterative procedures to analyse the large number of tunnelling cases. Multiple geological parameters for each tunnel case were simplified into a single strength parameter, and the rock mass deformation was quantified artificially as a function of the strength parameter using a nonlinear regression model. Among the studies, the functions enable to obtain the tunnel strain or the plastic zone radius for various tunnel cases with various geological scenarios. However, the limitation is obvious due to the difficulty when considering the strain of rock mass showing strain-softening behaviours, which is proved to be a common behaviour in numerous rock tests³. Also, many studies adopted only one fitting equation in the regression model, failing to consider the support pressure, the initial stress, and the strength classification (such as RMR, GSI, and the compressive strength). As a result, the application of analysis results with one fitting equation is limited to particular initial stress or rock mass quality.

In this paper, the index GSI is assigned with a group of values to represent the strength parameters and the deformation moduli for a strain-softening rock mass having various qualities. The tunnel strain around a circular opening under a hydrostatic stress state is obtained through a numerical scheme, which is validated through comparison with the previous studies. A more accurate estimation of the tunnel strain is further derived by semi-analytical procedures with different input geological parameters. Twelve fitting equations are proposed with the regression analysis method to correlate the tunnel strain with the support pressure, the GSI, the initial stress state, and the critical softening parameter; In particular, three equations are for the critical tunnel strain, the critical support pressure, and the tunnel strain in the elastic zone, and nine equations are for the tunnel strain in the plastic zone with different strain-softening behaviours.

Problem setup

Assumptions

Some assumptions are considered prior to the analysis:

1. A circular opening, with a radius of R₀, is under a hydrostatic stress field of ${\sigma }_0$ asymmetrically distributed around it; the radial stress ${\sigma }_{\text{r}}$ and the tangential stress ${\sigma }_{\mathrm{\theta }}$ correspond to the minor and major principal stresses ${\sigma }_3$ and ${\sigma }_1$, respectively;

2. Plane strain condition is considered as the deformation along the longitudinal direction of the tunnel is virtually uniform;

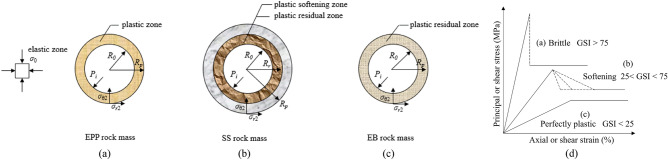
3. Material of the rock mass is isotropic, continuous, and initially elastic. Near underground excavations where confinement is reduced, most rock mass exhibits post-peak strength loss, which is called strain-softening property. The rock mass presents strain-softening (SS) behaviour; the elastic-perfectly-plastic (EPP) and elastic-brittle-plastic (EBP) behaviours are also considered, which are taken as special cases of the SS behaviour. The SS, EPP, and EBP behaviours of the rock mass induced by excavation operations are shown in Fig. 1. A support pressure p_i is evenly imposed around the tunnel. σ_r2 and σ_θ2 represent the radial and tangential stresses at the elasto-plastic boundary, respectively. Within a SS rock mass, σr1 and σθ1 are the radial and tangential stresses at the plastic softening-residual boundary, respectively. The radii of the plastic softening and residual areas are symbolised as R_p and R_r, respectively. For the EPP and EBP rock masses, the radius of plastic area is represented as R_p

4. The softening parameter η characterises the softening quantity in the rock mass and is calculated as the gap between the tangential and radial plastic strains for the axisymmetric problem:

   $$\eta ={\epsilon }_{\mathrm{\theta }}^{\text{plas}}-{\epsilon }_{\text{r}}^{\text{plas}}$$ 1

   The critical value of η is denoted as η^*, which occurs at the moment that the rock mass strength decays to its residual value. Specially, η^* has values of ∞ and 0 for the EPP and EBP rock masses, respectively.

5. The Mohr–Coulomb failure criterion is considered for the plastic potential function^22,23

   $$g\left({\sigma }_{\text{r}},{\sigma }_{\mathrm{\theta }},\psi \right)={\sigma }_{\mathrm{\theta }}-\frac{1+sin\psi }{1-sin\psi }{\sigma }_{\text{r}}$$ 2

   where ψ is the dilatancy angle and herein is taken as nil.
6. The Hoek–Brown (H-B) failure criterion is satisfactory in the quick estimate of the rock mass strength²⁴:

   $${\sigma }_1={\sigma }_3+{\sigma }_{\text{ci}}{\left(m_{\text{b}}{\sigma }_3/{\sigma }_{\text{ci}}+s\right)}^a$$ 3

   where σ_ci represents the uniaxial compression strength of the intact rock; m_b, s and a are strength parameters of the Hoek–Brown rock mass. Because of the axisymmetric condition, the radial stress σ_r and the tangential stress σ_θ correspond to the minor and major principal stresses σ₃ and σ₁, respectively. Equation (3) can be transformed as:

   $$f\left({\sigma }_{\text{r}},{\sigma }_{\mathrm{\theta }},\eta \right)={\sigma }_{\mathrm{\theta }}-{\sigma }_{\text{r}}-{\sigma }_{\text{ci}}{\left(m_{\text{b}}{\sigma }_{\text{r}}/{\sigma }_{\text{ci}}+s\right)}^a$$ 4
   According to the geological observations in the field, Reference^10,24,25 constructed the relation between the strength parameters (m_b, s and a) and GSI. The empirical equations are listed as follows:

   $$m_{\text{b}}=m_{\text{i}}exp\left(\frac{\text{GSI}-100}{28-14D}\right)$$ 5

   $$s=exp\left(\frac{\text{GSI}-100}{9-3D}\right)$$ 6

   $$a=\frac{1}{2}+\frac{1}{6}\left(e^{-\text{GSI}/15}-e^{-20/3}\right)$$ 7

   where D is a coefficient influenced by the disturbance from blast impact and the stress relaxation. An optimised blasting operation with an accurate drilling control technique is assumed during the tunnel excavation, thereby, the damage to the tunnel wall is negligible and D is regarded as 0 by Hoek²⁶. m_i in Eq. (5) characterises the friction between the composition minerals.

Figure 1.

Schematic graph of excavation problem and stress–strain relationship: (a) for EPP rock mass; (b) for SS rock mass; (c) for EBP rock mass; (d) stress–strain relationships (reference from³).

Strength classification of rock mass

The strength classification systems, such as the RMR, Q, and GSI, were successfully applied to many tunnel excavations. Various empirical equations by the systems are feasible to characterise the strength and deformation behaviours of the rock mass. Herein, GSI is incorporated to quantify the rock mass properties. Advantages of the GSI are demonstrated in three aspects: GSI is directly correlated to the strength constants in the Hoek–Brown failure criterion²⁴; GSI can be estimated by RMR and Q systems, thus some strength parameters related to RMR can also be represented by GSI; and the residual strength of the strain-softening rock mass could be calculated from the peak value of GSI based on the equation proposed²⁷.

Correlation between RMR and GSI

In the latest version, the relationship between GSI and RMR is:

$$\text{GSI = RMR}-5\text{, RMR > 23}$$ 8

It is noted that Eq. (8) is specialised for the dry condition of the rock mass and thus is not applicable to the weak rock mass with the RMR below 18.

Residual value of GSI

The guideline for the GSI was presented in²⁵, which are to characterise the peak strength parameters of the EPP rock mass. Considering the strain-softening effect, Reference²⁷ extended the GSI framework to consider the residual strength. In their study, through the in-situ block shear test at a number of real construction sites, the residual value of the GSI, denoted as GSI^r, was expressed with a function of the peak value of GSI, denoted as GSI^p:

$${\text{GSI}}^{\text{r}}={\text{GSI}}^{\text{p}}·e^{-0.0134{\text{GSI}}^{\text{p}}}$$ 9

Here, GSI^p varies between 25 and 75 with 5 even intervals to consider the rock mass from very poor to excellent qualities. GSI^r is calculated by substituting GSI^p into Eq. (9) with values of GSI^p and GSI^r listed in Table 1.

Table 1.

GSI^p and GSI^r.

GSIp	25	30	35	40	45	50	55	60	65	70	75
GSIr	17.9	20.1	21.9	23.4	24.6	25.6	26.3	26.9	27.2	27.4	27.5

Geological parameters

Within the plastic softening area

The parameters $m_b$, $s$, and $a$ for the SS rock mass can be calculated as²:

$$\omega (\eta )=\left\{\begin{array}{cc}& {\omega }^{\text{p}}-({\omega }^{\text{p}}-{\omega }^{\text{r}})\frac{\eta }{{\eta }^{\ast }},0<\eta <{\eta }^{\ast }\hfill \\ \hfill & {\omega }^{\text{r}},\eta \ge {\eta }^{\ast }\hfill \\ \hfill \end{array}\right)$$ 10

where $\omega$ represents any of $m_b$, $s$ and $a$. The peak and residual values of the strength parameters are denoted with superscripts ‘p’ and ‘r’, respectively, having $m_b^{\text{p}}$, $s^{\text{p}}$, $a^{\text{p}}$, and $m_b^{\text{r}}$, $s^{\text{r}}$, $a^{\text{r}}$. The value of $\omega$ decays linearly with the increase in $\eta$ when the rock mass is undergoing plastic softening, while it keeps unchanged with the value of $\eta$ above the critical value ${\eta }^{\ast }$. $\omega$ equates to ${\omega }^{\text{p}}$ within the EPP rock mass and is ${\omega }^r$ within the plastic area of the EBP rock mass. The deformation modulus $E_{\text{r}}$ and strength parameters, such as ${\sigma }_{\text{ci}}$ and $m_{\text{i}}$, also need to be determined. A number of compression tests show that $E_{\text{r}}$ deteriorates for the rock mass beyond the peak state^28,29. It is proposed that ${\sigma }_{\text{ci}}$ wanes from its peak value to the residual during the softening stage since the rock mass quality is weakened, and the variations of $E_{\text{r}}$ and ${\sigma }_{\text{ci}}$ also obey Eq. (10)⁴. Therefore, $E_{\text{r}}$, ${\sigma }_{\text{ci}}$, and $m_{\text{i}}$ within the plastic softening area are all assumed to obey Eq. (10).

As observed in Eq. (10), the prerequisite for obtaining $E_{\text{r}}$, ${\sigma }_{\text{ci}}$, $m_{\text{i}}$, $m_{\text{b}}$, $s$ and $a$ in the softening area is to predict the peak and residual values ($E_{\text{r}}^{\text{p}}$, $E_{\text{r}}^{\text{r}}$, ${\sigma }_{\text{ci}}^{\text{p}}$, ${\sigma }_{\text{ci}}^{\text{r}}$, $m_{\text{i}}^{\text{p}}$, $m_{\text{i}}^{\text{r}}$, $m_{\text{b}}^{\text{p}}$,$m_{\text{b}}^{\text{r}}$, $s^{\text{p}}$, $s^{\text{r}}$, $a^{\text{p}}$, $a^{\text{r}}$). Based on GSI^p and GSI^r, the derivation of $E_{\text{r}}^{\text{p}}$, $E_{\text{r}}^{\text{r}}$, ${\sigma }_{\text{ci}}^{\text{p}}$, ${\sigma }_{\text{ci}}^{\text{r}}$, $m_{\text{i}}^{\text{p}}$, $m_{\text{i}}^{\text{r}}$, $m_{\text{b}}^{\text{p}}$,$m_{\text{b}}^{\text{r}}$, $s^{\text{p}}$, $s^{\text{r}}$, $a^{\text{p}}$, $a^{\text{r}}$ is presented in the following.

Within the plastic elastic and plastic residual areas

Deformation modulus $E_{\text{r}}$

Empirical equations to determine E_r were proposed with GSI and RMR.

Reference⁷:

$$E_{\text{r}}=2\text{RMR}-100$$ 11

Reference³⁰:

$$E_{\text{r}}={10}^{\left(\text{RMR}-10\right)/40}$$ 12

Reference³¹:

$$E_{\text{r}}=0.1{\left(\frac{\text{RMR}}{10}\right)}^3$$ 13

Simplified Hoek and Diederichs equation³²:

$$E_{\text{r}}=100\left(\frac{1-D/2}{1+e^{\left(\left(75+25D-GSI\right)/11\right)}}\right)$$ 14

With GSI^p and GSI^r listed in Table 1, the calculated $E_{\text{r}}^{\text{p}}$ and $E_{\text{r}}^{\text{r}}$ from Eqs. (11)–(14) are shown in Table 2. In Table 3, E_r^p and E_r^r can be estimated as the average values from Eqs. (11)–(14).

Table 2.

Calculated values of E_r^p and E_r^r by Eqs. (11) to (14).

GSIp	Equation (11)	Equation (12)	Equation (13)	Equation (14)	GSIr	Equation (11)	Equation (12)	Equation (13)	Equation (14)
25		3.162	2.700	1.050	17.883		2.099	1.198	0.953
30		4.217	4.288	1.645	20.069		2.381	1.575	1.126
35		5.623	6.400	2.567	21.897		2.645	1.946	1.295
40		7.499	9.113	3.986	23.403		2.885	2.291	1.452
45		10.000	12.500	6.138	24.623		3.094	2.599	1.592
50	10	13.335	16.638	9.341	25.585		3.271	2.861	1.712
55	20	17.783	21.600	13.965	26.320		3.412	3.072	1.809
60	30	23.714	27.463	20.365	26.852		3.518	3.232	1.883
65	40	31.623	34.300	28.719	27.205		3.590	3.340	1.934
70	50	42.170	42.188	38.828	27.399		3.631	3.401	1.962
75	60	56.234	51.200	50.000	27.453		3.642	3.418	1.970

Table 3.

Estimated values of E_r^p and E_r^r.

GSIp	Erp (MPa)	GSIr	Err(MPa)
75	54.359	27.453	3.010
70	43.296	27.399	2.998
65	33.660	27.205	2.955
60	25.385	26.852	2.878
55	18.337	26.320	2.764
50	12.328	25.585	2.615
45	7.160	24.623	2.429
40	5.149	23.403	2.209
35	3.648	21.897	1.962
30	2.537	20.069	1.694
25	1.728	17.883	1.417

Strength constant m_i

In the previous works, such as Reference^33–35, $m_{\text{i}}$ was approximated by two methods. One is to determine the classification of $m_{\text{i}}$ from the rock type, such as in Hoek and Brown³⁴. The other method is to estimate $m_{\text{i}}$ from the rock mass quality. Although the latter method tends to be subjective, it enables to establish a direct relationship between $m_{\text{i}}$ and the rock mass strength classification¹⁴. Therefore, the latter method is utilised in this study to correlate $m_{\text{i}}$ with GSI. The test data of $m_{\text{i}}$ for different GSI by Hoek and Brown³³ and Hoek and Marinos³⁶ is listed in Table 4. The data for estimating $m_{\text{i}}$ by GSI can be best-fitted by,

$$m_{\text{i}}=0.7375{\text{GSI}}^{0.7586}$$ 15

Table 4.

Values of m_i with different GSI: (a) Hoek and Brown³³; (b) Hoek and Marino³⁶.

(a) GSI	75	50	30	75	75	65	20	24
mi	25	12	8	16.3	17.7	15.6	9.6	10

(b) GSI	20	5	13	28
mi	8.0	2.0	5.0	11.0

The coefficient of determination R² reaches 81.38%, which indicates that the fitting line is in agreement with the test results. By Eq. (15) (see Fig. 2), the calculated m_i^p and m_i^r with different GSI^p and GSI^r are presented in Table 5.

Figure 2.

Fitting for m_i.

Table 5.

Estimated values of m_i^p and m_i^r.

GSIp	mip	GSIr	mir
75	19.507	27.453	9.101
70	18.512	27.399	9.087
65	17.500	27.205	9.038
60	16.469	26.852	8.949
55	15.417	26.320	8.814
50	14.342	25.585	8.627
45	13.240	24.623	8.380
40	12.108	23.403	8.063
35	10.942	21.897	7.666
30	9.734	20.069	7.176
25	8.477	17.883	6.575
20	7.157	15.298	5.840

It is admitted that m_i is the inherent characteristic of the intact rock. In this respect, m_i corresponds to GSI = 100. But from many references^33–36, it is found that generally a greater GSI gives rise to a larger value of m_i. Hence, in the analysis, a rough and immature relation between GSI and m_i is proposed as shown in Eq. (15) is proposed. The aim of Eq. (15) is to solve the tunnel strain as one of the input parameter in the latter. And according to Eq. (15), the tunnel strain is greater in comparison to a constant m_i with no reduction. Then, the tunnel design will be conservative and safe. In this respect, Eq. (15) is reasonable. Furthermore, the sensitive analysis for the influence of multiple mechanical parameters on the tunnel strain has also been undertaken. It is found that in comparing with other input parameters such as the deformation modulus and the compressive rock strength, the effect of m_i on the rock deformation is trivial. In this aspect, although Eq. (15) is subjective, it seems to be not very important factor that affect the results in this analysis.

Strength constants m_b, s and a

According to Eqs. (5) to (7), when the disturbance factor D is 0, $m_{\text{b}}^{\text{p}}$ and $m_{\text{b}}^{\text{r}}$ can be obtained from GSI^p, GSI^r, $m_{\text{i}}^{\text{p}}$, and $m_{\text{i}}^{\text{r}}$; and $s^{\text{p}}$, $s^{\text{r}}$, $a^{\text{p}}$, $a^{\text{r}}$ can be calculated from GSI^p and GSI^r. The estimated result is listed in Table 6.

Table 6.

Estimated values of m_b^p, s^p, a^p and m_b^r, s^r, a^r.

GSIp	mbp	sp	ap	GSIr	mbr	sr	ar
75	7.988	62.177	0.501	27.453	0.682	0.316	0.527
70	6.341	35.674	0.501	27.399	0.680	0.314	0.527
65	5.014	20.468	0.502	27.205	0.671	0.307	0.527
60	3.947	11.744	0.503	26.852	0.656	0.295	0.528
55	3.090	6.738	0.504	26.320	0.634	0.278	0.529
50	2.405	3.866	0.506	25.585	0.605	0.257	0.530
45	1.857	2.218	0.508	24.623	0.568	0.230	0.532
40	1.421	1.273	0.511	23.403	0.523	0.201	0.535
35	1.074	0.730	0.516	21.897	0.471	0.170	0.539
30	0.799	0.419	0.522	20.069	0.413	0.139	0.544
25	0.582	0.240	0.531	17.883	0.350	0.109	0.550
20	0.411	0.138	0.544	15.298	0.284	0.082	0.560

Compressive strength of intact rock σ_ci

Here, σ_ci by GSI is calculated in three steps.

1. Estimation of σ_cm/σ_ci

   Considering different RMR, the reduction factor σ_cm/σ_ci was proposed by Wilson³⁷ to characterise the rock mass strength decreasing from its peak value to the residual. Assuming RMR-5 equals to GSI (see Eq. (8)), the estimated σ_cm/σ_ci by Asef et al.¹⁴ are listed in Table 7. Other fitting equations for σ_cm/σ_ci in the literature are presented in Eqs. (16) to (22):

   Reference³⁴:

   $$\frac{{\sigma }_{\text{cm}}}{{\sigma }_{\text{ci}}}=\sqrt{e^{\left(\frac{\text{RMR}-100}{9}\right)}}$$ 16
   Reference³⁸:

   $$\frac{{\sigma }_{\text{cm}}}{{\sigma }_{\text{ci}}}=e^{\left(0.0765\text{RMR}-7.65\right)}$$ 17
   Reference³⁹:

   $$\frac{{\sigma }_{\text{cm}}}{{\sigma }_{\text{ci}}}=e^{\left(\frac{\text{RMR}-100}{24}\right)}$$ 18
   Reference⁴⁰:

   $$\frac{{\sigma }_{\text{cm}}}{{\sigma }_{\text{ci}}}=e^{\left(\frac{\text{RMR}-100}{20}\right)}$$ 19
   Reference⁴¹:

   $$\frac{{\sigma }_{\text{cm}}}{{\sigma }_{\text{ci}}}=e^{\left(\frac{\text{RMR}-100}{18.75}\right)}$$ 20
   Reference⁴²:

   $$\frac{{\sigma }_{\text{cm}}}{{\sigma }_{\text{ci}}}=\frac{\text{RMR}}{\text{RMR}+6\left(100-\text{RMR}\right)}$$ 21
   Reference²⁶:

   $$\frac{{\sigma }_{\text{cm}}}{{\sigma }_{\text{ci}}}=0.019e^{0.05\text{GSI}},5\le \text{GSI}\le 35$$ 22
   The GSI was given values from 5 to 95 with 10 intervals, which is to compute σ_cm/σ_ci through Eqs. (16) to (22). The otained σ_cm/σ_ci by Eqs. (16) to (22), by Asef et al.¹⁴, and the field data retrieved from realistic construction sites⁴² are plotted in Fig. 3. With the estimated σ_cm/σ_ci, the best-fitting equation is expressed as:

   $$\frac{{\sigma }_{\text{cm}}}{{\sigma }_{\text{ci}}}=0.0103e^{0.0476\text{GSI}}$$ 23

   The coefficient of determination R² is 95.84%, which indicates the prediction by Eq. (23) is acceptable.

2. Estimation of σ_cm and σ_ci.

   Reference⁴³ claimed that σ_cm can be described as a function of RMR:

   $${\sigma }_{\text{cm}}=0.5e^{0.06\text{RMR}}$$ 24
   Combing Eqs. (23) and (24), the solution for σ_ci is derived as:

   $${\sigma }_{\text{ci}}=\frac{0.5e^{0.06\text{RMR}}}{0.0387+0.00474e^{\frac{\text{GSI}}{18.9086}}}$$ 25

   σ_ci^p and σ_ci^r with different values of GSI^p and GSI^r are calculated by Eq. (25), and the result is presented in Table 8.

Table 7.

Estimated values of σ_cm/σ_ci proposed by Asef et al.¹⁴.

RMR	20	30	40	50	60	70	80	90	100
σcm/σci	0.147	0.142	0.142	0.166	0.200	0.250	0.400	0.666	1.000

Figure 3.

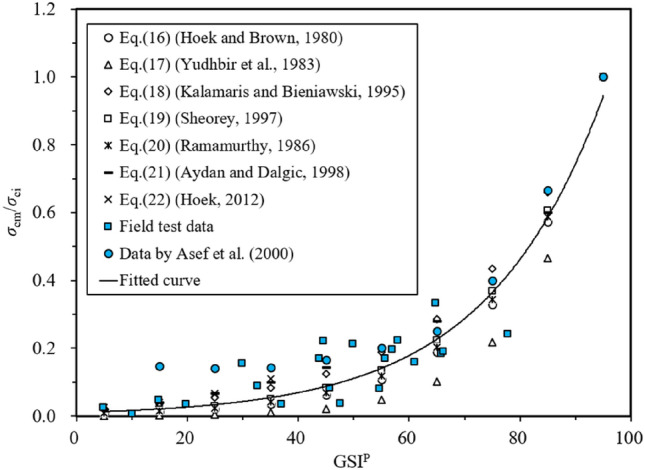
Fitting for σ_ci/σ_cm.

Table 8.

Estimated values of σ_ci^p and σ_ci^r.

GSIp	σcip (MPa)	GSIr	σcir (MPa)
75	237.222	27.4	66.781
70	219.950	27.4	66.629
65	201.942	27.2	66.088
60	183.276	26.9	65.111
55	164.134	26.3	63.656
50	144.813	25.6	61.682
45	125.708	24.6	59.160
40	107.271	23.4	56.066
35	89.957	21.9	52.406
30	74.155	20.1	48.201

Semi-analytical procedure

Governing equation

For the case of plane strain, the equilibrium equation is:

$$\frac{\partial {\sigma }_{\text{r}}}{\partial r}+\frac{{\sigma }_{\text{r}}-{\sigma }_{\mathrm{\theta }}}{r}=0$$ 26

In terms of small strain case, the displacement compatibility is:

$${\epsilon }_{\text{r}}=\frac{\mathit{du}}{\mathit{dr}},{\epsilon }_{\mathrm{\theta }}=\frac{u}{r}$$ 27

Stresses and strains in the plastic softening zone

The generalised H-B failure criterion³³ is :

$${\sigma }_1={\sigma }_3+{\sigma }_{\text{ci}}{\left(m_{\text{b}}{\sigma }_3/{\sigma }_{\text{ci}}+s\right)}^a$$ 28

where ${\sigma }_1$ and ${\sigma }_3$ are the major and minor principal stresses. ${\sigma }_{\text{ci}}$ is the uniaxial compression strength of intact rock. $m_{\text{b}}$ and $s$ are the strength constants, respectively. According to Eq. (28), the yielding function of the rock mass surrounding a circular opening is:

$$f({\sigma }_{\mathrm{\theta }},{\sigma }_{\text{r}},\eta )={\sigma }_{\mathrm{\theta }}-{\sigma }_{\text{r}}-{\sigma }_{\text{ci}}(\eta ){\left[m_{\text{b}}(\eta ){\sigma }_{\text{r}}/{\sigma }_{\text{ci}}+s(\eta )\right]}^{a(\eta )}$$ 29

First, ${\sigma }_{\text{r}2}$, the radial stress at the elastic–plastic boundary is solved by combing Eq. (26) with Eq. (29) through Runge–Kutta method.

A constant radial stress increment is assumed for each annulus, i.e.:

$$\mathrm{\Delta }{\sigma }_{\text{r}}={\sigma }_{\text{r}(i)}-{\sigma }_{\text{r}(i-1)}$$ 30

where ${\sigma }_{\text{r}(i)}$ and ${\sigma }_{\text{r}(i-1)}$ are the radial stresses at the inner and outer boundaries of each annulus (i.e. r = r_(i) and r_(i-1)).

The plastic strain is expressed as:

$$\left\{\begin{array}{c}{\epsilon }_{\text{r}(i)}\hfill \\ {\epsilon }_{1\mathrm{\theta }(i)}\hfill \end{array}\right\}=\left\{\begin{array}{c}{\epsilon }_{\text{r}(i-1)}\hfill \\ {\epsilon }_{\mathrm{\theta }(i-1)}\hfill \end{array}\right\}+\left\{\begin{array}{c}\mathrm{\Delta }{\epsilon }_{\text{r}(i)}^{\text{elas}}\hfill \\ \mathrm{\Delta }{\epsilon }_{\mathrm{\theta }(i)}^{\text{elas}}\hfill \end{array}\right\}+\left\{\begin{array}{c}\mathrm{\Delta }{\epsilon }_{\text{r}(i)}^{\text{plas}}\hfill \\ \mathrm{\Delta }{\epsilon }_{\mathrm{\theta }(i)}^{\text{plas}}\hfill \end{array}\right\}$$ 31

where ${\epsilon }_{\text{r}(i)}$ and ${\epsilon }_{{\mathrm{\theta }}_{(i)}}$ are the radial and tangential strains at r = r_(i); ${\epsilon }_{\text{r}(i-1)}$ and ${\epsilon }_{{\mathrm{\theta }}_{(i-1)}}$ are the radial and tangential strains at r = r_(i-1); $\mathrm{\Delta }{\epsilon }_{\text{r}(i)}^{\text{plas}}$ and $\mathrm{\Delta }{\epsilon }_{{\mathrm{\theta }}_{(i)}}^{\text{plas}}$ are the radial and tangential plastic strain increments; $\mathrm{\Delta }{\epsilon }_{\text{r}(i)}^{\text{elas}}$ and $\mathrm{\Delta }{\epsilon }_{{\mathrm{\theta }}_{(i)}}^{\text{elas}}$ are the radial and tangential elastic strain increments.

According to Hooke’s law, the elastic strain increments can be correlated to the stress increments, i.e.:

$$\left\{\begin{array}{c}\mathrm{\Delta }{\epsilon }_{\text{r}(i)}^{\text{elas}}\\ \mathrm{\Delta }{\epsilon }_{\mathrm{\theta }(i)}^{\text{elas}}\\ \end{array}\right\}=\frac{1+\mu }{E}\left[\begin{array}{c}1-\mu \\ -\mu \end{array}\right)\left(\begin{array}{c}-\mu \\ 1-\mu \end{array}\right]\left\{\begin{array}{c}\mathrm{\Delta }{\sigma }_{\text{r}(i)}\\ \mathrm{\Delta }{\sigma }_{{\mathrm{\theta }}_{(i)}}\\ \end{array}\right\}$$ 32

The relation between ${\epsilon }_{\mathrm{\theta }}^{\text{plas}}$ and ${\epsilon }_{\text{r}}^{\text{plas}}$ can be given as:

$${\epsilon }_{\text{r}}^{\text{plas}}=-K_{\psi }(\eta ){\epsilon }_{\mathrm{\theta }}^{\text{plas}}$$ 33

where $K_{\psi }(\eta )$ is the dilatancy coefficient and can be written as:

$$K_{\psi }(\eta )=\frac{1+sin\psi (\eta )}{1-sin\psi (\eta )}$$ 34

where $\psi$ is the dilatancy angle, it should be noted that $\psi$ is not equal to the friction angle $\phi$ when the non-associated flow rule is employed.

In order to solve the strain components, Eq. (27) can be rewritten as:

$${\epsilon }_{\text{r}(i)}=\frac{\mathrm{\Delta }{u}_{(i)}}{\mathrm{\Delta }{r}_{(i)}},{\epsilon }_{{\mathrm{\theta }}_{(i)}}=\frac{u_{(i)}}{r_{(i)}}$$ 35

where $u_{(i)}$ is the radial displacement at r = r_(i); substituting Eqs. (32) and (33) into Eqs. (31) and (36), one gains:

$${\epsilon }_{\mathrm{\theta }(i)}=\frac{u_{(i)}}{r_{(i)}}=\frac{A_{(i-1)}(r_{(i)}/r_{(i-1)}-1)+u_{(i-1)}/r_{(i-1)}}{r_{(i)}/r_{(i-1)}+K_{\psi (i)}(r_{(i)}/r_{(i-1)}-1)}$$ 36

$${\epsilon }_{\text{r}(i)}=\frac{\mathrm{\Delta }{u}_{(i)}}{\mathrm{\Delta }{r}_{(i)}}=-K_{\psi (i)}{\epsilon }_{\mathrm{\theta }(i)}+A_{(i-1)}·\frac{r_{(i)}/r_{(i-1)}-1}{1-r_{(i-1)}/r_{(i)}}$$ 37

$$u_{(i)}=\frac{A_{(i-1)}{r}_{(i)}(r_{(i)}-r_{(i-1)})+u_{(i-1)}{r}_{(i)}}{r_{(i)}+K_{\psi }(r_{(i)}-r_{(i-1)})}$$ 38

where

$$A_{(i-1)}=\frac{(1+\nu )}{E}\left\{\mathrm{\Delta }{\sigma }_{\text{r}(i)}(1-\nu -K_{\psi }\nu )+\left[-{\sigma }_{{\mathrm{\theta }}_{(i-1)}}+{\sigma }_{\text{r}(i)}+H({\sigma }_{\text{r}(i)},{\eta }_{(i-1)})\right](K_{\psi }-K_{\psi }\nu -\nu )\right\}+{\epsilon }_{\text{r}(i-1)}+K_{\psi }{\epsilon }_{{\mathrm{\theta }}_{(i-1)}}$$

$$H({\sigma }_{\text{r}(i)},{\eta }_{(i-1)})={\sigma }_{\text{ci}}{\left(m_{\text{b}(i-1)}{\sigma }_{\text{r}(i)}/{\sigma }_{\text{ci}}+s_{(i-1)}\right)}^{a\left(i\right)}$$

In accordance with Reference⁴, the relation between $r_{(i)}$ and $r_{(i-1)}$ can be derived as:

$$\frac{r_{(i)}}{r_{(i-1)}}=\frac{2H\left[({\sigma }_{\text{r}(i)}+{\sigma }_{\text{r}(i-1)})/2,{\eta }_{(i-1)}\right]+\mathrm{\Delta }{\sigma }_{\text{r}}}{2H\left[({\sigma }_{\text{r}(i)}+{\sigma }_{\text{r}(i-1)})/2,{\eta }_{(i-1)}\right]-\mathrm{\Delta }{\sigma }_{\text{r}}}$$ 39

As illustrated in Eqs. (36), (37) and (39), ${\epsilon }_{{\mathrm{\theta }}_{(i)}}$,${\epsilon }_{\text{r}(i)}$ and $r_{(i)}/r_{(i-1)}$ are independent of the radius $R_{\text{p}}$, or $R_{\text{r}}$. This means that with no need to obtain the value of $R_{\text{r}}$, stress and strain components in the plastic softening zone can be solved first.

Radii of plastic softening and residual zones

IN the plastic residual zone, by incorporating Eq. (29) into Eq. (26), one obtains:

$$\frac{\partial {\sigma }_{\text{r}}}{\partial r}=\frac{{\sigma }_{\text{ci}}{\left(m_{\text{b}}^{\text{r}}{\sigma }_{\text{r}}/{\sigma }_{\text{ci}}^{\text{r}}+s^{\text{r}}\right)}^{a^{\text{r}}}}{r}$$ 40

where $m_{\text{b}}^{\text{r}}$ and s^r are the strength parameters in the residual zone. The boundary conditions for Eq. (41) are: (1) r = R₀, σ_r = p_i; and (2) r = R_r, σ_r = σ_r1. Hence, the following equation can be derived from Eq. (40):

$$R_{\text{r}}=R_{0}exp\left[\frac{{\left({\sigma }_{\text{r}1}{m}_{\text{b}}^{\text{r}}/{\sigma }_{\text{ci}}^{\text{r}}+s^{\text{r}}\right)}^{a^{\text{r}}}-{\left(p_i{m}_{\text{b}}^{\text{r}}/{\sigma }_{\text{ci}}^{\text{r}}+s^{\text{r}}\right)}^{a^{\text{r}}}}{m_{\text{b}}^{\text{r}}(1-a^{\text{r}})}\right]$$ 41

Equation (41) illustrates that $R_{\text{r}}$ can be obtained by use of $m_{\text{b}}^{\text{r}}$, $s^{\text{r}}$ and ${\sigma }_{\text{r}1}$. In fact, from Eq. (40), the relation between $R_{\text{r}}$ and $R_{\text{p}}$ can be derived as follows:

$$\frac{R_{\text{r}}}{R_{\text{p}}}=\prod _{i=1}^j\frac{2H({\sigma }_{\text{r}(i)}^{\prime },{\eta }_{(i-1)})+\mathrm{\Delta }{\sigma }_{\text{r}}}{2H({\sigma }_{\text{r}(i)}^{\prime },{\eta }_{(i-1)})-\mathrm{\Delta }{\sigma }_{\text{r}}}$$ 42

where j is the number of the annulus immediately outside the plastic softening-residual boundary. Equation (42) shows that $R_{\text{p}}$ can be solved by $R_{\text{r}}$.

In addition, when only the plastic softening zone is formed, Eq. (42) can be rewritten into:

$$\frac{R_{\text{p}}}{R_0}=\prod _{i=1}^j\frac{2H({\sigma }_{\text{r}(i)}^{\prime },{\eta }_{(i-1)})+\mathrm{\Delta }{\sigma }_{\text{r}}}{2H({\sigma }_{\text{r}(i)}^{\prime },{\eta }_{(i-1)})-\mathrm{\Delta }{\sigma }_{\text{r}}}$$ 43

Radial displacement of plastic softening and residual zones

Essentially, after obtaining $R_{\text{p}}$, $u_{(i)}$ in the plastic softening zone can be solved by Eq. (38). As for u in the plastic residual zone, it can be obtained in a closed-form as shown in Eq. (44)⁴⁴. Since the plastic softening zone is considered herein, $R_{\text{r}}$ and ${\sigma }_{\text{r}1}$ of Eq. (44) are substituted for $R_{\text{p}}$ and ${\sigma }_0$ of Eq. (38) presented in the elastic-brittle-plastic solution⁴⁴.

$$\frac{u}{r}=\frac{1}{2G}\frac{1}{r^{K_{\psi }}}\left[D_1{f}_1(r)+D_2{f}_2(r)+D_3{f}_3(r)+2R_{\text{r}}^{K_{\psi }}{Gu|}_{r=R_{\text{r}}}-D_1{f}_1(r)-D_2{f}_2(r)-D_3{f}_3(r)\right]$$ 44

where G is the shear modulus, G = E/2(1 + μ).

$$A^{H-B}={\left(m_{\text{b}}^{\text{r}}{\sigma }_{\text{ci}}^{\text{r}}{p}_{\text{i}}+s^{\text{r}}{\sigma }_{\text{ci}}^{\text{r2}}\right)}^{a_{\text{r}}},B^{H-B}=m_{\text{b}}^{\text{r}}{\sigma }_{\text{ci}}^{\text{r}}/4$$

$$D_1=(K_{\psi }-\mu K_{\psi }-\mu )A^{H-B}+(K_{\psi }+1)(1-2\mu )(p_{\text{i}}-{\sigma }_{\text{r}1}),$$

$$D_2=(K_{\psi }+1)(1-2\mu )A^{H-B}+2(K_{\psi }-\mu K_{\psi }-\mu )B^{H-B},D_3=(K_{\psi }+1)(1-2\mu )B^{H-B},$$

$$f_1(r)=r^{K_{\psi }+1}/(K_{\psi }+1),f_2(r)=\frac{r^{K_{\psi }+1}}{(K_{\psi }+1)}\left[ln\left(\frac{r}{R_0}\right)-\frac{1}{K_{\psi }+1}\right]$$

$$f_3(r)=\frac{r^{K_{\psi }+1}}{(K_{\psi }+1)}\left[{ln}^2\left(\frac{r}{R_0}\right)-\frac{2}{K_{\psi }+1}ln\left(\frac{r}{R_0}\right)+\frac{2}{{(K_{\psi }+1)}^2}\right].$$

Verification

The strength parameters for a group of tunnel excavation cases are used to verify the proposed semi-analytical procedure (Table 9). The cases are from the References^2,3,6. Figure 4 demonstrates the distribution of the normalised radial displacement predicted by the semi-analytical procedure and a self-similar method² for the SS rock masses with different dilatancy behaviours, which show good agreement with each other. The normalised support pressure versus the normalised plastic radii is plotted in Fig. 5. Comparison of the Ground Reaction Curves for the SS rock mass obtained from the semi-analytical procedure and self-similar method² are presented in Fig. 6, also showing good convergence. Therefore, the semi-analytical procedure proposed in this study is sufficiently reliable in predicting the tunnel strain for the SS rock masses. It should be noted that EPP and EPB rock masses can be regarded as the special cases for the SS rock masses. In this aspect, the above can also serve as a verification of the EPP and EPB rock masses.

Table 9.

Parameters of the tunnel cases for verification.

	C1	C2	C3	C4	C5	C6
ψ/°	φp/2	φp/4	φp/8	0	3.75	3.1
φp/°	30	30	30	30	30	24.81
φr/°	22	22	22	22	22	15.69
η*	0.008	0.008	0.008	0.008	0.008	0.017
Er/GPa	10	10	10	10	3.837	3.837
$\mu$	0.25	0.25	0.25	0.25	0.25	0.25
R0/m	3	3	3	3	3	7
$c^{\text{p}}/\text{MPa}$	1	1	1	1	1	0.744
$c^{\text{r}}/\text{MPa}$	0.7	0.7	0.7	0.7	0.7	0.397
${\sigma }_0/\text{MPa}$	20	20	20	20	20	12

Figure 4.

Variations of dimensionless support pressure p_i/σ₀ versus dimensionless radial displacement u₀E_r/ 2R₀(1 + μ)(σ₀ – σ_r2) for case C1, C2, C3 and C4.

Figure 5.

Variations of dimensionless support pressure p_i/σ₀ versus plastic radius R_r/R₀, or R_p/R₀ for case C5.

Figure 6.

Ground reaction curve for case C6.

In some existing studies, efforts were given to calculate the tunnel strain ɛ_θ for the EPP rock mass with a wide range of qualities^13–16. Particularly, Reference¹⁶ established a regression model with 20 < RMR < 90:

$$u_0\left(\text{mm}\right)=\left\{\begin{array}{cc}& 24711\times 0.{43}^{p_{\text{i}}}\times {\text{RMR}}^{-2.42},{\sigma }_0=2.7\text{MPa}\hfill \\ \hfill & 157513\times 0.{59}^{p_{\text{i}}}\times {\text{RMR}}^{-2.71},{\sigma }_0=5.4\text{MPa}\hfill \\ \hfill & 696395\times 0.{65}^{p_{\text{i}}}\times {\text{RMR}}^{-2.99},{\sigma }_0=8.1\text{MPa}\hfill \\ \hfill & 3973329\times 0.{66}^{p_{\text{i}}}\times {\text{RMR}}^{-3.37},{\sigma }_0=10.8\text{MPa}\hfill \\ \hfill & 18531047\times 0.{67}^{p_{\text{i}}}\times {\text{RMR}}^{-3.72},{\sigma }_0=13.5\text{MPa}\hfill \\ \hfill \end{array}\right)$$ 45

Based on Eqs. (8), (45) can be transferred to the following equation,

$$u_0\left(\text{mm}\right)=\left\{\begin{array}{cc}& 24711\times 0.{43}^{p_{\text{i}}}\times {\left(\text{GSI}+5\right)}^{-2.42},{\sigma }_0=2.7\text{MPa}\hfill \\ \hfill & 157513\times 0.{59}^{p_{\text{i}}}\times {(\text{GSI}+5)}^{-2.71},{\sigma }_0=5.4\text{MPa}\hfill \\ \hfill & 696395\times 0.{65}^{p_{\text{i}}}\times {\text{(GSI + 5)}}^{-2.99},{\sigma }_0=8.1\text{MPa}\hfill \\ \hfill & 3973329\times 0.{66}^{p_{\text{i}}}\times {\text{(GSI + 5)}}^{-3.37},{\sigma }_0=10.8\text{MPa}\hfill \\ \hfill & 18531047\times 0.{67}^{p_{\text{i}}}\times {\text{(GSI + 5)}}^{-3.72},{\sigma }_0=13.5\text{MPa}\hfill \\ \hfill \end{array}\right)$$ 46

The value of ε_θ predicted by the proposed procedures in this study can be compared with that by Eq. (46).

Then GSI^p was varied between 40 and 65 with 5 intervals to compare the proposed method with that by Reference¹⁶. For each GSI^p value, σ₀ ranges from 2.7 to 13.5 MPa, p_i is 0 and R₀ is 5 m. ε_{θ_Basarir} is obtained by dividing u₀ by R₀¹⁶. The comparison of ε_θ obtained from the semi-analytical procedure and ε_{θ_basarir} by the scheme in Reference¹⁶ shows good agreement with the coefficient of determination R² up to 90.8% (see Fig. 7). Then the rationality of the input geological parameters (E_r^p, E_r^r, σ_ci^p, σ_ci^r, m_i^p, m_i^r, m_b^p, m_b^r,s^p, s^r, a^p, and a^r) in this study can be validated to some extent.

Figure 7.

Comparison between ε_θ and ε_{θ_Basarir}.

Regression model for tunnel strain

The strain ε_θ can be fitted as a function of GSI^p, σ₀ and p_i/σ₀ by a nonlinear regression method. The equations for ε_θ in the plastic and elastic areas differ from each other:

$${\epsilon }_{\mathrm{\theta }}=f_1\left({\text{GSI}}^{\text{p}},{\sigma }_0,p_{\text{i}}/{\sigma }_0\right),{\epsilon }_{\mathrm{\theta }}>{\epsilon }_{\mathrm{\theta }2},p_{\text{i}}<{\sigma }_{\text{r2}},\text{plastic}\text{area}$$ 47a

$${\epsilon }_{\mathrm{\theta }}=f_2\left({\text{GSI}}^{\text{p}},{\sigma }_0,p_{\text{i}}/{\sigma }_0\right),{\epsilon }_{\mathrm{\theta }}\le {\epsilon }_{\mathrm{\theta }2},p_{\text{i}}\ge {\sigma }_{\text{r2}},\text{elastic area}$$ 47b

In Eq. (38), the critical strain ε_θ2 and the critical support pressure σ_r2 need to be determined prior to solving ε_θ. Combining Eqs. (26) and (27), fitting equations for σ_r2 and ε_θ2 can be written as:

$${\sigma }_{\text{r2}}=f_3\left({\text{GSI}}^{\text{p}},{\sigma }_0\right)$$ 48a

$${\epsilon }_{\theta 2}=f_4\left({\text{GSI}}^{\text{p}},{\sigma }_0\right)$$ 48b

The Taylor series polynomial regression (PR) can be adopted to solve f₁, f₃ and f₄. Particularly for f₁, a nonlinear function can be constructed as:

$$\begin{array}{cc}\hfill y& =exp\left(a_1+b_1{x}_1+b_2{x}_2+b_3{x}_3+c_1{x}_1^2+c_2{x}_2^2+c_3{x}_3^2+c_4{x}_1{x}_2+c_5{x}_3{x}_2+c_6{x}_3{x}_1\right)\hfill \\ \hfill & +d_1{x}_3^2{x}_2+d_2{x}_3^2{x}_1+d_3{x}_3{x}_1^2+d_4{x}_3{x}_2^2+d_5{x}_1{x}_2{x}_3+d_6{x}_2^3+d_7{x}_1^3\hfill \\ \hfill & +e_1{x}_1^2{x}_2^2+e_2{x}_2^2{x}_3^2+e_3{x}_3^2{x}_1{x}_2+e_4{x}_3{x}_1^3+e_5{x}_3{x}_2^3\hfill \\ \hfill & \left(+f_1{x}_1^3{x}_3^2+f_2{x}_2^3{x}_3^2\right)\hfill \\ \hfill \end{array}$$ 49

For f₃ and f₄, the variable y (ε_θ2 or σ_r2) depends on x₁ (GSI^p) and x₂ (σ₀), as:

$$y=a_1+b_1{x}_1+b_2{x}_2+c_1{x}_1^2+c_2{x}_2^2+c_3{x}_1{x}_2+d_1{x}_1^3+d_2{x}_2^3+d_3{x}_1{x}_2^2+d_4{x}_2{x}_1^2$$ 50

As for f₂, the relation between the variable y (ε_θ) and the independent variables x₁ (GSI^p), x₂ (σ₀), and x₃ (p_i/σ₀) can be derived from Eq. (28) as:

$$y=\frac{x_2\left(1+\mu \right)\left(1-x_3\right)}{a_1{x}_1^3+b_1{x}_1^2+c_1{x}_1+d_1}$$ 51

To obtain the coefficients in Eqs. (40) to (42), ε_θ for a large number of tunnelling cases are calculated by the proposed iterative procedure. The input geological parameters (GSI^p, GSI^r, E_r^p, E_r^r, σ_ci^p, σ_ci^r, m_b^p, m_b^r, s^p, s^r, a^p, and a^r) for the calculation are given in Tables 1, 3, 6, and 8. Nine values for η^* within cases A1 to A9 are listed in Table 10. σ₀ varies from 5 to 50 MPa with intervals of 5 MPa. p_i/σ₀ ranges from 0 to 1 MPa and 10 to 20 values are selected for different combination of p_i and σ_r2. f₂, f₃ and f₄ are merely correlated to the peak geological parameters in the elastic zone. The regression model is composed of twelve equations: three equations are for f₂, f₃ and f₄, and nine equations are for f₁. Then the coefficients can be determined with the Levenberg Marquardt iteration algorithm (see Tables 11 and 12), which is validated through the analysis of variance ANOVA. The predictions with the twelve equations match well with those by the semi-analytical procedure.

Table 10.

Critical plastic softening parameter η^*.

Case	A1	A2	A3	A4	A5	A6	A7	A8	A9
η*	0	0.005	0.01	0.025	0.05	0.1	0.5	1	∞

Table 11.

Coefficients in f₄, f₃, and f₂.

	f4		f3		f2
a1 (10–5)	42.5845	a1	− 0.28589	a1	0.000273
b1 (10–5)	2.88088	b1	0.0338	b1	− 0.01925
b2 (10–5)	1.1807	b2	0.91007	c1	0.47982
c1 (10–5)	0.075412	c1	− 0.00195	d1	− 3.57994
c2 (10–5)	0.043128	c2	0.00938
c3 (10–5)	0.035988	c3	− 0.01975
d1 (10–5)	0.000485	d1 (10–5)	2.44631
d2 (10–5)	0.000479	d2 (10–5)	− 7.68786
d3 (10–5)	0.000468	d3 (10–5)	1.3393
d4 (10–5)	0.000488	d4 (10–5)	5.4923

Table 12.

Coefficients in f₁: (a) when η^* = ∞, 1, 0.5, 0.1, 0.05; (b) when η^* = 0.025, 0.01, 0.005, 0.

(a) η*	∞	1	0.5	0.1	0.05
a1	0.37576	− 0.74117	− 0.61639	1.08615	3.27504
b1	− 0.3432	− 0.24502	− 0.2742	− 0.43415	− 0.58165
b2	− 16.0768	− 16.14255	− 16.55177	− 16.45784	− 19.47774
b3	0.32959	0.41235	0.46672	0.53739	0.53157
c1	0.00788	0.00246	0.00225	0.00656	0.00967
c2	19.49741	21.77123	22.57404	21.46441	27.19204
c3	− 0.00289	− 0.00176	− 0.00156	− 0.00362	− 0.00485
c4	0.33925	0.34786	0.36874	0.38357	0.45668
c5	− 0.07987	− 0.22695	− 0.26771	− 0.70855	− 0.82604
c6	− 0.00862	− 0.02094	− 0.02172	− 0.01372	− 0.00686
d1	− 0.00059963	− 0.01182	− 0.00343	0.00441	0.00765
d2 (10–5)	2.24755	0.707777	− 0.862592	4.88805	10.3286
d3 (10–5)	4.96784	15.5397	17.8538	8.07328	− 8.19822
d4	− 0.01828	0.29111	0.37644	0.83708	0.87071
d5	− 0.00656	− 0.02268	− 0.00153	0.00261	0.00278
d6	− 15.49841	− 18.33127	− 18.88734	− 19.65351	− 25.08435
d7 (10–5)	− 1.72834	− 0.615086	− 0.667556	− 3.36496	− 5.69299
e1 (10–4)	− 7.9539	− 29.9	− 33.9	− 21.9	− 36.7
e2 (10–4)	14.6	23.1	16.2	− 76.6	− 95.5
e3 (10–5)	9.11563	8.73084	10.4683	1.56558	− 2.26792
e4 (10–7)	− 2.61481	− 9.51432	− 11.4793	− 0.354321	12.6512
e5	0.06741	− 0.27619	− 0.2907	− 0.48179	− 0.34204
f1 (10–9)	0.532421	1.95193	3.18653	− 3.039	− 8.42
f2	− 0.00215	− 0.00076716	0.00017157	0.00582	0.00517

(b) η*	0.025	0.01	0.005	0
a1	3.37806	− 1.23767	− 0.45896	3.37629
b1	− 0.56164	− 0.16611	− 0.15858	− 0.47128
b2	− 21.86517	− 21.45617	− 19.50907	− 16.89839
b3	0.48318	0.52196	0.38419	0.25426
c1	0.0088	− 0.00075226	− 0.00132	0.00759
c2	33.78561	37.16971	26.33782	28.57907
c3	− 0.00656	− 0.00627	− 0.00162	− 0.00173
c4	0.51334	0.43875	0.29709	0.15241
c5	− 0.96887	− 0.66871	− 0.00379	0.38674
c6	− 0.00277	− 0.00527	− 0.0063	0.00259
d1	0.01421	0.00686	− 0.0018	− 0.00575
d2 (10–5)	14.2824	10.6465	− 4.79792	− 2.97141
d3 (10–5)	− 19.9824	2.54789	19.5277	− 4.91271
d4	0.85951	0.57685	− 0.19027	− 0.13331
d5	0.0037	0.00075557	− 0.01386	− 0.02578
d6	− 30.75648	− 32.48237	− 20.64928	− 36.72157
d7 (10–5)	− 4.78882	2.51696	2.35951	− 5.6103
e1 (10–4)	− 68.6	− 81.9	25.7	109.2
e2 (10–4)	− 97.7	− 19.3	94.2	− 39.7
e3 (10–5)	− 7.26793	− 3.79109	12.6535	32.7694
e4 (10–7)	19.6994	− 4.32378	− 20.7783	4.66801
e5	− 0.18899	− 0.15045	0.17124	0.25735
f1 (10–9)	− 10.6367	− 2.62886	13.3079	2.50107
f2	0.00376	− 0.00163	− 0.00931	0.00429

Parametric study

Variation of tunnel strain with different critical softening parameters

Values of ε_θ are calculated by the proposed regression model, which are plotted for Cases A1 to A9 versus GSI^p, σ₀, and p_i/σ₀, respectively, as in Figs. 8 and 9. In Fig. 8, GSI^p is variable, σ₀ is 30 MPa and p_i/σ₀ is 0.1, and in Fig. 9, p_i/σ₀ is variable, GSI^p is 30 and σ₀ is 5 MPa. When GSI^p is 70 or 75, and p_i/σ₀ is 0.3, ε_θ maintains constant. The reason is that GSI^p and p_i/σ₀ are relatively large, so that the rock mass takes elastic deformations and is independent of η^*. With plastic deformations in the rock mass, ε_θ decreases to a substantial constant with the increase in η^*. The decrease of ε_θ is induced by the shrinkage of the plastic residual area. If η^* is nil, all rock mass within the plastic area is characterised with the residual strength; and the maximum ε_θ is therefore reached; as η^* increases, ε_θ falls rapidly since the softening area expands; and ε_θ becomes stable when the softening zone dominates in the plastic area. The expansion of the plastic residual area is the critical factor enhancing the deformation within the rock mass. In the practical engineering, the measures to decrease the plastic residual zone can substantially improve the tunnel stability. Furthermore, ε_θ falls quickly and becomes constant within a small η^* for excellent quality rock mass, whereas ε_θ for the weak rock mass decreases slowly and the decline process is prolonged until a plateau is reached (see Fig. 9). Hence, the rock mass deformation decreases more suddenly with a better quality rock while η^* increases.

Figure 8.

Variation of ε_θ versus cases A1 to A9: (a) GSI^p ranges from 25 to 75; (b) GSI^p = 65, 70, 75.

Figure 9.

Variation of ε_θ versus cases A1 to A9: (a) p_i/σ₀ ranges from 0 to 0.3; (b) p_i/σ₀ = 0.25, p_i/σ₀ = 0.30.

Difference of tunnel strain between the EPP and EBP rock masses

ε_θ for the EPP rock mass is symbolised by ε_{θ_EPP}. The increase ratio of ε_θ for the EBP rock mass in comparison to the EPP counterpart is denoted by Δε_θ/ε_{θ_EPP}. Δε_θ/ε_{θ_EPP} versus GSI^p for variations in σ₀ and p_i/σ₀ is plotted in Fig. 10.

Figure 10.

Variation of Δε_θ/ε_{θ_EPP} versus GSI^p : (a) p_i/σ₀ = 0; (b) p_i/σ₀ = 0.1; (c) p_i/σ₀ = 0.2; (d) p_i/σ₀ = 0.3.

When p_i/σ₀ is 0.1, 0.2 and 0.3, Δε_θ/ε_{θ_EPP} decreases as GSI^p increases (see Fig. 10b–d). Hence, while p_i/σ₀ exceeds 0.1, the effect of η^* on ε_θ for the weakest rock mass (GSI^p = 25) is the greatest, which should be highlighted. While p_i is 0, and σ₀ ranges from 10 to 20 MPa, Δε_θ/ε_{θ_EPP} rises but then decreases with the increase in GSI^p (Fig. 10a). The maximum Δε_θ/ε_{θ_EPP} appears while GSI^p is around 45 or 50. In this case, the influence of η^* on ε_θ for the moderate rock mass (GSI^p = 45, 50) is the largest. For GSI^p is 50 and σ₀ is 20 MPa, Δε_θ/ε_{θ_EPP} reaches almost 10.64 for p_i/σ₀ is 0 but drops to 1.77 for p_i/σ₀ is 0.1 (see Fig. 10a,b). This means that the growth of p_i effectively weakens the softening effect on the deformation for moderate quality rock mass with high initial stress. Furthermore, when GSI^p is greater than 55 and p_i/σ₀ exceeds 0.1, Δε_θ/ε_{θ_EPP} for most cases is 0, which means ε_θ by EPP and EBP rock masses are equivalent (see Fig. 10b–d). This is because that the rock mass undergoes an elastic deformation. Therefore, if p_i/σ₀ reaches 0.1, the rock mass deformation is inconsiderable and irrespective of η^* for the excellent rock mass quality (GSI^p ≥ 55).

Sensitive analysis

Figure 11 illustrates the sensitivity analysis concerning the tunnel strain ɛ_θ, showing the relative significance of the most significant input data (i.e. GSI^p, σ₀ and p_i/σ₀) on this final output (i.e. ɛ_θ). Three base cases with different rock mass qualities are given in Table 13. In the sensitive analysis, σ₀ varies between 5 and 30 MPa with even intervals of 5 MPa. p_i/σ₀ ranges from 0 to 0.225 with 0.025 intervals. GSI^p ranges from 25 to 75 with 5 intervals. GSI^p, σ₀ or p_i/σ₀ is represented by the variable m. GSI^p, σ₀ or p_i/σ₀ in cases B1 to B3 is represented by m_base. ɛ_θ calculated by cases B1 to B3 is represented by ɛ_θ,base.

Figure 11.

Sensitive analysis of GSI^p, σ₀ and p_i/σ₀ on ε_θ: (a) cases B1; (b) case B2; (c) case B3.

Table 13.

GSI, σ₀ and p_i/σ₀ for cases B1 to B3.

	Case B1	Case B2	Case B3
GSIp	70	50	30
σ0 (MPa)	20	20	20
pi/σ0	0.15	0.15	0.15

In comparison with the EBP rock mass, ε_θ/ε_θ,base of the EPP rock mass with the moderate and weak rock qualities tends to be closer to the line for ε_θ/ε_θ,base is 1 (see Fig. 11b,c). In this respect, ε_θ for the EBP rock mass is more sensitive to the change in GSI^p, p_i/σ₀ and σ₀. However, for the excellent quality rock mass, ε_θ/ε_θ,base of EBP rock mass coincides with that of EPP rock mass (Fig. 11a). This is attributed to that the rock mass exhibits the elastic behaviour, and thus ε_θ is independent of the plastic parameters. In this respect, the influence of GSI^p, p_i/σ₀ or σ₀ on ε_θ by EPP and EBP rock masses are equivalent.

Among the input parameters GSI^p, σ₀ and p_i/σ₀, the change in GSI^p gives rise to the greatest change in ε_θ. Especially for the excellent rock mass, ε_θ/ε_θ,base by GSI^p is considerably higher than σ₀ and p_i/σ₀ (Fig. 11a). Therefore, GSI^p is of vital importance in controlling ε_θ. The relative significance of p_i/σ₀ and σ₀ varies with different conditions. For the EBP rock mass, when p_i/σ₀ decreases and σ₀ increases with an equivalent variation, ε_θ/ε_θ,base affected by p_i/σ₀ is always higher than that by σ₀; and it becomes remarkably higher while p_i/σ₀ decreases to a small value. Hence, for the EBP rock mass, when p_i/σ₀ decreases and σ₀ increases, the influence of p_i/σ₀ on ε_θ is larger than that of σ₀. For all the other conditions, the influence of σ₀ on ε_θ is greater than that of p_i/σ₀. For instance, for the EPP rock mass, the change in σ₀ causes a larger variation in ε_θ; for the EBP rock mass, when p_i/σ₀ increases and σ₀ decreases with the equivalent variation, a decrease of σ₀ yields a higher reduction of ε_θ. As the weak rock mass shows the EPP behaviour³³, the reduction of σ₀ exerts greater influence than the increase in p_i/σ₀ in controlling the rock deformation for the weak rock mass. In the tunnelling engineering, the reduction of σ₀ and the increase of p_i/σ₀ can be obtained by relieving the stress and installing the rigid support, respectively.

Conclusions

Various GSI were considered to quantify the input geological parameters for the strain-softening rock masses with various qualities. A specialised numerical scheme was presented to calculate the tunnel strain around a circular opening within the rock mass. The proposed semi-analytical procedure and the input geological parameters were validated through comparison of the tunnel strain obtained by the semi-analytical procedure with that predicted by the previous studies. With the obtained input geological parameters, more accurate quantification of the tunnel strain was obtained by a semi-analytical procedure. A regression model, composed of 12 fitting equations, was further proposed: 3 equations were to calculate the critical tunnel strain, the critical support pressure and the tunnel strain with elastic behaviour, and 9 equations were for the tunnel strain with different strain-softening behaviours. The model provides practical guidelines to assess the deformations of the rock mass prior to the tunnel construction. Following conclusions can then be drawn:

The tunnel strain wanes to a constant value with the critical softening parameter keeps increasing, which is mainly ascribed to the shrinkage of the plastic residual area. Reversely, the rock deformation is mainly raised due to the expansion of the plastic residual area. In the practical engineering, the measures to decrease the plastic residual area can substantially improve the tunnel stability.

While the support pressure exceeds a certain value (p_i/σ₀ ≥ 0.1), the critical softening parameter makes the most significant influence on the tunnel strain for the weakest rock mass (GSI^p = 25). In comparison, with no support pressure (p_i/σ₀ ≥ 0) and relatively high initial stress (σ₀ ≥ 10 MPa), the influence of the critical softening parameter for the moderate rock mass (GSI^p is around 45 or 50) is the most significant. While the support pressure that acted on the good rock mass quality (GSI^p ≥ 55) exceeds a certain value, the rock mass deformation becomes inconsiderable.

While the rock mass exhibits a strain-softening behaviour, the tunnel strain for the EBP rock mass can be affected by the change in the rock mass quality, the support pressure and the initial stress state. Among the three input geological parameters (i.e. GSI^p, the support pressure, and the initial stress), GSI^p is of vital importance in controlling the tunnel strain. The relative significance of the support pressure and initial stress varies with different conditions. For the EBP rock mass, with the support pressure decreases and the initial stress increases, the tunnel strain is mostly influenced by the variation in the support pressure. For all other conditions, the initial stress state becomes the critical factor.

List of symbols

η

Softening parameter

${\sigma }_{\text{r}}$, ${\sigma }_{\mathrm{\theta }}$

Radial and tangential stresses

${\epsilon }_{\text{r(}i)}$,${\epsilon }_{{\mathrm{\theta }}_{(i)}}$

Radial and tangential strains at r = r_(i)

${\epsilon }_{\text{r}(i-1)}$, ${\epsilon }_{{\mathrm{\theta }}_{(i-1)}}$

Radial and tangential strains at r = r_(i-1)

${\epsilon }_{\text{r}}^{\text{plas}}$,${\epsilon }_{\mathrm{\theta }}^{\text{plas}}$

Radial and tangential plastic strains

$\mathrm{\Delta }{\epsilon }_{\text{r}(i)}^{\text{plas}}$,$\mathrm{\Delta }{\epsilon }_{\mathrm{\theta }(i)}^{\text{plas}}$

Radial and tangential plastic strain increments

$\mathrm{\Delta }{\epsilon }_{\text{r}(i)}^{\text{elas}}$,$\mathrm{\Delta }{\epsilon }_{\theta (i)}^{\text{elas}}$

Radial and tangential elastic strain increments

$u_{(i)}$

Radial displacement at r = r_(i)

p₀

Initial ground stress

μ

Poisson’s ratio

σ₁, σ₃

Major and minor principal stresses at failure, respectively

GSI

Geological Strength Index

GSI^p, GSI^r

Peak and residual values of the Geological Strength Index

ψ

Dilatancy angle

$K_{\psi }(\eta )$

Dilatancy coefficient

φ

Friction angle

${\sigma }_{\text{ci}}$

Uniaxial compression strength of intact rock

m_b, s, a

Strength parameters of the Hoek–Brown rock mass

$\omega$

m_b, s and α

D

Disturbance coefficient

RMR

Rock Mass Rating

η^*

Critical value of the softening parameter

${\sigma }_{\text{cm}}$

Strength of a rock mass

σ_r(i),σ_r(i-1)

Radial stresses at the inner and outer boundaries of each annulus

E_r^p , E_r^r

Peak and residual values of the deformation modulus

${\sigma }_{\text{r}2}$

Radial stress at the elastic–plastic boundary

Author contributions

Contributor roles taxonomy: Y.D. and L.C.: conceptualization, methodology, validation, investigation and writing-original draft; Q.S.: data curation, formal analysis; Y.D.: visualization, project administration; J.Z., Z.G. and L.C.: writing—review and editing.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Competing interests

The authors declare no competing interests.