Abstract
We review the theory of Lagrangian fibrations of hyperkähler manifolds as initiated by Matsushita. We also discuss more recent work of Shen–Yin and Harder–Li–Shen–Yin. Occasionally, we give alternative arguments and complement the discussion by additional observations.
Assume is a Lagrangian fibration of a compact hyperkähler manifold X of complex dimension 2n, and is a type III degeneration of compact hyperkähler manifolds of complex dimension 2n. Then the cohomology algebra of appears naturally in (at least) four different guises:
-
(i)As the cohomology algebra of (0, p) resp. (p, 0)-forms (both independent of f):
-
(ii)As the cohomology of the base of the fibration:1
-
(iii)As the image of the restriction to the generic fiber of f:
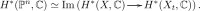
-
(iv)As the cohomology of the dual complex of the central fiber of :
In this survey we discuss these four situations and explain how they are related. We start by reviewing basic results on Lagrangian fibrations in Sect. 1, discuss the topology of the base and the restriction to the fiber in Sect. 2, and then explain in Sect. 3 how the various occurrences of are related, by sketching the proof of a key identity called P W.
Throughout, X denotes a compact hyperkähler manifold of complex dimension 2n. A fibration of X is a surjective morphism 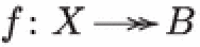 with connected fibers onto a normal variety B with . A submanifold of dimension n is Lagrangian if the restriction of the holomorphic two-form is zero.
with connected fibers onto a normal variety B with . A submanifold of dimension n is Lagrangian if the restriction of the holomorphic two-form is zero.
Basics on Lagrangian Fibrations
We first discuss Lagrangian submanifolds and in particular Lagrangian tori. Then we study the cohomology and the singularities of the base B. Next we show that the fibers, smooth ones as well as singular ones, of any fibration are Lagrangian and conclude that fibrations of hyperkähler manifolds over a smooth base are flat.
At the end, we mention further results and directions without proof: Matshushita’s description of the higher direct image sheaves , Beauville’s question whether Lagrangian tori are always Lagrangian fibers, smoothness of the base, etc.
Lagrangian Tori
We start with some general comments on Lagrangian manifolds and more specifically on Lagrangian tori.
Proposition 1.1
(Voisin) Any Lagrangian submanifold of a hyperkähler manifold X is projective. In particular, any Lagrangian torus is an abelian variety.
Proof
We follow the proof as presented in [11]. Since the restriction of any Kähler class on X to T is non-trivial, the restriction 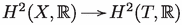 is a non-trivial morphism of Hodge structures. On the other hand, as T is Lagrangian, all classes in have trivial restrictions. Hence, the image of
is a non-trivial morphism of Hodge structures. On the other hand, as T is Lagrangian, all classes in have trivial restrictions. Hence, the image of  is contained in . More precisely, the images of
is contained in . More precisely, the images of 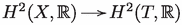 and of
and of 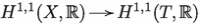 coincide. Therefore, for any Kähler class there exists a rational class such that the (1, 1)-class comes arbitrarily close to the Kähler class . Thus, is a rational Kähler class and, hence, T is projective.
coincide. Therefore, for any Kähler class there exists a rational class such that the (1, 1)-class comes arbitrarily close to the Kähler class . Thus, is a rational Kähler class and, hence, T is projective.
Remark 1.2
The normal bundle of a Lagrangian submanifold is isomorphic to the cotangent bundle of T, so . Hence, the (1, 1)-part of the restriction map 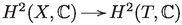 can be identified with the natural map
can be identified with the natural map 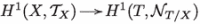 that sends a first order deformation of X to the obstruction to deform T sideways with it, see [69]:
that sends a first order deformation of X to the obstruction to deform T sideways with it, see [69]:
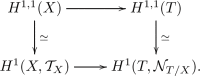 |
Clearly, as T is Lagrangian, the map 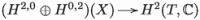 is trivial, see the proof above. Since the restriction of a Kähler class is again Kähler,
is trivial, see the proof above. Since the restriction of a Kähler class is again Kähler, 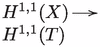 is certainly not trivial. Thus, deforms with X along a subset of codimension at least one. For smooth fibers of a Lagrangian fibration, so eventually Sect. 1.5.2 for all Lagrangian tori, the rank of the restriction map and hence the codimension of the image
is certainly not trivial. Thus, deforms with X along a subset of codimension at least one. For smooth fibers of a Lagrangian fibration, so eventually Sect. 1.5.2 for all Lagrangian tori, the rank of the restriction map and hence the codimension of the image 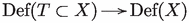 is exactly one.2
is exactly one.2
Proposition 1.3
Assume is a Lagrangian torus. Then the restrictions of the Chern classes are trivial.
Proof
The normal bundle sequence allows one to compute the restriction of the total Chern class of X to T. More precisely, . To conclude, use and the fact that the tangent bundle of a torus is trivial.
Remark 1.4
(i) In the case when is the fiber of a Lagrangian fibration 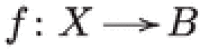 , as it always is, see Sect. 1.5.2, the restriction of the Beauville–Bogomolov–Fujiki form, thought of as a class , is also trivial:
, as it always is, see Sect. 1.5.2, the restriction of the Beauville–Bogomolov–Fujiki form, thought of as a class , is also trivial:
There does not seem to be a direct proof of this fact. However, using that the rank of the restriction map  is one, see Theorem 2.1, it can be shown as follows. The classes and in both have the distinguished property that the homogenous forms and defined on are non-trivial scalar multiples of and, therefore, of each other.3 If is the class of a fiber , then up to scaling for some . Hence, for a Kähler class on X we find (up to a non-trivial scalar factor)
is one, see Theorem 2.1, it can be shown as follows. The classes and in both have the distinguished property that the homogenous forms and defined on are non-trivial scalar multiples of and, therefore, of each other.3 If is the class of a fiber , then up to scaling for some . Hence, for a Kähler class on X we find (up to a non-trivial scalar factor)
Since and 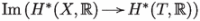 is generated by , this proves the claim.
is generated by , this proves the claim.
(ii) For other types of Lagrangian submanifolds, the restrictions of the Chern classes of X are not trivial. For example, for a Lagrangian plane one easily computes .
As remarked before, the normal bundle of a Lagrangian torus is trivial. The next observation can be seen as a converse, it applies in particular to the smooth fibers of any fibration 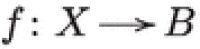 .
.
Lemma 1.5
Assume is Lagrangian submanifold with trivial normal bundle. Then T is a complex torus and, therefore, an abelian variety.
Proof
Since T is Lagrangian, the tangent bundle is trivial. Using the Albanese morphism, one easily proves that any compact Kähler manifold with trivial tangent bundle is a complex torus.
The Base of a Fibration
We pass on to (Lagrangian) fibrations.
Proposition 1.6
(Matsushita) Assume 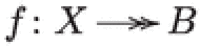 is a fibration with B smooth. Then B is a simply connected, smooth projective variety of dimension n satisfying for all and . In particular,
is a fibration with B smooth. Then B is a simply connected, smooth projective variety of dimension n satisfying for all and . In particular,
Proof
The smoothness of B implies that the pull-back 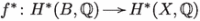 is injective; see Remark 1.14. Next, as for any class , we have and, therefore, . By [9, 68], this implies and hence , which implies . On the other hand, again by [9, 68], for every nonzero class from which we deduce .
is injective; see Remark 1.14. Next, as for any class , we have and, therefore, . By [9, 68], this implies and hence , which implies . On the other hand, again by [9, 68], for every nonzero class from which we deduce .
If , then is a non-trivial multiple of some power of . Hence, if p is odd. If , then and, hence, . Since and , one finds . A similar argument can be made to work for all even p and an alternative argument is provided by Theorem 2.1.
Next we show . Using [9, 68], we have
On the other hand, the image of is contained in which is just one-dimensional.4
Since X is Kähler, so is B, see [67]. Using , we can conclude that there exists a rational Kähler class on B. Hence, B is projective. According to [42, Prop. 2.10.2], the natural map 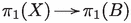 is surjective and, therefore, B is simply connected, as X is.5 Then, by the universal coefficient theorem, is torsion-free, i.e. . Since , the exponential sequence gives
is surjective and, therefore, B is simply connected, as X is.5 Then, by the universal coefficient theorem, is torsion-free, i.e. . Since , the exponential sequence gives 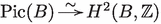 .
.
Remark 1.7
In fact, as we shall see, for all and , i.e. there is an isomorphism of rational Hodge structures
There are two proofs of this fact, both eventually relying on the isomorphism . It seems that unlike , which was proved above by exploiting the structure of the subring of , the proof of the identities for uses deeper information about the hyperkähler structure.
Lemma 1.8
(Markushevich, Matsushita) Under the above assumptions, B is a Fano variety, i.e. is ample.
Proof
Since B is dominated by X, we have by the known case of the Iitaka conjecture; see [36, Cor. 1.2]. Hence, or is ample. However, the first case is excluded by .
In [32, Prop. 24.8] the assertion is deduced from the fact that X admits a Kähler–Einstein metric. The case is excluded, because it would imply , which was excluded above.
Remark 1.9
It turns out that as soon as the base B is smooth, then . This result is due to Hwang [34] and its proof relies on the theory of minimal rational tangents. The results by Matsushita and more recently by Shen and Yin, see Remark 1.7 and Sect. 2, can be seen as strong evidence for the result. In dimension two, the result is immediate: Any smooth projective surface B with ample and is isomorphic to .
It is tempting to try to find a more direct argument in higher dimension, but all attempts have failed so far. For example, according to Hirzebruch–Kodaira [29] it suffices to show that such that the first Chern class of a line bundle L corresponding to a generator of satisfies , see [47] for a survey of further results in this direction.
Alternatively, by Kobayashi–Ochai [39], it is enough to show that is divisible by , i.e. the Fano manifold B has index . As a first step, one could try to show that is divisible by .
Singularities of the Base
It is generally expected that the base manifold B is smooth, but at the moment this is only known for , see [7, 35, 61]. The expectation is corroborated by the following computations of invariants of the singularities of B.
Denote by the intersection cohomology of the complex variety B with middle perversity and rational coefficients. It is the hypercohomology of the intersection cohomology complex , i.e. . In particular, if B is smooth or has quotient singularities, see [24, Prop. 3], then .
Proposition 1.10
Assume 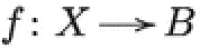 is a fibration over the complex variety B.
is a fibration over the complex variety B.
-
(i)
B is -factorial, 7 both in the Zariski and in the analytic topology.
-
(ii)
The intersection cohomology complex of B is quasi-isomorphic to the constant sheaf . In particular, .
-
(iii)
(Matsushita) B has log terminal singularities.
Proof
For (i) and (ii) one only needs that 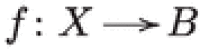 is a connected and equidimensional morphism from a smooth variety X, while in the proof of (iii) one also needs trivial.
is a connected and equidimensional morphism from a smooth variety X, while in the proof of (iii) one also needs trivial.
For any , choose a chart 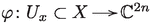 , centered at x, and the analytic subset , where is an n-dimensional affine subspace intersecting the fiber transversely. Since f is equidimensional, the restriction
, centered at x, and the analytic subset , where is an n-dimensional affine subspace intersecting the fiber transversely. Since f is equidimensional, the restriction 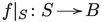 is finite over an analytic neighbourhood U of t. Therefore, U is -factorial by [38, Lem. 5.16].
is finite over an analytic neighbourhood U of t. Therefore, U is -factorial by [38, Lem. 5.16].
Denote . By the decomposition theorem [4].8 is a direct summand of . Taking stalks at t, we have
because of the finiteness of . Thus, the natural map 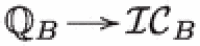 is a quasi-isomorphism in the constructible derived category with rational coefficients.
is a quasi-isomorphism in the constructible derived category with rational coefficients.
By the canonical bundle formula, there exists a -divisor such that the pair is log terminal; see [43, Thm. 8.3.7.(4)] and [56, Thm. 2]. By the -factoriality, B has log terminal singularities too.
Remark 1.11
(Quotient singularities) The finiteness of the restriction 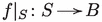 over b suggests that B should have at worst quotient singularities. This would follow from the following conjecture.
over b suggests that B should have at worst quotient singularities. This would follow from the following conjecture.
Conjecture 1.12
[44, §2.24] Let 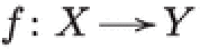 be a finite and dominant morphism from a smooth variety X onto a normal variety Y. Then Y has quotient singularities.
be a finite and dominant morphism from a smooth variety X onto a normal variety Y. Then Y has quotient singularities.
This is known for by [10, Lem. 2.6], but it is open in higher dimension. One of the main issue is that f itself need not be a quotient map, not even locally.
Corollary 1.13
The pullback 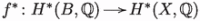 is injective.
is injective.
Proof
By Proposition 1.10 this follows from the inclusion 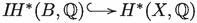 coming from the decomposition theorem.
coming from the decomposition theorem.
Remark 1.14
Let 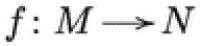 be a surjective holomorphic map between compact complex manifolds, with M Kähler. By [70, Lem. 7.28], the pullback
be a surjective holomorphic map between compact complex manifolds, with M Kähler. By [70, Lem. 7.28], the pullback 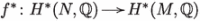 is injective. However, this may fail if N is singular, e.g. if f is a normalization of a nodal cubic, even if N has -factorial log terminal singularities, see for instance [52, Thm. 5.11].
is injective. However, this may fail if N is singular, e.g. if f is a normalization of a nodal cubic, even if N has -factorial log terminal singularities, see for instance [52, Thm. 5.11].
Remark 1.15
Assume that B is projective. By Corollary 1.13, the smoothness of B can be dropped from the assumptions of Proposition 1.6 and Lemma 1.8, see also [50].
The Fibers of a Fibration
Next we present Matsushita’s result that any fibration of a compact hyperkähler manifold is a Lagrangian fibration.
Lemma 1.16
(Matsushita) Assume 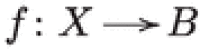 is a fibration. Then every smooth fiber is a Lagrangian torus and in fact an abelian variety.
is a fibration. Then every smooth fiber is a Lagrangian torus and in fact an abelian variety.
Proof
Comparing the coefficients of in the polynomial (in x and y) the equation
shows for all and all . Since for some class , this implies , which for a Kähler class and using that is semi-positive implies . Then conclude by Lemma 1.5.
Lemma 1.17
(Matsushita) The symplectic form is trivial when restricted to any subvariety contracted to a point t under f. In particular, all fibers of f are of dimension n, i.e. f is equidimensional, and if B is smooth, f is flat.
Proof
A theorem due to Kollár [40, Thm. 2.1] and Saito [63, Thm. 2.3, Rem. 2.9.] says that is torsion free. Since in our case , this shows that is torsion free. Let be the conjugate of the symplectic form, and be its image in . Since the general fiber is Lagrangian, must be torsion and hence zero. If  is a resolution of T, then the image of in is contained in the image of
is a resolution of T, then the image of in is contained in the image of
and hence trivial. This implies that the image of in is trivial, i.e. . By semi-continuity of the dimension of the fibers, , and so T is Lagrangian.
The flatness follows from the smoothness of X and B, see [25, Exer. III.10.9].
Remark 1.18
Note that the conclusion that f is flat really needs the base to be smooth. In fact, by miracle flatness, f is flat if and only if B is smooth.
Further Results
We summarize a few further results without proof.
Higher Direct Images
The first one is the main result of [51].
Theorem 1.19
(Matsushita) Assume 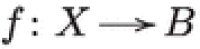 is a fibration of a projective9 hyperkähler manifold over a smooth base. Then
is a fibration of a projective9 hyperkähler manifold over a smooth base. Then
On the open subset over which 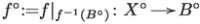 is smooth, the result can be obtained by dualising the isomorphism
is smooth, the result can be obtained by dualising the isomorphism
which holds because the smooth fibers of f are Lagrangian. A relative polarization is used to show that and are dual to each other. To extend the result from to the whole B, Theorem 1.19 uses a result of Kollár [40, Thm. 2.1] saying that are torsion free, which for X hyperkähler translates into being torsion free.
As mentioned in Remark 1.7, the theorem implies .
Lagrangian Tori are Lagrangian Fibers
In [6] Beauville asked whether every Lagrangian torus is the fiber of a Lagrangian fibration  . The question has been answered affirmatively:
. The question has been answered affirmatively:
-
(i)
Greb–Lehn–Rollenske in [20] first dealt with the case of non-projective X and later showed in [21] the existence of an almost10 holomorphic Lagrangian fibration in dimension four.
-
(ii)
A different approach to the existence of an almost holomorphic Lagrangian fibration with T as a fiber was provided by Amerik–Campana [1]. The four-dimensional case had been discussed before by Amerik [2].
-
(iii)
Hwang–Weiss [33] deal with the projective case and proved the existence of an almost Lagrangian fibration with fiber T. Combined with techniques of [20] this resulted in a complete answer.
Cohomology of the Base and Cohomology of the Fiber
The aim of this section is to prove the following result.
Theorem 2.1
Assume  is a fibration and let be a smooth fiber. Then
is a fibration and let be a smooth fiber. Then
The first isomorphism for X projective and B smooth is originally due to Matsushita [51], see Remark 1.7. The proof we give here is a version of the one by Shen and Yin [66] that works without assuming X projective. Note also that we do not assume that the base B is smooth.
The second isomorphism in degree two is essentially due to Oguiso [60], relying on results of Voisin [69]. The paper by Shen and Yin [66] contains two proofs of the general result, one using the -representation theory of the perverse filtration and another one, due to Voisin, relying on classical Hodge theory.
The proof we shall give avoids the perverse filtration as well as the various -actions central for the arguments in [66]. The discussion below also proves the second result in [66, Thm. 0.2], namely the equality
between the classical and perverse Hodge numbers, see Sect. 2.3. How it fits into the setting of P W is explained in Sect. 3.
Algebraic Preparations
To stress the purely algebraic nature of what follows we shall use the shorthand and consider it as a graded -algebra.
Consider a non-trivial, isotropic element of degree two, i.e. with . Then, according to Verbitsky and Bogomolov [9, 68], one has
In particular, multiplication by defines on the structure of a graded -algebra with x of degree two.
All that is needed in the geometric applications is then put into the following statement.
Proposition 2.2
For every two non-zero, isotropic elements the induced graded -algebra structures on are isomorphic.
Proof
Consider the complex algebraic group of automorphisms of the graded -algebra and its image G under 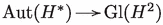 . Clearly, the assertion holds if are contained in the same G-orbit. As any two non-zero isotropic classes are contained in the same orbit of the complex special orthogonal group , it suffices to show that . This follows from [65, Prop. 3.4], up to taking complex coefficients in loc. cit.
. Clearly, the assertion holds if are contained in the same G-orbit. As any two non-zero isotropic classes are contained in the same orbit of the complex special orthogonal group , it suffices to show that . This follows from [65, Prop. 3.4], up to taking complex coefficients in loc. cit.
Remark 2.3
The arguments can be adapted to prove the following statement: Assume satisfy . Then the induced graded -algebra structures on , given by letting x act by multiplication with resp. , are isomorphic.
For with and we let
which is called the space of -primitive forms. Note, however, that does not satisfy the Hard Lefschetz theorem; otherwise we would have defined primitive classes in as elements in the kernel of .
We will also need the two spaces
| 2.1 |
It turns out that the map in the definition of is injective, but this is not needed for the argument. Note that for all .
Corollary 2.4
The dimensions of the spaces and are independent of the choice of the non-trivial, isotropic class .
Geometric Realizations
Let us begin by looking at the obvious choice for provided by the symplectic form .
Lemma 2.5
For one has
and
Proof
Concerning the first equality, one inclusion is obvious: Since , we have for d even and for d odd. For the other direction, use that 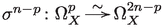 , for , is an isomorphism and that, therefore, for the composition
, for , is an isomorphism and that, therefore, for the composition
| 2.2 |
is injective. Hence, for , we have is injective, i.e. for , which is enough to conclude.
For the second part observe that .
As an immediate consequence of Corollary 2.4 one then finds.
Corollary 2.6
For any non-trivial, isotropic class there exist isomorphisms
of graded vector spaces.
Next let us consider a Lagrangian fibration 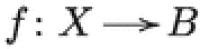 . We consider the class , which is isotropic since for dimension reasons.
. We consider the class , which is isotropic since for dimension reasons.
Lemma 2.7
For there exists an inclusion
Proof
The assertion follows from the Lefschetz decomposition
on B, with respect to the unique ample class , see [13, Thm. 2.2.3.(c)], and the observation that pull-back via f maps into .
Corollary 2.4 then immediately implies
see Remark 1.7, which proves the first part of Theorem 2.1.
We keep the isotropic class and observe that the natural inclusion
| 2.3 |
is actually an isomorphism.
Lemma 2.8
(Voisin) Let be as before and let be a smooth fiber of f. Then
Proof
The result is proved in [66, App. B]. The assertion is shown to be equivalent to the statement that the intersection pairing on the fiber is non-degenerate on the image of the restriction map, which in turn is deduced from Deligne’s global invariant cycle theorem.
From the result one obtains a surjection
Since by Corollary 2.6, its image in is the subring generated by the restriction of a Kähler class. Hence, is an isomorphism, which proves the second isomorphism in Theorem 2.1. However, it is easier to argue directly, as the equality holds in Lemma 2.8 by (2.3).
Perverse = Hodge
As in Sect. 2.1, we consider the abstract algebraic situation provided by and the additional structure induced by the choice of a non-zero isotropic class . The two spaces and defined there, both depending on , are part of a filtration
where is as defined before and .
In general, one defines
| 2.4 |
If we want to stress the dependence of , we write . The graded objects of this filtration
in particular , are used to define the Hodge numbers of the filtration as
As a further consequence of Proposition 2.2, one has
Corollary 2.9
The Hodge numbers of the filtration are independent of the choice of the isotropic class .
Let us quickly apply this to two geometric examples.
-
(i)First, consider , the anti-holomorphic symplectic form. Then the filtration gives back the Hodge filtration, i.e.
To see this, one needs to use the Lefschetz decomposition with respect to :
Note that from this example one can deduce that indeed for any choice of one has for and for . -
(ii)
For the second example consider a Lagrangian fibration
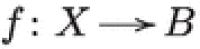 and let be the pull–back of an ample class . The induced filtration is called the perverse filtration11 and the Hodge numbers are denoted by .
and let be the pull–back of an ample class . The induced filtration is called the perverse filtration11 and the Hodge numbers are denoted by .
Then [66, Thm. 0.2] becomes the following immediate consequence of Proposition 2.2 or Corollary 2.9.
Corollary 2.10
(Shen–Yin) For any Lagrangian fibration 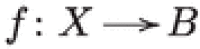 the Hodge numbers of the perverse filtration equal the classical Hodge numbers :
the Hodge numbers of the perverse filtration equal the classical Hodge numbers :
P W
P W for compact hyperkähler manifolds asserts that the perverse filtration associated with a Lagrangian fibration can be realised as the weight filtration of a limit mixed Hodge structure of a degeneration of compact hyperkäher manifolds. It boils down to the observation that the cup product by a semiample not big class and a logarithmic monodromy operator define nilpotent endomorphisms in cohomology which are not equal, but up to renumbering induce the same filtration.
Inspired by P W, we provide some geometric explanation or conjecture concerning the appearance of the cohomology of in the introduction and in Theorem 2.1.
The Weight Filtration of a Nilpotent Operator
Definition 3.1
Given a nilpotent endomorphism N of a finite dimensional vector space of index l, i.e. and , the weight filtration of N centered at l is the unique increasing filtration
with the property that (1) , and denoting again by N the induced endomorphism on graded pieces, (2) for every , see [16, §1.6].
The weight filtration of N on can be constructed inductively as follows: first let , and . We can replace with , on which N is still well-defined and . Then define
Continuing inductively, we obtain the unique (!) filtration on satisfying (1) and (2).
By the Jacobson–Morozov theorem, the nilpotent operator N can be extended to an -triple with Cartan subalgebra generated by an element which is unique up to scaling. By the representation theory of -triples, there exists a decomposition
called the weight decomposition, with the property that for all . In particular, the decomposition splits the weight filtration of N
let us apply this to some geometric examples.
-
(i)Any cohomology class defines a nilpotent operator on by cup product. If is Kähler, then the Hard Lefschetz theorem implies that the weight filtration of on centered at 2n is12
-
(ii)Consider a Lagrangian fibration
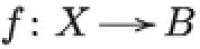 and let be the pull–back of an ample class . Up to renumbering, the weight filtration associated with the class on centered at n coincides with the perverse filtration, see Sect. 2.3
and let be the pull–back of an ample class . Up to renumbering, the weight filtration associated with the class on centered at n coincides with the perverse filtration, see Sect. 2.3
Indeed, the action of gives the morphisms
The isomorphism is called the perverse Hard Lefschetz theorem [13, Prop. 5.2.3]. By Proposition 2.2, this corresponds to the isomorphism .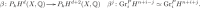
-
(iii)
Let
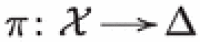 be a projective degeneration of hyperkähler manifolds over the unit disk which we assume to be semistable, i.e. the central fiber is reduced with simple normal crossings. For , let N denote the logarithmic monodromy operator on . The weight filtration of N centered at d on , denoted by , is the weight filtration of the limit mixed Hodge structure associated to , see [62, Thm. 11.40].
be a projective degeneration of hyperkähler manifolds over the unit disk which we assume to be semistable, i.e. the central fiber is reduced with simple normal crossings. For , let N denote the logarithmic monodromy operator on . The weight filtration of N centered at d on , denoted by , is the weight filtration of the limit mixed Hodge structure associated to , see [62, Thm. 11.40].
The degeneration 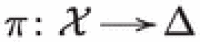 is called of type III if and on . In this case, the limit mixed Hodge structure is of Hodge–Tate type by [64, Thm. 3.8], and in particular . Then the even graded pieces of the weight filtration are used to define the Hodge numbers
is called of type III if and on . In this case, the limit mixed Hodge structure is of Hodge–Tate type by [64, Thm. 3.8], and in particular . Then the even graded pieces of the weight filtration are used to define the Hodge numbers
The Hodge numbers have a clear geometric description. The dual complex of , denoted by , is the CW complex whose k-cells are in correspondence with the irreducible components of the intersection of divisors . The Clemens–Schmid exact sequence then gives
| 3.1 |
see for instance [54, §3, Cor. 1 & 2].
In order to show P W, namely that the filtrations (ii) and (iii) can be identified, we need the notion of hyperkähler triples with their associated -action.
Hyperkähler Triples
A hyperkähler manifold is a Riemannian manifold (X, g) which is Kähler with respect to three complex structures I, J, and K, satisfying the standard quaternion relations . The corresponding hyperkähler triple is the triple of Kähler classes in given by
The set of all hyperkähler triples on X forms a Zariski-dense subset in
In particular, all algebraic relations that can be formulated for triples in and which hold for triples of the form hold in fact for all , see [66, Prop. 2.3].
The -Action
Recall the scaling operator
By the Jacobson–Morozov theorem, to any of Lefschetz type we can associate a -triple . Let . The -triples associated to x, y and z generate the Lie subalgebra , isomorphic to , with Cartan subalgebra
| 3.2 |
There is an associated weight decomposition
| 3.3 |
such that for all we have
The following -triples in
| 3.4 |
| 3.5 |
induce the same weight decomposition, since for any we have
Remark 3.2
The previous identities for hyperkähler triples are due to Verbitsky. The result for a general triple follows from the density of hyperkähler triples in , and the fact that the -representation associated to x, y and z have the same weights, since x, y, and z are all of Lefschetz type, see [66, §2.4].
P W
The main result of [30] is the following.
Theorem 3.3
(P = W) For any Lagrangian fibration 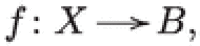 there exists a type III projective degeneration of hyperkähler manifolds
there exists a type III projective degeneration of hyperkähler manifolds 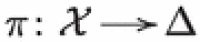 with deformation equivalent to X for all together with a multiplicative isomorphism such that
with deformation equivalent to X for all together with a multiplicative isomorphism such that
Proof
Let be the pullback of an ample class , and with . Since , we have . Up to replacing with for some , we can suppose that . Set
By scaling a nonzero vector perpendicular to y and z with respect to q, we obtain with
Soldatenkov showed that the nilpotent operator is the logarithmic monodromy N of a projective type III degeneration 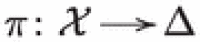 of compact hyperkähler manifolds deformation equivalent to X, see [64, Lem. 4.1, Thm. 4.6].13
of compact hyperkähler manifolds deformation equivalent to X, see [64, Lem. 4.1, Thm. 4.6].13
The weight decomposition for the -triple (3.4) splits the perverse filtration associated to f, since acts in cohomology via the cup product by . The weight decomposition for the -triple (3.5) splits the weight filtration of the limit mixed Hodge structure associated to , because . Hence, by Sect. 3.3, this implies P W.
P W also provides alternative proofs of Corollary 2.10 and Theorem 2.1.
Corollary 3.4
(Numerical P = W) .
Proof
By Theorem 3.3 we obtain . The equality is Corollary 2.10.
Alternatively, one can argue as follows. By [64, Thm. 3.8], the limit mixed Hodge structure associated to is of Hodge–Tate type, and so By the classical result [62, Cor. 11.25], we have We conclude that .
Corollary 3.5
At the boundary of the Hodge diamond of X, P W gives14
In the following, we provide conjectural conceptual explanations for these identities.
A Conjectural Explanation I
Assume that is Calabi–Yau. This can be always achieved via a MMP, at the cost of making mildly singular (precisely divisorial log terminal), see [18]. Under this assumption the homeomorphism class of is well-defined.
Then the SYZ conjecture predicts that carries a special Lagrangian fibration  with respect to a hyperkähler metric. By hyperkähler rotation [28, §3], f should become a holomorphic Lagrangian fibration
with respect to a hyperkähler metric. By hyperkähler rotation [28, §3], f should become a holomorphic Lagrangian fibration 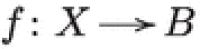 on a hyperkähler manifold X deformation equivalent to . It is conjectured that the base of a Lagrangian fibration on X is a projective space. So in brief, we should have the homeomorphisms
on a hyperkähler manifold X deformation equivalent to . It is conjectured that the base of a Lagrangian fibration on X is a projective space. So in brief, we should have the homeomorphisms
| 3.6 |
The latter equality is known to hold if , see Sect. 1.3, or conditional to the smoothness of the base [34]. The former equality is known for degenerations of Hilbert schemes or generalised Kummer varieties [8]. In both case, the most delicate problem is to assess the smoothness of or B. From this viewpoint, the identity
is a weak cohomological evidence for the conjecture (3.6).
A Conjectural Explanation II
We conjecture that the equality is the result of the identification of two Lagrangian tori up to isotopy.
Definition 3.6
Let x be a zero-dimensional stratum of . Choose local coordinates centered at x with . For fixed radii and , a profound torus is
Remark 3.7
The ambient-isotopy type of does not depend on the choice of the coordinates: is homotopic to , where is a neighbourhood of x in . More remarkably, if is Calabi–Yau, then the isotopy class of in is independent of x. This follows at once from Kollár’s notion of -link (see [45, Prop. 4.37] or [26, Lem. 3.10]), or equivalently because profound tori are fibers of the same smooth fibration, by adapting [17, Prop. 6.12.]
Conjecture 3.8
(Geometric P = W) For any Lagrangian fibration 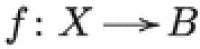 with general fiber T, there exists a projective minimal dlt type III degeneration of hyperkähler manifolds
with general fiber T, there exists a projective minimal dlt type III degeneration of hyperkähler manifolds 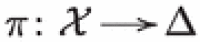 with deformation equivalent to X for all such that T is isotopic to a profound torus .
with deformation equivalent to X for all such that T is isotopic to a profound torus .
The conjecture is inspired by the geometric P W conjecture for character varieties, see the new version of [53] (to appear soon). Lemma 2.8 and (2.1) give
If has simple normal crossings (or dlt singularities modulo adapting [26, Thm. 3.12]), one obtains that
Therefore, Conjecture 3.8 would give a geometric explanation of P W at the highest weight
It is not clear what a geometric formulation of P W should be that could explain the cohomological statement in all weights.
Recent advance in the SYZ conjecture due to Li [48] suggests that profound tori can be made special Lagrangian, modulo a conjecture in non-archimedean geometry. A few months ago, the existence of a single special Lagrangian torus on was a complete mystery, see [23, §5, p.152]. Note also that Li’s result is compatible with the expectation in symplectic geometry [3, Conj. 7.3]. Profound tori appear as general fibers of the SYZ fibration that Li constructed on an open set which contains an arbitrary large portion of the mass of with respect to a Calabi–Yau metric, still modulo the non-archimedean conjecture. It is curious (but maybe not surprising) that also the previously quoted results [35] and [8] highly rely on non-archimedean techniques.
Multiplicativity of the Perverse Filtration
P W implies that the perverse filtration on is compatible with cup product.
Corollary 3.9
(Multiplicativity of the perverse filtration) Assume is a fibration. Then the perverse filtration on is multiplicative under cup product, i.e.
Proof
By P=W, it is sufficient to show that the weight filtration is multiplicative. To this end, endow the tensor product with the nilpotent endomorphism , and call the weight filtration of . Since the monodromy operator is an algebra homomorphism of , N is a derivation, i.e.
As a consequence, the construction of the weight filtration (see Sect. 3.1) gives
Together with [16, 1.6.9.(i)] which says that
we conclude that the weight filtration is multiplicative. Alternatively see [30, §5].
Remark 3.10
For an arbitrary morphism of projective varieties or Kähler manifolds, the perverse filtration is not always multiplicative [71, Exa. 1.5], but it is so for instance if it coincides with the Leray filtration, or if P W holds. Indeed, the Leray filtration and the weight filtration of the limit mixed Hodge structure are multiplicative.
It is natural to ask whether the multiplicativity holds at a sheaf theoretic level, for , or over an affine base. The motivation for this comes from the celebrated P W conjecture for twisted character varieties [12], which has been proved to be equivalent to the conjectural multiplicativity of the perverse filtration of the Hitchin map that is a proper holomorphic Lagrangian fibration over an affine base, see [14, Thm. 0.6]. From this viewpoint, it is remarkable that Shen and Yin give a proof of the multiplicativity in the compact case [66, Thm. A.1] which uses only the representation theory of -triples, with no reference to the weight filtration.
Nagai’s Conjecture for Type III Degenerations
Let 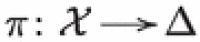 be a projective degeneration of hyperkähler manifolds with unipotent monodromy on . The index of nilpotence of is
be a projective degeneration of hyperkähler manifolds with unipotent monodromy on . The index of nilpotence of is
and by [22, Ch. IV]. It is known that determines the Hodge structure of by means of the LLV representation, see [65]. Nagai’s conjecture investigates to what extent determines . The ring structure of the subalgebra generated by implies the inequality , see [55, Lem. 2.4], but equality is expected.
Conjecture 3.11
(Nagai) for .
The previous inequalities imply Nagai’s conjecture for type III degenerations, i.e. . Remarkably, P W explains Nagai’s conjecture in terms of the level of the Hodge structure , and determines even for d odd. Recall that the level of a Hodge structure , denoted by , is the largest difference for which , or equivalently the length of the Hodge filtration on H.
Proposition 3.12
Let 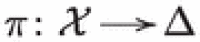 be a type III projective degeneration of hyperkähler manifolds with unipotent monodromy. Then
be a type III projective degeneration of hyperkähler manifolds with unipotent monodromy. Then
For the following identities hold :
-
(i)
-
(ii)
if .
Remark 3.13
The Statement (ii) is proved in [64, Prop. 3.15]. Here we present an alternative simple proof of (ii) which avoids the LLV representation.
Nagai’s conjecture is known to hold for degenerations of type I and III, i.e. for and 2, see [37, Thm. 6.5]. In order to establish Nagai’s conjecture in full, only the case of type II degenerations remains open, i.e. when . For type II there are partial results: for , see [37, Thm. 6.5], and , see [31, Thm. 1.2]. The full conjecture holds for all the known deformation types of hyperkähler manifolds by [19, Thm. 1.13]. Further comments on Nagai’s conjecture for type II can be found in [19, 27, 31].
Proof
Let be half of the length of the weight filtration of , i.e. By Definition 3.1, we have .
For any type III degeneration of Hodge structures of hyperkähler type with unipotent monodromy, we know by the proof of Theorem 3.3 that the logarithmic monodromy is of the form for some and x in with . Here, we use the assumption , see [64, §4.1]. Then, by Corollaries 2.9 and 3.4, we have . Hence, .
Finally, statements (i) and (ii) are equivalent to (i) , and (ii) if , which follows from (2.2).
Examples and Counterexamples
Example 4.1
In [57, Ex. 1.7.(iv)] Namikawa exhibits an example of a submanifold T of a hyperkähler manifold X which is isomorphic to a complex torus, but is not Lagrangian (actually it is symplectic). Let E, F be elliptic curves defined by the cubic equations f and g respectively, and let be the cubic fourfold given by the equation . The cyclic group acts on Y by
where is a primitive third root of unity. The induced action on the Fano variety of lines X is symplectic, i.e. for . Indeed, by [5] there is a G-equivariant isomorphism . Denoting by the canonical section of , is generated by the G-invariant residue , and so the action is symplectic. In particular, the fixed locus T of the G-action on X is a symplectic submanifold. One defines T as the set of lines which join two points on and respectively. Hence, . We conclude that T is a symplectic torus embedded in the hyperkähler manifold X.
Example 4.2
There exists a Lagrangian submanifold L of a hyperkähler manifold X with
Proof
Let 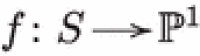 be an elliptic K3 surface with smooth fiber E. Define to be the locus of non-reduced length-two subschemes of S supported on E, which is isomorphic to the -bundle over E. Then, L is an irreducible component of the fiber of the Lagrangian fibration
be an elliptic K3 surface with smooth fiber E. Define to be the locus of non-reduced length-two subschemes of S supported on E, which is isomorphic to the -bundle over E. Then, L is an irreducible component of the fiber of the Lagrangian fibration 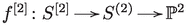 , thus L is Lagrangian. The exceptional divisor of the Hilbert–Chow morphism
, thus L is Lagrangian. The exceptional divisor of the Hilbert–Chow morphism 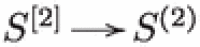 restricts to a multiple of the tautological line bundle on L. Therefore, the second cohomology group is generated by the restriction of and the pullback of an ample line bundle of .
restricts to a multiple of the tautological line bundle on L. Therefore, the second cohomology group is generated by the restriction of and the pullback of an ample line bundle of .
Example 4.3
There exists a Lagrangian submanifold L of a hyperkähler manifold X with
Proof
Let C be a smooth curve of genus two in an abelian surface A. Consider the moduli space of stable 1-dimensional sheaves on A supported on the curve class
and Euler characteristic . The fiber of the Albanese morphism 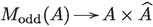 is a compact hyperkähler manifold X deformation equivalent to a generalised Kummer variety of dimension six. Taking Fitting supports defines a Lagrangian fibration
is a compact hyperkähler manifold X deformation equivalent to a generalised Kummer variety of dimension six. Taking Fitting supports defines a Lagrangian fibration
The fiber over the curve 2C contains the locus L of stable sheaves on A such that the composition 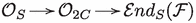 factors via the natural map
factors via the natural map 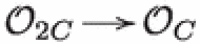 . As -module, is a rank-two vector bundle, and L can be identified with the moduli space of rank-two vector bundles on C of degree one, which is isomorphic to the intersection of two quadrics in , see [15, 59]. The cohomology is generated by so-called tautological classes, and is generated by their restrictions, see [49] and [58, Thm. 1]. Therefore, we have
. As -module, is a rank-two vector bundle, and L can be identified with the moduli space of rank-two vector bundles on C of degree one, which is isomorphic to the intersection of two quadrics in , see [15, 59]. The cohomology is generated by so-called tautological classes, and is generated by their restrictions, see [49] and [58, Thm. 1]. Therefore, we have
Acknowledgements
We wish to thank Paolo Cascini for bringing to our attention Kollár’s conjecture 1.12, Thorsten Beckmann for useful conversations and in particular for suggesting Example 4.1, Fabrizio Anella and Olivier Debarre for reading a first version of this note. The second author is supported by the Max Planck Institute for Mathematics.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Footnotes
Here and in (iii) and (iv), one expects isomorphisms of -algebras, but this seems not known.
Is there an a priori reason why this is the case for Lagrangian tori? It fails for general Lagrangian submanifolds; see Sect. 4.
The non-triviality of the scalar for follows from the fact that for any Kähler class .
The traditional proof goes as follows: First one shows that for any non-trivial class and any Kähler class on X one has . Indeed, otherwise the Hodge index theorem would imply and, therefore, , which contradicts . As a consequence, observe that for any two non-trivial classes there exists a linear combination with , which then implies , i.e. any two classes are linearly dependent.
By Lemma 1.8 below, B is a Fano manifold, which provides an alternative argument of the simply connectedness of B.
By evoking results due to Saito [63], it should be possible to avoid the projectivity assumption in [41].
Are the singularities of B actually factorial?
Alternatively, note that the trace map 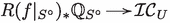 splits the natural morphism
splits the natural morphism 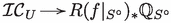 .
.
Again, the projectivity assumption can presumably be dropped by applying results of Saito.
A meromorphic map is almost holomorphic if there exists a Zariski-open subset such that 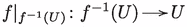 is holomorphic and proper.
is holomorphic and proper.
The classical definition of the perverse filtration for the constructible complex due to [4] or [13, Def. 4.2.1] coincides with the present one; see [13, Prop. 5.2.4.(39)].
The equality actually holds for any Kähler manifold, not necessary hyperkähler.
One can use the Lie algebra structure of the LLV algebra to compare the present description of with that of [64, Lem. 4.1], see [46, Lem. 3.9]. Mind that Soldatenkov’s existence result is not constructive: it relies on lattice theory and the geometry of the period domain, and does not produce an explicit type III degeneration.
The identity was first proved in [37, Thm. 7.13].
This review was prepared in the context of the seminar organized by the ERC Synergy Grant HyperK, Grant agreement ID 854361. The talk was delivered on June 4, 2021.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
D. Huybrechts, Email: huybrech@math.uni-bonn.de
M. Mauri, Email: mauri@mpim-bonn.mpg.de
References
- 1.Amerik E, Campana F. On families of Lagrangian tori on hyperkähler manifolds. J. Geom. Phys. 2013;71:53–57. [Google Scholar]
- 2.Amerik, E.: A remark on a question of Beauville about Lagrangian fibrations. Mosc. Math. J. 12(4), 701–704, 883 (2012)
- 3.Auroux D. Mirror symmetry and -duality in the complement of an anticanonical divisor. J. Gökova Geom. Topol. GGT. 2007;1:51–91. [Google Scholar]
- 4.Beilinson, A., Bernstein, J., Deligne, P., Gabber, O.: Faisceaux pervers. Astérisque, vol. 100, pp. 5–171. Société Mathématique de France, Paris (2018)
- 5.Beauville A, Donagi R. La variété des droites d’une hypersurface cubique de dimension . C. R. Acad. Sci. Paris Sér. I Math. 1985;301(14):703–706. [Google Scholar]
- 6.Beauville, A.: Holomorphic symplectic geometry: a problem list. In: Complex and Differential Geometry. Springer Proceedings in Mathematics, vol. 8, pp. 49–63. Springer, Heidelberg (2011)
- 7.Bogomolov, F., Kurnosov, N.: Lagrangian fibrations for IHS fourfolds (2018). arXiv:1810.11011
- 8.Brown M, Mazzon E. The essential skeleton of a product of degenerations. Compos. Math. 2019;155(7):1259–1300. [Google Scholar]
- 9.Bogomolov F. On the cohomology ring of a simple hyper-Kähler manifold (on the results of Verbitsky) Geom. Funct. Anal. 1996;6(4):612–618. [Google Scholar]
- 10.Brieskorn, E.: Rationale Singularitäten komplexer Flächen. Invent. Math. 4, 336–358 (1967/1968)
- 11.Campana F. Isotrivialité de certaines familles kählériennes de variétés non projectives. Math. Z. 2006;252(1):147–156. [Google Scholar]
- 12.de Cataldo M, Hausel T, Migliorini L. Topology of Hitchin systems and Hodge theory of character varieties: the case . Ann. Math. (2) 2012;175(3):1329–1407. [Google Scholar]
- 13.de Cataldo M, Migliorini L. The Hodge theory of algebraic maps. Ann. Sci. École Norm. Sup. (4) 2005;38(5):693–750. [Google Scholar]
- 14.de Cataldo, M., Maulik, D., Shen, J.: Hitchin fibrations, abelian surfaces, and the P=W conjecture. J. Am. Math. Soc. (2021)
- 15.de Cataldo M, Rapagnetta A, Saccà G. The Hodge numbers of O’Grady 10 via Ngô strings. J. Math. Pures Appl. 2021;9(156):125–178. [Google Scholar]
- 16.Deligne P. La conjecture de Weil. II. Inst. Hautes Études Sci. Publ. Math. 1980;52:137–252. [Google Scholar]
- 17.Evans JD, Mauri M. Constructing local models for Lagrangian torus fibrations. Ann. Henri Lebesgue. 2021;4:537–570. [Google Scholar]
- 18.Fujino O. Semi-stable minimal model program for varieties with trivial canonical divisor. Proc. Jpn. Acad. Ser. A Math. Sci. 2011;87(3):25–30. [Google Scholar]
- 19.Green, M., Kim, Y.-J., Laza, R., Robles, C.: The LLV decomposition of hyper-Kähler cohomology. Math. Ann. (2021)
- 20.Greb D, Lehn C, Rollenske S. Lagrangian fibrations on hyperkähler manifolds—on a question of Beauville. Ann. Sci. Éc. Norm. Supér. (4) 2013;46(3):375–403. [Google Scholar]
- 21.Greb D, Lehn C, Rollenske S. Lagrangian fibrations on hyper-Kähler four-folds. Izv. Ross. Akad. Nauk Ser. Mat. 2014;78(1):25–36. [Google Scholar]
- 22.Griffiths P. Topics in Algebraic and Analytic Geometry. Princeton: Princeton University Press; 2015. [Google Scholar]
- 23.Gross, M.: Mirror symmetry and the Strominger–Yau–Zaslow conjecture. In: Current developments in mathematics 2012, pp. 133–191. International Press, Somerville (2013)
- 24.Göttsche L, Soergel W. Perverse sheaves and the cohomology of Hilbert schemes of smooth algebraic surfaces. Math. Ann. 1993;296(2):235–245. [Google Scholar]
- 25.Hartshorne R. Algebraic Geometry. New York: Springer; 1977. [Google Scholar]
- 26.Harder, A.: Torus fibers and the weight filtration (2019). arXiv:1908.05110
- 27.Harder, A.: Mixed Hodge structures in log symplectic geometry (2020). arXiv:2005.11367
- 28.Hitchin, N.: The moduli space of complex Lagrangian submanifolds. In: Surveys in Differential Geometry. Surveys in Differential Geometry, vol. 7, pp. 327–345. International Press, Somerville (2000)
- 29.Hirzebruch F, Kodaira K. On the complex projective spaces. J. Math. Pures Appl. 1957;9(36):201–216. [Google Scholar]
- 30.Harder, A., Li, Z., Shen, J., Yin, Q.: P = W for Lagrangian fibrations and degenerations of hyper-Kähler manifolds. Forum Math. Sigma 9(e50) (2021)
- 31.Huybrechts, D., Mauri, M.: On type II degenerations of hyperkähler manifolds. Math. Res. Lett. (2022)
- 32.Huybrechts, D.: Compact hyperkähler manifolds. In: Calabi–Yau Manifolds and Related Geometries (Nordfjordeid, 2001). Universitext, pp. 161–225. Springer, Berlin (2003)
- 33.Hwang J-M, Weiss RM. Webs of Lagrangian tori in projective symplectic manifolds. Invent. Math. 2013;192(1):83–109. [Google Scholar]
- 34.Hwang J-M. Base manifolds for fibrations of projective irreducible symplectic manifolds. Invent. Math. 2008;174(3):625–644. [Google Scholar]
- 35.Huybrechts, D., Xu, C.: Lagrangian fibrations of hyperkähler fourfolds. J. Inst. Math. Jussieu 1–12 (2020)
- 36.Kawamata Y. Minimal models and the Kodaira dimension of algebraic fiber spaces. J. Reine Angew. Math. 1985;363:1–46. [Google Scholar]
- 37.Kollár J, Laza R, Saccà G, Voisin C. Remarks on degenerations of hyper-Kähler manifolds. Ann. Inst. Fourier (Grenoble) 2018;68(7):2837–2882. [Google Scholar]
- 38.Kollár J, Mori S. Birational Geometry of Algebraic Varieties. Cambridge: Cambridge University Press; 1998. [Google Scholar]
- 39.Kobayashi S, Ochiai T. Characterizations of complex projective spaces and hyperquadrics. J. Math. Kyoto Univ. 1973;13:31–47. [Google Scholar]
- 40.Kollár J. Higher direct images of dualizing sheaves. I. Ann. Math. (2) 1986;123(1):11–42. [Google Scholar]
- 41.Kollár J. Higher direct images of dualizing sheaves. II. Ann. Math. (2) 1986;124(1):171–202. [Google Scholar]
- 42.Kollár J. Shafarevich Maps and Automorphic Forms. Princeton: Princeton University Press; 1995. [Google Scholar]
- 43.Kollár, J.: Kodaira’s canonical bundle formula and adjunction. In: Flips for 3-Folds and 4-Folds. Oxford Lecture Series in Mathematics and its Applications, vol. 35, pp. 134–162. Oxford University Press, Oxford (2007)
- 44.Kollár J. Lectures on Resolution of Singularities. Princeton: Princeton University Press; 2007. [Google Scholar]
- 45.Kollár J. Singularities of the Minimal Model Program. Cambridge: Cambridge University Press; 2013. [Google Scholar]
- 46.Kurnosov N, Soldatenkov A, Verbitsky M. Kuga–Satake construction and cohomology of hyperkähler manifolds. Adv. Math. 2019;351:275–295. [Google Scholar]
- 47.Li P. Some remarks on the uniqueness of the complex projective spaces. Bull. Lond. Math. Soc. 2016;48(2):379–385. [Google Scholar]
- 48.Li, Y.: Metric SYZ conjecture and non-Archimedean geometry (2020). arXiv:2007.01384
- 49.Markman E. Generators of the cohomology ring of moduli spaces of sheaves on symplectic surfaces. J. Reine Angew. Math. 2002;544:61–82. [Google Scholar]
- 50.Matsushita D. On fibre space structures of a projective irreducible symplectic manifold. Topology. 1999;38(1):79–83. [Google Scholar]
- 51.Matsushita D. Higher direct images of dualizing sheaves of Lagrangian fibrations. Am. J. Math. 2005;127(2):243–259. [Google Scholar]
- 52.Mauri, M.: Intersection cohomology of rank two character varieties of surface groups. J. Inst. Math. Jussieu 1–40 (2021)
- 53.Mauri, M., Mazzon, E., Stevenson, M.: On the geometric P = W conjecture (2018). arXiv:1810.11837
- 54.Morrison, D.: The Clemens–Schmid exact sequence and applications. In: Topics in Transcendental Algebraic Geometry (Princeton, N.J., 1981/1982). Annals of Mathematics Studies, vol. 106, pp. 101–119. Princeton University Press, Princeton (1984)
- 55.Nagai Y. On monodromies of a degeneration of irreducible symplectic Kähler manifolds. Math. Z. 2008;258(2):407–426. [Google Scholar]
- 56.Nakayama N. The singularity of the canonical model of compact Kähler manifolds. Math. Ann. 1988;280(3):509–512. [Google Scholar]
- 57.Namikawa Y. Deformation theory of singular symplectic -folds. Math. Ann. 2001;319(3):597–623. [Google Scholar]
- 58.Newstead P. Characteristic classes of stable bundles of rank over an algebraic curve. Trans. Am. Math. Soc. 1972;169:337–345. [Google Scholar]
- 59.Narasimhan MS, Ramanan S. Moduli of vector bundles on a compact Riemann surface. Ann. Math. 1969;2(89):14–51. [Google Scholar]
- 60.Oguiso K. Picard number of the generic fiber of an abelian fibered hyperkähler manifold. Math. Ann. 2009;344(4):929–937. [Google Scholar]
- 61.Ou W. Lagrangian fibrations on symplectic fourfolds. J. Reine Angew. Math. 2019;746:117–147. [Google Scholar]
- 62.Peters C, Steenbrink J. Mixed Hodge Structures. Berlin: Springer; 2008. [Google Scholar]
- 63.Saito M. Decomposition theorem for proper Kähler morphisms. Tohoku Math. J. (2) 1990;42(2):127–147. [Google Scholar]
- 64.Soldatenkov A. Limit mixed Hodge structures of hyperkähler manifolds. Mosc. Math. J. 2020;20(2):423–436. [Google Scholar]
- 65.Soldatenkov A. On the Hodge structure of compact hyperkähler manifolds. Math. Res. Lett. 2021;28(2):623–635. [Google Scholar]
- 66.Shen J, Yin Q. Topology of Lagrangian fibrations and Hodge theory of hyper-Kähler manifolds. Duke. Math. J. 2022;171(1):209–241. [Google Scholar]
- 67.Varouchas J. Stabilité de la classe des variétés kählériennes par certains morphismes propres. Invent. Math. 1984;77(1):117–127. [Google Scholar]
- 68.Verbitsky M. Cohomology of compact hyperkähler manifolds and its applications. Geom. Funct. Anal. GAFA. 1996;6(4):601–611. [Google Scholar]
- 69.Voisin, C.: Sur la stabilité des sous-variétés lagrangiennes des variétés symplectiques holomorphes. In: Complex Projective Geometry (Trieste, 1989/Bergen, 1989). London Mathematical Society Lecture Note Series, vol. 179, pp. 294–303. Cambridge University Press, Cambridge (1992)
- 70.Voisin C. Hodge Theory and Complex Algebraic Geometry. I. Cambridge: Cambridge University Press; 2007. [Google Scholar]
- 71.Zhang Z. Multiplicativity of perverse filtration for Hilbert schemes of fibered surfaces. Adv. Math. 2017;312:636–679. [Google Scholar]


