Abstract
In the last two decades dengue cases increased significantly throughout the world, giving place to more frequent outbreaks in Latin America. In the non-endemic city of San Ramón de la Nueva Orán, located in Northwest Argentina, large dengue outbreaks alternate with several years of smaller ones. This pattern, as well as the understanding of the underlying mechanisms, could be essential to design proper strategies to reduce epidemic size. We develop a stochastic model that includes climate variables, social structure, and mobility between a non-endemic city and an endemic area. Climatic variables were input of a mosquito population ecological model, which in turn was coupled to a meta-population, spatially explicit, epidemiological model. Human mobility was included into the model given the high border crossing to the northern country of Bolivia, where dengue transmission is sustained during the whole year. We tested different hypotheses regarding people mobility as well as climate variability by fitting numerical simulations to weekly clinical data reported from 2009 to 2016. After assessing the number of imported cases that triggered the observed outbreaks, our model allows to explain the observed epidemic pattern. We found that the number of vectors per host and the effective reproductive number are proxies for large epidemics. Both proxies are related with climate variability such as rainfall and temperature, opening the possibility to test these meteorological variables for forecast purposes.
Keywords: Mathematical modelling, Dengue, Outbreak, Mosquitoes population
1. Introduction
Several vector-borne diseases affect tropical, subtropical and also temperate regions worldwide (Robert et al., 2019). Dengue in particular, causes 390 million infections in the world every year, with nearly 3.9 billion people at risk of infection (World Health Organization, 2020). Reported dengue cases increased significantly in some Latin American countries in the last 20 years (World Health Organization, 2020). Four different antigenically related serotypes, i.e. DENV-1, DENV-2, DENV-3 and DENV-4, produce a large variety of symptoms, from mild to severe and rarely fatal ones. Although each virus strain provides partial temporal immunity for that specific serotype, there is no cross-immunity (Iboi & Gumel, 2018). Antibodies generated by previous infections cross react with infections of a different strain, sometimes increasing symptoms severity (World Health Organization, 2020).
Dengue virus transmission occurs in a mosquito-human cycle. The vectors that transmit dengue disease in the Latin American region are Aedes albopictus and Aedes aegypti, being the last one more prevalent throughout the region (Kraemer et al., 2015a; Lopez-Gatell et al., 2015, pp. 203–224; Torres & Castro, 2007). Aedes aegypti has domestic habits and mainly breeds on artificial water containers (Edman et al., 1998). Therefore climate variability might not be a good candidate to drive dengue cases variability. However some studies show that vector survival and virus development are constrained, specially by rainfall and temperature (Romeo-Aznar et al., 2018), and others are successful in predicting dengue incidence with climate-driven models (Vásquez et al., 2019). Some studies for South East Asia have found a very limited association between synoptic variables and the reported number of dengue cases (Chen & Hsieh, 2012). However in the Central Region of Malaysia, the association between the disease and climate lead to develop a model capable to constitute an early warning system for dengue outbreaks (Yip et al., 2022). To which extent the variability of some climatic variables can anticipate the timing and relative intensity of dengue outbreaks in Northwest Argentina is still unknown and is one of the objectives of this study.
Dengue is endemic in many countries, i.e. transmission is present during the whole year. By contrast, in non-endemic regions, dengue outbreaks occur during a given season. A typical case with both regions is Taiwan, where the south is endemic while the north of the island is epidemic and seasonal (Valdez et al., 2018). In subtropical southern Taiwan was found that temperature was a relevant variable for the dynamic modeling of the vector–host interaction (Chen & Hsieh, 2012). In Latin America both endemic and epidemic/seasonal dengue dynamics are observed. For the particular case of Northwest Argentina, outbreaks occur during the hot rainy season (November–March) (Avilés et al., 1999; Rotela et al., 2007).
During most of the years there are just a few dengue cases but large epidemics occurred in 2004, 2009 and 2016 with thousands of cases and several deaths, with a significant economic impact (Tarragona et al., 2012). Therefore, forecasting the risk of a large epidemics in these non-endemic regions may help to take preventive actions to reduce negative impacts of the disease.
Recent studies indicate that some dengue vaccines applied to dengue-naive populations may induce increased risk of severe disease (Iboi & Gumel, 2018). Given that in Northwest Argentina there is only one dominant circulating serotype by season (being DENV-1 the predominant one in Orán during 2009–2010 and 2015–2016 outbreaks (Ministerio de Salud de Argentina, 2009; Ministerio de Salud de Argentina, 2016)) vaccines are still not applied and therefore the study of the relationship between climate and dengue becomes even more relevant to anticipate disease outbreaks.
Previous works developed different models (Kraemer et al., 2015b; Musa et al., 2020; Pinho et al., 2010; Reiner et al., 2014; Sardar et al., 2015) to describe the dynamics of dengue transmission. The reproductive number R0 and its evolution R(t) in time are relevant indicators of epidemics and have been assessed to help in the design of disease control strategies (Musa et al., 2019; Pinho et al., 2010). Those inspiring works lead us to couple a stochastic simulation model for the Aedes aegypti population dynamics (Valdez et al., 2018) to an epidemiological model, to explore the impact of imported cases flux and climate variability on dengue disease dynamics. We show how the interaction of all these factors influence the variability of dengue cases recorded between 2009 and 2016 for a non-endemic city of Northwest Argentina.
2. Materials and methods
We will take as a case study the city of San Ramón de la Nueva Orán (Oran from now on), although the model is applicable to any non-endemic city. This city has an extension of 3.75 km × 5 km, a population of 75697 people (17633 houses), and is located in Northwest Argentina (23°07′45.8”S, 64°19′16.9”W, see Fig. 1). It is 50 km south of the Bolivian-Argentinian border, where is connected with Bermejo city (Bolivia) through a bridge that crosses Bermejo river. Therefore social and business activities across the border are very intense.
Fig. 1.
Geographical location of the city of Oran. From left to right: map of South America, the zoomed region shows the Argentina-Bolivia border, sketch of the city of Oran. The map was done by the authors under the common creative license.
In 2010, a population census was conducted in Argentina (Argentine Institute of Statistics and Censuses (INDEC), 2010). For census purposes the city was partitioned in polygons or census sections, each of which will be considered as a patch for our meta-population model. From the census data we obtained population size and number of houses for each patch (Fig. 2). The city of Oran contains a total of sixty urban sections and two rural sections. Surrounding rural areas, including the two rural sections, are not considered in our model.
Fig. 2.
Distribution of populations and households in the city of Oran. Jenks categorization for the population (left) and households (right) of the city of Oran. In this work we do not consider the two largest rural ratios (rural areas) (Argentine Institute of Statistics and Censuses (INDEC), 2010).
Oran has a tropical climate; with dry, mild winters and hot summers with high rainfall (see Section S4 in Supplementary Material). As a consequence, the population of Aedes aegypti, the main dengue transmission vector in the region, shows marked seasonal variations (Estallo et al., 2011). In fact, the appearance of new cases of dengue is related in part with an increase in the vector population.
We developed a stochastic meta-population model for disease transmission and mosquito population dynamics. For each patch in Oran, we considered its human and vector population size, possible imported cases that arrive, the number of households, as well as an estimated number of mosquito breeding sites. Imported cases were recorded by the National Ministry of Health of Argentina (see Data Statement).
Given that Aedes mosquitoes usually breed in domestic containers, we assumed as a modeling hypotheses, that breeding sites were proportional to human population size that was estimated as the number of houses in each patch. Vector population size, as well as number of mosquitoes and breeding sites, were estimated by performing computer simulations with the mathematical model described in the section below (see “Ecological model for Aedes aegypti”).
Daily time series of relative humidity (RH), temperature (T) and precipitation for the period 2009–2017, were provided by the Argentinian Meteorological Service. Daily averages of those climatic variables were used as input for the ecological model for Aedes aegypti population, although qualitatively similar results were obtained when using their maximum or minimum values.
For the simulations we used the Poisson approximation (Aparicio & Solari, 2001) with a fixed time step Δt. For each event considered in the model we computed the corresponding transition rate, i.e. the probability of occurrence per unit of time, generating a pseudo random number following a Poisson distribution with parameter equal to the transition rate, times Δt (see S7 in Supplementary Material).
Demographic variables do not change in the studied time period, therefore we considered for each patch in the city a constant human host population of size H divided in four epidemiological classes: susceptible (HS), exposed (HE), infectious (HI) and recovered (HR). As mosquitoes are infected for life we considered only susceptible (VS), exposed (VE) and infectious (VI) vector populations. A scheme of the epidemic cycle is depicted in Fig. 3.
Fig. 3.
Scheme of the epidemiological model.HS, HE, HI, HR are susceptible, exposed, infected and recovered host populations respectively. Similarly are susceptible, exposed and infected vector populations respectively. Sub-index i refers to different mosquito stages in the exposed class. Processes are: Xj → VS: Recruitment of new susceptible vectors by oviposition (Xj are different stages of Aedes from the ecological model, VS are female Aedes mosquitoes), : Vector infection while biting, and VE → VI: Transition between different infected mosquito stages, HS → HE: Infection of a susceptible host by infected vector biting, HE → HI: Host transition from exposed to infectious (Infectious hosts can be increased by externally infected hosts, which come from the imported case model.), HI → HR: Recovery of an infected host.
The complete model implemented to perform the computer simulations consists in a compartmental model (see Fig. 3) in combination with an ecological model for the mosquitoes population and an imported cases model, together with the vector-host model. These models are applied on a meta-population structure that emulates a no-endemic city. For each patch, information such as the number of hosts and households is included, which allows to reproduce the real city heterogeneities. In the following sections we briefly describe those model components.
2.1. Epidemiological model
Virus transmission was modelled using frequency dependent rates. The susceptible mosquitoes get infected while in contact with an infected host. Thus the probability of vector infection per unit of time (GV(t; T)) at a given temperature T, is given by:
| (1) |
where b is the mosquito biting rate, θ(T) is the effect of temperature on the biting rate and pV is the probability of infection per bite for vectors. A similar probability could be written for human infection:
| (2) |
with pH the infection probability per bite for hosts.
To compute the latency period of vectors before becoming infectious we follow the model proposed in (Romeo-Aznar et al., 2015) which considers a series of steps, exponentially distributed in time, performed in sequence to complete an infectious process. The convolution of these steps leads to a gamma distribution for the latency period (see Supplementary Material S3.2).
For humans, the progression from latency to the infectious state takes place at a constant rate σH, while recovery rate γ is also constant. In other words, we assume that latency and infectious periods are exponentially distributed with mean values 1/σH and 1/γ respectively.
Dispersion of Aedes aegypti is estimated in a few hundred meters (Sowilem et al., 2013), while the size of the patch is of the order of 800m, therefore we only considered mosquito dispersion to neighbouring patches using a dispersion model (Gutierrez & Aparicio, 2015) with low diffusion values (DV < 0.1 and DV = 0). Simulations performed with both diffusion values show no significant variations. Therefore to save computational costs we choose DV = 0, avoiding the need to make the balance of agents (vectors and hosts) in each time step. The main source for disease spreading between patches is human mobility. For the spatial dynamics of the human population we will consider that individuals may visit any randomly chosen patch. In this way, it is possible the transmission of the virus from a visiting infected host to susceptible vectors in another patch, or the transmission to a susceptible host visiting a patch with infected vectors. To model this dynamics we included a term considering the possibility of disease transmission between vector and host of neighbouring patches or for a randomly chosen pair of patches at each time step. Under these assumptions the probability of vector infection per unit of time in patch j is:
| (3) |
where and PH are the sum of infected hosts and the total number of hosts in the patch, in its nearest neighbours, and in a randomly chosen patch in the time step. The number of new infected vectors was simulated by drawing a random number, Poisson distributed, with mean .
In an analogous way, the number of new infected hosts in a time step was simulated using the probability of human infection per unit of time given by:
| (4) |
where is the sum of infected vectors in patch j, in its nearest neighbours, and in a patch randomly chosen at each time step.
2.2. Model for imported cases
In our sub-tropical non-endemic region, dengue transmission is interrupted during the coolest dry season. Therefore, assuming a negligible vertical transmission for Aedes aegypti, new outbreaks mostly start by the influx of infected people. These imported cases, i.e. individuals who contracted the virus in endemic areas, can be people from Argentina returning from holidays in Bolivia, or people doing temporary travel to Argentina for commercial or working activities.
The flux of imported dengue cases is modelled as:
| (5) |
where FPS(t) is the number of people from the non-endemic area who are in contact with people from the endemic area, is the prevalence of infectiousness in the endemic area and pi is the rate of new imported cases per host. From Eq. (5) we constructed the time series of imported cases δI(t), sampling random numbers from a Poisson distribution with parameter λI(t)Δt. We tested the model for several FPS(t) representing the different imported cases scenarios considered.
Each imported case was assigned to a randomly chosen patch. See S6 of the Supplementary Material for more details.
2.3. Ecological model for Aedes aegypti
The mosquito population dynamic model (Fig. 4) is inspired on the abundance model (Valdez et al., 2018). Local weather conditions as temperature (T), precipitation level (R) and relative humidity (RH) strongly affect mosquito activity, development, and egg hatching.
Fig. 4.
Scheme of the ecological model for vector population. Circles represent the different stages of Aedes aegypti maturation: dried egg (ED), wet eggs (EW), larvae (L), pupae (P), young mosquitoes (M) and adult female mosquitoes (V). Solid arrows indicate those processes that occur at a constant rate, while the dotted arrow indicates a fixed period process that triggers depending on the rain. Processes are: V → ED: Eggs deposition, ED → EW: Eggs wetting, EW → L: Eggs hatching, L → P: Larvae pupate, P → M: Pupae maturation, M → V: Mosquito maturation. All arrows pointing out represent mortality processes.
We considered five stages for the mosquito population: eggs, larvae, pupae, pre-adults (adult mosquitoes with non fully developed wings) and adults. Eggs may be in two states, dry and wet, with population sizes ED and EW respectively. According to our model the larval capacity of each patch depends on the number of households, and on the climatic conditions.
Recruitment rate of new adult susceptible mosquitoes, Λ(T, R, RH), depends on temperature (T), rainfall (R) and relative humidity (RH) and it is obtained from an ecological model for the mosquito population dynamics described in S2 of the Supplementary Material. Mosquito mortality, μV(T), is temperature dependent and we assumed that it does not depend on the mosquito age. This is a reasonable assumption given that the consideration of mosquito age classes, would significantly increase model complexity and computational cost without need, because mosquito lifetime is only limited to the summer season.
The complete model, that integrates all the processes detailed in the previous sections, was implemented and its outcome together with field data are presented in the following section.
3. Results
Dengue re-emerged in Argentina in 1997. In the city of Oran there were large epidemics beginning in 2009 and 2016, with small outbreaks in between, as shown by the time series of laboratory confirmed dengue cases (Fig. 5).
Fig. 5.
Dengue cases in the city of Oran. Dengue monthly cases from December 2008 to December 2016. Positive cases are those confirmed by laboratory (viral confirmation and serotype identification, positive screening test). Epidemic outbreaks do not occur during the dry months (winter). Epidemics were mostly of DENV-1 in 2009 and 2016 (Ministerio de Salud de Argentina, 2009; Ministerio de Salud de Argentina, 2016).
Each year, the first dengue cases are imported cases, mostly due to infection of city residents who travelled to endemic areas of Bolivia, as reported for example in (Gil et al., 2016). Cases detected by the Argentinian Ministry of Health are classified as imported or locally transmitted (see Data Statement).
Usually, single-strain outbreaks are observed and, only in a few occasions, more than one strain circulates, being only one of them responsible of more than 90% of the reported cases. During 2008–2009 and 2015–2016 outbreaks the main circulating serotype was DENV-1, being also the main serotype circulating in the southern region of Bolivia, specially in Santa Cruz de la Sierra and Tarija cities, from where most of the imported cases come from (Ministerio de Salud de Argentina, 2009; Ministerio de Salud de Argentina, 2016). Therefore, computer simulations of the epidemiological model developed in the present work were performed considering only one virus strain.
In the following sections we present the results obtained from the combination of data and computer simulations with the complete model described in the previous section.
3.1. Meteorological variability and dengue dynamics
We simulated the evolution of the vector population with the ecological model for mosquito population dynamics, using meteorological time series as model input. The human population in each patch was estimated from census data. After computing the vector-host ratio for each patch, we computed its average over all the simulations for each of the patches. All the obtained values were summed up for each time step to obtain the V(t)/H time series. Our model predicts two significantly larger values for the vector-host ratio V/H for years 2009 and 2016 (Fig. 6).
Fig. 6.
V/H Factor. Representative simulation of the average vector-host ratio (V(t)/H) obtained with 100 simulations, with its standard error, summing up all the patches in Oran city.
Those years were the ones with the largest dengue epidemics (Fig. 5). Therefore the average vector-host ratio could be an indicator of a high probability of epidemics in these particular years.
Given that the vector population dynamics obtained from the ecological model mainly depends on meteorological variability, the evolution of the number of vectors per host (V(t)/H) shows little variation between different simulations. Mosquito population is different among patches as it depends on the number of houses in each patch. However during simulations, the disease spread produced by infected mosquitoes between patches is negligible compared with the long range movement of hosts. Additionally, mosquito population inside each patch did not change significantly, due to low mosquito dispersal between patches given that patch area is larger than the lifetime dispersal area of Aedes aegypti (Sowilem et al., 2013). Therefore, we can conclude that meteorological factors constitute the main source of dengue cases variability.
3.2. Basic and effective reproduction numbers
To model the dynamics of the mosquito population we considered k gamma distributed latency periods. Neglecting the spatial effects (diffusion from and to other regions), the basic reproduction number (R0) of our model is:
| (6) |
Where is the fraction of mosquitoes that survive to the different k latency stages. The basic reproduction number is proportional to the number of vector per human, V/H. Details of the derivation of Eq. (6) can be found in the Supplementary Material.
It is important to remark that we are interested in reproducing the observed pattern, with large epidemics and small outbreaks in between, and not the number of reported cases, because in many cases only a fraction of the suspected cases are sent for laboratory confirmation.
As we are interested in recurrent outbreaks dynamics, a more useful measure of epidemic probability is the effective reproduction number which takes into account that only a fraction of the host population is susceptible. Without considering spatial effects the effective reproduction number is:
| (7) |
The extra factor accounts for the amount of susceptible humans available in the system. As vector population is constantly renewing itself, for practical purposes we considered a constant proportion of susceptible mosquito population in (Eq. (7)).
For the maturation rates see S3.3. In all simulations we estimate a HS(0) ≈ 0.75H for the city of Oran, each patch has initially 75% population susceptible.
In this case we used the full model (see Eq. S1) to obtain estimations of the human susceptible population HS. We computed the moving average of expression in Eq. (7) using a time window of four days to smooth the variability introduced by considering four infected mosquito latent stages. The pattern obtained for (Fig. 7) is similar to the one of the fraction V/H (Fig. 6), with a large peak in 2016 besides the large peak of 2010. This is an interesting result despite the fact that a constant human population without recruitment of susceptibles is considered, and therefore the proportion of susceptible hosts necessarily decreases with successive outbreaks. Thus, due to meteorological variability is possible to obtain an epidemic after smaller outbreaks. We can conclude that the effective reproduction number (Eq. (7)) could be another indicator of dengue epidemics.
Fig. 7.
Basic effective reproductive number. Representative graph of 100 simulation's moving average of period four days for the effective reproductive number.
3.3. Influence of imported cases
For Oran, the majority of imported cases comes from the nearby endemic area of Bolivia, as there is a fluid movement of people across the border.
To model the influx of imported cases from Bolivia we used data of dengue incidence in Bolivia (Pan American Health Organization/World Health Organization, 2019) (see S5 in Supplementary Material) and estimations of people entering Salta from Bolivia (see S6 in Supplementary Material).
The influx of imported cases is a necessary source of new cases, as the disease cannot emerge every season in a non-endemic region without that input. Therefore as a first approach we assumed a number of imported cases proportional to the number of cases in Bolivia (IB(t) in Eq. (5)). We proposed two different functional forms for the number of people entering from the endemic country (FPS(t) in Eq. (5)), i.e. a constant influx during the whole year and a seasonal influx of imported cases. Averaged simulations do not reproduce the clinical cases time series. In other words, simulations assuming a fixed number of imported cases proportional to the number of cases in Bolivia, do not reproduce the observed time series, independently of how those imported cases are distributed throughout the year (See S6.1, Figs. S8 and S9 in Supplementary Material).
A more successful approach consisted in not imposing the functional shape for the flux of imported cases but instead in fitting λI(t) (Eq. (5)) for every year, to reproduce the time series of observed cases in Oran. This way, the number of imported cases emerges from the dataset and it is not necessarily proportional to the number of cases in Bolivia, which might be a reasonable assumption as we will discuss later.
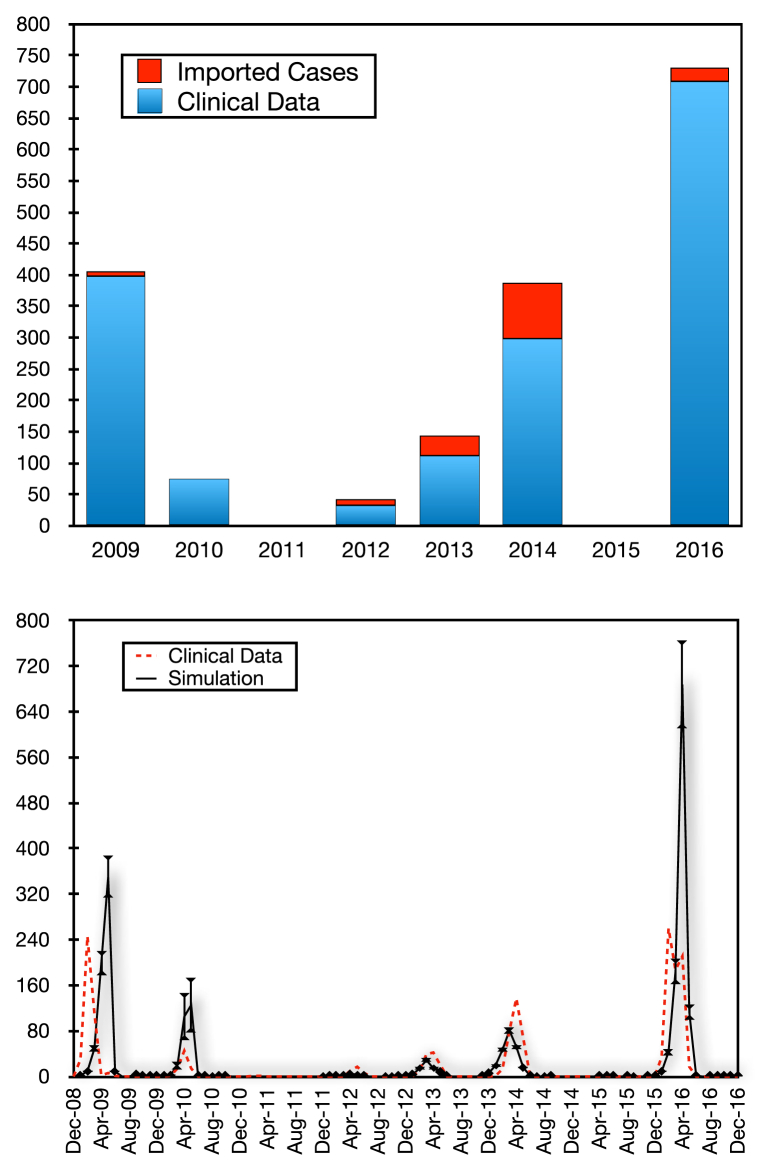
To construct the δI(t) time series, imported cases were randomly distributed evenly over the first four months of each year that correspond to the rainy period, fitting on average the observations (as explained in previous sections). The procedure is repeated for each iteration. A new time series δI(t) is constructed, that correlates with the reported cases for each year. Using the parameters of Table 1, we compare simulations and clinical data (see Fig. 8A), assessing the values and the corresponding error of imported cases for each epidemic year (see Fig. 8B).
Table 1.
Estimated values for the epidemiological model.
| Parameter | Value | Reference |
|---|---|---|
| βday | 2.39 (1.9–2.4) [egg day−1 ] | (Grech et al., 2010) and S3.1.1 |
| μDry | 120−1 [day−1 ] | Valdez et al. (2018) |
| μWet | 90−1 [day−1 ] | Valdez et al. (2018) |
| Rthres | 10.5 (7.5–12.5) [mm] | Valdez et al. (2018) |
| Hmax | 24 [mm] | Valdez et al. (2018) |
| kI | 3.9 × 10−5(3.3 × 10−6, 6.6 × 10−5) [mm oC2] | Valdez et al. (2018) |
| Kmax | 120 (70–220) | (Estallo et al., 2011; Valdez et al., 2018) |
| μV(T) | 10−1η(T) [day−1] | S3.4 |
| μM | 0.5 (0.25–0.5) [day−1] | |
| mM | 0.5 (0.25–1) [day−1] | |
| σV(T) | kζ(T) [day−1] | S3.2 |
| k | 4 (3–7) | S3.2 |
| DV | 0.0 (0–0.1) | |
| b | 0.30 [day−1 ] | Pandey et al. (2013) |
| pV | 0.75 | Wearing and Rohani (2006) |
| pH | 0.75 | Wearing and Rohani (2006) |
| σH | 4−1 [day−1 ] | Wearing and Rohani (2006) |
| γ | 7−1 [day−1 ] | Wearing and Rohani (2006) |
Fig. 8.
Top: bottom bars represent confirmed cases in Oran. Top bars show the number of imported cases from 2009 to 2016 after fitting to data in the bottom panel. The percentages of imported cases relative to the total number of cases resulted: 1.35%, 50.00%, 100%, 36.36%, 29.73%, 30.20%, 100.00% and 1.41%. Bottom: comparison between observed and simulated dengue incidence using the fitted values for imported cases. The series is an average of 100 simulations and the bars correspond to the standard error.
According to reports given by Argentina's epidemiological surveillance bulletin (Ministerio de Salud de Argentina, 2009; Ministerio de Salud de Argentina, 2016), imported dengue cases reported for 2016 represented no more than 10% of the total cases in the province of Salta. Most dengue fever cases in that province occur in the city of Oran, since Tartagal, the other comparable city of the region, has dengue prevention programmes ongoing (Mundo Sano Foundation, 2017). This percentage of imported cases reported in 2016, is in agreement with our estimation for that year (1.41% as shown in Fig. 8).
We can therefore conclude that the estimated number of imported cases per year trigger the corresponding outbreak but does not determine its size. In other words, years with large epidemics might be triggered by a small number of imported cases. Favorable meteorological conditions for the increase of vector population are an essential determinant for large epidemic size.
3.4. Role of stochasticity and spatiality
Deterministic models always produce a large initial epidemic followed by substantially smaller outbreaks (Gutierrez, 2018). Therefore, stochasticity is essential to reproduce the pattern of observed outbreaks, i.e. two epidemics and smaller outbreaks in between (see Fig. 8). In other words, because of the stochastic character of the system small outbreaks are common, and therefore the human susceptible population is almost not reduced, leaving enough susceptible individuals for future large outbreaks; something impossible to observe with deterministic models. However stochasticity alone is not enough.
Spatiality provides a small and clustered number of vector-human contacts which is also a critical factor to reduce the size of small outbreaks. Upon a mosquito population threshold, the probability of large outbreaks increases and therefore epidemics have a very high probability of occurrence.
4. Discussion
Qualitatively comparing model and data, we found two proxies for epidemics that might be of importance. On the one hand the fraction of vectors by host, that is closely related with rainfall and temperature. This dependence is presumably related to the maturation of mosquito eggs available to hatch at the beginning of the season, which is closely related to the amount of rainfall. Additionally it is necessary to have an stable high temperature without significant low values during the season. For instance, it's interesting to notice that for epidemic years 2009 and 2016 the frequency of four consecutive days in a given range of temperature was higher than most years with small outbreaks.
On the other hand the effective reproductive number , that is a product of the vector by host ratio and also a function of temperature, was found to be another epidemic proxy. The relevance of the link between vector abundance and human density for vector borne diseases was reported recently (Romeo-Aznar et al., 2018); therefore our findings indicate that, for quantitative comparisons between model and data, the functional dependence between vectors and hosts should be further explored.
The number of imported cases emerging after fitting the dataset was not proportional to the number of dengue cases in Bolivia. This is a reasonable result given that other factors might influence that quantity, e.g. economic exchange between countries, commercial activities as well as temporal work might drive the variability found in the number of imported cases. When imported cases appear in a sustained manner, and with conditions as previously described (by climate and location), the probability of an epidemic outbreak is very high.
The results obtained are quite satisfactory in terms of their qualitative comparison with clinical data. A quantitative comparison became extremely difficult given that confirmed cases are not the true total number of cases, not only because a considerable number of cases might be asymptomatic but also due to delays in cases recording, as the health system is centralized in Buenos Aires and becomes overwhelmed in epidemic situations.
Dengue is still non-endemic in northern Argentina, a region that was listed as one of the most affected by climate change, expecting a remarkable increase in temperatures according to high emission scenarios explored by the Intergovernmental Panel for Climate Change (IPCC) (Vera et al., 1029). Therefore, it could be expected that the region will become endemic in the future, with increased epidemics due to the El Niño Southern Oscilation (ENSO). Moreover, it is probable that the whole dengue endemic frontier will move south due to climate change.
The inclusion of spatiality, as it was introduced in the present model, gives the possibility that epidemic sizes are not as large as in a mean field model. Also, the model presented in this paper allows us to explore the development of risk maps, in cities where dengue is non-endemic. These maps can be useful to identify spreading hot spots in a city, that could help to design optimal dengue prevention programs.
5. Conclusion
Climate therefore constitutes a fundamental component in the population dynamics of Aedes aegypti and in the probability of dengue transmission. All these results open a promising door to explore the potential of meteorological data as a predictive tool for dengue epidemics. To address this formidable task is necessary to have access to good quality dengue cases records as well as to local rainfall and temperature forecasts. If these datasets were available, quantitative results would be obtained by fitting our model to data and performing intensive computer simulations with the ensemble of previously fitted parameters. Using climate forecasts as input it would be possible to obtain model hindcasts and, a posteriori, dengue outbreak forecasts (using for example V/H and as indicators). If the obtained uncertainties are acceptable, those forecasts can help to foresee new dengue outbreaks and alert the health system with enough anticipation to design strategies for dengue control. Given that Northwest Argentina is a hot spot for climate change, these relationships between climate and epidemics represent a valuable finding that should be deeply studied in the near future.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work was partially supported by grants PICT 2017-3117, PIP 112–2015 01-00644CO, SeCYT-UNC 05/B457, CIUNSa 2467, CIUNSa B-2572 and PICT-2019-2019-03558. We thank the Ministry of Health of Argentina and the National Meteorological Service of Argentina for providing the datasets. KL, GJS and JPA are members of Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Argentina.
Handling Editor: HE DAIHAI
Footnotes
Peer review under responsibility of KeAi Communications Co., Ltd.
Supplementary data to this article can be found online at https://doi.org/10.1016/j.idm.2022.10.004.
Contributor Information
Javier Armando Gutierrez, Email: g.javier.ar@gmail.com.
Karina Laneri, Email: karinalaneri@gmail.com.
Juan Pablo Aparicio, Email: juan.p.aparicio@gmail.com.
Gustavo Javier Sibona, Email: gsibona@unc.edu.ar.
Appendix A. Supplementary data
The following is the Supplementary data to this article:
References
- Aparicio J.P., Solari H.G. Population dynamics: Poisson approximation and its relation to the Langevin process. Physical Review Letters. 2001;86:4183–4186. doi: 10.1103/PhysRevLett.86.4183. [DOI] [PubMed] [Google Scholar]
- Argentine Institute of Statistics and Censuses (INDEC), National Population, Households and Housing Census 2010 and geography and geographic codes of the national statistical system - basic questionnaire processed with Redatam + SP, CEPAL/CELADE, https://www.indec.gob.ar/.
- Avilés G., Rangeón G., Vorndam V., Briones A., Baroni P., Enria D., Sabattini M.S. Dengue reemergence in Argentina. Emerging Infectious Diseases. 1999;5:575–578. doi: 10.3201/eid0504.990424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen S.-C., Hsieh M.-H. Modeling the transmission dynamics of dengue fever: Implications of temperature effects. Science of the Total Environment. 2012;431:385–391. doi: 10.1016/j.scitotenv.2012.05.012. https://www.sciencedirect.com/science/article/pii/S0048969712006584 URL. [DOI] [PubMed] [Google Scholar]
- Edman J.D., Scott T.W., Costero A., Morrison A.C., Harrington L.C., Clark G.G. Aedes aegypti (Diptera: Culicidae) movement influenced by availability of oviposition sites. Journal of Medical Entomology. 1998;35(4):578–583. doi: 10.1093/jmedent/35.4.578. arXiv:https://academic.oup.com/jme/article-pdf/35/4/578/18202180/jmedent35-0578.pdf. [DOI] [PubMed] [Google Scholar]
- Estallo E., Ludueña-Almeida F., Visintin A., Scavuzzo C., Introini M., Zaidenberg M., Almirón W. Prevention of dengue outbreaks through Aedes aegypti oviposition activity forecasting method, Vector borne and zoonotic diseases. Larchmont, N.Y.) 2011;11:543–549. doi: 10.1089/vbz.2009.0165. [DOI] [PubMed] [Google Scholar]
- Gil J.F., Palacios M., Krolewiecki A.J., Cortada P., Flores R., Jaime C., Arias L., Villalpando C., Alberti Dámato A.M., Nasser J.R., Aparicio J.P. Spatial spread of dengue in a non-endemic tropical city in northern Argentina. Acta Tropica. 2016;158:24–31. doi: 10.1016/j.actatropica.2016.02.003. [DOI] [PubMed] [Google Scholar]
- Grech M.G., Ludueña-Almeida F., Almirón W.R. Bionomics of Aedes aegypti subpopulations (Diptera: Culicidae) from Argentina. Journal of Vector Ecology. 2010;35(2):277–285. doi: 10.1111/j.1948-7134.2010.00083.x. arXiv:https://onlinelibrary.wiley.com/doi/pdf/10.1111/j.1948-7134.2010.00083.x. [DOI] [PubMed] [Google Scholar]
- Gutierrez J.A. 2018. Original codes used in the Phd. Thesis.https://github.com/javoxa/tesis [Google Scholar]
- Gutierrez J.A., Aparicio J.P. Quasi-deterministic population dynamics in stochastic coupled maps. Journal of Biological Systems. 2015;23(supp01):S151–S162. arXiv:https://doi.org/10.1142/S0218339015400124. [Google Scholar]
- Iboi E.A., Gumel A.B. Mathematical assessment of the role of Dengvaxia vaccine on the transmission dynamics of dengue serotypes. Mathematical Biosciences. 2018;304:25–47. doi: 10.1016/j.mbs.2018.07.003. https://www.sciencedirect.com/science/article/pii/S002555641730158X URL. [DOI] [PubMed] [Google Scholar]
- Kraemer M.U.G., Perkins T.A., Cummings D.A.T., Zakar R., Hay S.I., Smith D.L., Reiner R.C. Big city, small world: Density, contact rates, and transmission of dengue across Pakistan. Journal of The Royal Society Interface. 2015;12(111) doi: 10.1098/rsif.2015.0468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraemer M.U., Sinka M.E., Duda K.A., Mylne A.Q., Shearer F.M., Barker C.M., Moore C.G., Carvalho R.G., Coelho G.E., Van Bortel W., Hendrickx G., Schaffner F., Elyazar I.R., Teng H.-J., Brady O.J., Messina J.P., Pigott D.M., Scott T.W., Smith D.L.…Hay S.I. The global distribution of the arbovirus vectors Aedes aegypti and. Ae. albopictus, eLife. 2015;4 doi: 10.7554/eLife.08347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopez-Gatell H., Hernandez-Avila M., Hernández Avila J.E., Alpuche-Aranda C.M. Springer Vienna; Vienna: 2015. Dengue in Latin America: A persistent and growing public health challenge. [DOI] [Google Scholar]
- Ministerio de Salud de Argentina . 2009. Actas 2009, Anexo 6.a. Dengue, Situación de dengue en Argentina.https://www.argentina.gob.ar/salud/consejo-federal-salud/actas-2009 [Google Scholar]
- Ministerio de Salud de Argentina . 2016. Boletín integrado de Vigilancia se-32.http://www.msal.gob.ar/images/stories/boletines/Boletin-Integrado-De-Vigilancia-N322-SE32.pdf [Google Scholar]
- Mundo Sano Foundation Prevention program. 2017. https://www.mundosano.org/en/mosquito-borne-diseases/
- Musa S.S., Hussaini N., Zhao S., Daihai H. Dynamical analysis of chikungunya and dengue co-infection model. Discrete and Continuous Dynamical Systems - B. 2020;25(5):1907–1933. [Google Scholar]
- Musa S.S., Zhao S., Chan H.-S., Jin Z., He D. A mathematical model to study the 2014–2015 large-scale dengue epidemics in kaohsiung and tainan cities in taiwan, China. Mathematical Biosciences and Engineering. 2019;16(5):3841–3863. doi: 10.3934/mbe.2019190. https://www.aimspress.com/article/doi/10.3934/mbe.2019190 URL. [DOI] [PubMed] [Google Scholar]
- Pan American Health Organization/World Health Organization . 2019. PLISA health information platform for the Americas.http://www.paho.org/data/index.php/en/mnu-topics/indicadores-dengue-en/dengue-nacional-en/252-dengue-pais-ano-en.html [Google Scholar]
- Pandey A., Mubayi A., Medlock J. Comparing vector-host and SIR models for dengue transmission. Mathematical Biosciences. 2013;246(2):252–259. [PubMed] [Google Scholar]
- Pinho S., Ferreira C., Esteva L., Barreto F., Silva V., Teixeira M. Modelling the dynamics of dengue real epidemics. Philosophical transactions. Series A, Mathematical, physical, and engineering sciences. 2010;368:5679–5693. doi: 10.1098/rsta.2010.0278. [DOI] [PubMed] [Google Scholar]
- Reiner R.C., Stoddard S.T., Scott T.W. Socially structured human movement shapes dengue transmission despite the diffusive effect of mosquito dispersal. Epidemics. 2014;6:30–36. doi: 10.1016/j.epidem.2013.12.003. http://www.sciencedirect.com/science/article/pii/S1755436513000558 URL. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robert M.A., Tinunin D.T., Benitez E.M., Ludueña Almeida F.F., Romero M., Stewart-Ibarra A.M., Estallo E.L. Arbovirus emergence in the temperate city of Córdoba, Argentina, 2009 - 2018. Scientific Data. 2019;6:276. doi: 10.1038/s41597-019-0295-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romeo-Aznar V., De Majo M.S., Fisher S., Francisco D., Natiello M.A., Solari H.G. A model for the development of Aedes (Stegomyia) aegypti as a function of the available food. Journal of Theoretical Biology. 2015;365:311–324. doi: 10.1016/j.jtbi.2014.10.016. [DOI] [PubMed] [Google Scholar]
- Romeo-Aznar V., Paul R., Telle O., Pascual M. Mosquito-borne transmission in urban landscapes: The missing link between vector abundance and human density. Proc. R. Soc. B. 2018;285 doi: 10.1098/rspb.2018.0826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rotela C., Fouque F., Lamfri M., Sabatier P., Introini V., Zaidenberg M., Scavuzzo C. Spacetime analysis of the dengue spreading dynamics in the 2004 Tartagal outbreak, Northern Argentina. Acta Tropica. 2007;103(1):1–13. doi: 10.1016/j.actatropica.2007.05.003. http://www.sciencedirect.com/science/article/pii/S0001706X07001192 URL. [DOI] [PubMed] [Google Scholar]
- Sardar T., Rana S., Chattopadhyay J. A mathematical model of dengue transmission with memory. Communications in Nonlinear Science and Numerical Simulation. 2015;22(1):511–525. doi: 10.1016/j.cnsns.2014.08.009. http://www.sciencedirect.com/science/article/pii/S100757041400392X URL. [DOI] [Google Scholar]
- Sowilem M.M., Kamal H.A., Khater E.I. Life table characteristics of Aedes aegypti (Diptera:Culicidae) from Saudi Arabia. Tropical Biomedicine. 2013;30(2):301–314. http://europepmc.org/abstract/MED/23959496 URL. [PubMed] [Google Scholar]
- Tarragona S., Monteverde M., Marchioni S., Caporale J., Pereiro A., Palacios J. Dengue in Argentina: An economic analysis of the impact of the 2009 epidemic. Salud colectiva. 2012;8:151–162. doi: 10.1590/S1851-82652012000200004. [DOI] [PubMed] [Google Scholar]
- Torres J.R., Castro J. The health and economic impact of dengue in Latin America. Cadernos de Saúde Pública. 2007;23:S23–S31. doi: 10.1590/S0102-311X2007001300004. [DOI] [PubMed] [Google Scholar]
- Valdez L., Sibona G., Condat C. Impact of rainfall on Aedes aegypti populations. Ecological Modelling. 2018;385(C):96–105. [Google Scholar]
- Vásquez P., Loría A., Sanchez F., Barboza L. Climate-driven statistical models as effective predictors of local dengue incidence in Costa Rica: A generalized additive model and random forest approach. Revista de Matemática: Teoría y Aplicaciones. 2019;27(1):1–21. doi: 10.15517/rmta.v27i1.39931. [DOI] [Google Scholar]
- C. Vera, G. Silvestri, B. Liebmann, P. González, Climate change scenarios for seasonal precipitation in south America from ipcc-ar4 models, Geophysical Research Letters 33 (13). arXiv:https://agupubs.onlinelibrary.wiley.com/doi/pdf/10.1029/2006GL025759, doi:10.1029/2006GL025759.
- Wearing H.J., Rohani P. Ecological and immunological determinants of dengue epidemics. Proceedings of the National Academy of Sciences of the United States of America. 2006;103(31):11802–11807. doi: 10.1073/pnas.0602960103. https://pubmed.ncbi.nlm.nih.gov/16868086 URL. [DOI] [PMC free article] [PubMed] [Google Scholar]
- World Health Organization . 2020. Dengue and severe dengue.https://www.who.int/news-room/fact-sheets/detail/dengue-and-severe-dengue [Google Scholar]
- Yip S., Che Him N., Jamil N.I., He D., Sahu S.K. Spatio-temporal detection for dengue outbreaks in the central region of Malaysia using climatic drivers at mesoscale and synoptic scale. Climate Risk Management. 2022;36 doi: 10.1016/j.crm.2022.100429. https://www.sciencedirect.com/science/article/pii/S2212096322000365 URL. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.