fast.adonis: a computationally efficient non-parametric multivariate analysis of microbiome data for large-scale studies

Abstract

Motivation

Nonparametric multivariate analysis has been widely used to identify variables associated with a dissimilarity matrix and to quantify their contribution. For very large studies ($n\ge 5000$) and many explanatory variables, existing software packages (e.g. adonis and adonis2 in vegan) are computationally intensive when conducting sequential multivariate analysis with permutations or bootstrapping. Moreover, for subjects from a complex sampling design, we need to adjust for sampling weights to derive an unbiased estimate.

Results

We implemented an R function fast.adonis to overcome these computational challenges in large-scale studies. fast.adonis generates results consistent with adonis/adonis2 but much faster. For complex sampling studies, fast.adonis integrates sampling weights algebraically to mimic the source population; thus, analysis can be completed very fast without requiring a large amount of memory.

Availability and implementation

fast.adonis is implemented using R and is publicly available at https://github.com/jennylsl/fast.adonis.

Supplementary information

Supplementary data are available at Bioinformatics Advances online.

 

Nonparametric multivariate analysis (Anderson, 2001; McArdle and Anderson, 2001) based on a dissimilarity matrix has been widely used to analyze human microbiome data. This analysis quantifies the overall contribution of explanatory variables (R², coefficient of multiple determination), individually or collectively, by explaining the variation in the dissimilarity matrix [e.g. the UniFrac distance matrix (Lozupone and Knight, 2005)]. Then, statistical significance can be quantified using permutations and confidence intervals (CIs) are obtained using bootstrap sampling. The functions adonis and adonis2 in an R package vegan (Oksanen et al., 2020) are most commonly used for human microbiome data. While useful, they are computationally intensive for analyzing large-scale studies with thousands or tens of thousands of subjects and many explanatory variables (McDonald et al., 2018), particularly when performing sequential multivariate analysis (SMA) with permutations and bootstrapping. Moreover, we often perform many SMAs for variables included in the model in different orders because R² for individual variables depends on the order.

A more complicated problem is to analyze microbiome data from a study using complex sampling. For example, using a nested case-cohort design in a cohort study with N subjects, suppose that we have microbiome data for $n (n\ll N)$ subjects, each of which is sampled with a probability based on the fraction of the subjects selected from their sampling stratum. To derive an unbiased estimate of R² that reflects the source cohort population, we have to explicitly incorporate sampling weights (Korn and Graubard, 1999).

 

 

We first describe fitting multiple multivariate models simultaneously for subjects from a natural population. For a study with n samples, we have an n × n dissimilarity matrix $D=(d_{ij})$ and an n × p design matrix X for p explanatory variables with the first column $(1,\dots ,1)\prime$. We define an n × n matrix A with $a_{ij}=-d_{ij}^2/2$. The Gower’s centered matrix (Gower, 1966; Gower and Legendre, 1986) is defined as $G=(I-K/n)A(I-K/n)$, where K is an n × n matrix with k_ij = 1 and I is an n × n identity matrix. Let $H=X{(X^{\prime }X)}^{-1}{X}^{\prime }$ be the idempotent hat matrix. McArdle and Anderson (2001) showed that

$$tr(G)=tr(\mathit{HGH})+tr((I-H)G(I-H)).$$ (1)

Based on this partitioning, $R^2=tr(\mathit{HGH})/tr(G)$ is interpreted as the fraction of variance in matrix D explained by the p variables. In marginal multivariate analysis, we fit one model for each individual variable to derive R². In SMA for p variables with a given order, we calculate $R_k^2$ for the first k variables and then $R_1^2,R_2^2-R_1^2,\dots ,R_p^2-R_{p-1}^2$ are calculated as the incremental contribution of each individual variable. Obviously, SMA depends on the order of the variables.

In Supplementary Note, we show that $tr(G)=\sum _{i<j}{d}_{ij}^2/n$ and $tr(\mathit{HGH})=tr(HA)+\sum _{i<j}{d}_{ij}^2/n$. Thus, to calculate R², it remains to calculate tr(HA). Let $V=X[{(X^{\prime }X)}^{-1}]$ and $U=X^{\prime }A$. Here, V is an n × p matrix and U is an p × n matrix. Thus, $tr(HA)=tr\{(X[{(X^{\prime }X)}^{-1}])(X\prime A)\}=tr(VU)=\sum _{1\le i\le n;1\le j\le p}{V}_{ij}{U}_{ji}$. In Supplementary Note, we show that the computational complexity for tr(HA) is $n^{2}p$ when $p\ll n$, which is much less than n³ required for the multiplication of n × n matrices.

Now, we consider simultaneously fitting multivariate models for M subsets of the p variables with a given order (denoted as $S_1,\dots ,S_M$). We first calculate $U=X\prime A$ for all p variables. For any subset S_m, we do not need to calculate $U(S_m)$ individually; instead, we extract the corresponding rows of U. For a subset S_m with q variables, computing $U(S_m)$ has a complexity of $n^{2}q$ and is the most computationally intensive step for fitting the model when $q\ll n$. Thus, this extension is suitable for fitting many models simultaneously, including SMAs.

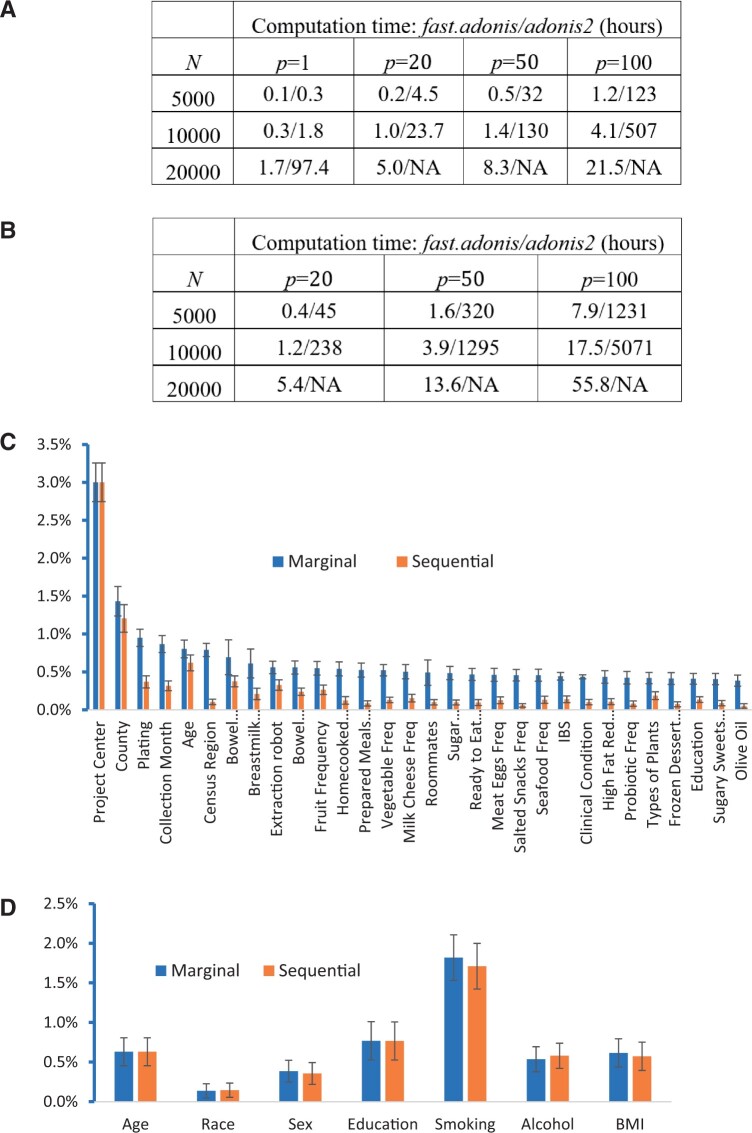
We compared the computational time between fast.adonis and adonis2 for performing one SMA with 1000 permutations on a MacBook Pro with Intel 2.3 GHz Core i9 CPU and 16 gigabytes of memory. No comparisons were made with adonis because of the requirement of memory ($\sim 30$ gigabytes of memory required when n = 10 000 and p = 20). For n = 10 000 and p > 20, fast.adonis is about 50–100 times faster than adonis2 (Fig. 1A). At n = 20 000, adonis2 did not run successfully when $p\ge 20$. Next, we compared the computing time for performing 10 SMAs for the same set of p variables included in different orders (Fig. 1B). fast.adonis simultaneously performed 10 SMAs while adonis2 performed SMA 10 times serially.

Fig. 1.

(A) Computation time (hours) for fast.adonis and adonis2 to perform one sequential multivariate analysis (SMA) for n subjects and p variables with 1000 permutations. For example, ‘1.2/123’ indicates 1.2 h for fast.adonis and 123 h for adonis2. ‘NA’: Analyses were not successful on the computer. (B) Computation time (hours) for adonis2 and fast.adonis to perform ten sequential multivariate analysis (SMA) for n subjects and p variables with 1000 permutations. Here, 10 SMAs mean SMA for 10 different orders of the same p variables. (C) Marginal and sequential R² for 30 variables and a weighted UniFrac dissimilarity matrix in the American Gut Project with n = 7096 subjects. Confidence intervals were calculated based on 1000 bootstrapping. (D) Multivariate analysis for the oral microbiome of n = 2487 subjects from the PLCO cohort with source population n = 32 763. Analyses were done for 29 dummy variables based on 7 categorical variables. Confidence intervals were derived based on within stratum bootstrapping.

We used fast.adonis to analyze the data from the American Gut Project (McDonald et al., 2018) with 111 variables (p = 559 after expanding categorical variables) and n = 7, 096 subjects. We evaluated the marginal R² of these variables and performed SMA with variables ordered by the marginal R² values. Analyses were performed for the weighted UniFrac dissimilarity matrix with 1000 permutations and 1000 bootstrap samples. Results for the top 30 variables are shown in Figure 1C. Consistent with the original publication (McDonald et al., 2018), technical factors were most associated with the dissimilarity matrix, followed by nutrition variables. For most nutrition variables, the R² from sequential analyses was much lower than those from marginal analyses. Because p = 559, this analysis took fast.adonis 8.8 h (1 SMA, 1000 permutations and 1000 bootstrapping); adonis2 was not able to finish analyses.

 

Next we extend the algorithm to complex sampling studies. The complex sample design used to sample the cohort to obtain a subcohort for the case-cohort study involved partitioning the subjects in the cohort into multiple strata, and subjects are randomly selected from each stratum with some sampling fraction. As an example, we have recently characterized the oral microbiome of n = 2487 subjects from the Prostate, Lung, Colorectal and Ovarian Cancer Screening Trial (PLCO) cohort (n = 37 263 eligible individuals with oral wash specimens) to prospectively investigate the association between the oral microbiome and the risk of multiple cancers, including lung cancer (Vogtmann et al., 2022). To select a referent subcohort for comparison to the cases, 24 strata were created based on age, sex and smoking variables and stratum-specific sampling fractions were determined based on the number of site-specific cancer cases in that stratum. To derive an unbiased estimate of R² in the dissimilarity matrix for many demographic and lifestyle factors, we extended the algorithm to explicitly incorporate the sampling weight (Supplementary Notes) following the philosophy of survey data analyses (Korn and Graubard, 1999).

We analyzed the PLCO data for p = 29 dummy variables generated from seven categorical variables (Vogtmann et al., 2022): age, race, sex, education, smoking history, alcohol consumption and body mass index (Fig. 1D). For each analysis, we used within-stratum bootstrapping by independently resampling the stratum-specific samples with replacement to derive the CI for R². Together, these seven variables explained 4.70% (95% CI = 3.84–5.68%) of the variance in the weighted UniFrac dissimilarity matrix, while smoking history alone explained 1.70% (95% CI = 1.20–2.22%) of the variance, conditioning on age, sex and education. Results based on marginal analyses and sequential analyses are similar in this data. It took 3.8 min to finish the analysis with 1000 bootstrap resampling for this data.

 

In summary, we developed fast.adonis to efficiently fit multivariate models to microbiome data from large-scale studies. fast.adonis can efficiently fit many multivariate models simultaneously, making it useful to identify important factors by forward selection (Blanchet et al., 2008). While results in this manuscript were obtained using a single core, fast.adonis has the option of parallel computation. Moreover, fast.adonis can analyze data from complex sampled studies which require analyses using sampling weights. When the interest centers on testing the association between one variable and a distance matrix, one can rely on the asymptotic P-value instead of permutations (Chen and Zhang, 2021).