App-SpaM: phylogenetic placement of short reads without sequence alignment

Abstract

Motivation

Phylogenetic placement is the task of placing a query sequence of unknown taxonomic origin into a given phylogenetic tree of a set of reference sequences. A major field of application of such methods is, for example, the taxonomic identification of reads in metabarcoding or metagenomic studies. Several approaches to phylogenetic placement have been proposed in recent years. The most accurate of them requires a multiple sequence alignment of the references as input. However, calculating multiple alignments is not only time-consuming but also limits the applicability of these approaches.

Results

Herein, we propose Alignment-free phylogenetic placement algorithm based on Spaced-word Matches (App-SpaM), an efficient algorithm for the phylogenetic placement of short sequencing reads on a tree of a set of reference sequences. App-SpaM produces results of high quality that are on a par with the best available approaches to phylogenetic placement, while our software is two orders of magnitude faster than these existing methods. Our approach neither requires a multiple alignment of the reference sequences nor alignments of the queries to the references. This enables App-SpaM to perform phylogenetic placement on a broad variety of datasets.

Availability and implementation

The source code of App-SpaM is freely available on Github at https://github.com/matthiasblanke/App-SpaM together with detailed instructions for installation and settings. App-SpaM is furthermore available as a Conda-package on the Bioconda channel.

Contact

matthias.blanke@biologie.uni-goettingen.de

Supplementary information

Supplementary data are available at Bioinformatics Advances online.

1 Introduction

Phylogeny reconstruction is a fundamental field of research in bioinformatics (Felsenstein, 2004). Here, the basic task is to reconstruct a phylogenetic tree for a set of nucleic acid or protein sequences, representing their evolutionary history. However, the de novo reconstruction of phylogenetic trees is resource-intensive and requires a well-curated set of biological sequences (Kapli et al., 2020). But if a reliable phylogenetic tree is already known for a subset of the input sequences, then it is possible to efficiently find the position of the remaining sequences within this existing tree. This procedure is called phylogenetic placement and a number of algorithms have been proposed for this task during the last years (Barbera et al., 2019; Brown and Truszkowski, 2013; Czech et al., 2019; Matsen et al., 2012; Mirarab et al., 2012; Rabiee and Mirarab, 2020). By now, phylogenetic placement is a common step in metabarcoding studies for purposes such as taxonomic identification and microbiome analyses (Darling et al., 2014; DeSalle and Goldstein, 2019; Mahé et al., 2017; Nguyen et al., 2014; Thompson et al., 2017). This development is also facilitated by large curated databases for marker genes such as 16S (DeSantis et al., 2006; Quast et al., 2013) or ITS2 (Ankenbrand et al., 2015) that make reference sequences readily available. It has also been argued that phylogenetic placement is more accurate than taxonomic read assignment (Barbera et al., 2019) and a variety of tools has been developed to analyse and visualize resulting placements between different samples (Barbera et al., 2021; Czech and Stamatakis, 2019; Czech et al., 2020; Matsen and Evans, 2013). The phylogenetic placement has also been used to update large phylogenetic trees (Balaban et al., 2021) and for the tracking of virus variants (Singer et al., 2020; Turakhia et al., 2021).

The first approaches to phylogenetic placement were pplacer (Matsen et al., 2010) and EPA (Berger et al., 2011). Both programs are based on probabilistic models of nucleotide substitutions. For a set of reference sequences, they require a multiple alignment of these sequences—the reference MSA—together with the reference tree. For a query read and a position in the tree, pplacer calculates the likelihood for observing the read at this position. The program then finds a position that maximizes this likelihood. It uses several heuristics to rapidly calculate the likelihood values and has a runtime linear with respect to the number of reference taxa, number of queries and sequence lengths. Similar to pplacer, EPA also calculates the likelihood for each query read at each possible edge in the reference tree. EPA-ng (Barbera et al., 2019) is a re-implementation of EPA designed to parallelize the computations and comes with additional improved placement heuristics. In addition to the reference alignment, all of the above approaches also require alignments of the query reads against the reference MSA. This alignment is often performed with hmmalign (Eddy, 1995; Finn et al., 2011). Alternatively, phylogeny-aware alignment algorithms such as PaPaRa (Berger and Stamatakis, 2011) or SEPP (Mirarab et al., 2012) can be used.

In comparison to pplacer and EPA, the more recently developed algorithm RAPPAS (Linard et al., 2019) does not align the read sequences to the reference alignment. Instead, RAPPAS uses so-called phylo-k-mers, which are calculated based on the reference tree and reference MSA in a pre-processing step. For each column of the reference alignment, for each edge e of the reference tree, and for each possible k-mer w, the program calculates the probability to see w at the corresponding position in a hypothetical sequence that would branch off from the reference tree at edge e (note that w does not need to be present in any of the reference sequences). If this probability is above a chosen threshold, the k-mer w is called a phylo-k-mer. RAPPAS creates a database with all phylo-k-mers and their associated probabilities to occur at a branch in the reference tree. Once this database is constructed, new query reads can be rapidly placed based on their k-mers that are also present in the database.

In contrast to the above methods, the recently proposed algorithm APPLES (Balaban et al., 2020) is a distance-based approach. The program chooses placement positions based on estimated phylogenetic distances between the reference sequences and the query read sequences. Then, APPLES finds a placement position in the reference tree such that the distances between the query and the reference sequences in the resulting tree approach the estimated phylogenetic distances. Here, a standard sum-of-squares criterion is applied. The distances between query and reference sequences can either be estimated from sequence alignments or by using an alignment-free method; in the latter case, APPLES uses Skmer (Sarmashghi et al., 2019).

In this paper, we present a new approach to phylogenetic placement that we call Alignment-free phylogenetic placement algorithm based on Spaced-word Matches (App-SpaM). Similar to APPLES, App-SpaM also performs distance-based phylogenetic placement; it neither needs a multiple alignment of the reference sequences nor alignments of the query reads to the reference sequences. Thus, it skips the time intensive alignment procedures that are needed for most other software tools. Additionally, in contrast to existing placement methods, App-SpaM can be applied to datasets where no multiple sequence alignment of the references can be created.

App-SpaM is based on an approach that was originally implemented in the program Filtered spaced-word Matches (FSWM; Leimeister et al., 2017): For any two of the input DNA sequences, FSWM estimates their Jukes–Cantor distances, i.e. the average number of nucleotide substitutions per position since the two sequences have evolved from their last common ancestor. This estimate is based on simple gap-free alignments of a fixed length, so-called spaced-word matches, that are created with respect to a pre-defined binary pattern of match and don’tcare positions. This concept has already been extended to calculate distances between an assembled genome from one species and a set of unassembled reads from a second genome, or between sets of unassembled reads from two genomes. This adaptation of FSWM is called Read-SpaM (Lau et al., 2019).

App-SpaM is a fast implementation of the FSWM approach designed to perform phylogenetic placement: given a set of reference sequences, a reference tree for these sequences and a set of reads, App-SpaM uses spaced-word matches to estimate pairwise phylogenetic distances between every query and every reference sequence. It then uses one of several fast heuristics to perform phylogenetic placement of the queries. The heuristics are either based on the calculated query-reference distances or based on the number of identified spaced-word matches. We show that App-SpaM achieves a placement accuracy that is comparable to alignment-based approaches on a variety of datasets while it is faster than those existing methods.

2 Materials and methods

As input, our approach takes a set of N reference sequences, a rooted and edge-weighted phylogenetic tree T—the reference tree—with N leaves, where each leaf is labelled with one of the reference sequences, and a set of query read sequences. Our algorithm can be divided into three consecutive steps: (i) First, we find so-called spaced-word matches between every query and every reference sequence; (ii) then, we estimate the phylogenetic distance between every query and reference sequence based on a ‘filtered’ subset of the identified spaced-word matches; (iii) at last, we determine a placement position for each query sequence in the reference tree T.

2.1 Definitions

For a set Σ of characters called the alphabet, a sequence over Σ is an ordered list of elements of Σ. For a sequence S, its length is denoted by $|S|$, and for $i\in \{1,\dots ,|S|\}$, the i-th element of S is denoted by $S[i]$. The set of sequences of length n over Σ is denoted by ${\Sigma }^n$. In the following, we are considering sequences over the set {0, 1}—so-called patterns—over the nucleotide alphabet $\mathcal{A}=\{A,C,G,T\}$, and over the extended nucleotide alphabet ${\mathcal{A}}^{*}=\mathcal{A}\cup \{*\}$. Here, ‘$*$’ is a symbol not contained in $\mathcal{A}$, a so-called wildcard character.

A spaced word is defined with respect to a given binary pattern $P\in {\{0,1\}}^{\ell }$ of length $\ell$. A position j in the pattern is called a match position if $P[j]=1$ and a don’t care position if $P[j]=0$. The number of match positions in a pattern P is called the weight of P. A spaced word W with respect to P is defined as a sequence of length $|P|$ over ${\mathcal{A}}^{*}$, with $W[i]\in \mathcal{A}$ if and only if i is a match position of P. We say that a spaced word W occurs in a sequence S over $\mathcal{A}$ at some position i—or that (W, i) is a spaced-word occurrence in S—if $S[i+j-1]=W[j]$ for all match positions j of P.

For two sequences S₁ and S₂ and positions i₁ and i₂ in S₁ and S₂, respectively, we say that there is a spaced-word match (SpaM) between S₁ and S₂ at $(i_1,i_2$), if $S_1[i_1+j-1]=S_2[i_2+j-1]$ for all match positions j of P. In other words, there is a SpaM at (i₁, i₂), if there is a spaced word W, such that $(W,i_1)$ is a spaced-word occurrence in S₁ and $(W,i_2)$ is a spaced-word occurrence in S₂. A spaced-word match with respect to P can, thus, be seen as a local gap-free alignment of length $|P|$ with matching nucleotides at the match positions of P and possible mismatches at the don’t care positions, see Figure  1 for an example. Furthermore, for a substitution matrix assigning a score to any two symbols of the nucleotide alphabet $\mathcal{A}$, we define the score of a spaced-word match as the sum of all substitution scores of nucleotide pairs aligned to each other at the don’t care positions of P. Spaced-word matches—called spaced seeds in this context—have been originally introduced in sequence-database searching (Li et al., 2003; Ma et al., 2002); later they were applied in sequence classification (Břinda et al., 2015) and alignment-free sequence comparison to estimate phylogenetic distances between DNA and protein sequences (Leimeister et al., 2017, 2019; Morgenstern et al., 2015; Röhling et al., 2020), see Morgenstern (2020) for a review. The results of these methods depend on the underlying binary pattern or set of patterns. It is well known that finding optimal pattern sets is an NP hard problem (Li et al., 2006), but efficient heuristics have been proposed for this task (Brejova et al., 2004; Ilie et al., 2011; Kucherov et al., 2006).

Fig. 1.

Toy example of a spaced-word match (SpaM) between two DNA sequences S₁ and S₂ with respect to a binary pattern P = 1101001, representing match positions (‘1’) and don’t care positions (‘0’). The same spaced word AT*G**C occurs in both sequences. A SpaM corresponds to a local gap-free pairwise alignment with matching nucleotides at all match positions of P, while mismatches are allowed at the don’t care positions. Note that, in practice, we are using much larger patterns than in this example; by default, App-SpaM uses a single pattern with 12 match positions and 32 don’t care positions.

2.2 Spaced-word matches between query and reference sequences

In a first step, we determine a fixed set $\mathcal{P}$ of binary patterns with a specified length and weight. For this, App-SpaM uses our previously developed software rasbhari to calculate pattern sets (Hahn et al., 2016). By default, App-SpaM uses a single pattern, thus $|\mathcal{P}|=1$, with a weight of w = 12 and 32 don’t care positions. Given a pattern set $\mathcal{P}$, first, we efficiently identify all spaced-word matches (SpaMs) between the query reads and the reference sequences. More precisely, for each pattern $P\in \mathcal{P}$, all spaced-word occurrences with respect to P in the queries and references are stored in two lists L₁ (references) and L₂ (queries) that are both sorted in lexicographic order. For the sorting procedure, only the nucleotides at the match positions are considered, the don’tcare positions are ignored. For every spaced-word occurrence (W, i), we also store all nucleotides of the don’t care positions. Thus, for each possible spaced word W, all occurrences of W in the read and reference sequences appear as consecutive blocks in the lists L₁ and L₂, respectively.

Once the sorted lists L₁ and L₂ have been established, they can be traversed simultaneously, such that for each spaced word W, the blocks with the occurrences of W in L₁ and L₂ are processed at the same time. Each pair of occurrences $(W,i_1)$ in L₁ and $(W,i_2)$ in L₂ corresponds to a spaced-word match at (i₁, i₂) between a reference sequence and a query read. For each such spaced-word match, we calculate its score and we discard all SpaMs with a score smaller or equal to a pre-set threshold t. The SpaMs with a score below t are considered to be background or random spaced-word matches. All remaining, high-scoring, SpaMs are referred to as filtered spaced-word matches. These filtered spaced-word matches are regarded as putative homologous matches. As in FSWM, we use the HOXD70 nucleotide substitution matrix (Chiaromonte et al., 2002) and a default threshold value of t = 0.

The above ‘filtering’ step is necessary since, in general, many of the spaced-word matches detected by our program will be random matches. In fact, for long input sequences with a low degree of similarity, the majority of the SpaMs will be background matches. Our inferred distance estimates are only unbiased if all background matches can be filtered out while all homologous matches remain. For dissimilar sequences, this assumption might not always hold and distances can be slightly biased depending on the threshold t; examples are given in our previous paper (Leimeister et al., 2017). In this previous paper, however, we could also demonstrate that, with the filtering procedure, homologous and background SpaMs can be easily distinguished in most cases. The threshold t = 0 that we are using by default works well for this purpose, but the value of t can be adapted by the user, if desired. There is a difference, however, between App-SpaM and the original program FSWM, in the way the filtered SpaMs are selected. In FSWM, each spaced-word occurrence $(W,i_1)$ in sequence S₁ can be involved in at most one of the filtered spaced-word matches. In contrast, a spaced-word occurrence in a read sequence can be matched with multiple spaced-word occurrences in the reference sequences—and vice versa—in App-SpaM, as long as the corresponding scores are larger than t.

For each query read Q and each reference sequence S, we store the number s(Q, S) of SpaMs between Q and S with score larger than t. Additionally, we calculate the proportion of mismatches at the don’t care positions of all filtered SpaMs between Q and S, and we estimate the phylogenetic distance d(Q, S) between Q and S using the well-known Jukes–Cantor formula (Jukes and Cantor, 1969).

In practice, we compute the list L₁ of spaced-word occurrences from the reference sequences once and hold it in main memory. The query sequences are processed in batches to limit the memory consumption. Thus, the list L₂ of spaced-word occurrences in the query sequences is calculated and processed for each batch separately. This also allows straightforward parallelization for multi-core systems: multiple batches of query reads can be processed simultaneously across multiple cores for datasets with many query sequences.

2.3 Choosing a position for a read in the reference tree

In the following, we propose five heuristics to find a suitable position in our reference tree T, where a query read sequence Q is added to T. For an edge e in an edge-weighted tree, let l(e) denote the length (‘weight’) of e. For each query Q, we first select an edge e_Q in T and insert a new internal node into this edge, thereby splitting e_Q into two new edges e₁ and e₂ with $l(e_1)+l(e_2)=l(e_Q)$. Then, we add a new leaf that is labelled with Q, together with a new edge $e_Q^{\prime }$ that connects this new leaf with the newly generated internal node. Finally, a length $l(e_Q^{\prime })$ is assigned to the newly generated edge $e_Q^{\prime }$.

To find a suitable edge e_Q for a query sequence Q and to assign lengths to the newly generated edges, we are using either the phylogenetic distances d(Q, S) or the number of spaced-word matches s(Q, S) with scores larger than t between Q and all reference sequences S. A detailed description how we determine the edge lengths for e₁, e₂, and the newly inserted edge $e{\prime }_Q$ are given in the Supplementary Section S1.1. In case we find no spaced-word matches for a query read to any reference sequence, the query placement is recorded at the root of T.

2.3.1 MIN-DIST

In this approach, we first select the reference sequence S that minimizes the distance d(Q, S) over all reference sequences, and we define e_Q to be the edge in T that is adjacent to the leaf labelled with S. If multiple references have the same smallest distance to Q, one of them is chosen randomly.

2.3.2 SpaM-COUNT

This works like the previous approach, but instead of selecting the reference sequence S that minimizes the distance to Q, we select the reference S that maximizes the number s(Q, S) of spaced-word matches with score $>t$ between S and Q.

2.3.3 LCA-DIST

Here, we identify the two reference sequences S₁ and S₂ with the lowest distances $d(Q,S_1)$ and $d(Q,S_2)$ to Q. Let v be the lowest common ancestor in T of the two leaves that are labelled with S₁ and S₂, respectively. The edge e_Q is then defined as the edge in T that connects v with its parental node.

2.3.4 LCA-COUNT

This is similar to the previous approach, but instead of using reference sequences S₁ and S₂ minimizing the distance with Q, we select the two references S₁ and S₂ with the maximal number $s(Q,S_1)$ and $s(Q,S_2)$ of spaced-word matches to Q with scores larger than t.

2.3.5 SpaM-X

The first four approaches will yield either only placement locations at branches directly above the leaves, or only placement locations at inner branches, respectively. Thus, in this approach, we combine the SpaM-COUNT and LCA-COUNT approaches: For S₁ and S₂ as in LCA-COUNT and a given X, we evaluate whether

$$|s(Q,S_1)-s(Q,S_2)|>\frac{s(Q,S_1)+s(Q,S_2)}{X}$$

is true. If so, the query is placed according to SpaM-COUNT, otherwise, the query is placed according to LCA-COUNT. As a result, when $d(Q,S_1)$ is substantially larger than $d(Q,S_2)$, then Q is placed at the branch directly above S₁. App-SpaM uses SpaM-X on default with X = 4 (referred to as SpaM-4 in the following).

SpaM+APPLES: As a sixth approach, in addition to five versions of App-SpaM, we used the distance values d(Q, S) as input for the program APPLES (Balaban et al., 2020). APPLES performs a least-squares optimization to find the position in the tree that fits the calculated distances best. For a reference tree T, a query sequence Q and input distances between Q and all reference sequences, it finds a position for Q in T, such that the sum of the squared differences between the input distances and the distances in the resulting tree is minimized.

2.4 Evaluation procedure

We primarily used the recently developed Placement Evaluation WOrkflows (PEWO) (Linard et al., 2021) to evaluate the placement accuracy and runtime of App-SpaM. For a given reference dataset, consisting of a set of reference sequences, a reference MSA of these sequences, and a reference tree in which the leaves are labelled with the reference sequences, the pruning-based accuracy evaluation (PAC) implemented in PEWO determines the placement accuracy of an evaluated method as follows: First, a randomly chosen subtree is removed (‘pruned’) from the reference tree. All sequences at the leaves of the chosen subtree are removed from the reference MSA as well. Next, artificial reads are generated by splitting the removed sequences into segments of a given length; these reads are used as query sequences. An algorithm under evaluation is then used to place the queries onto the pruned reference tree.

To measure the placement accuracy of a method, PEWO uses the so-called node distance (ND): For each query sequence Q, the distance between the proposed placement position of Q and the edge where the subtree was pruned is measured by counting the number of nodes on the corresponding path. The average of these distances over all query sequences is then a measure of accuracy for one pruning event. This procedure is repeated with randomly pruned subtrees and PEWO uses the average accuracy over all pruning events as the overall accuracy of the evaluated method. PEWO also provides a resources evaluation (RES) workflow to measure the runtime and memory usage of programs. This includes the alignment of queries against the MSA of references for those methods that are based on sequence alignments and the construction of the phylo-k-mer database in RAPPAS.

We used the PEWO PAC workflow to evaluate the placement accuracy of the five versions of App-SpaM that we outlined above. In addition, we evaluated the combination of SpaM and APPLES. Both programs were run with default parameter values. We also ran our program with non-default parameter values for the pattern weight w and the number of patterns by varying $w\in \{8,12,16\}$ and using between 1 and 5 different patterns per pattern set.

We compared the accuracy of App-SpaM to all programs that are currently supported by PEWO with the PAC workflow. At present, the programs pplacer, EPA, EPA-ng, RAPPAS and APPLES are included in the PEWO package. The datasets used for this evaluation vary with respect to the number and length of the reference sequences, with respect to the degree of similarity between the reference sequences, and with respect to the sequence locus. A short overview of the reference datasets is given in Table  1; a more detailed overview can be found in the Supplementary Section S1.3. In this analysis, in addition to the default parameters, we included a variety of parameter combinations for all placement programs. For APPLES, we used the updated version 2.0.1 that automatically re-estimates the branch lengths of the reference tree appropriately to match the evolutionary model of query-reference distances. For each reference dataset, we performed 100 pruning runs with randomly sampled subtrees and recorded the average ND. As default, we used a length of 150 base pairs (bp) for the simulated query reads. We also performed additional test runs with longer read lengths for three datasets (hiv-104, neotrop-512 and tara-3748).

Table 1.

Datasets used for evaluation

Name	Locus	Mean length (bp)	Query length (bp)
bac-150	16S	1256	150
hiv-104	Viral genomes	9096	150; 500
neotrop-512	16S	1766	150; 300
tara-3748	16S	1406	150; 300
bv-797	16S	1341	150
epa-218	16S	1483	150
epa-628	5.8S	780	150
epa-714	16S	1169	150
wol-43	Microbial genomes	52 768 066	150
CPU-652	16S	1315	150
CPU-512	16S	1766	150

Notes: Overview of datasets used in the evaluation. The columns show the dataset names used in this manuscript, the locus from which the sequences in the datasets originate from, the mean sequence length of the references and the simulated read lengths used during evaluation. The name of each dataset includes the number of reference sequences. The first nine datasets are used in the PAC workflow, the last two in the RES workflow.

To measure the runtime and memory requirements of the evaluated methods, we used PEWO’s RES workflow on two datasets of differing sizes (CPU-652 and CPU-512). We recorded the average runtime and memory usage over five repeats for each program. For CPU-652, we placed 100 000 query sequences, and for CPU-512, we placed 10 000 query sequences on the reference tree. In addition to these evaluations, we performed an additional runtime test with App-SpaM on the tara-3748 dataset, similarly to the runtime study conducted in EPA-ng: We recorded the runtime of App-SpaM to place up to 37 480 000 query reads with parallel execution on 30 cores. All of these tests were carried out on Intel(R) Xeon(R) E7-4850 CPUs with 2 GHz.

Lastly, we also performed test runs using simulated sets of unassembled sequencing reads as references, instead of contiguous reference sequences. In these experiments, we used the hiv-104 dataset that consists of complete HIV genomes, and wol-43, a dataset of complete microbial genomes of 43 different Wolbachia strains. Because PEWO does not support unassembled reference sequences, we used a simple leave-one-out procedure to assess the accuracy of App-SpaM in this scenario. For this, we simulated reads with a length of 150 bp and values for the sequencing coverage of 4, 2, 1, 0.5, 0.25, 0.125, 0.0625 and 0.03125 for all sequences. These ‘bags of reads’ constitute the reference sequences for the evaluation. Then, for a given coverage, a leaf is pruned from the reference tree, its corresponding reads are used as the query sequences, and the average ND across all reads is measured. This is repeated one by one for all references, and subsequently for all coverages. To assess the accuracy of App-SpaM in these tests, we used three control methods: First, we compared the placement accuracy to the accuracy achieved on contiguous (‘assembled’) reference sequences; this shows the decline in accuracy depending on the sequencing coverage. Second, we compared the achieved results to the accuracy when placing all query reads at the root of the tree; and third, when placing all query reads at the midpoint of the tree.

3 Results

Figure  2 shows the accuracy of the five different versions of App-SpaM described above, together with the combination of SpaM+APPLES, on the bac-150 dataset and a query read length of 150 bp. On average, SpaM-4 performed best among the five methods while MIN-DIST was the least accurate. These results are consistent across different values of w and across different datasets (see Supplementary Section S2.1). In general, w has little influence on the placement accuracy of App-SpaM and there is no value of w that performs best in all situations. The second best of the five placement methods was LCA-COUNT followed by SpaM+APPLES, while LCA-DIST, MIN-DIST and SpaM-COUNT perform not as well.

Fig. 2.

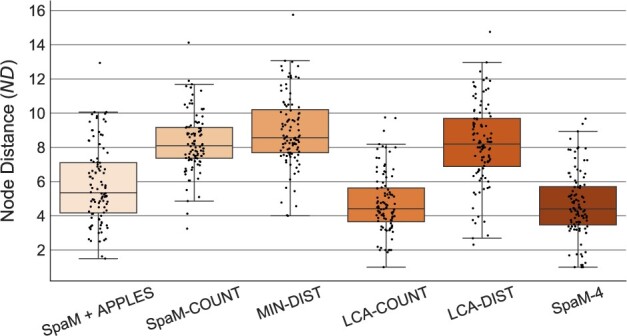
Average ND over n = 100 pruning experiments on the bac-150 dataset. ND was measured with PEWO for the five different versions of App-SpaM and the combination of SpaM and APPLES. A single pattern with weight w = 12 and 32 don’t care positions is used for all heuristics. Every box plot shows the overall distribution over all 100 pruning experiments (black dots).

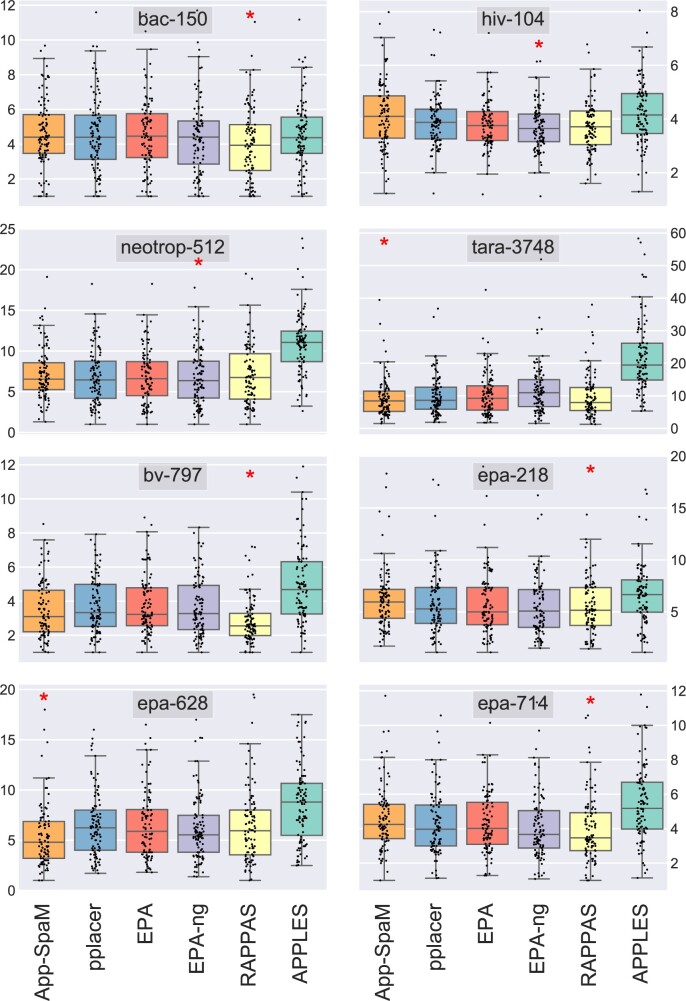
Figure  3 shows the ND for App-SpaM and five other placement methods on eight different datasets, again for a query read length of 150 bp. For each program, the placement accuracy for their default parameter settings is shown. App-SpaM is the most accurate program on the tara-3748 and epa-628 datasets, while EPA-ng performs best on the hiv-104 and neotrop-512 datasets; on the remaining four datasets, RAPPAS achieves the lowest average ND value among all evaluated programs. The exact statistics as well as results for other parameter settings for all programs are given in the Supplementary Material.

Fig. 3.

Average ND over n = 100 pruning experiments on all eight datasets (grey patches) for all six programs (coloured box plots). The y-axes show the ND, the x-axes are divided into six categories that correspond to the six programs. Every box plot shows the overall distribution over all 100 pruning experiments (black dots). The program that performs best on average is highlighted (red star).

Figure  4 shows the performance of the evaluated methods for different query read lengths. Additionally, to read lengths of 150 bp, here, we used the dataset hiv-104 with query read lengths of 500, and the datasets neotrop-512 and tara-3748 with query read lengths of 300. As expected, all programs are more accurate when longer query reads are used. The ND improves on average by 29% for hiv-104, by 27% for neotrop-512 and by 24% for tara-3748 across all methods, compared to a read length of 150 bp. In general, likelihood-based programs and RAPPAS benefit more from longer reads than App-SpaM and APPLES. For likelihood-based programs and RAPPAS, the ND drops on average by 30% across the three datasets when using longer query reads. In contrast, App-SpaM has a 25% lower ND and APPLES 12% lower ND on average across the three datasets when using longer queries.

Fig. 4.

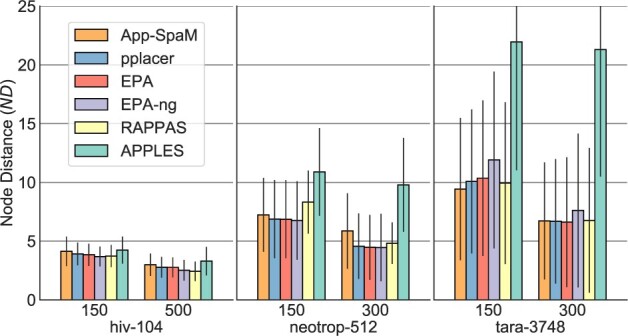
Average ND (n = 100) for different placement programs, for different read lengths on three datasets. For hiv-104 read lengths of 150 and 500 bp, and for neotrop-512 and tara-3748 results for read lengths of 150 and 300 bp were used. SDs across prunings are shown (black lines).

The accuracy of App-SpaM on unassembled reference sequences is shown in Figure  5 for different values of the sequencing coverage and for different values of the pattern weight w. For a coverage of 1, the ND for App-SpaM with w = 12 increases—in comparison to assembled references—by 30% on hiv-104 and by 31% on wol-43, respectively. The accuracy decreases for lower and increases for higher coverages of the reference sequences: With a coverage of 4, the ND is only 14% larger for hiv-104 and 15% larger for wol-43 in comparison to assembled references. On the hiv-104 dataset and a coverage of 0.0625, App-SpaM’s inferred positions are only as good as the control method that always places a query read at the midpoint of the tree. However, with this low coverage of the viral genomes, every reference genome is, on average, only represented by 3.8 reads with a length of 150 bp. For the same reason, no results could be produced for a coverage of 0.03125 for hiv-104.

Fig. 5.

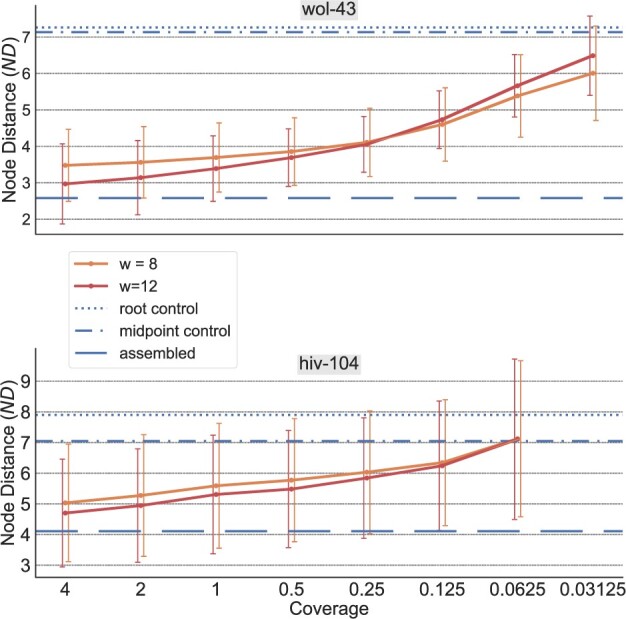
Average ND on unassembled reference sequences with different sequencing coverage on the wol-43 (n = 43) and hiv-104 (n = 104) datasets for App-SpaM with default parameters. Results for read lengths of 150 bp and a pattern weight of 8 and 12 are shown (orange and red) with SDs. Three control methods serve as reference for the performance of App-SpaM: The placement accuracy with assembled references (long dashed blue), always placing a query at the midpoint of the tree (dashed-dotted blue) and always placing a query at the root (dotted blue).

Runtime results for CPU-652 and CPU-512 are shown in Table  2. We report the runtimes for all pre-processing steps, the placement itself, as well as the total runtime (pre-processing plus placement). For some programs, the runtimes vary greatly depending on the chosen parameters. For RAPPAS, the pre-processing step—the assembly of the phylo-k-mer database—is relatively time-consuming. This database, however, needs to be assembled only once for a set of reference sequences. This is a considerable advantage of RAPPAS if multiple sets of query reads are placed on the same set of reference sequences. On these two datasets, App-SpaM performs 30–60 times faster than the next fastest program (EPA-ng) and 3–5 times faster than the placement step of RAPPAS. On CPU-652, App-SpaM has the lowest memory footprint and on CPU-512 the second lowest behind APPLES (see Supplementary Section S3.4). In the large runtime example on the tara-3748 dataset, App-SpaM placed a total of 37 480 000 queries in 613 min with parallel execution on 30 threads. When the pattern weight is increased to w = 16 the runtime drops to 475 min.

Table 2.

Runtime comparison of programs

	App-SpaM		RAPPAS		APPLES	EPA-ng	EPA	pplacer
	w = 12	w = 16	k = 6	k = 8
CPU-652
Pre-proc.	—	—	651	7253	3437	3437	3437	3437
Placement	152	79	710	454	2804	1315	194338	9257
Total	152	79	1361	7707	6241	4752	197775	12694
CPU-512
Pre-proc.	—	—	1070	12144	1879	1879	1879	1879
Placement	34	22	254	185	348	127	6626	1976
Total	34	22	1324	12329	2227	2006	8505	3855

Notes: Comparison of runtimes for all tested programs on two datasets. 10 000 queries were placed for CPU-512 and 100 000 queries for CPU-652. All runtimes are shown in seconds. For each dataset, we show the time for pre-processing (pre-proc.), placement and the total sum of pre-processing and placement with default parameters. Pre-processing includes generating the query alignment or building the phylo-k-mer database for RAPPAS.

4 Discussion

In this paper, we proposed a new method for phylogenetic placement called App-SpaM. To estimate phylogenetic distances, App-SpaM uses inexact word matches, so-called SpaMs, that are based on a binary pattern of match and don’tcare positions (Leimeister et al., 2017). As previously shown, such spaced-word matches can be used to accurately estimate phylogenetic distances based on the number of mismatches per position at the don’tcare positions. In the present paper, we applied this approach to the problem of phylogenetic placement, by estimating distances between query and reference sequences.

We are using sets of filtered SpaMs as a substitute for full pairwise sequence alignments of the input sequences. A SpaM can be seen as a pairwise local alignment of a given length that, by definition, does not include gaps. Thus, strictly spoken, this approach can only deal with un-gapped homologies; insertions and deletions (indels) can introduce a certain bias in our approach: If a local homology contains an indel, it is possible that an SpaM correctly aligns homologous sequence positions to each other on one side of the indel, but then aligns non-homologous positions on the other side. Since the score of such an SpaM may still be above the filtering threshold, such ‘partial homologies’ can pass our filtering procedure and would then be used to estimate the phylogenetic distance between the two sequences. As a result, the average number of substitutions per position—i.e. the Jukes–Cantor distance of the sequences—would be over-estimated. We investigated the influence of indels on the accuracy of the estimated distances based on simulated sequence data (Leimeister et al., 2017). The result was that, even in the presence of indels, our approach still provides fairly accurate distance estimates.

Our extensive evaluation shows that App-SpaM’s accuracy is close to the accuracy of the best-performing likelihood-based methods on most benchmark datasets that we used, see Figure  3. One exception is a set of complete viral genomes (hiv-104), where App-SpaM performed not as accurate as the competing programs that we evaluated. In contrast, App-SpaM achieved the best placement accuracy out of all programs that we tested on two other datasets: a large set of 16S sequences (tara-3748) and a set of fungal 5.8S sequences (epa-628). The runtime of App-SpaM on these datasets was considerably faster than for the alternative methods.

We also presented five different placement heuristics for App-SpaM in this paper. Two of them performed best across all datasets, namely LCA-Count and SpaM-4. There are situations, however, where SpaM-4 is superior to LCA-Count. If a leaf labelled with some reference sequence S_i is far away from the other leaves in the reference tree, but the distance between a query read q and S_i is small, then LCA-based methods would place q at the proximal branch of the node connecting S_i and its neighbour in the tree. The query would, thus, be placed far away from S_i. In contrast, our heuristic SpaM-4 would be able to correctly place q near the leaf labelled with S_i. Therefore, SpaM-4 is the default version of our program; we advise the user to always use App-SpaM with the default settings.

In comparison to existing programs, besides APPLES, App-SpaM does not rely on a multiple sequence alignment of the reference sequences. This gives App-SpaM distinct advantages over existing, alignment-based programs: Calculating a reference MSA in a pre-processing step is time-consuming, and errors in the reference alignment can be a source of errors in the placement results. Moreover, if the homologies between the reference sequences are not co-linear, due to evolutionary events such as genome rearrangements, it is not possible to find a meaningful multiple alignment for them in the first place. This advantage of App-SpaM also implies that it does not require assembled reference sequences as input, but can be applied to taxa for which only unassembled reads are available. Genome assembly is still a non-trivial task (Padovani de Souza et al., 2019; Sohn and Nam, 2018), and wrongly assembled reference sequences can be a source of errors in phylogenetic placement. Also, for a growing number of genomes, only unassembled reads are available, often with low sequencing depth (Coissac et al., 2016; Dodsworth, 2015). For this, as a proof of concept, we performed phylogenetic placement on two datasets of viral and bacterial genomes of varying coverage, respectively. Here, the placement accuracy predominantly depends on the coverage of the reference sequences. In general, with unassembled references, the placement is not as accurate as when using assembled references but it approaches similar accuracy if the sequencing coverage is sufficiently high. However, the placement on unassembled references also comes at the cost of an increased variance of the placement accuracy: Here, accurate placement is only possible for those query reads where the corresponding homologous regions are also present in the ‘bags of reads’ of the references.

In this context, another certain difficulty for our SpaM approach can be caused by low-complexity regions in the input sequences, e.g. by long runs of ‘ATATATATAT’. If such runs would be present in both compared sequences, a large number of SpaMs with 100% matches at the don’t care positions would be found. For the viral and bacterial sequences used in this paper, low-complexity regions are not an issue. However, we would recommend to filter out low-complexity regions prior to running our software on eukaryotic sequences by using a software such as RepeatMasker (Smit and Green, 2015).

Another drawback of App-SpaM, as well as APPLES, compared to other programs, is their inability to describe the uncertainty of inferred placement locations. While App-SpaM only reports a single placement location for every query sequence, other programs can specify multiple placement locations for a single query read and assign weights to these locations according to their likelihood, so-called likelihood-weight ratios.

We used the benchmarking system PEWO for our evaluations to ensure clearly defined and reproducible evaluation workflows. A certain draw-back of PEWO is the fact that it simulates query reads by simply splitting the pruned reference sequences into segments of the desired read length; sequencing errors are not modelled. To evaluate our method under more realistic conditions, we performed additional test runs with simulated query reads obtained with the simulation software ART (Huang et al., 2012), within the PEWO framework. Unlike PEWO, ART models sequencing errors. A conspicuous result of these test runs is that our method outperformed all other approaches substantially when we used reads simulated by the ART software (see Supplementary Section S4).

There are several possibilities to further improve App-SpaM. The placement heuristics that we implemented so far depend either on the number of spaced-word matches or on the estimated phylogenetic distances between a query read and the references. However, both sources of information may complement one another, so improved placement results might be obtained by combining both measures of distance and similarity, respectively. Such a placement method could also be used to express placement uncertainty similar to the likelihood-weight ratios used by ML-based methods. Hence, we are continuing to work on additional placement heuristics that use all available information to fully utilize the spaced-word matches approach for phylogenetic placement. Moreover, while the runtime of App-SpaM is already fast, the current implementation is not yet optimized for speed and memory efficiency and multiple strategies to further decrease the runtime are possible: All spaced words are held in main memory in a non-optimized data format instead of referencing the corresponding positions in the input sequences. This significantly increases the runtime and memory usage and can be improved by more efficient data handling. Given the test results shown in this study, App-SpaM should already be a useful tool for performing phylogenetic placement on large datasets and efforts should be made to further improve its accuracy and efficiency.