Concentrated poverty, ambient air pollution, and child cognitive development

Abstract

Why does growing up in a poor neighborhood impede cognitive development? Although a large volume of evidence indicates that neighborhood poverty negatively affects child outcomes, little is known about the mechanisms that might explain these effects. In this study, we outline and test a theoretical model of neighborhood effects on cognitive development that highlights the mediating role of early life exposure to neurotoxic air pollution. To evaluate this model, we analyze data from a national sample of American infants matched with information on their exposure to more than 50 different pollutants known or suspected to harm the central nervous system. Integrating methods of causal inference with supervised machine learning, we find that living in a high-poverty neighborhood increases exposure to many different air toxics during infancy, that it reduces cognitive abilities measured later at age 4 by about one-tenth of a standard deviation, and that about one-third of this effect can be attributed to disparities in air quality.

Early exposure to neurotoxic air pollution partly explains the harmful effects of neighborhood poverty on cognitive development.

INTRODUCTION

The United States stands out among economically advanced democracies for the depth and expanse of its poverty (1). Concentrated poverty in particular, which refers to the high incidence of economic deprivation in specific neighborhoods or geographic areas, is among its most disturbing and persistent problems. Since the “War on Poverty” in the 1960s, the proportion of families living in high-poverty neighborhoods has remained stubbornly high, and despite impressive progress in other areas, the problem deepened in recent decades as income inequality increased and lower income families became more spatially isolated from those with higher incomes (2, 3). The deteriorating situation portends a troubled future: A large volume of evidence indicates that, above and beyond family hardships, growing up in a poor neighborhood leads to diminished cognitive abilities (4), lower levels of educational achievement (5, 6), and worse economic fortunes in adulthood (7, 8).

Although the effects of neighborhood poverty on children have been extensively studied, their etiology remains poorly understood (9–11). Few analyses investigate the mechanisms thought to mediate, or explain, the impacts of growing up in a poor neighborhood, and a frequent criticism of research in this area is that neighborhood effects “have remained largely a black box” (12). In other words, “research findings…are too scant to draw any firm conclusions about the potential pathways through which neighborhood effects may be transmitted” (13). As a result, prior research on the effects of concentrated poverty has limited capacity to inform public policy because it reveals little about intermediate mechanisms that might serve as points of effective intervention.

Most studies of concentrated poverty hypothesize that its effects operate through social, cultural, or institutional pathways, such as differences in collective supervision (12), local norms and values (14), or school quality (15). These pathways, however important, are primarily relevant for older children and adolescents, although socioeconomic disparities in child development become entrenched during the first few years of life and change little thereafter (16–18). Human abilities are formed in a predictable sequence, where children are most sensitive to environmental inputs early during the course of development and later attainments are constrained by the foundations laid down earlier (17). It follows that the search for mechanisms linking neighborhood poverty to developmental outcomes should begin during early childhood.

Integrating research from the social sciences, neurology, and environmental epidemiology, we hypothesize that differences in early life exposure to contextual health hazards, and neurotoxic air pollution in particular, may help to explain the effects of neighborhood poverty on cognitive development (19). Because major roadways and other noxious infrastructure are more likely to be located in, near, or upwind of poor neighborhoods (20, 21), their residents are disproportionately exposed to air pollutants (22, 23), many of which harm the central nervous system. Young children are especially vulnerable (24, 25). They breathe more air per unit of body weight, absorb some chemicals more easily and efficiently, and have developing biological systems that are highly plastic. If growing up in a poor neighborhood impedes cognitive development, differences in exposure to neurotoxic air pollution may therefore play an explanatory role. In this study, we investigate whether exposure to air pollution during early childhood mediates the effects of living in a poor neighborhood on reading and math abilities measured around the time of school entry. Relatedly, we also examine which toxics among a large number of different organic compounds, gases, metals, and fine particulates are most closely linked with concentrated poverty and which, in turn, are the strongest predictors of subsequent skill formation.

Theoretical model

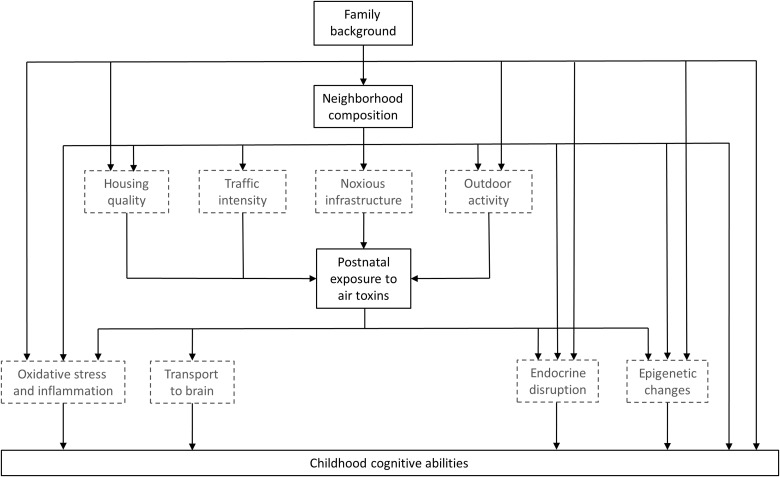
Figure 1 provides a graphical representation of our hypothesized causal model. In this figure, nodes represent variables and arrows represent causal relationships between them. The variables depicted in solid black boxes are those we are able to measure directly in the present study, while the variables in dashed gray boxes represent intermediate factors that we do not observe.

Fig. 1. A graphical causal model.

This figure describes the hypothesized causal process linking concentrated poverty to child cognitive ability via exposure to ambient air pollution. The dashed gray boxes denote intermediate factors that are not measured in the present study.

The figure shows that the socioeconomic composition of a child’s neighborhood affects their exposure to air pollution, consistent with prior research linking neighborhood poverty to higher concentrations of many different toxics (21–23). This pattern of environmental inequality is a function of several interrelated processes, including the siting of toxic infrastructure, traffic intensity, and residential sorting, which are closely related to race and class. The United States industrialized during a period of de jure racial segregation, and this created distinct and unequal patterns of infrastructure development across its communities. From this historical foundation, wealthier areas with fewer racial minorities were disproportionately shielded from noxious land use and development, cementing many environmental inequalities firmly in place. For example, governments and businesses typically confront the dilemma of where to place polluting infrastructure, such as factories and highways, by pursuing the “path of least political resistance” (20). This path often leads to communities with many poor and minority residents because they are not as well equipped as their more affluent counterparts to mount effective opposition. Once certain neighborhoods become highly polluted, families with the necessary means will pay to avoid them (26), tightening the connection between residential composition and outdoor air pollution.

Children in poor neighborhoods, however, may spend less time outdoors owing to parental fears about crime and safety or deficiencies of the built environment (27, 28). These differences in outdoor activity may partly shield resident children from the elevated levels of ambient air pollution often found in poor communities. Nevertheless, high-poverty neighborhoods also tend to have an older and more dilapidated housing stock, which may allow greater concentrations of outdoor pollutants into the household via damaged windows, doors, or weather-stripping (29, 30). Thus, wherever children spend their time, growing up in a high- versus low-poverty neighborhood may disproportionately expose them to a variety of different toxics in the air they breathe.

Figure 1 also shows that exposure to air pollution, in turn, affects child cognitive abilities. Prior research indicates that postnatal exposure to several different air pollutants—specifically, fine particulate matter, nitrogen oxides, ozone (O₃), and a number of heavy metals, such as lead (Pb), arsenic (As), and mercury (Hg)—is associated with subclinical deficits in cognitive test scores (31–33). It has also been linked with attention deficit hyperactivity disorder (ADHD) symptoms and externalizing behavioral problems in pediatric populations (34), among several other indicators of poor health, such as asthma and infant mortality (35, 36). Although the biological processes connecting air pollution to cognitive impairment are not as well established, emerging evidence implicates oxidative stress and inflammation, endocrine disruption, epigenetic changes, and alterations in brain structure (24). For example, exposure to fine particulate matter is correlated with reduced cortical thickness and thinner gray matter, which may influence information processing, learning, and memory (37, 38).

In sum, poor neighborhoods are disproportionately contaminated by air pollution, and many of these toxics are known or suspected to affect cognitive outcomes, especially when exposure occurs early during the course of child development. Thus, neighborhood poverty is hypothesized to inhibit formation of cognitive abilities during early childhood, in part, by increasing the risk of exposure to neurotoxic air pollution.

Research design

To evaluate our theoretical model, we follow n ≈ 10,700 children in the Early Childhood Longitudinal Study-Birth Cohort [ECLS-B; (39)] from wave 1, when sample members were infants around 9 months old, to wave 3, when they were age 4 years (all sample sizes are rounded to the nearest 100 in accordance with disclosure risk requirements from the U.S. Institute of Education Sciences). We match these children at wave 1 with multiple sources of information on their residential neighborhoods, defined using zip code tabulation areas (ZCTAs). Specifically, we match sample members in the ECLS-B to information on the socioeconomic composition of their neighborhoods from the GeoLytics Neighborhood Change Database [NCDB; (40)]. We also match them to outdoor concentrations for six “criteria air pollutants” monitored by the Environmental Protection Agency (EPA)—O₃, carbon monoxide (CO), sulfur dioxide (SO₂), nitrogen dioxide (NO₂), and particulate matter smaller than 10 μm (PM₁₀) and 2.5 μm (PM_2.5)—as estimated by the Center for Air, Climate, and Energy Solutions [CACES; (41)]. In addition to these pollutants, which arise mainly from mobile sources, we also match sample members to estimated outdoor concentrations of 46 different industrial-source neurotoxics from the EPA’s Risk-Screening Environmental Indicators Geographic Microdata [RSEI-GM; (42)]. With these matched data sources, we then analyze how living in a high- versus low-poverty neighborhood during infancy affects cognitive abilities measured later at age 4 and whether these effects are mediated by differences in exposure to air pollution.

Analyzing whether the effects of neighborhood poverty are mediated by air pollution presents several methodological challenges. First, consistently estimating these effects requires that exposure to concentrated poverty and to ambient air pollution are both unconfounded by unobserved factors. If unobserved confounding is present, then analyses of causal mediation may be biased and may lead to faulty inferences about the explanatory role of air pollution. Second, consistently estimating these effects also requires correctly modeling the relationship of child abilities to air pollution, neighborhood poverty, and a large set of observed confounders. This is especially challenging in the present study because air pollution is a diverse mixture of many different toxics. We measure exposures to more than 50 different types of air pollutants, including particulate matter, organic compounds, gases, and metals. Some of these toxics have atypical distributions (e.g., with large mass points at zero), and their relationship to cognitive ability may involve complex forms of nonlinearity and interaction (24, 31). Although most prior studies attempt to circumvent the challenge of high dimensionality by focusing on only one or just a handful of toxics, this approach could misrepresent whether and how air pollution may explain neighborhood effects if important chemicals are omitted.

We address these challenges by integrating methods of causal inference for observational data with supervised machine learning. To address the challenge of confounding bias, we adjust for the most powerful joint predictors of neighborhood selection and child cognitive outcomes that are measured by the ECLS-B, and we then construct a range of estimates under different hypothetical patterns of unobserved confounding in a formal sensitivity analysis (43). To address the challenge of high dimensionality, we implement a regression-imputation estimator for natural direct and indirect effects (44, 45) using random forests [RFs; (46, 47)]. An RF is an ensemble machine learning method that, by integrating recursive partitioning with random subspace selection and bootstrap aggregation, can accurately approximate complex forms of nonlinearity and interaction in high-dimensional data, including interactions among different air toxics. It is therefore well suited to constructing models of child cognitive ability from information on many different covariates and exposures to a large number of pollutants, which may combine in complex ways to produce their effects. A detailed description of our data, measures, and analytic procedure is provided in Materials and Methods.

Contribution

We extend research on concentrated poverty by providing, to our knowledge, the first empirical assessment of whether its effects on child cognitive development are explained by differences in early life exposure to neurotoxic air pollution. We also extend a growing body of work on environmental inequalities (21) and the neurological impacts of air pollution (24) by analyzing how exposures to a large set of pollutants differ across neighborhoods and predict cognitive abilities during early childhood in a national probability sample. On a technical level, we introduce methods for analyzing causal mediation with a high-dimensional set of putative mediators and with minimal functional form assumptions. Our approach has the potential for wide application in the social sciences, where the intermediate mechanisms thought to connect an exposure to an outcome are often numerous and complex.

In general, analyses of the mechanisms linking concentrated poverty with child development have broad implications. They are important for evaluating the consequences of residential segregation and the factors responsible for the reproduction of poverty from one generation to the next. They can also illuminate new points of intervention for policies intended to remediate these harms. Last, research on concentrated poverty, environmental inequality, and child development is also important for accurately diagnosing the etiology of many different social problems that stem, at least in part, from material deprivation during childhood.

RESULTS

In this section, we first present a set of descriptive results illustrating bivariate associations between concentrated poverty and air pollution. Next, we provide estimates that capture how early life exposures to air toxics would differ if children were born into a high- versus low-poverty neighborhood. We then present estimates for the total, direct, and indirect effects of living in a poor neighborhood during infancy on reading and math abilities measured at age 4. These estimates capture the degree to which differences in exposure to air pollution mediate the impact of concentrated poverty during early childhood. We conclude with a “mechanism sketch” (48), where measures of variable importance are consulted in an effort to identify which toxics, in particular, appear to play a central mediating role.

Place, poverty, and pollution

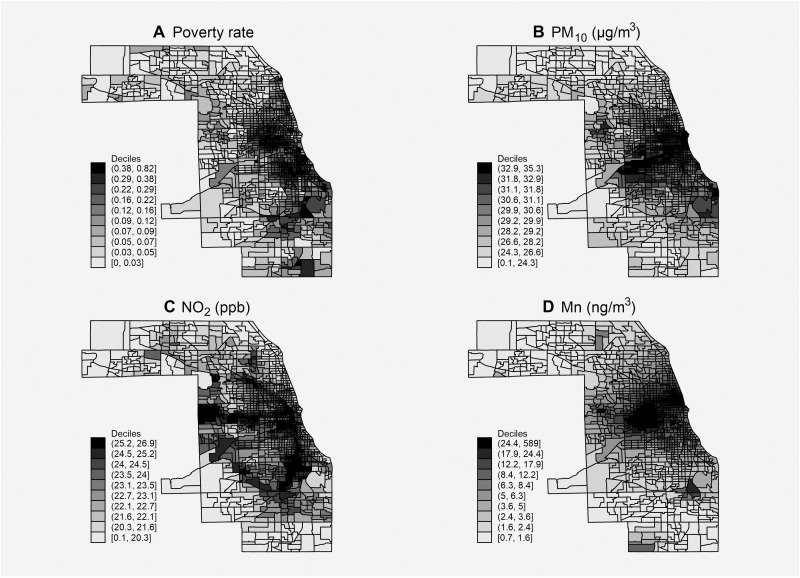
Figure 2 displays a set of chloropleth maps of Cook County, IL, depicting the spatial distribution of neighborhood poverty and selected air toxics in 2001, when the ECLS-B was beginning its first wave of data collection. Grayscale variations in the figure denote differences across census tracts in (i) the proportion of resident families that fall below the federal poverty threshold, (ii) concentrations of PM₁₀, (iii) concentrations of NO₂, and (iv) concentrations of manganese (Mn). We focus on Cook County, IL, which contains the City of Chicago, as an illustrative example because it is a large urban setting that suffers from both concentrated poverty and air pollution from multiple sources.

Fig. 2. Spatial distribution of poverty and selected air toxics, Cook County, IL, 2001.

(A) The poverty rate, (B) concentration of PM10, (C) concentration of NO2, (D) concentration of Mn Data sources: (40–42).

Several patterns are evident in these maps. First, poverty is concentrated mainly on Chicago’s South and West Sides, in several pockets on the North Side, and in several suburban communities located to the south of the city. Many of these neighborhoods are also predominantly Black or Hispanic, reflecting the city’s history of extreme racial segregation. Second, NO₂, which arises mainly from vehicle emissions, is concentrated along the major expressways that traverse the city. Because the expressways tend to abut neighborhoods with relatively higher poverty levels, these factors—NO₂ and concentrated poverty—appear weakly correlated. Third, PM₁₀ also appears weakly correlated with neighborhood poverty, as this pollutant is disproportionately concentrated on the South and, to a lesser degree, the West side of the city. Fourth, Mn, a neurotoxic heavy metal that arises mainly from manufacturing facilities, is concentrated in several industrial sections of the metro area that tend to be located in or near relatively poorer neighborhoods. Last, although concentrated poverty and the distribution of these toxics are associated in Cook County, neighborhoods with low poverty levels and high pollutant concentrations still exist in nontrivial numbers throughout the area.

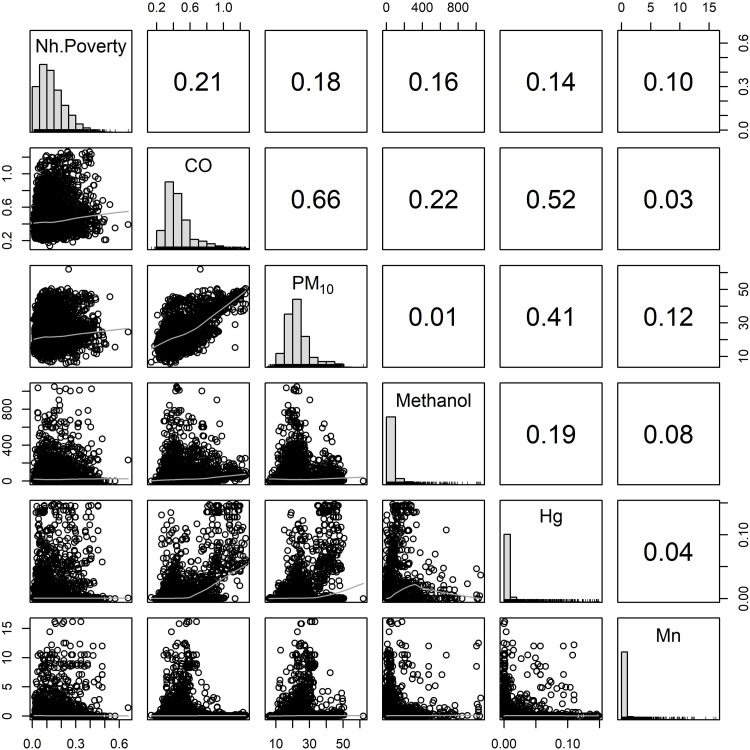
Because of its deeply concentrated poverty and history as a major industrial center, Chicago is an ideal but not representative site for illustrating patterns of environmental inequality. Figure 3 displays a scatterplot matrix describing the association of neighborhood poverty and exposure to another set of selected air toxics among a national sample of children in the ECLS-B, when they were about 9 months old. The main diagonal of the matrix presents histograms summarizing the marginal distribution of each pollutant, while the upper and lower triangular cells contain Pearson correlation coefficients and bivariate scatterplots, respectively. Consistent with the spatial patterns outlined previously in Cook County, IL, these results also show that neighborhood poverty is modestly correlated with exposure to several air pollutants on a national scale. The strongest correlations are observed with CO and PM₁₀. Weaker yet still noteworthy correlations are observed with methanol, Hg, and Mn, although the corresponding scatterplots indicate that a measure of linear association may not capture these relationships very well. Table S1 summarizes differences in exposure to all 52 toxics considered in this study across levels of neighborhood poverty among ECLS-B sample members. Overall, this table is consistent with the selected results presented in Figs. 2 and 3. It indicates that infants living in neighborhoods with high rates of poverty are more likely to be exposed to many different air toxics, although differences in exposure are often modest or appear nonlinear, and in several cases that we discuss below, the relationship is inverted.

Fig. 3. Scatterplot matrix of neighborhood poverty and selected air toxics.

The upper diagonal of the matrix presents Pearson correlation coefficients. The lower diagonal presents scatterplots with kernel regression smooths in light gray. Results are reported for a single imputation. Data sources: (39–42).

Effects of neighborhood poverty on exposure to air toxics during infancy

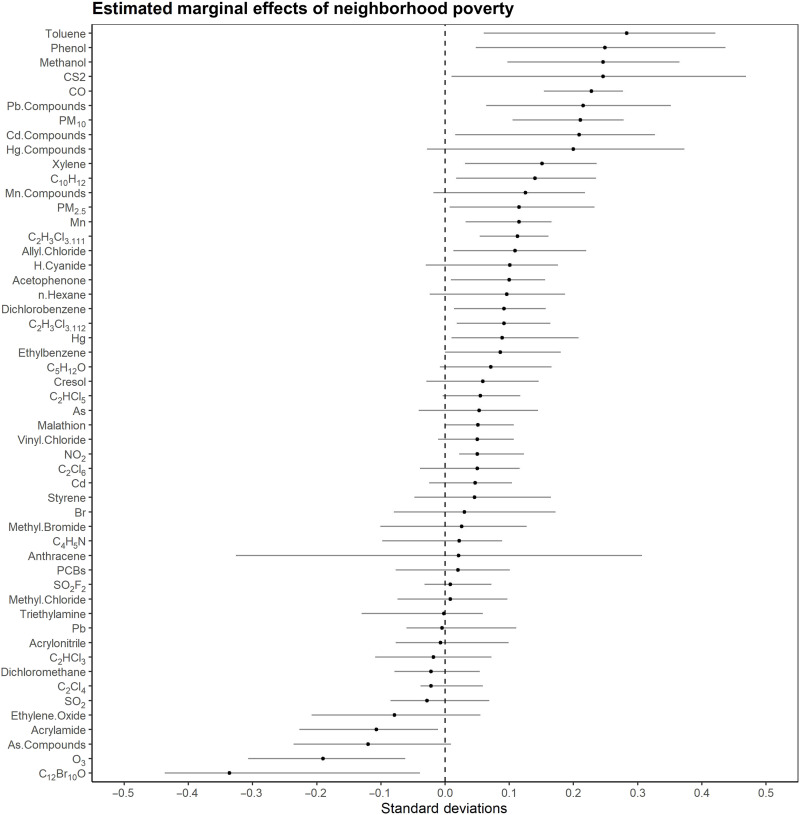
Figure 4 displays a dot-and-whisker plot summarizing the estimated marginal effects of neighborhood poverty on exposure to each of the 52 different air toxics considered in this analysis. These estimates contrast living in a neighborhood with a poverty rate of 25%, rather than 5%, during infancy, which roughly correspond to the 90th and 20th percentiles of the national exposure distribution, respectively. They are computed using RFs fit to data from the ECLS-B. For each toxic, the model is trained to predict exposure as a function of neighborhood poverty and the large set of potential confounders listed in table S2. The horizontal axis of the figure displays point estimates and [2.5, 97.5] percentile bootstrap intervals in standard deviation (SD) units, while the vertical axis displays each toxic sorted in descending order by effect size.

Fig. 4. Estimated marginal effects of neighborhood poverty on exposure to ambient air toxics during infancy.

Estimates are computed from RFs and contrast residence in a neighborhood with a poverty rate of 25% versus 5%. They are weighted and combined across five imputations. Confidence intervals are based on the [2.5, 97.5] percentiles of a pooled sampling distribution simulated via the repeated half-sample bootstrap with 1000 replications per imputation. Data sources: (39–42).

The estimates in this figure indicate that living in a high-poverty neighborhood increases exposure to many different air toxics by a nontrivial margin. Some of the largest effects of neighborhood poverty are observed for toluene, methanol, CO, and fine particulate matter. For example, living in a neighborhood with a poverty rate of 25%, rather than 5%, is estimated to increase exposure to each of these toxics by about 0.2 to 0.3 SDs, net of other factors. Neighborhood poverty also has nontrivial effects on exposure to several heavy metals emitted into the air by industrial facilities. In particular, living in a high- rather than low-poverty neighborhood is estimated to increase exposure to Mn and its compounds, Pb compounds, Hg, and cadmium (Cd) compounds. Exposure to a number of different petrochemicals, such as xylene, n-hexane, and ethylbenzene, is also elevated in high- compared to low-poverty neighborhoods.

Although living in a poor neighborhood increases the risk that infants are exposed to many different air toxics, Fig. 4 indicates that there are also chemicals for which neighborhood poverty has little effect or may even reduce exposure. For example, neighborhood poverty has no appreciable effect on exposure to industrial-source air pollution composed of several well-known and highly neurotoxic chemicals, including polychlorinated biphenyls (PCBs) and hydrogen cyanide. Furthermore, living in a neighborhood with a poverty rate of 25%, rather than 5%, is estimated to reduce exposure to O₃ by nearly 0.2 SDs (or about 1.25 parts per billion), net of measured controls. As a secondary pollutant, O₃ is not emitted directly into the air. Rather, it is formed by the influence of solar radiation on nitrogen oxides and hydrocarbons, which arise largely from vehicle emissions. It is also a highly reactive molecule that is easily degraded back into its precursors. A consequence of this is the so-called ozone paradox: O₃ levels tend to be lower in areas where there is greater traffic pollution, and thus a higher availability of nitrogen oxide (NO), which reacts with O₃ to form NO₂ and O₂ (49). As a result, poor neighborhoods tend to be contaminated by higher levels of NO₂ and other vehicle emissions, but lower levels of O₃, by virtue of their proximity to sources of traffic pollution.

Living in a high-poverty neighborhood also appears to reduce exposure to decabromodiphenyl ether (C₁₂Br₁₀O), although the interval estimate is rather imprecise. C₁₂Br₁₀O is a flame retardant used in the manufacture of several different consumer products, such as televisions and upholstered furniture. It is emitted by a relatively small number of facilities in the United States, and the largest of these polluters are located in or near higher-income areas, possibly because production of C₁₂Br₁₀O is an emergent industry and thus more likely to be housed in modern facilities constructed during an era of environmental regulation and not during earlier periods of central city industrialization.

Together, these results suggest that the causal process by which air pollution may mediate the effect of neighborhood poverty on cognitive development is quite complex, with several pathways involving toxics that operate in different, potentially offsetting directions. Nevertheless, the weight of the evidence from Fig. 4 indicates that living in a poor neighborhood generally increases the risk that resident children are exposed to many different pollutants that are known or suspected neurotoxics.

It is important to note that Figs. 2 to 4 compare concentrations of pollutants that are not adjusted for their variable neurotoxicity or effects on cognitive development. As some air toxics are more harmful than others, small differences in exposure to highly neurotoxic pollutants may be more consequential for cognitive development than are large differences in exposure to pollutants with relatively lower neurotoxicity. In the sections below, we examine whether exposure to any of these pollutants mediates the effect of neighborhood poverty on cognitive ability, and we then identify which toxics are most strongly linked with both child abilities and residence in a poor neighborhood.

Effects of neighborhood poverty on cognitive ability during early childhood

Table 1 presents point and interval estimates for total, direct, and indirect effects of living in a poor neighborhood on child cognitive ability. These estimates describe the effects of living in a neighborhood with a poverty rate of 25%, rather than 5%, during infancy on scores from standardized assessments of reading and math skills administered later at around age 4. They are computed using the method of regression-imputation (44, 45), which is a generic algorithm for simulating counterfactual outcomes from observed data, implemented with a set of RFs. In this analysis, the RFs are trained to predict test scores as a function of neighborhood poverty, exposures to more than 50 different air toxics, and a full set of baseline covariates. Confidence intervals are based on the [2.5, 97.5] percentiles of a bootstrap sampling distribution.

Table 1. Total, direct, and indirect effects of neighborhood poverty on reading and math test scores.

Notes: Estimates are reported in SD units and are computed using regression-imputation and RFs; they are weighted and combined across five imputations; confidence intervals are based on the [2.5, 97.5] percentiles of a pooled sampling distribution simulated via the repeated half-sample bootstrap with 1000 replications per imputation. Data sources: (39–42).

Estimands	Point estimate	[2.5, 97.5] Percentile bootstrap interval
Reading test scores
Average total effect	−0.088	[−0.154, −0.051]
Natural direct effect	−0.056	[−0.095, −0.031]
Natural indirect effect	−0.032	[−0.068, −0.013]
Math test scores
Average total effect	−0.116	[−0.176, −0.051]
Natural direct effect	−0.077	[−0.132, −0.032]
Natural indirect effect	−0.040	[−0.063, −0.013]

Estimates of the average total effect (ATE) suggest that living in a high-poverty neighborhood during infancy has a negative impact on reading and math abilities measured around the time of school entry. Specifically, they indicate that early life residence in a neighborhood with a poverty rate of 25%, rather than 5%, reduces reading abilities by 0.088 SDs and math abilities by 0.116 SDs. To put the size of these effects in perspective, they are roughly equivalent to the learning losses that would typically occur as a result of missing 1 month of elementary schooling (18). They are also comparable to effect estimates reported previously in both observational and quasi-experimental studies of neighborhood effects (4).

The ATE can be additively decomposed into the sum of a so-called natural direct effect (NDE) and a natural indirect effect (NIE) of neighborhood poverty (50). The NDE represents the expected difference in cognitive ability due to residence in a high- versus low-poverty neighborhood if each child were exposed to the configuration of air toxics that they would have experienced in a low-poverty neighborhood. It captures an effect of neighborhood poverty operating through all mechanisms other than those involving exposure to the measured air pollutants. The NIE, by contrast, represents the expected difference in cognitive ability if children lived in a high-poverty neighborhood but were then exposed to the configuration of air toxics that they would have experienced living in a high- rather than low-poverty area. It captures an effect of neighborhood poverty that jointly operates through exposure to all of the different pollutants considered in this analysis.

Estimates of the NDE and NIE suggest that the total effect of neighborhood poverty on cognitive development is mediated by exposure to air pollution. Specifically, estimates of the NIE indicate that if children lived in a neighborhood during infancy with a 25% poverty rate and then were exposed to the configuration of air toxics that they would encounter in this high-poverty neighborhood, rather than the pollutants they would encounter in a neighborhood with only a 5% poverty rate, their reading and math abilities would decline by about 0.03 to 0.04 SDs. These effects are small in substantive terms, but nevertheless, they suggest that exposure to air pollution at least partially mediates the impact of neighborhood poverty on cognitive development during early childhood. Dividing point estimates for the NIE and by those for ATE indicates that exposure to air pollution may explain about one-third of the overall impact of neighborhood poverty on both reading and math abilities at this development stage. The weight of the evidence therefore suggests that early life exposure to air pollution represents a nontrivial pathway through which concentrated poverty affects cognitive outcomes.

Estimates of the NDE, however, also clearly signal that exposure to air pollution is not the only mechanism through which concentrated poverty may affect early childhood development. The direct effects in Table 1 indicate that if children lived in neighborhoods with a poverty rate of 25%, rather than 5%, and then were exposed to the configuration of air pollutants they would have encountered in the low-poverty neighborhood, their reading and math test scores would still decrease by 0.056 and 0.077 SDs, respectively. This suggests that, while air pollution appears to play a noteworthy mediating role, the effects of concentrated poverty on early cognitive development also operate through other unobserved mechanisms. These may include exposure to environmental health hazards beyond those circulating in the outside air, more limited access to high-quality childcare, or the biological stress response to local violence, among other mechanisms that plausibly operate during early childhood but await empirical scrutiny (10).

Our estimates of direct and indirect effects only have a causal interpretation under several strong assumptions about the absence of unobserved confounding. These include assumptions that the relationships of neighborhood poverty and ambient air pollution with cognitive ability are both unconfounded by unobserved factors. If either of these assumptions is violated, our estimates would be biased. We attempt to mitigate these threats to causal inference by controlling for the most powerful joint predictors of residential selection and child cognitive outcomes, such as parental education, household income, and family structure, but the possibility of unobserved confounding remains. For example, we lack direct measures of parenting skills, which may affect selection into poor or polluted neighborhoods and is also a determinant of child development.

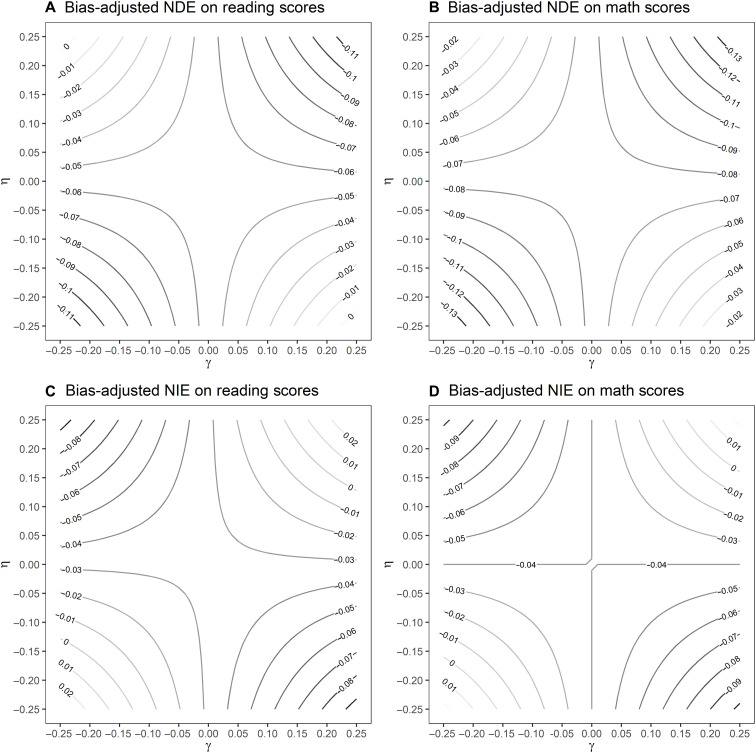
To assess the sensitivity of our estimates to different hypothetical patterns of unobserved confounding, Fig. 5 displays a set of contour graphs that plot bias-adjusted estimates of the NDE and NIE across values of two parameters, γ and η, that express the form and magnitude of unobserved confounding. The γ parameter represents the mean difference in cognitive ability associated with a unit increase in a hypothetical unobserved confounder, conditional on all other predictors. Similarly, η represents a mean difference in the unobserved confounder across neighborhoods with a 25%, rather than a 5%, poverty rate, given all other predictors. If the unobserved confounder affects exposures to air pollution and cognitive ability, but not neighborhood poverty, estimates of the NDE and NIE suffer from biases given by γη and −γη, respectively, under a set of simplifying assumptions outlined in Materials and Methods. If, alternatively, the unobserved confounder only affects exposure to neighborhood poverty and cognitive ability, but not exposures to air pollution, then estimates of the NDE suffer from a bias equal to ηγ, while estimates of the NIE remain unbiased, under a similar set of simplifying assumptions.

Fig. 5. Sensitivity of effect estimates to unobserved confounding.

This figure presents contour plots of (A) bias-adjusted natural direct effects on reading scores, (B) bias-adjusted natural direct effects on math scores, (C) bias-adjusted natural indirect effects on reading scores, and (D) bias-adjusted natural indirect effects on math scores across values of the sensitivity parameters. Data sources: (39–42).

The adjusted estimates in Fig. 5 are computed by subtracting these bias terms from their corresponding point estimates. They are then plotted across a range of values for the sensitivity parameters using contour lines. Specifically, the contour lines in this figure denote values of the bias-adjusted estimates at different levels of the two sensitivity parameters given on each axis. Grayscale variations in the color of the contour lines are used to visually signal effect size, where lighter shades denote bias-adjusted estimates that are close to zero or positive. In other words, lighter contour lines demarcate regions of the graph where the bias-adjusted estimates provide little or only weak support for our theoretical model, and thus, they highlight values of the sensitivity parameters that would undermine our conclusions.

These plots suggest that our mediation analysis is moderately robust to unobserved confounding. Bias-adjusted estimates for the NDE remain negative and substantively large across all but fairly extreme values of γ and η. Adjusted estimates for the NIE are reduced to zero under less extreme but still nontrivial levels of unobserved confounding—for example, when γ = η = −0.15 SDs. To put these values in perspective, consider that the conditional mean difference in reading ability associated with a 1 SD increase in household income is about 0.1 SDs, net of other predictors, while roughly 0.25 SDs is the conditional mean difference in household income associated with living in a neighborhood where 25%, rather than 5%, of the residents are poor.

Which toxics play the most important mediating role?

The direct and indirect effects discussed previously evaluate whether exposure to any of the multiple different air toxics—considered together—explain the effects of neighborhood poverty on cognitive development, but they do not identify which pollutants may play the most important mediating role. Identifying specific causal pathways operating through single intermediate exposures is exceedingly difficult with a high-dimensional set of mediators and, in general, cannot be accomplished without strong assumptions about parametric form or causal ordering (50), none of which are defensible in this analysis. Nevertheless, we attempt to shed at least some light on this question by providing a descriptive mechanism sketch (48) aimed at identifying which air toxics are (i) the strongest predictors of test scores and (ii) most strongly predicted by neighborhood poverty.

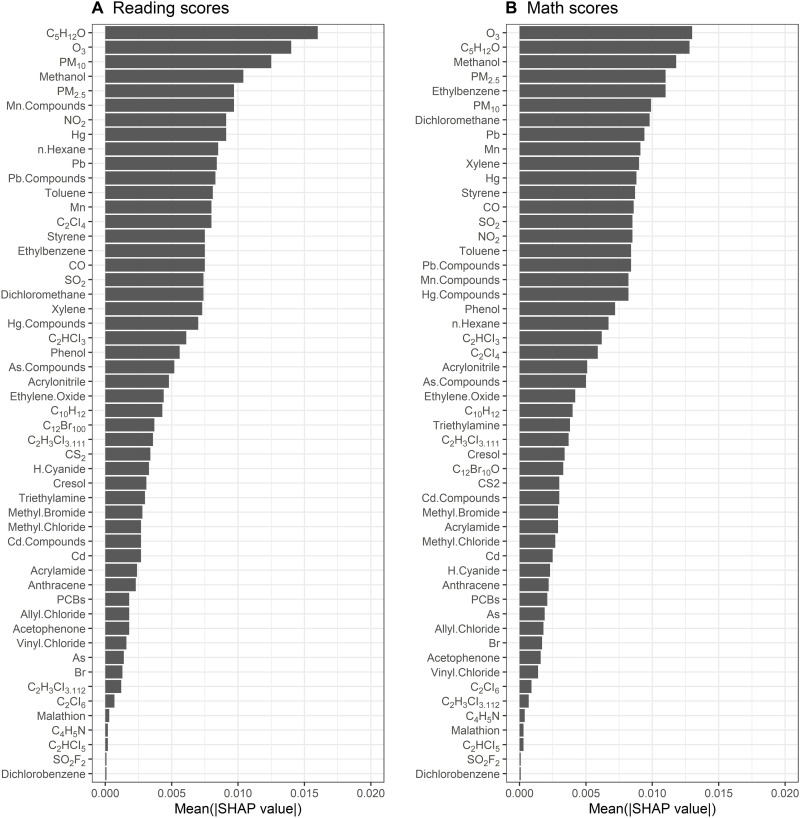
For each toxic included in this analysis, Fig. 6 summarizes Shapley additive explanation (SHAP) values from RFs predicting reading and math abilities. Mean absolute SHAP values measure the predictive importance of variables while taking account of potential interactions and collinearities among them (51). This is accomplished by comparing the predictions obtained with and without a variable in the model, where larger differences between these predictions signal greater importance. Because the order in which variables are added or excluded from a model can affect its predictions, these comparisons are made over every possible combination of covariates and then the differences are averaged together.

Fig. 6. Predictive importance of exposure to ambient air toxics during infancy for reading and math test scores at age 4.

This figure reports (A) mean absolute SHAP values for reading scores and (B) mean absolute SHAP values for math scores, both computed from RFs. Each RF includes neighborhood poverty, the full set of controls, and the full set of air toxics as predictors. Results are weighted and combined across five imputations. Data sources: (39–42).

The results in Fig. 6 indicate that, of all the air toxics considered in this analysis, exposures to O₃, NO₂, and particulate matter are among the more important predictors of reading and math abilities during early childhood. A number of heavy metals (Hg, Pb, Mn, and their compounds) and petrochemicals (C₅H₁₂O, methanol, xylene, toluene, styrene, n-hexane, and ethylbenzene) also appear to have a noteworthy degree of predictive importance. The importance of all these toxics, however, is relatively weak when compared against most sociodemographic variables. Figure S1 summarizes the SHAP values for every predictor considered in this analysis, not just the air toxics featured above. In this figure, for example, the mean absolute SHAP values for parental education and family income are about 0.15 and 0.08 SDs, respectively, based on the RF predicting reading scores. By contrast, this metric never exceeds 0.02 SDs for any single air toxic, although collectively the measured pollutants together have a nontrivial degree of predictive power. Note that the weak predictive importance of an air pollutant in these data should not be interpreted as evidence against its neurotoxicity; rather, it may simply reflect that sampled children are exposed only to low and thus relatively less toxic concentrations of a chemical in the ambient air of their neighborhoods—for example, exposure to hydrogen cyanide can lead to death within minutes at concentrations >200 μg/m³ of air, but it is not this harmful at the levels observed empirically in the ECLS-B, which range from 0 to 5.6 ng/m³.

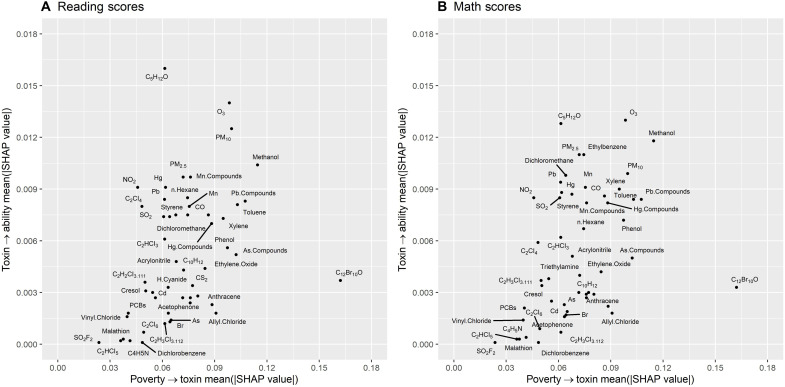
Figure 7 plots these measures against a second set of mean absolute SHAP values that capture the predictive importance of neighborhood poverty in a series of RFs modeling standardized exposures to each air toxic. Pollutants in or near the upper right quadrant of the plots are those that most strongly predict test scores and are themselves most strongly predicted by neighborhood poverty, which together suggest a potentially important mediating role. They include O₃, methanol, CO, and particulate matter as well as some of the heavy metals and petrochemicals mentioned previously.

Fig. 7. Predictive importance of exposure to ambient air toxics for cognitive ability classified against the predictive importance of neighborhood poverty for toxic exposure.

This figure shows, separately for (A) reading test scores and (B) math test scores, a scatterplot of air toxics classified according to (i) how strongly exposure predicts test scores and (ii) how strongly exposure is predicted by neighborhood poverty. Mean absolute SHAP values for each standardized toxic from RFs predicting test scores are plotted on the vertical axis, while mean absolute SHAP values for neighborhood poverty from RFs predicting standardized exposures to each toxic are plotted on the horizontal axis. Toxics located in or close to the top-right quadrant of the plots are those for which neighborhood poverty predicts exposure during infancy and for which exposure, in turn, predicts test scores. Results are weighted and combined across five imputations. Data sources: (39–42).

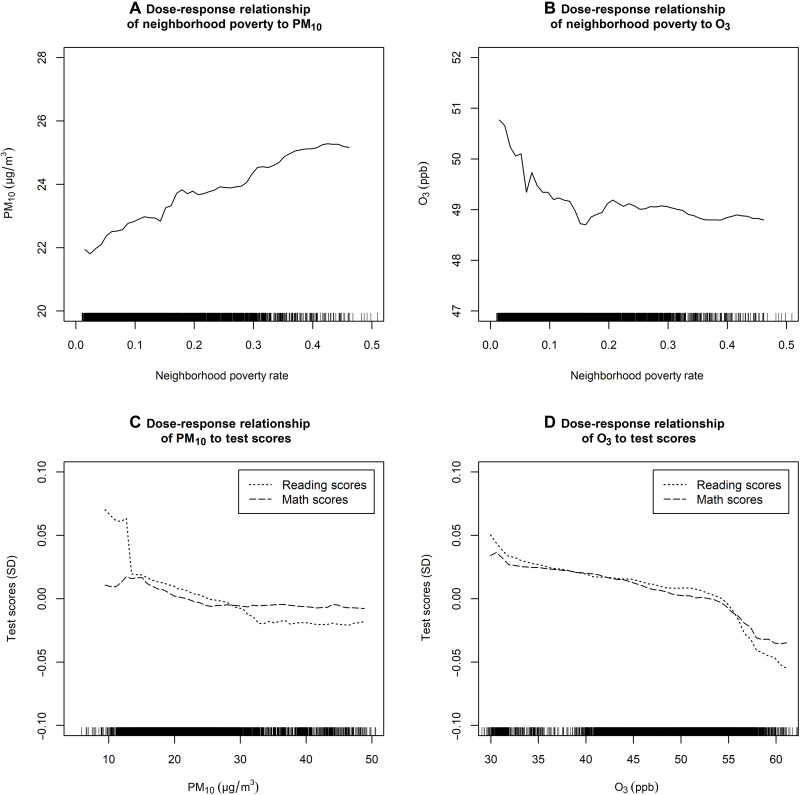
These different toxics, however, may not all transmit the effects of neighborhood poverty in the same manner. Figure 8 displays a set of partial dependence plots, which describe the marginal dose-response relationship between a predictor and an outcome. The top panel of the figure shows the relationship of neighborhood poverty with exposure to PM₁₀ and O₃, while the bottom panel shows the relationship between each of these chemicals and child test scores. Exposures to both PM₁₀ and O₃ during infancy are inversely related to reading and math abilities measured later at age 4, net of other predictors, but the relationship of neighborhood poverty with each pollutant differs. Consistent with results discussed previously, this figure shows that living in a neighborhood with an elevated poverty level is linked with exposure to higher concentrations of PM₁₀ but lower concentrations of O₃. This suggests that differences in exposure to particulate matter work to transmit the negative effects of early life residence in a poor neighborhood on cognitive development, while differences in exposure to O₃ may function to suppress them. These results must be interpreted cautiously, though, owing to the difficulty of isolating effects of single air toxics.

Fig. 8. Partial dependence plots for selected air toxics.

(A) Relationship of neighborhood poverty with exposure to PM₁₀. (B) Relationship of neighborhood poverty with exposure to O₃. (C) Relationship of PM₁₀ to child test scores. (D) Relationship of O₃ to child test scores. All results are weighted and combined across five imputations. Data sources: (39–42).

DISCUSSION

Why does growing up in a poor neighborhood negatively affect cognitive development? In this study, we provide evidence implicating early life exposures to neurotoxic air pollution. Specifically, we estimate that living in a high-poverty neighborhood increases exposure to many airborne neurotoxics and that the negative effects of neighborhood poverty on reading and math abilities during early childhood are mediated, at least in part, by these disparities in air quality. We also present preliminary evidence suggesting that, of all the toxics considered in this study, particulate matter, traffic-related pollutants, industrial-source heavy metals, and several petrochemicals may play the most important mediating role. However, the connection between concentrated poverty, air pollution, and cognitive development is complex. Our results suggest that these mediating pathways may not all operate in the same direction, and that no single pollutant or set of pollutants stand out from the others as a dominant explanatory mechanism. Rather, the causal process connecting neighborhood poverty to air pollution, and air pollution to cognitive ability, appears to involve the accumulation of many small effects, several of which may be partly offsetting.

This study has important implications for interdisciplinary research on concentrated poverty in sociology, developmental psychology, and economics. Although most prior research about the effects of concentrated poverty focuses on older children and posits mechanisms involving differences in socialization or institutional resources, we provide evidence that the etiology of neighborhood effects lies earlier during the course of development and is rooted in environmental inequalities (19). Our findings demonstrate how concentrated poverty is a “linked ecology of social maladies” (1), consisting not merely of material deprivation but also a morass of environmental health hazards, that may lead to neurological injury and impede the early stages of human development. Given that child cognitive skills predict many later life outcomes, such as higher earnings and better health in adulthood (52, 53), our results suggest that environmental inequalities may contribute to the reproduction of poverty from one generation to the next.

Our findings also have implications for the epidemiology of air pollution, which has previously focused mainly on cardiovascular and respiratory health (24). In particular, they contribute to an emerging literature on the effects of air pollution for early life cognitive development (31–33). Consistent with prior research in this area, we document that exposure to air toxics during infancy is linked with reading and math abilities measured around the time of school entry in a large, national, prospective study. In addition, we demonstrate the importance of considering the full set of air toxics to which young children are exposed. Because different toxics are linked in complex ways (e.g., O₃ and NO₂) and their overall impact on cognitive development appears to reflect the accumulation of many small effects, studies focusing on just one or only a handful of pollutants in isolation may provide an incomplete or possibly even misleading representation of the development impacts of air pollution.

An important policy implication of the present study is that interventions designed to improve environmental health may also promote upward social mobility. Regulations that reduce exposure to air pollution not only improve the health and well-being of the population overall but also may mitigate the harmful effects of concentrated poverty on early childhood development, thereby disrupting the intergenerational transmission of socioeconomic disadvantages. In other words, environmental policy may also function indirectly as anti-poverty policy, and these second-order effects should be accounted for in cost-benefit analyses of any program aimed at cleaning up the physical environment or otherwise reducing exposures to toxic hazards (54). Our results also point toward a potential role for small-scale public health interventions during a period of early life vulnerability. For example, disseminating technologies, such as indoor air filters, to childcare centers and households in poor communities or making targeted investments in housing repair (e.g., replacing damaged windows, doors, and weather-stripping) could potentially prevent early cognitive impairments that would otherwise reverberate throughout the later life course.

Although this study has important implications for research and policy, it is certainly not without limitations. In particular, it remains possible that our estimates overstate the magnitude of neighborhood effects and/or the mediating role of air pollution because of unobserved confounding, despite our best efforts to address this problem via covariate adjustment and a formal sensitivity analysis. Because the threat of unobserved confounding is ubiquitous in studies of causal mediation, our inferences are provisional and must be interpreted cautiously.

Nevertheless, several other limitations raise the possibility that our estimates may, in fact, be conservative. First, our measures of air pollution are subject to known error. They come from model-based estimates, and these models are themselves fit to imperfect data variously collected from air quality monitors or reports from industrial facilities. Because measurement error in a mediator can lead to attenuation bias in estimates of indirect effects, it is therefore possible that we have understated the explanatory role of air pollution.

Second, we focus only on point-in-time exposures during infancy, when it is likely that the effects of both concentrated poverty and air pollution accumulate over time if exposures to them are sustained (5, 24). Analyses that measure exposures cumulatively from birth through school entry could reveal more pronounced effects. Similarly, our narrow focus on the postnatal period is also a potential limitation, as exposure to neurotoxic pollutants earlier during gestation may have especially harmful effects on the central nervous system (24). By extension, prenatal exposure to air toxics could play an even more important mediating role connecting residential poverty to later cognitive development.

Third, although national data have many strengths, our estimates likely obscure a large amount of local heterogeneity. In some cities or metro areas, where the link between concentrated poverty and noxious infrastructure is especially tight, the mediating role of air pollution may be stronger, while in other areas that are less polluted, neighborhood effects may be weaker and alternative mechanisms would likely predominate. Unfortunately, we lack the data needed to precisely evaluate geographic variability in these causal processes. Moreover, the ECLS-B only allows for matching sample members to pollution concentrations at a relatively low geographic resolution (zip codes), when exposures to some air toxics can vary from block to block. If, within zip codes that are socioeconomically heterogeneous, poorer blocks tend to have higher levels of air pollution, our estimates may understate the causal process connecting concentrated poverty to child cognition via exposure to air toxics, as this process would operate at a more fine-grained spatial scale than we are able to observe.

Last, we also lack the data needed to empirically evaluate biological processes thought to connect air pollution with subclinical cognitive impairments. These processes may include neurological inflammation, alterations in brain structure, epigenetic changes, and interference with neurotransmitter release, cellular signaling, apoptosis, or protein synthesis, among several other mechanisms suggested by prior research (24, 37). Absent data on these intermediate factors, we cannot fully trace the hypothesized causal path from concentrated poverty to performance on cognitive tasks, as linked through pollution exposures and their biological consequences for developing children.

Despite its limitations, this study provides considerable evidence that differences in early life exposure to air pollution partly transmit the effects of neighborhood poverty on child cognitive development. Future research should elaborate on this causal process by identifying the cities in which it operates most strongly, by investigating whether the effects that compose it accumulate or intensify over time, by developing scalable interventions that might help to mitigate these harms, and by investigating the biological mechanisms thought to explain them. Our findings suggest that children in poor neighborhoods are—disproportionately and with alarming frequency—poisoned by their environments from the moment they take their first breaths. Amid growing public concern about economic inequality and environmental injustice, unraveling the link between poverty and pollution, and designing effective means to spare children their deleterious impacts, is essential.

MATERIALS AND METHODS

Data

To investigate whether exposure to neurotoxic air pollution mediates the effects of neighborhood poverty, we combine and analyze data from the ECLS-B, CACES, RSEI-GM, and NCDB. The ECLS-B is a multisource longitudinal cohort study sponsored by the U.S. Institute of Education Sciences. Designed to provide comprehensive data on early childhood development, the study followed a large national sample of children born in 2001 from infancy through kindergarten entry. Data were collected via caregiver surveys and direct child assessments for all sample members when they were approximately 9 months old (wave 1, fielded during 2001–2002), 2 years old (wave 2, fielded during 2003–2004), 4 years old (wave 3, fielded during 2005–2006), and just after they had begun kindergarten (waves 4 and 5, fielded during the fall of 2006 and fall of 2007, respectively, depending on when a child started school). The analytic sample for our analysis includes all n ≈ 10,700 children enrolled in the study at wave 1.

Restricted-access data from the ECLS-B identify the ZCTA in which sample members lived at each wave of the study. We use these data to match children with information on both the socioeconomic composition and the air quality of their residential area at wave 1. Formulated by the U.S. Census Bureau, ZCTAs are spatial representations of postal service delivery areas. They differ from census tracts—the geographic units most commonly used to define neighborhoods in studies of concentrated poverty—in that their boundaries are determined primarily by physical size rather than population. As a result, ZCTAs typically subsume several different census tracts in more densely populated areas, while in areas with lower population density, tracts are often larger. Like census tracts, ZCTAs may not reflect local perceptions of neighborhood boundaries, and owing to their larger geographic size in urban areas, they may blend together several distinct and potentially heterogeneous communities. Nevertheless, ZCTAs are the highest resolution data on residential location provided by the ECLS-B, and they provide a defensible, if also imperfect, proxy for neighborhoods.

Data on criteria air pollutants, which are composed of six common toxics monitored by the EPA in accordance with the Clean Air Act amendments of 1970, come from the CACES database. This database contains estimates of outdoor concentrations for O₃, CO, SO₂, NO₂, PM₁₀, and PM_2.5 throughout the United States. Concentration estimates are based on geographic regression models fit to measurements from EPA regulatory monitors. Using universal kriging, partial least squares, and several different approaches to covariate selection, the models use information on more than 300 geographic characteristics, such as measures of traffic intensity, land use, topography, and satellite data, to interpolate pollutant concentrations for areas between monitors. The optimal models typically achieve an out-of-sample predictive accuracy of 0.5 < R² < 0.9. Their estimates give annual-average concentrations at the census tract level, which we translate to ZCTAs using land area weights from the Census Geographic Correspondence Engine [Geocorr; (55)].

We also use data on a large set of other air toxics from the RSEI-GM, version 2.3.8. This database is constructed using information from the EPA’s Toxic Release Inventory (TRI) program, which requires manufacturing, mining, utility, hazardous waste, and chemical processing facilities to report their annual emissions of nearly 800 chemicals deemed toxic to human health. Similar to the CACES data, the RSEI-GM provides concentration estimates from air dispersion models that incorporate information on the source of the chemical release (e.g., smokestack versus valve leak), the chemical’s molecular weight and rate of decay, features of the local topography, and weather patterns around the facility. The models predict where the emitted chemicals were likely to have dispersed within a 49-km radius around each reporting facility, and the resulting database contains estimates for the amount of each chemical in every 1 km² of the United States. As before, we translate these estimates to ZCTAs using land area weights from Geocorr.

Data on the socioeconomic composition of neighborhoods come from the NCDB, version 2.1. The NCDB contains harmonized tract-level data on population characteristics collected as part of the 1970–2010 U.S. Censuses and the 2006–2010 American Community Surveys, which we translate to ZCTAs using Geocorr population weights. For intercensal years, we use linear interpolation to impute the demographic characteristics of neighborhoods.

Measures

The outcome of interest, denoted by Y, is child cognitive ability. We measure cognitive ability using reading and math assessments administered at wave 3 of the ECLS-B, when most children were 4 years old and had not yet entered kindergarten. These assessments were administered during a home visit by trained field interviewers. They were designed to evaluate skills across several domains, with an emphasis on abilities that are important for school readiness and that are typically covered by curriculum content, such as letter knowledge, word recognition, basic numeracy, and spatial relationships. Ability scores for reading and math are estimated from these assessments using a three-parameter item-response theory model, which accounts for differences in item difficulty and discrimination. These scores have desirable psychometric properties, including high reliability and validity and low differential item functioning (56). In all analyses, they are standardized to have zero mean and unit variance.

The exposure of interest, denoted by X, is the socioeconomic composition of a child’s neighborhood, or ZCTA, at wave 1 of the ECLS-B, when sample members were around 9 months old. We operationalize the socioeconomic composition of neighborhoods using an income poverty rate, which is computed as the ratio of families falling below the federal poverty threshold to the total number of families in a given area. Although poverty is multidimensional and the socioeconomic composition of neighborhoods can be measured with a wide variety of indicators, we focus on a conventional poverty rate because it is closely intertwined with the underlying social processes thought to be responsible for neighborhood effects, it is highly correlated with other dimensions of socioeconomic disadvantage, and it has a simple interpretation, unlike multidimensional scales. In table S3, we report effect estimates based on a composite index of neighborhood disadvantage, which combines information on income poverty, unemployment, education, family structure, and the racial composition of a sample member’s ZCTA. These effects are similar to those based on the poverty rate alone, although they are somewhat smaller and less precisely estimated.

The mediators of interest, collectively denoted by M = {M₁, …, M_j}, include all known or suspected air neurotoxics to which a nontrivial number of children are exposed at wave 1 of the ECLS-B and that have been consistently monitored by the EPA during the study period. Of the nearly 800 chemicals that are monitored in accordance with the TRI program, and thus are included in the RSEI-GM, 45 are classified by the EPA as known or suspected neurotoxics and developmental disruptors. This classification is based on the research synthesized in the EPA’s Integrated Risk Information System, the Office of Pesticide Programs’ Toxicity Tracking Reports, and the Agency for Toxic Substances and Disease Registry’s Toxicological Profiles, among several other sources. We include all but eight of these neurotoxics in our analysis. We exclude hydrogen sulfide because the TRI reporting requirements for this chemical were inconsistent during the ECLS-B study period, and we exclude cycloate, diazinon, dichlorvos, fenthion, propetamphos, thiodicarb, and triallate because less than 1% of children in the ECLS-B were exposed to them. Beyond the chemicals officially classified as neurotoxics in the RSEI-GM, we additionally include nine other pollutants from this database—anthracene, Cd, decabromodiphenyl ether, PCBs, and compounds that contain As, Cd, Pb, Mn, or Hg—based on our own independent review of research on pollution and child health, which indicated that there is at least some empirical evidence linking each of these pollutants to cognitive or neurological outcomes. Last, we include the six criteria air pollutants from the CACES database. In total, our vector of mediators contains concentration estimates for 52 air toxics in a child’s ZCTA of residence at wave 1 of the ECLS-B. Table S1 provides a complete list of all these pollutants, their units of measurement, and basic summary statistics about their distribution in our sample.

Because data from the RSEI-GM are based on facility reports subject to human error, it contains concentration estimates for some chemicals that appear to be extreme outliers. To address this problem systematically, we truncate and then multiply impute values above the 99th percentile in our analytic sample for all measures from the RSEI-GM. We also experimented with truncating values in the top 0.5% and the top 0.025% as well as with censoring rather than truncating values above these thresholds, all of which generated similar results.

To control for confounding, we measure and adjust for a large set of covariates in the ECLS-B, denoted by C = {C₁, …, C_l}. These include factors thought to have strong effects on neighborhood selection, the risk of pollution exposure, and child development or that are proxies for unobserved determinants of these variables. Specifically, we adjust for a child’s age at baseline and at the time of assessment, gender, race, birth weight, and whether they were part of a multiple birth. A child’s age is measured in months. Gender is coded as a binary variable denoting whether the child is male or female, as is our measure for whether the child was part of a multiple birth. Race is coded as a categorical variable capturing whether the child is white, Black, Hispanic, Asian, or another race. Birth weight is measured in grams.

We additionally adjust for the following characteristics of a child’s family at baseline: parental education, employment status, occupational status, and age, total family income, whether the family owns their home, whether a child’s biological father lives in the household, whether a child’s mother is currently married, the total number of household members, the primary language spoken at home, a measure of parental involvement in their child’s early education, and indicators for whether a family received several different types of government support. Parental education is defined as the highest level of education attained by either parent in a household, and it includes categories for “less than a high school diploma,” “high school diploma or equivalent,” “vocational/technical degree or some college education,” “bachelor’s degree,” and “graduate degree.” Maternal employment status is a categorical variable capturing whether the parent is currently “working 35 or more hours per week,” “working less than 35 hours per week,” or “not in the labor force.” For fathers, employment status is coded as a binary variable denoting whether or not this parent is working at all. Parental occupational status is measured using a variant of the Duncan Socioeconomic Index (57) and assigned on the basis of the parent with the highest score on this metric. Both paternal and maternal age are measured in years. The ECLS-B measures family income using interval response categories, and we imputed dollar values based on interval midpoints. Homeownership is a binary variable distinguishing between families that own and those that rent their place of residence. The presence of a child’s biological father is a binary variable indicating whether he currently lives in the same household as the child, while maternal marital status is another indicator variable that records whether a child’s mother is currently married. Household size is a count of the total number of individuals currently living within the child’s residence. We measure the home language environment with a binary variable indicating whether English is the primary language spoken in the household. Parental involvement in a sample member’s early education is defined as the amount of time the mother typically reads to her child, with response categories for “not at all,” “once or twice per week,” “three to six times per week,” or “every day.” Participation in government assistance programs is measured with a series of binary variables denoting whether, in the past year, the family received benefits from the Program for Women, Infants, and Children (WIC), the Supplemental Nutrition Assistance Program (SNAP), Medicaid, or Temporary Assistance for Needy Families (TANF).

Last, we also adjust for several ecological characteristics, including geographic region, urbanicity, and population density. Region is operationalized using census divisions, while urbanicity is a categorical variable that captures whether a child lives in an urban, suburban, or rural area. Population density refers to the number of people per square kilometer living in a child’s ZCTA of residence.

Estimands

To evaluate whether neighborhood effects are mediated by differences in exposure to neurotoxic air pollution, we focus on estimating total, natural direct, and natural indirect effects (50, 58). Using potential outcomes notation, the average total effect can be formally defined as follows

$$\mathit{ATE}=E(Y(x*)-Y(x))$$ (1)

where E( ∙ ) denotes the expectation operator, {x*, x} denote different levels of neighborhood poverty, and {Y(x*), Y(x)} denote potential outcomes of the cognitive assessments under these different neighborhood exposures. In words, the ATE is the expected difference in cognitive ability at age 4 had children previously been exposed to the level of neighborhood poverty given by x*, rather than x, during infancy.

The ATE can be additively decomposed into a natural direct and a natural indirect effect, which describe the causal process by which differences in neighborhood poverty bring about differences in cognitive ability. Let M(x) denote the vector of air toxics to which a child would be exposed under residence in a neighborhood with poverty level x. Similarly, let Y(x) = Y(x, M(x)) denote a child’s cognitive ability under exposure to a level of neighborhood poverty x and, by extension, under exposure to the set of air toxics, M(x), that the child would encounter as a result of their residence in a neighborhood with this level of poverty. Using this expanded notation for the potential outcomes, the ATE can be expressed as E(Y(x*) − Y(x)) = E(Y(x*, M(x*)) − Y(x, M(x))) and then decomposed as follows

$$\begin{array}{c}E(Y(x*,\mathbf{M}(x*))-Y(x,\mathbf{M}(x)))=\\ E(Y(x*,\mathbf{M}(x))-Y(x,\mathbf{M}(x)))+E(Y(x*,\mathbf{M}(x*))\\ -Y(x*,\mathbf{M}(x)))=\mathit{NDE}+\mathit{NIE}\end{array}$$ (2)

where the first term in this decomposition, NDE = E(Y(x*, M(x)) − Y(x, M(x))), is the natural direct effect, and the second term, NIE = E(Y(x*, M(x*)) − Y(x*, M(x))), is the natural indirect effect.

The NDE is the expected difference in cognitive ability at age 4 under residence in a neighborhood with a poverty level given by x*, rather than x, during infancy, if children were exposed to the set of air toxics that they would have encountered in the neighborhood with poverty level x. For example, with x* > x, the NDE captures the effect of living in a higher rather than a lower poverty neighborhood, if children were exposed to the air pollution they would have encountered by virtue of residing in the lower poverty neighborhood. It measures an effect of neighborhood poverty operating through all mechanisms other than exposure to the observed air toxics. This is accomplished by fixing all of the mediators to the levels they would have “naturally” been for each child under the reference level of concentrated poverty, which deactivates the component of the total effect mediated via air pollution.

The NIE is the expected difference in cognitive ability under residence in a neighborhood with poverty level x*, if children were then exposed to the set of air toxics they would have encountered by virtue of living in this neighborhood rather than another neighborhood with a poverty level given by x. For example, with x* > x, the NIE captures the effect of exposure to the toxics that children would encounter in the air if they lived in a higher rather than a lower poverty neighborhood during infancy. It measures an effect of neighborhood poverty on cognitive ability operating only through differences in exposure to neurotoxic air pollution—that is, an effect mediated by all of the measured toxics jointly. This is accomplished by holding neighborhood composition fixed for each child, which deactivates the component of the total effect that operates directly, and then comparing outcomes across differences in the vector of pollutants that would have occurred under exposure to different levels of concentrated poverty.

We focus on effects contrasting residence in neighborhoods with a 25% rather than a 5% poverty rate, which are approximately equal to the 90th and 20th percentiles of the national exposure distribution, respectively. Thus, we prioritize a comparison between neighborhoods with high versus low levels of concentrated poverty. In table S4, we additionally report effect estimates based on several other contrasts, including comparisons of low-poverty neighborhoods with areas that have moderate levels of poverty (10 to 20%) and with neighborhoods that have extreme levels of poverty (30%).

We also report effect estimates separately by race, family income, geographic region, and homeownership. These results are presented in tables S5 to S8. They provide suggestive evidence of effect heterogeneity, although estimates of conditional effects for these selected subpopulations are too imprecise to draw firm conclusions about differences between them. In general, we observe larger point estimates among Hispanic children and among those living in the Southern and Western regions of the country.

Identification

The total, direct, and indirect effects of interest can be identified from the observed data under a set of four assumptions about unobserved confounding (58). These assumptions can be formally expressed as follows, using a series of conditional independence restrictions

$$\begin{array}{c}Y(x,\mathbf{m})\mathbf{\perp }X\mid \mathbf{C};\mathbf{M}(x)\mathbf{\perp }X\mid \mathbf{C};Y(x,\mathbf{m})\mathbf{\perp }\mathbf{M}\mid \{\mathbf{C},X\};\\ \text{and} Y(x,\mathbf{m})\mathbf{\perp }\mathbf{M}(x*)\mid \mathbf{C}\end{array}$$ (3)

In substantive terms, the first of these assumptions, Y(x, m) ⊥ X∣C, requires that there must not be any unobserved confounding for the exposure-outcome relationship. The second assumption, M(x) ⊥ X∣C, requires that there must also not be any unobserved confounding for the exposure-mediator relationships. The third and fourth assumptions, given by Y(x, m) ⊥ M∣{C, X} and Y(x, m) ⊥ M(x*)∣C, respectively, require that there must not be any unobserved or exposure-induced confounding for the relationship between the mediators and outcome.

These are strong assumptions. They would be violated, for example, if unobserved factors like parenting skills affect both neighborhood attainment and child cognitive ability, above and beyond our set of measured controls, leading to bias. We attempt to satisfy them approximately by adjusting for a large set of predictors linked with residential selection and child development. Then, because this identification strategy is imperfect, we also perform a sensitivity analysis that evaluates how our results would change under hypothetical patterns of unobserved confounding.

Even if some of these assumptions are violated, however, our results may still have an alternative causal interpretation provided that certain of them continue to hold. In particular, if the exposure-outcome relationship is confounded but the mediator-outcome relationship is not, our estimates can be interpreted as reflecting the degree to which descriptive disparities in test scores across neighborhoods with different poverty levels are explained by differences in pollution exposure between them. If none of these assumptions are met, our results merely summarize how test scores vary with exposures to air pollution and concentrated poverty, conditional on a set of baseline controls.

Estimation

If, however, the identification assumptions outlined previously are all satisfied, then the means of the potential outcomes can be expressed in terms of the observed data as follows

$$\begin{array}{c}E(Y(x*))=E(E(Y\mid \mathbf{C},X=x*)),\\ E(Y(x))=E(E(Y\mid \mathbf{C},X=x)),\text{and}\\ E(Y(x*,\mathbf{M}(x)))=E(E(E(Y\mid \mathbf{C},X=x*,\mathbf{M})\mid \mathbf{C},X=x))\end{array}$$ (4)

which are sufficient for computing the ATE, NDE, and NIE. We use the method of regression-imputation to estimate these quantities (44, 45). In words, this approach involves fitting models for the conditional means shown above and then using them to impute, or simulate, counterfactuals by (re)setting the value of the exposure variable at different levels for all sample members and obtaining model predictions.

Specifically, in analyses of causal mediation, the regression-imputation algorithm can be implemented according to the following steps:

first, fit a model for the mean of the observed outcome conditional on the exposure and baseline confounders, which can be expressed as E(Y∣C, X) = f(C, X);

second, use this model to estimate the mean of the potential outcomes under x* by setting X = x* for all sample members, computing predicted values $\widehat{f}(\mathbf{C},x*)$, and then taking the sample average of these values, $\frac{1}{n}\sum \widehat{f}(\mathbf{C},x*)$, which yields an estimate for E(Y(x*)) = E(E(Y∣C, X = x*));

third, use the same model to estimate the mean of the potential outcomes under x by now setting X = x for all sample members, computing predicted values $\widehat{f}(\mathbf{C},x)$, and then taking the sample average of these values, $\frac{1}{n}\sum \widehat{f}(\mathbf{C},x)$, which yields an estimate for E(Y(x)) = E(E(Y∣C, X = x));

fourth, fit a second model for the mean of the observed outcome conditional on the exposure, baseline confounders, and the full set of mediators, which can be expressed as E(Y∣C, X, M) = g(C, X, M), and then set X = x* for all sample members to obtain a set of predicted values $\widehat{g}(\mathbf{C},x*,\mathbf{M})$;

fifth, use these predicted values to estimate the mean of the potential outcomes under {x*, M(x)} by fitting a third model for $\widehat{g}(\mathbf{C},x*,\mathbf{M})$ conditional on the observed exposure and baseline confounders, which can be expressed as $E(\hat{g}(\mathbf{C},x*,\mathbf{M})\mid \mathbf{C},X)=h(\mathbf{C},X)$, and then by setting X = x for all sample members, computing predicted values $\widehat{h}(\mathbf{C},x)$, and taking the sample average of these predictions, $\frac{1}{n}\sum \widehat{h}(\mathbf{C},x)$, which yields an estimate for E(Y(x*, M(x))) = E(E(E(Y∣C, X = x*, M)∣C, X = x));

last, compute estimates for the effects of interest using these quantities—that is, calculate $\widehat{\mathit{ATE}}=\frac{1}{n}\sum (\widehat{f}(\mathbf{C},x*)-\widehat{f}(\mathbf{C},x))$, $\widehat{\mathit{NDE}}=\frac{1}{n}\sum (\widehat{h}(\mathbf{C},x)-\widehat{f}(\mathbf{C},x))$, and $\widehat{\mathit{NIE}}=\frac{1}{n}\sum (\widehat{f}(\mathbf{C},x*)-\widehat{h}(\mathbf{C},x))$.

The method of regression-imputation yields consistent estimates under the identification assumptions outlined previously and provided that f(C, X), g(C, X, M), and h(C, X) are themselves consistently estimated.

This approach to estimation is ideal for the present analysis, which involves a continuous measure of neighborhood poverty and a large number of air pollutants, because it does not require modeling the distributions of the exposure or mediators, as is necessary with most other approaches to analyzing causal mediation. That is, unlike other methods, our approach can recover estimates of the NDE and NIE without models for (i) the probability of exposure to neighborhood poverty given the baseline covariates or (ii) the joint probability of exposure to different air toxics conditional on neighborhood poverty and prior covariates, which would be exceedingly difficult to correctly specify and fit given the complexity of these distributions and the challenge of data sparsity. Our approach does, however, require correctly modeling several conditional mean functions for the outcome given different sets of predictors. Because the true form of these functions is unknown and potentially complex, especially when the predictors include a high-dimensional set of mediators, conventional approaches to modeling them (e.g., linear regression) are likely to suffer from severe bias due to misspecification, even if our key assumptions about unobserved confounding are all satisfied. For example, the relationships between cognitive ability and the many different air toxics included in this analysis may be nonlinear or nonadditive or they may otherwise differ across levels of the exposure or confounders (24, 31). In this situation, it is difficult to accurately approximate the true conditional mean functions with conventional parametric models, leading to bias. We mitigate this problem by constructing models for f(C, X), g(C, X, M), and h(C, X) using data-adaptive machine learning algorithms.

Specifically, we model these functions using RFs (46), an ensemble method that combines recursive partitioning with random subspace selection and bootstrap aggregation. Recursive partitioning involves repeatedly dividing the sample into subgroups, or nodes, based on binary partitions of the predictors that minimize a loss function at each step of the algorithm—in our case, mean squared error. The algorithm initiates by considering all possible partitions, and then it selects the one that minimizes squared error around the mean of the outcome in the two resulting nodes. This partitioning process is then repeated, where the nodes created at each previous step of the procedure are further partitioned themselves, over and over, until the algorithm reaches a stopping criterion. The result is a so-called “regression tree,” which yields a set of predicted values equal to the mean of the outcome within each terminal node. Recursive partitioning can approximate complex forms of nonlinearity and interaction with high accuracy, but the method also tends to produce estimates with excessive variance because it overfits random variation in the sample data. RFs overcome this limitation by creating and then combining an ensemble, or “forest,” of many different regression trees. Each tree in the ensemble differs because it is created using (i) a random sample of observations selected from the data with replacement and (ii) a random subset of predictors selected as candidates for partitioning at each step of the algorithm. Predictions from the RF are obtained by taking the average of the predictions from all the different trees that compose it. By averaging over the predictions from many complex but weakly correlated trees, RFs yield a regression surface that is capable of approximating the true conditional mean function with a high degree of accuracy while minimizing excessive variance due to overfitting.

RFs require specifying a set of hyperparameters that control the algorithm and determine its stopping criterion. In particular, they require specifying the minimum number of observations allowed in a terminal node (a_n), the number of predictors to select for partitioning at each step (a_p), and the total number of trees to construct for the ensemble (b). We construct ensembles of b = 200 trees and then tune the other hyperparameters using a grid search and k = 5 fold cross-validation. For each RF, we search over a_p ∈ {floor(0.3p), floor(0.4p), …, floor(0.7p)}, where p denotes the total number of predictors, and a_n ∈ {5,10,15,20}, selecting the combination of values that maximize predictive accuracy.

As a robustness check, we also compute a set of effect estimates using RFs with commonly used default values for these hyperparameters—specifically, a_n = 5 and a_p = floor(p/3)—and by using a variant of the algorithm that involves constructing each tree in the ensemble with a random sample of size s_n = floor(s × n) selected without replacement from the observed data (47). For this implementation of RFs, the sampling fraction, s, is an additional hyperparameter that we tune using a cross-validated grid search over s ∈ {0.6,0.7, …,0.9}. In addition, we compute effect estimates using a stacking algorithm, known as a “super learner” [SL; (59)], that constructs a weighted average of predictions from each of the different RF implementations considered in our analysis. This weighted average is designed so that it may perform better asymptotically, while being guaranteed to perform no worse, than the predictions from any single RF taken in isolation. Estimates for the total, direct, and indirect effects of interest based on these different modeling approaches are presented in table S9. They are very similar to those that we prioritize in Table 1. We focus on RFs over other methods in this analysis because they can accurately approximate complex forms of interaction and nonlinearity, because they can easily accommodate a high-dimensional set of predictors while minimizing problems due to overfitting, and because predictions from this class of algorithms are consistent under fairly general conditions (47, 60).

To account for the stratified multistage sample design used by the ECLS-B, we use sampling weights that adjust for unequal probabilities of selection and compute interval estimates using a repeated half-sample bootstrap that adjusts for the geographic clustering of study participants (61). This involves repeating the regression-imputation procedure, with weights, on independent samples drawn from the observed data, where each sample is constructed by randomly selecting one of the two primary sampling units from within each design stratum and duplicating these observations. To adjust for the bias that may arise in the presence of missing data, we replicate this entire analysis across five complete datasets, with missing values for all variables simulated via chained RFs (62, 63). The proportion of missing information in this analysis is 0.04, which is due to a combination of item-specific nonresponse, truncation of extreme values in the RSEI-GM, and panel attrition in the ECLS-B. After pooling results across imputations, the upper and lower limits of our interval estimates are given by the 97.5th and 2.5th percentiles of the combined bootstrap distribution, respectively (64). We also performed a parallel analysis under the assumption that the ECLS-B sample design is ignorable and therefore computed effect estimates without sampling weights, which may be relatively more efficient in certain situations (65). Results from this analysis are reported in table S10. They are similar to those constructed with sampling weights but are somewhat more precise.

Sensitivity analysis

We assess the sensitivity of our results to unobserved confounding by computing bias terms and then using them to construct a set of adjusted point estimates for the NDE and NIE (43, 45). In the scenario where unobserved confounding exists for the relationship between the mediators and outcome (i.e., there are unmeasured factors that affect both pollution exposure and child cognitive ability), estimates for both the NDE and NIE are biased. In this setting, the bias terms can be expressed as follows

$$\text{bias}(\widehat{\mathit{NDE}})=\mathrm{\gamma }\mathrm{\eta } \text{and} \text{bias}(\widehat{\mathit{NIE}})=-\mathrm{\gamma }\mathrm{\eta }$$ (5)

where η = E(U∣C, X = x*, M) − E(U∣C, X = x, M), γ = E(Y∣C, X, M, U = 1) − E(Y∣C, X, M, U = 0), and U represents an unobserved variable that is assumed to affect the outcome and to differ across levels of the exposure in a manner that does not depend on the observed covariates or mediators. In the scenario where unobserved confounding exists for the relationship between the exposure and outcome (i.e., there are unmeasured factors that affect selection into poor neighborhoods and child cognitive ability), estimates for the NDE, but not the NIE, are biased. In this setting, the unobserved variable, U, can be recast as an exposure-outcome confounder rather than a mediator-outcome confounder, and estimates for the NDE suffer the same bias as outlined above. We construct bias-adjusted estimates by subtracting γη from $\widehat{\mathit{NDE}}$, and −γη from $\widehat{\mathit{NDE}}$, and then we plot them across a range of plausible values for γ and η to identify the magnitude of unobserved confounding that would suffice to reduce our effect estimates to zero.

Model explanation

Although RFs are well equipped to accurately model complex conditional mean functions, especially with a high-dimensional set of predictors, they are more difficult to interpret than conventional parametric models. We address this tension between accuracy and interpretability using SHAP values (51, 66), which quantify the contribution that each covariate brings to the predictions made by an RF. This allows us to identify the predictive importance of different variables considered in our analysis and, by extension, to illuminate which toxics are likely to play a more versus less important role in mediating the effects of neighborhood poverty on child cognitive ability. SHAP values enjoy several advantages over alternative measures of variable importance, including a game theoretic motivation, the ability to handle correlated predictors, and the ability to fairly attribute influence to both high- and low-cardinality predictors.

Formally, SHAP values are based on an additive attribution model with the following form

$$\widehat{v}(\mathbf{z})={\mathrm{\varphi }}_0+{\displaystyle {\sum }_{i=1}^p}{\mathrm{\varphi }}_i\mathbf{1}(z_i)$$ (6)

In this model, $\widehat{v}(\mathbf{z})$ denotes a predicted value from some focal model (e.g., an RF) given the vector of predictors z = {z₁, …z_p}, ${\mathrm{\varphi }}_0=\widehat{v}(\varnothing )$ denotes the prediction given by a null model with no covariates, 1(z_i) is an indicator function denoting that a predictor is included in the model, and ϕ_i is the SHAP value for predictor z_i, which provides a single number summary of its contribution to the prediction of interest.

The SHAP value for z_i is obtained by comparing the difference between predictions from models with and without the variable included as a predictor. Because the effect of withholding a covariate on a model’s prediction may depend on all the other variables included, these differences are computed for every possible combination of the other predictors, and then the SHAP value is given by their weighted average. Specifically, if p denotes the total number of predictors and d_−i denotes subsets of these variables that do not include the predictor z_i, then the SHAP value for this predictor is equal to

$${\mathrm{\varphi }}_i={\sum }_{d_{-i} }\left(\frac{\mid d_{-i}\mid !(p-\mid d_{-i}\mid -1)!}{p!}\right)(\hat{v}(d_{-i},z_i)-\hat{v}(d_{-i}))$$ (7)

where $\widehat{v}(d_{-i},z_i)$ denotes the prediction from a model trained with the covariate set {d_−i, z_i} and $\widehat{v}(d_{-i})$ is the prediction from a model trained without z_i. Computing SHAP values exactly as in Eq. 7. would require fitting 2^p different models, which becomes computationally intractable even with a relatively small number of predictors. SHAP values are therefore estimated using a Monte Carlo approximation that greatly reduces the time complexity of the computations (66).

To summarize the influence of a predictor over the entire regression surface, as opposed to its influence on a single predicted value, we compute the mean of the absolute SHAP values, $\frac{1}{n}\sum \mid {\mathrm{\varphi }}_i\mid$, where the sum is taken over sample members. The mean absolute SHAP value is a global measure of variable importance. It can be interpreted as the average influence of a predictor, in absolute terms, on a model’s output. Figures S1 and S2 display mean absolute SHAP values for every predictor included in our RFs for E(Y∣C, X) and E(Y∣C, X, M), while figs. S3 and S4 plot the individual SHAP values themselves, which additionally provide information about the general direction of the relationship between the predictors and outcome. Figures 6 and 7 are based on the subset of these values that are directly relevant to neighborhood effect mediation via air pollution.

Supplementary Materials

This PDF file includes:

Figs. S1 to S4

Tables S1 to S10