Time-dependent diffusivity and kurtosis in phantoms and head and neck cancer patients

Abstract

Purpose:

To assess the reliability of measuring diffusivity, diffusional kurtosis and cellular-interstitial water exchange time with long diffusion times (100–800 ms) using stimulated-echo diffusion-weighted imaging.

Methods:

Time-dependent diffusion MRI (dMRI) was tested on two well-established diffusion phantoms and in five patients with head and neck cancer. Measurements were conducted using an in-house diffusion-weighted STEAM-EPI pulse sequence with multiple diffusion times at a fixed echo time on three scanners. We used the weighted linear least-squares fit method to estimate time-dependent diffusivity, D(t) and diffusional kurtosis, K(t). Additionally, the Kärger model (KM) was used to estimate cellular-interstitial water exchange time (τ_ex) from K(t).

Results:

Diffusivity measured by time-dependent STEAM-EPI measurements and commercial SE-EPI showed comparable results with R² of above 0.98 and overall 5.4±3.0% deviation across diffusion times. Diffusional kurtosis phantom data showed expected patterns: constant D and K = 0 for negative controls and slow varying D and K for samples made of nanoscopic vesicles. Time-dependent dMRI in head and neck cancer patients found that KM could be considered valid in 72±23% of the voxels in the metastatic lymph nodes. The median cellular-interstitial water exchange time estimated for lesions was between 58.5 and 70.6 ms.

Conclusion:

Based on two well-established diffusion phantoms, we found that time-dependent dMRI measurements can provide stable diffusion and kurtosis values over a wide range of diffusion times and across multiple MRI systems. Moreover, estimation of cellular-interstitial water exchange time can be achieved using KM for the metastatic lymph nodes in head and neck cancer patients.

INTRODUCTION

Diffusion MRI (dMRI) has become the modality of choice to assess the cellular properties of tumors as the diffusion of water molecules is highly sensitive to tissue microstructure (1–3). While dMRI signal is sensitive to different biophysical properties of tissue, such as cell size and density, quantitative assessment of those microstructural properties remains challenging. Among these microstructural properties are the presence of barriers (e.g. cell membranes), cellular compartments (e.g. intracellular and extracellular spaces) and various cellular organelles. Diffusivity is typically interpreted as a measure of cell density and extracellular water fraction (4). Consistent with this interpretation, dMRI of malignant tumors typically showed a decrease in diffusivity (5,6) which was correlated with increased cell density measured by histology (7) and thus a decrease in extracellular space. However, the diffusivity derived from dMRI acquisition is not a constant for a given biological tissue, but a function of measurement conditions, such as diffusion weighting strength and the diffusion time (8–12). Hence, it is crucial to consider both factors carefully when planning dMRI experiments.

It is even more important to consider the dependency of dMRI derived parameters on diffusion time when a higher-order term of diffusion signal, such as diffusional kurtosis, is included with a stronger diffusion weighting. Quantifying the degree of deviation from Gaussian diffusion can be useful in characterizing the associated tissue structures. For this purpose, Diffusional Kurtosis Imaging (DKI) provides a practical clinical technique to probe the microscopic structure of biologic tissues (13). It has been demonstrated that diffusional kurtosis is a more specific measure of tissue structure, such as cellular compartments and membranes, than diffusivity (14,15). It was also shown that diffusional kurtosis has greater sensitivity and specificity than diffusivity for assessment of hepatocellular carcinoma viability after treatment (16) and as a marker to assess cell viability to evaluate early treatment response (17). However, the variability of diffusion kurtosis parameters as a function of diffusion time is still not fully understood.

Diffusional kurtosis increases with the diffusion time when the cellular barriers are impermeable, as in the white matter (18). When the diffusion time is long enough and the tissue contains permeable barriers, the diffusional kurtosis monotonically decreases as diffusion time increases (19). These study results support that it is important to report the diffusion time used for a diffusional kurtosis measurement. More importantly, these studies show that by utilizing two-compartment modeling, the time-dependent diffusional kurtosis can be used to measure the cellular-interstitial water exchange time (14,19,20).

Cellular-interstitial water exchange time (τ_ex) has been suggested as a marker of cellular metabolism (21). τ_ex can be used to assess the increased metabolic activity associated with cancer (22), and the metastatic potential that could be associated with long term survival as shown for head and neck cancer (23). DKI parameters, D,K and τ_ex, can be useful imaging biomarkers for monitoring both cellular viability and metabolism. Based on former Monte Carlo simulations (24) and breast cancer measurements (20), the water exchange time in cancer cells is expected to be around 100 ms. Thus, to measure the cellular-interstitial water exchange time, it is necessary to conduct a series of DKI scans with multiple diffusion times longer than 100 ms. However, conventional spin echo-based diffusion-weighted imaging (DWI) pulse sequences are not adequate for this purpose, due to the increased echo time (TE) to accommodate a long diffusion time. Instead, Stimulated Echo Acquisition Mode (STEAM) DWI pulse sequences have been adopted to achieve long diffusion time without the need to increase the echo time (8,20,25). Nevertheless, the evaluation of STEAM-based imaging for diffusion kurtosis has not been conducted with commercially available clinical scanners for a range of diffusional kurtosis values expected for cancer.

The purpose of this study is to investigate how reliably diffusivity and diffusional kurtosis can be measured for long diffusion times (100 – 800 ms) using STEAM DWI. We used two well-established diffusion phantoms: one from the National Institute of Standards and Technology (NIST) and another from the University of Michigan in collaboration with the Quantitative Imaging Network (QIN) of the National Cancer Institute (NCI). The same pulse sequence was also tested to measure diffusion parameters and cellular-interstitial water exchange time in head and neck cancer patients.

METHODS

Theory

The diffusion MRI signal can be expressed as the cumulant expansion (14):

$$\ln \left[S\left(b\right)\right]=\ln \left(S_0\right)-bD+\frac{1}{6}{b}^2{D}^{2}K+O(b^3)$$ [1]

where S(b) and S₀ are the signal intensities with and without diffusion weighting, D is diffusivity, K is diffusional kurtosis, and O(b³) is the approximation error. The diffusion weighting, also known as b-value, is defined as a single parameter, b = q² t, where q is defined as the accumulated diffusion gradient strength during the gradient pulse duration δ: $q={\int }_0^{\delta }g\left(t^{\prime }\right)d{t}^{\prime }$ and t is defined as the diffusion time (also typically known as Δ). The signal equation in Eq.1 is constrained by a maximum b-value (10): b_max < 3/(DK). When a voxel has multiple Gaussian compartments with impermeable barriers (i.e., no water exchange), K is given by the relative variance of compartmental diffusivities, $K=3\frac{var\left(D\right)}{D^2}$. In the absence of microscopic structures, the variance of diffusivity is zero such that K = 0, which is the case of simple Gaussian diffusion.

A non-Gaussian diffusion environment can be characterized by a non-zero kurtosis term K and the time-dependence of all the cumulants, such as D(t) and K(t) (26). In this case, tissue complexity can be probed in two complementary approaches: (i) by quantifying higher-order cumulants at a given diffusion time, i.e. by increasing the b-value at fixed t, or by (ii) probing the time dependence of the cumulants by varying the diffusion time t. For both approaches, biophysical modeling of the diffusional tissue microenvironment is required.

The diffusion time-dependence of the cumulants is affected by both the time for water molecules to travel between the barriers and the permeability of the barriers. When the permeability is not known, it is helpful to consider the diffusion time-dependence with respect to t_c, the characteristic time for restrictive effects determined by a typical time to diffuse between cell membranes, as t_c would be the lower limit of τ_ex. In the barrier limited exchange case t_c ≪ τ_ex, it has been shown that K(t) peaks around t ~ t_c (19). For short diffusion times t ≪ t_c, the increase of the kurtosis with diffusion time can be viewed as resulting from the restriction of water molecules by membranes. For long diffusion times t ≫ t_c, as measured in this study (≥100ms), both intra- and extra-cellular compartments are coarse-grained by diffusion (i.e., long-time diffusion regime) (27), and the overall diffusivity D(t) becomes constant and behaves like a Gaussian diffusion, as predicted by the Kärger model (KM) (28). KM assumes that a tissue has two molecular spin-carrying pools (intra- and extra-cellular) with Gaussian diffusion, each characterized by diffusion coefficients (D_i and D_e), fractions v_i and v_e, and mean lifetime in individual compartments (residence times) τ_i and τ_e, respectively. t_c is related to the characteristic diffusion times of the extecellular and intracellular compartments, t_D,e and t_D,i: t_c = max{t_D,e, t_D,i} and t_c ≪ τ_i and τ_e (24). Following KM, D is constant when t ≫ t_c:

$$D=\left(1-v_e\right)D_e+v_e{D}_i=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.$$ [2]

And K(t) can be described as a function of the exchange time τ_ex = v_iτ_{e =} v_eτ_i (14):

$$K\left(t\right)={K_{\mathrm{\infty }}+K}_0\frac{2{\tau }_{ex}}{t}\left[1-\frac{{\tau }_{ex}}{t}\left(1-e^{-\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{${\tau }_{ex}$}\right.}\right)\right]$$ [3]

where K₀ + K_∞ is the maximum of K in the case of impermeable barriers and K_∞ accounts for a partial volume effect of any tissue compartments not involved in water exchange. A Monte Carlo numerical simulation study (24) showed that KM is a valid model when t ≫ t_c thus the exchange time τ_ex can be measured from K(t) using Eq.3. This was previously demonstrated with mouse tumor models (20). Furthermore, the time dependence of the cumulants D and K(t) in Eqs. 2 and 3 can be used to estimate diffusion weighted signals:

$$S_e\left(t,b\right)=S_{e0}\left(t\right)exp\left(-bD+{\frac{1}{6}b}^2{D}^{2}K\left(t\right)\right)$$ [4]

The estimated signal S_e(t, b) can be linearly scaled by adjusting S_e0(t) to match the measured signal S_m(t, b) for each diffusion time. Then, estimation of four KM parameters is conducted by minimizing the sum of squared differences between the estimated and measured signals for each voxel:

$$\left\{K_0,K_{\mathrm{\infty }},{\tau }_{ex},D\right\}=\arg min{\sum }_{t,b}{\left(S_e\left(t,b\right)-S_m\left(t,b\right)\right)}^2$$ [5]

where the upper b-value limit (b < 3/(DK)) is applied per diffusion time.

Time-dependent Diffusion Experiments

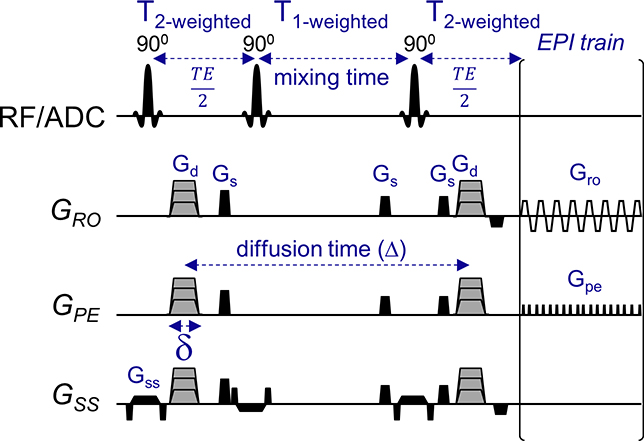
Time-dependent diffusion experiments were performed using a STEAM pulse sequence. An in-house STEAM pulse sequence (Fig. 1) has been developed based on a conventional Echo-Planar Imaging (EPI) acquisition (STEAM-EPI). The sequence calculates the total diffusion weighting from all the gradients for a given diffusion time (i.e., t = Δ) and adjusts the diffusion-weighted gradients (G_d) in accordance to the desired b-value. To avoid potential directional bias along the 3 orthogonal directions, the strength of the gradient for each direction and diffusion time was adjusted in order to achieve the same b-value for all three directions. G_d was kept lower than 70 mT/m in all our scans. Flexible diffusion times are manually set by varying the mixing time (TM) while keeping other key diffusion and imaging parameters constant such as: b-value and echo-time (TE). In our study, diffusion times were varied from 100 to 800 ms and b-values held constant.

Figure 1.

Time-dependent diffusion and kurtosis experiments using Stimulated-Echo sequence (STEAM). This in-house STEAM sequence allows to use a flexible range of long diffusion times by extending the mixing time. In this study, diffusion times ranging from 100 ms and above were used while keeping TE and b-values constant by adjusting the diffusion weighting gradients (G_d) accordingly. Diffusion gradients indicated by stepped gray gradients are separated by a diffusion time Δ. Refocusing echo with $\frac{TE}{2}$ delay is placed symmetrically after the excitation pulse and before acquisition. Spoiler gradients G_s rotate with the diffusion gradients. G_ro, readout gradient; G_pe, phase-encode gradients; G_d, diffusion-weighting gradients; G_ss, slice-selective gradient; G_s, spoiler gradients.

Diffusion Phantom

We tested the time-dependent dMRI on two diffusion phantoms. The first phantom (29) is a diffusion phantom provided by National Institute of Standards and Technology (NIST) and was tested on three MAGNETOM MRI 3T systems (Siemens Healthcare, Erlangen, Germany) at two imaging centers using a 20-channel head coil array. A Prisma scanner at New York University was designated as ‘Site1’, and Prisma and Skyra scanners at Weill Cornell Medicine were designated as ‘Site2’ and ‘Site3’, respectively. The NIST phantom is a well-established tool for assessing measurement of isotropic water Gaussian diffusion coefficients. This phantom contains thirteen 30 ml vials with different polyvinylpyrrolidone (PVP) concentrations: 0%, 10%, 20%, 30%, 40% and 50%, bathed in ice water keeping the temperature of the phantom close to 0°C. To minimize temperature variance across sites, while preparing the phantom ice-water bath, we performed temperature measurements using a digital temperature probe, until the temperature inside the phantom reached 0°C.

This phantom was used to test the reproducibility of measuring diffusivity over different diffusion times using our in-house STEAM-EPI pulse sequence. The imaging parameters for the STEAM-EPI sequence were TR/TE=6000/56 ms, 1.6 × 1.6 × 5.0 mm³ resolution, BW = 1200 Hz/pixel, and 6 slices acquired in coronal orientation with fat suppression. The STEAM-EPI diffusion parameters included δ = 8 ms with five diffusion times, [Δ = 200, 400, 600, 700, 800 ms], one b=0 and five b-shells [b = 200, 600, 1000, 1600, 2000 s/mm²] with three diffusion directions along x, y, and z axes. For the diffusion times, the mixing times were [TM = 186, 386, 586, 686, 786 ms]. The scan time of STEAM-EPI for one diffusion time was 1:54 min. For comparison, the standard vendor-provided SE-EPI sequence was run with the following imaging parameters: TR/TE=10000/101 ms, 0.5 × 0.5 × 4.0 mm³ resolution, with fat suppression, BW = 1184 Hz/pixel, and 25 slices acquired in coronal orientation. SE-EPI was used with a bipolar twice-refocused scheme (Δ ~TE/2=50, three b-shells [b = 500, 900, 2000 s/mm²] and scan time = 2:12 min).

Diffusional Kurtosis Imaging (DKI) Phantom

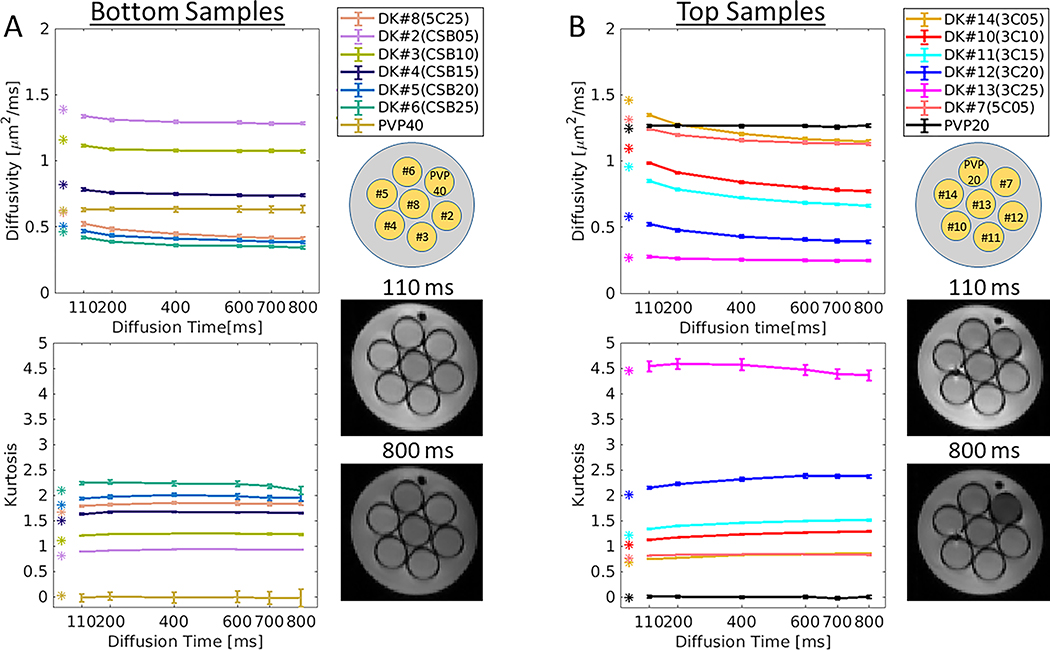
A DKI phantom (30) developed at the University of Michigan was provided as part of a collaboration with the Quantitative Imaging Network (QIN) at the National Cancer Institute (NCI). This phantom was tested on a Prisma 3T system at Weill Cornell Medicine. The kurtosis phantom samples were made from cetearyl alcohol (CA), behentrimethyl ammonium chloride (B), stearylamidoproply dimethylamine (S) and cetyltrimethyl ammonium bromide (CTAB). Each sample has a unique identification (ID) where C indicates a mixture of CA and CTAB with an alcohol-to-surfactant molar ratio of 3:1 or 5:1 (labeled in the beginning of the sample ID). CSB indicates a mixture of CA, B and S in a ratio of 7:1:1. The %(w/w) solid-in-water range between 0.5% and 2.5% as indicated by the number at the end of the sample ID. To simplify, in the legend of Figure 3, each sample ID was also numbered (DK#), while the sample ID mapping is provided in brackets. Additionally, the phantom includes two negative controls (K = 0) of 20% and 40% PVP solutions in water, designated as PVP20 and PVP40, respectively.

The kurtosis phantom was used for evaluation of the diffusivity and kurtosis values measured by our STEAM-EPI sequence. The imaging parameters were identical to the ones used for the NIST phantom. The scans were performed at room temperature of 20–21°C. The STEAM-EPI diffusion parameters included δ = 10 ms with six diffusion times, [Δ = 110, 200, 400, 600, 700, 800 ms], one b=0 and ten b-shells [b = 70, 80, 100, 200, 500, 800, 1000, 1500, 2000, 2500 s/mm²] with three diffusion directions along x, y, and z axes. For varying diffusion time, the mixing times were [TM = 86, 186, 386, 586, 686, 786 ms]. The scan time of STEAM-EPI for one diffusion time was 3:24 min. The conventional SE-EPI sequence included the following imaging parameters: TR/TE=5000/91 ms, 1.6 × 1.6 × 5.0 mm³ resolution, with fat suppression, BW = 1202 Hz/pixel, and 6 slices acquired in coronal orientation. For the Kurtosis phantom, SE-EPI was used with a bipolar twice-refocused scheme (Δ ~TE/2=45, nine b-shells [b = 50, 100, 200, 500, 800, 1000, 1500, 2000, 2500 s/mm²] and scan time = 2:52 min).

Head and Neck Cancer Patient Study

Five tonsil biopsy-proven oropharyngeal squamous cell carcinoma (OPSCC) patients with metastatic lymph nodes were recruited for measurement of dMRI with long diffusion times. This Health Insurance Portability and Accountability Act-compliant prospective study was performed with approval from our institutional review board, and written informed consent was obtained from all subjects. All data were acquired with our STEAM-EPI sequence on a 3T MAGNETOM Prisma MRI system (Siemens Healthcare, Erlangen, Germany) using a 20-channel head/neck coil array. The STEAM-EPI imaging parameters included: TR/TE=5000/60 ms, resolution=1.5×1.5×4.0 mm³, FOV=190 mm, partial Fourier 6/8, and GRAPPA with R=2. The STEAM-EPI diffusion parameters included δ = 15 ms with five diffusion times, [Δ = 100, 200, 300, 500, 700 ms], one b=0 and 4 b-shells [b = 200, 1000, 2000, 3000 s/mm²] with 3 diffusion directions along x, y, and z axes. For the varying diffusion time, the mixing time was [TM=80, 180, 280, 480, 680 ms]. The scan time for one diffusion time was 1:54 min. To avoid the intravoxel incoherent motion (IVIM) effect, b0 data was not included in the final analysis.

dMRI Data Analysis

Each set of images were denoised (31) and de-Gibbsed (32). The estimated noise level (33) was then used to correct the signal for Rician bias. Data was also corrected for eddy currents and off-resonance effects using FSL package (34). To further correct for motion effects in the patient scans, each dataset was registered to a reference b0 image by a rigid image registration function (Matlab ‘imregtform’ function, MathWorks, Natick, MA), over all b-values and diffusion times. Additionally, non-local means filtering was applied on the final images (35). Following post-processing, diffusion and kurtosis maps were generated via a weighted linear least square fit method (36). The Kärger model was used for estimating K₀, K_∞, D and τ_ex for each voxel by minimization function (Matlab ‘fminsearch’ function, MathWorks, Natick, MA). For minimizing Eq.5, we chose a set of 100 initial random values between: K₀ = [0 1], K_∞ = [0 1], D = [0 2] and τ_ex = [10 100]. Moreover, the final estimates were selected only if: a) minimization function successfully converged to a solution and b) fit values and their objective function values were above zero. The final KM estimates were the median over these values. To test the assumption that the median value indeed reflects a good estimate of the solution, Figure S1 shows an example how each parameter yields similar results to the final chosen median solution (circled in red). Regions of interest (ROIs) for the metastatic lymph nodes were manually drawn over b0 dMRI images with the shortest diffusion time (100 ms) and then duplicated to other diffusion times. The metastatic nodes were used instead of the primary tumor because they are less sensitive to susceptibility artifacts and physiological involuntary motion, such as breathing and swallowing. According to KM (Eqs. 2 and 3) and as discussed above, for the long time regime, diffusivity is expected to be constant. To apply KM to voxels meeting this criteria, Eq. 5 model was applied to voxels with the mean diffusivity between 0.5 and 1.5 μm²/ms and standard deviation smaller than 15% of its mean, across all diffusion times.

RESULTS

Diffusion phantom

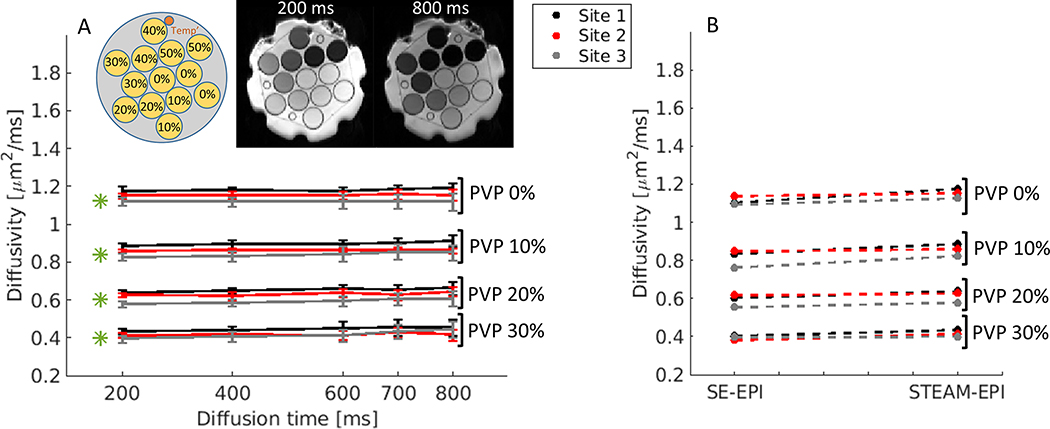
Figure 2A shows plots of diffusivity values across the different diffusion times for 0%, 10%, 20% and 30% PVP concentrations vials, described for each of the three sites. As shown in the b0 images at 200 ms and 800 ms, 40% and 50% PVP concentration vials showed poor signal intensity close to the noise level due to their short T1 of 360 ms and 650 ms, respectively (29), thus they were not included in this study. The mean signal-to-noise ratios (SNR; mean signal intensity/standard deviation of background voxels) of b0 images with diffusion time = 800 ms are 243.7 (0% PVP), 212.7 (10% PVP), 148.8 (20% PVP), 73.1 (30% PVP), 17.6 (40% PVP) and 5.3 (50% PVP).

Figure 2.

Diffusivity measurements of NIST diffusion phantom at 0°C. (A) Time-dependent experiments included multiple diffusion times [Δ =200, 400, 600, 700, 800 ms] with same b-values up to 2000 for each diffusion time. Measurements were performed at three different 3T sites (see Methods section). Reported NIST diffusivity values are indicated by green asterisks. The phantom includes thirteen vials of polymer concentration: 0%, 10%, 20%, 30%, 40% and 50% PVP (see the inset for the schematic diagram of the phantom). STEAM-EPI b0 images at 200 ms and 800 ms show how signal varies as a function of PVP concentration. (B) Measured diffusion values of SE-EPI vs. STEAM-EPI with the shortest diffusion time of 200 ms. The plots values represent the average over the multiple vials, per concentration.

For the vials with PVP 0, 10, 20, and 30%, the diffusivity difference measured had overall 5.4±3.0% deviation across the diffusion times from 200 ms to 800 ms (Fig. 2A.): 2.9±1.4% for site 1, 2.4±0.8% for site 2 and 5.4±3.0% for site 3. Among the data from three sites, there are differences with 5.8±2.6% between site 1 and site 2, 8.5±1.6% between site 1 and site 3, and 5.6±2.1% between site 2 and site 3 (Fig.2A and Supplemental Fig.S2). The same differences are also observed among the data from SE-EPI data acquired within the same imaging sessions (Fig.2B and Supplemental Fig.S3), indicating that the differences are likely from the slightly different temperature of the phantom at three sites. Comparing the diffusivity values measured by the STEAM-EPI with the values reported by the NIST (Fig.2A, green asterisks), the differences found for the longest diffusion time (800 ms) were 9±3.1% for site 1, 3.5±1.8% for site 2 and 2.7±4.4% for site 3. Additionally, regression analysis (Supplemental Fig. S4) and Bland-Altman plots (Supplemental Fig. S5) between the two shows good correlations with a slight negative bias for Site 1 and Site 2.

DKI phantom

Figure 3 shows a summary of D(t) and K(t) measures from the DKI phantom. For the vials in the bottom layer (Fig. 3A, indicated by CSB), diffusivity and kurtosis show low permeability characterized by weak dependency across the diffusion times where D(t) decreases maximally by 27.8 % (DK#8) from 110 ms to 800 ms, and K(t) increases maximally by 4.2 % (DK#2). For top layer (Fig. 3B, indicated by C), D(t) and K(t) changes are more noticeable than in CSB samples: D(t) decreases maximally by 34.3 % (DK#12) from 110 ms to 800 ms, and K(t) increases maximally by 14.7 % (DK#14). The C sample with 2.5% (DK#13, 3C25) shows that D(t) approaches a constant value in long diffusion times beyond 400 ms where K(t) decreases monotonically (Supplemental Figure S6). The diffusivity and kurtosis values measured by SE-EPI (Fig. 3, indicated by asterisks at diffusion time = ~45 ms) are well in line with the trends of D(t) and K(t) measured by STEAM-EPI (indicated by lines in Fig.3). Negative controls designated as PVP40 and PVP20, show D(t) ~ constant (0.63±0.002 μm²/ms and 1.27±0.004 μm²/ms, respectively) and K(t) ~ 0 (0.0±0.013 and 0.017±0.014, respectively) across the diffusion times.

Figure 3.

Diffusivity and kurtosis measurements of the diffusional kurtosis phantom. The phantom is composed of two clusters of samples: (A) bottom and (B) top, each composed of combinations of different chemical compositions (see Methods section). Time-dependent experiments included multiple diffusion times [Δ =110, 200, 400, 600, 700, 800 ms] with same b-values up to 2500 per diffusion time. Bottom and top clusters are characterized by their coded samples and their corresponding STEAM-EPI b0 images at 110 ms and 800 ms diffusion time. Measured SE-EPI diffusivity and kurtosis values are indicated by colored asterisks.

Head and neck cancer patients

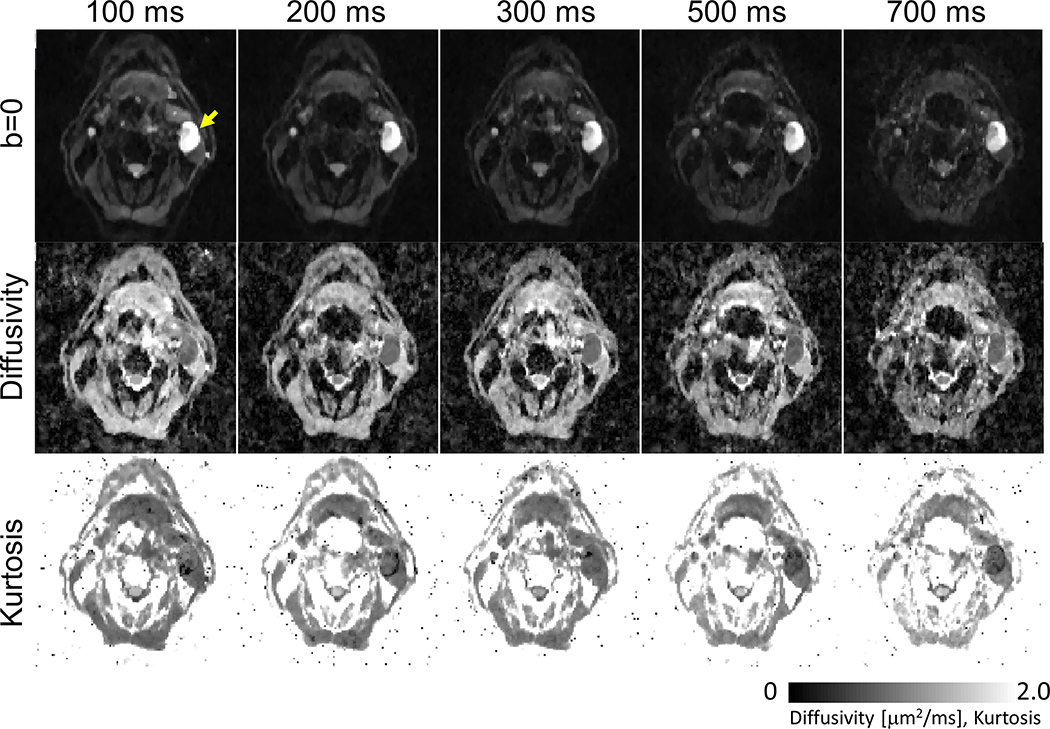
Next, we tested time-dependent diffusion measurements in head and neck cancer. Figure 4 shows b0 images, diffusivity and kurtosis maps calculated from a patient with a metastatic cervical node measuring about 27 mm × 17 mm. The images demonstrate good SNR and quality of diffusion-weighted images along with the estimated diffusivity and kurtosis maps for each diffusion time. For diffusion time of 700 ms, the signal intensity of the lymph node (marked by yellow arrow) remains high enough for estimation of diffusivity and kurtosis, compared to the surrounding tissue.

Figure 4.

Representative b0, diffusivity and kurtosis images acquired by time-dependent STEAM-EPI diffusion experiments of a patient (65 year old) with oropharyngeal squamous cell carcinoma and a metastatic left-sided cervical node (yellow arrow).

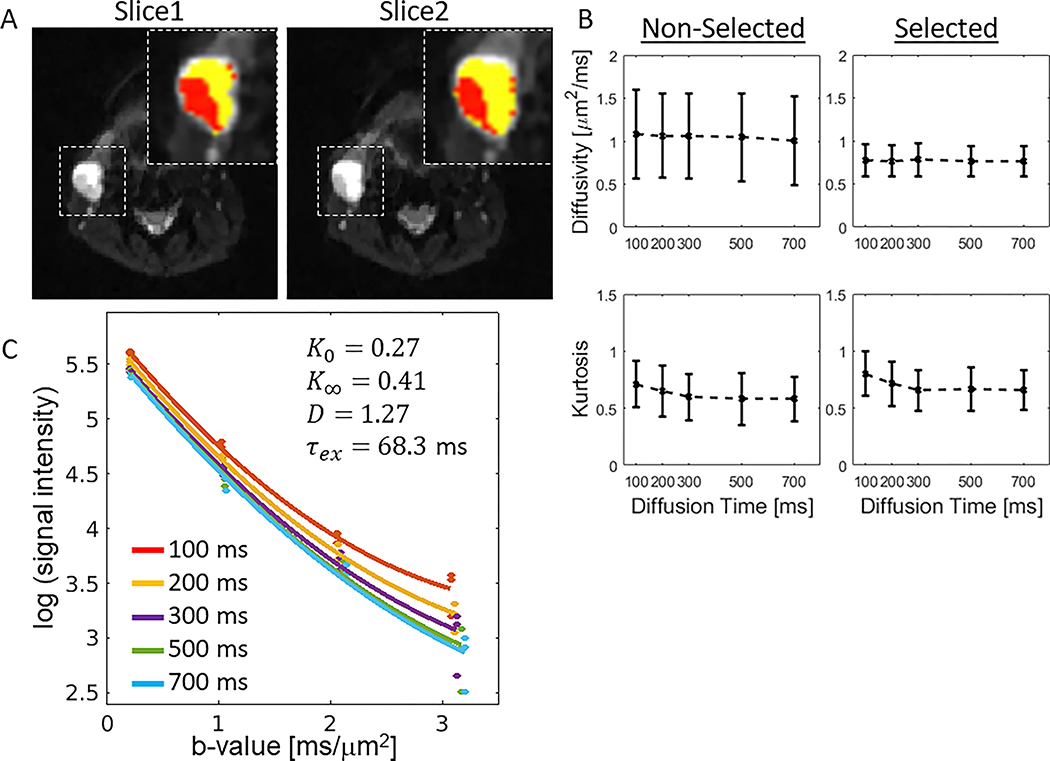
Figure 5A shows a representative case with a lymph node that has a cluster of voxels suitable for KM, based on the diffusivity and its standard deviation over the diffusion times as described in the Method section. For the two slices shown in Figure 5A, selected voxels were 47% and 35% of the whole lesion in each slice, respectively. The results of applying this criteria to select voxels suitable for KM in all five head and neck cancer patients are shown in Figure 5B, where a higher variance is observed in diffusivity for the non-selected voxels than the variance for the selected voxels: D =[0.773±0.183, 0.769±0.186, 0.782±0.189, 0.764±0.179, 0.764±0.178 μm²/ms] for diffusion times [t = 100, 200, 300, 500, and 700 ms] in the selected voxels; D =[1.085±0.516, 1.065±0.487, 1.061±0.495, 1.045±0.515, 1.007±0.516 μm²/ms] for the non-selected voxels. Moreover, K(t) decreases gradually from the shortest diffusion time to the longest: 0.803±0.194 to 0.66±0.176 for the selected voxels, and 0.712±0.204 to 0.582±0.197 for the non-selected voxels. Additionally, a representative voxel signal taken from the selected region was plotted as a function of b-value (Fig. 5C) for all 5 diffusion times together with their corresponding fits.

Figure 5.

Voxel selection for data analysis using Kärger Model. (A) A metastasis lesion shown in two slices of a 50 year old patient with oropharyngeal squamous cell carcinoma. The voxels in the metastatic lymph node (noted by the dashed box) are divided into non-selected (yellow) and selected tumor voxels (red) based on the variability of D(t) (see Method). (B) Diffusivity and kurtosis values calculated from the non-selected and selected voxels of the five head and neck patients with lymph metastasis lesions. (C) A representative voxel-wise signal (taken from the selected region) is plotted as a function of b-value for all 5 diffusion times.

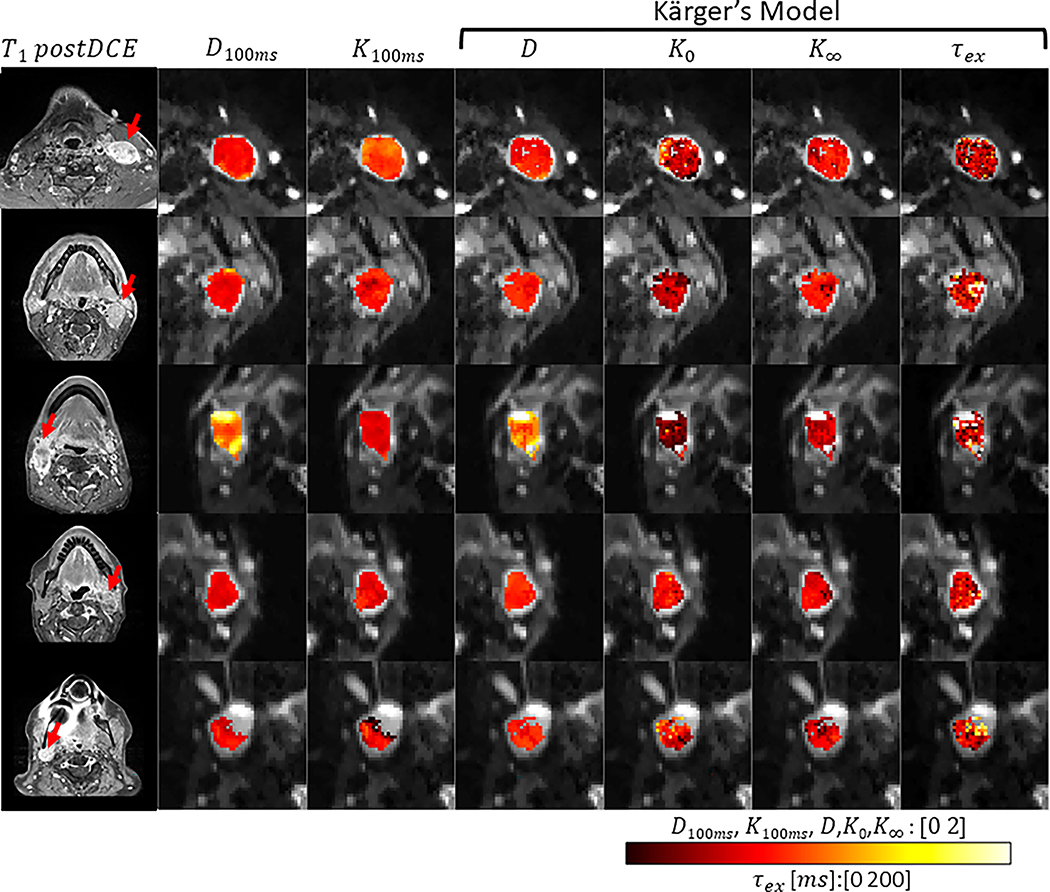
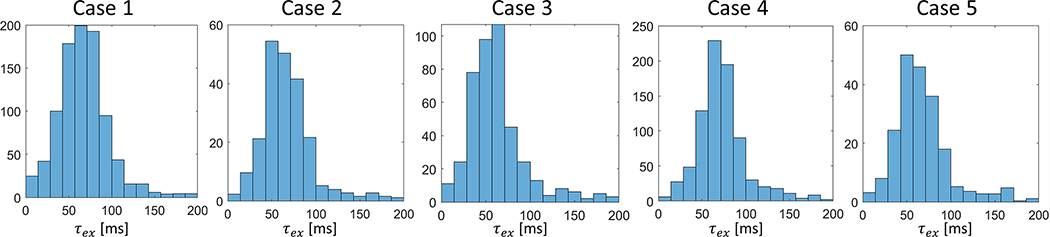
Figure 6 shows representative parameter maps of 5 patients with KM analysis applied to the selected voxels. Among the five patients, 72±23% of all voxels within the lymph nodes ROIs were selected for KM analysis according to the D(t) trend. For comparison, Supplemental Figure S7 shows the KM parameter maps of all voxels regardless of the selection step. The median K₀, the magnitude of K(t) decay, is between 0.3 and 0.65. The median cellular-interstitial exchange time τ_ex is between 58.5 and 70.6 ms. The KM analysis results of the selected voxels in all 5 cases are summarized in Table 1 and Figure 7. To examine the potential difference between T1 values of the intra- and extra-cellular compartments, we show a voxel-wise linear model fit of a representative lymph node, demonstrating a mono-exponential decay (Supplemental Fig. S8). Finally, the upper b-value limit (b < 3/(DK)) as defined in the theory section, yielded that, for a representative case (including all slices), 73.7% of all pixels included the highest b-value (i.e., 3000 s/mm²) while 26.1% included b-value = 2000 s/mm² and less than 1% below that.

Figure 6.

Parametric maps as calculated by Kärger model for the selected voxels of the five patients included in the study. Diffusivity (D) and kurtosis (K) maps with 100ms diffusion time were calculated by a weighted linear least square fit method. Diffusivity (D), K₀, K∞ and τ_ex maps were calculated by the Kärger model.

Table 1.

Summary of Kärger model parameters of the metastatic lymph nodes of all five patients. The values are the median [25^th and 75^th percentiles] from the selected voxels in all slices of each lymph node of individual patients. Diffusional parameter is in μm²/ms units and exchange time in millisecond.

	D		K 0		K ∞		τex
Case1	0.76	[0.69 0.86]	0.65	[0.40 0.87]	0.75	[0.61 0.88]	66.87	[49.60 84.15]
Case2	0.85	[0.80 0.89]	0.46	[0.33 0.59]	0.81	[0.72 0.88]	63.71	[49.96 82.72]
Case3	1.15	[0.99 1.28]	0.3	[0.21 0.40]	0.61	[0.51 0.68]	58.47	[43.54 79.04]
Case4	0.87	[0.82 0.92]	0.61	[0.47 0.73]	0.69	[0.60 0.77]	70.57	[57.15 85.64]
Case5	0.92	[0.85 0.97]	0.48	[0.33 0.69]	0.72	[0.60 0.81]	63.05	[48.60 80.25]

Figure 7.

Histograms of τ_ex values for all five head and neck patient cases.

DISCUSSION

In many biological tissues, and specifically in cancer lesions, the highly heterogeneous tissue microstructure and variable permeability can lead to non-Gaussian and time-dependent water diffusion (37). To examine this phenomenon, we explored time-dependent diffusion and kurtosis measurements in phantoms and in head and neck cancer using an in-house STEAM-EPI pulse sequence with a range of relatively long diffusion times. We found that the phantom data support that the STEAM-EPI sequence can be used to reliably measure diffusivity and diffusional kurtosis (14) for a constant-b value experiment over diffusion times ranging from 100 ms to 800 ms. Our study results also suggest that the cellular-interstitial water exchange time can be measured using a biophysical modeling approach known as the Kärger model (28).

Phantoms

Diffusion phantoms are used for validation of diffusion acquisition and analysis methods and also serve as a good quality control tool (38). In this study, we used an established NIST diffusion phantom (29) to perform time-dependent diffusion measurements by STEAM-EPI acquisition. To assess the reproducibility of our STEAM-EPI method, we repeated the measurements across three MRI 3T systems at two imaging centers. Our results suggest that diffusion time does not affect diffusivity values of the phantoms at near zero Celsius degree. It was further confirmed by comparing them with the results measured by the conventional SE-EPI method acquired with much shorter diffusion times (~50 ms). We also show that our results agree with the reported diffusivity values from the NIST (29). All these test results confirm that the diffusion weighting applied at the range of long diffusion times is accurately accounted for calculation of the b-matrices that are used for estimation of diffusivities and kurtosis for the corresponding diffusion times.

The comparison of diffusivity values measured at three sites showed a small, but noticeable difference among the sites (Fig. 2) in the data collected using both our in-house STEAM-EPI and the vendor-provided SE-EPI sequences. The phantom was filled with ice water until it reached 0°C, however, temperature was not consistently monitored during scans. Hence, we assume that some discrepancy can arise from differences in the actual temperature inside the phantom which apparently related to temperature drift. In addition, we cannot rule out any potential differences in the performances of the gradient systems, phantom positioning off isocenter and gradient rise times, which could also affect the accuracy of the diffusivity measurement among the three sites. These discrepancies can occur between sites but also during the experiment itself. In our study, since the different diffusion times were acquired in ascending order, we observed a slight increase in diffusivity between the shortest and the longest diffusion: 5.1% for site 1, 2.81% for site 2 and 10.5% for site 3, which can imply of an increase in temperature along time. In any rate, our observations in this study substantiate that, with careful control and monitoring of the temperature of the phantom during the scan, this type of diffusion phantom can be used to assess any changes in the hardware and/or software. This is consistent with the negative control measurements for DKI phantom performed at equilibrium room temperature.

We also examined a novel DKI phantom that provides realistic diffusional kurtosis values in a physiologically plausible range (30). This new generation DKI phantom is composed of nanoscopic vesicles made with a combination of alcohols and surfactants. Using the DKI phantom, time-dependent diffusion experiments were performed to measure both diffusion and kurtosis. In principle, the high molecular weight alcohol samples, characterized by impenetrable barrier, are not expected to show exchange. Looking closer at few of the samples in the supplementary material (Fig . S6), diffusivity of the lower concentration composed of C and CTAB (indicated by C), showed gradual decrease in diffusion and increase in kurtosis, which implies an impermeable membrane or a short diffusion regime (Fig. S6A). For the 2.5% concentration (Fig. S6B), diffusivity initially shows a gradual decrease for the short diffusion times and then approaches to a constant diffusivity value for the long diffusion times (>400 ms). Interestingly, for the same long diffusion times, kurtosis shows a monotonically decrease, rather similar to what is expected in the Karger regime with long diffusion times. The exchange time estimated from the time course is 102 ms. One possible explanation for these exchange properties is the mixture of C and CTAB, which have long-chain alcohols and likely have some “intermediate” vesicle permeability. Nevertheless, this observation requires further investigation of the material chemical properties with improved precision which could also be extended to make a phantom with different exchange times. Further characterization of cross-scanner reproducibility would require temperature calibration of the DKI phantom (ongoing) to rule out contribution of different scanner room environment temperatures (27). Lastly, please note that due to the temperature difference between the DKI phantom (room temperature) and the NIST phantom (~0°C) and its potential effect on T1 relaxation timing, we had sufficient signal in the DKI phantom to include the PVP40 data (39).

Head and Neck Cancer patients

Cellular-interstitial water exchange time has been suggested to be associated with a number of important cellular properties such as membrane permeability, tumor aggressiveness (40) and treatment response (23). Being able to measure water exchange can help understanding some of its mechanisms mainly governed by molecules diffusivity across the plasma membrane and transport via aquaporins (41). Moreover, it was shown that cancer cells with increased metabolic activity can be associated with higher water exchange rates compared with normal tissues (22). Here, we examine the use of KM for measuring water exchange time in head and neck cancer without an exogenous contrast agent. To achieve the long time diffusion regime where diffusivity is expected to be constant, we have selected voxels that meet this criteria. As a result, only a portion of the whole metastasis lymph node was selected (Figure 5) experiencing significant (p= 2.2e-06) lower diffusivity variance, compared to the non-selected voxels. This difference stems from the KM criteria defined in the Method section. In the supplementary materials (Fig. S7), we show additional parametric maps analyzed for the whole lesion without selecting voxels. Overall, the constant diffusivity and water exchange time exhibited in this study can reflect many possible microstructural arrangements between intra and extra cellular compartments. However, our present study was not designed to specifically probe other microstructural properties, such as cell size and extracellular volume fraction, which would require to have much shorter diffusion times as shown in our earlier study (11). For the voxels that do not meet the criteria for KM, future study is warranted to explore the options of using other biophysical models, including the random permeable barrier model (42) or Mitra model (43).

The median exchange times measured in this study ranged between 58.5 ms and 70.6 ms. These values are similar to the exchange times reported in perfused glial cells measured by NMR (44) and slightly lower than the ones recently reported for two breast cancers (70 and 106 ms) (20). Since the time to diffuse across a cancer cell with a radius of 4 μm and diffusivity ~1.5 μm²/ms is 10 ms, these water exchange times from our study and previous studies indicate that the exchange is barrier limited, meaning that the estimated exchange times exceed the characteristic time (20,24). There is only a limited number of studies that used time-dependent diffusion experiments to measure water exchange times in tumors to date. A majority of studies have measured the intracellular water lifetime parameter (τ_i = τ_ex/v_e) using dynamic contrast-enhanced (DCE) MRI (21,23). In head and neck cancer DCE studies, the exchanges values estimated from the intracellular water lifetime and extracellular volume fraction are 71 ± 33 ms for metastatic lymph nodes (45) and 96 and 107 ms for cancer patients with partial and complete response, respectively (46). These exchange times are close to those measured using the KM in our present study. To date, there is no histological method to measure water exchange time and no in vivo imaging method has been established as a gold standard method. The main advantage of using the proposed time-dependent diffusion experiment is the fact that, unlike DCE, dMRI does not require contrast injection.

This study had several limitations. Optimization of the diffusion MRI protocol was not within the scope of this proof of concept study. The diffusion times used in this study were arbitrary selected over the range between 100 and 700 ms. Future studies need to be conducted to determine optimal combinations of diffusion times and b-values for robust estimation of diffusion and KM parameters including water exchange time. Moreover, as KM solutions for D and K(t) apply under the narrow pulse assumption (47), future studies should restrict diffusion gradient duration as short as possible. Additionally, since the STEAM-EPI is heavily dependent on effective spoiler gradients, in charge of crushing residual magnetization after storage, some consideration in the choice of b-values is needed in order to avoid the possibility that spoiler gradients become stronger than the diffusion gradients which may lead to slightly shortening effect in diffusion timing. Another limitation is a small number of patients included in the study. A follow-up study with a larger cohort will further strengthen the finding and confirm the feasibility of using KM to measure water exchange time. Moreover, our study did not include repeatability measures over the same patient which could further strengthen the findings presented in this study. Future study is warranted to include repeatability measures on the same patient in one site (48). Lastly, from plotting the b0 signal of a representative lymph node as a function of TM (Fig. S8), we observed the T1 recovery is monoexponential. This suggests that the potential difference between T1 values of the intra- and extra-cellular compartments is negligible. However, future study is warranted to investigate more in depth the potential influence of T1 in the cellular-interstitial water exchange among head and neck cancer patients.

CONCLUSIONS

In this study we investigated the reliability of measuring water exchange times based on diffusivity and diffusional kurtosis at long diffusion times using a stimulated echo diffusion weighted imaging. We used two well-established diffusion phantoms and found that diffusion and kurtosis show stable values over a wide range of diffusion times. In head and neck cancer patients, we found that the Kärger model is a valid model for measuring water exchange time in a large portion (72±23%) of metastasis lymph node voxels.