An approach for reliably identifying high‐frequency oscillations and reducing false‐positive detections

Abstract

Objective

Aiming to improve the feasibility and reliability of using high‐frequency oscillations (HFOs) for translational studies of epilepsy, we present a pipeline with features specifically designed to reject false positives for HFOs to improve the automatic HFO detector.

Methods

We presented an integrated, multi‐layered procedure capable of automatically rejecting HFOs from a variety of common false positives, such as motion, background signals, and sharp transients. This method utilizes a time‐frequency contour approach that embeds three different layers including peak constraints, power thresholds, and morphological identification to discard false positives. Four experts were involved in rating detected HFO events that were randomly selected from different posttraumatic epilepsy (PTE) animals for a comprehensive evaluation.

Results

The algorithm was run on 768‐h recordings of intracranial electrodes in 48 PTE animals. A total of 453 917 HFOs were identified by initial HFO detection, of which 450 917 were implemented for HFO refinement and 203 531 events were retained. Random sampling was used to evaluate the performance of the detector. The HFO detection yielded an overall accuracy of $0.95\pm 0.03$, with precision, recall, and F1 scores of $0.92\pm 0.05$, $0.99\pm 0.01$, and $0.94\pm 0.03$, respectively. For the HFO classification, our algorithm obtained an accuracy of $0.97\pm 0.02$. For the inter‐rater reliability of algorithm evaluation, the agreement among four experts was $0.94\pm 0.03$ for HFO detection and $0.85\pm 0.04$ for HFO classification.

Significance

Our approach shows that a segregated pipeline design with a focus on false‐positive rejection can improve the detection efficiency and provide reliable results. This pipeline does not require customization and uses fixed parameters, making it highly feasible and translatable for basic and clinical applications of epilepsy.

Key Points.

A novel algorithm was introduced to reject false positives after initial HFO detection.

A high level of accuracy and reliability was achieved in the comprehensive evaluation of multiple datasets.

Translatable and adaptable to other HFO detection algorithms.

1. INTRODUCTION

High‐frequency oscillation (HFO), classified as ripples (80‐240 Hz) and fast ripples (240‐500 Hz), is regarded as a promising biomarker of epilepsy. ¹ , ² , ³ , ⁴ Such biomarkers can help localize the epileptogenic zone, the brain region that is indispensable for generating seizures in patients with drug‐resistant epilepsy (DRE). ⁵ , ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ Yet, the clinical utility of HFOs in the presurgical evaluation of patients with DRE is limited. Currently, clinicians perform the detection of HFO through visual inspection, a process that is challenging and time‐consuming since artifacts and environmental noise often mimic HFOs. A reliable, automated computational method is preferred to discard these artifacts and extract the true HFOs.

Conventional HFO detection methods implement bandpass filters for local field potentials (LFPs) followed by multiple thresholding in terms of amplitude and power to identify HFOs. ¹¹ , ¹² , ¹³ , ¹⁴ , ¹⁵ , ¹⁶ The short‐time‐energy (STE) method proposed by our group ¹⁷ is one of these methods, whose main advantages are the low computational cost and the short processing time. This method does not require a prior information of HFO labels and has been shown to be effective for detecting HFOs in animals and patients with epilepsy. ¹⁷ , ¹⁸ , ¹⁹ However, bandpass filtering and the use of amplitude thresholds do not separate true HFOs from sharp transients, ²⁰ sharp‐contoured epileptiform spikes, ²¹ and other physiological events. Therefore, STE methods still require expert review and manual flagging of true positives from a database, rendering the detection pipeline labor‐intensive and not fully automated.

Similar methodological approaches based on filtered signals have been proposed aiming to improve the HFO detection. ²¹ , ²² , ²³ Several research groups have suggested that an isolated “island” in the time‐frequency plot is the biosignature that characterize a true HFO. ²⁰ , ²³ , ²⁴ Yet, nontrue HFO events may also present a similar distinct biosignature, ²⁵ making it more challenging to exclude false HFOs by using this approach. Moreover, fast brain activities, such as the physiological sharp spikes, and transient motion artifacts also show the “blob‐like” feature in the time‐frequency analysis plot. ²⁶ Thus, there is an urgent need to develop new methodological approaches that discard false HFO positives (HFO FPs) in order to improve the reliability of the HFO detectors.

To address the above challenges, we proposed here a novel HFO fully automated method that combines the extraction of HFOs spectral feature with the analysis of events morphology. ²⁶ , ²⁷ , ²⁸ , ²⁹ This method categorized three common HFO FPs, including sharp transients, sharply contoured epileptiform spikes, and background signals. Our main hypothesis is that the rejection of these three types of HFO FPs can significantly improve the robustness of the intracranial HFO detection. Here, we analyzed a dataset of posttraumatic epileptic animals with long‐term sustained intracranial electrophysiological recordings to test the above hypothesis. This algorithm was developed as a separate module to reversely reject the events after the HFO detection. The module‐based design provides more step‐by‐step performance information than the integrated pipeline. A comprehensive evaluation was designed to evaluate each step of HFO rejection. The assessment of the validity and reliability of this new approach was reported.

2. METHOD

2.1. Experimental setups

The data pool consisted of 48 male Sprague‐Dawley rats (300‐350 g) that were treated with lateral fluid percussion injury (FPI) in a posttraumatic epilepsy model from our early studies. ¹⁹ , ³⁰ , ³¹ , ³² The data pool consisted of LFPs recorded at depth electrodes with sampling frequencies of 3000‐10 000 Hz. Specifically, 16 electrodes were implanted in the following areas: prefrontal cortex, thalamus, traumatic brain injury (TBI) areas, and hippocampal. The recordings were selected from the interictal period with a length of 3 h. A total of 768 h of LFPs during the epileptogenesis were analyzed in this study. Details of the experimental setup and data acquisition have been presented in our previous publications. ¹⁸ , ³²

2.2. Data preprocessing

Prior to the HFO analysis, raw data were first down‐sampled to 3KHz and then manually selected for the interictal period. During the data selection, recordings contaminated by long‐lasting (>5 s) noise, poor connections, or large shocks were removed. Instead of using all 16 channels of data, we manually identified high‐quality 8 channels for data analysis because our electrodes were designed as dual channels at each location. The main remaining disturbances of the signal were background noise and sharp transients that were difficult to be removed by visual inspection. Therefore, the core algorithm was built aiming to distinguish these two types of events from true HFOs. Specifically, eight brain regions were selected for our study, including bilateral prefrontal cortex (LFC, RFC), striatum (LST, RST), perilesional areas (LTBI, RTBI), and hippocampus (LHP, RHP). ¹⁹ , ³⁰ , ³¹ , ³²

2.3. HFO initial detection

Before we run the algorithm, a HFO initial detection was performed based on the two purposes. The first is to provide the small portion of dataset for feature selection, and the second is to include as many potential HFOs as possible for refinement. In this step, STE method ¹⁷ was implemented to find all HFO candidates and retrieve a 2‐s HFO epoch (with HFO peak at the center) for further analysis.

2.4. Algorithm Framework

The complete pipeline consists of three major modules, including: (1) feature selection module, (2) HFO detection module, and (3) HFO classification module (Figure 1).

FIGURE 1.

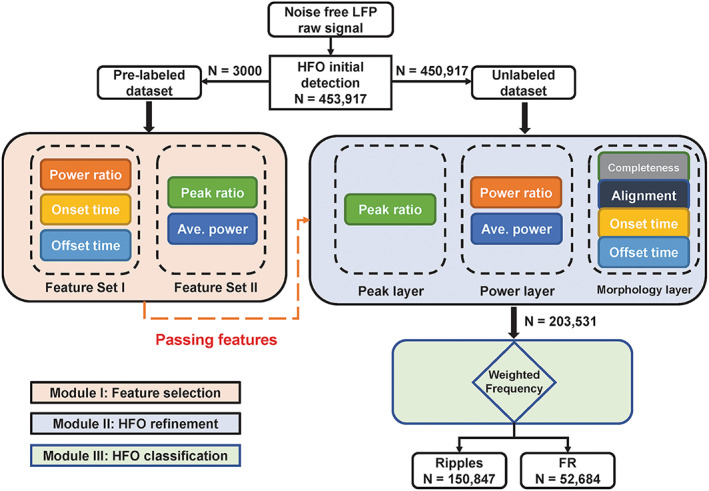
Schematic diagram of the HFO detection pipeline. In the HFO refinement module, the completeness and alignment subsystems are introduced from the previous study. All remaining are the re‐combination of features from the feature selection module.

2.4.1. Module 1: Feature selection

To explore key features that lead to different types of events, two experts were invited to review the database generated by the HFO initial detection. Experts manually selected 1000 true HFO events, 1000 all except sharp transients and true HFOs (AESH), and 1000 sharp transients (ST). Only events that were agreed by both reviewers were used for feature selection. The labeled datasets were excluded from the further HFO refinement process. The HFO refinement process was performed based on the remaining unlabeled datasets (n = 450 917) (Figure 1).

The reviewers scored the events by examining the local field potential (LFP). Specifically, the reviewers screened the LFP raw signal, filtered signal, and the time‐frequency plot and created the descriptive characteristics of HFOs from them. Guided by reviewers' criterions, we analyzed the labeled data generated two feature sets and they were defined as follows: (1) set A included the normalized average power and power ratio, and (2) set B included peak ratio and the start/end time of the peak. The interpretation of constructing two sets was that the reviewers found set A to be effective in distinguishing sharp transients from the data pool (Figure 2A), and meanwhile set B worked in differentiating HFOs from AESH (Figure 2B). Based on the analysis of these two numerical distributions, the thresholds used to establish the HFO refinement were set, and they are as follows: normalized average power: 0.2; power ratio: 0.7; peak ratio: 0.6; start time: less than 0; end time: greater than 0.

FIGURE 2.

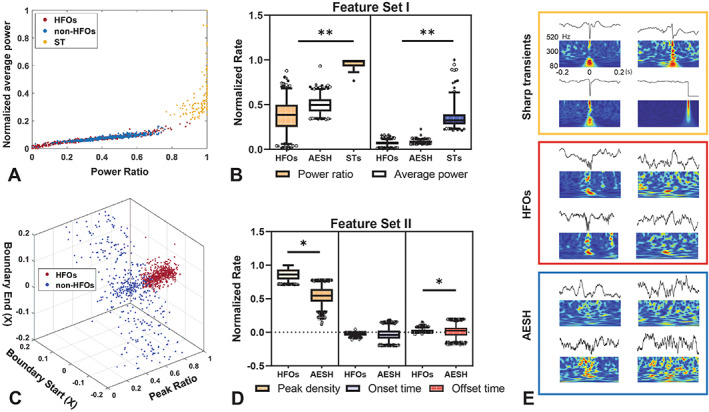
HFO selection process. A, 2D distribution of three types of events based on power ratio ${\mathit{HPR}}_k$ and normalized power ${\overline{Z}}_k$, with red, blue, and yellow dots representing HFOs, AESH, and sharp transients (ST), respectively. B, The statistical analysis of feature set one with respect to HFOs, AESH, and STs. C, 3D distribution of HFO and AESH regards to peak ratio, start/end time of POE. The red dots refer to HFOs, while blue dots represent AESH. D. The statistical analysis of feature set two with respect to HFOs and AESH. E. The demonstrative events of the ST (top), HFO (middle), and AESH (bottom).

2.4.2. Module 2: HFO refinement

To discard HFO FPs from the original database, a multi‐threshold layer was created based on the two feature sets generated by feature selection module. There are three layers in this section, and the detailed design is described below.

2.4.2.1. (1) Peak constraint layer

Based on the LFP of labeled dataset, we found that the HFOs always represent rapid oscillations around the center, which contrasts with the AESH. Consequently, it is plausible to assume that the difference in shape between the true HFOs and AESH will be reflected and enhanced after implementing the 80‐520 Hz bandpass filter on the LFPs. Then, it is also feasible to separate the HFOs from the background noise by quantifying the burst of peaks on filtered data. Thus, we calculated the ratio between the peaks in the center 0.1 s range and the total number of peaks for that event. The ratio is denoted as $P_d$ and peaks are defined as follows: if points are above or below the mean ± 2 times of standard deviation of the baseline, they will be considered as peaks. We set the ratio to 0.6 by looking at the 3D distribution on labeled dataset (Figure 2B).

2.4.2.2. (2) Power thresholding layer

It is worth noting that sharp transients also reflect a burst of peaks, inevitably making it hard to differentiating them from true HFOs. Therefore, adding a layer that can distinguish sharp transients is necessary. During the feature selection process, the reviewers found that the time‐frequency maps obtained by Gabor wavelets clearly showed differences. Hotspots of ST reflected a thin and long candle‐shaped contour, while HFOs typically represent more of a squeezed or orb shape around the center, with AESH not indicating any obvious hotspot. Here, we introduced a similar approach to quantify the predominant characteristic of sharp transients. ³³ The first property introduced was the average power $\overline{Z}$, and the power of the $k^{\mathit{th}}$ time window is denoting as: ${\overline{Z}}_k=\frac{1}{\mathit{TF}}\sum _l\sum _{m=t_k}^{t_{k+1}-1}{Z}_{\mathit{lm}}$, it was set to $\frac{1}{\mathit{TF}}\sum _l\sum _m{Z}_{\mathit{lm}}$, which was identical to our previous study. ³³ The other was the power ratio $\mathit{HPR}$, and the ratio of the $k^{\mathit{th}}$ window is as follows: ${\mathit{HPR}}_k=\frac{1}{\mathit{TF}}{1}^T\left({\sum }_{m=t_k}^{t_{k+1}-1}{Z}_{\mathit{lm}}\ge {\overline{Z}}_k\right)$, which was set to 0.7 following the value of previous study. ³³ Specifically, the terms $T$, $F$, and $t_k$ refer to the length of the time vector, frequency vector, and start point of the $k^{\mathit{th}}$ time window, respectively. $Z$ represents the time‐frequency matrix of an epoch, and $1$ is the vector whose all entries are 1. Moreover, the length of the time window was set to 100 ms, and the stride was set to ensure the 90% overlap of two consecutive windows.

2.4.2.3. (3) Contour morphology layer

The feature $P_d$ demonstrates its effectiveness in separating HFOs from background signals. The HFO usually reflects the blob shape around the center, while the AESH show no sign of energy concentration. The location of hotspot can be considered as another key factor to distinguish these two. The hotspot was quantified by the contour method, ²⁶ , ²⁷ , ²⁸ , ²⁹ and the contour analysis can be generalized into three aspects. The first aspect is the completeness of the contour. In this study, only closed‐loop contours (CLCs) are included for further analysis. Specifically, contours with identical starting and ending points are defined as CLCs, while open‐loop contours (OLCs) refer to the ones that have different starting and ending points. The second aspect is the alignment. The purpose is to discard epochs that do not follow certain rules, and they are defined as follows. (i) Discard the low power‐level CLCs by setting the threshold to $0.6\times \left(\max Z-\min Z\right)+\min Z$ to make a trade‐off between too many false positives and too few true HFOs. (ii) Discard those groups with the highest energy CLC located in the inner circle. (iii) Discard the groups containing less than 3 CLCs. After the three‐step threshold processing, the outermost CLC in each group is defined as the boundary of the group (BOG) and the CLC with the highest power level is defined as the peak of the group (POG). The third aspect is the on/offset of the hotspot, and the purpose is to ensure the events reflect a blob shape on the time‐frequency map. The details are described as follows: (i) Find the highest power‐level POG among all candidates and its BOG. These two parameters are denoted as the peak of epoch (POE) and boundary of epoch (BOE), respectively. (ii) Denote the left and right edge of the POE as the starting and ending points of the events. Set the starting points boundary <0 and set the ending points boundary >0 (Figure 2). All other parameters in this section follow the settings in the previous study. ³³

2.4.3. Module 3: HFO classification

All unlabeled data were processed according to the pipeline to form a refined dataset. The POE of each individual HFO was implemented to compute the corresponding weighted frequency $F$, which is defined as: $F_{\mathit{ij}}={f_D}^T{Z}_D$, where $D$ denotes all complete grid cells covered by the POE. The terms $f_D$ and $Z_D$ represent the frequency value and power level of a specific grid cell retrieved from the time‐frequency matrix. If $F$ is above 240 Hz, then this epoch is classified as a fast ripple. Otherwise, it is classified as ripple.

2.5. Comprehensive evaluation of the HFO detection algorithm

At present, there is little consensus on how HFO detection algorithms should be comprehensively evaluated. ³⁴ One of the problems is the difficulty of assembling a team of experts in HFO identification. Previous studies have found both disagreement ³⁵ and relatively good agreement ³⁶ among raters on HFO detection. HFO events are most often observed in the hippocampal CA1 region and the entorhinal cortex. ³⁷ However, it is more difficult to confidently label HFO events in other brain regions and when the recording microelectrodes are away from the soma. ³⁸ , ³⁹ , ⁴⁰ , ⁴¹ In addition, scoring a large sample of events is very laborious. To assess the accuracy and reliability of the algorithm, we implemented a rating protocol involving four experts, either clinical epileptologists or neurology researchers. Given the very long recordings (nearly thousands of hours in total), visual inspection of all HFOs was impractical, so a random sampling was introduced for evaluation. Specifically, epochs were randomly selected among several subjects to create test sets to comprehensively evaluate the HFO detection accuracy and ripple/fast ripple distinguishability. We constructed four different event subgroups in the evaluation dataset, including 1000 detected HFOs, 1000 rejected HFOs, 500 ripples, and 500 fast ripples. Specifically, the 1000 detected HFOs used to evaluate HFO detection were separated from the 500 ripples/fast ripples used to evaluate HFO classification. All individual events were independently labeled by four experts. No platform/software was given to the reviewer, instead we provided the unfiltered LFPs and their corresponding time‐frequency plots (see Supplementary Figure S1) for evaluation.

2.6. Statistics

2.6.1. Assessing the effectiveness of HFO detection and classification

To evaluate the performance of HFO detection, the task of the raters was to label: (1) true HFOs from 1000 detector‐dropped HFO events, and (2) false HFOs from 1000 algorithm‐identified HFO events. In the first experiment, the expert labeled HFO events were referred to as false negatives (FNs) and the remaining unlabeled events were referred to as true negatives (TNs). In the second experiment, expert labeled AEH (all events except HFOs) were considered as false positives (FPs) and the remaining unlabeled events were denoted as true positives (TPs). The results of evaluation from raters formed a 2‐by‐2 confusion matrix that further quantified accuracy ($\mathit{Acc}$), precision ($P$), recall ($R$), and F1 score ($F1$) according to the following equations. (i) $\mathit{Acc}=\frac{\mathit{TP}+\mathit{TN}}{N}$; (ii) $P=\frac{\mathit{TP}}{\mathit{TP}+\mathit{FP}}$; (iii) $R=\frac{\mathit{TP}}{\mathit{TP}+\mathit{FN}}$; (iv) $F1=\frac{2*P*R}{P+R}$. The term $N$ represents the total number of samples used for review, which in this study corresponds to 2000.

To verify the distinguishability of the HFO classification, the rater needs to indicate the source of the error from the dataset of 500 detector‐identified ripples, 500 detector‐identified fast ripple, and 500 detector‐dropped events. Specifically, the rater should empirically indicate that an incorrectly detected ripple should be classified as a fast ripple or as other (either a AESH or a sharp transient). Therefore, a 3‐by‐3 confusion matrix was created to retrieve the overall accuracy ($\mathit{Acc}$), precision, recall, and F1 score for ripple ($P_r,R_r,F{1}_r$) and fast ripple ($P_{\mathit{fr}},R_{\mathit{fr}},F{1}_{\mathit{fr}}$), respectively. Specifically, these parameters were computed as follows (i) $\mathit{Acc}=\frac{{\sum }_{i=j}{N}_{\mathit{ij}}}{{\sum }_{i=1}^3\sum _j^3{N}_{\mathit{ij}}}$; (ii) $P_r=\frac{N_{11}}{{\sum }_{i=1}^3{N}_{i1}}$, $P_{\mathit{fr}}=\frac{N_{22}}{{\sum }_{i=1}^3{N}_{i2}}$; (iii) $R_r=\frac{N_{11}}{{\sum }_{j=1}^3{N}_{1j}}$, $R_{\mathit{fr}}=\frac{N_{22}}{{\sum }_{j=1}^3{N}_{2j}}$; (iv) $F{1}_r=\frac{2*P_r*R_r}{P_r+R_r}$, $F{1}_{\mathit{fr}}=\frac{2*P_{\mathit{fr}}*R_{\mathit{fr}}}{P_{\mathit{fr}}+R_{\mathit{fr}}}$. The term $N_{\mathit{ij}}$ is denoted as the ${\mathit{ij}}^{\mathit{th}}$ entry of the confusion matrix.

2.6.2. Assessment of the inter‐rater reliability

To evaluate the validity of the test and the stability of the results, we conducted an inter‐rater reliability analysis. We chose Cohen's kappa to measure the inter‐rater reliability of the scores from the previous step (section 2.5.1). For more details on computing Cohen's Kappa, see the supplementary materials. In this paper, the conventional description of $\kappa$ is implemented, which follows: less than 0, poor reliability; 0 to 0.2, slight agreement; 0.21 to 0.4, fair; 0.41 to 0.6, moderate; 0.61 to 0.8, substantial; 0.81 to 1, almost perfect agreement. ⁴²

3. RESULTS

3.1. Results of feature selection module

As described in 2.3.1, five features were included in the feature library, namely $P_d$, ${\overline{Z}}_k$, ${\mathit{HPR}}_k$, and onset/offset time of POE. ${\overline{Z}}_k$ and ${\mathit{HPR}}_k$ comprised the feature set 1 and are mainly responsible for separating sharp transients from the database (Figure 2A). The histogram of ${\overline{Z}}_k$ and ${\mathit{HPR}}_k$ shows statistical differences in distribution among all three categories, revealing that the power and shape of the hotspot do help to distinguish sharp transients (Figure S2A). On the contrary, the $P_d$ and the onset/offset time of POE constitute the feature set 2, which aims to distinguish HFOs from the background signal. The true HFOs are clustered in a certain region of this 3D space, while the AESH are sparsely distributed (Figure 2C). The bar plot of the three attributes of feature set 2 shows the probability distribution of selected features in these two categories, reflecting the more concentrated energy of HFOs compared with the background signals (Figure S2B). Thus, a favorable HFO detection pipeline was generated by these two feature sets being integrated into the thresholding process. The detailed distributions of these five selected features across different data types are represented in Figure 2B and Figure 2D, and the significant differences are listed in Table S1.

3.2. Results of HFO detection and classification module

To investigate the details of HFO refinement, each processing layer of HFO rejection was carefully screened (Figure 3). Sharp transients revealed a long and narrow hotspot that spans across the entire frequency range, which was substantially different from HFOs/AESH, suggesting the effectiveness of power and shape of the contour in differentiating sharp transients and others (Figure 3A&B). Contours were split into OLCs and CLCs, and only CLCs with higher power level than the hyperparameters were kept for the following steps (Figure 3C&D). At last, the onset and offset time of POE was implemented to check the position of the hotspot with the left dashed line representing onset time of the event and the right dashed line referring to the offset time (Figure 3E). The AESH revealed the off‐centered hotspot, which was captured by this layer and substantializing the effectiveness of feature selection layer.

FIGURE 3.

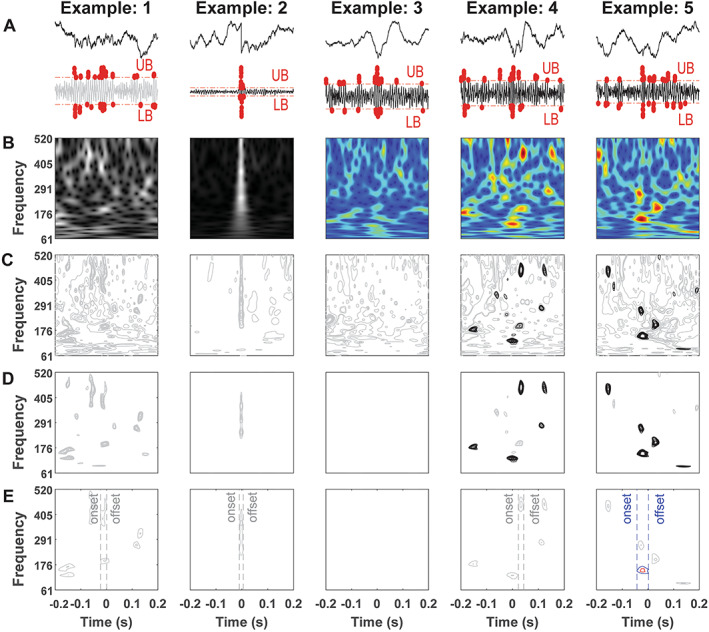
Details of HFO rejection. A, Raw plot of selected epochs and the details of peak thresholding layer. UB, upper bound. LB, lower bound. Red dots, peaks outside of the boundary. Gray line, epoch declined by thresholding. B, Time‐frequency plot. Gray picture, epoch failed in sharp transients rejection. C, Decomposed contour plot. Gray contours, contours removed due to low‐energy CLCs. D, The process of group checking layer. Gray contours, contours less than 4 times CLCs. Black contours, qualified contour. E, Off‐center checking layer. Red circle, POE. Blue circle, BOE. Gray contour, unqualified POG and BOG.

The HFO classification was performed after HFO detection, and weighted frequency was the threshold implemented in this process. In this study, a total number of 453 917 HFOs candidates in 228 LFP epochs were identified after HFO rough detection. In total, 250 368 events were rejected during the HFO refinement process, including 84 320 events deleted in the peak constraint layer, 15 668 events deleted in the power thresholding layer, 4492 events deleted in the contour morphology layer, and 145 906 events deleted at off‐center checking layer. After the HFO rejection, 203 531 events (44% of total) were retained in the HFO events library.

The data analysis was computed on a 64‐core CPU, 264GB ram Dell Precision 7920 workstation and took 89.5 h to complete the entire process. The computation load was also tested on a conventional computer with 8‐core i7 CPU and 16GB memory capacity. With this build, the HFO initial detection ran for 1 min for a 30‐min file containing 8 channels. For the HFO refinement process, the time varied and the average processing time per file was 5‐10 min.

3.3. Comprehensive evaluation for the HFO processing

3.3.1. Evaluation of the HFO rejection

The evaluation of HFO detection included data from two perspectives: (1) labeling true HFO events from the 1000 algorithm‐discarded HFOs and (2) labeling false HFOs from 1000 algorithm‐detected HFOs. The confusion matrices based on the evaluation of each rater are presented along with the $\mathit{Acc}$, $P$, $R$, and $F1$ scores (Table 1). Specifically, the highest and lowest $F1$ scores among all raters were 0.99 and 0.92, indicating a solid performance in the HFO detection and reliability of features we selected for HFO refinement process. We obtained a $P$ of $0.92\pm 0.05$, $R$ of $0.99\pm 0.01$, with the $\mathit{Acc}$ = $0.95\pm 0.03$ and the $F1$ score=$0.94\pm 0.03$.

TABLE 1.

Confusion matrix of HFO detection

	Predicted HFO	Predicted AEH	ACC	P	R	F1‐Score
R1
Labeled HFO	869	13	92.8%	86.9%	98.5%	0.92
Labeled AEH	131	987
R2
Labeled HFO	937	8	96.5%	93.7%	99.2%	0.96
Labeled AEH	63	992
R3
Labeled HFO	983	2	99.1%	98.3%	99.8%	0.99
Labeled AEH	17	998
R4
Labeled HFO	865	11	92.7%	86.5%	98.7%	0.92
Labeled AEH	135	989

3.3.2. Evaluation of the ripple fast ripple classification

Table 2 not only reflects that our model is reliable in terms of distinguishing ripples and fast ripples, but more importantly summarizes the effectiveness of weighted frequencies in determining the category of the events. The overall accuracy was $0.97\pm 0.02$, revealing the high quality of the classifier. Specifically, the overall $P_r$, $R_r$, and $F{1}_r$ were $0.98\pm 0.02$, $0.98\pm 0.01$, and $0.98\pm 0.01$. On the contrary, the overall $P_{\mathit{fr}}$, $R_{\mathit{fr}}$, and $F{1}_{\mathit{fr}}$ were $0.94\pm 0.05$, $0.98\pm 0.01$, and $0.96\pm 0.03$.

TABLE 2.

Confusion matrix of HFO classification

	Predicted Ripple	Predicted Fast Ripple	Predicted AEH	$\mathit{Acc}$	$\mathit{Pr}$	$\mathit{Rr}$	$F1r$	$\mathit{Pfr}$	$\mathit{Rfr}$	$F1\mathit{fr}$
R1
Labeled Ripple	495	0	1	99.1%	99%	99.8%	0.994	99.6%	98.6%	0.99
Labeled Fast Ripple	1	498	6
Labeled AEH	4	2	493
R2
Labeled Ripple	499	5	3	97.2%	99.8%	98.4%	0.991	92.8%	99.4%	0.96
Labeled Fast Ripple	1	464	2
Labeled AEH	0	31	495
R3
Labeled Ripple	496	3	0	98.9%	99.2%	99.4%	0.993	97.8%	99.0%	0.98
Labeled Fast Ripple	3	489	2
Labeled AEH	1	8	498
R4
Labeled Ripple	481	6	5	94.5%	96.2%	97.8%	0.97	89.4%	97.6%	0.93
Labeled Fast Ripple	5	447	6
Labeled AEH	14	47	489

3.3.3. Inter‐rater reliability of HFO identification

As described in section 2.4.3, Cohen's kappa was introduced to analyze the inter‐rater reliability. Figure 4A provides details of raters' decision for each randomly selected event in HFO detection. Experts tended to have more disagreements on the incorrectly detected HFOs, indicating that raters were more confident in the events that were rejected by multi‐layers. Strong inter‐rater agreement was found in the HFO detection section, with an overall $\kappa$ of $0.94\pm 0.03$ (Figure 4C). Figure 4B documents rater disagreements with the detector in HFO classification. The raster plot shows that raters disagreed the most on the cases in the fast ripple labeling. The overall inter‐rater reliability was slightly weaker than the HFO classification (Figure 4D), with a corresponding $\kappa$ of $0.85\pm 0.04$, but still in the range of excellent agreement.

FIGURE 4.

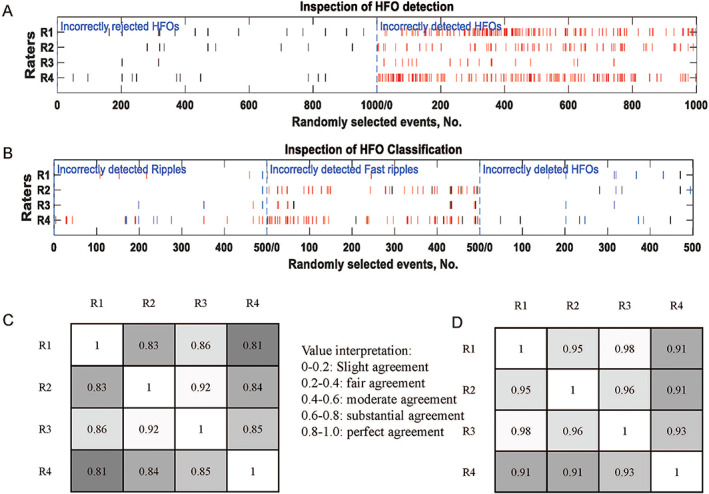
Evaluation of our approach. A, Raster plot of HFO algorithm evaluation. The black bars referred to the disputes over HFO events rejected by detector and red bars referred to disagreements over the detected HFOs. B, Raster plot of HFO classification evaluation. Incorrectly detected ripples: Blue bar from fast ripple, red bar from AESH. Incorrectly detected fast ripples: Black bar from ripple, red bar from non‐HFO events. Incorrectly deleted HFOs: black bar from ripple, blue bar from fast ripple. C, Correlation matrix of HFO detection between four raters, the lighter color the stronger agreement, with the overall $0.94\pm 0.03$ $\kappa$. D, Correlation matrix of HFO detection evaluation between four raters, the lighter color the stronger agreement, with the overall $0.85\pm 0.04$ $\kappa$.

3.3.4. Performance comparison against other methods

To further test that our detector accurately selects true HFOs and discards false detections, we compared our approach with other detectors. As shown in Figure S4, our approach reached the accuracy rate of $0.91\pm 0.049$, while the short line detector method ¹³ , ⁴³ showed a rate of $0.54\pm 0.082$, and the Hilbert approach ⁴⁴ showed an accuracy of $0.54\pm 0.08$. The details of reviewers' agreements have been well documented with each bar representing a false positive (Figure S5). It was worth noting that the co‐occurrence of high rater agreements on wrong detections and the low agreements on correct identifications are due to the inconsistent performance of the detectors. In our method, the agreement for detectors to incorrectly identify HFO events was 13.5%, while the agreement to correctly identify HFOs improved to 85%. In contrast, in the Hilbert method, the agreement for incorrect detection raised to 35.9%, while the agreement for accurate identification dropped to 42.3%. Again, the short line length method performed similarly to the Hilbert method on this metric. Agreement on incorrectly detected events rose to 29.4%, while agreement on correctly detected HFOs fell to 36.9% (Figure S6).

We implemented our approach to a new dataset with the Kainic Acid animal model of epilepsy ¹⁸ to evaluate the effectiveness of our algorithm. Notably, we did not manually inspect and remove artifacts in the KA dataset as we did in the TBI dataset, and thus, the accuracy on the KA dataset should decrease given the variation in data quality. Specifically, we randomly selected 500 algorithm‐detected HFOs on the KA dataset and asked reviewers to mark AEH (Figure S7). Our method obtained an accuracy of $0.92\pm 0.05$ and $0.77\pm 0.08$ for HFO detection on the TBI dataset and KA dataset, respectively. The precision decreased on KA dataset, but it still remains at a high level even though the recordings were affected by motion artifacts. In terms of the recall rate for HFO detection, our method has a solid performance, reaching $0.99\pm 0.01$ and $1.00\pm 0.00$ on TBI and KA dataset, respectively. Finally, the $F1$ score reached $0.94\pm 0.03$ on the TBI dataset and $0.87\pm 0.05$ on the KA dataset, indicating the reliability and feasibility of the selected feature sets for refinement process (Figure S8).

4. DISCUSSION

This study presented a novel approach to reliably and effectively reject HFO FPs, one of the most common problems that hinders the clinical use of HFO. Our approach focused on the analysis of LFPs without machine noise, using AESH and sharp transients as the main rejection targets. We designed a method based on a library of relevant features, followed by a multi‐layer threshold processing method for event rejection. Four experts thoroughly evaluated the method and achieved high F1 scores in both detection and classification tests, thus confirming the feasibility of our method. The stability of this study was further validated by high inter‐rater reliability, indicating the advanced nature of our method in improving the quality of the HFO database. The highlight of this study is the introduction of the multi‐layer threshold module. Five critical features were selected to distinguish between HFOs, background signals, and sharp transients. The experts marked small portion of events for each category, and they empirically evaluated event type from the shape, power, and locations of the LFPs and time‐frequency plots. We used these features and designed the HFO rejection pipeline that simulates the expert reviewing process. Specifically, the peak constraint and morphological identification layers are responsible for identifying HFOs and AESH, while the power thresholding layer aims to distinguish sharp transients.

In the HFO initial detection, the main drawback was the large number of HFO FPs; specifically, 84% of the detected events were later found to be either background noise or sharp transients, which indicated a need for HFO FP rejection. In our multi‐layer thresholding process, 33.73% of the HFO FPs were removed by the peak constraint layer and 6.28% of sharp transients by the power thresholding layer and the remaining 59.98% were rejected in the morphological identification layer. According to the evaluation of HFO detection, our algorithm reached the accuracy rate of 92% and a precision rate of 99%. This result is close to the machine learning approaches with powerful recognition capabilities brought by neural networks. ⁴⁵ , ⁴⁶ , ⁴⁷ , ⁴⁸ , ⁴⁹ , ⁵⁰ However, the machine learning models hold an end‐to‐end design, which lack the interpretation and mathematical description of HFOs important to clinical utilization. ⁴⁵ , ⁴⁶ , ⁴⁷ , ⁴⁸ The HFO classification module of our method distinguished ripples and fast ripples with high accuracy presumably because high‐quality HFO candidates had already passed through the feature selection module. Specifically, our design had the precision rate of 98% and 94% in ripple and fast ripple classification, and 98% and 98% in recall rate of ripple and fast ripple, respectively.

It is important to clarify that intracranial EEG implementations of HFO detection using the topographical method consider “candles” as exclusively physiological sharp spikes. ¹³ , ²⁹ , ³⁴ , ³⁵ In contrast, in the current LFP implementation, we considered candles as nonphysiological sharp transients and sharp spikes. The major difference is that in LFP recordings from rodents, sharp transients occur frequently and need to be automatically redacted, along with sharp spikes (eg, Figure 2E). In the current version of the topographic analysis, we do not distinguish HFOs on oscillations from HFOs on spikes, but this can be implemented in later versions. Other potential issue comes from the use of the same parameters for topographical detection of ripple and fast ripples. In our approach, the ripples and fast ripples are processed simultaneously, which inevitably introduces bias to contour morphology layer and then leading to fewer fast ripples been detected since power level of CLC in high‐frequency range (>240 Hz) is typically lower than the one in the lower frequency region (<240 Hz). Additionally, our algorithm identifies only one class of event for each epoch, either ripple or fast ripple. It would omit the case when ripples and fast ripples occur simultaneously. Under this circumstance, our algorithm would be forced to choose the one with higher energy even if the power levels of these two POGs are similar. The case of “fast ripple on ripple” provides valuable information in epilepsy assessment ¹⁴ and may not be well addressed in our approach.

In this study, we are still manually selecting thresholds in the feature selection process. In future work, as more data are visually inspected and more features are added to the feature selection process, we hope to establish a tree model that selects the most critical features based on their importance ranking and then automatically detects HFOs without the need to manually set criteria for HFO rejection.

Inter‐rater reliability test has been implemented in many studies and has become a golden standard to justify the performance of the automatic detection method. The inter‐rater agreement was applied to identify interictal epileptiform discharges (IEDs) and justify the robustness of the detection method. ⁵¹ It was also introduced in seizure detection to make a collective clinical decision. ⁵² Former studies reported the inter‐rater reliability in the HFO analysis. ⁴⁵ , ⁴⁹ However, one of the issues was the difficulties to obtain the “ground truth,” especially when the dataset was large. In our approach, the deleted epochs were assembled to form the negative dataset. Instead of labeling all the data, we reported the true negatives by sampling and rating the events from the negative dataset. Our results indicated a high degree of consistency across raters, suggesting that features selected are representative and able to generate the detector without instability issues. Consequently, the implementation of important features and mathematical description of HFOs would be beneficial to HFO study in academic and clinical scenarios.

One issue to note is that we did not test our algorithm in a clinical dataset. Considering that common SEEG data has hundreds of channels, it is expected to take longer to compute compared with the animal data we tested in this study. Additional adjustments may be needed because of the different sampling rates. In addition, we note that our method is not computationally efficient, especially slow in computing the morphological layers.

Instead of one‐dimensional data, the morphological analysis in our algorithm expands the data into a two‐dimensional graph, which increases the computational load to a large extent. For the 768‐h dataset we tested, it took about 90 h to complete the entire process on a 64‐core Intel workstation. More optimization efforts should be implemented in future studies to improve the processing efficiency.

5. CONCLUSION

In this study, we presented a refined pipeline with a segregated design focused on rejecting false positives for HFOs. Through comprehensive expert evaluation, our algorithm showed a promising reliability and accuracy in rejecting HFO FPs. Future work can focus on refining the algorithm by testing larger populations and different recording environments.

CONFLICTS OF INTEREST

The authors report no conflicts of interest. We confirm that we have read the Journal's position on issues involved in ethical publication and affirm that this report is consistent with those guidelines.

Supporting information

Table S1: Computing the Cohen’s Kappa.

Zhou Y, You J, Kumar U, Weiss SA, Bragin A, Engel J, et al. An approach for reliably identifying high‐frequency oscillations and reducing false‐positive detections. Epilepsia Open. 2022;7:674–686. 10.1002/epi4.12647