A unique cardiac electrocardiographic 3D model. Toward interpretable AI diagnosis

Summary

Mathematical models of cardiac electrical activity are one of the most important tools for elucidating information about heart diagnostics. In this paper, we present an efficient mathematical formulation for this modeling simple enough to be easily parameterized and rich enough to provide realistic signals. It relies on a five dipole representation of the cardiac electric source, each one associated with the well-known waves of the electrocardiogram signal. Beyond the physical basis of the model, the parameters are physiologically interpretable as they characterize the wave shape, similar to what a physician would look for in signals, thus making them very useful in diagnosis. The model accurately reproduces the electrocardiogram signals of any diseased or healthy heart. This new discovery represents a significant advance in electrocardiography research. It is especially useful for diagnosis, patient follow-up or decision-making on new therapies; is also a promising tool for well-performing, transparent and interpretable AI approaches.

Graphical abstract

Highlights

• •A solid mathematical modeling of the cardiac electric activity
• •The model accurately reconstructs, and generates, 12-lead ECG signals
• •Three markers for the diagnosis of LBBB, CBBB, and HYP pathologies
• •An APP analyses and diagnoses ECGs for any heart condition

Artificial intelligence; Cardiovascular medicine; Computer-aided diagnosis method

Introduction

The development of models and algorithms for the study of the cardiac electric system helps to better understand the physical processes governing the system and helps to guide therapeutic planning. In particular, the development of automatic methods with interpretable decisions is in high demand. The relevance of the topic has attracted the interest of scientists from different fields, such as mathematics, physics, bioengineering, and medicine.

The heart muscle is a composite tissue with a complex structure that consists of various cell types. The electric activation of the heart begins at the sinus node where pacemarker cells activate spontaneously. The corresponding current results in the excitation of the neighboring cells, and it then spreads, first along the atria, and then along the ventricles.^6,28

Generalized assumptions on cardiac electrophysiological models that date back to the 1960s,²³ and remain part of the conventional approach are: the electric field is represented by a single or multiple dipoles, whereas the total electric activity is represented by a three-dimensional vector. This vector, denoted by $\overrightarrow{D}\left(t\right)$ at time $t$, is the sum of all the individual dipole vectors. Because the depolarization wavefront spreads through the heart, $\overrightarrow{D}\left(t\right)$ changes in magnitude and direction as a function of time. $\overrightarrow{D}\left(t\right)$typically describes a trajectory with three loops corresponding to consecutive time segments: the $P$ wave (atrial depolarization), the $QRS$ complex (ventricular depolarization) and the $T$ wave (ventricular repolarization), respectively. The loops described by the $P$ and $T$ waves are elliptical, whereas the $QRS$ has an irregular shape.²⁵ Furthermore, the voltage measurements registered by the electrocardiogram (ECG) signal are the projections of $\overrightarrow{D}\left(t\right)$ in the directions of the axes of the recording electrodes located on the thoracic surface. In general, positive (negative) signals are produced when the depolarization front propagates toward (away from) a positive electrode. The opposite happens for the repolarization front. The standard ECG has signals from 12 projections or leads recorded using 10 electrodes.⁶

Despite the previous assumptions, mathematical formulations for ECG signals remain quite complex. Classical formulations include differential equation systems, representing the process with more or less biophysical detail. Aside from the mathematical complexity of the model formulation, some common criticisms of these models are that they hardly generate realistic 12-lead ECG signals, and that they depend on a large number of parameters which are hardly identifiable. In practice, a meaningful parameter identification is essential.

The literature dealing with dipole models for the electric activity of the heart is very extensive.^{5,12,13,14,15,16,32,37,38,54,58} Alternative approaches dealing with specific aspects of the heart’s electric activity are also too many to be easily summarised.^{21,22,30,50,51,52} Furthermore, many papers since the early 1950s have been devoted to vectorcardiography (VCG) models.²⁵ Instead of 12-lead standard ECG models, they only consider three leads scanned in quasi-orthogonal axes. However, the VCG system is not common in clinical practice as there are fewer experts trained in these signals. ECG and VCG models have contributed to an improved understanding of the functioning of the heart, but have so far had little success in convincing clinicians. In particular, they fail in an important prerequisite for clinical applications, the ability to faithfully replicate ECG recorded from any diseased or healthy heart.

Here we present a novel model, named 3DFMM_ecg that is formulated for the 12-lead signals. The term 3D is used because it is assumed that these signals are projections of a three-dimensional electrical signal. The model relies on the classical physiological premise: the electric source is represented by a multiple dipole model. The novelty, however, is that it assumes that $\overrightarrow{D}\left(t\right)$ combines the electric signals from exactly five different sources, which represent differentiated myocardium segments, further associated with the five fundamental waves in ECG signals. Namely, $\overrightarrow{D}\left(t\right)={\overrightarrow{d}}_P\left(t\right)+{\overrightarrow{d}}_Q\left(t\right)+{\overrightarrow{d}}_R\left(t\right)+{\overrightarrow{d}}_S\left(t\right)+{\overrightarrow{d}}_T\left(t\right)$, where $t$ represents the real time and varies in $(\mathrm{0,2}\pi ]$ for each heartbeat. Furthermore, the new model is also based on a key idea and original assumption: ${\overrightarrow{d}}_J\left(t\right)$, with $J\in \left\{P,Q,R,S,T\right\}$, moves in the same plane as time progress, and its trajectory is described as a complex FMM signal, a parameterized mathematical equation that describes an elliptical trajectory. Accordingly, the magnitude of ${\overrightarrow{d}}_J\left(t\right)$ in a given direction is represented by a one-dimensional FMM wave, which reflects depolarization and repolarization voltage changes. An FMM wave, $W\left(t,A,\alpha ,\beta ,\omega \right)$, is an equation defined in terms of four parameters.⁴⁴ The parameter $A$, a positive real number, measures the wave amplitude; $\alpha$ is a location parameter with values in $(\mathrm{0,2}\pi ]$; whereas $\beta$, with values in $(\mathrm{0,2}\pi ]$, describes the asymmetry degree of the wave shape and also informs when the unimodal pattern corresponds to a crest or a trough. Finally, the parameter $\omega$, with values in 0,1, measures the sharpness of the peak. The value $\omega =1$ corresponds to an exact sinusoidal shape. Figure 1 illustrates each parameter in a simulated ECG signal. These four parameters are wave-specific, but, whereas $A$ and $\beta$ are also lead-specific, $\alpha$ and $\omega$ are the same across leads. The role of these common parameters is essential in the modeling process. They provide connectivity between the signals from different leads thus, simplifying the model substantially. For a given lead $L$ and wave $J$, the quadruple $\left[A_J^L,{\alpha }_J,{\beta }_J^L,{\omega }_J\right]$ describes precisely the wave shape, in the same way a physician looks at the signal. From the model definition it also follows that projections of $\overrightarrow{D}\left(t\right)$, in directions different from those in the standard 12-lead system, are also formulated as a sum of five FMM waves where $\alpha$ and $\omega$ do not change. Thus, the approach unifies VCG and ECG systems within a single formulation.

Figure 1.

FMM parameter description

An ECG healthy heartbeat with waves decomposition and morphological parameter description

The inclusion of an intercept and an error term that accounts for data noise results in a powerful statistical model. To make the model identifiable and even more biologically interpretable, we assume that ${\alpha }_P\le {\alpha }_Q\le {\alpha }_R\le {\alpha }_S\le {\alpha }_T$. These restrictions respond to the natural depolarization order of different myocardium segments. These restrictions and the fact that the number of parameters is small, some of them common to different leads, guarantee an accurate identification of the model parameters, even in the cases of highly anomalous patterns or noisy signals. A quadratic optimization problem must be solved to obtain the model parameters. Here, we design a backfitting iterative approach to solve the problem. Specifically, the common parameters, $\alpha$ and $\omega$, are identified using a grid search. Then, the lead-specific parameter estimates $A$ and $\beta$ are easily derived using standard linear regression models. An algorithm is designed to analyze 12-lead ECG fragments of any length. In the preprocessing stage, the signal is divided beat by beat. Then, for each beat, parameter estimates are derived. The output of the algorithm provides, for each wave, the series of parameter values, corresponding to consecutive beats, which can be summarized to get average patterns as well as the changes in the patterns over time. These quantities can be used directly in the clinic. For example, a specific measure of the QRS complex duration, a very well-known feature in cardiology, can be defined with the distance between ${\alpha }_Q$ and ${\alpha }_S$. In the literature, there is no universal way to calculate this measurement. First, because the definition is vague: the QRS interval starts from the beginning of the Q wave to the end of the S wave. Second, because the observed signal is noisy, and finally, because different values may be derived from different leads. Compared to the commonly used measures of QRS duration, that based on FMM parameters have a more precise meaning and, more importantly, are not dependent on the lead, the measurement device, or the investigator eye.

The evaluation of the 3DFMM_ecg model is an integral question but the evaluation technique and the model to compare with, depend on the specific tasks we want to solve. The 3DFMM_ecg model is a multi-purpose approach and there is no an alike model to compare with. Indeed, there is no other multiple lead model, useful for automatic diagnosis, beyond black-box models. The better performance of the FMM single lead model against alternatives has been already shown in Rueda et al.,⁴³ in terms of global goodness of fit, consistency, robustness, and also for fiducial marks detection and pattern identification. In this paper, to evaluate the performance of the 3DFMM_ecg model, we proceed as follows. First, we analyze the model’s ability to reconstruct realistic ECG signals using 1D, 2D, and 3D representations generated from different parameter configurations. Second, all the ECG fragments from patients in the Database:PTB-XL⁵⁶ were analyzed with the new model. PTB-XL is a benchmark database, that contains a great variety of healthy, pathological, and noisy cases. To illustrate how the model works see Figure 2 and Figures S5–S12 for healthy and different heart conditions, respectively. We emphasize that the input and output of the 3DFMM_ecg model are the 12-lead signals although is based on the assumption that these signals are projections of a 3D signal. Specifically, the model generates a predicted multivariate signal that mirrors the original 12-lead ECG signal with high reliability, as we quantify in the paper. This is something that other models are very far from reaching except for methods specifically designed for data compression or denoising, which are useless for solving other issues, particularly in automatic diagnostics. Third, the applicability of the model in clinical practice is illustrated with three markers, defined in terms of the model parameters, which are proved to be very useful for the detection of three well-known cardiac pathologies. Specifically, ROC curves from the Database:PTB-XL are given. These markers have at least the following advantages compared to black-box models: (1) The definition is very simple, it is applied to each patient individually and the result does not depend on the rest of the patients or their pathologies. In particular, no training set is used. (2) Its universal character allows the analysis of signals obtained with any recording device or preprocessing. (3) The cardiographic interpretation is clear and in accordance with standard medical diagnostic criteria. (4) The markers can be easily monitored and their evolution can be studied, providing valuable diagnostic information over time.

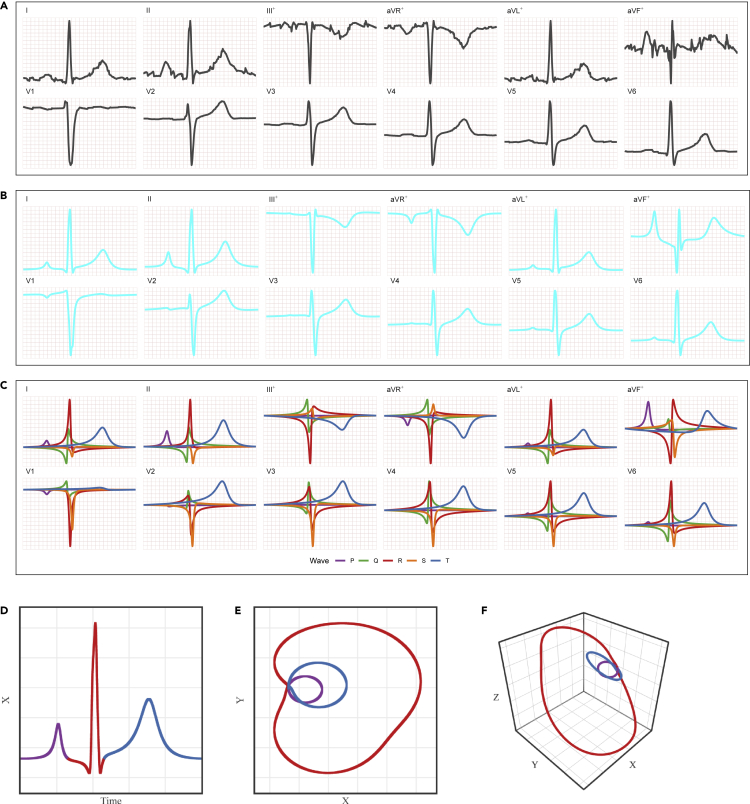
Figure 2.

ECG from patient id 8 (beat n°9) in the Database:PTB-XL

(A) 12-lead observed signals (scaled).

(B) 12-lead FMM predicted signals.

(C) 12-lead FMM wave patterns. The symbol + indicates linear combinations of other signals.

(D), (E) and (F): 1D, 2D and 3D representations of the predicted signals, respectively, where $X=LeadII;Y=LeadI{I}^{\left(i\right)};Z=LeadV2-2\ast Y$. The colors differentiate the $P$ (purple), $QRS$ (red) and $T$ loops (blue)

Furthermore, the model validation can be extended to any other dataset as an app is provided: https://fmmmodel.shinyapps.io/fmmEcg3D/, which allows the researchers to check the model with their own data. It includes a variety of examples that clearly illustrate how well our model reconstructs multivariate ECG signals, and help in diagnosis providing the markers values.

Results

Next sections show how the 3DFMM_ecg successfully solves the main challenges of the forward and inverse problems in electrocardiography, and give an overview of the contributions to interpretable AI. Furthermore, a simulation study that shows how the identification algorithm provides sensible and robust parameter estimates across different configuration scenarios was conducted (see STAR Methods). The analysis of real ECG data requires a preprocessing stage to remove baseline and other noise artifacts. Data preprocessing is detailed in the STAR Methods.

Reconstruction of realistic ECG signals

A configuration of parameters for a healthy heart, labeled NORM, has been identified using the median values for all patients, labeled NORM in the Database:PTB-XL. This configuration is used as a reference. Alternative configurations describing different pathological conditions of the heart have been generated by changing the reference values of the most relevant parameters, summarized in Table S1, see the STAR Methods. The standard 12-lead unidimensional signals, and selected 2D and 3D representations, are provided for each configuration scenario. The axes we have selected for the 2D and 3D representations are defined as follows;

$$X=LeadII;Y=LeadI{I}^{\left(i\right)};Z=LeadV2-2\ast Y$$

$X$ is the most commonly used lead in studies, and $\left(X,Y\right)$ is a natural bidimensional representation described by the Analytic Signal, defined in the complex plane^45,47 (additional details are given in the Methods Section). Finally, $Z$ has been selected after checking other alternatives, as it offers an interesting visualization of the three loops: $P$, $QRS$ and $T$ across different patterns.

To conserve space, the figures for these configurations are shown in the Supplemental Information (see Figures S1–S4). In particular, the figure for the NORM configuration looks similar to Figure 2. The other configurations generate representations with characteristic and differentiated patterns.

Accuracy of 3DFMM_ecg predictions and markers

To validate the performance of the 3DFMM_ecg model in real practice, and in particular the three new markers, the ECG signals from the Database:PTB-XL have been analyzed. Using the preprocessing step, 210 patients (less than 1%) out of 21,837, were discarded because of very noisy patterns. In addition, 295 patients with pacemakers were discarded because of their highly atypical but predictable ECG patterns. A diagnostic label has been assigned to each patient in the database using SNOMED CT ontology,³⁴ (bioportal.bioontology.org/ontologies/SNOMEDCT). Labels are assigned only to patients with a diagnostic likelihood of 80 or more. Examples of observed and predicted signals from diverse heart conditions and noisy cases are given from Figures S5–S9 in Supplemental Information, illustrating the ability of the model to successfully handle pathological patterns. Some of the more recognized SNOMED labels used here are Complete Bundle Branch Blocks (CLBBB, CRBBB) left and right, respectively, and ventricular Hypertrophy (HYP).

ECG data at the patient level are a series of consecutive beats. The new markers are defined for a given patient, in a given center and device, and at a given moment of time; and these are obtained using median values of FMM parameters from individual beat values. Specifically, we define three new markers, namely: and $omeS$ as the median of the ${\omega }_R$ and${\omega }_S$ individual beat values, respectively; and $maxAR$ as the maximum, across leads, of the median of the $A_R$ individual beat values.

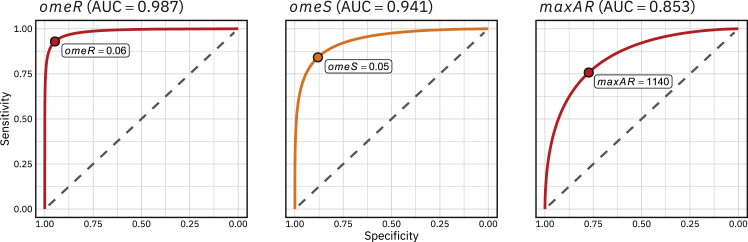
Table 1 gives percentiles for different measures obtained for CLBBB, CRBBB, HYP and NORM patients. On the one hand, a global model quality measure, named $\overline{R}$, is given. It is defined as the mean across leads of an$R^2$ measure, which is, in turn, the proportion of variation in the signal that is explained by the model (see Methods section for details). The figures in Table 1show that the $\overline{R}$ values are quite high across diagnostics, being higher than 90% for more than 95% of patients. The only candidate models with which to compare the values of $R^2$ in Table 1 are the models designed for data compression or denoising. These models are calibrated in the literature using measures similar to $R^2$, such as $PRD\left(\mathit{PR}{D}^2=1-R^2\right)$. $PRD$ values of the order of 10% or less are considered sufficient to maintain the specific characteristics of an ECG signal.³¹ The average $PRD$ values were obtained using the 3DFMM models with 5–12 components, ranging from 20% to 9%, for the Database:PTB-XL. These values show that the FMM approach is also a very interesting method for data compression tasks while retaining diagnostics markers. On the other hand, Table 1 also shows that $omeR$ and $omeS$ are directly associated with CLBBB and CRBBB, respectively, whereas $maxAR$ does with HYP, as long as $omeR$ is within the percentile range of NORM. The interest of the $omega$ FMM parameters in the diagnosis had already been evidenced in Rueda et al.,⁴² where simple diagnostic rules for CLBBB and CBBB (Complete Bundle Branch Block) have been defined, and can be used even when only one of the lead signals is available. To better illustrate the diagnostic ability of binary classifier systems based on these markers, ROC curves have been plotted in Figure 3. There are many proposed rules in the literature to classify these diagnoses with surprisingly high AUC values in some cases.⁴⁸ The AUC values obtained with the FMM markers are not far from them whereas the rules based on the new markers have several advantages compared to black-box models, as commented in the Introduction.

Table1.

Percentiles of $\overline{R}$, $omeR$, $omeS$ and $maxAR$ across NORM, CLBBB, CRBBB, HYP and ALL patients in Database:PTB-XL

		$\overline{R}$			omeR			omeS			maxAR
Diagnostic	N°	5$th$	Median	95$th$	5$th$	Median	95$th$	5$th$	Median	95$th$	5$th$	Median	95$th$
NORM	8,578	0.91	0.95	0.97	0.03	0.03	0.04	0.02	0.03	0.05	525	837	1,379
CLBBB	505	0.91	0.96	0.98	0.07	0.14	0.21	0.04	0.06	0.10	806	1,585	2,673
CRBBB	523	0.87	0.94	0.97	0.03	0.04	0.11	0.04	0.08	0.14	396	811	1,627
HYP	599	0.92	0.96	0.98	0.03	0.04	0.09	0.02	0.03	0.06	852	1,465	2,403
ALL	21,331	0.92	0.95	0.97	0.03	0.04	0.09	0.02	0.03	0.07	520	888	1,677

Figure 3.

ROC curves and AUC values for the markers $omeR$, $omeS$ and $maxAR$ for CLBBB, CRBBB and HYP, respectively

Figures S10–S12 in the Supplemental Information, illustrate how the model works under other heart conditions.

Contributions to interpretable AI

Black-box Machine Learning (ML) algorithms rapidly growing in cardiology, lack interpretability and can cause problems in high-stakes decision making.^{2,17,21,22,36,41,52,55,61} The ways the 3DFMM_ecg approach helps to explain how ML models work are diverse but mainly rely on two powerful properties. On the one hand, the model provides a set of robust indexes that characterize in detail the morphology of ECG signals. These indexes can be incorporated as features in a classification or prediction task generating inherently interpretable ML models. Besides, they can be used to explain the decision of an ML algorithm with statistic summaries and visualization. In particular, the relevance of different waves and/or leads can be easily illustrated, identifying the heart regions related to the algorithm decision as well. On the other hand, the 3DFMM_ecg model is able to reconstruct any real 12 lead ECG signal. This property allows us to elucidate how the ML model operates through well designed simulations, detecting possible shortcomings problems and identifying the causes of its decisions. Furthermore, a human-like interpretable and trustworthy AI FMM-based system could be developed by taking advantage of the ability of the FMM indexes to mimic almost any electrocardiographic feature, in such a way that the system is able to reproduce approximately the steps that a physician follows to read and interpret an ECG. Beyond the transparency and interpretability, other property that makes the 3DFMM_ecg model a very promising tool is its universal character. It works regardless of the preprocessing and denoising, the recording device, the number of leads, the length of data, or the differences between datasets label distributions. It provides consensus indexes for relevant features such as the QRS complex duration that would also contribute to reduce the differences in the interpretation of electrocardiograms.

Discussion

Here we present a unique cardiac electrophysiological model, the 3DFMM_ecg. The model is formulated under the assumption that the 12-lead signals are projections of a three-dimensional electric signal. Furthermore, the equations in the 3D model and in the univariate model in Rueda et al.⁴³ are identical. This is a great advantage of the 3D model as the generalization of the univariate model. The key of the 3D model is that the $\alpha$’s and $\omega$’s parameters are common to the 12 leads. These parameter are estimated using information from all the leads, avoiding problems if, for example, one of the signals had large disturbances. In addition, a set of parameters, two for each wave and lead, complete the description of the signals. The estimation approach using the 3D model is much more robust, the model parameters are accurately estimated avoiding identifiability problems.

The 3DFMM_ecg model also succeeds in providing reliable quantitative results to enhance the understanding of biophysical processes, starting with the $\alpha$’s and $\omega$’s parameters that represent the underlying electric signal and synchronize the waves across leads. Actually, all the parameters have a morphological interpretation and are reliable for extrapolation and prediction, thus simplifying the diagnostic task. Another crucial contribution of the 3D Model is that it permits to generate realist 12-lead ECG signals whereas those signals generated using univariate models do not necessarily correspond to projections of the same 3D underlying signal.

Furthermore, the results in the paper validate the premise that the electrical source can be represented with a five dipole model, on which the new model is built. Of interest, dipole models have been widely used in different forms in the literature. An additional motivation of this study is the capacity of the FMM approach for data compression, as minimal hard disk space is needed to fully reconstruct the signal. The monitoring of patients and, in particular, telemedicine requires the storage of ECG signals and a fast on-line transmission of information,^7,8 and therefore efficient data compression methods are in high demand. No other model had ever come close to achieving these goals.

Many challenges arise from this study. On the one hand, there is much work to do from a research perspective, such as the design of new diagnostic rules based on the FMM parameters; the identification of wave patterns specific to exceptional conditions such as atrial flutter, which do not adapt so well to the model; the integration of the 3DFMM_ecg model in AI systems; or the inclusion of new terms accounting for different sources of variability. Specifically, we will start by studying a rule for HYP, using a combination of markers including the $maxAR$ defined in this paper. On the other hand, there is the committed objective of getting the new markers to be used in clinical practice. To that end, devices that record the signals should provide the new markers, and more importantly, physicians need to be trained. Moreover, the current paper opens up great research opportunities for studying biological electric systems beyond the cardiac one, which have an impact on the knowledge of the effect and causes of multiple diseases, as well as the development of drugs and therapies. In particular, electric signals from other organs, such as the brain or the eyes, can be modeled using adapted 3DFMM models. Thus, the important question of analyzing the relationship between signals recorded in different regions, could also be addressed with these models. Some work in this line is in progress.

Limitations of the study

Regarding the limitations, the computational time is still too high to give interactive outputs. This is because of the exhaustive search and the backfitting loop, which are time-consuming processes. However, by implementing the current method in C and using general-purpose computing on graphics processing units, the computational cost could be greatly reduced. Furthermore, the algorithm, as described here, does not identify the $P$ wave when it is not located before the $QRS$ complex. New research into detecting and adapting the algorithm in these cases could bring about the correct identification of the $P$ wave.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
PTB-XL Database. Version: 1.0.2	https://doi.org/10.1038/s41597-020-0495-6	https://doi.org/10.13026/zx4k-te85
Software and algorithms
R statistical language, version 4.4.1	The Comprehensive R Archive Network	https://www.r-project.org/
FMM package version 3.0.0	https://cran.r-project.org/web/packages/FMM/index.html	https://doi.org/10.32614/rj-2022-015
Data generation, simulations, analysis and figure production scripts	This paper	https://github.com/FMMGroupVa
Online app	This paper	https://fmmmodel.shinyapps.io/fmmEcg3D/

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Cristina Rueda (cristina.rueda@uva.es).

Materials availability

This study did not generate new unique reagents.

Method details

Data preprocessing

Electrocardiogram (ECG) signals are usually interfered with baseline drifts, noises, or conduction artifices which severely affect ECG signal analysis quality.⁵⁰ Data preprocessing is required both to achieve reliable ECG fragments and to divide them beat by beat.^9,26,53 However, the preprocessed signal may still be affected by other sources of variability, see Figure S8 in the Supplemental Information. The preprocessing is designed in four steps, as illustrated in Figure S13 of the Supplemental Information. The inputs of the algorithm are the raw ECG signals from the 12 leads. The four steps are: 1) Baseline removing; 2) Single-lead$QRS$detections and checking; 3) Multi-lead$QRS$detections; and 4) ECG segmentation and checking. Unlike most of the preprocessing algorithms,^3,9,49 the denoising step is dismissed from our proposal, due to the robustness of the 3DFMM_ecg model. The details of the algorithm are given below.

Step 1: Baseline removing

For each ECG fragment, a low-frequency filter based on the fitting of a local polynomial regression model is used. Following the ideas in Rahul et al.,³⁹ these estimates subtracted to the signals which corrects the baseline wander.

Step 2: Single-lead $QRS$ detections and checking

Signals are independently analyzed with the Pan Tompkins algorithm³³ to obtain lead-specific $QRS$ detections.

• •QRS Revision. The median $RR$ length of the fragment is used as benchmark to remove too short/long detections^40,42,46 preventing false positive detections. $RR$is the time elapsed between two consecutive $QRS$ detections.

Step 3: Multi-lead $QRS$ detection

Single-lead $QRS$ detections provided in Step 2 are combined to obtain a common reference annotation set. Following the ideas given in Mondelo et al.,²⁹ the single detections are increasingly sorted to build groups of at least four nearby detections, in a way that the groups are far enough from each others. The median of the nearby detections within groups, called $t^{QRS}$, are computed. Hence, $t^{QRS}$ are the annotations on the reference set, that is common across leads. This procedure ensures false positives detections and overcomes the problems caused by undetected $QRS$ in some leads. One may refer to Mondelo et al.²⁹ for details. From now on, only the leads on the set $Lred=\left\{I,II,V1,V2,V3,V4,V5,V6\right\}$ will be considered.

Step 4: ECG segmentation and checking

As it was done in Rueda et al.,⁴² the heartbeat segmentation across leads is given by $\left[t^{QRS}-40\%RR,t^{QRS}+60\%RR\right]$.

• •
  ECG Segmentation Revision. To avoid meaningless heartbeats,^27,60 remove from the ECG fragment:

  • 1.
    The first (resp. last) beats which are notably shorter than the median $RR$ length; or with a high percentage of initial (resp. ending) observations being constant.
  • 2.
    The beats for which$t^{QRS}$ locates out of the $35\%-45\%$ of the beat length.
  • 3.
    The beats with a marked difference between the signal endpoints regarding the beat amplitude.
  • 4.
    The beats that exhibit conduction issues with amplitudes exceeding the standard limits; or anomalous relative beat amplitudes regarding the signal.

ECG signals pass through the analysis iff there are at least i) three beats in the reference annotation set; ii) three leads with more than three beats; and iii) a 20$\%$ of expected beats according to sampling frequency. The latter conditions allow discarding unacceptable levels of noise or distorted signals.

The outputs of the preprocessing are the $t^{QRS}$ annotations and ECG beat segmentation.

The 3DFMM_ecg model

Without loss of generality, it is assumed that the time points are in $(\mathrm{0,2}\pi ]$. In any other case, transform the time points $t^{\prime }\in \left[t_0,T+t_0\right]$to $t=\frac{\left(t^{\prime }-t_0\right)2\pi }{T}$.

Let us define an FMM wave as follows: $W\left(t,A,\alpha ,\beta ,\omega \right)=A\cos \left(\phi \left(t,\alpha ,\beta ,\omega \right)\right)$, where $A$ is the wave amplitude and,

$$\phi (t,\alpha ,\beta ,\omega )=\beta +2\arctan \left(\omega \tan \left(\frac{t-\alpha }{2}\right)\right),t\in (\mathrm{0,2}\pi ]$$ (Equation 1)

is the wave phase.

$W\left(t,A,\alpha ,\beta ,\omega \right)$ is suitable for describing rhythmic up-down-up (or down-up-down) patterns, as is well justified in Rueda et al.⁴⁴ The parameters characterise various morphological aspects of the wave, as detailed in the introduction.

The Analytic Signal (AS) of a unit FMM wave, $A=1$, is defined using the Hilbert Transform (HT) as follows: $S\left(t\right)=\mu \left(t\right)+i\nu \left(t\right)$; where, $\mu \left(t\right)=W\left(t,1,\alpha ,\beta ,\omega \right)$, and $\nu \left(t\right)=HT\left(\mu \left(t\right)\right)$. The AS signal has interesting properties and researchers often assume that the underlying complex signal associated with an oscillatory process is an AS.⁴⁷ Now, the FMM complex signal is defined generalizing the AS of an FMM unit wave as: $S\left(t\right)=A_{Re}\mu \left(t\right)+i{A}_{Im}\nu \left(t\right)$, where $A_{Re},A_{Im}\in {\mathfrak{R}}^{+}$. A complex FMM wave has elliptical trajectories. Furthermore, in this paper, the AS is also used to generate 2D and 3D representations of ECG signals, specifically, we consider that when $\mu \left(t\right)=P\left(\overrightarrow{D}\left(t\right)|LeadII\right)=\sum _{J=1}^m{A}_J\cos \left({\phi }_J\left(t\right)\right)$then $\nu \left(t\right)=\sum _{J=1}^m{A}_J\sin \left({\phi }_J\left(t\right)\right)=P\left(\overrightarrow{D}\left(t\right)|LeadI{I}^{\left(i\right)}\right)$, where $P\left(\right)$ denotes the projection operator.

The 3DFMM_ecg model relies on two premises. Namely; 1.- the heart electric field originates from a multi dipole; and 2.- each dipole is represented by a vector, which moves in a plane as time progress and is mathematically described as a complex FMM signal.

Below, we prove that the projection of such a vector is an FMM wave with the property that the values of $\alpha$ and $\omega$ do not depend on the direction of the projection.

Theorem 1

Let $\left\{\overrightarrow{d}\left(t\right),t\in (\mathrm{0,2}\pi \right]\}$ be a set of vectors in the same plane, $\wp$, describing a complex FMM signal, let the projection of $\overrightarrow{d}\left(t\right)$ in the principal axe of the ellipse, $L$, is an FMM wave, as follows;

$$P\left(\overrightarrow{d}\right(t\left)\right|L)=M^L+W(t_{,}{A}^L,{\alpha }^L,{\beta }^L,{\omega }^L),t\in (\mathrm{0,2}\pi ]$$

Then, the projection of $\overrightarrow{d}\left(t\right)$ in any other direction, $L^{\prime }$, is also an FMM wave, verifying that ${\alpha }^{L^{\prime }}={\alpha }^L$ and ${\omega }^{L^{\prime }}={\omega }^L$.

• Proof:

First, assume that ${\left(\mathrm{0,0,0}\right)}^{\prime }\in \wp$. Consider the orthogonal system $\left(X,Y,Z\right)=\left(L,L^{\perp },Z\right)$, where $L,L^{\perp }\in \wp$ are the axes of the ellipse describing the trajectory of $\overrightarrow{d}\left(t\right),t\in (\mathrm{0,2}\pi ]$; also define the center of the ellipse as $\overrightarrow{O}=\left(O_L,O_{L^{\perp }},0\right)$. Then, the coordinates of ${\overrightarrow{d}}_{\ast }\left(t\right)=\left(\overrightarrow{d}\left(t\right)-\overrightarrow{O}\right)$ are $\left(x,y,z\right)=\left(A^L\cos \left(\theta \left(t\right)\right),A^{L^{\perp }}\sin \left(\theta \left(t\right)\right),0\right)$. From the theorem assumptions consequently: $\theta \left(t\right)=\phi \left(t,{\alpha }^L,{\beta }^L,{\omega }^L\right)$

Now, for any other direction $L^{\prime }$, there exist ${\lambda }^{L^{\prime }},{\mu }^{L^{\prime }},{\kappa }^{L^{\prime }}$ such that the projection of a vector $\overrightarrow{v}={\left(x,y,z\right)}^{\prime }$ in $L^{\prime }$ is:

$$P\left(\overrightarrow{v}|L^{\prime }\right)={\lambda }^{L^{\prime }}x+{\mu }^{L^{\prime }}y+{\kappa }^{L^{\prime }}z\text{.}$$ (Equation 2)

Then, consequently,

$$P\left({\overrightarrow{d}}_{\ast }\left(t\right)|L^{\prime }\right)={\lambda }^{L^{\prime }}{A}^L\cos \left(\phi \left(t,{\alpha }^L,{\beta }^L,{\omega }^L\right)\right)+{\mu }^{L^{\prime }}{A}^{L^{\perp }}\sin \left(\phi \left(t,{\alpha }^L,{\beta }^L,{\omega }^L\right)\right)\text{.}$$ (Equation 3)

and,

$$P\left(\overrightarrow{d}\left(t\right)|L^{\prime }\right)=P\left(\overrightarrow{O}|L^{\prime }\right)+{\lambda }^{L^{\prime }}{A}^L\cos \left(\phi \left(t,{\alpha }^L,{\beta }^L,{\omega }^L\right)\right)+{\mu }^{L^{\prime }}{A}^{L^{\perp }}\sin \left(\phi \left(t,{\alpha }^L,{\beta }^L,{\omega }^L\right)\right)\text{.}$$ (Equation 4)

Now, considering the trigonometric relation:

$$\lambda \cos \left(\theta \right)+\mu \sin \left(\theta \right)=\sqrt{{\lambda }^2+{\mu }^2}\cos \left(\theta +\mathit{atan}\left(\frac{\lambda }{\mu }\right)+\frac{3\pi }{2}\right)$$

and applying this relation to equation (4), where $\theta =\phi \left(t,{\alpha }^L,{\beta }^{L^{\prime }},{\omega }^L\right)$, $\lambda ={\lambda }^{L^{\prime }}{A}^L$, and $\mu ={\mu }^{L^{\prime }}{A}^{L^{\perp }}$, it is immediate to derive that,

$$P\left(\overrightarrow{d}\left(t\right)|L^{\prime }\right)=P\left(\overrightarrow{O}|L^{\prime }\right)+A^{L^{\prime }}\cos \left(\phi \left(t,{\alpha }^L,{\beta }^{L^{\prime }},{\omega }^L\right)\right)$$

where,

$$A^{L^{\prime }}=\sqrt{{\left({\lambda }^{L^{\prime }}{A}^L\right)}^2+{\left({\mu }^{L^{\prime }}{A}^{L^{\perp }}\right)}^2};{\beta }^{L^{\prime }}={\beta }^L+\mathit{atan}\left(\frac{{\lambda }^{L^{\prime }}{A}^L}{{\mu }^{L^{\prime }}{A}^{L^{\perp }}}\right)+\frac{3\pi }{2}$$

and the result of the theorem follows when $M^L=0$.

Now, when ${\left(\mathrm{0,0,0}\right)}^{\prime }\notin \wp$, the projections in any direction are FMM waves, but they also include an intercept term that accounts for the location of $\wp$ relative to the origin. Specifically, let $z_0=P\left(\left(\mathrm{0,0,0}\right)|\wp \right)$, for each $\overrightarrow{d}\left(t\right)\in \wp$, then $\overrightarrow{v}\left(t\right)=\overrightarrow{d}\left(t\right)-z_0\in {\wp }_{d_0}$, where ${\wp }_{d_0}$ is a plane passing through the origin.

Therefore, $P\left(z_0|L\right)=M_0^L$ and $P\left(\overrightarrow{v}\left(t\right)|L\right)=O_L+A^L\cos \left(\phi \left(t,{\alpha }^L,{\beta }^L,{\omega }^L\right)\right)$.

Finally,

$$P\left(\overrightarrow{d}\left(t\right)|L^{\prime }\right)=M^{L^{\prime }}+A^{L^{\prime }}\cos \left(\phi \left(t,{\alpha }^L,{\beta }^{L^{\prime }},{\omega }^L\right)\right)$$

where, $M^{L^{\prime }}=M_0^{L^{\prime }}+P\left(\overrightarrow{O}|L^{\prime }\right)$, and the theorem follows. $\square$

Now, consider the tridimensional space with its origin of the central point in the chest and the voltage recorder with the ten electrodes generating the 12-lead ECG signals: $Lset=\left\{I,II,III,aVR,aVL,aVF,V1,V2,V3,V4,V5,V6\right\}$. Each of these signals is the projection of $\overrightarrow{D}\left(t\right)$ in a given direction and, in turn, the projection of $\overrightarrow{D}\left(t\right)$ is the sum of the projections of the five dipole vectors, for each of which the result of the theorem can be applied individually.

Finally, the 3DFMM_ecg model is derived, taking into account all the above considerations. Specifically, the ECG unidimensional signals are formulated as a signal plus error model in Definition 1, where the error term accounts for artifacts in the data and the intercept accounts for location changes as follows.

Definition 1. 3DFMM_ecg model

Let $X^L\left(t_i\right)$, $t_1<\dots <t_n$, be an observation from lead $L$, $L\in Lset$. Then,

$$X^L\left(t_i\right)=M^L+\sum _{J\in \left\{P,Q,R,S,T\right\}}W\left(t_i,A_J^L,{\alpha }_J,{\beta }_J^L,{\omega }_J\right)+e^L\left(t_i\right)\text{;}$$ (Equation 5)

where, for $L\in Lset$, and, $J\in \left\{P,Q,R,S,T\right\}$:

• •$M^L\in \mathfrak{R}$,
• •${\beta }_J^L\in (\mathrm{0,2}\pi ]$,
• •${\alpha }_P\le {\alpha }_Q\le {\alpha }_R\le {\alpha }_S\le {\alpha }_T\le {\alpha }_P$,
• •${\omega }_J\in \left[\mathrm{0,1}\right]$,
• •$A_J^L\in {\mathfrak{R}}^{+}$,
• •${\left(e^L\left(t_1\right),\dots ,e^L\left(t_n\right)\right)}^{\prime }\sim N_n(\mathbf{0},{\sigma }^L\mathbf{I})$.

It is relevant to note that restrictions imposed on the $\alpha$ parameters, response to the assumption that the atrial depolarization is previous to the ventricles depolarization. Occasionally, the atria may repolarize later. In such a case, the $P$ wave would not go before the $QRS$. To prevent these cases, the model can also be defined by numbering the waves and making a subsequent identification of the numbers with the letters, maintaining the relationship between the $QRS$ and the $T$.

Other important parameters of practical use are the peak and trough times. They are defined as functions of the basic parameters.⁴³ In addition, other indices, such as the distances between waves, are easily derived from the set of basic 3DFMM_ecg model parameters. Obtaining good estimators of these indices is crucial for clinicians because they are useful tools in the diagnosis.

Evaluation metrics

In this study, a global model quality measure, named $\overline{R}$, is defined for a given patient. Namely,

$$\overline{R}=\frac{1}{12}\sum _{L\in Lset}median\left(R_{L_b}^2\right)\text{,}$$

where, for a fixed beat $b$ and lead $L$,

$$R_{L_b}^2=1-\frac{{{\sum }_{i=1}^n\left(X_b^L\left(t_i\right)-\widehat{X_b^L}\left(t_i\right)\right)}^2}{{{\sum }_{i=1}^n\left(X_b^L\left(t_i\right)-{\overline{X}}_b^L\left(t_i\right)\right)}^2}$$

is the proportion of variation in the signal that is explained by the predicted values. The higher the $\overline{R}$, the better the model.

The $PRD$, a related measure that is widely used in the data compression literature is defined as follows:

$$\mathit{PR}{D}_{L_b}=\sqrt{\frac{{\sum }_{i=1}^n{\left(X_b^L\left(t_i\right)-\widehat{X_b^L}\left(t_i\right)\right)}^2}{{\sum }_{i=1}^n{\left(X_b^L\left(t_i\right)-{\overline{X}}_b^L\left(t_i\right)\right)}^2}}=\sqrt{1-R_{L_b}^2}$$

Identification algorithm

The identification problem reduces to solving the following optimization problem:

$$Mi{n}_{\theta \in \Theta }\sum _{L\in Lset}\frac{1}{{\sigma }^L}\sum _{i=1}^n{\left[X^L\left(t_i\right)-{\mu }^L(t_i,\theta )\right]}^2\text{,}$$

where $\theta$ is the vector of the model parameters, $\Theta$ is the parametric space, and ${\mu }^L\left(t_i,\theta \right)=M^L+{\sum }_{J\in \left\{P,Q,R,S,T\right\}}W\left(t_i,A_J^L,{\alpha }_J,{\beta }_J^L,{\omega }_J\right)$. For a typical ECG pattern, $\Theta$ is initially defined as in Definition 1. However, $\Theta$ is reduced when atypical or very noisy patterns are analyzed to achieve a correct physiological identification of waves. The values ${\sigma }^L,L\in Lset$ are identified as part of the optimization process.

For computational efficiency, the $Lset$ is reduced to $Lred=\left\{I,II,V1,V2,V3,V4,V5,V6\right\}$, as the rest of the lead signals are linear combinations of $I$ and $II$. However, the weight of $I$ and $II$ increase by a factor of 3 in order to maintain the global weight of the derivations from the frontal plane.⁶

From a statistical point of view, the optimization problem defined above is that of finding the Maximun Likelihood Estimates of the parameters. We adapt an iterative algorithm⁴⁵ to the multivariate setting. The algorithm alternates M and I steps. It is assumed that the preprocessing stage provides a $QRS$ annotation point, denoted as $t^{QRS}$, for each beat. Moreover, exceptionally, one or more than one, of the eight leads are discarded in the preprocessing stage due to noise artifacts; only information on at least one of $I$, $II$, $V2$, or $V5$ lead is required. In those cases, the identification stage is conducted with the selected leads, providing estimates for the common parameters; while the estimates for the lead-specific parameters of missing leads are derived by solving a standard multiple linear regression problem at the end of each M step.

The M step obtains $K\ge 5$ FMM waves using a backfitting algorithm and the I step assigns $K\le 5$ letters to, at most, five of these waves. Typically, $K=5$; however, in the presence of significant noise or when the morphology is pathological, it is possible that the interesting waves may be hidden between the sixth and seventh waves (exceptionally up to the tenth). The values ${\sigma }^L$ are updated in each iteration of the algorithm, averaging the squared difference between the expected values and the predicted values by the model. They are initially set to 1.

M step

A standard backfitting algorithm is designed by fitting a single FMM wave simultaneously to the leads in Lred. The fitting of a single FMM is repeated successively to the residuals. The numbers of backfitting passes programmed in each step M is five. The final estimates of $M^L$, $A_J^L$ and ${\beta }_J^L$ ; $L\in Lred;J\in \left\{P,Q,R,S,T\right\}$, are derived by solving a standard multiple linear regression problem.

I step

The $R$ wave is assigned in the first I step. It corresponds to the one with the highest explained variability among those closest to $t^{QRS}$, which also has a positive peak on leads $I$ or $II$ and a negative peak in lead $V2$. In the few cases where these assumptions do not hold, additional conditions are used. Next, the preassignation of $P,Q,S$ and $T$ to the free components among the first five is done using ${\alpha }_P\le {\alpha }_Q\le {\alpha }_R\le {\alpha }_S\le {\alpha }_T$. This preassigment corresponds, in most cases, to the final assignment. However, in the presence of significant noise, or when the morphology is pathological, the interesting waves may sometimes be hidden between the sixth and seventh waves, which are checked for reassignments using thresholds on the main model parameters. In particular, noisy components are detected with too small or too high $\omega$ values.

The algorithm finishes when there is no significant increase in the objective function of the optimization problem.

In addition, the predictions from other leads in the frontal plane, $III$, $aVL$, $aVR$ and $aVF$ are derived using the predictions of the $I$ and $II$ leads, using the known linear relations between them.⁶ In the case that any of the $I$ and $II$ leads is tentatively eliminated in the preprocessing step, the estimates for leads in the frontal plane can be derived by solving a standard multiple linear regression problem, as is done with the missing leads in step M. A flow chart of the algorithm is given in Figure S14 of the Supplemental Information.

Model validation

A simulation study is performed to evaluate the properties of the parameter estimators provided by the identification algorithm across different ECG signal patterns. Four different parameter configurations defining the 3DFMM_ecg signal are considered, representing healthy (NORM), complete left bundle-branch block (CLBBB), complete right bundle-branch block (CRBBB) and hypertrophy (HYP) hearts. Figures S1–S4 show the simulated 3D signals and Table S1 gives the values of the main parameters of the different configurations. The parameter for the NORM configuration corresponds to the median values of the patients labeledNORM in PTB-XL database. As it is shown in Table S1, the main changes in CLBBB, CRBBB and HYP in relation to NORMare ${\omega }_R$, ${\omega }_S$ and $maxAR$, respectively.

For each configuration, 100 synthetic beats are simulated at 300 equally time spaced points using the 3DFMM_ecg model (see Definition 1 of the main text). The error term is generated using a normal distribution with mean zero and lead-dependent SD. The choice of SD values is based on the residual SD from NORMsubjects of PTB-XL database. Depending upon the lead, three values of SD are considered: ${\sigma }^L=25$ for $L\in \left\{I,II\right\}$, ${\sigma }^L=20$ for $L\in \left\{V1,V2,V3\right\}$ and ${\sigma }^L=12$ for $L\in \left\{V4,V5,V6\right\}$.

Three measures of the estimation performance are shown in Table S2: bias, defined as the average difference between the true parameter value and its estimate across the 100 simulated beats in each ECG pattern; empirical SE(empSE), computed as the SD of the estimates over the 100 synthetic beats; and a coefficient of variation (CV) that, for the euclidean parameters $\theta \in \left\{{\omega }_J,maxAR\right\}$, $J\in \left\{P,Q,R,S,T\right\}$ is defined as,

$$C{V}_{\theta }=\sqrt{\frac{\frac{1}{N}{\sum }_{j=1}^N{\left({\theta }_0-{\hat{\theta }}_j\right)}^2}{{\theta }_0^2}}$$ (Equation 6)

where${\theta }_0$ is the true parameter value and $N$ the number of simulated beats. For the angular parameters, ${\alpha }_J$, this CV is defined as

$$C{V}_{\theta }=\sqrt{\frac{\frac{1}{N}{\sum }_{j=1}^N{\left(({\hat{\theta }}_j-{\theta }_1)-\pi \right)}^2}{{\pi }^2}}$$ (Equation 7)

where ${\theta }_1={\theta }_0-\pi$. For the angular parameters, circular mean and SD are computed using the circular R package.¹ The median and percentile ranges of global model quality measure, $\overline{R}$, are shown in Table S3.

Estimates for $\alpha$ and $\omega$’s parameters exhibit a bias near zero and a very small empirical SE ECG patterns, pointing that the proposed algorithm provides high accurate and precise parameter estimates. As expected, the CVs are low in these cases, below the 10% for almost all of the estimates. The higher CV values are observed for ${\omega }_Q$ in the HYP pattern and for ${\omega }_S$ in the CLBBB pattern, both near an acceptable 30%. Although, in absolute terms, the bias of the $maxAR$ estimates is higher, this bias is small with respect to the true parameter value, ranging from 600 to 1700. It is worth noting that this parameter is the maximum, across leads, of the $A_R$ values, so bias is to be expected. Additionally, this estimate has a very high precision. Furthermore, by observing the distribution of this estimate in PTB-XL (see Table 1), it is clear that such biases have no effect on the ability of $maxAR$ as a diagnostic marker. Regarding the values for the $\overline{R}$, in all patterns are above the 97%, showing an excellent match between the predicted and simulated ECG signals.

The performance of the 3DFMM_ecg in real cases for healthy and pathological heart conditions is illustrated in Figures S5–S12 of the Supplemental Information.

3DFMM_ecgapp

The 3DFMM_ecgapp has been developed using shiny¹¹ from the programming language R. Shiny applications are mainly composed of two modules: the frontend or user interface, designed with HTML widgets and CSS elements, and the backend or server, responsible for the computational tasks implemented in R. User interface flexibility is achieved through several R packages.^{4,10,24,35,59} While the backend has been mainly implemented using the R package FMM.^18,19

ECG data can be analyzed in the app by uploading the data in tabular format (extensions.csv,.xls, or.xlsx), and indicating the sampling rate in Hertz (Hz). Data must contain multiple beats recorded in the standard twelve leads, and include at least one of I, II, V2, or V5 leads. The more of these derivations provided, the better the estimates obtained will be. Each column of the file should correspond to a lead and the column header names should indicate the lead name (labeledI, II, III, aVL, aVR, aVF, V1, V2, V3, V4, V5, or V6).

Once the file is uploaded, data is preprocessed and fragmented in beats using the preprocessing described in this document. Then, the user must select the beat to be analyzed, which is displayed in the app interface, and the number of backfittings desired in the estimation algorithm. In particular, a higher number of backfittings can improve the predictions at the cost of a higher computational time. Finally, the analysis starts by pressing the prediction button. The following outputs are given:

• •The predicted FMM signal plotted along with the input data for each lead.
• •Individual waves plot for each lead. Plot of estimated $W\left(t,A_J^L,{\alpha }_J,{\beta }_J^L,{\omega }_J\right)$, $L\in Lset$, $Lset=\left\{I,II,III,aVL,aVR,aVF,V1,V2,V3,V4,V5,V6\right\}$, $J\in \left\{P,Q,R,S,T\right\}$, $t\in (\mathrm{0,2}\pi ]$.
• •Accuracy measure, in particular $100\times \overline{R}$.
• •The estimates for the relevant parameters given in Tables S1 and S2.

To illustrate the app functionality, four ECG fragments from PTB-XL database are provided, labeledNORM, CLBBB, CBBB and HYP, respectively. The recordings sampling rate is 500 Hz, default value in the app. In particular, signals are from patients 976 (NORM), 11,174 (CLBBB), 10,938 (CBBB), and 15,260 (HYP).

Published: December 22, 2022

Data and code availability

• •This work makes use of the Database:PTB-XL⁵⁷ that is publicly available at Physionet.²⁰
• •All the presented results are reproducible through the 3DFMM_ecg app, publicly available at https://fmmmodel.shinyapps.io/fmmEcg3D/. A detailed description of the 3DFMM_ecg app, including implementation and usage examples, is provided in the STAR Methods.
• •The code is available at https://github.com/FMMGroupVa.