Abstract
Fast-paced yield improvement in strategic crops such as soybean is pivotal for achieving sustainable global food security. Precise genomic selection (GS), as one of the most effective genomic tools for recognizing superior genotypes, can accelerate the efficiency of breeding programs through shortening the breeding cycle, resulting in significant increases in annual yield improvement. In this study, we investigated the possible use of haplotype-based GS to increase the prediction accuracy of soybean yield and its component traits through augmenting the models by using sophisticated machine learning algorithms and optimized genetic information. The results demonstrated up to a 7% increase in the prediction accuracy when using haplotype-based GS over the full single nucleotide polymorphisms-based GS methods. In addition, we discover an auspicious haplotype block on chromosome 19 with significant impacts on yield and its components, which can be used for screening climate-resilient soybean genotypes with improved yield in large breeding populations.
Keywords: Food security, Haplotype block, Machine learning algorithms, Soybean yield, Soybean breeding
Food security; Haplotype block; Machine learning algorithms; Soybean yield; Soybean breeding.
1. Introduction
Moderate to severe food insecurity has been increasing significantly due to the exponential increase in the world's population [1]. This, in turn, requires a fast-paced yield improvement in major crops, including soybean as one of the world's four key crops [2]. In conventional soybean breeding programs, yield improvement that is currently at an annual rate of ∼1% highly depends on the end-season yield selection strategy [3]. However, the current rate falls well short of the required rate of 2.4% to double global soybean production by 2050 [4]. In the last two decades, soybean breeders have made tremendous efforts to increase the yield by selecting superior genotypes not necessarily based on yield per se but yield components as well [5]. Secondary yield-related traits in soybeans can be categorized into four yield component layers based on their importance in determining the overall yield [6, 7]. The first layer of the yield components in soybean includes the number of nodes per plant (NP), number of non-reproductive nodes per plant (NRNP), number of reproductive nodes per plant (RNP), and number of pods per plant (PP), directly explained the variation of yield in genotypes [7, 8]. However, due to the complex nature of these traits, several intrinsic and extrinsic interactions need to be considered and manipulated for a successful, fast-paced yield improvement [9].
Agricultural genomics has been a promising area for investigating and discovering genetic and phenotype interactions using a wide range of genetic approaches in order to shorten the lengthy breeding process and lead to breakthroughs in yield genetic gains [10]. Previously Varshney, Graner and Sorrells [11] proposed the use of different genomic tools to identify candidate genes and molecular markers associated with the traits of interest. Recently, genomic selection (GS) has been added to this portfolio as an effective method to select superior genotypes based on their genetic profiles [12]. The basis of GS is to exploit different genomic predicting models on a large set of genetic markers distributed across the genome to predict the desirable phenotypic performance of a given trait in a wide range of genotypes [13, 14]. Genome prediction (GP) models are developed over phenotypic and genetic information of the training population and predict the phenotype of the testing population based on its genotypic data [14, 15]. Unlike other genomic tools, GS does not require prior knowledge about the marker-trait association, but the inclusion of the significant marker-trait associations into GP models can improve its prediction accuracy [12, 13]. Nevertheless, the actual yield improvement with GS depends on several factors, including the selection of appropriate algorithms and precise genetic information, which hinder its important role in future sustainability and global food security [16].
Significant efforts have been made to increase the efficiency of GS in selecting superior genotypes [12, 13, 15, 17]. Those efforts included but not limited to the use of haplotype blocks instead of genetic markers and sophisticated bigdata analyzing methods. Haplotype refers to a set of different alleles in different genetic markers on a single chromosome with strong linkage disequilibrium (LD) that are inherited together with the least chance of recombination [18]. Due to the high variable linkage disequilibrium (LD) patterns in soybean populations, incorporating all genetic markers in GP models may significantly increase the overfitting and false-positive rates. However, redundant genetic markers can be eliminated by the use of haplotypes [18, 19]. Abdel-Shafy, Bortfeldt, Tetens and Brockmann [20] reported the efficiency of using the haplotype approach for detecting genomic regions associated with the trait of interest instead of using a single-marker approach. Haplotypes can be obtained using different approaches such as (1) estimating haplotype diversity in a given segment of a chromosome, (2) calculating pairwise LD between the adjacent genetic markers in a chromosome, and (3) clustering genetic markers using sliding – windows or variable length [21]. Previous studies suggested the effectiveness of LD-based approaches in identifying haplotypes in a given chromosome [19, 20, 21]. Although using haplotypes in GS can improve the prediction accuracy per se, it can be accelerated if using appropriate and sophisticated GP models [12].
By the recent advances in bigdata analyzing methods, machine learning (ML) algorithms have been considered as high potential analytical approaches to be exploited in different breeding aspects such as early-stage yield prediction [22], genome-wide association studies [23], and GS [24]. The basis of ML algorithms is to learn from the available dataset and improve automatically without completely programming [25]. Each ML algorithm can learn the data pattern from the training dataset in a specific way and predict the target variable in the testing dataset [25, 26]. For instance, random forest (RF) as one of the most widely used ML algorithms, can predict the target variable by using the average results of identical decision trees that are obtained from the bootstrapped samples of the training dataset [27]. Support vector regression (SVR), as the regression form of the support vector machine, provides different sets of hyperplanes to select the best regression line with the minimum possible errors in the model [28]. Radial basis function (RBF) regressor, as the regression form of RBF network algorithm, quantifies the inherent existing knowledge in the training dataset and detects all possible connections between inputs and target variables using the radial basis function as an activation function [29].
Although all ML algorithms have revolutionized the bigdata analysis methods, recent studies showed that the individual use of ML algorithms might be subject to overfitting and false-positive rate [30]. Data fusion, in which the results of two or more individual ML algorithms are combined by using an ensemble strategy, can be considered as one of the common approaches to tackle this shortage [31]. Previous studies demonstrated the efficiency of using data fusion techniques for improving the yield prediction in soybean [22], synergizing off-target in cannabis through CRISPR/CAS [31], and nicosia wastewater treatment plant [32]. However, the possible use of data fusion techniques in GS to improve prediction accuracy is still unexplored and requires comprehensive investigations. This study was aimed to (1) investigate the possible use of haplotype-based GS for predicting soybean yield and its component traits, (2) conduct a comparative study on the success of ensemble and individual ML algorithms for improving the prediction accuracy in GS, and (3) determine the best haplotype profiles for improving soybean yield and its component traits. Overall, the findings from this study shed light on the use of optimized GS in selecting superior genotypes, which will facilitate the development of soybean cultivars with improved yield genetic gains as a sustainable way to tackle global food insecurity.
2. Results
2.1. Phenotyping and genotyping evaluations
The phenotypic evaluations and data collecting process of the tested traits are explained in detail in Yoosefzadeh-Najafabadi, Tulpan and Eskandari [5, 33]. In brief, the average yield performance of genotypes in a panel of 250 soybeans ranged between 2.58 to 5.71 ton ha−1. Also, the average mean for the number of nodes per plant (NP), non-reproductive nodes per plant (NRNP), reproductive nodes per plant (RNP), and pods per plant (PP) were 15.21, 3.33, 11.89, and 45.02, respectively. While the highest estimated heritability of the tested traits was found for NP (0.34), seed yield had the lowest value (0.24). A full description of the genetic evaluation can be found in Yoosefzadeh Najafabadi, Torabi, Tulpan, Rajcan and Eskandari [34]. In brief, a total of 17,958 SNPs out of 40,712 SNPs were selected as the polymorphic and mapped onto 20 soybean chromosomes with an average 898 SNPs in each chromosome. In addition, the mean genetic density of the tested population was 0.12 cM for every SNP across the whole genome.
2.2. SNPs-based GS vs. haplotypes-based GS
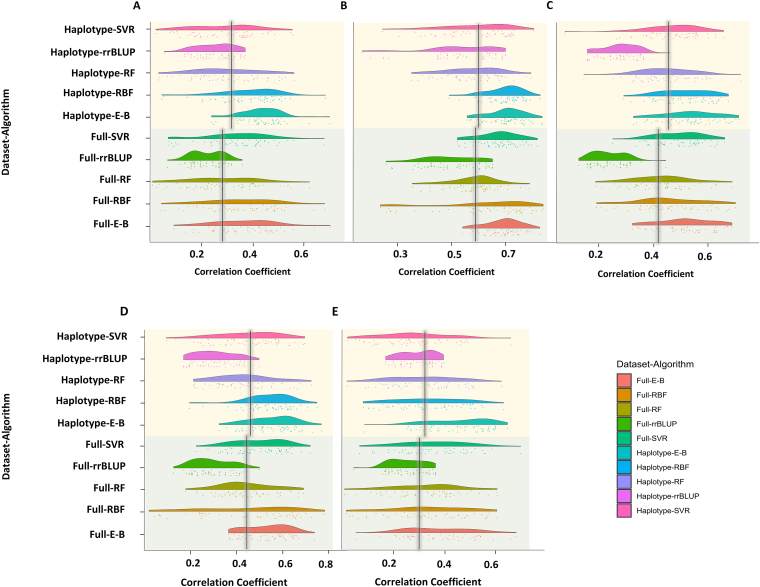
To predict the breeding values of the genotypes for yield and its component traits, different learning algorithms were performed on full SNPs and haplotype blocks as input variables. Linear Pearson correlation coefficient values, between training and testing prediction values for each dataset, were used to evaluate the efficacies of the datasets. Using haplotype blocks as input variables resulted in greater correlation values for all the tested traits (Figure 1A–E). The average correlation coefficient between training and testing prediction values using the full SNPs dataset was 0.41, while the haplotype blocks dataset had an average value of 0.48. Therefore, further GS analysis was conducted on the haplotype blocks dataset only.
Figure 1.
Estimated correlation coefficient values of the tested algorithms for (A) yield, (B) NP, (C) NRNP, (D) RNP, and (E) PP using full SNP (Full-) and haplotype block (Haplotype-) dataset. Ensemble-Bagging (E-B), Radial basis function (RBF), Random forest (RF), support vector regression (SVR), Ridge regression best linear unbiased prediction (rrBLUP).
2.3. Haplotype-based GS analysis
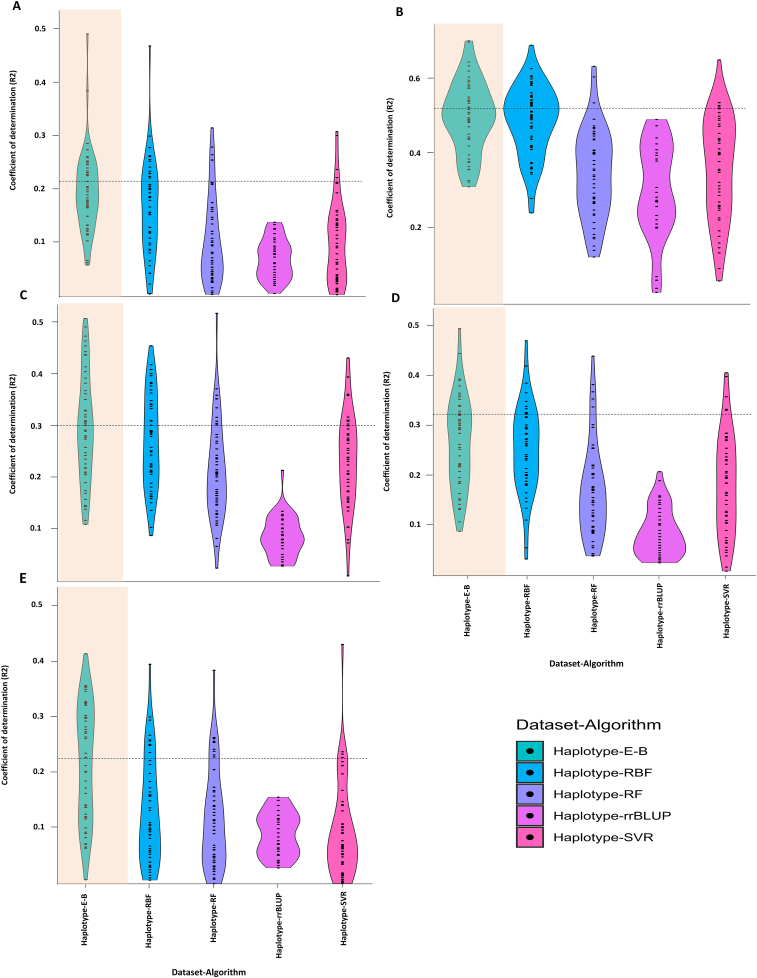
To perform the comparative haplotype-based GS analysis, coefficient of determination (R2) values were estimated for the individual method, including ridge regression best linear unbiased prediction (rrBLUP) and each machine learning (ML) algorithm, and for the combined ML strategy of Ensemble-Bagging (E-B). For yield, the highest R2 value was obtained using the E-B method (R2 = 0.21), and the lowest value was obtained using rrBLUP (0.07). The SVR algorithm was the second-best algorithm for predicting the breeding value of the yield using the haplotypes with the R2 value of 0.16 (Figure 2A). For NP, the highest R2 was obtained using E-B (0.51), while the lowest value was for rrBLUP (0.30). Other tested ML algorithms had the R2 ranging from 0.35 to 0.47 in predicting the breeding value of NP using the haplotype dataset (Figure 2B). For NRNP, the highest R2 was obtained using EB (0.30), followed by SVR (0.26), RBF (0.23), RF (0.21), and rrBLUP with an R2 value of 0.10 (Figure 2C). The same pattern was observed for RNP as the E-B had the highest R2 (0.32) among all other tested algorithms while the rrBLUP had the lowest value of 0.10 (Figure 2D). E-B was also the best algorithm for predicting the breeding value of the PP with the R2 value of 0.23. The SVR and RF algorithms were the second and third best algorithms for predicting the breeding value of PP with the R2 values of 0.13 and 0.11, respectively. The lowest R2 (0.09) was obtained using rrBLUP (Figure 2E).
Figure 2.
Estimated coefficient of determination (R2) values of the tested algorithms for (A) yield, (B) NP, (C) NRNP, (D) RNP, and (E) PP using haplotype block (Haplotype-) dataset. Ensemble-Bagging (E-B), Radial basis function (RBF), random forest (RF), support vector regression (SVR), ridge regression best linear unbiased prediction (rrBLUP).
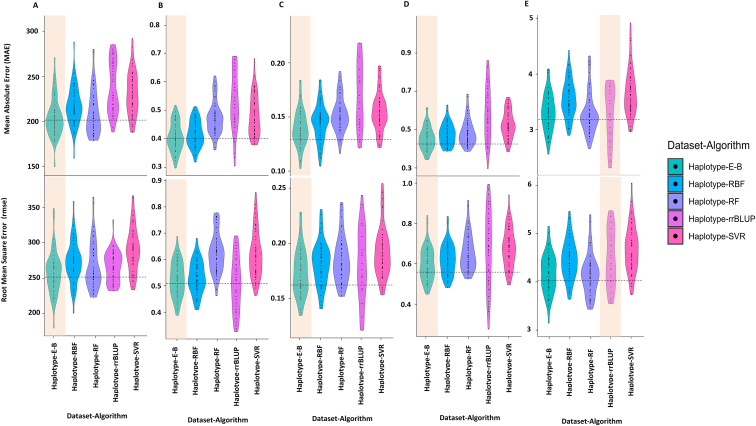
In addition to estimating R2 values of the tested methods for evaluating their performance, the mean absolute error (MAE) and root mean square error (RMSE) values were also estimated for them (Figure 3A-E). Among all the tested algorithms, E-B had the lowest MAE and RMSE in predicting the breeding values of all the tested traits except for PP, in which rrBLUP had the lowest values for MAE (3.27) and RMSE (4.17). The rrBLUP method had the highest MAE and RMSE values for yield, NP, NRNP, and RNP (Figure 3A–D). For PP, E-B was the second-best algorithm for this trait, with MAE and RMSE values of 3.31 and 4.47, respectively (Figure 3E). Based on the average values of MAE and RMSE in all the tested traits, E-B outperformed all other algorithms in predicting the breeding values for soybean yield and its components.
Figure 3.
The Mean Absolute Error (MAE, Top) and Root Mean Square Error (RMSE, Bottom) values of the tested algorithms for (A) yield, (B) NP, (C) NRNP, (D) RNP, and (E) PP using haplotype blocks (Haplotype-) dataset. Ensemble-Bagging (E-B), radial basis function (RBF), random forest (RF), Support vector regression (SVR), ridge regression best linear unbiased prediction (rrBLUP).
2.4. Top score associated haplotypes
The importance scores for each haplotype block were measured using recursive feature elimination (RFE). All the haplotype blocks with importance scores of over 50% were selected as the best haplotype blocks for predicting the breeding values of the tested traits. The 50% threshold was achieved based on using a global empirical threshold for estimating the significant threshold of haplotype blocks associated with the tested traits. For soybean yield, seven haplotype blocks were selected as best for predicting the breeding value. Most of the high importance haplotype blocks underlying yield were located on chromosomes 16 and 19, with an average length of 731.4 kbp (Supplementary Table 1). The haplotype blocks 16 and 23 located on chromosomes 19 and 16, respectively, had the highest frequencies in predicting the breeding value for soybean yield.
For NP, 10 haplotype blocks were selected to predict the breeding value of this trait. Most of the high importance haplotype blocks were located on chromosomes 19 and 8, with an average length of 2,278.0 kbp (Supplementary Table 2). Haplotype block 16 on chromosome 19 was the most frequent haplotype among all other high-scored haplotype blocks important for predicting the breeding value of NP. For NRNP, 20 haplotype blocks, mostly located on chromosomes 8 and 13 with an average length of 761.2 kbp, were identified as highly associated with this trait. Haplotype block 16 on chromosome 19 was one of the high-scored ones associated with this trait, and it was also detected as associated with NP and yield. Haplotype block 65 on chromosome 8 was also detected as the high importance one associated with both NP and NRNP (Supplementary Table 3). For predicting the breeding value of RNP, we identified 16 highly important haplotype blocks on eight chromosomes. The most influential haplotype block was located on chromosome 1, with the highest importance score of 98.9 (Supplementary Table 4). The haplotype block 16 on chromosome 19 was also one of the detected haplotypes that was highly associated with RNP. For PP, the high importance score haplotype blocks were located on chromosomes 1, 8, 9, 11, 12, 14, 16, and 19. The highest scored haplotype block was located on chromosome 16, with an importance score of 98.2 (Supplementary Table 5). The haplotype block 16 on chromosome 19 was also one of the high importance haplotypes underlying the breeding value of PP.
2.5. Extracting candidate genes underlying detected haplotype
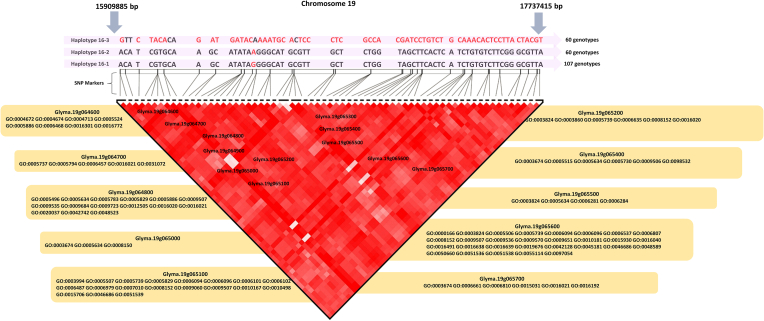
Since haplotype block 16, located on chromosome 19, was found to be associated with all the tested traits, potential candidate genes underlying yield and its components located in this block were extracted using the existing knowledge from previous studies and gene ontology (GO) enrichment analyses. With 1,827 kbp length, the haplotype block contained 69 SNPs in total, as illustrated in Figure 4. Three different sub-haplotypes, namely 16–1, 16–2, and 16–3, were identified in this block with the frequency rates of 0.47 (107 genotypes), 0.26 (60 genotypes), and 0.26 (60 genotypes), respectively (Figure 4). Out of 12 candidate genes located in this block, six genes namely, Glyma.19G064700, Glyma.19G064800, Glyma.19G065100, Glyma.19G065200, Glyma.19G065600, and Glyma.19G065700 were previously reported as being associated with soybean yield and its related traits (Table 1). All six candidate genes seem to be related to the plastid, plasma membrane, cytosol, endoplasmic reticulum, mitochondrion, nucleolus, nucleus, and membrane. Based on the GO annotation results, 18 GO profiles were identified for the selected six genes that mainly encode oxidative stress, glycolyse and nitrogen cycles, fatty acid beta-oxidation, developmental growth, and cellular process (Table 1). Out of 18 GO profiles, nine were detected in Glyma.19G065600, which mainly encodes the glutamate biosynthetic process, ammonia assimilation cycle, nitrate assimilation and compound metabolic process, developmental growth, NADH and NADPH activities, gluconeogenesis, and glycolysis (Table 1).
Figure 4.
The haplotype block 16, on chromosome 19, with its 12 putative candidate genes and 18 GO profiles, underlying soybean yield improvement.
Table 1.
The list of detected genes for the selected haplotype blocks in the tested soybean panel.
| Gene ID | Go enrichment ID | GO Description |
|---|---|---|
| Glyma.19G064700 | GO:0031072 | Heat shock protein binding |
| Glyma.19G064800 | GO:0009684 | Indoleacetic acid biosynthetic process |
| GO:0048523 | Negative regulation of cellular process | |
| GO:0006979 | Response to oxidative stress | |
| Glyma.19G065100 | GO:0007010 | Cytoskeleton organization |
| GO:0006094 | Gluconeogenesis | |
| GO:0006096 | Glycolysis | |
| Glyma.19G065200 | GO:0006635 | Fatty acid beta-oxidation |
| Glyma.19G065600 | GO:0006537 | Glutamate biosynthetic process |
| GO:0019676 | Ammonia assimilation cycle | |
| GO:0042128 | Nitrate assimilation | |
| GO:0006807 | Nitrogen compound metabolic process | |
| GO:0048589 | Developmental growth | |
| GO:0016040 | Glutamate synthase (NADH) activity | |
| GO:0045181 | Glutamate synthase activity, NAD(P)H as acceptor | |
| GO:0006094 | Gluconeogenesis | |
| GO:0006096 | Glycolysis | |
| Glyma.19G065700 | GO:0006661 | Phosphatidylinositol biosynthetic process |
3. Discussion
The most dominant strategy to increase the pace of soybean yield improvement is to select the superior genotypes based on their yield performance and its component traits. According to previous studies, soybean yield components such as NP, NRNP, RNP, and PP play important roles in determining the final yield production [33, 35]. Yoosefzadeh-Najafabadi, Tulpan and Eskandari [5] reported that PP and NP had the highest positive correlation with yield, which indicated that manipulating NP could result in significant changes in PP, leading to an increase or decrease in the formation of final soybean seed yield. Therefore, selecting superior genotypes based on yield influential characteristics can accelerate the breeding process of cultivar development programs.
With the emergence and fast advancement of the next-generation sequencing (NGS) technologies, the cost and time of sequencing breeding plant materials continue to decrease. This enables breeders to exploit genetic information as a reasonable and sustainable tool in selecting superior genotypes for accelerating genetic yield improvement in soybean [12]. In addition to exploiting diverse genomic tools for selecting genes and molecular markers associated with the trait of interest [13], GS has recently been added to this portfolio as an effective method to select superior genotypes based on their entire genetic profiles [12]. However, one of the major obstacles to using GS in applied breeding programs is relatively low rates of prediction accuracy that need to be improved. In this study, the efficiency of most common ML algorithms individually and collectively, using E-B strategy, were evaluated using a full SNPs-based dataset vs. an optimized haplotype-based dataset. Based on the results, all the tested algorithms had higher performances using the haplotype-based dataset, which indicated the efficiency of using haplotype blocks over the full complement of SNPs in predicting the breeding values of soybean yield and its components. Bhat, Yu, Bohra, Ganie and Varshney [12] (2021) reported that by using haplotype blocks in GS, breeders could extract the multidimensional relationships between phenotypic and genotypic information better than using full SNP markers. It can be mostly explained by the better capturing of the genomic similarity and LD in different genotypes, which resulted in capturing the high allelic order interactions [12, 18]. Recently, Jan, Guan, Yao, Liu, Wei, Abbadi, Zheng, He, Chen and Guan [36] compared the prediction performance of haplotype and SNPs-based datasets in Brassica and detected a higher prediction ability using haplotype-based datasets.
In addition to using haplotype blocks for a prominent improvement of prediction accuracies in GS, choosing an appropriate GP model is paramount to avoid overfitting issues and reduce false-positive rates. This study demonstrated the efficiency of using the E-B data fusion technique for increasing the prediction accuracy of soybean yield and its related traits using the haplotype blocks dataset. The effectiveness of using E-B over individual ML algorithms is due to the ability of the E-B to combine multiple individual algorithms to construct a combined robust algorithm. The E-B strategy is built upon using the decision trees for different individual ML algorithms that significantly reduce the variance and improve the accuracy, which results in a reliable strategy to deal with overfitting rates. However, more studies are required to confirm the efficiency of E-B for increasing the prediction accuracy in soybean and other plant species.
In addition, RFE was used to estimate the importance scores of all the haplotype blocks for predicting the breeding values of the soybean yield and its secondary related traits. The results showed that haplotype 16 on chromosome 19 was highly influential on all the tested traits. Furthermore, we identified six candidate genes, with 18 GO profiles associated with all the tested traits, which need further evaluations before being used in future genetic engineering and genome design activities. Glyma.19G064700 (GO:0031072) encodes heat shock protein (HSP) binding, which is important for both growth and abiotic stresses tolerance in plant species [37]. Li, Wong, Cheng, Cheng, Li, Mansveld, Bergsma, Huang, van Eijk and Lam [38] reported that HSP, which was significantly induced under a wide range of abiotic stress treatments in soybean, affected plant growth and development. Another candidate gene that was found significantly important for soybean yield and its secondary-related traits was Glyma.19G064800 (GO:0006979), which encodes response to oxidative stress. It can be read that abiotic stresses played a major role in determining the overall yield of the tested genotypes, and these two candidate genes might be exploited further as a marker for selecting superior genotypes that have a high abiotic stress tolerance.
Many of the identified candidate genes, such as Glyma.19G065100 (GO:0007010), Glyma.19G064800 (GO:0009684 and GO:0048523), and Glyma.19G065600 (GO:0048589) encode cytoskeleton organization, indoleacetic acid biosynthetic process, negative regulation of cellular process, and developmental growth, respectively. Cytoskeleton and indoleacetic acid are major components for building, expanding, and modifying cell walls, which affects the internode length and NP in plant species [39, 40]. Changing the hormone balance in plants can greatly affect the growth pattern, which results in increasing/decreasing the overall yield. Besides hormonal balances, the optimal use of products of the primary metabolism, such as nitrogen and carbon ratio, can influence plant growth and development [41]. In this study, one of the identified genes, Glyma.19G065600 (GO:0019676, GO:0042128, and GO:0006807), encodes ammonia assimilation cycle, nitrate assimilation, and nitrogen compound metabolic process. Ammonium assimilation plays an important role in incorporating ammonium into proteins, directly affecting plant growth and development [42, 43]. Nitrate assimilation is another important component in plants that greatly influences crop yield, plant biomass, and productivity [44, 45]. These results indicate that nitrogen and ammonium assimilation rates are strongly associated with the overall performance of the genotypes suggesting that the candidate genes underlying these characteristics may be used as markers for selecting superior genotypes.
In conclusion, a fast-paced yield improvement in soybean is conceivable through exploiting GS methods that are built on precise algorithms as well as using optimized genetic information. Our findings suggested using the E-B strategy as an effective approach for increasing the accuracy of GS over conventional GS methods. In addition, using haplotype block datasets can increase the prediction accuracy of GS up to 7% compared to using full SNP datasets for complex yield component traits. Overall, the optimization process in GS can be done using both the E-B strategy and haplotype dataset, and the information derived from the optimized GS can be used to select the superior genotypes with improved yield genetic gains. Through his study, we discovered a haplotype block on chromosome 19 (block 16) with significant effects on yield and its component traits, which can be used as a reliable genomic fragment for screening genotypes with improved yield genetic potential. The identified candidate genes positioned in this haplotype block revealed the importance of genes associated with plant growth and development as well as genes underlying abiotic resilience for enhancing yield production in soybean. Although the results of this study seem to be promising for improving yield in soybean, there are some limitations with this study that may need to be taken into account before generalizing the results to our germplasm and environments. The tested soybean panel probably covers only a portion of the available genetic variation in worldwide soybean germplasm. Therefore, the authors recommend applying the same approach to more diverse populations using whole-genome sequencing data to validate the results and give a better estimation of the efficiency of using ML algorithms in haplotype-based GS analysis for increasing the prediction accuracy. In addition, we used the cross-validation technique to minimize false-positive rates in our results; however, upstream analyses such as gene expression and transcriptomics-related evaluations are recommended to confirm the causal relationship between the identified genes and the target traits in this study.
4. Methods
4.1. Plant materials and experimental data
A panel of 250 soybean genotypes was cultivated in the field at the University of Guelph, Ridgetown Campus (200m above sea level, 42°27′14.8″N 81°52′48.0″W) and Palmyra (195 m above sea level, 42°25′50.1″N 81°45′06.9″W), Ontario, Canada in two consecutive years (2018 and 2019). The field experiments were based on randomized complete block design (RCBD) with two replications in each environment. Overall, there were four environments consisting of two locations × two years. Each phenotypic plot in each replication consisted of five 4.2 m long rows with a row spacing of 43 cm and seedling rate of 57 per m2. There were 250 plots per replication, 500 soybean plots per environment, 1000 plots per year, and 2000 plots in total.
4.2. Seed yield and yield components data collection
Soybean seed yield (ton ha−1) was collected by harvesting three middle rows of each plot and adjusting to 13% seed moisture and days to maturity. Soybean yield component traits information such as PP, NP, RNP, and NRNP were collected from 10 randomly selected plants in each plot for each genotype [5].
4.3. Statistical analyses
In order to control the possible error in the field, the nearest-neighbor analysis (NNA) as one of the most common spatial analyzing methods [46] was implemented to reduce the possible error in the field caused by spatial variability in the field. All the tested traits were scaled, centered, and standardized in the pre-treatment and pre-processing steps. The best linear unbiased prediction (BLUP) mixed model was used to estimate the average value of each yield component trait. The effect of the environment was considered as a fixed effect, and the effect of genotypes and block was assumed to be random in the BLUP analysis [47]. Overall, the following statistical model was used in this study (Eq. (1)):
| (1) |
where Y is the phenotypic value (yield and yield component traits), g in the vector of random genotype effects, in which g ∼ N(0, σ2g), a is the vector of block effects includes all the environments, added to the overall mean (fixed), i stands for the GxE interaction effects (random), which i ∼ N(0, σ2int), and is the vector of residuals, which ∼ N(0, σ2). Z, X, and W represent the incidence matrices of g, a, and i effects, respectively. The Pearson correlation and the heritability of soybean yield and its related traits were measured previously by Yoosefzadeh-Najafabadi, Tulpan and Eskandari [5].
4.4. Genotyping
The young trifoliate leaf tissue of each genotype was collected from the first plot at the Ridgetown location. Afterward, DNA was extracted using the NucleoSpin Plant II kit (Macherey–Nagel, Düren, Germany), and the DNA quality was checked with Qubit® 2.0 fluorometer (Invitrogen, Carlsbad, CA). Genotyping-by-sequencing (GBS) was conducted at Genomic Analysis Platform at Université Laval (Laval, Quebec, Canada), using ApeKI as the common enzymatic digestion for soybean [48]. The Fast-GBS pipeline [49] was conducted for each genotype based on the Gmax_275_v2 reference genome. Imputing missing loci and removing markers with a minor allele frequency less than 0.05 was done through Markov model in Beagle v5 pipeline. Overall, 23 soybean genotypes were eliminated, and a total of 17,958 high-quality SNPs were obtained from 227 soybean genotypes.
4.5. SNP-based haplotype blocks
A total of 2103 haplotype blocks that were characterized from 17,958 SNPs were used in haplotype-based GS (Supplementary Table 6). Haplotype blocks were constructed using Haploview version 4.1 [50] based on the solid spline method. This method provides more robust block boundaries by considering the first and last markers in a block with a strong LD. A cut-off of 1% was set to exclude SNPs from the block if adding particular SNPs resulted in more than 1% recombinant allele frequency. The Tagger was used to tag the best SNPs representing specific blocks in a chromosome. Then, all the untagged SNPs were excluded from the dataset to construct the haplotype-based dataset.
4.6. Genomic prediction models
4.6.1. Ridge regression best linear unbiased predictor (rrBLUP)
The basis of rrBLUP is to exploit the genetic relationship to calculate the breeding value of each genotype [51, 52]. The rrBLUP method considers all genetic markers that explain the equal amount of variance in the trait of interest based on the following equation (Eq. (2)):
| (2) |
where Y is the phenotypic value (yield and yield component traits in this study), is the overall mean, g stands for the marker effects follow g ∼ N(0, σ2m) distribution, in which σ2m is the amount of the genetic variance that is explained by each genetic marker, z in the design matrix for the genetic marker effects instead of an incident matrix, and is the vector of residuals [51].
4.6.2. Data fusion technique
Three commonly used ML algorithms, namely RBF, SVR, and RF, were exploited in GS individually and collectively using the ensemble Bagging data fusion technique.
4.6.2.1. Radial basis function (RBF) regressor
RBF regressor is known as one of the most important neural network algorithms that predict the target variable using a linear combination of RBF from neurons and input variables [53]. RBF regressor consists of different layers, including a linear output layer, a hidden layer with non-linear RBF, and an input layer. In this study, RBF regressor was constructed based on the radial basis function (RBF) as follows (Eq. (3)):
| (3) |
where, is the kernel function based on the RBF, σ2 is the variance, and is the Euclidean distance measurement between two Xa and Xb points.
4.6.2.2. Support vector regression (SVR)
SVR is the regression form of the support vector machine that is widely used in different regression analyses. SVR is constructed based on different sets of hyperplanes known as decision boundaries that are used to predict the target variable [54]. SVR also takes benefits from different types of kernels, which transform the input variables to the required form. In this study, SVR was constructed based on the polynomial kernel as follows (Eq. (4)):
| (4) |
where, is the polynomial kernel between two data points, a is the constant number, b is the degree of the kernel, and T is the transpose element.
4.6.2.3. Random forest (RF)
RF is another supervised ML algorithm, which is constructed with different sets of parallel trees with no interaction [55]. After constructing several decision trees based on the training dataset, the output would be the mean of all classes derived from the prediction results of all constructed decision trees. Overall, the following equation was used to solve the regression problem in this study (Eq. (5)):
| (5) |
where Yi is the predicted value of the genotype Xi, T stands for the total number of constructed trees, and B stands for the total number of samples.
4.6.2.4. Ensemble bagging strategy (E-B)
Ensemble techniques have been used broadly to improve the prediction accuracy by combining the final prediction output of all individual ML algorithms. In this study, (E-B) was used by the following steps: (1) train each ML algorithm individually using the training dataset, (2) select the best ML algorithm that can best predict the output variable as the metaClassifier for (E-B), and (3) combine and aggregate the results of all tested ML algorithms in order to increase the prediction accuracy of soybean yield and its related traits.
4.7. Haplotype importance score
The RFE method as one of the most commonly used methods to estimate the importance of haplotype blocks, was used for estimating the importance of each haplotype in predicting soybean yield and its components. The RFE method identifies the score of each haplotype block in the following steps: (1) construct the model based on the complete set of inputs, (2) calculate the importance score using a sequential selection strategy, (3) remove the least important haplotype blocks and eliminate them from the model, and (4) recursively repeat the process [56]. In this study, RFE was used based on considering the haplotype blocks as inputs and soybean yield and its components as output variables.
4.8. Extracting candidate genes underlying detected haplotype
The haplotype block 16, on chromosome 19 that was found to be associated all the tested traits was chosen to extract the candidate genes within the fragment. For this, the Glycine max William 82 reference gene 2.0 by the SoyBase database (https://www.soybase.org) was used. The flanking regions of the detected haplotype were determined based on the solid spline method with the expected spin if the coefficient of linkage disequilibrium (D′) was higher than 0.5. Finally, the associated genes with traits of interest were detected using discoveries from previous studies and GO enrichment analysis.
4.9. Quantification of model performance and error estimations
The tested dataset consisted of the genetic information from 227 genotypes was randomly decided into the training and testing dataset using a five-fold cross-validation (CV) technique with ten repetitions [57]. The MAE (Eq. (6)) and The RMSE (Eq. (7)) as the two most common error estimated measurements, were calculated to quantify the performance of each tested GS method.
| (6) |
| (7) |
where Y stands for the observed value, Y′ is the predicted value, and n stands for the number of observations.
In addition to the error estimation metrics, the R2 (Eq. (8)) was calculated to estimate the goodness of fit between predicted and observed values. The full definitions and descriptions of the tested metrics can be found in [58, 59, 60].
| (8) |
where SST and SSE stand for the sum of squares for total and error, respectively.
4.10. Visualizing and statistical analyzing
The results were visualized using Haploview [50], ggplot2 [61], and ggvis [62] packages in the R software version 3.6.1. All pre-processing steps and all description statistical procedures were conducted by R software. Also, all ML algorithms were implemented using Weka software version 3.8.5 [63] and caret [64] package in the R software.
Declarations
Author contribution statement
Mohsen Yoosefzadeh-Najafabadi: Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Istvan Rajcan: Contributed reagents, materials, analysis tools or data; Wrote the paper.
Milad Eskandari: Conceived and designed the experiments; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Funding statement
None.
Data availability statement
Data will be made available on request.
Declaration of interest's statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
Acknowledgements
The authors are grateful to the past and current members of Eskandari laboratory at the University of Guelph, Ridgetown, Bryan Stirling, John Kobler, and Robert Brandt for their technical support. We would like to thank Dr. Sepideh Torabi for his assistance with data collection.
Contributor Information
Mohsen Yoosefzadeh-Najafabadi, Email: myoosefz@uoguelph.ca.
Milad Eskandari, Email: meskanda@uoguelph.ca.
Appendix A. Supplementary data
The following is the supplementary data related to this article:
References
- 1.IFAD, UNICEF, WFP, WHO . FAO Rome; Italy: 2021. The State of Food Security and Nutrition in the World 2021. Transforming Food Systems for Food Security, Improved Nutrition and Affordable Healthy Diets for All. [Google Scholar]
- 2.Liu Z., Ying H., Chen M., Bai J., Xue Y., Yin Y., Batchelor W.D., Yang Y., Bai Z., Du M. Optimization of China’s maize and soy production can ensure feed sufficiency at lower nitrogen and carbon footprints. Nat. Food. 2021:1–8. doi: 10.1038/s43016-021-00300-1. [DOI] [PubMed] [Google Scholar]
- 3.Ray D.K., Mueller N.D., West P.C., Foley J.A. Yield trends are insufficient to double global crop production by 2050. PLoS One. 2013;8 doi: 10.1371/journal.pone.0066428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ray D.K., Ramankutty N., Mueller N.D., West P.C., Foley J.A. Recent patterns of crop yield growth and stagnation. Nat. Commun. 2012;3:1293. doi: 10.1038/ncomms2296. [DOI] [PubMed] [Google Scholar]
- 5.Yoosefzadeh-Najafabadi M., Tulpan D., Eskandari M. Application of machine learning and genetic optimization algorithms for modeling and optimizing soybean yield using its component traits. PLoS One. 2021;16 doi: 10.1371/journal.pone.0250665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yoosefzadeh Najafabadi M. University of Guelph; 2021. Using Advanced Proximal Sensing and Genotyping Tools Combined with Bigdata Analysis Methods to Improve Soybean Yield. [Google Scholar]
- 7.Board J., Kang M., Bodrero M. Yield components as indirect selection criteria for late-planted soybean cultivars. Agron. J. 2003;95:420–429. [Google Scholar]
- 8.Cui S., Yu D. Estimates of relative contribution of biomass, harvest index and yield components to soybean yield improvements in China. Plant Breed. 2005;124:473–476. [Google Scholar]
- 9.Wei X., Qiu J., Yong K., Fan J., Zhang Q., Hua H., Liu J., Wang Q., Olsen K.M., Han B. A quantitative genomics map of rice provides genetic insights and guides breeding. Nat. Genet. 2021;53:243–253. doi: 10.1038/s41588-020-00769-9. [DOI] [PubMed] [Google Scholar]
- 10.Decker J.E. Agricultural genomics: commercial applications bring increased basic research power. PLoS Genet. 2015;11 doi: 10.1371/journal.pgen.1005621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Varshney R.K., Graner A., Sorrells M.E. Genomics-assisted breeding for crop improvement. Trends Plant Sci. 2005;10:621–630. doi: 10.1016/j.tplants.2005.10.004. [DOI] [PubMed] [Google Scholar]
- 12.Bhat J.A., Yu D., Bohra A., Ganie S.A., Varshney R.K. Features and applications of haplotypes in crop breeding. Commun. Biol. 2021;4:1–12. doi: 10.1038/s42003-021-02782-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sandhu K.S., Patil S.S., Pumphrey M.O., Carter A.H. bioRxiv; 2021. Multi-Trait Machine and Deep Learning Models for Genomic Selection Using Spectral Information in a Wheat Breeding Program. [DOI] [PubMed] [Google Scholar]
- 14.Goddard M., Hayes B. Genomic selection. J. Anim. Breed. Genet. 2007;124:323–330. doi: 10.1111/j.1439-0388.2007.00702.x. [DOI] [PubMed] [Google Scholar]
- 15.Jannink J.-L., Lorenz A.J., Iwata H. Genomic selection in plant breeding: from theory to practice. Brief. Funct. Genom. 2010;9:166–177. doi: 10.1093/bfgp/elq001. [DOI] [PubMed] [Google Scholar]
- 16.Singh S., Jighly A., Sehgal D., Burgueño J., Joukhadar R., Singh S.K., Sharma A., Vikram P., Sansaloni C.P., Govindan V., Bhavani S., Randhawa M., Solis-Moya E., Singh S., Pardo N., Arif M.A.R., Laghari K.A., Basandrai D., Shokat S., Chaudhary H.K., Saeed N.A., Basandrai A.K., Ledesma-Ramírez L., Sohu V.S., Imtiaz M., Sial M.A., Wenzl P., Singh G.P., Bains N.S. Direct introgression of untapped diversity into elite wheat lines. Nat. Food. 2021;2:819–827. doi: 10.1038/s43016-021-00380-z. [DOI] [PubMed] [Google Scholar]
- 17.Wartha C.A., Lorenz A.J. Implementation of genomic selection in public-sector plant breeding programs: current status and opportunities. Crop Breed. Appl. Biotechnol. 2021;21 [Google Scholar]
- 18.Hamazaki K., Iwata H. RAINBOW: haplotype-based genome-wide association study using a novel SNP-set method. PLoS Comput. Biol. 2020;16 doi: 10.1371/journal.pcbi.1007663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Contreras-Soto R.I., Mora F., de Oliveira M.A.R., Higashi W., Scapim C.A., Schuster I. A genome-wide association study for agronomic traits in soybean using SNP markers and SNP-based haplotype analysis. PLoS One. 2017;12 doi: 10.1371/journal.pone.0171105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Abdel-Shafy H., Bortfeldt R.H., Tetens J., Brockmann G.A. Single nucleotide polymorphism and haplotype effects associated with somatic cell score in German Holstein cattle. Genet. Sel. Evol. 2014;46:1–10. doi: 10.1186/1297-9686-46-35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Liu J.S., Sabatti C., Teng J., Keats B.J., Risch N. Bayesian analysis of haplotypes for linkage disequilibrium mapping. Genome Res. 2001;11:1716–1724. doi: 10.1101/gr.194801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Yoosefzadeh-Najafabadi M., Tulpan D., Eskandari M. Using hybrid artificial intelligence and evolutionary optimization algorithms for estimating soybean yield and fresh biomass using hyperspectral vegetation indices. Rem. Sens. 2021;13:2555. [Google Scholar]
- 23.Szymczak S., Biernacka J.M., Cordell H.J., González-Recio O., König I.R., Zhang H., Sun Y.V. Machine learning in genome-wide association studies. Genet. Epidemiol. 2009;33:S51–S57. doi: 10.1002/gepi.20473. [DOI] [PubMed] [Google Scholar]
- 24.Montesinos-López O.A., Montesinos-López A., Pérez-Rodríguez P., Barrón-López J.A., Martini J.W., Fajardo-Flores S.B., Gaytan-Lugo L.S., Santana-Mancilla P.C., Crossa J. A review of deep learning applications for genomic selection. BMC Genom. 2021;22:1–23. doi: 10.1186/s12864-020-07319-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kodratoff Y. Elsevier; 2014. Introduction to Machine Learning. [Google Scholar]
- 26.Yoosefzadeh-Najafabadi M., Rajcan I., Vazin M. High-throughput plant breeding approaches: moving along with plant-based food demands for pet food industries. Front. Vet. Sci. 2022:1467. doi: 10.3389/fvets.2022.991844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Qi Y. Ensemble Machine Learning. Springer; 2012. Random forest for bioinformatics; pp. 307–323. [Google Scholar]
- 28.Noble W.S. What is a support vector machine? Nat. Biotechnol. 2006;24:1565–1567. doi: 10.1038/nbt1206-1565. [DOI] [PubMed] [Google Scholar]
- 29.Hesami M., Jones A.M.P. Application of artificial intelligence models and optimization algorithms in plant cell and tissue culture. Appl. Microbiol. Biotechnol. 2020:1–37. doi: 10.1007/s00253-020-10888-2. [DOI] [PubMed] [Google Scholar]
- 30.Yoosefzadeh-Najafabadi M., Earl H.J., Tulpan D., Sulik J., Eskandari M. Application of machine learning algorithms in plant breeding: predicting yield from hyperspectral reflectance in soybean. Front. Plant Sci. 2021;11:2169. doi: 10.3389/fpls.2020.624273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hesami M., Yoosefzadeh Najafabadi M., Adamek K., Torkamaneh D., Jones A.M.P. Synergizing off-target predictions for in silico insights of CENH3 knockout in cannabis through CRISPR/CAS. Molecules. 2021;26:2053. doi: 10.3390/molecules26072053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Nourani V., Elkiran G., Abba S. Wastewater treatment plant performance analysis using artificial intelligence–an ensemble approach. Water Sci. Technol. 2018;78:2064–2076. doi: 10.2166/wst.2018.477. [DOI] [PubMed] [Google Scholar]
- 33.Yoosefzadeh-Najafabadi M., Torabi S., Torkamaneh D., Tulpan D., Rajcan I., Eskandari M.M. Machine-learning-based genome-wide association studies for uncovering QTL underlying soybean yield and its components. Int. J. Mol. Sci. 2022;10:5538. doi: 10.3390/ijms23105538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Yoosefzadeh Najafabadi M., Torabi S., Tulpan D., Rajcan I., Eskandari M. Genome-wide association analyses of soybean yield-related hyperspectral reflectance bands using machine learning-mediated data integration methods. Front. Plant Sci. 2021:2555. doi: 10.3389/fpls.2021.777028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Xavier A., Rainey K.M. Quantitative genomic dissection of soybean yield components. G3: Genes Genomes Genet. 2020;10:665–675. doi: 10.1534/g3.119.400896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Jan H.U., Guan M., Yao M., Liu W., Wei D., Abbadi A., Zheng M., He X., Chen H., Guan C. Genome-wide haplotype analysis improves trait predictions in Brassica napus hybrids. Plant Sci. 2019;283:157–164. doi: 10.1016/j.plantsci.2019.02.007. [DOI] [PubMed] [Google Scholar]
- 37.Al-Whaibi M.H. Plant heat-shock proteins: a mini review. J. King Saud Univ. Sci. 2011;23:139–150. [Google Scholar]
- 38.Li K.P., Wong C.H., Cheng C.C., Cheng S.S., Li M.W., Mansveld S., Bergsma A., Huang T., van Eijk M.J., Lam H.M. GmDNJ1, a type-I heat shock protein 40 (HSP40), is responsible for both Growth and heat tolerance in soybean. Plant Direct. 2021;5 doi: 10.1002/pld3.298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wasteneys G.O., Galway M.E. Remodeling the cytoskeleton for growth and form: an overview with some new views. Annu. Rev. Plant Biol. 2003;54:691–722. doi: 10.1146/annurev.arplant.54.031902.134818. [DOI] [PubMed] [Google Scholar]
- 40.Lecube M.L., Noriega G.O., Santa Cruz D.M., Tomaro M.L., Batlle A., Balestrasse K.B. Indole acetic acid is responsible for protection against oxidative stress caused by drought in soybean plants: the role of heme oxygenase induction. Redox Rep. 2014;19:242–250. doi: 10.1179/1351000214Y.0000000095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Allen D.K., Young J.D. Carbon and nitrogen provisions alter the metabolic flux in developing soybean embryos. Plant Physiol. 2013;161:1458–1475. doi: 10.1104/pp.112.203299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Li Q., Li B.H., Kronzucker H.J., Shi W.M. Root growth inhibition by NH4+ in Arabidopsis is mediated by the root tip and is linked to NH4+ efflux and GMPase activity. Plant Cell Environ. 2010;33:1529–1542. doi: 10.1111/j.1365-3040.2010.02162.x. [DOI] [PubMed] [Google Scholar]
- 43.Sun H., Wang L.H., Zhou Q., Huang X.H. Effects of bisphenol A on ammonium assimilation in soybean roots. Environ. Sci. Pollut. Control Ser. 2013;20:8484–8490. doi: 10.1007/s11356-013-1771-1. [DOI] [PubMed] [Google Scholar]
- 44.Stitt M., Müller C., Matt P., Gibon Y., Carillo P., Morcuende R., Scheible W.R., Krapp A. Steps towards an integrated view of nitrogen metabolism. J. Exp. Bot. 2002;53:959–970. doi: 10.1093/jexbot/53.370.959. [DOI] [PubMed] [Google Scholar]
- 45.Huang G., Wang L., Zhou Q. Lanthanum (III) regulates the nitrogen assimilation in soybean seedlings under ultraviolet-B radiation. Biol. Trace Elem. Res. 2013;151:105–112. doi: 10.1007/s12011-012-9528-0. [DOI] [PubMed] [Google Scholar]
- 46.Goldberger A.S. Best linear unbiased prediction in the generalized linear regression model. J. Am. Stat. Assoc. 1962;57:369–375. [Google Scholar]
- 47.Bowley S. Any Old Subject Books; Guelph, Ont.: 1999. A Hitchhiker's Guide to Statistics in Plant Biology. [Google Scholar]
- 48.Sonah H., Bastien M., Iquira E., Tardivel A., Légaré G., Boyle B., Normandeau É., Laroche J., Larose S., Jean M., Belzile F. An improved genotyping by sequencing (GBS) approach offering increased versatility and efficiency of SNP discovery and genotyping. PLoS One. 2013;8 doi: 10.1371/journal.pone.0054603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Torkamaneh D., Laroche J., Belzile F. Fast-GBS v2.0: an analysis toolkit for genotyping-by-sequencing data. Genome. 2020;63:577–581. doi: 10.1139/gen-2020-0077. [DOI] [PubMed] [Google Scholar]
- 50.Barrett J.C., Fry B., Maller J., Daly M.J. Haploview: analysis and visualization of LD and haplotype maps. Bioinformatics. 2005;21:263–265. doi: 10.1093/bioinformatics/bth457. [DOI] [PubMed] [Google Scholar]
- 51.Tan B., Grattapaglia D., Martins G.S., Ferreira K.Z., Sundberg B., Ingvarsson P.K. Evaluating the accuracy of genomic prediction of growth and wood traits in two Eucalyptus species and their F1 hybrids. BMC Plant Biol. 2017;17:1–15. doi: 10.1186/s12870-017-1059-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Endelman J.B. Ridge regression and other kernels for genomic selection with R package rrBLUP. Plant Genome. 2011;4 [Google Scholar]
- 53.Broomhead D.S., Lowe D. Royal Signals and Radar Establishment Malvern (United Kingdom) 1988. Radial basis functions, multi-variable functional interpolation and adaptive networks. [Google Scholar]
- 54.Vapnik Vladimir N. Springer; 1999. The Nature of Statistical Learning Theory (Information Science and Statistics) [Google Scholar]
- 55.Breiman L. Bagging predictors. Mach. Learn. 1996;24:123–140. [Google Scholar]
- 56.Guyon I., Weston J., Barnhill S., Vapnik V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002;46:389–422. [Google Scholar]
- 57.Siegmann B., Jarmer T. Comparison of different regression models and validation techniques for the assessment of wheat leaf area index from hyperspectral data. Int. J. Rem. Sens. 2015;36:4519–4534. [Google Scholar]
- 58.Farifteh J., Van der Meer F., Atzberger C., Carranza E.J.M. Quantitative analysis of salt-affected soil reflectance spectra: a comparison of two adaptive methods (PLSR and ANN) Remote Sens. Environ. 2007;110:59–78. [Google Scholar]
- 59.Cacuci D.G., Ionescu-Bujor M., Navon I.M. CRC Press; 2005. Sensitivity and Uncertainty Analysis, Volume II: Applications to Large-Scale Systems. [Google Scholar]
- 60.Taylor J. 1997. Introduction to Error Analysis, the Study of Uncertainties in Physical Measurements. [Google Scholar]
- 61.Wickham H., Wickham M.H. The ggplot package. 2007. https://cran.r-project.org/web/packages/ggplot2/index.html URL:
- 62.Dennis T. 2016. Using R and Ggvis to Create Interactive Graphics for Exploratory Data Analysis, Data Visualization: a Guide to Visual Storytelling for Libraries. [Google Scholar]
- 63.Hall M., Frank E., Holmes G., Pfahringer B., Reutemann P., Witten I.H. The WEKA data mining software: an update. ACM SIGKDD Explor. Newslett. 2009;11:10–18. [Google Scholar]
- 64.Kuhn M. Astrophysics Source Code Library; 2015. Caret: Classification and Regression Training. ascl: 1505.1003. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data will be made available on request.