BMI-CNV: a Bayesian framework for multiple genotyping platforms detection of copy number variants

Abstract

Whole-exome sequencing (WES) enables the detection of copy number variants (CNVs) with high resolution in protein-coding regions. However, variants in the intergenic or intragenic regions are excluded from studies. Fortunately, many of these samples have been previously sequenced by other genotyping platforms which are sparse but cover a wide range of genomic regions, such as SNP array. Moreover, conventional single sample-based methods suffer from a high false discovery rate due to prominent data noise. Therefore, methods for integrating multiple genotyping platforms and multiple samples are highly demanded for improved copy number variant detection. We developed BMI-CNV, a Bayesian Multisample and Integrative CNV (BMI-CNV) profiling method with data sequenced by both whole-exome sequencing and microarray. For the multisample integration, we identify the shared copy number variants regions across samples using a Bayesian probit stick-breaking process model coupled with a Gaussian Mixture model estimation. With extensive simulations, BMI-copy number variant outperformed existing methods with improved accuracy. In the matched data from the 1000 Genomes Project and HapMap project data, BMI-CNV also accurately detected common variants and significantly enlarged the detection spectrum of whole-exome sequencing. Further application to the data from The Research of International Cancer of Lung consortium (TRICL) identified lung cancer risk variant candidates in 17q11.2, 1p36.12, 8q23.1, and 5q22.2 regions.

Introduction

Copy number variants (CNVs) are a major type of structural variants comprised of deletions and duplications of the genomic segments. They play an important role in complex diseases, such as cancer, muscle diseases, and neuropsychiatric diseases (Shlien and Malkin 2009; Välipakka et al. 2017; Takumi and Tamada 2018). In addition, recurrent and common CNVs have also been revealed to be risk factors for many diseases, such as autism spectrum disorders and schizophrenia (Moreno-De-Luca et al. 2010) and cardiovascular disease (Wang et al. 2019).

With the dramatic growth and the accompanying cost drop in sequencing technologies, massive whole-exome sequencing (WES) datasets have been generated from large-scale biomedical studies, which allows for the identification of genomic variants in functional protein-coding regions (Amos et al. 2017). However, exons only encompass 1% of the genome, limiting the possibility to investigate the impact of genetic variations such as CNVs located in the noncoding regions (Venter et al. 2001). Therefore, cohort projects often used both WES and SNP arrays for a combined genome-wide scanning and fine exome scanning. For example, the international Transdisciplinary Research In Cancer of the Lung (TRICL) consortium genotyped 2,003 subjects with both WES and SNP array data (Amos et al. 2017), the Alzheimer’s Disease Genetics Consortium (ADGC) and the Alzheimer’s Disease Sequencing Project (ADSP) (Karch et al. 2016; Beecham et al. 2017) have also collected such multiplatform data. Consequently, the demand for multiplatform (e.g. WES and SNP) integration methods that accurately study CNV in a full-coverage manner has dramatically increased but is still unfulfilled. Another challenge is that WES is subject to the nonuniform coverage of sequence reads in the assembly procedure due to the existence of short duplications or deletions, resulting in many dropped-out segments that were originally mapped to the exome. For example, Fang et al. (2014) found that more than 16% of the exons cannot be captured by WES experiments, losing the opportunity to detect short CNVs. Theoretically, integrating the information from SNP array can overcome this challenge and improve calling accuracy.

Similar efforts, such as iCNV, have been made by Zhou et al. (2018) for integrative segmentation. In iCNV, data from different platforms were first normalized and standardized and then jointly segmented by a Hidden Markov Model (Zhou et al. 2018). This method presented a significant boost in accuracy compared to WES. However, it only used information from a single sample. As we know, technological and biological factors are prominent in real data and increase the variations and noise in data intensities, leading to unreliable findings with single-sample scanning of CNVs. Consequently, multiple sample strategies previously introduced for detecting common CNVs have great potential to improve the robustness and detection power with noisy data. Such a direction has been supported by various existing studies (Zhang et al. 2010; Siegmund et al. 2011; Klambauer et al. 2012; Song et al. 2016), but none has focused on the direction of multiplatform integration. Moreover, the most widely used WES methods, such as CODEX2 and EXCAVATOR, are also used for single-sample scanning (Magi et al. 2013; Jiang et al. 2018).

Collectively, the development of a full-spectrum CNV detection method that can achieve high performance using comprehensive information from all samples and all platforms is essential. In this study, we developed BMI-CNV, a Bayesian Multisample and Integrative CNV calling method, as the first of its kind to enhance the detection of both intergenic or intragenic and common CNVs. The significant improvement of BMI-CNV on CNV calling was demonstrated by simulation studies (Simulations showed superior performance of BMI-CNV in multiplatform integrative analysis, Simulations showed superior performance of BMI-CNV in single platform analysis) as well as the analyses of real datasets from the HapMap project (Altshuler et al. 2010) and the 1000 Genomes Project (Application to the 1000 Genomes Project and HapMap data) (Auton et al. 2015). The further application of BMI-CNV to the international TRICL dataset identified new lung cancer-associated CNVs (Integrative CNV detection and association analyses with TRICL dataset). This new method has a wide scope of applications and has great potential to be further extended to profile CNVs for whole-genome sequencing and single-cell sequencing data.

Materials and methods

Our method mainly focuses on CNV detection by integrating the SNP array and WES data, which can also be naturally applied to single platform data (Numerical simulations). The overview of the framework is shown in Fig. 1. First, WES read counts and SNP array data are integrated using a series of data integration procedures. The main segmentation algorithm consists of 2 stages: Stage I uses a Bayesian probit stick-breaking process (PSBP) method (Stage-I: shared CNV inference by Bayesian probit stick-breaking process model) coupled with a Gaussian mixture model-based initial data filtering (Supplementary A.2) to identify shared CNV regions, and Stage II uses the individual CNV calling procedure to identify sample-specific CNVs (Stage-II: Individual CNV calling).

Fig. 1.

Analysis workflow of BMI-CNV. BMI-CNV uses 2 inputs: (1) WES raw read count data from testing and control samples that are computed by using genotyping tools such as SAMtools; and (2) SNP array intensities. WES read counts are normalized to correct exon length, GC-content, and mappability biases. Logarithms of normalized values between testing and pooled control samples are calculated. SNP array intensities are normalized to adjust the genomic waves. The WES and SNP array data are standardized by a robust scaling approach and then integrated. For CNV calling, BMI-CNV carries out a 2-stage framework to generate CNV calls. In stage I, an initial data filtering procedure is coupled with a Bayesian PSBP method to identify shared CNV regions. In stage II, an individual CNV calling procedure is performed to call CNVs in each sample.

Data description and multiplatform integration

First, we performed platform-specific normalization procedures for the original data. For WES data, with raw read depth data from test and external negative control samples, we used the exon mean read count (EMRC; Magi et al. 2013). EXCAVATOR2 median normalization procedure was utilized to mitigate the effects from 3 observed sources of bias: exon length, GC-content, and mappability (D’Aurizio et al. 2016). All negative control samples were pooled by averaging the EMRC on each exon across all samples and the logarithm between the ratio of test and pooled control samples was calculated, referred to as the $lo{g}_{2}R$ intensities. These $lo{g}_{2}R$ data were then processed by the lowess-scatter plot procedure to adjust read-depth differences between testing and control samples and remove coverage-dependent bias. For array data, PennCNV was used to adjust the genomic wave on genetic intensities (i.e. Log R ratio [LRR]) (Wang et al. 2007).

To combine the SNP array LRR data and the WES $lo{g}_{2}R$ data, we standardized each dataset via a robust scaling approach (Rousseeuw and Croux 1993). Compared to the conventional standardization method, the robust scaling approach used median and interquartile ranges to mitigate the influence from potential outliers and signals from double deletions (Details in Supplementary A.1). The WES and SNP array data were then merged by chromosomal coordinates for joint segmentation (details in Supplementary A.1).

Notations and basic model

Let Y denote a n × m data matrix obtained from the precalling procedures described above, where Y_ij represented the processed genetic intensities (e.g. LRR from array or $lo{g}_{2}R$ from WES) for the j—th ($j=1,2,\dots ,m$) marker (e.g. SNPs from array or exons from WES) in sample i ($i=1,2,\dots ,n$). We assumed a classic normal kernel for Y_ij,

$$Y_{ij}\sim N(Y_{ij}|{\varphi }_{ij}).$$

${\varphi }_{ij}=({\mu }_{ij},{\sigma }_{ij}^2)$ was an unknown matrix of the underlying mean and variance. Different values of ${\varphi }_{ij}$ indicated the existence of different copy number states. Five copy number states, including the deletion of single copy or double copies, diploid, duplication of a single copy or double copies were assumed in our study. We considered τ to be a change point for sample i if ${\varphi }_{i,\tau }\ne {\varphi }_{i,\tau +1}$. The goal is to estimate the locations of change points, CNV segments can then be generated by connecting adjacent change points.

To achieve this, we estimate change points shared by all samples and then identify their individual carriers. We use a 2-stage method: Stage I with a probit stick-breaking process (PSBP) to identify shared CNV regions across samples (Stage-I: shared CNV inference by Bayesian probit stick-breaking process model) and Stage II calling sample-specific CNVs individually (Stage-II: Individual CNV calling). We also initially filter samples without CNVs in Stage I (Supplementary A.2).

Stage-I: shared CNV inference by Bayesian probit stick-breaking process model

Let ${\mathit{Y}}_j={(Y_{1j},Y_{2j},\dots ,Y_{nj})}^T$ denote the genetic intensity for the jth marker ($j=1,2,\dots ,m$) across all samples. The classic normal kernel can be rewritten as

$${\mathit{Y}}_j\sim N({\mathit{Y}}_j|{\varphi }_j).$$

${\varphi }_j=({\mu }_j,{\sigma }_j^2)$ represented the shared mean and variance scalars of position j across all samples, the parameters in which needed to be estimated. We modeled the corresponding latent means and variances using the Bayesian PSBP model (Chung and Dunson 2009; Rodriguez and Dunson 2011). The favorable shrinkage property of PSBP allows for efficiently clustering of all ${\varphi }_j$’s to a small number of clusters (i.e. copy number states). Moreover, the PSBP mixture model can capture multimodal and heavy-tailed distribution, which relaxed the normality assumption of the latent means, providing more flexible scenarios for modeling the complex CNV data. Specifically, we assumed ${\varphi }_j$ followed an unknown distribution $G\sim \mathit{PSBP}(\alpha G_0)$ with centering distribution G₀ where the shape measure α reflected how far away the random distribution is from the center. Following Rodriguez and Dunson (2011), G admitted a representation of the form:

$${\varphi }_j\sim G(.)=\sum _{l=1}^L{\omega }_l{\delta }_{{\theta }_l}(.)$$ (1)

where L represented the number of all possible copy number states (e.g. L = 5), ${\theta }_l=({\mu }_l,{\sigma }_l^2)$ were possible distinct mean and variance specific to each copy number state ($l=1,2,\dots ,L$), ${\delta }_{{\theta }_l}(.)$ was a degenerate distribution at θ_l, and ${\omega }_l=\Phi ({\alpha }_l)\prod _{r<l}(1-\Phi ({\alpha }_r))$ represented the probability of assigning θ_l to each position where $\Phi (.)$ was the probit function and ${\alpha }_l\sim N({\mu }_{\alpha },{\sigma }_{\alpha }^2)$. Following this structure, ${\varphi }_j$ was assigned to one of the $\left\{{\theta }_l\right\}$ based on the observed intensities across all potential carriers of the copy number state for locus j, where the carriers were initially identified using a Gaussian mixture model-based strategy described in Supplementary A.2. To simultaneously implement the variable selection and clustering procedures for the purpose of CNV detection, we further reconstructed the PSBP model (George and McCulloch 1993; Cai and Bandyopadhyay 2017):

$${\varphi }_j\sim {\gamma }_j{G}_{\mu =0}+(1-{\gamma }_j)G(.)$$ (2)

where the $G_{\mu =0}$ was the underlying distribution of the normal copy number states with the mean fixed at zero (i.e. diploids). ${\gamma }_j\sim \mathit{Bernoulli}(\kappa )$ was an indicator of ${\varphi }_j$ being in $G_{\mu =0}$ (i.e. normal state) or not, which incorporated variable selection of the locus across samples. Specifically, when ${\gamma }_j=1,\hspace{0.17em}{\varphi }_j$ followed a distribution $G_{\mu =0}$; ${\gamma }_j=0$ indicated a potential CNV locus following $G(.)$ defined in equation (1). Within this framework, the posterior probability of ${\varphi }_j$ being $G_{\mu =0}$ or not was calculated through inference on γ_j (Supplementary A.3–A.4). In this way, each shared change-point is the position such that ${\gamma }_{{\tau }_t}\ne {\gamma }_{{\tau }_{t+1}}$ and locations of all shared change-points (i.e. $\tau =\{{\tau }_1,{\tau }_2,\dots ,{\tau }_T\}$) can be identified. In order to efficiently perform the posterior inference for all the parameters, we developed a Markov Chain Monte Carlo (MCMC) algorithm relying on a modification of the Gibbs sampler (Ishwaran and James 2001). With the proper choices of priors and hyperpriors, all full conditional distributions of the parameters can be analytically derived which ensured the computational speed and the convergence to the true posterior distributions (Supplementary A.3–A.4).

Stage-II: Individual CNV calling

Note that for shared CNV regions identified in the stage I, only a proportion of the samples carry the CNV for each region. We then determined the carriers for each shared CNV, that is, to call CNVs in each sample. Specifically, using the posterior mean and variance estimates specific to each copy number state (i.e. ${\widehat{\mu }}_l$ and ${\widehat{\sigma }}_l^2,\hspace{0.17em}l=1,\dots ,5$), we constructed the interval for each state as $C_l=[{\widehat{\mu }}_l-c_{1l}{\widehat{\sigma }}_l,{\widehat{\mu }}_l+c_{2l}{\widehat{\sigma }}_l]$. The individual segment would be classified into l—th copy number state if its segmental mean fell within one specific interval C_l. Here, C₃ represented the interval for diploid (i.e. noncarrier). Values of c₁ and c₂ should be carefully chosen according to empirical evidence about the magnitude of mean shifts of each CNV state, which may vary by genotyping platforms. In practice, to provide calibration of c₁ and c₂ and optimize the performance of our method, we will suggest users to initiate a pilot study and plot the genotyping signals of CNV segments identified under different combinations of c₁ and c₂ for visualization. True positive rate (TPR) can be calculated for each combination and the optimal choices for c₁ and c₂ will achieve the highest TPR. In our applications (Numerical simulations, Application to the 1000 Genomes Project and HapMap datasets, Analysis of the TRICL consortium case-control dataset), $c_1=c_2=1.2$ were used.

Numerical simulations

To evaluate the performance of our method, we conducted simulations under various settings. Four copy number states were simulated, including single copy deletion (del.S), double copy deletion (del.D), single copy duplication (dup.S), and double copy duplication (dup.D). The CNV length (i.e. SNPs and exons) varied from 10–30 markers, 30–60 markers, and 60–100 markers. The CNV population frequency was 20%, 50%, or 100%, respectively.

First, we evaluated our method when both WES and SNP array data were available. For WES data, to generate data retaining the true noise background and exon distribution, we conducted a spike-in design (Jiang et al. 2018; Zhou et al. 2018). We started with read-depth data on chromosome 1 in 81 samples from the 1000 Genomes Project (Auton et al. 2015). Exons harboring CNVs identified by EXCAVATOR2 and CODEX2 and reported in the Database of Genomic Variants (DGV) were initially removed (MacDonald et al. 2014; D’Aurizio et al. 2016; Jiang et al. 2018). The read depth data of the remaining exons were treated as WES random noise background. We multiplied the background read depth by $c/2$, where c was sampled from a normal distribution with mean and variance provided in Supplementary A.5. For SNP array data, we utilized the similar strategy used in Xiao et al. (2019) to simulate intensities, which mimicked the real data from the Altshuler et al. (2010). 50 dispersed CNV segments of varying length and frequency were then randomly selected and spiked randomly in coding regions (i.e. exonic CNVs) or noncoding regions (i.e. intergenic or intragenic CNVs).

Our method was compared to the only existing multiplatform integrative method iCNV (Zhou et al. 2018). The performance of these methods was assessed by precision rate, recall rate, and F1 score (Supplementary A.5). We also evaluated the performance of our method in the single-platform mode when only WES data was available. In this scenario, only exonic CNVs were simulated and our method was compared against 3 commonly used CNV detection methods CODEX2 (Jiang et al. 2018), EnsembleCNV (Zhang et al. 2019), and EXCAVATOR2 (D’Aurizio et al. 2016); a multisample based method, cn. MOPS (Klambauer et al. 2012); and iCNV in the single-platform mode (Zhou et al. 2018).

Application to the 1000 Genomes Project and HapMap datasets

We analyzed the same 81 individuals with SNP array and WES data from the 1000 Genomes Project and the international HapMap consortium. A detailed description of the experimental samples and genotyping platforms was provided in previous literature (Altshuler et al. 2010; Auton et al. 2015). Raw read counts and SNP array data were processed and normalized to generate $lo{g}_{2}R$ and LRR intensities. For the WES data, we arbitrarily selected 4 normal samples from the 1000 Genomes Project as negative controls (details in Supplementary A.6). The posterior inference of BMI-CNV was based on 2,000 MCMC samples with a burn-in period of 500 iterations.

Analysis of the TRICL consortium case-control dataset

We further applied BMI-CNV to the international lung cancer consortium TRICL (Amos et al. 2017), which consists of 1,163 samples genotyped by both OncoArray and WES data (i.e. integrative analysis mode), and 829 samples that only had WES data (i.e. single platform analysis mode) (details in Supplementary A.6 and A.7).

CNV calls were annotated by known gene regions obtained from the University of California, Santa Cruz (UCSC) Genome Browser (Kent et al. 2002). A gene-based association test was performed to investigate the influence of CNVs on lung cancer susceptibility:

$$\mathit{logit}(P(\mathit{disease}=1))={\beta }_0+{\beta }_{\mathit{del}}DEL+{\beta }_{\mathit{dup}}DUP+\mathit{\beta X}+\mathit{\beta }\prime \sum _{i=1}^{4}P{C}_i.$$ (3)

DEL and DUP were 2 indicator variables for deletions and duplications separately. We adjusted the covariates, including smoking status (ever/never), age, and gender, ancestry-related PCs representing the top principal components (Patterson et al. 2006). In addition to studying overall lung cancer risk, we also performed stratification analyses by histological types of lung cancer [squamous cell lung cancer (SQC) and lung adenocarcinoma (LUAD)]. The effects from deletions and duplications were tested via the Wald test, and all nominal P-values were adjusted by the Benjamini–Hochberg (BH) procedure (Benjamini and Hochberg 1995).

Results

Simulations showed superior performance of BMI-CNV in multiplatform integrative analysis

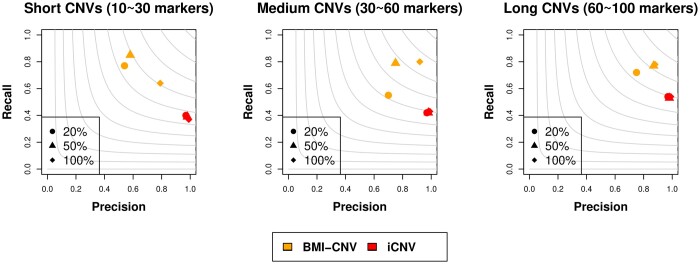
We first evaluated the performance of BMI-CNV with simulated data. In various simulation settings including different CNV sizes and population frequencies, BMI-CNV outperformed iCNV in all scenarios with higher F1 scores (Fig. 2, Supplementary Table 1). iCNV tended to be conservative compared to our method, which maintained a high precision rate, although the recall rate was compromised. For example, when the simulated CNVs had a length of 30–60 markers and the population frequency was 20%, BMI-CNV had a precision at 0.70, a recall rate at 0.83, and an F1 score at 0.76. The corresponding values for iCNV were 0.99, 0.37, and 0.54, respectively. Moreover, at a fixed CNV size, the performance of BMI-CNV was improved when CNV frequencies increased from 20% to 100%, achieving the highest F1 score when all the samples were carriers, whereas the performance of the iCNV method was not sensitive to the CNV frequencies.

Fig. 2.

Performance assessment of BMI-CNV and iCNV on simulated data in the integrative analysis. Simulated CNVs were of frequency 20%, 50%, and 100% and length 10–30 markers (short), 30–60 markers (medium), and 60–100 markers (long). The grey contours are F1 scores calculated as the harmonic mean of precision and recall rates.

We further assessed the performance of BMI-CNV to detect CNVs in different regions as 25% of simulated CNVs were mainly located in the intergenic or intragenic regions which are difficult to be detected for methods using WES data alone. By integrating available SNP array data, BMI-CNV can identify most of these CNVs, and it still outperformed iCNV in all scenarios (Supplementary Table 2). For example, when the simulated CNVs had 60–100 markers and the population frequency was 20%, BMI-CNV detected 94% of the CNVs, and iCNV only detected 59%. For computational speed, our method took about 280 min to screen a chromosome with 90,739 markers from 81 samples based on 2,000 MCMC sampling runs which was 54 min for iCNV, 20 min for EXCAVATOR2, 70 min for CODEX2, and 30 min for cn. MOPs. The computation was performed on a regular laptop with an Intel Core i7 processor and 24.00 GB of RAM.

Simulations showed superior performance of BMI-CNV in single platform analysis

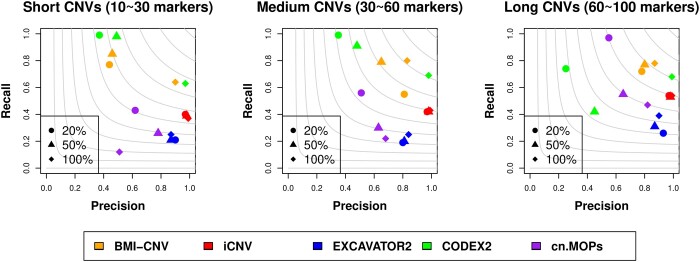
For single platform analysis, we assessed the performance of BMI-CNV benchmarking against existing WES methods. As a result, the performance of our method was superior in detecting medium and long CNVs reflected by the largest F1 scores (Fig. 3, Supplementary Table 3). iCNV, cn. MOPS, and EXCAVATOR2 tended to be conservative, as they achieved high precision rates but with significant sacrifice on recall rates. It is also noteworthy when the CNV size was fixed, the performance of BMI-CNV and CODEX2 were both improved with increased CNV frequencies, achieving the highest F1 scores when all the samples were carriers, and cn. MOPS tended to be conservative when CNV frequencies increased. Still, the performance of EXCAVATOR2 and iCNV were not subject to CNV frequencies, which was expected as the shared information from multiple samples was not utilized.

Fig. 3.

Performance assessment of BMI-CNV, iCNV, EXCAVATOR2, CODEX2, cn. MOPs and EnsembleCNV on simulated data in WES analysis. Simulated CNVs are of frequency 20%, 50%, and 100% and length 10–30 markers (short), 30–60 markers (medium), and 60–100 markers (long). The grey contours are F1 scores calculated as the harmonic mean of precision and recall rates.

In conclusion, the BMI-CNV method, integrating information from multiple samples, presented evidence of superior performance in common CNV detection for both multiplatform integration and single-platform analyses. By incorporating SNP array data, BMI-CNV enabled the accurate detection of intergenic or intragenic CNVs for integrative analysis.

Application to the 1000 Genomes Project and HapMap data

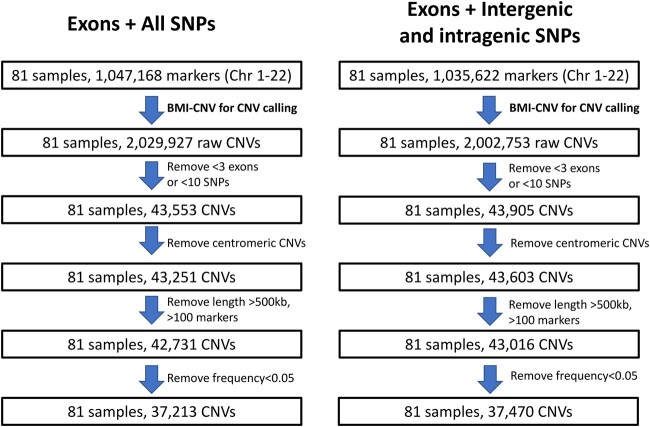
We applied BMI-CNV to the public datasets from the 1000 Genomes Project and HapMap data. In total, 37,213 CNVs were identified from 81 samples (Fig. 4), 28% of which have been previously reported by DGV (MacDonald et al. 2014). Most CNVs tended to be short (<20 markers) and had a frequency of less than 50%. Supplementary Fig. 1 showed the summary of CNVs, which suggested no significant difference in CNV length and frequency between deletions and duplications. Moreover, by integrating the SNP array data, our method retrieved 4,418 CNVs that were located in the noncoding regions which were missed by methods using WES data alone.

Fig. 4.

Overview of the application to the 1000 Genomes Project and HapMap data. The figure outlines the study design with a brief description of quality control (QC) methods. Summary of key results includes the sample size and number of CNVs at various stages of analysis. Left: CNV calling results using all SNPs and exons; right: CNV calling results using intergenic and intragenic SNPs and exons. Chr, chromosome.

A clear pattern of the signal in the shared deletion suggested high detection accuracy of our method. We illustrated a common deletion region in Supplementary Fig. 2, suggesting that 27 out of 81 samples were carriers of this variant. Besides, we explored an alternative data integration strategy that only used intronic SNPs from the array data. Compared to the main method using all SNPs, a lower concordance rate with DGV (26% vs 28%) was observed, implying that utilizing information from all SNPs slightly improved the detection accuracy (Fig. 4, Supplementary Fig. 3).

Integrative CNV detection and association analyses with TRICL dataset

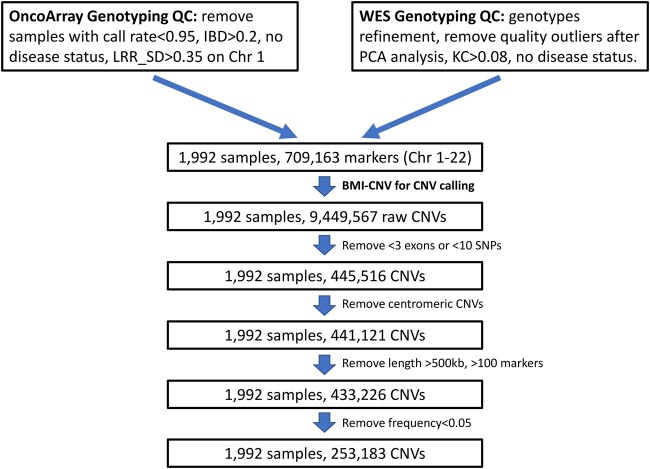
With the TRICL datasets, we identified 253,183 autosomal CNVs from 1,992 samples (Fig. 5) in total. Overall, there was no significant difference in the size of detected deletions or duplications (31.46 kb vs 32.51 kb), but the deletions covered more markers than the duplications (13.46 markers vs 8.72 markers) (Supplementary Table 4). No significant difference was observed in the overall proportion of deletions and duplications between cases and controls (49% vs 51% for deletions and 52% vs 48% for duplications, respectively).

Fig. 5.

Overview of the integrative analysis of the TRICL case-control study. The figure outlines the study design with a brief description of quality control (QC) steps. The summary of the key results includes the sample size and number of CNVs at various stages of analysis. IBD, identical by descent; KC, kinship coefficient; LRR SD, standard deviation of Log R ratio; Chr, chromosome; PCA, principal component analysis.

The identified CNVs were mapped to 3,472 genes. Association tests in SQC subgroup highlighted the deletion gene LGALS9 in 17q11.2 region (OR = 4.14, 95% CI = 1.65–10.38, P-value = 0.002), the duplication genes HSPG2 in 1p36.12 region (OR = 4.79, 95% CI = 1.75–13.10, P-value = 0.002) and EIF3E in 8q23.1 region (OR = 2.19, 95% CI = 1.31–3.64, P-value = 0.003). Association in the LUAD subgroup identified the duplication gene YTHDC2 in 5q22.2 region (OR = 2.88, 95% CI = 1.62–5.12, P-value = 0.0003), which was also identified in the overall lung cancer risk model by adjusting the histological subtypes as a covariate (Supplementary Table 5). The intensity plots indicated those were valid CNV segments that showed distinct data patterns from other noncarriers and adjacent regions (Supplementary Fig. 4). Although these genes became not significant after multiple comparison adjustments, they still provided potential evidence for further studies and great insight into revealing the role of CNVs in lung cancer risk.

Discussion

The importance of CNVs for elucidating the mechanism underlying many diseases has been increasingly remarked upon. Improving the accuracy of CNV detection is fundamental for downstream CNV-disease risk association and diagnostic classification. In this study, we developed a novel multiple sample-based method, BMI-CNV, to improve common CNV detection with WES data, allowing for the integration of available SNP array data. The simulation results demonstrated the desirable performance across different scenarios of CNV sizes and population frequencies. The improvement for calling long and high-frequency CNVs was the most substantial. We analyzed the WES data from the 1000 Genomes Project and SNP array data previously generated by the HapMap project 3 and demonstrated the advantage of multiplatform integration over the single-platform analysis. Finally, our application of BMI-CNV to WES and OncoArray datasets of the TRICL consortium indicated potential lung cancer-associated CNVs.

Among the top associations with the TRICL study, the discovered significantly associated gene LGALS9 was previously found to be a prognostic factor for lung cancer, low expression of which was correlated with poorer survival outcome (He et al. 2019). The significant amplification genes HSPG2, EIF3E, and YTHDC2 have also been extensively found as oncogenes in diverse tumor types, including lung cancer, gastrointestinal cancers, and breast cancer (Li et al. 2014; Chen et al. 2018; Kalscheuer et al. 2019). Our study mainly focuses on identifying germline CNV; however, the method is also suitable for the detection of somatic aberrations, where long and recurrent copy number changes are prominent. Due to the tumor complexity and heterogeneity, it may require different strategies in data normalization and filtering procedures (Zare et al. 2017).

This report demonstrated the improved performance of integrative CNV detection by utilizing a multisample and multiplatform strategy. The advantages of our method in theory lie in 2 aspects. First, utilizing information across samples will dramatically reduce false positives and boost detection power. We showed that BMI-CNV presented essential advantages over other single-sample methods in detecting common variants. The advantage was previously shown in Song et al. (Song et al. 2016), which revealed that the underlying statistical power of multisample methods converged to one at a faster rate than single-sample methods. Second, BMI-CNV integrates available SNP data to detect CNVs in noncoding regions, allowing for full-spectrum genomic variants investigation. Indeed, the important role of CNVs in noncoding regions has been revealed in numerous studies. For example, Kumaran et al. identified 1,812 breast cancer-associated CNVs mapping to noncoding regions (Kumaran et al. 2018). Other similar efforts in integrating data from noncoding regions have been made. EXCAVATOR2 and CopywriteR used both the targeted reads and the nonspecifically captured off-target reads (i.e. from the noncoding region) (Kuilman et al. 2015; D’Aurizio et al. 2016), in which the information is usually biased and incomplete. Our method utilizes the more complete SNP array data from the matched samples and therefore provides a more reliable and unbiased solution. Besides, iCNV assumes that those overlapping markers (i.e. exons and SNPs) share the same copy number and indeed use one platform to validate calls from the other using a single hidden Markov model (Zhou et al. 2018). In contrast, BMI-CNV systematically combines data sequences from multiplatforms and allows heterogenous copy number states for the overlapping markers.

In this study, we developed a Bayesian statistical framework that has several essential advantages over other modeling strategies. First, the nonparametric PSBP can relax the restrictive parametric assumption and allows flexible modeling of the complex high-throughput data. A common critique of the Bayesian method is its computational speed. In our framework, all conditional distributions implemented in the Gibbs sampling algorithm can be analytically derived, which guarantees efficient sample generation and fast computation. Second, the Bayesian framework enables great flexibility and possibility to incorporate prior relevant information such as the documented CNV hotspot information (Wang et al. 2007). Finally, the PSBP framework can be easily extended to accommodate the complex data dependence structure by replacing the independent weights with stochastic processes (e.g. Gaussian process) without sacrificing computational tractability (Rodriguez and Dunson 2011).

Our method presents some limitations. First, it does not detect rare CNVs, as the power will be attenuated in the existence of a large proportion of noncarriers. Second, it will have low power to detect CNVs with similar proportions of duplications and deletions in the samples, which might be less likely for germline variations. Our method may split those CNVs into several smaller deletions and duplications, as each CNV locus is equally likely to be assigned to deletion or duplication. Our study primarily focuses on systematically integrating matched WES and SNP array data, since there are many unexplored large-scale datasets that have been previously sequenced by multiple platforms (e.g. SNP array and WES). As whole genome sequencing is becoming more affordable nowadays, it is prominent to combine such data with data generated from other low-resolution platforms. Our proposed method can also be extended in such direction accompanied with the development of appropriate normalization methods. For future directions, the detection performance of BMI-CNV can be improved by combining B allele frequency (BAF) data. One strategy is to construct a composite score using both total genetic intensities and allele-specific information, similar effort has been pursued in SNP array data in a previous study of our team (Xiao et al. 2019). With WES, efficient derivation of allele-specific information and normalization methods will be desirable for optimal performance of the method. Moreover, our method can be extended to integrate other data types (e.g. gene expression data) and may incorporate case-control status to directly identify disease-associated CNVs in a single model.

Data Availability

WES data from the 1000 Genomes Project were downloaded from the FTP site hosted at the EBI ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/ (accessed 2022 June 10). SNP array data from the International HapMap project are available from the FTP site ftp://ftp.ncbi.nlm.nih.gov/hapmap (accessed 2022 June 10). The TRICL SNP array and WES data are available at dbGaP with study accession numbers: phs000877.v2.p1 and phs000878 v2.p1. BMI-CNV source code is available on GitHub at https://github.com/FeifeiXiaoUSC/BMI-CNV (accessed 2022 June 10).

Supplemental material is available at GENETICS online.