Trigeminal afferents sense locomotion-related meningeal deformations

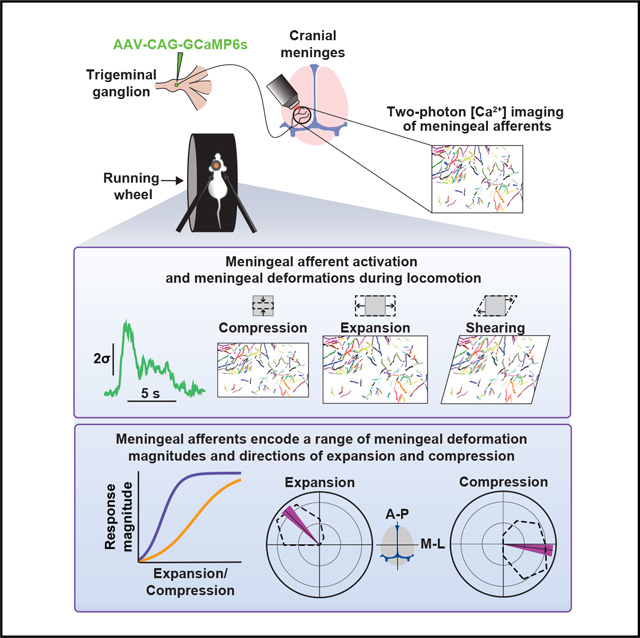
SUMMARY

The trigeminal sensory innervation of the cranial meninges is thought to serve a nociceptive function and mediate headache pain. However, the activity of meningeal afferents under natural conditions in awake animals remains unexplored. Here, we used two- and three-dimensional two-photon calcium imaging to track the activity of meningeal afferent fibers in awake mice. Surprisingly, a large subset of afferents was activated during non-noxious conditions such as locomotion. We estimated locomotion-related meningeal deformations and found afferents with distinct dynamics and tuning to various levels of meningeal expansion, compression, shearing, and Z-axis motion. Further, these mechanosensitive afferents were often tuned to distinct directions of meningeal expansion or compression. Thus, in addition to their role in headache-related pain, meningeal sensory neurons track the dynamic mechanical state of the meninges under natural conditions.

In brief

The trigeminal sensory innervation of the cranial meninges mediates headache pain, but its function under normal conditions is poorly understood. Blaeser et al. report that a subset of meningeal afferents encode diverse aspects of meningeal deformation associated with locomotion, suggesting their role as intracranial interoceptors under physiological conditions.

Graphical Abstract

INTRODUCTION

The cranial meninges envelop the brain parenchyma and serve as a protective barrier and a neuroimmune interface between the brain and the periphery.^1,2 The cranial meninges are densely innervated by primary afferent neurons, whose cell bodies are located in the trigeminal ganglion (TG). Acute electrical or mechanical stimulation of the cranial meninges in awake human patients produces headache-like pain.^3,4 These observations, together with data from animal studies, support the notion that the meningeal sensory innervation plays a key role in the origin of intracranial headaches, including migraines.^5–7 In contrast, it remains unknown whether trigeminal meningeal afferents are also recruited under normal physiological conditions.

Current knowledge about the response properties of meningeal afferents in vivo is almost exclusively based on acute experiments involving single-unit recordings from their TG somata.⁸ In these recordings, direct application of mechanical or chemical stimuli to the afferents’ meningeal receptive fields revealed response properties consistent with a nociceptive function.⁹ However, the above studies were carried out in anesthetized animals with surgically exposed and depressurized meninges. Hence, there is a large gap in our understanding of how meningeal afferents actually interact with the unique and complex mechanical and chemical landscape of the intact intracranial space.

To fill this gap, we employed high-speed two-photon calcium imaging of the activity of individual trigeminal meningeal afferents in the intact intracranial space of awake mice. We combined these recordings with behavioral tracking of locomotion and estimates of instantaneous, local meningeal deformation based on two- and three-dimensional imaging. Afferents exhibited diverse sensitivities to locomotion and to the amplitude and direction of local meningeal deformation. Our findings suggest a surprising degree of sensitivity of meningeal afferents to natural meningeal deformations that occur during and after locomotion and other natural behaviors and enable investigation of the potentially multi-functional roles of meningeal afferents in health and disease.

RESULTS

Monitoring calcium activity in meningeal afferent nerve terminals in behaving mice

We developed a calcium imaging approach to monitor the activity of dozens of meningeal afferent peripheral nerve endings simultaneously in the intact intracranial space of awake, behaving mice through a chronically implanted cranial window (Figure 1). Microinjection of AAV5-CAG-GCaMP6s into the TG produced labeling of TG neuronal somata and afferent fibers in the ipsilateral dural meninges (Figures S1A–S1C). GCaMP6 colocalized with calcitonin gene-related peptide (CGRP) in a subset of fibers (Figure S1C), confirming expression in peptidergic and non-peptidergic meningeal primary afferent neurons.

Figure 1. Imaging meningeal afferent activity in awake, behaving mice.

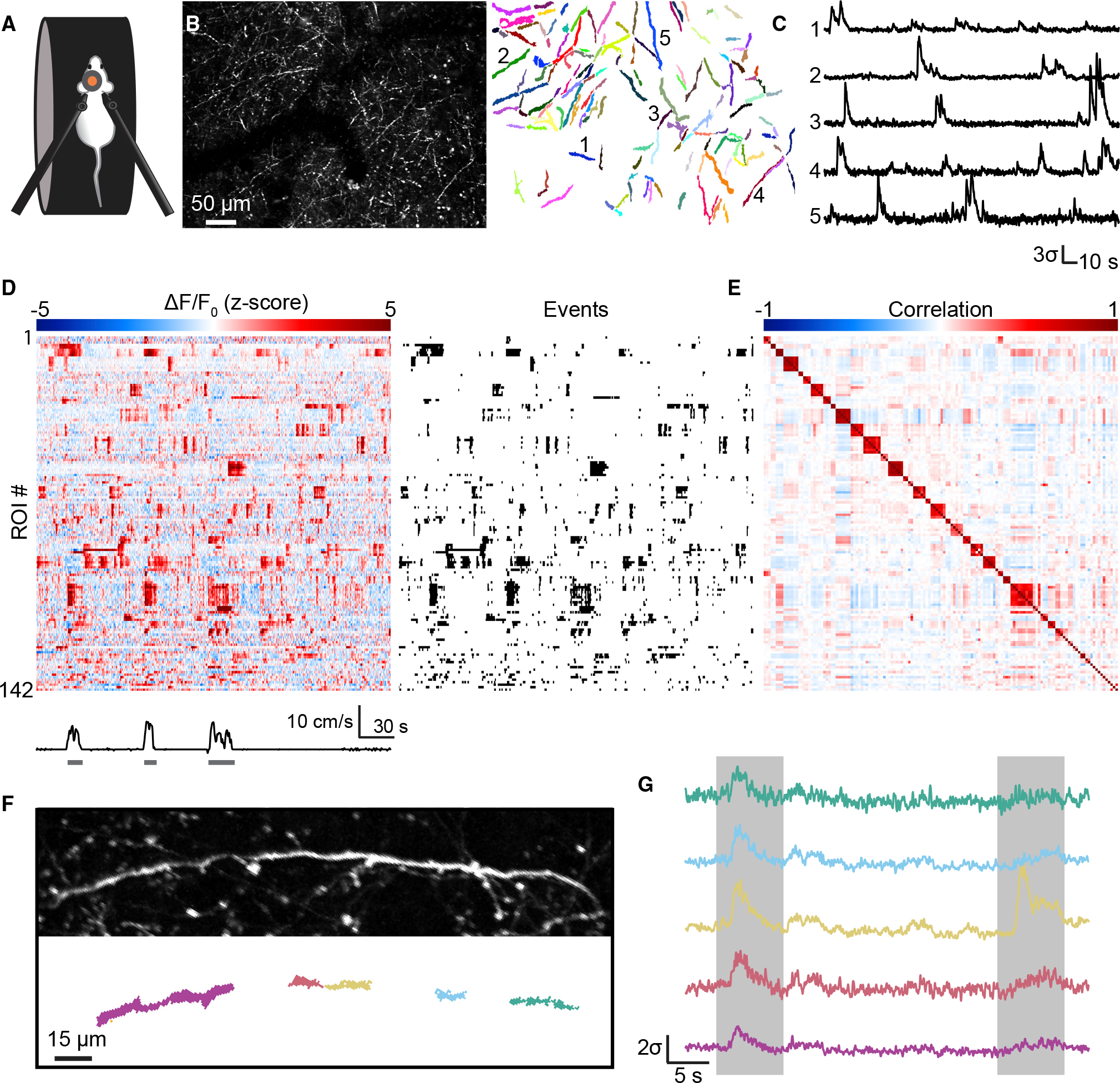
(A) Two-photon imaging of meningeal afferents was conducted in awake, head-fixed mice that could run freely on a treadmill.

(B) Left: maximum projection across all frames from a field of view (FOV) with dense GCaMP6s-expressing fibers. Right: regions of interest (ROIs) obtained from this field of view.

(C) Example fluorescence traces from the five ROIs indicated in (B). Traces are standardized and plotted in standard deviation units (σ).

(D) Meningeal afferents exhibited ongoing activity during quiet wakefulness and increased activity during locomotion. Left: example heatmap of standardized fluorescence signals for all ROIs from the FOV shown in (B). Right: raster of binarized events detected from those signals.

(E) Correlation matrix for ROI signals from the FOV in (B). Sets of ROIs were clustered into putative fibers based on activity correlations during quiet wakefulness.

(F) Example of a single fiber spanned by multiple ROIs.

(G) Fluorescence traces from the five ROIs in (F). ROI activity was highly correlated within fibers (left box), but occasional fluorescence events were localized to a single ROI (right box, yellow trace).

See also Figure S1 and Video S1.

Following implantation of a headpost and chronic cranial window above the intact dura overlying the posterior neocortex and at least 7 days of recovery, mice were gradually habituated across multiple sessions to head restraint while free to run on a wheel (Figure 1A). The cranial window remained clear for over 12 weeks, allowing imaging of the activity of afferents from the same mouse across months. Vascular imaging using this cranial window approach confirmed no leakage of macromolecules from dural or pial vessels at similar time points (Figure S1D), suggesting no persistent meningeal inflammation below the window.

We tracked the activity of meningeal afferents using two-photon calcium imaging in awake, head-fixed mice as follows. First, during each imaging session, we identified a field of view (FOV) containing dense GCaMP6s labeling of meningeal afferents (Figure 1B). We then conducted two consecutive 30-min imaging runs while the mouse was free to stand or run. A total of 30 FOVs were imaged from 12 mice. Some FOVs were imaged at a single focal plane to maximize temporal resolution (15.5 frames/s; two-dimensional [2D] imaging dataset: 14 FOVs from 6 mice). In other experiments, to sample afferents throughout the entire meningeal thickness, we used volume scanning for near-simultaneous imaging of 15 or 30 planes evenly spaced across 60 μm in depth (1.03 or 0.52 volumes/s, respectively; 3D imaging dataset: 16 FOVs from 7 mice).

We used a modified principal component analysis (PCA)/independent component analysis (ICA) approach¹⁰ to identify active regions of interest (ROIs; e.g., Figure 1B) and detected 4,537 ROIs in the 2D dataset (18–790 ROIs per FOV, median: 300) and 3,085 ROIs in the 3D dataset (48–735 ROIs per FOV, median: 145). ROIs were found throughout the meningeal thickness but were enriched in the most superficial 20 μm (Figure S1E). Afferents demonstrated sporadic, transient elevations of calcium activity (Video S1; Figure 1C). Such elevations were defined as active events if (1) the fluorescence signal continuously exceeded one standard deviation above the mean for at least 1 s and (2) the peak fractional change in fluorescence from baseline (ΔF/F₀) was at least 5% (Figure 1D). We observed a high degree of correlated activity between certain pairs of ROIs (Figure 1E), many of which appeared to be subregions of the same afferent fiber based on their location and orientation (Figure 1F). While sets of ROIs belonging to the same putative afferent fiber were highly correlated, we observed rare calcium events that were localized to only one among these ROIs (Figures 1F and 1G). Therefore, analyses were performed on individual ROIs rather than fibers as we could not rule out the possibility that different local regions of a meningeal afferent axon may exhibit at least partially distinct activity patterns.

A subset of meningeal afferents are sensitive to locomotion

Throughout each imaging session, mice toggled between periods of stillness and brief, sporadic bouts of running. Using high-speed 2D imaging, we observed occasional calcium activity in most ROIs (99%) during quiet wakefulness (Video S1; Figures 1D and S2A; median event rate: 1.31 events/min). Median event durations rarely exceeded 2 s (Figure S2B), and median event amplitude (ΔF/F₀) was ~30% (Figure S2C). In every experiment, a subpopulation of ROIs (7%–61% of ROIs, median: 23.5%; 14 FOV from 6 mice) exhibited robust activation during locomotion (significant mean increase in fluorescence of >5% during running bouts relative to pre-bout baseline; Video S2; Figures 2A, 2B, and S2D). A smaller subpopulation of ROIs (0%–23%, median: 4.8%) exhibited decreased fluorescence during locomotion (Figures 2B and S2D) that was commonly followed by rebound activation above baseline following the termination of locomotion (Figures 2B and 2C). Control experiments using mice that expressed GFP in a subset of meningeal afferents confirmed that the locomotion sensitivity described above was not due to motion artifacts (Figures S2E–S2G).

Figure 2. Locomotion activates or suppresses subpopulations of meningeal afferents.

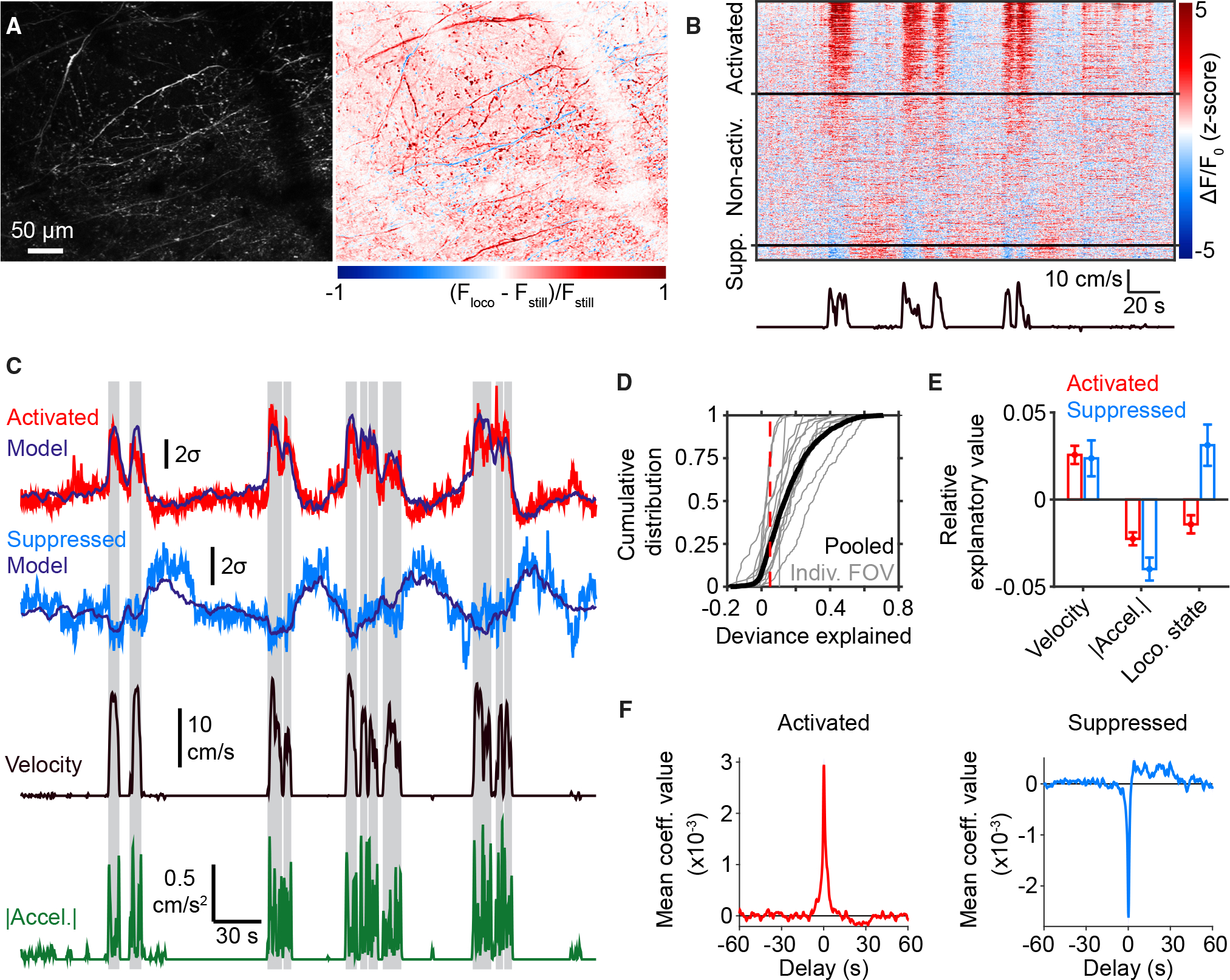
(A) Left: maximum projection from an example FOV. Right: heatmap of the normalized difference between maximum projections of fluorescence across moments of locomotion (F_loco) or stillness (F_still).

(B) Example data from the same FOV as in (A), illustrating sets of ROIs that became activated or suppressed (“Supp.”) during locomotion bouts (bottom trace).

(C) Fluorescence traces from running-bout-activated (red) and running-bout-suppressed (light blue) ROIs. Traces from both ROIs were well fit by a general linear model (GLM; dark blue traces) using velocity (black), acceleration (green), and locomotion state (shaded regions) as predictor variables. Traces are plotted in units of standard deviation (σ).

(D) Cumulative distributions of deviance explained by the GLM for bout-modulated ROIs from each individual FOV (gray) and pooled across FOVs (black). Red dashed line indicates cut-off value for substantial deviance explained.

(E) Systematic exclusion of one predictor variable at a time from the GLM yielded estimates of relative explanatory value of that variable compared with the full model (difference in total deviance explained with versus without that variable; see STAR Methods). This revealed that velocity is a valuable predictor of afferent activity both for bout-activated and bout-suppressed ROIs. Values are mean ± SEM (activated: n = 983 ROIs from 14 FOVs in 6 mice; suppressed: n = 289 ROIs from 14 FOVs in 6 mice).

(F) Temporal profiles of mean GLM coefficient values for velocity averaged across all bout-activated (red, n = 983) and bout-suppressed (blue, n = 289) ROIs. Note that bout-suppressed ROIs show a sustained increase in activity that lags velocity by tens of seconds.

See also Figure S2 and Video S2.

This diversity of afferent sensitivities to locomotion could relate directly to the kinematics of mouse movement that couple mechanically to brain motion (i.e., locomotion velocity and acceleration) and/or to other latent variables indirectly coupled to the general state of locomotion. Thus, we first fit the fluorescence signal of each locomotion-activated or locomotion-suppressed ROI to a general linear model (GLM) using three predictor variables: running velocity, acceleration, and locomotion state (for example, Figure 2C; see STAR Methods). Overall, the activity time courses of 25%–100% (median: 78%) of running-bout-modulated ROIs were reasonably well fit by this model, suggesting that these ROIs track at least one of these predictor variables to some degree (Figure 2D). We further observed that locomotion velocity provided roughly equal explanatory power for activated and suppressed subpopulations of ROIs, that locomotion state was more informative for explaining the activity of suppressed ROIs, and that acceleration was generally uninformative (Figure 2E). For the suppressed subpopulation, velocity was negatively related to activity at short delays but, interestingly, exhibited a sustained positive relationship at longer delays from ~2 to 30 s (Figure 2F).

Locomotion drives sustained meningeal deformation

Locomotion is associated with increased intracranial pressure and with rigid and non-rigid brain motion related to stretch and compression driven by external forces applied to the brain, as well as forces related to vascular changes.^11–13 Given the known mechanosensitivity of trigeminal meningeal afferents,⁹ we reasoned that some of the activity we observed around bouts of locomotion might be driven by mechanical deformation of the meninges. Hence, we first assessed time-varying deformation in the meninges during natural behaviors. We obtained estimates of translation, scaling, and shearing along both anterior-posterior (A-P) and medial-lateral (M-L) axes (Figure 3A). We further calculated instantaneous translational speed (time derivative of translation), stretch (time derivative of scaling), and shear rate (time derivative of shearing).

Figure 3. Locomotion drives multiple forms of meningeal deformation across distinct time scales.

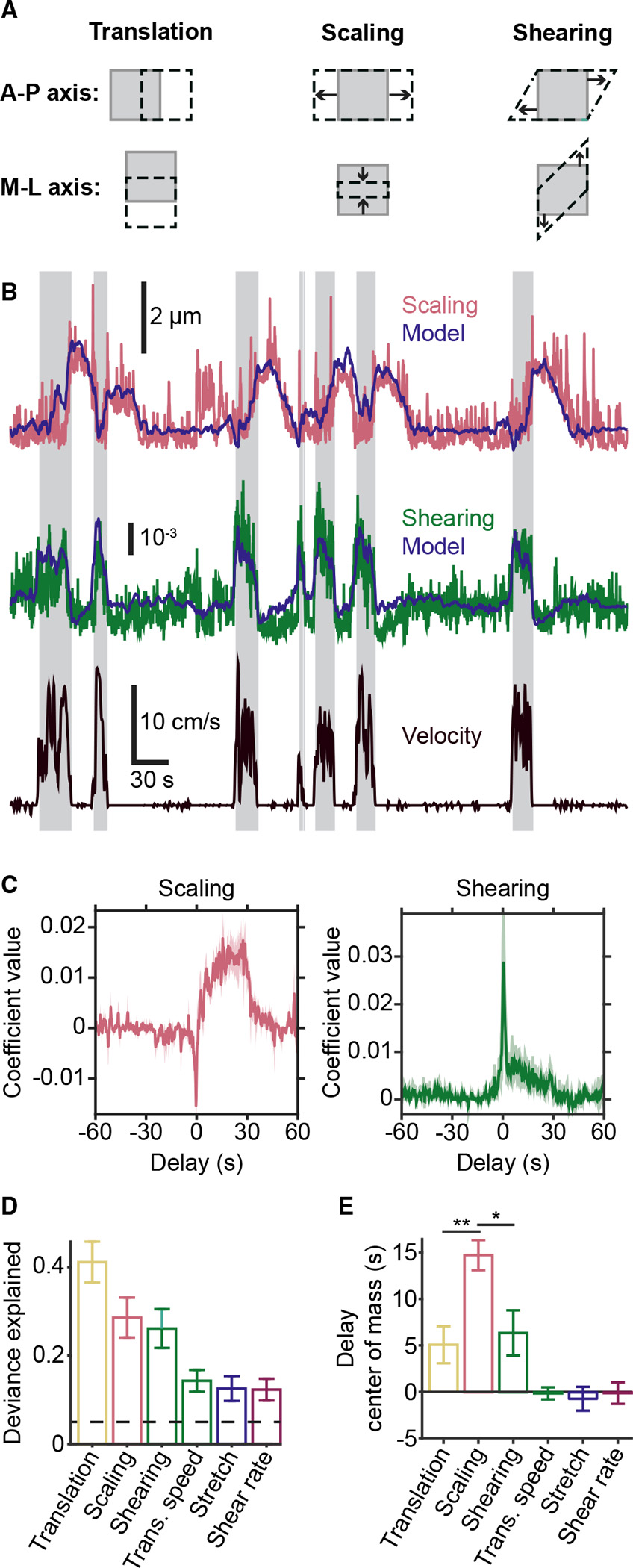
(A) Cartoons illustrating the three types of deformation measured by affine registration. Gray squares represent a FOV before deformation, and the black dashed shapes represent the FOV after deformation. The top row illustrates positive-valued deformations along the anterior-posterior axis, and the bottom row illustrates negative-valued deformations along the medial-lateral axis. Note: scaling deformations include expansion (top middle) or compression (bottom middle).

(B) Example of successful prediction of absolute magnitude of meningeal deformation (scaling and shearing) from a GLM based on locomotion variables. Shaded regions indicate locomotion bouts.

(C) Temporal profiles of GLM coefficients used to predict scaling (left) and shearing (right) from locomotion state. Traces indicate mean across all well-fit FOVs, and shaded regions indicate SEM.

(D) All forms of deformation are consistently well fit by this GLM. Dashed line indicates threshold for being considered well fit.

(E) Center-of-mass (COM) estimates of GLM coefficients across all delays indicate that locomotion drives scaling at a longer delay compared with other forms of meningeal deformation (ANOVA, p = 0.0056; translation versus scaling: **p = 0.0082; scaling versus shearing: *p = 0.0203, post hoc tests). Error bars for (D) and (E) represent mean ± SEM. n = 14 FOV from 6 mice. See also Figure S3.

We used a GLM to characterize the relationship between mouse locomotion parameters and meningeal movement and deformation measures (Figure 3B). All movement/deformation measures were well fit in most FOVs (9/14; Figure 3D), suggesting that various aspects of meningeal deformation are correlated, to some extent, with certain mouse movement parameters. Interestingly, different forms of deformation were observed at distinct delays relative to locomotion (Figures 3B, 3D, and S3B). For example, coefficients for meningeal shearing peaked near zero delay relative to locomotion and then gradually returned to baseline over subsequent delays up to ~30 s. In contrast, coefficients for meningeal scaling deformation exhibited a transient drop near zero delay, followed by a sustained elevation that decayed gradually to baseline after ~30 s (Figure 3C). Locomotion state was a stronger predictor of this scaling deformation than mouse velocity or acceleration, again consistent with the greater influence of locomotion state versus velocity on bout-suppressed afferents (Figure 2E). These data suggest that scaling deformation of the meninges may be driven by a latent variable associated with locomotion (Figure S3A), potentially related to direct mechanical forces produced by intracranial pressure elevations and/or meningeal vasodilation.¹²

Meningeal deformation may underlie locomotion-associated afferent activity

The delayed nature of the meningeal scaling deformation following locomotion was reminiscent of the rebound activation of running bout-suppressed meningeal afferents (Figure 2B). To more directly assess if locomotion-evoked local deformation and/or other variables associated with mouse locomotion could explain afferent activation, we considered both meningeal deformation and mouse locomotion as predictors of afferent activity using a GLM (Figures 4A and S4A). Indeed, 55% of the ROIs (n = 2,453/4,537) were well fit by this model (Figure S4B). We also determined that several distinct meningeal deformation variables helped explain afferent activity dynamics, that local scaling was the single most effective predictor (Figure S4C), and that the full combination of all meningeal deformation variables provided the most explanatory power by far (Figure S4D).

Figure 4. Locomotion-associated meningeal afferent activity is partially predicted by locomotion-induced deformation and encodes the direction of scaling.

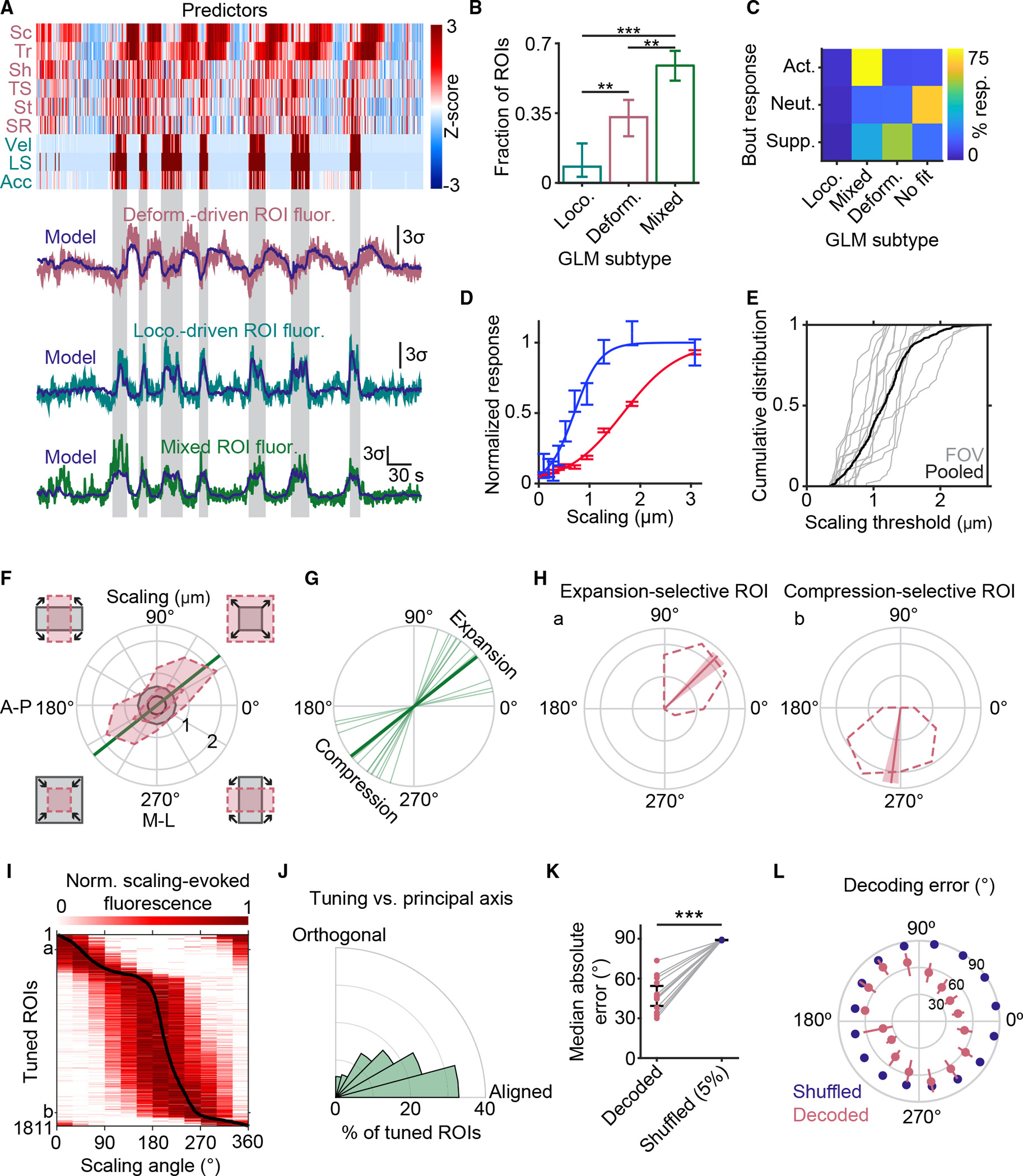
(A) Example data illustrating the three subtypes of afferent ROIs identified by a GLM. Top: standardized deformation predictors (pink labels; Sc, scaling; Tr, translation; Sh, shearing; TS, translation speed; St, stretch; SR, shearing rate) and locomotion predictors (teal labels; Vel, velocity; LS, locomotion state; Acc, acceleration). Bottom: examples of ROI subtypes identified by this model. Shaded regions indicate bouts of locomotion.

(B) Breakdown of the proportions of well-fit ROIs identified by the GLM as having activity time courses predicted by changes in locomotion (loco.), deformation (deform.), or a mix of both (mixed). p values: loco. versus mixed: p < 0.001; loco. versus deform., p = 0.0078; deform. versus mixed, p = 0.0058 (iterated, bootstrapped null hypothesis test). Values are mean ±95% confidence interval, n = 14 FOV from 6 mice.

(C) Breakdown of overlap between ROIs that were activated (n = 1,273), neutral (n = 2,843), or suppressed (n = 421) during locomotion bouts (rows) and their GLM-defined subtypes (columns).

(D) Two examples of afferent ROIs from the same FOV exhibiting sigmoidal relationships to meningeal scaling. Scaling thresholds (scaling magnitude at 50% of peak fitted response) were 0.7 and 1.7 μm (corresponding to 0.14% and 0.34% scaling of a ~500 × 500 μm² FOV) for the blue and red ROIs, respectively. Values are mean ± SEM.

(E) Cumulative distributions of scaling threshold values for all ROIs with sigmoidal stimulus-response curves (505 ROIs from 14 FOVs across 6 mice).

(F) Scaling was considered in polar coordinates, with cartoons outside each quadrant illustrating moments involving different combinations of expansion and/or compression along the anterior-posterior (A-P) and medial-lateral (M-L) axes (top right quadrant: expansion along both axes; bottom left: compression along both axes). This plot shows the angular distribution of the 95th percentile of scaling magnitude (outer dashed line) and 60^th percentile (inner dashed line) for each type of scaling. The annular region between the minima of these two dashed lines (i.e., the region between the two gray circles) indicates a subset of moments of scaling of approximately equal magnitude but spanning all directions. These moments were used to test for angular sensitivity of afferent responses to scaling. The straight green line indicates the principal axis of scaling for this FOV.

(G) Principal axis of scaling for each FOV. The thick line represents the axis from (F).

(H) Two example ROIs, from the same experiment as in (F), exhibiting tuning selectivity to scaling deformation along distinct angles, with preferential responses to uniform expansion along both axes (left ROI) or to compression along the M-L axis but not along the A-P axis (right ROI). Dashed curves represent mean fluorescence evoked by similar-magnitude scaling deformation at different angles (see also F). Solid lines indicate preferred tuning angle (from vector average), and shaded regions indicate 90% confidence intervals on preferred tuning angles.

(I) Heatmap with rows showing peak-normalized, scaling-evoked fluorescence tuning curves of all tuned ROIs (pooled across FOVs), sorted by preferred scaling angle (black curve). The letters “a” and “b” indicate the example ROIs in (H).

(J) Angular distribution of tuning angles relative to the principal axis of scaling. There was a significant bias in afferent tuning toward the principal axis of scaling (p < 0.001, bootstrapped one-way, two-tailed ANOVA).

(K) Maximum likelihood decoding of the angle of scaling deformation using population activity is significantly better than chance (p = 1.6 × 10⁻⁸, paired, two-tailed t test, n = 14 FOV) compared with the 5^th percentile of decoding estimates (lower percentile = better decoding) across all shuffles of the real data. This indicates that meningeal afferents contain information about the direction and nature of scaling deformations. Values are mean ± SEM.

(L) Analysis of the error in maximum likelihood decoding for each scaling angle (mean ± SEM across all 14 FOVs, red). 5^th percentile error in decoding across shuffles (blue) is also presented for comparison. Note that A-P and M-L meningeal expansion (0° and 90°, respectively) can each be decoded above chance using population afferent activity.

See also Figures S4 and S5.

We then determined the apparent selectivity of each ROI to aspects of meningeal deformation and/or mouse locomotion by identifying ROIs where a good fit depended on the inclusion of deformation variables (deformation-sensitive afferents) and/or locomotion variables (locomotion-sensitive afferents). Among the 2,453 well-fit ROIs, most were either purely deformation sensitive (32.7%) or exhibited mixed sensitivity to both local deformation and locomotion (61.6%), while only 5.8% were considered purely locomotion sensitive (Figure 4B). Notably, afferents initially classified as activated by locomotion (Figure 2) were mainly of the mixed-sensitivity type, while those initially classified as suppressed by locomotion were more often of the deformation-only type (Figure 4C; likely due to their sensitivity to the delayed scaling deformation that followed locomotion; Figures 2B, 2F, and 3C). Taken together, these findings indicate that local meningeal deformations—in particular, scaling (i.e., expansion/compression in A-P and/or M-L)—are strongly predictive of (and may directly contribute to) the activation of certain afferents during locomotion and quiet wakefulness but that other physiological variables also likely contribute to locomotion-related afferent activation.

To further explore the relationship between afferent responses and meningeal deformation, we investigated stimulus-response relationships as described previously between mechanical indentation of the dura and dural afferent activity in anesthetized animals with exposed meninges.¹⁴ We focused on deformation-sensitive and mixed-sensitivity units and obtained sigmoidal fits of their activity as a function of the instantaneous magnitude of local meningeal scaling deformation (Figure 4D). A variable fraction of ROIs in each FOV (0–51%, median: 22%) exhibited activity that increased sigmoidally with increasing scaling deformation magnitude. Notably, afferents exhibited diverse stimulus-response curves and sensitivity thresholds (Figures 4D and 4E), with a median sensitivity threshold of ~1 μm (corresponding to a ~0.2% scaling of the FOV). These findings demonstrate distributed coding of meningeal deformations by this set of meningeal afferents, which could enhance the dynamic range of sensitivity to both small and large mechanical deformations.

Afferent population activity encodes the angle of scaling deformation

Given the predictive power of local meningeal scaling in explaining meningeal afferent activation, we investigated this deformation variable in greater detail. While the above analyses focused only on the absolute magnitude of scaling, our image registration approach produced separate estimates of scaling along the A-P and M-L axes, each of which yielded both positive values (expansion) and negative values (compression) at each time point. Therefore, the mechanical scaling of the meninges at any given moment can be represented in polar coordinates as a point on a 2D plane specified by a magnitude and an angle (Figure 4F). For example, a 45° scaling represents equal expansion along the A-P and M-L axes, while a 135° scaling represents simultaneous compression along the A-P axis and expansion along the M-L axis. In each FOV, the angular distribution of scaling values was not uniform. Instead, both A-P and M-L axes typically underwent expansion or compression simultaneously but with some variability in the degree of scaling in A-P versus M-L (Figures 4F and 4G; concurrent compression and expansion along different axes was less common and of smaller magnitude).

Given that scaling was consistently biased toward concurrent A-P and M-L expansion or compression, we wondered whether meningeal afferents exhibited differential sensitivity to different proportions of expansion/compression along the A-P versus M-L axes (Figure 4F). We, therefore created tuning curves of the average activity at each angle (excluding time points with very large or small net scaling amplitudes; see STAR Methods). For every afferent identified as putatively mechanosensitive in the previous analyses, we calculated an angle selectivity index (ASI) and a preferred angle. Afferents with ASI >0.5 and preferred angles with 95% confidence intervals narrower than 60° exhibited angular tuning (Figures 4H and S5A). Strikingly, 82% (1,887 of 2,312) of the mechanosensitive ROIs exhibited angular tuning.

While preferred angles spanned the full 360° range (Figure 4I), many ROIs were preferentially activated by deformations involving concurrent compression or expansion along both axes—angles that align with the most common axis of scaling deformation in each FOV (Figure 4J). Notably, the physical orientation of each ROI mask (i.e., elongation) within the imaging plane did not confer any particular sensitivity to scaling along that axis (Figure S5B).

The existence of a substantial population of ROIs exhibiting angular tuning suggested that meningeal afferents may encode information about the anatomical direction (i.e., A-P or M-L axis) and valence (compression or expansion) of meningeal deformation. To test this, we attempted to decode the angle of mechanical scaling using afferent population activity alone. Using a maximum-likelihood approach (see STAR Methods), we found that the angle of meningeal scaling deformation could be inferred from the population neuronal activity with accuracy that greatly exceeded chance (Figure 4K). Moreover, decoding accuracy was significantly above chance for nearly all angles (Figure 4L). Notably, performance was best for moments of pure expansion or compression and poorer for moments of mixed scaling, presumably due to the aforementioned enrichment of afferents exhibiting tuning along the most common axis of scaling. Thus, meningeal afferents exhibit diverse angular sensitivities but are differentially sensitive to the axis of naturalistic meningeal deformation and to the expansive or compressive nature of this scaling.

Meningeal afferents respond to locomotion-induced meningeal z-motion

We next performed similar experiments using volumetric imaging (Figure 5A; Video S3). We corrected for small motions along the z-axis for every plane in each acquired 3D volume,¹⁵ which provided a measure of how much each plane moved up or down relative to a reference volume (“z-shift”). In this way, volumetric imaging enabled near-simultaneous 3D quantification of deformation and afferents’ activity (Figure 5B).

Figure 5. Volumetric imaging of afferent activity and deformation at different depths within the meninges.

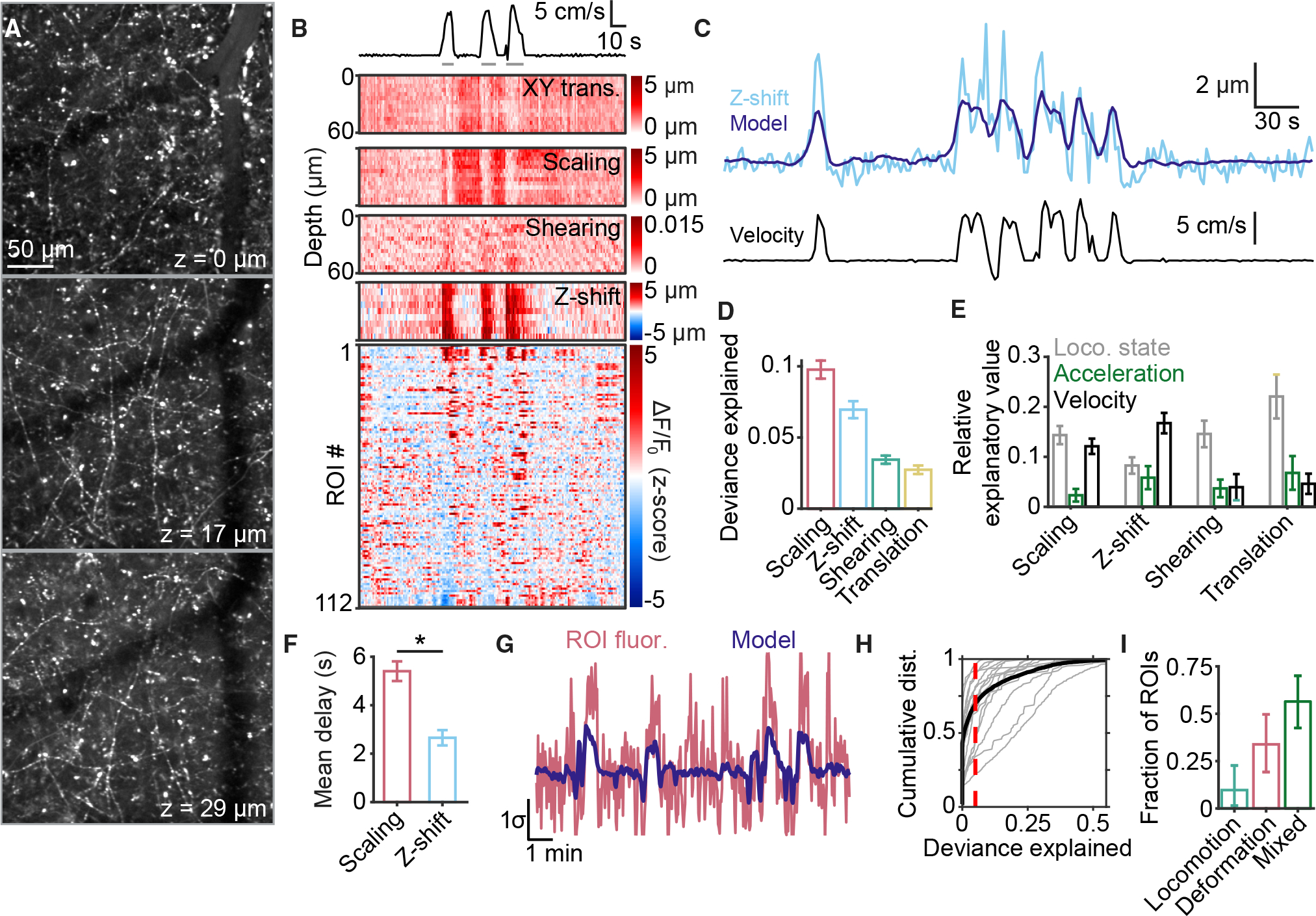
(A) Multiple layers of afferents are visible at different depths throughout the thickness of the meninges. Z-values increase with depth relative to the most superficial plane imaged.

(B) Example data showing simultaneous afferent activity (bottom heatmap) and meningeal deformation parameters (top heatmaps) during quiet wakefulness and locomotion (trace at top; gray lines indicate locomotion state).

(C) Comparison of observed z-shift (top, light blue) and the prediction (top, dark blue) of GLM trained on mouse locomotion parameters, including velocity (bottom).

(D) Scaling and z-shift were consistently well fit by a GLM trained on locomotion parameters. Values are mean ± SEM.

(E) Breakdown, for each form of deformation in (D), of the relative explanatory value of each locomotion parameter. Values are mean ± SEM.

(F) GLM coefficients for z-shift were concentrated at earlier temporal delays from locomotion compared with scaling (p = 0.0199, paired t test). Values are mean ± SEM.

(G) Example of a fluorescence trace (red) extracted from a 3D ROI that was well fit by a GLM (dark blue line) based on locomotion and meningeal deformation data.

(H) Cumulative distribution of deviance explained by the GLM for all ROIs from each experiment (gray) and pooled across experiments (black). Dashed line indicates threshold for being considered well fit.

(I) Comparison of the proportions of well-fit ROIs identified as locomotion sensitive, deformation sensitive, or of mixed sensitivity. Values are mean ± 95% confidence interval.

n = 16 FOV from 7 mice for (D)–(F), (H), and (I). See also Figure S6 and Video S3.

Locomotion was consistently accompanied by a positive z-shift of similar amplitude across all imaging planes, indicating movement of the meningeal sheet toward the skull, consistent with the rapid increase in intracranial pressure observed in mice during locomotion.¹² Similar to the above analyses of mechanical deformation using the 2D dataset, we fit seven deformation measures with a GLM using velocity, acceleration, and locomotion state as predictors (Figure 5C; each plane was fit separately). Scaling and z-shift were consistently well fit (Figure 5D). Interestingly, z-shifts were primarily explained by concurrent increases in mouse locomotion velocity (Figure 5E) and tracked locomotion with shorter delays compared with scaling (Figure 5F), suggesting a direct coupling to body movement.

We used a GLM to predict each afferent’s activity using meningeal deformation and mouse locomotion variables (Figure 5G), analogous to earlier analyses (Figure 4A). Overall, 30% (931/3,085) of ROIs were well fit by this model (Figure 5H). The proportion of well-fit afferents sensitive to locomotion and/or deformation was similar to that observed for the 2D dataset (Figure 5I versus Figure 4B). These proportions match despite the fact that the 3D datasets were corrected for minor z-shifts prior to GCaMP6 fluorescence time course extraction. This insensitivity of our 2D imaging results to minor z-shifts is likely due to the sparsity of GCaMP6-expressing dural afferents and the large two-photon imaging point spread function along the z-axis.

The minor z-shifts in the meninges were the single strongest predictor of afferent activity for deformation-sensitive afferents and the second strongest for mixed-sensitivity afferents (Figure S6). These results suggest that the movement of the meningeal tissue toward the skull during locomotion may be a potent driver of afferent activation but that there is sufficient redundancy between this z-shift and other x-y deformation variables such that mechanosensitive units can be identified with similar accuracy using both 2D and 3D imaging strategies.

DISCUSSION

Activation of meningeal sensory neurons is considered to play a key role in mediating headaches of intracranial origin, including during migraines.^5–7 However, very little is known about the function of these sensory neurons under normal physiological conditions. Here, we used adeno-associated virus (AAV)-mediated expression of a calcium indicator in trigeminal primary afferent neurons, followed by single-plane and volumetric two-photon calcium imaging of the meninges under normally pressurized conditions, to characterize the activity dynamics of individual meningeal afferent fibers in awake, behaving mice. We observed low levels of spontaneous calcium activity during quiet wakefulness in a subset of meningeal afferents and further discovered afferent subpopulations that were highly sensitive to locomotion and/or distinct mechanical deformations of the meninges. These findings suggest that, in addition to mediating headache, a subpopulation of mechanosensitive meningeal sensory neurons also monitor the mechanical state of the meninges under normal, innocuous conditions. In the future, this approach can be used to study these diverse potential roles for the meningeal sensory system in monitoring other interoceptive mechanical signals and maintaining homeostasis, as well as the potential sensitization of these afferents as a driver of migraine headache.⁶

Locomotion drives meningeal deformation

Our data suggest that during locomotion, the meninges undergo significant deformations—specifically, scaling and shearing—that produce localized intracranial forces that are likely sensed by mechanosensitive meningeal afferents. Interestingly, these deformation variables exhibited distinct time courses. x-y shearing and z-shifts closely tracked locomotion velocity, while scaling deformations ramped up slowly and often persisted for tens of seconds after the offset of locomotion. The slower change in scaling during locomotion may be driven, at least partially, by the slow recovery dynamics of the meningeal vascular response to voluntary locomotion.¹² Mechanical properties of the meninges related to stiffness and a slower relaxation rate¹⁶ may also play a role.

Meningeal afferents sense and encode meningeal deformation

In previous studies, meningeal afferent mechanosensitivity has been characterized using punctate stimuli applied to the exposed dura mater, which elicits a compressive strain.⁹ These studies revealed a range of thresholds mostly above the normal range of physiological intracranial pressure fluctuations, suggesting a purely nociceptive function.^9,14 However, the meningeal deformations we observed during locomotion in mice with a closed cranial window instead produce tensile loads. Studies on cutaneous nociceptors indicate that activation thresholds for tensile loads are an order of magnitude lower than for compressive loads.¹⁷ It is also possible that a subset of the afferents that respond to meningeal deformations are A-type low-threshold mechanoreceptors (A-LTMRs) with unencapsulated Ruffini-like endings.^18,19 The finding of a diversity of meningeal scaling sensitivity thresholds with a median threshold of ~0.2% points to an extremely sensitive sensory system capable of responding to naturalistic mechanical deformation. Additionally, the apparent sensitivity to small z-shifts further suggests that mechanosensitive meningeal afferents may also sense volumetric changes in the intracranial space, potentially related to normal intracranial pressure elevations during locomotion.¹²

The changes we observed in afferent calcium activity and meningeal deformations during locomotion are unlikely to produce painful sensations. However, during migraines, amplification of such responses could mediate the exacerbation of the headache pain during physical activity and minor movements, such as sneezing or coughing, that are likely to produce meningeal deformations but are normally innocuous.²⁰ Amplification of afferent mechanosensitivity at peripheral terminals (i.e., peripheral sensitization) has been suggested to play a key role in mediating the intracranial hypersensitivity in migraines.⁶ However, given the exquisite mechanosensitivity of these afferents under non-pathological conditions, amplification of the afferents’ signals at the level of the CNS (i.e., central sensitization)²¹ may be sufficient to produce this pain response.

In addition to detecting the magnitude of scaling deformations, meningeal sensory afferents also appear to encode the general orientation (M-L or A-P) and sign (expansion or compression) of scaling. This finding suggests a role for meningeal afferents as primary interoceptive sensors engaged in proprioception and/or vestibular sensing, potentially preventing meningeal damage by signaling abnormal meningeal stretch during rapid head movements. Such sensors may also become engaged during concussions and more severe head impacts. Moreover, abnormal activation of these sensory neurons during migraine or head impact may explain the relationship between migraine or head injury and dizziness and other vestibular symptoms.²² The neural pathways responsible for these functions remain to be established but may involve direct inputs from trigeminal dural afferents to nuclei in the parabrachial complex that process nociceptive and other interoceptive modalities.²³

Technical considerations and study limitations

The ability to track meningeal afferent activity across weeks using our approach will allow longitudinal testing of the effects of various models of headache and pharmacological treatments, similar to preparations used for long-term imaging of neurons in the CNS (e.g., Andermann et al.,¹¹ Burgess et al.,²⁴ and Lutas et al.^11,24,25). The chronic cranial window approach we employed with a large FOV (~7 mm²) allowed us to locate and image numerous meningeal afferent fibers in each mouse. This approach produces minimal inflammatory responses in the cortex²⁶ and meninges (Figure S1A) below the window when assessed during the period when we imaged meningeal afferent activity. The very low level of afferent activity during quiet wakefulness further points to a lack of afferent sensitization associated with an inflammatory response.

Our analyses depend on using GLMs to identify which of the sets of locomotion and/or deformation variables are most useful for predicting response variables (deformation or neural activity). While this modeling was often successful, it must be noted that this approach cannot definitively establish causality. For instance, while it is well known that mechanosensitive fibers innervate the cranial meninges, it remains possible that some of the apparent mechanosensitivity we observed was actually due to a correlation between deformation and other variables (e.g., meningeal vasomotion, intracranial pressure changes) that were not considered in the model. Conversely, it is also possible that some high-threshold mechanosensitive afferents were not driven strongly enough by spontaneous locomotion to be detected but that a more substantial local deformation would have activated them. Future studies could combine the imaging of afferent activity during natural meningeal deformations with pharmacological or genetic manipulations to disentangle contributions of mechanosensitive ion channels (i.e., Piezo2) and neurotransmitter release (i.e., nitric oxid) during locomotion that might underlie the afferent responses.

STAR★METHODS

RESOURCE AVAILABILITY

Lead contact

Requests for information or resources should be directed to the lead contact, Dan Levy (dlevy1@bidmc.harvard.edu).

Materials availability

This study did not generate any new reagents.

Data and code availability

The code used to analyze locomotion data is available at: https://github.com/ablaeser/LocomotionAnalysis. Code for organizing and processing two-photon imaging data is available at: https://github.com/ablaeser/MovieProcessing. The code for analysis of calcium imaging is available at: https://github.com/ablaeser/CalciumAnalysis. Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Male and female C57BL/6J adult mice were used for calcium imaging. Nav1.8Cre:: B6.Cg-Gt(ROSA)26Sor^{tm6(CAG-ZsGreen1)Hze}/J (Ai6(RCL-ZsGreen)) transgenic mice were used as controls. Mice were group housed in standard conditions before stereotaxic injection. After AAV injection, mice were singly housed and provided a running wheel, a hut, and a chew bar. Experimental procedures were approved by the Beth Israel Deaconess Medical Center Institutional Animal Care and Use Committee.

METHOD DETAILS

Viral injection

Mice (8–10 weeks) were anesthetized by isoflurane in 100% O2 (induction, 3%–5%; maintenance, 1.5%–2%) and placed on a heating pad (CWE) in a stereotaxic apparatus (KOPF). A 1 × 1 mm² square craniotomy was made 1–2 mm lateral to and 0–1 mm anterior to Bregma on the right hemisphere. To label meningeal afferent axons, 2.0 μL of AAV5.CAG.GCaMP6s.WPRE.SV40 (titer: 1 × 10¹³; Addgene,²⁹) was stereotactically injected into the left TG at 1.5 mm lateral and 0.3–0.8 mm anterior to Bregma and 7.0–7.2 mm ventral to the dura, at a lateral-to-medial tilt with an angle of 22.5° relative to the dorsal-ventral axis (see Figure 1A). The scalp was then stapled closed, and the mouse was moved to a post-surgery single-housing cage with enrichment for recovery.

Immunohistochemistry

To verify GCaMP6s expression in TG somata and meningeal afferents, 8 weeks after AAV injection, mice were given a lethal dose of urethane (2 g/kg) and perfused transcardially with 0.025% heparin in PBS, followed by 4% paraformaldehyde (PFA). Mice were decapitated, and heads were postfixed in 4% PFA at 4°C for 24 h. The skull cap was cut, and meningeal whole mounts were prepared by dissecting it from the skull cap using fine surgical forceps. The TGs were also harvested and transferred to 30% sucrose in PBS for cryoprotection (24–48 h) before being embedded in OCT (Fisher Scientific), rapidly frozen over dry ice and 20 μm cryosections, cut on a cryostat (Leica) and washed 3 times with PBS. Wholemount meninges were blocked and permeabilized for one hour at room temperature in 24-well plates with PBS with 0.2% Triton X-100 and 2% chicken serum. Meningeal whole mounts were then incubated with rabbit anti-CGRP (cat. C8198, Sigma, St. Louis, MO, USA) and chicken anti-GFP (cat. AB13970 Abcam, Waltham, MA, USA) at 4°C for 24 h, washed three times with PBS with 0.2% triton-X and incubated with a goat anti-rabbit IgG-Alexa 594 (Invitrogen, Cambridge, UK), and rabbit anti-chicken IgG-Alexa 488 (Jackson Immunoresearch, West Grove, PA, USA) at room temperature for two hours and washed again three times in PBS. TG sections and meningeal whole mounts were mounted on Superfrost Plus slides (Fisher Scientific) and coverslipped with Fluoromount-G (electron microscopy sciences). Immunofluorescence was acquired using a confocal microscope (Zeiss LSM880/Imaris 9.8.2).

Headpost and cranial window implantation

Six weeks after viral injection, a headpost and cranial window were implanted using a previously described protocol.²⁶ Briefly, mice were given 0.03 mL of dexamethasone (4 mg/mL, i.m.) 3 h before surgery to reduce inflammation. Mice were anesthetized using isoflurane in 100% O₂ (induction, 3%–5%; maintenance, 1.5%–2%) and placed on a heating pad in a stereotaxic apparatus. Opthalmic ointment (Vetropolycin) was applied to the eyes. A two-pronged headpost was affixed to the skull, centered roughly 1.5 mm lateral and 2 mm posterior to Bregma over the left hemisphere. A circular craniotomy (3 mm diameter) was performed at the center of the headpost to expose the dura. A compound coverglass composed of 4 #1 coverslips (3 × 3 mm below 1 × 5 mm) was inserted into the craniotomy and affixed to the skull with Vetbond (3M) and C&B Metabond (Parkell) to form a permanent seal. A neodymium ring (Indigo Instruments) was glued to the headpost to create a low-profile adaptor to accommodate the water-immersion objective and light shielding made from blackout fabric (Thorlabs). Meloxicam SR (4 mg/kg, s.c.) was administered, and the mouse was allowed to recover.

This craniotomy could conceivably impact the maintenance of homeostatic intracranial pressure or cerebrospinal fluid circulation. However, while these variables were not monitored in these experiments, we previously found that normal intracranial pressure was maintained several weeks after an even more invasive procedure (deep brain implant of a 3-mm cannula; data not shown), justifying our assumption that intracranial pressure is relatively normal during our experiments. Furthermore, these mice were imaged ~8 weeks after the window surgery, so it is unlikely that intracranial pressure changed dramatically over the 2 h imaging sessions. Finally, the cranial window strategy is clearly superior in this regard to the open skull preparation that represented the primary method for monitoring meningeal innervation in vivo prior to this study.

Wheel training

After the cranial window surgery, mice were allowed to recover for at least a week. To habituate the mice to head fixation and wheel running, mice received multiple wheel training sessions (10 min to 1 h over 3–4 days). In each session, the mouse was placed on a 3D printed running wheel, with its headpost attached to two clamps, and allowed to locomote freely. Care was taken to minimize movement-related forces on the headpost and skull that might not occur in untethered mice. Of note, forward forces during locomotion were mitigated by the freely-turning wheel, while forces due to the mouse pushing upwards against the headpost were reduced by mounting the wheel on a cantilever (see³⁰). Moreover, the strong cement used to bind all skull plates and headpost together²⁶ further mitigated any movement-induced strain on the skull. Mice displaying signs of stress were immediately removed from head fixation, and additional habituation days were added until mice tolerated head fixation without visible signs of stress.

Two-photon imaging

Starting at 8 weeks after AAV injection, calcium imaging was performed using a Nikon 16X, 0.8 NA objective on a resonant-scanning two-photon microscope (Neurolabware), acquiring 796 × 512 pixel images at 15.5 Hz. A MaiTai DeepSee laser, set to 920 nm with 25–40 mW power, was used to excite fluorescence. Emitted light was filtered (510/84 nm, Semrock) and measured with a photomultiplier tube (H10770B-40; Hamamatsu). The Scanbox package for MATLAB (Neurolabware) was used to control the microscope and acquire images and wheel running data. Digital zoom was set at 2X or 2.4X (751 × 483 μm² or 626 × 423 μm² FOVs, respectively). Some experiments were performed using 60 μm thick, volumetric imaging of the meninges, using an electrically tunable lens (Optotune), imaging either 15 or 30 planes spanning this range of depths, resulting in effective sampling rates of 1.03 or 0.52 volumes/s, respectively. Each experiment consisted of at least two 30-min runs of continuous imaging. Vascular imaging (Figure S1D) was conducted 30 min after retro-orbital administration of a 2 MDa FITC-Dextran tracer (50 μL, 50 mg/mL; Sigma-Aldrich), 2–6 weeks after window surgery.

QUANTIFICATION AND STATISTICAL ANALYSIS

Locomotion signals

Wheel position during each imaging run was recorded using an Arduino Uno board at 15.5 Hz. The instantaneous velocity was calculated as the time derivative of this signal and convolved with a Gaussian kernel (standard deviation 0.26 s, total width 1 s). For 3D imaging, velocity was downsampled to match the sampling rate of volume scans. Acceleration was calculated as the derivative of velocity. To infer the locomotion state, we first concatenated all velocity signals obtained from a given mouse across all experiments and trained a two-state Hidden Markov Model using the MATLAB function ‘hmmtrain’. Then, the locomotion state was inferred for each individual imaging run by applying the MATLAB function ‘hmmviterbi’ with the model trained on the concatenated data. Locomotion bouts were defined as periods when the locomotion state was sustained for at least two seconds.

Image processing and signal extraction

All image processing and analyses were performed in MATLAB 2020a (Mathworks) and ImageJ (FIJI, NIH).

Image analysis for 2D imaging datasets

For single-plane experiments, all imaging runs were concatenated into a single movie. A reference image was defined as the mean projection over the middle 50% of frames from either the first run (for two-run experiments) or the second run (for four-run experiments). Each frame of the concatenated movie was then affine registered to the reference using the TurboReg plugin for ImageJ. In some cases, histogram equalization was used to improve registration results. The registered movie was analyzed using a PCA/ICA package¹⁰ to extract masks of pixels with correlated activity. Users then screened each prospective region of interest (ROI) for quality of morphology and fluorescence signal. In cases where at least 50% of one ROI’s pixels overlapped with another ROI, the two ROIs were merged. Otherwise, overlapping pixels were excluded from both ROIs. In some cases, excluding overlapping pixels had the effect of cleaving a single putative ROI into two ROIs, as ROIs were always required to be contiguous. After the above steps, ROIs smaller than 50 pixels were rejected. For each ROI included in subsequent analyses, a dilated mask extending from 8–21 pixels from the outer edge of the ROI, excluding any pixels that belonged to another ROI, was generated as a “neuropil” ROI for subtraction of background neuropil signal (see below).

Image analysis for 3D imaging datasets

For 3D experiments, each run of volumetric data was independently subjected to several preprocessing steps as described in.¹⁵ First, the lensing effect due to the electrically tunable lens was estimated from a sample volume generated by temporal mean projection across 30 acquired volumes. This correction was then applied to all volumes. Second, rigid registration using the discrete Fourier transform was used to correct for within-volume translations and translations along the z-axis. Next, z-interpolation was used to correct for z-translations of individual imaged planes within each volume. The corrected data from each run was then aligned to the second run, and all runs were concatenated into a single 3D movie.

The concatenated data for each plane of the 3D volume was then affine registered in a manner similar to the 2D case: a reference volume was formed from the mean projection of the middle 50% of frames from the second run, and all images from a given plane were independently registered to the corresponding plane of the reference volume. Volume imaging raised the issue that images obtained from the superficial planes are acquired at a substantial delay relative to those from deep planes. Each plane of each volume was therefore subjected to linear interpolation (using the same plane from the prior and following volumes) to correct for this delay across planes.

A mean projection over all planes containing afferents was then generated for each volume, and the resulting 2D movie was run through the same PCA/ICA procedure previously described, yielding an initial set of 2D masks that represented putative 3D ROIs (this was a reasonable approach given the sparsity of active afferents). An initial fluorescence trace extracted from each 2D mask was calculated by averaging fluorescence across all pixels in the mask. To identify which voxels in the original volumetric dataset contributed most strongly to each fluorescence trace, we calculated the Pearson correlation of this trace with the fluorescence time course of each voxel, resulting in a 3D volume of correlation values. These 3D correlation volumes were then screened manually, as in the 2D case, based on the quality of morphology and signal. The surviving volumes were thresholded at the value of the 75^th percentile of correlation across all voxels to form putative 3D ROI masks (“ROIs”). As in the 2D case, putative ROIs with overlapping voxels were either merged or trimmed depending on the extent of overlap so that no voxel was shared by two ROIs. Sets of non-contiguous voxels were split into separate ROIs. Finally, ROIs with fewer than 50 voxels were rejected. For each afferent ROI, a corresponding neuropil ROI was generated from a shell of voxels extending 8–21 pixels from the surface in the XY dimensions and 2–3 planes above and below in the Z dimension, excluding voxels belonging to other afferent ROIs. Background subtraction with the neuropil signal and all subsequent processing of fluorescence signals was identical to the 2D case.

Deformation signals

Estimates of meningeal translation, scaling, and shearing were extracted from the affine transformation matrices. Translation and scaling were converted from pixels to microns. Their first-order time derivatives were also calculated using the difference between neighboring frames at 15.5 Hz for 2D data and the difference between adjacent volume scans at 1.03 Hz or 0.51 Hz for volumetric data.

Fluorescence signals

The raw fluorescence signals at each time point for the i^th ROI (Fⁱ_ROI) and its corresponding neuropil shell (Fⁱ_np), were calculated as the simple arithmetic means of all pixels/voxels within each ROI mask. Next, we calculated Fⁱ = Fⁱ_ROI − Fⁱ_np + <Fⁱ_np>, where brackets denote temporal averaging. Then we calculated the corresponding baseline signal Fⁱ₀ as the 10^th percentile of a moving window for the previous 32 s.³¹ We then calculated the normalized, baseline subtracted time series ΔF/F₀ = (Fⁱ − Fⁱ₀)/Fⁱ₀. This signal was standardized akin to a z-score operation by subtracting the median value and dividing by the standard deviation (calculated during quiet wakefulness, an epoch with low levels of evoked activity). Fluorescence events were defined as periods where the signal consistently exceeded a value of 1 for at least one second and where the maximum ΔF/F₀ within the event exceeded 5%.

Identifying afferent fibers

Sets of ROIs putatively belonging to the same axon were initially identified using the custom MATLAB function MergeROI3D, available in the GitHub repository. Briefly, following the approach of Liang et al.³² we calculated the pairwise fluorescence event correlation between ROIs during quiet wakefulness, thresholding at 0.7 correlation. We then calculated the cosine dissimilarity between the full set of correlation coefficients for each pair of ROIs, which in turn was used to calculate the linkage between each pair. Finally, hierarchical clustering was performed using a cutoff value of 2. This procedure generated sets of ROIs that were mutually highly correlated but not necessarily corresponding to the same fiber. For example, it often picked up ROIs from the same putative axonal arbor but from different branches. Therefore, we visually inspected each cluster and manually identified the subsets of ROIs that unambiguously covered the same specific afferent fiber without any branching.

General linear models

Gaussian general linear models for deformation and fluorescence were fit using the glmnet package, with elastic net regularization (α = 0.01) and ten-fold cross-validation. All signals were downsampled to 5.16 Hz (for 2D data) or 0.516 Hz (for 3D data). To allow for the possibility of a delay between the predictor and response, we expanded the set of predictors.^30,33 Specifically, for each basic predictor (e.g., velocity), we generated a set of temporally shifted versions spanning a time window from −4 s to +4 s. For models that relied solely on locomotion-related predictors, the time window was set to −60 to 60 s instead to capture the long delay between locomotion and fluorescence or some forms of deformation. These sets of arrays of temporal shifts for each predictor were joined to form an array of temporally shifted predictor signals. Fitting was performed on 75% of the data and tested on the remaining 25%. The training subset was drawn from 20 evenly spaced periods. We then applied the GLM coefficients to the testing data to calculate the deviance explained by the model. The relative explanatory value of each predictor, or family of predictors, was calculated by refitting the GLM after excluding one predictor or family of predictors (including all its temporal shifts) and then calculating 1–(deviance explained by the reduced model)/(deviance explained by the full model). Every predictor yielded a series of coefficients corresponding to each temporal shift. To characterize the delay between predictor and response, we calculated the centroids of the absolute value of this series of coefficients.

Angular tuning analysis

For each frame, TurboReg produced estimates of scaling along the anterior-posterior (X) and medial-lateral (Y) axes. Positive values correspond to expansion, and negative values correspond to compression. Thus, each frame’s instantaneous, signed scaling was represented as a point on the Cartesian plane. Each point was converted to polar coordinates. For all FOVs, we found that scaling distribution was not uniform across angles. Therefore, we sought to identify a subset of time points for which scaling values were relatively uniformly distributed in angle and of sufficient magnitude to plausibly activate the fiber. To do so, we first divided the full set of scaling values into 30° bins. Within each bin, we calculated the 60^th and 95^th percentile magnitudes. The set of all scaling values that fell between the minimal 60^th percentile value and the minimal 95^th percentile value was defined as the test range used to assess each ROI’s sensitivity to the scaling angle. All values below the lower limit of the test range were considered baseline time points. Next, for each ROI, we gathered the set of fluorescence values in the test range and subtracted the mean baseline value. The mean scaling-evoked response for each angular bin was then calculated as the mean of baseline-subtracted fluorescence values. Any negative mean responses were set to zero. The ROI’s preferred angle was calculated as the angle of the resultant vector obtained from adding all mean scaling-evoked response vectors. The axis selectivity index was defined as: ASI = (magnitude of resultant vector)/(sum of magnitudes of responses across all angular bins). The 95% confidence interval for the preferred angle was calculated from bootstrapping (500 resamplings, with replacement, of the mean scaling-evoked response). All scaling values (in Cartesian coordinates) were entered into a principal component analysis (MATLAB’s ‘pca’ function), and the first component was defined as the principal axis.

Decoding scaling angle from fluorescence

Maximum likelihood decoding of scaling angle was performed using a custom MATLAB function, ‘DecodeDirection.m’. Briefly, all scaling and fluorescence data for a given FOV was binned by angle (22.5° bins) and divided into training and testing subsets (75% and 25% of data, respectively). The probabilities p(F), p(θ_bin), and conditional probability p(F|θ_bin), where F is the set of fluorescence values from all ROIs for a given frame, and θ_bin is the bin of scaling angle for that frame, were estimated from training data under the simplifying assumption that each ROI’s fluorescence was independent. Subsequently, for each frame of the testing data, we applied Bayes’ theorem: p(θ_bin|F) = p(F|θ_bin) p(θ_bin)/p(F), and read off θ_est as the angle with the highest probability across all values of θ_bin. Median absolute error was calculated as MAE = median(|θ−θ_est|).

Statistics

All analysis was performed in MATLAB 2020a. Sample sizes were not predetermined by power analysis but are similar to previous studies.³¹ Parametric hypothesis tests, such as t-tests and ANOVA, were performed using native MATLAB functions. Bootstrapped confidence intervals and hypothesis tests were generated using the ‘iboot’ iterated bootstrapping package. p-values are indicated as follows: p ≤ 0.05 (*), p ≤ 0.01 (**), and p ≤ 0.001 (***).

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Rabbit anti-CGRP	Sigma-Aldrich	Cat#C8198; RRID:AB_259091
Chicken anti-GFP	Abcam	Cat#13970; RRID:AB_300798
Goat anti-Rabbit IgG-Alexa 594	Invitrogen	Cat#11012; RRID:AB_2534079
rabbit anti-chicken IgG-Alexa 488	Jackson Immunoresearch	Cat# 303-545-003; RRID:AB_2339327
Bacterial and virus strains
AAV5.CAG.GCaMP6s.WPRE.SV40	Addgene	Cat#100844
Chemicals, peptides, and recombinant proteins
FITC Dextran-2M Da	Sigma-Aldrich	Cat# 2000S
Experimental models: Organisms/strains
Mouse: wild-type: C57BL/6J	The Jackson Laboratory	JAX:000664
Mouse: Ai6: B6.Cg-Gt(ROSA)26Sortm6(CAG-ZsGreen1)Hze/J	The Jackson Laboratory	JAX:007906
Mouse:Nav1.8Cre: Scn10atm2(cre)Jnw	Nassar et al.27	MGI:3053096
Mouse: NaV1.8Cre/+:: Ai6fl/wt	This paper	N/A
Software and algorithms
ImageJ	NIH	RRID:SCR_003070
MATLAB 2020a	Mathworks	RRID:SCR_001622
MIJ	D. Sage, D. Prodanov, J.-Y. Tinevez, and J. Schindelin	https://www.mathworks.com/matlabcentral/fileexchange/47545-mij-running-imagej-and-fiji-within-matlab
Turboreg	Thévenaz et al.28	RRID:SCR 014308
Iboot statistics MATLAB package	A.C. Penn	Zenodo. https://doi.org/10.5281/zenodo.3992392
Glmnet	J. Qian, T. Hastie, J. Friedman, R. Tibshirani, N. Simon	RRID:SCR_015505; http://hastie.su.domains/glmnet_matlab/
MATLAB code for image processing	This paper	https://github.com/ablaeser/MovieProcessing https://doi.org/10.5281/zenodo.7153228
MATLAB code for locomotion analysis	This paper	https://github.com/ablaeser/LocomotionAnalysis https://doi.org/10.5281/zenodo.7153241
MATLAB code for calcium imaging analysis	This paper	https://github.com/ablaeser/CalciumAnalysis https://doi.org/10.5281/zenodo.7153347

Highlights.

• Two-photon calcium imaging of trigeminal meningeal afferents in awake mice

• Brief locomotion causes sustained meningeal deformation

• Afferents encode diverse aspects of meningeal deformation during locomotion

• Meningeal afferents may guide cranial interoception in addition to headache pain

INCLUSION AND DIVERSITY

While citing references scientifically relevant to this work, we actively worked to promote gender balance in our reference list.