Robust Methods for Quantifying the Effect of A Continuous Exposure from Observational Data

Abstract

A cornerstone of clinical medicine is intervening on a continuous exposure, such as titrating the dosage of a pharmaceutical or controlling a laboratory result. In clinical trials, continuous exposures are dichotomized into narrow ranges, excluding large portions of the realistic treatment scenarios. The existing computational methods for estimating the effect of continuous exposure rely on a set of strict assumptions. We introduce new methods that are more robust towards violations of these assumptions. Our methods are based on the key observation that changes of exposure in the clinical setting are often achieved gradually, so effect estimates must be “locally” robust in narrower exposure ranges. We compared our methods with several existing methods on three simulated studies with increasing complexity. We also applied the methods to data from 14k sepsis patients at M Health Fairview to estimate the effect of antibiotic administration latency on prolonged hospital stay. The proposed methods achieve good performance in all simulation studies. When the assumptions were violated, the proposed methods had estimation errors of one half to one fifth of the state-of-the-art methods. Applying our methods to the sepsis cohort resulted in effect estimates consistent with clinical knowledge.

I. Introduction

Estimating the effect of exposures and interventions on outcomes is one of the cornerstones of biomedical research. When the exposure is binary, a multitude of effective methods exist. However, the exposures of interest in biomedicine are often continuous. For example, the effect of A1c value on cardiovascular risk [14], [38], the effect of time to antibiotics on sepsis-related adverse outcomes [27], [32], [41], and the effect of potassium level on mortality due to acute myocardial infarction [13] are all examples of continuous exposures. Quantifying the effect of continuous exposures remains a challenge.

Randomized clinical trials (RCT) are considered the gold standard for estimating the effect of interventions. For some questions, however, the use of RCTs would be deemed unethical, and even when RCTs are applicable, they have difficulty handling continuous exposures. Typically, the exposure is dichotomized into two clinically meaningful narrow ranges to compare. In a diabetes example [38], patients with A1c of 6.0% (intensive control) are compared to patients with A1c between 7.0 and 7.9% (standard control) in terms of cardiovascular outcomes. The desired interpretation is that more intensive A1c control (being in the 6.0% range as opposed to the 7.0–7.9% range) leads to lower cardiovascular risk. Unfortunately, this leaves gaps in our knowledge about the potential benefit of the intervention in patients who are outside the range of exposure. Patients with A1c levels far in excess of 8% could potentially also benefit from more intensive control, however reducing their A1c to 6.0% may not be safe or even possible. To experimentally determine the effect of reducing A1c along the entire range of A1c measurements would require multiple RCTs.

In lieu of running multiple RCTs, effects can be estimated from observational studies. These studies, in turn, suffer from their own problems. Key among these problems is confounding, when the contribution of observed (or unobserved) variables is incorrectly attributed to the exposure. To overcome this problem, a vast array of causal modeling techniques have been developed. These techniques are used for better prediction [7], [12], [30], [39], learning the causal mechanisms underlying the data [11], [31], [33], [36], and estimating the effect of exposures or interventions on outcomes [8], [23], [32] in a broad range of contexts including time-series data (e.g. Granger causality in [12]), longitudinal data [30], pre-post analyses [29], retrospective subpopulation analysis [43], and propensity score (PS) analysis using aggregated Electronic Health Records (EHR) data [8].

In this paper, our focus is on estimating the effect size of a continuous exposure variable E on an outcome variable Y. We consider the most common study design in observational EHR data, where patients’ longitudinal data is aggregated into a single cross section. Commonly applied effect estimation methods include the basic Direct Adjustment (DA) method (our implementation is equivalent to G-computation method in [3]) and methods of the Generalized Propensity Score (GPS) class, which were first introduced as extensions of the binary exposure problem [35] to the continuous exposure [19], [22].

These methods critically depend on three assumptions, which are often violated in practice, yielding potentially misleading results or results that hold no clinical value.

Common support.

Common support assumes that patients who are identical, except for their exposure level, exist along the entirety of the exposure range. Returning to the A1c example, the common support assumption implies that there are patients along the entire A1c range, who are comparable in all respects relevant to A1c and the outcome, and only differ in their A1c levels. The common support assumption is often violated at the extreme values of the exposure range: e.g. patients with normal A1c and those with excessively high A1c are typically not comparable; disease in the latter patients has progressed beyond comparability.

Validity of the outcome model.

A popular and straightforward method to estimate the effect of a continuous exposure on an outcome is to regress the outcome on the continuous exposure and potential confounders [13]. After acquiring this model, the average effect size between two levels of exposure can be estimated as the average of the difference in model predictions calculated at these two levels. Correct effect estimation is dependent on the correct specification of the outcome model, which could be a difficult task for real world problems where complex and non-linear relationships exist.

Validity of the propensity model.

Many of the methods that adjust for confounding utilize propensity scores to this end. The use of propensity score methods can allow us to sidestep issues regarding the validity of the outcome model as long as the propensity model itself is correctly specified. However, the correct specification of the propensity model can be challenging when explicit knowledge about the causal mechanism is absent.

Many recent methods that are technically in the GPS class [6], [10], [18], [24], [44], [45], either try to estimate only a single global propensity model and/or a single outcome model, and assume global common support. The term global refers to the requirement that common support exists throughout the entire range of possible exposure values, while the term local means that common support is required only in a narrower range of exposure values. In this paper, we relax the global common support assumption to the local common support assumption and suggest a framework where the effect gradient is estimated locally and some of the effect gradients are then integrated into an effect estimate. Using local samples relaxes the assumption of validity of propensity (or outcome) model, because we focus on a more uniform sample with common support in the distribution of confounders (no extrapolation). We also introduce a common support diagnostic and show how to interpret the result of integrating the effect gradient based on the result of this diagnostic.

There are also some very recent novel techniques for estimating the effect of continuous exposures. These methods include the entropy balancing method [16], which has been extended from the binary to the continuous exposure problem very recently [40], [42], and the generative adversarial deconfounding method [25]. Both of these methods follow similar assumptions to GPS relying on global common support or global positivity. These methods rely on weighting the samples so that in different exposure levels the distribution of confounders become more similar in a certain sense.

Contributions.

The main contributions of this paper are (i) to point out that in biomedical studies, the common support assumption is often too strong and when the common support assumption is violated, the effect estimates by GPS can suffer considerably; (ii) to establish a general framework that can use any existing GPS or binary PS methods locally to estimate the effect gradient when only local common support is present (relaxing global common support assumption); and (iii) to estimate the extent of common support for the integrated effect curve and discuss the causal interpretation of this curve. Specifically, in (ii), we introduce two example methods using the proposed framework and compare them to several existing methods on simulated datasets, where the true effect size is known. We also apply these methods to a real-world clinical problem, where we estimate the effect of the latency of the first antibiotic administration on prolonged hospital stay for sepsis patients.

II. Materials and Methods

A. Problem Definition

For a continuous exposure E and two of its levels e₁ and e₂, we wish to estimate the average effect of changing E from e₁ to e₂ with respect to an outcome Y. This is analogous to ATT for binary treatment, where control group is E = e₁ and treated (or exposed) group is E = e₂. We denote this average effect by A(e₁, e₂).

B. Proposed Methods

Fig 1 shows an illustration of the proposed method. To estimate the effect of changing the exposure from e₁ to e₂, we create a sequence of propensity matched populations at a sequence of exposure levels ϵ between e₁ and e₂. Then, in each propensity matched population, we estimate the local effect a(ϵ) of the exposure in the small neighborhood of ϵ and finally, we sum up the local effects to obtain A(e₁, e₂). Local estimation allows for more relaxed assumptions: we only need common support locally, in the neighborhood of ϵ, as opposed to globally (along the entire exposure range) and similarly, the propensity and outcome models only need to provide a good approximation of the true relationship between exposure, confounders, and the outcome locally, in the small neighborhood around ϵ.

Fig. 1:

After selecting a sequence of samples S_ϵ, the local samples are matched $S_{ϵ}^{(m)}$ and the local effect a(ϵ) is computed. A(e₁, e₂) is estimated by numerically integrating over local effects a(ϵ). Finally the extent of common support is estimated e.g. by checking the matching ratio from e₁ to further exposures.

Specifically, we propose two methods for estimating A(e₁, e₂), the Local Gradient Propensity Score Matching (grad-PSM) and the Greater Than Less Than Propensity Score Matching (gtlt-PSM).

$$\begin{array}{l}\mathbf{Data:}\hspace{0.17em}\hspace{0.17em}\left\{X_i,E_i,Y_i\right\}\hspace{0.17em}\hspace{0.17em}\text{for patinets}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,N_{\text{tot }}\\ \mathbf{Result:}\text{ Effect curve}\hspace{0.17em}\hspace{0.17em}A\left(e_1,e_2\right)\\ \mathbf{Step 1.}\text{ Initialization:}\\ \text{Generate}\hspace{0.17em}{ϵ}_k\hspace{0.17em}\text{sequence along exposure,}\hspace{0.17em}\hspace{0.17em}k=1,\dots ,n\\ \text{Choose}\hspace{0.17em}{S}_{ϵ}\hspace{0.17em}\text{local sample, a minumum sample size }N\text{ selected by}\\ \hspace{0.33em}\text{power sample analysis of local models;}\\ \mathbf{Step 2.}\text{ Local PSM:}\\ \text{Fit binary propensity score model for each}\hspace{0.17em}{S}_{ϵ}\left(\text{above vs below}\hspace{0.17em}ϵ\right)\\ \hspace{0.33em}\text{and compute matched sample at}\hspace{0.17em}ϵ\text{,}\hspace{0.17em}{S}_{ϵ}^{(m)};\\ \text{(Use}\hspace{0.17em}\delta \hspace{0.17em}\text{parameter as minimum difference between matched samples}\\ \hspace{0.33em}\text{to numerically stabilize gradient estimation}.\text{ See Appendix A for}\\ \hspace{0.33em}\text{details}.)\\ \mathbf{Step 3.}\text{ Fit local outcome model and compute}\\ \hspace{0.33em}a(ϵ)={\mathbb{E}}_{S_{ϵ}^{(m)}}[\partial \widehat{y}/\partial ϵ];\\ \mathbf{Step 4.}\text{ Use trapezoid rule numerical integration to compute,}\\ \hspace{0.33em}A\left(e_1,e_2\right)={\int }_{e_1}^{e_2} \text{d}ϵa(ϵ);\\ \mathbf{Step 5.}\text{ Estimate the extent of common support: Use matching}\\ \hspace{0.33em}\text{efficiency (under the exact conditions of Step 2 for balance criteria}\\ \hspace{0.33em}\text{etc}.) \text{from}\hspace{0.17em}{e}_{\text{1}}\hspace{0.17em}\text{to further and further target exposures}\hspace{0.17em}{e}_{\text{2}}.\hspace{0.17em}\text{Compute}\\ \hspace{0.33em}\text{extent of common support for each}\hspace{0.17em}{e}_{\text{1}}\hspace{0.17em}\text{as exposure}\hspace{0.17em}{e}_{\text{2}}\hspace{0.17em}\text{on each side}\\ \hspace{0.33em}\text{of}\hspace{0.17em}{e}_{\text{1}}\hspace{0.17em}\text{where matching efficiency drops to a cut-off value (e}.\text{g}.\hspace{0.17em}\text{90\%)}.\\ \mathbf{Algorithm\hspace{0.33em}1:}\text{ grad-PSM}\hspace{0.33em}\text{algorithm}.\end{array}$$

$$\begin{array}{l}\mathbf{Data:}\hspace{0.17em}\hspace{0.17em}\left\{X_i,E_i,Y_i\right\}\hspace{0.17em}\text{for patinets}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,N_{\text{tot }}\\ \mathbf{Result:}\text{ Effect curve}\hspace{0.17em}\hspace{0.17em}A\left(e_1,e_2\right)\\ \mathbf{Step 1.}\text{ Initialization:}\\ \text{Generate}\hspace{0.17em}\hspace{0.17em}{ϵ}_k\hspace{0.17em}\hspace{0.17em}\text{sequence along exposure, }\hspace{0.17em}\hspace{0.17em}k=1,\dots ,n;\\ \mathbf{Step 2.}\text{ Local PSM:}\\ \text{Fit binary propensity score model for each}\hspace{0.17em}\hspace{0.17em}ϵ\hspace{0.17em}\hspace{0.17em}\text{(greater than vs less}\\ \hspace{0.33em}\text{than}\hspace{0.17em}\hspace{0.17em}ϵ\hspace{0.17em}\hspace{0.17em}\text{using all data) and compute matched sample at}\hspace{0.17em}\hspace{0.17em}ϵ,\hspace{0.17em}\hspace{0.17em}{S}_{ϵ}^{(m)};\\ \text{(Use}\hspace{0.17em}\hspace{0.17em}\delta \hspace{0.17em}\hspace{0.17em}\text{parameter as minimum difference between matched samples}\\ \hspace{0.33em}\text{to numerically stabilize gradient estimation}. \text{See Appendix A for}\\ \hspace{0.33em}\text{details}.)\\ \mathbf{Step 3.}\text{ Use mean difference in outcome divided to change in}\\ \hspace{0.17em}\hspace{0.17em}\text{exposure for matched pairs to estimate the effect gradient,}\\ \hspace{0.33em}a(ϵ)={\mathbb{E}}_{(i,j)\in S_{ϵ}^{(m)}}\left[\left(Y_i-Y_j\right)/\left(E_i-E_j\right)\right];\\ \mathbf{Step 4.}\text{ Same as grad-PSM;}\\ \mathbf{Step 5.}\text{ Same as grad-PSM}.\\ \mathbf{Algorithm\hspace{0.33em}2:}\text{ gtlt-PSM}\hspace{0.33em}\text{algorithm}.\end{array}$$

1). Local Gradient Propensity Score Matching (grad-PSM):

(Step 1) Consider a sample of patients i with covariates X_i, exposure E_i and outcome Y_i. A sequence ϵ₁, ϵ₂, …, ϵ_n of exposure values is generated and the exposure range is divided into a sequence of (possibly overlapping) neighborhoods centered around ϵ_k(k = 1, 2, …, n). For brevity, below we use ϵ ∈ {ϵ₁, ϵ₂, …, ϵ_n}, dropping the index.

(Step 2) In the neighborhood around each ϵ, propensity score matching is carried out resulting in a matched set of patients $S_{ϵ}^{(m)}$,

$$\begin{array}{l}{S}_{ϵ}^{(m)}=\left\{(i,j)\mid i,j\in S_{ϵ},\hspace{1em}{E}_i\le ϵ,\hspace{1em}ϵ<E_j\right.,\hfill \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left.p_i\approx p_j,\hspace{1em}{E}_j-E_i>\delta \right\},\hfill \end{array}$$ (1)

where S_ϵ is a set of patients around ϵ, i (and j) are patients with exposure levels E_i (and E_j, respectively) and propensity scores p_i and p_j that fall within the required calipers (p_i ≈ p_j), and their exposure levels differ at least by δ. The minimum difference δ in exposure levels numerically stabilizes the gradient estimate by avoiding division by very small numbers. More details about selecting S_ϵ and matching procedure are covered in Appendix A.

(Step 3) In the propensity matched population $S_{ϵ}^{(m)}$, a(ϵ) is computed. To this end, we apply an outcome model, which is a logistic regression model for binary outcome Y, Y ∼ E + X, constructed on the matched samples $S_{ϵ}^{(m)}$, and estimate,

$$a(ϵ)={\mathbb{E}}_{S_{ϵ}^{(m)}}\left[\frac{\partial \widehat{y}}{\partial ϵ}\right]={\mathbb{E}}_{S_{ϵ}^{(m)}}\left[\frac{{\beta }_E}{4{\cosh }^2([1,X,E]\beta /2)}\right],$$ (2)

where $\widehat{y}$ is a model-based estimate of the outcome, β = [β₀, β_X, β_E] is denoting the intercept, coefficients for confounders, and coefficient for exposure, respectively, and a reminder that cosh(x) = (e^x + e^−x)/2. Notice that this model needs to approximate the true relationships between X, E, and Y only in the narrow neighborhood of E = ϵ. The quantity a(ϵ) can be interpreted as the gradient of the average treatment effect in the treated (ATT) when exposure level is reduced approximately from ϵ + δ/2 to ϵ − δ/2.

(Step 4) We integrate a(ϵ) to obtain A(e₁, e₂), the effect of changing exposure from e₁ to e₂ using the trapezoid rule,

$$A\left(e_1,e_2\right)={\int }_{e_1}^{e_2} \text{d}ϵ\hspace{0.33em}a(ϵ),$$ (3)

keeping in mind that A(e₁, e₂) in only meaningful up to the extent of common support from e₁ to e₂.

(Step 5) To estimate the extent of common support, we use the same matching method as above, and the proportion of samples at e₁ that could be matched to samples at e₂ or beyond can be used (e.g. using a 90% cut-off) as the extent of common support.

2). Greater than vs Less than Propensity Score Matching (gtlt-PSM):

Inspired by [32], [41], gtlt-PSM is a simplified version of grad-PSM. The gtlt-PSM is identical to the grad-PSM except for steps 2 and 3. In gtlt-PSM, we use the entire population when matching,

$$\begin{array}{l}{S}_{ϵ}^{(m)}=\left\{(i,j)\mid \hspace{1em}{E}_i\le ϵ,\hspace{1em}ϵ<E_j\right.,\hfill \\ \left.\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{p}_i\approx p_j,\hspace{1em}{E}_j-E_i>\delta \right\},\hfill \end{array}$$ (4)

and the gradient a(ϵ) is computed with mean difference in outcome (no outcome model),

$$a(ϵ)={\mathbb{E}}_{(i,j)\in S_{ϵ}^{(m)}}\left[\frac{Y_i-Y_j}{E_i-E_j}\right].$$ (5)

The details regarding the selection of the sequence of ϵ, propensity matching, and the choice of δ are identical to grad-PSM. These implementation details are covered in the Appendix A.

C. Comparison methods

Unadjusted is the most naive calculation of effect size, without adjusting for the confounders,

$$A\left(e_1,e_2\right)=\mathbb{E}\left[Y\left(E_i\approx e_2\right)\right]-\mathbb{E}\left[Y\left(E_i\approx e_1\right)\right],$$ (6)

where “E_i ≈ e” is implemented as the 200 nearest samples to e (i denotes the samples).

Direct Adjustment is the most commonly used method to estimate the effect of continuous exposures, where a model is constructed for the outcome using the covariates. The effect curve in this case is calculated as,

$$A\left(e_1,e_2\right)=\mathbb{E}\left[\widehat{y}\left(E_i=e_2,X_i\right)-\widehat{y}\left(E_i=e_1,X_i\right)\right],$$ (7)

where $\widehat{y}$ denotes the estimated outcome from the model. Specifically we consider two different models. GLM-DA utilizes a generalized linear model and GBM-DA uses gradient boosted trees as implemented in the gbm R package.

Covariate Balancing Generalized Propensity Score (CB-GPS) As discussed earlier, the GPS methods follow very similar assumptions, especially regarding the global common support. Here we include the CB-GPS method [10], a representative method from this class, that was recently found to stands out as one of the top-performing methods [3].

D. Simulation Studies

Real data with complex confounding is often observational data and the true effect of the interventions are not known. To know the true effect sizes and to be able to judge whether a causal method is successful in removing the confounding bias, the use of simulated data is necessary and common practice. We use a sequence of increasingly challenging studies designed to highlight the limitations of the different methods. Fig. 2 shows the causal graph used for data generation in all three studies. In Study 1, none of the assumptions are violated and our aim is to see whether the proposed method can perform as well as the theoretically best method. In Study 2, although both the propensity and the outcome models for the GPS methods are specified correctly, the global common support assumption is violated. This study demonstrates the importance of the global common support assumption. In Study 3, neither the propensity nor the outcome model is specified correctly and the global common support assumption is also partially violated.

Fig. 2:

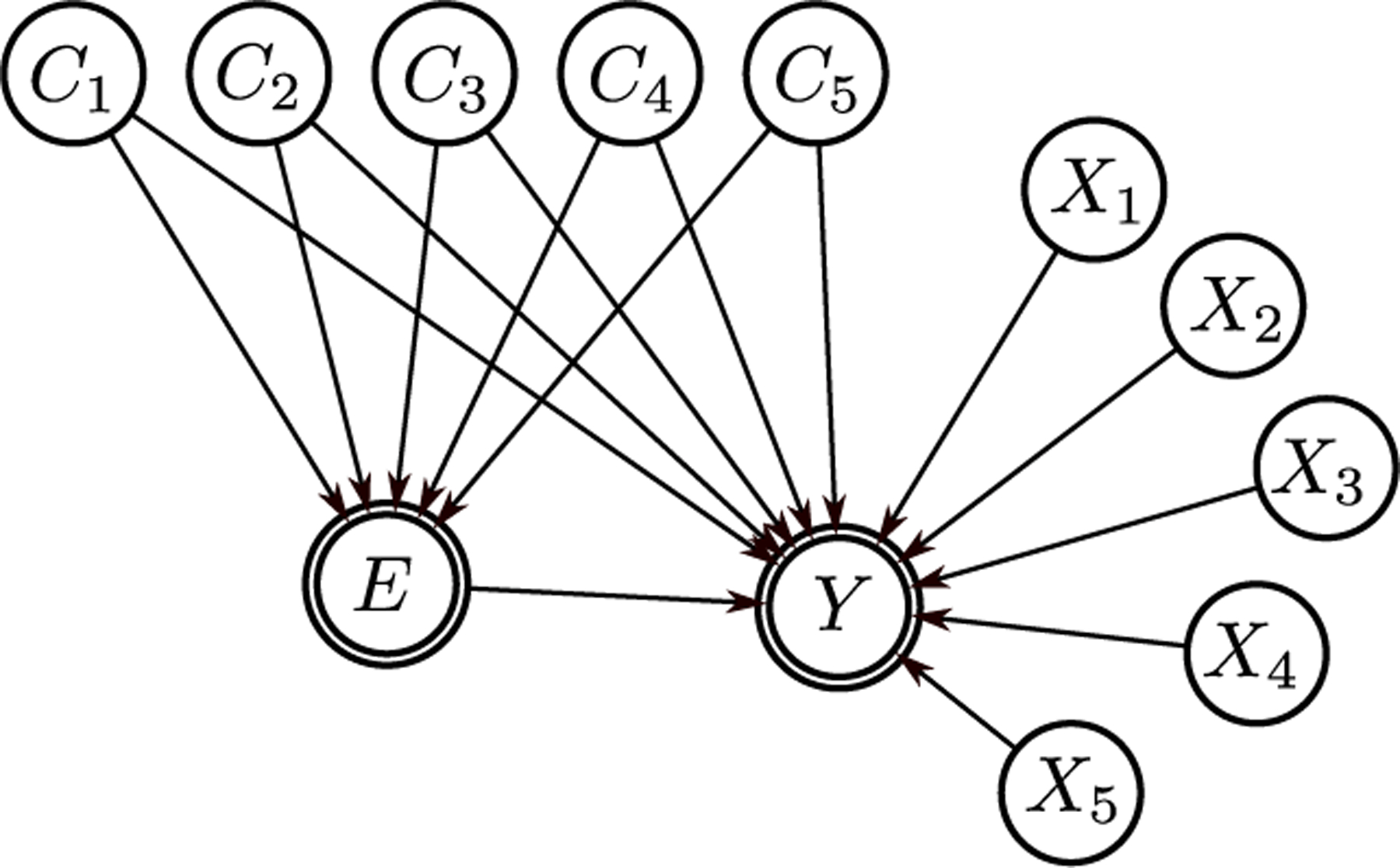
The causal graph used for data generation in simulation studies. For clarity the true confounder variables X₅, …, X₁₀ are called C₁, …, C₅, respectively.

Study 1 is simple, patients are comparable across the entire range of the exposure. The exposure model is linear in the confounders and the outcome is linear in all variables; the outcome model we use is correctly specified,

$$E=\sum _j{C}_j+2.25\hspace{0.17em}\hspace{0.17em}\xi ,$$ (8)

$$O=-1+0.2E+0.5\sum _j{C}_j+0.5\sum _j{X}_j+\epsilon .$$ (9)

where $\xi ~\mathcal{N}(0,1)$, $\epsilon ~\mathcal{N}(0,1)$, and the available outcome data is binary, Y = binom(logit(O)). Notice that about half the variation in exposure is due to noise (the choice of SD=2.25).

This study meets all the theoretical assumptions for GLM-DA and CB-GPS methods.

Study 2 is exactly the same as Study 1, except,

$$E=1.4\sum _j{C}_j+\xi ,$$ (10)

and $\xi ~\mathcal{N}(0,1)$. We kept the total variation of E almost the same as Study 1, but now most of this variation is due to confounders. This way the global common support assumption is violated.

In Study 3 we vary the effect size across exposure (non-linear U-shaped relation) and make patients only locally comparable across the exposure range. Also we use piecewise linear curves both in the exposure and the outcome models (still monotonic in each variable). This reflects the common behavior of labs and vitals in real biomedical studies, where a lab value mostly affects the exposure or outcome above or below a threshold.

$$\begin{gathered} E=2.5\left[r\left(C_1,a\right)+l\left(C_2,b\right)+r\left(C_3,a\right)+l\left(C_4,b\right)+C_5\right] \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\xi \end{gathered}$$ (11)

$$\begin{array}{l}O=-2\hfill \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+1.5\left[l\left(C_1,-c\right)+l\left(C_2,b\right)+r\left(C_3,c\right)+r\left(C_4,a\right)+C_5\right]\hfill \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+r\left(X_1,a\right)+l\left(X_2,b\right)+r\left(X_3,a\right)+l\left(X_4,b\right)+X_5\hfill \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+0.1\hspace{0.17em}\hspace{0.17em}u(E,-0.5,1)+\epsilon ,\hfill \end{array}$$ (12)

where $\xi ~\mathcal{N}(0,1)$, $\epsilon ~\mathcal{N}(0,1)$, a = 0.5, b = −0.25, and c = 1 are used. l(X, a) is a left-hinged curve, where the curve is linearly decreasing on the left of ‘a’ and is constant on the right; r(X, a) is a right-hinged curve that is linearly increasing on the right of ‘a’ and is constant on the left; finally, u(X, a, b) is a u-shaped curve that quadratically decreases on the left of ‘a’, quadratically increases on the right of ‘b’, and zero in between (a < b),

$$l(X,a)=\left\{\begin{array}{ll}X\hfill & X\le a,\hfill \\ a\hfill & X>a.\hfill \end{array}\right.$$ (13)

$$r(X,a)=\left\{\begin{array}{ll}a\hfill & X<a,\hfill \\ X\hfill & X\ge a.\hfill \end{array}\right.$$ (14)

$$u(X,a,b)=\left\{\begin{array}{ll}{(X-a)}^2\hfill & X\le a,\hfill \\ 0\hfill & a<X<b,\hfill \\ {(X-b)}^2\hfill & X\ge b.\hfill \end{array}\right.$$ (15)

Again available outcome data is binary Y = binom(logit(O)). This example is an attempt to mimic the considered real data set and a bit more challenging test for methods introduced.

Usually in biomedical studies one knows the direction of effect size (it being positive or negative). Given that we defined the effect size to be U-shaped, for GLM-DA and CB-GPS, we estimate the effect size for E < 0 and E > 0 separately and combine the results. These methods have no built-in facility to handle U-shaped effect curves.

Evaluation:

Since the data generation method assumes path/direction independence for A(e₁, e₂) function, for any e₀ we have,

$$A\left(e_1,e_2\right)=A\left(e_1,e_0\right)+A\left(e_0,e_2\right)=A\left(e_0,e_2\right)-A\left(e_0,e_1\right).$$ (16)

It is thus sufficient to reconstruct the A(e₀, e) curve, a single-valued function of e, for all exposure levels e relative to a “reference” initial exposure e₀. In other words, evaluating A(e₁, e₂) in two dimensions will not add any new information. The path independence assumption can be interpreted as averaging over a distribution of paths that patients take from e₁ to e₂; or more formally, ⟨A(γ(e₁, e₂))⟩ =: A(e₁, e₂) where γ is the paths patients take from e₁ to e₂ in the population that is comparable between e₁ and e₂ (confounders or propensity of exposure are changed by a very small amount).

We chose e₀ = 0 as the reference level, because it is the approximate median of the exposure data. Changing e₀ to $e_0^{\prime }$ only shifts all the curve by a constant A(e₀, $e_0^{\prime }$) and does not affect the evaluation results in any other way.

Similar to simulations in previous studies, e.g. [10], the population in simulation is taken to be homogeneous (a single outcome model is used) and the effect size does not depend on the direction, meaning,

$$A\left(e_1,e_2\right)=-A\left(e_2,e_1\right),$$ (17)

therefore different treatment effects are equal, i.e. ATE=ATT, which helps simplify and focus our discussion in this paper.

For improved visibility, smoothing is applied to the curve for all the methods. We use Gaussian kernel smoother with the same smoothing widths (bandwith) across all methods. See Appendix B.

We generated 10k samples for Studies 1 and 2, and 15k for Study 3. We applied the algorithms to estimate the effect curves and plotted them. We computed the RMSEs for three exposure ranges of decreasing data density: 35–65th, 25–75th and 5–95th percentiles. To quantify the variability of the RMSE, we generated 400 additional data sets and computed the RMSE on each. We report the mean and 95% CI of the 400 RMSEs for each exposure range. Also we use t-test for all method pairs to check whether the mean differences are significant, using p-value < 0.001 as the significance level with Holm-Bonferroni method to adjust for multiple comparisons.

Finally, to evaluate the extent of common support we use bins with 400 sample size at initial exposure, plot the heat-map plot of matching proportions for different target exposures and mark the 90% contours.

E. Antibiotic Latency Effect on Prolonged Hospital Stay for Patients with Sepsis on Admission

Study design and setting.

This is a retrospective cohort study of 14k hospitalized septic patients from M Health Fairview (FV) from Sep 2010 to Dec 2016. Septic patients are identified as those who are Systemic Inflammatory Response Syndrome (SIRS) positive or have acute organ dysfunction within two days of admission and follow a full course of antibiotics [34]. For patients with multiple hospitalizations, only one, a randomly chosen hospitalization is included.

Outcome.

The primary outcome is prolonged hospital stay, defined as length of stay of 10 days or longer.

Exposure.

We define the continuous exposure variable antibiotic latency as the elapsed time from first the time the patient was SIRS positive (which we call onset time) until the first antibiotic administration, measured in hours.

Variables of interest.

We consider the following variables as potential confounders: chronic comorbidities (e.g. tumor, chronic kidney disease, liver disease, chronic obstructive pulmonary disease), baseline labs, the variables related to acuity of infection at the onset time: vital signs, WBC, lactate, and PCO2, plus other labs which can be related to organ dysfunction, again measured up to the onset time.

Statistical Analysis.

The proposed methods grad-PSM and gtlt-PSM were applied. As part of the method, propensity models are constructed. We use causal feature discovery [28] to discover the actual confounders and these confounders were used in the propensity model. As discussed, grad-PSM uses an outcome model for further adjustment after matching.

Evaluation.

Given that exposure is time, the path independence assumption holds (similar to the simulated studies), meaning that we can study a single valued curve rather than two-dimensional A(e₁, e₂). Given that the latency distribution is concentrated around 2.5h, we focus on estimating the ATT of moving a patient from latency e to 2.5h denoted by −A(e, 2.5h), where the negative sign is used to denote the benefit (outcome is adverse).

Estimating variability with propensity score methods is debated [4], [17], [37]. Here we simply report the estimated variability using 95% CI of bootstrap sampling (with replacement) following [17], [32]. Using all sample bootstrap (with replacement) potentially overestimates sample variation (especially for grad-PSM), but arguably it is the safer choice when reporting the existence or significance of effect sizes.

III. Results

A. Simulation Studies

First we applied the methods to the data generated for Study 1. Fig 3a shows the estimated effect size for each method from a single run. The vertical axis depicts the effect size of A(0, e), changing the exposure from 0 to the target exposure e, e ranging from −5.3 to 5.2 (5%−95% percentile of data) depicted on the horizontal axis. The effect size is ATE for GLM-DA and GBM-DA and ATT for the other methods. The solid black line represents the true effect size, for which ATE=ATT, and the dashed line is the raw (unadjusted) effect size.

Fig. 3:

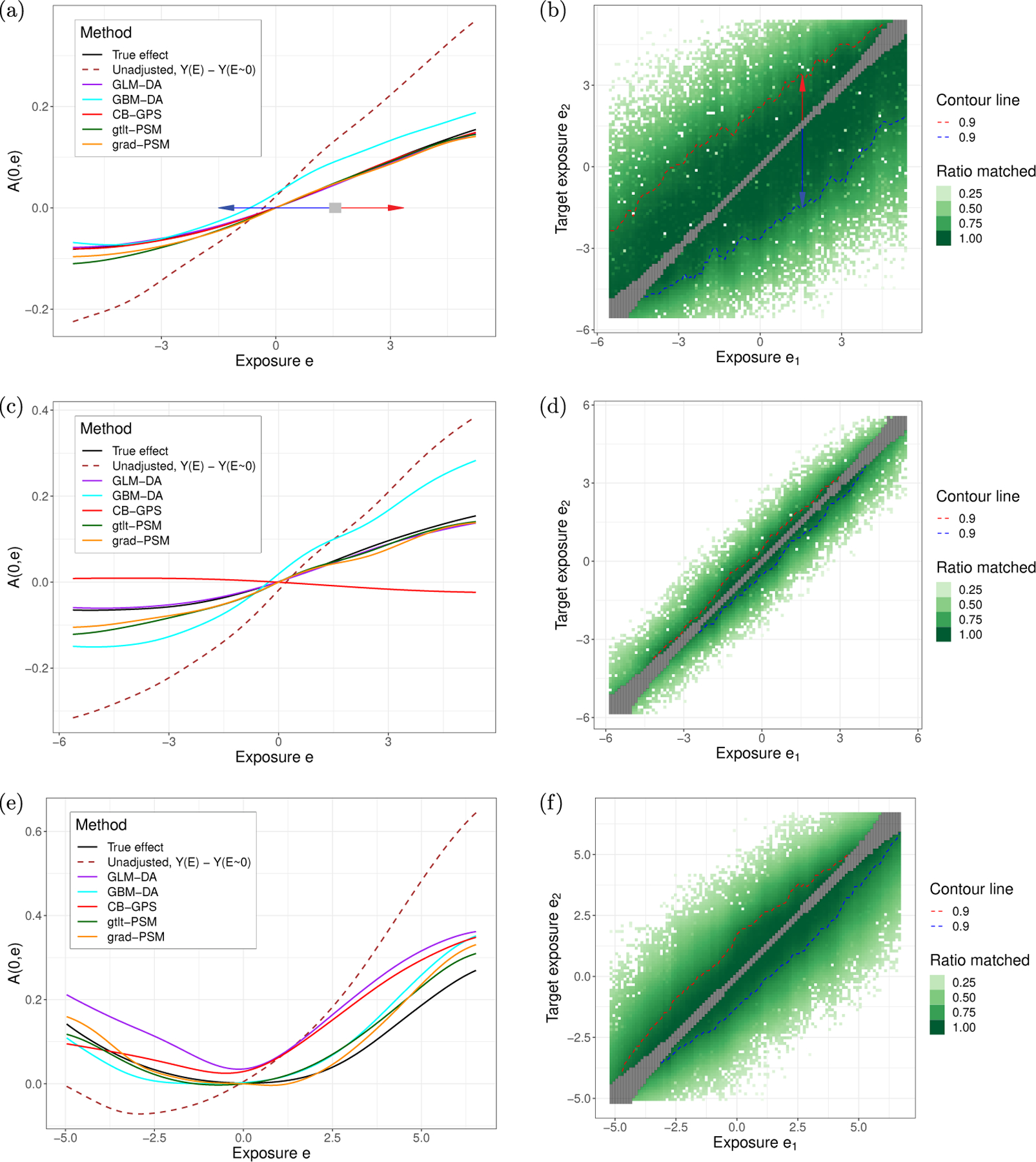
(a) The effect curve A(0, e) for Study 1, a single run. (b) Extent of common support. Matching a bin of 400 samples around a initial exposure (horizontal axis) with a matching proportion of 90% (360/400) was possible to the exposure range (vertical axis) shown by red and blue dashed lines. For example, a sample from e = 1.5 is likely to have a match from e = −1.5 (blue arrow) to e = 3.5 (red arrow). In this example, the extent of common support is large. (c) A(0, e) results for Study 2, a single run. (d) Extent of common support in Study 2. It is much smaller than Study 1 and to achieve 90% matching, one can only change exposure by about ≲ 0.5 below or above. In other words, on A(0, e) plot the estimated effects from e = e₁ to e = e₂ are only meaningful for |e₂ − e₁| ≲ 0.5. (e) The effect curve for Study 3, a single run. (f) The extent of common support for Study 3.

Fig 3b visualizes the extent of common support. The horizontal axis corresponds to the original level e₁ of exposure and the vertical axis corresponds to the target level e₂. The greenness of the pixel represents the percentage of samples within gray box that could be matched. The contour lines corresponds to the range within which 90% of the samples was matched. For example, when the source exposure is 1.5 (1.5 on the horizontal axis), at least 90% of the samples can be matched for target exposures between almost −1.5 and positive 3.5 (this is where the two contour lines are).

Table Ia displays the errors (RMSE) from the various methods in different ranges of exposure (35%−65%, 25%−75%, and 5%−95%) (scaled up by 10² for easier reading). It shows the mean RMSE and its empirical 95% CI over the 400 runs. ‘Unadjusted’ has the highest error, followed by GBM-DA. The other methods perform very comparably and their RMSE is about 10% of the RMS of actual effect size. The mean differences can be read from this table and except the difference between CB-GPS and grad-PSM, all other differences were significant (using t-test for all the method pairs with significance level of p-value < 0.001 with Holm-Bonferroni adjustment for multiple comparisons).

TABLE I:

RMSE ×100 for different methods over three intervals of exposure for (a) Study 1, (b) Study 2, and (c) Study 3. Reported values are the mean (95% CI) of the 400 RMSEs for each exposure range, comparing methods in regions with high density (35%−65%) going towards extreme exposure values with less densities (25%−75% and 5%−95%), pushing methods to rely more and more on extrapolating. t-test is used for all method pairs with significance level of p-value < 0.001 with Holm-Bonferroni adjustment for multiple comparisons.

	35%−65%	25%−75%	5%−95%
GLM-DA	0.10 (0.01,0.3)	0.17 (0.03,0.6)	0.38 (0.08,1.2)
gtlt-PSM	0.18 (0.05,0.4)	0.32 (0.08,0.7)	1.11 (0.43,1.9)
grad-PSM	0.29 (0.07,0.7)	0.49 (0.16,1.1)	1.22 (0.47,2.2)
CB-GPS	0.26 (0.02,1.0)	0.44 (0.04,1.7)	0.96 (0.12,3.7)
GBM-DA	1.16 (0.35,3.0)	1.47 (0.57,3.5)	1.90 (0.90,3.8)
Unadjusted	3.42 (2.10,7.2)	5.07 (3.79,8.0)	10.90 (9.85,13.0)
(a) RMSE ×100 results for Study 1. t-tests are conducted for all method pairs. The only non-significant mean differences are between grad-PSM and CB-GPS.
	35%−65%	25%−75%	5%−95%
GLM-DA	0.24 (0.02,0.8)	0.39 (0.04,1.3)	0.84 (0.13,2.9)
gtlt-PSM	0.51 (0.11,1.2)	0.83 (0.26,2.0)	2.08 (0.75,4.0)
grad-PSM	0.50 (0.12,1.2)	0.84 (0.22,1.9)	2.16 (0.82,4.3)
CB-GPS	0.77 (0.05,3.0)	1.29 (0.10,5.0)	2.80 (0.30,11.2)
GBM-DA	2.35 (0.88,3.9)	3.74 (1.46,5.7)	7.89 (3.21,12.6)
Unadjusted	4.22 (2.87,7.0)	6.66 (5.47,8.8)	14.85 (13.68,16.4)
(b) RMSE ×100 results for Study 2. t-tests are conducted for all method pairs. The only non-significant mean differences are between grad-PSM and gtlt-PSM.
	35%−65%	25%−75%	5%−95%
grad-PSM	0.5 (0.2,1.6)	0.9 (0.3,2.0)	3.3 (1.9,4.9)
gtlt-PSM	1.4 (0.7,2.1)	2.0 (1.1,2.9)	3.1 (1.7,4.6)
GBM-DA	1.8 (0.3,3.4)	2.5 (0.6,4.1)	5.4 (2.4,7.7)
GLM-DA	6.8 (6.1,7.6)	8.3 (7.4,9.2)	10.0 (8.6,11.4)
CB-GPS	6.3 (4.3,9.0)	7.6 (5.0,11.2)	8.5 (4.9,14.4)
Unadjusted	6.5 (4.1,9.7)	9.0 (7.0,11.3)	18.0 (16.4,19.9)
(c) RMSE ×100 results for Study 3. t-tests are conducted for all method pairs. All the mean differences are significant.

Next, we performed the analysis on Study 2. Results are shown in Fig 3 second row. Recall that Study 2 violates the (global) common support assumption, but allows for correct specification of the outcome and exposure models. The results are similar to those from Study 1 but unlike in Study 1, CB-GPS fails to reliably estimate the effect size. Table Ib contains the RMSE for the various methods. All the mean differences were significant other than the difference between grad-PSM and gtlt-PSM (using t-test for all method pairs and significance level of p-value < 0.001).

Finally, the analyses were carried out on Study 3 and are shown in Fig 3 third row. Given that all three assumptions are violated, all methods performed worse than in the previous studies, but the two proposed methods performed better than the others. GBM-DA was slightly more biased towards the Unadjusted curve. RMSE values are reported in Table Ic. In the middle (25%−75%) grad-PSM performs exceptionally well, but at the edges it becomes similar to gtlt-PSM as the sample density decreases. All the mean differences in Table Ic were significant (using t-test for all method pairs and significance level of p-value < 0.001).

B. Antibiotic Latency Effect on Prolonged Hospital Stay for Sepsis Cohort

The effect curves for grad-PSM and gtlt-PSM are shown in Fig 4(a). The vertical axis is −A(e, 2.5h) which denotes the effect size of reducing the outcome (benefit) by changing the latency from e to e₀ = 2.5h.

Fig. 4:

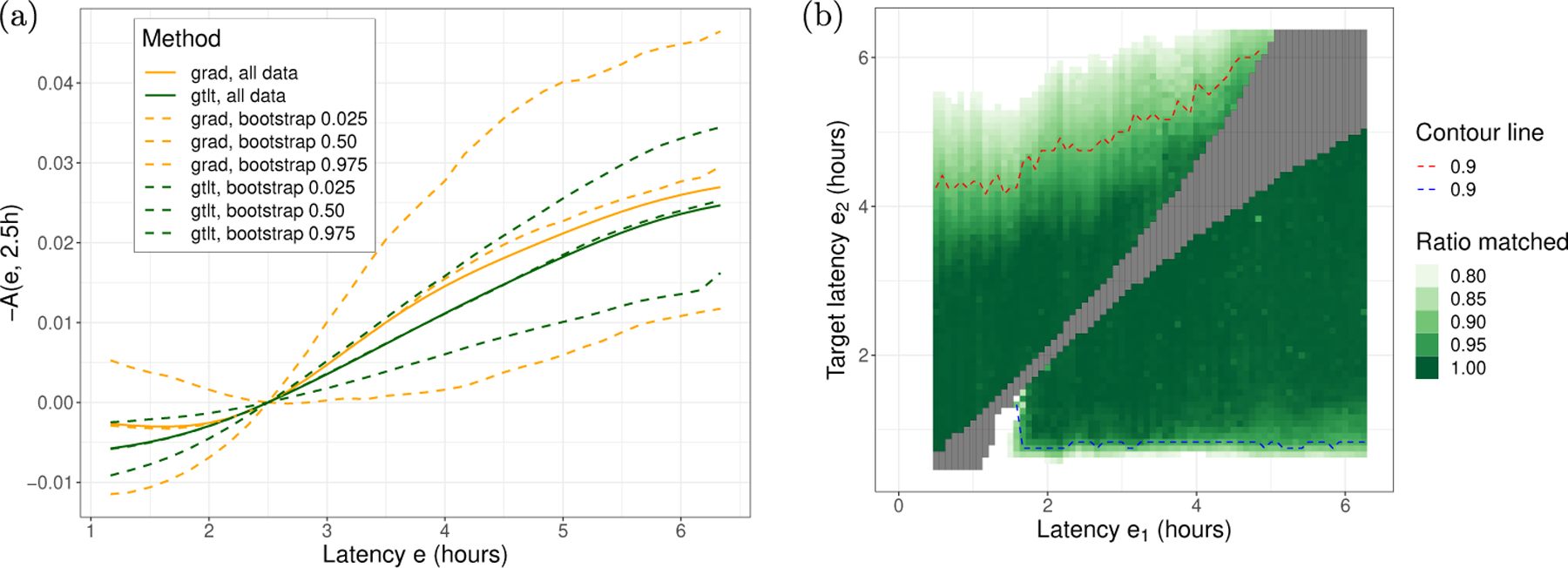
(a) Effect of antibiotic latency on prolonged (10+ days) hospital stay (excluding in-hospital mortality). −A(e, 2.5h) means how much patients will benefit (lowering the adverse outcome) if their latency is changed from e to 2.5h. (b) An estimation of the extent of common support. Patients with antibiotic latency of 2h or above can be matched down to 1h. So using the effect size curve in (a) it is reasonable to start from exposure 2h or above and reduce latency all the way down to 1h.

Fig 4(b) shows that we have a rather large unconfounded variation in exposure, which allows patients to be matched down to about 1h (blue dashed line). This means we can get reliable effect estimates for reducing the exposure (latency) from 6h not only to 2.5h but all the way down to 1h and estimate the effect using equation (16): A(e, 1h) = A(e, 2.5h)+A(2.5h, 1h) for any e ≳ 2h. Using the average curves, reducing the delay in antibiotic administration from 6h to 1h can reduce prolonged hospital stay by about 3%.

IV. Discussion

We consider the problem of estimating the effect of changing a continuous exposure from an original value e₁ to another e₂. Currently existing methods make three critical assumptions. These are (global) common support, validity of the outcome model, and validity of the propensity model. We designed a new method that reduces reliance on these assumptions and we demonstrated that the proposed methods can achieve good performance in face of violations of these three assumptions.

In a series of three simulation studies of escalating difficulty, the first one was very simple, where none of the assumptions were violated, and accordingly, most methods performed well, except for GBM-DA which overestimated the effect of exposure. The other methods (with their assumptions met) performed well with minimal differences (RMSE range from 0.0046 to 0.012, which is 5.7% to 15% of the RMS of estimated effect.). GBM-DA could fit the outcome data almost perfectly, yet its effect estimates were biased because the confounders had similar coefficients in the exposure and the outcome models, allowing GBM to mistakenly attribute the confounders’ effect to the exposure. This is an example where a flexible (and less interpretable) outcome model, that fits the outcome data well, does not help with better causal effect estimation.

The second study primarily differs from the first one in that it violates the (global) common support assumption, only having local common support. With the outcome and propensity models being correctly specified, most models performed well, except for CB-GPS and GBM-DA. CB-CPS relies on the global common support assumption heavily and even failed to determine the effect direction correctly. Similarly to the first study, the flexibility of GBM-DA hurt its performance.

The second study highlights one of the key differences between the proposed method and existing methods, which is the departure from the (global) common support assumption. Interpretation for Study 2 is driven by the local common support: A(e₁, e₂) = A(0, e₂) − A(0, e₁) is the ATT of changing the exposure level from e₁ to e₂, provided that e₁ and e₂ has sufficient common support (but neither e₁ nor e₂ has to have common support with E = 0). In practice this means that e₁ and e₂ cannot be arbitrarily far from each other. This reflects clinical practice. For example in patients with very high A1c levels, the target A1c level can be raised (to the more attainable 8% in the Minnesota Community Measures [1]) instead of the normal target of 7% [2].

The third study highlights that under more realistic conditions, where none of the assumptions are met, the proposed method still performs adequately. Study 3 simulates a situation where the exact functional form of the propensity and outcome models are unknown. This favors flexible methods such as GBM-DA and the proposed methods. Even though the models were incorrectly specified, using many local point estimates helped the proposed methods achieve a reasonably good approximation.

For the antibiotics treatment latency example, there is no gold standard thus we did not perform a thorough comparison and only included the results for the proposed methods. The findings are consistent with prior studies [27], [32], [41], and provide evidence that starting antibiotics earlier may also benefit “healthier” patients (“healthier” in the sense that we excluded in-hospital mortality). This is not to say that patients with about 6h latency can necessarily be compared to patients with about 2h latency and will benefit according to the resultant effect curve. The diagnostic ambiguities that cause large latency are very challenging to address, if at all possible. But looking at this result and the methods used, physicians will know how much benefit there is in reducing everyone’s latency by about an hour or two, which is an attainable amount. The interpretability and the focus on measuring attainable changes in exposure, better helps physicians make necessary changes in treatment planning.

Contrasting grad-PSM and gtlt-PSM.

In terms of the global support assumption, an assumption critical to the causal interpretability of the results, the various methods lie on a continuum. On one extreme are the existing methods that require global support. On the other extreme is grad-PSM that only requires local support. In between these two is gtlt-PSM, which is local due to binarization, but can use more data than grad-PSM. Also fusing grad-PSM and gtlt-PSM is possible. Rather than using a sharp cutoff at N samples in S_ϵ for grad-PSM or using all possible samples in gtlt-PSM, S_ϵ can be constructed by weighting the samples. More generally, many method variaties can be created from our proposed framework, for example, by replacing the PSM estimator with inverse propensity weighting or the doubly robust estimator in grad-PSM.

Limitations.

(1) The methods used in the study, the proposed and comparison methods alike, rely on having sufficient local sample size for estimation. This is why in all studies above, the proposed methods performed better around central regions of exposure with higher sample density compared to the edge regions where the density was much lower. (2) The proposed methods use binary propensity matching as an operation and support virtually any such method [5], [9], [15], [20], [21], [26], [37]. Therefore, all the limitations of binary propensity score matching apply to the framework discussed in this paper. Though, due to the pointwise estimation, as we have shown, the provided framework can be more robust compared to single PS effect analyses (e.g. common binary PS or GPS methods).

V. Conclusion

When the three critical assumptions are met (having global common support and correctly specifying outcome and propensity models), the effect analysis problem is simple and most methods perform well. When they, especially the common support assumption, are violated, the proposed methods (grad-PSM and gtlt-PSM) can estimate the effects better than the existing methods. By focusing on estimating the effect of attainable or clinically actionable changes in exposure, the proposed methods can make more realistic assumptions and obtain more reliable effect estimates, thus they can better inform clinical decision making.

Appendix

A. Proposed Methods

(Step 1) A sequence ϵ₁, ϵ₂, …, ϵ_n of exposure values is generated and the exposure range is divided into a sequence of (possibly overlapping) neighborhoods centered around ϵ_k, k = 1, …, n.

Recall that we perform three simulation studies and an application to a real-world clinical problem of estimating the effect of delay in antibiotic administration for sepsis cohort. In the simulation studies we used n = 100 points across the exposure range, and in the sepsis study, the sequence of ϵ is equally spaced at 5 min increments of delayed antibiotic administration, total of n = 73.

(Step 2) In the neighborhood around each ϵ, propensity score matching is carried out resulting in a matched set of patients $S_{ϵ}^{(m)}$.

Propensity scores are estimated by binarizing the exposure around E = ϵ and fitting a logistic regression model (E < ϵ vs E ≥ ϵ). For matching, we are using nearest neighbor matching with caliper 0.25. Balance diagnosis utilizes the standardized mean differences (SMD) of each variable: whenever SMD exceeds 0.1 (a commonly used SMD threshold), we re-match the population using univariate subclassification matching on that variable [37], which refers to exact matching for binary and categorical variables, and to matching within quintiles for continuous variables. Additionally, matched pairs of patients are required to have a minimum exposure difference of δ. If sufficient balance could not be achieved following this matching procedure, we discard this ϵ from the gradient estimation.

The required number of patients in S_ϵ (for propensity model) is determined based on power sample analysis and selecting a least sample size of N below and above E = ϵ. Here we use N = 500 for simulated studies and N = 1000 for the sepsis study.

We require that the matched pair’s exposure levels differ at least by δ. The minimum difference in exposure levels numerically stabilizes the gradient estimate by avoiding division by very small numbers.

The selection of δ can be domain driven: differences in antibiotic administration delays of less than 1 hour are not expected to impact outcomes measurably so we set δ = 1h; or can be chosen arbitrarily: we chose δ = 0.25 for all simulation studies. Sensitivity analysis is carried to verify that the choice of N and δ did not unduly influence the results.

(Step 3) In the propensity matched population $S_{ϵ}^{(m)}$, the effect gradient a(ϵ) is computed. As explained in the main text, for grad-PSM method we use the mean of derivative of outcome modelh preidiction with respect to exposure variable, $a(ϵ)={\mathbb{E}}_{S_{ϵ}^{(m)}}\left[\frac{\partial \widehat{y}}{\partial ϵ}\right]$, and for gtlt-PSM we use the mean of outcome differences divided by exposure differences, $a(ϵ)={\mathbb{E}}_{(i,j)\in S_{ϵ}^{(m)}}\left[\frac{Y_i-Y_j}{E_i-E_j}\right]$. Other estimation methods are also possible, e.g. using inverse propensity weighting or doubly robust (DR) estimators.

(Step 4) We integrate a(ϵ) to obtain the A(e₁, e₂), the effect of changing exposure from E = e₁ to E = e₂. The way we use PSM makes A(e₁, e₂) directional, meaning that we are estimating ATT going from E = e₁ (control) to E = e₂ (treated). Using other estimators one can estimate ATE instead.

The numerical integration is done using the trapezoid rule. For the simulation studies, 100 point estimates were used for the gradient a(ϵ). About 10 points got dropped from distribution tails with insufficient sample size for S_ϵ or $S_{ϵ}^{(m)}$. In the sepsis study every 5 minutes a point estimate is acquired (73 points from 60min to 420min, and again, about 10 of them dropped from tails for not having enough samples).

(Step 5) The exact same criteria used in Step 2 for accepting matched groups is applied for matching from E ≈ e₁ to further exposure value. E ≈ e₁ means 400 samples around E = e₁. The target exposure samples are selected from samples at E = e₂ or further than E = e₂ (measured from E = e₁). And the extent of common support is defined as 90% matching ratio between 400 samples at E ≈ e₁ and samples that are at E = e₂ or further (at least 360 matched pairs which must satisfy the same matching/balancing criteria given in Step 2).

Computational complexity.

The computational complexity is linear in the number of ϵ steps n, multiplied to PS matching complexity (PSM). For PSM we used nearest neighbor greedy algorithm in our code, which is linear in sample size. So computational complexities are O(nN ) for grad-PSM and O(nN_tot) for gtlt-PSM. For evaluating the extent of common support (or when path/direction independence assumption does not hold) one has to estimate the matching efficiency (or causal effect) on the surface of (e₁, e₂). This makes the complexity quadratic in the number of steps. We should mention that the algorithm is straightforward to fully parallelize in step iterations (independent for-loop parallelization). So with access to a computational grid, one can parallelize away the linear or quadratic in steps part and only deal with the underlying PSM complexity (or any propensity score method used in each local region).

B. Simulated Studies

Smoothing.

A final smoothing is applied on the effect curves. The integration step in proposed methods result in a smooth curve, however, to make all the results comparable, we use Gaussian kernel smoother on the final results for all the methods studied, with the same smoothing widths: 0.1 for simulated data and 20min for the real study.

U-shaped effect in GPS or GLM models.

Usually in biomedical studies one knows the direction of effect size (it being positive or negative). In Study 3, we defined the effect size to be U-shaped, so for GLM-DA and CB-GPS, we estimated the effect size for E < 0 and E > 0 separately and combined the results. These methods have no built-in facility to handle U-shaped effect curves.