Exercise increases information content and affects long-term stability of hippocampal place codes

Summary

Physical exercise is known to augment brain functioning, improving memory and cognition. However, while some of the physiological effects of physical activity on the brain are known, little is known about its effects on the neural code. Using calcium imaging in freely behaving mice, we study how voluntary exercise affects the quality and long-term stability of hippocampal place codes. We find that running accelerates the emergence of a more informative spatial code in novel environments and increases code stability over days and weeks. Paradoxically, although runners demonstrated an overall more stable place code than their sedentary peers, their place code changed faster when controlling for code quality level. A model-based simulation shows that the combination of improved code quality and faster representational drift in runners, but neither of these effects alone, could account for our results. Thus, exercise may enhance hippocampal function via a more informative and dynamic place code.

Graphical abstract

Highlights

• •Ca²⁺ imaging in behaving mice allows studying how exercise affects hippocampal codes
• •Voluntary physical exercise increases information content in hippocampal neurons
• •Runners exhibit faster changes in spatial codes if code quality levels are considered
• •Results favor the “memory resolution” over the “pattern separation” hypothesis

Rechavi et al. study how physical exercise affects neural coding underlying spatial cognition using longitudinal calcium imaging in the hippocampus of mice as they explore the same environments over weeks. Exercise supports the emergence of a more informative spatial code in novel environments and accelerates code dynamics over days.

Introduction

Physical activity is vital for maintaining a healthy brain, promoting memory and cognition in both humans (Kramer et al., 1999; Yaffe et al., 2001; Weuve et al., 2004; Hillman et al., 2005; Creer et al., 2010; Erickson et al., 2011, 2015; Bherer et al., 2013; Hayes et al., 2016; Basso and Suzuki, 2017; Kramer and Colcombe, 2018) and animals (Fordyce and Farrar, 1991b; van Praag et al., 1999a; Anderson et al., 2000; Cotman and Engesser-Cesar, 2002; Baruch et al., 2004; van Praag, 2005; Falls et al., 2010; Speisman et al., 2013). Exercise is particularly beneficial for hippocampal-dependent cognitive abilities (Fordyce and Farrar, 1991a; Anderson et al., 2000; Baruch et al., 2004; van Praag, 2005). The mechanisms by which physical activity aids hippocampal cognition and memory involve multiple factors, acting systemically and locally within the brain. These include an increase in neurotrophic factors (Neeper et al., 1995; Cotman and Berchtold, 2002; Vaynman et al., 2003, 2004; Liu et al., 2008; Rasmussen et al., 2009; Griffin et al., 2011; Marlatt et al., 2012; Sleiman et al., 2016), changes in neurotransmitters and their receptors (Fordyce and Farrar, 1991a; Gómez-Pinilla et al., 1997; Carro et al., 2000; Farmer et al., 2004; Fisher et al., 2013; Moon et al., 2016), vasculature alterations (Swain et al., 2003; Lopez-Lopez et al., 2004; Maass et al., 2015), increased dendritic spine density (Stranahan et al., 2007), reduced inflammation (de Miguel et al., 2021), and enhanced synaptic plasticity (O’Callaghan et al., 2007). One of the prominent effects of exercise is enhanced neurogenesis in the adult hippocampal dentate gyrus (van Praag et al., 1999a, 1999b; Wu et al., 2008), which, in turn, improves spatial and contextual discrimination (Clelland et al., 2009; Creer et al., 2010; Sahay et al., 2011a).

Given the well-established relationship between hippocampal activity and the above-mentioned cognitive functions (Scoville and Milner, 1957; Broadbent et al., 2006; Goshen et al., 2011), it is plausible that the improvement in these functions due to physical activity is mediated via changes in the hippocampal neural code. However, although much is known about the molecular and cellular factors that mediate the effects of exercise on hippocampal-dependent spatial cognition, it remains unknown how exercise affects hippocampal neural coding. To address this question, we performed longitudinal imaging of Ca²⁺ activity in the CA1 of mice as they repeatedly explored initially novel environments over weeks, and compared the hippocampal place codes of mice that voluntarily ran on wheels in their home cage with those of sedentary mice.

Results

We combined head-mounted miniaturized fluorescence microscopes (Ghosh et al., 2011; Ziv et al., 2013), chronic microendoscopy (Barretto et al., 2011), and viral-vector-based expression of a genetically encoded Ca²⁺ indicator (Chen et al., 2013) to perform longitudinal imaging of Ca²⁺ dynamics of large populations of hippocampal CA1 pyramidal cells in freely behaving mice. Two weeks after surgical implantation of a guide tube above the CA1, we randomly assigned mice to cages with functional (“runners”) or dysfunctional (“sedentary”) running wheels, where they acclimatized for 3 weeks. Then, we conducted a behavioral experiment (Figure 1A). First, mice were subjected to four pre-training sessions to become accustomed to running with a head-mounted microscope and learn to run back and forth along a linear track in order to obtain water rewards. Then, over the 3-week-long experiment, mice explored two different, initially novel linear tracks (environments A and B), marked by a distinct geometry, floor texture, surrounding proximal and distal visual cues, odor, and flavor of the water reward. Time-lapse imaging was performed in both environments every 3 days for a total of 16 sessions (eight sessions per environment). Each imaging session comprised five separate 3-minute-long visits (trials) to the same environment. In addition, to examine the contribution of voluntary physical activity to pattern separation (Creer et al., 2010; Sahay et al., 2011a), we imaged the mice while they visited two highly similar, novel, open-field environments (environments C and D).

Figure 1.

Studying the effects of voluntary physical exercise on adult neurogenesis and hippocampal CA1 spatial codes

(A) Top: Mice housed with either a functional (“Run”) or dysfunctional (“Sed”) running wheel were trained to run back and forth and collect rewards in two linear tracks. Bottom: Experimental timeline. After a pre-training period, we trained and imaged mice in the two environments every 3 days for 22 days. On day 25, the mice visited two circular, open-field arenas in a session consisting of four trials. They were injected with BrdU a day later and perfused 4 days later.

(B) Staining for BrdU and DCX in the DG.

(C) DCX expression per DG slice is higher in the runners (n = 6) versus sedentary (n = 7) group (two-sample one-sided t test, p < 0.01). Data presented as mean ± SEM across mice.

(D) Number of BrdU + cells per DG slice is higher in the runners (n = 6) versus sedentary (n = 7) group (two-sample one-sided t test, p < 0.05). Data presented as mean ± SEM across mice.

(E) Example place cells tracked across all days of the experiment. Dots represent Ca²⁺ events.

(F) Spatial tuning (rate maps) for the same cells across 8 recording days, ordered by the place fields’ centroid positions. The maps depict the changes in place cell activity patterns on different days.

(G) Population vector (PV) correlations between the representations of different locations (pooled from both running directions) across 8 recording days and averaged over all mice from the runners (left, n = 5) and sedentary (right, n = 5) mice.

(H) Average population vector correlations across all spatial locations and running directions, averaged across mice in each group. PVs were obtained by pooling data from all sessions in each environment.

We found that despite running extended distances in their home cage (4.2 ± 0.5 km per day, mean ± SEM, and up to more than 200 km throughout the experiment) (Figure S1A), runners ran similar distances, obtained a similar number of rewards, and had a similar running velocity to sedentary mice during the linear-track exploration (Figures S1B–S1D).

To assess the levels of hippocampal neurogenesis, we injected mice with Bromodeoxyuridine (BrdU), a marker for proliferating cells. In accordance with previous results (van Praag et al., 1999b), we found a higher number of BrdU-positive cells and increased labeling density of doublecortin (DCX), a protein transiently expressed in newborn neurons, in the DG of runners (Figures 1B–1D). This increase in adult neurogenesis indicates that physical activity affected the physiology of hippocampal circuits in our experiments.

We examined the consistency and quality of the code within each environment and asked (1) does physical activity lead to a more refined and informative spatial code? (2) How does physical activity affect the evolution of spatial representations as a function of the familiarization with the environments? The elevated neurogenesis levels of runners might suggest less stable place codes (over days), since the incorporation of new neurons into the hippocampal network could continuously change neuronal representations (Akers et al., 2014). Alternatively, place codes could be more stable over days due to the contribution of the hyperexcitable newborn neurons to the existing circuitry (Schmidt-Hieber et al., 2004). As expected, we found intact spatial representations of the linear tracks (Figures 1E–1H, S1E–S1I, S2A, and S2B). Consistent with recent work (Rubin et al., 2015), we found low population vector (PV) and ensemble activity-rate correlations between the different environments, confirming that the hippocampus distinctly represented the two environments in both groups (Figures S1E and S1F). Also in line with previous work (Karlsson and Frank, 2008), the number of neurons active in a given environment modestly decreased over time (Figure 2A), while the fraction of place cells increased, reflecting place code refinement with familiarization (Figures 2A and 2B). While exercise did not change the number of active neurons, the fraction of place cells, and their reliability in runners (Figures 2A, 2B, and S1G), it increased Ca²⁺ activity rates and event amplitudes relative to sedentary mice (Figures 2C and 2D). Furthermore, runners’ place cells had finer place fields and were more spatially informative than those in sedentary mice (Figures 2E–2G, S1J, and S1K).

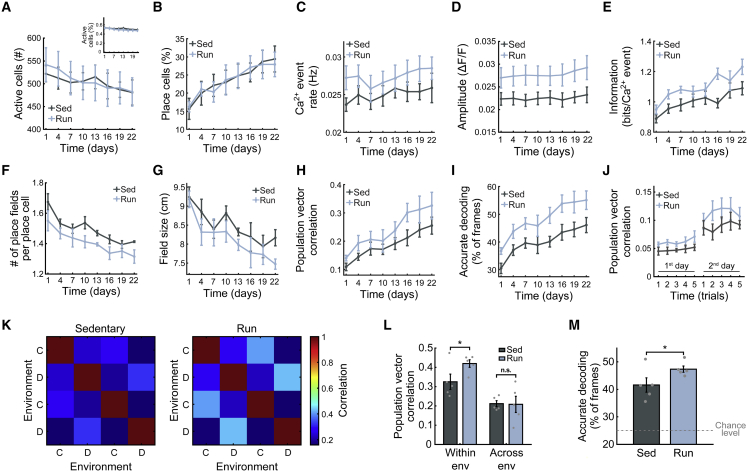
Figure 2.

The effects of voluntary physical exercise on the accuracy of hippocampal CA1 spatial codes

(A) Number of active cells per day. Both groups show a similar number of active cells per day (Friedman test, p > 0.5). Inset: the percentage of active cells out of the total number of cells that were active throughout the experiment.

(B) Percentage of place cells out of the population of active cells. Both groups show a comparable fraction of place cells (Friedman test, p > 0.5). Each group showed an increase in the portion of place cells with learning (paired-sample two-sided t test between the first and last sessions, p < 0.001 and p < 0.01, for sedentary and runners, respectively).

(C) Average Ca²⁺ event rate was higher in the runners versus sedentary group (Friedman test, p < 0.005).

(D) Average Ca²⁺ event amplitude in the runners was higher than in the sedentary group (Friedman test, p < 5^∗10⁻⁷).

(E) The average spatial information conveyed by CA1 place cells in the runners was higher than in the sedentary group (Friedman test, p < 0.00002).

(F) The average number of place fields per place cell decreased with time and was lower in the runners relative to the sedentary group (Friedman test, p < 0.00001).

(G) The average place-field size was smaller in the runners compared with the sedentary group (Friedman test, p < 0.015).

(H) PV correlations during running epochs across different trials within the same session were higher in the runners versus sedentary group (Friedman test, p < 0.0005).

(I) Performance of a within-session spatial decoder was better in the runners versus sedentary group (Friedman test, p < 5^∗10⁻⁷).

(J) Place code similarity between each trial on the first days of learning (days 1 and 4) and the spatial representations on the last days of learning (days 19 and 22). This similarity was lower for the last trial on the first day of learning than for the first trial on the second day of learning, for both groups (two-sided t test, p < 0.05 for both groups).

(K) PV correlation between the representations of different open-field environments (environments C and D) across different trials, averaged across mice.

(L) PV correlation between trials in which mice visited the same open-field environment was higher in the runners (two-sample one-sided t test, p < 0.05), but was similar to the sedentary group between trials in different environments (two-sample one-sided t test, p > 0.05).

(M) The performance of a spatial decoder in the open-field arena was higher in the runners versus sedentary group (two-sample one-sided t test, p < 0.05). The dashed line indicates chance level performance (25%). Data presented as mean ± SEM across mice. For all t tests: two groups, five mice per group. For all Friedman tests: same groups over eight sessions per mouse.

Next, we sought to determine how the consistency of the spatial representation within a session changes over time and between runners and sedentary mice. We found that the similarity between spatial representations across different trials within the same session increased with time, and was higher throughout the experiment in runners (Figure 2H). To measure the reliability of the population’s spatial representation at a higher temporal resolution, we devised a decoder for mouse position (see STAR Methods). Decoding accuracy improved with time in both the runners and sedentary mice, but was consistently better in runners (Figure 2I). The gradual increase in the fraction of place cells, neuronal activity rates, and spatial information indicates an improvement in the quality of CA1 spatial representations, reflecting a gradual familiarization process. For both groups, the similarity of the place code at a given trial to the code on the last days of learning was lower for the last trials on the first day than for the first trials on the second day (Figure 2J). This result suggests that offline plasticity processes may also contribute to establishing place codes in novel environments. Overall, we found a higher quality of CA1 place codes in runners than in sedentary mice (Figures 2 and S2). Importantly, we obtained similar results using different definitions of place cells and active cells (Figure S3), indicating our findings are not limited to any one definition of these subsets.

It is known that running (Creer et al., 2010), in part via adult neurogenesis, improves the performance of mice in tasks that require discriminating between similar spatial contexts (i.e., behavioral pattern separation). Two different cognitive mechanisms have been proposed to support such enhanced spatial discrimination ability: (1) Higher “memory resolution,” suggesting that the improvement results from an increase in the information content of neuronal representations (Aimone et al., 2011). (2) Improved “pattern separation,” suggesting that the enhanced discrimination arises from more distinct neuronal representations of different sensory inputs (Sahay et al., 2011b). While it is challenging to discern the exact mechanism using solely behavioral-level measurements, it could be readily determined using measurements at the neuronal-code level. Therefore, we imaged the mice as they explored two highly similar, novel, open-field environments on the same day (Figure 1A). Both groups showed comparable levels of similarity between the representations of the two different environments, but the runners exhibited higher similarity between the representations of the same environment (Figures 2K and 2L). The performance of a spatial decoder was likewise better in the runners than in sedentary mice (Figure 2M), suggesting a more informative representation of these environments in runners. These results did not stem from differences in the running velocities, exploration time, or overall activity rates (Figures S1L–S1N). Thus, our findings are consistent with the “memory resolution” hypothesis.

To assess the effect of running on the long-term stability of hippocampal place codes, we tracked cells across multiple sessions and estimated the registration accuracy for each registered cell using an established probabilistic method for cell registration (Sheintuch et al., 2017). We found no difference in registration quality between the groups (Figure S4A–E). When examining the level of similarity between representations of the linear tracks over days, we found that the PV correlations between pairs of subsequent sessions in the same environment increased with time in both groups (Figure S1O). A comparison of the across-days similarity of spatial codes in the two groups showed that the PV correlations were significantly higher in runners, irrespective of the elapsed time between sessions (Figure 3A), which may reflect increased code stability.

Figure 3.

The effects of voluntary physical exercise on the stability of hippocampal CA1 spatial codes

(A) PV correlations between the place cell activity patterns across days. The correlations between the neuronal representations on different sessions in the same environment were higher in the runners (Friedman test, p < 0.005).

(B) The correlations between the activity rates of all cells in different environments and on different days in the runners and sedentary mice were similar (Friedman test, p > 0.5).

(C) Correlations between the neuronal tuning curves in different environments and different days. The spatial tuning curve correlations as a function of elapsed time were more stable in runners versus sedentary mice (Friedman test, p < 0.001).

(D) The percentage of stable place cells out of the population of place cells was higher in runners versus sedentary mice as a function of elapsed time (Friedman test, p < 0.0005).

(E) The performance of a spatial decoder between adjacent days was higher in runners versus sedentary group (Friedman test, p < 0.0005).

(F) The performance of a spatial decoder as a function of elapsed time was higher in runners versus sedentary group (Friedman test, p < 5^∗10⁻⁸). Chance level in (E) and (F) = 5%. Data presented as mean ± SEM across mice. For all statistics: two groups, five mice per group, seven session-pairs per mouse.

As place code stability may be affected by the spatial tuning and activity levels of individual neurons (Ziv et al., 2013; Rubin et al., 2015), we examined which of these factors contributed to the observed place code stabilization. Previous work indicated that continuous changes in cells’ activity rates over days conveyed information about the temporal relationships between experienced events (Rubin et al., 2015). Similarly, ongoing changes in the population of highly excitable newborn neurons in the DG over timescales of days and weeks have been proposed as a mechanism for encoding time in episodic memory (Aimone et al., 2006). Thus, given the increased levels of neurogenesis in the runners, we hypothesized that the changes in place cell activity patterns result from changes in activity rates. To our surprise, across-day correlations in cells’ activity rates were similar between the two groups (Figures 3B and S1P). However, the spatial tuning of place cells in runners was more stable than in sedentary mice (Figures 3C and 3D). Moreover, the performance of an across-days spatial decoder improved as a function of time in both groups (Figure 3E). Similar to the PV correlation analysis results (Figure 3A), the performance of this spatial decoder was consistently better in the runners group than in the sedentary mice (Figures 3E and 3F).

However, poor code quality is characterized by a low signal-to-noise ratio, which inherently hinders the estimation of code stability (Figure 4A). Thus, we assessed to what extent are the differences in code stability between the groups linked to code quality. Rather than analyzing the PV correlation between neighboring days (a measure of code stability) as a function of time, we analyzed it as a function of the average information conveyed by place cells (a measure of code quality), as illustrated by the vertical and horizontal shaded areas in Figure 4B. We found that for a given level of code quality, runners showed lower PV correlations across neighboring days, i.e., faster changes in their place codes (Figures 4C and 4D). Therefore, the observed differences between the two groups (Figure 3A) could be explained by the difference in the distribution of code quality levels in each group. When we treated coding quality as a controlled variable, the difference between the groups was inverted (an effect known as “Simpson’s paradox,” Figure 4E, Simpson, 1951).

Figure 4.

Runners demonstrate a more rapid representational drift when accounting for code quality, and model-based simulated data recapitulates the experimental findings

(A) We posit that physical activity affects code stability via two pathways with opposite effects: (1) through representational drift (gradual time-dependent changes in the responsiveness of neurons) and (2) through the increase in code quality (learning dynamics), which, in turn, effectively stabilizes the code.

(B) Schematic overview: Instead of examining the difference between the two groups for a given time (vertical gray area), we compared the two groups for a given code quality level (horizontal gray area).

(C and D) Information versus code stability. For a given code quality (i.e., information), the code stability (PV correlation across adjacent days) was higher in the sedentary group, indicating slower changes in encoding relative to the runners. (C) Data averaged per day. (D) Each data point represents a single day in a single mouse (two-sample, two-sided t test, p < 0.05). This difference between the two groups remained significant when applying a method for bias-free estimation of spatial information (Sheintuch et al., 2022) (two-sample, two-sided t test, p < 0.016, inset).

(E) Illustration of Simpson’s paradox: Overall, y values are higher for the blue group, although lower for the blue group for any given value of x. For all statistics: two groups, five mice per group, seven session-pairs per mouse.

(F) Model illustration: To represent learning, the spatial tuning of place cells improved over time (left panel). To capture representational drift, each of these place cells' preferred position randomly shifted along days (right panel).

(G–J) Simulated data (data presented as mean ± SEM): (G) The average information conveyed by place cells in the runners was higher than in the sedentary group. (H) Code similarity across adjacent days (i.e., PV correlation) in the runners was higher than in the sedentary group. (I) Code similarity as a function of elapsed time in the runners was higher than in the sedentary group. (J) Average information versus adjacent days code similarity, day-averaged data. For a given code quality, the code stability was higher in the sedentary group.

Previous work demonstrated representational drift in mice that explored familiar environments (Ziv et al., 2013; Rubin et al., 2015; Cai et al., 2016; Driscoll et al., 2017; Hainmueller and Bartos, 2018; Sheintuch et al., 2020). In our experiment, mice learned to navigate in novel environments, and therefore some of the observed changes in the CA1 place codes are due to the mouse familiarization with these environments. To better tease apart the effect of code quality on code stability across days from changes in the code due to ongoing representational drift, we devised a model and used it to simulate the spatial tuning of place cells on the different days of the experiment. Our model included a population of place cells, each with a defined spatial tuning that improved over days (“Learning”), and a preferred position that randomly shifted over days (“Representational drift”) (Figure 4F). This allowed us to study the combination of these two factors, as well as the effect of each of them in isolation, on the differences between coding dynamics in the two groups. When simulating both improved learning dynamics and faster representational drift in the runners compared with the sedentary group, the model yielded qualitatively similar results to those observed in the experimental data: (1) higher code quality (i.e., information content) per day in the runners group (Figure 4G), (2) higher code similarity across adjacent days (i.e., PV correlation) in the runners group (Figure 4H), (3) higher code similarity as a function of elapsed time in the runners group (Figure 4I), and (4) higher code similarity across adjacent days for a given code quality in the sedentary group (Figure 4J). Importantly, when accounting for only one of these factors, the model did not recapitulate the experimental data. Specifically, considering different learning dynamics but with the same representational drift rates yields qualitatively similar results to those observed in the experimental data with regard to higher code quality per day, code stability across adjacent days, and code stability as a function of elapsed time in the runners (Figures S4F–S4H), but failed to capture the higher across adjacent days code stability for a given code quality in the sedentary group (Figure S4I). Correspondingly, considering different representational drift rates but with the same learning dynamics yields qualitatively similar results to those observed in the experimental data with regard to the higher code stability across adjacent days for a given code quality in the sedentary group, but fails to capture the effects seen in code quality per day, across adjacent days code stability, and code stability as a function of elapsed time (Figures S4J–S4M). Overall, these results imply a role for physical activity in both improving the spatial code and accelerating representational drift in the hippocampus.

Discussion

Here, we studied how physical activity affects the neural coding mechanisms underlying spatial cognition and memory by longitudinally imaging the activity of large neuronal populations in the hippocampus of freely behaving physically active or sedentary mice as they became familiarized with two distinct environments over the course of 3 weeks. While the number of active cells and fraction of place cells did not differ between the groups, runners exhibited higher Ca²⁺ event rates and amplitudes, higher information rates, and more refined and stabler place fields. Since the velocity and number of traversals on the linear track were similar between the two groups, it is unlikely that the effects of exercise on spatial coding simply resulted from improved physical fitness or track coverage. In the open-field environments, the runners showed improved decoder performance and a more consistent population representation of the same environment. However, we found no differences between the groups in Ca²⁺ event rates and spatial information, implying the susceptibility of these cell-level measures to short sample durations.

Although the naive analysis suggested that spatial representations are more stable in the runners, we found that representations changed faster in runners when accounting for the level of code quality. Importantly, our simulations show both improved code quality and faster representational drift in the runners, but neither of these effects alone could explain our results. Thus, exercise may benefit hippocampal function by increasing the information content while accelerating representational drift.

In agreement with previous studies, the level of neurogenesis in the dentate gyrus increased in the runners. One of the most accepted hypotheses suggests that adult neurogenesis contributes to pattern separation (Sahay et al., 2011a, 2011b; Yassa and Stark, 2011), i.e., it supports the encoding of events with similar features as distinct neuronal representations in downstream areas. Specifically, by recruiting distinct sets of newborn neurons to encode different episodes, neurogenesis reduces interference between stored memories. Accordingly, animals with increased neurogenesis should better distinguish between events that occurred in distinct but similar environments. The “memory resolution” hypothesis is comparable to the “pattern separation” hypothesis in that it predicts similar outcomes at the behavioral level for varying rates of neurogenesis, but suggests a different underlying coding mechanism: that newborn neurons in the DG increase the information content of neuronal representations, thereby enhancing the resolution of the encoded memories (Aimone et al., 2011; Johnston et al., 2015). Our findings that under conditions in which neurogenesis was elevated, mice exhibited a more informative neuronal activity (Figure 2E), but not more distinct representations of similar novel environments (Figures 2K–2M), favor the “memory resolution” over the “pattern separation” hypothesis.

Another theory suggests that the continuously changing subsets of immature neurons provide common signatures for events that occur close in time, effectively binding them in memory in temporal clusters (Aimone et al., 2006). Accordingly, neurogenesis may benefit episodic memory by having relative time represented in a continuum of memory associations. This hypothesis emphasizes the “rolling” impact of turnover in the newborn neuron population on memory encoding. We previously found that ongoing gradual changes in the activity rates of CA1 neurons confer information about the temporal relationships between experienced events, even if these events occurred in distinct environments (Rubin et al., 2015). Surprisingly, in the current study, changes in neuronal activity rates were similar between the runners and sedentary mice (Figure 3B), suggesting that elevated neurogenesis levels did not contribute to improved “temporal binding” capabilities over timescales of weeks.

Previous studies showed that animals with increased neurogenesis rates perform worse than control animals on tasks that require the retention of memory over timescales of days and weeks. This suggests that the continuous integration of new neurons into existing circuitry disrupts information already stored in these circuits, resulting in the clearance of and even forgetting stored memories (Frankland et al., 2013; Akers et al., 2014; Epp et al., 2016; Ishikawa et al., 2016). According to this idea, which attributes a negative, retrograde impact of neurogenesis on pre-existing representations, increased neurogenesis should destabilize hippocampal memory codes. Indeed, although the naive analysis showed that the fraction of place cells with a stable place field was higher in the runners than in the sedentary mice (Figure 3D), when accounting for code quality levels, we found that place codes in the runners changed faster (i.e., were less stable).

Notably, several recent studies demonstrated representational drift over timescales of days in various brain areas, including the hippocampus (Rubin et al., 2015; Cai et al., 2016; Hainmueller and Bartos, 2018; Sheintuch et al., 2020), posterior parietal cortex (Driscoll et al., 2017), visual cortex (Deitch et al., 2021; Marks and Goard, 2021), and olfactory cortex (Schoonover et al., 2021). The mechanisms underlying representational drift remain elusive, but it is likely that network architecture determines code stability to some extent since drift rates differ across different brain areas (Deitch et al., 2021). Importantly, since physical activity is associated with improved brain function, the observed increased representational drift in runners hints at the possibility that drift has a functional role. One such role may be expediting neural code reconfiguration, which underlies protracted learning of new spatial environments and long-term memory consolidation (Mau et al., 2020). Thus, our results warrant reconsidering the naive, commonly assumed relationship between code stability and circuit functionality.

Limitations of the study

Here we demonstrate the effect of voluntary physical activity on hippocampal spatial code properties, and show the known effect of exercise-induced adult neurogenesis enhancement. However, increased adult neurogenesis is one of numerous effects of voluntary physical activity, and the observed changes in hippocampal coding may be mediated in part or in full by other mechanisms. Another limitation is that the results were obtained for learning of novel environments. It is yet to be determined what are the effects of physical activity on code quality, code stability, and the interaction between them in a familiar environment. In addition, our experimental design does not provide an explicit behavioral readout of a hippocampal-dependent function. However, the link between physical activity and improved cognition is well established in the literature.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and virus strains
pAAV2/5-CaMKIIα-GCaMP6f	UNC vector core	Cat #5834
Chemicals, peptides, and recombinant proteins
C&B Metabond	Parkell	S380
Ultraviolet-curing adhesive	Norland Products Inc.	NOA 81
Flow-It ALC	Pentron	Univ. Opaque
Bromodeoxyuridine	Sigma-Aldrich	Cat #B5002
anti-doublecortin	Santa Cruz	SC-8066
anti-BrdU	Bio-Rad	MCA-2060
Biotin-SP AffiniPure Donkey Anti-Goat IgG	Jackson Immuno Research	RRID: AB_2340397
Cy3-Streptavidin	Jackson Immuno Research	RRID: AB_2337244
Cy5-Donkey anti-rat	Jackson Immuno Research	RRID: AB_2340672
Experimental models: Organisms/strains
C57BL/6J	Envigo Israel	RRID:IMSR_JAX:000,664
Software and algorithms
Original code	This paper	https://doi.org/10.5281/zenodo.7229556
nVista Acquisition Software	Inscopix inc.	Version 2.0
IC Capture	The imaging source	Version 2.3
MATLAB (version 2014a and onward)	mathworks	https://www.mathworks.com/products/matlab.html
Mosaic	Inscopix inc.	1.1.1b
CellReg – cell registration method	Sheintuch et al. (2017)	https://github.com/zivlab/CellReg
Deposited data
Data to produce figures	This paper	https://doi.org/10.5281/zenodo.7229556
Other
Integrated miniature fluorescence microscope	Inscopix inc.	nVista 2.0
Gradient refractive index (GRIN) lens	Inscopix inc.	Cat # 1050-002176
Overhead camera for recording animal behavior	The imaging source	DFK 33G445

Resource availability

Lead contact

Further information and requests should be directed to the lead contact, Yaniv Ziv (yaniv.ziv@weizmann.ac.il).

Materials availability

This study did not generate new unique reagents.

Experimental model and subject details

Animals

All procedures were approved by the Weizmann Institute’s IACUC. A total of 13 male mice, aged 15 weeks at the start of imaging, were used in this study. Out of these 13 mice, 10 were used for the neuronal analyses (n = 5 for each group), while 3 were excluded due to poor imaging quality. Mice were initially housed with 2 cage-mates in cages without a running wheel in a 12:12 h reverse light cycle (lights off 10am-10pm). At age 11–12 weeks, the mice were divided into the ‘runners’ and ‘sedentary’ groups, and were housed accordingly with either a functional or a stuck (dysfunctional) running wheel. Five days later, all the mice were single housed in order to assess each individual’s home cage running distance. Two days later, water restriction started. From this point and until the end of the experiment, mice underwent a daily health inspection (Guo et al., 2014), and their body weight was kept above 80% of their initial weight.

Method details

Surgical procedures

We first injected into the CA1, under isoflurane anesthesia (1.5–2% volume), 500nL of viral vector AAV2/5-CaMKIIa-GCaMP6f (∼2X10¹³ particles per ml, packed by University of North Carolina Vector Core) (Chen et al., 2013) at stereotatic coordinates: −1.9 mm anterio-posterior, −1.4 mm mediolateral, −1.6 mm dorsoventral from bregma. Mice were then allowed to recover for at least a week. We then implanted all mice with a glass guide tube directly above the CA1. We used a trephine drill to remove a circular part of the skull centered posteriolateral to the viral injection site. We removed the dura and cortex above the CA1 by suction with a 29-gauge blunt needle while constantly washing the exposed tissue with sterile PBS. We then implanted an optical guide tube with its window just dorsal to, but not within, area CA1 and sealed the space between the skull and the guide tube using 1.5% agarose in PBS. The exposed areas of the skull were then sealed with Metabond (Parkell, Edgewood, NY) and dental acrylic.

Home cage running wheels

Mice in the ‘runners’ group were given continuous access to a running wheel (Low Profile Running Wheel, Med Associates Inc.) in their home cage. Wheel revolutions were recorded on non-imaging days to track the running distance. Mice ran an average of 4.2 ± 0.5 km per day, mean ± SEM.

Histology

To assess the levels of neurogenesis at the end of the experiment, we injected the mice with Bromodeoxyuridine (BrdU; a marker for proliferating cells), and euthanized them four days later. Mice were deeply anesthetized with Pental and perfused transcardially with 4% buffered formaldehyde. Brains were extracted and post-fixed in 4% formaldehyde for 24 hours. Sections 70μm in width were cut on a vibratome, and free-floating sections were stored in 0.01% sodium azide in PBS. Sections were incubated at 37°C for 30 min in 2N hydrochloric acid and then transferred to Borate buffer for 10 min at room temp. The sections were then blocked with 20% normal horse serum before being incubated overnight at room temp with anti-doublecortin (Santa Cruz, SC-8066) and anti-BrdU (Bio-Rad, MCA-2060) primary antibodies, both diluted 1:100 in 0.5% Triton X- and 2% normal horse serum. The sections were then incubated for 90 min in Biotin-SP AffiniPure Donkey Anti-Goat IgG (Jackson Immuno Research, 705-065-147) and afterward incubated for 30 min in Cy3-Strepavidin (diluted 1:100 in PBS) and Cy5-Donkey anti-rat (diluted 1:100 in PBS) secondary antibody. Quantification was performed using confocal microscopy with an ×20 objective. BrdU-positive cells were counted through the anterior–posterior extent of the dentate gyrus using a 1/5 sampling fraction. This was done for each slice from a given mouse and then averaged over all slices from that individual mouse. For DCX quantification, we manually detected two areas in each slice: the DG area and a background area. We defined the intensity threshold to determine DCX-positive pixels as the intensity of the 99th percentile in the background area. To quantify DCX expression for each mouse, we divided the number of pixels above the aforementioned threshold by the number of total pixels in the selected DG area for each slice from a given mouse and then averaged over all the slices from that individual mouse.

Ca²⁺ imaging and behavioral setup

To perform time-lapse imaging in freely behaving mice using an integrated miniature fluorescence microscope (nVistaHD, Inscopix), we followed an established protocol (Ziv et al., 2013). Mice were water-restricted and habituated to human handling by allowing them to walk on the experimenters’ hands. At least three weeks after guide-tube implantation, mice were imaged under isoflurane anesthesia using a two-photon microscope (Ultima IV, Bruker, Germany). We inserted a microendoscope consisting of a single gradient refractive index lens (1 mm diameter, GRINtech GmbH, Germany) into the guide tube and examined Ca²⁺ indicator expression and tissue health. We selected for further imaging only those mice that exhibited homogeneous GCaMP6f expression and appeared to have healthy tissue. For the selected mice, we then affixed the microendoscope within the guide tube using an ultraviolet-curing adhesive (Norland, NOA81, Edmund Optics, Barrington, NJ). Next, we attached the microscope’s base plate to the dental acrylic cap using a light cured adhesive (Flow-It ALC, Pentron, Orange, CA). To record mouse behavior, we used an overhead camera (DFK 33G445, The Imaging Source, Germany), which we synchronized with the integrated microscope. Ca²⁺ imaging was performed at 20Hz. After a few days, we began pre-training the mice to run back and forth on an elevated 50-cm-long linear track for water rewards. The pre-training consisted of four sessions at two-day intervals. Afterward, we began imaging the mice while running back and forth on two novel linear tracks (environments A and B). Environment A was a straight 96-cm-long track and Environment B was an L-shaped track consisting of two 48-cm-long arms. Each environment had distinct sets of visual and tactile cues, overhead lights, flavored liquid rewards, and odor cues, and both differed from the short (50 cm) track on which they were pre-trained. Before the beginning of each pre-training or imaging session, we wiped the tracks with differently scented paper towels (10% ethanol for environment A and 0.5% acetic acid for environment B). We trained the mice to run back and forth along the track by giving them a measured amount of water sweetened with either a commercial fruit juice concentrate or sucrose (lemon flavored with 2% added sugar by weight for track A and 6% sucrose water for track B). The water reward was dispensed using a custom-made computer-controlled device. Pre-training and imaging sessions consisted of five 3-min-long trials, with an inter-trial interval of 3 min. During the 3-min inter-trial interval, mice were placed in a bucket near the track. We imaged the mice every three days for 22 days, 8 recording days altogether. Each day of the experiment consisted of two sessions (AM and PM) separated by 4–5 h.

Three days later (day 25), we conducted an additional imaging session in which all of the mice freely explored two round open arenas (environments C and D). The circular arenas (30 cm in diameter) differed in their floor texture and proximal cue. This session consisted of four 7-min-long trials, with an inter-trial interval of 4 min. During the 4-min inter-trial interval, mice were placed in a bucket near the arena.

Tracking the mouse’s position

We analyzed mouse behavioral videos using a custom MATLAB (Mathworks) routine that detects the mouse’s center of mass in each frame. We then used the estimated position to calculate its velocity, and applied a smoothing filter (rectangular window of 250 msec) to the calculated velocity.

Processing of Ca²⁺ imaging data

We processed the Ca²⁺ imaging data using commercial software (Mosaic, version 1.1.1b, Inscopix) and custom MATLAB routines (Ziv et al., 2013; Rubin et al., 2015). To increase the computation speed, we spatially down-sampled the data by a factor of four in each dimension (final pixel size of 2.3 × 2.3 μm). To correct for non-uniform illumination, both in space and time, we normalized the images by dividing each pixel by the corresponding value from a smoothed image. The smoothed image was obtained by applying a Gaussian filter with a radius of 100μm to the movies. Normalization also enhanced the appearance of the blood vessels, which were later used as stationary fiducial markers for image registration. We used a rigid-body registration to correct for lateral displacements of the brain. This procedure was performed on a high-contrast sub-region of the normalized movies in which the blood vessels were most prominent. The movies were transformed into relative fluorescence changes, $\frac{\Delta \text{F}\left(\text{t}\right)}{{\text{F}}_0}=\left(\text{F}\left(\text{t}\right)-{\text{F}}_0\right)/{\text{F}}_0$, where F₀ is the value for each pixel averaged over the entire recording duration. For cell detection, the movies were down-sampled in time by a factor of five. We detected spatial footprints corresponding to individual cells using an established cell-detection algorithm that applies principal and independent component analyses (PCA and ICA; Mukamel et al., 2009). For each spatial footprint, we used a threshold of 50% of the footprint’s maximum intensity, and each pixel that did not cross this threshold was set to zero. After the cells were detected, further cell sorting was performed to identify the spatial footprints that follow a typical cellular structure. This was done by measuring the footprint area and circularity, discarding those whose radius was smaller than 5μm or larger than 15μm or that had a circularity smaller than 0.8. In some cases, the output of the PCA/ICA algorithm included more than one component that corresponded to a single cell. To eliminate such occurrences, we examined all pairs of cells with centroid distances <18μm; whenever their traces had a correlation >0.9, the cell with the lower average event peak amplitude was discarded. We detected 387–646 cells per imaging session.

Detection of Ca²⁺ events

Ca²⁺ activity was extracted by applying the thresholded spatial footprints to the Ca²⁺ movies at full temporal resolution (20Hz) $\Delta \text{F}\left(\text{t}\right)/{\text{F}}_0$. Baseline fluctuations were removed by subtracting the median trace (20 s sliding window). The Ca²⁺ traces were smoothed with a low-pass filter with a cutoff frequency of 2Hz. Ca²⁺ candidate events were detected whenever the amplitude crossed a threshold of 5 median absolute deviations (MAD). We considered for further analysis only candidate Ca²⁺ events with an indicator decay time equal to or longer than 200 msec. In order to avoid the detection of several peaks corresponding to a single Ca²⁺ event, only peaks 5 MAD higher than the previous peak (within the same candidate event) and 2.5 MAD higher than the next peak were regarded as true events. We set the Ca²⁺ event occurrence to the time of the peak fluorescence. To mitigate the effects of crosstalk (i.e., spillover of Ca²⁺ fluorescence from neighboring cells), we adopted a conservative approach, allowing only one cell from a group of neighbors (pairs of cells with centroid distances <18μm) to register a Ca²⁺ event in any 200 msec time window. If multiple Ca²⁺ events occurred within ∼200 msec in neighboring cells, we retained only the event with the highest peak $\Delta \text{F}\left(\text{t}\right)/{\text{F}}_0$ value. If two neighboring cells had a correlation >0.9 in their events, the cell with the lower average peak amplitude was discarded. After the events were identified, further event sorting was performed to find the cells with sufficient signal-to-noise ratios. This was done by measuring the event rate and the average event peak amplitude for each cell and discarding those whose event rate was smaller than 0.01Hz or which had an average event amplitude smaller than 1% ($\Delta \text{F}\left(\text{t}\right)/{\text{F}}_0$).

Registration of cells across sessions

To identify the same neurons across multiple imaging sessions, we used a probabilistic method for cell registration (Sheintuch et al., 2017). This method models the distribution of spatial correlations and centroid distances for neighboring cells from different recording sessions (candidates to be the same cell) as a weighted sum of the distributions of two subpopulations of cell pairs, representing the same cells and different cells. Then, based on the model that best fits the data, the method estimates the probability of each candidate in the dataset to be the same cell (P_same). This allows the estimation of the overall rates of false-positive (different cells falsely registered as the same cells) and false-negative (the same cells falsely registered as different cells) errors, providing a registration threshold that is optimized to the dataset of each mouse. The threshold used for registration controls the tradeoff between false-positive and false-negative errors. Therefore, we chose a registration threshold that corresponds to P_same = 0.5, which constitutes an appropriate balance between false-positive and false-negative registration errors (Sheintuch et al., 2017). Note that while some of the same-cell candidates had intermediate spatial correlation values, the vast majority of such cell pairs exhibited either very high spatial correlations (suggesting they are the same cells), or very low spatial correlations (suggesting they are different cells). Overall, we could track the same neurons across multiple imaging days with estimated cell scores (Sheintuch et al., 2017) of 0.86 ± 0.14 (“runners group”) and 0.84 ± 0.15 (“sedentary group”) with no significant difference between the two groups (two-sample two-sided t test, p = 0.243, Figure S3E). Furthermore, in cases with multiple candidates that cross the registration threshold, only the pair with the highest P_same was registered as the same cell, thus avoiding some of the false-positive errors, resulting in lower percentages of false-positive errors than those estimated by the probabilistic model. Importantly, since the microscope remained head-mounted throughout each session (i.e., maintaining exactly the same focal plane and field of view), the data processing and cell detection was done together for all trials within each session. Therefore, no cell registration was required across trials from the same session. Overall, we recorded from five mice per group and a total of: 958, 1028, 1002, 944, and 1164 cells per mouse in the runners group, and: 888, 940, 1083, 941, and 1031 cells per mouse in the sedentary group.

Rate maps

For the place field analysis, we considered periods wherein the mouse ran >2 cm/s. We divided each track into 24 bins (4 cm each) and calculated the time spent in each bin and the number of Ca²⁺ events per bin (Rubin et al., 2015; Ziv et al., 2013). We then calculated the activity map (event rate per bin, excluding the last 2 bins at each end of the tracks) for each neuron by dividing the overall number of Ca²⁺ events per bin by the overall occupancy per bin. We separately considered place fields for the two running directions on the linear tracks. The same procedure was applied also for visualization of single place cells (Figures 1 and S2). For each running direction, we defined the preferred position as the position with a peak value within the activity map.

Place tuning analysis

Active cells were defined as cells with ≥5 detected events in a given session (we further verified that our results are not susceptible to this definition; see Figure S3). We calculated the spatial information (in bits per event) of these cells using the events-rate map of each cell (Markus et al., 1994):

$$Spatial\mathit{inf}ormation=\sum _i{p}_i\left(\frac{r_i}{\overline{r}}\right)lo{g}_2\left(\frac{r_i}{\overline{r}}\right),$$

where p_i is the probability of the mouse to be in the i^th bin (time spent in i^th bin/total running time); r_i is the Ca²⁺ event rate in the i^th bin; and $\overline{r}$ is the overall mean Ca²⁺ event rate. We then performed 10,000 distinct shuffles of animal locations during Ca²⁺ events, accounting for the spatial coverage statistics for the relevant trial and running direction, and calculated the spatial information for each shuffle. This yielded the p value of the calculated spatial information relative to the shuffles. Cells with spatial information higher than that of 95% of their shuffles were considered significant place cells (we further verified that our results are not susceptible to this definition; see Figure S3). To reduce the estimation bias of the spatial information, we subtracted from the spatial information of each cell the mean spatial information calculated for its shuffles. The fraction of place cells in each trial was defined as the number of significant cells out of the number of active cells in that trial. When the average spatial information is presented, average and SEM are calculated over mice. The spatial information per mouse was calculated by averaging over all place cells in each given running direction and session, then averaging over the two running directions, and then averaging over same-day sessions (the two linear tracks). We further validated our results (Figures 2, 4, and S1) by applying scaled shuffle reduction (SSR) correction for bias-free estimation of spatial information (Sheintuch et al., 2022). When plotting the PV correlation as a function of the mean spatial information (Figures 3, 4, and S5), the PV correlation was calculated between neighboring days and the spatial information was averaged across these two days.

Population vector correlation

To determine the level of similarity between representations of the environment on different trials, we calculated the mean population vector correlation between them (Leutgeb et al., 2005). For the linear tracks, we defined the population vector for each spatial bin (excluding the last 2 bins at each end of the tracks, and separating between right and left running directions) as the mean event rate for each neuron in that bin. We calculated the Pearson’s correlation between the population vector in one session with that of the matching location in the other session, and averaged the values over all positions (for the across-sessions analysis) or between the population vector in one trial with the population vector compiled by the rest of the trials within the same session, and averaged the values over all the positions and over all the trials within the session (for the within-session analysis). For the open-field arenas, we defined the population vector for each spatial bin (each arena was divided into four spatial bins) as the mean event rate for each neuron in that bin. We then calculated the correlation between the population vector in each trial with that of the population vector corresponding to the matching location in other trials, and averaged the correlations over all the positions.

Tuning-curve correlation

To quantify the similarities in the spatial tuning preference of individual place cells across sessions (regardless of changes in their activity rates), we calculated for each place cell the Pearson’s correlation between its rate maps in different sessions and then averaged the obtained values across all cells for each pair of sessions.

Average activity rate and event amplitude

To calculate the activity rate, we measured the overall Ca²⁺ event rate for each neuron in each session (regardless of position or running direction, with an activity threshold of ≥5 detected events in a given session). We then averaged this for each mouse and each session over all active neurons. Afterward, we averaged over same-day sessions (the two linear tracks). The average Ca²⁺ event amplitude was calculated for each cell, averaged over cells and then averaged over mice.

Ensemble-rate correlation

To quantify the similarities in activity patterns between trials, without accounting for place tuning, we measured the overall Ca²⁺ event rate for each neuron in each trial (regardless of position or running direction). We then defined the ensemble-rate correlation as the Pearson’s correlation between the vectors (for all neurons) of the Ca²⁺ event rates.

Place fields

A place field’s center was defined as the bin in which the maximal Ca²⁺ event rate was detected for each place cell (done for each running direction separately). Stable cells were defined as place cells that retained their place-field center between sessions (≤4 cm shift). For the calculation of place field width, we considered the overall area of spatial bins with a rate >0.33 of the maximum event rate.

Spatial decoder

For the linear tracks, we constructed a decoder to infer the position of the mouse at each frame in a given trial or session (test data) based on the relations between the neuronal activity patterns during the exploration of the same environment on other trials within the same session or other sessions (training data), respectively. We defined the activity pattern of each spatial bin in the training data as the vector of the activity rate per neuron at that bin. For each frame in the test data (50 ms), we inferred the mouse’s position by maximizing the correlation of the activity pattern in that frame with the activity pattern of a bin in the training data (namely, the decoded position was the bin whose activity pattern had the highest correlation with that of the decoded frame). For this analysis, we considered only running epochs (velocity>2 cm/s and excluding the last 2 bins at each end of the tracks). We smoothed the neuronal activity data by applying a sliding window of 2 frames (100 ms) and excluded frames without any neuronal activity (<1 event/frame). For the calculation of accurate decoding percentage, we defined frames whose decoded position was >4 cm (one spatial bin) away from a true position as erroneous.

For the open-field arenas, we constructed a decoder designed to decode the specific position of the mouse within the given environment it is exploring. Each of the open-field environments was divided into four spatial bins, and we defined the activity pattern of each spatial bin in one trial (training data) as the vector of the activity rate per neuron at that bin. For each frame from the other trial (test data) in the same environment, we inferred the mouse’s position by maximizing the correlation of the activity pattern in that frame with the activity pattern of a bin in the training data. For each one of the two open arenas, we calculated the accurate decoding percentage twice: once with the first trial as training data and the second trial in the same environment as the test data, and vice versa. Finally, we averaged over these two values and then over the values for the two open-field arenas (Environments C and D) to define one accurate decoding percentage value for each mouse. The Ca²⁺ activity was smoothed using a rectangular sliding window of 250 ms.

Model-based simulation

We simulated a model of code dynamics in place cells that is driven by both learning and representational drift (Ziv et al., 2013; Rubin et al., 2015), as well as two additional variants of the model, ones considering only learning or only representational drift. All three models assume a population of place cells. For each place cell, we defined a spatial tuning with a single Gaussian place field. The preferred position (peak activity rate, i.e., place-field center) of the cells was uniformly distributed along the linear track. To match the experimental design, we simulated neuronal tuning for the same neurons over eight days; each day consisted of five trials. The code quality of a given cell on a given day was defined by the variance of its preferred position across the different trials within that day.

The variance was equal for all cells within the same mouse on the same day. The evolution of the spatial code was composed of two factors: (1) Learning; realized as a decay of the within-day variance (${\sigma }_{noise}^2$) over days, and (2) Representational drift; realized as stationary day-to-day changes in the spatial-tuning curves. The changes in the spatial tuning curves driven by representational drift were simulated as random (normal, $\mu =0$ ${\sigma }_{drift}^2$) changes in the mean preferred position of the cell. In each day, the change was defined relative to the mean preferred position of the cell at the previous day; hence, these changes accumulated over days. The same place cell had different place-field centers on different trials, which were rendered using the mean preferred position of the cell and the across-trial variance for that given day. We simulated neuronal representations of the environment over the different days of the experiment in mice from two groups, runners and sedentary mice. These groups differed solely in their learning dynamics and their representational-drift rates. Runners had better learning dynamics (lower and faster decaying across-trials variance) and higher representational drift rates (greater changes in the mean preferred position of each cell over days) compared to sedentary mice. We simulated spatial tuning over a 1D track that was divided into 20 spatial bins (similar to the analysis of the neuronal data, in which we divided the track into 24 spatial bins and omitted two bins from each end due to the stationary behavior at the edges). For each mouse, we simulated 400 place cells. All the cells had a unimodal Gaussian spatial tuning with sigma = 1 bin around the preferred position. The drift constant (${\sigma }_{drift}$) was 1.2 bins and 0.9 bins for runners and sedentary mice, respectively. Improvement in the code quality over days (learning dynamics) was modeled as an exponential decay of the within-day noise constant (${\sigma }_{noise}$). The noise constant started at 3.6 and exponentially decayed to 1.5 with a time constant of 0.06 for mice in the runners group, and started at 4 and exponentially decayed to 2 with a time constant of 0.05 for the sedentary group. To model the sole effect of learning dynamics on the difference between the two groups, we set the drift constant to be identical in both groups (${\sigma }_{drift}$ = 1.2 bins). To model the sole effect of representational drift on the difference between the two groups, we set the parameters of the learning dynamics to be identical in both groups (noise constant ${\sigma }_{noise}$ started at 4 and exponentially decayed to 2 with a time constant of 0.05). We simulated five mice per group, matching the experimental design, and rendered the simulation 50 times. Mean and SEM are calculated per repetition; for visualization (Figures 4C–4E and S5A–S5H), the data are averaged over all repetitions.

Behavioral analysis

To compare the mice’s behavior across the different groups, we measured the track traversal and the median speed of each mouse. The number of track traversals was measured based on the number of times a mouse reached either of the two track ends. The median speed was calculated based on the periods for which a mouse was not stationary (≥2 cm/s). For the open-field arenas, we also measured the exploration time, which we defined as the percentage of time for which the mice ran at >2 cm/s out of the total time of each trial.

Quantification and statistical analysis

The statistical analysis was conducted using MATLAB 2018b software. We analyzed unrelated samples by way of a t test or Friedman test. Statistical details of experiments can be found in the figure legends, Results section, and STAR Methods section. Throughout the paper, the results of the Friedman tests for comparison between runners and sedentary mice were consistent with those of a two-way repeated-measures analysis of variance (ANOVA).

Published: November 22, 2022

Data and code availability

• •Data to reproduce the figures is available as of the date of publication at https://github.com/zivlab/hpc_physical_exercise. DOI is listed in the key resources table.
• •All original code has been deposited at Zenodo and is publicly available as of the date of publication. DOIs are listed in the key resources table.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.