Abstract
As supplying adequate blood in multiple countries has failed due to the Covid-19 pandemic, the importance of redesigning a sensible protective-resilience blood supply chain is underscored. The outbreak-as an extensive disruption-has caused a delay in ordering and delivering blood and its by-products, which leads to severe social and financial loss to healthcare organizations. This paper presents a robust multi-phase optimization approach to model a blood supply network ensuring blood is collected efficiently. We evaluate the effectiveness of the model using real-world data from two mechanisms. Firstly, a Geographic Information System (GIS)-based method is presented to find potential alternative locations for blood donation centers to maximize availability, accessibility, and proximity to blood donors. Then, a protective mathematical model is developed with the incorporation of (a) blood perishability, (b) efficient collation centers, (c) multiple-source of suppliers, (d) back-up centers, (e) capacity limitation, and (f) uncertain demand. Emergency back-up for laboratory centers to supplement and offset the processing plants against the possible disorders is applied in a two-stage stochastic robust optimization model to maximize the level of hospitals' coverage. The results highlight the fraction cost of considering back-up facilities in the total costs and provide more resilient decisions with lower risks by examining resource limitations.
Keywords: Blood supply chain, Alternative collection facilities, Disruption management, Robust optimization, Geographic information system, Pandemic
1. Introduction
One of the vital roles of national healthcare systems is to transfer blood and its components from donation centers to demand zones by ensuring quality and safety [1]. The Coronavirus outbreak (Covid-19), as one of the severest disruptions due to its long term [2,3], increases the risk of unexpected failures, for it has had adverse influences on both the number of potential donors and physicians in the supply chain [4,5]. As a highly perishable and time-sensitive product, blood requires different strategies from those used in business supply chains [6,7]. Red blood cells or Red Packed cells (RPC) - with a lifespan between 35 and 42 days - are one of the vital components of whole blood, making up about 45% of whole blood [8,9]. The only way to achieve the availability of this perishable product is to sufficiently prepare a situation to increase the number of potential blood donors. Notably, donating blood in most countries is free, and blood transfusion organizations do not pay the donors [10]. In addition, various items -such as blood extraction technologies, different types of cross-matching, the distance between located donation centers and processing plants, and a high rate of perishability-boost the importance of the blood supply network. This research employs a multiphase approach to address this issue by integrating a GIS-based location method and a two-stage stochastic robust optimization model. Regarding this, the concern of blood supply in pandemics and gap analysis are described as follows.
1.1. Background and context of real study
In the light of the COVID-19 pandemic, individuals use public transportation less than usual because of coronavirus dangers. This situation also affects the number of donors in the system, and donors are unwilling to travel a long distance to donate their blood. For example, in India, the Covid-19 outbreak creates many challenges in blood transfusion [11], including finding healthy blood, inventory management, and staff safety. Therefore, a strategic plan is needed to curb the demand dissatisfaction rate, outdated blood units, and supply cost. In a sprawling metropolis like Tehran, easy access to donation centers, processing plants, and medical centers plays a vital role in the supply chain. Accordingly, the importance of donation centers' geographic location to manage both supply and demand in the network is being considered to face this problem. Spatial differences in maximum coverage distance, availability to potential donors in a city, proximity to hospitals, and accessibility to the road network make these candidate locations distinguished.
Moreover, the outbreak creates a worse condition and increases complexity in hospitals' blood supplies. After business closures in March 2020 due to the coronavirus pandemic, some donation centers were closed, and blood supply decreased abruptly in the United States [12]. This situation can be even more complicated in developing countries due to less stability and capacity limitation in processing plants. Besides that, the number of medical staff may be fluctuated by being infected with the coronavirus [13]. Therefore, to have a reliable system, it is crucial to manage data uncertainty and the processing plant's vulnerability [[14], [15], [16]]. Apart from the critical issues in the blood supply chain (BSC) that have arisen due to pandemic conditions, the blood supply chain's importance is increased by its unique features, such as blood extraction technologies and different types of cross-matching. Cross-matching is chosen depending on the time of blood transfusion and whether the injection should be given immediately, which affects managing inventory and patients' demands [10,17]. With this in mind, an efficient redesign of blood supply is crucial as ignoring these issues increases the mismatch between demand and capacity and escalates the possibility of irreversible occurrence in healthcare organizations. Fig. 1 shows the different layers of the supply chain and their connections after a massive disruption. The green flow shows the transportation of blood and its sub-products to hospitals in the case of disruption in processing plants. The dash-dot red arrows connect the donors to candidate donation centers, which need to be established first, and the red arrows show the available centers for donor arrival.
Fig. 1.
Conceptual representation of designing a blood supply network in a massive disruption or pandemics.
1.2. Gap analysis and contributions
Failures in processing plants and demanding access to donation centers have unfavorable consequences for the system, especially in hospitals and medical centers. The unfavorable consequences include chronic shortage, delay in order, poor quality, and a high risk of cross-matching transfusion-transmitted infections. The Covid-19 pandemic has increased the risk of this situation. Accordingly, motivated by the real case, in which “back-up facilities” help the system not only to be reliable and resilient but also be protective against potential disruption and additional costs, we aim to generalize the case in analytical modeling with the following features:
-
a)
Efficient potential donation centers, which help decision-makers to establish the ones with higher efficiency and limitations.
-
b)
Perishability of RPC and rate of inappropriate production based on cross-matching type (based on patients' demand and laboratory product, Anti-globulin Cross-match (AC), and Immediate spin Cross-match (IC)).
-
c)
Different types of collection centers as suppliers (mobile and fixed), and the importance of availability, accessibility, and proximity in finding the best candidate location for donation centers to control donors' fluctuation
-
d)
A disruption in laboratories' supply capacity, which shows the importance of a back-up plan to test and analyze the collected whole-blood units.
-
e)
The coverage distance limitation for allocating donors due to the pandemic.
-
f)
Uncertainty in the number of arrival patients
The purposes of the presented mixed-integer linear programming model are as follows:
-
•
Taking accurate and micro-scale vector data into account based on a GIS method to find the optimal locations for blood donation centers to maximize coverage and provide a boosted and more precise input for the optimization model.
-
•
Developing a two-stage stochastic framework in analytical mathematical modeling to optimize the BSC network, considering different types of cross-matching and protective approaches for processing plants.
-
•
Evaluating the demand fluctuation and disruption conditions in processing plants in the mathematical model.
-
•
Locating back-up facilities to support the processing plants and increasing the resiliency in the healthcare system.
-
•
Assessing the conservative level in the system by considering different amounts of the price of robustness to calculate both penalty value and unexpected penalty costs.
This paper is organized as follows. Section 2 shows the relevant literature. The problem statement is presented in Section 3. In Section 4, the case description and solution methodology are discussed. Computational results and managerial insights are respectively defined in Sections 5, 6. Finally, conclusions and future opportunities are mentioned in Section 7.
2. Literature review
Many studies have worked on city logistics and disruption conditions, and operations research models have become powerful approaches to manage logistics in emergencies [18]. Several related surveys on blood supply networks and healthcare management have been reviewed to highlight the research gaps and contributions better. Osorio et al. [19], Pirabán et al. [20], and Williams et al. [21] are the three important review papers in the field of BSC. Osorio et al. [19] reviewed the papers up to 2014 and categorized them based on the BSC echelons. Recently, Pirabán et al. [20] investigated documents up to 2019 based on network design, decision makings, processes, management of inventory, and data characteristics. Williams et al. [21] reviewed 46 papers on collection echelon and categorized them in appointment scheduling, collection policy, crisis, donor demographics, location/clinic planning, staff utilization, and vehicle routing.
In the following, Section 2.1 highlights the concept of healthcare management and blood supply network in relevant essays by considering different features –such as perishability, cross-matching, variable demands, and capacity limitation. Section 2.2 categorized literature undertaking disastrous situations. The importance of epidemic outbreaks in healthcare analysis is mentioned in Section 2.3.
2.1. Healthcare management and blood supply chain
One of our contributions is considering RPC perishability and rate of production based on cross-matching type. Limited essays have paid attention to testing and processing, especially cross-matching and ABO-RH(D) compatibility issues [20]. To describe briefly, the antigens' absence or existence classifies RPC into four different groups, A, B, AB, and O, subdivided into two classifications based on blood antibodies, named RH+ and RH_. Testing before RPC transfusion includes three steps, (1) Testing the ABO group of blood, (2) evaluating RH (D) matching, and (3) Cross-matching [22,23]. The third one is identifying and preventing harmful interactions between donors and recipients, including two different types, Antiglobulin Cross-match (AC) and Immediate spin Cross-match (IC). According to Achmadi & Mansur [24], the severity of cross-matching in the supply chain is 9 out of 9, illustrating the importance of this issue in the system. Most of the related works focused on cross-matching by healthcare analysis and management viewpoint [[25], [26], [27]], and a few are from analytical modeling and supply chain points of view. Gunpinar & Centeno [28] presented a model as a stochastic integer programming framework for RPC and platelets by considering two different types of demand based on the age of the product. Also, the cross-match-to-transfusion ratio was taken into account. Zahiri & Pishvaee [29] outlined a bi-objective mixed-integer linear programming model to design a BSC network. Their model aimed to minimize shortage and total costs by making a trade-off between these two objective functions. Baş Güre et al. [30] focused on a donation scheduling problem and balanced supply and demand using a robust possibilistic programming approach. Hosseini-Motlagh et al. [31] proposed a BSC network design by considering ABO-RH(D) compatibility to minimize the system's total costs. They used a robustness approach to tackle data uncertainty in their model. Hosseini-Motlagh, Samani, & Cheraghi [32] presented a location-allocation model for BSC to increase donors. Advertisement, education, and medical credits are motivational initiatives to boost blood donation. Our mathematical model, which distinguishes from the previous studies, tries to redesign a patient-centered BSC to manage a sudden massive disruption, such as the Covid-19 pandemic, simultaneously minimizing total costs and increasing healthcare resilience by considering different types of blood cross-matching.
2.2. Healthcare management in disastrous situations
Disruption and disastrous conditions are concerns in production and supply chain environments [33]. An organization's entire plan can be distorted due to disruption, causing a deficiency in goods and unfulfilled customer requests. The development of fit policies can support minimizing losses and maintaining the goodwill of a company [34]. Several studies considered emergency response plans in the wake of disruptions. However, limited essays used mobility in facilities to manage the disastrous conditions. Acar and Kaya [35] presented a model based on a real case in Turkey, in which mobile hospitals are deployed to cover patient demand better. A scenario-based model was proposed by Li et al. [36] to manage uncertain data and transportation time in a combination of disasters.
Blood is different from business models due to its prominent features, such as time sensitivity, perishability, and irreplaceability. Dealing with shortages and wastages are important issues in a blood network, especially in disruption conditions. Some researchers investigated the effect of disruptions in the BSC. Using a Lagrangian relaxation algorithm, Rahmani [37] presented a robust BSC network design to simultaneously control the solution against the disruption risks and uncertainty (in cost and demand). Yaghoubi et al. [38] used a two-objective mathematical model to make a trade-off between minimizing the total costs and delivery time for different types of platelets by assuming various types of production methods. They considered both partial and complete disruptions in their formulation. Haghjoo et al. [6] presented a scenario-based model of designing a BSC by considering the risk of uncertainty in demand and temporary facilities' disruption. The model aims to fulfill the demand by minimizing the total cost and considering the budget limitation. Hosseini-Motlagh, Samani, & Homaei [39] presented a fuzzy stochastic robust programming model in a BSC to simultaneously minimize shortage and cost in a disastrous situation. Patra and Jha [40] focused on the lack of replenishment opportunities after a disaster by formulating a prepositioning problem in a two-period newsvendor model. Our study, inspired by the previous articles in the crisis area, presents a robust-stochastic mixed-integer programming model to respond to emergencies with lower penalty costs and higher satisfaction rates for the Covid-19 patients. Partial or complete disruption in processing centers and demand fluctuations are the two primary uncertain data in this study. Thus, our approach finds an optimized solution for providing sufficient blood units for patients by considering simultaneously high penalty costs for shortage, and potential backup plans for processing centers and mobile clinics for donation.
2.3. Pandemic outbreak in healthcare management
The roles played by the Covid-19 outbreak in supply chain designs are, of course, a significant disruption [41]. Blood -as a highly perishable product-needs to be supplied in a short interval period. However, many existing potential donors are unwilling to participate in donations because of the risk of disease transmission [42]. Choi [43] shows the effects of mobile centers in absorbing more customers in a business during a pandemic, showing that increasing and reorganizing the available donation centers around a region will positively affect the number of available donors in the supply network. It is because donors do not need to travel a long distance to reach the donation centers.
For one thing, production procedures and donors' absorption are critical issues in supplying blood. For another, social distancing is vital to avoid contact during pandemics, similar to the COVID-19 [44]. Finding a way to increase donors' attraction to the system to produce sufficient blood can provide patients and healthcare organizations with an excellent opportunity to handle this critical situation better. Geographic information systems (GIS) is a method that allows the decision-makers to gather and manage data accurately, quickly, and precisely, which can be used in BSC network design [45]. Mollalo et al. [46] developed a GIS-based multiscale weighted regression model to investigate the interaction between several socio-demographic factors and the COVID-19 pandemic. After evaluating the effectiveness of the COVID-19 measures in India using the Bayesian probability model, Bherwani et al. [47] applied the GIS-based Voronoi approach to identify high-risk areas. Franch-Pardo et al. [48] also conducted a literature review on scientific articles that employed statistical analysis and GIS to study the geographical dimension of COVID-19.
Moreover, a considerable number of related healthcare studies considered the optimal design in a strategic decision by integrating GIS. GIS technology not only analyze as well as visualize spatial data, it also has contributed to the widespread use of location models due to its user-friendly nature and low cost [49,50]. Delen et al. [45] presented a model based on operations research, data mining, and GIS approach to manage the blood supply chain and increase its availability. Kaveh & Mesgari [51] presented a location-allocation based on improved biogeography-based optimization to maximize the coverage of emergency centers. Comber [52], Dell'Ovo [53], and Özceylan [54] are the relevant papers, which utilized a GIS method to find the candidate locations. Concerning social aspects and reliability of donation centers is a critical topic in the blood supply network, especially in pandemic situations that availability, accessibility, and proximity are of utmost importance for both the donors and the blood transportation system. Given the power of GIS in analyzing spatial data, GIS-based location models in commercial GIS packages such as ArcGIS have been a significant part of optimization modeling [50]. However, in order to solve location problems more efficiently to reduce computing time and resources, commercial GIS packages employ heuristic methods to carry out faster analysis [49]. Given there is no need to use a solver that models the exact location in heuristic methods, the reliability of location models in commercial GIS packages is, therefore, questionable, and they are likely to render no optimal or sometimes even good solutions [50,55]. Another problem with location models in GIS packages is the assumption that the capacity of the facilities is unlimited, and that each can meet demand as much as possible. As most facilities are limited in terms of their service capacities, this problematic assumption can lead to questionable results [56].
Nonetheless, GIS can still be an effective tool in location modeling, especially for large datasets. For example, in the case of this study, which aims to serve the entire population of Tehran with more than eight million residents, the power of GIS can be used. The population of a city is not evenly distributed and significant demographic variations can be seen in a city's regions or statistical divisions. GIS is able to take into account such significant demographic dispersions in large datasets, while such a problem renders mathematical models impractical. Therefore, to use the power of both exact and heuristic methods, we used a GIS-integrated multi-phase mathematical model to find the donation centers' optimal location.
The summary of the reviewed literature is shown in Table A1 (see in Appendix A) to highlight the research gaps. To the best of our knowledge, many of the papers have paid attention to the disruption condition in the first layer (collection procedure), and none of the mentioned papers present an alternative to cope with the effects of disruption in distribution and laboratories endangering patients' safety. Noteworthy, the number of processing plants (responsible for distributing the blood to hospitals on time) in a city is much lower than the donation centers (i.e., Tehran only has one processing plant, but six fixed donation centers). By this motivation, we utilized a GIS-based analytical model with the combination of back-up plans to better respond to the demands in the wake of disruption in pandemic conditions. Therefore, to maximize availability, accessibility, and proximity for the blood-donors to timely response in these emergencies, we reorganized more donation centers, as mobile and fixed, which helps us to increase potential donors and meet demands on time. Also, leveraging the back-up facility strategy implements low vulnerability and high reliability for the supply network against disorders. A robust analytical mathematical model with a service-oriented and cost-efficient approach is presented to combat demand variations and manage blood flow.
3. Problem statement
This paper redesigned a four-echelon BSC network to prepare sufficient RPC units from donor groups to demand zones. Donor groups can donate their blood in three places: main donation centers, mobile facilities, and blood processing plants. The extracted blood from main donation centers and mobile facilities are sent to blood processing plants for testing, analyzing the quality of the product, and cross-matching the RPC based on hospitals' requirements. At the last echelon, the appropriate RPC will be distributed to demand zones. Fig. 2 shows a schematic summary of the phases in the proposed supply chain.
Fig. 2.
Flow chart of the main phases in the proposed BSC.
3.1. Location-allocation analysis in ArcGIS
The three main factors, availability, accessibility, and proximity, play an important role in finding the best location for blood donation in a city [45]. The closer the blood donation centers are to the city's population centers, the more available blood donation centers are to donors, and the more likely residents are to donate blood [57].
Accessibility of these centers to the city's main routes also plays an essential role in the timely delivery of blood to hospitals and donors' access.
The proximity of blood donation centers to city hospitals is also crucial, particularly in times of crisis. The need for blood in hospitals increases in times of crisis and blood can be used for a maximum of 8 h. Thus, the proximity of blood donation centers to hospitals in improving crisis response is essential.
GIS is effective in studies that aim to find the optimal location for facilities to maximize services. Location-Allocation Analysis is one of the Network Analyst tools in ArcGIS that finds the optimal location for facilities based on the demand generated by different variables. In this method, candidate locations are selected to maximize coverage, or minimize costs, or maximize market share. Therefore, using ArcGIS 10.5, Location-Allocation Analysis includes demand points, facilities, and the network database, and it was set to cover the most demand. This analysis aims to provide the most coverage of demand points by facilities in the network database. The demand points of the analysis were the main hospitals as well as the population of the city. The population of census tracts had to be converted to population centroids to be used as demand points. A census tract consists of several adjacent urban blocks to form a homogeneous neighborhood, i.e., a census tract. Before that, the city's road network, which included the maximum speed limit and the direction of traffic on the street, was used as the input for the network dataset. The existing and the proposed facilities should also be identified in Location-Allocation Analysis, and they are referred to as required facilities and candidate facilities, respectively. Tehran has 22 districts whose activity centers can potentially be the best locations to build new blood collection centers. Thus, the existing blood donation centers and the activity centers of the districts were used as required facilities and candidate facilities, respectively.
3.2. Supply chain resiliency strategy with protective approach
Using analytical mathematical modeling as a mixed-integer linear programming (MILP) framework, this study aims to combat the uncertain input data and possible disruption based on non-resiliency, partial-resiliency, and complete resiliency. Regarding this, based on the conservative robustness approach, the non-resilience model has considered no level of conservatism. In the partial-resilience model, this approach is less risky than the former to face unexpected penalty costs, although the highest level of conservatism has not been considered. The complete-resilience approach manages the system with the highest conservative level. Noteworthy, although the total cost of the supply chain might be increased in general conditions, it would significantly lessen the unexpected expenses in disastrous situations. Moreover, the flow of cross-matched blood between the echelons and the importance of each located donation center for absorbing donors and transshipping the extracted blood to both the processing plant and demand zones (in the case of disruption in the processing plant) need to be managed. In specific terms, the assumptions of the mathematical models are as follows:
-
•
Six main donation centers have already been established in Tehran.
-
•
Disruption occurs in processing plants in both partial and complete scenarios. Main donation centers and mobile facilities are considered as reliable centers in the supply chain.
-
•
Only located main donation centers can be considered as back-up facilities in the system.
-
•
The capacity of main donation centers, mobile facilities, and processing plants is fixed and bounded.
-
•
After transferring whole blood to processing plants, the process of extracting RPC begins.
-
•
Based on patients' demands, the extracted RPC divides into two types of cross-matching, AC and IC.
-
•
RPC perishability and inappropriate production rate are considered in the model, as the outdated RPC in processing plants or hospitals has wastage costs.
The following indices, parameters, and variables are introduced in Table 1 to present the MILP model in a two-stage stochastic programming framework, in which patients' demand parameter is considered deterministically. Noteworthy, the three main disruption conditions incorporated in the formulation, can be dedicated as follows:
-
•
Condition 1: In the first condition, the processing plant is the only option for testing and analyzing the extracted blood and transferring them to hospitals. The blood will be extracted in donation centers, mobile facilities, and the processing plant. Then, all the extracted blood in donation centers and mobile facilities will be delivered to the processing plant as the only place equipped with expert staff and required technologies.
-
•
Condition 2: In the second condition, partial disruption occurs in the processing plant. Therefore, both the processing plant and donation centers can test and then transfer the extracted blood to the hospitals. Noteworthy, Condition 2 is the same as Condition 1 if the number of total demands is less than the non-disrupted capacity of the processing plant. In this situation, there is no need to assign back-up facilities in other centers.
-
•
Condition 3: In the third condition, the processing plant completely fails. Therefore, the only options to deliver the required blood units to the hospitals are the equipped main donation centers. It is noteworthy to mention that lateral transshipment between the located donation centers is not allowed, for it makes it hard to check the blood flow path.
Table 1.
Notations applied in the mathematical formulation.
| Indices | |
| I | index of available donors in each region |
| J | index of possible main donation centers |
| U | index of possible mobile facilities |
| B | index of blood processing plants |
| H | index of public therapy centers |
| R | index of cross-matching types |
| T | index of time-periods |
| S | index of probable scenarios (probable conditions) |
| Parameters | |
| Holding cost of one blood unit | |
| Cost of blood extraction through blood donors | |
| Demand of RPC cross-matched type r at public therapy center h in time-period t | |
| Available blood donors in area i in time-period t | |
| Moving cost of per RPC unit from processing plant b to public therapy center h | |
| Moving cost of per RPC unit from the located main donation center j to public therapy center h (In the case of disruption in the processing plant) | |
| Fixed cost of establishing one main donation center in location j | |
| & | Transportation fee of one unit of RPC from location j (u for) to processing plant b |
| Rate of appropriate RPC units cross-matched type r produced at the processing plant | |
| Cost of moving a mobile facility from location u1 to location u2 | |
| Transportation cost of one RPC unit from mobile facility at location u to main donation center j | |
| A big number | |
| Disruption parameter in each scenario, 0: if a disruption does not occur in processing plant b | |
| Shortage penalty per unit of RPC demand cross-matched type r | |
| Probability of each scenario | |
| The full length between donor group i and main donation center j | |
| The full length between donor group i and mobile facility u | |
| The full length between donor group i and processing plant b | |
| Maximum vacancy of the blood bank in processing plant b | |
| Maximum vacancy of processing plant b to accept blood donors | |
| Wastage penalty per unit of RPC demand cross-matched type r | |
| Coverage distance of each main donation center, processing plant, and mobile facility, respectively | |
| Cost of considering main donation center j as a back-up facility | |
| , | Maximum vacancy of main donation center j and temporary facility u, respectively |
| Positive variables | |
| , | Fraction of maximum RPC requirement cross-matched type r at public therapy center h in time-period t supplied by processing plant b and main donation center j, respectively |
| Inventory level of RPC units cross-matched type r at processing plant b in each scenario | |
| Inventory level of RPC units cross-matched type r at public therapy center h in each scenario | |
| Number of required mobile blood facilities | |
| Quantity of RPC extracted through donor area i at main donation center j in time-period t in each scenario | |
| Quantity of RPC extracted through donor area i at mobile facility u in time-period t in each scenario | |
| Quantity of RPC extracted through donor area i at processing plant b in time-period t in each scenario | |
| Quantity of RPC delivered from a mobile facility located in u to a main facility at location j in time-period t in each scenario | |
| Quantity of RPC delivered from a main facility located in j to processing plant b in time-period t in each scenario | |
| Quantity of RPC delivered from a mobile facility located in u to processing plant b in period t in each scenario | |
| Shortage level of RPC units cross-matched type r at public therapy center h in time-period t in each scenario | |
| Wastage level of RPC units cross-matched type r at processing plant b in each scenario | |
| Wastage level of RPC units cross-matched type r at public therapy center h in each scenario | |
| Binary variables | |
| 1: if main donation center j assigned as a back-up facility in scenario s; 0 otherwise | |
| 1: if a mobile facility moved from location u1 to location u2 in period t in scenario s; 0: otherwise | |
| 1: if a main donation center is established in location j; 0: otherwise | |
| 1: if mobile facility u is dedicated to main facility j in time t in scenario s; 0: otherwise | |
| 1: if donor area i donates in main donation center j in time t in scenario s; 0: otherwise | |
| 1: if donor area i donates in mobile facility u in time t in scenario s; 0: otherwise | |
| 1: if donor area i donates in processing plant b in time t in scenario s; 0: otherwise | |
Objective function:
| (1) |
The objective function aims to minimize the overall costs in the supply chain, including costs of inventory in hospitals and the processing plant, shortage and wastage costs of each type of patient, costs of establishing main donation centers and mobile facilities, transportation costs (i.e., the amount of blood that moved from one echelon to another; and moving mobile facilities), and considering an established main donation center as a back-up facility.
The constraints are divided into seven groups, mentioned in Appendix B. Equations (B.2) to (B.8) refer to assigning blood donors to mobile facilities. Equations (B.9) to (B.14) refer to the main donation centers' constraints. The blood processing plant constraints are mentioned in equations (B.15) to (B.17). Constraints (B.18) to (B.22) are the inventory constraints. The back-up plan in the mathematical model has mentioned in Constraints (B.23) to (B.26). Constraints (B.27) and (B.28) refer to the wastage amount in the model. The last two constraints show the domain of decision variables.
3.3. Robustness approach for blood demand tailoring problem
Fluctuation in blood demands in different periods is inseparable in reality, as inaccurate estimation poses a delay in its access, which may cause an escalating rate of unsatisfied demand in the system [58]. Regarding this, a conservative robustness approach is applied in this study [[59], [60]] (Refer to Appendix C).
4. Data collection
This section demonstrates the data used for the GIS approach and the mathematical model from a realistic case study to evaluate its possibility and practicality.
Tehran is the capital of Iran and its largest city with the best equipment and treatment staff. The demand points for the Location-Allocation Analysis include 18 main hospitals of Tehran, whose beds vary from 1300 to 119, representing the weight of the demand points (Fig. 3 ). Information on the hospitals and the number of their beds were obtained from the Iran Blood Transfusion Organization (IBTO) and the hospitals, respectively. Also, Tehran's census tracts were the rest of the demand points for analysis obtained from the last Iranian national census in 2016. Tehran is made up of 4330 census tracts, and they were converted to population centroids. Thus, there are 4330 population centroids or demand points used in this article, the population of which represented their weight in the analysis. The road network, which was extracted from the vector maps of Tehran's master plan, formed the network database, in which the maximum speed limit and the direction of traffic on the street were included. Also, facilities included the existing main donation centers as required facilities and 29 activity centers of Tehran's districts as candidate facilities. There are 22 districts in Tehran; however, some districts had two activity centers due to their size or large population. According to IBTO and hospitals' reports, the rate of producing cross-matched unit type AC and IC are 70% and 30%, respectively. The reason for the lower use of the second type is that the ABO-RH (D) of the donor and recipient must be equal as a prerequisite. The rest of the parameters are gained through experts' knowledge, IBTO, and relevant papers [[61], [62], [63]] (Refer to Appendix D).
Fig. 3.
Major roads in 22 districts of Tehran, as well as the geographical distribution of activity centers, existing main donation centers, and main hospitals.
5. Results and discussion
The applicability and sensitivity analysis of the proposed model and the solution techniques are presented in this section. All the models are solved with GAMS 24.1.2 using CPLEX solver on a PC with CORE i7 and 8 GB memory.
First, the candidate location of the main donation centers is calculated by the GIS approach. Then, the resilience model with a protective approach against the processing plant disruption is analyzed in two steps. In the first step, the protective model is applied in different disruption scenarios. In the second step, the protective model is validated in a robustness approach, in which the analytical approach aims to combat both demand fluctuations and possible disruption.
5.1. Locating main donation centers
Assuming that each person is willing to spend 30 min to reach the blood donation centers, location-allocation analysis located 22 potential blood donation centers from 36 existing blood collection centers and activity centers (Fig. 4 ). Since the population of census tracts and main hospitals with different bed capacities have not been evenly distributed across Tehran, districts 4, 5, and 12 each had two potential locations for blood collection centers. On the other hand, the analysis proposed no potential blood collection center in the 22nd district of Tehran, which has a low population density. These potential blood collection centers were then used in the optimization model as input data to eventually determine the optimum blood collection centers and the back-up facilities needed in times of crisis.
Fig. 4.
Proposed blood donation centers located by Location-Allocation Analysis.
5.2. The impact of coverage distance on logistics costs
Due to the pandemic and to increase the available donors in the system, this model considered restricted coverage distance for each mobile and fixed donation center (see Table 2 ). For one thing, this limitation would increase the logistics cost in comparison to normal situations. For another, this decision increases donors' satisfaction rate and makes a proper condition to donate blood by traveling a short distance. Table 3 shows different distance limitations in the system, which would help the decision-makers (DMs) choose the best-fit decision based on the budget limitation. In the optimistic case, DMs can ignore adding one more donation center (DC) and two mobiles, and in the pessimistic point of view, adding two more DCs and using all mobile DCs are recommended. Also, the existing facility 1 is useless for its location cannot cover considerable donors. This result also highlights the impact of mobile centers in pandemics, as if the DMs prefer to limit each collection center coverage, adding more mobile facilities is preferred.
Table 2.
The acronym of each donation center.
| 1 | Vesal | 6 | Piroozi | 11 | Al-Qadir Sq. | 16 | Shoosh Sq. | 21 | Tehransar |
|---|---|---|---|---|---|---|---|---|---|
| 2 | Sattari | 7 | Imam Khomeini SW | 12 | Enghelab Sq. | 17 | Nabard Sq. | 22 | Shahed Sq. |
| 3 | Tehranpars | 8 | Tajrish Sq. | 13 | Azadi Sq. | 18 | Basij Sq. | ||
| 4 | Shahre Ray | 9 | Sanaat Sq. | 14 | Shamshiri Sq. | 19 | Yaftabad | ||
| 5 | Sadr | 10 | Resalat Sq. | 15 | Imam Khomeini Sq. | 20 | Sarvi Sq. |
Table 3.
The effect of distance limitation in total costs and number of DCs.
| Coverage distance |
Total cost | number of located DCs | number of located mobile DCs | Inefficiency in existed DCs | |
|---|---|---|---|---|---|
| Mobile facility | Fixed DCs | ||||
| 1500 | 1500 | 3330000 | 15 | 4 | facility 1 |
| 1500 | 3500 | 1570000 | 15 | 4 | facility 1 |
| 1500 | 4000 | 1350000 | 15 | 4 | facility 1 |
| 2250 | 5250 | 825150 | 14 | 2 | – |
| 3000 | 7000 | 779000 | 13 | 2 | – |
| 3375 | 7875 | 701000 | 13 | 1 | – |
| 4500 | 10500 | 645000 | 12 | 0 | – |
5.3. Back-up facility and resiliency sensitivity analysis
As stated before, IBTO has considered several methods to protect the model against disruption in the processing centers. For this purpose, it has been considered that the processing center's capacity in Tehran should be twice as big as the expected demand. Therefore, failures over 50% need back-up facilities. The first scenario (S = 0) demonstrates that the model is reliable and in stable conditions, in which disruption cannot affect the system. The second and third scenarios show the model in partial disruption, and the fourth scenario (S = 4) is when the processing center has wholly failed. Fig. 5 illustrates the number of main donation centers and back-up centers in different scenarios. As can be seen, the number of back-up facilities has a direct relationship with the failure rate. Moreover, the number of considered main donation centers and mobile facilities has increased due to the disruption in the supply chain. Noteworthy, to fulfill all blood demands in the system, at least seven more donation centers need to be established in non-critical situations.
Fig. 5.
Number of located main donation center and mobile facilities in deterministic form of demand.
Table 4 demonstrates the logistics costs, back-up facility costs, transportation costs, and inventory costs in all periods in the healthcare system. Since the proposed blood supply network is service-based, we investigate different incident scenarios and a two-stochastic approach. The first row (S = 0) shows the supply chain in the deterministic condition. Rows two to four respectively reveal the outcome costs in 50%, 70%, and 100% disruption in the processing plant, and the fifth row illustrates the model based on the two-stage stochastic approach. The last row, titled “Gap%," points to the solutions gained through the MILP approach, which means the difference between the current solution and the best lower bound (optimal answer) when the problem-solving process ends. The columns are divided into three groups. The first category reveals the outputs by considering back-up facilities for increasing the resiliency of the system. The second group shows the costs without a protection strategy for the processing plant with the exact probable disruption. The last column of the table shows the fraction cost of the back-up facility in the total logistics costs in different disruption situations, which fluctuate in the range of 21%–67% based on the level of destruction in processing plants. As can be seen, the total costs increase under disruption occurrence in the processing plant. However, this cost is much more if no resiliency strategy applies to the system. Based on Table 4, if the system is protected for 50% disruption, the total costs will increase by 11%. The total logistics costs in scenarios 2, 3, and the stochastic model are 2, 3.84, and 2.13 times higher than the deterministic one. On the other side, if the network faces disruption without any prior management, not only do higher logistics costs incur to the system, but the cost of patient dissatisfaction will also be added. Noteworthy, not assigning back-up facilities in complete disruption in the processing plant gives infeasible results, as no other supplier is considered to satisfy hospitals' demands. By applying the stochastic model, not only the proposed supply chain is protected against partial or complete failure, but the total logistics costs will also be decreased to 1663100 IRR (Rials/unit). The required resilient conditions will be met if costs increase by 36% to allocate support centers and back-up facilities.
Table 4.
Logistics costs' reports (Rials/unit).
| Disruption Scenarios | with protective centers |
without protective centers |
|||||
|---|---|---|---|---|---|---|---|
| Total logistics costs | Back-up facility costs | Transportation costs | Inventory costs | Total logistics costs | Shortage costs | ||
| S = 0 | 778760 | 0.0 | 35642.4 | 743.604 | 778760 | 0.0 | 0.0 |
| S = 1 | 881220 | 192500 | 39866.2 | 9.5 | 5696940.1 | 5285700 | 0.21 |
| S = 2 | 1572400 | 927850 | 70287.1 | 22 | 24297558.7 | 24276420 | 0.59 |
| S = 3 | 2991600 | 2020287 | 201584.4 | 0 | infeasible | infeasible | 0.67 |
| TSS | 1663100 | 613112.5 | 49412.7 | 116.8 | – | 0.0 | 0.36 |
| Gap%: 0.00 | Gap%: 0.00 | ||||||
*TSS: Two-stage stochastic model.
* The fraction cost of back-up facility in the total logistics costs.
Fig. 6 illustrates the percentage of donation participation in each region in the deterministic situation. As can be seen, activity centers 4, 8, and 15 are the three critical points in supplying the blood demand. Therefore, if healthcare organizations and IBTO wish to persuade other regions and donation centers to increase donations, rewarding these three donor groups can be beneficial. These areas are very close to the processing plant, illustrating the importance of transportation in locating donation centers.
Fig. 6.
Blood donation in each area in the deterministic form of demand without disruption in all periods.
Fig. 7 explicitly demonstrates the effect of incident scenarios in transferring extracted blood units from donation centers to the demand zones. As can be seen, the higher the failure rate in the processing plant, the more donation centers will be considered as back-up centers. Since lateral transshipment between donation centers cannot be considered due to the rules of blood transshipment according to IBTO, all the located donation centers are considered back-up centers if a complete disruption occurs in the processing plant. Noteworthy, the number of located donation centers depends on various factors, such as limited capacity, coverage distance, available blood donors, establishment cost, implemented in the problem formulation with two mechanisms. Firstly, the GIS approach is used to find the optimal candidate centers, and then, the proposed MILP model is presented to find the best fit. According to the Figure, alternative facilities 6, 15, and 16 are the three most important ones in collecting and transferring blood units to hospitals in the situation of high rate or complete failure in the supply chain. This result also shows that among all DCs, DCs 14, 19, and 20 have the least role. It means that in case of budget limitations, it would be better to eliminate them from the candidate DCs.
Fig. 7.
Effect of each main donation center in transferring blood to hospitals in different scenarios.
The importance of each mobile facility is illustrated in Table 5 . As can be seen through the results of assessment metrics, mobile centers are moved among activity areas 7, 10, and 18 and preferred not to meet the two other facilities. The main reasons for this result are that the donation rate of activity centers 22 and 16 is lower than the other areas, and the transportation costs to reach the destination are not affordable. Therefore, DMs prefer to lose the available donors in those areas (see Table 6 ).
Table 5.
The movement among candidate mobile areas in different periods.
| Period 1 | 10 → 18→2 |
|---|---|
| Period 2 | 18 → 10→2 |
| Period 3 | 7 → 10→18 |
| Period 4 | 18 → 10→7 |
| Period 5 | 7 → 10→7 |
| Total number of located mobile facilities | 2 |
Table 6.
Evaluation of the expected value solution based on different weights of each scenario.
| Weight of each scenario | Total cost | Transportation cost | Back-up cost | DAM | DAF | DAP |
|---|---|---|---|---|---|---|
| = 0 | 805119 | 37639 | 41195 | 88 | 7489 | 1382 |
| = 0.1 | 1133075 | 56382 | 310598 | 74 | 7784 | 1240 |
| = 0.1 | 1159684 | 59766 | 338703 | 124 | 7802 | 1132 |
| 1236126 | 62517 | 416473 | 162 | 7374 | 1291 | |
| 1246704 | 61742 | 436878 | 172 | 7358 | 1272 |
*DAM: Donor absorption to mobile centers.
*DAF: Donor absorption to fixed collection centers.
*DAP: Donor absorption to processing plants.
5.4. The impact of price of dissatisfaction rate in the supply network
The shortage cost parameter is given from Ensafian & Yaghoubi [61], which is 1500 $/unit (6300 × 103 Toman/unit or 6300 × 104 Rials/unit). This large number is considered to minimize and avoid shortages in the proposed network. Fig. 8 reveals the deficiency rate changes in all periods based on different unfulfillment costs for each cross-matching type. S and S′ indicate the shortage level of AC and IC cross-matching types in different scenarios, respectively. As shown in Fig. 8, the deficiency amount-especially the IC type-will escalate considerably by decreasing the importance of facing shortages in the supply chain. The ratio of deficit cost to the total cost (RCT) varies in different shortage costs, so the lower the shortage cost, the higher RCT. Calculating RCT, the cost of the deficit is divided by the total logistics costs. RCT gives its higher amount if the shortage cost is considered its least value (130 × 103 Toman/unit), about 90% of logistics cost. It means that if patients are not in emergency status, DMs may decide not to respond to the hospital's demand due to limited supply and logistics costs. It would be logical for DMs not to add extra DCs when the price of dissatisfaction rate downs to 3 times than the emergency one.
Fig. 8.
Amount of shortage of each cross-matched RPC based on different values of shortage costs.
5.5. Analyzing the quality of the expected value solution
Different weights for each scenario are considered, and the value of each variable is assessed [64]. As can be seen, as the weights of partial or complete disruption scenarios increase, the total logistics costs also escalate. This change also reveals an upward trend in the number of donors to mobile centers and transportation costs.
5.6. Sensitivity of robust-stochastic approach and realization
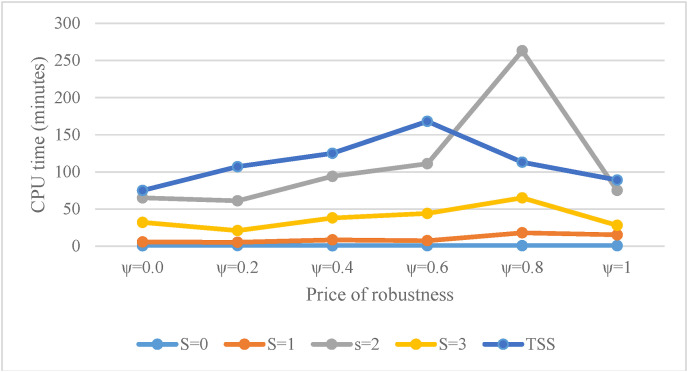
One of the critical parameters, which is the inseparable part of the blood supply, is demand fluctuation. The scenario-based approach is a risk-averse method to combat and control the adverse effects of demand uncertainty in the healthcare system. Table 7 analyses the model's robustness when the model faces uncertainty in both demand and probable processing center's disruption. The first row of the table shows different budget levels of uncertainty in the system, and the first column shows the results in different scenarios. The last part of the table reveals the optimal data in the two-stage stochastic approach. The results in the deterministic form of both demand and disruption can be seen in . The uncertainty effects will be escalated as the values of budget of uncertainties and S are close to one and three, respectively (The last column of the fourth row). The results reveal that by increasing uncertainty in the supply network, the expected logistics costs – to control and manage-will intensify. Moreover, as can be seen from Fig. 9 , by considering both fluctuations in demand and failure in the processing center, the computational time rises significantly. However, by combining the TSS method to protect the system, the computational time only increased up to 1.47 times than the worst scenario time.
Table 7.
The costs result of the model in deterministic, robust, and stochastic framework ().
| Budget of uncertainty |
|
|
|
|
|
|
|
|---|---|---|---|---|---|---|---|
| S=0 | Logistic costs |
778760 |
887230 |
993100 |
1115700 |
1256200 |
1402100 |
| Back-up facility costs | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| S = 1 | Logistic costs | 881220 | 1042000 | 1225400 | 1416300 | 1617700 | 1825100 |
| Back-up facility costs | 192500 | 274312 | 351312 | 442750 | 534187 | 620812 | |
| S = 2 | Logistic costs | 1794360 | 1881091 | 1921200 | 2105800 | 2309800 | 2505200 |
| Back-up facility costs | 927850 | 1020250 | 1091475 | 1178100 | 1267612 | 1339800 | |
| S = 3 | Logistic costs | 2991600 | 3152300 | 3315600 | 3439700 | 3613200 | 3802300 |
| Back-up facility costs | 2020287 | 2111725 | 2150225 | 2265725 | 2353312 | 2444750 | |
| TSS | Logistic costs | 1663100 | 1784165 | 1813441 | 1910350 | 2074377 | 2238993 |
| Back-up facility costs | 613112 | 835714 | 951440 | 1001371 | 1117941 | 1199899 | |
*TSS = Two-stage stochastic form.
Fig. 9.
Computational time comparison of the proposed solution techniques based on different conservative levels.
We proposed ten different realizations to examine the applicability of the robustness approach. The impact of different budgets of uncertainty levels between the deterministic and robustness strategy is described in Table 8a, Table 8b . The penalty cost (PC) and unexpected penalty cost (UPC) have been highlighted in each realization. Symbol Re shows the realization number.
Table 8a.
The model effectiveness under different realization.
| Re | Deterministic |
Robustness approach |
||||
|---|---|---|---|---|---|---|
|
|
|
|
||||
| PC | UPC | PC | UPC | PC | UPC | |
| 1 | 6233268 | 4570168 | 4654885 | 2870720 | 4143263 | 2329822 |
| 2 | 5025164 | 3362064 | 4959105 | 3174940 | 4239070 | 2425629 |
| 3 | 6222866 | 4559766 | 4917935 | 3133770 | 4229249 | 2415808 |
| 4 | 5217873 | 3554773 | 4937357 | 3153192 | 4079985 | 2266544 |
| 5 | 5342685 | 3679585 | 4535473 | 2751308 | 4035069 | 2221628 |
| 6 | 5710973 | 4047873 | 4904441 | 3120276 | 4075860 | 2262419 |
| 7 | 5757660 | 4094560 | 4816854 | 3032689 | 4035178 | 2221737 |
| 8 | 5267115 | 3604015 | 4463038 | 2678873 | 4245374 | 2431933 |
| 9 | 6292726 | 4629626 | 4668846 | 2884681 | 4113709 | 2300268 |
| 10 | 5069447 | 3406347 | 4995066 | 3210901 | 4252205 | 2438764 |
| AVG | 5613978 | 3950878 | 4785300 | 3001135 | 4144896 | 2331455 |
| SDV | 473185 | 473185 | 180817 | 180817 | 84646.28 | 84646.28 |
Table 8b.
The model effectiveness under different realization.
| Re | Robustness approach |
|||||
|---|---|---|---|---|---|---|
|
|
|
|
||||
| PC | UPC | PC | UPC | PC | UPC | |
| 1 | 3617836 | 1707486 | 2221392 | 147015 | 1470148 | 0 |
| 2 | 3513031 | 1602681 | 1904442 | 0 | 1196958 | 0 |
| 3 | 3813999 | 1903649 | 2278453 | 204076 | 1802371 | 0 |
| 4 | 3666908 | 1756558 | 2265369 | 190992 | 2142477 | 0 |
| 5 | 3246586 | 1336236 | 2156937 | 82560 | 1174362 | 0 |
| 6 | 3136721 | 1226371 | 1923605 | 0 | 1365288 | 0 |
| 7 | 3254834 | 1344484 | 1989375 | 0 | 1367795 | 0 |
| 8 | 3596658 | 1686308 | 2384515 | 310138 | 1854911 | 0 |
| 9 | 3546673 | 1636323 | 1904551 | 0 | 1326835 | 0 |
| 10 | 3083708 | 1173358 | 2224493 | 150116 | 1140194 | 0 |
| AVG | 3447695 | 1537345 | 2125313 | 108489.7 | 1484134 | 0 |
| SDV | 235428.9 | 235428.9 | 169412.6 | 103718.2 | 319607.1 | 0 |
As can be observed, the optimal value of the objective function in the robustness approach is notably better than the deterministic one. The PC, UPC, and average also take lower values in the robust optimization. Besides that, the average and standard deviation of the penalty and unexpected penalty costs decrease considerably by increasing the conservatism level.
When the level of conservatism escalates, the price of robustness would be more than the deterministic status. On the other hand, the PC and UPC would be controlled significantly when the system meets a fluctuation in the number of unexpected new patients. By enhancing the conservatism level from 0 to 0.2, the robustness price would be 121,065 × 104 IRR, but the system would save 1,699,448 × 104 IRR when there is an extra patient in a period. Moreover, by extending the conservatism level from 0.2 to 1, the robustness price will be only 25%. However, the system can reduce its cost by 68% if newly sudden patients are in the supply network.
6. Managerial insights
According to the WHO, the COVID-19 pandemic has caused blood supply in emergencies, and the healthcare systems should be reliable enough to work properly during this pandemic. With this in mind, a resilient and optimized strategic-tactical decision-making process must be evaluated by considering BSC features to manage the supply network entirely. The results provided the following findings as managerial implications:
-
(a)
Perishability consideration can combat with wastage amount and its cost in the system. Regarding this, the amount of useable blood units increases in the blood banks. Moreover, perishability forces the system not to hold the blood unit up to the last lifetime period, bringing about lower inventory cost for the supply chain and higher quality of blood for patients.
-
(b)
The population of a city is never evenly distributed across the city. Furthermore, the quality of the road network has a significant effect on access to facilities. In other words, while each component of the road network has a different maximum speed, traffic flow, and traffic direction, the Euclidean distance between different variables in conventional models does not give an accurate picture of accessibility between facilities and demand points (i.e., potential donors and hospitals). GIS addresses this issue by employing accurate and micro-scale data. By conducting location-allocation analysis in ArcGIS 10.5, blood donation centers were optimally located to have better access to the road network, are available to potential donors, and are proximate to hospitals.
-
(c)
The rate of collecting and delivering RPC (in the case of disruption and by considering the center as a back-up) in donation centers helps us find the importance of each donation center in the system. Factors –such as coverage distance, available potential donors, and the establishment and transportation costs-endow the decision-makers to choose a candidate center to be located. Therefore, in the case of budget limitations, DCs with the highest contribution should be selected.
-
(d)
The fraction cost of the back-up facility in the total logistics costs gives a logical view to decision-makers to choose the best decision for the system by considering the budget limitation. It is notable to mention that due to the pandemic, medical staff is endangered by the threats of being infected, which means that a portion of them might become deactivated. According to our results, by increasing almost 36% of the expected total costs, the supply network can be supported entirely by the potential disruption.
-
(e)
The decision-makers can reorganize the proposed BSC for applying a protective network in the healthcare system. For this purpose, the maximum capacity of the service level in the processing plant plays a leading role in disruption situations. The current Tehran processing plant can support up to 50% of the disruption without back-up in the system. This percentage can be varied in different supply chain networks, in which the lower value requires higher back-up importance in the healthcare organization.
-
(f)
Due to the natural uncertainty in demand and lack of information on possible disruption in the supply chain, sensitivity analysis should be implemented in the uncertainty budget based on the probability of each scenario. This study evaluated the total logistics cost and RPC production in a demand-protection model to face possible data fluctuations. Regarding this, PC and UPC decline by raising the conservative level, the average and standard deviation of the objective function. Moreover, a minor increase in the system's total cost can protect the blood supply network from failure by considering fluctuations in the number of new patients. By increasing the price of robustness from 0 to 0.2, the system can save 23% of the penalty costs, and by increasing the level of conservatism from 0.2 to 0.4, this value will grow significantly by only a 1.6% increase in total costs. By turning the value of robustness to 1, the price of UPC would reach almost 0. This point can turn on lights for DMs to choose the best decision for the blood supply chain.
7. Conclusion
The outbreak of COVID-19 has caused a substantial reduction in blood transfusion activities, including blood donations. Under the guidance of blood transfusion and organization, several visible systemic issues (i.e., RPC cross-matching type, blood perishability, multiple-source of suppliers, back-up centers, capacity limitation, and pandemic situations) have been found in the blood supply network, which ushered us to incorporate the GIS approach with an analytical mathematical model. By considering three different conditions, namely non-disrupted, partial disrupted, and complete failure, the application of our MILP model presented an incentive mechanism to minimize both the total logistics costs and RPC flow disorder. The summary of this paper is provided as follows:
-
•
To come closer to reality, availability, accessibility, and proximity, as the three main factors, are considered and evaluated by the GIS approach. By applying a GIS-based method, 22 potential blood donation centers were located to be optimally available to potential donors throughout the city, most accessible through the city's road network, and finally proximate to the city's main hospitals.
-
•
Then, a protective blood supply network designed to combat the uncertain data and failures in the system based on a real case. The proposed study includes four leading echelons from donor arrival to hospitals for collecting, testing, distributing, and consuming the extracted blood. In this study, the possible disorders were managed in three statuses. (a) As during the Covid-19 pandemic, many potential donors prefer to travel the shortest distance for donation, we assessed the effectiveness of existing DCs based on limited coverage distance. The results illustrated that even some existing DCs might need to be closed for the donation rate at negligible areas. Also, the outcome revealed the importance of mobility in facilities when the maximum coverage distance becomes more limited. (b) The test and distribution echelon may face disruption, where the extracted blood units need to be analyzed and subdivided into two cross-matching types (i.e., AC and IC). Besides that, the number of processing plants in the blood supply network is limited. Therefore, some DCs as alternative facilities were incorporated into the analytical model to protect the system. Among different disruption possibilities, four situations were considered in a scenario-based approach to handle the blood flow and control the shortage level. (c) There is a fluctuation in the number of patients in the healthcare system. Therefore, a robust optimization approach was presented at first, and then, ten different realizations were provided to show the price of robustness effectiveness in the supply network. The conservative level of each budget of uncertainty has shown, and the penalty costs and unexpected penalty costs are dedicated to shedding some light on this subject better. The practical management insights through the findings of the proposed model can be seen in the preceding section.
Future works can focus on dynamic routing strategies to absorb more donors in disruption and disastrous conditions. As during an outbreak, the number of available blood donors would decrease, practitioners can manage this issue by mobile facilities and absorbing donors from farther areas. Besides that, the high rate of perishability in the system as a distance limitation and the other type of mobile facility (without extraction technology, which is used only for transferring blood to the laboratory centers) need to be considered. Further research can be focused on different types of production procedures for blood extraction. In the end, evaluating the concept of resource sharing in hospitals and its efficiency is another direction on this subject of interest.
Acknowledgement
We would like to show our gratitude to the: (1) Bita Hadinejad, Head-nurse (2) Mahtab Moradi Koohbad, physician; And (3) Naser Gilani Larimi, physician for sharing their knowledge and information with us during this research study. We sincerely thank the Editor and two anonymous reviewers for their kind and helpful comments on this paper.
Appendix A.
Table A1.
An overview of related studies
| References | Product type | Hierarchical level | Donation mode | Planning horizon | Goal and objective | Time period | Back-up facility | Solution approach | Cross-matching | ABO-RH compatibility | Real case | Uncertainty | Different patients | Network design | Perishability | Disaster/disruption |
Other feature | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Processing plant | Donation center | |||||||||||||||||
| Larimi and Yaghoubi [10] | Platelet | Integrated | Apheresis-whole blood | Tactical | Min Cost& Max donors | Multi | – | Robust-stochastic | – | Yes | Demand | Yes | – | Yes | – | – | – | |
| Hosseini-Motlagh et al. [31] | Blood | Integrated | whole blood | Strategic- tactical | Min cost& max service | Multi | – | Robust | – | Yes | Yes | Demand | – | Yes | Yes | – | – | – |
| Ensafian et al. [23] | Platelet | Integrated | Apheresis-whole blood | Tactical-operational | Min cost | Multi | – | Robust-stochastic | – | Yes | Yes | Demand | Yes | – | Yes | – | – | – |
| Gunpinar and Centeno [28] | Blood-platelet | Distribution | whole blood | Tactical-operational | Min cost | Multi | – | Stochastic | Yes | – | – | Demand | Yes | – | Yes | – | – | – |
| Zahiri and Pishvaee [29] | Blood | Collection | whole blood | Strategic- tactical | Min cost& shortage | Multi | – | Fuzzy-robust | – | Yes | Yes | Demand | – | Yes | – | – | – | – |
| Beheshtifar and Alimoahmmadi [68] | – | Network design | – | Strategic | Min cost& max service | single | – | exact | – | – | Yes | – | – | Yes | – | – | – | GIS-approach for locating hospitals |
| Kizito andWilliam [65] | – | Network design | – | Strategic | Min non-standard hospitals | single | – | exact | – | – | Yes | – | – | Yes | – | – | – | GIS-approach for locating hospitals |
| Yaghoubi et al. [38] | Platelet | Inventory- distribution | whole blood | Strategic- tactical | Min cost& time delivery | Multi | – | Robust& p-robust | – | – | Yes | Demand | Yes | Yes | Yes | – | Yes | |
| Samani et al.[66] | Blood | Inventory- distribution | Not-mentioned | tactical | Min cost& max service | Multi | – | Robust | – | – | Yes | Demand, supply, costs | – | Yes | Yes | – | – | – |
| Rahmani [37] | Blood | Collection | Not-mentioned | Strategic | Min cost | Multi | – | Robust& lagrangian relaxation | – | – | – | Demand& cost | – | Yes | – | – | Yes | – |
| Hosseini-Motlagh et al. [39] | Plasma | Integrated | Apheresis-whole blood | Strategic- tactical | Min cost | Multi | – | Robust& p-robust | – | – | Yes | Demand& cost | Yes | Yes | Yes | – | Yes | – |
| Haghjoo et al. [6] | Blood | Collection | Not-mentioned | Strategic | Min cost | Multi | – | stochastic | – | – | Demand& failure | – | Yes | – | – | Yes | – | |
| Liu et al. [16] | Blood-platelet | Inventory- distribution | Not-mentioned | Tactical | Min cost | Multi | – | decomposition-based algorithm | – | – | – | – | – | – | Yes | – | – | – |
| Achmadi & Mansur [24] | Blood products | Inventory | Not-mentioned | – | Cross-matching | – | – | Operations management | Yes | – | – | – | – | – | – | – | – | – |
| Baş Güre et al. [30] | Blood | Donation | – | Operational | Min time | Single | – | Robust-possiblistic | – | – | – | Demand | – | – | – | – | – | Scheduling |
| Hosseini-Motlagh et al. [32] | Blood | Network design | – | Strategic | Min costs | Multi | – | Fuzzy | – | – | Yes | Demand | – | Yes | – | – | – | Donor motivation, advertisement |
| Acar and Kaya [35] | – | Network design | – | Tactical | Max satisfaction rate | – | – | Scenario-based | – | – | Yes | Demand- transportation time | Yes | Yes | – | – | – | Disastrous situation in hospitals |
| Patra and Jha [40] | – | Network design | – | Tactical-operational | max service | Multi | – | Scenario-based | – | – | Yes | – | – | – | – | – | Yes | lack of replenishment opportunities |
| Choi [43] | – | Network design | – | Tactical | Min costs | Multi | – | Scenario-based | – | – | – | – | – | – | – | – | Yes | Mobile centers considered |
| Mollalo et al. [46] | – | Supplier | – | Strategic | max service | – | – | – | – | – | Yes | – | – | – | – | – | Yes | GIS-based approach |
| Bherwani et al. [47] | – | Supplier | – | Strategic | max service | – | – | Bayesian probability model | – | – | – | – | – | – | – | – | – | GIS-based approach in Pandemics |
| Delen et al. [45] | Blood | Collection | – | Strategic | max service | – | – | data mining | – | – | Yes | – | – | – | – | – | – | Max availability |
| Kaveh & Mesgari [49] | – | Network design | – | Strategic- tactical | Min costs | – | – | – | – | – | – | – | – | Yes | – | – | – | Max coverage in emergencies |
| Samani et al. [69] | blood | Integrated | – | Strategic- tactical | Min cost-Max quality | Multi-period | – | Fuzzy | – | – | Yes | Costs- demand- quality | – | Yes | Yes | – | – | – |
| This research | Blood | Integrated | whole blood | Strategic- tactical | Min cost& max protect | Multi-period | Yes | Robust & scenario-based | Yes | No | Yes | Demand& failure | No | Yes | Yes | Yes | – | GIS-approach for finding the candidate donation centers' location |
Appendix B.
Subject to:
Constraints of assigning blood donors to mobile facilities:
| (B2) |
| (B3) |
| (B4) |
| (B5) |
| (B6) |
| (B7) |
| (B8) |
Constraint (B.2) assures that at most one mobile facility can move from other locations to a specific area in each period. The third constraint points to the number of open mobile facilities in each time period. Constraint (B.4) guarantees that a mobile facility can move to another location only if it is first allocated in location u. Constraint (B.5) points to the coverage distance limitation for assigning donor groups to mobile facilities. Constraint (B.6) makes sure that donors can donate their blood in a mobile facility only if it has been established. Constraint (B.7) refers to the capacity limitation in each mobile facility. Constraint (B.8) ensures that each group of donors can donate in only one of the three centers of mobile facilities, main donation centers, or the processing plant.
Constraints of main donation centers:
| (B9) |
| (B10) |
| (B11) |
| (B12) |
| (B13) |
| (B14) |
Constraints (B.9) and (B.10) refer to the point that each donor group only can assign to a main donation center if the donation center has been founded before in its coverage distance. Constraints (B.11) and (B.13) ensure that each mobile facility can assign to a main donation center if both the donation center and mobile facility have been established. Constraint (B.14) limits the maximum capacity in each main donation center.
Constrains of processing plant:
| (B15) |
| (B16) |
| (B17) |
Constraint (B.15) refers to the coverage distance for each processing plant. Constraint (B.16) limits the number of donors that can be accepted to donate their blood in the processing plant. Constraint (B.17) ensures that amount of blood units in the processing plant is not more than its capacity. on the left side of the equation refers to the probable disruption situation in the processing plant, which decreases the processing plant's capacity.
Flow balance and inventory constraints:
| (B18) |
| (B19) |
| (B20) |
| (B21) |
| (B22) |
Constraint (B.18) limits the maximum supply achieved by donors. The flow balance for the mobile facilities in different periods has shown in constraint (B.19). Constraint (B.20) illustrates the flow balance for each main donation center. Constraints (B.21) and (B.22) evaluate the inventory level of each kind of cross-matched product in each processing plant and hospital, respectively.
Back-up facilities and protective approach constraints:
| (B23) |
| (B24) |
| (B25) |
| (B26) |
Constraint (B.23) ensures that the delivery rate of a hospital cannot be more than one. It means that a hospital can gain at most 100% of its demand from both the back-up facilities and processing plant. Constraint (B.24) ensures that a main donation center can directly transfer their blood units to hospitals only if considered a back-up facility. Constraint (B.25) guarantees that none of the main donation centers can be regarded as a back-up center unless there is a disruption in the processing plant. Constraint (B.26) states that only a located main donation center can be considered as a back-up center.
Constraints of wastages amount
| (B27) |
| (B28) |
Constraints (B.27) and (B.28) calculate the number of wastages units of both types of cross-matched blood in the processing plant and hospitals, respectively.
Domain of decision variables
| (B29) |
| (B30) |
Appendix C.
Based on Bertsimas & sim [59] robustness approach, the following MILP model is considered, where are respectively convex polyhedron, the n-vector of objective coefficients, and right-hand side constraints:
| (C31) |
| (C32) |
| (C33) |
If is considered as the uncertain parameter, which can be changed in the range of , where refers to the deviation of , its uncertain formulation can be written as follows,
| (C34) |
| (C35) |
In which, and are an uncertainty set and budget of uncertainty for each constraint i, respectively. can take a value between [0, ]. The lower bound of the budget of uncertainty illustrates the model in the lower protected situation, as means the model cannot be protected against demand fluctuation. Regarding this, shows the fully protected system against uncertainty.
The duality of the robust model can be formulated as:
| (C36) |
| (C37) |
| (C38) |
| (C39) |
| (C40) |
| (C41) |
Similar to the above formulation, if is the uncertain parameter, which can be changed in the range of , where refers to the deviation of , its uncertain formulation can be written as follows [70],
| (C42) |
| (C43) |
Accordingly, the conservatism level in this model is in the range of [0, 100%]. As this value goes to the upper bound [100%], the level of protection of the model increases. If the uncertain demand varies in the range of [, the revision of equation (1), (B.20), (B.21), and (B.22) can be seen in the following:
| (C44) |
| (C45) |
| (C46) |
| (C47) |
| (C48) |
| (C49) |
| (C50) |
| (C51) |
| (C52) |
| (C53) |
| (C54) |
where and are dual auxiliary variables. To find the maximum deviation of , an index named perturbation level () is defined as a given data to take a value between [0,1]. With this in mind, can be calculated as . Budget of uncertainty can be changed between , is in the range between , can be changed between and can be changed between For further information, readers can see Refs. [36,[66], [67]].
Appendix D.
Table. D1.
shows the sources of the input data.
| The value of input data | |||
|---|---|---|---|
| Parameter | Reference | Parameter | Reference |
| i | Real case, Tehran is divided into 22 areas | s | Decision-makers, divided into four different scenarios, no disruption, 50% disruption, 70% disruption, and complete disruption. |
| j | Based on the IBTO website | Decision-makers, 0.4 for s = 0, 0.2 for the rest scenarios | |
| u | Based on the IBTO website | Cost parameters | Based on experts' knowledge, and relevant literature [7,38,61,71] |
| b | Real case, Tehran has one processing plant | Distance parameters | Based on the real case by GIS approach |
| h | Number of main consumers of blood, based on the IBTO website | Capacity parameters | The real data, based on IBTO experts' knowledge and documents |
| r | Based on medical facts | Real case, based on IBTO reports and related studies [58] | |
| t | Real case, the weekly period up to blood lifespan | Relevant articles [23] and IBTO reports | |
The description of each area in Tehran is illustrated in Table D2, including population, number of available donation centers, number of potential donation centers as alternative care facilities, and donation rate.
Table D2.
The data of each activity center in Tehran
| Activity center | Population () | No. of available DC | No. of Potential DC | No. of Potential mobile clinics | Available donation rate () |
|---|---|---|---|---|---|
| 1 | 381003 | 1 | 1 | – | 1905 |
| 2 | 608918 | – | 1 | – | 3045 |
| 3 | 655718 | – | 1 | – | 3279 |
| 4 | 856072 | 1 | 2 | – | 4280 |
| 5 | 687377 | 1 | 2 | – | 3437 |
| 6 | 240751 | 1 | – | – | 1204 |
| 7 | 310184 | – | – | 1 | 1551 |
| 8 | 379036 | – | 1 | – | 1895 |
| 9 | 167000 | – | 2 | – | 835 |
| 10 | 316620 | – | – | 1 | 1583 |
| 11 | 275595 | – | 1 | – | 1378 |
| 12 | 250188 | – | 2 | – | 1251 |
| 13 | 246407 | 1 | 1 | – | 1232 |
| 14 | 690609 | – | 1 | – | 3453 |
| 15 | 655277 | – | 1 | – | 3276 |
| 16 | 315115 | – | – | 1 | 1576 |
| 17 | 256439 | – | 1 | – | 1282 |
| 18 | 322656 | – | – | 1 | 1613 |
| 19 | 255027 | – | 1 | – | 1275 |
| 20 | 336339 | 1 | 1 | – | 1682 |
| 21 | 160107 | – | 1 | – | 801 |
| 22 | 112711 | – | – | 1 | 564 |
*Note that DC is the acronym of donation center.
References
- 1.Williamson L.M., V Devine D. Challenges in the management of the blood supply. Lancet. 2013;381(9880):1866–1875. doi: 10.1016/S0140-6736(13)60631-5. [DOI] [PubMed] [Google Scholar]
- 2.Govindan K., Mina H., Alavi B. A decision support system for demand management in healthcare supply chains considering the epidemic outbreaks: a case study of coronavirus disease 2019 (COVID-19) Transport Res Part E Logist Transp Rev. 2020;138:101967. doi: 10.1016/j.tre.2020.101967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Verikios G. The dynamic effects of infectious disease outbreaks: the case of pandemic influenza and human coronavirus. Socioecon. Plann. Sci. 2020;71:100898. doi: 10.1016/j.seps.2020.100898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Politis C., et al. Strategies for blood collection and optimization of the blood supply chain during the COVID‐19 pandemic in Greece. ISBT Sci Ser. 2020;15(4):386–392. [Google Scholar]
- 5.Leung J.N.S., Lee C.-K. Impact of the COVID‐19–a regional blood centre's perspective. ISBT Sci Ser. 2020;15(4):362–364. [Google Scholar]
- 6.Haghjoo N., Tavakkoli-Moghaddam R., Shahmoradi-Moghadam H., Rahimi Y. Reliable blood supply chain network design with facility disruption: a real-world application. Eng Appl Artif Intell. 2020;90:103493. [Google Scholar]
- 7.Hosseini-Motlagh S.-M., Larimi N.G., Nejad M.O. A qualitative, patient-centered perspective toward plasma products supply chain network design with risk controlling. Oper Res. 2020:1–46. [Google Scholar]
- 8.Hamdan B., Diabat A. Robust design of blood supply chains under risk of disruptions using Lagrangian relaxation. Transport Res Part E Logist Transp Rev. 2020;134:101764. [Google Scholar]
- 9.Jafarkhan F., Yaghoubib S., Gilani Larimi N., Farhang Moghadam B. The inventory–routing problem for distribution of red blood cells considering compatibility of blood group and transshipment between hospitals. Adv. Ind. Eng. 2020;53(3):31–44. [Google Scholar]
- 10.Larimi N.G., Yaghoubi S. A robust mathematical model for platelet supply chain considering social announcements and blood extraction technologies. Comput Ind Eng. 2019;137:106014. [Google Scholar]
- 11.Dhiman Y., Patidar G.K., Arora S. Covid‐19 pandemic‐response to challenges by blood transfusion services in India: a review report. ISBT Sci Ser. 2020;15(4):365–373. [Google Scholar]
- 12.Gniadek T.J., et al. Expansion of hospital‐based blood collections in the face of COVID‐19 associated national blood shortage. Transfusion. 2020;60(7):1470–1475. doi: 10.1111/trf.15869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Teng Z., et al. Psychological status and fatigue of frontline staff two months after the COVID-19 pandemic outbreak in China: a cross-sectional study. J Affect Disord. 2020;275:247–252. doi: 10.1016/j.jad.2020.06.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ratick S., Meacham B., Aoyama Y. Locating backup facilities to enhance supply chain disaster resilience. Growth Change. 2008;39(4):642–666. [Google Scholar]
- 15.Jabbarzadeh A., Fahimnia B., Seuring S. Dynamic supply chain network design for the supply of blood in disasters: a robust model with real world application. Transport Res Part E Logist Transp Rev. 2014;70:225–244. [Google Scholar]
- 16.Liu K., Li Q., Zhang Z.-H. Distributionally robust optimization of an emergency medical service station location and sizing problem with joint chance constraints. Transp Res part B Methodol. 2019;119:79–101. [Google Scholar]
- 17.Lowalekar H., Ravi R.R. Revolutionizing blood bank inventory management using the TOC thinking process: an Indian case study. Int J Prod Econ. 2017;186:89–122. [Google Scholar]
- 18.Caunhye A.M., Nie X., Pokharel S. Optimization models in emergency logistics: a literature review. Socioecon. Plann. Sci. 2012;46(1):4–13. [Google Scholar]
- 19.Osorio A.F., Brailsford S.C., Smith H.K. A structured review of quantitative models in the blood supply chain: a taxonomic framework for decision-making. Int J Prod Res. 2015;53(24):7191–7212. [Google Scholar]
- 20.Pirabán A., Guerrero W.J., Labadie N. Survey on blood supply chain management: models and methods. Comput Oper Res. 2019;112:104756. [Google Scholar]
- 21.Williams E.P., Harper P.R., Gartner D. Modeling of the collections process in the blood supply chain: a literature review. IISE Trans Healthc Syst Eng. 2020;10(3):200–211. [Google Scholar]
- 22.Bandarenko N., King K. eleventh ed. American Association of Blood Banks (AABB); Bethesda, Maryland: 2014. Blood transfusion therapy: a physician's handbook. [Google Scholar]
- 23.Ensafian H., Yaghoubi S., Yazdi M.M. Raising quality and safety of platelet transfusion services in a patient-based integrated supply chain under uncertainty. Comput Chem Eng. 2017;106:355–372. [Google Scholar]
- 24.Achmadi R.E., Mansur A. Proceedings of the international conference on industrial engineering and operations management. 2018. Design mitigation of blood supply chain using supply chain risk management approach; pp. 1763–1772. [Google Scholar]
- 25.Bozorgi A., Najafi M. 2020 IEEE 7th international conference on industrial engineering and applications. ICIEA); 2020. Improving blood bank inventory management using double cross-match and hybrid issuance policy; pp. 819–826. [Google Scholar]
- 26.Dumas M.B., Rabinowitz M. Policies for reducing blood wastage in hospital blood banks. Manag Sci. 1977;23(10):1124–1132. [Google Scholar]
- 27.Katsaliaki K. Cost-effective practices in the blood service sector. Health Pol. 2008;86(2–3):276–287. doi: 10.1016/j.healthpol.2007.11.004. [DOI] [PubMed] [Google Scholar]
- 28.Gunpinar S., Centeno G. Stochastic integer programming models for reducing wastages and shortages of blood products at hospitals. Comput Oper Res. 2015;54:129–141. [Google Scholar]
- 29.Zahiri B., Pishvaee M.S. Blood supply chain network design considering blood group compatibility under uncertainty. Int J Prod Res. 2017;55(7):2013–2033. [Google Scholar]
- 30.Baş Güre S., Carello G., Lanzarone E., Yalçındağ S. Unaddressed problems and research perspectives in scheduling blood collection from donors. Prod Plann Control. 2018;29(1):84–90. [Google Scholar]
- 31.Hosseini-Motlagh S.-M., Samani M.R.G., Homaei S. Blood supply chain management: robust optimization, disruption risk, and blood group compatibility (a real-life case) J Ambient Intell Hum Comput. 2020;11(3):1085–1104. [Google Scholar]
- 32.Hosseini-Motlagh S.-M., Samani M.R.G., Cheraghi S. Robust and stable flexible blood supply chain network design under motivational initiatives. Socioecon. Plann. Sci. 2020;70:100725. [Google Scholar]
- 33.Fan D., Lo C.K.Y., Zhou Y. Sustainability risk in supply bases: the role of complexity and coupling. Transport Res Part E Logist Transp Rev. 2021;145:102175. [Google Scholar]
- 34.Qiu R., Sun Y., Sun M. A distributionally robust optimization approach for multi-product inventory decisions with budget constraint and demand and yield uncertainties. Comput Oper Res. 2021;126:105081. [Google Scholar]
- 35.Acar M., Kaya O. A healthcare network design model with mobile hospitals for disaster preparedness: a case study for Istanbul earthquake. Transport Res Part E Logist Transp Rev. 2019;130:273–292. [Google Scholar]
- 36.Li Y., Zhang J., Yu G. A scenario-based hybrid robust and stochastic approach for joint planning of relief logistics and casualty distribution considering secondary disasters. Transport Res Part E Logist Transp Rev. 2020;141:102029. [Google Scholar]
- 37.Rahmani D. Designing a robust and dynamic network for the emergency blood supply chain with the risk of disruptions. Ann Oper Res. 2019;283(1):613–641. [Google Scholar]
- 38.Yaghoubi S., Hosseini-Motlagh S.-M., Cheraghi S., Larimi N.G. Designing a robust demand-differentiated platelet supply chain network under disruption and uncertainty. J Ambient Intell Hum Comput. 2020;11(8):3231–3258. [Google Scholar]
- 39.Hosseini-Motlagh S.-M., Samani M.R.G., Homaei S. Toward a coordination of inventory and distribution schedules for blood in disasters. Socioecon. Plann. Sci. 2020;72:100897. [Google Scholar]
- 40.Patra T.D.P., Jha J.K. A two-period newsvendor model for prepositioning with a post-disaster replenishment using Bayesian demand update. Socioecon. Plann. Sci. 2021:101080. [Google Scholar]
- 41.Khan S.A.R., Razzaq A., Yu Z., Shah A., Sharif A., Janjua L. Disruption in food supply chain and undernourishment challenges: an empirical study in the context of Asian countries. Socioecon. Plann. Sci. 2021:101033. [Google Scholar]
- 42.Stanworth S.J., et al. Effects of the COVID-19 pandemic on supply and use of blood for transfusion. Lancet Haematol. 2020;7(10):756–764. doi: 10.1016/S2352-3026(20)30186-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Choi T.-M. Innovative ‘bring-service-near-your-home’ operations under Corona-virus (COVID-19/SARS-CoV-2) outbreak: can logistics become the messiah? Transport Res Part E Logist Transp Rev. 2020;140:101961. doi: 10.1016/j.tre.2020.101961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Jorfi M., et al. 2020. Diagnostic technology for COVID-19: comparative evaluation of antigen and serology-based SARS-CoV-2 immunoassays, and contact tracing solutions for potential use as at-home products,” medRxiv. [Google Scholar]
- 45.Delen D., Erraguntla M., Mayer R.J., Wu C.-N. Better management of blood supply-chain with GIS-based analytics. Ann Oper Res. 2011;185(1):181–193. [Google Scholar]
- 46.Mollalo A., Vahedi B., Rivera K.M. GIS-based spatial modeling of COVID-19 incidence rate in the continental United States. Sci Total Environ. 2020;728:138884. doi: 10.1016/j.scitotenv.2020.138884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bherwani H., et al. Understanding COVID-19 transmission through Bayesian probabilistic modeling and GIS-based Voronoi approach: a policy perspective. Environ Dev Sustain. 2020;23(4):5846–5864. doi: 10.1007/s10668-020-00849-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Franch-Pardo I., Napoletano B.M., Rosete-Verges F., Billa L. Spatial analysis and GIS in the study of COVID-19. A review. Sci Total Environ. 2020;739:140033. doi: 10.1016/j.scitotenv.2020.140033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Murray A.T. Contemporary optimization application through geographic information systems. Omega. 2021;99:102176. [Google Scholar]
- 50.Murray A.T., Xu J., Wang Z., Church R.L. Commercial GIS location analytics: capabilities and performance. Int J Geogr Inf Sci. 2019;33(5):1106–1130. [Google Scholar]
- 51.Kaveh M., Mesgari M.S. Improved biogeography-based optimization using migration process adjustment: an approach for location-allocation of ambulances. Comput Ind Eng. 2019;135:800–813. [Google Scholar]
- 52.Comber A., Dickie J., Jarvis C., Phillips M., Tansey K. Locating bioenergy facilities using a modified GIS-based location–allocation-algorithm: considering the spatial distribution of resource supply. Appl Energy. 2015;154:309–316. [Google Scholar]
- 53.Dell'Ovo M., Capolongo S., Oppio A. Combining spatial analysis with MCDA for the siting of healthcare facilities. Land Use Pol. 2018;76:634–644. [Google Scholar]
- 54.Özceylan E., Çetinkaya C., Erbaş M., Kabak M. Logistic performance evaluation of provinces in Turkey: a GIS-based multi-criteria decision analysis. Transport Res Part A Policy Pract. 2016;94:323–337. [Google Scholar]
- 55.Tong D., Murray A.T. Spatial optimization in geography. Ann Assoc Am Geogr. 2012;102(6):1290–1309. [Google Scholar]
- 56.Xu J., Murray A., Wang Z., Church R. Challenges in applying capacitated covering models. Trans GIS. 2020;24(2):268–290. [Google Scholar]
- 57.Piersma T.W., Bekkers R., de Kort W., Merz E.-M. Altruism in blood donation: out of sight out of mind? Closing donation centers influences blood donor lapse. Health Place. 2021;67:102495. doi: 10.1016/j.healthplace.2020.102495. [DOI] [PubMed] [Google Scholar]
- 58.Larimi N.G., Yaghoubi S., Hosseini-Motlagh S.-M. Itemized platelet supply chain with lateral transshipment under uncertainty evaluating inappropriate output in laboratories. Socioecon. Plann. Sci. 2019;68:100697. [Google Scholar]
- 59.Bertsimas D., Sim M. Robust discrete optimization and network flows. Math Program. 2003;98(1):49–71. [Google Scholar]
- 60.Hanks R.W., Lunday B.J., Weir J.D. Robust goal programming for multi-objective optimization of data-driven problems: a use case for the United States transportation command's liner rate setting problem. Omega. 2020;90:101983. [Google Scholar]
- 61.Ensafian H., Yaghoubi S. Robust optimization model for integrated procurement, production and distribution in platelet supply chain. Transport Res Part E Logist Transp Rev. 2017;103:32–55. [Google Scholar]
- 62.Cheraghi S., Hosseini-Motlagh S.-M. Responsive and reliable injured-oriented blood supply chain for disaster relief: a real case study. Ann Oper Res. 2020;291(1):129–167. [Google Scholar]
- 63.Wang C., Chen S. A distributionally robust optimization for blood supply network considering disasters. Transport Res Part E Logist Transp Rev. 2020;134:101840. [Google Scholar]
- 64.Maggioni F., Wallace S.W. Analyzing the quality of the expected value solution in stochastic programming. Ann Oper Res. 2012;200(1):37–54. [Google Scholar]
- 65.Kizito A., William C.M.P. Geospatial location-allocation approach to optimize healthcare facilities in peri-urban dwellers in mbeya city, Tanzania. MUST J Res Dev. 2020;1(1):56–78. [Google Scholar]
- 66.Samani M.R.G., Hosseini-Motlagh S.-M., Ghannadpour S.F. A multilateral perspective towards blood network design in an uncertain environment: methodology and implementation. Comput Ind Eng. 2019;130:450–471. [Google Scholar]
- 67.Paul J.A., Wang X.J. Robust location-allocation network design for earthquake preparedness. Transp Res part B Methodol. 2019;119:139–155. [Google Scholar]
- 68.Beheshtifar S., Alimoahmmadi A. A multiobjective optimization approach for location‐allocation of clinics. Int Trans Oper Res. 2015;22(2):313–328. [Google Scholar]
- 69.Samani M.R., Hosseini-Motlagh S.M., Sheshkol M.I., Shetab-Boushehri S.N. A bi-objective integrated model for the uncertain blood network design with raising products quality. Eur J Ind Eng. 2019;13(5):553–588. [Google Scholar]
- 70.Hatefi S.M., Jolai F. Robust and reliable forward–reverse logistics network design under demand uncertainty and facility disruptions. Appl Math Model. 2014;38(9–10):2630–2647. [Google Scholar]
- 71.Rajendran S., Ravindran A.R. Platelet ordering policies at hospitals using stochastic integer programming model and heuristic approaches to reduce wastage. Comput Ind Eng. 2017;110:151–164. [Google Scholar]