A Feature-based Affine Registration Method for Capturing Background Lung Tissue Deformation for Ground Glass Nodule Tracking

Abstract

Lung nodule tracking assessment relies on cross-sectional measurements of the largest lesion profile depicted in initial and follow-up computed tomography (CT) images. However, apparent changes in nodule size assessed via simple image-based measurements may also be compromised by the effect of the background lung tissue deformation on the GGN between the initial and follow-up images, leading to erroneous conclusions about nodule changes due to disease. To compensate for the lung deformation and enable consistent nodule tracking, here we propose a feature-based affine registration method and study its performance vis-a-vis several other registration methods. We implement and test each registration method using both a lung- and a lesion-centered region of interest on ten patient CT datasets featuring twelve nodules, including both benign and malignant GGO lesions containing pure GGNs, part-solid, or solid nodules. We evaluate each registration method according to the target registration error (TRE) computed across 30 – 50 homologous fiducial landmarks surrounding the lesions and selected by expert radiologists in both the initial and follow-up patient CT images. Our results show that the proposed feature-based affine lesion-centered registration yielded a 1.1 ± 1.2 mm TRE, while a Symmetric Normalization deformable registration yielded a 1.2 ± 1.2 mm TRE, and a least-square fit registration of the 30–50 validation fiducial landmark set yielded a 1.5 ± 1.2 mm TRE.

Although the deformable registration yielded a slightly higher registration accuracy than the feature-based affine registration, it is significantly more computationally efficient, eliminates the need for ambiguous segmentation of GGNs featuring ill-defined borders, and reduces the susceptibility of artificial deformations introduced by the deformable registration, which may lead to increased similarity between the registered initial and follow-up images, over-compensating for the background lung tissue deformation, and, in turn, compromising the true disease-induced nodule change assessment. We also assessed the registration qualitatively, by visual inspection of the subtraction images, and conducted a pilot pre-clinical study that showed the proposed feature-based lesion-centered affine registration effectively compensates for the background lung tissue deformation between the initial and follow-up images and also serves as a reliable baseline registration method prior to assessing lung nodule changes due to disease.

1. Introduction

Thin-slice helical chest CT images are used as standard-of-care to identify pulmonary nodules Henschke, McCauley, et al. (1999) and classify them as either part-solid (also known as sub-solid) or solid nodules Hansell, Bankier, et al. (2008). When smaller than 1 cm in diameter, these nodules are typically classified as incidental, benign findings, and only require follow-up CT imaging Fischbach, Knollmann, et al. (2003). Part-solid nodules, on the other hand, feature a “ground-glass appearance” — hence they are commonly referred to as ground-glass opacities (GGOs) nodules or ground-glass nodules (GGNs) — and are characterized by hazy, increased lung tissue opacities that don’t completely obscure pulmonary structures; in contrast, pure GGNs only feature ground-glass appearance, with no solid components. Unlike GGNs, solid nodules appear as focal homogeneous regions that completely obscure other different lung structures.

The Early Lung Cancer Action Project (ELCAP) study reported that 81% of the positive findings correspond to solid nodules, while the remaining 19% correspond to part-solid nodules. Compared to solid nodules, which feature a 7% malignancy risk, part-solid nodules pose a higher risk for malignancy (63%), while pure GGNs have pose a 18% risk for malignancy Henschke, Yankelevitz, et al. (2002); Jacobs, van Rikxoort, et al. (2014); Godoy and Naidich (2012). Unlike transient GGNs, which regress or disappear within three months of their appearance either due to their transient nature Lee, Park, et al. (2010) or in response to proper treatment Wormanns, Kohl, et al. (2004), other nodules are persistent and exhibit a slow growth rate or no change in size or opacity upon follow-up, often suggesting early-stage lung cancer.

Longitudinal analysis and tracking of nodule progression in current clinical practice resorts to visual comparison, as well as largest lesion diameter measurements between initial and follow-up CT scans to quantify growth rate. Radiologists rely on manual one- (1D) or two-dimensional (2D) annotations from the axial slices that depict the largest lesion diameter and the visual appearance of the margins Ko, Berman, et al. (2012) to quantify the solid portion and the whole nodule size. Subsequently, the lesion volume and volumetric growth rate, such as the doubling time, are often estimated based on a shape approximation of the lesion depicted in the initial and the follow-up scans displayed side-by-side, however, without first registering the initial and follow-up images.

Several factors may cause significant error in the nodule assessment. Intrinsic factors entail nodule orientation relative to the chest wall or other structures, irregular nodule margins, and asymmetric nodule shape and attenuation. Although three-dimensional (3D) shape and size quantification was suggested to provide more accurate and precise nodule tracking, especially for small nodules Ko, Berman, et al. (2012), volumetric analysis is rarely used in clinical practice, as it requires segmentation of the nodule. This process is highly subjective to intra- and inter-observer variability, especially for GGNs that often feature blurry and not clearly distinctive margins, rendering 2D slice-based analysis as the clinical standard of care for longitudinal lung nodule tracking.

Extrinsic factors, on the other hand, include patient position and changes in the parenchyma surrounding the nodules in response to heart rate and respiratory motion, which significantly change lung volume and shape Zheng, Kambhamettu, et al. (2009); Ko, Berman, et al. (2012). Zheng et al. Zheng, Kambhamettu, et al. (2009) reported that estimates at end-inspiration vs. end-expiration may lead to nodule volume detection error on the order of 12% induced by local deformations alone. Similarly, an additional study by Kim et al. Kim, Park, et al. (2013) reported an overall ±18% mass (volume x HU) and volume measurement fluctuations for part-solid GGNs as a result of inter-scan variability, patient position, heart rhythm, and inspiration levels. These findings suggest that true, disease-induced nodule changes may be reliably characterized only if a significant change in lesion size, independent of the background lung deformation, is detected Kakinuma, Ashizawa, et al. (2012).

Not only is a single CT slice a poor predictor of the geometry, orientation, and volume of a 3D lesion, but the different appearance of the lesion may also be influenced by deformations of the surrounding lung tissue between the initial and the follow-up scans. To quantify the effect of the background lung tissue deformation on nodule geometry to correctly assess the disease-induced nodule changes, accurate registration of the initial and follow-up scans is critical prior to comparing the lesion appearance in the initial and follow-up scans. Moreover, the use of image registration to align the initial and follow-up scans showed improved inter-observer agreement and clinical confidence when the radiologists used the digitally subtracted post-registration image to assess GGN volume and density changes Staring, Pluim, et al. (2009). According to this study, the perceived need for standard nodule diameter or volume measurements dropped substantially when the subtraction images of the registered initial and follow-up scans were available. Moreover, our collaborating radiologist also confirmed the usefulness of the subtraction image over the traditional nodule diameter measurements, therefore emphasizing the need for accurate registration to account for the extrinsic changes on nodule geometry due to background lung deformation and eliminate the need for lesion segmentation or diameter measurements to track nodule progression.

A large body of work has been dedicated to using lung image registration to compensate for the surrounding tissue deformation prior to nodule progression assessment, while preserving the true nodule volumes in the two scans. One of the first approaches was proposed by Zhao, Yankelevitz, et al. (1999) and uses the Jacobian of the registration transformation to eliminate false negative or false positive lesion expansion or shrinkage caused by the background lung deformation. Other approaches employ a rigid constraint on the nodule region using explicit or implicit segmentation of the nodule Tustison, Cook, et al. (2011); Werner, Schmidt-Richberg, et al. (2014); K., van Ginneken, et al. (2011). To explicitly evaluate the local deformation of the surrounding tissue around the nodule, a reasonable approach is to separate the foreground (i.e., nodule) and background (i.e., surrounding lung tissue) deformations by excluding (i.e., masking out) the lesion region. However, this approach also requires segmentation of the nodule, which inherently affects nodule growth estimates based on the segmented nodule shape. To address this limitation, implicit segmentation is preferable, especially for GGNs El-Baz, Beache, et al. (2013) that feature challenging to segment shapes and margins.

Although rigid registration is thought to appropriately handle the global deformation of the solid portion of the lesion and maintain nodule volume, it may not correctly capture the behavior of the non-solid portion or the lung tissue, which may be best portrayed by deformable registration, given the inherent soft tissue characteristics of the lung. Zheng et al. Zheng, Steiner, et al. (2007) leveraged a previous study that involved breast MR images Tanner, Schnabel, et al. (2000) to develop a framework that allowed different transformations to the lung and to the nodule, while coupling the segmentation and registration simultaneously into a single optimization problem. Their method modeled the lung tissue as non-rigid and the nodule as a rigid structure; the deformable registration followed the B-spline free-form deformation (FFD) implementation, while the rigid transformation imposed on the nodule preserved nodule volume and shape to avoid artificial changes.

A more sophisticated method proposed a geometric metamorphosis formulation, which simultaneously solves for the background and foreground deformation fields Niethammer, Hart, et al. (2011). The formulation also includes an image composition model to account for changes in image appearance. This method allows non-rigid deformation of both the lung and lesion, but still requires manual segmentation of the nodule, which is highly sensitive to irregular margins characteristic to GGNs.

Affine registration, on the other hand, was deemed most efficient to handle global transformations that are inherently non-rigid, such as the alignment of the inspiration/expiration image pairs that are often difficult to register accurately because of the large deformations present K., van Ginneken, et al. (2011). As such, most registration algorithms used in the EMPIRE10 (Evaluation of Methods for Pulmonary Image REgistration 2010) challenge relied on rigid, affine, or multi-resolution registration to handle the initial image alignment prior to deformable registration. Lastly, fluid-based deformable registration methods were also deemed optimal to handle large deformations by using the velocity field rather than displacement field to impose diffeomorphic transformations Werner, Schmidt-Richberg, et al. (2014); Lorenzi, Ayache, et al. (2013); Niethammer, Hart, et al. (2011) via the Large Deformation Diffeomorphic Metric Mapping (LDDMM) algorithm Cao, Miller, et al. (2005). Nevertheless, fluid-based registration methods are still highly dependent on the initial affine alignment and may still result in artificial deformations that could yield erroneous nodule tracking and mislead diagnosis.

The effectiveness of different lung image registration techniques for different applications, including local measurement of lung density changes for quantifying tissue destruction for emphysema detection and progression, was demonstrated in phantom data Staring, Bakker, et al. (2014). The results showed accurate prediction of solid nodule progression in phantom data that was reasonably consistent with global results in patient data, featuring a median TRE of 1 mm and effective elimination of the dependency on the inspiration level at image acquisition time.

In the effort to quantify “correspondence” and to validate image registration techniques, Murphy et al. K., van Ginneken, et al. (2011) recommended that the computed TRE between corresponding homologous landmarks in both the initial and follow-up images still provides the most useful reference standard for distinguishing between registration algorithm results. To provide a consistent framework for assessment of various image registration methods, two benchmarks featuring evaluation criteria for thoracic CT image registration were launched. The first benchmark — EMPIRE10 — provides a dataset for comparison of registration algorithms based on intra-patient thoracic CT image pairs K., van Ginneken, et al. (2011). The second benchmark — MIDRAS (Multi-Institution Deformable Registration Accuracy Study) — includes a set of lung and liver 4D CT image pairs Brock (2010). EMPIRE10 has conducted an ongoing challenge in registering thoracic CT image data and one of the evaluation criteria included the TRE calculated across a set of 100 homologous lung fiducial landmarks identified in both the initial and follow-up images. Following initialization via affine registration, the deformable fluid-based registration method achieved the highest accuracy, characterized by a TRE of 1.14 – 1.20 mm as reported by Werner et al. in their comprehensive comparison study of variational intensity-based parametric registration methods Werner, Schmidt-Richberg, et al. (2014).

Although deformable registration may be considered optimal, most deformable registration algorithms are highly dependent on the parameter initialization, are computationally inefficient, and pose a high risk of convergence to local rather than global minima, resulting in unrealistic deformations. As such, depending on the optimization trade-off between the similarity and regularization terms, if the registration is allowed to proceed extensively, the lesion depicted by the registered follow-up image will look similar to the lesion in the initial image, therefore compromising nodule progression assessment. As such, the added computational cost and high risk of artificial deformations that could mislead diagnosis, at the expense of only modest accuracy improvement, have contributed to limited use of deformable registration techniques beyond the research arena. In spite of the promising results reported in these studies, the difficulty of assessing background lung tissue deformation and using it as a baseline when quantifying the disease-induced lesion changes still exists in clinical practice, and a simple, sufficiently reliable solution is still pending.

To assess true nodule changes due to disease alone, beyond the changes induced by the deformation of the background lung tissue, and based on the premise that a global affine registration has the potential to provide a more realistic and accurate means to portray the background lung tissue deformation than a local deformable registration, here we propose and validate a feature-based affine registration method to co-register the initial and follow-up lung CT images.

2. Methods

2.1. Overview

In the effort to comprehensively evaluate the proposed feature-based affine registration to other registration techniques, our study entails several stages: automated segmentation and separation of the lungs, centroid alignment of the region of interest, intensity- and/or feature-based rigid and affine registration, then final refinement via intensity-based deformable registration. Moreover, since the region of interest is known to have a significant impact on the registration outcome, we explore the effect of using a lung- or lesion-centered RoIs. Lastly, we examined the use of local deformable registration accompanied by inclusion or exclusion of the lesion region from the registration domain by masking out the lesion segmented by radiologists.

Each registration algorithm was assessed according to the TRE evaluated across 30–50 homologous fiducial landmarks located at vessel branches in the vicinity of each lesion selected by two expert radiologists in each image pair. In addition, the residual error following rigid and 12 degree-of-freedom (DoF) affine least squared fit of the homologous landmarks identified in the initial and follow-up images were also computed and treated as baseline, control registration errors.

2.2. Imaging Data

This study was conducted on ten pairs of chest CT datasets featuring an initial and follow-up scan. The CT image datasets were acquired on either a 16-slice Lightspeed or a 64-slice VCT scanner (GE Medical Systems, Milwaukee, WI). All imaging data was retrieved following retrospective review of patient charts at a single site following informed consent granted by all patients, in compliance with the United States Health Insurance Portability and Accountability Act of 1996, and approved by the Institutional Review Board. The ten datasets contained twelve lesions identified and classified by two radiologists: one patient featured one lesion in each lung (Cases 5 and 6), while another patient featured two non-overlapping lesions in the same lung (Cases 11 and 12). The datasets contained solitary GGNs, multiple GGNs, and solid nodules.

All scans were acquired in a single breath-hold with sub-millimeter resolution (0.5 – 0.7 mm in-plane resolution and 0.62 mm slice thickness) and featured lesions localized in different regions of the lung that showed different extent of progression as evaluated at different stages ranging from 0.5 months to almost 3 years. As an example, Case 9 featured a part-solid GGN with a large solid part attached to the chest wall that was classified by both radiologists as a malignant juxtapleural nodule, justified by the large change detected at 32 month follow-up. Moreover, Case 2 featured a common transient part-solid nodule that showed almost complete regression in the follow-up scan. Lastly, Case 3 featured a new nodule in the follow-up scan that was not visible in the initial scan.

An expert radiologist manually segmented the nodules and also selected 30 – 50 homologous fiducial landmarks located both within and in the vicinity of each lesion in both the initial and follow-up scans. Most landmarks were selected at vasculature branching points as, according to the radiologists, these locations are least susceptible to non-rigid lung deformation due to breathing. The landmarks were used to quantify the TRE associated with all registration algorithms implemented in this study.

2.3. Trachea and Lung Segmentation and Separation, and RoI Definition

2.3.1. Lung Segmentation and Separation

We first resampled each follow-up CT scan to match the resolution of the initial scan and classified the image regions according to the typical Hounsfield scale of medical grade CT images that renders lung tissue between −1000 and −500 HU. In short, we segmented the lung as the largest connected region spanning the −1000 to −500 HU range not connected to the image borders. We then used the trachea segmentation and its branching into the left and right bronchi to identify and separate the lungs from the dual lung segmentation.

To segment the trachea, we first isolated the voxels in the −1050 to −850 HU range that separates the trachea from the lungs. We then employed several morphological operations to identify the circular tracheal cross-section in the first superior axial slice and used this geometry to track the trachea in subsequent inferior slices, until it branched into the left and right bronchi. This operation helped us separate and label the lungs.

2.3.2. Region of Interest Definition and Centroid Alignment

The lung-centered RoI was defined as a bounding box enclosing the entire lung and was centered at the centroid of the lung mask. The lesion-centered RoI was centered at the centroid of each lesion, determined either according to its approximate location identified by the radiologists or based on a rough, preliminary nodule segmentation, and extended 3–5 cm beyond the lesion boundaries to ensure full nodule enclosure and sufficient image clues for registration. For consistency, the size and resolution of the initial and follow-up image RoIs were the same after re-sampling.

Following RoI definition, the centroid of the RoI from the follow-up scan (i.e., the moving image) was aligned with the centroid of the homologous RoI in the initial scan (i.e., the fixed image). The resulting 3D translation was then subsequently applied to transform the fiducial dataset, later used for registration evaluation, corresponding to the follow-up scan into the same coordinate system as the initial scan. This preliminary RoI centroid alignment served as a global initial registration of the initial and follow-up images prior to the application of the subsequent registration transformations.

2.4. Intensity- and Feature-based Rigid and Affine Registration Algorithms

2.4.1. Intensity-based Registration

The optimal rigid and affine intensity-based registration utilized normalized cross-correlation (NCC), also known as the Pearson correlation coefficient, as the similarity measure. The NCC measure is invariant to the size of the overlap region between the images and hence can be computed efficiently. To solve the optimization problem, we used the linear programming simplex algorithm Cormen, Stein, et al. (2001), which was previously shown to outperform, in terms of accuracy, computational efficiency, and robustness to local minima, both the gradient descent and quasi-Newton Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithms Gill, Murray and Wright (1981). Moreover, we used different scales for each transformation type (i.e., rotation, scaling, shear, and translation) in the simplex solver implementation.

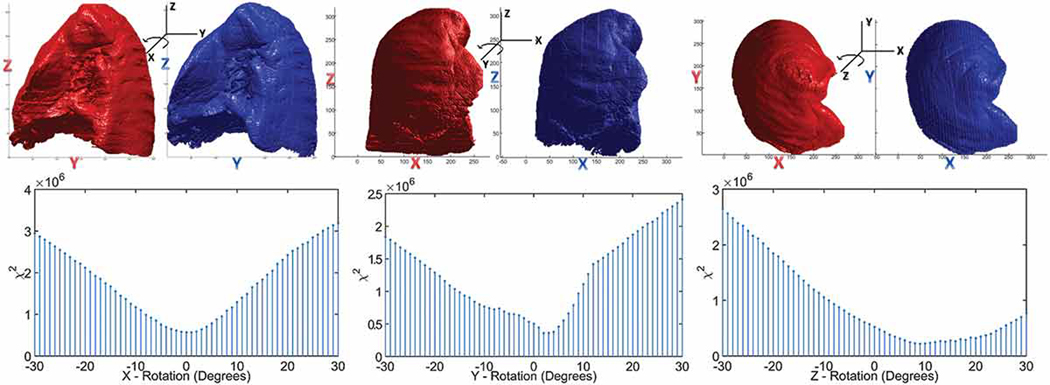
To initialize the rotation transformation, we sequentially estimated the optimal rotation about the x, y and z axes by minimizing the ${\chi }^2$ statistic between two the 2D image histograms of the initial and follow-up lung mask images h₁ and h₂ for each integer rotation within ±30°, using:

$$D_{{\chi }^2}=\sum _i\sum _j\frac{{\left(h_1(i,j)-h_2(i,j)\right)}^2}{h_1(i,j)+h_2(i,j)},$$ (1)

The 2D image histogram is the histogram of all non-zero voxels of the 3D lung mask projected onto the 2D image plane orthogonal to the rotation axis. The ${\chi }^2$ statistic was adopted from Pearson’s chi-square statistical test and was deemed effective when comparing the image histograms of similar objects at different orientations Meshgi and Ishii (2015). As such, we compared the histogram of the initial (i.e., fixed) lung mask with that of the rotated follow-up (i.e., moving) lung mask, computed the ${\chi }^2$ statistic, and select the rotation parameters that minimize the ${\chi }^2$ statistic ( Fig. 1). The optimal initial rotations about the x, y and z axes suggested by the minima of the ${\chi }^2$ statistic were similar to the final rotation parameters obtained post-registration and to the rotation parameters estimated via the rigid least-square fitting of the initial and follow-up fiducial markers datasets.

Figure 1.

Illustration of the lung masks from the initial scan (red) and follow-up scan (blue) rotated about the x, y and z axes along with the rotation angles determined by minimizing the χ² statistic between the histograms of the lung masks projected on the plane orthogonal to the rotation axis.

2.4.2. Feature-based Registration

The feature-based registration approach, illustrated in Fig. 2, followed a modified formulation and implementation of the widely-known iterative closest point (ICP) algorithm employed in the registration of point clouds. The features used for registration were edges extracted from both the initial and follow-up CT scans using the monogenic filtering approach proposed by Rajpoot et al. Rajpoot, Grau and Noble (2009). Unlike the traditional ICP algorithm in which the objective function minimizes the distance between estimated corresponding points using the closed-form solution for the Euclidean distance, we constructed a distance map Maurer, Qi and Raghavan (2003) of the initial scan by assigning each voxel a value equal to its distance from the closest edge. We then multiplied the distance map of the initial edge image by the transformed follow-up edge image, then computed the sum of the distances from the transformed edges to the edges in the initial image, which served as the objective function to be minimized.

Figure 2.

Illustration of the feature-based similarity metric. Mid-slices from the initial (a) and follow-up (b) CT images. The lung boundary edges are outlined in blue, while the content edges are overlaid in red; separation of the boundary (c) and content (d) edges for the initial and follow-up images; e) initial (white) and follow-up (black) lung boundary edges before registration; initial and follow-up content edges before (f) and after (g) registration.

The employed distance map function was defined as follows: given a subset of metric space $\text{Ω}\subset R^3$ with metric d, $\partial \text{Ω}$ denotes the boundary of $\text{Ω}$ and $x\in R^3$, then the distance function, is defined by:

$$f(x)=d(x,\partial \text{Ω})\mathbf{\text{if}}x\in R^3\setminus \partial \text{Ω}$$ (2)

$$\begin{gathered} =0\mathbf{\text{if}}x\in \partial \text{Ω} \\ \mathbf{\text{when}}d(x,\partial \text{Ω}):=\underset{y\in \partial \text{Ω}}{\inf }d(x,y) \end{gathered}$$ (3)

where ${\inf }_{y\in \partial \text{Ω}}d(x,y)$ denotes the infimum of the Euclidean distance between (x, y)

When constructing the objective function to be minimized during either rigid or affine registration, we separated the edges of the lung boundaries and the edges of the lung content. We defined the Energy Dissimilarity (E_D) function as the sum of the distances between lung boundary edges and lung content edges of the initial and follow-up scans.

$$\begin{gathered} Boundar{y}_{dist}=\sum f_{flb}\left(T\left[\partial {\text{Ω}}_{mlb}\right]\right), \\ Conten{t}_{dist}=\sum f_{flc}\left(T\left[\partial {\text{Ω}}_{mlc}\right]\right), \\ {E}_D=\alpha *Boundar{y}_{dist}+(1-\alpha )*Conten{t}_{dist}, \end{gathered}$$ (4)

where f _flb is the distance map function of the lung boundary edges in the initial scan and f _flc is the distance map function of the lung content edges in the initial scan (i.e., mostly the vessel boundaries). Similarly, $\partial {\text{Ω}}_{mlb}$ is the moving lung boundary edge image and $\partial {\text{Ω}}_{mlc}$ is the moving lung content edge image. $T[\partial \text{Ω}]$ represents the transformed edges, where the transformation can be rigid or affine. while α is a scalar weighting factor that modulates the weight of the lung boundary and lung content regions in the registration. Hence, α = 0 will only align the content edges, while α = 1 will only align the lung boundaries ( Fig. 2). Lastly, since most lesions are located within the lung and are rarely attached to the wall, and the selected fiducials used for registration validation are also within the lung content, our algorithm assigns heavier weights to the lung content edges than the lung boundary edges. Nevertheless, to ensure the most appropriate α values for each case, our algorithm evaluates the registration (centroid alignment followed by rigid and affine registration) for several α values (i.e., α = 0, 0.3, 0.5) and selects the optimal α value that yielded the highest NCC.

To initialize the rotation parameters prior to registration, we used the same ${\chi }^2$ statistic minimization approach. Moreover, we also used the same solver with similar options to solve the unconstrained linear objective function as those used in the intensity-based registration, specifically, the linear programming simplex algorithm Cormen, Stein, et al. (2001) featuring different scales for each transformation type. We first scaled the parameters to enlarge the search space and bounded the translation, rotation, shearing, and scaling parameters by ±20 mm, ±20°,±2°,and ±15%, respectively. Note that these bounds are only used to limit the search space, and are not mandatory to achieve the reported accuracy.

2.5. Nonrigid, Deformable Registration

The result of the affine intensity- or feature-based registration served as input for the non-rigid, deformable registration. We used the high-degree of freedom diffeomorphic transformation method proposed in Song, Tustison, et al. (2010), with several pre-processing steps recommended by the authors, including the rescaling and truncation of the image intensities, followed by de-noising. This technique is referred to as the Greedy Symmetric Normalization (SyN) registration and is based on the LDDMM algorithm available via the ANTS (Advanced Normalization Tools) open source package integrated within ITK. This registration is initiated via a global affine registration of the lungs masks, rather than the CT data. The mutual information (MI) similarity measure is used on a four-level image pyramid, together with successive gradient descent optimization to control the affine registration parameters.

The affine transformation is used to establish boundary conditions for the diffeomorphic registration, which is defined using Euler Lagrange equation (ELE) on the velocity field that varies over time, where the deformation field is the Euler integration on the smooth velocity field at t = 1. To construct a symmetric diffeomorphism, the deformation is decomposed into two components: the first component represents the deformation from the reference image into the template image and minimizes the variational energy from t = 0; the second component represents the deformation from template image to the reference image, and minimize the variational energy from t = 1. Both images are moving and the stationary solution is obtained at the midway when t = 0.5. To reduce the computation of the gradient and integration steps, a greedy gradient descent multi-resolution optimization is proposed, while fixing the affine registration on the boundaries. In addition, an approximated Green kernel accompanied by a Gaussian regularization kernel of the differential operator was used to solve for and update both components in each iteration. The local cross-correlation integrated over the entire lung volume was used as a similarity metric, as its invariance to the linear intensity changes renders it as a suitable similarity function.

For the sake of completeness and reproducibility, here we provide a summary of the optimal configuration of the Symmetric Normalization algorithm, starting with the authors’ recommendations Song, Tustison, et al. (2010) and adapted for our lesion- and lung-centered RoIs. The optimal configuration for the lesion-centered RoI deformable registration entails the following parameters: convergence — 200 × 150 × 100; convergence threshold — 1e-6; convergence window size — 10; shrink-factors (in each level) — 4 × 2 × 1; no smoothing; gradient step — 0.1; update field mesh size at base level — 8; total field mesh size at base level — 0; spline order — 3. To achieve an optimal configuration for the lung-centered RoI deformable registration, the following parameters were adjusted as indicated: update field mesh size at base level — 32; iterations in each level — 200 × 200 × 200 × 150 × 100; smoothing in each pyramid level — 2 × 1 × 0 × 0 × 0; shrink factors — 8 × 6 × 4 × 2 × 1. In addition, the lesion-centered RoI knot spacing for the updated field of 8 mm at the base level is reduced by a factor of two for each of the three sequential multi-resolution level, yielding a knot spacing of 2 mm at the final level. For the lung-centered RoI, the knot spacing for the updated field at the base level was 32 mm and was also reduced by a factor of two for each of the five sequential multi-resolution levels, also yielding a 2 mm spacing at the final level. Moreover, for the average resolution of the initial and follow-up scans (0.66 × 0.66 × 0.77 mm), and average size of the lung-centered RoI (331 × 248 × 406) and lesion-centered RoI (188 × 190 × 89), the corresponding number of control points was 110 × 83 × 157 and 63 × 64 × 35, resulting in ((110 × 83 × 157 × 3) and (63 × 64 × 35 × 3) degrees of freedom, respectively. As such, the number of degrees of freedom (i.e., 10⁶ for the lung-centered RoI and 10⁵ for the lesion-centered RoI) associated with the deformable registration is significantly higher than the 12 degrees of freedom of an affine registration, and significantly increase the complexity of the optimization problem.

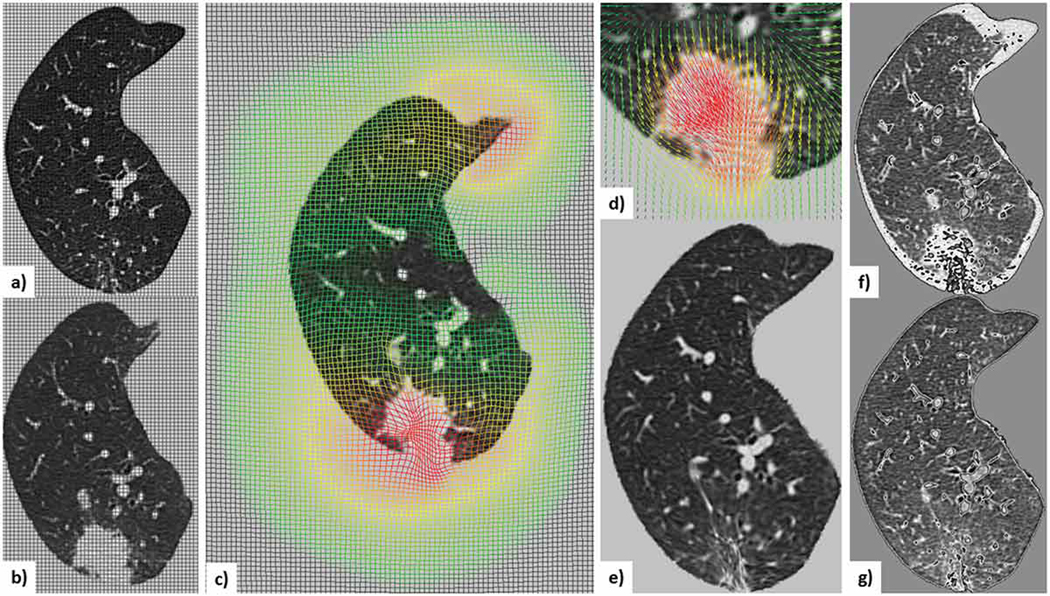
This deformable registration workflow applied to Case 9 — the most challenging nodule in our dataset — is illustrated in Fig. 3, along with the deformation field showing the shrinkage of the lesion in the registered follow-up image to match the lesion geometry in the initial scan acquired 32 months prior to the follow-up scan, hence clearly suggesting nodule progression. Recall than we register the follow-up scan to the initial scan, so shrinkage of the follow-up scan to match the initial scan suggests nodule growth.

Figure 3.

Illustration of the deformable registration workflow applied to Case 9, the most challenging nodule in the dataset: a) mid-slice from the initial lung-centered-RoI image with overlaid non-deformed grid; b) mid-slice from the follow-up lung-centered-RoI (i.e., moving) image with overlaid non-deformed grid; c) scaled moving image with overlaid deformed grid showing the deformation field; d) moving lesion-centered RoI image and corresponding deformed field; e) scaled deformed moving image; subtraction image between the initial and follow-up images before (f) and after (g) registration.

2.6. Registration Evaluation and Baseline Control Metrics

Each registration step was assessed according to the TRE evaluated across 30–50 homologous fiducial landmarks located at vessel branches in the vicinity of each lesion selected by two expert radiologists in each image pair.

To obtain a measure of the ideal, best possible alignment of the fiducial datasets selected in both the initial and follow-up CT scans, we computed the rigid and affine best fit transforms that minimize the residual least-square error between the initial and follow-up sets of 30–50 homologous fiducial landmarks. For the rigid least-square fit, we used the singular value decomposition (SVD) of the estimated covariance matrix to extract the rotation angles and translation parameters Sorkine-Hornung and Rabinovich (2017), while for the 12 DoF affine transformation, we used the pseudo-inverse approach described in Bjerhammar (1928). The achieved residual error served not only as a measure of the “best possible alignment” between the initial and follow-up landmark datasets, but also a measure of how “homologous” the two fiducial datasets were, and how reliably they were selected by the clinicians under the assumption that either a rigid or 12 DoF affine transformation were sufficient to portray their deformation from their initial to follow-up configuration. In essence, the residual error following best rigid and 12 DOF affine alignment of the two point clouds indicates the lowest achievable registration error and hence serve as baselines against which the TRE of all the implemented registration algorithms could be assessed.

Note that the 12 DoF affine transformation is not just a simple affine transformation, but also featured a projective transformation in addition to the affine transformation, because of the twelve degrees of freedom not being restricted to only translation, rotation, shearing and scaling, as shown in the visual (qualitative) image registration evaluation section. Therefore, these unwanted projective transformation effects render the rigid least squared fit transform as a more reliable control for establishing a baseline for registration accuracy.

3. Evaluation and Results

3.1. Quantitative Image Registration Accuracy Evaluation

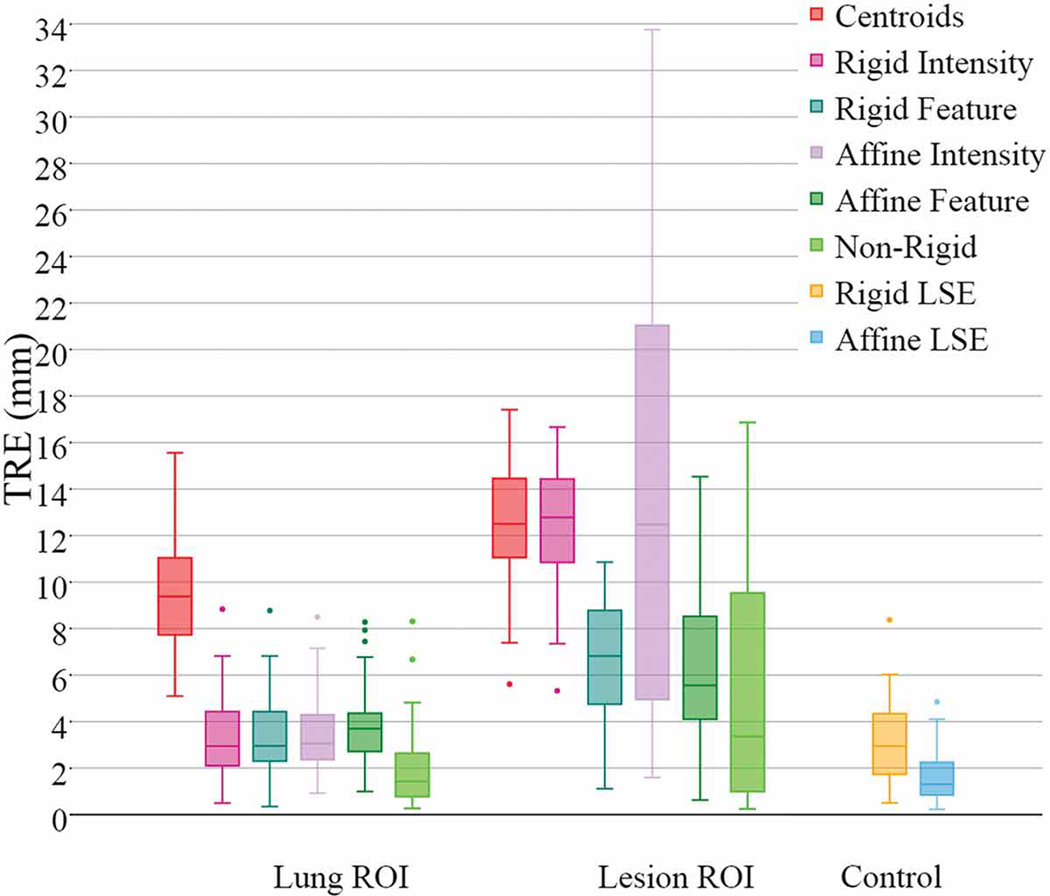
Table 1 summarizes the accuracy performance of each registration algorithm (rigid, affine and deformable) operating on both the lung- and lesion-centered RoI in terms of their mean ± standard deviation and median TRE.

Table 1.

Summary of the Target Registration Error (TRE) across cases 1–11 for each registration method (TRE (mm) Mean ± Std. Dev. and Median) operating on the lung- and lesion-centered RoI. Recall that the Case 12 lesion was located within the same lung as the Case 11 lesion, however all landmarks were centered around the Case 11 lesion; hence the deformable registration operating on the Case 11 lesion-centered RoI cannot be evaluated using the landmarks surrounding Case 11.)

TRE (mm)	Lung RoI		Lesion RoI
	μ±σ	Median	μ±σ	Median
Rigid Intensity	2.57±1.85	2.04	1.83±1.33	1.41
Rigid Feature	2.22±1.19	1.98	1.72±1.29	1.35
Affine Intensity	1.82±1.27	1.43	1.42±1.13	1.07
Affine Feature	1.95±1.64	1.44	1.47±1.22	1.10
Non-Rigid	1.17±1.18	0.80	1.14±1.25	0.80
Rigid LSE	1.63±1.14	1.34	1.53±1.16	1.22

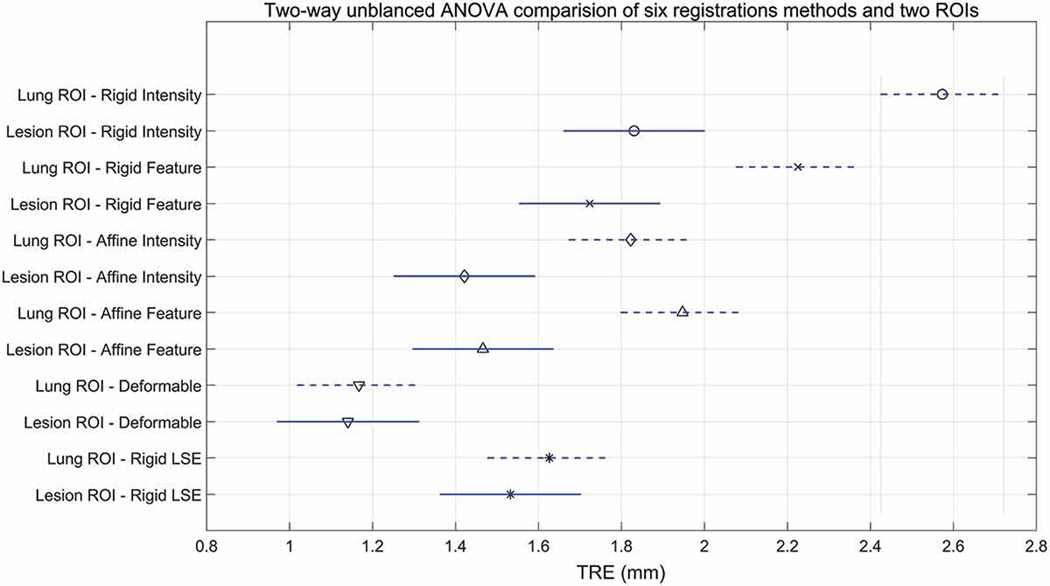
To test for statistically significant differences between the TRE achieved using different registration algorithm across both the lesion- and lung-centered RoIs across all patients, we first preformed an unbalanced (since not all fiducial landmarks were included in the lesion RoIs) two-way ANOVA followed by a Tukey-Kramer pairwise comparison post-hoc test with a standard significance level of α = 0.05. Note that the deformable registration is not greatly influenced by the RoI selection due to its local nature, but it still nevertheless depends on the precursor affine registration step to handle the initial large deformations, when present.

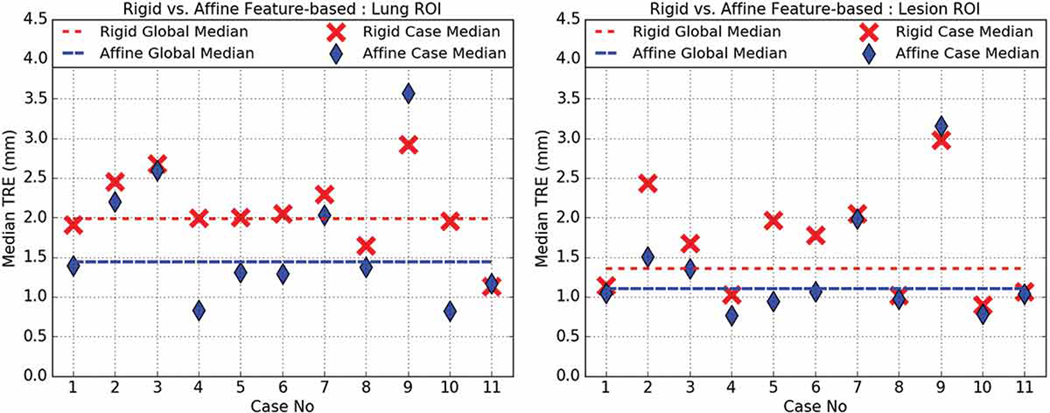
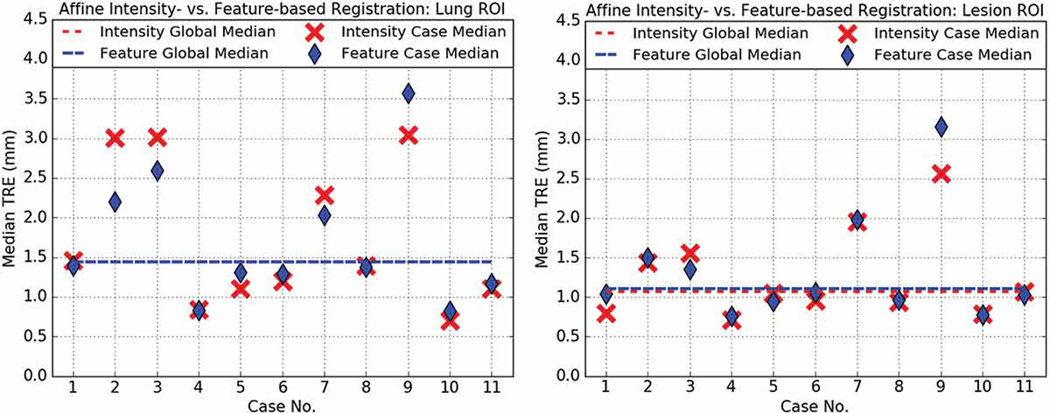
Figures 5 - 8 show the overall median TRE for each registration method across all cases, with Case 12 illustrating the importance of the lesion-centered RoI and its improved local effect and unchanged global effect.

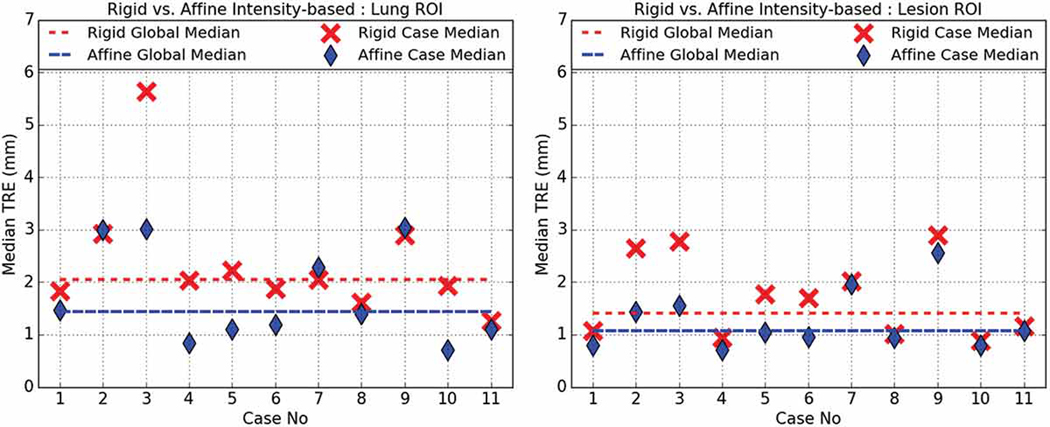
Figure 5.

Rigid (red) vs. affine (blue) intensity-based registration median TRE for lung- (left) and lesion-centered RoI (right).

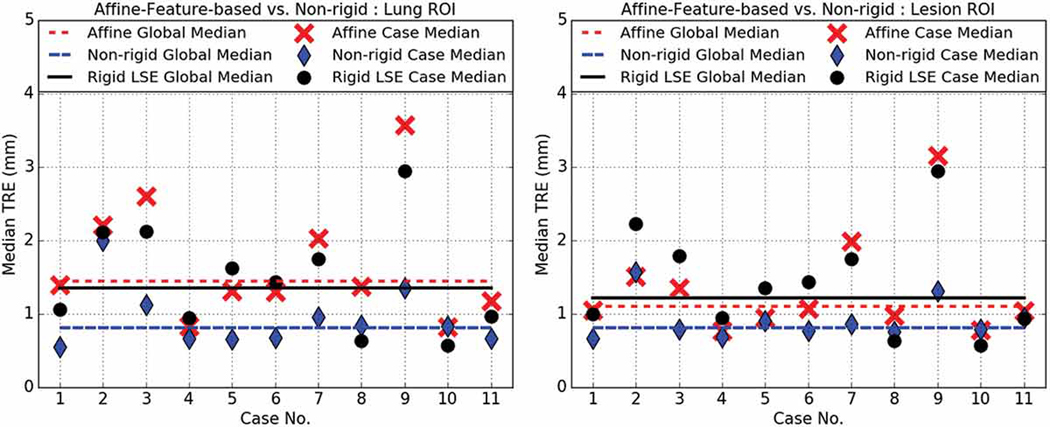
Figure 8.

Affine feature-based (red) vs. deformable (blue) median TRE for lung- (left) and lesion-centered (right) RoI registration. Also shown is the landmark-based rigid least squared fit TRE (black) treated as control. Note that since the Case 12 lesion was co-located within the same lung as the Case 11 lesion, but remote from the Case 11 lesion, and all selected landmarks were in the vicinity of the Case 11 lesion, hence the deformable registration operating on the Case 12 lesion-centered RoI could not be evaluated. Therefore, this figure only illustrates the median TRE achieved across 11 cases under feature-based affine, deformable and rigid least-square fit registration.

Fig. 5 shows that the intensity-based affine registration operating on the lung-centered RoI (1.82.±1.27 mm) was significantly more accurate (p = 0.0000) than the intensity-based rigid registration (2.57±1.85 mm). A similar trend was observed for the lesion-centered RoI registration, which yielded a 1.42±1.13 mm affine TRE vs. a 1.83±1.33 mm rigid TRE, with statistical significance (p = 0.0041).

Fig. 6 compares the feature-based rigid vs. affine registration algorithms. On the lung-centered RoI, the affine TRE (1.95±1.64 mm) was not significantly different (p = 0.0865) from the rigid TRE (2.22±1.19 mm). Similarly, on the lesion-centered RoI, the affine TRE (1.47±1.22 mm) was also not significantly different (p = 0.3405) from the rigid TRE (1.72±1.29 mm). However, it is worthwhile noting that when Case 9 is excluded from the statistic, the affine feature-based TRE is significantly more accurate than the rigid registration. Case 9 features a malignant nodule attached to the chest wall with significant progression between the scans, which was posed difficulties in identifying reliable fiducials, and it therefore may be considered an outlier when evaluating the lesion-centered RoI.

Figure 6.

Rigid (red) vs. affine (blue) feature-based registration median TRE for lung- (left) and lesion-centered RoI (right).

Fig. 7 shows no statistically significant difference (p = 0.9668) between the feature-based (1.95±1.64 mm) and intensity-based (1.82±1.27 mm) affine registration TRE when operating on the lung-centered RoI, and, similarly, no statistically significant difference (p = 1.0000) between the feature- (1.47±1.22 mm) and intensity-based (1.42±1.13 mm) affine registration TRE when operating on the lesion-centered RoI.

Figure 7.

Intensity- (red) vs. feature-based (blue) affine registration median TRE for lung- and lesion-centered RoI.

Fig. 8 compares the affine feature-based registration to the deformable (SyN) intensity-based registration, as well as the rigid landmark-based least squared fit. When operating on the lung-centered RoI, significant statistical differences (p = 0.001) were observed between the deformable registration (1.17±1.18) and feature-based affine registration (1.95±1.64), as well as between the rigid LSE (1.63±1.14) registration and the feature-based affine registration (p = 0.0194). However, when operating on the lesion-centered RoI, the feature-based affine registration TRE (1.47±1.22) was not significantly different (p = 0.0711) from the deformable registration TRE (1.14±1.25), and also not significantly different (p = 1.000) from the rigid least squared fit TRE (1.53±1.16) treated as control. Lastly, it should be noted that the deformable lesion-centered RoI registration for the Case 12 lesion could not be evaluated, as Case 12 represents a second nodule within the same lung as Case 11, but all fiduciall landmarks used to asses the registration were proximal to the Case 11 nodule.

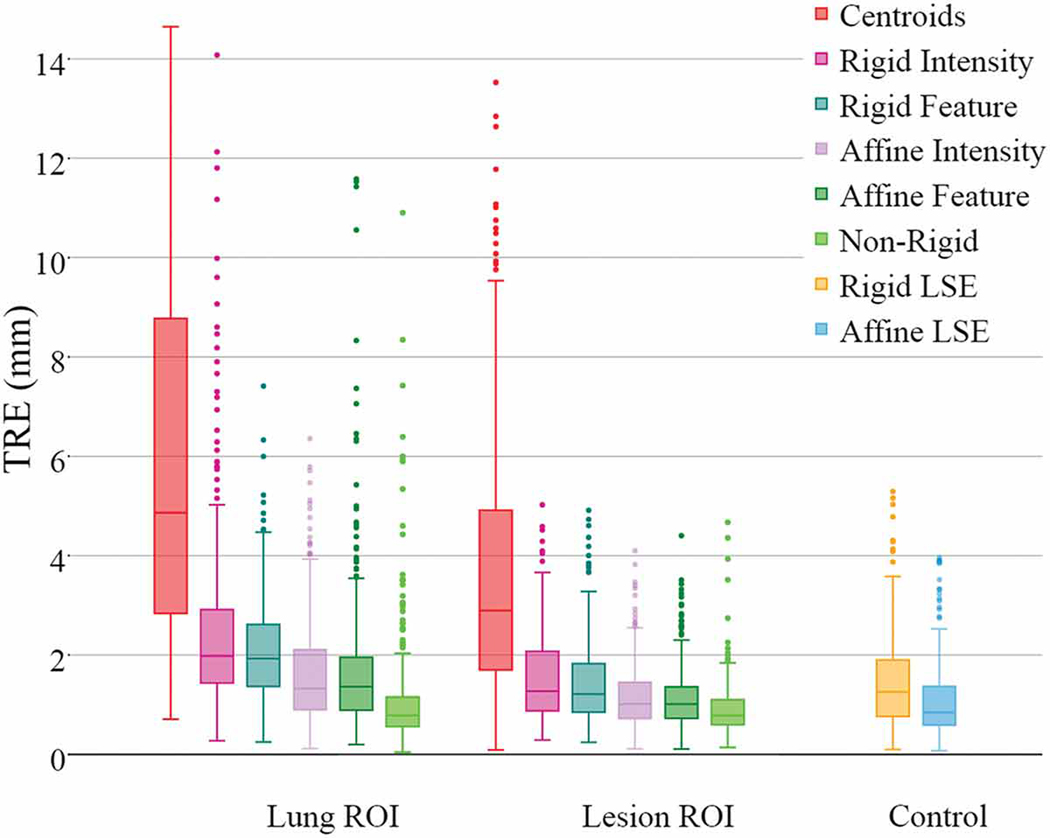
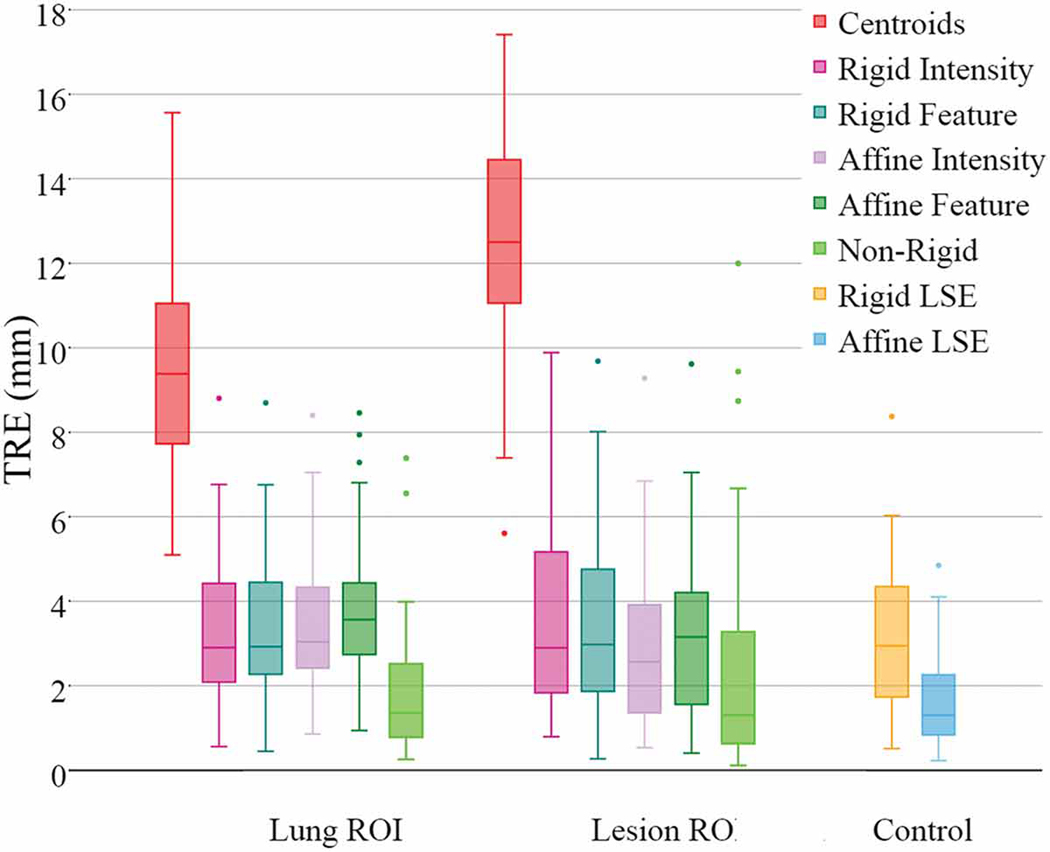
Fig. 9 shows the achieved TRE for both lung- and lesion-centered RoI registrations vs. “best fit” landmark-based rigid and 12 DOF least squared transformation TREs. This figure shows the overall advantage of using the lesion- vs. lung-centered RoI registration, the advantage of using affine vs. rigid registration, as well as the benefit of feature- vs. intensity based registration, including deformable registration.

Figure 9.

Cases 1–10 TRE box-plots comparing the performance of lung- and lesion-centered RoI registration, vis-a-vis the rigid and 12 DoF affine residual error baseline controls. Note that Case 11 and 12 lesions are shown separately.

According to our study, all registration methods performed best when operating on the lesion-centered RoI. Moreover, all affine registration methods, intensity- and feature-based, yielded better accuracy than their rigid counterparts. Lastly, the lesion-centered feature-based affine registration yielded comparable TRE to the non-rigid, deformable registration, and also to the control TRE estimated via the residual rigid least-square fit, hence suggesting no significant difference in performance between the lesion-centered feature-based affine and the non-rigid deformable registration.

3.2. Quantitative Image Registration Performance Evaluation

Table 2 summarizes the computational performance of each registration algorithm (rigid, affine, and deformable registration) on average sizes of lung- and lesion-centered RoIs. The experiments were conducted on a Windows 7 64 bit PC featuring a 3.6 GHz Intel CPU with 32 GB RAM using non-optimized MATLAB code featuring a three and five pyramid-level approach for the lesion- and lung-centered RoIs, respectively. We chose relatively small tolerance values (i.e., 10⁻¹²) for the changes in both the objective function and parameter values, to ensure ideal stopping criteria at the expense of longer processing times for enhanced registration accuracy. When limiting the maximum number of iterations and using higher tolerance values (i.e., 10⁻⁶), the performance times were significantly reduced, approaching 17 min for the intensity-based registration and 2 min for the feature-based registration operating on the lung-centered RoI. While further improved performance can be achieved for both the intensity- and feature-based affine registrations, here we focused on achieving the best registration accuracy. Nevertheless, the feature-based implementation will always feature a higher computational performance than its intensity-based counterpart.

Table 2.

Summary of registration performance (Mean ± Standard Deviation (minutes)) achieved using lung- and lesion-centered RoI across all cases.

	357×248×455		144×152×93
	Intensity	Edge	Intensity	Edge
Rigid Registration	122.8±20.5	45.0±1.1	2.4±3.2	2.3±1.5
Affine Registration	119.0±10.3	8.0±10	1.3±2.3	0.7±1.5
Deformable Registration	245.0±40.0	NA	17.2±10.2	NA

3.3. Visual (Qualitative) Image Registration Evaluation

To visualize the registration results, we generated subtraction images i.e., initial (i.e., fixed) image minus the registered follow-up (i.e., moving) image from the lesion mid-slices after each registration step. As mentioned earlier, subtraction images were shown to be efficient when assessing nodule growth-rate and reducing variability according to Staring, Pluim, et al. (2009).

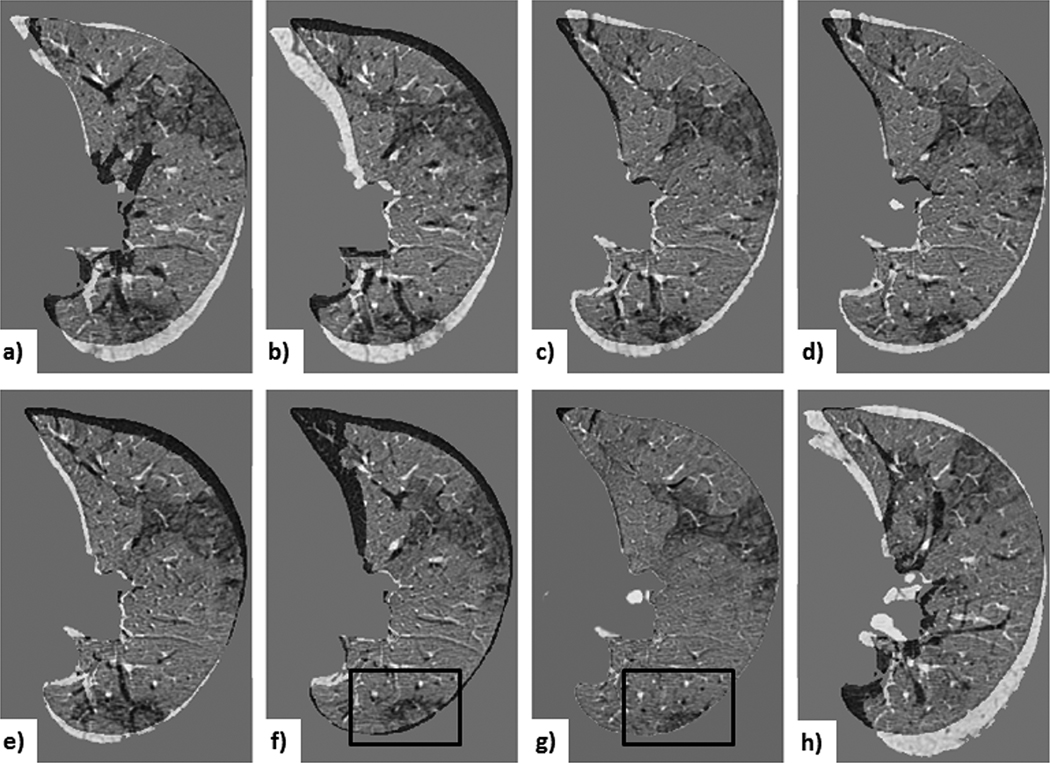
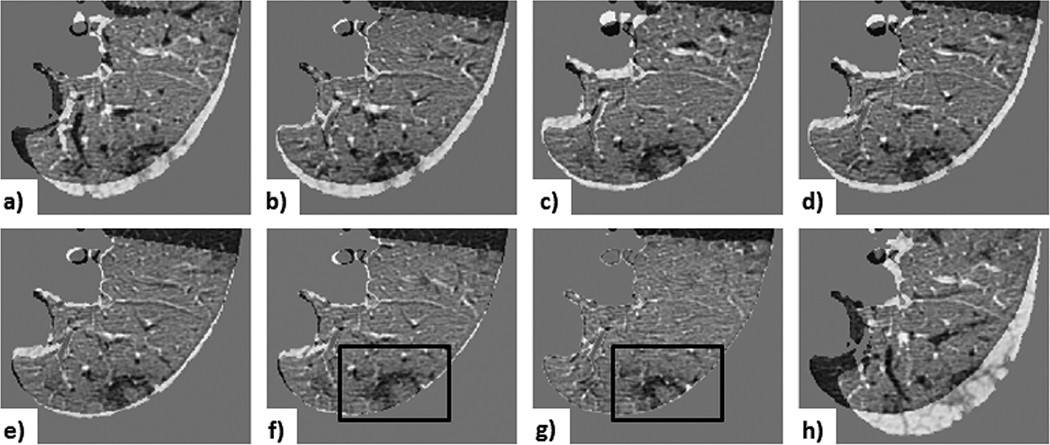
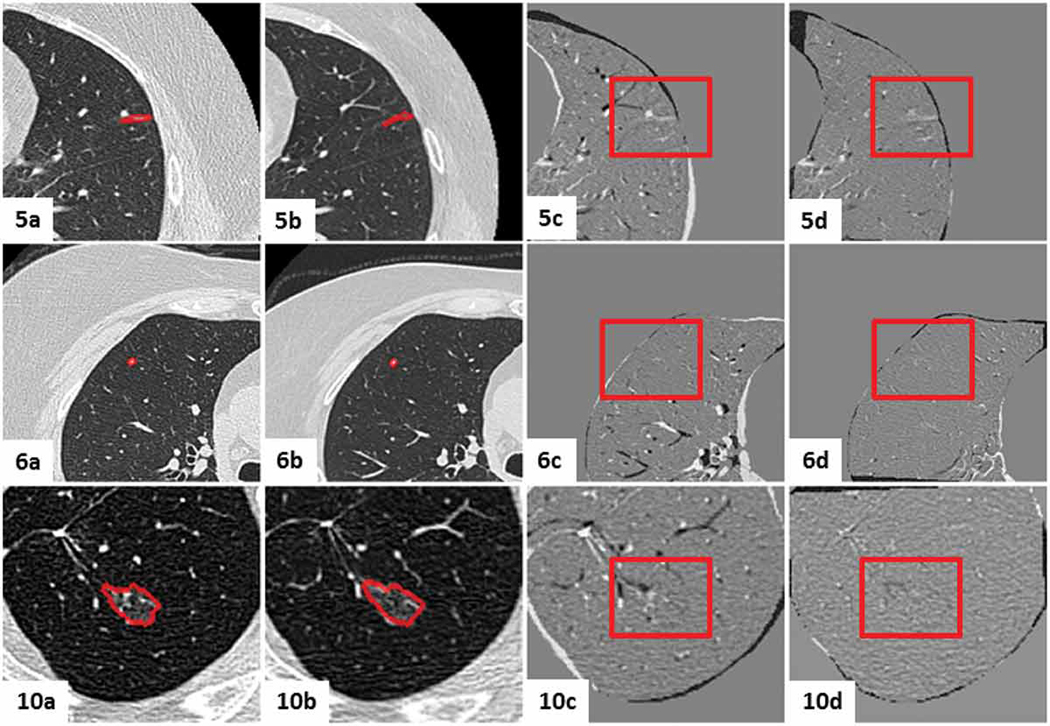
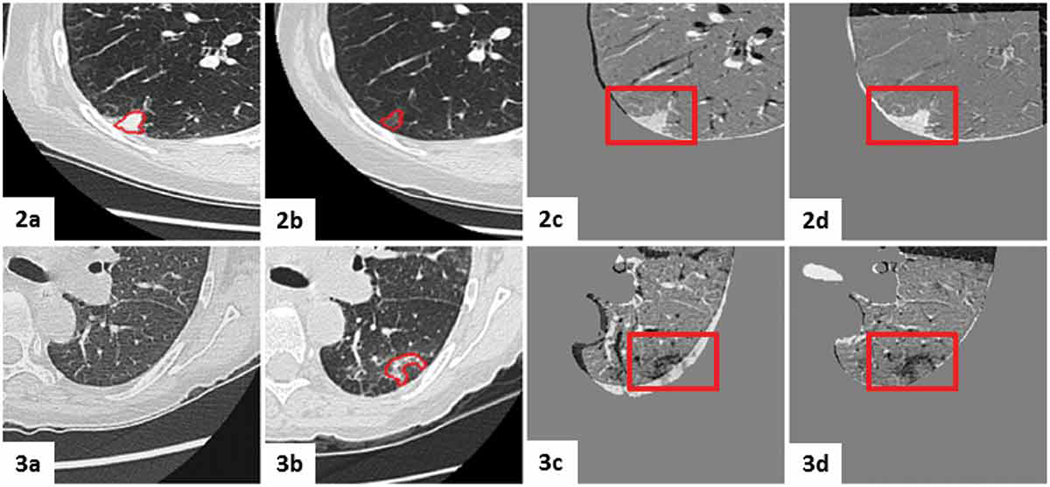
Figures 10 - 12 show subtraction images for all registration steps. Fig. 10 shows the subtraction images for the least problematic lesion (Case 10) for lesion-centered RoI registration; note that both the affine and deformable registrations yielded similar visual results.

Figure 10. Case 10 — least challenging lesion:

visual assessment of lesion-centered RoI registration showing the subtraction between the initial and registered follow-up image at each registration stage. a) centroid alignment; b) intensity-based rigid registration; c) feature-based rigid registration; d) landmark-based rigid transformation; e) intensity-based affine registration; f) feature-based affine registration (with black box outlining the lesion); g) deformable registration (with black box outlining the lesion); h) landmark-based 12 DoF affine transformation (note lung boundary misalignment caused by the projective transformation component.

Figure 12. Case 3 — a common lesion:

visual assessment of lung-centered RoI registration showing the subtraction between the initial and registered follow-up image at each registration step: a) centroid alignment; b) intensity-based rigid registration; c) feature-based rigid registration; d) landmark-based rigid transformation; e) intensity-based affine registration; f) feature-based affine registration (with black box outlining the lesion); g) deformable registration (with black box outlining the lesion); h) landmark-based affine with projective transformation. Note that the landmark-based rigid least-square fit transformation serves as a control, since the projective components of the 12 DoF affine transformation led to unreliable alignment (depicted by the projective transformation effect visible around the lung boundary), despite the lower TRE computed across the fiducials.

Fig. 11 and Fig. 12 show the subtraction images for Case 3 — an average case — for both lesion- and lung-centered RoI registration, respectively. These images provide a visual interpretation of a ∼ 0.4 mm TRE difference between the feature-based affine and deformable registration.

Figure 11. Case 3 — a common lesion:

visual assessment of lesion-centered RoI registration showing the subtraction between the initial and registered follow-up image at each registration stage: a) centroid alignment; b) intensity-based rigid registration; c) feature-based rigid registration; d) landmark-based rigid transformation; e) intensity-based affine registration; f) feature-based affine registration (with black box outlining the lesion); g) deformable registration (with black box outlining the lesion); h) landmark-based affine with projective transformation. Note that the landmark-based rigid least-square fit transformation serves as a control, since the projective components of the 12 DoF affine transformation led to unreliable alignment (depicted by the projective transformation effect visible around the lung boundary), despite the lower TRE computed across the fiducials.

The deformable registration shows an improved 0.8 mm median TRE, compared to 1.2 mm median TRE yielded by the both the lesion-centered affine feature- and intensity-based lesion-centered RoI registration; nevertheless, these improvements are insignificant.

As shown in the subtraction images (Fig. 11f-g), the depicted lesion changes following both feature-based affine and the deformable registration are also very similar, hence suggesting that the overall improvement in median TRE on the order of 0.4 mm represents, in fact, less than one voxel, and is therefore physically and physiologically insignificant, despite its statistical significance.

Conversely, the improved alignment following deformable registration may be an artifact caused by the non-rigid registration algorithm deforming the moving image beyond realism, making it look too similar to the fixed image, hence removing the ability to assess any true nodule changes due to disease. Such unrealistic, unreliable deformations are caused by the registration algorithm attempting to reduce image dissimilarity subject to the chosen regularization method, transformation space, selected solver, weighting of the objective terms, as well as any parameters that are inherent to the complexity of the deformable registration. Such deformation artifacts are challenging to identify and avoid, as the ground truth registration is not known, especially in vivo.

3.4. Initial Pre-clinical Demonstration and Evaluation

As a first attempt to demonstrate clinical relevance and utility, we conducted a pilot study involving a collaborating radiologist. The study was designed to compare the nodule changes assessed using the clinical standard of care (i.e., analysis of the initial and follow-up images) vs. using the digital subtraction images post-registration.

We presented the radiologist with either the mid-slice lesion-centered RoI images of the initial and follow-up CT scans, or the digital subtraction image of the lesions following feature-based affine registration. The twelve cases were presented in random order and the radiologist was asked to classify each case in one of the four categories — no nodule change, new or transient nodule, slight nodule change, or significant nodule change — under each of the two assessment methods.

Both assessment methods (side-by-side initial and follow-up scan visualization and post registration digital subtraction image) yielded consistent nodule classification across all twelve cases, hence confirming the utility of the digital subtraction images for clinical decision making. In addition, the radiologist also states that the post-registration digital subtraction images eliminated the need to perform any lesion measurements to assess nodule changes, hence confirming the findings of the previous study Staring, Pluim, et al. (2009) that reported the benefit of using digital subtraction images to assess nodule growth-rate.

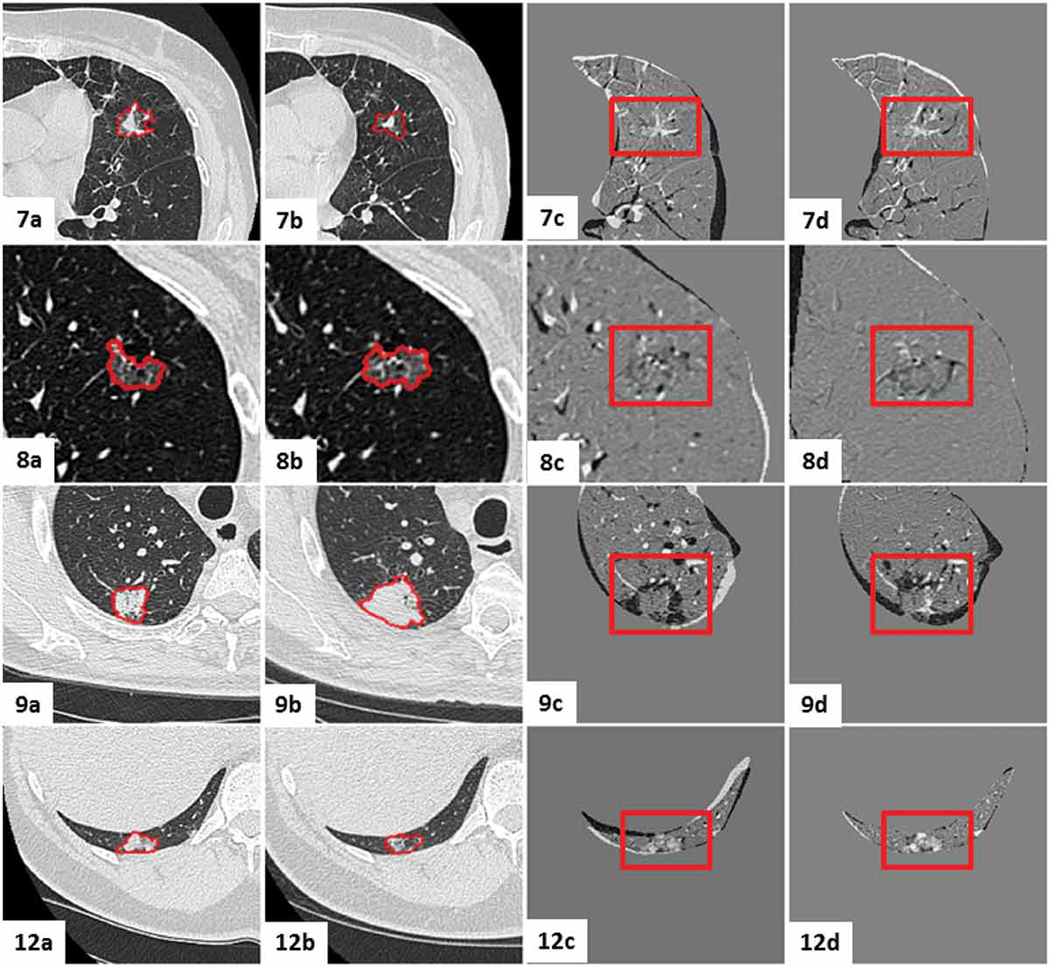
Figures 13 - 16 show the mid-slices containing the lesion-centered RoI of the initial and follow-up CT scans, as well as the digitally subtracted images following centroid alignment and feature-based affine registration for all twelve cases. Moreover, the cases were organized according to the extent of the changes detected by the radiologist, as follows: no nodule changes (Case 5, 6 and 10), new or transient nodules (Case 2 and 3), slight nodule changes (Case 1, 4 and 11), and definite nodule changes (Case, 7, 8, 9 and 12).

Figure 13.

Visual assessment of the lesion-centered RoI registration for the clinical cases featuring no nodule changes. Initial and follow-up lesion-centered RoI in the mid-slice image, followed by the subtraction image post centroid alignment and post feature-based affine registration. Gray regions infer no change, while black and white regions suggest changes.

Figure 16.

Visual assessment of the lesion-centered RoI registration for the clinical cases featuring significant nodule changes. Initial and follow-up lesion-centered RoI in the mid-slice image, followed by the subtraction image post centroid alignment and post feature-based affine registration. Gray regions infer no change, while black and white regions suggest changes.

4. Discussion

In this paper, we conducted a head-to-head comparison between several registration algorithms tested on twelve lesions from ten patient CT image pairs and operating on a lung- or lesion-centered region of interest, with the overall objective to identify the most suitable approach to account for the background lung tissue deformation between initial and follow-up lung CT images, to help objectively assess lung nodule changes induced by disease alone. Within this context, we proposed, implemented, and validated a feature-based affine registration algorithm that yielded less than 0.5 mm TRE difference compared to the Symmetric Normalization non-rigid, deformable registration, and baseline control registration, as well as significantly improved computational performance. Moreover, the qualitative visual assessment conducted by two radiologists confirmed similar conclusions about the nodule changes using the digital subtraction image post-registration as the current standard of care assessment method.

While deformable registration may be viewed as the preferred technique for longitudinal lung nodule follow-up studies thanks to its added accuracy, our quantitative registration accuracy findings, along with the visual visual assessment of the digitally subtracted image, show minimal differences between the registered images using feature-based affine or deformable registration, despite their ∼ 1.47 mm and ∼ 1.14 mm mean TRE, respectively. It is also worth mentioning that previous study Kakinuma, Ashizawa, et al. (2012) required a minimum difference of ∼ 1.72 mm change in the maximal lesion diameter between the initial and follow-up scans confirmed by two radiologists in order to render a particular lesion as progressive. Based on these criteria, our proposed feature-based affine registration operating on both the lung- and lesion-centered RoI provides an accuracy better than 1.72 mm.

Although the feature-based affine registration is less accurate by ∼ 0.3 mm according to the median TRE and ∼ 0.4 mm according to the mean TRE than the deformable registration, no statistically significant difference (p = 0.0711) was reported by the multi-comparison statistical tests. Moreover, this residual error is not physically relevant, not only because the difference in TRE was on the order of the in-plane resolution of the clinical quality CT images (lower than 0.5 mm), but such errors are also too small to be visually noticeable in the actual images, as shown in the visual inspection evaluation section, and also confirmed by our radiologists. Furthermore, the need for improvement is minimal, as the SyN median TRE is already less than 1 mm, which is optimal according to previous studies Werner, Schmidt-Richberg, et al. (2014), and also lower than the user variability associated with the fiducial selection, quantified via the residual error following the rigid landmark-based least square fit, assuming the vessels deformed rigidly.

Our proposed feature-based registration also does not require segmentation of the lesion, hence further simplifying the workflow by eliminating the additional lesion segmentation and masking step. The feature-based rather than intensity-based registration was also preferred to avoid image-inherent noise, which was “filtered out” during monogenic filtering, along with the small edges (associated with higher frequencies), only maintaining the meaningful, representative edges. While different frequency thresholds and edge strength parameters generate images featuring different edges, a distance metric is still preferred to other similarity metrics, as it is sufficiently robust to provide accurate registration even in absence of corresponding edges. Furthermore, instead of using features reconstructed using monogenic filtering, similar or better performance could be achieved using segmented pulmonary vessels as real features.

The feature-based affine and intensity-based deformable registration results are neither statistically significant in terms of registration accuracy, nor visually significant in terms of the image information, the implementation efficiency, computing time, and reduced susceptibility to registration artifacts render the feature-based affine registration as an overall safer, ore reliable, and more effective technique for this application, considering its low risk for artificial deformations, compared to deformable registration methods. The building blocks of deformable registration algorithms, specifically the regularizer, solver, and selected weighting factors, significantly influence the results and while there is no regularization term that can guarantee to correctly capture the true, actual deformation, the optimal regularizer may only control the properties of the deformation field to achieve smoother results, as previously confirmed by Werner et al. (Werner, Schmidt-Richberg, et al. (2014)), but does not ensure their reliability. Moreover, identifying an optimal solver to guarantee convergence to a global minimum rather than local minima is still challenging, not only for intensity-based deformable registration, but also for the feature-based affine registration, as small initialization variations may cause large changes in the output, due to the algrithm’s non-convex behavior. Nevertheless, to mitigate this challenge, we used the statistic minimzation strategy to objectively initialize the rotation parameters with our proposed framework.

In addition to the Symmetric Normalization deformable registration algorithm, we also considered another algorithm developed by the same team, which was slightly modified to use Exponential Mapping — DARTEL (Diffeomorphic Anatomical Registration using Exponentiated Lie algebra) — rather than the SyN time-varying diffeomorphism introduced by Ashburner (2007). The Exponential Mapping maintains a vector field that is constant in time, but time-variable only in the deformation field, reducing the diffeomorphism space and illustrating the benefit of time-dependent velocity over constant exponential velocity. Moreover, we also performed a comparison between several other techniques, including the ITK B-spline registration Balci, Golland, et al. (2007) based on free form deformation (FFD) Rueckert, Sonoda, et al. (1999), and a variation of the demons algorithm Thirion (1995) featuring the motion-coherent method proposed in Cahill (2012), the latter of which features a user control parameter — the variance of the Gaussian regularizer — used to constrain the spread of local deformation and ensure physically realistic behavior. Our comparison showed that the SyN algorithm outperformed both the FFD and the motion-coherent featuring optimal Gaussian variance. Moreover, the Greedy SyN method was already evaluated in the EMPIRE10 lung registration challenge reported by K., van Ginneken, et al. (2011) and it achieved competitive results in terms of overall accuracy, robustness to large deformations with affine initialization, and computational efficiency when compared to other state-of-the-art methods.

As described in the introduction, several prior works explored the inclusion vs. exclusion of the lesion region from the registration domain. In the effort to estimate the true deformation of the background lung tissue, we also explored the effect of including or excluding the lesion from the registration domain on four of the twelve cases.Case 9 lesion, featuring a large malignant nodule exhibiting significant disease progression according to the clinicians, was the one that demonstrated the greatest effect of lesion exclusion vs. inclusion from the similarity computation domain.

Fig. 17 and Fig. 18 show that the exclusion of the lesion region does not improve the surrounding registration, but rather increase the TRE associated with the intensity-based registration. Furthermore, when the global (rigid and affine) intensity-based registration is less accurate, it also leads to higher deformable registration TRE. On the other hand, the same figures clearly show that both the feature-based rigid and affine registrations are much more robust and less susceptible to the inclusion or exclusion of the lesion than their intensity-based counterparts, therefore emphasizing the uncompromised robustness of feature-based registration compared to intensity-based registration when removing image clues from the lesion region.

Figure 17.

Case 9 TRE box-plots following each registration stage for the lung- and lesion-centered RoI registration, as well as the rigid and 12 DoF affine least-square residual error, with inclusion of the lesion region in the registration domain.

Figure 18.

Case 9 TRE box-plots following each registration step for the lung- and lesion-centered RoI registration, as well as the rigid and 12 DoF affine least-square residual error, with exclusion of the lesion region in the registration domain.

In summary, our sub-study on lesion inclusion/exclusion for the registration doman showed no significant difference in response to the inclusion or exclusion of the lesion region from the similarity metric computation, with the exception of one single case featuring a very large (>3 cm) nodule that represented a significant portion of the registration RoI. This difference was caused by the lack of sufficient image clues for accurate registration when excluding a large region from the small lesion RoI. Nevertheless, as evident from Fig. 17 and Fig. 18, the lung-centered RoI registration was not affected by the exclusion of the lesion region.

5. Conclusion and Future Work

In this paper, we described and validated a feature-based affine registration algorithm designed to account for the background lung tissue deformation between initial and follow-up CT scans, to enable true assessment of lung nodule changes induced by disease. Specifically, a new distance similarity metric was formulated and implemented using image features extracted using monogenic filtering. Furthermore, our proposed feature-based registration also does not require segmentation of the lesion, hence further simplifying the workflow by eliminating the highly challenging and uncertain lesion segmentation process, which often misleads diagnosis due to segmentation uncertainties caused by the irregular and ambiguous GGN margins.

The proposed registration algorithm was evaluated against several other rigid, affine and deformable registration algorithm operating on a lung- and lesion-centered region of interest as part of a multi-stage registration protocol using a dataset consisting of 10 patient CT images featuring 12 nodules. Our study suggested that the feature-based affine registration was the most appropriate technique for lung image registration, in light of its computational efficiency (3.4±0.5 min) vis-a-vis 17.2±10.2 min computing time for deformable registration operating on the lesion-centered RoI, and minimal compromise on registration accuracy (1.1 mm median TRE) vs. a 0.8 mm median TRE achieved using deformable registration operating lesion-centered RoI.

Despite a mere 0.4 mm median TRE improvement using deformable vs. feature-based affine registration, no statistically significant differences (p = 0.0711) were reported by the multi-comparison statistical tests. Moreover, the error difference between the affine and deformable registration is neither physically nor clinically relevant; not only is the 0.4 mm median TRE difference smaller than the voxel size of typical clinical quality CT images, but such errors are also too small to be visually noticeable in the actual images, as shown in the visual inspection evaluation section, and also confirmed by our radiologists during our pre-clinical pilot study. Nevertheless, the implementation efficiency, computing time, and reduced susceptibility to registration artifacts render the feature-based affine registration as an overall safer and more reliable technique for this application, considering its low risk for artificial deformations, compared to deformable registration.

Future work may focus on extending the study to include additional lung imaging data, as well as append other registration techniques to the analysis in the effort to perform a more in-depth head-to-head comparison of the top-rated lung image registration methods. Specifically, one tentative approach is the registration of the vessel segmentation maps using the distance metric, similar to the technique proposed here for our feature-based registration. Lastly, we plan to also extend the preliminary clinical demonstration to include additional cases, as well as additional radiologists, to help us emphasize the robustness and impact of correcting for the background lung tissue deformation, as well as the benefit of using post-registration digital subtraction images prior to assess the true nodule changes due to disease.

Figure 4.

A pairwise multi-comparison test across all patients between the six registration methods (centroid alignment, imtensity and feature-based rigid registration, intensity- and feature-based affine registration, and non-rigid, deformable registration) and the two RoIs (lung- and lesion-centeres RoI). Note that the lesion-centered RoI TRE is significantly lower than the lung-centered RoI TRE for all registration methods, with the exception of the deformable registration, which is local in nature and hence not susceptible to the selected RoI, and the rigid LSE, which only depends on the fiducial configuration.

Figure 14.

Visual assessment of the lesion-centered RoI registration for the clinical cases featuring new or transient nodules. Initial and follow-up lesion-centered RoI in the mid-slice image, followed by the subtraction image post centroid alignment and post feature-based affine registration. Gray regions infer no change, while black and white regions suggest changes.

Figure 15.

Visual assessment of the lesion-centered RoI registration for the clinical cases featuring slight nodule changes. Initial and follow-up lesion-centered RoI in the mid-slice image, followed by the subtraction image post centroid alignment and post feature-based affine registration. Gray regions infer no change, while black and white regions suggest changes.