On the mechanics of thin films and growing surfaces

Abstract

Many living structures are coated by thin films, which have distinct mechanical properties from the bulk. In particular, these thin layers may grow faster or slower than the inner core. Differential growth creates a balanced interplay between tension and compression and plays a critical role in enhancing structural rigidity. Typical examples with a compressive outer surface and a tensile inner core are the petioles of celery, caladium, or rhubarb. While plant physiologists have studied the impact of tissue tension on plant rigidity for more than a century, the fundamental theory of growing surfaces remains poorly understood. Here, we establish a theoretical and computational framework for continua with growing surfaces and demonstrate its application to classical phenomena in plant growth. To allow the surface to grow independently of the bulk, we equip it with its own potential energy and its own surface stress. We derive the governing equations for growing surfaces of zero thickness and obtain their spatial discretization using the finite-element method. To illustrate the features of our new surface growth model we simulate the effects of growth-induced longitudinal tissue tension in a stalk of rhubarb. Our results demonstrate that different growth rates create a mechanical environment of axial tissue tension and residual stress, which can be released by peeling off the outer layer. Our novel framework for continua with growing surfaces has immediate biomedical applications beyond these classical model problems in botany: it can be easily extended to model and predict surface growth in asthma, gastritis, obstructive sleep apnoea, brain development, and tumor invasion. Beyond biology and medicine, surface growth models are valuable tools for material scientists when designing functionalized surfaces with distinct user-defined properties.

1. Introduction

The phenomenon of growing surfaces has been known to developmental biologists for more than a century [1]. In plant biology, surface growth plays a critical role in creating form and function through the balanced interplay between tension and compression [2]. Surface growth generates a mechanical environment of residual stress, stress that is present even in the absence of external loading [3]. Plant biologists refer to this phenomenon as tissue tension [4].

Figure 1 illustrates growth-induced longitudinal tissue tension in the petiole, the stalk, of Rheum rhabarbarum, commonly known as rhubarb [2]. In most plants, the epithelial cells of the outer surface, shown in red, grow slower than the parenchyma cells of the inner core, shown in green [5]. Differential growth creates a state of surface tension and bulk compression [6], which gives the stalk its characteristic rigidity to support the heavy rhubarb leaves [1]. When the surface layers are peeled off the inner core, they contract and bend outward, while the inner core expands as tissue tension is released. Bending and curvature changes in the classical split pea test have played an important role in the discovery of the plant growth hormone auxin [7], and are one of the major topics in many introductory textbooks on botany [4].

Figure 1.

Growth-induced longitudinal tissue tension in a stalk of rhubarb. The red outer surface of the stalk grows slower than the green inner core and generates a state of surface tension and bulk compression. The balanced interplay between tension and compression gives the stalk its characteristic rigidity. When the surface layers are peeled off the inner core, they contract and bend outward, while the inner core expands as tissue tension is released. The release of tissue tension is associated with a significant loss of rigidity. (Adapted from [2].)

Figure 2 illustrates the microstructure of growing rhubarb. The outer surface, shown in red, consists of a continuous layer of densely packed, brick-shaped epidermal cells, while the inner core, shown in green, consists primarily of thin-walled parenchyma cells and longitudinal fibers. Epidermal cells display a distinct behavior from parenchyma cells [5]; in particular, they grow at a different rate [8]. In cylindrical plant stems, different growth rates generate longitudinal tissue tension, or, in mechanical terms, a state of residual stress [9].

Figure 2.

Microstructure of growing rhubarb. The red outer surface consist of epidermal cells; the green inner core consists primarily of parenchyma cells and longitudinal fibers. The epithelial cells of the outer surface grow slower than the parenchyma cells of the inner core creating a state of longitudinal tissue tension to enhance stalk rigidity.

In continuum mechanics, the phenomenon of residual stress is inherently related to the notion of growth [10, 11]. The first continuum model to characterize the interplay between growth and residual stress was proposed almost two decades ago [12]. Motivated by the introduction of an incompatible growth configuration [13], it is based on the multiplicative decomposition of the deformation gradient into a reversible elastic part and an irreversible growth part [14]. In the most generic sense, this growth part can be represented through a second-order tensor [15]. Two key ingredients determine the particular type of growth: the functional form of the growth tensor and the driving force for its evolution [16]. The functional form of the growth tensor typically depends on the underlying tissue microstructure [17, 18]. In the simplest case, growth is isotropic [19, 20]. In the presence of fibers, like in rhubarb, growth is typically transversely isotropic, with a pronounced growth or shrinkage along the fiber direction [21, 22]. Area growth is also usually transversely isotropic, i.e. isotropic in the plane tangent to the surface [23, 24]. In complex tissues with multiple fiber families growth can be orthotropic [25], or even generally anisotropic [26]. The driving force for growth can either be morphogenetic, mechanical, or a combination of both. In evolution and developmental biology, the growth process is usually prescribed morphogenetically [27]. This implies that growth and mechanics are only coupled unidirectionally: growth influences mechanics, but mechanics does not influence growth [28, 29]. In biomechanics, the growth process is typically driven by strain [30], stress [31], or energy. This implies that growth and mechanics are coupled bidirectionally: growth influences mechanics and, at the same time, mechanics influences growth [32, 33]. Motivated by the differential growth in plant stems in Figure 1, here, we focus on transversely isotropic growing surfaces and prescribe the evolution of growth through morphogenesis.

The distinguishing feature of the type of growth we are interested in here is that the growing surface is extremely thin as compared with the bulk [34]. As shown in Figure 2, many biological structures are coated by thin films of epidermal cells, which are only a few micrometers thick. The modeling of thin films is conceptually challenging and has attracted increasing attention within the past two decades. An elegant way to model thin growing surfaces at the zero-thickness limit [35, 36] is to equip the surface with its own potential energy, which can evolve independently of the bulk [37]. The concept of surface energies has been established more than two centuries ago, formalized through the famous Young–Laplace equation, which relates the pressure difference across a fluid surface to surface tension and mean curvature [38, 39]. More than three decades ago, the familiar concept of scalar-valued surface tension was generalized to the tensorial notion of surface stress in the first continuum theory of elastic material surfaces [40]. Since then, the concept of material surfaces has gained wide attention in various fields of metallurgy, material sciences, micro- and nanofabrication, and soft lithography [41], broadly speaking, whenever the surface displays distinct characteristic properties [42, 43]. For fluids, the theory of surface tension is classic and well-developed. Computationally, finite-element formulations exist to simulate droplets and free surfaces with scalar-valued surface tension [44]. For solids, however, a generic finite-element approach towards elastic surfaces with tensorial surface stresses has only been proposed recently [45]. This approach models the surface as a hyperelastic membrane of zero thickness, kinematically constrained to move with the solid body, but equipped with its own potential energy [46]. The concept of surface energies is mathematically elegant and easily generalizable to anisotropic surfaces [47], thermomechanical surfaces [48] and surfaces with diffusion [49]. Motivated by Figures 1 and 2, we adopt the concept of surface energies to model differential growth of a thin film of epidermal cells, kinematically constrained to move with the parenchyma bulk, but allowed to grow at a different rate.

Characterizing differential growth experimentally is a challenging task. The classic opening angle experiment is probably the most established setup to quantify differential growth of living structures ex vivo [50]. While new methods have been proposed to characterize tissue growth in vivo [51], these approaches typically introduce the growth tensor as the gradient of a displacement field, implying that growth is a compatible process [52]. In their classical textbooks, plant physiologists suggest two conceptually simple experiments to visualize differential growth in plants: the peel test to quantify changes in length upon layer separation [4] and the longitudinal cutting test to quantify changes in curvature upon release of residual stress [2]. The petiole of rhubarb is an excellent model system for these two experiments, since its epidermal surface layer is easily distinguishable by its bright red color from the green bulk of the parenchyma ground substance. Figure 3 illustrates the classic peel test to quantify growth-induced changes in length. When the outer surface layer is peeled off the inner core, it contracts by approximately 1% generating a stretch of λ = 0.99, while the inner core expands by approximately 4% corresponding to a stretch of λ = 1.04. The peel test can serve as an easily reproducible experiment to calibrate the model and to identify the surface-to-volume growth ratio. Here, the surface-to-volume growth ratio is 0.99 : 1.04 = 0.952. In the following, we systematically vary the surface-to-volume growth ratio and explore its impact on tissue form and function.

Figure 3.

Peel test for model calibration. The red epidermal surface grows slower than the green parenchymal core. When the outer surface layer is peeled off the inner core, the epidermal surface contracts by ~ 1%, i.e. its stretch is λ = 0.99, while the parenchymal core expands by ~ 4%, i.e. its stretch is λ = 1.04. The peel test can serve to calibrate the relative surface growth to $\widehat{\vartheta }=0.99/1.04=0.952$.

This manuscript is organized as follows. In Section 2, we introduce the kinematic equations, the equilibrium equations, and the constitutive equations of finite surface growth. In each subsection, we independently discuss the equations for the inner bulk and for the outer boundary. In Section 3, we derive the weak forms of these equations and discretize them in space using a combination of volume elements for the bulk and surface elements for the boundary. In Section 4, we demonstrate the features of growing surfaces using the model problem of growth-induced longitudinal tissue tension in a stalk of rhubarb. We close with a critical discussion in Section 5.

2. Governing equations

2.1. Kinematics

To model growing surfaces, we kinematically characterize the motion of material particles $\mathit{X}\in {\mathcal{B}}_0$, where ${\mathcal{B}}_0\subset {\mathbb{R}}^3$ denotes the material placement of a continuum body with a smooth surface ${\mathcal{S}}_0=\partial {\mathcal{B}}_0$ in the reference configuration.

We label points on the surface ${\mathcal{S}}_0$ as $\widehat{\mathit{X}}={\mathit{X}|}_{{\mathcal{S}}_0}$ and denote the unit outward normal to ${\mathcal{S}}_0$ as N, see Figure 4. We characterize the smooth motion of the material placement X onto its spatial placement x during the time interval of interest $\mathbb{T}=\left[0,T\right]\subset {\mathbb{R}}^{+}$ through the bulk deformation map $\mathit{\phi }:{\mathcal{B}}_0\times \mathbb{T}\to {\mathbb{R}}^3$ . Similarly, we characterize the motion of the corresponding surface placement $\widehat{\mathit{X}}$ onto $\widehat{\mathit{x}}={\mathit{x}|}_{{\mathcal{S}}_t}$ through the boundary deformation map $\widehat{\mathit{\phi }}:{\mathcal{S}}_0\times \mathbb{T}\to {\mathbb{R}}^3$,

$$\begin{array}{ccc}\mathit{x}=\mathit{\phi }(\mathit{X},t)& \text{and}& \widehat{\mathit{x}}=\widehat{\mathit{\phi }}(\widehat{\mathit{X}},t)\end{array}.$$ (1)

Figure 4.

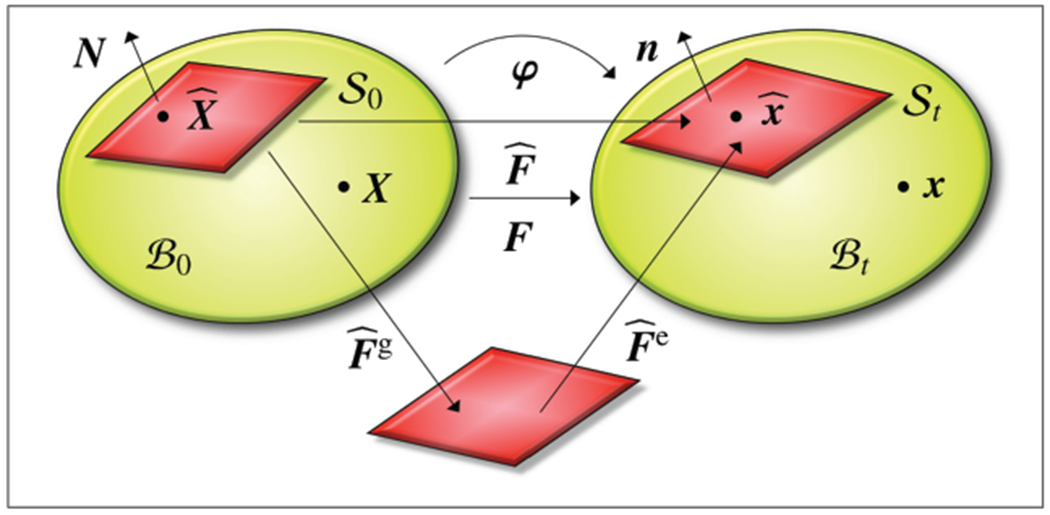
Kinematics of growing surfaces. Material and spatial configurations ${\mathcal{B}}_0$ and ${\mathcal{B}}_t$ with bulk deformation map F shown in green. Material and spatial surfaces ${\mathcal{S}}_0$ and ${\mathcal{S}}_t$ with boundary deformation gradient $\widehat{\mathit{F}}$ and its multiplicative decomposition $\widehat{\mathit{F}}={\widehat{\mathit{F}}}^{\text{e}}\cdot {\widehat{\mathit{F}}}^{\text{g}}$ into an elastic part ${\widehat{\mathit{F}}}^{\text{e}}$ and a growth part ${\widehat{\mathit{F}}}^{\text{g}}$ shown in red.

As indicated in Figure 4, we label the current placement of the body at time t as ${\mathcal{B}}_t=\mathit{\phi }\left({\mathcal{B}}_0\right)$ and the associated surface as ${\mathcal{S}}_t=\widehat{\mathit{\phi }}\left({\mathcal{S}}_0\right)$. Next we introduce the bulk deformation gradient F, which maps material line elements dX onto spatial line elements dx = F · dX and the corresponding boundary deformation gradient $\widehat{\mathit{F}}$, which maps tangential line elements from the material surface $\text{d}\widehat{\mathit{X}}$ onto the spatial surface $\text{d}\widehat{\mathit{x}}=\widehat{\mathit{F}}\cdot \text{d}\widehat{\mathit{X}}$,

$$\begin{array}{ccc}\mathit{F}=\nabla \mathit{\phi }& \text{and}& \widehat{\mathit{F}}=\widehat{\nabla }\widehat{\mathit{\phi }}=\mathit{F}\cdot \widehat{\mathit{I}}.\end{array}$$ (2)

The bulk gradient $\nabla \{\circ \}={\partial }_{\mathit{X}}{\{\circ \}|}_t$ follows from its standard definition, where ${\{\circ \}|}_t$ denotes a fixed position in time. The boundary gradient gradient $\widehat{\nabla }\{\circ \}=\nabla \{\circ \}\cdot \widehat{\mathit{I}}$ follows from the projection of the bulk gradient using the second order surface unit tensor $\widehat{\mathit{I}}=\mathit{I}-\mathit{N}\otimes \mathit{N}$ . Here I is the classical second-order unit tensor and N is the outward surface normal. The bulk Jacobian J of the deformation gradient F relates material volume elements dV₀ to spatial volume elements dV_t = J dV₀. Similarly, the boundary Jacobian $\widehat{J}$ of the deformation gradient $\widehat{\mathit{F}}$ relates material surface elements dA₀ to spatial surface elements $\text{d}{A}_t=\widehat{J}\text{d}{A}_0$,

$$\begin{array}{ccc}J=\det (\mathit{F})>0& \text{and}& \widehat{J}=\widehat{\det }(\widehat{\mathit{F}})=\Vert J{\mathit{F}}^{-\text{t}}\cdot \mathit{N}\Vert >0.\end{array}$$ (3)

Note that Equation (3.2) is a version of Nanson’s formula for surface elements. To characterize surface growth, we multiplicatively decompose the boundary deformation gradient $\widehat{\mathit{F}}$ into an elastic part ${\widehat{\mathit{F}}}^{\text{e}}$ and a growth part ${\widehat{\mathit{F}}}^g$,

$$\widehat{\mathit{F}}={\widehat{\mathit{F}}}^{\text{e}}\cdot {\widehat{\mathit{F}}}^{\text{g}}.$$ (4)

Recall that in contrast to the surface deformation gradient $\widehat{\mathit{F}}=\widehat{\nabla }\widehat{\mathit{\phi }}$, the individual contributions ${\widehat{\mathit{F}}}^{\text{e}}$ and ${\widehat{\mathit{F}}}^{\text{g}}$ can, in general, be incompatible [53]. Similarly, we multiplicatively decompose the surface Jacobian $\widehat{J}$ into an elastic part ${\widehat{J}}^{\text{e}}$ and a growth part ${\widehat{J}}^{\text{g}}$,

$$\begin{array}{ccc}\widehat{J}={\widehat{J}}^{\text{e}}{\widehat{J}}^{\text{g}}& \text{with}& {\widehat{J}}^{\text{g}}=\widehat{\det }({\widehat{\mathit{F}}}^{\text{g}})=\frac{\Vert [{\widehat{\mathit{F}}}^{\text{g}}\cdot {\mathit{A}}_1]\times [{\widehat{\mathit{F}}}^{\text{g}}\cdot {\mathit{A}}_2]\Vert }{\Vert {\mathit{A}}_1\times {\mathit{A}}_2\Vert }\end{array},$$ (5)

where ${\widehat{J}}^g$ is defined in terms of the covariant base vectors A₁ and A₂ on the material surface $T{\mathcal{S}}_0$ (see [42]).

Remark 1. The second-order surface unit tensor $\widehat{\mathit{I}}$ serves as projection tensor to map the bulk deformation gradient F onto the boundary deformation gradient $\widehat{\mathit{F}}$,

$$\begin{array}{ccc}\widehat{\mathit{F}}=\mathit{F}\cdot \widehat{\mathit{I}}& \mathit{with}& \widehat{\mathit{I}}=\mathit{I}-\mathit{N}\otimes \mathit{N},\end{array}$$ (6)

where N is the unit outward normal to the material surface ${\mathcal{S}}_0$. Since $\widehat{\mathit{I}}$ is rank deficient, the boundary deformation gradient $\widehat{\mathit{F}}$ is typically non-invertible. However, it possesses a generalized inverse according to the following singular value decomposition,

$$\begin{array}{ccc}{\widehat{\mathit{F}}}^{-1}\cdot \widehat{\mathit{F}}=\widehat{I},& \widehat{\mathit{F}}=\mathit{U}\cdot \mathit{\Sigma }\cdot {\mathit{V}}^{\text{t}},& {\widehat{\mathit{F}}}^{-1}=\mathit{V}\cdot {\left[{\mathit{\Sigma }}^{+}\right]}^{-1}\cdot {\mathit{U}}^{\text{t}}\end{array}$$ (7)

where the diagonal entries of Σ correspond to the singular values of $\widehat{\mathit{F}}$, the columns of U and V are the left- and right-singular vectors associated with these singular values, and Σ⁺ is the pseudoinverse of Σ, which is formed by replacing every non-zero diagonal entry by its reciprocal value.

2.2. Equilibrium equations

To characterize the mechanical equilibrium of growing surfaces, we introduce two sets of equilibrium equations, one in the bulk and one on the boundary. The former balances the divergence of the volume stresses P with the volume forces b; the latter balances the divergence of the surface stresses $\widehat{\mathit{P}}$ with the surface tractions $\widehat{\mathit{b}}-\mathit{P}\cdot \mathit{N},$

$$\begin{array}{ccc}\text{Div}\mathit{P}+\mathit{b}=\mathbf{0}& \text{and}& \widehat{\text{Div}}\widehat{\mathit{P}}\end{array}+[\widehat{\mathit{b}}-\mathit{P}\cdot \mathit{N}]=\mathbf{0}.$$ (8)

Here we simply adopt these two equations from thermodynamic considerations of continua with boundary energies [37], and refer to the literature for their detailed derivation, either using the principle of virtual power [54, 55] or the principle of virtual work [45, 46]. In the above equations, Div {∘} = ∇{∘} : I and $\widehat{\mathrm{Div}}\{\circ \}=\nabla \{\circ \}:\widehat{\mathit{I}}$ denote the bulk divergence operator and the boundary divergence operator. The volume stresses P and volume forces b have the dimensions of force per unit area and force per unit volume, while the surface stresses $\widehat{\mathit{P}}$ and surface tractions $\widehat{\mathit{b}}-\mathit{P}\cdot \mathit{N}$ have the dimensions of force per unit length and force per unit area. The surface tractions consist of two contributions, the prescribed surface tractions $\widehat{\mathit{b}}$ and the surface tractions imposed by the underlying bulk through the projected volume Piola stress P · N [46]. The strong forms of the equilibrium equation (8) are related to the corresponding weak forms,

$$\begin{array}{l}{\int }_{{\mathcal{B}}_0}\nabla \delta \mathit{\phi }:\mathit{P}\text{d}{V}_0={\int }_{{\mathcal{B}}_0}\delta \mathit{\phi }\cdot \mathit{b}\text{d}{V}_0+{\int }_{{\mathcal{S}}_0}\delta \mathit{\phi }\cdot \mathit{P}\cdot \mathit{N}\text{d}{A}_0\\ {\int }_{{\mathcal{S}}_0}\widehat{\nabla }\delta \mathit{\phi }:\widehat{\mathit{P}}\text{d}{A}_0={\int }_{{\mathcal{S}}_0}\delta \mathit{\phi }\cdot \widehat{\mathit{b}}\text{d}{A}_0-{\int }_{{\mathcal{S}}_0}\delta \mathit{\phi }\cdot \mathit{P}\cdot \mathit{N}\text{d}{A}_0+{\int }_{{\mathcal{C}}_0}\delta \mathit{\phi }\cdot \widehat{\mathit{P}}\cdot \mathit{N}\text{d}{L}_0,\end{array}$$ (9)

through the multiplication with the test function δφ, the integration over the volume ${\mathcal{B}}_0$ and over the surface ${\mathcal{S}}_0$, and the integration by parts. The weak form of the equilibrium equation in the bulk (9.1) balances the internal volume forces with the external volume and surface forces. The weak form of the equilibrium equation on the boundary (9.2) balances the internal surface forces with the external surface forces, the projected forces imposed by the underlying bulk, and the external line forces along the boundary curve ${\mathcal{C}}_0$ of the surface ${\mathcal{S}}_0$.

2.3. Constitutive equations

To characterize the hyperelastic response of the bulk, we introduce the bulk energy ψ, parameterized in terms of the bulk deformation gradient F. To characterize growth of the boundary, we introduce an independent boundary energy $\widehat{\psi }$, parameterized in terms of the boundary deformation gradient $\widehat{\mathit{F}}$ and the growth tensor ${\widehat{\mathit{F}}}^{\text{g}}$, or, alternatively, in terms of the elastic tensor ${\widehat{\mathit{F}}}^e=\widehat{\mathit{F}}\cdot {\widehat{\mathit{F}}}^{\text{g}-1}$ [37],

$$\begin{array}{ccc}\psi =\psi \left(\mathit{F}\right)& \text{and}& \widehat{\psi }=\widehat{\psi }(\widehat{\mathit{F}},{\widehat{\mathit{F}}}^{\text{g}})=\widehat{\psi }({\widehat{\mathit{F}}}^{\text{e}})\end{array}.$$ (10)

We can then express the volume and surface Piola stresses P and $\widehat{\mathit{P}}$ as stress measures conjugate to the bulk and boundary deformation gradients F and $\widehat{\mathit{F}}$,

$$\begin{array}{ccccc}\mathit{P}=\frac{\partial \psi }{\partial \mathit{F}}& \text{and}& \widehat{\mathit{P}}=\frac{\partial \widehat{\psi }}{\partial \widehat{\mathit{F}}}=\frac{\partial \widehat{\psi }}{\partial {\widehat{\mathit{F}}}^{\text{e}}}:\frac{\partial {\widehat{\mathit{F}}}^{\text{e}}}{\partial \widehat{\mathit{F}}}={\widehat{\mathit{P}}}^{\text{e}}\cdot {\widehat{\mathit{F}}}^{\text{g}-\text{t}}& \text{with}& {\widehat{\mathit{P}}}^{\text{e}}=\frac{\partial \psi }{\partial {\widehat{\mathit{F}}}^{\text{e}}}\end{array},$$ (11)

where ${\widehat{\mathit{P}}}^{\text{e}}$ denotes the elastic surface stress. The total derivatives of the volume and surface stresses P and $\widehat{\mathit{P}}$ with respect to the deformation gradients F and $\widehat{\mathit{F}}$ introduce the fourth-order volume and surface tangent moduli $\mathbb{A}$ and $\widehat{\mathbb{A}}$,

$$\begin{array}{ccccc}\mathbb{A}=\frac{\text{d}\mathit{P}}{\text{d}\mathit{F}}& \text{and}& \widehat{\mathbb{A}}=\frac{\text{d}\widehat{\mathit{P}}}{\text{d}\widehat{\mathit{F}}}=\frac{\text{d}\widehat{\mathit{P}}}{\text{d}{\widehat{\mathit{F}}}^{\text{e}}}:\frac{\text{d}{\widehat{\mathit{F}}}^{\text{e}}}{\text{d}\widehat{\mathit{F}}}={\widehat{\mathbb{A}}}^{\text{e}}:[{\widehat{\mathit{F}}}^{\text{g}-\text{t}}\overline{\otimes }{\widehat{\mathit{F}}}^{\text{g}-\text{t}}]& \text{with}& {\widehat{\mathbb{A}}}^{\text{e}}=\frac{\text{d}{\widehat{\mathit{P}}}^e}{\text{d}\widehat{\mathit{F}}}\end{array}$$ (12)

where ${\widehat{\mathbb{A}}}^{\text{e}}$ denotes the elastic surface tangent moduli. These tangent moduli will prove critical to guarantee optimal convergence of the algorithmic Newton–Raphson procedure.

2.4. Growth

To characterize growth, we prescribe the functional form of the growth tensor and its evolution in time. We consider the two simplest possible cases, isotropic and transversely isotropic surface growth, for which the growth tensors ${\widehat{\mathit{F}}}_{\text{iso}}^{\text{g}}$ and ${\widehat{\mathit{F}}}_{\mathrm{trs}}^{\text{g}}$ can be parameterized in terms of a single scalar-valued growth multiplier $\widehat{\vartheta }$, which characterizes the amount of growth,

$$\begin{array}{ccc}{\widehat{\mathit{F}}}_{\text{iso}}^{\text{g}}=\widehat{\vartheta }\widehat{\mathit{I}}& \text{and}& {\widehat{\mathit{F}}}_{\text{trs}}^{\text{g}}=\widehat{\mathit{I}}+[\widehat{\vartheta }-1]\widehat{\mathit{M}}\otimes \widehat{\mathit{M}}.\end{array}$$ (13)

Here, the surface unit vector $\widehat{\mathit{M}}$ defines the direction of growth for the transversely isotropic case. We can quantify the amount of surface growth through the Jacobians,

$$\begin{array}{ccc}{\widehat{J}}_{\text{iso}}^{\text{g}}={\widehat{\vartheta }}^2& \text{and}& {\widehat{J}}_{\text{trs}}^{\text{g}}=\widehat{\vartheta },\end{array}$$ (14)

such that $\widehat{\vartheta }=1$ characterizes the initial ungrown state, $\widehat{\vartheta }>1$ indicates surface growth, and $\widehat{\vartheta }<1$ indicates surface shrinkage. In the following, we assume that surface growth is plain morphogenetic. This implies that the growth multiplier $\widehat{\vartheta }$ is not governed by mechanical driving forces, but rather follows directly from a constitutively prescribed evolution law. In particular, we adopt a simple exponential evolution equation [37],

$$\frac{\text{d}\widehat{\vartheta }}{\text{d}t}=[{\widehat{\vartheta }}_{\infty }-{\widehat{\vartheta }}_0][\exp (-t/\widehat{\tau })]/\widehat{\tau },$$ (15)

which we can integrate explicitly to directly identify the amount of growth $\widehat{\vartheta }$ at any given point in time t,

$$\widehat{\vartheta }(t)={\widehat{\vartheta }}_{\infty }+[{\widehat{\vartheta }}_0-{\widehat{\vartheta }}_{\infty }]\exp (-t/\widehat{\tau }).$$ (16)

Here $\text{d}\widehat{\vartheta }/\text{d}t$ denotes the material time derivative, $\widehat{\tau }$ characterizes the speed of surface growth, ${\widehat{\vartheta }}_0=1.0$ is the initial growth value, and ${\widehat{\vartheta }}_{\infty }$ limits the final amount of surface growth towards which the growth multiplier $\widehat{\vartheta }$ converges gradually as time increases.

3. Discretization

Since surface growth is typically a highly nonlinear and possibly heterogeneous process, we suggest to solve its governing equations computationally within an incremental iterative nonlinear finite-element scheme. We begin by summarizing the weak forms of the equilibrium equation (9) in the volume ${\mathcal{B}}_0$ and on the surface ${\mathcal{S}}_0$,

$${\int }_{{\mathcal{B}}_0}\nabla \delta \mathit{\phi }:\mathit{P}\text{d}{V}_0-{\int }_{{\mathcal{B}}_0}\delta \mathit{\phi }\cdot \mathit{b}\text{d}{V}_0+{\int }_{{\mathcal{S}}_0}\widehat{\nabla }\delta \mathit{\phi }:\widehat{\mathit{P}}\text{d}{A}_0-{\int }_{{\mathcal{S}}_0}\delta \mathit{\phi }\cdot \widehat{\mathit{b}}\text{d}{A}_0-{\int }_{{\mathcal{C}}_0}\delta \mathit{\phi }\cdot \widehat{\mathit{P}}\cdot \mathit{N}\text{d}{L}_0\doteq 0.$$ (17)

To discretize the weak form in space, we partition the bulk ${\mathcal{B}}_0={\mathbf{\cup }}_{\text{e}=1}^{{\text{n}}_{\text{be}}}{\mathcal{B}}_{\text{0}}^{\text{e}}$ into n_se finite-volume elements ${\mathcal{B}}_0^{\text{e}}$, and the boundary ${\mathcal{S}}_0={\mathbf{\cup }}_{\text{e}=1}^{{\text{n}}_{\text{se}}}{\mathcal{S}}_{\text{0}}^{\text{e}}$ into n_se finite surface elements ${\mathcal{S}}_0^{\text{e}}$. Each surface element shares its nodes with its corresponding volume element as illustrated in Figure 5. This implies that the surface element acts like a shell element, which moves in consistency with the bulk, however, it is equipped with its own independent free energy function.

Figure 5.

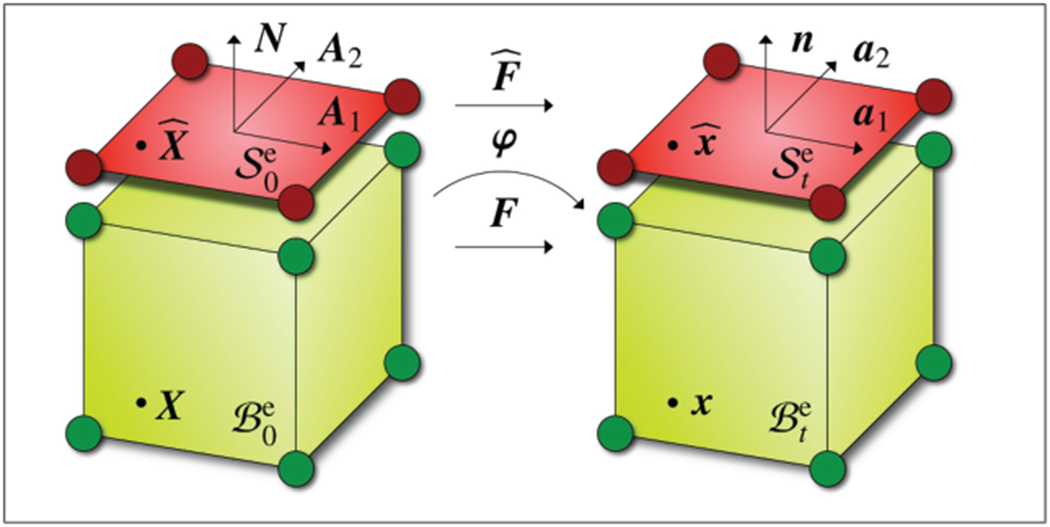
Discretization of the bulk with finite-volume elements ${\mathcal{B}}_0^{\text{e}}$ and ${\mathcal{B}}_t^{\text{e}}$, shown in green, and of its boundary with finite surface elements ${\mathcal{S}}_0^{\text{e}}$ and ${\mathcal{S}}_t^{\text{e}}$, shown in red. Surface elements share their nodes with the corresponding volume elements, however, they are equipped with their own energies $\widehat{\psi }$, stresses $\widehat{\mathit{P}}=\partial \widehat{\psi }/\partial \widehat{\mathit{F}},$ , and tangent operators $\widehat{\mathbb{A}}=\text{d}\widehat{\mathit{P}}/\text{d}\widehat{\mathit{F}}.$

To approximate the test functions δφ, trial functions φ, and nodal coordinates X in the bulk and on the boundary, we apply an isoparametric Bubnov–Galerkin-type finite-element interpolation,

$$\begin{array}{l}\begin{array}{ccccc}\delta \mathit{\phi }={\sum }_{i=1}^{{\text{n}}_{\mathrm{vn}}}{N}^i\delta {\mathit{\phi }}_i& \text{and}& \mathit{\phi }={\sum }_{j=1}^{{\text{n}}_{\mathrm{vn}}}{N}^j{\mathit{\phi }}_j& \text{and}& \mathit{X}={\sum }_{i=1}^{{\text{n}}_{\mathrm{vn}}}{N}^i{\mathit{X}}_i\end{array}\\ \begin{array}{ccccc}\delta \mathit{\phi }={\sum }_{i=1}^{{\text{n}}_{\mathrm{sn}}}{\widehat{N}}^i\delta {\mathit{\phi }}_i& \text{and}& \mathit{\phi }={\sum }_{j=1}^{{\text{n}}_{\mathrm{sn}}}{\widehat{N}}^j{\mathit{\phi }}_j& \text{and}& \mathit{X}={\sum }_{i=1}^{{\text{n}}_{\mathrm{sn}}}{\widehat{N}}^i{\mathit{X}}_i\end{array}.\end{array}$$ (18)

Here N^i,j and ${\widehat{N}}^{i,j}$ are the element shape functions in the bulk and on the boundary and i,j = 1, … , n_vn and i,j = 1, … , n_sn are the volume and surface nodes. The gradients of the test and trial functions in the bulk and on the boundary

$$\begin{array}{l}\begin{array}{ccc}\delta \mathit{F}=\nabla \delta \mathit{\phi }={\sum }_{i=1}^{{\text{n}}_{\mathrm{vn}}}\delta {\mathit{\phi }}_i\otimes \nabla N^i& \text{and}& \mathit{F}=\nabla \mathit{\phi }={\sum }_{j=1}^{{\text{n}}_{\mathrm{vn}}}{\mathit{\phi }}_j\otimes \nabla N^j\end{array}\\ \begin{array}{ccc}\delta \mathit{F}=\widehat{\nabla }\delta \mathit{\phi }={\sum }_{i=1}^{{\text{n}}_{\mathrm{sn}}}\delta {\mathit{\phi }}_i\otimes \widehat{\nabla }{N}^i& \text{and}& \mathit{F}=\widehat{\nabla }\mathit{\phi }={\sum }_{j=1}^{{\text{n}}_{\mathrm{sn}}}{\mathit{\phi }}_j\otimes \widehat{\nabla }{N}^j\end{array}\end{array}$$ (19)

then follow naturally in terms of the gradients of the bulk and boundary shape functions

$$\begin{array}{l}\begin{array}{ccccc}\nabla N^i=\frac{\text{d}{N}^i\left(\mathit{\xi }\right)}{\text{d}\mathit{X}}={\mathbf{J}}^{-\text{t}}\cdot \frac{\text{d}{N}^i\left(\mathit{\xi }\right)}{\text{d}\mathit{\xi }}& \text{with}& \mathbf{J}=\frac{\text{d}\mathit{X}}{\text{d}\mathit{\xi }}& \text{and}& \mathit{X}={\sum }_{i=1}^{{\text{n}}_{\mathrm{vn}}}{N}^i\left(\mathit{\xi }\right){\mathit{X}}_i\end{array}\\ \begin{array}{ccccc}\widehat{\nabla }{N}^i=\frac{\text{d}{\widehat{N}}^i\left(\mathit{\xi }\right)}{\text{d}\mathit{X}}={\widehat{\mathbf{J}}}^{-\text{t}}\cdot \frac{\text{d}{\widehat{N}}^i\left(\mathit{\xi }\right)}{\text{d}\mathit{\xi }}& \text{with}& \widehat{\mathbf{J}}=\frac{\text{d}\mathit{X}}{\text{d}\mathit{\xi }}=\left[{\mathit{A}}_{1,}{\mathit{A}}_2\right]& \text{and}& {\mathit{A}}_{\alpha }={\sum }_{i=1}^{{\text{n}}_{\mathrm{sn}}}{\mathit{X}}_i{\widehat{N}}_{,\xi \alpha }^i.\end{array}\end{array}$$ (20)

Herein A_α for α = 1, 2 are the contravariant material base vectors. With these discretizations, Equation (17) transforms into the following discrete residual

$${\mathbf{\text{R}}}_I=\underset{\text{e}=1}{\overset{{\text{n}}_{\text{el}}}{\mathbf{\text{A}}}}{\int }_{{\mathcal{B}}_0^{\text{e}}}\nabla N^i\cdot \mathit{P}\text{d}{V}_{\text{e}}-{\int }_{{\mathcal{B}}_0^{\text{e}}}{N}^{i}b\text{d}{V}_{\text{e}}+{\int }_{{\mathcal{S}}_0^{\text{e}}}\widehat{\nabla }{N}^i\cdot \widehat{P}\text{d}{A}_{\text{e}}-{\int }_{{\mathcal{S}}_0^{\text{e}}}{\widehat{N}}^i\widehat{b}d{A}_{\text{e}}-{\int }_{{\mathcal{C}}_0^{\text{e}}}{\widehat{N}}^i\widehat{P}\cdot \mathit{N}\text{d}{L}_{\text{e}}\doteq \mathbf{0},$$ (21)

where the operator A symbolizes the assembly of all element residuals at the i = 1, … , n_vn element nodes to the global residual at the global node points I = 1, … , n_gn. To solve the above equation, we use an incremental iterative Newton–Raphson algorithm based on the consistent linearization of the residual R_I with respect to the nodal vector of unknowns φ_J. This linearization introduces the global stiffness matrix K_IJ at all global nodes I, J = 1, … , n_ng,

$$K_{IJ}=\frac{\text{d}{R}_I}{\text{d}{\mathit{\phi }}_J}=\underset{\text{e}=1}{\overset{{\text{n}}_{\text{e}1}}{A}}{\int }_{{\mathcal{B}}_0^{\text{e}}}[I\cdot \nabla N^i]:\mathbb{A}\cdot \nabla N^j\text{d}{V}_{\text{e}}+{\int }_{{\mathcal{S}}_0^{\text{e}}}[\widehat{I}\cdot \widehat{\nabla }{N}^i]:\widehat{\mathbb{A}}\cdot \widehat{\nabla }{N}^j\text{d}{A}_{\text{e}}.$$ (22)

For each global Newton iteration step, we iteratively update the current deformation state ${\mathit{\phi }}_J\leftarrow {\mathit{\phi }}_J-K_{IJ}^{-1}\cdot {\mathbf{R}}_I$ until we achieve algorithmic convergence. Upon convergence, we store the surface growth multipliers ${\widehat{\vartheta }}^{\text{g}}$ at the integration points of the corresponding surface elements.

4. Results

We illustrate the performance of the proposed surface growth model by simulating differential growth in a stalk of rhubarb. Unless stated otherwise, we model the stalk as a cylindrical tube with a length of l = 7.0 cm and a radius of r = 0.375 cm. To visualize the effect of different surface-to-volume growth ratios, we virtually cut the stalk in quarters, fix it at one end, and allow its surface to shrink by gradually decreasing the surface growth multiplier $\widehat{\vartheta }$. We discretize one quarter of the inner parenchyma core with 32 elements along the length and 80 elements across the cross section. In each cross-section, we discretize the corresponding epidermal surface with eight additional surface elements around the circumference. This results in a discretization with 2560 elastic 8-noded volume elements and 256 growing 4-noded surface elements with a total of 3201 nodes and 9603 degrees of freedom. We characterize the hyperelastic responses of the bulk and of the boundary using independent isotropic bulk and boundary energies ψ₀ and ${\widehat{\psi }}_0$ of neo-Hookean type,

$$\begin{array}{l}{\psi }_0=\frac{1}{2}\mu [F:F-3-2\ln J]+\frac{1}{2}\lambda {\ln }^{2}J\\ {\widehat{\psi }}_0=\frac{1}{2}\widehat{\mu }[{\widehat{F}}^{\text{e}}:{\widehat{F}}^{\text{e}}-2-2\ln {\widehat{J}}^{\text{e}}]+\frac{1}{2}\widehat{\lambda }{\ln }^2{\widehat{J}}^{\text{e}}.\end{array}$$

Here, λ and μ are the standard Lamé constants of the bulk and $\widehat{\lambda }$ , and $\widehat{\mu }$ are the Lamé constants of the boundary. To evaluate the discrete residual (21), we calculate the volume and surface Piola stresses P and $\widehat{\mathit{P}}={\widehat{\mathit{P}}}^{\text{e}}\cdot {\widehat{\mathit{F}}}^{\text{g}-\text{t}}$ using the general definitions (11),

$$\begin{array}{l}P=\mu F+[\lambda \ln J-\mu ]F^{-\text{t}}\\ {\widehat{P}}^{\text{e}}=\widehat{\mu }{\widehat{F}}^{\text{e}}+[\widehat{\lambda }\ln {\widehat{J}}^e-\widehat{\mu }]{\widehat{F}}^{\text{e}-\text{t}}.\end{array}$$

To evaluate the consistent algorithmic linearization of the residual (22), we calculate the volume and surface tangent moduli $\mathbb{A}$ and $\widehat{\mathbb{A}}={\widehat{\mathbb{A}}}^{\text{e}}:[{\widehat{\mathit{F}}}^{\text{g}-\text{t}}\overline{\otimes }{\widehat{\mathit{F}}}^{\text{g}-\text{t}}]$ using the general definitions (12),

$$\begin{array}{l}\mathbb{A}=\mu I\overline{\otimes }I+[\mu -\lambda \ln J]{\mathit{F}}^{-t}\underset{\_}{\otimes }{\mathit{F}}^{-1}+\lambda {\mathit{F}}^{-\text{t}}\otimes {\mathit{F}}^{-\text{t}}\\ {\widehat{\mathbb{A}}}^{\text{e}}=\widehat{\mu }I\overline{\otimes }\widehat{I}+[\widehat{\mu }-\widehat{\lambda }\ln {\widehat{J}}^{\text{e}}][{\widehat{\mathit{F}}}^{\text{e}-\text{t}}\underset{\_}{\otimes }{\widehat{\mathit{F}}}^{\text{e}-1}-{\widehat{i}}^{\perp }\overline{\otimes }[{\widehat{\mathit{F}}}^{\text{e}-1}\cdot {\widehat{\mathit{F}}}^{\text{e}-\text{t}}]]+\widehat{\lambda }{\widehat{\mathit{F}}}^{\text{e}-\text{t}}\otimes {\widehat{\mathit{F}}}^{\text{e}-\text{t}},\end{array}$$

where we have introduced the abbreviation i^⊥ for the spatial second-order normal projection tensor i^⊥ = F · N ⊗ F · N. To model the elastic response of the parenchyma core, we choose the Lamé constants of the bulk to λ = 0.577 N/mm² and μ = 0.385 N/mm². While the epidermal surface in plants typically tends to be stiffer and stronger than the parenchyma bulk, here, for the sake of simplicity, we choose similar values for the Lamé constants of the boundary to $\widehat{\lambda }=0.577$ N/mm and $\widehat{\mu }=0.385$ N/mm for outer epidermal cell layer. To model the difference in growth between the inner parenchyma core and the outer epidermal surface, we gradually decrease the surface growth multiplier $\widehat{\vartheta }$ by choosing an infinite growth multiplier of ${\widehat{\vartheta }}_{\infty }=0.5$, a time constant of $\widehat{\tau }=1.0$, and an initial discrete time step size of Δt = 0.1. The choice of the latter two parameters influences the speed of growth but not the growth process itself. As such, these two parameters do not affect the results we present in the following.

Figure 6 illustrates the effect of growth-induced longitudinal tissue tension in the rhubarb stalk. The snapshots correspond to surface-to-volume growth ratios gradually decreasing from $\widehat{\vartheta }=1.000$, to $\widehat{\vartheta }=0.967,$ $\widehat{\vartheta }=0.933,$ $\widehat{\vartheta }=0.900,$ and $\widehat{\vartheta }=0.867,$ from left to right. As the surface-to-volume growth ratio decreases, the tissue tension increases and induces a higher curvature when the stalk is cut into quarters. Since the outer epidermal surface shrinks with respect to the inner parenchyma core, the four sections of the stalk gradually bend outward. The colorcode indicates the growth-induced increase in tissue stress with red colors indicating tissue compression and green and blue colors indicating tissue tension.

Figure 6.

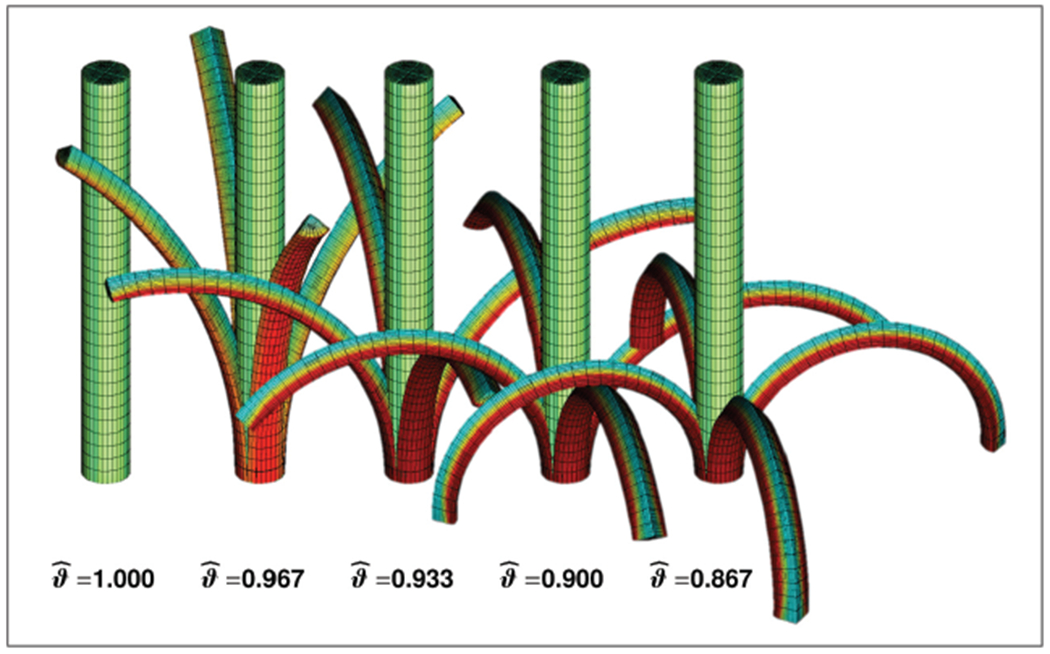
Growth-induced longitudinal tissue tension in a stalk of rhubarb. The stalk is modeled as a cylindrical tube with elastic volume elements and growing surface elements. With decreasing surface-to-volume growth ratios from $\widehat{\vartheta }=1.000$, to $\widehat{\vartheta }=0.967$, $\widehat{\vartheta }=0.933$, $\widehat{\vartheta }=0.900$, and $\widehat{\vartheta }=0.867$, from left to right, the tissue tension increases and induces a higher curvature when the stalk is cut in fourths. Red colors indicate compression, green and blue colors indicate tension.

Figure 7 displays the effect of different surface-to-volume growth ratios overlaid in a single image. With decreasing surface-to-volume growth ratios from $\widehat{\vartheta }=1.000$, to $\widehat{\vartheta }=0.980$, $\widehat{\vartheta }=0.960$, and $\widehat{\vartheta }=0.940$, the surface tension increases and induces a higher curvature when the stalk is cut in four sections. Again, red colors indicate tissue compression, green and blue colors indicate tissue tension.

Figure 7.

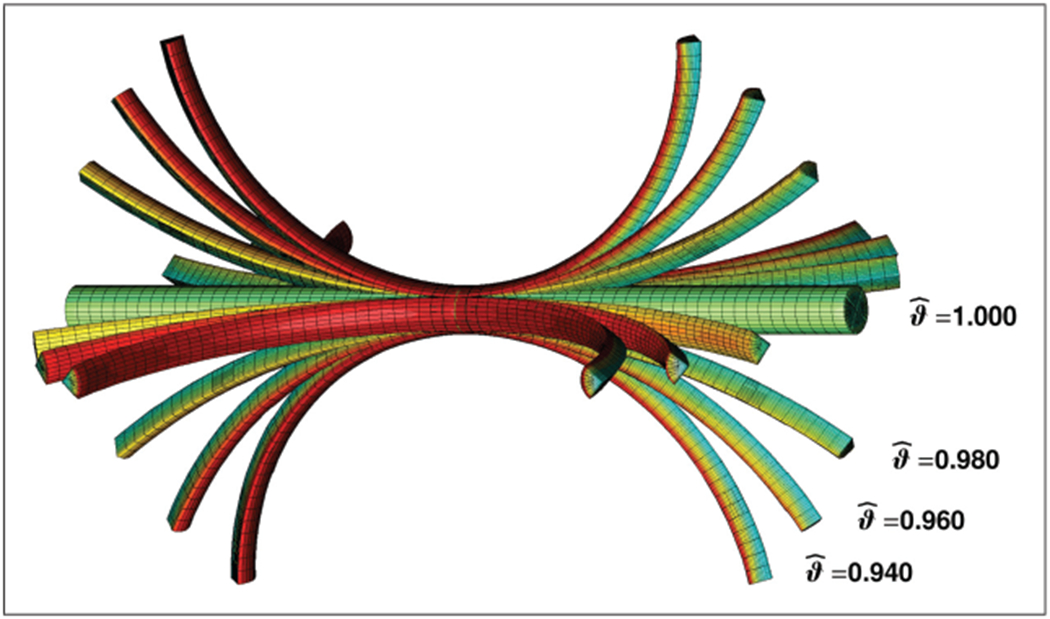
Growth-induced longitudinal tissue tension in a stalk of rhubarb. The stalk is modeled as a cylindrical tube with elastic volume elements and growing surface elements. With decreasing surface-to-volume growth ratios from $\widehat{\vartheta }=1.000$, to $\widehat{\vartheta }=0.980$, $\widehat{\vartheta }=0.960$, and $\widehat{\vartheta }=0.940$, the surface tension increases and induces a higher curvature when the stalk is cut in fourths. Red colors indicate compression, green and blue colors indicate tension.

Figure 8 illustrates the effect of surface growth as the surface-to-volume growth ratio decreases gradually until the rhubarb stalk forms a closed loop. With decreasing surface-to-volume growth ratios from $\widehat{\vartheta }=1.000$, to $\widehat{\vartheta }=0.975$, $\widehat{\vartheta }=0.950$, $\widehat{\vartheta }=0.925$, $\widehat{\vartheta }=0.900$, $\widehat{\vartheta }=0.850$, and $\widehat{\vartheta }=0.750$, the surface tension increases and induces a higher curvature when the stalk is cut in four sections. Again, red colors indicate tissue compression, green and blue colors indicate tissue tension.

Figure 8.

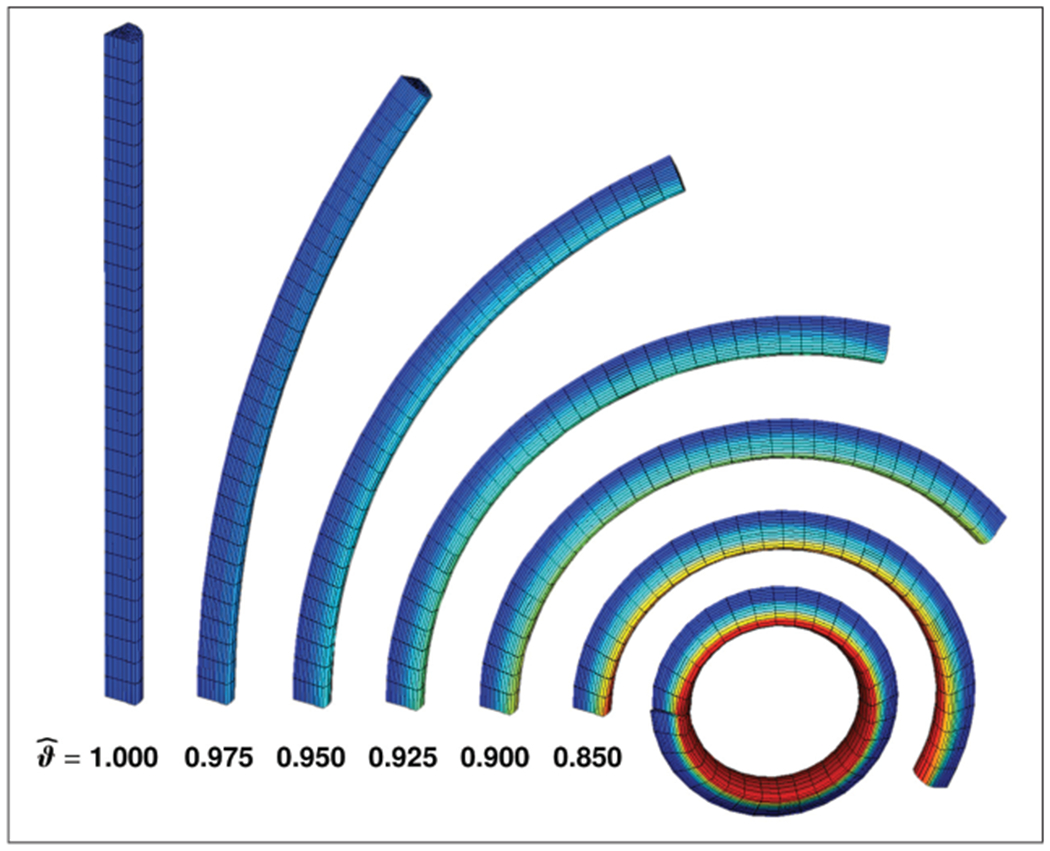
Growth-induced longitudinal tissue tension in a stalk of rhubarb. The stalk is modeled as a quarter of a cylindrical tube with elastic volume elements and growing surface elements. With decreasing surface-to-volume growth ratios from $\widehat{\vartheta }=1.000$, to $\widehat{\vartheta }=0.975$, $\widehat{\vartheta }=0.950$, $\widehat{\vartheta }=0.925$, $\widehat{\vartheta }=0.900$, $\widehat{\vartheta }=0.850$, and $\widehat{\vartheta }=0.750$, the surface tension increases and induces a higher curvature when the stalk is cut into quarters. Red colors indicate compression, green and blue colors indicate tension.

Figure 9 quantifies the growth-induced curvature change in rhubarb stalks with different radius-to-length ratios. For this simulation, we decrease the mesh size to 16 elements along the length, 40 elements across the cross-section, and 4 surface elements per cross-section. This results in a discretization with 320 elastic 8-noded volume elements and 64 growing 4-noded surface elements with a total of 493 nodes and 1479 degrees of freedom. We keep the length of the stalk constant at l = 7.0 cm and vary the radius from r = 0.250 cm to r = 0.375 cm, r = 0.500 cm, r = 0.675 cm, and r = 0.750 cm. A decrease in the surface-to-volume growth ratio $\widehat{\vartheta }$ increases tissue tension. This induces an increase in relative curvature κ/κ₀ from κ/κ₀ = 0.0, corresponding to a straight line, to κ/κ₀ = 1.0, corresponding to a closed loop, where κ₀ = 2π/l. The surface-to-volume growth ratio $\widehat{\vartheta }$ required to form this closed loop decreases with increasing radius-to-length ratios, from $\widehat{\vartheta }=0.894$, to $\widehat{\vartheta }=0.887$, $\widehat{\vartheta }=0.872$, $\widehat{\vartheta }=0.853$, and $\widehat{\vartheta }=0.838$, from blue to red lines. Upon isometric scaling, e.g. when doubling both, the stalk length l and radius r, the resulting curvature versus surface-to-volume growth curves remain identical as expected.

Figure 9.

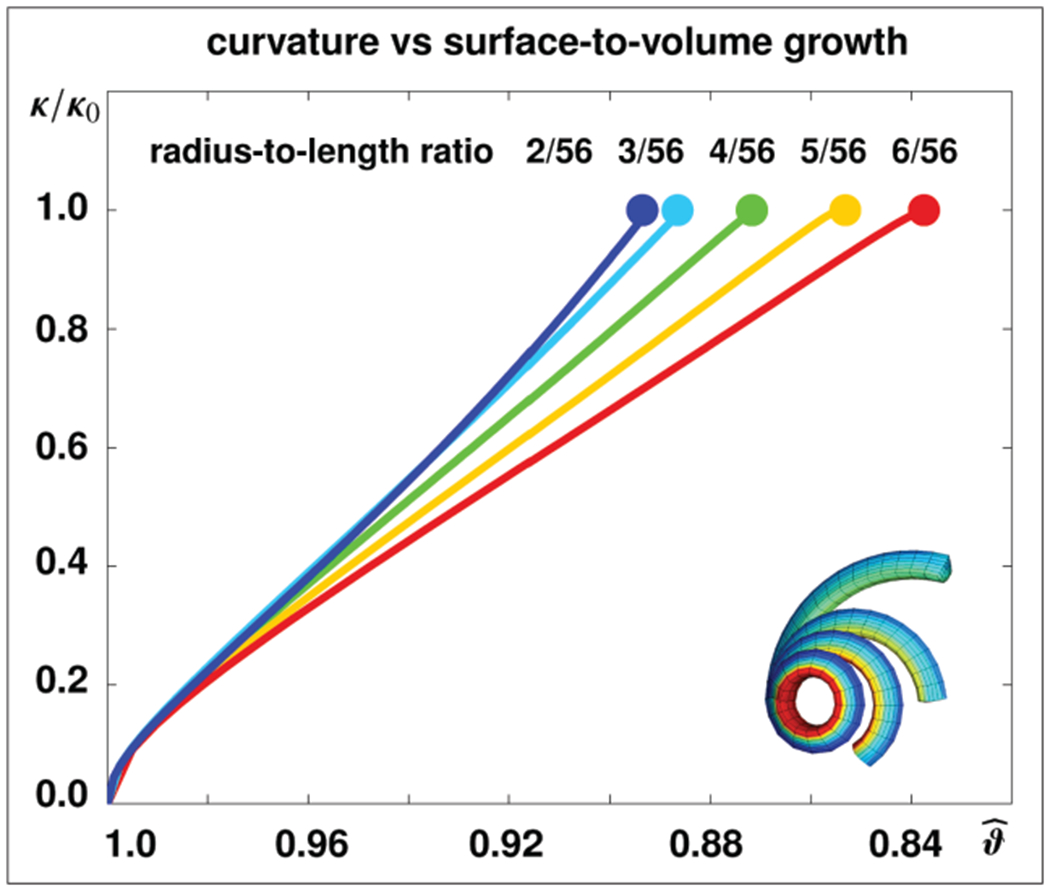
Growth-induced curvature changes in stalk of rhubarb for different radius-to-length ratios. A decrease in the surface-to-volume growth ratio $\widehat{\vartheta }$ increases tissue tension and induces an increase in relative curvature κ/κ₀. At a relative curvature of κ/κ₀ = 1.0, indicated throughout the solid dots, each stalk forms a closed loop. The surface-to-volume growth ratio $\widehat{\vartheta }$ required to form a closed loop, as shown in Figure 10, bottom row, decreases with increasing radius-to-length ratios, from $\widehat{\vartheta }=0.894$, to $\widehat{\vartheta }=0.887$, $\widehat{\vartheta }=0.872$, $\widehat{\vartheta }=0.853$, and $\widehat{\vartheta }=0.838$, from blue to red.

Figure 10 illustrates snapshots associated with the curves in Figure 9. In particular, the top row corresponds to the straight line at a relative curvature of κ/κ₀ = 0.0, while the bottom row corresponds to the formation of a closed loop at κ/κ₀ = 1.0 indicated through the solid dots in Figure 9. For the same curvature configuration, displayed in the individual rows, tissue stresses increase with increasing radius-to-length ratios, from left to right.

Figure 10.

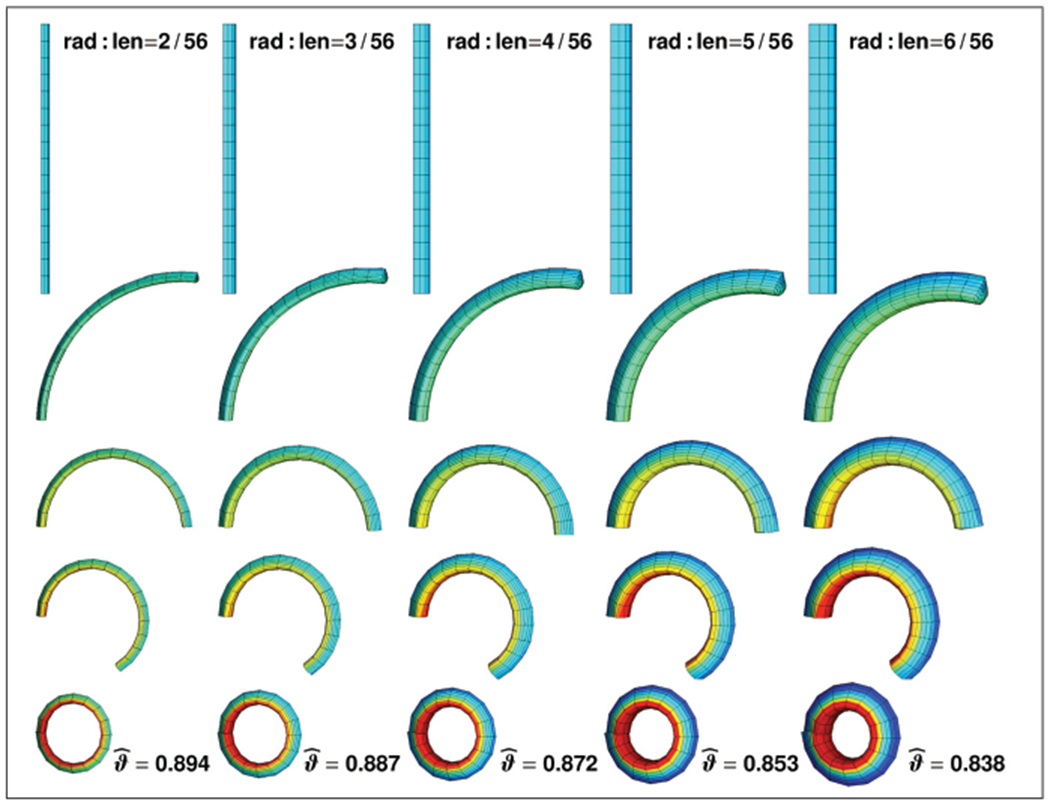
Growth-induced curvature changes in a stalk of rhubarb for different radius-to-length ratios. A decrease in the surface-to-volume growth ratio, from top to bottom, increases tissue tension and induces an increase in curvature. The top row corresponds to the straight stalk at a relative curvature of κ/κ₀ = 0.0, while the bottom row corresponds to the formation of a closed loop at κ/κ₀ = 1.0 indicated through the solid dots in Figure 9. The surface-to-volume growth ratio required to form a closed loop decreases with increasing radius-to-length ratios, from left to right. Red colors indicate compression, green and blue colors indicate tension.

5. Discussion

Growth of thin surfaces plays a central role in the morphogenesis of many biological structures [27]. In plants, the differential growth of thin layers of cells is critical to establishing structural form and function [4]. While the individual layers of a plant stem are relatively compliant when considered in plain isolation, differential growth creates a mechanical environment of residual stress that stiffens the structure as a whole [1]. Residual stresses can be generated by a fast growing inner core of parenchyma cells covered by a slowly growing thin layer of epidermal cells. By peeling off the thin surface layer, we can release residual stresses and observe a significant lengthening of the inner core, while the surface layer contracts as illustrated in Figure 1 (see [2]).

Modeling differential growth of thin films can be conceptually challenging, especially because most biological surfaces are typically only a few micrometers thick [5]. An elegant way to model growing thin biological layers is the concept of surface energies [40]. Introduced more than two centuries ago to characterize surface tension in droplets [38, 39], surface energies allow us to represent extremely thin surfaces as two-dimensional manifolds at the zero-thickness limit. This dimensional reduction is particularly valuable in the context of numerics, since the fully three-dimensional discretization of thin surfaces would either require very fine meshes, or generate numerically ill-conditioned systems [47]. To avoid these numerical difficulties, we simply equip the surface with its own free energy, which we allow to evolve independently of the bulk [36, 46]. In particular, our surface energy not only accounts for the elastic behavior of the surface itself, but also for its growth or shrinkage with respect to the bulk [37]. To kinematically characterize the amount of surface growth, we adopt the multiplicative decomposition of the surface deformation gradient into an elastic tensor and a growth tensor [56].

A conceptually elegant approach to experimentally characterize the surface growth tensor in plants is the classical peel test [2] as demonstrated in Figure 3. In this experiment, surface growth can simply be interpreted as the ratio between surface shortening and volume lengthening after both substructures are separated [4]. Virtually anybody can perform a simple peel test with rhubarb in their own kitchen, measure surface shortening and volume lengthening, and verify correct layer separation simply by the distinct red and green tissue colors [5]. Upon peeling several stalks of rhubarb, we observed surface shortening of the order of −1% and the volume lengthening of the order of +4%. These values are slightly less pronounced than the surface shortening of −2–4% and the volume lengthening of +6% reported in the literature [9], most likely because our rhubarb was not freshly harvested and its lower water content might play an important role.

An equally simple model experiment to quantify growth upon releasing tissue tension is the longitudinal cutting test [2]. When cutting the cylindrical plant stem into four equal parts, the epidermal surface layers contract and bend outward, while the inner parenchyma core expands [4]. The release of tissue tension generates a state of bending, which we can quantify kinematically in terms of the stalk curvature [57]. Here, we have simulated the longitudinal cutting tests, and systematically varied the amount of surface growth and the radius-to-length ratio. Intuitively, as illustrated in Figure 9, the relative stalk curvature increases with increasing surface growth. For the same surface growth, thicker stems curve less upon longitudinal cutting than thinner stems. While the stalk curvature is sensitive to the amount surface growth and to the radius-to-length ratio, it is unaffected by isometric scaling: Proportional changes in radius and length do not affect curvature and shape. Despite the large deformations associated with bending a straight line to a closed loop illustrated in Figures 8 and 10, our surface growth algorithm always performed stably and robustly, with no evidence of ill-conditioning or loss of convergence [37].

Our results demonstrate that the framework for continua with growing surfaces is an elegant setting to model growing thin biological films. Plant biology presents an illustrative area of application for growing surfaces, especially because the underlying experiments are simple, illustrative, and easily reproducible, even outside an advanced laboratory setting. Growing plants can serve as elegant model problems to calibrate surface growth models and validate computational algorithms. Beyond classical model problems in plant biology, our novel theoretical and computational framework for growing surfaces has immediate biomedical applications in asthma [58], gastritis [59], obstructive sleep apnoea [60], brain development [61], and tumor invasion [19]. It naturally captures the distinct mechanical behavior of a thin epidermal layer, which is typically only a few micrometers thick. Similar thin-film phenomena are inherent to applications in material sciences, manufacturing, and microfabrication [62]. We believe that the proposed framework can provide insight into the complex interplay between thin films and the bulk, which might be particularly valuable when designing novel functionalized surfaces with distinct user-defined properties.