Designing humanitarian logistics network for managing epidemic outbreaks in disasters using Internet-of-Things. A case study: An earthquake in Salas-e-Babajani city

Abstract

Along with the destructive effects of catastrophes throughout the world, the COVID-19 outbreak has intensified the severity of disasters. Although the global aid organizations and philanthropists aim to alleviate the adverse impacts, many employed actions are not impactful in dealing with the epidemic outbreak in disasters. However, there is a gap in controlling the epidemic outbreak in the aftermath of disasters. Therefore, this paper proposes a novel humanitarian location-allocation-inventory model by focusing on preventing COVID-19 outbreaks with IoT-based technology in the response phase of disasters. In this study, IoT-based systems enable aid and health-related organizations to monitor people remotely, suspect detection, surveillance, disinfection, and transportation of relief items. The presented model consists of two stages; the first is defining infected cases, transferring patients to temporary hospitals promptly, and accommodating people in evacuation centers. Next, distribution centers are located in the second stage, and relief items are transferred to temporary hospitals and evacuation centers equally regarding shortage minimization. The model is solved by the LP-metric method and applied in a real case study in Salas-e-Babajani city, Kermanshah province. Then, sensitivity analysis on significant model parameters pertaining to the virus, relief items, and capacity has been conducted. Using an IoT-based system in affected areas and evacuation centers reduces the number of infected cases and relief item's shortages. Finally, several managerial insights are obtained from sensitivity analyses provided for healthcare managers.

1. Introduction

Annually, cataclysms, e.g., earthquakes, hurricanes, volcanic eruptions, and floods, claim people's lives worldwide. Based on information released from the international disaster database (https://www.emdat.be/emdat_atlas), Japan's deadliest earthquake had more than 20,033 fatalities. The last decade has experienced significant earthquakes triggering more than 400,000 deaths and 500,000 injuries. Two of the most destructive earthquakes, the Sichuan earthquake in China and earthquakes in Haiti, affected more than 56 million people in both countries (Ahmadi et al., 2020). Regarding the statistics published recently, Iran is seventh of the world's top ten countries with the most dangerous earthquake (Zolfaghari and Peyghaleh, 2016, Heydari et al., 2021). There is evidence that the most frequent natural catastrophe in Iran is the earthquake. Managing the disaster in the situation of occurrence of an earthquake is one of the most critical issues. Aside from a massive proportion of casualties, the economy of Affected Areas (AAs) may deteriorate after disasters, along with the healthcare system (Bakhshi et al., 2022).

While an unprecedented SARS-CoV-2 outbreak emerged in Wuhan on 31st December 2019, World Health Organization (WHO) disseminated information about the fatal disease to ensure people's safety (Sohrabi et al., 2020). Until now, many patients who are infected have mild symptoms, e.g., a dry cough, a sore throat, and a mild fever, which improve over a few days. However, others are faced with more severe symptoms such as organ failure, septic shock, and severe pneumonia (Chen et al., 2020). As noted by the online statistics platform (https://www.worldometers.info/coronavirus ), the number of confirmed cases worldwide is now more than 145 million, with 3.1 million deaths. As far as COVID-19 is concerned, the global economy has declined due to preventative measures such as social distancing and lockdowns to eradicate coronavirus (Heydari & Bakhshi, 2022). To summarize, industries, international trade, and the global supply chain all suffer during the given timeframe (Ibn-Mohammed et al., 2021). Along with the crippling effect of COVID-19 on the supply chain network, relief logistics, encompassing vaccine, medicine, and ventilators distribution, have been experiencing some disruptions throughout the period (Sharma et al., 2020).

Regarding the destructive impacts of COVID-19, the spread of epidemic outbreaks amid the disaster can pose a potential menace to people's lives and increase the number of casualties noticeably. The outbreak of acute gastroenteritis in Hurricane Katrina in August 2005 and cholera followed by the Haiti Earthquake in January 2010 are the cases in point (Barzilay et al., 2013). Unambiguously, the lack of alcohol-based disinfectants, masks, paper towels, medical supplies, and drinkable water brings about unhygienic circumstances within the disaster-affected zones (Sakamoto et al., 2020). Therefore, planning the evacuation procedure that will apply during the COVID-19 pandemic has the utmost importance.

Prevention, preparedness, response, and recovery constitute the four phases of managing a disaster (Goretti et al., 2017). Disaster prevention has become a global problem to lessen the impact of disasters. One strategic aspect of the pre-disaster phase is the facilities' location and the quantity of relief items (RIs) to be processed, as they are closely linked to timely service and cost of response within the Humanitarian Relief Logistics (HRL) (Duhamel et al., 2016). Aim in HRL is the reducing the response time and the rate of casualty (Momeni et al., 2020). The response phase involves the evacuation measures and transferring of affected people from AAs. During the epidemic outbreak, the response phase should be combined with continuous surveillance and assessment. Additionally, in the preparedness stage, locating facilities and Evacuation Centers (ECs) and distributing RIs should be based on virus features.

To tackle the COVID-19 outbreak in AAs, Sakamoto et al. (2020) suggested a recommendation obtained from previous experiences mentioned in the following: (1) The total area required per person is six square meters. (2) Thermometers and sensors can be deployed to find symptomatic patients. (3) Public places, i.e., schools, can be utilized to accommodate unoccupied people along with ECs. (4) About one-third of ECs' capacity should be accepted to occupy. (5) Tankers replete with drinkable water should be allocated to ECs. (6) The mask and alcohol-based disinfectants should be distributed to evacuees immediately. (7) A system is necessary to ensure that information and guidelines reach evacuees. (8) Continuous surveillance and tests would be implemented in ECs to find infected people. (9) The isolation space is crucial for symptomatic patients.

As noted above, mitigating the shambolic situation amid the disaster outbreak is one of the main challenges severely impacted by the COVID-19 outbreak (Dehghan-Bonari et al., 2021). Planning and executing guidelines, accommodating symptomatic and asymptomatic patients simultaneously, utilizing the IoT-based technology, using cargo drones for distribution, and distributing RIs fairly and quickly can control the epidemic outbreak. The proposed IoT framework in this study collects the data of the symptoms from individuals and patients to define the infected cases and calculate the infection rate. A decision support system is incorporated into the IoT framework to make critical decisions based on the infection rate in the aftermath of a disaster. Also, the framework is utilized for virtual communication between patients and physicians and for informing people of the latest guidelines.

The discrepancies between the management of disasters simultaneous with a pandemic and without it are as follows: (1) Relief items should contain sanitization and personal protective equipment, along with excess hygienic water; (2) allocation of patients and symptomatic people should be based on guidelines; (3) the medical IoT framework, along with the PCR test, should be used to detect suspects in a timely manner; (4) quarantine places should be considered to separate infected cases from the crowds; (5) novel vehicles and transportation methods (i.e., autonomous drones) should be hired to distribute RIs without human intervention. Therefore, these differences make management complicated.

Questions that need to be answered in this study are as follows:

• •Where and how many Temporary Hospitals (THs) and Distribution Centers (DCs) should be instituted to cope with COVID-19 in the aftermath of disasters?
• •Are IoT-based technologies impactful for controlling COVID-19 in disasters?
• •What is the optimum inventory level for DCs?
• •How many drones and trucks are needed?
• •How many RIs are required?

Therefore, the multi-objective, multi-period, multi-fleet location-allocation-inventory mixed-integer IoT-based mathematical programming model with uncertain parameters is developed for the response phase based on Japan's experiences proposed by Sakamoto et al. (2020) to answer the questions mentioned above. Additionally, an IoT framework for finding suspected and infected cases, enriched with a novel decision support system for logistics management, is proposed in our study. Due to the paramount importance of disaster management amid the COVID-19 outbreak, affected people are allocated to ECs and THs regarding the allocation policy and time consideration. Then, RIs are distributed from DCs to ECs and THs swiftly. The main goals of our RI logistics problem are to minimize the delivery time of RIs, the shortage and surplus of RIs in demand zones, and total cost. As a main result of this study, reducing the infection rate can be impactful on cost reduction. Also, the infection rate in AAs has more impact on cost, shortage, and the number of the infected cases in THs than the rate in ECs. In terms of item distribution, drones have more impact on the shortage reduction than trucks. Furthermore, increasing the capacity of distribution centers has less effect on a shortage than increasing the fleet capacity or the number of fleets.

This paper is composed of six main sections. The introduction is considered the first one. The literature of previous studies is analysed in Section 2. In Section 3, the problem description and suggested mathematical model are presented, along with tackling uncertainty. Section 4 points out the solution methodology. Next, in Section 5, the proposed model is evaluated by the actual case study, and comprehensive sensitivity analyses are conducted concerning model parameters. Finally, the managerial insight, as well as the conclusion, are reported in Section 6.

2. Literature review

2.1. The location-allocation problems in humanitarian relief logistics (HRL)

The location problem has numerous supply chain network applications, capturing the scholar's attention in recent years. Some studies in humanitarian logistics are highlighted below.

In the aftermath of floods, the telecommunication network may be disrupted as well as accommodation may be demolished. Mohammadi et al. (2016) presented the stochastic mathematical model to locate DCs, shelters, and telecommunication towers to enhance service efficiency and communication in disasters. Paul and Hariharan (2012) conducted the research to mitigate disaster-impacted zones, taking into account the reduction of delays in allocating stockpiles and evacuation. Survivability time and severity of injuries have a significant role in the mentioned study. While AAs encounter severe devastations, donations from non-governmental organizations (NGOs) and international contributions are requisite to evacuate people. Sarma et al. (2019) introduced the mathematical model, including minimizing total costs and operational time for inventory and allocation of daily consumed RIs, and supplying machinery equipment delivered by NGOs. In the recovery phase of disasters, Ahmadi et al. (2020) presented a two-stage mathematical model to allocate Save and Response (SAR) teams to AAs as soon as possible. The model aims to maximize demand coverage and minimize operational time to identify the casualties in the shortest time.

Tofighi et al. (2016) proposed the two-stage inventory-location-allocation model to define the location of warehouses and DCs in the first phase and distribute the RIs to DCs in the second phase. Considering demands and items' priority, the model aims to minimize total cost and transportation time. Furthermore, Aslan and Çelik (2019) designed the location-routing-inventory model consisting of two stages; the first aims to locate DCs and warehouses during the preparedness phase, and the latter tries to find the indefectible roads at the post-disaster time. The road's vulnerability amid the disaster and restoration time of affected roads is incorporated in the mentioned model. Since RIs have various lifetimes, ordering policy plays a crucial role in HRL. Rezaei-Malek et al. (2016) proposed the model considering selling surplus perishable items and buying them periodically to decrease the surplus amount of perishable RI. Amid the catastrophe, Road disruptions and people's foreboding will bring about massive traffic congestion in the aftermath of disasters. To cope with the rampant problem, Wang and Nie (2019) proposed the location-allocation single-objective model involving traffic function incorporated into transportation costs. The model aims to find the road with the lowest traffic congestion. Vahdani et al. (2018) developed the comprehensive two-stage multi-period multi-commodity multi-vehicle mathematical model that encompasses locating DCs and warehouses in the first stage and routing and distributing RIs in the second one. To fulfil people's demand and deliver RIs promptly, the priority of damage AAs, split delivery, and hard time window are incorporated into the model. A novel transportation method has emerged regarding the road disruptions during calamities, which name is aeromedical logistics. Abazari et al. (2021) tackled the problem of distribution of perishable and imperishable RIs by minimizing total traveling time and distance and considering the time window. Jenkins et al. (2020) addressed mobile aeromedical facility location and allocation of helicopters to stages. The model aims to maximize the demand coverage in AAs and facilitate distributions. Bozorgi-Amiri and Khorsi (2016) considered people's satisfaction in AAs by minimizing the maximum amount of shortage, total travel time, and total cost. The proposed model regards multi-modal transportation encompassing a heterogeneous fleet of vehicles.

In the response phase, patient hospitalization and provision of medical supplies decrease the disaster's fatality rate. Habibi-Kouchaksaraei et al. (2018) considered the problem of temporary blood facility location and blood distribution to the temporary and existing hospitals. The bi-objective multi-echelon model aims to minimize the total costs and blood deficiency. Additionally, Salehi et al. (2017) developed the previous work and presented the multi-objective multi-period, multi-product model considering all types of blood types, their derivations, and the possible blood substitution. Moreover, to transfer casualty aftermath earthquakes, Haghi et al. (2017) considered THs in HRL. The mathematical model entails minimizing costs and maximum demand shortage, and neglected casualties. Ghasemi et al. (2019) proposed the bi-objective model regarding the distribution of RIs and injured people's hospitalization simultaneously. Due to the severity of injuries, the patients are divided into two groups; the first is outpatients transferred to temporary medical centers, and the latter is seriously injured patients transferred to hospitals.

2.2. Uncertainty in humanitarian logistics

Due to the unpredictable nature of disasters, embracing the uncertain environment can make the model more real-world and efficacious. Based on the literature review conducted by Peidro et al. (2009), in most logistics models, the inventory parameters (i.e., inventory cost and capacity of the storage), supplier-side parameters (i.e., establishment cost, production cost, and quality parameters), distribution parameters (i.e., transportation cost and the capacity of vehicles), and demand parameters (i.e., demand quantity) were taken as uncertain parameters. As shown in numerous studies in HRL, uncertainty stems from supply, demand, inventory, and network connectivity.

Specifically, for the demand side, Mohamadi et al. (2016) used Fuzzy Mathematical Programming (FMP) for demand uncertainties. The uncertain population in each region (demand level) for maximizing demand coverage in the problem of selecting telecommunication towers Also, the hired possibilistic method does not control the level of uncertainty. Additionally, Jenkins et al. (2020) considered volatile demands in the aeromedical location-allocation problem.

To predict disasters' unspecified behaviours, some researchers have considered uncertain demand and supply simultaneously whether many scholars have presented all the facets of uncertainty sources. It is worth noticing that disaster time walks hand in hand with demand levels at specific locations. For instance, in working hours, the total population can increase in the business district. Simultaneously, considering location and demand level are found in Rezaei-Malek et al., 2016, Salehi et al., 2017, and Habibi-Kouchaksaraei et al. (2018).

Aside from fluctuating demand, Abazari et al. (2021) focused on uncertainty corresponding to distribution parameters, including travel, loading, unloading time, transportation, and inventory cost. This work did not consider the uncertainty in either demand or supply. However, the study developed by Tofighi et al. (2016) considered demand sides with the accompaniment of parameters mentioned in the previous work. Note that in this study, the uncertain capacity of distribution centers is added into model to concentrate more on the uncertainty for the distribution side. Similarly, Sarma et al. (2019) embraced the FMP method to convert transportation and inventory costs and demand levels into the crisp model. However, this study did not consider time and capacity as fuzzy numbers. In addition, in the problem of pre-positioning and procurement planning, Torabi et al. (2018) utilized both FMP and scenario-based methods for uncertain parameters in all fields, involving uncertain capacity, production and procurement costs, transportation costs, and demand level. This study focused on the supplier side and prepositioning planning, which model is not appropriate for the disaster response phase. Similar to Mohamadi et al. (2016), the utilized fuzzy method cannot control the degree of uncertainty. Danesh Alagheh Band et al. (2020) presented a multi-objective problem to maximize the gain from the assessment of roads and areas with uncertain parameters.

2.3. Impact of COVID-19 on supply chain management

Regarding the business closure, lack of workforce, and massive lockdowns, the logistics network's efficiency decreases considerably amid the coronavirus (Wu et al., 2021, Spieske and Birkel, 2021). Some studies are conducted pertaining to the COVID-19 outbreak to tackle the lack of products and emergency items mentioned below.

Regarding the distribution of critical items to tackle the COVID-19 outbreak, Tirkolaee et al. (2022) proposed the location-allocation closed-loop green network for distributing and collecting face masks, considering all components wrestling with COVID-19 (i.e., quarantine, distribution, and recycling centers). In order to eradicate the Hazardous Medical Wastes (HMW), including masks, among the COVID-19, Kargar et al. (2020) designed the network enriched by Temporary Treatment Centers (TTCs) and all potential waste generators (hospitals, treatment centers, and quarantine places). The multi-period model aims to locate the TTCs and allocate the influx volume of HMW to TTCs in terms of minimizing the maximum quantity of uncollected waste, which is similar to minimizing the unmet demand in Goodarzian et al. (2022). Similarly, in Goodarzian et al. (2021), the sustainable production–distribution–inventory–allocation–location model was developed for perishable medicine amid the coronavirus, taking into consideration of minimizing maximum shortage. Aside from masks and their waste management, Mondal and Roy (2021) designed a production–distribution model to distribute required items for COVID-19 to hospitals concerning the minimizing time and backlogged works to increase people’s satisfaction. In the HRL network, distributing foods, along with relief items, plays a pivotal role, which is considered in Azani et al. (2022). In this study, food is allocated to reduce the virus transmission and people’s communication.

In order to utilize the state-of-the-art technologies for eradicating COVID-19, Zahedi et al. (2021) proposed the application of the medical internet of things (m-IoT) for ambulance allocation for COVID-19 patients with consideration of their priorities that are efficacious in reducing COVID-19 patients noticeably. The role of IoT in this paper is to define suspected cases and allocate the ambulance to them. In addition, Goodarzian et al. (2022) designed the COVID-19 vaccine supply chain network with the goal of minimizing the maximum unmet demand, total cost, and delivery time. Similar to Zahedi et al. (2021), the IoT framework plays a critical role in gathering people’s information and prioritizing sensitive tiers. Hence, the impact of IoT on supply chain management became stark after the emerging of the virus that the proposed Methods and IoT equipment are discussed in Yousif et al. (2021).

2.4. Research gaps

To sum up the literature, a meticulous analysis of Table 1 provides research gaps of the HRL. Some specifications of research gaps are mentioned below.

• •None of the research considers the management of epidemic and disease outbreaks among the disasters (i.e., earthquake, tsunami, flood, storm). There are several guidelines in essays, but this problem lacks mathematical modelling. Also, none of the aforementioned essays consider time, cost, distance, and demand coverage as objective functions simultaneously.
• •In a few recent articles, fleet management and multi-modal transportation play a crucial role in distribution and delivery. It should be mentioned that none of the previous research does not consider various types of transportation, including road, air, rail, and sea methods, along with the heterogeneous types of fleets.
• •Practically speaking, evacuating people and distributing RIs happen concurrently, which is considered in numerous essays separately. There is an stark gap to make a mathematical model that involves both of them.
• •In the aftermath of a disaster, the level of uncertainty surges in all aspects. Most papers concentrated on demand fluctuations at the time of the disaster. Based on the systematic review conducted in Section 2.2, none of the research considered all types of uncertainty for the response phase of a disaster.
• •Based on two recent articles (Zahedi et al., 2021, Goodarzian et al., 2022), they combined IoT-based technology into supply chain management to tackle the impact of COVID-19 on the logistics network. However, there is a gap in incorporating the medical IoT into the humanitarian logistics network.

Table 1.

A comparison of relevant literature on the topic of HRL network design.

Author	Objective function					Type of problem				Period		Commodity		Uncertainty					Fleet	IoT	Solution method
	H	D	DC	T	C	L	A	R	I	S	M	S	M	SB	F	S	R	N
Paul and Hariharan. (2012)				*	*	*	*			*		*		*							commercial solver
Bozorgi-Amiri and Khorsi (2016)			*	*	*	*	*		*		*		*	*							ε-constraint method
Mohamadi et al. (2016)	*	*	*			*	*			*		*		*	*						commercial solver
Rezaei-Malek et al. (2016)				*	*	*	*				*		*	*			*				tchebycheff method
Tofighi et al. (2016)				*	*	*	*		*	*			*	*	*						metaheuristic
Vahdani et al. (2018)				*	*	*	*	*	*		*		*	*			*		*		metaheuristic
Haghi et al. (2017)	*				*	*	*			*			*	*			*				metaheuristic + ε-constraint method
Habibi-Kouchaksaraei et al. (2018)			*		*	*	*				*	*		*			*				commercial solver
Aslan and Çelik (2019)				*	*	*		*	*	*			*			*					heuristic
Salehi et al. (2017)					*	*	*		*		*		*	*		*	*				branch and cut method
Sarma et al. (2019)				*	*	*	*			*			*		*						commercial solver
Ghasemi et al. (2019)	*				*	*	*		*		*		*	*					*		metaheuristic
Wang and Nie (2019)					*	*	*			*		*		*							general benders decomposition
Ahmadi et al. (2020)			*	*			*	*			*	*					*				commercial solver
Abazari et al. (2021)		*		*	*	*	*		*	*			*		*				*		metaheuristic
Jenkins et al. (2020)	*		*			*	*			*				*							ε-constraint method
This Study	*	*		*	*	*	*		*		*		*	*	*				*	*	commercial solver

Cue: [Objective function: H = humanitarian, D = distance, DC = demand coverage, T = time, C = cost], [Type of problem: L = location, A = allocation, R = routing, I = inventory], [Period and Commodity: S = single, M = multi], [Uncertainty: SB = scenario-based, F = fuzzy, S = stochastic, R = robust, N = none].

After a meticulous analysis of research gaps, the novelties of our paper are listed below:

• •The study herein seeks to cope with natural cataclysms amid the epidemic outbreak. In this study, the mathematical model is presented to address the location of THs and DCs, determination of required RI's quantity, e.g., sanitizers, water, Personal Protective Equipment (PPE), transferring people and patients, and allocation of them to THs and ECs. The proposed IoT-based multi-echelon multi-commodity multi-period model aims to make a trade-off between unmet demand, costs, distances, and travel time simultaneously to increase people's satisfaction and fairness in distribution. Also, some practical experiments, proposed by Sakamoto et al. (2020), were added to our model; these can be seen in model assumptions.
• •The heterogeneous fleet is utilized in the study to deliver RIs swiftly. In our article, two models of transportation are deployed, including air and road. Drones are utilized for air transportation, and trucks are considered for road distribution.
• •The transferring of people along with the distribution of RIs to individuals is considered concurrently in our model.
• •The novel IoT framework is incorporated into our humanitarian logistics network for calculating and reducing the infection rate of COVID-19. Note that this framework is based on Otoom et al. (2020), that we make it specific for the disaster situation by adding some components (e.g., quarantine centers).
• •To cope with uncertainty, all types of uncertainty, involving supply (institutional cost), demand (number of people living in city zones), inventory (capacity of storage and inventory cost), and distribution (capacity of fleet and distribution cost), are covered in our study. Aside from parameters, fuzzy mathematical programming and scenario-based optimization cope with uncertainty in all aspects of this study. Finally, the proposed model is evaluated in three different scenarios by a real-world case study in Salas-e-Babajani city, located in Iran.

3. Problem description

Our problem is composed of two interconnected sections, including a proposed IoT framework and a decision support system. Note that this IoT framework is the developed version of the study proposed by Otoom et al. (2020), specifically for monitoring and detecting infected cases in disasters. Regarding the review article written by Asadzadeh et al. (2020), one of the DSS applications that was made to deal with the COVID-19 epidemic is supply chain management. As a significant novelty of this work, a novel decision support system as a part of an IoT system is proposed to make critical decisions in the aftermath of disasters.

3.1. The proposed IoT framework

The Internet of Things (IoT) is a system of interconnected computer, electronic, and mechanical equipment capable of transmitting data across a specified network without human intervention. What makes IoT capable of the COVID-19 Pandemic is its significant benefits, including a lower probability of error, lower costs, superior treatment, improved diagnosis, proper monitoring system during the quarantine, reduction in medical staff’s workload, and effective control (Singh et al., 2020). The lack of this framework can increase the infection rate noticeably because doing a COVID-19 PCR test on all individuals and then allocating people based on the test result takes a great deal of time and also, a huge number of tests are not available at that time.

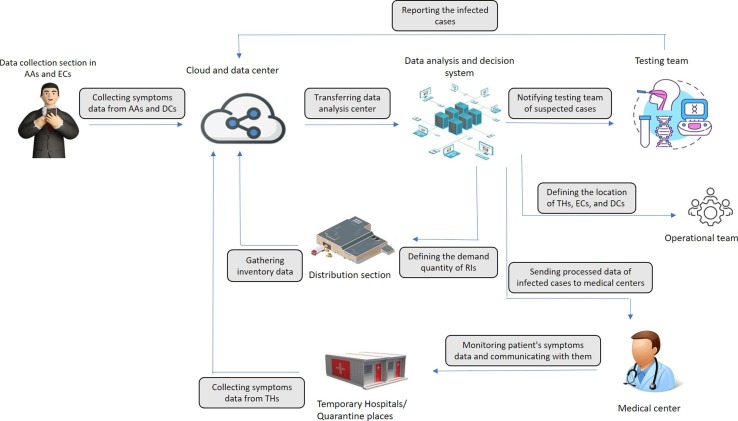
Practically speaking, the medical IoT system is utilized in numerous countries to cope with the COVID-19 issue. Some practical examples of IoT are presented in the following. For the first time, China hired the IoT to build the questionnaire-based application used for COVID-19 treatment and diagnosis (Bai et al., 2020). The Health Beats application was developed along with the phone application for monitoring vital signs and diagnosing suspected COVID-19 cases (https://www.healthbeats.co/covid-19/). Also, the Mhero application is utilized for physician-patient communications by using text messages and SMS (https://www.mhero.org/). Aside from a mobile phone-bed infected detector, Shanghai Public Health Clinical Center (SPHCC) deployed a continuous body temperature monitoring system with wearable sensors, which are based on Bluetooth (https://www.mobihealthnews.com/news/asia/sphcc-employs-iot-tech-and-wearable-sensors-monitor-covid-19-patients). Additionally, to illustrate the accuracy of the ML-driven infected detector models, the study proposed by Otoom et al. (2020) showed that five out of eight supervised classification models have more than 90 % accuracy in detecting COVID-19 suspects. This section illustrates our planned IoT-based infrastructure for monitoring coronavirus infections in real-time and making critical decisions automatically. The framework of our suggested IoT is depicted in Fig. 1 , comprising eight major components specifically for disaster management amid the outbreak.

• 1.Data collection section in THs and ECs:

Fig. 1.

The proposed IoT-driven framework.

This section seeks to collect real-time symptom data from individuals’ bodies using a set of sensors. Based on the study proposed by Alzubaidi et al. (2021), these symptoms were recognized as Fever, Cough, Fatigue, Sore Throat, and Breathlessness.

In our study, biosensors, involving thermal and infrared sensors for monitoring people's body temperature and detecting fever, heart-rate sensors located on wearable rings for measuring oxygen level and detecting breathlessness, and a web-based application for assessing the general wellbeing of patients based on the daily questionnaire, notifying people to comply with the regulations, and sending symptoms data to the cloud, are utilized in ECs and THs. Noteworthy, in AAs, body temperature data is based on thermal sensors located on the drones and medical infrared thermometer guns, and then other symptoms are measured after allocating people to ECs and THs.

• 2.Cloud and data center:

With cloud infrastructure, it is possible to gather real-time symptom data from each person in AAs, THs, and DCs and store personal health records. It should be mentioned that the data collection is based on the internet, Bluetooth, and Wi-Fi systems. The use of each way is regarded as the destruction of network connection in AAs. In our study, the data of the symptoms from THs, ECs, and AAs, the data of RIs inventory level from DCs, and data from the PCR team are transferred to the data center.

• 3.Data analysis and decision support system:

The most significant part of the IoT infrastructure is data analysis. The symptom data stored in the data centers is analyzed by Machine Learning (ML) algorithms to detect suspected COVID-19 cases based on the ML approaches proposed by Otoom et al. (2020). Note that the utilization of IoT for the detection of suspected cases is not enough in the aftermath of a disaster because suspected cases should take the PCR test. After analyzing the result of PCR test team, infection rate in AAs and ECs by dividing the total number of individuals in AAs and ECs by the number of infected cases in these centers, respectively. The related parameters used in our mathematical model were $P_1$ and $P_2$. Moreover, our study proposes a novel decision-making system based on the infection rate determined by the mentioned ML approaches and data analysis. This decision system aims to (1) allocate individuals from AAs to THs and ECs in a timely manner; (2) define the best location for DCs; (3) define the number of required vehicles and drones for DCs; and (4) calculate the demand for RIs and distribute them to demand points regarding time and satisfaction. The decision-making system is based on mathematical modeling, which is solved by optimization software, e.g., GAMS and LINDO.

• 4.Testing team

Using a machine learning-based identification algorithm, the testing team performs a PCR test on suspected cases with abnormal symptom data, which is defined by the data analysis section. After defining the results, those results are transmitted to the cloud, and then the data analysis section determines the exact number of infected cases and the infection rate of COVID-19 in ECs and AAs.

• 5.Temporary Hospitals or Quarantine places

This section shoulders the responsibility of gathering vital signs, e.g., body temperature, pulse rate, respiration rate, and blood pressure, from patients who are isolated in THs. Additionally, other data, including gender, age, and incurable diseases, is transmitted with vital signs with tablets allocated to each patient to the cloud and data analysis section. Aside from data transmission, the tablets provide mutually virtual physician-patient communication.

• 6.Medical center

After allocating the infected cases to THs, physicians will monitor the real-time symptom data in THs. Therefore, this integrated system allows physicians to communicate with patients remotely.

• 7.Distribution section

The indispensable decision after transferring people is to distribute the RIs to the used THs and ECs. The proposed decision-making system calculates the exact quantity of required RIs for each demand point in each period. Additionally, DCs will monitor the inventory level of RIs based on scanning the barcode of RIs with the barcode reader and sending the real-time inventory data to the cloud and decision system.

• 8.Operational team

Operational teams will receive the final decision pertaining to the location of DCs, THs, and ECs from the decision support system, and they will institute and equip these points properly with regards to the number of individuals allocated to each center. Note that data transfer is based on the team’s phone and internet.

3.2. The proposed decision support system

In the aftermath of a disaster, the casualties must be allocated to hospitals, RIs should be distributed to ECs, and affected people should be transferred to ECs as soon as possible. However, the COVID-19 outbreak affects the distribution of RIs and the evacuation of people. Detecting infected people in crowds is complicated, and disasters worsen the situation. Until now, no effective medications have been discovered for COVID-19. Thus, isolation and reducing the infection rate of COVID-19 is the only solution in this period. This rate, playing a critical role in our decision system, will be calculated by dividing the total number of individuals by the number of infects cases determined by the proposed IoT framework.

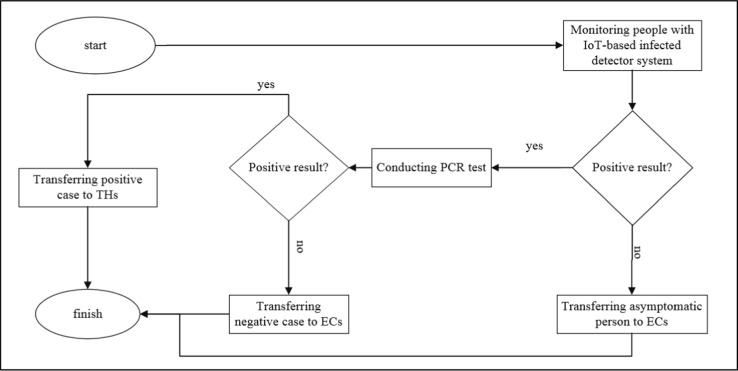
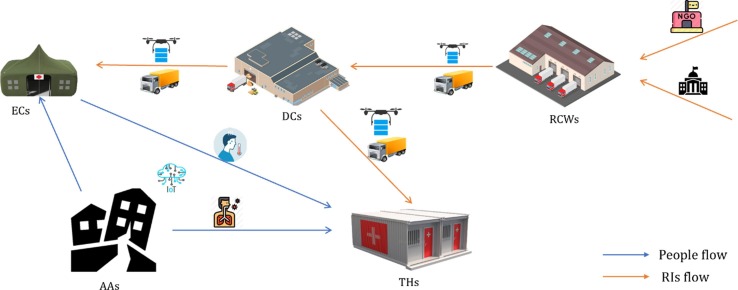
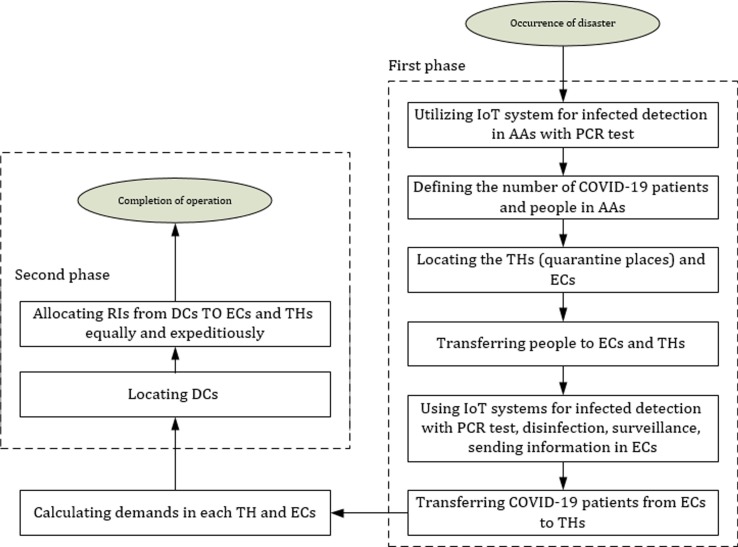
Similar to the situation before the COVID-19 pandemic, the severely wounded patients are transferred to hospitals. Due to the transmission of the virus, people, along with mildly wounded patients, are allocated to ECs and THs according to the allocation guideline shown in Fig. 2 . Unambiguously, testing all people sensitively with a PCR diagnostic kit in the aftermath of a disaster is robustly impossible because it is time-consuming. PCR tests with IoT-based infected detector systems can be taken as a viable solution throughout the period. Among rapid tests, symptomatic individuals should take the PCR test to transfer COVID-19 patients to THs. In contrast, asymptomatic people are transferred to ECs with the accompaniment of symptomatic people who have negative PCR tests. The TH is a place where symptomatic patients are quarantined to prevent the spread of the COVID-19 pandemic amid the earthquake. After transferring people to ECs, they will undergo continuous monitoring based on the proposed IoT-driven system. Aside from patients' allocation, RIs encompassing face masks, sanitizers, hygienic products, and drinkable water should be provided in Relief Collection Warehouses (RCW). Governmental Organizations (GO) and NGOs contribute towards RCWs (Bakhshi et al., 2022). RIs are distributed to DCs, and then they are allocated to ECs and THs according to their needs. Therefore, it is necessary to locate temporary DCs and THs based on cost, distance, time minimization, the increase in people's satisfaction, and fair distribution. Moreover, a heterogeneous fleet of trucks and IoT-based cargo drones are hired to deliver RIs expeditiously. Note that drones and trucks can simultaneously operate in all distributional sections. Therefore, the location-allocation-inventory multi-period, multi-commodity, multi-fleet, and multi-objective IoT-based models are presented in this study. The structure of this network has been depicted in Fig. 3 . The proposed model is the two-phase model illustrated in Fig. 4 . In the first phase, the critical decisions correspond to COVID-19 patients and people transferring, defining their numbers, and determining which ECs are used and which THs are instituted are made. In the second phase, the strategic decisions on the location of DCs and the distribution of RIs equally between selected THs and ECs are made.

Fig. 2.

People allocation guidelines amid the COVID-19 outbreak in AAs and DCs.

Fig. 3.

The considered HRL network.

Fig. 4.

The relevance between two phases of the mathematical model in each period.

3.3. Assumption

The principal assumptions are made for the HRL model:

• •Each period is considered 24 h in this study.
• •The model involves three periods after an earthquake occurred.
• •The capacity and potential location of temporary DCs are defined.
• •The heterogeneous fleets, including cargo drones and trucks, are considered for RIs transportation.
• •RIs are provided by NGOs and GOs, which are collected in RCWs.
• •The number and location of RCWs, AAs, and ECs are known.
• •The heterogeneous fleet can work simultaneously at each period.
• •The distances between RCWs, DCs, ECs, THs, and AAs are known.
• •DCs and THs may be instituted in potential locations.
• •Uncertainties of the model encompass capacities, demands, transportation cost, and inventory holding costs.
• •Six square meters are provided for each individual in ECs
• •The RIs, including drinkable water, sanitizers, and essential items, are delivered to ECs and THs.
• •THs are taken as the quarantine place for COVID-19 patients.
• •The allocation of people in AAs is based on the mentioned guideline.
• •The model is only designed for non-severely wounded patients and impeccable people.

3.4. Proposed mathematical model

The mathematical model is formulated on two levels, and the necessary notations are explained in this regard. The first stage specifies the number of individuals in ECs and THs. Then the demand for RIs in each center is calculated by Eqs (14), (15). Afterward, the second level locates the suitable DCs and distributes RIs.

Set of indices
$j$	Index of ${\mathit{DC}}_{j}j=1,\cdots ,J$
$i$	Index of $\mathit{RCWsi}=1,\cdots ,I$
$p$	Index of relief items $p=1,\cdots ,P$
$h$	Index of $\mathit{THsh}=1,\cdots ,H$
$k$	Index of $\mathit{ECsk}=1,\cdots ,K$
$m$	Index of $\mathit{AAsm}=1,\cdots ,M$
$t$	Index of periods $t=1,\cdots ,T$
$x$	Index of periods $x=1,\cdots ,X$
$s$	Index of scenarios $s=1,\cdots ,S$
$f$	Index of fleet types $f=1,\cdots ,F$
Parameters
${\mathit{IHC}}_{\mathit{pj}}^{}$	Inventory holding cost at ${\mathit{DC}}_j$ for product $p$
${\mathit{ICD}}_j$	Institution cost of ${\mathit{DC}}_j$
${\mathit{ICH}}_h$	Institution cost of ${\mathit{TH}}_h$
${\mathit{TC}}_{\mathit{pf}}^{\mathit{ts}}$	Transportation cost for product $p$ using fleet type $f$ at period $t$(tomans/(km. kg))in scenario $s$
${\mathit{PCS}}_{\mathit{pk}}$	Penalty cost of shortage of product $p$ in ${\mathit{EC}}_k$
${\mathit{PCSu}}_{\mathit{pk}}$	Penalty cost of surplus of product $p$ in ${\mathit{EC}}_k$
$d_{\mathit{ijfs}}$	Distance between ${\mathit{RCW}}_i$ and ${\mathit{DC}}_j$ with fleet type $f$ in scenario $s$
$d_{\mathit{jkfs}}$	Distance between ${\mathit{DC}}_j$ and ${\mathit{EC}}_k$ with fleet type $f$ in scenario $s$
$d_{\mathit{jhfs}}$	Distance between ${\mathit{DC}}_j$ and ${\mathit{TH}}_h$ with fleet type $f$ in scenario $s$
${\mathit{PC}\stackrel{´}{S}}_{\mathit{ph}}$	Penalty cost of shortage of product $p$ in ${\mathit{TH}}_h$
${\mathit{PCSu}}_{\mathit{ph}}$	Penalty cost of surplus of product $p$ in ${\mathit{TH}}_h$
${\mathit{imp}}_{\mathit{pk}}$	Importance of product $p$ at ${\mathit{EC}}_k$
${\mathit{im}\stackrel{´}{p}}_{\mathit{ph}}$	Importance of product $p$ at ${\mathit{TH}}_h$
${\mathit{CapF}}_f$	Capacity of fleet type $f$
${\mathit{Cap}\stackrel{´}{H}}_{\mathit{hs}}$	Capacity of ${\mathit{TH}}_h$ in scenario s
${\mathit{CapD}}_{\mathit{js}}$	Capacity ${\mathit{DC}}_j$ in scenario $s$
${\mathit{CapEC}}_{\mathit{ks}}$	Capacity of ${\mathit{EC}}_k$ in scenario $s$
$M$	Big M
${\mathit{Vol}}_p$	Volume of product $p$
${\mathit{As}}_f$	Average speed of fleet type $f$
${\alpha }_p$	Consumption coefficient of product $p$
${\mathit{PS}}_s$	Probability of occurrence of scenario $s$
${\stackrel{´}{t}}_{\mathit{mhs}}$	Transferring time of patients from ${\mathit{AA}}_m$ to ${\mathit{TH}}_h$ in scenario $s$
$t_{\mathit{mks}}$	Transferring time of patients from ${\mathit{AA}}_m$ to ${\mathit{EC}}_k$ in scenario $s$
${\mathit{MDC}}_s$	Maximum number of distribution centers that can be instituted under scenario s
${\mathit{MNF}}_f$	Maximum number of fleet type f that can be used
$P_1$	infection rate of COVID-19 in AAs
$P_2$	infection rate of COVID-19 in ECs
${\mathit{Op}}_m^{\mathit{ts}}$	Total population in ${\mathit{AA}}_m$ that should be transferred to $\mathit{EC}$ s at period $t$ in scenario $s$
${\mathit{PCO}}_m^{\mathit{ts}}$	Total population in ${\mathit{AA}}_m$ that should be transferred to ${\mathit{TH}}_h$ at period $t$ in scenario $s$
${\mathit{PA}}_m^{\mathit{ts}}$	Population should be evacuated in ${\mathit{AA}}_m$ at period t in scenario $s$
Decision variables
$Q_{\mathit{pjhf}}^{\mathit{ts}}$	Quantity of delivered product p from ${\mathit{DC}}_j$ to ${\mathit{TH}}_h$ using fleet $f$ at period $t$ in scenario $s$
$Q_{\mathit{pijf}}^{\mathit{ts}}$	Quantity of delivered product $p$ from ${\mathit{RCL}}_i$ to ${\mathit{DC}}_j$ using fleet $f$ at period $t$ in scenario $s$
$Q_{\mathit{pjkf}}^{\mathit{ts}}$	Quantity of delivered product $p$ from ${\mathit{DC}}_j$ to ${\mathit{EC}}_k$ using fleet $f$ at period $t$ in scenario $s$
${\mathit{numF}}_{\mathit{fij}}^{\mathit{ts}}$	Number of fleet type $f$ from ${\mathit{RCL}}_i$ to ${\mathit{DC}}_j$ at period $t$ in scenario $s$
${\mathit{num}\stackrel{´}{F}}_{\mathit{fij}}^{\mathit{ts}}$	Number of fleet type $f$ from ${\mathit{DC}}_j$ to ${\mathit{EC}}_k$ at period $t$ in scenario $s$
${\mathit{num}\stackrel{´}{\stackrel{´}{F}}}_{\mathit{fij}}^{\mathit{ts}}$	Number of fleet type $f$ from ${\mathit{DC}}_j$ to ${\mathit{TH}}_h$ at period $t$ in scenario $s$
$I_{\mathit{pj}}^{\mathit{ts}}$	Inventory level of product p in ${\mathit{DC}}_j$ at period $t$ in scenario $s$
${\mathit{TH}}_{\mathit{hs}}$	(Binary variable) = 1, if ${\mathit{TH}}_h$ is opened in scenario $s$; ow = 0
${\mathit{EC}}_{\mathit{ks}}$	(Binary variable) = 1, if ${\mathit{EC}}_k$ is used in scenario $s$; ow = 0
${\mathit{TDC}}_{\mathit{js}}$	(Binary variable) = 1, if ${\mathit{DC}}_j$ is opened in scenario $s$;ow = 0
$Z_{\mathit{phts}}^2$	Surplus amount of product $p$ in ${\mathit{TH}}_h$ at period $t$ in scenario $s$
$Z_{\mathit{phts}}^3$	Shortage amount of product $p$ in ${\mathit{TH}}_h$ at period t in scenario $s$
${\stackrel{´}{Z}}_{\mathit{pkts}}^2$	Surplus amount of product $p$ in ${\mathit{EC}}_k$ at period $t$ in scenario $s$
${\stackrel{´}{Z}}_{\mathit{pkts}}^3$	Shortage amount of product $p$ in ${\mathit{EC}}_k$ at period $t$ in scenario $s$
${\stackrel{´}{P}}_{\mathit{mh}}^{\mathit{ts}}$	Number of symptomatic patients transferred from ${\mathit{AA}}_m$ to ${\mathit{TH}}_h$ at period $t$ in scenario $s$
$P_{\mathit{mk}}^{\mathit{ts}}$	Number of affected people transferred from ${\mathit{AA}}_m$ to ${\mathit{EC}}_k$ at period t in scenario $s$
${\stackrel{´}{\stackrel{´}{p}}}_{\mathit{kh}}^{\mathit{ts}}$	Number of infected cases in ${\mathit{EC}}_k$ detected by IoT system and transferred to ${\mathit{TH}}_h$ at period $t$ in scenario $s$
${\stackrel{´}{\stackrel{´}{\mathit{Pk}}}}_k^{\mathit{xs}}$	Number of people entering in ${\mathit{EC}}_k$ at period $x$ in scenario $s$ from $\mathit{AA}$ s
${\mathit{PC}}_h^{\mathit{xs}}$	Number of people entering in ${\mathit{TH}}_h$ at period $x$ in scenario $s$ from $\mathit{AA}$ s
${\mathit{RQC}}_{\mathit{pkts}}$	Required demand of product $p$ by ${\mathit{EC}}_k$ at period $t$ in scenario $s$
${\mathit{RQH}}_{\mathit{phts}}$	Required demand of product $p$ by ${\mathit{TH}}_h$ at period $t$ in scenario $s$

3.4.1. The first level

$$\mathit{min}{Z}_1=\sum _{h,s}{\mathit{PS}}_s\times \left({\mathit{ICH}}_h\times {\mathit{TH}}_{h,s}\right)$$ (1)

$$\mathit{min}{Z}_2=\sum _s{\mathit{PS}}_s\times \left(\sum _{m,h}{\stackrel{´}{t}}_{\mathit{mhs}}\times {\mathit{TH}}_{\mathit{hs}}+\sum _{m,k}{t}_{\mathit{mks}}\times {\mathit{EC}}_{\mathit{ks}}\right)$$ (2)

St.

$$\sum _{m,t}{\stackrel{´}{p}}_{\mathit{mh}}^{\mathit{ts}}+\sum _{k,t}{\stackrel{´}{p}}_{\mathit{kh}}^{\mathit{ts}}\le \stackrel{\sim }{{\mathit{CapH}}_{\mathit{hs}}}\times {\mathit{TH}}_{\mathit{hs}}\forall h,s$$ (3)

$$\sum _{m,t}{P}_{\mathit{mk}}^{\mathit{ts}}-\sum _{t,h}{\stackrel{´}{p}}_{\mathit{kh}}^{\mathit{ts}}\le \stackrel{\sim }{{\mathit{CapEC}}_{\mathit{ks}}}\times {\mathit{EC}}_{\mathit{ks}}\forall k,s$$ (4)

$${\stackrel{´}{p}}_{\mathit{mh}}^{\mathit{ts}}+{\stackrel{´}{p}}_{\mathit{kh}}^{\mathit{ts}}\le M\times {\mathit{TH}}_{\mathit{hs}}\forall m,h,t,k,s$$ (5)

$$p_{\mathit{mk}}^{\mathit{ts}}\le M\times {\mathit{EC}}_{\mathit{ks}}\forall m,k,t,s$$ (6)

$$\stackrel{\sim }{{\mathit{PCO}}_m^{\mathit{ts}}}={\stackrel{\sim }{\mathit{PA}}}_m^{\mathit{ts}}\times P_1\forall t,m,s$$ (7)

$$\stackrel{\sim }{{\mathit{Op}}_m^{\mathit{ts}}}={\stackrel{\sim }{\mathit{PA}}}_m^{\mathit{ts}}\times \left(1-P_1\right)\forall t,m,s$$ (8)

$$\stackrel{\sim }{{\mathit{Op}}_m^{\mathit{ts}}}=\sum _k{p}_{\mathit{mk}}^{\mathit{ts}}\forall t,m,s$$ (9)

$$\stackrel{\sim }{{\mathit{PCO}}_m^{\mathit{ts}}}=\sum _h{\stackrel{´}{p}}_{\mathit{mh}}^{\mathit{ts}}\forall t,m,s$$ (10)

$$\left(\sum _{x\le t}{\stackrel{´}{\stackrel{´}{\mathit{Pk}}}}_k^{\mathit{xs}}-\sum _h{\stackrel{´}{p}}_{\mathit{kh}}^{t-1,s}\right)\times P_2=\sum _h{\stackrel{´}{\stackrel{´}{p}}}_{\mathit{kh}}^{\mathit{ts}}\forall t,k,s$$ (11)

$${\stackrel{´}{\stackrel{´}{\mathit{Pk}}}}_k^{\mathit{xs}}=\sum _{m,t\le x}{p}_{\mathit{mk}}^{\mathit{ts}}-\sum _{m,t\le x}{p}_{\mathit{mk}}^{t-1,s}\forall x,k,s$$ (12)

$${\mathit{PC}}_h^{\mathit{xs}}=\sum _{m,t\le x}\left({\stackrel{´}{p}}_{\mathit{mh}}^{\mathit{ts}}-{\stackrel{´}{p}}_{\mathit{mh}}^{t-1,s}\right)\forall x,h$$ (13)

$$\left(\sum _{x\le t}{\stackrel{´}{\stackrel{´}{\mathit{Pk}}}}_k^{\mathit{xs}}-\sum _h{p}_{\mathit{kh}}^{\mathit{ts}}\right)\times {\alpha }_p={\mathit{RQH}}_{\mathit{pht}}^{}\forall p,h,t$$ (14)

$$\left(\sum _{x\le t}{\mathit{PC}}_h^{\mathit{xs}}+\sum _k{\stackrel{´}{p}}_{\mathit{kh}}^{\mathit{ts}}\right)\times {\alpha }_p={\mathit{RQC}}_{\mathit{pkt}}^{}\forall p,h,t$$ (15)

$${\stackrel{´}{p}}_{\mathit{mh}}^{\mathit{ts}},p_{\mathit{mk}}^{\mathit{ts}},{\mathit{RQH}}_{\mathit{pht}}^{},{\mathit{RQC}}_{\mathit{pkt}}^{},{\stackrel{´}{\stackrel{´}{\mathit{Pk}}}}_k^{\mathit{xs}},{\mathit{PC}}_h^{\mathit{xs}},{\stackrel{´}{p}}_{\mathit{mh}}^{\mathit{ts}},{\stackrel{´}{\stackrel{´}{p}}}_{\mathit{kh}}^{\mathit{ts}}\ge 0\forall m,k,x,t,h,s$$ (16)

$${\mathit{TH}}_{\mathit{hs}},{\mathit{EC}}_{\mathit{ks}}\in \left\{0,1\right\}\forall k,h,s$$ (17)

The first objective function aims to minimize the institutional cost of temporary hospitals. The second objective function concentrates on the transferring time of patients and people to THs and ECs, respectively. Constraints (3), (4) imply that the number of patients and people allocated to THs and DCs, respectively, must be less than their capacities. Constraint (5) represents that patients in an AA and EC can be transferred to a TH if the TH is instituted. Likewise, people in an AA are allocated to an EC if used in the constraint (6). Eq (8) calculates the number of infected cases in AAs, and other people in AA are assigned to ECs, which is calculated in Eq (7) based on the infection rate defined by the IoT framework. Constraints (9), (10) illustrate the total number of individuals, including patients and people, transferred to each TH and EC. Eqs (11), (12) calculate the number of positive cases detected by IoT and PCR tests in an EC. The number of patients transferred from AAs and DCs to a TH is multiplied by the RI consumption coefficient to calculate the patient's demand in a TH for each RI. Likewise, the people's demand in an EC is computed by multiplying the number of people accommodated in an EC by the consumption coefficient. Eqs. (13), (14), (15) imply the amount of demand in each demand zone. Note that the demand for each TH and EC accumulates by period $t$. Eventually, constraints (16), (17) are related to the problem's decision variables.

3.4.2. The second level

$$\mathit{min}\stackrel{´}{Z_1}=\sum _s{\mathit{PS}}_s\times \left(\left(\sum _{j,p,t}\stackrel{\sim }{\mathit{IH}{C}_{\mathit{pj}}^{}}\times I_{\mathit{pj}}^{\mathit{ts}}\right)+\left(\sum _{f,t,p}\stackrel{\sim }{{\mathit{TC}}_{\mathit{fp}}^{\mathit{ts}}}\times \left(\sum _{i,j}{d}_{\mathit{ijfs}}\times Q_{\mathit{pijf}}^{\mathit{ts}}+\sum _{j,k}{d}_{\mathit{jkfs}}\times Q_{\mathit{pjkf}}^{\mathit{ts}}+\sum _{j,h}{d}_{\mathit{jhfs}}\times Q_{\mathit{pjhf}}^{\mathit{ts}}\right)\right)+\left(\sum _j{\mathit{ICD}}_j\times {\mathit{TDC}}_{\mathit{js}}\right)+\left(\sum _{p,k}{\mathit{imp}}_{\mathit{pk}}\times {\mathit{PCS}}_{\mathit{pk}}\times \sum _t{Z}_{\mathit{pkts}}^3+\sum _{p,h}{\stackrel{´}{\mathit{imp}}}_{\mathit{ph}}\times {\stackrel{´}{\mathit{PCS}}}_{\mathit{ph}}\times \sum _t{\stackrel{´}{Z}}_{\mathit{phts}}^3\right)+\left(\sum _{p,k}{\mathit{PCSu}}_{\mathit{pk}}\times \sum _t{Z}_{\mathit{pkts}}^2+\sum _{p,h}{\stackrel{´}{\mathit{PCSu}}}_{\mathit{ph}}\times \sum _t{\stackrel{´}{Z}}_{\mathit{phts}}^2\right)\right)$$ (18)

$$\mathit{min}\stackrel{´}{Z_2}={\mathit{max}}_{p,k,t,s}\left\{{\mathit{imp}}_{\mathit{pk}}\times ({\mathit{RQC}}_{\mathit{pk}}^{\mathit{ts}}-\sum _{j,f}{Q}_{\mathit{pjkf}}^{\mathit{ts}})\right\}+{\mathit{max}}_{p,h,t,s}\left\{{\mathit{imp}}_{\mathit{ph}}\times ({\mathit{RQH}}_{\mathit{ph}}^{\mathit{ts}}-\sum _{j,f}{Q}_{\mathit{pjhf}}^{\mathit{ts}})\right\}$$ (19)

$$\mathit{min}\stackrel{´}{Z_3}={\sum }_s{\mathit{PS}}_s\times \left(\sum _{i,j,f,t}\left(\frac{d_{\mathit{ijfs}}}{{\mathit{As}}_f}\right)\times {\mathit{numF}}_{\mathit{fij}}^{\mathit{ts}}+\sum _{j,k,f,t}\left(\frac{d_{\mathit{jkfs}}}{{\mathit{As}}_f}\right)\times {\mathit{num}\stackrel{´}{F}}_{\mathit{fjk}}^{\mathit{ts}}+\sum _{j,hf,t}\left(\frac{d_{\mathit{jhfs}}}{{\mathit{As}}_f}\right)\times {\mathit{num}\stackrel{´}{\stackrel{´}{F}}}_{\mathit{fjh}}^{\mathit{ts}}\right)$$ (20)

(27)(26)(29)St.

$$\sum _p{I}_{\mathit{pj}}^{\mathit{ts}}\times {\mathit{vol}}_p\le \stackrel{\sim }{{\mathit{CapD}}_{\mathit{js}}}\times {\mathit{TDC}}_{\mathit{js}}\forall j,t,s$$ (21)

$$\sum _p{Q}_{\mathit{pijf}}^{\mathit{ts}}\times {\mathit{vol}}_p\le \stackrel{\sim }{{\mathit{CapF}}_f}\times {\mathit{numF}}_{\mathit{fij}}^{\mathit{ts}}\forall f,i,j,t,s$$ (22)

$$\sum _p{Q}_{\mathit{pjkf}}^{\mathit{ts}}\times {\mathit{vol}}_p\le \stackrel{\sim }{{\mathit{CapF}}_f}\times {\mathit{num}\stackrel{´}{F}}_{\mathit{fjk}}^{\mathit{ts}}\forall f,j,k,t,s$$ (23)

$$\sum _p{Q}_{\mathit{pjhf}}^{\mathit{ts}}\times {\mathit{vol}}_p\le \stackrel{\sim }{{\mathit{CapF}}_f}\times {\mathit{num}\stackrel{´}{\stackrel{´}{F}}}_{\mathit{fjh}}^{\mathit{ts}}\forall f,j,h,t,s$$ (24)

$$I_{\mathit{pj}}^{t-1,s}+\sum _{i,f}{Q}_{\mathit{pijf}}^{\mathit{ts}}-\sum _{h,f}{Q}_{\mathit{pjhf}}^{\mathit{ts}}-\sum _{h,f}{Q}_{\mathit{pjkf}}^{\mathit{ts}}=I_{\mathit{pj}}^{\mathit{ts}}\forall p,t,j,s$$ (25)

$$\sum _{f,p}{Q}_{\mathit{pjhf}}^{\mathit{ts}}\le M\times {\mathit{TH}}_{\mathit{hs}}\forall j,h,t,s$$ (26)

$$\sum _{f,p}{Q}_{\mathit{pijf}}^{\mathit{ts}}\le M\times {\mathit{TDC}}_{\mathit{js}}\forall i,j,t,s$$ (27)

$$\sum _{p,f}{Q}_{\mathit{pjkf}}^{\mathit{ts}}\le M\times {\mathit{TDC}}_{\mathit{js}}\forall k,j,t,s$$ (28)

$$\sum _{f,j}{Q}_{\mathit{pjkf}}^{\mathit{ts}}-{\mathit{RQC}}_{\mathit{pkts}}=Z_{\mathit{pkts}}^2-Z_{\mathit{pkts}}^3\forall p,k,t,s$$ (29)

$$\sum _{f,j}{Q}_{\mathit{pjhf}}^{\mathit{ts}}-{\mathit{RQH}}_{\mathit{phts}}={\stackrel{´}{Z}}_{\mathit{phts}}^2-{\stackrel{´}{Z}}_{\mathit{phts}}^3\forall p,h,t,s$$ (30)

$$Z_{\mathit{pkts}}^3\le {\mathit{RQC}}_{\mathit{pkts}}-\sum _{f,j}{Q}_{\mathit{pjkf}}^{\mathit{ts}}\forall p,k,t,s$$ (31)

$${\stackrel{´}{Z}}_{\mathit{phts}}^3\le {\mathit{RQH}}_{\mathit{phts}}-\sum _{f,j}{Q}_{\mathit{pjhf}}^{\mathit{ts}}\forall p,h,t,s$$ (32)

$$Z_{\mathit{pkts}}^2\ge \sum _{f,j}{Q}_{\mathit{pjkf}}^{\mathit{ts}}-{\mathit{RQC}}_{\mathit{pkts}}\forall p,k,t,s$$ (33)

$${\stackrel{´}{Z}}_{\mathit{phts}}^2\ge \sum _{f,j}{Q}_{\mathit{pjhf}}^{\mathit{ts}}-{\mathit{RQH}}_{\mathit{phts}}\forall p,h,t,s$$ (34)

$$\sum _{i,j}{\mathit{numF}}_{\mathit{fij}}^{\mathit{ts}}+\sum _{j,k}{\mathit{num}\stackrel{´}{F}}_{\mathit{fjk}}^{\mathit{ts}}+\sum _{j,h}{\mathit{num}\stackrel{´}{\stackrel{´}{F}}}_{\mathit{fjh}}^{\mathit{ts}}\le {\mathit{MNF}}_f\forall t,s,f$$ (35)

$$\sum _j{\mathit{TDC}}_{j,s}\le {\mathit{MDC}}_s\forall s$$ (36)

$$Q_{\mathit{pijf}}^{\mathit{ts}},Q_{\mathit{pjkf}}^{\mathit{ts}},Q_{\mathit{pjhf}}^{\mathit{ts}},{\mathit{numF}}_{\mathit{fij}}^{\mathit{ts}},{\mathit{num}\stackrel{´}{F}}_{\mathit{fjh}}^{\mathit{ts}},{\mathit{num}\stackrel{´}{\stackrel{´}{F}}}_{\mathit{fjh}}^{\mathit{ts}},I_{\mathit{pj}}^{\mathit{ts}},Z_{\mathit{phts}}^2,Z_{\mathit{phts}}^3,{\stackrel{´}{Z}}_{\mathit{pkts}}^2,{\stackrel{´}{Z}}_{\mathit{pkts}}^3\ge 0\forall p,k,t,i,h,j,f,s$$ (37)

$${\mathit{TDC}}_{j,s}\in \left\{0,1\right\}\forall j,s$$ (38)

The objective function (18) consists of five main sections. The first term aims to minimize the inventory holding cost of RIs stored in temporary DCs. The transportation costs of RIs between RCWs, DCs, ECs, and THs are considered in the second term, taking into account distances and RIs quantities. The third part of this objective function is related to institution costs of THs and temporary DCs. The fourth and fifth terms aim to penalize the shortage and surplus RIs in THs and ECs, respectively. To increase the affected people's satisfaction and equality in RI distribution, the first term of the objective function (19) reduces the maximum difference between people's demand in each ECs and the amount of RIs shipped from DCs to ECs. Likewise, the other term does a similar way for patients in THs. It is worth noticing that the importance level of RIs is incorporated to distribute RIs being in dire need. The objective function (20) minimizes the delivery time of RIs carried by fleet type f. Time is obtained by dividing distances by the average speed of vehicle type f. That is to say, Eq (20) aims to minimize the number of fleets with higher delivery times.

Constraint (21) guarantees that the volume of RIs stored in the DC is less than the DC's capacity. Constraints (22), (23), (24) state the capacity of RIs transportation from RCW to DC, DC to TH, and DC to EC using fleet type f, respectively. Constraint (25) represents the inventory balance at the DC. Constraint (26) implies that RIs can be distributed to the TH on the condition that the TH is instituted in the location h. Constraint (27) states that RIs are delivered from RCWs to the DC when the DC is opened in location j. Constraint (28) represents that the RIs transfer from DCs to the EC when the DC in location j is opened. Constraints (29), (30) express the balancing equations for the amount of shortage and surplus of RIs in ECs and THs, respectively. Constraints (31), (32) illustrate the upper bound of RI's shortage in demand zones, and whether the lower bound of RI's surplus is represented in constraints (33), (34). Constraint (35) implies that the total number of fleets at each period in the supply chain network does not exceed the maximum number. Constraint (36) implies that the instituted DCs must be lower than the maximum number. Eventually, constraints (37), (38) are related to the problem's decision variables.

3.5. Linearization

In order to linearize the objective function (19), it can be converted to the objective function (39) and two constraints (40), (41) by two free variables proposed in the following:

$$\mathit{min}\stackrel{´}{Z_2}=y_1+y_2$$ (39)

s.t.

$$y_1\ge ({\mathit{imp}}_{\mathit{pk}}\times ({\mathit{RQC}}_{\mathit{pk}}^{\mathit{ts}}-\sum _{j,f}{Q}_{\mathit{pjkf}}^{\mathit{ts}}))\forall p,k,t,s$$ (40)

$$y_2\ge ({\mathit{imp}}_{\mathit{ph}}\times ({\mathit{RQH}}_{\mathit{ph}}^{\mathit{ts}}-\sum _{j,f}{Q}_{\mathit{pjhf}}^{\mathit{ts}}))\forall p,h,t,s$$ (41)

3.6. The proposed credibility-based fuzzy chance-constrained programming model

Regarding the discrepancies between Fuzzy Mathematical Programming and the stochastic approach, stochastic modeling uses probabilistic modeling and theory to cope with uncertainty. Hence, a known probability distribution for the uncertain parameters is required in this approach. In contrast, FMP deploys the Fuzzy Set Theory to tackle uncertain data, which is not stochastic. In other words, the uncertain parameters do not have a specific probability distribution (Zadeh, 1996). Furthermore, the major benefit of FMP is that it models a problem with linguistic variables instead of exact numerical variables to illustrate the imprecise data (a soft approach to tackle uncertainty), and it considers these parameters as fuzzy numbers (Ross, 2005). Similar to FMP, the probability distribution of uncertain parameters is not defined in robust optimization. However, these variables belong to an uncertainty set and they do not have an exact central value (Ghaffarinasab, 2022).

In our case study, the distribution of uncertain parameters is not well-defined, and we encounter imprecise data with no distributional information. Many parameters are defined by experts and officials of humanitarian organizations in the aftermath of a disaster, which are based on linguistics and their perception. For instance, to calculate the imprecise transportation cost after an earthquake, experts assess the roads by aerial pictures and define the price based on the road demolition linguistically (e.g., if the roads are destroyed badly, the transportation cost is around 1$, otherwise it is 0.75$).

Regarding the uncertain ambiance prevailing in the aftermath of disasters, some parameters corresponding to the demand, supply, distribution, and network connection are considered uncertain in our study. Therefore, the input parameters involving inventory holding cost, transportation cost, the capacity of DCs, and the number of individuals residing in each AA that affects the demand of RIs quantity are considered fuzzy numbers. Regarding the severity of disasters, it is possible that some distribution centers or parts of them cannot be utilized. Hence, uncertainty in capacity of DCs and inventory holding cost make the model real-life. Also, Transportation costs may be volatile by the destruction of roads and fluctuation in the gasoline price because many fuel suppliers may fall into disuse. Additional information regarding the ambiguities of many of these parameters can be seen in Sarma et al., 2019, Torabi et al., 2018.

The reasons for hiring FCCP approach are presented in the following: (Pishvaee et al., 2012).

• •In general, this method is a computationally efficient FMP depending on mathematical concepts, e.g., credibility measure and expected value.
• •It can support all kinds of fuzzy numbers, including triangular, trapezoidal, and pentagonal fuzzy numbers.
• •At least defined confidence levels, FCCP allows the decision-maker to meet those chance constraints.
• •FCCP uses the credibility measure instead of possibility and necessity measures, which allow decision-makers to consider both optimistic and pessimistic views concurrently. In other words, a fuzzy event may fail even if its possibility hits 1 and happen even if its necessity equals 0. The fuzzy event must happen if its credibility is 1, and fail to happen if its credibility equals 0, though.”

Assume $\stackrel{\sim }{\vartheta }$ is a fuzzy number defined by three prominent value as $\stackrel{\sim }{\vartheta }=\left({\vartheta }_{(1)},{\vartheta }_{(2)},{\vartheta }_{(3)}\right)$, $\mu \left(x\right)$ is the membership function, and $r$ is a real number. The credibility measure can be defined as below like Liu & Liu (2002).

$$Cr\left\{\stackrel{\sim }{\vartheta }\le r\right\}=\frac{1}{2}\left({\sup }_{x\le r}\mu \left(x\right)+1-{\sup }_{x>r}\mu \left(x\right)\right)=\frac{1}{2}\left(Pos\left\{\stackrel{\sim }{\vartheta }\le r\right\}+Nec\left\{\stackrel{\sim }{\vartheta }\le r\right\}\right)$$ (42)

Noteworthy, the FCCP utilized possibility and necessity measures simultaneously called the average of both measures. Additionally, the expected value of $\stackrel{\sim }{\vartheta }$ can be calculated as follows using credibility measure.

$$E\left[\stackrel{\sim }{\vartheta }\right]={\int }_0^{\infty }Cr\left\{\stackrel{\sim }{\vartheta }\ge r\right\}dr-{\int }_{-\infty }^{0}Cr\left\{\stackrel{\sim }{\vartheta }\le r\right\}dr$$ (43)

Based on Eq. (43) and credibility measure functions (44), (45) the expected value of $\stackrel{\sim }{\vartheta }$ is $\left({\vartheta }_{(1)}+2\times {\vartheta }_{(2)}+{\vartheta }_{(3)}\right)/4$.

$$Cr\left\{\stackrel{\sim }{\vartheta }\le r\right\}\left\{\begin{array}{c}\genfrac{}{}{0.0pt}{}{0,r\in \left(-\infty ,{\vartheta }_{\left(1\right)}\right)}{\frac{r-{\vartheta }_{\left(1\right)}}{2\left({\vartheta }_{\left(2\right)}-{\vartheta }_{\left(1\right)}\right)},r\in \left({\vartheta }_{\left(1\right)},{\vartheta }_{\left(2\right)}\right)}\\ \genfrac{}{}{0.0pt}{}{\frac{r-2{\vartheta }_{\left(2\right)}+{\vartheta }_{\left(3\right)}}{2\left({\vartheta }_{\left(3\right)}-{\vartheta }_{(2)}\right)},r\in \left({\vartheta }_{\left(2\right)},{\vartheta }_{\left(3\right)}\right)}{1,r\in \left({\vartheta }_{\left(3\right)},+\infty \right)}\end{array}\right)$$ (44)

$$Cr\left\{\stackrel{\sim }{\mathrm{\xi }}\ge r\right\}\left\{\begin{array}{c}\genfrac{}{}{0.0pt}{}{1,r\in (-\infty ,{\vartheta }_{(1)})}{\frac{2{\vartheta }_{\left(2\right)}-{\vartheta }_{\left(1\right)}-r}{2\left({\vartheta }_{\left(2\right)}-{\vartheta }_{\left(1\right)}\right)},r\in ({\vartheta }_{(1)},{\vartheta }_{\left(2\right)})}\\ \genfrac{}{}{0.0pt}{}{\frac{{\vartheta }_{(3)}-r}{2\left({\vartheta }_{\left(3\right)}-{\vartheta }_{(2)}\right)},r\in ({\vartheta }_{\left(2\right)},{\vartheta }_{(3)})}{0,r\in ({\vartheta }_{(3)},+\infty )}\end{array}\right)$$ (45)

Also, it can be calculated if $\stackrel{\sim }{\vartheta }$ is a triangular fuzzy number and $\omega >0.5$ then:

$$Cr\left\{\stackrel{\sim }{\vartheta }\le r\right\}\ge \omega \iff r\ge \left(2-2\omega \right){\vartheta }_2+\left(2\omega +1\right){\vartheta }_3$$ (46)

$$Cr\left\{\stackrel{\sim }{\vartheta }\ge r\right\}\ge \omega \iff r\ge \left(2-2\omega \right){\vartheta }_2+\left(2\omega +1\right){\vartheta }_1$$ (47)

Eqs. (46), (47) can be deployed to convert the fuzzy constraint to crisp ones (Zhu & Zhang, 2009).

Based on Pishvaee et al. (2012), the hybrid approach of FCCP is embraced because using only expected values to make a crisp model makes the optimization simpler, but it does not consider control on the confidence level. However, considering credibility-based measures for objectives and constraints may increase the number of constraints and complexity of the model, it needs the ideal solution for each objective. Hence, hybrid models are hired to convert uncertain objective functions with expected values and chance constraints with credibility measures into a crisp model. It does not increase the number of constraints and does not require additional information, e.g., confidence level and ideal solution. According to the descriptions mentioned above, the proposed FCCP can be formulated for this HRL problem.

3.6.1. The first level of the fuzzy model

$$\mathit{min}{Z}_1,Z_2$$

St.

Constraints (5), (6), (7), (8), (11), (12), (13), (14), (15), (16), (17) and

$$Cr\left\{\sum _{m,t}{\stackrel{´}{p}}_{\mathit{mh}}^{\mathit{ts}}+\sum _{k,t}{\stackrel{´}{\stackrel{´}{p}}}_{\mathit{kh}}^{\mathit{ts}}\le \stackrel{\sim }{{\mathit{CapH}}_{\mathit{hs}}}\times {\mathit{TH}}_{\mathit{hs}}\right\}\ge {\alpha }_h\forall h,s$$

$$Cr\left\{\sum _{m,t}{P}_{\mathit{mK}}^{\mathit{ts}}-\sum _{h,t}{\stackrel{´}{\stackrel{´}{p}}}_{\mathit{kh}}^{\mathit{ts}}\le \stackrel{\sim }{{\mathit{CapEC}}_{\mathit{ks}}}\times {\mathit{EC}}_{\mathit{ks}}\right\}\ge \stackrel{´}{{\alpha }_h}\forall k,s$$

$$Cr\left\{\stackrel{\sim }{{\mathit{Op}}_m^{\mathit{ts}}}=\sum _k{p}_{\mathit{mk}}^{\mathit{ts}}\right\}\ge {\gamma }_m\forall t,m,s$$

$$Cr\left\{\stackrel{\sim }{{\mathit{PCO}}_m^{\mathit{ts}}}=\sum _h{\stackrel{´}{p}}_{\mathit{mh}}^{\mathit{ts}}\right\}\ge {\mu }_m\forall t,m,s$$

3.6.2. The second level of the fuzzy model

$$\mathit{min}\stackrel{´}{Z_1}=\sum _s{\mathit{PS}}_s\times \left(\left(\sum _{j,p,t}IH{C}_{\mathit{pj}}^t\times I_{\mathit{pj}}^{\mathit{ts}}\right)+\left(\sum _{f,t}E\left[{\mathit{TC}}_f^{\mathit{ts}}\right]\times \left(\sum _{i,j}{d}_{\mathit{ijfs}}\times Q_{\mathit{pijf}}^{\mathit{ts}}+\sum _{j,k}{d}_{\mathit{jkfs}}\times Q_{\mathit{pjkf}}^{\mathit{ts}}+\sum _{j,h}{d}_{\mathit{jhfs}}\times Q_{\mathit{pjhf}}^{\mathit{ts}}\right)\right)+\left(\sum _{j}E\left[{\mathit{ICD}}_j\right]\times {\mathit{TDC}}_{\mathit{js}}\right)+\left(\sum _{p,k}{\mathit{imp}}_{\mathit{pk}}\times {\mathit{PCS}}_{\mathit{pk}}\times \sum _t{Z}_{\mathit{pkts}}^3+\sum _{p,h}{\stackrel{´}{\mathit{imp}}}_{\mathit{ph}}\times {\stackrel{´}{\mathit{PCS}}}_{\mathit{ph}}\times \sum _t{\stackrel{´}{Z}}_{\mathit{phts}}^3\right)+\left(\sum _{p,k}{\mathit{PCSu}}_{\mathit{pk}}\times \sum _t{Z}_{\mathit{pkts}}^2+\sum _{p,h}{\stackrel{´}{\mathit{PCSu}}}_{\mathit{ph}}\times \sum _t{\stackrel{´}{Z}}_{\mathit{phts}}^2\right)\right)$$

$$\mathit{min}\stackrel{´}{Z_2},\stackrel{´}{Z_3}$$

St.

Constraints (25), (26), (27), (28), (29), (30), (31), (32), (33), (34), (35), (36), (37), (38) and

$$Cr\left\{\sum _p{I}_{\mathit{pj}}^{\mathit{ts}}\times {\mathit{vol}}_p\le \stackrel{\sim }{{\mathit{CapD}}_{\mathit{js}}}\times {\mathit{TDC}}_{\mathit{js}}\right\}\ge {\ddot{\alpha }}_j\forall j,t,s$$

$$\begin{array}{c}Cr\left\{{\sum }_p{Q}_{\mathit{pijf}}^{\mathit{ts}}\times {\mathit{vol}}_p\le \stackrel{\sim }{{\mathit{CapF}}_f}\times {\mathit{numF}}_{\mathit{fij}}^{\mathit{ts}}\right\}\ge {\beta }_f\forall f,i,j,t,s\\ Cr\left\{{\sum }_p{Q}_{\mathit{pjkf}}^{\mathit{ts}}\times {\mathit{vol}}_p\le \stackrel{\sim }{{\mathit{CapF}}_f}\times {\mathit{num}\stackrel{´}{F}}_{\mathit{fjk}}^{\mathit{ts}}\right\}\ge \stackrel{´}{{\beta }_f}\forall f,j,k,t,s\\ Cr\left\{{\sum }_p{Q}_{\mathit{pjhf}}^{\mathit{ts}}\times {\mathit{vol}}_p\le \stackrel{\sim }{{\mathit{CapF}}_f}\times {\mathit{num}\stackrel{´}{\stackrel{´}{F}}}_{\mathit{fjh}}^{\mathit{ts}}\right\}\ge \stackrel{´}{\stackrel{´}{{\beta }_f}}\forall f,j,h,t,s\end{array}$$

Based on Eqs. (46), (47) and expected value formula, the credibility-based model can be converted to the crisp model.

3.6.3. The first level of the crisp model

$$\mathit{min}{Z}_1,Z_2$$

St.

Constraints (5), (6), (7), (8), (11), (12), (13), (14), (15), (16), (17) and

$$\sum _{m,t}{\stackrel{´}{p}}_{\mathit{mh}}^{\mathit{ts}}+\sum _{k,t}{\stackrel{´}{p}}_{\mathit{kh}}^{\mathit{ts}}\le \left[{\left(2{\alpha }_h-1\right)CapH}_{h\left(1\right)s}+\left(2-2{\alpha }_h\right){\mathit{CapH}}_{h\left(2\right)s}\right]\times {\mathit{TH}}_{\mathit{hs}}\forall h,s$$

$$\sum _{m,t}{\mathrm{P}}_{\mathit{mk}}^{\mathit{ts}}-\sum _{h,t}{\stackrel{´}{p}}_{\mathit{kh}}^{\mathit{ts}}\le \left[{\left(2\stackrel{´}{{\alpha }_h}-1\right)CapEC}_{k(1)s}+\left(2-2\stackrel{´}{{\alpha }_h}\right){\mathit{CapEC}}_{k(2)s}\right]\times {\mathit{EC}}_{\mathit{ks}}\forall k,s$$

$$\left(2{\gamma }_m-1\right){\mathit{Op}}_{m(1)}^{\mathit{ts}}+\left(2-2{\gamma }_m\right){\mathit{Op}}_{m(2)}^{\mathit{ts}}\le \sum _k{p}_{\mathit{mk}}^{\mathit{ts}}\forall t,m$$

$$\left(2{\gamma }_m-1\right){\mathit{Op}}_{m(3)}^{\mathit{ts}}+\left(2-2{\gamma }_m\right){\mathit{Op}}_{m(2)}^{\mathit{ts}}\ge \sum _k{p}_{\mathit{mk}}^{\mathit{ts}}\forall t,m,s$$

$$\left(2{\mu }_m-1\right){\mathit{PCO}}_{m(1)}^{\mathit{ts}}+\left(2-2{\mu }_m\right){\mathit{PCO}}_{m(2)}^{\mathit{ts}}\le \sum _h{\stackrel{´}{p}}_{\mathit{mh}}^t\forall t,m,s$$

$$\left(2{\mu }_m-1\right){\mathit{PCO}}_{m(3)}^{\mathit{ts}}+\left(2-2{\mu }_m\right){\mathit{PCO}}_{m(2)}^{\mathit{ts}}\ge \sum _h{\stackrel{´}{p}}_{\mathit{mh}}^t\forall t,m,s$$

3.6.4. The second level of the crisp model

$$\mathit{min}\stackrel{´}{Z_1}=\sum _s{\mathit{PS}}_s\times \left(\left(\sum _{j,p,t}IH{C}_{\mathit{pj}}^{}\times I_{\mathit{pj}}^{\mathit{ts}}\right)+\sum _{p,f,t}\left(\frac{{\mathit{TC}}_{\mathit{pf}(1)}^{\mathit{ts}}{+2\bullet TC}_{\mathit{pf}(2)}^{\mathit{ts}}+{\mathit{TC}}_{\mathit{pf}(3)}^{\mathit{ts}}}{4}\right)\times \left(\sum _{i,j}{d}_{\mathit{ijfs}}\times Q_{\mathit{pijf}}^{\mathit{ts}}+\sum _{j,k}{d}_{\mathit{jkfs}}\times Q_{\mathit{pjkf}}^{\mathit{ts}}+\sum _{j,h}{d}_{\mathit{jhfs}}\times Q_{\mathit{pjhf}}^{\mathit{ts}}\right)+\left(\sum _j\left(\frac{{\mathit{ICD}}_{j(1)}+{2\bullet ICD}_{j(2)}+{\mathit{ICD}}_{j(3)}}{4}\right)\times {\mathit{TDC}}_{\mathit{js}}\right)+\left(\sum _{p,k}{\mathit{imp}}_{\mathit{pk}}\times {\mathit{PCS}}_{\mathit{pk}}\times \sum _t{Z}_{\mathit{pkts}}^3+\sum _{p,h}{\stackrel{´}{\mathit{imp}}}_{\mathit{ph}}\times {\stackrel{´}{\mathit{PCS}}}_{\mathit{ph}}\times \sum _t{\stackrel{´}{Z}}_{\mathit{phts}}^3\right)+\left(\sum _{p,k}{\mathit{PCSu}}_{\mathit{pk}}\times \sum _t{Z}_{\mathit{pkts}}^2+\sum _{p,h}{\stackrel{´}{\mathit{PCSu}}}_{\mathit{ph}}\times \sum _t{\stackrel{´}{Z}}_{\mathit{phts}}^2\right)\right)$$

$$\mathit{min}\stackrel{´}{Z_2},\stackrel{´}{Z_3}$$

St.

Constraints (25), (26), (27), (28), (29), (30), (31), (32), (33), (34), (35), (36), (37), (38) and

$$\sum _p{I}_{\mathit{pj}}^{\mathit{ts}}\times {\mathit{vol}}_p\le \left[{\left(2{\alpha }_j-1\right)CapD}_{j(1)s}+\left(2-2{\alpha }_j\right){\mathit{CapD}}_{j(2)s}\right]\times {\mathit{TDC}}_{\mathit{js}}\forall j,t,s$$

$$\begin{array}{c}{\sum }_p{Q}_{\mathit{pijf}}^{\mathit{ts}}\times {\mathit{vol}}_p\le \left[{\left(2{\beta }_f-1\right)CapF}_{f\left(1\right)}+\left(2-2{\beta }_f\right){\mathit{CapF}}_{f\left(2\right)}\right]\times {\mathit{numF}}_{\mathit{fij}}^t\forall f,i,j,t,s\\ {\sum }_p{Q}_{\mathit{pjkf}}^{\mathit{ts}}\times {\mathit{vol}}_p\le \left[{\left(2\stackrel{´}{{\beta }_f}-1\right)CapF}_{f\left(1\right)}+\left(2-2\stackrel{´}{{\beta }_f}\right){\mathit{CapF}}_{f\left(2\right)}\right]\times {\mathit{num}\stackrel{´}{F}}_{\mathit{fjk}}^{\mathit{ts}}\forall f,j,k,t,s\\ {\sum }_p{Q}_{\mathit{pjhf}}^{\mathit{ts}}\times {\mathit{vol}}_p\le \left[{\left(2\stackrel{´}{\stackrel{´}{{\beta }_f}}-1\right)CapF}_{f\left(1\right)}+\left(2-2\stackrel{´}{\stackrel{´}{{\beta }_f}}\right){\mathit{CapF}}_{f\left(2\right)}\right]\times {\mathit{num}\stackrel{´}{\stackrel{´}{F}}}_{\mathit{fjh}}^{\mathit{ts}}\forall f,j,h,t,s\end{array}$$

It should be assumed in the model mentioned above, the confidence level in chance constraints should be met by more than 0.5.

4. Solution method

The proposed two-phase model is a multi-objective linear model. There are several methods in the literature to convert multi-objective functions to single-objective functions. To deal with the multi-objective function, we use the LP-metric method in this study for both phases. The LP-metric technique aims to minimize the deviation (distance) of objective functions from the ideal solution. This method was elaborated clearly in the study proposed by Bagheri and Bashiri (2013).

$$\mathit{LP}={\{{\sum _{y=1}^Y{w}_j\times [\frac{f_i(x^{\ast j})-f_i(x)}{f_i(x^{\ast j})-f_i({\overline{x}}^j)}]}^p\}}^{1/p}$$ (48)

First, the optimal value or ideal solution, considered as $f_i(x^{\ast j})$, (in this study, the minimum values are calculated) for each objective function must be calculated separately. Afterward, the anti-ideal solution, considered as $f_i({\overline{x}}^j)$, (the maximum values are calculated) must be calculated. Also, the obtained values should be placed in Eq (48). In order to minimize derivations from the ideal solution, Eq (48) should be minimized. Note that, wj represents the importance (weight) of each objective function. Moreover, p emphasizes the deviation. It should be noted that all calculations are conducted by GAMS 28.2 with a LINDO solver. Additionally, a laptop with a 2.71 GHz processor and 4 GB of internal memory is utilized.

5. Case study

5.1. Case description

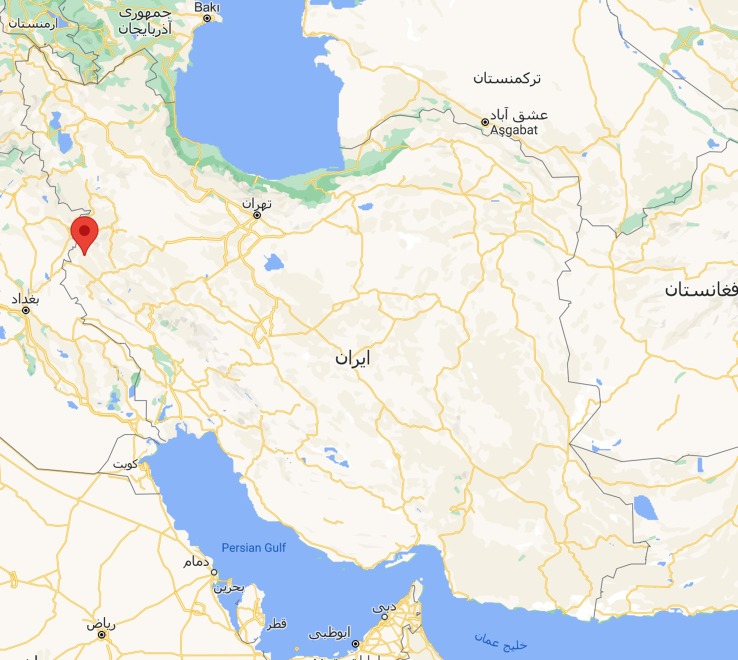
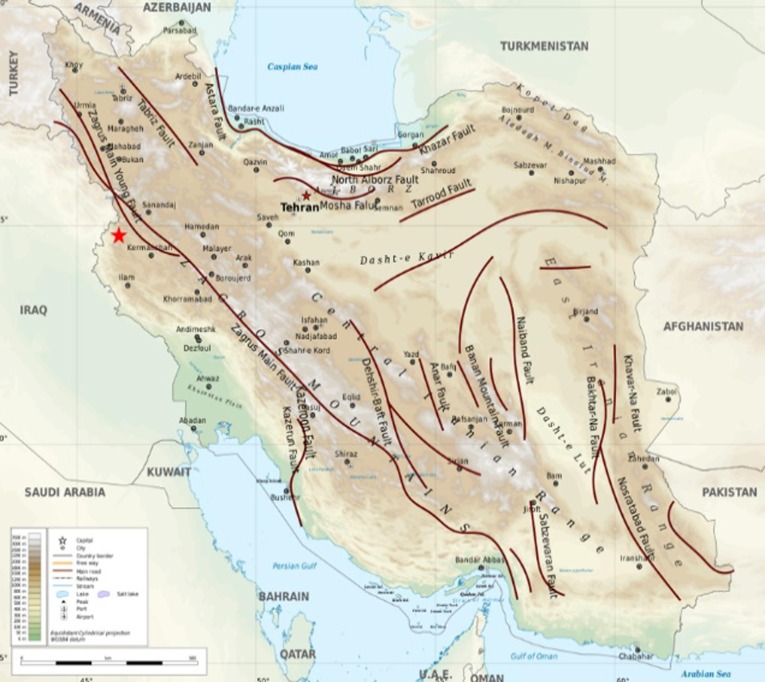
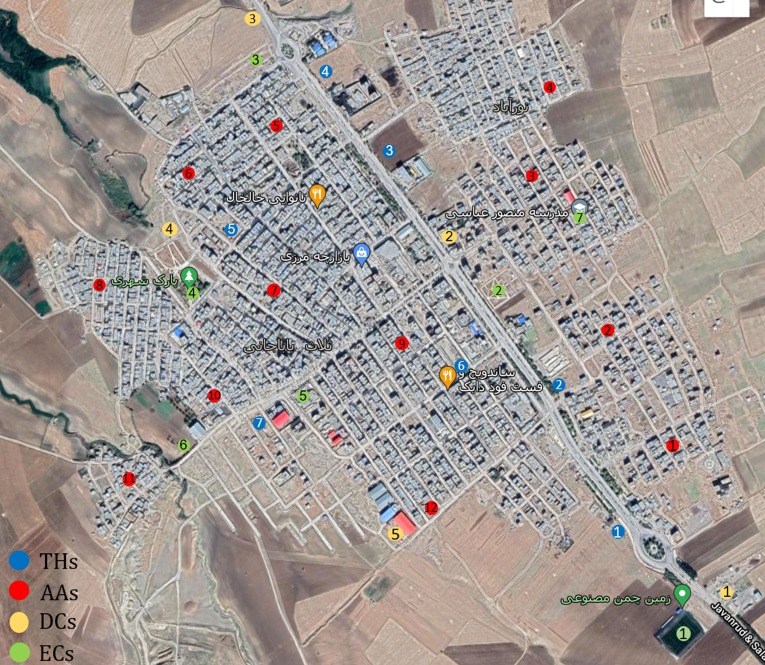
As mentioned above, the proposed model has two interconnected phases, evacuating people from AAs and distributing RIs equally regarding the COVID-19 outbreak. In order to model and solve the problem, the data is collected from Salas-e-Babajani city, located in Kermanshah province, in the east of Iran. The exact location of this city in Iran is depicted in Fig. 5 . This city is selected because of the occurrence of numerous severe earthquakes in recent years, explained in the following. Also, this city is surrounded by two faults, increasing the earthquake dangers, as shown in Fig. 6 .

Fig. 5.

Location of Salas Babajani city.

Fig. 6.

Iran fault lines.

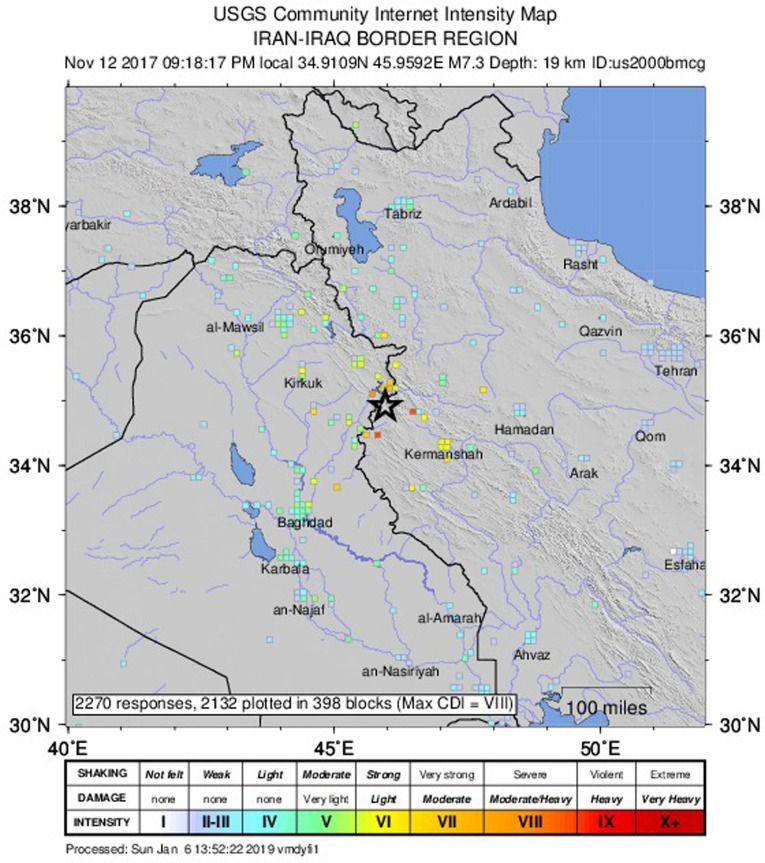
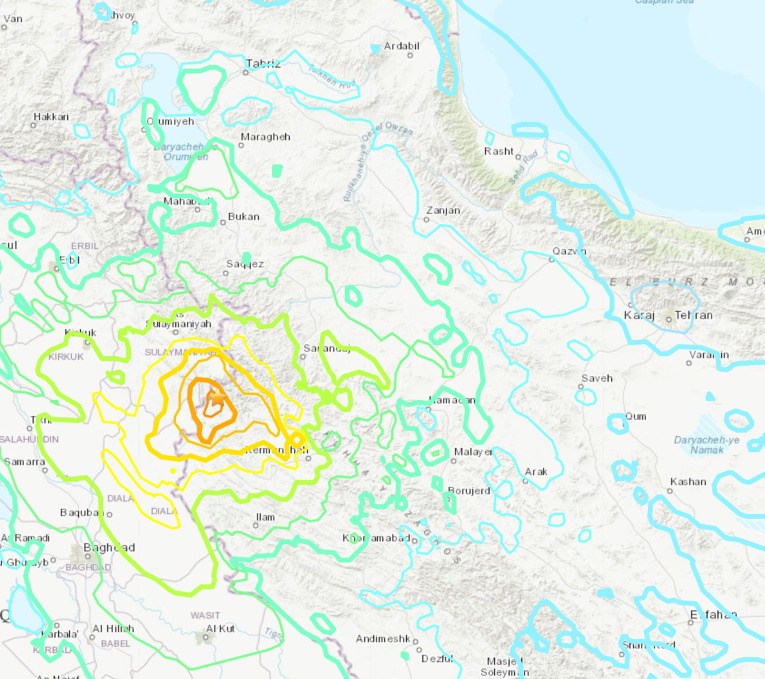
Based on statistics (Jamalreyhani et al., 2017), in the most severe earthquake with Mw 7.3 that occurred on 12 November 2017, more than 600 people were killed, and over 8000 people were injured in Salas-Babajani and Sarpol-zahab cities. Moreover, in August and November 2018, two severe earthquakes with Mw 6.0 and Mw 6.4 occurred in the proximity of both cities, respectively. It is worth noticing that this region experienced more than 133 aftershocks continuously, exceeding Mw 4.0 until 30 December 2019. The epicentre and intensity of the most severe earthquake are illustrated in Fig. 7 and Fig. 8 , respectively. What makes this city more sensitive amid the COVID-19 outbreak is the lack of appropriate healthcare sectors because of the earthquake that occurred in 2017 crippled this section. According to the COVID-19 outbreak throughout the world, evacuation of people and transferring RIs are conducted difficultly. Akin to the world situation, this city has been experiencing a dangerous situation more than five times, shown as the red area on the Iranian COVID-19 interactive map (https://app.mask.ir/map).

Fig. 7.

Epicentre of Mw 7.3 earthquake.

Fig. 8.

The intensity of Mw 7.3 earthquake.

In order to handle the disaster effectively, RCWs, DCs, THs, and ECs are utilized in this real case. The location of the above-mentioned centers is illustrated in Fig. 9 . The RCW is located in Kermanshah city, the capital of Kermanshah province. Regarding severe earthquakes mentioned above, three scenarios are considered to involve all types of intensive earthquakes. Each scenario relates to the Richter scale. The first scenario is considered for the fifth Richter scale, and the second and third one is taken for the sixth and seventh Richter scales, respectively. The planning horizon of this model is 72 h, which is made up of three days because most aftershocks happened in the 3-day period in this region.

Fig. 9.

Location of centers in Salas Babajani city.

According to the Iranian Seismological Center (http://irsc.ut.ac.ir/index.php?lang=ea?lang=fa), most earthquakes that occurred in Kermanshah range from 4.5 to 5.5 Richter scale. The probability of earthquake occurrence with five Richter is 50 percent, and for 6 and 7 scale are 30 % and 20 %, respectively. The infection rate determined by IoT systems and diagnostic tests is considered 3 % in AAs and ECs. Also, the sensitivity analysis on the infection rate is conducted to illustrate different situations before an earthquake occurs.

RIs in this study include sanitizing package, 1.5L hygienic drinkable water, PPE package, and prepared foods. The consumption rate for the first and second items is one. Also, two PPE packages and three cans of conserved food are considered for people in ECs and THs for daily consumption. The volume of RIs packages are 0.0015, 0.003, 0.005, and 0.0015 $m^3$ respectively. In the proposed model, trucks and cargo drones transport RIs simultaneously. The maximum volume of products transferred by a truck and a drone is 6 and 1 $m^3$. The capacity of THs, DCs, and ECs has been presented in Table 2 . Data relating to costs are obtained by interviews with officers of the Red Crescent Society of Kermanshah province. The ECs capacity is calculated by $\mathit{areaofEC}/6m^2$ because based on Sakamoto et al. (2020), each person needs 6 m in ECs. It is noteworthy that the uncertain parameters in the proposed model are considered a triangular fuzzy number with a 10 % deviation from the center.

Table 2.

Capacity of ECs, THs, and DCs.

Capacity	$s$ = 1			$s$ = 2			$s$ = 3
	EC	TH	DC	EC	TH	DC	EC	TH	DC
1	1000	150	10	950	143	9.5	900	135	9
2	950	120	8	903	114	7.6	855	108	7.2
3	1000	160	10	950	152	9.5	900	144	9
4	850	150	8	808	143	7.6	765	135	7.2
5	650	100	8	618	95	7.6	585	90	7.2
6	950	100	–	903	95	–	855	90	–
7	550	150	–	523	143	–	495	135	–

In previous articles, most of them considered Tehran (capital of Iran) or other metropolitans in Iran as a case study. In these cities, the level of uncertainty is somewhat controllable, but in our case, this level may be difficult to control because this location has experienced a lot of harsh earthquakes and it has become underdeveloped in recent years. All uncertain parameters with the accompaniment of FMP and scenario-based optimization are considered to tackle the ambiguous environment. In addition, because of the lack of an airport in this city, airplanes and helicopters cannot have high efficiency. Thus, we added drones to our logistics networks, along with trucks to distribute RIs. As mentioned before, the distributional infrastructure of the city is weak in comparison to other giant cities. To control the outbreak, the distribution of RIs is based on minimizing costs, transportation time, distance, and demand coverage. Furthermore, the IoT framework is widely used in COVID-19 management worldwide (some practical examples are discussed in 3.1). In our study, we developed the framework that a basic version of this was utterly practical in finding COVID-19 suspects.

Based on the centers located in Fig. 9, the distances and travel time between centers are acquired by Google map (https://www.google.com/maps) listed in Table S1 – S3, S12, and S13, respectively. All data about costs, including inventory holding costs, institution costs, penalty costs, and transportation costs, have been presented in Tables S4 – S11. The number of individuals in each AA who needs accommodation is presented in Table S14, changed in each scenario. This number is estimated by officers of the Red Crescent Society based on their recent experiences with earthquakes.

5.2. Results

Regarding Fig. 4, our solution comprises two phases, including selection of the location of ECs and THs and calculation of the individuals number living in them in the first phase and selection of DCs locations and allocation RIs to them in the second phase, along with an intermediate stage, called the calculation of demand for RIs. It is worth mentioning that demand quantity is obtained by the multiplication of the number of individuals by consumption coefficients.

5.2.1. Results of phase 1

In order to distribute RIs among people in THs and ECs, the number of individuals in both centers should be defined first. This result is obtained by solving the first phase of the proposed model. In the first phase, the best locations for instituting THs and ECs are selected from potential ones. Then, the individuals are allocated to ECs based on Fig. 2. In our case, the results are depicted in Table 3 and Table 4 .

Table 3.

Number of people living in ECs.

People in EC	$s$ = 1			$s$ = 2			$s$ = 3
	$t$ = 1	$t$ = 2	$t$ = 3	$t$ = 1	$t$ = 2	$t$ = 3	$t$ = 1	$t$ = 2	$t$ = 3
$k$ = 1
$k$ = 2	423	576	626	592	685	731	892	892	892
$k$ = 3				437	898	972	198	669	909
$k$ = 4							798	798	798
$k$ = 5							610	611	611
$k$ = 6	712	919	981	873	883	938	2	702	860
$k$ = 7							379	380	379

Table 4.

Number of people living in THs.

People in TH	$s$ = 1			$s$ = 2			$s$ = 3
	$t$ = 1	$t$ = 2	$t$ = 3	$t$ = 1	$t$ = 2	$t$ = 3	$t$ = 1	$t$ = 2	$t$ = 3
$h$ = 1	1	1	7	15	100	58	50	93	80
$h$ = 2							5	49	71
$h$ = 3	72	96	96	107	56	109	99	76	52
$h$ = 4							27	36	76

After defining the number of individuals in both centers, the demand for RIs can be computed simply by multiplying the consumption rate with data in Table 3 and Table 4.

5.2.2. Result of phase 2

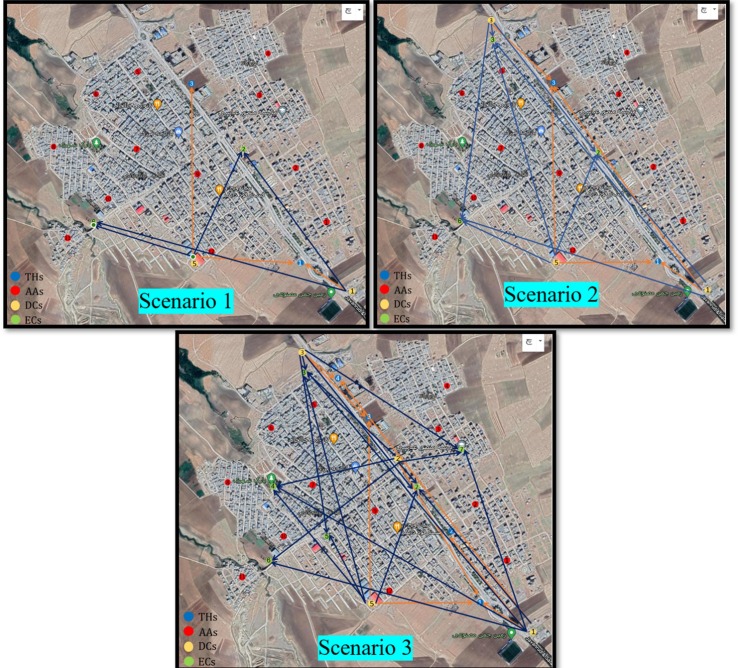
In the second phase, first, the location of DCs should be selected from the potential ones, and afterwards the RIs should be distributed from DCs to ECs and THs. Flows of RIs between the instituted and used centers are presented in Fig. 10 . The total quantity of RIs transferred from RCWs to DCs is illustrated in Table 5 . Also, the RIs quantity transferred from DCs to ECs and THs is represented in Table 6 and Table 7 . It is worth noticing that the objective function weights in the second phase are considered 0.3, 0.5, and 0.2, respectively.

Fig. 10.

The flow of RIs in three different scenarios (green arrows illustrate the flow between DCs and THs and yellow arrows define the flow for ECs). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Table 5.

Quantity of RIs transferred from RCW to DCs.

$Q$	$s$ = 1			$s$ = 2			$s$ = 3
$i\to j$	$t$ = 1	$t$ = 2	$t$ = 3	$t$ = 1	$t$ = 2	$t$ = 3	$t$ = 1	$t$ = 2	$t$ = 3
	→$j$ = 1	1226	3716	3328	2309	4819	3472	3399	4450	4859
$i$ = 1	→$j$ = 2							3926	3685	4636
	→$j$ = 3				5474	4085	4832	4666	5764	4739
	→$j$ = 5	4690	4416	4583	3614	4418	5412	3713	5279	5227

Table 6.

Quantity of RIs transferred from DCs to THs.

Q		$s$ = 1			$s$ = 2			$s$ = 3
$j\to h$		$t$ = 1	$t$ = 2	$t$ = 3	$t$ = 1	$t$ = 2	$t$ = 3	$t$ = 1	$t$ = 2	$t$ = 3
$j$ = 1	→$h$ = 1		3				292	262
	→$h$ = 2								321	344
	→$h$ = 3					278
	→$h$ = 4									149
$j$ = 2	→$h$ = 1									465
	→$h$ = 3						544	533	308	404
	→$h$ = 4							115	273
$j$ = 5	→$h$ = 1			35	104	498			642
	→$h$ = 3	363	482		643

Table 7.

Quantity of RIs transferred from DCs to ECs.

$Q$		$s$ = 1			$s$ = 2			$s$ = 3
$j\to k$		$t$ = 1	$t$ = 2	$t$ = 3	$t$ = 1	$t$ = 2	$t$ = 3	$t$ = 1	$t$ = 2	$t$ = 3
$j$ = 1	→ $k$=2	196	784	3328	1198	3757	2004	656
	→$k$ = 3					980	1274			653
	→$k$ = 4							2236		2538
	→$k$ = 5
	→$k$ = 6	638	3321		817				2504	1502
	→$k$ = 7							22	1522
$j$ = 2	→$k$ = 2								653	1590
	→$k$ = 3							601	521
	→$k$ = 4								1825
	→$k$ = 6							1826	653	2613
	→$k$ = 7							1499
$j$ = 3	→$k$ = 2				1924	392			2613
	→$k$ = 3					2613	2613		2570
	→$k$ = 4							1702
	→$k$ = 5							2317		2461
	→$k$ = 6				3549	1081	1675
	→$k$ = 7									1875
$j$ = 5	→$k$ = 2	2086	2371		1021	644	2432	3713		1960
	→$k$ = 3				1749					2613
	→$k$ = 4								2116	653
	→$k$ = 5								2521
	→$k$ = 6	2241	1223	4889		3336	3018

One of the essential objectives of the study is to minimize the amount of shortage and surplus of RIs. It is clear that the shortage in the first scenario is lower than in other scenarios because of the lower Richter scale. The surplus amount, in this case, is zero in all scenarios due to RIs shortage. The amount of shortage in THs and DCs is represented in Table 8, Table 9 . The result of the shortage demonstrates that the area of the city with a higher population density has more shortages. The RIs stored in the inventory are illustrated in Table 10 .

Table 8.

RIs shortage in THs.

Shortage in TH	$s$ = 1			$s$ = 2			$s$ = 3
	$t$ = 1	$t$ = 2	$t$ = 3	$t$ = 1	$t$ = 2	$t$ = 3	$t$ = 1	$t$ = 2	$t$ = 3
$h$ = 1	1	2	14		3		52	185	157
$h$ = 2									65
$h$ = 3	145	193	192	214	111	148	209	57	162
$h$ = 4							46	109	112

Table 9.

RIs shortage in ECs.

Shortage in EC	$s$ = 1			$s$ = 2			$s$ = 3
	$t$ = 1	$t$ = 2	$t$ = 3	$t$ = 1	$t$ = 2	$t$ = 3	$t$ = 1	$t$ = 2	$t$ = 3
$k$ = 2	751	651	1058		428	789	1647	3208	3593
$k$ = 3				1201	2695	2916	435	2206	3103
$k$ = 4							1575	2116	2283
$k$ = 5							1219	1730	1822
$k$ = 6	1246	1818	1956	1746	1767	2005	731	1524	1821
$k$ = 7							608	609	941

Table 10.

Quantity of RIs stored in DCs.

Inventory	$s$ = 1			$s$ = 2			$s$ = 3
	$t$ = 1	$t$ = 2	$t$ = 3	$t$ = 1	$t$ = 2	$t$ = 3	$t$ = 1	$t$ = 2	$t$ = 3
$j$ = 1	262			425	98		98
$j$ = 3				98	327		1624	292
$j$ = 5	223			98				327

Aside from RIs quantity, the number of trucks and drones used in this case is represented in Table 11 . As shown in Table 11, most drones are allocated to centers with lower distances between them.

Table 11.

number of required trucks and drones in mentioned routes.

Fleet		$\mathrm{s}$ = 1			$\mathrm{s}$ = 2			$\mathrm{s}$ = 3
		$\mathrm{t}$ = 1	$\mathrm{t}$ = 2	$\mathrm{t}$ = 3	$\mathrm{t}$ = 1	$\mathrm{t}$ = 2	$\mathrm{t}$ = 3	$\mathrm{t}$ = 1	$\mathrm{t}$ = 2	$\mathrm{t}$ = 3
$\mathrm{f}$ = 1	$\mathrm{i}\to \mathrm{j}$	3	4	4	6	6	6	7	8	8
	$\mathrm{j}\to \mathrm{k}$	3	5	5	7	7	7	8	7	7
	$\mathrm{j}\to \mathrm{h}$	1			1	2	1
$\mathrm{f}$ = 2	$\mathrm{i}\to \mathrm{j}$				2	3	4	4	2
	$\mathrm{j}\to \mathrm{k}$	2				5	5	2	3	5
	$\mathrm{j}\to \mathrm{h}$	1	2	1	1	2	1	3	5	5

5.3. Sensitivity analyses and discussion

Sensitivity analysis is conducted on critical parameters of this study. In order to reduce the redundancy, all analyses are executed on the third scenario (the most severe earthquake) presented in the following.

5.3.1. Sensitivity analysis of virus parameters

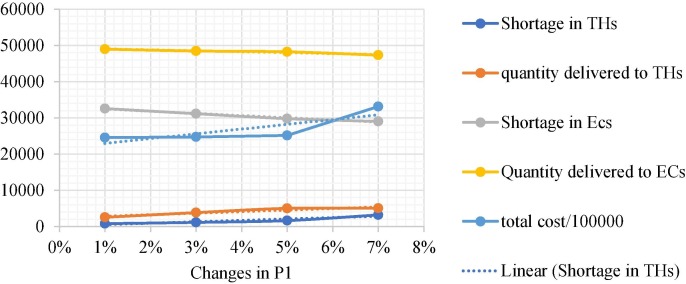
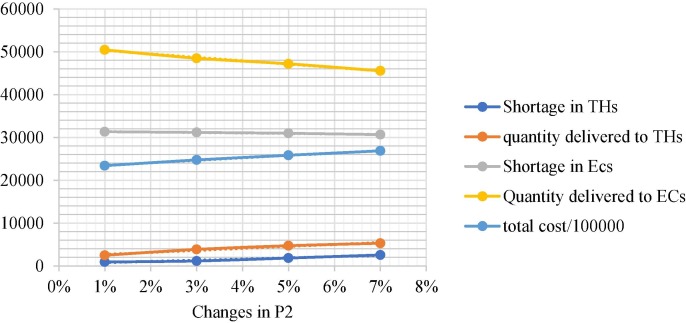
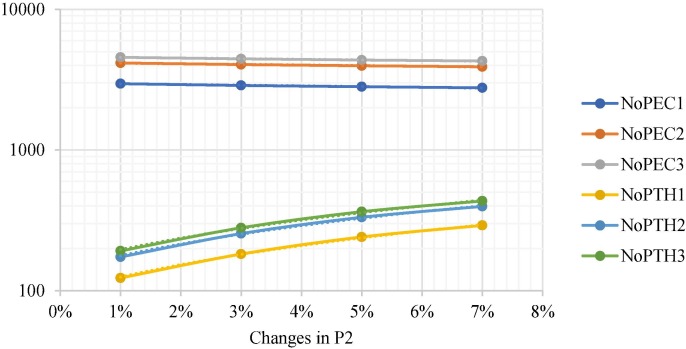
Parameters of virus transmission directly impact the number of infected patients transferred to hospitals. Since the most significant objective is to minimize the shortage and surplus of RIs, the effect of the infection rate of the virus on RIs shortage, RIs quantity, number of people living in THs and ECs, and total cost are analyzed.

According to Fig. 11, Fig. 12 and Tables S15 and S16, the infection rate defined by IoT system and PCR test in AAs directly impacts the number of people living in THs and affects the number of people living in ECs reversely. Because of that, RIs shortage and RIs quantity in ECs decreased. Adversely, the trend of shortage and quantity in THs is increased because more people are transferred to THs. Moreover, this rate incurs an extra cost in this supply chain which is noticeable in the aftermath of disasters. Notably, the more deployment of IoT-based equipment can reduce this probability which is impactful in reducing the infection rate of the virus in ECs.

Fig. 11.

The effects of infection rate in AAs on shortage, quantity, and cost.

Fig. 12.

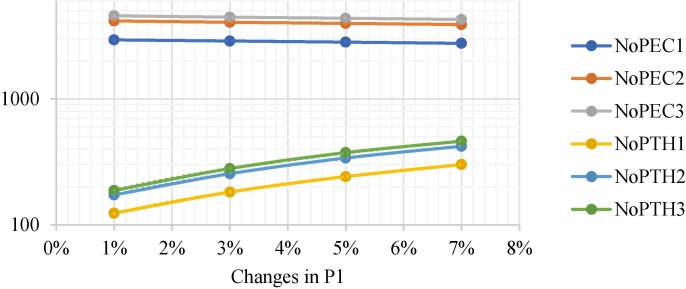
The effects of infection rate in AAs on the number of people living in THs and ECs. Cue: (NoPEC: number of people living in ECs) & (NoPTH: number of people living in THs).

As shown in Fig. 13, Fig. 14 and Tables S17 and S18, the infection rate calculated by IoT systems and PCR tests in interiors and ECs has similar behaviour to AAs' rate. Based on the meticulous analysis of Fig. 12, Fig. 14, the utilization of the system mentioned above in AAs can detect more infected cases than in ECs. However, faster detection of infected cases increases the supply chain costs.

Fig. 13.

The effects of infection rate in ECs on shortage, quantity, and cost.

Fig. 14.

The effects of infection rate in ECs on number of people living in THs and ECs. Cue: (NoPEC: number of people living in ECs) & (NoPTH: number of people living in THs).

5.3.2. Sensitivity analysis of capacity parameters

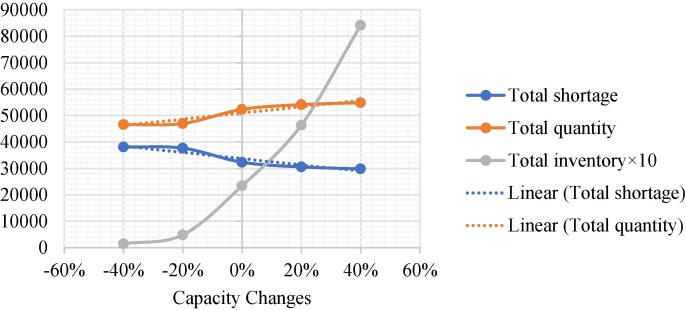
The second sensitivity analysis is based on the capacity of DCs and transportation capacity. The available number of vehicles represents the transportation capacity in this model. The SA results are shown in Fig. 15, Fig. 16, Fig. 17 . As shown in Fig. 15 and Table S19, the increase in ECs capacity can decrease RIs shortage and increase RIs quantity transferred from DCs to THs and ECs. Furthermore, a significant increase in the capacity of distribution centers alone would not alleviate the shortage but would only increase storage capacity because the transportation capacity is limited.

Fig. 15.

The effect of DCs capacity on RIs shortage, quantity, and inventory.

Fig. 16.

The impact of number of available trucks on RIs quantity and shortage (number of trucks represents ${\mathrm{M}\mathrm{N}\mathrm{F}}_{\mathrm{f}}$ for $\mathrm{f}=1$).

Fig. 17.

The impact of number of available drones on RIs quantity and shortage (number of drones represents ${\mathrm{M}\mathrm{N}\mathrm{F}}_{\mathrm{f}}$ for $\mathrm{f}=2$).

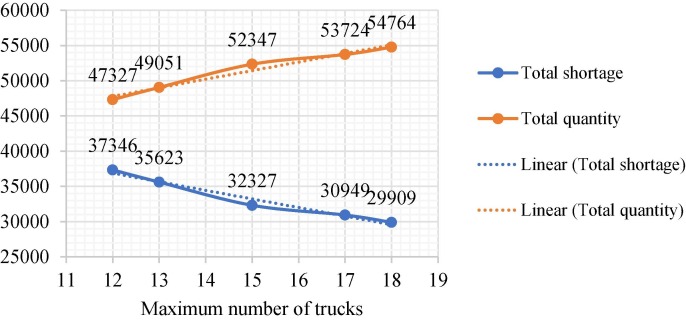
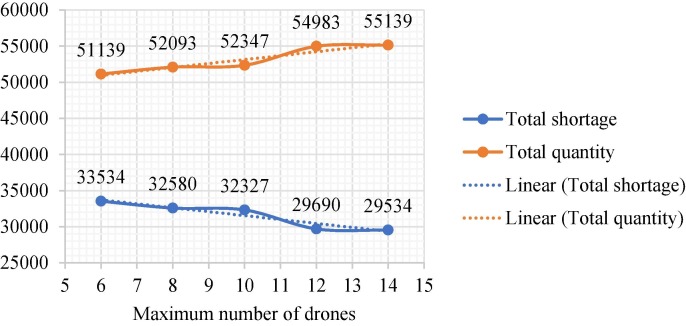
According to Fig. 16, Fig. 17 and Tables S20 and S21, the transportation capacity plays a significant role in decreasing shortage along with DCs capacity. The utilization of more trucks and cargo drones, interconnected with IoT systems, can deliver more quantity to demand points. Therefore, it is concluded that RIs shortage can be depleted on the condition transportation and DCs capacities increase simultaneously. Regarding the comparison between drones and trucks, the increase in drones is more impactful for transferring RIs and reduction of shortages because drones can carry items to remote areas in a shorter time.

5.3.3. Sensitivity analysis of RIs parameters

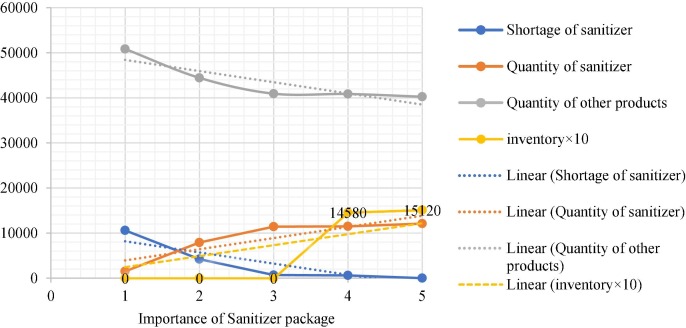
In this section, SA is performed on the RIs specifications involving the importance and consumption coefficient of RIs. The decision-maker determines both coefficients according to the criteria defined by the IoT surveillance and monitoring system. As shown in Fig. 18 and Table S22, the importance of RIs may differ in enhancing the hygienic condition and reducing virus transmission. To illustrate, if the importance of sanitizer package in ECs increases, the shortage of sanitizer package decrease drastically and reaches zero in the highest importance, and the delivered quantity of this package increases and reaches the peak. The quantity of other RIs transferred to demand points decreases because an item with higher priority should be transferred at first. Note that less important RI requires less storage because the warehouse should be allocated to items with high priority.

Fig. 18.

The effect of importance of an RI (type 1) on shortage, quantity, and inventory.

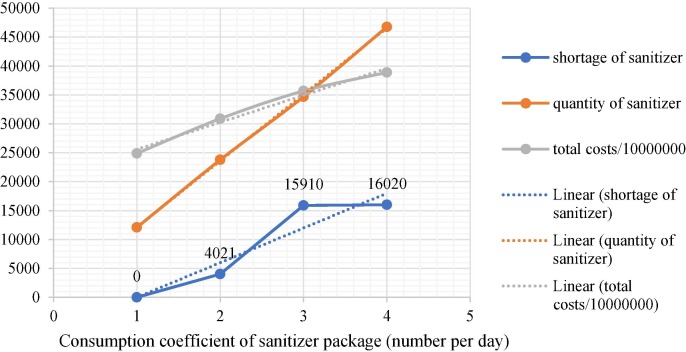
Moreover, the changes in RIs importance may engender changes in RIs consumption coefficient. The more people consume RIs in demand points, the more shortage of RIs we have. According to Fig. 19 and Table S23, the amount of sanitizer package transferred to demand increases noticeably because of the increase in sanitizer demand. Therefore, the total costs experience tremendous growth.

Fig. 19.

The effect of consumption coefficient of an RI (type 1) on shortage, quantity, and total cost.

5.4. Managerial insights and discussion

The main goal of the research is to detect and transfer people and infected patients along with planning a fair and prompt distribution of RIs in catastrophes among the COVID-19 outbreak. The main contribution of this article is the extensive use of IoT-based systems in the humanitarian supply chain, which distinguishes it from the article written by Ghasemi et al. (2019), who considered only patient transfer and RI allocation with shortage reduction. Notably, IoT frameworks proposed by Zahedi et al., 2021, Goodarzian et al., 2022 cannot be utilized for disaster management. In our work, a novel framework is presented, connected with our mathematical model. Also, fleet management is considered in the article by Abazari et al. (2021). However, they did not consider the shortage reduction of RIs. In addition, Torabi et al. (2018) considered all aspects of uncertainty in humanitarian logistics networks, but the model is not commensurate with the response phase of disaster. Regarding the specification of this model, several implications are presented to managers of health-related and Red Cross organizations. Some of the managerial insights obtained by the results and sensitivity analysis are mentioned in the following:

• 1.According to Fig. 12, Fig. 14, one way to manage disasters in a COVID-19 epidemic is to reduce the infection rate because an outbreak can spread quickly. The presence of domestic and foreign humanitarian workers and aid organizations may increase the risk of transmitting the virus. There are some practical solutions to tackle this inevitable problem mentioned below:
• A.Informing people about the instructions and keeping them posted about how to get aid can significantly reduce the rate of virus transmission. It is recommended to managers that IoT-based systems are an appropriate way to send information quickly and securely, consisting of Web-based applications and announcement drones shown in Fig. 20 .
• B.In addition to suitable announcements, surveillance of people for paying obedience to guidelines and social distancing plays a pivotal role. The utilization of two types of IoT surveillance systems can be taken as a panacea. Surveillance drones, shown in Fig. 21 , and monitoring cameras can detect people's neglect.
• C.Prompt and timely detection of infected people and their transfer to quarantine centers can reduce the spread of the COVID-19 virus (infection rate). It is also impossible to test all people with PCR-kit in the affected areas because it imposes a high cost and time. Due to emerging new mutations of the coronavirus, e.g., Indian and Brazilian, which have higher transmission rates, patients should be diagnosed and transferred immediately. Therefore, the use of the IoT monitoring system can quickly identify suspects. This interconnected system comprises web-based applications, thermal sensors and cameras, and monitoring drones and powered by Artificial Intelligence, as shown in Fig. 22, Fig. 23, Fig. 24 . Suspects detected by this system are shown on monitors. So, taking PCR tests from suspects to ensure the virus infects them is not complicated via this real-time data. Note that all people should answer a questionnaire in the web-based application and report their general well-being continuously.
• D.Replacing clinical care robots and IoT-based systems with humans in hospitals and quarantine places to treat and care for infected patients can prevent the healthcare section from being crippled significantly in the aftermath of disasters. That is to say, China has been utilizing disinfection and clinical care robots in a field hospital located in Wuhan,1 which city designed for 20,000 patients. The mentioned systems are illustrated in Fig. 25, Fig. 26 .
• 2.Along with controlling the virus transmission rate in disasters, the fair and rapid distribution of RIs plays a crucial role in controlling the virus. Also, either the lack or surplus of items or unfair distribution causes dissatisfaction among people in ECs and THs. Therefore, several recommendations have been made for the distribution of RIs:
• A.Regarding Fig. 15, one of the critical recommendations for managers is to increase the capacity of distribution centers to the extent determined by the model. It should be noted that an excessive increase in the centers' capacity cannot help improve the situation noticeably. Also, more RIs with lower priority can be stored in DCs, and RIs with higher importance can be transferred to THs and ECs if the capacity of DCs increases, but the total cost increases drastically. It is worth mentioning that it is better to extend storage in densely populated areas because most of the shortage happens in these zones.
• B.Based on Fig. 16, Fig. 17, one way to increase the amount of transported RIs is to improve transportation capacity. Managers are advised that instead of spending much money to increase distribution centers, increasing the number of trucks is better. In addition, cargo drones can be used with trucks to quickly send RIs to remote and inaccessible areas, albeit with lower capacity to expand transportation capacity. Thus, Investing in IoT-based cargo drones can also improve shortages and equitable distribution. For example, JD Company2 in china has used cargo drones to transfer commercial items and rapid covid-19 test kits to remote locations illustrated in Fig. 27, Fig. 28 .
• C.According to Fig. 18, due to new COVID-19 virus mutations, the importance of RIs can be changed by the medical decision-maker. These changes lead to increase demands and shortages of RIs. Paying more attention to the above-mentioned recommendations for reducing virus transmission is a way to control the changes in importance.
• D.Regarding Fig. 19, daily RIs should include the necessary items for people and patients. Consuming RIs without a predefined plan can increase shortage and unfair distribution. Determining the proper consumption pattern by managers for people in THs and DCs, along with timely announcement and consumption surveillance with IoT-based systems, can modify the situation.
• 3.In terms of results obtained from this case study, infected cases detected by IoT-based technology and PCR test should be transferred to quarantine swiftly. Location of temporary quarantine places plays a pivotal role in controlling outbreaks because the more accessibility centers have, the less time it takes to transfer infected, and the more patients are transferred

Fig. 20.

Announcement drone.

Fig. 21.

Surveillance drone.

Fig. 22.

IoT thermal sensor.

Fig. 23.

IoT monitoring system for infected people detection.

Fig. 24.

Monitoring drone.

Fig. 25.

Disinfection drone.

Fig. 26.

Autonomous robot.

Fig. 27.

Cargo drone introduced by JD Company.

Fig. 28.

Cargo drone.

6. Conclusion and further research

In this paper, an uncertain, scenario-based, two-stage, multi-objective, multi-products, multi-fleet, multi-period, IoT-based, location-allocation-inventory, mixed-integer mathematical programming model was proposed for the response phase of disasters in the epidemic outbreak. The proposed model has five echelons involving Affected Areas (AAs), Relief Collection Warehouse (RCW), Distribution Centers (DCs), Temporary Hospitals (THs), and Evacuation Centers (ECs). Fuzzy mathematical programming is hired to cope with uncertainty in this problem. Also, due to the uncertain behaviour of the COVID-19 outbreak, the infection rate of the virus is obtained by the proposed IoT framework. Two objective functions, including minimizing the establishment cost of ECs, and minimizing transferring time of patients to THs, are considered for patients and people transferring. In the next phase, three objective functions involve minimizing the total cost, shortage of RIs, and the number of used fleets. The preliminary decision of the proposed model was locating ECs and THs, finding infected cases in AAs and ECs using an IoT system, transferring them to THs, locating DCs based on people's demand, allocating RIs fairly between people in THs and ECs, and finding an optimum number of drones and trucks.

The proposed two-level model was solved using the LP-metric method with GAMS software. Then, this model was evaluated by a real case study in Salas-e-Babajani city, Kermanshah province. Finally, sensitivity analyses were conducted on obtained data that might differ in three scenarios of earthquakes and presence of a new mutation of COVID-19. The results of sensitivity analyses indicate that the increase the infection rate of COVID-19 in AAs and ECs leads to increase patients’ numbers, demand in THs, and RIs shortage in THs. We find that the utilization of IoT-based systems in monitoring and informing can alleviate the situation in ECs and THs. Notably, using this system in AAs meticulously can be more effective than detecting infected cases in ECs, but it incurs an extra cost on the supply chain. We also find that the increase in the number of fleets and DCs capacity simultaneously reduce the shortage effectively, which is not very impactful if one increases solely. One of the study's findings is the use of cargo drones instead of trucks. Although they have less capacity than trucks, but have a more significant impact on reducing shortage. It should be noted that the use of drones also increases supply chain costs. The last finding is the effect of the importance and consumption coefficient of RIs on the shortage, inventory, and quantity of RIs transferred to demand points. If the importance and consumption rate increase, the RIs shortage will increase in ECs. Also, we find that the inventory is allocated to RIs with higher priority.

Our model has some limitations but can be developed in many ways. For further research, it is recommended that the routing problems of fleets be considered, along with traffic congestion and road disruption. Second, waste is an inevitable problem that should be treated. Locating temporary treatment centers for this problem can be taken as future work. Third, incorporating the location problem of portable blood distribution centers and the allocation problem of portable ventilators can modify decision-making. Researchers can incorporate the injured patients into this model and consider the problem of location-allocation-routing of ambulances for this supply chain network amid the COVID-19 outbreak. Another significant novelty that can enrich this study is to model a location-allocation problem for IoT equipment. For instance, because of the internet's interruption after a severe disaster, the location and number of the internet antennas to provide the internet for IoT devices can be an intriguing issue for future research. Furthermore, in some logistics networks, in order to reduce the shortage, we can consider the min–max type objective function on the transportation objective function (minimizing transportation time), along with minimizing shortage quantity and the penalty costs.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary material

The following are the Supplementary data to this article: