Abstract
The trucking sector contributes significantly to the economic vitality of the United States. Large trucks are primarily used for transporting goods within and across states. Despite its economic importance, large truck crashes constitute public safety concerns. To minimize the consequences, there is a need to understand the factors that contribute to the severity outcomes of truck-involved crashes. Since many large truck drivers transport goods across several states, the driver-centered crash factors are expected to differ between in-state and out-of-state drivers. For this reason, this study developed two random parameters multinomial logit models with heterogeneity in means and variances to examine the factors contributing to the severity of crashes involving in-state and out-of-state large truck drivers in Alabama. The study was based on the 2016–2020 large truck crashes in Alabama. After data cleaning and preparation, it was observed that approximately 20% of in-state and 23% of out-of-state large truck crashes were fatigue-related. There were more speeding related crashes (12.4%) among in-state large truck drivers, but the contribution of speeding to crash severity outcomes was only significant in the out-of-state model. More crashes related to red light running violation (14.2%) were observed among out-of-state drivers, pointing to the fundamental issues of fatigue and unfamiliarity with the operations of signalized intersections in Alabama. The study contributes to the literature on large truck crashes by uncovering the nuances in crashes involving in-state and out-of-state large truck drivers. Despite the seeming similarity in factors that influence crash outcomes, this study provides the basis for truck drivers’ training and communication campaigns on the differences that may exist in roadway characteristics from state to state. Also, policy formulations and strategies that prioritizes the well-being of the large truck drivers and creates a better working condition for them should be explored.
Keywords: Large truck safety, In-state drivers, Out-of-state drivers, Fatigue, Random parameter modelling
Large truck safety; In-state drivers; Out-of-state drivers; Fatigue; Random parameter modelling.
1. Introduction
The trucking sector contributes significantly to the economic vitality of the United States. In 2020, over 900,000 active truck drivers were in the sector, generating approximately $732 billion in revenue and representing 1% of the country's annual revenue (Duffin, 2022; Placek, 2022). The sector relies primarily on large trucks to transport goods within and across different states. The outbreak of COVD-19 in 2020 and the following lockdown did not significantly impact the trucking industry as its regarded as an essential service. Despite the economic importance of the trucking sector, large truck (with a gross vehicle weight rating greater than 10,000 pounds) crashes constitute public safety concerns. These vehicle types represent 4% of all registered vehicles but contribute about 9% to fatal crashes (National Safety Council, 2022; NHTSA, 2022a). Occupants of other vehicles and non-vehicle occupants (like pedestrians and bicyclists) are more vulnerable to severe or fatal injury in crashes involving large trucks (NHTSA, 2022b).
Moreover, large truck crashes often result in severe and fatal injuries compared to other vehicle crashes due to their size and weight (Behnood and Mannering, 2019; Liu and Fan, 2022). Data from the National Safety Council (National Safety Council, 2022) showed that fatalities in large truck crashes increased between 2014 and 2019, with 70% of the fatalities representing occupants of other vehicles. Despite the decrease in large truck-related fatalities observed in 2020 compared to the previous year, the number of non-vehicle occupants (like pedestrians and bicyclists) killed increased by 9.1% (NHTSA, 2022b). These statistics demonstrate the need to mitigate large truck crashes and their impact on public safety by identifying the significant contributing factors to implement effective countermeasures.
Aside from the public health safety concerns associated with large truck crashes, the stressful working conditions among professional truck drivers encourage unhealthy lifestyles resulting in higher risks of chronic diseases (Garbarino et al., 2018). Compared to the population average, the life expectancy of male truck drivers in the U.S is 16.1% and 25.8% lower for unionized and independent drivers, respectively (Apostolopoulos et al., 2010). Long-haul routes expose truck drivers to various mental health-related risks associated with the transportation environment (Apostolopoulos et al., 2010). In most cases, truck drivers spend consecutive days away from their families and engage in stimulants, alcohol, and drug use to meet the high delivery requirements (Heaton, 2005). These enormous industry demands often result in stress and health challenges for truck drivers and can significantly impact road safety. Therefore, understanding the peculiar challenges of truck drivers will inform more effective countermeasures that complement the results of large truck-involved crash models.
Previous studies have examined the association between large truck injury severity outcomes and their contributing factors with a diverse focus (Alrejjal et al., 2021; Azimi et al., 2019, 2020; Behnood and Mannering, 2019; Hosseinzadeh et al., 2021; Liu and Fan, 2022; Tahfim and Yan, 2021). Azimi et al. (2019) conducted a severity analysis of large truck crashes in Florida between 2007 and 2017 using a random parameter ordered logit model. They found that vision obstruction, running red light, and following too close increased crash severity significantly. By developing a mixed logit model as a baseline compared to selected machine learning models, Li et al. (2020) examined the factors contributing to the severity of large truck crashes in Texas using data from the Texas Crash Records Information System between 2011 and 2015. They identified that driving under the influence of drugs or alcohol and fatigue were the most significant factors contributing to the severity outcomes. They also found that the presence of curbs and medians and lanes and shoulders with adequate widths can prevent severe large truck crashes. Pulugurtha et al. (2022) study of truck-involved crashes in North Carolina revealed that fatigue, inattention, and impairment are the driver-related factors contributing significantly to crash occurrence.
Some other studies considered specific crash types like rollover or run-off-road crashes and single-vehicle or multi-vehicle crashes. For instance, Azimi et al. (2020) conducted a severity analysis of large truck rollover crashes in Florida using a random parameter ordered logit model and identified lighting condition, time of the crash, and driver vision obstruction as significant contributing factors. Also, Liu & Fan (2022) study of rear-end large truck crashes in North Carolina found that driving under the influence of drugs or alcohol, rural roadways, dark lightning condition, grade roadway configuration, and speed limits above 50 mph increased injury severity significantly. Adanu et al., 2021a, Adanu et al., 2021b, on the other hand, considered the injury severity of lane change crashes involving commercial motor vehicles on interstate highways. The study showed that lane changing crashes on unlit roadway and involving older drivers, at-fault commercial vehicles, and female drivers are more likely to result in major injury.
Spatio-temporal differences like time of the day or location (urban/rural areas, interstates, intersections) have also been explored among large truck-involved crashes. For instance, Pahukula et al. (2015) conducted a time-of-the-day analysis of crashes involving large trucks in urban areas using reported data by Texas Peace Officer's Crash Reports. For the analysis, they separated the data into five time periods and found seatbelt use, sideswipe collision, driver age less than 25, and male drivers to be significant factors in each period. For large truck crashes on mountainous interstates, Alrejjal et al. (2021), used correlated random parameters binary logit model and found that strong winds, overcorrections, and run-off-road increased the risk of rollover. Thereby, increasing the possibility of a severe crash outcomes. Additionally, Islam et al. (2014) developed four different random parameter logit models to comprehensively analyze single and multi-vehicle large truck at-fault crashes on rural and urban roadways in Alabama. Their results revealed that driver fatigue, wet surface, overtaking, and hitting fixed objects contributed significantly to single and multi-vehicle crashes in rural areas. These studies identified several factors contributing to the severity of large truck-related crashes given different circumstances.
Despite the studies uncovering the association between explanatory variables and severity outcomes of crashes involving large trucks, no known research effort has explored crashes involving in-state and out-of-state large truck drivers. Viewing large truck crashes from the lens of the drivers' primary state of residence is important to understand whether familiarity with driving in a state plays a role in the types of crashes that involve truck drivers. Indeed, drivers licensed and residing within the state are more likely to be familiar with the state's driving environment than drivers from other states. Similar factors might contribute differently to the severity of crashes involving in-state and out-of-state large truck drivers. It is imperative to capture such similarities and differences to be able to target driver-centered countermeasures.
Familiarity with the road network and traffic conditions influence driving styles and driving behaviors. Generally, in-state drivers are familiar with the local context of the transportation system. This knowledge, or lack thereof on the part of out-of-state drivers, influences traffic safety. This study aims to identify differences in the contributing factors to large truck crashes in Alabama involving in-state and out-of-state drivers and proposes some countermeasures. To achieve this, separate random parameters multinomial logit models with heterogeneity in means and variances were developed to identify the explanatory variables associated with crashes involving in-state and out-of-state large truck drivers in Alabama. Five-year (2016–2020) crash data from the Critical Analysis Reporting Environment (CARE) developed by the University of Alabama Center for Advanced Public Safety were used for the analysis.
2. Data description
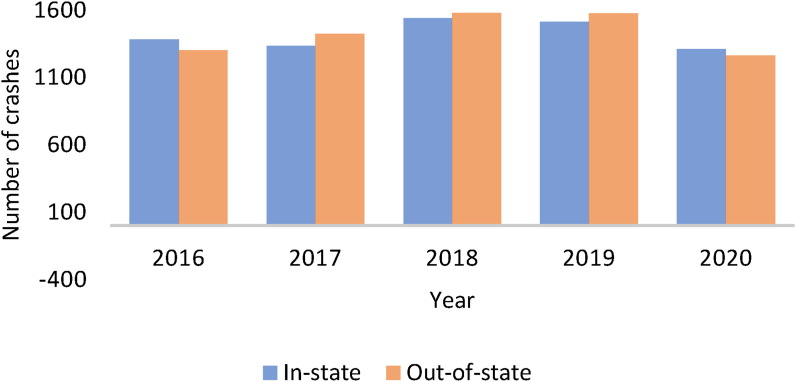
The study data was extracted from the Critical Analysis Reporting Environment (CARE) developed by the University of Alabama Center for Advanced Public Safety. Data from 2016 to 2020 was obtained, representing the most recent 5-year records of large truck crashes. The data contained five crash severity levels classified on the KABCO scale, where K = fatal injury, A = incapacitating injury, B = evident injury, C = possible injury, and O = no injury. We reclassified K and A as severe injury (SI), B and C as minor injury (MIN), and O as no injury (NI). Crashes involving large trucks licensed in Alabama were separated as in-state crashes and other trucks as out-of-state crashes. A total of 6943 in-state and 6863 out-of-state large truck-involved crash observations were used for the modeling. Figure 1 shows the number of crashes over the study period. It indicates an increasing trend from 2016 to 2019 and a decrease in 2020. There were more in-state crashes in 2016 and 2020 than out-state crashes. The reduction in crashes observed in 2020 can be related to the Covid-19 pandemic when traffic volume decreased. However, the proportion of severe crashes in 2019 and 2020 are similar for both in-state and out-of-state crashes despite the reduction in total crashes in 2020.
Figure 1.
Frequency of large truck crashes over the study period.
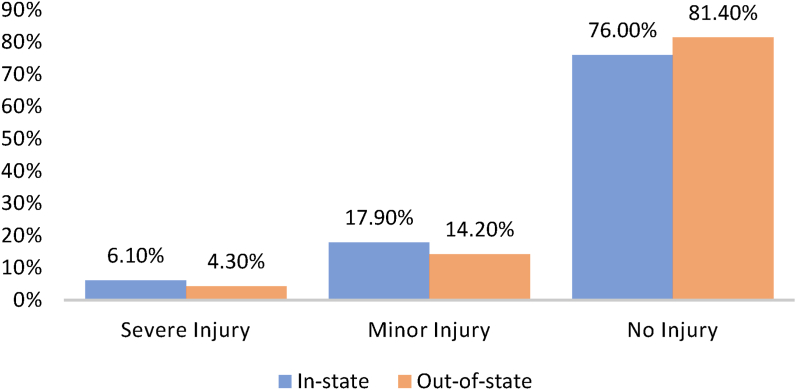
Figure 2 shows the proportion of in-state and out-of-state crashes for severe, minor, and no injury. In-state crashes resulted in a higher proportion of severe and minor crash severity, and out-of-state crashes resulted in a higher proportion of no injury crash severity.
Figure 2.
Proportion of in-state and out-of-state large truck crash severity.
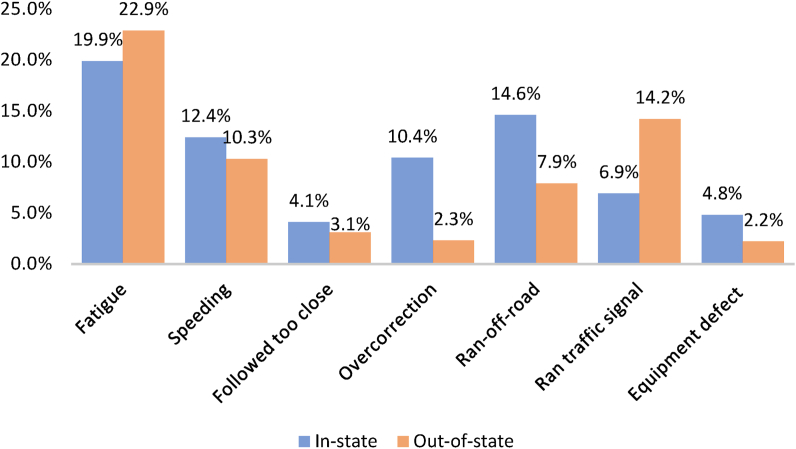
Figure 3 gives the proportions of selected primary contributing factors to severe crashes. “Fatigue” and “ran traffic light” contributed 22.9% and 14.2% to out-of-state major crashes, respectively, higher than the in-state crash observations. Overcorrection and run-off-road contributed more to in-state severe crashes than out-of-state severe crashes.
Figure 3.
Selected primary contributing factors for in-state and out-of-state severe crashes.
Tables 1 and 2 present the detailed descriptive statistics of the in-state and out-of-state large truck crash variables used in the model estimation.
Table 1.
Descriptive statistics of selected in-state large truck crash variables.
| Variable | Severe Injury |
Minor Injury |
No Injury |
Total |
|||
|---|---|---|---|---|---|---|---|
| Count | Percent | Count | Percent | Count | Percent | Count | |
| Driver age | |||||||
| Less than 25 years old | 14 | 6.1% | 47 | 20.6% | 167 | 73.2% | 228 |
| 25–40 years old | 120 | 5.8% | 367 | 17.8% | 1580 | 76.4% | 2067 |
| 41–65 years old | 240 | 5.8% | 737 | 17.9% | 3145 | 76.3% | 4122 |
| Above 65 years old | 47 | 9.0% | 95 | 18.2% | 381 | 72.8% | 523 |
| Driver race | |||||||
| Caucasian | 290 | 6.7% | 781 | 18.1% | 3249 | 75.2% | 4320 |
| Black | 125 | 4.9% | 448 | 17.5% | 1983 | 77.6% | 2556 |
| Others | 20 | 7.5% | 71 | 26.7% | 175 | 65.8% | 266 |
| Crash location | |||||||
| Intersection | 137 | 4.1% | 564 | 17.0% | 2624 | 78.9% | 3325 |
| Non-intersection | 284 | 7.9% | 682 | 18.9% | 2650 | 73.3% | 3616 |
| Primary contributing factor | |||||||
| Fatigue | 29 | 19.9% | 41 | 28.1% | 76 | 52.1% | 146 |
| Speeding | 39 | 12.4% | 99 | 31.5% | 176 | 56.1% | 314 |
| Followed too close | 21 | 4.1% | 126 | 24.8% | 362 | 71.1% | 509 |
| Improper turn | 4 | 1.1% | 32 | 9.1% | 315 | 89.7% | 351 |
| Overcorrection | 11 | 10.4% | 29 | 27.4% | 66 | 62.3% | 106 |
| Ran-off-road | 37 | 14.6% | 69 | 27.2% | 148 | 58.3% | 254 |
| Ran traffic signal | 7 | 6.9% | 40 | 39.6% | 54 | 53.5% | 101 |
| Equipment defect | 24 | 4.8% | 54 | 10.9% | 417 | 84.2% | 495 |
| Improper load/size | 0 | 0.0% | 3 | 7.3% | 38 | 1.4% | 41 |
| Others | 249 | 5.4% | 753 | 16.3% | 3624 | 78.3% | 4626 |
| First harmful event | |||||||
| Collision with a ditch | 36 | 17.7% | 57 | 28.1% | 110 | 54.2% | 203 |
| Collision with a guardrail | 13 | 11.8% | 23 | 20.9% | 74 | 67.3% | 110 |
| Collision with a tree | 23 | 18.4% | 27 | 21.6% | 75 | 60.0% | 125 |
| Others | 349 | 5.4% | 1139 | 17.5% | 5017 | 77.1% | 6505 |
| Most harmful event | |||||||
| Rollover | 153 | 15.9% | 337 | 35.0% | 473 | 49.1% | 963 |
| Collision with vehicle in traffic | 159 | 4.3% | 662 | 18.0% | 2860 | 77.7% | 3681 |
| Others | 109 | 4.7% | 247 | 10.7% | 1943 | 84.5% | 2299 |
| Manner of crash | |||||||
| Single vehicle | 204 | 9.4% | 453 | 20.9% | 1506 | 69.6% | 2163 |
| Rear-end | 81 | 6.0% | 310 | 22.8% | 967 | 71.2% | 1358 |
| Head-on | 14 | 38.9% | 6 | 16.7% | 16 | 44.4% | 36 |
| Others | 122 | 3.6% | 477 | 14.1% | 2787 | 82.3% | 3386 |
| Roadway condition | |||||||
| Dry | 365 | 6.4% | 1054 | 18.4% | 4320 | 75.3% | 5739 |
| Wet | 52 | 5.4% | 175 | 18.2% | 737 | 76.5% | 964 |
| Others | 4 | 1.7% | 17 | 7.1% | 219 | 91.3% | 240 |
| Roadway lighting | |||||||
| Daylight | 306 | 5.6% | 948 | 17.5% | 4163 | 76.9% | 5417 |
| Dark without streetlights | 82 | 9.0% | 172 | 18.9% | 654 | 72.0% | 908 |
| Others | 33 | 5.3% | 126 | 20.4% | 459 | 74.3% | 618 |
| Opposing lane separation | |||||||
| No separation | 26 | 4.4% | 85 | 14.5% | 477 | 81.1% | 588 |
| Concrete barrier | 19 | 2.9% | 129 | 19.6% | 510 | 77.5% | 658 |
| Metal/cable barrier | 19 | 4.4% | 63 | 14.5% | 352 | 81.1% | 434 |
| Others | 357 | 6.8% | 969 | 18.4% | 3937 | 74.8% | 5263 |
| Development | |||||||
| Rural | 313 | 10.1% | 610 | 19.6% | 2185 | 70.3% | 3108 |
| Urban | 108 | 2.8% | 636 | 16.6% | 3091 | 80.6% | 3835 |
| Locale | |||||||
| Open Country | 326 | 8.9% | 736 | 20.0% | 2612 | 71.1% | 3674 |
| Residential | 29 | 4.2% | 102 | 14.8% | 556 | 80.9% | 687 |
| Shopping or Business | 51 | 2.4% | 335 | 15.5% | 1779 | 82.2% | 2165 |
| Others | 15 | 3.6% | 73 | 17.5% | 329 | 78.9% | 417 |
| Driver residence distance | |||||||
| Less than 25 miles | 10 | 4.1% | 33 | 14.2% | 202 | 80.5% | 245 |
| More than 25 miles | 295 | 4.4% | 969 | 14.4% | 5475 | 81.2% | 6739 |
| Highway classification | |||||||
| Federal | 90 | 7.3% | 248 | 20.1% | 894 | 72.6% | 1232 |
| Interstate | 70 | 4.5% | 276 | 17.8% | 1205 | 77.7% | 1551 |
| State | 146 | 8.7% | 331 | 19.7% | 1204 | 71.6% | 1681 |
| County | 85 | 9.7% | 187 | 21.4% | 600 | 68.8% | 872 |
| Others | 30 | 1.9% | 204 | 12.7% | 1373 | 85.4% | 1607 |
| Functional class | |||||||
| Interstate | 69 | 4.4% | 282 | 18.1% | 1205 | 77.4% | 1556 |
| Minor arterial | 98 | 7.8% | 230 | 18.3% | 926 | 73.8% | 1254 |
| Major collector | 69 | 8.7% | 171 | 21.5% | 554 | 69.8% | 794 |
| Local | 30 | 4.5% | 88 | 13.2% | 551 | 82.4% | 669 |
| Others | 155 | 5.8% | 475 | 17.8% | 2040 | 76.4% | 2670 |
| Time of day | |||||||
| Dawn (1 am–6 am) | 159 | 5.7% | 486 | 17.3% | 2160 | 77.1% | 2803 |
| Morning (7 am–12 pm) | 59 | 8.5% | 151 | 21.8% | 483 | 69.7% | 693 |
| Afternoon (1 pm–6 pm) | 46 | 6.3% | 125 | 17.1% | 562 | 76.7% | 733 |
| Night (7 pm–12 am) | 157 | 5.8% | 485 | 17.9% | 2071 | 76.3% | 2713 |
Table 2.
Descriptive statistics of selected out-of-state large truck crash variables.
| Variable | Severe Injury |
Minor Injury |
No Injury |
Total |
|||
|---|---|---|---|---|---|---|---|
| Count | Percent | Count | Percent | Count | Percent | Count | |
| Driver age | |||||||
| Less than 25 years old | 14 | 5.1% | 38 | 13.8% | 223 | 81.1% | 275 |
| 25–40 years old | 92 | 4.3% | 304 | 14.2% | 1748 | 81.5% | 2144 |
| 41–65 years old | 179 | 4.3% | 596 | 14.2% | 3422 | 81.5% | 4197 |
| Above 65 years old | 27 | 6.3% | 78 | 18.2% | 323 | 75.5% | 428 |
| Driver race | |||||||
| Caucasian | 155 | 4.4% | 511 | 14.6% | 2831 | 81.0% | 3497 |
| Black | 110 | 4.3% | 370 | 14.5% | 2075 | 81.2% | 2555 |
| Others | 47 | 4.1% | 145 | 12.6% | 962 | 83.4% | 1154 |
| Crash location | |||||||
| Intersection | 122 | 3.6% | 485 | 14.2% | 2820 | 82.3% | 3427 |
| Non-intersection | 190 | 5.0% | 541 | 14.3% | 3047 | 80.7% | 3778 |
| Primary contributing factor | |||||||
| Fatigue | 24 | 22.9% | 25 | 23.8% | 56 | 53.3% | 105 |
| Speeding | 24 | 10.3% | 55 | 23.6% | 154 | 66.1% | 233 |
| Followed too close | 15 | 3.1% | 106 | 22.1% | 359 | 74.8% | 480 |
| Improper turn | 2 | 1.1% | 10 | 5.7% | 162 | 93.1% | 174 |
| Overcorrection | 1 | 2.3% | 8 | 18.6% | 34 | 79.1% | 43 |
| Ran-off-road | 14 | 7.9% | 28 | 15.7% | 136 | 76.4% | 178 |
| Ran traffic signal | 17 | 14.2% | 45 | 37.5% | 58 | 48.3% | 120 |
| Equipment defect | 11 | 2.2% | 36 | 7.1% | 461 | 90.7% | 508 |
| Improper load/size | 0 | 0.0% | 2 | 10.0% | 18 | 90.0% | 20 |
| Others | 190 | 3.8% | 646 | 12.9% | 4166 | 83.3% | 5002 |
| First harmful event | |||||||
| Collision with a ditch | 10 | 12.5% | 13 | 16.3% | 57 | 71.3% | 80 |
| Collision with guard rail | 10 | 11.1% | 7 | 7.8% | 73 | 81.1% | 90 |
| Others | 277 | 4.2% | 934 | 14.0% | 5440 | 81.8% | 6651 |
| Most harmful event | |||||||
| Rollover | 43 | 15.9% | 82 | 30.3% | 146 | 53.9% | 271 |
| Collision with vehicle in traffic | 143 | 3.8% | 621 | 16.6% | 2970 | 79.5% | 3734 |
| Others | 112 | 3.9% | 258 | 9.0% | 2488 | 87.1% | 2858 |
| Manner of crash | |||||||
| Single vehicle | 115 | 6.0% | 223 | 11.6% | 1591 | 82.5% | 1929 |
| Rear-end | 72 | 5.6% | 269 | 21.0% | 938 | 73.3% | 1279 |
| Others | 111 | 3.0% | 469 | 12.8% | 3075 | 84.1% | 3655 |
| Roadway condition | |||||||
| Dry | 258 | 4.6% | 813 | 14.4% | 4585 | 81.1% | 5656 |
| Wet | 50 | 4.3% | 194 | 16.7% | 919 | 79.0% | 1163 |
| Others | 4 | 1.0% | 19 | 4.9% | 364 | 94.1% | 387 |
| Roadway Lighting | |||||||
| Daylight | 191 | 3.9% | 703 | 14.2% | 4048 | 81.9% | 4942 |
| Dark without streetlights | 80 | 6.2% | 185 | 14.3% | 1031 | 79.6% | 1296 |
| Others | 41 | 4.2% | 138 | 14.3% | 789 | 81.5% | 968 |
| Opposing lane separation | |||||||
| No separation | 14 | 2.8% | 54 | 10.7% | 439 | 86.6% | 507 |
| Concrete barrier | 30 | 2.6% | 177 | 15.4% | 940 | 82.0% | 1147 |
| Metal or cable barrier | 26 | 3.4% | 125 | 16.3% | 616 | 80.3% | 767 |
| Others | 242 | 5.1% | 670 | 14.0% | 3873 | 80.9% | 4785 |
| Development | |||||||
| Rural | 202 | 6.3% | 460 | 14.3% | 2549 | 79.4% | 3211 |
| Urban | 96 | 2.6% | 501 | 13.7% | 3054 | 83.6% | 3651 |
| Locale | |||||||
| Open Country | 245 | 6.1% | 600 | 14.8% | 3199 | 79.1% | 4044 |
| Residential | 10 | 2.2% | 45 | 10.0% | 396 | 87.8% | 451 |
| Shopping or Business | 46 | 2.1% | 310 | 13.9% | 1880 | 84.1% | 2236 |
| Others | 11 | 2.3% | 71 | 14.9% | 393 | 82.7% | 475 |
| Driver residence distance | |||||||
| Less than 25 miles | 14 | 5.2% | 38 | 14.2% | 215 | 80.5% | 267 |
| More than 25 miles | 283 | 4.4% | 910 | 14.1% | 5267 | 81.5% | 6460 |
| Highway classification | |||||||
| Federal | 69 | 6.7% | 186 | 18.2% | 768 | 75.1% | 1023 |
| Interstate | 139 | 4.6% | 439 | 14.6% | 2427 | 80.8% | 3005 |
| State | 66 | 6.4% | 164 | 15.9% | 803 | 77.7% | 1033 |
| County | 12 | 3.5% | 39 | 11.4% | 292 | 85.1% | 343 |
| Others | 12 | 0.8% | 133 | 9.1% | 1314 | 90.1% | 1459 |
| Functional class | |||||||
| Interstate | 146 | 4.6% | 473 | 14.9% | 2552 | 80.5% | 3171 |
| Minor arterial | 42 | 5.7% | 98 | 13.3% | 595 | 81.0% | 735 |
| Major collector | 14 | 3.2% | 51 | 11.8% | 368 | 85.0% | 433 |
| Local | 6 | 1.4% | 31 | 7.2% | 395 | 91.4% | 432 |
| Others | 104 | 4.3% | 373 | 15.3% | 1958 | 80.4% | 2435 |
| Time of day | |||||||
| Dawn (1 am–6 am) | 92 | 3.5% | 357 | 13.7% | 2158 | 82.8% | 2607 |
| Morning (7 am–12 pm) | 70 | 7.9% | 135 | 15.2% | 684 | 76.9% | 889 |
| Afternoon (1 pm–6 pm) | 89 | 4.1% | 305 | 14.2% | 1757 | 81.7% | 2151 |
| Night (7 pm–12 am) | 48 | 3.9% | 164 | 13.5% | 1004 | 82.6% | 1216 |
3. Methodology
Over the years, highway agencies and vehicle manufacturers have focused on reducing traffic injury severities resulting from motor vehicle crashes. While visible progress has been made in this regard, there still exists the need for additional insights through empirical assessment of the impacts of complex interactions of vehicle, roadway, environment, and human attributes on crash-injury severity outcomes (Savolainen et al., 2011). Traffic researchers have adopted several methodological approaches to uncover the association between crash-injury severity levels and observed and unobserved contributing factors to facilitate the development of effective countermeasures. The recent methodological advances have created robust techniques that accommodate and account for the randomity and unobserved heterogeneity across crash observations. In most cases, the researcher's choice of methodological approach is contingent on the nature of the dependent variable and associated data limitations (Savolainen et al., 2011). Typically, the dependent variable in crash injury severity analysis can be modeled as a binary response outcome (e.g., minor injury or major injury) or multiple response outcomes (e.g., severe injury, minor injury, or no injury). Researchers have also treated response variables with multiple outcomes as either ordinal (ordered) or categorical (unordered) in nature. The application of these various methodological approaches has provided useful insights, but the inherent characteristics of the crash data often result in unaccounted methodological limitations (Savolainen et al., 2011).
Methodological techniques that account for heterogeneity in crash observations are popular within the traffic safety research community. Such approaches include random parameter ordered probability models (Azimi et al., 2020), random parameter multinomial logit models (Ahmadi et al., 2020; Cheng et al., 2019), random parameter models with heterogeneity in means and variances (Behnood and Mannering, 2017; Damsere-Derry et al., 2021), latent class model (Shaheed and Gkritza, 2014), and latent class logit and mixed logit models (Behnood and Mannering, 2016).
Contextually, Guo et al. (2019) used full Bayesian random parameters multivariate Tobit model to examine the correlation and heterogeneity in crash rates by collision types. They found that accounting for heterogeneity improved the model fit significantly in comparison with other Tobit model variants. Random parameter bivariate probit model has been used to examine the impact of driver fatigue, gender and distracted driving on aggressive driving behavior (Fountas et al., 2019). More recent studies have adopted random parameters logit model with heterogeneity in means and variances for traffic crash analysis (Damsere-Derry et al., 2021; Liu et al., 2021; Waseem et al., 2019). Wassem et al. (2019), used random parameters logit model with heterogeneity in means and variances to identify the significant contributing factors to motorcyclists-injury severities in the Pakistian city of Rawalpindi. Damsere-Derry et al. (2021) adopted the same approach to model injury severity of intercity bus crashes in Ghana. In their study Behnood and Mannering (2019) explored the effects of time variation and temporal instability on injury severity in large-truck crashes.
For this study, two separate random parameter multinomial logit models were developed for crashes involving in-state and out-of-state large truck drivers in Alabama while allowing for heterogeneity in the random parameters means and variances. The multinomial logit model is a discrete outcome model that extends the binary logit model to include more than two response outcomes without explicitly considering the existence of potential ordering in the response outcomes. Hence, it is used to model each injury severity class as a categorical response variable with its unique utility function. Marginal effects or pseudo-elasticities are then used to understand the marginal effect of an explanatory variable in one utility function on others. The extended consideration of heterogeneity in means and variances of the random parameters allows for a more generalized approach that captures unobserved heterogeneity across the crash observations (Mannering et al., 2016). For analysis, the response outcomes or dependent variables are usually the various crash or injury severity levels in the data or those modified for the study. Most crash records have five categories of injury severity (i.e., fatal, incapacitating injury, evident injury, minor injury, and no injury) in the data. However, for research purposes, the injury severity levels are often reclassified into three categories, namely, major or severe injury, minor injury, and no injury (Uddin et al., 2020).
While various models can exhibit inherent limitations, the random parameters multinomial logit models with heterogeneity in means and variances approach has produced more statistically superior outcomes in recent crash or injury severity studies. The term crash severity represents the injury level of the most severely injured crash victim. For a crash involving large trucks, the most severely injured victim could be the truck driver or an occupant, another vehicle occupant, or a vulnerable road user. To start with, we define a crash severity function as shown in Eq. (1).
| (1) |
where is the crash severity function that determines the probability of large truck crash severity category in crash , is a vector of explanatory variables that influence the likelihood of large truck crash severity level in crash , is a vector of estimable parameters for crash severity , and is the distributed error term (Washington et al., 2020). If is assumed to follow an independent and identically distributed extreme value Type I distribution (McFadden, 1981), and parameter variations are allowed across observations by introducing a mixing distribution. According to McFadden and Train (2000), the resulting mixed logit model is expressed as shown in Eq. (2).
| (2) |
where is the density function of with representing a vector of parameters of the density function (mean and variance), is the probability of crash severity category in crash conditioned on and all other terms as previously defined. can now account for observation-specific variations in the effect of on crash severity probabilities, with used to determine . Mixed-logit probabilities are then a weighted average for the different values of across observations where some elements of the vector can be fixed or allowed to vary across observations. The parameters that vary across observations are known as random parameters.
The random parameters (mixed) logit models can identify variables that exhibit randomness but cannot account for the factors that explain the randomness in the random variables. We addressed this limitation by adopting random parameters (mixed) logit modeling approach with heterogeneity in means and variances. The technique enables the identification of other variables (within the modeling dataset or from another set of observations) that could further explain the random parameters and their association with the response variables in the presence of other explanatory variables. Therefore, the random parameter (mixed) logit model with heterogeneity in means and variances model can account for unobserved heterogeneity in the dataset than the conventional random parameter models.
The heterogeneity in means and variances of random parameters are modeled according to Eq. (3) by allowing to vary across crashes (Islam and Mannering, 2020; Waseem et al., 2019).
| (3) |
where is the mean parameter estimate across all crashes, is a vector of attributes that captures the heterogeneity in the mean, is the corresponding vector estimable parameters, is the vector of attributes that captures heterogeneity in the standard deviation with corresponding parameter vector and a disturbance term . The vectors and may contain crash factors or other potential sources of heterogeneity that might be unavailable in the crash database. Model parameters were estimated using simulated maximum likelihood with 1000 Halton draws, which are sufficient for accurate estimation based on previous studies (Anastasopoulos and Mannering, 2009; Bhat, 2003; Halton, 1960; Savolainen, 2016). Additionally, the marginal effects were computed to examine the impact of explanatory variables on the reclassified crash severity outcome probabilities (Washington et al., 2020). By coding all the explanatory variables as indicator variables, the marginal effects are calculated using Eq. (4).
| (4) |
The marginal effect of the indicator variable, is the probability difference when changes from 0 to 1 while other variables are constant. Marginal effects for variables with random parameters across all observations are calculated using only the estimated mean coefficients. Each marginal parameter effect is computed as the average of the marginal effects of all crash observations.
4. Model input variables
The outcome of a crash is influenced by several factors usually referred to as the crash contributing factors. For the modeling, the explanatory variables are selected based on the knowledge of significant variables from previous studies on large truck crashes (e.g., Alrejjal et al., 2021; Azimi et al., 2019, 2020; Uddin et al., 2020; Li et al., 2020). The variables cut across driver characteristics, vehicle attributes, and roadway and environmental features. Attention was given to selecting variables that are significant and also improve the model fit. The variable categories included in the final models are briefly described below.
Primary contributing factor: This parameter describes the main factor that contributed to the occurrence of the crash. Some common primary contributing factors include speeding, fatigue, overcorrection, and driving under the influence of alcohol or drugs.
Highway classification: It describes the type of highway where a crash occurred. The common highway classes are federal, interstate, state, municipal, and county highways. The data shows that most crashes involving in-state and out-of-state drivers were recorded on state and interstate highways, respectively.
Rural or urban: This parameter describes the development of the environment where the crash occurred, either as rural or urban.
First harmful event: Most crashes are associated with multiple events before the vehicle eventually halts. This parameter describes the preceding event in the crash. In some instances, the first harmful event might not be the most harmful in a crash. Examples of first harmful events include collision with a ditch, collision with a guardrail, and ran-off-road.
Most harmful event: This parameter describes the event that seems to contribute mostly to the severity outcome of a crash. It can be the only event in a crash or among the number of events leading to the final crash outcome. Examples include rollover or collision with a vehicle in traffic.
Opposing lane separation: This data element describes the separation between the opposing traffic. Examples are concrete barriers (median) and metal/cable barriers.
Locale: This variable describes the vicinity of the crash and the common activities in the area. A locale can be a shopping or business area or an open country.
Driver residence distance: This variable describes the distance of the crash location from the truck driver's residence. In the data, the distance could either be less than 25 miles or more than 25 miles.
Road condition: This parameter describes the condition of the road during the crash. The common road conditions are dry or wet.
Lighting condition: This variable describes the lightning state of the road at the time of the crash. Aside from daylight conditions, other lightning conditions include dark with streetlights and dark without streetlights.
Manner of crash: This data element describes the form of the crash. Aside from single vehicle large truck crashes, other common “manner of crash” are head-on and rear-end collisions. Head-on or rear-end collisions involves two or more vehicles.
Road curvature: This data element describes if a curve on the road contributed to the crash outcome. The road curvatures included in the model are curve left and level and curve right and level.
Airbag status: This parameter explains if the vehicle's airbag was deployed or not during the crash. This is a safety related variable and usually have a significant influence on crash outcomes.
Time of day (TOD): This variable describes the period when the crash occurred. As shown in the descriptive statistics, TOD was divided into dawn, morning, afternoon, and night.
5. Results
Separate random parameter multinomial logit models with heterogeneity in means and variances were estimated for analyzing crashes involving in-state and out-of-state large truck drivers in Alabama. As explained under the data description, three crash severity categories were considered in the models: SI (fatal and incapacitating injury), MI (evident and possible injury), and NI (no injury). The -statistics of all variables included in the model estimation are statistically significant at a 90% confidence interval or above on a two-tailed t-test. The random parameters were included in the model specification if their standard deviation -statistics corresponds to a 90% confidence interval or more. Tables 3 and 4 present the detailed model results with their computed marginal effects. The marginal effects indicate the impact of the explanatory variables on the different crash severity categories. From Tables 3 and 4, the McFadden pseudo- values for the in-state and out-of-state random parameter (mixed) logit models with heterogeneity in means and variances are and , respectively. The McFadden pseudo- value represents the ratio of the model log-likelihood at constant (model with zero variables except for constants) to the log-likelihood at convergence of the measure (model with all the significant variables). According to Ulfarsson et al. (2010), a value more than 0.1 indicates meaningful model improvement. Hence, the obtained values from the two models, as shown in Tables 3 and 4, reflect significant improvement in their goodness-of-fit.
Table 3.
Model estimation and marginal effects for crashes involving in-state large truck drivers.
| Category | Variables | Parameter estimate | -score | Marginal effects |
||
|---|---|---|---|---|---|---|
| Severe Injury |
Minor Injury |
No Injury |
||||
| [SI] | [MI] | [NI] | ||||
| Random parameter | ||||||
| Rural or Urban | Rural [SI] | -1.010 | -1.45 | 0.0354 | -0.0083 | -0.0271 |
| Standard deviation of “Rural” (normally distributed) | 2.210 | 3.58 | ||||
| Heterogeneity in means of random parameter | ||||||
| Highway Classification | Interstate | -0.570 | -1.8 | |||
| Driver race | Caucasian | 0.492 | 2.27 | |||
| Heterogeneity in variance of random parameter | ||||||
| First harmful event | Collision with a tree | 0.631 | 3.02 | |||
| Defined for severe injury | ||||||
| Primary contributing factor | Ran off-road | 0.458 | 1.72 | 0.0014 | -0.0003 | -0.0011 |
| First harmful event | Collision with a ditch | 0.876 | 2.68 | 0.0023 | -0.0006 | -0.0017 |
| Most harmful event | Rollover | 1.332 | 6.59 | 0.0163 | -0.0041 | -0.0122 |
| Intersection | Yes | -0.407 | -2.74 | -0.006 | 0.0012 | 0.0048 |
| Opposing Lane Separation | Metal/cable barrier | -0.725 | -2.64 | -0.003 | 0.0006 | 0.0024 |
| Locale | Shopping or business area | -0.641 | -3.44 | -0.0042 | 0.0007 | 0.0035 |
| Driver residence distance | More than 25 miles | -0.279 | -2.08 | -0.0062 | 0.0014 | 0.0048 |
| Road Condition | Wet | -0.357 | -1.76 | -0.0018 | 0.0004 | 0.0014 |
| Lighting condition | Daylight | -0.858 | -5.5 | -0.0255 | 0.0055 | 0.0201 |
| Dark without streetlights | -0.660 | -2.95 | -0.0046 | 0.0011 | 0.0035 | |
| Defined for minor severity | ||||||
| Primary contributing factor | Fatigue | 0.516 | 2.63 | -0.0002 | 0.0022 | -0.002 |
| Ran traffic signal | 1.484 | 7.06 | -0.0001 | 0.0051 | -0.0049 | |
| Overcorrection | 0.578 | 2.4 | -0.0002 | 0.0016 | -0.0015 | |
| Swerved to avoid animal | 0.626 | 2.02 | -0.0001 | 0.0009 | -0.0008 | |
| Defective equipment | -0.611 | -3.99 | 0.0003 | -0.0041 | 0.0039 | |
| Highway Classification | Federal | 0.330 | 3.67 | -0.0006 | 0.009 | -0.0085 |
| County | 0.307 | 2.73 | -0.0006 | 0.0062 | -0.0056 | |
| Functional class | Major collector | 0.196 | 1.82 | -0.0003 | 0.0036 | -0.0033 |
| Locale | Open Country | 0.254 | 3.58 | -0.0017 | 0.0206 | -0.0189 |
| Road curvature | Curve left and level | 0.347 | 2.05 | -0.0002 | 0.0019 | -0.0017 |
| Manner of crash | Single vehicle | 0.447 | 5.51 | -0.0021 | 0.0222 | -0.0201 |
| Defined for no injury | ||||||
| Constant | 2.024 | 24.82 | ||||
| Primary contributing factor | Improper load/size | 1.217 | 1.95 | -0.0001 | -0.0004 | 0.0005 |
| Ran stop sign | -1.591 | -3.46 | 0.0002 | 0.0009 | -0.0011 | |
| Manner of crash | Rear-end | -0.709 | -8.97 | 0.0044 | 0.0227 | -0.027 |
| Highway Classification | State | -0.241 | -3.1 | 0.0024 | 0.0081 | -0.0105 |
| Opposing Lane Separation | Concrete barrier | -0.294 | -2.69 | 0.0006 | 0.0041 | -0.0046 |
| Airbag status | Deployed | 0.258 | 3.94 | -0.0032 | -0.0146 | 0.0178 |
| number of observations | 6943 | |||||
| Log-likelihood at convergence | -4480.001 | |||||
| Log-likelihood at zero | -7627.665 | |||||
| McFadden Pseudo R-sq | 0.413 | |||||
Table 4.
Model estimation and marginal effects for crashes involving out-of-state large truck drivers.
| Category | Variables | Parameter estimate | -score | Marginal effects |
||
|---|---|---|---|---|---|---|
| Severe Injury [SI] | Minor Injury [MI] | No Injury [NI] | ||||
| Random parameter | ||||||
| Lighting condition | Daylight [SI] | -1.953 | -2.18 | 0.0091 | -0.0013 | -0.0078 |
| Standard deviation of “Daylight” (normally distributed) | 1.868 | 2.60 | ||||
| Heterogeneity in means of random parameter | ||||||
| Primary contributing factor | Improper turning | -1.737 | -2.11 | |||
| Heterogeneity in variance of random parameter | ||||||
| Most harmful event | Rollover | 0.571 | 3.36 | |||
| Defined for severe injury | ||||||
| Driver age | Above 60 years old | -0.409 | -1.72 | -0.0137 | 0.0022 | 0.0116 |
| Primary contributing factor | Speeding | 0.899 | 2.72 | 0.0018 | -0.0003 | -0.0015 |
| Run off-road | 0.579 | 1.7 | 0.0009 | -0.0001 | -0.0008 | |
| First harmful event | Collision with a ditch | 0.763 | 2.41 | 0.0014 | -0.0002 | -0.0012 |
| Collision with guardrail | 0.985 | 3.38 | 0.0020 | -0.0003 | -0.0017 | |
| Functional class | Major corridor | -0.787 | -2.14 | -0.0011 | 0.0001 | 0.0010 |
| Opposing Lane Separation | Metal/cable barrier | -0.888 | -4.59 | -0.0057 | 0.0009 | 0.0048 |
| Locale | Shopping or business area | -0.782 | -3.78 | -0.0043 | 0.0007 | 0.0036 |
| Road Condition | Dry | 0.400 | 2.04 | 0.0111 | -0.0018 | -0.0093 |
| Airbag status | Deployed | -0.854 | -5.1 | -0.0093 | 0.0014 | 0.0079 |
| Time of day | Night (7 pm–12 am) | -0.429 | -2.27 | -0.0027 | 0.0004 | 0.0023 |
| Season of year | Summer | 0.403 | 2.61 | 0.0040 | -0.0006 | -0.0034 |
| Defined for minor severity | ||||||
| Primary contributing factor | Fatigue | 1.108 | 6.58 | -0.0005 | 0.0062 | -0.0057 |
| Ran traffic signal | 1.409 | 7.45 | -0.0002 | 0.0058 | -0.0056 | |
| Overcorrection | 0.853 | 3.58 | -0.0001 | 0.0022 | -0.0021 | |
| Defective equipment | -0.594 | -3.34 | 0.0001 | -0.0029 | 0.0028 | |
| Highway Classification | Federal | 0.509 | 4.55 | -0.0005 | 0.0109 | -0.0104 |
| Interstate | 0.417 | 4.36 | -0.0011 | 0.0226 | -0.0215 | |
| Road curvature | Curve Left and Level | 0.516 | 2.57 | -0.0001 | 0.0019 | -0.0018 |
| Vehicle age | New truck (2010–2020) | -0.272 | -3.69 | 0.0009 | -0.0212 | 0.0202 |
| Defined for no injury | ||||||
| Constant | 2.273 | 20.84 | ||||
| Manner of crash | Rear-end | -0.566 | -6.89 | 0.0032 | 0.0165 | -0.0197 |
| Most Harmful event | Collision with vehicle in traffic | -0.307 | -3.95 | 0.0041 | 0.0218 | -0.0259 |
| Road curvature | Curve right and level | -0.673 | -3.37 | 0.0006 | 0.0021 | -0.0027 |
| Highway Classification | State | -0.447 | -4.23 | 0.0025 | 0.0082 | -0.0107 |
| Local | 0.633 | 3.33 | -0.0007 | -0.0021 | 0.0028 | |
| Number of observations | 7206 | |||||
| Log-likelihood at convergence | -3935.43 | |||||
| Log-likelihood at zero | -7916.60 | |||||
| McFadden Pseudo R-sq | 0.503 | |||||
Two variables were obtained as random parameters for both the in-state and out-of-state drivers’ models. The normal distribution provided the most appropriate fit for the random parameters among the various tested statistical distributions (like normal, lognormal, Weibull, etc.).
For the in-state model, the rural variable (defined for severe injury) was estimated as a random parameter with a mean of and a standard deviation of . These values indicate that with a normal distribution, the variable (rural) is positive for 32.4% of the large truck crash observations (increasing the likelihood of severe injury) and negative for the remaining 67.6% of the observations (decreasing the probability of severe injury). The marginal effect also shows that the rural indicator variable increased the probability of severe injury by 0.0354. Only the interstate and white driver indicators produced significant heterogeneity in means among the explanatory variables. The explanatory variable collision with a tree (as a first harmful event) produced heterogeneity in the variance of the random parameter. The mean of the rural random parameter decreased if the highway classification was interstate, suggesting a decrease in the likelihood of severe injury and an increase in the likelihood of minor and no injury. Ran-off-road, rollover, collision with a ditch, rear-end collision, and collision with vehicle in traffic increase the likelihood of severe injury outcomes. Rollover indicator variable increased the probability of severe injury by 0.0163 marginal points. In daylight condition and at an intersection, the probability of severe injury is significantly decreased by 0.0255 and 0.006 marginal points, respectively. Fatigue, overcorrection, ran traffic light, and single vehicle increase the probability of minor injury. Single vehicle crashes increased the possibility of minor injury by 0.0222 marginal points. For crashes that occurred in an open country, the likelihood of minor injury increases by 0.0206 marginal points.
In the out-of-state model, the daylight variable was estimated as a random parameter (Table 4), having a mean of – 1.953 and a standard deviation of 1.868. These values indicate that the daylight variable decreases the likelihood of severe injury for 85.2% of the crash observations and increases the likelihood of severe injury for the remaining crash observations. Among the explanatory variables, the improper turning (as a primary contributing factor) indicator produced significant heterogeneity in means of the random parameter. The rollover (as a most harmful event) indicator produced significant heterogeneity in the variance of the random parameter. The improper turning indicator variable decreased the mean of the daylight parameter, implying a decrease in the probability of a severe injury and an increase in the probability of minor or no injury. In other words, crashes that involve improper turning in daylight are less likely to result in severe crashes but more likely to result in minor or no injury. Also, in the out-of-state model, speeding, collision with guardrail, dry road condition, and summer increased the probability of severe injury. Older drivers (above 65 years) variable decreased the probability of severe injury but increased the likelihood of minor and no injury.
The explanatory variables, ran-off-road, and collision with a ditch increased the likelihood of severe injury in both models. On the other hand, indicator variables for fatigue, ran traffic signal, overcorrection, federal highway, and road with left curvature and level grade increased the likelihood of minor injury in both models. Table 5 presents a comparison of both model estimates.
Table 5.
Model results comparison for in-state and out-of-state large truck crashes.
| Category | Variable | In-state | Out-of-state |
|---|---|---|---|
| Driver age | >65 years old | ↓ SI | |
| Vehicle age | New truck (2010–2020) | ↓ MI | |
| Primary contributing factor | Ran off-road | ↑ SI | ↑ SI |
| Fatigue | ↑ MI | ↑ MI | |
| Ran traffic signal | ↑ MI | ↑ MI | |
| Overcorrection | ↑ MI | ↑ MI | |
| Swerved to avoid animal | ↑ MI | ||
| Defective equipment | ↓ MI | ↓ MI | |
| Overload | ↑ NI | ||
| Ran stop sign | ↓ NI | ||
| Speeding | ↑ SI | ||
| First harmful event | Collision with a ditch | ↑ SI | ↑ SI |
| Collision with guardrail | ↑ SI | ||
| Most harmful event | Rollover | ↑ SI | |
| Collision with vehicle in traffic | ↓ NI | ||
| Manner of crash | Single vehicle | ↑ MI | |
| Rear-end | ↓ NI | ↓ NI | |
| Intersection | Yes | ↓ SI | |
| Locale | Shopping or business area | ↓ SI | ↓ SI |
| Open Country | ↑ MI | ||
| Driver residence distance | More than 25 miles | ↓ SI | |
| Opposing lane separation | Physical separation | ↓ SI | ↓ SI |
| Concrete | ↓ NI | ||
| Highway classification | Federal | ↑ MI | ↑ MI |
| Interstate | ↑ MI | ||
| County | ↑ MI | ||
| State | ↓ NI | ↓ NI | |
| Local | ↑ NI | ||
| Rural or Urban | Rural | ↓ SI | |
| Road condition | Wet | ↓ SI | |
| Dry | ↑ SI | ||
| Lightning condition | Daylight | ↓ SI | ↓ SI |
| Dark without streetlights | ↓ SI | ||
| Functional class | Major corridor | ↑ MI | ↓ SI |
| Road curvature | Curve Left and Level | ↑ MI | ↑ MI |
| Curve right and level | ↓ NI | ||
| Airbag status | Deployed | ↑ NI | ↓ SI |
| Time of day | Night (7 pm–12 am) | ↓ SI | |
| Season of year | Summer | ↑ SI |
↑ indicates an increase in a severity category, ↓ indicates a decrease in a severity category, SI = severe injury, MI = minor injury, and NI = No injury.
6. Model specification test
Researchers have used the Likelihood Ratio (LR) test to determine the suitability of separate models for traffic crash studies (Islam et al., 2014). In this study, an LR test was conducted to justify the estimation of different models for crashes involving in-state and out-of-state large truck drivers using Eq. (5).
| (5) |
where is the log-likelihood at convergence estimated for all the crashes, is the log-likelihood at convergence estimated for crashes involving in-state large truck drivers, and is the log-likelihood at convergence estimated for crashes involving out-of-state large truck drivers. The test statistic is the distribution having degrees of freedom equal to the sum of the estimated parameters in all the separate models minus the number of estimated parameters in the corresponding model estimated for all crashes. The result showed that the test statistic ( is more than the corresponding value of () with degree of freedom () at a 99.99% confidence interval. We can then reject the null hypothesis that the combined model log-likelihood is not significantly different from the corresponding separate models and conclude that a separate model specification is suitable.
7. Discussion
Freight transport contributes significantly to the overall economic development of a state (Wang et al., 2021). A prerequisite for this, however, is the timely arrival of goods at their destinations. Truck-involved crashes are one of the leading causes of disruption to the timely delivery of goods. As such, much effort has been devoted to understanding the factors that contribute to truck-involved crashes and crash outcomes. Considering that crash incident clearance time is significantly impacted by the crash severity (Ding et al., 2015; Islam et al., 2021; Ji et al., 2014), this study contributes to this effort by exploring differences and similarities in crashes involving in-state and out-of-state truck drivers. It is worth noting that a preliminary analysis of the data used in the study showed similar proportions of crashes involving in-state and out-of-state drivers across the years. This indicates that irrespective of truck drivers’ state of residence, the factors contributing to their crashes are perhaps generally very similar.
However, viewing large truck crashes through the lens of the driver's state of residence is particularly important as familiarity with the roadway and driver fatigue are major contributing factors to crashes. Indeed, Figure 3 revealed a clear difference in the proportion of fatigue-related crashes between in-state and out-of-state drivers. Similarly, it was observed that out-of-state drivers were involved in more crashes related to running traffic signals. These findings point to the fundamental issues of fatigue among long distance truck drivers and their unfamiliarity with the operations of signalized intersections in Alabama. Speeding was found to contribute to more crashes among in-state drivers. In-state drivers might be more familiar with the roadway characteristics than their out-of-state counterparts. However, such familiarity could encourage unsafe actions like speeding, possibly compromising traffic safety. Figure 2 further revealed that the injury outcomes of truck-involved crashes are not significantly different between in-state and out-of-state drivers.
To better understand the crash factors that significantly influence crash outcomes, two separate injury-severity models were estimated. For ease of comparison, Table 5 was developed to present the variables significantly contributing to large truck-involved crash outcomes between in-state and out-of-state drivers. From Table 5, it can be observed that the factors that influence large truck crash outcomes do not significantly differ between in-state and out-of-state drivers. This finding is interesting because, whereas different factors may contribute to the occurrence of crashes, the outcome of the crashes are similar. Perhaps, this may be more related to the vehicle characteristics (e.g., age, size, configuration, etc.) and less to driver demographics. However, it should be noted that even though the crash factors have similar effects on crash outcomes, they do so to varying degrees. For instance, for the collision with a ditch variable, the marginal effects indicate that this variable increases the probability of severe injury by 0.0023 and 0.0014 in the in-state and out-of-state models, respectively. This difference in magnitude shows that truck crashes involving in-state drivers are more likely to result in severe injury compared to out-of-state drivers. There were more speeding related crashes among the in-state large truck drivers, but the contribution of speeding to minor crash severity outcomes was only significant in the out-of-state model. It is quite interesting that speeding was not significant in the in-state model as one would have expected. However, since speeding contribute to significant proportion of the crashes, measures should be taken to adequately enforce speeding regulations.
In this study, it was observed that fatigue and red light running were associated with increased crash severity in both in-state and out-of-state truck large truck crashes. These findings are generally consistent with previous studies (Azimi et al., 2019; Hosseinzadeh et al., 2021). Contrary to Islam and Hernandez (2013), the results of this study revealed that summer season was more likely to be linked with severe injury outcomes for crashes involving out-of-state large truck drivers. FHWA (2020) made an interesting finding that summer months are associated with vehicle overheating and traffic congestion and these usually result in vehicle malfunctioning and increased traffic incidents. Indeed, statistics have also shown that severe road crashes involving large trucks are more likely in summer compared to other seasons (Ahmed et al., 2020).
Despite the seeming similarity in factors that influence crash outcomes, this study provides the basis for truck driver training and awareness creation on differences that may exist in roadway characteristics from state to state. Communication campaigns should be incorporated with training programs as evidence has shown that simultaneously implementing both measures is more effective (Faus et al., 2021). Long-distance truck drivers should be encouraged to use rest areas to reduce the likelihood of getting into fatigue-related crashes (Adanu et al., 2021a, Adanu et al., 2021b; Pulugurtha et al., 2022). Driver-assist technologies also have the potential to complement the driving task for truck drivers, hence minimizing the chances of getting into crashes. Regular sensitization and adequate traffic law enforcement are necessary to ensure road safety compliance among truck drivers. In the long term, this is expected to promote a positive safety culture among truck drivers. Policy formulations and strategies that prioritize truck drivers’ well-being and create better working conditions for them should be explored. Also, exchange driver(s) should be provided for long-distance trips to minimize fatigue driving and keep the main driver engaged.
8. Conclusion
This study extends the understanding of truck-involved crashes by examining in-state and out-of-state large truck crashes in Alabama. The analysis was based on 2016–2020 large truck crashes obtained from the Critical Analysis Reporting Environment (CARE) developed by the University of Alabama Center for Advanced Public Safety. Crashes involving in-state and out-of-state drivers were classified based on the driver's state of residence. Crashes involving truck drivers residing in Alabama were classified as in-state and others as out-of-state. Two random parameter logit models with heterogeneity in means and variances were estimated to identify the significant contributing factors to the severity outcomes of crashes involving in-state and out-of-state drivers. An initial descriptive analysis of the data revealed that speeding contributes to more in-state crashes and running traffic light contributes to more out-of-state crashes. Of all the primary contributing factors, fatigue contributed to a significant proportion of the crashes and more for crashes involving out-of-state drivers.
The model results revealed that the crash contributing factors do not differ significantly among in-state and out-of-state drivers. Factors like fatigue, ran off-road, ran traffic signal, overcorrection, and collision with a ditch significantly increased severity outcomes in both models. Speeding was associated with more in-state crashes but was only significant in the out-of-state crash model. Perhaps, familiarity with the roadway among in-state drivers encourage more speeding but is probably less likely to result in severe crash outcomes. Also, overcorrection was predominant among in-state drivers. However, overcorrection increased the probability of minor injury for crashes involving out-of-state crashes by 0.0022 marginal points compared to 0.0016 for in-state drivers. Interstate, dry road condition, and summer season are other factors that significantly increase severe or minor injury outcomes for crashes involving out-of-state drivers.
Regarding heterogeneity, the impact of rural areas and daylight lightning conditions showed significant variations among crash observations involving in-state and out-of-state drivers, respectively. This suggests that truck-involved crashes in rural areas or under daylight conditions are less likely to result in severe injury outcomes. However, the presence of other variables like fatigue, speeding, or running traffic light could increase the injury severity outcomes. Besides the theoretical advantages of this study, the consideration of heterogeneity across the crash observations ensured better model estimations and proposal of efficient countermeasures. Compared to the existing literature on severity analysis of truck-involved crashes, this study identified similar significant contributing factors. Consistent with prior studies, factors such as fatigue, ran off-road, overcorrection, running red light, speeding, collision with vehicle in traffic, dry road condition, curve left and level, and summer season increased the probability of severe injury outcomes. The study also identified that single vehicle and rollover crashes involving in-state large truck drivers in open country are associated with an increased likelihood of severe outcomes. Despite the seeming significant similarity in factors that influence crash outcomes, this study provides the basis for truck driver training and awareness creation on differences that may exist in roadway characteristics from state to state.
In spite of the findings of this study which are interesting and consistent with previous works, there are few limitations that should be noted. The quality of any statistical model depends on the quality of the data used. Underreporting is a common limitation of crash data (Kayani et al., 2014; Watson et al., 2015), especially for minor or no injury crashes. Crash reporting officers usually rely on their discretion, drivers, and eyewitness accounts to determine the contributing factors in a crash. The collected information, based on a standard reporting system format, might not accurately represent all contributing factors. Where the driver refused to disclose some information regarding the crash, the reporting officer would have to rely on their experience to make a decision. These discrepancies can create “bias” in the dataset, usually called unobserved heterogeneity. However, in the absence of other sources of crash information, researchers often rely on police-reported crash records and adopt statistical methods to account for some of the unobserved heterogeneity in the data. In that regard, this study developed a random parameter multinomial logit model with heterogeneity in the means and variances. Traffic volume during the crash was not available as an input variable for this study. As a contributing factor, traffic volume could improve the model and provide additional insights into the difference between crashes involving in-state and out-of-state drivers. The classification of in-state or out-of-state drivers was based on the driver's license state (i.e., the state that issued the driving license) regarded as the state of residence. The assumption was that most drivers reside in the state where their driving license was issued. This approach might not be accurate given that some drivers might obtain their license in one state but reside or work in the state where the crash occurred. This possible interlink within the data could create a distinctive classification challenge. Based on the study outcome and highlighted limitations, the following suggestions are provided for future research direction.
-
•
Future studies should explore better ways to classify crashes involving in-state and out-of-state drivers by interpolating two or more variables. For instance, if the truck driver's origin-destination is known (which was not available for this study), a better classification of in-state and out-of-state crashes could be obtained by interpolating it with the driver state of residence considered as the driver's license state in this study.
-
•
The imbalance in the dataset, as shown in Figure 2, where observations from a particular injury severity class have a significantly lower frequency than the other classes, could present a challenge of inadequate variability in model estimations. Therefore, future works should compare different modeling techniques including machine learning to identify the method (s) with improved model performance.
-
•
The study could benefit from additional information from a survey of truck drivers for countermeasures proposition. Therefore, future studies can incorporate a survey of truck drivers in and outside Alabama to understand the challenges of the drivers that might be critical to traffic safety.
Declarations
Author contribution statement
Sunday Okafor: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.
Emmanuel Kofi Adanu: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Steven Jones: Contributed reagents, materials, analysis tools or data; Wrote the paper.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data availability statement
Data will be made available on request.
Declaration of interest's statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
Acknowledgements
The authors are thankful for the support from the Alabama Transportation Institute at the University of Alabama. The study data was obtained from the Critical Analysis Reporting Environment (CARE) developed by the University of Alabama Center for Advanced Public Safety.
References
- Adanu E.K., Hu Q., Liu J., Jones S. Better rested than sorry: data-driven approach to reducing drowsy driving crashes on interstates. J. Transport. Eng., Part A: Systems. 2021;147(10) [Google Scholar]
- Adanu E.K., Lidbe A., Tedla E., Jones S. Injury-severity analysis of lane change crashes involving commercial motor vehicles on interstate highways. J. Saf. Res. 2021;76:30–35. doi: 10.1016/j.jsr.2020.11.001. [DOI] [PubMed] [Google Scholar]
- Ahmadi A., Jahangiri A., Berardi V., Machiani S.G. Crash severity analysis of rear-end crashes in California using statistical and machine learning classification methods. J. Transport. Saf. Secur. 2020;12(4):522–546. [Google Scholar]
- Ahmed I.U., Gaweesh S.M., Ahmed M.M. Exploration of hazardous material truck crashes on Wyoming’s interstate roads using a novel Hamiltonian Monte Carlo Markov chain bayesian inference. Transport. Res. Rec.: J. Transport. Res. Board. 2020;2674(9):661–675. [Google Scholar]
- Alrejjal A., Farid A., Ksaibati K. A correlated random parameters approach to investigate large truck rollover crashes on mountainous interstates. Accid. Anal. Prev. 2021;159 doi: 10.1016/j.aap.2021.106233. [DOI] [PubMed] [Google Scholar]
- Anastasopoulos P.C., Mannering F.L. A note on modeling vehicle accident frequencies with random-parameters count models. Accid. Anal. Prev. 2009;41(1):153–159. doi: 10.1016/j.aap.2008.10.005. [DOI] [PubMed] [Google Scholar]
- Apostolopoulos Y., Sönmez S., Shattell M.M., Belzer M. Worksite-induced morbidities among truck drivers in the United States. AAOHN J. 2010;58(7):285–296. doi: 10.3928/08910162-20100625-01. [DOI] [PubMed] [Google Scholar]
- Azimi G., Asgari H., Rahimi A., Jin X. Transportation Research Board 98th Annual Meeting. 2019. Investigation of heterogeneity in severity analysis for large truck crashes.https://trid.trb.org/view/1658006 [Google Scholar]
- Azimi G., Rahimi A., Asgari H., Jin X. Severity analysis for large truck rollover crashes using a random parameter ordered logit model. Accid. Anal. Prev. 2020;135 doi: 10.1016/j.aap.2019.105355. [DOI] [PubMed] [Google Scholar]
- Behnood A., Mannering F. The effect of passengers on driver-injury severities in single-vehicle crashes: a random parameters heterogeneity-in-means approach. Anal. Methods Accid. Res. 2017;14:41–53. [Google Scholar]
- Behnood A., Mannering F. Time-of-day variations and temporal instability of factors affecting injury severities in large-truck crashes. Anal. Methods Accid. Res. 2019;23 [Google Scholar]
- Behnood A., Mannering F.L. An empirical assessment of the effects of economic recessions on pedestrian-injury crashes using mixed and latent-class models. Anal. Methods Accid. Res. 2016;12:1–17. [Google Scholar]
- Bhat C.R. Simulation estimation of mixed discrete choice models using randomized and scrambled Halton sequences. Transp. Res. Part B Methodol. 2003;37(9) [Google Scholar]
- Cheng L., Caset F., de Vos J., Derudder B., Witlox F. Investigating walking accessibility to recreational amenities for elderly people in Nanjing, China. Transport. Res. Transport Environ. 2019;76:85–99. [Google Scholar]
- Damsere-Derry J., Adanu E.K., Ojo T.K., Sam E.F. Injury-severity analysis of intercity bus crashes in Ghana: a random parameters multinomial logit with heterogeneity in means and variances approach. Accid. Anal. Prev. 2021;160 doi: 10.1016/j.aap.2021.106323. [DOI] [PubMed] [Google Scholar]
- Ding C., Ma X., Wang Y., Wang Y. Exploring the influential factors in incident clearance time: disentangling causation from self-selection bias. Accid. Anal. Prev. 2015;85:58–65. doi: 10.1016/j.aap.2015.08.024. [DOI] [PubMed] [Google Scholar]
- Duffin E. 2022. U.S. Government Revenues in the Fiscal Year of 2020, by Category. Statista. [Google Scholar]
- Faus M., Alonso F., Fernández C., Useche S.A. Are traffic announcements really effective? A systematic review of evaluations of crash-prevention communication campaigns. Saf. Now. 2021;7(4):66. [Google Scholar]
- FHWA . 2020. Traffic Congestion and Reliability: Trends and Advanced Strategies for Congestion Mitigation.https://ops.fhwa.dot.gov/congestion_report/chapter2.htm [Google Scholar]
- Fountas G., Pantangi S.S., Hulme K.F., Anastasopoulos P.C. The effects of driver fatigue, gender, and distracted driving on perceived and observed aggressive driving behavior: a correlated grouped random parameters bivariate probit approach. Anal. Methods Accid. Res. 2019;22 [Google Scholar]
- Garbarino S., Guglielmi O., Sannita W., Magnavita N., Lanteri P. Sleep and mental health in truck drivers: descriptive review of the current evidence and proposal of strategies for primary prevention. Int. J. Environ. Res. Publ. Health. 2018;15(9):1852. doi: 10.3390/ijerph15091852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo Y., Li Z., Liu P., Wu Y. Modeling correlation and heterogeneity in crash rates by collision types using full bayesian random parameters multivariate Tobit model. Accid. Anal. Prev. 2019;128:164–174. doi: 10.1016/j.aap.2019.04.013. [DOI] [PubMed] [Google Scholar]
- Halton J.H. On the efficiency of certain quasi-random sequences of points in evaluating multi-dimensional integrals. Numer. Math. 1960;2(1) [Google Scholar]
- Heaton K. Truck driver hours of service regulations: the collision of policy and public health. Pol. Polit. Nurs. Pract. 2005;6(4):277–284. doi: 10.1177/1527154405282841. [DOI] [PubMed] [Google Scholar]
- Hosseinzadeh A., Moeinaddini A., Ghasemzadeh A. Investigating factors affecting severity of large truck-involved crashes: comparison of the SVM and random parameter logit model. J. Saf. Res. 2021;77:151–160. doi: 10.1016/j.jsr.2021.02.012. [DOI] [PubMed] [Google Scholar]
- Islam M., Hernandez S. Large truck–involved crashes: exploratory injury severity analysis. J. Transport. Eng. 2013;139(6):596–604. [Google Scholar]
- Islam M., Mannering F. A temporal analysis of driver-injury severities in crashes involving aggressive and non-aggressive driving. Anal. Methods Accid. Res. 2020;27 [Google Scholar]
- Islam N., Adanu E.K., Hainen A.M., Burdette S., Smith R., Jones S. A comparative analysis of freeway crash incident clearance time using random parameter and latent class hazard-based duration model. Accid. Anal. Prev. 2021;160 doi: 10.1016/j.aap.2021.106303. [DOI] [PubMed] [Google Scholar]
- Islam S., Jones S.L., Dye D. Comprehensive analysis of single- and multi-vehicle large truck at-fault crashes on rural and urban roadways in Alabama. Accid. Anal. Prev. 2014;67:148–158. doi: 10.1016/j.aap.2014.02.014. [DOI] [PubMed] [Google Scholar]
- Ji Y., Jiang R., Qu M., Chung E. Traffic incident clearance time and arrival time prediction based on hazard models. Math. Probl Eng. 2014;2014:1–11. [Google Scholar]
- Kayani A., Fleiter J.J., King M.J. Underreporting of road crashes in Pakistan and the role of fate. Traffic Inj. Prev. 2014;15(1):34–39. doi: 10.1080/15389588.2013.793797. [DOI] [PubMed] [Google Scholar]
- Li J., Liu J., Liu P., Qi Y. Analysis of factors contributing to the severity of large truck crashes. Entropy. 2020;22(11):1191. doi: 10.3390/e22111191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu P., Fan W. (David) Analyzing injury severity of rear-end crashes involving large trucks using a mixed logit model: a case study in North Carolina. J. Transport. Saf. Secur. 2022;14(5):723–736. [Google Scholar]
- Liu S., Fan W.D., Li Y. Injury severity analysis of rollover crashes for passenger cars and light trucks considering temporal stability: a random parameters logit approach with heterogeneity in mean and variance. J. Saf. Res. 2021;78:276–291. doi: 10.1016/j.jsr.2021.06.013. [DOI] [PubMed] [Google Scholar]
- Mannering F.L., Shankar V., Bhat C.R. Unobserved heterogeneity and the statistical analysis of highway accident data. Anal. Methods Accid. Res. 2016;11 [Google Scholar]
- McFadden D. 198272nd ed. The MIT Press; Cambridge, MA: 1981. Econometric Models of Probabilistic Choice. Structural Analysis of Discrete Data with Econometric Applications. [Google Scholar]
- McFadden D., Train K. Mixed MNL models for discrete response. J. Appl. Econom. 2000;15(5) [Google Scholar]
- National Safety Council . National Safety Council; 2022. Large Trucks.https://injuryfacts.nsc.org/motor-vehicle/road-users/large-trucks/ [Google Scholar]
- NHTSA . 2022. Fatality Analysis Reporting System.https://www-fars.nhtsa.dot.gov/Vehicles/VehiclesAllVehicles.aspx [Google Scholar]
- NHTSA . 2022. Traffic Safety Facts: Overview of Motor Vehicle Crashes in 2020.https://crashstats.nhtsa.dot.gov/Api/Public/ViewPublication/813266 [Google Scholar]
- Pahukula J., Hernandez S., Unnikrishnan A. A time of day analysis of crashes involving large trucks in urban areas. Accid. Anal. Prev. 2015;75:155–163. doi: 10.1016/j.aap.2014.11.021. [DOI] [PubMed] [Google Scholar]
- Placek M. 2022. Trucking Industry in the U.S. - Statistics & Facts. Statista. [Google Scholar]
- Pulugurtha S.S., Duvvuri S., Mathew S. 2022. Risk Factors Associated with Crash Injury Severity Involving Trucks. [Google Scholar]
- Savolainen P.T. Examining driver behavior at the onset of yellow in a traffic simulator environment: comparisons between random parameters and latent class logit models. Accid. Anal. Prev. 2016;96:300–307. doi: 10.1016/j.aap.2016.01.006. [DOI] [PubMed] [Google Scholar]
- Savolainen P.T., Mannering F.L., Lord D., Quddus M.A. The statistical analysis of highway crash-injury severities: a review and assessment of methodological alternatives. Accid. Anal. Prev. 2011;43(5):1666–1676. doi: 10.1016/j.aap.2011.03.025. [DOI] [PubMed] [Google Scholar]
- Shaheed M.S., Gkritza K. A latent class analysis of single-vehicle motorcycle crash severity outcomes. Analytic Methods in Accident Research. 2014;2:30–38. [Google Scholar]
- Tahfim S.A.-S., Yan C. Analysis of severe injuries in crashes involving large trucks using K-prototypes clustering-based GBDT model. Saf. Now. 2021;7(2):32. [Google Scholar]
- Uddin M., Huynh N. Injury severity analysis of truck-involved crashes under different weather conditions. Accid. Anal. Prev. 2020;141 doi: 10.1016/j.aap.2020.105529. [DOI] [PubMed] [Google Scholar]
- Ulfarsson G.F., Kim S., Booth K.M. Analyzing fault in pedestrian–motor vehicle crashes in North Carolina. Accid. Anal. Prev. 2010;42(6):1805–1813. doi: 10.1016/j.aap.2010.05.001. [DOI] [PubMed] [Google Scholar]
- Wang H., Han J., Su M., Wan S., Zhang Z. The relationship between freight transport and economic development: a case study of China. Res. Transport. Econ. 2021;85 [Google Scholar]
- Waseem M., Ahmed A., Saeed T.U. Factors affecting motorcyclists’ injury severities: an empirical assessment using random parameters logit model with heterogeneity in means and variances. Accid. Anal. Prev. 2019;123:12–19. doi: 10.1016/j.aap.2018.10.022. [DOI] [PubMed] [Google Scholar]
- Washington S., Karlaftis M., Mannering F., Anastasopoulos P. Chapman and Hall/CRC; 2020. Statistical and Econometric Methods for Transportation Data Analysis. [Google Scholar]
- Watson A., Watson B., Vallmuur K. Estimating under-reporting of road crash injuries to police using multiple linked data collections. Accid. Anal. Prev. 2015;83:18–25. doi: 10.1016/j.aap.2015.06.011. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.