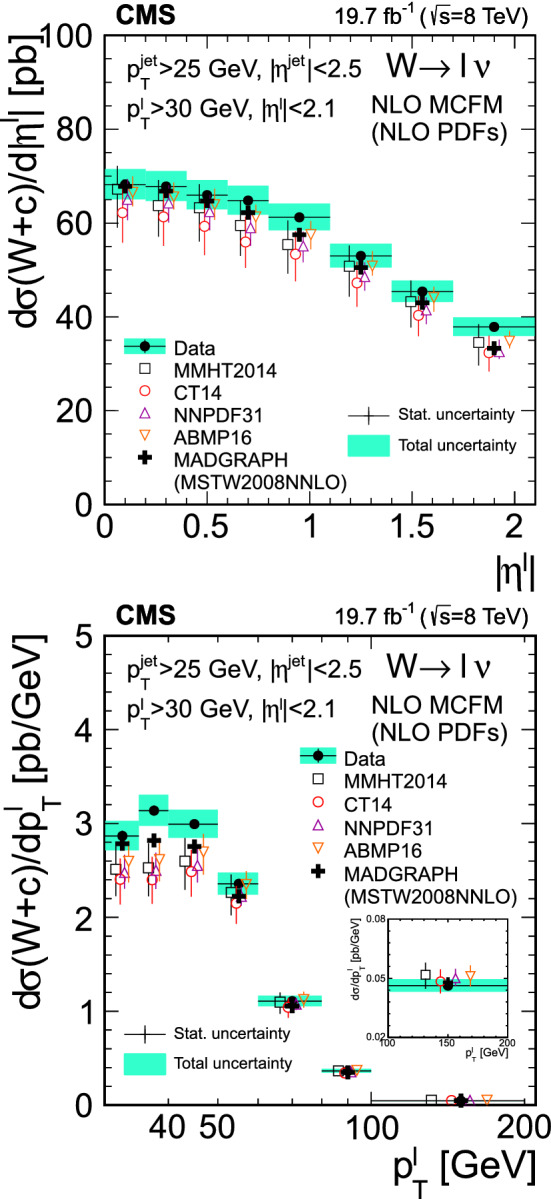
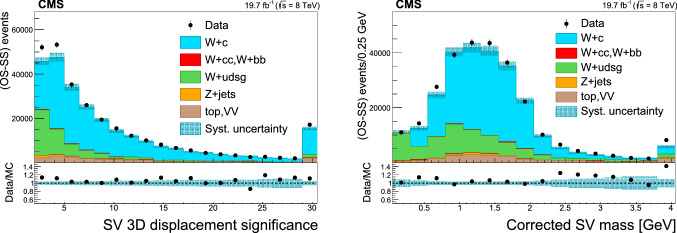
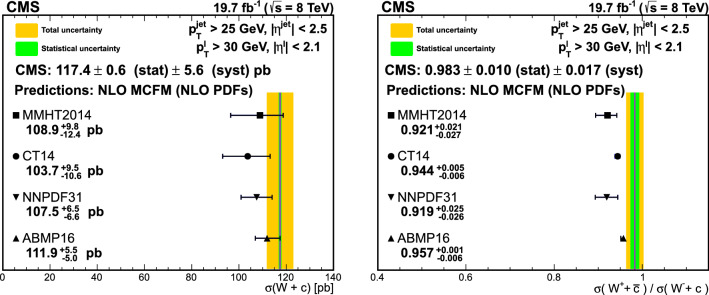
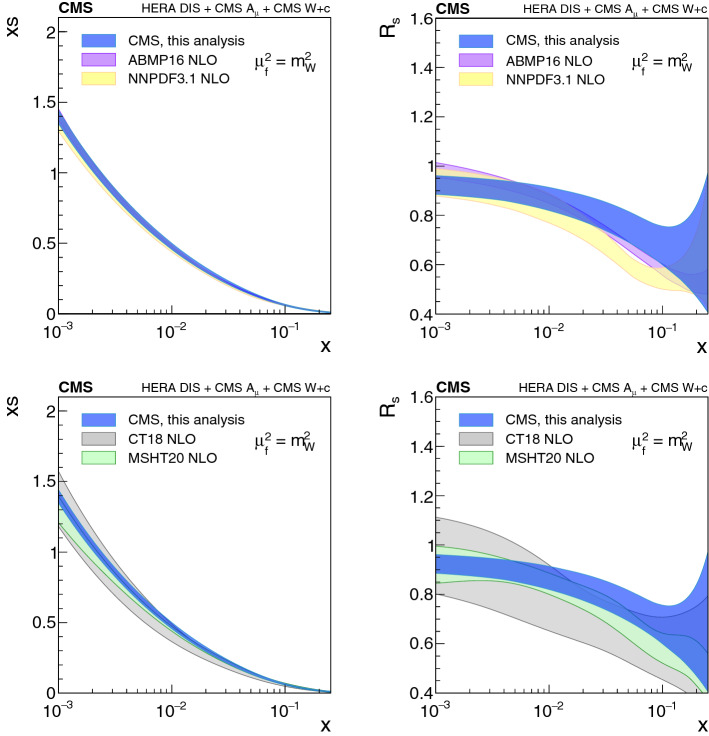
A Tumasyan
A Tumasyan
1Yerevan Physics Institute, Yerevan, Armenia
1,
W Adam
W Adam
2Institut für Hochenergiephysik, Vienna, Austria
2,
T Bergauer
T Bergauer
2Institut für Hochenergiephysik, Vienna, Austria
2,
M Dragicevic
M Dragicevic
2Institut für Hochenergiephysik, Vienna, Austria
2,
J Erö
J Erö
2Institut für Hochenergiephysik, Vienna, Austria
2,
A Escalante Del Valle
A Escalante Del Valle
2Institut für Hochenergiephysik, Vienna, Austria
2,
R Frühwirth
R Frühwirth
2Institut für Hochenergiephysik, Vienna, Austria
196 TU Wien, Wien, Austria
2,196,
M Jeitler
M Jeitler
2Institut für Hochenergiephysik, Vienna, Austria
196 TU Wien, Wien, Austria
2,196,
N Krammer
N Krammer
2Institut für Hochenergiephysik, Vienna, Austria
2,
L Lechner
L Lechner
2Institut für Hochenergiephysik, Vienna, Austria
2,
D Liko
D Liko
2Institut für Hochenergiephysik, Vienna, Austria
2,
T Madlener
T Madlener
2Institut für Hochenergiephysik, Vienna, Austria
2,
I Mikulec
I Mikulec
2Institut für Hochenergiephysik, Vienna, Austria
2,
F M Pitters
F M Pitters
2Institut für Hochenergiephysik, Vienna, Austria
2,
N Rad
N Rad
2Institut für Hochenergiephysik, Vienna, Austria
2,
J Schieck
J Schieck
2Institut für Hochenergiephysik, Vienna, Austria
196 TU Wien, Wien, Austria
2,196,
R Schöfbeck
R Schöfbeck
2Institut für Hochenergiephysik, Vienna, Austria
2,
M Spanring
M Spanring
2Institut für Hochenergiephysik, Vienna, Austria
2,
S Templ
S Templ
2Institut für Hochenergiephysik, Vienna, Austria
2,
W Waltenberger
W Waltenberger
2Institut für Hochenergiephysik, Vienna, Austria
2,
C-E Wulz
C-E Wulz
2Institut für Hochenergiephysik, Vienna, Austria
196 TU Wien, Wien, Austria
2,196,
M Zarucki
M Zarucki
2Institut für Hochenergiephysik, Vienna, Austria
2,
V Chekhovsky
V Chekhovsky
3Institute for Nuclear Problems, Minsk, Belarus
3,
A Litomin
A Litomin
3Institute for Nuclear Problems, Minsk, Belarus
3,
V Makarenko
V Makarenko
3Institute for Nuclear Problems, Minsk, Belarus
3,
J Suarez Gonzalez
J Suarez Gonzalez
3Institute for Nuclear Problems, Minsk, Belarus
3,
M R Darwish
M R Darwish
4Universiteit Antwerpen, Antwerpen, Belgium
197 Institute of Basic and Applied Sciences, Faculty of Engineering, Arab Academy for Science, Technology and Maritime Transport, Alexandria, Egypt
4,197,
E A De Wolf
E A De Wolf
4Universiteit Antwerpen, Antwerpen, Belgium
4,
D Di Croce
D Di Croce
4Universiteit Antwerpen, Antwerpen, Belgium
4,
T Janssen
T Janssen
4Universiteit Antwerpen, Antwerpen, Belgium
4,
T Kello
T Kello
4Universiteit Antwerpen, Antwerpen, Belgium
198 Université Libre de Bruxelles, Bruxelles, Belgium
4,198,
A Lelek
A Lelek
4Universiteit Antwerpen, Antwerpen, Belgium
4,
M Pieters
M Pieters
4Universiteit Antwerpen, Antwerpen, Belgium
4,
H Rejeb Sfar
H Rejeb Sfar
4Universiteit Antwerpen, Antwerpen, Belgium
4,
H Van Haevermaet
H Van Haevermaet
4Universiteit Antwerpen, Antwerpen, Belgium
4,
P Van Mechelen
P Van Mechelen
4Universiteit Antwerpen, Antwerpen, Belgium
4,
S Van Putte
S Van Putte
4Universiteit Antwerpen, Antwerpen, Belgium
4,
N Van Remortel
N Van Remortel
4Universiteit Antwerpen, Antwerpen, Belgium
4,
F Blekman
F Blekman
5Vrije Universiteit Brussel, Brussel, Belgium
5,
E S Bols
E S Bols
5Vrije Universiteit Brussel, Brussel, Belgium
5,
S S Chhibra
S S Chhibra
5Vrije Universiteit Brussel, Brussel, Belgium
5,
J D’Hondt
J D’Hondt
5Vrije Universiteit Brussel, Brussel, Belgium
5,
J De Clercq
J De Clercq
5Vrije Universiteit Brussel, Brussel, Belgium
5,
D Lontkovskyi
D Lontkovskyi
5Vrije Universiteit Brussel, Brussel, Belgium
5,
S Lowette
S Lowette
5Vrije Universiteit Brussel, Brussel, Belgium
5,
I Marchesini
I Marchesini
5Vrije Universiteit Brussel, Brussel, Belgium
5,
S Moortgat
S Moortgat
5Vrije Universiteit Brussel, Brussel, Belgium
5,
A Morton
A Morton
5Vrije Universiteit Brussel, Brussel, Belgium
5,
Q Python
Q Python
5Vrije Universiteit Brussel, Brussel, Belgium
5,
S Tavernier
S Tavernier
5Vrije Universiteit Brussel, Brussel, Belgium
5,
W Van Doninck
W Van Doninck
5Vrije Universiteit Brussel, Brussel, Belgium
5,
P Van Mulders
P Van Mulders
5Vrije Universiteit Brussel, Brussel, Belgium
5,
D Beghin
D Beghin
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
B Bilin
B Bilin
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
B Clerbaux
B Clerbaux
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
G De Lentdecker
G De Lentdecker
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
B Dorney
B Dorney
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
L Favart
L Favart
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
A Grebenyuk
A Grebenyuk
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
A K Kalsi
A K Kalsi
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
I Makarenko
I Makarenko
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
L Moureaux
L Moureaux
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
L Pétré
L Pétré
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
A Popov
A Popov
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
N Postiau
N Postiau
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
E Starling
E Starling
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
L Thomas
L Thomas
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
C Vander Velde
C Vander Velde
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
P Vanlaer
P Vanlaer
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
D Vannerom
D Vannerom
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
L Wezenbeek
L Wezenbeek
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
T Cornelis
T Cornelis
7Ghent University, Ghent, Belgium
7,
D Dobur
D Dobur
7Ghent University, Ghent, Belgium
7,
M Gruchala
M Gruchala
7Ghent University, Ghent, Belgium
7,
I Khvastunov
I Khvastunov
7Ghent University, Ghent, Belgium
199 IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
7,199,
M Niedziela
M Niedziela
7Ghent University, Ghent, Belgium
7,
C Roskas
C Roskas
7Ghent University, Ghent, Belgium
7,
K Skovpen
K Skovpen
7Ghent University, Ghent, Belgium
7,
M Tytgat
M Tytgat
7Ghent University, Ghent, Belgium
7,
W Verbeke
W Verbeke
7Ghent University, Ghent, Belgium
7,
B Vermassen
B Vermassen
7Ghent University, Ghent, Belgium
7,
M Vit
M Vit
7Ghent University, Ghent, Belgium
7,
G Bruno
G Bruno
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
F Bury
F Bury
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
C Caputo
C Caputo
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
P David
P David
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
C Delaere
C Delaere
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
M Delcourt
M Delcourt
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
I S Donertas
I S Donertas
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
A Giammanco
A Giammanco
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
V Lemaitre
V Lemaitre
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
K Mondal
K Mondal
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
J Prisciandaro
J Prisciandaro
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
A Taliercio
A Taliercio
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
M Teklishyn
M Teklishyn
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
P Vischia
P Vischia
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
S Wuyckens
S Wuyckens
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
J Zobec
J Zobec
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
G A Alves
G A Alves
9Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
9,
C Hensel
C Hensel
9Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
9,
A Moraes
A Moraes
9Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
9,
W L Aldá Júnior
W L Aldá Júnior
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
E Belchior Batista Das Chagas
E Belchior Batista Das Chagas
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
H BRANDAO MALBOUISSON
H BRANDAO MALBOUISSON
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
W Carvalho
W Carvalho
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
J Chinellato
J Chinellato
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
200 Universidade Estadual de Campinas, Campinas, Brazil
10,200,
E Coelho
E Coelho
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
E M Da Costa
E M Da Costa
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
G G Da Silveira
G G Da Silveira
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
201 Federal University of Rio Grande do Sul, Porto Alegre, Brazil
10,201,
D De JesusDamiao
D De JesusDamiao
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
S Fonseca De Souza
S Fonseca De Souza
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
J Martins
J Martins
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
202 UFMS, Nova Andradina, Brazil
10,202,
D Matos Figueiredo
D Matos Figueiredo
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
M Medina Jaime
M Medina Jaime
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
203 Universidade Federal de Pelotas, Pelotas, Brazil
10,203,
C Mora Herrera
C Mora Herrera
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
L Mundim
L Mundim
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
H Nogima
H Nogima
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
P Rebello Teles
P Rebello Teles
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
L J Sanchez Rosas
L J Sanchez Rosas
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
A Santoro
A Santoro
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
S M Silva Do Amaral
S M Silva Do Amaral
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
A Sznajder
A Sznajder
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
M Thiel
M Thiel
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
F Torres Da Silva DeAraujo
F Torres Da Silva DeAraujo
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
A Vilela Pereira
A Vilela Pereira
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
C A Bernardes
C A Bernardes
11Universidade Estadual Paulista (a), Universidade Federal do ABC (b), São Paulo, Brazil
11,
L Calligaris
L Calligaris
11Universidade Estadual Paulista (a), Universidade Federal do ABC (b), São Paulo, Brazil
11,
T R Fernandez Perez Tomei
T R Fernandez Perez Tomei
11Universidade Estadual Paulista (a), Universidade Federal do ABC (b), São Paulo, Brazil
11,
E M Gregores
E M Gregores
11Universidade Estadual Paulista (a), Universidade Federal do ABC (b), São Paulo, Brazil
11,
D S Lemos
D S Lemos
11Universidade Estadual Paulista (a), Universidade Federal do ABC (b), São Paulo, Brazil
11,
P G Mercadante
P G Mercadante
11Universidade Estadual Paulista (a), Universidade Federal do ABC (b), São Paulo, Brazil
11,
S F Novaes
S F Novaes
11Universidade Estadual Paulista (a), Universidade Federal do ABC (b), São Paulo, Brazil
11,
Sandra S Padula
Sandra S Padula
11Universidade Estadual Paulista (a), Universidade Federal do ABC (b), São Paulo, Brazil
11,
A Aleksandrov
A Aleksandrov
12Institute for Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences, Sofia, Bulgaria
12,
G Antchev
G Antchev
12Institute for Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences, Sofia, Bulgaria
12,
I Atanassov
I Atanassov
12Institute for Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences, Sofia, Bulgaria
12,
R Hadjiiska
R Hadjiiska
12Institute for Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences, Sofia, Bulgaria
12,
P Iaydjiev
P Iaydjiev
12Institute for Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences, Sofia, Bulgaria
12,
M Misheva
M Misheva
12Institute for Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences, Sofia, Bulgaria
12,
M Rodozov
M Rodozov
12Institute for Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences, Sofia, Bulgaria
12,
M Shopova
M Shopova
12Institute for Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences, Sofia, Bulgaria
12,
G Sultanov
G Sultanov
12Institute for Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences, Sofia, Bulgaria
12,
M Bonchev
M Bonchev
13University of Sofia, Sofia, Bulgaria
13,
A Dimitrov
A Dimitrov
13University of Sofia, Sofia, Bulgaria
13,
T Ivanov
T Ivanov
13University of Sofia, Sofia, Bulgaria
13,
L Litov
L Litov
13University of Sofia, Sofia, Bulgaria
13,
B Pavlov
B Pavlov
13University of Sofia, Sofia, Bulgaria
13,
P Petkov
P Petkov
13University of Sofia, Sofia, Bulgaria
13,
A Petrov
A Petrov
13University of Sofia, Sofia, Bulgaria
13,
W Fang
W Fang
14Beihang University, Beijing, China
198 Université Libre de Bruxelles, Bruxelles, Belgium
14,198,
Q Guo
Q Guo
14Beihang University, Beijing, China
14,
H Wang
H Wang
14Beihang University, Beijing, China
14,
L Yuan
L Yuan
14Beihang University, Beijing, China
14,
M Ahmad
M Ahmad
15Department of Physics, Tsinghua University, Beijing, China
15,
Z Hu
Z Hu
15Department of Physics, Tsinghua University, Beijing, China
15,
Y Wang
Y Wang
15Department of Physics, Tsinghua University, Beijing, China
15,
E Chapon
E Chapon
16Institute of High Energy Physics, Beijing, China
16,
G M Chen
G M Chen
16Institute of High Energy Physics, Beijing, China
204 University of Chinese Academy of Sciences, Beijing, China
16,204,
H S Chen
H S Chen
16Institute of High Energy Physics, Beijing, China
204 University of Chinese Academy of Sciences, Beijing, China
16,204,
M Chen
M Chen
16Institute of High Energy Physics, Beijing, China
16,
T Javaid
T Javaid
16Institute of High Energy Physics, Beijing, China
204 University of Chinese Academy of Sciences, Beijing, China
16,204,
A Kapoor
A Kapoor
16Institute of High Energy Physics, Beijing, China
16,
D Leggat
D Leggat
16Institute of High Energy Physics, Beijing, China
16,
H Liao
H Liao
16Institute of High Energy Physics, Beijing, China
16,
Z-A Liu
Z-A Liu
16Institute of High Energy Physics, Beijing, China
16,
R Sharma
R Sharma
16Institute of High Energy Physics, Beijing, China
16,
A Spiezia
A Spiezia
16Institute of High Energy Physics, Beijing, China
16,
J Tao
J Tao
16Institute of High Energy Physics, Beijing, China
16,
J Thomas-Wilsker
J Thomas-Wilsker
16Institute of High Energy Physics, Beijing, China
16,
J Wang
J Wang
16Institute of High Energy Physics, Beijing, China
16,
H Zhang
H Zhang
16Institute of High Energy Physics, Beijing, China
16,
S Zhang
S Zhang
16Institute of High Energy Physics, Beijing, China
204 University of Chinese Academy of Sciences, Beijing, China
16,204,
J Zhao
J Zhao
16Institute of High Energy Physics, Beijing, China
16,
A Agapitos
A Agapitos
17State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
17,
Y Ban
Y Ban
17State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
17,
C Chen
C Chen
17State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
17,
Q Huang
Q Huang
17State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
17,
A Levin
A Levin
17State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
17,
Q Li
Q Li
17State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
17,
M Lu
M Lu
17State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
17,
X Lyu
X Lyu
17State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
17,
Y Mao
Y Mao
17State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
17,
S J Qian
S J Qian
17State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
17,
D Wang
D Wang
17State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
17,
Q Wang
Q Wang
17State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
17,
J Xiao
J Xiao
17State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
17,
Z You
Z You
18Sun Yat-Sen University, Guangzhou, China
18,
X Gao
X Gao
19Institute of Modern Physics and Key Laboratory of Nuclear Physics and Ion-beam Application (MOE), Fudan University, Shanghai, China
198 Université Libre de Bruxelles, Bruxelles, Belgium
19,198,
M Xiao
M Xiao
20Zhejiang University, Hangzhou, China, Zhejiang, China
20,
C Avila
C Avila
21Universidad de Los Andes, Bogota, Colombia
21,
A Cabrera
A Cabrera
21Universidad de Los Andes, Bogota, Colombia
21,
C Florez
C Florez
21Universidad de Los Andes, Bogota, Colombia
21,
J Fraga
J Fraga
21Universidad de Los Andes, Bogota, Colombia
21,
A Sarkar
A Sarkar
21Universidad de Los Andes, Bogota, Colombia
21,
M A Segura Delgado
M A Segura Delgado
21Universidad de Los Andes, Bogota, Colombia
21,
J Jaramillo
J Jaramillo
22Universidad de Antioquia, Medellin, Colombia
22,
J Mejia Guisao
J Mejia Guisao
22Universidad de Antioquia, Medellin, Colombia
22,
F Ramirez
F Ramirez
22Universidad de Antioquia, Medellin, Colombia
22,
J D Ruiz Alvarez
J D Ruiz Alvarez
22Universidad de Antioquia, Medellin, Colombia
22,
C A Salazar González
C A Salazar González
22Universidad de Antioquia, Medellin, Colombia
22,
N Vanegas Arbelaez
N Vanegas Arbelaez
22Universidad de Antioquia, Medellin, Colombia
22,
D Giljanovic
D Giljanovic
23University of Split, Faculty of Electrical Engineering, Mechanical Engineering and Naval Architecture, Split, Croatia
23,
N Godinovic
N Godinovic
23University of Split, Faculty of Electrical Engineering, Mechanical Engineering and Naval Architecture, Split, Croatia
23,
D Lelas
D Lelas
23University of Split, Faculty of Electrical Engineering, Mechanical Engineering and Naval Architecture, Split, Croatia
23,
I Puljak
I Puljak
23University of Split, Faculty of Electrical Engineering, Mechanical Engineering and Naval Architecture, Split, Croatia
23,
T Sculac
T Sculac
23University of Split, Faculty of Electrical Engineering, Mechanical Engineering and Naval Architecture, Split, Croatia
23,
Z Antunovic
Z Antunovic
24University of Split, Faculty of Science, Split, Croatia
24,
M Kovac
M Kovac
24University of Split, Faculty of Science, Split, Croatia
24,
V Brigljevic
V Brigljevic
25Institute Rudjer Boskovic, Zagreb, Croatia
25,
D Ferencek
D Ferencek
25Institute Rudjer Boskovic, Zagreb, Croatia
25,
D Majumder
D Majumder
25Institute Rudjer Boskovic, Zagreb, Croatia
25,
M Roguljic
M Roguljic
25Institute Rudjer Boskovic, Zagreb, Croatia
25,
A Starodumov
A Starodumov
25Institute Rudjer Boskovic, Zagreb, Croatia
205 Institute for Theoretical and Experimental Physics named by A.I. Alikhanov of NRC ‘Kurchatov Institute’, Moscow, Russia
25,205,
T Susa
T Susa
25Institute Rudjer Boskovic, Zagreb, Croatia
25,
M W Ather
M W Ather
26University of Cyprus, Nicosia, Cyprus
26,
A Attikis
A Attikis
26University of Cyprus, Nicosia, Cyprus
26,
E Erodotou
E Erodotou
26University of Cyprus, Nicosia, Cyprus
26,
A Ioannou
A Ioannou
26University of Cyprus, Nicosia, Cyprus
26,
G Kole
G Kole
26University of Cyprus, Nicosia, Cyprus
26,
M Kolosova
M Kolosova
26University of Cyprus, Nicosia, Cyprus
26,
S Konstantinou
S Konstantinou
26University of Cyprus, Nicosia, Cyprus
26,
G Mavromanolakis
G Mavromanolakis
26University of Cyprus, Nicosia, Cyprus
26,
J Mousa
J Mousa
26University of Cyprus, Nicosia, Cyprus
26,
C Nicolaou
C Nicolaou
26University of Cyprus, Nicosia, Cyprus
26,
F Ptochos
F Ptochos
26University of Cyprus, Nicosia, Cyprus
26,
P A Razis
P A Razis
26University of Cyprus, Nicosia, Cyprus
26,
H Rykaczewski
H Rykaczewski
26University of Cyprus, Nicosia, Cyprus
26,
H Saka
H Saka
26University of Cyprus, Nicosia, Cyprus
26,
D Tsiakkouri
D Tsiakkouri
26University of Cyprus, Nicosia, Cyprus
26,
M Finger
M Finger
27Charles University, Prague, Czech Republic
206 Joint Institute for Nuclear Research, Dubna, Russia
27,206,
M Finger Jr
M Finger Jr
27Charles University, Prague, Czech Republic
206 Joint Institute for Nuclear Research, Dubna, Russia
27,206,
A Kveton
A Kveton
27Charles University, Prague, Czech Republic
27,
J Tomsa
J Tomsa
27Charles University, Prague, Czech Republic
27,
E Ayala
E Ayala
28Escuela Politecnica Nacional, Quito, Ecuador
28,
E Carrera Jarrin
E Carrera Jarrin
29Universidad San Francisco de Quito, Quito, Ecuador
29,
H Abdalla
H Abdalla
30Academy of Scientific Research and Technology of the Arab Republic of Egypt, Egyptian Network of High Energy Physics, Cairo, Egypt
207 Cairo University, Cairo, Egypt
30,207,
Y Assran
Y Assran
30Academy of Scientific Research and Technology of the Arab Republic of Egypt, Egyptian Network of High Energy Physics, Cairo, Egypt
208 Suez University, Suez, Egypt
209 British University in Egypt, Cairo, Egypt
30,208,209,
A Mohamed
A Mohamed
30Academy of Scientific Research and Technology of the Arab Republic of Egypt, Egyptian Network of High Energy Physics, Cairo, Egypt
210 Zewail City of Science and Technology, Zewail, Egypt
30,210,
M A Mahmoud
M A Mahmoud
31Center for High Energy Physics (CHEP-FU), Fayoum University, El-Fayoum, Egypt
31,
Y Mohammed
Y Mohammed
31Center for High Energy Physics (CHEP-FU), Fayoum University, El-Fayoum, Egypt
211 Fayoum University, El-Fayoum, Egypt
31,211,
S Bhowmik
S Bhowmik
32National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
32,
A Carvalho Antunes De Oliveira
A Carvalho Antunes De Oliveira
32National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
32,
R K Dewanjee
R K Dewanjee
32National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
32,
K Ehataht
K Ehataht
32National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
32,
M Kadastik
M Kadastik
32National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
32,
M Raidal
M Raidal
32National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
32,
C Veelken
C Veelken
32National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
32,
P Eerola
P Eerola
33Department of Physics, University of Helsinki, Helsinki, Finland
33,
L Forthomme
L Forthomme
33Department of Physics, University of Helsinki, Helsinki, Finland
33,
H Kirschenmann
H Kirschenmann
33Department of Physics, University of Helsinki, Helsinki, Finland
33,
K Osterberg
K Osterberg
33Department of Physics, University of Helsinki, Helsinki, Finland
33,
M Voutilainen
M Voutilainen
33Department of Physics, University of Helsinki, Helsinki, Finland
33,
E Brücken
E Brücken
34Helsinki Institute of Physics, Helsinki, Finland
34,
F Garcia
F Garcia
34Helsinki Institute of Physics, Helsinki, Finland
34,
J Havukainen
J Havukainen
34Helsinki Institute of Physics, Helsinki, Finland
34,
V Karimäki
V Karimäki
34Helsinki Institute of Physics, Helsinki, Finland
34,
M S Kim
M S Kim
34Helsinki Institute of Physics, Helsinki, Finland
34,
R Kinnunen
R Kinnunen
34Helsinki Institute of Physics, Helsinki, Finland
34,
T Lampén
T Lampén
34Helsinki Institute of Physics, Helsinki, Finland
34,
K Lassila-Perini
K Lassila-Perini
34Helsinki Institute of Physics, Helsinki, Finland
34,
S Laurila
S Laurila
34Helsinki Institute of Physics, Helsinki, Finland
34,
S Lehti
S Lehti
34Helsinki Institute of Physics, Helsinki, Finland
34,
T Lindén
T Lindén
34Helsinki Institute of Physics, Helsinki, Finland
34,
H Siikonen
H Siikonen
34Helsinki Institute of Physics, Helsinki, Finland
34,
E Tuominen
E Tuominen
34Helsinki Institute of Physics, Helsinki, Finland
34,
J Tuominiemi
J Tuominiemi
34Helsinki Institute of Physics, Helsinki, Finland
34,
P Luukka
P Luukka
35Lappeenranta University of Technology, Lappeenranta, Finland
35,
T Tuuva
T Tuuva
35Lappeenranta University of Technology, Lappeenranta, Finland
35,
C Amendola
C Amendola
36IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
36,
M Besancon
M Besancon
36IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
36,
F Couderc
F Couderc
36IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
36,
M Dejardin
M Dejardin
36IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
36,
D Denegri
D Denegri
36IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
36,
J L Faure
J L Faure
36IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
36,
F Ferri
F Ferri
36IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
36,
S Ganjour
S Ganjour
36IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
36,
A Givernaud
A Givernaud
36IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
36,
P Gras
P Gras
36IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
36,
G Hamel de Monchenault
G Hamel de Monchenault
36IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
36,
P Jarry
P Jarry
36IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
36,
B Lenzi
B Lenzi
36IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
36,
E Locci
E Locci
36IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
36,
J Malcles
J Malcles
36IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
36,
J Rander
J Rander
36IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
36,
A Rosowsky
A Rosowsky
36IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
36,
MÖ Sahin
MÖ Sahin
36IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
36,
A Savoy-Navarro
A Savoy-Navarro
36IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
212 Purdue University, West Lafayette, IN USA
36,212,
M Titov
M Titov
36IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
36,
G B Yu
G B Yu
36IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
36,
S Ahuja
S Ahuja
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
F Beaudette
F Beaudette
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
M Bonanomi
M Bonanomi
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
A Buchot Perraguin
A Buchot Perraguin
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
P Busson
P Busson
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
C Charlot
C Charlot
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
O Davignon
O Davignon
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
B Diab
B Diab
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
G Falmagne
G Falmagne
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
R Granier de Cassagnac
R Granier de Cassagnac
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
A Hakimi
A Hakimi
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
I Kucher
I Kucher
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
A Lobanov
A Lobanov
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
C Martin Perez
C Martin Perez
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
M Nguyen
M Nguyen
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
C Ochando
C Ochando
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
P Paganini
P Paganini
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
J Rembser
J Rembser
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
R Salerno
R Salerno
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
J B Sauvan
J B Sauvan
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
Y Sirois
Y Sirois
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
A Zabi
A Zabi
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
A Zghiche
A Zghiche
37Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
37,
J-L Agram
J-L Agram
38Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
213 Université de Haute Alsace, Mulhouse, France
38,213,
J Andrea
J Andrea
38Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
38,
D Bloch
D Bloch
38Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
38,
G Bourgatte
G Bourgatte
38Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
38,
J -M Brom
J -M Brom
38Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
38,
E C Chabert
E C Chabert
38Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
38,
C Collard
C Collard
38Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
38,
J -C Fontaine
J -C Fontaine
38Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
213 Université de Haute Alsace, Mulhouse, France
38,213,
D Gelé
D Gelé
38Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
38,
U Goerlach
U Goerlach
38Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
38,
C Grimault
C Grimault
38Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
38,
A -C Le Bihan
A -C Le Bihan
38Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
38,
P Van Hove
P Van Hove
38Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
38,
E Asilar
E Asilar
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
S Beauceron
S Beauceron
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
C Bernet
C Bernet
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
G Boudoul
G Boudoul
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
C Camen
C Camen
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
A Carle
A Carle
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
N Chanon
N Chanon
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
D Contardo
D Contardo
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
P Depasse
P Depasse
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
H El Mamouni
H El Mamouni
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
J Fay
J Fay
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
S Gascon
S Gascon
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
M Gouzevitch
M Gouzevitch
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
B Ille
B Ille
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
Sa Jain
Sa Jain
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
I B Laktineh
I B Laktineh
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
H Lattaud
H Lattaud
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
A Lesauvage
A Lesauvage
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
M Lethuillier
M Lethuillier
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
L Mirabito
L Mirabito
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
L Torterotot
L Torterotot
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
G Touquet
G Touquet
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
M Vander Donckt
M Vander Donckt
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
S Viret
S Viret
39Institut de Physique des 2 Infinis de Lyon (IP2I ), Villeurbanne, France
39,
G Adamov
G Adamov
40Georgian Technical University, Tbilisi, Georgia
40,
Z Tsamalaidze
Z Tsamalaidze
40Georgian Technical University, Tbilisi, Georgia
206 Joint Institute for Nuclear Research, Dubna, Russia
40,206,
L Feld
L Feld
41RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
41,
K Klein
K Klein
41RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
41,
M Lipinski
M Lipinski
41RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
41,
D Meuser
D Meuser
41RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
41,
A Pauls
A Pauls
41RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
41,
M Preuten
M Preuten
41RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
41,
M P Rauch
M P Rauch
41RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
41,
J Schulz
J Schulz
41RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
41,
M Teroerde
M Teroerde
41RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
41,
D Eliseev
D Eliseev
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
M Erdmann
M Erdmann
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
P Fackeldey
P Fackeldey
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
B Fischer
B Fischer
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
S Ghosh
S Ghosh
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
T Hebbeker
T Hebbeker
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
K Hoepfner
K Hoepfner
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
H Keller
H Keller
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
L Mastrolorenzo
L Mastrolorenzo
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
M Merschmeyer
M Merschmeyer
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
A Meyer
A Meyer
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
G Mocellin
G Mocellin
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
S Mondal
S Mondal
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
S Mukherjee
S Mukherjee
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
D Noll
D Noll
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
A Novak
A Novak
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
T Pook
T Pook
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
A Pozdnyakov
A Pozdnyakov
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
T Quast
T Quast
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
Y Rath
Y Rath
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
H Reithler
H Reithler
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
J Roemer
J Roemer
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
A Schmidt
A Schmidt
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
S C Schuler
S C Schuler
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
A Sharma
A Sharma
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
S Wiedenbeck
S Wiedenbeck
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
S Zaleski
S Zaleski
42RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
42,
C Dziwok
C Dziwok
43RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
43,
G Flügge
G Flügge
43RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
43,
W Haj Ahmad
W Haj Ahmad
43RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
214 Erzincan Binali Yildirim University, Erzincan, Turkey
43,214,
O Hlushchenko
O Hlushchenko
43RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
43,
T Kress
T Kress
43RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
43,
A Nowack
A Nowack
43RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
43,
C Pistone
C Pistone
43RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
43,
O Pooth
O Pooth
43RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
43,
D Roy
D Roy
43RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
43,
H Sert
H Sert
43RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
43,
A Stahl
A Stahl
43RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
215 CERN, European Organization for Nuclear Research, Geneva, Switzerland
43,215,
T Ziemons
T Ziemons
43RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
43,
H Aarup Petersen
H Aarup Petersen
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
M Aldaya Martin
M Aldaya Martin
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
P Asmuss
P Asmuss
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
I Babounikau
I Babounikau
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
S Baxter
S Baxter
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
O Behnke
O Behnke
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
A Bermúdez Martínez
A Bermúdez Martínez
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
A A Bin Anuar
A A Bin Anuar
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
K Borras
K Borras
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
216 RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
44,216,
V Botta
V Botta
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
D Brunner
D Brunner
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
A Campbell
A Campbell
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
A Cardini
A Cardini
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
P Connor
P Connor
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
S Consuegra Rodríguez
S Consuegra Rodríguez
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
V Danilov
V Danilov
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
A De Wit
A De Wit
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
M M Defranchis
M M Defranchis
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
L Didukh
L Didukh
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
D Domínguez Damiani
D Domínguez Damiani
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
G Eckerlin
G Eckerlin
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
D Eckstein
D Eckstein
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
T Eichhorn
T Eichhorn
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
L I Estevez Banos
L I Estevez Banos
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
E Gallo
E Gallo
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
217 University of Hamburg, Hamburg, Germany
44,217,
A Geiser
A Geiser
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
A Giraldi
A Giraldi
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
A Grohsjean
A Grohsjean
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
M Guthoff
M Guthoff
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
A Harb
A Harb
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
A Jafari
A Jafari
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
218 Isfahan University of Technology, Isfahan, Iran
44,218,
N Z Jomhari
N Z Jomhari
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
H Jung
H Jung
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
A Kasem
A Kasem
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
216 RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
44,216,
M Kasemann
M Kasemann
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
H Kaveh
H Kaveh
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
C Kleinwort
C Kleinwort
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
J Knolle
J Knolle
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
D Krücker
D Krücker
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
W Lange
W Lange
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
T Lenz
T Lenz
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
J Lidrych
J Lidrych
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
K Lipka
K Lipka
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
W Lohmann
W Lohmann
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
219 Brandenburg University of Technology, Cottbus, Germany
44,219,
R Mankel
R Mankel
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
I-A Melzer-Pellmann
I-A Melzer-Pellmann
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
J Metwally
J Metwally
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
A B Meyer
A B Meyer
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
M Meyer
M Meyer
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
M Missiroli
M Missiroli
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
J Mnich
J Mnich
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
A Mussgiller
A Mussgiller
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
V Myronenko
V Myronenko
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
Y Otarid
Y Otarid
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
D Pérez Adán
D Pérez Adán
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
S K Pflitsch
S K Pflitsch
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
D Pitzl
D Pitzl
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
A Raspereza
A Raspereza
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
A Saggio
A Saggio
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
A Saibel
A Saibel
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
M Savitskyi
M Savitskyi
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
V Scheurer
V Scheurer
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
C Schwanenberger
C Schwanenberger
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
A Singh
A Singh
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
R E Sosa Ricardo
R E Sosa Ricardo
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
N Tonon
N Tonon
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
O Turkot
O Turkot
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
A Vagnerini
A Vagnerini
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
M Van De Klundert
M Van De Klundert
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
R Walsh
R Walsh
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
D Walter
D Walter
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
Y Wen
Y Wen
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
K Wichmann
K Wichmann
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
C Wissing
C Wissing
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
S Wuchterl
S Wuchterl
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
O Zenaiev
O Zenaiev
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
R Zlebcik
R Zlebcik
44Deutsches Elektronen-Synchrotron, Hamburg, Germany
44,
R Aggleton
R Aggleton
45University of Hamburg, Hamburg, Germany
45,
S Bein
S Bein
45University of Hamburg, Hamburg, Germany
45,
L Benato
L Benato
45University of Hamburg, Hamburg, Germany
45,
A Benecke
A Benecke
45University of Hamburg, Hamburg, Germany
45,
K De Leo
K De Leo
45University of Hamburg, Hamburg, Germany
45,
T Dreyer
T Dreyer
45University of Hamburg, Hamburg, Germany
45,
A Ebrahimi
A Ebrahimi
45University of Hamburg, Hamburg, Germany
45,
M Eich
M Eich
45University of Hamburg, Hamburg, Germany
45,
F Feindt
F Feindt
45University of Hamburg, Hamburg, Germany
45,
A Fröhlich
A Fröhlich
45University of Hamburg, Hamburg, Germany
45,
C Garbers
C Garbers
45University of Hamburg, Hamburg, Germany
45,
E Garutti
E Garutti
45University of Hamburg, Hamburg, Germany
45,
P Gunnellini
P Gunnellini
45University of Hamburg, Hamburg, Germany
45,
J Haller
J Haller
45University of Hamburg, Hamburg, Germany
45,
A Hinzmann
A Hinzmann
45University of Hamburg, Hamburg, Germany
45,
A Karavdina
A Karavdina
45University of Hamburg, Hamburg, Germany
45,
G Kasieczka
G Kasieczka
45University of Hamburg, Hamburg, Germany
45,
R Klanner
R Klanner
45University of Hamburg, Hamburg, Germany
45,
R Kogler
R Kogler
45University of Hamburg, Hamburg, Germany
45,
V Kutzner
V Kutzner
45University of Hamburg, Hamburg, Germany
45,
J Lange
J Lange
45University of Hamburg, Hamburg, Germany
45,
T Lange
T Lange
45University of Hamburg, Hamburg, Germany
45,
A Malara
A Malara
45University of Hamburg, Hamburg, Germany
45,
C E N Niemeyer
C E N Niemeyer
45University of Hamburg, Hamburg, Germany
45,
A Nigamova
A Nigamova
45University of Hamburg, Hamburg, Germany
45,
K J Pena Rodriguez
K J Pena Rodriguez
45University of Hamburg, Hamburg, Germany
45,
O Rieger
O Rieger
45University of Hamburg, Hamburg, Germany
45,
P Schleper
P Schleper
45University of Hamburg, Hamburg, Germany
45,
S Schumann
S Schumann
45University of Hamburg, Hamburg, Germany
45,
J Schwandt
J Schwandt
45University of Hamburg, Hamburg, Germany
45,
D Schwarz
D Schwarz
45University of Hamburg, Hamburg, Germany
45,
J Sonneveld
J Sonneveld
45University of Hamburg, Hamburg, Germany
45,
H Stadie
H Stadie
45University of Hamburg, Hamburg, Germany
45,
G Steinbrück
G Steinbrück
45University of Hamburg, Hamburg, Germany
45,
B Vormwald
B Vormwald
45University of Hamburg, Hamburg, Germany
45,
I Zoi
I Zoi
45University of Hamburg, Hamburg, Germany
45,
S Baur
S Baur
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
J Bechtel
J Bechtel
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
T Berger
T Berger
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
E Butz
E Butz
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
R Caspart
R Caspart
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
T Chwalek
T Chwalek
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
W De Boer
W De Boer
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
A Dierlamm
A Dierlamm
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
A Droll
A Droll
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
K El Morabit
K El Morabit
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
N Faltermann
N Faltermann
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
K Flöh
K Flöh
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
M Giffels
M Giffels
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
A Gottmann
A Gottmann
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
F Hartmann
F Hartmann
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
215 CERN, European Organization for Nuclear Research, Geneva, Switzerland
46,215,
C Heidecker
C Heidecker
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
U Husemann
U Husemann
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
M A Iqbal
M A Iqbal
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
I Katkov
I Katkov
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
220 Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
46,220,
P Keicher
P Keicher
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
R Koppenhöfer
R Koppenhöfer
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
S Maier
S Maier
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
M Metzler
M Metzler
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
S Mitra
S Mitra
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
D Müller
D Müller
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
Th Müller
Th Müller
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
M Musich
M Musich
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
G Quast
G Quast
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
K Rabbertz
K Rabbertz
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
J Rauser
J Rauser
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
D Savoiu
D Savoiu
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
D Schäfer
D Schäfer
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
M Schnepf
M Schnepf
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
M Schröder
M Schröder
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
D Seith
D Seith
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
I Shvetsov
I Shvetsov
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
H J Simonis
H J Simonis
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
R Ulrich
R Ulrich
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
M Wassmer
M Wassmer
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
M Weber
M Weber
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
R Wolf
R Wolf
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
S Wozniewski
S Wozniewski
46Karlsruher Institut fuer Technologie, Karlsruhe, Germany
46,
G Anagnostou
G Anagnostou
47Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
47,
P Asenov
P Asenov
47Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
47,
G Daskalakis
G Daskalakis
47Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
47,
T Geralis
T Geralis
47Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
47,
A Kyriakis
A Kyriakis
47Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
47,
D Loukas
D Loukas
47Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
47,
G Paspalaki
G Paspalaki
47Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
47,
A Stakia
A Stakia
47Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
47,
M Diamantopoulou
M Diamantopoulou
48National and Kapodistrian University of Athens, Athens, Greece
48,
D Karasavvas
D Karasavvas
48National and Kapodistrian University of Athens, Athens, Greece
48,
G Karathanasis
G Karathanasis
48National and Kapodistrian University of Athens, Athens, Greece
48,
P Kontaxakis
P Kontaxakis
48National and Kapodistrian University of Athens, Athens, Greece
48,
C K Koraka
C K Koraka
48National and Kapodistrian University of Athens, Athens, Greece
48,
A Manousakis-Katsikakis
A Manousakis-Katsikakis
48National and Kapodistrian University of Athens, Athens, Greece
48,
A Panagiotou
A Panagiotou
48National and Kapodistrian University of Athens, Athens, Greece
48,
I Papavergou
I Papavergou
48National and Kapodistrian University of Athens, Athens, Greece
48,
N Saoulidou
N Saoulidou
48National and Kapodistrian University of Athens, Athens, Greece
48,
K Theofilatos
K Theofilatos
48National and Kapodistrian University of Athens, Athens, Greece
48,
K Vellidis
K Vellidis
48National and Kapodistrian University of Athens, Athens, Greece
48,
E Vourliotis
E Vourliotis
48National and Kapodistrian University of Athens, Athens, Greece
48,
G Bakas
G Bakas
49National Technical University of Athens, Athens, Greece
49,
K Kousouris
K Kousouris
49National Technical University of Athens, Athens, Greece
49,
I Papakrivopoulos
I Papakrivopoulos
49National Technical University of Athens, Athens, Greece
49,
G Tsipolitis
G Tsipolitis
49National Technical University of Athens, Athens, Greece
49,
A Zacharopoulou
A Zacharopoulou
49National Technical University of Athens, Athens, Greece
49,
I Evangelou
I Evangelou
50University of Ioánnina, Ioánnina, Greece
50,
C Foudas
C Foudas
50University of Ioánnina, Ioánnina, Greece
50,
P Gianneios
P Gianneios
50University of Ioánnina, Ioánnina, Greece
50,
P Katsoulis
P Katsoulis
50University of Ioánnina, Ioánnina, Greece
50,
P Kokkas
P Kokkas
50University of Ioánnina, Ioánnina, Greece
50,
S Mallios
S Mallios
50University of Ioánnina, Ioánnina, Greece
50,
K Manitara
K Manitara
50University of Ioánnina, Ioánnina, Greece
50,
N Manthos
N Manthos
50University of Ioánnina, Ioánnina, Greece
50,
I Papadopoulos
I Papadopoulos
50University of Ioánnina, Ioánnina, Greece
50,
J Strologas
J Strologas
50University of Ioánnina, Ioánnina, Greece
50,
M Bartók
M Bartók
51MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
221 Institute of Physics, University of Debrecen, Debrecen, Hungary
51,221,
R Chudasama
R Chudasama
51MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
51,
M Csanad
M Csanad
51MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
51,
M M A Gadallah
M M A Gadallah
51MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
222 Physics Department, Faculty of Science, Assiut University, Assiut, Egypt
51,222,
S Lökös
S Lökös
51MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
223 MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
51,223,
P Major
P Major
51MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
51,
K Mandal
K Mandal
51MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
51,
A Mehta
A Mehta
51MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
51,
G Pasztor
G Pasztor
51MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
51,
O Surányi
O Surányi
51MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
51,
G I Veres
G I Veres
51MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
51,
G Bencze
G Bencze
52Wigner Research Centre for Physics, Budapest, Hungary
52,
C Hajdu
C Hajdu
52Wigner Research Centre for Physics, Budapest, Hungary
52,
D Horvath
D Horvath
52Wigner Research Centre for Physics, Budapest, Hungary
224 Institute of Nuclear Research ATOMKI, Debrecen, Hungary
52,224,
F Sikler
F Sikler
52Wigner Research Centre for Physics, Budapest, Hungary
52,
V Veszpremi
V Veszpremi
52Wigner Research Centre for Physics, Budapest, Hungary
52,
G Vesztergombi
G Vesztergombi
52Wigner Research Centre for Physics, Budapest, Hungary
52,
S Czellar
S Czellar
53Institute of Nuclear Research ATOMKI, Debrecen, Hungary
53,
J Karancsi
J Karancsi
53Institute of Nuclear Research ATOMKI, Debrecen, Hungary
221 Institute of Physics, University of Debrecen, Debrecen, Hungary
53,221,
J Molnar
J Molnar
53Institute of Nuclear Research ATOMKI, Debrecen, Hungary
53,
Z Szillasi
Z Szillasi
53Institute of Nuclear Research ATOMKI, Debrecen, Hungary
53,
D Teyssier
D Teyssier
53Institute of Nuclear Research ATOMKI, Debrecen, Hungary
53,
P Raics
P Raics
54Institute of Physics, University of Debrecen, Debrecen, Hungary
54,
Z L Trocsanyi
Z L Trocsanyi
54Institute of Physics, University of Debrecen, Debrecen, Hungary
54,
B Ujvari
B Ujvari
54Institute of Physics, University of Debrecen, Debrecen, Hungary
54,
T Csorgo
T Csorgo
55Karoly Robert Campus, MATE Institute of Technology, Gyongyos, Hungary
55,
F Nemes
F Nemes
55Karoly Robert Campus, MATE Institute of Technology, Gyongyos, Hungary
55,
T Novak
T Novak
55Karoly Robert Campus, MATE Institute of Technology, Gyongyos, Hungary
55,
S Choudhury
S Choudhury
56Indian Institute of Science (IISc), Bangalore, India
56,
J R Komaragiri
J R Komaragiri
56Indian Institute of Science (IISc), Bangalore, India
56,
D Kumar
D Kumar
56Indian Institute of Science (IISc), Bangalore, India
56,
L Panwar
L Panwar
56Indian Institute of Science (IISc), Bangalore, India
56,
P C Tiwari
P C Tiwari
56Indian Institute of Science (IISc), Bangalore, India
56,
S Bahinipati
S Bahinipati
57National Institute of Science Education and Research, HBNI, Bhubaneswar, India
225 IIT Bhubaneswar, Bhubaneswar, India
57,225,
D Dash
D Dash
57National Institute of Science Education and Research, HBNI, Bhubaneswar, India
57,
C Kar
C Kar
57National Institute of Science Education and Research, HBNI, Bhubaneswar, India
57,
P Mal
P Mal
57National Institute of Science Education and Research, HBNI, Bhubaneswar, India
57,
T Mishra
T Mishra
57National Institute of Science Education and Research, HBNI, Bhubaneswar, India
57,
V K Muraleedharan Nair Bindhu
V K Muraleedharan Nair Bindhu
57National Institute of Science Education and Research, HBNI, Bhubaneswar, India
57,
A Nayak
A Nayak
57National Institute of Science Education and Research, HBNI, Bhubaneswar, India
226 Institute of Physics, Bhubaneswar, India
57,226,
D K Sahoo
D K Sahoo
57National Institute of Science Education and Research, HBNI, Bhubaneswar, India
225 IIT Bhubaneswar, Bhubaneswar, India
57,225,
N Sur
N Sur
57National Institute of Science Education and Research, HBNI, Bhubaneswar, India
57,
S K Swain
S K Swain
57National Institute of Science Education and Research, HBNI, Bhubaneswar, India
57,
S Bansal
S Bansal
58Panjab University, Chandigarh, India
58,
S B Beri
S B Beri
58Panjab University, Chandigarh, India
58,
V Bhatnagar
V Bhatnagar
58Panjab University, Chandigarh, India
58,
S Chauhan
S Chauhan
58Panjab University, Chandigarh, India
58,
N Dhingra
N Dhingra
58Panjab University, Chandigarh, India
227 G.H.G. Khalsa College, Punjab, India
58,227,
R Gupta
R Gupta
58Panjab University, Chandigarh, India
58,
A Kaur
A Kaur
58Panjab University, Chandigarh, India
58,
S Kaur
S Kaur
58Panjab University, Chandigarh, India
58,
P Kumari
P Kumari
58Panjab University, Chandigarh, India
58,
M Meena
M Meena
58Panjab University, Chandigarh, India
58,
K Sandeep
K Sandeep
58Panjab University, Chandigarh, India
58,
S Sharma
S Sharma
58Panjab University, Chandigarh, India
58,
J B Singh
J B Singh
58Panjab University, Chandigarh, India
58,
A K Virdi
A K Virdi
58Panjab University, Chandigarh, India
58,
A Ahmed
A Ahmed
59University of Delhi, Delhi, India
59,
A Bhardwaj
A Bhardwaj
59University of Delhi, Delhi, India
59,
B C Choudhary
B C Choudhary
59University of Delhi, Delhi, India
59,
R B Garg
R B Garg
59University of Delhi, Delhi, India
59,
M Gola
M Gola
59University of Delhi, Delhi, India
59,
S Keshri
S Keshri
59University of Delhi, Delhi, India
59,
A Kumar
A Kumar
59University of Delhi, Delhi, India
59,
M Naimuddin
M Naimuddin
59University of Delhi, Delhi, India
59,
P Priyanka
P Priyanka
59University of Delhi, Delhi, India
59,
K Ranjan
K Ranjan
59University of Delhi, Delhi, India
59,
A Shah
A Shah
59University of Delhi, Delhi, India
59,
M Bharti
M Bharti
60Saha Institute of Nuclear Physics, HBNI, Kolkata, India
228 Shoolini University, Solan, India
60,228,
R Bhattacharya
R Bhattacharya
60Saha Institute of Nuclear Physics, HBNI, Kolkata, India
60,
S Bhattacharya
S Bhattacharya
60Saha Institute of Nuclear Physics, HBNI, Kolkata, India
60,
D Bhowmik
D Bhowmik
60Saha Institute of Nuclear Physics, HBNI, Kolkata, India
60,
S Dutta
S Dutta
60Saha Institute of Nuclear Physics, HBNI, Kolkata, India
60,
S Ghosh
S Ghosh
60Saha Institute of Nuclear Physics, HBNI, Kolkata, India
60,
B Gomber
B Gomber
60Saha Institute of Nuclear Physics, HBNI, Kolkata, India
229 University of Hyderabad, Hyderabad, India
60,229,
M Maity
M Maity
60Saha Institute of Nuclear Physics, HBNI, Kolkata, India
230 University of Visva-Bharati, Santiniketan, India
60,230,
S Nandan
S Nandan
60Saha Institute of Nuclear Physics, HBNI, Kolkata, India
60,
P Palit
P Palit
60Saha Institute of Nuclear Physics, HBNI, Kolkata, India
60,
A Purohit
A Purohit
60Saha Institute of Nuclear Physics, HBNI, Kolkata, India
60,
P K Rout
P K Rout
60Saha Institute of Nuclear Physics, HBNI, Kolkata, India
60,
G Saha
G Saha
60Saha Institute of Nuclear Physics, HBNI, Kolkata, India
60,
S Sarkar
S Sarkar
60Saha Institute of Nuclear Physics, HBNI, Kolkata, India
60,
M Sharan
M Sharan
60Saha Institute of Nuclear Physics, HBNI, Kolkata, India
60,
B Singh
B Singh
60Saha Institute of Nuclear Physics, HBNI, Kolkata, India
228 Shoolini University, Solan, India
60,228,
S Thakur
S Thakur
60Saha Institute of Nuclear Physics, HBNI, Kolkata, India
228 Shoolini University, Solan, India
60,228,
P K Behera
P K Behera
61Indian Institute of Technology Madras, Madras, India
61,
S C Behera
S C Behera
61Indian Institute of Technology Madras, Madras, India
61,
P Kalbhor
P Kalbhor
61Indian Institute of Technology Madras, Madras, India
61,
A Muhammad
A Muhammad
61Indian Institute of Technology Madras, Madras, India
61,
R Pradhan
R Pradhan
61Indian Institute of Technology Madras, Madras, India
61,
P R Pujahari
P R Pujahari
61Indian Institute of Technology Madras, Madras, India
61,
A Sharma
A Sharma
61Indian Institute of Technology Madras, Madras, India
61,
A K Sikdar
A K Sikdar
61Indian Institute of Technology Madras, Madras, India
61,
D Dutta
D Dutta
62Bhabha Atomic Research Centre, Mumbai, India
62,
V Kumar
V Kumar
62Bhabha Atomic Research Centre, Mumbai, India
62,
K Naskar
K Naskar
62Bhabha Atomic Research Centre, Mumbai, India
231 Indian Institute of Technology (IIT), Mumbai, India
62,231,
P K Netrakanti
P K Netrakanti
62Bhabha Atomic Research Centre, Mumbai, India
62,
L M Pant
L M Pant
62Bhabha Atomic Research Centre, Mumbai, India
62,
P Shukla
P Shukla
62Bhabha Atomic Research Centre, Mumbai, India
62,
T Aziz
T Aziz
63Tata Institute of Fundamental Research-A, Mumbai, India
63,
M A Bhat
M A Bhat
63Tata Institute of Fundamental Research-A, Mumbai, India
63,
S Dugad
S Dugad
63Tata Institute of Fundamental Research-A, Mumbai, India
63,
R Kumar Verma
R Kumar Verma
63Tata Institute of Fundamental Research-A, Mumbai, India
63,
G B Mohanty
G B Mohanty
63Tata Institute of Fundamental Research-A, Mumbai, India
63,
U Sarkar
U Sarkar
63Tata Institute of Fundamental Research-A, Mumbai, India
63,
S Banerjee
S Banerjee
64Tata Institute of Fundamental Research-B, Mumbai, India
64,
S Bhattacharya
S Bhattacharya
64Tata Institute of Fundamental Research-B, Mumbai, India
64,
S Chatterjee
S Chatterjee
64Tata Institute of Fundamental Research-B, Mumbai, India
64,
M Guchait
M Guchait
64Tata Institute of Fundamental Research-B, Mumbai, India
64,
S Karmakar
S Karmakar
64Tata Institute of Fundamental Research-B, Mumbai, India
64,
S Kumar
S Kumar
64Tata Institute of Fundamental Research-B, Mumbai, India
64,
G Majumder
G Majumder
64Tata Institute of Fundamental Research-B, Mumbai, India
64,
K Mazumdar
K Mazumdar
64Tata Institute of Fundamental Research-B, Mumbai, India
64,
S Mukherjee
S Mukherjee
64Tata Institute of Fundamental Research-B, Mumbai, India
64,
D Roy
D Roy
64Tata Institute of Fundamental Research-B, Mumbai, India
64,
S Dube
S Dube
65Indian Institute of Science Education and Research (IISER), Pune, India
65,
B Kansal
B Kansal
65Indian Institute of Science Education and Research (IISER), Pune, India
65,
S Pandey
S Pandey
65Indian Institute of Science Education and Research (IISER), Pune, India
65,
A Rane
A Rane
65Indian Institute of Science Education and Research (IISER), Pune, India
65,
A Rastogi
A Rastogi
65Indian Institute of Science Education and Research (IISER), Pune, India
65,
S Sharma
S Sharma
65Indian Institute of Science Education and Research (IISER), Pune, India
65,
H Bakhshiansohi
H Bakhshiansohi
66Isfahan University of Technology, Isfahan, Iran
232 Deutsches Elektronen-Synchrotron, Hamburg, Germany
66,232,
S Chenarani
S Chenarani
67Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
233 Department of Physics, University of Science and Technology of Mazandaran, Behshahr, Iran
67,233,
S M Etesami
S M Etesami
67Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
67,
M Khakzad
M Khakzad
67Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
67,
M Mohammadi Najafabadi
M Mohammadi Najafabadi
67Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
67,
M Felcini
M Felcini
68University College Dublin, Dublin, Ireland
68,
M Grunewald
M Grunewald
68University College Dublin, Dublin, Ireland
68,
M Abbrescia
M Abbrescia
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
R Aly
R Aly
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
234 INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,234,
C Aruta
C Aruta
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
A Colaleo
A Colaleo
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
D Creanza
D Creanza
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
N De Filippis
N De Filippis
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
M De Palma
M De Palma
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
A Di Florio
A Di Florio
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
A Di Pilato
A Di Pilato
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
W Elmetenawee
W Elmetenawee
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
L Fiore
L Fiore
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
A Gelmi
A Gelmi
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
M Gul
M Gul
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
G Iaselli
G Iaselli
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
M Ince
M Ince
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
S Lezki
S Lezki
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
G Maggi
G Maggi
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
M Maggi
M Maggi
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
I Margjeka
I Margjeka
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
V Mastrapasqua
V Mastrapasqua
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
J A Merlin
J A Merlin
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
S My
S My
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
S Nuzzo
S Nuzzo
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
A Pompili
A Pompili
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
G Pugliese
G Pugliese
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
A Ranieri
A Ranieri
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
G Selvaggi
G Selvaggi
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
L Silvestris
L Silvestris
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
F M Simone
F M Simone
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
R Venditti
R Venditti
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
P Verwilligen
P Verwilligen
69INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
69,
G Abbiendi
G Abbiendi
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
C Battilana
C Battilana
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
D Bonacorsi
D Bonacorsi
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
L Borgonovi
L Borgonovi
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
S Braibant-Giacomelli
S Braibant-Giacomelli
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
R Campanini
R Campanini
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
P Capiluppi
P Capiluppi
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
A Castro
A Castro
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
F R Cavallo
F R Cavallo
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
C Ciocca
C Ciocca
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
M Cuffiani
M Cuffiani
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
G M Dallavalle
G M Dallavalle
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
T Diotalevi
T Diotalevi
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
F Fabbri
F Fabbri
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
A Fanfani
A Fanfani
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
E Fontanesi
E Fontanesi
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
P Giacomelli
P Giacomelli
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
L Giommi
L Giommi
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
C Grandi
C Grandi
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
L Guiducci
L Guiducci
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
F Iemmi
F Iemmi
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
S Lo Meo
S Lo Meo
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
235 Italian National Agency for New Technologies, Energy and Sustainable Economic Development, Bologna, Italy
70,235,
S Marcellini
S Marcellini
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
G Masetti
G Masetti
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
F L Navarria
F L Navarria
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
A Perrotta
A Perrotta
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
F Primavera
F Primavera
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
T Rovelli
T Rovelli
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
G P Siroli
G P Siroli
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
N Tosi
N Tosi
70INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
70,
S Albergo
S Albergo
71INFN Sezione di Catania, Università di Catania, Catania, Italy
236 Centro Siciliano di Fisica Nucleare e di Struttura Della Materia, Catania, Italy
71,236,
S Costa
S Costa
71INFN Sezione di Catania, Università di Catania, Catania, Italy
236 Centro Siciliano di Fisica Nucleare e di Struttura Della Materia, Catania, Italy
71,236,
A Di Mattia
A Di Mattia
71INFN Sezione di Catania, Università di Catania, Catania, Italy
71,
R Potenza
R Potenza
71INFN Sezione di Catania, Università di Catania, Catania, Italy
71,
A Tricomi
A Tricomi
71INFN Sezione di Catania, Università di Catania, Catania, Italy
236 Centro Siciliano di Fisica Nucleare e di Struttura Della Materia, Catania, Italy
71,236,
C Tuve
C Tuve
71INFN Sezione di Catania, Università di Catania, Catania, Italy
71,
G Barbagli
G Barbagli
72INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
72,
A Cassese
A Cassese
72INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
72,
R Ceccarelli
R Ceccarelli
72INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
72,
V Ciulli
V Ciulli
72INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
72,
C Civinini
C Civinini
72INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
72,
R D’Alessandro
R D’Alessandro
72INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
72,
F Fiori
F Fiori
72INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
72,
E Focardi
E Focardi
72INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
72,
G Latino
G Latino
72INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
72,
P Lenzi
P Lenzi
72INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
72,
M Lizzo
M Lizzo
72INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
72,
M Meschini
M Meschini
72INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
72,
S Paoletti
S Paoletti
72INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
72,
R Seidita
R Seidita
72INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
72,
G Sguazzoni
G Sguazzoni
72INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
72,
L Viliani
L Viliani
72INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
72,
L Benussi
L Benussi
73INFN Laboratori Nazionali di Frascati, Frascati, Italy
73,
S Bianco
S Bianco
73INFN Laboratori Nazionali di Frascati, Frascati, Italy
73,
D Piccolo
D Piccolo
73INFN Laboratori Nazionali di Frascati, Frascati, Italy
73,
M Bozzo
M Bozzo
74INFN Sezione di Genova, Università di Genova, Genoa, Italy
74,
F Ferro
F Ferro
74INFN Sezione di Genova, Università di Genova, Genoa, Italy
74,
R Mulargia
R Mulargia
74INFN Sezione di Genova, Università di Genova, Genoa, Italy
74,
E Robutti
E Robutti
74INFN Sezione di Genova, Università di Genova, Genoa, Italy
74,
S Tosi
S Tosi
74INFN Sezione di Genova, Università di Genova, Genoa, Italy
74,
A Benaglia
A Benaglia
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
75,
A Beschi
A Beschi
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
75,
F Brivio
F Brivio
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
75,
F Cetorelli
F Cetorelli
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
75,
V Ciriolo
V Ciriolo
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
215 CERN, European Organization for Nuclear Research, Geneva, Switzerland
75,215,
F De Guio
F De Guio
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
75,
M E Dinardo
M E Dinardo
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
75,
P Dini
P Dini
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
75,
S Gennai
S Gennai
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
75,
A Ghezzi
A Ghezzi
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
75,
P Govoni
P Govoni
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
75,
L Guzzi
L Guzzi
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
75,
M Malberti
M Malberti
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
75,
S Malvezzi
S Malvezzi
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
75,
D Menasce
D Menasce
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
75,
F Monti
F Monti
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
75,
L Moroni
L Moroni
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
75,
M Paganoni
M Paganoni
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
75,
D Pedrini
D Pedrini
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
75,
S Ragazzi
S Ragazzi
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
75,
T Tabarelli de Fatis
T Tabarelli de Fatis
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
75,
D Valsecchi
D Valsecchi
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
215 CERN, European Organization for Nuclear Research, Geneva, Switzerland
75,215,
D Zuolo
D Zuolo
75INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
75,
S Buontempo
S Buontempo
76INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Napoli, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
76,
N Cavallo
N Cavallo
76INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Napoli, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
76,
A De Iorio
A De Iorio
76INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Napoli, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
76,
F Fabozzi
F Fabozzi
76INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Napoli, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
76,
F Fienga
F Fienga
76INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Napoli, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
76,
A O M Iorio
A O M Iorio
76INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Napoli, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
76,
L Lista
L Lista
76INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Napoli, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
76,
S Meola
S Meola
76INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Napoli, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
215 CERN, European Organization for Nuclear Research, Geneva, Switzerland
76,215,
P Paolucci
P Paolucci
76INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Napoli, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
215 CERN, European Organization for Nuclear Research, Geneva, Switzerland
76,215,
B Rossi
B Rossi
76INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Napoli, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
76,
C Sciacca
C Sciacca
76INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Napoli, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
76,
E Voevodina
E Voevodina
76INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Napoli, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
76,
P Azzi
P Azzi
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
N Bacchetta
N Bacchetta
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
D Bisello
D Bisello
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
A Boletti
A Boletti
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
A Bragagnolo
A Bragagnolo
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
R Carlin
R Carlin
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
P Checchia
P Checchia
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
P De CastroManzano
P De CastroManzano
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
T Dorigo
T Dorigo
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
F Gasparini
F Gasparini
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
U Gasparini
U Gasparini
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
S Y Hoh
S Y Hoh
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
L Layer
L Layer
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
237 Università di Napoli ’Federico II’, Naples, Italy
77,237,
M Margoni
M Margoni
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
A T Meneguzzo
A T Meneguzzo
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
M Presilla
M Presilla
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
P Ronchese
P Ronchese
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
R Rossin
R Rossin
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
F Simonetto
F Simonetto
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
G Strong
G Strong
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
A Tiko
A Tiko
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
M Tosi
M Tosi
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
H YARAR
H YARAR
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
M Zanetti
M Zanetti
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
P Zotto
P Zotto
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
A Zucchetta
A Zucchetta
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
G Zumerle
G Zumerle
77INFN Sezione di Padova, Università di Padova, Padova, Italy, Università di Trento, Trento, Italy
77,
C Aime‘
C Aime‘
78INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
78,
A Braghieri
A Braghieri
78INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
78,
S Calzaferri
S Calzaferri
78INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
78,
D Fiorina
D Fiorina
78INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
78,
P Montagna
P Montagna
78INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
78,
S P Ratti
S P Ratti
78INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
78,
V Re
V Re
78INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
78,
M Ressegotti
M Ressegotti
78INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
78,
C Riccardi
C Riccardi
78INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
78,
P Salvini
P Salvini
78INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
78,
I Vai
I Vai
78INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
78,
P Vitulo
P Vitulo
78INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
78,
M Biasini
M Biasini
79INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
79,
G M Bilei
G M Bilei
79INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
79,
D Ciangottini
D Ciangottini
79INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
79,
L Fanò
L Fanò
79INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
79,
P Lariccia
P Lariccia
79INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
79,
G Mantovani
G Mantovani
79INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
79,
V Mariani
V Mariani
79INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
79,
M Menichelli
M Menichelli
79INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
79,
F Moscatelli
F Moscatelli
79INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
79,
A Piccinelli
A Piccinelli
79INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
79,
A Rossi
A Rossi
79INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
79,
A Santocchia
A Santocchia
79INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
79,
D Spiga
D Spiga
79INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
79,
T Tedeschi
T Tedeschi
79INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
79,
K Androsov
K Androsov
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
P Azzurri
P Azzurri
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
G Bagliesi
G Bagliesi
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
V Bertacchi
V Bertacchi
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
L Bianchini
L Bianchini
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
T Boccali
T Boccali
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
R Castaldi
R Castaldi
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
M A Ciocci
M A Ciocci
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
R Dell’Orso
R Dell’Orso
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
M R Di Domenico
M R Di Domenico
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
S Donato
S Donato
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
L Giannini
L Giannini
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
A Giassi
A Giassi
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
M T Grippo
M T Grippo
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
F Ligabue
F Ligabue
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
E Manca
E Manca
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
G Mandorli
G Mandorli
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
A Messineo
A Messineo
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
F Palla
F Palla
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
G Ramirez-Sanchez
G Ramirez-Sanchez
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
A Rizzi
A Rizzi
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
G Rolandi
G Rolandi
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
S Roy Chowdhury
S Roy Chowdhury
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
A Scribano
A Scribano
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
N Shafiei
N Shafiei
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
P Spagnolo
P Spagnolo
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
R Tenchini
R Tenchini
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
G Tonelli
G Tonelli
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
N Turini
N Turini
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
A Venturi
A Venturi
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
P G Verdini
P G Verdini
80INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
80,
F Cavallari
F Cavallari
81INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
81,
M Cipriani
M Cipriani
81INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
81,
D Del Re
D Del Re
81INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
81,
E Di Marco
E Di Marco
81INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
81,
M Diemoz
M Diemoz
81INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
81,
E Longo
E Longo
81INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
81,
P Meridiani
P Meridiani
81INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
81,
G Organtini
G Organtini
81INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
81,
F Pandolfi
F Pandolfi
81INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
81,
R Paramatti
R Paramatti
81INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
81,
C Quaranta
C Quaranta
81INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
81,
S Rahatlou
S Rahatlou
81INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
81,
C Rovelli
C Rovelli
81INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
81,
F Santanastasio
F Santanastasio
81INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
81,
L Soffi
L Soffi
81INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
81,
R Tramontano
R Tramontano
81INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
81,
N Amapane
N Amapane
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
R Arcidiacono
R Arcidiacono
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
S Argiro
S Argiro
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
M Arneodo
M Arneodo
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
N Bartosik
N Bartosik
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
R Bellan
R Bellan
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
A Bellora
A Bellora
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
C Biino
C Biino
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
A Cappati
A Cappati
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
N Cartiglia
N Cartiglia
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
S Cometti
S Cometti
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
M Costa
M Costa
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
R Covarelli
R Covarelli
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
N Demaria
N Demaria
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
B Kiani
B Kiani
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
F Legger
F Legger
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
C Mariotti
C Mariotti
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
S Maselli
S Maselli
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
E Migliore
E Migliore
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
V Monaco
V Monaco
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
E Monteil
E Monteil
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
M Monteno
M Monteno
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
M M Obertino
M M Obertino
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
G Ortona
G Ortona
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
L Pacher
L Pacher
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
N Pastrone
N Pastrone
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
M Pelliccioni
M Pelliccioni
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
G L Pinna Angioni
G L Pinna Angioni
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
M Ruspa
M Ruspa
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
R Salvatico
R Salvatico
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
F Siviero
F Siviero
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
V Sola
V Sola
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
A Solano
A Solano
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
D Soldi
D Soldi
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
A Staiano
A Staiano
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
D Trocino
D Trocino
82INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
82,
S Belforte
S Belforte
83INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
83,
V Candelise
V Candelise
83INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
83,
M Casarsa
M Casarsa
83INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
83,
F Cossutti
F Cossutti
83INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
83,
A Da Rold
A Da Rold
83INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
83,
G Della Ricca
G Della Ricca
83INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
83,
F Vazzoler
F Vazzoler
83INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
83,
S Dogra
S Dogra
84Kyungpook National University, Daegu, Korea
84,
C Huh
C Huh
84Kyungpook National University, Daegu, Korea
84,
B Kim
B Kim
84Kyungpook National University, Daegu, Korea
84,
D H Kim
D H Kim
84Kyungpook National University, Daegu, Korea
84,
G N Kim
G N Kim
84Kyungpook National University, Daegu, Korea
84,
J Lee
J Lee
84Kyungpook National University, Daegu, Korea
84,
S W Lee
S W Lee
84Kyungpook National University, Daegu, Korea
84,
C S Moon
C S Moon
84Kyungpook National University, Daegu, Korea
84,
Y D Oh
Y D Oh
84Kyungpook National University, Daegu, Korea
84,
S I Pak
S I Pak
84Kyungpook National University, Daegu, Korea
84,
B C Radburn-Smith
B C Radburn-Smith
84Kyungpook National University, Daegu, Korea
84,
S Sekmen
S Sekmen
84Kyungpook National University, Daegu, Korea
84,
Y C Yang
Y C Yang
84Kyungpook National University, Daegu, Korea
84,
H Kim
H Kim
85Chonnam National University, Institute for Universe and Elementary Particles, Kwangju, Korea
85,
D H Moon
D H Moon
85Chonnam National University, Institute for Universe and Elementary Particles, Kwangju, Korea
85,
B Francois
B Francois
86Hanyang University, Seoul, Korea
86,
T J Kim
T J Kim
86Hanyang University, Seoul, Korea
86,
J Park
J Park
86Hanyang University, Seoul, Korea
86,
S Cho
S Cho
87Korea University, Seoul, Korea
87,
S Choi
S Choi
87Korea University, Seoul, Korea
87,
Y Go
Y Go
87Korea University, Seoul, Korea
87,
S Ha
S Ha
87Korea University, Seoul, Korea
87,
B Hong
B Hong
87Korea University, Seoul, Korea
87,
K Lee
K Lee
87Korea University, Seoul, Korea
87,
K S Lee
K S Lee
87Korea University, Seoul, Korea
87,
J Lim
J Lim
87Korea University, Seoul, Korea
87,
J Park
J Park
87Korea University, Seoul, Korea
87,
S K Park
S K Park
87Korea University, Seoul, Korea
87,
J Yoo
J Yoo
87Korea University, Seoul, Korea
87,
J Goh
J Goh
88Kyung Hee University, Department of Physics, Seoul, Republic of Korea, Seoul, Korea
88,
A Gurtu
A Gurtu
88Kyung Hee University, Department of Physics, Seoul, Republic of Korea, Seoul, Korea
88,
H S Kim
H S Kim
89Sejong University, Seoul, Korea
89,
Y Kim
Y Kim
89Sejong University, Seoul, Korea
89,
J Almond
J Almond
90Seoul National University, Seoul, Korea
90,
J H Bhyun
J H Bhyun
90Seoul National University, Seoul, Korea
90,
J Choi
J Choi
90Seoul National University, Seoul, Korea
90,
S Jeon
S Jeon
90Seoul National University, Seoul, Korea
90,
J Kim
J Kim
90Seoul National University, Seoul, Korea
90,
J S Kim
J S Kim
90Seoul National University, Seoul, Korea
90,
S Ko
S Ko
90Seoul National University, Seoul, Korea
90,
H Kwon
H Kwon
90Seoul National University, Seoul, Korea
90,
H Lee
H Lee
90Seoul National University, Seoul, Korea
90,
K Lee
K Lee
90Seoul National University, Seoul, Korea
90,
S Lee
S Lee
90Seoul National University, Seoul, Korea
90,
K Nam
K Nam
90Seoul National University, Seoul, Korea
90,
B H Oh
B H Oh
90Seoul National University, Seoul, Korea
90,
M Oh
M Oh
90Seoul National University, Seoul, Korea
90,
S B Oh
S B Oh
90Seoul National University, Seoul, Korea
90,
H Seo
H Seo
90Seoul National University, Seoul, Korea
90,
U K Yang
U K Yang
90Seoul National University, Seoul, Korea
90,
I Yoon
I Yoon
90Seoul National University, Seoul, Korea
90,
D Jeon
D Jeon
91University of Seoul, Seoul, Korea
91,
J H Kim
J H Kim
91University of Seoul, Seoul, Korea
91,
B Ko
B Ko
91University of Seoul, Seoul, Korea
91,
J S H Lee
J S H Lee
91University of Seoul, Seoul, Korea
91,
I C Park
I C Park
91University of Seoul, Seoul, Korea
91,
Y Roh
Y Roh
91University of Seoul, Seoul, Korea
91,
D Song
D Song
91University of Seoul, Seoul, Korea
91,
I J Watson
I J Watson
91University of Seoul, Seoul, Korea
91,
H D Yoo
H D Yoo
92Department of Physics, Yonsei University, Seoul, Korea
92,
Y Choi
Y Choi
93Sungkyunkwan University, Suwon, Korea
93,
C Hwang
C Hwang
93Sungkyunkwan University, Suwon, Korea
93,
Y Jeong
Y Jeong
93Sungkyunkwan University, Suwon, Korea
93,
H Lee
H Lee
93Sungkyunkwan University, Suwon, Korea
93,
Y Lee
Y Lee
93Sungkyunkwan University, Suwon, Korea
93,
I Yu
I Yu
93Sungkyunkwan University, Suwon, Korea
93,
Y Maghrbi
Y Maghrbi
94College of Engineering and Technology, American University of the Middle East (AUM), Egaila, Kuwait, Dasman, Kuwait
94,
V Veckalns
V Veckalns
95Riga Technical University, Riga, Latvia
238 Riga Technical University, Riga, Latvia
95,238,
A Juodagalvis
A Juodagalvis
96Vilnius University, Vilnius, Lithuania
96,
A Rinkevicius
A Rinkevicius
96Vilnius University, Vilnius, Lithuania
96,
G Tamulaitis
G Tamulaitis
96Vilnius University, Vilnius, Lithuania
96,
W A T Wan Abdullah
W A T Wan Abdullah
97National Centre for Particle Physics, Universiti Malaya, Kuala Lumpur, Malaysia
97,
M N Yusli
M N Yusli
97National Centre for Particle Physics, Universiti Malaya, Kuala Lumpur, Malaysia
97,
Z Zolkapli
Z Zolkapli
97National Centre for Particle Physics, Universiti Malaya, Kuala Lumpur, Malaysia
97,
J F Benitez
J F Benitez
98Universidad de Sonora (UNISON), Hermosillo, Mexico
98,
A Castaneda Hernandez
A Castaneda Hernandez
98Universidad de Sonora (UNISON), Hermosillo, Mexico
98,
J A Murillo Quijada
J A Murillo Quijada
98Universidad de Sonora (UNISON), Hermosillo, Mexico
98,
L Valencia Palomo
L Valencia Palomo
98Universidad de Sonora (UNISON), Hermosillo, Mexico
98,
G Ayala
G Ayala
99Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
99,
H Castilla-Valdez
H Castilla-Valdez
99Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
99,
E De La Cruz-Burelo
E De La Cruz-Burelo
99Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
99,
I Heredia-De La Cruz
I Heredia-De La Cruz
99Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
239 Consejo Nacional de Ciencia y Tecnología, Mexico City, Mexico
99,239,
R Lopez-Fernandez
R Lopez-Fernandez
99Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
99,
C A Mondragon Herrera
C A Mondragon Herrera
99Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
99,
D A Perez Navarro
D A Perez Navarro
99Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
99,
A Sánchez Hernández
A Sánchez Hernández
99Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
99,
S Carrillo Moreno
S Carrillo Moreno
100Universidad Iberoamericana, Mexico City, Mexico
100,
C Oropeza Barrera
C Oropeza Barrera
100Universidad Iberoamericana, Mexico City, Mexico
100,
M Ramírez García
M Ramírez García
100Universidad Iberoamericana, Mexico City, Mexico
100,
F Vazquez Valencia
F Vazquez Valencia
100Universidad Iberoamericana, Mexico City, Mexico
100,
J Eysermans
J Eysermans
101Benemerita Universidad Autonoma de Puebla, Puebla, Mexico
101,
I Pedraza
I Pedraza
101Benemerita Universidad Autonoma de Puebla, Puebla, Mexico
101,
H A Salazar Ibarguen
H A Salazar Ibarguen
101Benemerita Universidad Autonoma de Puebla, Puebla, Mexico
101,
C Uribe Estrada
C Uribe Estrada
101Benemerita Universidad Autonoma de Puebla, Puebla, Mexico
101,
A Morelos Pineda
A Morelos Pineda
102Universidad Autónoma de San Luis Potosí, San Luis Potosí, Mexico
102,
J Mijuskovic
J Mijuskovic
103University of Montenegro, Podgorica, Montenegro
199 IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
103,199,
N Raicevic
N Raicevic
103University of Montenegro, Podgorica, Montenegro
103,
D Krofcheck
D Krofcheck
104University of Auckland, Auckland, New Zealand
104,
S Bheesette
S Bheesette
105University of Canterbury, Christchurch, New Zealand
105,
P H Butler
P H Butler
105University of Canterbury, Christchurch, New Zealand
105,
A Ahmad
A Ahmad
106National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
106,
M I Asghar
M I Asghar
106National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
106,
M I M Awan
M I M Awan
106National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
106,
H R Hoorani
H R Hoorani
106National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
106,
W A Khan
W A Khan
106National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
106,
M A Shah
M A Shah
106National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
106,
M Shoaib
M Shoaib
106National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
106,
M Waqas
M Waqas
106National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
106,
V Avati
V Avati
107AGH University of Science and Technology Faculty of Computer Science, Electronics and Telecommunications, Kraków, Poland
107,
L Grzanka
L Grzanka
107AGH University of Science and Technology Faculty of Computer Science, Electronics and Telecommunications, Kraków, Poland
107,
M Malawski
M Malawski
107AGH University of Science and Technology Faculty of Computer Science, Electronics and Telecommunications, Kraków, Poland
107,
H Bialkowska
H Bialkowska
108National Centre for Nuclear Research, Swierk, Poland
108,
M Bluj
M Bluj
108National Centre for Nuclear Research, Swierk, Poland
108,
B Boimska
B Boimska
108National Centre for Nuclear Research, Swierk, Poland
108,
T Frueboes
T Frueboes
108National Centre for Nuclear Research, Swierk, Poland
108,
M Górski
M Górski
108National Centre for Nuclear Research, Swierk, Poland
108,
M Kazana
M Kazana
108National Centre for Nuclear Research, Swierk, Poland
108,
M Szleper
M Szleper
108National Centre for Nuclear Research, Swierk, Poland
108,
P Traczyk
P Traczyk
108National Centre for Nuclear Research, Swierk, Poland
108,
P Zalewski
P Zalewski
108National Centre for Nuclear Research, Swierk, Poland
108,
K Bunkowski
K Bunkowski
109Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
109,
A Byszuk
A Byszuk
109Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
240 Warsaw University of Technology, Institute of Electronic Systems, Warsaw, Poland
109,240,
K Doroba
K Doroba
109Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
109,
A Kalinowski
A Kalinowski
109Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
109,
M Konecki
M Konecki
109Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
109,
J Krolikowski
J Krolikowski
109Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
109,
M Olszewski
M Olszewski
109Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
109,
M Walczak
M Walczak
109Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
109,
M Araujo
M Araujo
110Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
110,
P Bargassa
P Bargassa
110Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
110,
D Bastos
D Bastos
110Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
110,
P Faccioli
P Faccioli
110Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
110,
M Gallinaro
M Gallinaro
110Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
110,
J Hollar
J Hollar
110Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
110,
N Leonardo
N Leonardo
110Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
110,
T Niknejad
T Niknejad
110Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
110,
J Seixas
J Seixas
110Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
110,
K Shchelina
K Shchelina
110Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
110,
O Toldaiev
O Toldaiev
110Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
110,
J Varela
J Varela
110Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
110,
S Afanasiev
S Afanasiev
111Joint Institute for Nuclear Research, Dubna, Russia
111,
V Alexakhin
V Alexakhin
111Joint Institute for Nuclear Research, Dubna, Russia
111,
M Gavrilenko
M Gavrilenko
111Joint Institute for Nuclear Research, Dubna, Russia
111,
A Golunov
A Golunov
111Joint Institute for Nuclear Research, Dubna, Russia
111,
I Golutvin
I Golutvin
111Joint Institute for Nuclear Research, Dubna, Russia
111,
N Gorbounov
N Gorbounov
111Joint Institute for Nuclear Research, Dubna, Russia
111,
I Gorbunov
I Gorbunov
111Joint Institute for Nuclear Research, Dubna, Russia
111,
A Kamenev
A Kamenev
111Joint Institute for Nuclear Research, Dubna, Russia
111,
V Karjavine
V Karjavine
111Joint Institute for Nuclear Research, Dubna, Russia
111,
A Lanev
A Lanev
111Joint Institute for Nuclear Research, Dubna, Russia
111,
A Malakhov
A Malakhov
111Joint Institute for Nuclear Research, Dubna, Russia
111,
V Matveev
V Matveev
111Joint Institute for Nuclear Research, Dubna, Russia
241 Institute for Nuclear Research, Moscow, Russia
242 National Research Nuclear University ’Moscow Engineering Physics Institute’ (MEPhI), Moscow, Russia
111,241,242,
V V Mitsyn
V V Mitsyn
111Joint Institute for Nuclear Research, Dubna, Russia
111,
P Moisenz
P Moisenz
111Joint Institute for Nuclear Research, Dubna, Russia
111,
V Palichik
V Palichik
111Joint Institute for Nuclear Research, Dubna, Russia
111,
V Perelygin
V Perelygin
111Joint Institute for Nuclear Research, Dubna, Russia
111,
M Savina
M Savina
111Joint Institute for Nuclear Research, Dubna, Russia
111,
S Shmatov
S Shmatov
111Joint Institute for Nuclear Research, Dubna, Russia
111,
V Smirnov
V Smirnov
111Joint Institute for Nuclear Research, Dubna, Russia
111,
O Teryaev
O Teryaev
111Joint Institute for Nuclear Research, Dubna, Russia
111,
V Trofimov
V Trofimov
111Joint Institute for Nuclear Research, Dubna, Russia
111,
N Voytishin
N Voytishin
111Joint Institute for Nuclear Research, Dubna, Russia
111,
A Zarubin
A Zarubin
111Joint Institute for Nuclear Research, Dubna, Russia
111,
G Gavrilov
G Gavrilov
112Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
112,
V Golovtcov
V Golovtcov
112Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
112,
Y Ivanov
Y Ivanov
112Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
112,
V Kim
V Kim
112Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
243 St. Petersburg Polytechnic University, St. Petersburg, Russia
112,243,
E Kuznetsova
E Kuznetsova
112Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
244 University of Florida, Gainesville, FL USA
112,244,
V Murzin
V Murzin
112Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
112,
V Oreshkin
V Oreshkin
112Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
112,
I Smirnov
I Smirnov
112Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
112,
D Sosnov
D Sosnov
112Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
112,
V Sulimov
V Sulimov
112Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
112,
L Uvarov
L Uvarov
112Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
112,
S Volkov
S Volkov
112Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
112,
A Vorobyev
A Vorobyev
112Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
112,
Yu Andreev
Yu Andreev
113Institute for Nuclear Research, Moscow, Russia
113,
A Dermenev
A Dermenev
113Institute for Nuclear Research, Moscow, Russia
113,
S Gninenko
S Gninenko
113Institute for Nuclear Research, Moscow, Russia
113,
N Golubev
N Golubev
113Institute for Nuclear Research, Moscow, Russia
113,
A Karneyeu
A Karneyeu
113Institute for Nuclear Research, Moscow, Russia
113,
M Kirsanov
M Kirsanov
113Institute for Nuclear Research, Moscow, Russia
113,
N Krasnikov
N Krasnikov
113Institute for Nuclear Research, Moscow, Russia
113,
A Pashenkov
A Pashenkov
113Institute for Nuclear Research, Moscow, Russia
113,
G Pivovarov
G Pivovarov
113Institute for Nuclear Research, Moscow, Russia
113,
D Tlisov
D Tlisov
113Institute for Nuclear Research, Moscow, Russia
113,
A Toropin
A Toropin
113Institute for Nuclear Research, Moscow, Russia
113,
V Epshteyn
V Epshteyn
114Institute for Theoretical and Experimental Physics named by A.I. Alikhanov of NRC ‘Kurchatov Institute’, Moscow, Russia
114,
V Gavrilov
V Gavrilov
114Institute for Theoretical and Experimental Physics named by A.I. Alikhanov of NRC ‘Kurchatov Institute’, Moscow, Russia
114,
N Lychkovskaya
N Lychkovskaya
114Institute for Theoretical and Experimental Physics named by A.I. Alikhanov of NRC ‘Kurchatov Institute’, Moscow, Russia
114,
A Nikitenko
A Nikitenko
114Institute for Theoretical and Experimental Physics named by A.I. Alikhanov of NRC ‘Kurchatov Institute’, Moscow, Russia
245 Imperial College, London, UK
114,245,
V Popov
V Popov
114Institute for Theoretical and Experimental Physics named by A.I. Alikhanov of NRC ‘Kurchatov Institute’, Moscow, Russia
114,
G Safronov
G Safronov
114Institute for Theoretical and Experimental Physics named by A.I. Alikhanov of NRC ‘Kurchatov Institute’, Moscow, Russia
114,
A Spiridonov
A Spiridonov
114Institute for Theoretical and Experimental Physics named by A.I. Alikhanov of NRC ‘Kurchatov Institute’, Moscow, Russia
114,
A Stepennov
A Stepennov
114Institute for Theoretical and Experimental Physics named by A.I. Alikhanov of NRC ‘Kurchatov Institute’, Moscow, Russia
114,
M Toms
M Toms
114Institute for Theoretical and Experimental Physics named by A.I. Alikhanov of NRC ‘Kurchatov Institute’, Moscow, Russia
114,
E Vlasov
E Vlasov
114Institute for Theoretical and Experimental Physics named by A.I. Alikhanov of NRC ‘Kurchatov Institute’, Moscow, Russia
114,
A Zhokin
A Zhokin
114Institute for Theoretical and Experimental Physics named by A.I. Alikhanov of NRC ‘Kurchatov Institute’, Moscow, Russia
114,
T Aushev
T Aushev
115Moscow Institute of Physics and Technology, Moscow, Russia
115,
O Bychkova
O Bychkova
116National Research Nuclear University ‘Moscow Engineering Physics Institute’ (MEPhI), Moscow, Russia
116,
M Chadeeva
M Chadeeva
116National Research Nuclear University ‘Moscow Engineering Physics Institute’ (MEPhI), Moscow, Russia
246 P.N. Lebedev Physical Institute, Moscow, Russia
116,246,
A Oskin
A Oskin
116National Research Nuclear University ‘Moscow Engineering Physics Institute’ (MEPhI), Moscow, Russia
116,
E Popova
E Popova
116National Research Nuclear University ‘Moscow Engineering Physics Institute’ (MEPhI), Moscow, Russia
116,
V Rusinov
V Rusinov
116National Research Nuclear University ‘Moscow Engineering Physics Institute’ (MEPhI), Moscow, Russia
116,
V Andreev
V Andreev
117P.N. Lebedev Physical Institute, Moscow, Russia
117,
M Azarkin
M Azarkin
117P.N. Lebedev Physical Institute, Moscow, Russia
117,
I Dremin
I Dremin
117P.N. Lebedev Physical Institute, Moscow, Russia
117,
M Kirakosyan
M Kirakosyan
117P.N. Lebedev Physical Institute, Moscow, Russia
117,
A Terkulov
A Terkulov
117P.N. Lebedev Physical Institute, Moscow, Russia
117,
A Belyaev
A Belyaev
118Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
118,
E Boos
E Boos
118Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
118,
M Dubinin
M Dubinin
118Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
247 California Institute of Technology, Pasadena, CA USA
118,247,
L Dudko
L Dudko
118Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
118,
A Ershov
A Ershov
118Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
118,
A Gribushin
A Gribushin
118Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
118,
V Klyukhin
V Klyukhin
118Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
118,
O Kodolova
O Kodolova
118Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
118,
I Lokhtin
I Lokhtin
118Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
118,
S Obraztsov
S Obraztsov
118Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
118,
S Petrushanko
S Petrushanko
118Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
118,
V Savrin
V Savrin
118Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
118,
A Snigirev
A Snigirev
118Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
118,
V Blinov
V Blinov
119Novosibirsk State University (NSU), Novosibirsk, Russia
248 Budker Institute of Nuclear Physics, Novosibirsk, Russia
119,248,
T Dimova
T Dimova
119Novosibirsk State University (NSU), Novosibirsk, Russia
248 Budker Institute of Nuclear Physics, Novosibirsk, Russia
119,248,
L Kardapoltsev
L Kardapoltsev
119Novosibirsk State University (NSU), Novosibirsk, Russia
248 Budker Institute of Nuclear Physics, Novosibirsk, Russia
119,248,
I Ovtin
I Ovtin
119Novosibirsk State University (NSU), Novosibirsk, Russia
248 Budker Institute of Nuclear Physics, Novosibirsk, Russia
119,248,
Y Skovpen
Y Skovpen
119Novosibirsk State University (NSU), Novosibirsk, Russia
248 Budker Institute of Nuclear Physics, Novosibirsk, Russia
119,248,
I Azhgirey
I Azhgirey
120Institute for High Energy Physics of National Research Centre ‘Kurchatov Institute’, Protvino, Russia
120,
I Bayshev
I Bayshev
120Institute for High Energy Physics of National Research Centre ‘Kurchatov Institute’, Protvino, Russia
120,
V Kachanov
V Kachanov
120Institute for High Energy Physics of National Research Centre ‘Kurchatov Institute’, Protvino, Russia
120,
A Kalinin
A Kalinin
120Institute for High Energy Physics of National Research Centre ‘Kurchatov Institute’, Protvino, Russia
120,
D Konstantinov
D Konstantinov
120Institute for High Energy Physics of National Research Centre ‘Kurchatov Institute’, Protvino, Russia
120,
V Petrov
V Petrov
120Institute for High Energy Physics of National Research Centre ‘Kurchatov Institute’, Protvino, Russia
120,
R Ryutin
R Ryutin
120Institute for High Energy Physics of National Research Centre ‘Kurchatov Institute’, Protvino, Russia
120,
A Sobol
A Sobol
120Institute for High Energy Physics of National Research Centre ‘Kurchatov Institute’, Protvino, Russia
120,
S Troshin
S Troshin
120Institute for High Energy Physics of National Research Centre ‘Kurchatov Institute’, Protvino, Russia
120,
N Tyurin
N Tyurin
120Institute for High Energy Physics of National Research Centre ‘Kurchatov Institute’, Protvino, Russia
120,
A Uzunian
A Uzunian
120Institute for High Energy Physics of National Research Centre ‘Kurchatov Institute’, Protvino, Russia
120,
A Volkov
A Volkov
120Institute for High Energy Physics of National Research Centre ‘Kurchatov Institute’, Protvino, Russia
120,
A Babaev
A Babaev
121National Research Tomsk Polytechnic University, Tomsk, Russia
121,
A Iuzhakov
A Iuzhakov
121National Research Tomsk Polytechnic University, Tomsk, Russia
121,
V Okhotnikov
V Okhotnikov
121National Research Tomsk Polytechnic University, Tomsk, Russia
121,
L Sukhikh
L Sukhikh
121National Research Tomsk Polytechnic University, Tomsk, Russia
121,
V Borchsh
V Borchsh
122Tomsk State University, Tomsk, Russia
122,
V Ivanchenko
V Ivanchenko
122Tomsk State University, Tomsk, Russia
122,
E Tcherniaev
E Tcherniaev
122Tomsk State University, Tomsk, Russia
122,
P Adzic
P Adzic
123University of Belgrade: Faculty of Physics and VINCA Institute of Nuclear Sciences, Belgrade, Serbia
249 Faculty of Physics, University of Belgrade, Belgrade, Serbia
123,249,
P Cirkovic
P Cirkovic
123University of Belgrade: Faculty of Physics and VINCA Institute of Nuclear Sciences, Belgrade, Serbia
123,
M Dordevic
M Dordevic
123University of Belgrade: Faculty of Physics and VINCA Institute of Nuclear Sciences, Belgrade, Serbia
123,
P Milenovic
P Milenovic
123University of Belgrade: Faculty of Physics and VINCA Institute of Nuclear Sciences, Belgrade, Serbia
123,
J Milosevic
J Milosevic
123University of Belgrade: Faculty of Physics and VINCA Institute of Nuclear Sciences, Belgrade, Serbia
123,
M Aguilar-Benitez
M Aguilar-Benitez
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
J Alcaraz Maestre
J Alcaraz Maestre
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
A Álvarez Fernández
A Álvarez Fernández
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
I Bachiller
I Bachiller
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
M Barrio Luna
M Barrio Luna
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
CristinaF Bedoya
CristinaF Bedoya
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
J A Brochero Cifuentes
J A Brochero Cifuentes
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
C A Carrillo Montoya
C A Carrillo Montoya
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
M Cepeda
M Cepeda
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
M Cerrada
M Cerrada
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
N Colino
N Colino
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
B De La Cruz
B De La Cruz
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
A Delgado Peris
A Delgado Peris
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
J P Fernández Ramos
J P Fernández Ramos
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
J Flix
J Flix
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
M C Fouz
M C Fouz
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
A García Alonso
A García Alonso
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
O Gonzalez Lopez
O Gonzalez Lopez
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
S Goy Lopez
S Goy Lopez
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
J M Hernandez
J M Hernandez
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
M I Josa
M I Josa
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
J León Holgado
J León Holgado
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
D Moran
D Moran
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
Á Navarro Tobar
Á Navarro Tobar
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
A Pérez-Calero Yzquierdo
A Pérez-Calero Yzquierdo
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
J Puerta Pelayo
J Puerta Pelayo
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
I Redondo
I Redondo
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
L Romero
L Romero
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
S Sánchez Navas
S Sánchez Navas
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
M S Soares
M S Soares
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
A Triossi
A Triossi
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
L Urda Gómez
L Urda Gómez
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
C Willmott
C Willmott
124Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
124,
C Albajar
C Albajar
125Universidad Autónoma de Madrid, Madrid, Spain
125,
J F de Trocóniz
J F de Trocóniz
125Universidad Autónoma de Madrid, Madrid, Spain
125,
R Reyes-Almanza
R Reyes-Almanza
125Universidad Autónoma de Madrid, Madrid, Spain
125,
B Alvarez Gonzalez
B Alvarez Gonzalez
126Universidad de Oviedo, Instituto Universitario de Ciencias y Tecnologías Espaciales de Asturias (ICTEA), Oviedo, Spain
126,
J Cuevas
J Cuevas
126Universidad de Oviedo, Instituto Universitario de Ciencias y Tecnologías Espaciales de Asturias (ICTEA), Oviedo, Spain
126,
C Erice
C Erice
126Universidad de Oviedo, Instituto Universitario de Ciencias y Tecnologías Espaciales de Asturias (ICTEA), Oviedo, Spain
126,
J Fernandez Menendez
J Fernandez Menendez
126Universidad de Oviedo, Instituto Universitario de Ciencias y Tecnologías Espaciales de Asturias (ICTEA), Oviedo, Spain
126,
S Folgueras
S Folgueras
126Universidad de Oviedo, Instituto Universitario de Ciencias y Tecnologías Espaciales de Asturias (ICTEA), Oviedo, Spain
126,
I Gonzalez Caballero
I Gonzalez Caballero
126Universidad de Oviedo, Instituto Universitario de Ciencias y Tecnologías Espaciales de Asturias (ICTEA), Oviedo, Spain
126,
E Palencia Cortezon
E Palencia Cortezon
126Universidad de Oviedo, Instituto Universitario de Ciencias y Tecnologías Espaciales de Asturias (ICTEA), Oviedo, Spain
126,
C Ramón Álvarez
C Ramón Álvarez
126Universidad de Oviedo, Instituto Universitario de Ciencias y Tecnologías Espaciales de Asturias (ICTEA), Oviedo, Spain
126,
J Ripoll Sau
J Ripoll Sau
126Universidad de Oviedo, Instituto Universitario de Ciencias y Tecnologías Espaciales de Asturias (ICTEA), Oviedo, Spain
126,
V Rodríguez Bouza
V Rodríguez Bouza
126Universidad de Oviedo, Instituto Universitario de Ciencias y Tecnologías Espaciales de Asturias (ICTEA), Oviedo, Spain
126,
S Sanchez Cruz
S Sanchez Cruz
126Universidad de Oviedo, Instituto Universitario de Ciencias y Tecnologías Espaciales de Asturias (ICTEA), Oviedo, Spain
126,
A Trapote
A Trapote
126Universidad de Oviedo, Instituto Universitario de Ciencias y Tecnologías Espaciales de Asturias (ICTEA), Oviedo, Spain
126,
I J Cabrillo
I J Cabrillo
127Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
127,
A Calderon
A Calderon
127Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
127,
B Chazin Quero
B Chazin Quero
127Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
127,
J Duarte Campderros
J Duarte Campderros
127Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
127,
M Fernandez
M Fernandez
127Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
127,
P J Fernández Manteca
P J Fernández Manteca
127Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
127,
G Gomez
G Gomez
127Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
127,
C Martinez Rivero
C Martinez Rivero
127Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
127,
P Martinez Ruiz del Arbol
P Martinez Ruiz del Arbol
127Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
127,
F Matorras
F Matorras
127Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
127,
J Piedra Gomez
J Piedra Gomez
127Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
127,
C Prieels
C Prieels
127Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
127,
F Ricci-Tam
F Ricci-Tam
127Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
127,
T Rodrigo
T Rodrigo
127Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
127,
A Ruiz-Jimeno
A Ruiz-Jimeno
127Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
127,
L Scodellaro
L Scodellaro
127Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
127,
I Vila
I Vila
127Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
127,
J M Vizan Garcia
J M Vizan Garcia
127Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
127,
M K Jayananda
M K Jayananda
128University of Colombo, Colombo, Sri Lanka
128,
B Kailasapathy
B Kailasapathy
128University of Colombo, Colombo, Sri Lanka
250 Trincomalee Campus, Eastern University, Sri Lanka, Nilaveli, Sri Lanka
128,250,
D U J Sonnadara
D U J Sonnadara
128University of Colombo, Colombo, Sri Lanka
128,
D D C Wickramarathna
D D C Wickramarathna
128University of Colombo, Colombo, Sri Lanka
128,
W G D Dharmaratna
W G D Dharmaratna
129Department of Physics, University of Ruhuna, Matara, Sri Lanka
129,
K Liyanage
K Liyanage
129Department of Physics, University of Ruhuna, Matara, Sri Lanka
129,
N Perera
N Perera
129Department of Physics, University of Ruhuna, Matara, Sri Lanka
129,
N Wickramage
N Wickramage
129Department of Physics, University of Ruhuna, Matara, Sri Lanka
129,
T K Aarrestad
T K Aarrestad
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
D Abbaneo
D Abbaneo
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
B Akgun
B Akgun
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
E Auffray
E Auffray
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
G Auzinger
G Auzinger
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
J Baechler
J Baechler
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
P Baillon
P Baillon
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
A H Ball
A H Ball
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
D Barney
D Barney
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
J Bendavid
J Bendavid
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
N Beni
N Beni
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
M Bianco
M Bianco
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
A Bocci
A Bocci
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
P Bortignon
P Bortignon
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
E Bossini
E Bossini
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
E Brondolin
E Brondolin
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
T Camporesi
T Camporesi
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
G Cerminara
G Cerminara
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
L Cristella
L Cristella
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
D d’Enterria
D d’Enterria
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
A Dabrowski
A Dabrowski
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
N Daci
N Daci
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
V Daponte
V Daponte
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
A David
A David
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
A De Roeck
A De Roeck
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
M Deile
M Deile
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
R Di Maria
R Di Maria
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
M Dobson
M Dobson
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
M Dünser
M Dünser
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
N Dupont
N Dupont
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
A Elliott-Peisert
A Elliott-Peisert
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
N Emriskova
N Emriskova
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
F Fallavollita
F Fallavollita
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
251 INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
130,251,
D Fasanella
D Fasanella
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
S Fiorendi
S Fiorendi
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
A Florent
A Florent
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
G Franzoni
G Franzoni
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
J Fulcher
J Fulcher
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
W Funk
W Funk
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
S Giani
S Giani
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
D Gigi
D Gigi
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
K Gill
K Gill
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
F Glege
F Glege
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
L Gouskos
L Gouskos
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
M Guilbaud
M Guilbaud
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
D Gulhan
D Gulhan
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
M Haranko
M Haranko
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
J Hegeman
J Hegeman
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
Y Iiyama
Y Iiyama
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
V Innocente
V Innocente
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
T James
T James
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
P Janot
P Janot
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
J Kaspar
J Kaspar
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
J Kieseler
J Kieseler
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
M Komm
M Komm
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
N Kratochwil
N Kratochwil
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
C Lange
C Lange
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
P Lecoq
P Lecoq
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
K Long
K Long
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
C Lourenço
C Lourenço
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
L Malgeri
L Malgeri
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
M Mannelli
M Mannelli
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
A Massironi
A Massironi
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
F Meijers
F Meijers
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
S Mersi
S Mersi
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
E Meschi
E Meschi
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
F Moortgat
F Moortgat
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
M Mulders
M Mulders
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
J Ngadiuba
J Ngadiuba
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
J Niedziela
J Niedziela
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
S Orfanelli
S Orfanelli
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
L Orsini
L Orsini
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
F Pantaleo
F Pantaleo
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
215 CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,215,
L Pape
L Pape
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
E Perez
E Perez
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
M Peruzzi
M Peruzzi
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
A Petrilli
A Petrilli
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
G Petrucciani
G Petrucciani
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
A Pfeiffer
A Pfeiffer
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
M Pierini
M Pierini
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
D Rabady
D Rabady
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
A Racz
A Racz
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
M Rieger
M Rieger
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
M Rovere
M Rovere
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
H Sakulin
H Sakulin
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
J Salfeld-Nebgen
J Salfeld-Nebgen
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
S Scarfi
S Scarfi
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
C Schäfer
C Schäfer
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
C Schwick
C Schwick
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
M Selvaggi
M Selvaggi
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
A Sharma
A Sharma
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
P Silva
P Silva
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
W Snoeys
W Snoeys
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
P Sphicas
P Sphicas
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
252 National and Kapodistrian University of Athens, Athens, Greece
130,252,
J Steggemann
J Steggemann
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
S Summers
S Summers
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
V R Tavolaro
V R Tavolaro
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
D Treille
D Treille
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
A Tsirou
A Tsirou
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
G P Van Onsem
G P Van Onsem
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
A Vartak
A Vartak
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
M Verzetti
M Verzetti
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
K A Wozniak
K A Wozniak
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
W D Zeuner
W D Zeuner
130CERN, European Organization for Nuclear Research, Geneva, Switzerland
130,
L Caminada
L Caminada
131Paul Scherrer Institut, Villigen, Switzerland
253 Universität Zürich, Zurich, Switzerland
131,253,
W Erdmann
W Erdmann
131Paul Scherrer Institut, Villigen, Switzerland
131,
R Horisberger
R Horisberger
131Paul Scherrer Institut, Villigen, Switzerland
131,
Q Ingram
Q Ingram
131Paul Scherrer Institut, Villigen, Switzerland
131,
H C Kaestli
H C Kaestli
131Paul Scherrer Institut, Villigen, Switzerland
131,
D Kotlinski
D Kotlinski
131Paul Scherrer Institut, Villigen, Switzerland
131,
U Langenegger
U Langenegger
131Paul Scherrer Institut, Villigen, Switzerland
131,
T Rohe
T Rohe
131Paul Scherrer Institut, Villigen, Switzerland
131,
M Backhaus
M Backhaus
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
P Berger
P Berger
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
A Calandri
A Calandri
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
N Chernyavskaya
N Chernyavskaya
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
A De Cosa
A De Cosa
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
G Dissertori
G Dissertori
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
M Dittmar
M Dittmar
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
M Donegà
M Donegà
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
C Dorfer
C Dorfer
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
T Gadek
T Gadek
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
T A Gómez Espinosa
T A Gómez Espinosa
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
C Grab
C Grab
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
D Hits
D Hits
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
W Lustermann
W Lustermann
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
A -M Lyon
A -M Lyon
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
R A Manzoni
R A Manzoni
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
M T Meinhard
M T Meinhard
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
F Micheli
F Micheli
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
F Nessi-Tedaldi
F Nessi-Tedaldi
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
F Pauss
F Pauss
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
V Perovic
V Perovic
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
G Perrin
G Perrin
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
L Perrozzi
L Perrozzi
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
S Pigazzini
S Pigazzini
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
M G Ratti
M G Ratti
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
M Reichmann
M Reichmann
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
C Reissel
C Reissel
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
T Reitenspiess
T Reitenspiess
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
B Ristic
B Ristic
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
D Ruini
D Ruini
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
D A Sanz Becerra
D A Sanz Becerra
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
M Schönenberger
M Schönenberger
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
V Stampf
V Stampf
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
M L Vesterbacka Olsson
M L Vesterbacka Olsson
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
R Wallny
R Wallny
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
D H Zhu
D H Zhu
132ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
132,
C Amsler
C Amsler
133Universität Zürich, Zurich, Switzerland
254 Stefan Meyer Institute for Subatomic Physics, Vienna, Austria
133,254,
C Botta
C Botta
133Universität Zürich, Zurich, Switzerland
133,
D Brzhechko
D Brzhechko
133Universität Zürich, Zurich, Switzerland
133,
M F Canelli
M F Canelli
133Universität Zürich, Zurich, Switzerland
133,
R Del Burgo
R Del Burgo
133Universität Zürich, Zurich, Switzerland
133,
J K Heikkilä
J K Heikkilä
133Universität Zürich, Zurich, Switzerland
133,
M Huwiler
M Huwiler
133Universität Zürich, Zurich, Switzerland
133,
A Jofrehei
A Jofrehei
133Universität Zürich, Zurich, Switzerland
133,
B Kilminster
B Kilminster
133Universität Zürich, Zurich, Switzerland
133,
S Leontsinis
S Leontsinis
133Universität Zürich, Zurich, Switzerland
133,
A Macchiolo
A Macchiolo
133Universität Zürich, Zurich, Switzerland
133,
P Meiring
P Meiring
133Universität Zürich, Zurich, Switzerland
133,
V M Mikuni
V M Mikuni
133Universität Zürich, Zurich, Switzerland
133,
U Molinatti
U Molinatti
133Universität Zürich, Zurich, Switzerland
133,
I Neutelings
I Neutelings
133Universität Zürich, Zurich, Switzerland
133,
G Rauco
G Rauco
133Universität Zürich, Zurich, Switzerland
133,
A Reimers
A Reimers
133Universität Zürich, Zurich, Switzerland
133,
P Robmann
P Robmann
133Universität Zürich, Zurich, Switzerland
133,
K Schweiger
K Schweiger
133Universität Zürich, Zurich, Switzerland
133,
Y Takahashi
Y Takahashi
133Universität Zürich, Zurich, Switzerland
133,
S Wertz
S Wertz
133Universität Zürich, Zurich, Switzerland
133,
C Adloff
C Adloff
134National Central University, Chung-Li, Taiwan
255 Laboratoire d’Annecy-le-Vieux de Physique des Particules, IN2P3-CNRS, Annecy-le-Vieux, France
134,255,
C M Kuo
C M Kuo
134National Central University, Chung-Li, Taiwan
134,
W Lin
W Lin
134National Central University, Chung-Li, Taiwan
134,
A Roy
A Roy
134National Central University, Chung-Li, Taiwan
134,
T Sarkar
T Sarkar
134National Central University, Chung-Li, Taiwan
230 University of Visva-Bharati, Santiniketan, India
134,230,
S S Yu
S S Yu
134National Central University, Chung-Li, Taiwan
134,
L Ceard
L Ceard
135National Taiwan University (NTU), Taipei, Taiwan
135,
P Chang
P Chang
135National Taiwan University (NTU), Taipei, Taiwan
135,
Y Chao
Y Chao
135National Taiwan University (NTU), Taipei, Taiwan
135,
K F Chen
K F Chen
135National Taiwan University (NTU), Taipei, Taiwan
135,
P H Chen
P H Chen
135National Taiwan University (NTU), Taipei, Taiwan
135,
W-S Hou
W-S Hou
135National Taiwan University (NTU), Taipei, Taiwan
135,
Y y Li
Y y Li
135National Taiwan University (NTU), Taipei, Taiwan
135,
R -S Lu
R -S Lu
135National Taiwan University (NTU), Taipei, Taiwan
135,
E Paganis
E Paganis
135National Taiwan University (NTU), Taipei, Taiwan
135,
A Psallidas
A Psallidas
135National Taiwan University (NTU), Taipei, Taiwan
135,
A Steen
A Steen
135National Taiwan University (NTU), Taipei, Taiwan
135,
E Yazgan
E Yazgan
135National Taiwan University (NTU), Taipei, Taiwan
135,
B Asavapibhop
B Asavapibhop
136Department of Physics, Faculty of Science, Chulalongkorn University, Bangkok, Thailand
136,
C Asawatangtrakuldee
C Asawatangtrakuldee
136Department of Physics, Faculty of Science, Chulalongkorn University, Bangkok, Thailand
136,
N Srimanobhas
N Srimanobhas
136Department of Physics, Faculty of Science, Chulalongkorn University, Bangkok, Thailand
136,
F Boran
F Boran
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
137,
S Damarseckin
S Damarseckin
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
256 Şırnak University, Sirnak, Turkey
137,256,
Z S Demiroglu
Z S Demiroglu
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
137,
F Dolek
F Dolek
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
137,
C Dozen
C Dozen
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
257 Department of Physics, Tsinghua University, Beijing, China
137,257,
I Dumanoglu
I Dumanoglu
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
258 Near East University, Research Center of Experimental Health Science, Nicosia, Turkey
137,258,
E Eskut
E Eskut
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
137,
G Gokbulut
G Gokbulut
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
137,
Y Guler
Y Guler
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
137,
E Gurpinar Guler
E Gurpinar Guler
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
259 Beykent University, Istanbul, Turkey
137,259,
I Hos
I Hos
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
260 Istanbul Aydin University, Application and Research Center for Advanced Studies, Istanbul, Turkey
137,260,
C Isik
C Isik
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
137,
E E Kangal
E E Kangal
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
261 Mersin University, Mersin, Turkey
137,261,
O Kara
O Kara
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
137,
A Kayis Topaksu
A Kayis Topaksu
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
137,
U Kiminsu
U Kiminsu
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
137,
G Onengut
G Onengut
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
137,
K Ozdemir
K Ozdemir
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
262 Piri Reis University, Istanbul, Turkey
137,262,
A Polatoz
A Polatoz
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
137,
A E Simsek
A E Simsek
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
137,
B Tali
B Tali
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
263 Adiyaman University, Adiyaman, Turkey
137,263,
U G Tok
U G Tok
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
137,
S Turkcapar
S Turkcapar
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
137,
I S Zorbakir
I S Zorbakir
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
137,
C Zorbilmez
C Zorbilmez
137Çukurova University, Physics Department, Science and Art Faculty, Adana, Turkey
137,
B Isildak
B Isildak
138Physics Department, Middle East Technical University, Ankara, Turkey
264 Ozyegin University, Istanbul, Turkey
138,264,
G Karapinar
G Karapinar
138Physics Department, Middle East Technical University, Ankara, Turkey
265 Izmir Institute of Technology, Izmir, Turkey
138,265,
K Ocalan
K Ocalan
138Physics Department, Middle East Technical University, Ankara, Turkey
266 Necmettin Erbakan University, Konya, Turkey
138,266,
M Yalvac
M Yalvac
138Physics Department, Middle East Technical University, Ankara, Turkey
267 Bozok Universitetesi Rektörlügü, Yozgat, Turkey
138,267,
I O Atakisi
I O Atakisi
139Bogazici University, Istanbul, Turkey
139,
E Gülmez
E Gülmez
139Bogazici University, Istanbul, Turkey
139,
M Kaya
M Kaya
139Bogazici University, Istanbul, Turkey
268 Marmara University, Istanbul, Turkey
139,268,
O Kaya
O Kaya
139Bogazici University, Istanbul, Turkey
269 Milli Savunma University, Istanbul, Turkey
139,269,
Ö Özçelik
Ö Özçelik
139Bogazici University, Istanbul, Turkey
139,
S Tekten
S Tekten
139Bogazici University, Istanbul, Turkey
270 Kafkas University, Kars, Turkey
139,270,
E A Yetkin
E A Yetkin
139Bogazici University, Istanbul, Turkey
271 Istanbul Bilgi University, Istanbul, Turkey
139,271,
A Cakir
A Cakir
140Istanbul Technical University, Istanbul, Turkey
140,
K Cankocak
K Cankocak
140Istanbul Technical University, Istanbul, Turkey
258 Near East University, Research Center of Experimental Health Science, Nicosia, Turkey
140,258,
Y Komurcu
Y Komurcu
140Istanbul Technical University, Istanbul, Turkey
140,
S Sen
S Sen
140Istanbul Technical University, Istanbul, Turkey
272 Hacettepe University, Ankara, Turkey
140,272,
F Aydogmus Sen
F Aydogmus Sen
141Istanbul University, Istanbul, Turkey
141,
S Cerci
S Cerci
141Istanbul University, Istanbul, Turkey
263 Adiyaman University, Adiyaman, Turkey
141,263,
B Kaynak
B Kaynak
141Istanbul University, Istanbul, Turkey
141,
S Ozkorucuklu
S Ozkorucuklu
141Istanbul University, Istanbul, Turkey
141,
D Sunar Cerci
D Sunar Cerci
141Istanbul University, Istanbul, Turkey
263 Adiyaman University, Adiyaman, Turkey
141,263,
B Grynyov
B Grynyov
142Institute for Scintillation Materials of National Academy of Science of Ukraine, Kharkiv, Ukraine
142,
L Levchuk
L Levchuk
143National Scientific Center, Kharkov Institute of Physics and Technology, Kharkiv, Ukraine
143,
E Bhal
E Bhal
144University of Bristol, Bristol, UK
144,
S Bologna
S Bologna
144University of Bristol, Bristol, UK
144,
J J Brooke
J J Brooke
144University of Bristol, Bristol, UK
144,
E Clement
E Clement
144University of Bristol, Bristol, UK
144,
D Cussans
D Cussans
144University of Bristol, Bristol, UK
144,
H Flacher
H Flacher
144University of Bristol, Bristol, UK
144,
J Goldstein
J Goldstein
144University of Bristol, Bristol, UK
144,
G P Heath
G P Heath
144University of Bristol, Bristol, UK
144,
H F Heath
H F Heath
144University of Bristol, Bristol, UK
144,
L Kreczko
L Kreczko
144University of Bristol, Bristol, UK
144,
B Krikler
B Krikler
144University of Bristol, Bristol, UK
144,
S Paramesvaran
S Paramesvaran
144University of Bristol, Bristol, UK
144,
T Sakuma
T Sakuma
144University of Bristol, Bristol, UK
144,
S Seif El Nasr-Storey
S Seif El Nasr-Storey
144University of Bristol, Bristol, UK
144,
V J Smith
V J Smith
144University of Bristol, Bristol, UK
144,
J Taylor
J Taylor
144University of Bristol, Bristol, UK
144,
A Titterton
A Titterton
144University of Bristol, Bristol, UK
144,
K W Bell
K W Bell
145Rutherford Appleton Laboratory, Didcot, UK
145,
A Belyaev
A Belyaev
145Rutherford Appleton Laboratory, Didcot, UK
273 School of Physics and Astronomy, University of Southampton, Southampton, UK
145,273,
C Brew
C Brew
145Rutherford Appleton Laboratory, Didcot, UK
145,
R M Brown
R M Brown
145Rutherford Appleton Laboratory, Didcot, UK
145,
D J A Cockerill
D J A Cockerill
145Rutherford Appleton Laboratory, Didcot, UK
145,
K V Ellis
K V Ellis
145Rutherford Appleton Laboratory, Didcot, UK
145,
K Harder
K Harder
145Rutherford Appleton Laboratory, Didcot, UK
145,
S Harper
S Harper
145Rutherford Appleton Laboratory, Didcot, UK
145,
J Linacre
J Linacre
145Rutherford Appleton Laboratory, Didcot, UK
145,
K Manolopoulos
K Manolopoulos
145Rutherford Appleton Laboratory, Didcot, UK
145,
D M Newbold
D M Newbold
145Rutherford Appleton Laboratory, Didcot, UK
145,
E Olaiya
E Olaiya
145Rutherford Appleton Laboratory, Didcot, UK
145,
D Petyt
D Petyt
145Rutherford Appleton Laboratory, Didcot, UK
145,
T Reis
T Reis
145Rutherford Appleton Laboratory, Didcot, UK
145,
T Schuh
T Schuh
145Rutherford Appleton Laboratory, Didcot, UK
145,
C H Shepherd-Themistocleous
C H Shepherd-Themistocleous
145Rutherford Appleton Laboratory, Didcot, UK
145,
A Thea
A Thea
145Rutherford Appleton Laboratory, Didcot, UK
145,
I R Tomalin
I R Tomalin
145Rutherford Appleton Laboratory, Didcot, UK
145,
T Williams
T Williams
145Rutherford Appleton Laboratory, Didcot, UK
145,
R Bainbridge
R Bainbridge
146Imperial College, London, UK
146,
P Bloch
P Bloch
146Imperial College, London, UK
146,
S Bonomally
S Bonomally
146Imperial College, London, UK
146,
J Borg
J Borg
146Imperial College, London, UK
146,
S Breeze
S Breeze
146Imperial College, London, UK
146,
O Buchmuller
O Buchmuller
146Imperial College, London, UK
146,
A Bundock
A Bundock
146Imperial College, London, UK
146,
V Cepaitis
V Cepaitis
146Imperial College, London, UK
146,
G S Chahal
G S Chahal
146Imperial College, London, UK
274 IPPP Durham University, Durham, UK
146,274,
D Colling
D Colling
146Imperial College, London, UK
146,
P Dauncey
P Dauncey
146Imperial College, London, UK
146,
G Davies
G Davies
146Imperial College, London, UK
146,
M Della Negra
M Della Negra
146Imperial College, London, UK
146,
G Fedi
G Fedi
146Imperial College, London, UK
146,
G Hall
G Hall
146Imperial College, London, UK
146,
G Iles
G Iles
146Imperial College, London, UK
146,
J Langford
J Langford
146Imperial College, London, UK
146,
L Lyons
L Lyons
146Imperial College, London, UK
146,
A -M Magnan
A -M Magnan
146Imperial College, London, UK
146,
S Malik
S Malik
146Imperial College, London, UK
146,
A Martelli
A Martelli
146Imperial College, London, UK
146,
V Milosevic
V Milosevic
146Imperial College, London, UK
146,
J Nash
J Nash
146Imperial College, London, UK
275 Monash University, Faculty of Science, Clayton, Australia
146,275,
V Palladino
V Palladino
146Imperial College, London, UK
146,
M Pesaresi
M Pesaresi
146Imperial College, London, UK
146,
D M Raymond
D M Raymond
146Imperial College, London, UK
146,
A Richards
A Richards
146Imperial College, London, UK
146,
A Rose
A Rose
146Imperial College, London, UK
146,
E Scott
E Scott
146Imperial College, London, UK
146,
C Seez
C Seez
146Imperial College, London, UK
146,
A Shtipliyski
A Shtipliyski
146Imperial College, London, UK
146,
M Stoye
M Stoye
146Imperial College, London, UK
146,
A Tapper
A Tapper
146Imperial College, London, UK
146,
K Uchida
K Uchida
146Imperial College, London, UK
146,
T Virdee
T Virdee
146Imperial College, London, UK
215 CERN, European Organization for Nuclear Research, Geneva, Switzerland
146,215,
N Wardle
N Wardle
146Imperial College, London, UK
146,
S N Webb
S N Webb
146Imperial College, London, UK
146,
D Winterbottom
D Winterbottom
146Imperial College, London, UK
146,
A G Zecchinelli
A G Zecchinelli
146Imperial College, London, UK
146,
J E Cole
J E Cole
147Brunel University, Uxbridge, UK
147,
P R Hobson
P R Hobson
147Brunel University, Uxbridge, UK
147,
A Khan
A Khan
147Brunel University, Uxbridge, UK
147,
P Kyberd
P Kyberd
147Brunel University, Uxbridge, UK
147,
C K Mackay
C K Mackay
147Brunel University, Uxbridge, UK
147,
I D Reid
I D Reid
147Brunel University, Uxbridge, UK
147,
L Teodorescu
L Teodorescu
147Brunel University, Uxbridge, UK
147,
S Zahid
S Zahid
147Brunel University, Uxbridge, UK
147,
A Brinkerhoff
A Brinkerhoff
148Baylor University, Waco, TX USA
148,
K Call
K Call
148Baylor University, Waco, TX USA
148,
B Caraway
B Caraway
148Baylor University, Waco, TX USA
148,
J Dittmann
J Dittmann
148Baylor University, Waco, TX USA
148,
K Hatakeyama
K Hatakeyama
148Baylor University, Waco, TX USA
148,
A R Kanuganti
A R Kanuganti
148Baylor University, Waco, TX USA
148,
C Madrid
C Madrid
148Baylor University, Waco, TX USA
148,
B McMaster
B McMaster
148Baylor University, Waco, TX USA
148,
N Pastika
N Pastika
148Baylor University, Waco, TX USA
148,
S Sawant
S Sawant
148Baylor University, Waco, TX USA
148,
C Smith
C Smith
148Baylor University, Waco, TX USA
148,
J Wilson
J Wilson
148Baylor University, Waco, TX USA
148,
R Bartek
R Bartek
149Catholic University of America, Washington, DC USA
149,
A Dominguez
A Dominguez
149Catholic University of America, Washington, DC USA
149,
R Uniyal
R Uniyal
149Catholic University of America, Washington, DC USA
149,
A M Vargas Hernandez
A M Vargas Hernandez
149Catholic University of America, Washington, DC USA
149,
A Buccilli
A Buccilli
150The University of Alabama, Tuscaloosa, AL USA
150,
O Charaf
O Charaf
150The University of Alabama, Tuscaloosa, AL USA
150,
S I Cooper
S I Cooper
150The University of Alabama, Tuscaloosa, AL USA
150,
S V Gleyzer
S V Gleyzer
150The University of Alabama, Tuscaloosa, AL USA
150,
C Henderson
C Henderson
150The University of Alabama, Tuscaloosa, AL USA
150,
P Rumerio
P Rumerio
150The University of Alabama, Tuscaloosa, AL USA
150,
C West
C West
150The University of Alabama, Tuscaloosa, AL USA
150,
A Akpinar
A Akpinar
151Boston University, Boston, MA USA
151,
A Albert
A Albert
151Boston University, Boston, MA USA
151,
D Arcaro
D Arcaro
151Boston University, Boston, MA USA
151,
C Cosby
C Cosby
151Boston University, Boston, MA USA
151,
Z Demiragli
Z Demiragli
151Boston University, Boston, MA USA
151,
D Gastler
D Gastler
151Boston University, Boston, MA USA
151,
J Rohlf
J Rohlf
151Boston University, Boston, MA USA
151,
K Salyer
K Salyer
151Boston University, Boston, MA USA
151,
D Sperka
D Sperka
151Boston University, Boston, MA USA
151,
D Spitzbart
D Spitzbart
151Boston University, Boston, MA USA
151,
I Suarez
I Suarez
151Boston University, Boston, MA USA
151,
S Yuan
S Yuan
151Boston University, Boston, MA USA
151,
D Zou
D Zou
151Boston University, Boston, MA USA
151,
G Benelli
G Benelli
152Brown University, Providence, RI USA
152,
B Burkle
B Burkle
152Brown University, Providence, RI USA
152,
X Coubez
X Coubez
152Brown University, Providence, RI USA
216 RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
152,216,
D Cutts
D Cutts
152Brown University, Providence, RI USA
152,
Y t Duh
Y t Duh
152Brown University, Providence, RI USA
152,
M Hadley
M Hadley
152Brown University, Providence, RI USA
152,
U Heintz
U Heintz
152Brown University, Providence, RI USA
152,
J M Hogan
J M Hogan
152Brown University, Providence, RI USA
276 Bethel University, St. Paul, Minneapolis, USA
152,276,
K H M Kwok
K H M Kwok
152Brown University, Providence, RI USA
152,
E Laird
E Laird
152Brown University, Providence, RI USA
152,
G Landsberg
G Landsberg
152Brown University, Providence, RI USA
152,
K T Lau
K T Lau
152Brown University, Providence, RI USA
152,
J Lee
J Lee
152Brown University, Providence, RI USA
152,
M Narain
M Narain
152Brown University, Providence, RI USA
152,
S Sagir
S Sagir
152Brown University, Providence, RI USA
277 Karamanoğlu Mehmetbey University, Karaman, Turkey
152,277,
R Syarif
R Syarif
152Brown University, Providence, RI USA
152,
E Usai
E Usai
152Brown University, Providence, RI USA
152,
W Y Wong
W Y Wong
152Brown University, Providence, RI USA
152,
D Yu
D Yu
152Brown University, Providence, RI USA
152,
W Zhang
W Zhang
152Brown University, Providence, RI USA
152,
R Band
R Band
153University of California, Davis, Davis, CA USA
153,
C Brainerd
C Brainerd
153University of California, Davis, Davis, CA USA
153,
R Breedon
R Breedon
153University of California, Davis, Davis, CA USA
153,
M Calderon De La BarcaSanchez
M Calderon De La BarcaSanchez
153University of California, Davis, Davis, CA USA
153,
M Chertok
M Chertok
153University of California, Davis, Davis, CA USA
153,
J Conway
J Conway
153University of California, Davis, Davis, CA USA
153,
R Conway
R Conway
153University of California, Davis, Davis, CA USA
153,
P T Cox
P T Cox
153University of California, Davis, Davis, CA USA
153,
R Erbacher
R Erbacher
153University of California, Davis, Davis, CA USA
153,
C Flores
C Flores
153University of California, Davis, Davis, CA USA
153,
G Funk
G Funk
153University of California, Davis, Davis, CA USA
153,
F Jensen
F Jensen
153University of California, Davis, Davis, CA USA
153,
W Ko
W Ko
153University of California, Davis, Davis, CA USA
153,
O Kukral
O Kukral
153University of California, Davis, Davis, CA USA
153,
R Lander
R Lander
153University of California, Davis, Davis, CA USA
153,
M Mulhearn
M Mulhearn
153University of California, Davis, Davis, CA USA
153,
D Pellett
D Pellett
153University of California, Davis, Davis, CA USA
153,
J Pilot
J Pilot
153University of California, Davis, Davis, CA USA
153,
M Shi
M Shi
153University of California, Davis, Davis, CA USA
153,
D Taylor
D Taylor
153University of California, Davis, Davis, CA USA
153,
K Tos
K Tos
153University of California, Davis, Davis, CA USA
153,
M Tripathi
M Tripathi
153University of California, Davis, Davis, CA USA
153,
Y Yao
Y Yao
153University of California, Davis, Davis, CA USA
153,
F Zhang
F Zhang
153University of California, Davis, Davis, CA USA
153,
M Bachtis
M Bachtis
154University of California, Los Angeles, CA USA
154,
R Cousins
R Cousins
154University of California, Los Angeles, CA USA
154,
A Dasgupta
A Dasgupta
154University of California, Los Angeles, CA USA
154,
D Hamilton
D Hamilton
154University of California, Los Angeles, CA USA
154,
J Hauser
J Hauser
154University of California, Los Angeles, CA USA
154,
M Ignatenko
M Ignatenko
154University of California, Los Angeles, CA USA
154,
T Lam
T Lam
154University of California, Los Angeles, CA USA
154,
N Mccoll
N Mccoll
154University of California, Los Angeles, CA USA
154,
W A Nash
W A Nash
154University of California, Los Angeles, CA USA
154,
S Regnard
S Regnard
154University of California, Los Angeles, CA USA
154,
D Saltzberg
D Saltzberg
154University of California, Los Angeles, CA USA
154,
C Schnaible
C Schnaible
154University of California, Los Angeles, CA USA
154,
B Stone
B Stone
154University of California, Los Angeles, CA USA
154,
V Valuev
V Valuev
154University of California, Los Angeles, CA USA
154,
K Burt
K Burt
155University of California, Riverside, Riverside, CA USA
155,
Y Chen
Y Chen
155University of California, Riverside, Riverside, CA USA
155,
R Clare
R Clare
155University of California, Riverside, Riverside, CA USA
155,
J W Gary
J W Gary
155University of California, Riverside, Riverside, CA USA
155,
S M A Ghiasi Shirazi
S M A Ghiasi Shirazi
155University of California, Riverside, Riverside, CA USA
155,
G Hanson
G Hanson
155University of California, Riverside, Riverside, CA USA
155,
G Karapostoli
G Karapostoli
155University of California, Riverside, Riverside, CA USA
155,
O R Long
O R Long
155University of California, Riverside, Riverside, CA USA
155,
N Manganelli
N Manganelli
155University of California, Riverside, Riverside, CA USA
155,
M Olmedo Negrete
M Olmedo Negrete
155University of California, Riverside, Riverside, CA USA
155,
M I Paneva
M I Paneva
155University of California, Riverside, Riverside, CA USA
155,
W Si
W Si
155University of California, Riverside, Riverside, CA USA
155,
S Wimpenny
S Wimpenny
155University of California, Riverside, Riverside, CA USA
155,
Y Zhang
Y Zhang
155University of California, Riverside, Riverside, CA USA
155,
J G Branson
J G Branson
156University of California, San Diego, La Jolla, CA USA
156,
P Chang
P Chang
156University of California, San Diego, La Jolla, CA USA
156,
S Cittolin
S Cittolin
156University of California, San Diego, La Jolla, CA USA
156,
S Cooperstein
S Cooperstein
156University of California, San Diego, La Jolla, CA USA
156,
N Deelen
N Deelen
156University of California, San Diego, La Jolla, CA USA
156,
J Duarte
J Duarte
156University of California, San Diego, La Jolla, CA USA
156,
R Gerosa
R Gerosa
156University of California, San Diego, La Jolla, CA USA
156,
D Gilbert
D Gilbert
156University of California, San Diego, La Jolla, CA USA
156,
V Krutelyov
V Krutelyov
156University of California, San Diego, La Jolla, CA USA
156,
J Letts
J Letts
156University of California, San Diego, La Jolla, CA USA
156,
M Masciovecchio
M Masciovecchio
156University of California, San Diego, La Jolla, CA USA
156,
S May
S May
156University of California, San Diego, La Jolla, CA USA
156,
S Padhi
S Padhi
156University of California, San Diego, La Jolla, CA USA
156,
M Pieri
M Pieri
156University of California, San Diego, La Jolla, CA USA
156,
V Sharma
V Sharma
156University of California, San Diego, La Jolla, CA USA
156,
M Tadel
M Tadel
156University of California, San Diego, La Jolla, CA USA
156,
F Würthwein
F Würthwein
156University of California, San Diego, La Jolla, CA USA
156,
A Yagil
A Yagil
156University of California, San Diego, La Jolla, CA USA
156,
N Amin
N Amin
157Department of Physics, University of California, Santa Barbara, Santa Barbara, CA USA
157,
C Campagnari
C Campagnari
157Department of Physics, University of California, Santa Barbara, Santa Barbara, CA USA
157,
M Citron
M Citron
157Department of Physics, University of California, Santa Barbara, Santa Barbara, CA USA
157,
A Dorsett
A Dorsett
157Department of Physics, University of California, Santa Barbara, Santa Barbara, CA USA
157,
V Dutta
V Dutta
157Department of Physics, University of California, Santa Barbara, Santa Barbara, CA USA
157,
J Incandela
J Incandela
157Department of Physics, University of California, Santa Barbara, Santa Barbara, CA USA
157,
B Marsh
B Marsh
157Department of Physics, University of California, Santa Barbara, Santa Barbara, CA USA
157,
H Mei
H Mei
157Department of Physics, University of California, Santa Barbara, Santa Barbara, CA USA
157,
A Ovcharova
A Ovcharova
157Department of Physics, University of California, Santa Barbara, Santa Barbara, CA USA
157,
H Qu
H Qu
157Department of Physics, University of California, Santa Barbara, Santa Barbara, CA USA
157,
M Quinnan
M Quinnan
157Department of Physics, University of California, Santa Barbara, Santa Barbara, CA USA
157,
J Richman
J Richman
157Department of Physics, University of California, Santa Barbara, Santa Barbara, CA USA
157,
U Sarica
U Sarica
157Department of Physics, University of California, Santa Barbara, Santa Barbara, CA USA
157,
D Stuart
D Stuart
157Department of Physics, University of California, Santa Barbara, Santa Barbara, CA USA
157,
S Wang
S Wang
157Department of Physics, University of California, Santa Barbara, Santa Barbara, CA USA
157,
D Anderson
D Anderson
158California Institute of Technology, Pasadena, CA USA
158,
A Bornheim
A Bornheim
158California Institute of Technology, Pasadena, CA USA
158,
O Cerri
O Cerri
158California Institute of Technology, Pasadena, CA USA
158,
I Dutta
I Dutta
158California Institute of Technology, Pasadena, CA USA
158,
J M Lawhorn
J M Lawhorn
158California Institute of Technology, Pasadena, CA USA
158,
N Lu
N Lu
158California Institute of Technology, Pasadena, CA USA
158,
J Mao
J Mao
158California Institute of Technology, Pasadena, CA USA
158,
H B Newman
H B Newman
158California Institute of Technology, Pasadena, CA USA
158,
T Q Nguyen
T Q Nguyen
158California Institute of Technology, Pasadena, CA USA
158,
J Pata
J Pata
158California Institute of Technology, Pasadena, CA USA
158,
M Spiropulu
M Spiropulu
158California Institute of Technology, Pasadena, CA USA
158,
J R Vlimant
J R Vlimant
158California Institute of Technology, Pasadena, CA USA
158,
S Xie
S Xie
158California Institute of Technology, Pasadena, CA USA
158,
Z Zhang
Z Zhang
158California Institute of Technology, Pasadena, CA USA
158,
R Y Zhu
R Y Zhu
158California Institute of Technology, Pasadena, CA USA
158,
J Alison
J Alison
159Carnegie Mellon University, Pittsburgh, PA USA
159,
M B Andrews
M B Andrews
159Carnegie Mellon University, Pittsburgh, PA USA
159,
T Ferguson
T Ferguson
159Carnegie Mellon University, Pittsburgh, PA USA
159,
T Mudholkar
T Mudholkar
159Carnegie Mellon University, Pittsburgh, PA USA
159,
M Paulini
M Paulini
159Carnegie Mellon University, Pittsburgh, PA USA
159,
M Sun
M Sun
159Carnegie Mellon University, Pittsburgh, PA USA
159,
I Vorobiev
I Vorobiev
159Carnegie Mellon University, Pittsburgh, PA USA
159,
J P Cumalat
J P Cumalat
160University of Colorado Boulder, Boulder, CO USA
160,
W T Ford
W T Ford
160University of Colorado Boulder, Boulder, CO USA
160,
E MacDonald
E MacDonald
160University of Colorado Boulder, Boulder, CO USA
160,
T Mulholland
T Mulholland
160University of Colorado Boulder, Boulder, CO USA
160,
R Patel
R Patel
160University of Colorado Boulder, Boulder, CO USA
160,
A Perloff
A Perloff
160University of Colorado Boulder, Boulder, CO USA
160,
K Stenson
K Stenson
160University of Colorado Boulder, Boulder, CO USA
160,
K A Ulmer
K A Ulmer
160University of Colorado Boulder, Boulder, CO USA
160,
S R Wagner
S R Wagner
160University of Colorado Boulder, Boulder, CO USA
160,
J Alexander
J Alexander
161Cornell University, Ithaca, NY USA
161,
Y Cheng
Y Cheng
161Cornell University, Ithaca, NY USA
161,
J Chu
J Chu
161Cornell University, Ithaca, NY USA
161,
D J Cranshaw
D J Cranshaw
161Cornell University, Ithaca, NY USA
161,
A Datta
A Datta
161Cornell University, Ithaca, NY USA
161,
A Frankenthal
A Frankenthal
161Cornell University, Ithaca, NY USA
161,
K Mcdermott
K Mcdermott
161Cornell University, Ithaca, NY USA
161,
J Monroy
J Monroy
161Cornell University, Ithaca, NY USA
161,
J R Patterson
J R Patterson
161Cornell University, Ithaca, NY USA
161,
D Quach
D Quach
161Cornell University, Ithaca, NY USA
161,
A Ryd
A Ryd
161Cornell University, Ithaca, NY USA
161,
W Sun
W Sun
161Cornell University, Ithaca, NY USA
161,
S M Tan
S M Tan
161Cornell University, Ithaca, NY USA
161,
Z Tao
Z Tao
161Cornell University, Ithaca, NY USA
161,
J Thom
J Thom
161Cornell University, Ithaca, NY USA
161,
P Wittich
P Wittich
161Cornell University, Ithaca, NY USA
161,
M Zientek
M Zientek
161Cornell University, Ithaca, NY USA
161,
S Abdullin
S Abdullin
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
M Albrow
M Albrow
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
M Alyari
M Alyari
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
G Apollinari
G Apollinari
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
A Apresyan
A Apresyan
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
A Apyan
A Apyan
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
S Banerjee
S Banerjee
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
L A T Bauerdick
L A T Bauerdick
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
A Beretvas
A Beretvas
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
D Berry
D Berry
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
J Berryhill
J Berryhill
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
P C Bhat
P C Bhat
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
K Burkett
K Burkett
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
J N Butler
J N Butler
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
A Canepa
A Canepa
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
G B Cerati
G B Cerati
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
H W K Cheung
H W K Cheung
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
F Chlebana
F Chlebana
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
M Cremonesi
M Cremonesi
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
V D Elvira
V D Elvira
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
J Freeman
J Freeman
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
Z Gecse
Z Gecse
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
E Gottschalk
E Gottschalk
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
L Gray
L Gray
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
D Green
D Green
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
S Grünendahl
S Grünendahl
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
O Gutsche
O Gutsche
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
R M Harris
R M Harris
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
S Hasegawa
S Hasegawa
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
R Heller
R Heller
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
T C Herwig
T C Herwig
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
J Hirschauer
J Hirschauer
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
B Jayatilaka
B Jayatilaka
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
S Jindariani
S Jindariani
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
M Johnson
M Johnson
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
U Joshi
U Joshi
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
P Klabbers
P Klabbers
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
T Klijnsma
T Klijnsma
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
B Klima
B Klima
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
M J Kortelainen
M J Kortelainen
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
S Lammel
S Lammel
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
D Lincoln
D Lincoln
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
R Lipton
R Lipton
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
M Liu
M Liu
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
T Liu
T Liu
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
J Lykken
J Lykken
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
K Maeshima
K Maeshima
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
D Mason
D Mason
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
P McBride
P McBride
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
P Merkel
P Merkel
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
S Mrenna
S Mrenna
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
S Nahn
S Nahn
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
V O’Dell
V O’Dell
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
V Papadimitriou
V Papadimitriou
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
K Pedro
K Pedro
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
C Pena
C Pena
162Fermi National Accelerator Laboratory, Batavia, IL USA
247 California Institute of Technology, Pasadena, CA USA
162,247,
O Prokofyev
O Prokofyev
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
F Ravera
F Ravera
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
A Reinsvold Hall
A Reinsvold Hall
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
L Ristori
L Ristori
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
B Schneider
B Schneider
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
E Sexton-Kennedy
E Sexton-Kennedy
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
N Smith
N Smith
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
A Soha
A Soha
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
W J Spalding
W J Spalding
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
L Spiegel
L Spiegel
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
S Stoynev
S Stoynev
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
J Strait
J Strait
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
L Taylor
L Taylor
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
S Tkaczyk
S Tkaczyk
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
N V Tran
N V Tran
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
L Uplegger
L Uplegger
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
E W Vaandering
E W Vaandering
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
H A Weber
H A Weber
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
A Woodard
A Woodard
162Fermi National Accelerator Laboratory, Batavia, IL USA
162,
D Acosta
D Acosta
163University of Florida, Gainesville, FL USA
163,
P Avery
P Avery
163University of Florida, Gainesville, FL USA
163,
D Bourilkov
D Bourilkov
163University of Florida, Gainesville, FL USA
163,
L Cadamuro
L Cadamuro
163University of Florida, Gainesville, FL USA
163,
V Cherepanov
V Cherepanov
163University of Florida, Gainesville, FL USA
163,
F Errico
F Errico
163University of Florida, Gainesville, FL USA
163,
R D Field
R D Field
163University of Florida, Gainesville, FL USA
163,
D Guerrero
D Guerrero
163University of Florida, Gainesville, FL USA
163,
B M Joshi
B M Joshi
163University of Florida, Gainesville, FL USA
163,
M Kim
M Kim
163University of Florida, Gainesville, FL USA
163,
J Konigsberg
J Konigsberg
163University of Florida, Gainesville, FL USA
163,
A Korytov
A Korytov
163University of Florida, Gainesville, FL USA
163,
K H Lo
K H Lo
163University of Florida, Gainesville, FL USA
163,
K Matchev
K Matchev
163University of Florida, Gainesville, FL USA
163,
N Menendez
N Menendez
163University of Florida, Gainesville, FL USA
163,
G Mitselmakher
G Mitselmakher
163University of Florida, Gainesville, FL USA
163,
D Rosenzweig
D Rosenzweig
163University of Florida, Gainesville, FL USA
163,
K Shi
K Shi
163University of Florida, Gainesville, FL USA
163,
J Wang
J Wang
163University of Florida, Gainesville, FL USA
163,
S Wang
S Wang
163University of Florida, Gainesville, FL USA
163,
X Zuo
X Zuo
163University of Florida, Gainesville, FL USA
163,
T Adams
T Adams
164Florida State University, Tallahassee, FL USA
164,
A Askew
A Askew
164Florida State University, Tallahassee, FL USA
164,
D Diaz
D Diaz
164Florida State University, Tallahassee, FL USA
164,
R Habibullah
R Habibullah
164Florida State University, Tallahassee, FL USA
164,
S Hagopian
S Hagopian
164Florida State University, Tallahassee, FL USA
164,
V Hagopian
V Hagopian
164Florida State University, Tallahassee, FL USA
164,
K F Johnson
K F Johnson
164Florida State University, Tallahassee, FL USA
164,
R Khurana
R Khurana
164Florida State University, Tallahassee, FL USA
164,
T Kolberg
T Kolberg
164Florida State University, Tallahassee, FL USA
164,
G Martinez
G Martinez
164Florida State University, Tallahassee, FL USA
164,
H Prosper
H Prosper
164Florida State University, Tallahassee, FL USA
164,
C Schiber
C Schiber
164Florida State University, Tallahassee, FL USA
164,
R Yohay
R Yohay
164Florida State University, Tallahassee, FL USA
164,
J Zhang
J Zhang
164Florida State University, Tallahassee, FL USA
164,
M M Baarmand
M M Baarmand
165Florida Institute of Technology, Melbourne, FL USA
165,
S Butalla
S Butalla
165Florida Institute of Technology, Melbourne, FL USA
165,
T Elkafrawy
T Elkafrawy
165Florida Institute of Technology, Melbourne, FL USA
278 Ain Shams University, Cairo, Egypt
165,278,
M Hohlmann
M Hohlmann
165Florida Institute of Technology, Melbourne, FL USA
165,
D Noonan
D Noonan
165Florida Institute of Technology, Melbourne, FL USA
165,
M Rahmani
M Rahmani
165Florida Institute of Technology, Melbourne, FL USA
165,
M Saunders
M Saunders
165Florida Institute of Technology, Melbourne, FL USA
165,
F Yumiceva
F Yumiceva
165Florida Institute of Technology, Melbourne, FL USA
165,
M R Adams
M R Adams
166University of Illinois at Chicago (UIC), Chicago, IL USA
166,
L Apanasevich
L Apanasevich
166University of Illinois at Chicago (UIC), Chicago, IL USA
166,
H Becerril Gonzalez
H Becerril Gonzalez
166University of Illinois at Chicago (UIC), Chicago, IL USA
166,
R Cavanaugh
R Cavanaugh
166University of Illinois at Chicago (UIC), Chicago, IL USA
166,
X Chen
X Chen
166University of Illinois at Chicago (UIC), Chicago, IL USA
166,
S Dittmer
S Dittmer
166University of Illinois at Chicago (UIC), Chicago, IL USA
166,
O Evdokimov
O Evdokimov
166University of Illinois at Chicago (UIC), Chicago, IL USA
166,
C E Gerber
C E Gerber
166University of Illinois at Chicago (UIC), Chicago, IL USA
166,
D A Hangal
D A Hangal
166University of Illinois at Chicago (UIC), Chicago, IL USA
166,
D J Hofman
D J Hofman
166University of Illinois at Chicago (UIC), Chicago, IL USA
166,
C Mills
C Mills
166University of Illinois at Chicago (UIC), Chicago, IL USA
166,
G Oh
G Oh
166University of Illinois at Chicago (UIC), Chicago, IL USA
166,
T Roy
T Roy
166University of Illinois at Chicago (UIC), Chicago, IL USA
166,
M B Tonjes
M B Tonjes
166University of Illinois at Chicago (UIC), Chicago, IL USA
166,
N Varelas
N Varelas
166University of Illinois at Chicago (UIC), Chicago, IL USA
166,
J Viinikainen
J Viinikainen
166University of Illinois at Chicago (UIC), Chicago, IL USA
166,
X Wang
X Wang
166University of Illinois at Chicago (UIC), Chicago, IL USA
166,
Z Wu
Z Wu
166University of Illinois at Chicago (UIC), Chicago, IL USA
166,
M Alhusseini
M Alhusseini
167The University of Iowa, Iowa City, IA USA
167,
K Dilsiz
K Dilsiz
167The University of Iowa, Iowa City, IA USA
279 Bingol University, Bingol, Turkey
167,279,
S Durgut
S Durgut
167The University of Iowa, Iowa City, IA USA
167,
R P Gandrajula
R P Gandrajula
167The University of Iowa, Iowa City, IA USA
167,
M Haytmyradov
M Haytmyradov
167The University of Iowa, Iowa City, IA USA
167,
V Khristenko
V Khristenko
167The University of Iowa, Iowa City, IA USA
167,
O K Köseyan
O K Köseyan
167The University of Iowa, Iowa City, IA USA
167,
J -P Merlo
J -P Merlo
167The University of Iowa, Iowa City, IA USA
167,
A Mestvirishvili
A Mestvirishvili
167The University of Iowa, Iowa City, IA USA
280 Georgian Technical University, Tbilisi, Georgia
167,280,
A Moeller
A Moeller
167The University of Iowa, Iowa City, IA USA
167,
J Nachtman
J Nachtman
167The University of Iowa, Iowa City, IA USA
167,
H Ogul
H Ogul
167The University of Iowa, Iowa City, IA USA
281 Sinop University, Sinop, Turkey
167,281,
Y Onel
Y Onel
167The University of Iowa, Iowa City, IA USA
167,
F Ozok
F Ozok
167The University of Iowa, Iowa City, IA USA
282 Mimar Sinan University, Istanbul, Istanbul, Turkey
167,282,
A Penzo
A Penzo
167The University of Iowa, Iowa City, IA USA
167,
C Snyder
C Snyder
167The University of Iowa, Iowa City, IA USA
167,
E Tiras
E Tiras
167The University of Iowa, Iowa City, IA USA
167,
J Wetzel
J Wetzel
167The University of Iowa, Iowa City, IA USA
167,
K Yi
K Yi
167The University of Iowa, Iowa City, IA USA
283 Nanjing Normal University Department of Physics, Nanjing, China
167,283,
O Amram
O Amram
168Johns Hopkins University, Baltimore, MD USA
168,
B Blumenfeld
B Blumenfeld
168Johns Hopkins University, Baltimore, MD USA
168,
L Corcodilos
L Corcodilos
168Johns Hopkins University, Baltimore, MD USA
168,
M Eminizer
M Eminizer
168Johns Hopkins University, Baltimore, MD USA
168,
A V Gritsan
A V Gritsan
168Johns Hopkins University, Baltimore, MD USA
168,
S Kyriacou
S Kyriacou
168Johns Hopkins University, Baltimore, MD USA
168,
P Maksimovic
P Maksimovic
168Johns Hopkins University, Baltimore, MD USA
168,
C Mantilla
C Mantilla
168Johns Hopkins University, Baltimore, MD USA
168,
J Roskes
J Roskes
168Johns Hopkins University, Baltimore, MD USA
168,
M Swartz
M Swartz
168Johns Hopkins University, Baltimore, MD USA
168,
TÁ Vámi
TÁ Vámi
168Johns Hopkins University, Baltimore, MD USA
168,
C Baldenegro Barrera
C Baldenegro Barrera
169The University of Kansas, Lawrence, KS USA
169,
P Baringer
P Baringer
169The University of Kansas, Lawrence, KS USA
169,
A Bean
A Bean
169The University of Kansas, Lawrence, KS USA
169,
A Bylinkin
A Bylinkin
169The University of Kansas, Lawrence, KS USA
169,
T Isidori
T Isidori
169The University of Kansas, Lawrence, KS USA
169,
S Khalil
S Khalil
169The University of Kansas, Lawrence, KS USA
169,
J King
J King
169The University of Kansas, Lawrence, KS USA
169,
G Krintiras
G Krintiras
169The University of Kansas, Lawrence, KS USA
169,
A Kropivnitskaya
A Kropivnitskaya
169The University of Kansas, Lawrence, KS USA
169,
C Lindsey
C Lindsey
169The University of Kansas, Lawrence, KS USA
169,
N Minafra
N Minafra
169The University of Kansas, Lawrence, KS USA
169,
M Murray
M Murray
169The University of Kansas, Lawrence, KS USA
169,
C Rogan
C Rogan
169The University of Kansas, Lawrence, KS USA
169,
C Royon
C Royon
169The University of Kansas, Lawrence, KS USA
169,
S Sanders
S Sanders
169The University of Kansas, Lawrence, KS USA
169,
E Schmitz
E Schmitz
169The University of Kansas, Lawrence, KS USA
169,
J D Tapia Takaki
J D Tapia Takaki
169The University of Kansas, Lawrence, KS USA
169,
Q Wang
Q Wang
169The University of Kansas, Lawrence, KS USA
169,
J Williams
J Williams
169The University of Kansas, Lawrence, KS USA
169,
G Wilson
G Wilson
169The University of Kansas, Lawrence, KS USA
169,
S Duric
S Duric
170Kansas State University, Manhattan, KS USA
170,
A Ivanov
A Ivanov
170Kansas State University, Manhattan, KS USA
170,
K Kaadze
K Kaadze
170Kansas State University, Manhattan, KS USA
170,
D Kim
D Kim
170Kansas State University, Manhattan, KS USA
170,
Y Maravin
Y Maravin
170Kansas State University, Manhattan, KS USA
170,
T Mitchell
T Mitchell
170Kansas State University, Manhattan, KS USA
170,
A Modak
A Modak
170Kansas State University, Manhattan, KS USA
170,
A Mohammadi
A Mohammadi
170Kansas State University, Manhattan, KS USA
170,
F Rebassoo
F Rebassoo
171Lawrence Livermore National Laboratory, Livermore, CA USA
171,
D Wright
D Wright
171Lawrence Livermore National Laboratory, Livermore, CA USA
171,
E Adams
E Adams
172University of Maryland, College Park, MD USA
172,
A Baden
A Baden
172University of Maryland, College Park, MD USA
172,
O Baron
O Baron
172University of Maryland, College Park, MD USA
172,
A Belloni
A Belloni
172University of Maryland, College Park, MD USA
172,
S C Eno
S C Eno
172University of Maryland, College Park, MD USA
172,
Y Feng
Y Feng
172University of Maryland, College Park, MD USA
172,
N J Hadley
N J Hadley
172University of Maryland, College Park, MD USA
172,
S Jabeen
S Jabeen
172University of Maryland, College Park, MD USA
172,
G Y Jeng
G Y Jeng
172University of Maryland, College Park, MD USA
172,
R G Kellogg
R G Kellogg
172University of Maryland, College Park, MD USA
172,
T Koeth
T Koeth
172University of Maryland, College Park, MD USA
172,
A C Mignerey
A C Mignerey
172University of Maryland, College Park, MD USA
172,
S Nabili
S Nabili
172University of Maryland, College Park, MD USA
172,
M Seidel
M Seidel
172University of Maryland, College Park, MD USA
172,
A Skuja
A Skuja
172University of Maryland, College Park, MD USA
172,
S C Tonwar
S C Tonwar
172University of Maryland, College Park, MD USA
172,
L Wang
L Wang
172University of Maryland, College Park, MD USA
172,
K Wong
K Wong
172University of Maryland, College Park, MD USA
172,
D Abercrombie
D Abercrombie
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
B Allen
B Allen
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
R Bi
R Bi
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
S Brandt
S Brandt
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
W Busza
W Busza
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
I A Cali
I A Cali
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
Y Chen
Y Chen
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
M D’Alfonso
M D’Alfonso
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
G Gomez Ceballos
G Gomez Ceballos
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
M Goncharov
M Goncharov
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
P Harris
P Harris
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
D Hsu
D Hsu
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
M Hu
M Hu
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
M Klute
M Klute
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
D Kovalskyi
D Kovalskyi
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
J Krupa
J Krupa
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
Y-J Lee
Y-J Lee
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
P D Luckey
P D Luckey
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
B Maier
B Maier
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
A C Marini
A C Marini
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
C Mcginn
C Mcginn
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
C Mironov
C Mironov
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
S Narayanan
S Narayanan
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
X Niu
X Niu
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
C Paus
C Paus
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
D Rankin
D Rankin
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
C Roland
C Roland
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
G Roland
G Roland
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
Z Shi
Z Shi
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
G S F Stephans
G S F Stephans
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
K Sumorok
K Sumorok
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
K Tatar
K Tatar
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
D Velicanu
D Velicanu
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
J Wang
J Wang
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
T W Wang
T W Wang
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
Z Wang
Z Wang
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
B Wyslouch
B Wyslouch
173Massachusetts Institute of Technology, Cambridge, MA USA
173,
R M Chatterjee
R M Chatterjee
174University of Minnesota, Minneapolis, MN USA
174,
A Evans
A Evans
174University of Minnesota, Minneapolis, MN USA
174,
S Guts
S Guts
174University of Minnesota, Minneapolis, MN USA
174,
P Hansen
P Hansen
174University of Minnesota, Minneapolis, MN USA
174,
J Hiltbrand
J Hiltbrand
174University of Minnesota, Minneapolis, MN USA
174,
Sh Jain
Sh Jain
174University of Minnesota, Minneapolis, MN USA
174,
M Krohn
M Krohn
174University of Minnesota, Minneapolis, MN USA
174,
Y Kubota
Y Kubota
174University of Minnesota, Minneapolis, MN USA
174,
Z Lesko
Z Lesko
174University of Minnesota, Minneapolis, MN USA
174,
J Mans
J Mans
174University of Minnesota, Minneapolis, MN USA
174,
M Revering
M Revering
174University of Minnesota, Minneapolis, MN USA
174,
R Rusack
R Rusack
174University of Minnesota, Minneapolis, MN USA
174,
R Saradhy
R Saradhy
174University of Minnesota, Minneapolis, MN USA
174,
N Schroeder
N Schroeder
174University of Minnesota, Minneapolis, MN USA
174,
N Strobbe
N Strobbe
174University of Minnesota, Minneapolis, MN USA
174,
M A Wadud
M A Wadud
174University of Minnesota, Minneapolis, MN USA
174,
J G Acosta
J G Acosta
175University of Mississippi, Oxford, MS USA
175,
S Oliveros
S Oliveros
175University of Mississippi, Oxford, MS USA
175,
K Bloom
K Bloom
176University of Nebraska-Lincoln, Lincoln, NE USA
176,
S Chauhan
S Chauhan
176University of Nebraska-Lincoln, Lincoln, NE USA
176,
D R Claes
D R Claes
176University of Nebraska-Lincoln, Lincoln, NE USA
176,
C Fangmeier
C Fangmeier
176University of Nebraska-Lincoln, Lincoln, NE USA
176,
L Finco
L Finco
176University of Nebraska-Lincoln, Lincoln, NE USA
176,
F Golf
F Golf
176University of Nebraska-Lincoln, Lincoln, NE USA
176,
J R González Fernández
J R González Fernández
176University of Nebraska-Lincoln, Lincoln, NE USA
176,
I Kravchenko
I Kravchenko
176University of Nebraska-Lincoln, Lincoln, NE USA
176,
J E Siado
J E Siado
176University of Nebraska-Lincoln, Lincoln, NE USA
176,
G R Snow
G R Snow
176University of Nebraska-Lincoln, Lincoln, NE USA
176,
B Stieger
B Stieger
176University of Nebraska-Lincoln, Lincoln, NE USA
176,
W Tabb
W Tabb
176University of Nebraska-Lincoln, Lincoln, NE USA
176,
F Yan
F Yan
176University of Nebraska-Lincoln, Lincoln, NE USA
176,
G Agarwal
G Agarwal
177State University of New York at Buffalo, Buffalo, NY USA
177,
H Bandyopadhyay
H Bandyopadhyay
177State University of New York at Buffalo, Buffalo, NY USA
177,
C Harrington
C Harrington
177State University of New York at Buffalo, Buffalo, NY USA
177,
L Hay
L Hay
177State University of New York at Buffalo, Buffalo, NY USA
177,
I Iashvili
I Iashvili
177State University of New York at Buffalo, Buffalo, NY USA
177,
A Kharchilava
A Kharchilava
177State University of New York at Buffalo, Buffalo, NY USA
177,
C McLean
C McLean
177State University of New York at Buffalo, Buffalo, NY USA
177,
D Nguyen
D Nguyen
177State University of New York at Buffalo, Buffalo, NY USA
177,
J Pekkanen
J Pekkanen
177State University of New York at Buffalo, Buffalo, NY USA
177,
S Rappoccio
S Rappoccio
177State University of New York at Buffalo, Buffalo, NY USA
177,
B Roozbahani
B Roozbahani
177State University of New York at Buffalo, Buffalo, NY USA
177,
G Alverson
G Alverson
178Northeastern University, Boston, MA USA
178,
E Barberis
E Barberis
178Northeastern University, Boston, MA USA
178,
C Freer
C Freer
178Northeastern University, Boston, MA USA
178,
Y Haddad
Y Haddad
178Northeastern University, Boston, MA USA
178,
A Hortiangtham
A Hortiangtham
178Northeastern University, Boston, MA USA
178,
J Li
J Li
178Northeastern University, Boston, MA USA
178,
G Madigan
G Madigan
178Northeastern University, Boston, MA USA
178,
B Marzocchi
B Marzocchi
178Northeastern University, Boston, MA USA
178,
D M Morse
D M Morse
178Northeastern University, Boston, MA USA
178,
V Nguyen
V Nguyen
178Northeastern University, Boston, MA USA
178,
T Orimoto
T Orimoto
178Northeastern University, Boston, MA USA
178,
A Parker
A Parker
178Northeastern University, Boston, MA USA
178,
L Skinnari
L Skinnari
178Northeastern University, Boston, MA USA
178,
A Tishelman-Charny
A Tishelman-Charny
178Northeastern University, Boston, MA USA
178,
T Wamorkar
T Wamorkar
178Northeastern University, Boston, MA USA
178,
B Wang
B Wang
178Northeastern University, Boston, MA USA
178,
A Wisecarver
A Wisecarver
178Northeastern University, Boston, MA USA
178,
D Wood
D Wood
178Northeastern University, Boston, MA USA
178,
S Bhattacharya
S Bhattacharya
179Northwestern University, Evanston, IL USA
179,
J Bueghly
J Bueghly
179Northwestern University, Evanston, IL USA
179,
Z Chen
Z Chen
179Northwestern University, Evanston, IL USA
179,
A Gilbert
A Gilbert
179Northwestern University, Evanston, IL USA
179,
T Gunter
T Gunter
179Northwestern University, Evanston, IL USA
179,
K A Hahn
K A Hahn
179Northwestern University, Evanston, IL USA
179,
N Odell
N Odell
179Northwestern University, Evanston, IL USA
179,
M H Schmitt
M H Schmitt
179Northwestern University, Evanston, IL USA
179,
K Sung
K Sung
179Northwestern University, Evanston, IL USA
179,
M Velasco
M Velasco
179Northwestern University, Evanston, IL USA
179,
R Bucci
R Bucci
180University of Notre Dame, Notre Dame, IN USA
180,
N Dev
N Dev
180University of Notre Dame, Notre Dame, IN USA
180,
R Goldouzian
R Goldouzian
180University of Notre Dame, Notre Dame, IN USA
180,
M Hildreth
M Hildreth
180University of Notre Dame, Notre Dame, IN USA
180,
K Hurtado Anampa
K Hurtado Anampa
180University of Notre Dame, Notre Dame, IN USA
180,
C Jessop
C Jessop
180University of Notre Dame, Notre Dame, IN USA
180,
D J Karmgard
D J Karmgard
180University of Notre Dame, Notre Dame, IN USA
180,
K Lannon
K Lannon
180University of Notre Dame, Notre Dame, IN USA
180,
N Loukas
N Loukas
180University of Notre Dame, Notre Dame, IN USA
180,
N Marinelli
N Marinelli
180University of Notre Dame, Notre Dame, IN USA
180,
I Mcalister
I Mcalister
180University of Notre Dame, Notre Dame, IN USA
180,
F Meng
F Meng
180University of Notre Dame, Notre Dame, IN USA
180,
K Mohrman
K Mohrman
180University of Notre Dame, Notre Dame, IN USA
180,
Y Musienko
Y Musienko
180University of Notre Dame, Notre Dame, IN USA
241 Institute for Nuclear Research, Moscow, Russia
180,241,
R Ruchti
R Ruchti
180University of Notre Dame, Notre Dame, IN USA
180,
P Siddireddy
P Siddireddy
180University of Notre Dame, Notre Dame, IN USA
180,
S Taroni
S Taroni
180University of Notre Dame, Notre Dame, IN USA
180,
M Wayne
M Wayne
180University of Notre Dame, Notre Dame, IN USA
180,
A Wightman
A Wightman
180University of Notre Dame, Notre Dame, IN USA
180,
M Wolf
M Wolf
180University of Notre Dame, Notre Dame, IN USA
180,
L Zygala
L Zygala
180University of Notre Dame, Notre Dame, IN USA
180,
J Alimena
J Alimena
181The Ohio State University, Columbus, OH USA
181,
B Bylsma
B Bylsma
181The Ohio State University, Columbus, OH USA
181,
B Cardwell
B Cardwell
181The Ohio State University, Columbus, OH USA
181,
L S Durkin
L S Durkin
181The Ohio State University, Columbus, OH USA
181,
B Francis
B Francis
181The Ohio State University, Columbus, OH USA
181,
C Hill
C Hill
181The Ohio State University, Columbus, OH USA
181,
A Lefeld
A Lefeld
181The Ohio State University, Columbus, OH USA
181,
B L Winer
B L Winer
181The Ohio State University, Columbus, OH USA
181,
B R Yates
B R Yates
181The Ohio State University, Columbus, OH USA
181,
P Das
P Das
182Princeton University, Princeton, NJ USA
182,
G Dezoort
G Dezoort
182Princeton University, Princeton, NJ USA
182,
P Elmer
P Elmer
182Princeton University, Princeton, NJ USA
182,
B Greenberg
B Greenberg
182Princeton University, Princeton, NJ USA
182,
N Haubrich
N Haubrich
182Princeton University, Princeton, NJ USA
182,
S Higginbotham
S Higginbotham
182Princeton University, Princeton, NJ USA
182,
A Kalogeropoulos
A Kalogeropoulos
182Princeton University, Princeton, NJ USA
182,
G Kopp
G Kopp
182Princeton University, Princeton, NJ USA
182,
S Kwan
S Kwan
182Princeton University, Princeton, NJ USA
182,
D Lange
D Lange
182Princeton University, Princeton, NJ USA
182,
M T Lucchini
M T Lucchini
182Princeton University, Princeton, NJ USA
182,
J Luo
J Luo
182Princeton University, Princeton, NJ USA
182,
D Marlow
D Marlow
182Princeton University, Princeton, NJ USA
182,
K Mei
K Mei
182Princeton University, Princeton, NJ USA
182,
I Ojalvo
I Ojalvo
182Princeton University, Princeton, NJ USA
182,
J Olsen
J Olsen
182Princeton University, Princeton, NJ USA
182,
C Palmer
C Palmer
182Princeton University, Princeton, NJ USA
182,
P Piroué
P Piroué
182Princeton University, Princeton, NJ USA
182,
D Stickland
D Stickland
182Princeton University, Princeton, NJ USA
182,
C Tully
C Tully
182Princeton University, Princeton, NJ USA
182,
S Malik
S Malik
183University of Puerto Rico, Mayaguez, PR USA
183,
S Norberg
S Norberg
183University of Puerto Rico, Mayaguez, PR USA
183,
V E Barnes
V E Barnes
184Purdue University, West Lafayette, IN USA
184,
R Chawla
R Chawla
184Purdue University, West Lafayette, IN USA
184,
S Das
S Das
184Purdue University, West Lafayette, IN USA
184,
L Gutay
L Gutay
184Purdue University, West Lafayette, IN USA
184,
M Jones
M Jones
184Purdue University, West Lafayette, IN USA
184,
A W Jung
A W Jung
184Purdue University, West Lafayette, IN USA
184,
B Mahakud
B Mahakud
184Purdue University, West Lafayette, IN USA
184,
G Negro
G Negro
184Purdue University, West Lafayette, IN USA
184,
N Neumeister
N Neumeister
184Purdue University, West Lafayette, IN USA
184,
C C Peng
C C Peng
184Purdue University, West Lafayette, IN USA
184,
S Piperov
S Piperov
184Purdue University, West Lafayette, IN USA
184,
H Qiu
H Qiu
184Purdue University, West Lafayette, IN USA
184,
J F Schulte
J F Schulte
184Purdue University, West Lafayette, IN USA
184,
M Stojanovic
M Stojanovic
184Purdue University, West Lafayette, IN USA
212 Purdue University, West Lafayette, IN USA
184,212,
N Trevisani
N Trevisani
184Purdue University, West Lafayette, IN USA
184,
F Wang
F Wang
184Purdue University, West Lafayette, IN USA
184,
R Xiao
R Xiao
184Purdue University, West Lafayette, IN USA
184,
W Xie
W Xie
184Purdue University, West Lafayette, IN USA
184,
T Cheng
T Cheng
185Purdue University Northwest, Hammond, IN USA
185,
J Dolen
J Dolen
185Purdue University Northwest, Hammond, IN USA
185,
N Parashar
N Parashar
185Purdue University Northwest, Hammond, IN USA
185,
A Baty
A Baty
186Rice University, Houston, TX USA
186,
S Dildick
S Dildick
186Rice University, Houston, TX USA
186,
K M Ecklund
K M Ecklund
186Rice University, Houston, TX USA
186,
S Freed
S Freed
186Rice University, Houston, TX USA
186,
F J M Geurts
F J M Geurts
186Rice University, Houston, TX USA
186,
M Kilpatrick
M Kilpatrick
186Rice University, Houston, TX USA
186,
A Kumar
A Kumar
186Rice University, Houston, TX USA
186,
W Li
W Li
186Rice University, Houston, TX USA
186,
B P Padley
B P Padley
186Rice University, Houston, TX USA
186,
R Redjimi
R Redjimi
186Rice University, Houston, TX USA
186,
J Roberts
J Roberts
186Rice University, Houston, TX USA
186,
J Rorie
J Rorie
186Rice University, Houston, TX USA
186,
W Shi
W Shi
186Rice University, Houston, TX USA
186,
A G Stahl Leiton
A G Stahl Leiton
186Rice University, Houston, TX USA
186,
A Bodek
A Bodek
187University of Rochester, Rochester, NY USA
187,
P de Barbaro
P de Barbaro
187University of Rochester, Rochester, NY USA
187,
R Demina
R Demina
187University of Rochester, Rochester, NY USA
187,
J L Dulemba
J L Dulemba
187University of Rochester, Rochester, NY USA
187,
C Fallon
C Fallon
187University of Rochester, Rochester, NY USA
187,
T Ferbel
T Ferbel
187University of Rochester, Rochester, NY USA
187,
M Galanti
M Galanti
187University of Rochester, Rochester, NY USA
187,
A Garcia-Bellido
A Garcia-Bellido
187University of Rochester, Rochester, NY USA
187,
O Hindrichs
O Hindrichs
187University of Rochester, Rochester, NY USA
187,
A Khukhunaishvili
A Khukhunaishvili
187University of Rochester, Rochester, NY USA
187,
E Ranken
E Ranken
187University of Rochester, Rochester, NY USA
187,
R Taus
R Taus
187University of Rochester, Rochester, NY USA
187,
B Chiarito
B Chiarito
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
188,
J P Chou
J P Chou
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
188,
A Gandrakota
A Gandrakota
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
188,
Y Gershtein
Y Gershtein
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
188,
E Halkiadakis
E Halkiadakis
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
188,
A Hart
A Hart
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
188,
M Heindl
M Heindl
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
188,
E Hughes
E Hughes
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
188,
S Kaplan
S Kaplan
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
188,
O Karacheban
O Karacheban
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
219 Brandenburg University of Technology, Cottbus, Germany
188,219,
I Laflotte
I Laflotte
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
188,
A Lath
A Lath
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
188,
R Montalvo
R Montalvo
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
188,
K Nash
K Nash
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
188,
M Osherson
M Osherson
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
188,
S Salur
S Salur
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
188,
S Schnetzer
S Schnetzer
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
188,
S Somalwar
S Somalwar
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
188,
R Stone
R Stone
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
188,
S A Thayil
S A Thayil
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
188,
S Thomas
S Thomas
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
188,
H Wang
H Wang
188Rutgers, The State University of New Jersey, Piscataway, NJ USA
188,
H Acharya
H Acharya
189University of Tennessee, Knoxville, TN USA
189,
A G Delannoy
A G Delannoy
189University of Tennessee, Knoxville, TN USA
189,
S Spanier
S Spanier
189University of Tennessee, Knoxville, TN USA
189,
O Bouhali
O Bouhali
190Texas A &M University, College Station, TX USA
284 Texas A &M University at Qatar, Doha, Qatar
190,284,
M Dalchenko
M Dalchenko
190Texas A &M University, College Station, TX USA
190,
A Delgado
A Delgado
190Texas A &M University, College Station, TX USA
190,
R Eusebi
R Eusebi
190Texas A &M University, College Station, TX USA
190,
J Gilmore
J Gilmore
190Texas A &M University, College Station, TX USA
190,
T Huang
T Huang
190Texas A &M University, College Station, TX USA
190,
T Kamon
T Kamon
190Texas A &M University, College Station, TX USA
285 Kyungpook National University, Daegu, Korea
190,285,
H Kim
H Kim
190Texas A &M University, College Station, TX USA
190,
S Luo
S Luo
190Texas A &M University, College Station, TX USA
190,
S Malhotra
S Malhotra
190Texas A &M University, College Station, TX USA
190,
R Mueller
R Mueller
190Texas A &M University, College Station, TX USA
190,
D Overton
D Overton
190Texas A &M University, College Station, TX USA
190,
L Perniè
L Perniè
190Texas A &M University, College Station, TX USA
190,
D Rathjens
D Rathjens
190Texas A &M University, College Station, TX USA
190,
A Safonov
A Safonov
190Texas A &M University, College Station, TX USA
190,
J Sturdy
J Sturdy
190Texas A &M University, College Station, TX USA
190,
N Akchurin
N Akchurin
191Texas Tech University, Lubbock, TX USA
191,
J Damgov
J Damgov
191Texas Tech University, Lubbock, TX USA
191,
V Hegde
V Hegde
191Texas Tech University, Lubbock, TX USA
191,
S Kunori
S Kunori
191Texas Tech University, Lubbock, TX USA
191,
K Lamichhane
K Lamichhane
191Texas Tech University, Lubbock, TX USA
191,
S W Lee
S W Lee
191Texas Tech University, Lubbock, TX USA
191,
T Mengke
T Mengke
191Texas Tech University, Lubbock, TX USA
191,
S Muthumuni
S Muthumuni
191Texas Tech University, Lubbock, TX USA
191,
T Peltola
T Peltola
191Texas Tech University, Lubbock, TX USA
191,
S Undleeb
S Undleeb
191Texas Tech University, Lubbock, TX USA
191,
I Volobouev
I Volobouev
191Texas Tech University, Lubbock, TX USA
191,
Z Wang
Z Wang
191Texas Tech University, Lubbock, TX USA
191,
A Whitbeck
A Whitbeck
191Texas Tech University, Lubbock, TX USA
191,
E Appelt
E Appelt
192Vanderbilt University, Nashville, TN USA
192,
S Greene
S Greene
192Vanderbilt University, Nashville, TN USA
192,
A Gurrola
A Gurrola
192Vanderbilt University, Nashville, TN USA
192,
R Janjam
R Janjam
192Vanderbilt University, Nashville, TN USA
192,
W Johns
W Johns
192Vanderbilt University, Nashville, TN USA
192,
C Maguire
C Maguire
192Vanderbilt University, Nashville, TN USA
192,
A Melo
A Melo
192Vanderbilt University, Nashville, TN USA
192,
H Ni
H Ni
192Vanderbilt University, Nashville, TN USA
192,
K Padeken
K Padeken
192Vanderbilt University, Nashville, TN USA
192,
F Romeo
F Romeo
192Vanderbilt University, Nashville, TN USA
192,
P Sheldon
P Sheldon
192Vanderbilt University, Nashville, TN USA
192,
S Tuo
S Tuo
192Vanderbilt University, Nashville, TN USA
192,
J Velkovska
J Velkovska
192Vanderbilt University, Nashville, TN USA
192,
M Verweij
M Verweij
192Vanderbilt University, Nashville, TN USA
192,
M W Arenton
M W Arenton
193University of Virginia, Charlottesville, VA USA
193,
B Cox
B Cox
193University of Virginia, Charlottesville, VA USA
193,
G Cummings
G Cummings
193University of Virginia, Charlottesville, VA USA
193,
J Hakala
J Hakala
193University of Virginia, Charlottesville, VA USA
193,
R Hirosky
R Hirosky
193University of Virginia, Charlottesville, VA USA
193,
M Joyce
M Joyce
193University of Virginia, Charlottesville, VA USA
193,
A Ledovskoy
A Ledovskoy
193University of Virginia, Charlottesville, VA USA
193,
A Li
A Li
193University of Virginia, Charlottesville, VA USA
193,
C Neu
C Neu
193University of Virginia, Charlottesville, VA USA
193,
B Tannenwald
B Tannenwald
193University of Virginia, Charlottesville, VA USA
193,
Y Wang
Y Wang
193University of Virginia, Charlottesville, VA USA
193,
E Wolfe
E Wolfe
193University of Virginia, Charlottesville, VA USA
193,
F Xia
F Xia
193University of Virginia, Charlottesville, VA USA
193,
P E Karchin
P E Karchin
194Wayne State University, Detroit, MI USA
194,
N Poudyal
N Poudyal
194Wayne State University, Detroit, MI USA
194,
P Thapa
P Thapa
194Wayne State University, Detroit, MI USA
194,
K Black
K Black
195University of Wisconsin-Madison, Madison, WI USA
195,
T Bose
T Bose
195University of Wisconsin-Madison, Madison, WI USA
195,
J Buchanan
J Buchanan
195University of Wisconsin-Madison, Madison, WI USA
195,
C Caillol
C Caillol
195University of Wisconsin-Madison, Madison, WI USA
195,
S Dasu
S Dasu
195University of Wisconsin-Madison, Madison, WI USA
195,
I De Bruyn
I De Bruyn
195University of Wisconsin-Madison, Madison, WI USA
195,
P Everaerts
P Everaerts
195University of Wisconsin-Madison, Madison, WI USA
195,
C Galloni
C Galloni
195University of Wisconsin-Madison, Madison, WI USA
195,
H He
H He
195University of Wisconsin-Madison, Madison, WI USA
195,
M Herndon
M Herndon
195University of Wisconsin-Madison, Madison, WI USA
195,
A Hervé
A Hervé
195University of Wisconsin-Madison, Madison, WI USA
195,
U Hussain
U Hussain
195University of Wisconsin-Madison, Madison, WI USA
195,
A Lanaro
A Lanaro
195University of Wisconsin-Madison, Madison, WI USA
195,
A Loeliger
A Loeliger
195University of Wisconsin-Madison, Madison, WI USA
195,
R Loveless
R Loveless
195University of Wisconsin-Madison, Madison, WI USA
195,
J Madhusudanan Sreekala
J Madhusudanan Sreekala
195University of Wisconsin-Madison, Madison, WI USA
195,
A Mallampalli
A Mallampalli
195University of Wisconsin-Madison, Madison, WI USA
195,
D Pinna
D Pinna
195University of Wisconsin-Madison, Madison, WI USA
195,
T Ruggles
T Ruggles
195University of Wisconsin-Madison, Madison, WI USA
195,
A Savin
A Savin
195University of Wisconsin-Madison, Madison, WI USA
195,
V Shang
V Shang
195University of Wisconsin-Madison, Madison, WI USA
195,
V Sharma
V Sharma
195University of Wisconsin-Madison, Madison, WI USA
195,
W H Smith
W H Smith
195University of Wisconsin-Madison, Madison, WI USA
195,
D Teague
D Teague
195University of Wisconsin-Madison, Madison, WI USA
195,
S Trembath-Reichert
S Trembath-Reichert
195University of Wisconsin-Madison, Madison, WI USA
195,
W Vetens
W Vetens
195University of Wisconsin-Madison, Madison, WI USA
195;
CMS Collaboration286