Occurrence and stability of anion–π interactions between phosphate and nucleobases in functional RNA molecules

Abstract

We present a systematic structural and energetic characterization of phosphate(OP)–nucleobase anion…π stacking interactions in RNAs. We observed OP–nucleobase stacking contacts in a variety of structural motifs other than regular helices and spanning broadly diverse sequence distances. Apart from the stacking between a phosphate and a guanine or a uracil two-residue upstream in specific U-turns, such interactions in RNA have been scarcely characterized to date. Our QM calculations showed an energy minimum at a distance between the OP atom and the nucleobase plane centroid slightly below 3 Å for all the nucleobases. By sliding the OP atom over the nucleobase plane we localized the optimal mutual positioning of the stacked moieties, corresponding to an energy minimum below -6 kcal•mol⁻¹, for all the nucleobases, consistently with the projections of the OP atoms over the different π-rings we observed in experimental occurrences. We also found that the strength of the interaction clearly correlates with its electrostatic component, pointing to it as the most relevant contribution. Finally, as OP–uracil and OP–guanine interactions represent together 86% of the instances we detected, we also proved their stability under dynamic conditions in model systems simulated by state-of-the art DFT-MD calculations.

INTRODUCTION

Among the non-covalent interactions governing the complex 3D architecture of RNAs, edge-to-edge hydrogen bonding and π–π stacking between nucleobases are the most frequent and most thoroughly characterized (1–6). In addition, to achieve a compact three-dimensional (3D) fold, RNA molecules employ a variety of stabilizing strategies - including posttranscriptional modifications (7–10), environmental factors such as structural water molecules (11–14) and metal ions (15–17), protonation of nucleobases (18–20) - and establish different types of backbone-backbone and backbone-nucleobase interactions (21–25).

Focusing on the interactions between the ribophosphate backbone and the nucleobases, the relevance of the stacking between the O4' atom of a ribose and the aromatic ring of a nucleobase, a lone pair–π (lp-–π) interaction in nature, is now widely recognized. First reported as stabilizing structural elements of the Z-DNA double-helix structure (26,27) and of Z-turns in RNA (28–30), we then found occurrences of them in basically all the RNA molecules that need to adopt a complex 3D structure to be functional (31). Further, by QM calculations, we showed that they contribute an energy comparable to the stacking between two bases in a regular double helix (31).

Another type of stacking contact between the RNA backbone and the nucleobases is the lp-π or, more specifically, the anion…π interaction that may establish between the non-bridging oxygen atoms of the phosphate and the aromatic ring of a nucleobase. While anion…π interactions are nowadays overall vastly reported in literature, also as tools in catalysis and for the design of anion receptors (32–35), this type of interaction has been so far much less explored in RNA (29,36). Just to give a taste of the chemical and biochemical relevance of such interactions, anion–π interactions are now constructively exploited in fields such as anion sensing (37), supramolecular assembly (38,39) and anion transport through membranes (40), including biological systems (35). Several experimental and theoretical studies have in fact shown the existence of such contacts in a variety of organic and biological molecules (41–46). To quote some examples, a systematic study of crystal structures of organic molecules, such as pentafluorophenyl rings, have captured halide anions (Cl⁻, Br⁻, I⁻) facing the aromatic ring surface (47).

In the context of biological macromolecules, the presence in protein structures of anion–π interactions between standard aromatic residues (Trp, Phe, Tyr, His) and anions, such as chloride and phosphate was shown in a Protein Data Bank (PDB) survey performed in 2012 (48). Similarly, Hinde and co-workers observed the occurrence in protein experimental structures of attractive interactions between the aromatic ring of Phe and the negatively charged side chains of Asp and Glu (49). However their findings, like those obtained on similar systems by Moore et al. (50), have been questioned by a later study (51) based on an accurate analysis of the electron density of residues involved in the putative interactions in considered structures. Still in the context of protein systems, Smith et al. proposed the anion…π interactions to strongly affect the stability of the β-sheet protein WW (52). Deyà and co-workers integrated the PDB search with ab initio calculations showing that anion–π interactions play a role in the activity of flavin-dependent enzymes (53) and, recently, Frontera and co-workers studied long-range effects in anion–π interactions and their role in the mycobacterium tuberculosis malate synthase inhibition mechanism (54). Moore and co-workers also searched high-resolution structures of nucleic acids for the presence of anion–π contacts, with the anion placed directly above the center of a six-membered ring (50). For nucleic acids, they especially observed anion…π contacts in loop/hairpin structures, such as tetraloops, between an oxygen atom of a phosphate and a base of a nucleotide two residues upstream (50). More recently, a comprehensive screening of the PDB has been carried on, searching for anion…aromatic motifs involving different anions and aromatic rings (amino acids, nucleobases and ligands) and featuring different mutual positioning: ‘canonical’, i.e. with the anion localized over the ring, or ‘peripheral’, i.e. with the anion close to the ring plane or above the ring substituents (55). This study confirmed the abundance of anion…aromatic interactions in basically all investigated systems and showed that nucleobases and ligands exhibit a considerable preference for ‘canonical’ anion…π contacts.

In the context of RNA, when the current view in chemistry was that forces between anions and the seemingly electron-rich π-system of an aromatic ring could be repulsive (56), it was debated whether such an interaction would be a stabilizing or a merely tolerated short contact (36). Nowadays, the anion…π stacking contact between phosphate and uracil is known to occur in 3- and 4-nt U-turns (29,36,57), and the contact between phosphate and guanine is described as a conserved and key feature of GNRA tetraloops (frequently occurring structural motifs, where N stands for any nucleobase and R stands for A or G) (29,55). In addition, by quantum mechanics (QM) calculations, this specific interaction between a phosphate and a guanine two residues upstream in the context of GNRA motifs has been estimated to be stabilizing by 3–4 kcal•mol⁻¹ (58). Although for some tetraloops (specifically GAAA and GGAG) classical molecular dynamics (MD) has shown that they maintain the overall stability and the anion…π contact under dynamic conditions all over the simulation time (58), other tetraloops in RNAs, such as UUCG, have been shown to be highly challenging for MD simulations (59).

While the structural role of the phosphate…π stacking interactions in the RNA GNRA tetraloops is now recognized and studies are currently exploring the possibility of bolstering their stability by incorporation of a thiophosphate modification (60,61), a thorough structural characterization of phosphate-nucleobase anion…π stacking interactions in general in RNA molecules and a full understanding of their physico-chemical nature and strength are not yet available in literature. To fill this gap, in this contribution we have carried out a systematic search of ‘canonical’ anion…π phosphate–nucleobase stacking interactions, which are indeed the preferred type of anion…π interactions for RNA (55), in a high-resolution non-redundant database of RNA structures (62). More importantly, we complemented this survey with statistical and structural analyses and with a state-of-the-art static and dynamic energetic characterization.

As a result of these analyses, we found phosphate-nucleobase anion…π stacking interactions to be widespread in functional RNAs, with the GNRA tetraloops and the 3- or 4-nt U-turns with stacked uracil representing roughly one third of all the cases. In the following, we discuss such interactions and relative energetics in detail for each of the nucleobases. We also present the distribution of the sequence distance between the nucleobase and the stacked phosphate and, using a case study, their strategic location in RNA structural motifs, also as inter-domain and inter-molecular contacts. Further, we report the first molecular dynamics DFT calculations (referred to as DFT-MD in the following) on two different RNA structural motifs featuring anion…π contacts involving a guanine and a uracil, respectively. Although currently limited in the time scale of ps (versus the ns time scale of classical MD), such simulations do not suffer from the limitations highlighted for the current state-of-the-art MD force fields in the description of RNA tetraloops (59).

Overall our statistical and structural analyses, along with our energetic and dynamic calculations, confirm the relevance of the anion…π contacts, not only in the context of GNRA tetraloops, and propose them as relevant contacts besides these structural motifs, adding themselves to the variety of non-covalent interactions employed by RNA molecules to fine tune their stability.

MATERIALS AND METHODS

Structural dataset

We started from the non-redundant 3D structure dataset for RNA by Leontis and Zirbel (62), version 1.89. The 699 structures that have a resolution ≤3.0 Å were collected, and we refer to them as the nrRNA3.0 dataset in the following. For some analyses, we also used a reduced dataset of 221 structures with a resolution ≤2.0 Å that we named the nrRNA2.0 dataset. These are the same datasets we used in (31,63), and we selected them here for the sake of consistency.

Identification of phosphate–nucleobase Contacts

Identification of anion…π interactions between the non-bridging oxygen atoms of the phosphate groups (OP1, OP2) and the nucleobases was achieved by using a geometrical setup analogous to that used in (31,63) and shown in Figure 1. The nucleobases of all the entries in the nrRNA3.0 dataset were oriented in a Cartesian frame as follows. The origin of the frame was placed at the geometric center of the heterocycle skeleton, the x-axis passing through the N3 atom for pyrimidines and through the middle point of the N1–C2 bond for purines (see Figure 1). The y-axis formed a 90^o angle with the x-axis, with the C6 atom of purines and the C4 atom of pyrimidines lying in the xy-plane at positive y values. A right-handed frame was formed by building the z-axis vector as the cross product of the vectors along the x-axis and y-axis. Orienting the base in the reference frame facilitated definition of the position of the OP1/OP2 atom of a phosphate group with respect to the nucleobase, using the three translational parameters Δx(shift), Δy(slide) and Δz(rise).

Figure 1.

Definition of the reference Cartesian frame on the nucleobases. The origin is at the geometrical center of the heterocycle skeleton, the x-axis passing through the N3 atom for pyrimidines and through the middle point of N1–C2 bond for purines; the y-axis forms a 90° angle with the x-axis, with the C6 atom of purines and the C4 atom of pyrimidines lying in the xy-plane at positive y values; the z-axis is the cross product of the versors along the x and y-axes, thus forming a right-handed frame. The yellow curve defines a circle of radius 1.5 Å in the xy-plane of pyrimidines, and an ellipse in the xy-plane of purines, with minor and major axes equal to 1.5 Å and 2.5 Å. A phosphate and a nucleobase are considered to be interacting if the projection of either OP1 or OP2 on the xy-plane is within the yellow circle/ellipse, with the vertical distance (z-distance) in the –4.0 Å to +4.0 Å range.

Phosphate-base contacts were defined based on two conditions. First, the rise of the OP atom (either OP1 or OP2) had to fall in the –4.0 Å to + 4.0 Å range. Second, the projection of the OP atom had to fall within a circle of radius 1.5 Å (centered at the frame origin) for pyrimidines and on an ellipse with major axis of 2.5 Å and minor axis of 1.5 Å (again centered at the origin). This procedure allowed us to identify 675 phosphate–base contacts in 147 PDB structures involving all four nucleobases (Supplementary Table S1). Of course, choosing cutoff values in a structural search always implies some arbitrariness. In the present case, the cutoff values that we chose were selected to enforce that the projection of OP atoms on the base plane is within the heterocycle ring. For the vertical distance, we considered a cutoff of ±4.0 Å, similar to our previous studies (31,63). This choice was reinforced by both our structural and energetic analyses, reported below. A plot of the distribution of the vertical distances of the OP from the nucleobase plane is reported in Figure 2.

Figure 2.

(A) Pie chart of the total number of instances (count and percentage) of phosphate-nucleobase anion…π contacts. The distance cutoff between OP and the nucleobase plane was set at 4.0 Å. (B) Distribution of the vertical distances: distances between OP and the nucleobase plane in the recorded interactions are reported for each nucleobase. Projections of the OP atoms on the base plane are also shown as red dots.

Quantum mechanics calculations

The phosphate–nucleobase interaction energies were evaluated using quantum mechanics (QM). To obtain an initial geometry for the QM calculations, coordinates of guanine-2659 and of the phosphate group of residue 2661 were taken from the crystal structure of the Sarcin/Ricin domain from E. coli 23 S rRNA (PDB ID: 3DVZ, resolution 1.0 Å), truncating the phosphate moiety at the O3′ and O5′ bridging oxygens and capping them with methyl groups, thus obtaining a dimethyl phosphate (DMP), as shown in Figure 1. Then, the isolated G and DMP were optimized using the PBE0 functional and triple-ζ TZVP basis sets (64,65) as implemented in the Gaussian 09 package and the optimized geometries were best superimposed on the respective moieties in the crystal structure, to obtain an optimized DMP-guanine interaction. Isolated adenine, cytosine, uracil and pseudouracil (PSU) moieties were also optimized and best superimposed on the guanine base in the above DMP-guanine interaction. For pyrimidines, best superimposition was performed on the 6-membered ring of the guanine and then the DMP was translated along the x-axis, to have the OP projecting into the centroid of the pyrimidine ring. During the optimization, a C_s symmetry constraint was imposed on the nucleobases, in order to maintain planarity and avoid the formation of H-bonds with the DMP, thus allowing the formation of stacking interactions only. The potential energy surface (PES) calculations for the modeled DMP-nucleobases were performed with the distance between the OP atom of the DMP and the nucleobases centroid varied at 0.1 Å increments, in the 2.0–7.0 Å range, and at 1.0 Å increments in the 7.0–14.0 Å range, with the DMP and the nucleobases frozen at the PBE0/TZVP optimized geometries.

In this work, we calculated the interaction energy of the DMP-base pairs, E_int, as in Equation (1):

(1)

where E_DMP-B is the electronic energy of the DMP-base complex and E_DMP and E_B are the electronic energies of the isolated DMP and base fragments forming the complex. Geometries of the nucleobases and DMP alone were not optimized, which means the isolated bases and DMP have exactly the same geometry that they have in the complex. It should be noted that the calculated interaction energies cannot directly be compared to the experimental free energies of RNA folding or stem formation, as they do not include several corrections, such as approximating the solvent with a continuum model and entropy (66). It should be noted that quantum mechanics calculations, discussed in this work, localize minima on the potential energy surface of isolated systems at formally 0 K (67). This implies that the calculated interaction energies cannot directly be compared to the experimental free energies of RNA folding or stem formation. In fact, in addition to the intrinsic stability of the phosphate-base stacking contacts, as calculated in this work, the experimental values depend also on the specific environment, which means other surrounding RNA bases and cations surrounding the RNA and solvent molecules.

The DMP–base anion…π interaction energies were evaluated at the coupled cluster level of theory, with iterative inclusion of single and double excitations and perturbative inclusion of triple excitations (CCSD(T)), which is considered the golden standard in electronic structure calculations including H-bonding and stacking interactions in nucleic acids (68,69). The domain-based local pair-natural orbital (DLPNO) approximation (70–72), as implemented in the ORCA package (73), was used to accelerate calculations. Tighter than the default ‘TightPNO’ DLPNO settings (TCutPairs = 10⁻⁵, TCutPNO = 10⁻⁷, and TCutMKN = 10⁻³) were used (74). The correlation consistent Dunning cc-pVTZ basis set was used in these calculations (75). The tight PNO settings (TCutPairs = 10⁻⁴, TCutPNO = 3.3 × 10⁻⁷, TCutMKN = 10⁻³) were used to reduce any numerical noise in the calculations. The default SCF convergence criterion NormalSCF (energy change 1 × 10⁻⁶ au) was replaced with the tighter TightSCF (energy change 1 × 10⁻⁸ au) to achieve better converging wave functions. All the interaction energies are corrected for basis set superposition error with the counterpoise method of Boys and Bernardi (76).

Electrostatic potentials were calculated as previously described (31), and are here mapped on electron density isosurfaces corresponding to a value of 0.0004 atomic units, scaled between –30 and + 30 kcal•mol⁻¹.

Potential energy interaction maps were built by scanning the grid positions located on the lines connecting the nucleobase centroid to each atom of the ring (see Supplementary Figure S1). On all the grid points the distance between OP of DMP and the nucleobase plane was fixed to the ideal value of 2.9 Å. Energies of the DMP-base anion…π interaction were calculated for all the scanned grid single points at the DLPNO-CCSD (T)/aug-cc-pVTZ level. Test calculations at the higher DLPNO-CCSD (T)/aug-cc-pVQZ level were also performed for representative instances of the DMP-cytosine interaction (see Supplementary Table S2), showing differences in energies within 0.05 kcal•mol⁻¹ from those obtained at the DLPNO-CCSD (T)/aug-cc-pVTZ level. This reinforces the choice of the DLPNO-CCSD (T)/aug-cc-pVTZ level for all the energies reported in the present work.

Energy decomposition analysis (EDA)

According to the EDA method, developed independently by Morokuma (77,78) and Ziegler and Rauk (79,80), ΔE_int can be decomposed into four physically meaningful components representing different steps towards the formation of a complex from two individual moieties. These four components are: the electrostatic energy, ΔE_elstat, the Pauli energy, ΔE_Pauli, the orbital energy, ΔE_orb and the dispersion energy, ΔE_dispersion (Equation 2):

(2)

The electrostatic energy, ΔE_elstat, corresponds to the electrostatic interaction between the moieties and being usually attractive, while the Pauli energy, ΔE_Pauli, corresponds to the steric repulsion originating from the Pauli antisymmetry principle and being responsible for the destabilizing interaction between occupied orbitals. Further, the orbital energy, ΔE_orb, accounts for the charge transfer (donor−acceptor interaction between the occupied molecular orbitals on one moiety and the unoccupied molecular orbitals on the other moiety) and the intra-moiety polarization (mixing of occupied and unoccupied orbitals). Finally, the empirical dispersion term, ΔE_dispersion, accounts for the long-range dispersion effects, as introduced by Grimme et al. (81); this term is computed independently from the Kohn−Sham energy to yield the total interaction energy of the system.

Decomposition analysis was carried out using the Amsterdam Density Functional (ADF) 2016 program package (82). Decomposed components of the interaction energies were calculated using the generalized gradient approximation (GGA) with the BLYP functional (83–85) and the DFTD3(BJ) correction (86), with the TZ2P basis set.

DFT-MD simulations

For the DFT-MD simulations, we used two 6- and 5-nt long systems, featuring an OP–guanine and an OP–uracil contact, respectively. For the OP–guanine contact, we selected the U-turn tetraloop containing G₂₆₅₉AGAGC sequence from a Sarcin/Ricin domain of E. coli 23S rRNA (PDB ID: 3DVZ, resolution: 1.00 Å), presenting an anion…π contact between G2661(OP) and the G2659 base. For the OP–uracil contact, we selected the U-turn in the T loop (U₅₄UCAA sequence) of mouse tRNA(Sec) (PDB ID: 3RG5, resolution: 2.00 Å), where A57(OP) interacts with the U55 base. We performed DFT-MD simulations in the NVT ensemble at 300 K, using the CP2K simulation package (87,88) and the PBE (89) level of exchange-correlation functional. The DZVP-MOLOPT-SR-GTH pseudo-potential was used to describe the Na and P elements, and DZVP-MOLOPT-GTH pseudo-potential was used to describe the electronic properties of C, H, O and N elements (90). We included the third generation of Grimme's dispersion interaction (81) to describe the vdW interactions. The Parinello's CSVR thermostat (91) was used to control the temperature. The systems were neutralized by adding 5 Na⁺ ions to the G₂₆₅₉AGAGC sequence and 4 Na⁺ ions to the U₅₄UCAA system. Simulations were performed for 25 ps, and the last 20 ps of the trajectories were recorded for further analyses. All the 20 000 recorded frames were used for the radial distribution analysis, and 1000 frames were extracted every 20 fs for the distances calculation and for visualization of the OP projection on the nucleobase plane.

RESULTS AND DISCUSSION

Statistical and structural analysis of phosphate-nucleobase anion…π interactions

Occurrences of phosphate-nucleobase anion…π interactions, from here on referred to as OP–nucleobase interactions/contacts, were searched in a non-redundant dataset of 699 RNA crystal structures, featuring a resolution of 3.0 Å or better, by using the geometrical criteria shown in Figure 1.

We identified 675 instances of OP–nucleobase contacts in 147 structures (which correspond to 21% of the available PDB structures in the dataset), including 36 tRNAs, 10 ribozymes, 22 riboswitches and 12 ribosomes. It is worth noting that the average length of the RNA molecules in the above ensemble of 147 structures is 199 nts when including and 68 nts when excluding the 12 ribosomal structures. In contrast, the average length for the dataset of 552 RNA structures where no OP–nucleobase contact was detected drops to 20 nucleotides.

Focusing on the participation of specific nucleobases to the anion…π interactions, out of the 675 detected contacts, 51 involve an adenine, 331 a guanine, 32 a cytosine and 249 an uracil (see Figure 2), while 12 instances correspond to OP–pseudouracil contacts from tRNA T-loops. From the numbers above it emerges the prevalent involvement of guanine and uracil as nucleobases in detected contacts. OP–guanine and OP–uracil contacts indeed represent together 86% of the total instances (49% for G and 37% for U), while OP–adenine and OP–cytosine represent 8 and 5%, respectively, of them. The overrepresentation of guanine and uracil in the OP–nucleobase contacts still persists if the resolution of the dataset is reduced from 3.0 to 2.0 Å (see Supplementary Figure S2A). Such a distribution does not simply reflect different frequencies of the 4 nucleobases in the analysed dataset, which are actually comparable. In the set of 147 structures presenting at least one OP–base contact, we counted overall 7464 adenines, 6167 uracils, 9409 guanines and 7355 cytosine, corresponding to 25, 20, 31 and 24% of the total, respectively. It is also noteworthy that, out of the total 26 pseudouridine nucleobases present in the dataset, 12 (46%) were found involved in OP–nucleobase contacts. We also investigated the identity of the nucleotides carrying the stacked phosphate, finding the following distribution: 366 contacts involve an adenine, 201 a guanine, 61 a cytosine and 47 a uracil. Therefore, a clear prevalence of A and G emerges, which provide together the 84% of all the phosphates involved in the observed phosphate-nucleobase interactions (see Supplementary Figure S2B). However, we cannot exclude the fine details of the presented statistical distributions to be dependent on the structural dataset selected for the analyses.

As for the distance between the OP atom and the nucleobase plane, it was found to be around 3.2 Å, and specifically 3.28 ± 0.36 Å for the OP–adenine, 3.13 ± 0.28 Å for the OP–uracil, 3.18 ± 0.24 Å for the OP–guanine and 3.25 ± 0.44 Å for the OP–cytosine contact. Figure 2B also reports, as red dots, the projection of the OP atoms on the plane of the stacked nucleobases for all the detected contacts. For OP–uracil, a large number of OP atoms point in proximity of the C2 atom, while for OP–guanine, a large number of them point to the center of the heterocycle, around the C4–C5 bond. For the OP–cytosine and OP–adenine contacts, the trend is less defined, however a slight preference is observed for an OP projection into the imidazole ring for adenine and around the ring center and the N1 atom for cytosine.

We also investigated the sequence distance in the 5′→3′ direction of the RNA chain between the phosphate (residue number n) and the nucleobase (residue number n ± i) involved in the anion…π interactions. The results of this analysis are reported in Figure 3. The large majority of the interactions are observed between a phosphate and a nucleobase that is two residues upstream (n-2), especially for guanine and uracil, where the n-2 interactions represent 84 and 68% of the total occurrences, respectively. This finding is not surprising since a n-2 OP–nucleobase interaction, has already been described as a key descriptor for U-turns, such as the GNRA tetraloop and the T loop in tRNAs, specifically between the first nucleobase of the loop (a U or PSU) and an OP atom on the third nucleotide (57,92). However, we also observed n-2 OP–nucleobase contacts in other structural motifs, such as the pentaloop (shown in Figure 4) and others discussed in the next paragraph. The large prevalence of n-2 interactions also explains the high proportion of A and G within the nucleotides involved in the interactions with their phosphate (discussed above and reported in Supplementary Figure S2B). The nucleotide at the n position is indeed a purine by definition in GNRA tetraloops (third position of the loop) and a G or A also in tRNA T-loops (position 57 according to the canonical numbering (93,94)). Furthermore, the vast majority of the n-2 OP–nucleobase contacts that we analysed in other structural motifs (see text and figures below) also feature an A or G nucleotide at the n position.

Figure 3.

Sequence distance between the phosphate(n) and the nucleobase(n± i) moieties involved in anion…π interactions, reported for each of the four bases. The residue numbering is in the 5'→3' direction. ‘n’ means that the interacting phosphate and nucleobase belong to the same nucleotide. In addition, 1 n+ 2 and 1 n-1 instance were observed for uracil and 2 n-1 instances were observed for guanine, which are not shown in the plots for the sake of readability.

Figure 4.

Examples of phosphate–base anion…π contacts involving different nucleobases in different structural motifs and with different sequence distances. 3D representations with the stacked OP shown as a red sphere; corresponding RNA molecules, PDB IDs, residues numbering and structural motifs are reported. H-bonds of the stacked nucleobase with surrounding residues are shown as dark-blue dotted lines, while H-bonds of the base pair closing the loop are shown as light-blue dotted lines.

In addition, roughly 6% of the interactions occur between phosphate and nucleobase moieties belonging to the same nucleotide (n, examples are reported in Supplementary Figure S3). Moreover, examples of interactions of the phosphate with a nucleobase that is 1 or 3 residues upstream (n-1, n-3), as well as with nucleobases 1 and 2 residues downstream (n + 1, n + 2) are also observed. Finally, long range interactions, i.e. interactions involving a phosphate and a nucleobase over 4 residues apart in the corresponding RNA sequence (i ≤ –4 or ≥ 4) are also observed for all the four nucleobases, while being more frequent, in proportion, for A and C. It is worth noticing that OP–nucleobase interactions with a sequence distance of n-2, located in structural motifs other than specific U-turns (GNRA tetraloops and 3- or 4-nt turns with a uracil/pseudouracil stacked) and those with a different sequence distance have never been reported before in literature, except for a n-1 interaction reported and a long-distance one mentioned in ref. (50). An example of a long-range interaction (n-9) in a C-loop motif is shown for cytosine in Figure 4, together with few examples of n-2 interactions for the other nucleobases.

23S-5S rRNA, a case-study

We detected 61 OP–nucleobase contacts in the 23S-5S rRNA from H. marismortui, (PDB ID: 1S72, resolution: 2.40 Å (95), that we will discuss in the following as a case study (Figure 5). Of the above 61 contacts, widespread all over the molecule, 50 (82%) involve a guanine or a uracil, in line with the nucleobases distribution observed in the overall dataset. As reported in Figure 5B, the observed contacts involve nucleobases located in a variety of structural elements, other than regular helices (stems), especially hairpin loops, but also junctions, internal loops and bulges (Figure 5C). In line with the above results on the sequence distance, in the 23S-5S rRNA from H. marismortui overall 67% (41 out of 61) of the contacts are of the n-2 type.

Figure 5.

OP–nucleobase contacts in 23S-5S rRNA from H. marismortui (PDB ID: 1S72). (A) 3D representation with blue, red, green and purple spheres representing adenine, guanine, uracil, cytosine bases involved in OP–nucleobase anion…π interactions. (B) Fraction of different nucleobases involved in the interactions (top) and number of occurrences of bases involved in the interactions in different structural motifs (bottom). (C) Count of the occurrences of OP–nucleobase contacts in different structural motifs. (D) An example for uracil (left) and one for guanine (right) of n-2 stacking contacts in structural motifs unreported before; stacked residues and those involved in motif-defining H-bonds are labeled. H-bonds of the stacked nucleobase with surrounding residues are shown as dark-blue dotted lines, while H-bonds of the base pair closing the loop are shown as light-blue dotted lines. (E) Examples of very long-range (inter-domain) and inter-molecular OP–nucleobase contacts; stacked residues and hosting domains are labeled.

We took advantage of this case study to verify whether the observed n-2 contacts involving a uracil or a guanine as the stacked nucleobase corresponded to the n-2 contacts already reported in literature. One example each of n-2 stacking contacts involving uracil or guanine in structural motifs not reported before are shown in Figure 5D. Specifically, for uracil a contact in a 7-nt U-turn is shown. For guanine a contact is shown in a motif that may seem a GNRA tetraloop at first sight but is not because it misses the 1–4 G506•A509 non canonical base pairing characteristic of GNRA loops, and features instead a 1–6 G506•A511 H-bonding (while A509 H-bonds to C505) (29,96). For uracil, we observed a total of 13 n-2 contacts, of which, surprisingly, only 3 correspond to the 3-nt T-loop reported in (36,97) and an additional one to a 4-nt U-turn similar to that discussed by Auffinger et al. (29); the remaining nine cases correspond to U-turns of variable length, some examples of which (for a length of 6-, 8- and 9-nt) are shown in Supplementary Figure S4, while a complete list is given in Supplementary Table S3. As for guanine, we observed overall 23 n-2 contacts, of which 17 are located in standard GNRA tetraloops, while the remaining six are located in motifs other than GNRA; examples of them are shown in Supplementary Figure S5, and a complete list is reported in Supplementary Table S4. Assuming a similar trend for the other RNA structures in the dataset, we may approximately estimate that overall only at most one third of the OP–nucleobase stacking contacts we recorded here strictly belong to the cases (structural motifs) already discussed in literature.

Finally, we note that seven contacts have the OP atom and the nucleobase more than 100 residues apart in sequence, connecting different structural domains of the 23S rRNA and one inter-molecular contact is observed between 23S and 5S rRNAs; examples are shown in Figure 5E. Among the inter-domains contacts, three involve domain 0, at the core of the 23S structure, to which the other six domains are rooted, while two involve domain V, which is mainly responsible for the 23S peptidyl transferase activity (98).

Potential energy surfaces

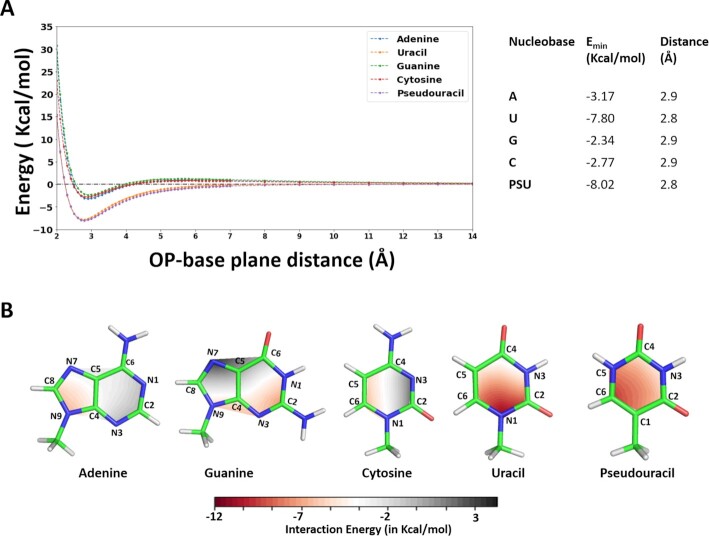
Potential energies of phosphate-nucleobase anion…π interactions have been calculated for the four canonical nucleobases and for pseudouracil. The distance between OP and the geometric center of nucleobases was varied at 0.1 Å increments, in the 2.0–7.0 Å range, and at 1.0 Å increments in the 7.0–14.0 Å range (see Materials and Methods for details). The single point energy values calculated at all the vertical distances for each nucleobase are reported in Supplementary Table S5. Resulting potential energy surfaces (PESs) are reported in Figure 6A.

Figure 6.

(A) Potential Energy Surfaces for all the nucleobases (A, U, G, C, PSU) with an OP of DMP oriented to give rise to anion…π interactions. Interaction energies in kcal•mol⁻¹ (y-axis) are reported versus the OP–nucleobase distances, varying between 2.0 Å and 14.0 Å (x-axis). (B) Contour diagrams showing the interaction energies between for the OP atom of DMP and the bases. Energy values are color coded, from red (−12.0 kcal•mol⁻¹) to blue (+3.0 kcal•mol⁻¹). Single point energies were calculated on a grid made of 4 points for each line connecting the nucleobase centroid to each atom of the ring (see Materials and Methods and Supplementary Figure S1). The OP–nucleobase distances were frozen at 2.9 Å.

PESs show well-defined energy minima for all the five nucleobases at a distance below 3.0 Å. Adenine, guanine and cytosine show similar trends with mimima located at a distance of 2.9 Å, corresponding to energy values of −3.17, −2.34 and v2.77 kcal•mol⁻¹ respectively. For uracil and pseudouracil, the interactions remain favorable in a wide range of distances (up to ≈ 8.0 Å), with energy minima, assuming values as low as −7.80 and −8.02 kcal•mol⁻¹, respectively, observed at a distance of 2.8 Å. It may be noted that Egli and coworkers have calculated the interaction energies of the phosphate-guanine and phosphate-uracil anion…π contacts, at the DFT/6–31G* level of theory, as +5.1 kcal•mol⁻¹ and −4.8 kcal•mol⁻¹ (36). However, their calculated interaction energies did not include the dispersion correction term and cannot therefore be meaningfully compared with ours. More recently, Bauza and coworkers have calculated the interaction energy at the RI-MP2/TZVPD level (which accounts for dispersion interactions) of a series of phosphate-guanine anion…π contacts to be in the −0.3 to −4.3 kcal•mol⁻¹ range (58), in line with the energies reported herein.

Interaction energies for different projections of OP on the nucleobase plane

Our structural analysis, (see Figure 2B) showed that, in the experimental occurrences of OP–nucleobase contacts, the OP atom is not always projected towards the centroid of the nucleobase. Therefore, in order to evaluate whether and how the energetics of the anion…π interactions is affected by the OP position relatively to the nucleobase centroid, we calculated the DMP-nucleobase interaction energy at different positions corresponding to the DMP sliding horizontally in a plane parallel to the nucleobase (see Materials and Methods for details). The distance between OP and the nucleobase plane was set to the ideal values of 2.9 Å, corresponding to the minima in the potential energy curves for most of the bases. On a quantitative ground, the average interaction energies for A, G, C, U and PSU are −2.92 ± 1.55, −2.21 ± 2.65, −2.50 ± 2.24, −6.85 ± 2.44 and −7.25 ± 1.33 kcal•mol⁻¹, respectively, thus all pointing to a stabilizing effect, with again U and PSU involved in clearly stronger interactions.

Analysis of the contour maps of Figure 6B indicates that sliding the DMP molecule above the nucleobase has a distinct effect on the interaction energies. For adenine, the energy minimum of −6.48 kcal•mol⁻¹ is observed around the C8−N9 atoms. For guanine, the most stable interaction at −7.22 kcal•mol⁻¹ is observed around the C2-N3 atoms. For cytosine, the OP projection of the energy minimum at −6.33 kcal•mol⁻¹ is located around the C5−C6 atoms. For uracil and pseudouracil, favorable energies are observed all over the surface of each of the nucleobases, with the most favorable site for interaction of U, at −11.68 kcal•mol⁻¹, around the N1 atom and encompassing the C2 and C6 atoms. This is consistent with the large proportion of OP projections towards these atoms in the experimental structures (see Figure 2B). Finally, for pseudouracil the energy minimum, at −10.1 kcal•mol⁻¹, is centered around the C6 atom.

Decomposition of the interaction energies: role of the electrostatic component

First of all, we checked that the interaction energies calculated using the BLYP-D3/TZ2P method are in good agreement with the same energies computed by the higher level CCSD(T)-DLPNO methodology (see Table 1). The mean absolute deviation of 0.74 kcal•mol⁻¹ between the B3LYP-D3 and CCSD(T)-DLPNO energies, together with a Pearson correlation coefficient of 0.99 between them, validate using the B3LYP-D3 energies in the following energy decomposition analysis (EDA) (77). Table 1 reports the decomposed interaction energy values for selected OP–nucleobase contacts. EDA analysis was carried out for 3 instances corresponding to individual DMP-nucleobase contacts, with one representing the geometric centroid and the other two corresponding to minimum (most negative) and maximum (least negative) interaction energy values, as calculated along the grid points.

Table 1.

Energy decomposition analysis of the OP–nucleobase contacts under study at the BLYP-D3(BJ)/TZ2P level of theory. By definition, ΔE_int = ΔE_elstat + ΔE_Pauli + ΔE_disp + ΔE_orb (see Materials and Methods). Interaction energies calculated at the DLPNO/aug-cc-pVTZ level of theory are also reported for the sake of comparison

Base pair	ΔEint (DLPNO)	ΔEint	ΔEelstat	ΔEPauli	ΔEdisp	ΔEorb
DMP-A-min	−6.48	−7.48	−1.88	6.20	−6.08	−5.73
DMP-A-max	0.04	−0.45	3.64	4.78	−3.51	−5.36
DMP-A-cen	−3.17	−4.32	0.66	6.47	−5.78	−5.67
DMP-U-min	−11.68	−12.78	−7.91	5.97	−5.25	−5.59
DMP-U-max	−1.87	−2.12	1.72	5.12	−3.91	−5.04
DMP-U-cent	−7.61	−8.14	−3.46	5.61	−5.06	−5.23
DMP-G-min	−7.22	−7.97	−3.20	5.30	−4.52	−5.55
DMP-G-max	4.48	4.32	9.18	4.96	−4.58	−5.23
DMP-G-cent	−2.34	−3.49	1.85	6.54	−5.91	−5.96
DMP-C-min	−6.33	−7.30	−2.51	6.64	−5.75	−5.68
DMP-C-max	2.47	2.00	5.65	4.66	−3.47	−4.83
DMP-C-cent	−2.77	−3.42	1.26	5.70	−5.12	−5.26
DMP-PSU-min	−10.10	−11.29	−6.82	6.59	−5.64	−5.42
DMP-PSU-max	−4.54	−5.08	−1.75	4.62	−3.50	−4.45
DMP-PSU-cent	−7.88	−8.51	−4.06	5.54	−5.02	−4.96

Of the four components of the interaction energy, the orbital and energy dispersion terms always contribute favorably and comparably to the total interaction energy, with the orbital energy ranging from −4.83 to −5.96 kcal•mol⁻¹ and the dispersion energy from −3.47 to −6.08 kcal•mol⁻¹. Therefore, differences in the total interaction energies stem from differences in the remaining components of the interaction energy. The other two components include the electrostatic energy between DMP and the nucleobase and the Pauli energy, corresponding to the steric repulsion originating from repulsive interaction between occupied orbitals. While the Pauli energy is consistently unfavorable for all the investigated OP–nucleobase contacts (ranging between 4.62 and 6.64 kcal•mol⁻¹), the electrostatic energy is favorable or unfavorable depending on the specific nucleobase involved and on the specific geometry. It explores in fact a range of ≈17 kcal•mol⁻¹, being +9.18 kcal•mol⁻¹ for the OP–guanine contact in the maximum energy geometry, and −7.91 kcal•mol⁻¹ for the OP–uracil contact in the minimum energy geometry.

Therefore, the electrostatic component is the one that tunes the interaction energy of these contacts, determining whether they are favorable or not. As it can be seen from Figure 7A, a strong correlation exists in fact between the overall interaction energy of the analyzed systems and its electrostatic component, with a R² value as high as 0.98.

Figure 7.

(A) Plot showing the correlation between the interaction energy, ΔE_int, and its electrostatic component, ΔE_elstat, for the OP–nucleobase contacts under study. (B) Electrostatic potentials of nucleobases and DMP, mapped on electron density isosurfaces corresponding to a value of 0.0004 atomic units, and scaled between –30 and 30 kcal•mol⁻¹.

The same finding is visually apparent when looking at the electrostatic maps for the nucleobases reported in Figure 7B. Due to the negative charge of DMP, it is not surprising that a clear positive correlation exists between the energy minima calculated above and the regions of the nucleobases characterized by positive electrostatic potential values.

DFT-MD simulations of RNA motifs featuring anion…π OP–guanine and OP–uracil contacts

Our statistical analysis showed the prevalent involvement of guanine and uracil in the OP–nucleobase contacts, representing together the 86% of the total instances. We decided therefore to simulate by a DFT-MD approach the dynamics of an OP–guanine and of an OP–uracil contact in a 6-nt and 5-nt long model system, respectively, to test their stability under dynamic conditions. For the OP–guanine contact, we selected the ‘U-turn’ tetraloop containing C₂₆₅₈GAGAG sequence from a Sarcin/Ricin domain of 23S rRNA from E. coli (PDB ID: 3DVZ, resolution: 1.0 Å) (99), with an OP of G2661 over the G2659 base. For the OP–uracil contact, we selected the U-turn in the T loop, U₅₄UCAA sequence, of tRNA(Sec) from Mus musculus (PDB ID: 3RG5, resolution: 2.0 Å) (100), with an OP of A57 over the U55 base. Although the tRNA T-loop is also known as T-PSU-C loop for the prevalent presence of a thymine and a pseudouracil at the first and second position of it (101), neither of these modifications is present in the selected structure. For each model system, we ran a 25-ps long simulation, collecting the last 20 ps for further analyses, whose results are reported in Figure 8.

Figure 8.

(A) Dynamic behavior of an OP–guanine anion…π contact in the C₂₆₅₈GAGAG motif from a Sarcin/Ricin domain of E.coli 23S rRNA (PDB ID: 3DVZ, resolution: 1.0 Å). Left: best superimposition on the G2659 nucleobase of 100 frames from the DFT-MD trajectory; oxygens of the stacked phosphate from G2661 are shown as small spheres. Middle: top view of the projection of OP–G2661 on the G2659 nucleobase plane (the black sphere indicates the projection of the OP atom in the initial structure), and time evolution of their distance, with average value and standard deviation also reported. Right: Two-dimensional radial distribution function (g(Δz, Δxy)), where Δz is the OP–base plane distance and Δxy is the lateral shift between the projection of the OP atom on the nucleobase plane (the xy-plane) and the geometrical center of the nucleobase (Figure 1). In the map, red and blue correspond to the most and least populated geometries, respectively. (B) Same analysis as in A) for the dynamic behavior of an OP–uracil anion…π contact in the U₅₄UCAA motif from the Mus musculus tRNA(Sec) structure (PDB ID: 3RG5, resolution: 2.0 Å.

As for the first model system, featuring the OP–guanine contact, the structural motif overall remained stable along the whole simulation. The average C1′-C1′ distance along the simulation between the 5′ C2658 and the 3′ G2663 nucleotides was 10.52 ± 0.15 Å, thus being very close to the initial value of 10.64 Å from the starting experimental structure (see Figure 8). The average distance between the OP atom of G2661 and the G2659 nucleobase plane is 3.21 ± 0.21 Å, which perfectly matches the value of 3.22 Å of the experimental distance. The OP–guanine contact was indeed maintained in all the 1000 analyzed frames, with minimum and maximum distances of 2.54 and 3.92 Å, respectively (Figure 8). Not surprisingly, the projection of the OP atom on the nucleobase plane is clustered around the centroid of the 6-membered ring, where it falls in the starting X-ray structure. We also extracted 10 snapshots from the simulation, at 2-ps intervals, and calculated their gas phase interaction energies at the DLPNO/aug-cc-pVTZ level of theory. The average calculated energy for the above 10 snapshots is −4.60 ± 1.58 kcal•mol⁻¹, in good agreement with the energies calculated for the OP–guanine contact along the grid points (see Figure 6B).

Also for the second model system, featuring the OP–uracil contact, the structural motif remained overall stable along the simulation. Here the average C1′-C1′ distance between the 5′ U54 and the 3′ A58 nucleotides is 9.63 ± 0.14 Å, which perfectly matches the initial static distance of 9.63 Å (Figure 8). The calculated average distance between the OP atom of A57 and the U55 nucleobase plane is 2.95 ± 0.21 Å, being extremely close to the initial experimental distance of 2.94 Å. The OP–uracil contact was in fact maintained in all the analyzed frames with a minimum and a maximum distance of 2.19 and 3.97 Å respectively (Figure 8). The projection of the OP atom on the nucleobase plane is clustered between the ring centroid and the N3 atom, similarly to the starting X-ray geometry. Also for this system we extracted 10 snapshots from the simulation, at 2-ps intervals, and calculated their gas phase interaction energy, on average, as −6.72 ± 1.75 kcal•mol⁻¹; again in fair agreement with the energies we calculated previously for the OP–uracil contact along the grid points (Figure 6B).

The position of the OP atom relatively to the nucleobase plane was also characterized through a radial distribution function (g(Δz, Δxy)), where Δz is OP–base plane distance, and Δxy is the lateral shift between the projection of the OP atom on the nucleobase plane (the xy-plane) and the geometrical center of the nucleobase (Figures 1 and 8). The color code of the maps, reported in Figure 8, follows the density of the population, with red corresponding to the most and blue corresponding to the least explored geometries. Results of this analysis clearly indicate a higher population, therefore in Boltzmann terms a more stable structure, at distances between 3.0 and 3.5 Å, and at a lateral shift between 0.5 and 1.0 Å, both for the OP–guanine and OP–uracil contacts.

CONCLUSIONS

The importance of anion…π interactions in biological systems cannot be overestimated (29,35,36,45,50,52–55,58,60,61,102,103). In the last two decades they have turned from controversial to well-established non-covalent interactions of functional relevance in a variety of biomolecules (56).

Herein we addressed the first systematic characterization of the phosphate(OP)-nucleobase anion…π stacking interactions in RNAs, based on a synergic structural and energetic approach. Our results indicate the OP–nucleobase interaction to be widespread in RNA molecules, with the already characterized stacking in GNRA tetraloops (between a phosphate and the guanine nucleobase two residues upstream, n-2) (29,36,50) and in 3- or 4-nt U-turns (between a phosphate and a uracil/pseudouracil two residues upstream, n-2) (29,36) representing roughly one third of the occurrences. We observed in fact OP–nucleobase stacking interactions with largely diverse sequence distances, ranging from 0 to hundreds, and including interactions with a n-2 sequence distance but located in other structural motifs. Except for a n-1 interaction reported and a long-distance one mentioned in ref. (50), such interactions have not been discussed in literature to date.

We also show that OP–nucleobase interactions mostly involve a stacked guanine or uracil ring and are located in a variety of structural motifs other than regular helices. Furthermore, in the H. marismortui 23S rRNA case-study several interactions are established between a phosphate and a nucleobase located on different structural domains, thus possibly contributing to maintaining its overall 3D fold and functionality. In addition, an inter-molecular stacking interaction was observed between a 23S phosphate and a 5S nucleobase.

QM calculations show an energy minimum at a distance between the OP atom and the nucleobase plane centroid slightly below 3 Å for all the nucleobases. While the stabilization energy is not negligible for any of the nucleobases (energy minima deeper than –2.3 kcal•mol⁻¹), it is stronger for uracil (and pseudouracil), where it almost doubles the energy of the stacking between two bases in a regular double helix calculated at a similar level of theory (on average –4.7 ± 3.38 kcal•mol⁻¹) (31).

By sliding the OP atom over the nucleobase plane, an optimal geometry corresponding to an energy minimum below −6 kcal•mol⁻¹ is reached by all the nucleobases. This indicates that any nucleobase can give a considerably stable stacking interaction with a phosphate at the proper geometry. We also found that the strength of the interaction clearly correlates with its electrostatic component, while all other energetic terms contribute similarly to their stability. This suggests that the electrostatic term is the discriminant between stable and unstable OP–nucleobase interactions, depending on the electrostatic profile of the involved nucleobase and on its mutual positioning with the stacked phosphate. Uracil and pseudouracil have a mostly positive electrostatic potential, and this results in particularly stable OP–nucleobase stacking interactions for many possible geometries. The electrostatic potential of other nucleobases also feature positive regions and, consequently, stacking of a phosphate over such regions results in quite favorable interactions. Noteworthily, these QM findings are consistent with the projections of the OP atoms over the aromatic rings of the different nucleobases we observed in the experimental occurrences. Finally, our DFT-MD calculations proved the stability under dynamic conditions, in the explored time range, of representative OP–nucleobase interactions featuring the most frequently observed stacked bases, i.e. guanine and uracil.

On these grounds, we believe that the stacking contacts between phosphate and nucleobases add themselves to the family of relatively weak interactions contributing to the 3D fold of RNAs. In this study, we provide a comprehensive structural overview of these interactions, together with a reference system to estimate the energy contribution of similar contacts in newly characterized structures.

DATA AVAILABILITY

The data underlying this article are available in the article and in its online supplementary material.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

KAUST baseline research funding (to L.C.); MIUR-FFABR ‘Fondo per il Finanziamento Attività Base di Ricerca’ (to R.O.). Funding for open access charge: KAUST baseline research funding.

Conflict of interest statement. None declared.