Abstract
Solid state quantum defects are promising candidates for scalable quantum information systems which can be seamlessly integrated with the conventional semiconductor electronic devices within the 3D monolithically integrated hybrid classical-quantum devices. Diamond nitrogen-vacancy (NV) center defects are the representative examples, but the controlled positioning of an NV center within bulk diamond is an outstanding challenge. Furthermore, quantum defect properties may not be easily tuned for bulk crystalline quantum defects. In comparison, 2D semiconductors, such as transition metal dichalcogenides (TMDs), are promising solid platform to host a quantum defect with tunable properties and a possibility of position control. Here, we computationally discover a promising defect family for spin qubit realization in 2D TMDs. The defects consist of transition metal atoms substituted at chalcogen sites with desirable spin-triplet ground state, zero-field splitting in the tens of GHz, and strong zero-phonon coupling to optical transitions in the highly desirable telecom band.
Subject terms: Two-dimensional materials, Quantum information, Electronic devices
Defect centers in two-dimensional materials has shown promise for applications in quantum information and sensing. Lee et al. computationally discover a class of substitutional defect centers in monolayer transition metal dichalcogenides with promising qubit characteristics operating at telecom wavelengths.
Introduction
An isolated point defect in a crystalline solid can be regarded as an artificial atom whose properties stem from the host material and bonding environment1–3. The experimental demonstration of defects exhibiting long spin coherence times (T2) and spin-selective optical transitions have made crystalline point defects one of the most promising platforms for the realization of long-distance quantum networks1,4. However, finding a single-point defect that exhibits all the desirable traits for quantum entanglement network generation remains elusive. For example, the popular nitrogen-vacancy (NV) center (NCVC−1 defect complex in diamond) does not operate at telecom wavelengths for low-loss fiber transmission (optical fiber telecom band: λ = 1260–1675 nm, or hν = 0.74–0.98 eV). On the other hand, Er-based qubits do but exhibit small optical oscillator strengths5,6. All of the most promising point defects occur in three-dimensional (3D) bulk crystalline materials (diamond7–9, SiC10, and oxides6), in which heterostructure fabrication, doping, and device fabrication remain challenging.
Here, we report on a family of point defects in 2D materials that combine moderate optical oscillator strengths, telecom operation, and low nuclear spin noise. Relative to 3D hosts, 2D hosts provide multiple advantages, including heterostructure engineering11,12, reduced sensitivity to nuclear spin environment13, and ease of integration with photonic platforms. Furthermore, the placement of defects in a 2D layer (versus one buried in 3D) could be precisely controlled using a scanning tunneling microscope (STM)14–16 or focused electron beam lithography17. In this regard, defects in monolayer hBN were theoretically investigated as qubit candidates in a 2D host18–20. Long, ms-scale, longitudinal spin relaxation times have been demonstrated with a defect ensemble in hBN21, and optically detected magnetic resonance of single defects in hBN has been reported22. However, spin coherence times (also called quantum memory times) are limited to microseconds in hBN due to the nuclear spin environment (nuclear spins of all B and N isotopes). Ye et al. predicted that a nuclear-spin limited quantum memory time in MoS2 can exceed milliseconds, even considering the natural abundance of nuclear spins before isotopic purification13. Moreover, the feasibility of isotopic purification of transition metal dichalcogenides (TMDs) further suppresses decoherence. Despite these promising properties, spin defect qubits in 2D TMDs remain uncharted territory even while defect-based single-photon emitters have been proposed and demonstrated23–26.
The first-principles calculations based on density functional theory (DFT)27,28 have extensively contributed to the characterization and identification of defect qubits in a wide range of solid hosts18–20,29–33. In this work, we computationally search through defects for a spin defect qubit in 2D monolayer TMDs by means of hybrid DFT34,35, known to be a quantitatively accurate method for solid-state defect calculations29,36. As a result of the comprehensive characterization of fundamental qubit properties—electronic, magnetic, vibrational, optical properties, and thermodynamic stability—we report on a defect family of MX in monolayer TMDs which turns out to be a promising candidate for quantum network applications.
Results
MX defect family
To computationally discover spin defect qubits realized in monolayer TMDs, we first search through intrinsic (native) and dopant defects in H-MoS, where H is the notation for semiconducting monolayer TMDs37. In this initial screening, we consider two criteria: (i) the spin-triplet ground state analogous to the NV center in diamond; (ii) spin-conserving intradefect optical transition without ionization of the defect29. High spin states are desirable to decouple the spin from the S = 1/2 paramagnetic background and to allow spin control at zero magnetic field2. Spin-conserving optical transitions are required for spin-state readout. First, we conducted DFT calculations based on the Perdew–Burke–Ernzerhof (PBE) functional38 to quickly explore densities of states for various defect states (Supplementary Fig. 1). As a result of the initial screening in terms of the spin-triplet ground state, we identify three spin-triplet ground-state defect types: negatively charged donor-vacancy complexes (FSVS−1 and ReMoVS−1), Mo substitution for two S (MoS2), and Mo substitution for S (MoS). The donor-vacancy complexes have the spin-triplet ground state, but their occupied energy levels are not far enough away from the conduction band minimum to avoid ionization of the defects during intradefect optical excitation. Although MoS2 meets the two criteria, the defect is made of MoI and two VS, so MoS2 is less likely to form than MoS, which can result in imprecise defect positioning, suffering from a random diffusion process during annealing; furthermore, a sulfur vacancy of MoS2 locates at the bottom sulfur layer of H-MoS2 does not allow the STM tip manipulation. Out of the initial set of the spin-triplet donor-vacancy, substitution-type defects, we found MoS turns out to meet the screening criteria and was selected for a systematic study. We then further characterized the MX defect family in the semiconducting H-MX2 (M = Mo, W; X = S, Se, Te). WTe2 is excluded because the most stable bulk phase of WTe2 is the metallic Td phase, not the semiconducting 2H phase39, and thus unsuitable for hosting an optically active defect. In addition to the criteria above, it is practically desirable that the dopant M is different from the transition metal atoms constituting the host TMD so that we can optically distinguish the synthesized defect qubit from native anti-site defects and reach concentrations low enough for single qubit isolation.
Defect energy levels
We investigate the detailed electronic structures of selected defects in H-MX2 using hybrid functional DFT calculations34,35. The MX defect family exhibits similar properties, and we focus the main text discussion on the WSe defect in monolayer MoSe2, which is found to have optical transitions in the telecom band along with WS in MoS2. The complete data for the family of defects investigated are listed in Table 1. We note that some defects in the family are not suitable spin qubit candidates. For example, WTe in MoTe2 does not have a spin-triplet ground state. For MoSe in WSe2, the occupied defect levels calculated with spin–orbit coupling (SOC) are lower than the valance band maximum (VBM). Therefore, MoTe2 and MoSe2 can be excluded from the desirable host materials accommodating the MX defect family. In addition to the MX defects in monolayer TMDs, Table I includes our simulation results of the NV center in diamond29 and the CBVN defect in monolayer hBN18,19, which have been reported to meet the aforementioned criteria, although quantum chemistry approaches beyond the hybrid functional demonstrated that the ground state of the CBVN in hBN could be spin-singlet by taking into account multireference nature of the singlet state26,40. These computational results are consistent with the previous reports for the NV center in diamond and CBVN in hBN, confirming that our simulation approaches are well-founded for defect qubit predictions. Comparison to these known centers also highlights the distinct features of the MX defect family.
Table 1.
Summary of calculated defect properties in diamond, hBN, and TMDs
| Hosts | Eg (eV) | Defects | Point groups | Defect levels (eV) | EZPL (eV) | S | DW | D (GHz) | τR (μs) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Spin up | Spin down | |||||||||||||
| ex | ey | a1 | ex | ey | a1 | |||||||||
| Diamond | 5.47 | NCVC−1 | C3v | 1.87 | 1.87 | 0.69 | 4.64 | 4.64 | 1.62 | 2.10 | 2.93 | 0.05 | 2.86 | 0.014 |
| hBN | 5.62 | CBVN | C2v | 1.53 | 3.00 | 5.30 | 4.76 | 5.05 | 5.77 | 1.71 | 2.21 | 0.11 | 10.77 | 0.032 |
| MoS2 | 2.37 (1.98) | MoS | C3v | 0.40 (0.18) | 0.40 (0.22) | 1.80 (1.59) | 2.34 (2.10) | 2.34 (2.10) | 2.35 (2.12) | 1.11 (1.09) | 0.74 | 0.48 | 20.51 | 37.7 |
| WS | C3v | 0.84 (0.48) | 0.84 (0.71) | 1.98 (1.89) | 2.33 (2.04) | 2.33 (2.06) | 2.35 (2.09) | 0.91 (0.94) | 1.47 | 0.23 | 13.44 | 20.5 | ||
| WS2 | 2.46 (1.85) | WS | C3v | 0.81 (0.44) | 0.81 (0.48) | 2.04 (1.70) | 2.44 (1.94) | 2.44 (1.94) | 2.46 (1.97) | 1.03 (1.01) | 1.01 | 0.36 | 14.44 | 14.1 |
| MoS | C3v | 0.38 (0.04) | 0.38 (0.06) | 1.92 (1.55) | 2.44 (1.95) | 2.44 (1.96) | 2.44 (1.97) | 1.22 (1.18) | 0.45 | 0.64 | 21.65 | 54.2 | ||
| MoSe2 | 2.07 (1.72) | MoSe | C3v | 0.27 (0.04) | 0.27 (0.06) | 1.63 (1.42) | 2.04 (1.79) | 2.04 (1.79) | 2.08 (1.81) | 1.08 (1.08) | 0.75 | 0.47 | 19.13 | 5.6 |
| WSe | C3v | 0.71 (0.29) | 0.71 (0.52) | 1.81 (1.57) | 2.03 (1.75) | 2.03 (1.78) | 2.08 (1.80) | 0.79 (0.74) | 1.95 | 0.14 | 12.43 | 4.2 | ||
| WSe2 | 2.15 (1.58) | WSe | C3v | 0.69 (0.34) | 0.69 (0.35) | 1.84 (1.47) | 2.10 (1.61) | 2.10 (1.62) | 2.16 (1.66) | 0.88 (0.84) | 1.63 | 0.20 | 12.88 | 3.2 |
| MoSe | C3v | 0.25 (−0.03) | 0.25 (−0.02) | 1.74 (1.35) | 2.12 (1.63) | 2.12 (1.65) | 2.17 (1.66) | 1.19 (1.08) | 0.50 | 0.60 | 19.82 | 4.7 | ||
| MoTe2 | 1.71 (1.39) | MoTe | C3v | 0.19 (−0.09) | 0.39 (0.01) | 1.26 (0.85) | 1.66 (1.06) | 1.70 (1.23) | 1.73 (1.30) | 0.49 (0.36) | 4.51 | 0.01 | 0.47 | 7.8 |
| WTe | C3v | 1.51 (1.24) | 1.51 (1.27) | 0.86 (0.60) | 1.51 (1.24) | 1.51 (1.27) | 0.86 (0.60) | |||||||
Note: Bold numbers indicate occupied states.
All the values in the table were theoretically estimated in this work, and the numbers between parentheses correspond to results with SOC. Defect levels are relative to the VBM. Majority (minority) spin is referred to as spin up (down). The ex, ey, and a1 columns indicate a1, b2, and for CBVN in hBN, respectively89. Note that the notations, ex, ey, and a1, are not valid anymore within SOC.
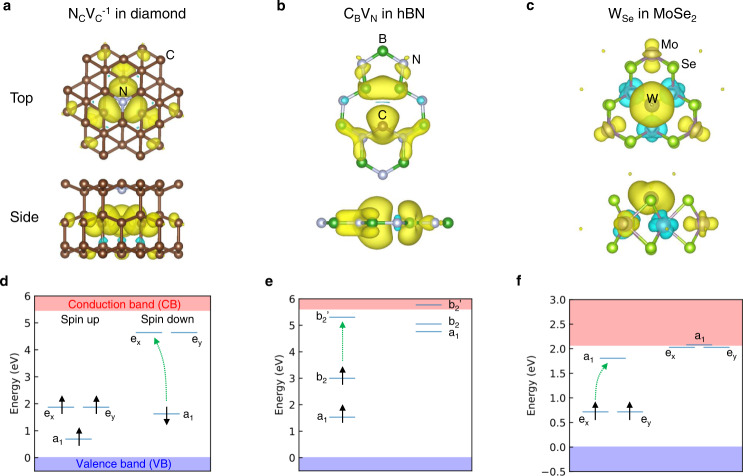
The structural geometry and spin density of the NCVC−1, CBVN, and WSe defects are shown in Fig. 1a–c. All three defects possess the spin-triplet ground states with optical excitation pathways of spin-conserving intradefect transitions. The optical transitions lie within the bandgap Eg, prohibiting single-photon ionization of the defect [Fig. 1d–f]; since its estimation based on Kohn–Sham eigenvalues can be erroneous owing to the ambiguous interpretation of the Kohn–Sham eigenvalues, we further confirmed this from the comparison of the zero-phonon line energy and the ionization energy determined by the charge transition level, more precisely (e.g., the zero phonon line energy of WSe in MoSe2 is 0.79 eV, and the ionization energy of that is 1.2 eV). Similar to the NV center in diamond, the WSe defect belongs to the C3v point group, and the electron configuration of the 2D defects is identical to the hole configuration of the NV center. Two majority-spin electrons occupy doubly degenerate ex and ey orbitals, and the optical transition takes place between ex,y and a1 orbitals. The quantities between parentheses in Table 1 are given to estimate the SOC effects with heavy elements, where SOC reduces Eg and lifts the degeneracy of the ex and ey orbitals. More detailed calculations are required to determine SOC effects on spin coherence times, coherent spin-light interactions, and inter-system crossing2 and will be addressed in future research work.
Fig. 1. Defect geometries and calculated electronic structures of (a,d) NCVC−1 in diamond, (b, e) CBVN in hBN, and (c,f) WSe in MoSe2.
a–c Top (top) and side (bottom) views of defect geometries and spin densities of the defect qubits in the ground state (isosurface level = 0.003 Å−3). d–f Energy levels of the defect qubits. The green arrows indicate spin-conserving intradefect optical transition. Detailed physical quantities of possible combinations of MX defects and MX2 hosts are summarized in Table 1.
Defect formation energy
Defect formation energy is a crucial quantity to determine whether a proposed defect can be physically realized in a host solid. The defect formation energy of a defect Xq in a charge state q is given by41–43
| 1 |
where Etot[Xq] and Etot[pristine] are the total energies of a supercell with and without the defect Xq, respectively. ni is the number of atoms of a species i added (positive) or removed (negative) from the pristine supercell, μi is the chemical potential of a species i. The chemical potential range was determined by considering competing phases (Supplementary Fig. 2) given in phase stability diagrams provided by Materials Project44; based on the phase stability diagrams, we further computed the chemical potentials within the HSE06 hybrid functional to plot the formation energy diagrams at extreme conditions, such as the M-rich condition. The chemical potentials of C and N are obtained in the diamond crystal and the N2 molecule, respectively. is the electrostatic correction, is the Fermi level, is the VBM energy level in the pristine supercell, and ΔV0/p is the potential alignment term. The electrostatic correction is employed to take into account spurious image charge due to periodic cells and uniform background charge, where the Freysoldt–Neugebauer–Van de Walle (FNV) correction scheme41–43,45 enables us to handle defects in anisotropic medium, such as 2D materials.
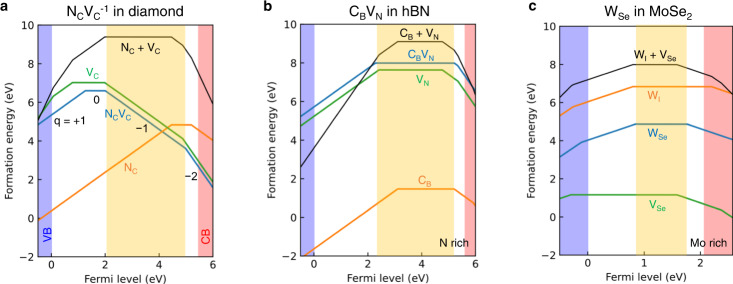
Figure 2 and Supplementary Fig. 4 show that the formation energy of an MX defect is lower than the sum of formation energies of the two independent defects of MI and VX (i.e., Ef[Mx] < Ef[MI] + Ef[Vx]), indicating that the formation of MX defects is favorable. Compared with the NV center in diamond and CBVN in hBN, the formation energy of MX in TMDs is small, so that the MX defect family is expected to be readily created. Based on this formation energy, we can create the MX defects by annealing a system with preexisting MI and VX defects. The formation of an antisite defect MoS in a MoS2, which is among the MX defect family, has been confirmed experimentally46,47. Along with the experimental observation of MoS, the similar formation energy diagrams for the MX defects in the family (Supplementary Fig. 4) support the feasible creation of the MX defect family. Note that the dopant M needs to be different from transition metal atoms constituting the h ost TMD to distinguish the intentionally created defect. Since VX is prevalent in TMDs48, the MX defect would be formed near the additional MI after annealing. Supplementary Figure 6 shows defect formation energies of possible competing defects, where VSe is much easier to be formed than VMo; thus, once we introduce WI in the presence of abundant VSe, the WSe complex can be readily formed. The M atom could be incorporated via ion implantation or STM lithography.
Fig. 2. Defect formation energy diagrams.
Defect formation energies of the defect qubits for a NCVC−1 in diamond, b CBVN in hBN in N-rich condition, and c WSe in MoSe2 in Mo-rich condition. The M-rich condition for MX2 (N-rich condition for hBN) provides lower defect formation energies than the X-rich condition (B-rich condition) (Supplementary Fig. 3). c WI + VSe indicates the sum of formation energies of the two independent defects, WI and VSe. The orange-shaded area shows the range of stability of NCVC−1, CBVN0, and WSe0. Defect formation energy diagrams for other MX in TMDs are displayed in Supplementary Fig. 4.
Zero-phonon line emission
Photon emission of defects plays a key role in qubit operation. Spin-conserving cycling transitions are utilized to read out the spin-qubit state. Zero-phonon-line (ZPL) transitions are utilized to realize spin-photon entanglement, which is required for generating spin-entangled quantum networks via photon measurement49,50. The ZPL emission is also utilized as a spectroscopic fingerprint to identify the defect qubit2,31,32. A photoluminescence line shape is composed of the ZPL and phonon sidebands. The contribution of the ZPL emission to the total emission is estimated by the Debye-Waller (DW) factor31,32. Only the ZPL emission is useful for photon-spin entanglement schemes, and thus a high DW factor is desirable. The configuration coordinate diagram (adiabatic potential energy against configuration coordinate) is often utilized to investigate the ZPL emission (Fig. 3)51,52. Here, the configuration coordinate displacement ΔQ is calculated as51,52
| 2 |
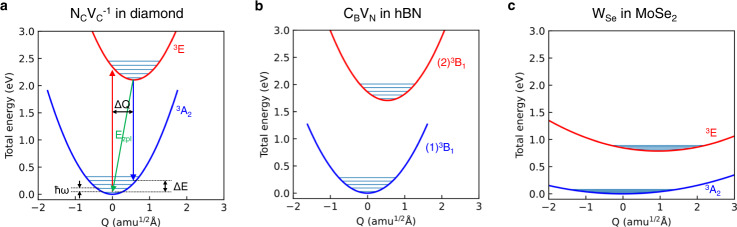
where i = {x, y, z}, mα is the mass of atom α, is the equilibrium position in the ground (excited) state. The electronic excited state is calculated by using the constrained DFT53. The number of phonons emitted during the optical transition can be quantified by the Huang–Rhys factor S. In the one-dimensional (1D) effective phonon approximation51, , where ΔE and ℏω are described in Fig. 3a, and the effective phonon frequency ω is obtained using the harmonic oscillator approximation . Here, ΔE is the difference between the ZPL energy EZPL and the vertical emission energy. The DW factor is given by DW = e−S 31,32,52. The ZPL energies, the Huang–Rhys factors, and the DW factors for the MX defect family are shown in Table 1. The MX defect family exhibits larger DW factors than the NV center in diamond and the CBVN in hBN except for in the MoTe2 host (which is not promising from the energy level point of view, as discussed earlier). The large DW factors stem from the small curvature of the MX defect family configuration coordinate diagram compared with the NV center in diamond and the CBVN in hBN (Fig. 3). In Table 1, the SOC-corrected ZPL energies between parentheses are approximated by estimating shifts in the defect energy levels shown in the same table. The ZPL energies of the MX defect family typically lie around 1 eV, close or in the telecom band, with the SOC-corrected ZPL energies at 0.74 eV and 0.94 eV of the WSe in MoSe2 and WS in MoS2, respectively. As we show further below, the 2D host environment enables fine-tuning of the ZPL energy by applying strain to further minimize optical fiber transmission loss. While photoluminescence measurements in 2D TMDs have identified localized excitons and chalcogen vacancies54–56, a ZPL that can be attributed to the MX defect family has not been experimentally identified yet.
Fig. 3. Configuration coordinate diagrams responsible for ZPL emission.
Configuration coordinate diagrams of the defect qubits for a NCVC−1 in diamond, b CBVN in hBN, and c WSe in MoSe2. The solid horizontal lines correspond to the phonon energy levels in the harmonic approximation. The ground state and the excited state are labeled as 3A2 and 3E for NCVC−1 in diamond31 and MX in TMDs; the states are labeled as (1)3B1 and (2)3B1 for CBVN in hBN40.
Zero-field splitting and hyperfine tensors
Magnetic properties of a spin qubit are of paramount importance for realizing quantum information applications2,31,32. For instance, the zero-field splitting (ZFS) between the ms = 0 and ms = ±1 spin sublevels corresponds to the microwave energy to manipulate the qubit state at zero applied magnetic field and enables spin-selective resonant optical excitation. Furthermore, utilizing ZFS TMD-based defects may also be attractive for quantum sensing applications. In these applications, changes in the ZFS can be used to sense electric fields, strain, and temperature57,58, while splitting of the ms = ±1 state due to the Zeeman effect is used for magnetic sensing applications59,60. Also important is the magnetic coupling of the spin-qubit to the crystal spin bath. A ZFS allows one to decouple the qubit spin from a paramagnetic electron spin-1/2 bath. In addition to a qubit spin state coupling to paramagnetic electron spins, there will also be hyperfine couplings to the crystal host nuclear bath13. In spin Hamiltonian, the ZFS and the hyperfine interaction are described as and , respectively, where is the electron spin, is the nuclear spin of nucleus n, D is the ZFS tensor, and A(n) is the hyperfine tensor.
The ZFS tensor determines the dipolar spin–spin interaction between electrons and is given by32,61
| 3 |
where μ0 is the magnetic permeability of vacuum, ge is the electron g-factor, μB is the Bohr magneton, χij is +1 for parallel spins and −1 for antiparallel spins, ra,b = (r1 − r2)a,b, and |Ψij(r1, r2)〉 is the slater determinant of ith and jth Kohn-Sham orbitals. After diagonalizing the ZFS tensor, one can obtain the ZFS value , presented in Table 1 (see Supplementary Table 1 for the tensor elements, Dxx, Dyy, and Dzz). For the NV center in diamond, D calculated in this work is 2.86 GHz, which is close to the reported one2,32. D of the MX defect family are 10–20 GHz, about an order of magnitude larger than that of the NV center, which is within the experimentally accessible range of microwave control62,63 and could enable higher-temperature resonant spin readout as well as the compatibility of higher Purcell factors64 with resonant optical spin selectivity. The large D of the MX defect family is attributed to stronger dipolar spin-spin interaction due to the more localized electron wavefunctions than the NV center. Note that because of the additional contribution of SOC65, the ZFS could be even greater than the value presented in Table 1, especially with a heavy element, such as W.
The hyperfine tensor of nucleus n at r = 0 is calculated by using32,66
| 4 |
where ns(r) is the electron spin density [Fig. 1(a–c)], gn is the nuclear g-factor67, and μn is the nuclear magneton. In Eq. (4), the first parenthesis is the non-dipolar Fermi contact term, and the second parenthesis is the dipole–dipole interaction term. Table 2 displays the calculated and diagonalized hyperfine tensors of the NV center in diamond, CBVN in hBN, and WSe in MoSe2 (see Supplementary Table 2 for a full list of hyperfine tensors, including other MX in the family) at the defect and nearest neighbor sites. The 183W and 77Se nuclear spins of the WSe defect exhibits large hyperfine tensor elements, similar to the on-site interaction CBVN defect in hBN and the nearest neighbor 13C in the NV. Considering the number of equivalent sites, the total hyperfine coupling between the electron spin and nearby nuclear spins is not necessarily stronger than the NV center. Furthermore, the advantageous dimensionality13 and the isotopic purification for 2D TMDs are expected to provide an exceptionally coherent time, whereas 2D hBN is incapable of excluding spinful nuclear isotopes. One intriguing possibility with 2D TMDs is to completely engineer a nuclear spin quantum memory register68 by STM lithography15. In this case, one would begin with an isotope-purified spin-0 host and incorporate a handful of nonzero spin nuclei in proximity to the defect.
Table 2.
Calculated hyperfine tensors for NCVC−1 in diamond, CBVN in hBN, and WSe in MoSe2
| Hosts | Defects | Nuclear spins | Number of equivalent sites | Hyperfine tensors (MHz) (convention: |Azz| > |Axx| > |Ayy|) | ||
|---|---|---|---|---|---|---|
| Axx | Ayy | Azz | ||||
| Diamond | NCVC−1 | 14N (I = 1, 99.632%) | 1 | −2.9 | −2.6 | −2.9 |
| 15N (I = 1/2, 0.368%) | 1 | 4.1 | 3.6 | 4.1 | ||
| 13C (I = 1/2, 1.07%) | 3 | 145.0 | 144.8 | 227.2 | ||
| 13C (I = 1/2, 1.07%) | 6 | 14.2 | 14.1 | 19.9 | ||
| hBN | CBVN | 13C (I = 1/2, 1.07%) | 1 | 474.7 | 400.9 | 478.8 |
| 10B (I = 3, 19.9%) | 1 | 24.9 | 22.2 | 26.4 | ||
| 11B (I = 3/2, 80.1%) | 2 | 74.4 | 66.3 | 78.9 | ||
| 14N (I = 1, 99.632%) | 2 | 7.3 | 7.2 | 9.9 | ||
| 15N (I = 1/2, 0.368%) | 2 | −10.3 | −10.1 | −13.9 | ||
| MoSe2 | WSe | 183W (I = 1/2, 14.31%) | 1 | 332.9 | 253.0 | 333.0 |
| 95Mo (I = 5/2, 15.92%) | 3 | 14.6 | 8.4 | 16.5 | ||
| 97Mo (I = 5/2, 9.55%) | 3 | 14.9 | 8.6 | 16.8 | ||
| 77Se (I = 1/2, 7.63%) | 6 | 68.2 | 65.4 | 78.2 | ||
The nuclear spin quantum number I and natural abundance are displayed in the nuclear spins column.
Radiative decay
In addition to the DW factor, the radiative recombination rate is an important optical property. For quantum information protocols, recombination rates should be fast enough to realize efficient spin initialization and readout2,31,32. Practically, radiative rates should also exceed the rates of any nonradiative recombination processes. The radiative recombination rate, which is the inverse of the radiative recombination lifetime τR, is calculated using32,69
| 5 |
where n is the refractive index, ϵ0 is the vacuum permittivity, Eij is the excitation energy that is substituted with EZPL, and is the transition dipole moment between the initial state |ψi〉 and the final state |ψj〉. Under the Frank-Condon approximation, we consider only the electronic component of the initial and final wavefunctions, which are occupied and empty Kohn-Sham orbitals of the spin-triplet ground state. Table 1 shows the calculated τR for the systems that we have examined so far. The WSe in MoSe2 exhibits a 4.2 µs decay time, which is four times shorter than the 20.5 µs decay time of the WS in MoS2. Overall, τR of the MX defect family is 100–1000 times larger compared with the NV center in diamond and CBVN in hBN. In the MX defect family, the optical transition between ex,y, and a1 is smaller due to the orbital selection rule (Laporte rule)70 associated with distinct d orbital characters of their defect states, ex, ey, and a1 (Supplementary Figure 6). While (slightly) shorter τR may be desirable, we note τR is already 5 orders of magnitude shorter than the current most promising defect telecom qubit, Er:3+Y2SiO5 where the intra-f-shell transitions are utilized, unlike the transition metal defects with d-orbital physics6. Moreover, for efficient photon collection, cavity integration is required, which can reduce τR by 4 orders of magnitude via the Purcell effect6. Due to the large ZFS, the system should still retain frequency-selective spin excitation for spin-photon entanglement and spin read-out even with the 4 orders of magnitude frequency broadening. TMDs can also provide multiple advantages in sensing. Due to the proximity to the surface, the exposed defect qubit on the surface of monolayer TMDs can compensate for the low radiative decay rate by suppressing internal reflection. Together with the radiative process, nonradiative recombination is a vital process determining quantum yield. The absence of crossing between the potential energy curves of 3E and 3A2 shown in Fig. 3c indicates that the nonradiative transition between the triplet states is less likely to occur; however, further investigation is necessary to make sure the rare nonradiative transition because the transition could depend on many critical factors.
Intersystem crossing (ISC)
The transition between a triplet state and a singlet state can play an important role in a nonradiative process and can enable the low-fidelity room-temperature optical initialization and readout of the qubit-based sensors. The MX defect family symmetrically resembles the antisite defect in monolayer TMDs and is expected to exhibit symmetry-allowed ISCs as in the antisite defect71. ISC is mediated by a combination of SOC and electron-phonon interaction. The crossing rate was calculated by the application of Fermi’s golden rule according to the formula72,73:
| 6 |
| 7 |
where λ⊥ is the transverse SOC constant between spin-singlet and spin-triplet states, is the phonon wavefunction overlap between initial state i with phonon quantum number m and final state f with phonon quantum number n, ϕim and ϕfn are the phonon wavefunctions, ωi and ωf are the phonon frequencies, wm is the occupation number of phonon according to Bose-Einstein distribution, and ΔEif is the energy difference between the initial state and final state (See Methods for further details of phonon wavefunction overlap and SOC strength calculations). The ISC from the triplet excited states 3E to the singlet shelving state 1A1 can be symmetrically allowed when ms = ±171. The simulated transition rate of ISC from the triplet excited state to the singlet shelving state is 0.031 μs, which is shorter than the radiative lifetime 4.2 μs of the triplet excited state, which tells us that the proposed quantum defect can exhibit the initialization and readout operation via the spin-selective decay pathways (Fig. 4). We note, however, that for the high-fidelity initialization and readout required for computation and network, resonant, spin selective excitation is required along with avoided or minimized ISCs74. Since SOC underlies the ISC transition72, we will be able to engineer ISC by utilizing various transition metal dopants with different SOCs.
Fig. 4. Sublevel structure of WSe in MoSe2.
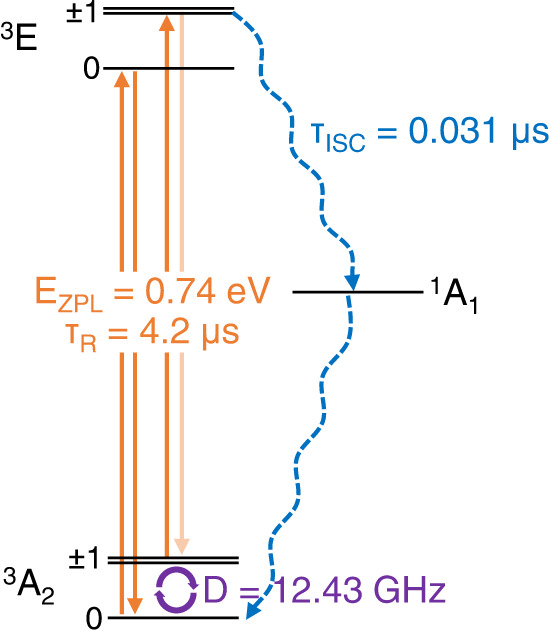
The radiative processes are shown in the orange vertical line. The blue dashed lines show the symmetry-allowed ISC transitions from the triplet excited state 3E to the singlet state 1A1 and the transition from 1A1 to 3A2, which are responsible for spin-selective decay, enabling the initialization and readout operations. The purple circular arrows within ZFS indicate the manipulation of qubit states by microwave.
Strain engineering
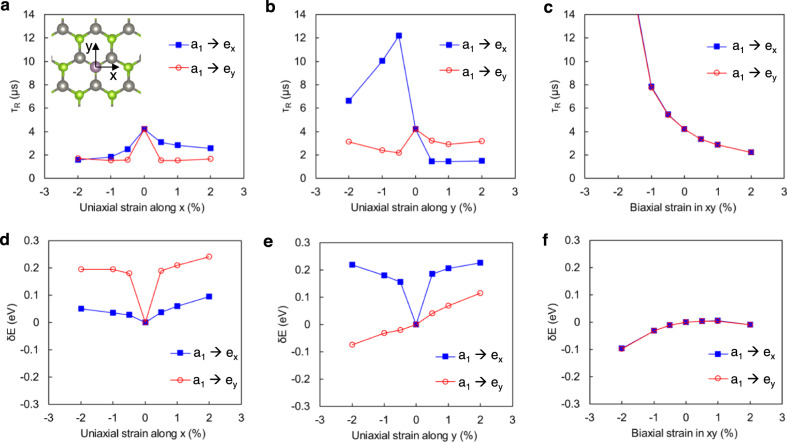
Strain can be effective in altering the dominant d orbital character by reducing the defect-crystal symmetry, which significantly modulates defect qubit properties, including the optical transition properties. Therefore, we can modify the radiative recombination rate under applied strain. As shown in Fig. 5, uniaxial strain along x or y breaks the C3v symmetry and lifts the ex and ey degeneracy. Technically, the notation ex,y is not valid when uniaxial strain is applied, and the notation is associated with their original orbital without strain. Although the biaxial strain does not break the C3v symmetry, the biaxial strain affects orbital mixing, resulting in the modulation of τR and EZPL. If we consider the lowest excitation for qubit operation (ex → a1 for uniaxial strain along x, ey → a1 for uniaxial strain along y), uniaxial strain is always beneficial to achieve a shorter lifetime. The tensile biaxial strain would also be helpful. In addition to τR, the strain technique can be used to engineer the ZPL energy. As shown in Fig. 5d–f, strain shifts energy levels and changes the energy gaps between a1 state and ex,y states by a few hundred meV, which would provide a useful way to tune defects to a single operational frequency in a targeted communication band. 2D host materials are beneficial for the strain engineering of defect qubit properties because a single atomic sheet can accommodate a more significant mechanical strain (up to a few %) than bulk materials (typically less than 0.1%), and the strain will depend on the 2D material-substrate interfaces75. Interestingly, δE pertaining to the second-lowest energy excitation, changes abruptly with small uniaxial strains as a consequence of the lifted degeneracy due to the symmetry breaking. The drastic response to external strain could be promising for highly susceptible quantum strain sensors.
Fig. 5. Strain effects on radiative recombination lifetime and ZPL energy.
a, b Uniaxial and c biaxial strain effects on radiative recombination lifetime τR. The inset in a shows the directions x and y. d, e Uniaxial and f biaxial strain effects on δE, modulation of the gap between corresponding eigenvalues (a1 to ex,y) in the ground state. The δE approximates the change of the ZPL energy, assuming the vertical shift of adiabatic potential energy curves occurs in the configuration coordinate diagram.
Discussion
We proposed the MX defect family in monolayer TMDs as a promising solid-state defect qubit through systematic computational investigation of essential criteria: defect energy levels, defect formation energy, ZPL emission, ZFS, hyperfine tensor, radiative recombination rate, and ISC transition rate. Compared with the NV center in diamond and the CBVN defect in hBN, the proposed defects exhibited desirable qubit properties, operating at telecom wavelengths. Finally, we demonstrated strain effects on radiative recombination lifetime and defect energy levels, which provides a technique that we can exploit for further engineering qubit properties and applications to sensitive quantum strain sensors.
Among the various combinations of M and X, the WSe defect in MoSe2 and the WS defect in MoS2 are particularly promising candidates for quantum network applications with a ZPL transition in the telecom band. However, many of the family’s defects are promising candidates for the first demonstration of experimentally detected spin defect qubits in a 2D TMD host. Computationally, there is also further work to be performed. In particular, the role of spin-orbit coupling on spin T1 lifetimes and coherent spin-light interactions should be investigated. The Debye temperatures of TMDs76 are an order of magnitude smaller than those of the NV center in diamond and the CBVN defect in hBN; thus, it is reasonable to expect that spin relaxation time T1 of the MX defect family could be shorter than those of the counterparts due to a strong spin-phonon interaction3,77. If T2, such that T2 ≤ 2T1, is limited by T1, one can explore different combinations of defects and hosts in the family to mitigate the spin-phonon interaction by reducing SOC. Other transition metal atoms in adjacent columns of the periodic table can also be explored to substitute for X along with a nonzero change state, implying expansive room for further exploration and qubit property engineering of 2D quantum defect systems. Having theoretically discovered and characterized the promising spin-defect qubits in monolayer TMDs, we opened a new door to the 2D world of research on spin-defect qubits.
Methods
First-principles calculations
We used Vienna Ab initio Simulation Package (VASP)78,79 to perform the first-principles calculations based on density functional theory (DFT)27,28. The Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional34,35, partially incorporating the Hartree-Fock exchange interaction, is used to overcome the bandgap problem with local exchange-correlation functionals. The pseudopotential is given by the projector-augmented wave method80,81. The energy cutoff for the plane-wave basis set is 250 eV for monolayer TMDs (350 eV for diamond and monolayer hBN). We prepared a supercell of 6 × 6 × 1 primitive cells for pristine monolayer TMDs and hBN (3 × 3 × 3 cubic unit cells for diamond), including a 15-Å-thick vacuum region. The single Γ-centered k-point is adopted for the Brillouin zone sampling. A pristine cell geometry is optimized until the maximum atomic force is smaller than 0.02 eV/Å; then, a defective cell geometry is relaxed within a fixed cell shape and volume based on the optimized pristine cell. The SOC is not considered unless otherwise stated. We utilized subroutines implemented in VASP to compute the magnetic properties—the ZFS tensors and the hyperfine tensors. We used the Corrections For Formation Energy and Eigenvalues (CoFFEE) code43 to calculate defect formation energies with the FNV charge correction scheme42.
Phonon wavefunction overlap and SOC strength
ISC is attributed to a combination of SOC and electron-phonon interaction. To obtain the phonon wavefunction overlap between the initial and final state, a one-dimensional harmonic oscillation approximation was used, which introduces the general configuration coordinate diagram. The potential surfaces of spin-triplet excited state 3E and spin-singlet state 1A1 were obtained by linearly interpolating between initial 3E and final 1A1 structures involved in the ISC. Energies of the interpolated structure were calculated using constrained-occupation DFT73. Since Kohn-Sham DFT theory cannot describe states composed of multiple Slater determinates, approximate electron occupations—|a1 ex〉 for 3E and for 1A1—were adopted, where indicate the different spin channel of ey orbital, and we made an approximation to access the energy of the 1A1 at the equilibrium geometry following Mackoit-Sinkeviciene et al.82. All constrained DFT computations were performed using VASP, facilitated by modified Nonrand83 preprocessing and postprocessing for interpolated structure energy calculation. The calculated configuration coordinate diagram for 3E and 1A1 is shown in Supplementary Fig. 7.
SOC strength was computed with the ORCA code84 using time-dependent density functional theory85. Different from VASP, ORCA does not have the feature of periodic boundary conditions. We thus constructed cluster models for both NCVC−1 and WSe defects by cutting relaxed structures from bulk and saturating dangling bonds to reproduce the electronic structures of bulk structures. The dangling bonds in the diamond cluster are easily saturated by H, while TMD is well-known for complicated edge states and charge transfer between edges and defects for over 10 Å86. After testing with different sizes, boundaries, and termination groups, a cluster with hybrid zigzag and arm-chair boundary and termination groups of H, OH, and NH was found using B3LYP functional to have both the same spin density as a periodic result [Supplementary Fig. 8a, b] and HOMO-LUMO gap of 1.22 eV to get reasonably excited states [Supplementary Figure 8(c)]. We obtained SOC values of 4.71 GHz for λ∥ and 44.6 GHz for λ⊥ for NCVC−1 defect using PBE functionals with def2-TZVP basis, which agrees well with previously computed values and experimentally measured values72,73,87. With the calculated λ⊥, we obtained the 3E → 1A1 ISC rate for the NV center in diamond at 30.6 MHz which is in fair agreement with the literature-reported value of 60.7 MHz88. We then computed the SOC strength for the axial λ∥ and non-axial λ⊥ components of the WSe defect in MoSe2 using B3LYP functionals to be 69 and 109 GHz, respectively.
Supplementary information
Acknowledgements
This work was supported by ASCENT, one of six centers in JUMP, a Semiconductor Research Corporation (SRC) program sponsored by DARPA (Grant no. 2018-JU-2776). This work was also supported by UTD Quantum Center, UTD SPIRe Award, National R&D Program (2022M3H4A1A04096496) and Basic Science Research Program (Grant no. 2022R1F1A1073068) through the National Research Foundation of Korea (NRF) funded by Ministry of Science and ICT. K.-M.C.Fu acknowledges support from the Army Research Office MURI (Ab-Initio Solid-State Quantum Materials) Grant no. W911NF-18-1-0431. Y.P. acknowledges support from the National Science Foundation under Grant no. DMR-2143233.
Author contributions
K.C. conceived the research idea and supervised the overall project development. Y.L. developed the idea, performed the first-principles calculations, and analyzed data. Y.H., X.L., K.L., and Y.P. performed the ISC calculation. Y.L., D.K., K.-M.C.F., and K.C. contributed to the discussion and preparation of the first draft of the paper.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Data availability
The data that support the findings of this study are available within the paper and Supplementary Information. Additional relevant data are available from the corresponding authors upon reasonable request.
Code availability
The codes used for data acquisition and processing are available from the corresponding authors upon reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Yeonghun Lee, Email: y.lee@inu.ac.kr.
Kyeongjae Cho, Email: kjcho@utdallas.edu.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-022-35048-0.
References
- 1.Awschalom DD, Hanson R, Wrachtrup J, Zhou BB. Quantum technologies with optically interfaced solid-state spins. Nat. Photonics. 2018;12:516–527. doi: 10.1038/s41566-018-0232-2. [DOI] [Google Scholar]
- 2.Bassett LC, Alkauskas A, Exarhos AL, Fu K-MC. Quantum defects by design. Nanophotonics. 2019;8:1867–1888. doi: 10.1515/nanoph-2019-0211. [DOI] [Google Scholar]
- 3.Wolfowicz, G. Quantum guidelines for solid-state spin defects. Nat. Rev. Mater. 10.1038/s41578-021-00306-y (2021).
- 4.Kimble HJ. The quantum internet. Nature. 2008;453:1023–1030. doi: 10.1038/nature07127. [DOI] [PubMed] [Google Scholar]
- 5.Thiel CW, Böttger T, Cone RL. Rare-earth-doped materials for applications in quantum information storage and signal processing. J. Lumin. 2011;131:353–361. doi: 10.1016/j.jlumin.2010.12.015. [DOI] [Google Scholar]
- 6.Raha M, et al. Optical quantum nondemolition measurement of a single rare earth ion qubit. Nat. Commun. 2020;11:1605. doi: 10.1038/s41467-020-15138-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wrachtrup J, Jelezko F. Processing quantum information in diamond. J. Phys. 2006;18:S807–S824. [Google Scholar]
- 8.Pompili M, et al. Realization of a multinode quantum network of remote solid-state qubits. Science. 2021;372:259–264. doi: 10.1126/science.abg1919. [DOI] [PubMed] [Google Scholar]
- 9.Nguyen CT, et al. Quantum network nodes based on diamond qubits with an efficient nanophotonic interface. Phys. Rev. Lett. 2019;123:183602. doi: 10.1103/PhysRevLett.123.183602. [DOI] [PubMed] [Google Scholar]
- 10.Son NT, et al. Developing silicon carbide for quantum spintronics. Appl. Phys. Lett. 2020;116:190501. doi: 10.1063/5.0004454. [DOI] [Google Scholar]
- 11.Geim AK, Grigorieva IV. Van der Waals heterostructures. Nature. 2013;499:419–425. doi: 10.1038/nature12385. [DOI] [PubMed] [Google Scholar]
- 12.Ajayan P, Kim P, Banerjee K. Two-dimensional van der Waals materials. Phys. Today. 2016;69:38–44. doi: 10.1063/PT.3.3297. [DOI] [Google Scholar]
- 13.Ye M, Seo H, Galli G. Spin coherence in two-dimensional materials. npj Comput. Mater. 2019;5:44. doi: 10.1038/s41524-019-0182-3. [DOI] [Google Scholar]
- 14.Cho K, Joannopoulos JD. Tip-surface interactions in scanning tunneling microscopy. Phys. Rev. Lett. 1993;71:1387–1390. doi: 10.1103/PhysRevLett.71.1387. [DOI] [PubMed] [Google Scholar]
- 15.Randall JN, et al. Highly parallel scanning tunneling microscope based hydrogen depassivation lithography. J. Vac. Sci. Technol. B. 2018;36:06JL05. doi: 10.1116/1.5047939. [DOI] [Google Scholar]
- 16.Liu P, et al. First-principle prediction on STM tip manipulation of Ti adatom on two-dimensional monolayer YBr 3. Scanning. 2019;2019:1–7. doi: 10.1155/2019/5434935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Robertson AW, et al. Spatial control of defect creation in graphene at the nanoscale. Nat. Commun. 2012;3:1144. doi: 10.1038/ncomms2141. [DOI] [PubMed] [Google Scholar]
- 18.Cheng GD, et al. A paramagnetic neutral CBVN center in hexagonal boron nitride monolayer for spin qubit application. Comput. Mater. Sci. 2017;129:247–251. doi: 10.1016/j.commatsci.2016.12.032. [DOI] [Google Scholar]
- 19.Wu F, Galatas A, Sundararaman R, Rocca D, Ping Y. First-principles engineering of charged defects for two-dimensional quantum technologies. Phys. Rev. Mater. 2017;1:071001. doi: 10.1103/PhysRevMaterials.1.071001. [DOI] [Google Scholar]
- 20.Ivády V, et al. Ab initio theory of the negatively charged boron vacancy qubit in hexagonal boron nitride. npj Comput. Mater. 2020;6:41. doi: 10.1038/s41524-020-0305-x. [DOI] [Google Scholar]
- 21.Gottscholl A, et al. Room temperature coherent control of spin defects in hexagonal boron nitride. Sci. Adv. 2021;7:eabf3630. doi: 10.1126/sciadv.abf3630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Stern HL, et al. Room-temperature optically detected magnetic resonance of single defects in hexagonal boron nitride. Nat. Commun. 2022;13:618. doi: 10.1038/s41467-022-28169-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gupta S, Yang J-H, Yakobson BI. Two-level quantum systems in two-dimensional materials for single photon emission. Nano Lett. 2019;19:408–414. doi: 10.1021/acs.nanolett.8b04159. [DOI] [PubMed] [Google Scholar]
- 24.Klein J, et al. Site-selectively generated photon emitters in monolayer MoS2 via local helium ion irradiation. Nat. Commun. 2019;10:2755. doi: 10.1038/s41467-019-10632-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Dang J, et al. Identifying defect-related quantum emitters in monolayer WSe2. npj 2D Mater. Appl. 2020;4:2. doi: 10.1038/s41699-020-0136-0. [DOI] [Google Scholar]
- 26.Sajid A, Ford MJ, Reimers JR. Single-photon emitters in hexagonal boron nitride: a review of progress. Rep. Prog. Phys. 2020;83:044501. doi: 10.1088/1361-6633/ab6310. [DOI] [PubMed] [Google Scholar]
- 27.Hohenberg P, Kohn W. Inhomogeneous electron gas. Phys. Rev. 1964;136:B864–B871. doi: 10.1103/PhysRev.136.B864. [DOI] [Google Scholar]
- 28.Kohn W, Sham LJ. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965;140:A1133–A1138. doi: 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
- 29.Weber JR, et al. Quantum computing with defects. Proc. Natl Acad. Sci. USA. 2010;107:8513–8518. doi: 10.1073/pnas.1003052107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Seo H, Ma H, Govoni M, Galli G. Designing defect-based qubit candidates in wide-gap binary semiconductors for solid-state quantum technologies. Phys. Rev. Mater. 2017;1:075002. doi: 10.1103/PhysRevMaterials.1.075002. [DOI] [Google Scholar]
- 31.Dreyer CE, Alkauskas A, Lyons JL, Janotti A, Van de Walle CG. First-principles calculations of point defects for quantum technologies. Annu. Rev. Mater. Res. 2018;48:1–26. doi: 10.1146/annurev-matsci-070317-124453. [DOI] [Google Scholar]
- 32.Gali Á. Ab initio theory of the nitrogen-vacancy center in diamond. Nanophotonics. 2019;8:1907–1943. doi: 10.1515/nanoph-2019-0154. [DOI] [Google Scholar]
- 33.Ma H, Sheng N, Govoni M, Galli G. First-principles studies of strongly correlated states in defect spin qubits in diamond. Phys. Chem. Chem. Phys. 2020;22:25522–25527. doi: 10.1039/D0CP04585C. [DOI] [PubMed] [Google Scholar]
- 34.Heyd J, Scuseria GE, Ernzerhof M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003;118:8207–8215. doi: 10.1063/1.1564060. [DOI] [Google Scholar]
- 35.Krukau AV, Vydrov OA, Izmaylov AF, Scuseria GE. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006;125:224106. doi: 10.1063/1.2404663. [DOI] [PubMed] [Google Scholar]
- 36.Freysoldt C, et al. First-principles calculations for point defects in solids. Rev. Mod. Phys. 2014;86:253–305. doi: 10.1103/RevModPhys.86.253. [DOI] [Google Scholar]
- 37.Gong C, et al. Band alignment of two-dimensional transition metal dichalcogenides: application in tunnel field effect transistors. Appl. Phys. Lett. 2013;103:053513. doi: 10.1063/1.4817409. [DOI] [Google Scholar]
- 38.Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 39.Lee C-H, et al. Tungsten Ditelluride: a layered semimetal. Sci. Rep. 2015;5:10013. doi: 10.1038/srep10013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Reimers JR, Sajid A, Kobayashi R, Ford MJ. Understanding and calibrating density-functional-theory calculations describing the energy and spectroscopy of defect sites in hexagonal boron nitride. J. Chem. Theory Comput. 2018;14:1602–1613. doi: 10.1021/acs.jctc.7b01072. [DOI] [PubMed] [Google Scholar]
- 41.Freysoldt C, Neugebauer J, Van de Walle CG. Electrostatic interactions between charged defects in supercells. Phys. Status Solidi B. 2011;248:1067–1076. doi: 10.1002/pssb.201046289. [DOI] [Google Scholar]
- 42.Komsa H-P, Rantala TT, Pasquarello A. Finite-size supercell correction schemes for charged defect calculations. Phys. Rev. B. 2012;86:045112. doi: 10.1103/PhysRevB.86.045112. [DOI] [PubMed] [Google Scholar]
- 43.Naik MH, Jain M. CoFFEE: corrections for formation energy and eigenvalues for charged defect simulations. Comput. Phys. Commun. 2018;226:114–126. doi: 10.1016/j.cpc.2018.01.011. [DOI] [Google Scholar]
- 44.Jain A, et al. Commentary: the materials project: a materials genome approach to accelerating materials innovation. APL Mater. 2013;1:011002. doi: 10.1063/1.4812323. [DOI] [Google Scholar]
- 45.Hwang J, Zhang C, Kim Y-S, Wallace RM, Cho K. Giant renormalization of dopant impurity levels in 2D semiconductor MoS2. Sci. Rep. 2020;10:4938. doi: 10.1038/s41598-020-61675-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Hong J, et al. Exploring atomic defects in molybdenum disulphide monolayers. Nat. Commun. 2015;6:6293. doi: 10.1038/ncomms7293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Khan MA, Leuenberger MN. Optoelectronics with single layer group-VIB transition metal dichalcogenides. Nanophotonics. 2018;7:1589–1600. doi: 10.1515/nanoph-2018-0041. [DOI] [Google Scholar]
- 48.Amani M, et al. Near-unity photoluminescence quantum yield in MoS2. Science. 2015;350:1065–1068. doi: 10.1126/science.aad2114. [DOI] [PubMed] [Google Scholar]
- 49.Barrett SD, Kok P. Efficient high-fidelity quantum computation using matter qubits and linear optics. Phys. Rev. A. 2005;71:060310. doi: 10.1103/PhysRevA.71.060310. [DOI] [Google Scholar]
- 50.Humphreys PC, et al. Deterministic delivery of remote entanglement on a quantum network. Nature. 2018;558:268–273. doi: 10.1038/s41586-018-0200-5. [DOI] [PubMed] [Google Scholar]
- 51.Alkauskas A, Lyons JL, Steiauf D, Van de Walle CG. First-principles calculations of luminescence spectrum line shapes for defects in semiconductors: the example of GaN and ZnO. Phys. Rev. Lett. 2012;109:267401. doi: 10.1103/PhysRevLett.109.267401. [DOI] [PubMed] [Google Scholar]
- 52.Alkauskas A, Buckley BB, Awschalom DD, Van de Walle CG. First-principles theory of the luminescence lineshape for the triplet transition in diamond NV centres. N. J. Phys. 2014;16:073026. doi: 10.1088/1367-2630/16/7/073026. [DOI] [Google Scholar]
- 53.Kaduk B, Kowalczyk T, Van Voorhis T. Constrained density functional theory. Chem. Rev. 2012;112:321–370. doi: 10.1021/cr200148b. [DOI] [PubMed] [Google Scholar]
- 54.Perebeinos V. Two dimensions and one photon. Nat. Nanotech. 2015;10:485–486. doi: 10.1038/nnano.2015.104. [DOI] [PubMed] [Google Scholar]
- 55.Koperski M, et al. Single photon emitters in exfoliated WSe2 structures. Nat. Nanotech. 2015;10:503–506. doi: 10.1038/nnano.2015.67. [DOI] [PubMed] [Google Scholar]
- 56.Zhang G, Cheng Y, Chou J-P, Gali A. Material platforms for defect qubits and single-photon emitters. Appl. Phys. Rev. 2020;7:031308. doi: 10.1063/5.0006075. [DOI] [Google Scholar]
- 57.Schirhagl R, Chang K, Loretz M, Degen CL. Nitrogen-vacancy centers in diamond: nanoscale sensors for physics and biology. Annu. Rev. Phys. Chem. 2014;65:83–105. doi: 10.1146/annurev-physchem-040513-103659. [DOI] [PubMed] [Google Scholar]
- 58.Degen CL, Reinhard F, Cappellaro P. Quantum sensing. Rev. Mod. Phys. 2017;89:035002. doi: 10.1103/RevModPhys.89.035002. [DOI] [Google Scholar]
- 59.Degen CL. Scanning magnetic field microscope with a diamond single-spin sensor. Appl. Phys. Lett. 2008;92:243111. doi: 10.1063/1.2943282. [DOI] [Google Scholar]
- 60.Fu K-MC, Iwata GZ, Wickenbrock A, Budker D. Sensitive magnetometry in challenging environments. AVS Quantum Sci. 2020;2:044702. doi: 10.1116/5.0025186. [DOI] [Google Scholar]
- 61.Ivády V, Simon T, Maze JR, Abrikosov IA, Gali A. Pressure and temperature dependence of the zero-field splitting in the ground state of NV centers in diamond: a first-principles study. Phys. Rev. B. 2014;90:235205. doi: 10.1103/PhysRevB.90.235205. [DOI] [Google Scholar]
- 62.Oliver WD, Welander PB. Materials in superconducting quantum bits. MRS Bull. 2013;38:816–825. doi: 10.1557/mrs.2013.229. [DOI] [Google Scholar]
- 63.Xue X, et al. Quantum logic with spin qubits crossing the surface code threshold. Nature. 2022;601:343–347. doi: 10.1038/s41586-021-04273-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Purcell EM. Spontaneous emission probabilities at radio frequencies. Phys. Rev. 1946;69:681. [Google Scholar]
- 65.Biktagirov T, Gerstmann U. Spin-orbit driven electrical manipulation of the zero-field splitting in high-spin centers in solids. Phys. Rev. Res. 2020;2:023071. doi: 10.1103/PhysRevResearch.2.023071. [DOI] [Google Scholar]
- 66.Gali A, Fyta M, Kaxiras E. Ab initio supercell calculations on nitrogen-vacancy center in diamond: Electronic structure and hyperfine tensors. Phys. Rev. B. 2008;77:155206. doi: 10.1103/PhysRevB.77.155206. [DOI] [Google Scholar]
- 67.Stone NJ. Table of nuclear magnetic dipole and electric quadrupole moments. At. Data Nucl. Data. 2005;90:75–176. doi: 10.1016/j.adt.2005.04.001. [DOI] [Google Scholar]
- 68.Bradley CE, et al. A ten-qubit solid-state spin register with quantum memory up to one minute. Phys. Rev. X. 2019;9:031045. [Google Scholar]
- 69.Derbenyova NV, Burdov VA. Effect of doping with shallow donors on radiative and nonradiative relaxation in silicon nanocrystals: ab initio study. J. Phys. Chem. C. 2018;122:850–858. doi: 10.1021/acs.jpcc.7b09882. [DOI] [Google Scholar]
- 70.Laporte O, Meggers WF. Some rules of spectral structure*. J. Opt. Soc. Am. 1925;11:459. doi: 10.1364/JOSA.11.000459. [DOI] [Google Scholar]
- 71.Tsai J-Y, Pan J, Lin H, Bansil A, Yan Q. Antisite defect qubits in monolayer transition metal dichalcogenides. Nat. Commun. 2022;13:492. doi: 10.1038/s41467-022-28133-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Smart TJ, Li K, Xu J, Ping Y. Intersystem crossing and exciton–defect coupling of spin defects in hexagonal boron nitride. npj Comput. Mater. 2021;7:59. doi: 10.1038/s41524-021-00525-5. [DOI] [Google Scholar]
- 73.Thiering G, Gali A. Ab initio calculation of spin-orbit coupling for an NV center in diamond exhibiting dynamic Jahn-Teller effect. Phys. Rev. B. 2017;96:081115. doi: 10.1103/PhysRevB.96.081115. [DOI] [Google Scholar]
- 74.Robledo L, et al. High-fidelity projective read-out of a solid-state spin quantum register. Nature. 2011;477:574–578. doi: 10.1038/nature10401. [DOI] [PubMed] [Google Scholar]
- 75.Dai Y, Zhao Y, Wang J, Xu J, Yang F. First principle simulations on the effects of oxygen vacancy in HfO 2 -based RRAM. AIP Adv. 2015;5:017133. doi: 10.1063/1.4906792. [DOI] [Google Scholar]
- 76.Peng B, et al. Thermal conductivity of monolayer MoS 2, MoSe 2, and WS 2: interplay of mass effect, interatomic bonding and anharmonicity. RSC Adv. 2016;6:5767–5773. doi: 10.1039/C5RA19747C. [DOI] [Google Scholar]
- 77.Norambuena A, et al. Spin-lattice relaxation of individual solid-state spins. Phys. Rev. B. 2018;97:094304. doi: 10.1103/PhysRevB.97.094304. [DOI] [Google Scholar]
- 78.Kresse G, Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996;6:15–50. doi: 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
- 79.Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B. 1996;54:11169–11186. doi: 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
- 80.Blöchl PE. Projector augmented-wave method. Phys. Rev. B. 1994;50:17953–17979. doi: 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
- 81.Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B. 1999;59:1758–1775. doi: 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
- 82.Mackoit-Sinkevičienė M, Maciaszek M, Van de Walle CG, Alkauskas A. Carbon dimer defect as a source of the 4.1 eV luminescence in hexagonal boron nitride. Appl. Phys. Lett. 2019;115:212101. doi: 10.1063/1.5124153. [DOI] [Google Scholar]
- 83.Turiansky ME, et al. Nonrad: Computing nonradiative capture coefficients from first principles. Comput. Phys. Commun. 2021;267:108056. doi: 10.1016/j.cpc.2021.108056. [DOI] [Google Scholar]
- 84.Neese F. The ORCA program system. WIREs Comput Mol. Sci. 2012;2:73–78. doi: 10.1002/wcms.81. [DOI] [Google Scholar]
- 85.de Souza B, Farias G, Neese F, Izsák R. Predicting phosphorescence rates of light organic molecules using time-dependent density functional theory and the path integral approach to dynamics. J. Chem. Theory Comput. 2019;15:1896–1904. doi: 10.1021/acs.jctc.8b00841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Han N, et al. Remote passivation in two-dimensional materials: the case of the monolayer–bilayer lateral junction of MoSe 2. J. Phys. Chem. Lett. 2021;12:8046–8052. doi: 10.1021/acs.jpclett.1c02457. [DOI] [PubMed] [Google Scholar]
- 87.Bassett LC, et al. Ultrafast optical control of orbital and spin dynamics in a solid-state defect. Science. 2014;345:1333–1337. doi: 10.1126/science.1255541. [DOI] [PubMed] [Google Scholar]
- 88.Tetienne J-P, et al. Magnetic-field-dependent photodynamics of single NV defects in diamond: an application to qualitative all-optical magnetic imaging. N. J. Phys. 2012;14:103033. doi: 10.1088/1367-2630/14/10/103033. [DOI] [Google Scholar]
- 89.Abdi, M., Chou, J.-P., Gali, A. & Plenio, M. B. Color centers in hexagonal boron nitride monolayers: a group theory and Ab initio analysis. ACS Photonics5, 1967–1976 (2018).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available within the paper and Supplementary Information. Additional relevant data are available from the corresponding authors upon reasonable request.
The codes used for data acquisition and processing are available from the corresponding authors upon reasonable request.