Evaluation of gowns and coveralls used by medical personnel working with Ebola patients against simulated bodily fluids using an Elbow Lean Test

Abstract

Gowns and coveralls are important components of protective ensembles used during the management of known or suspected Ebola patients. In this study, an Elbow Lean Test was used to obtain a visual semi-quantitative measure of the resistance of medical protective garments to the penetration of two bodily fluid simulants. Tests were done on swatches of continuous and discontinuous regions of fabrics cut from five gowns and four coveralls at multiple elbow pressure levels (2–44 PSI). Swatches cut from the continuous regions of one gown and two coveralls did not have any strike-through. For discontinuous regions, only the same gown consistently resisted fluid strike-through. As hypothesized, with the exception of one garment, fluid strike-through increased with higher applied elbow pressure, was higher for lower fluid surface tension, and was higher for the discontinuous regions of the protective garments.

Introduction

Scientific evidence suggests that the Ebola virus is mainly spread through direct contact with blood or bodily fluids of a person who is sick with Ebola or with objects that have been contaminated with the virus.^[1–4] The Centers for Disease Control and Prevention (CDC) has suggested that healthcare workers use single-use (disposable) fluid resistant or impermeable gowns and coveralls during the management of patients infected with Ebola.^[4] The Occupational Safety and Health Administration (OSHA) requires employers to be responsible for ensuring that workers are protected from exposure to the Ebola virus.^[5]

The objective of this study was to evaluate the barrier resistance offered by a set of garment types, with the manufacturers of several of these having reported their protective level using a standard classification system. In selecting the most appropriate personal protective equipment (PPE), employers should consider all of the available performance specifications on recommended protective clothing, including the potential limitations. The American National Standards Institute (ANSI) and Association for the Advancement of Medical Instrumentation (AAMI) have established a classification system and set minimum requirements for liquid barrier performance of gowns and drapes.^[6] This standard includes four standard tests to evaluate barrier effectiveness, including the American Association of Textile Chemists and Colorists (AATCC) 42 for impact penetration, AATCC 127 for hydrostatic pressure resistance, ASTM F1670^[7] for synthetic blood penetration resistance (applies only to drapes), and ASTM F1671^[8] for viral penetration resistance tests (see Appendix A). Based on the results of these standardized tests, four levels of barrier performance are defined, with Level 1 being the lowest level of protection, and Level 4 being the highest level of protection.^[9]

Among the test methods used to assign AAMI levels, ASTM F1670, and ASTM F1671 are the most stringent. These tests involve the use of bodily fluid and blood-borne pathogen simulants and are performed under conditions designed to differentiate among the various barrier materials. Only gowns that pass ASTM F1671 are considered impermeable to viral penetration, and are defined as Level 4 garments. Gowns that comply with the lower levels (Levels 1, 2, and 3) cannot be considered impermeable to viruses in blood or bodily fluids. However, Levels 1, 2, and 3 gowns, which are tested against water, are considered to have an increasing resistance to test liquids with higher surface tension than synthetic blood.^[10]

The ANSI/AAMI PB70 standard includes both surgical gowns and isolation gowns. Unlike isolation gowns, coveralls are typically not classified by the AAMI level system. However, in the specifications of garments, manufacturers typically report their performance against ASTM F1671 and sometimes AATCC 42 and 127. There are also test methods, more common in Europe, from ISO that evaluate similar barrier performance properties and can be applied to gowns or coveralls.^[11] While most coverall manufacturers readily report data for continuous regions of their products, less information is available on their discontinuous regions (e.g., seams, ties, and zippers).

Penetration of bodily fluids through garments can be influenced by several factors. The major factors include external forces acting against the garments, such as a Medical worker leaning on a contaminated surface or carrying an infected patient with exposed bodily fluids, or the surface tension of the liquid carrying the virus or pathogen, since liquid penetration through fabrics commonly increases with decreasing surface tension.^[11] Additionally, penetration of liquid is a function of clothing material thickness and pore radius, the liquid’s viscosity, exposure time, the contact angle, and amount of applied pressure.^[12] The surface tension of blood is lower than that of other bodily fluids that have higher portions of water. For such fluids, it has been reported that for many fabrics, blood has a greater chance of penetrating protective garment fabrics.^[13,14] Thus, in this study, blood is considered a “worst-case” scenario. However, since water resistance depends on the repellency of the fibers and yarns, as well as the fabric construction,^[15] it was expected in this study that fabrics treated by the manufacturer with a water resistant or water repellent finish may have a greater resistance to bodily fluids that are more water-based than blood, while fabrics that were not treated may have had the opposite effect.

In this study, we used the “Elbow Lean Test” (ELT), a 1 min visual evaluation of garment resistance to bodily fluids, originally developed by W.L. Gore and Associates.^[13] In contrast to the aforementioned standard tests, such as the ASTM F1670 hydrostatic screening test or the ASTM F1819 machine operated test, it is substantially quicker and simulates real-use conditions by providing immediate results for situations in which exterior areas of healthcare worker’s protective clothing are exposed to blood or other bodily fluids.^[16] Despite being an attractive test method for use in the field, little data exists in the peer-reviewed literature on the effect of key test parameters on test outcomes.

This article presents resistance data of two types of simulated bodily fluids for nine models of medical garments (five isolation gowns, and four coveralls) in both continuous and discontinuous regions (e.g., ties, seams and zippers) based on a series of ELTs at low and high elbow pressures. Colored water served as an upper limit of the surface tension of bodily fluids and was compared to synthetic blood. It was expected that garments with manufacturer claims of passing ASTM F1671 would have lower rates of strike-through failures (passage of a fluid through a barrier product) than garments without claims of passing ASTM F1671. Additionally, it was hypothesized that failure rates of the tests would decrease with increasing surface tensions of simulated bodily fluids, and increase with increasing pressure applied on the fabrics. Furthermore, failure rates would be lower for continuous regions compared to those for discontinuous regions.

Materials and methods

Test garments

There were five isolation gowns tested, including one without ANSI/AAMI PB70 barrier resistant claims (Model NON27SMS2, Medline, Mundelein, Illinois): one ANSI/AAMI PB70 Level 1 gown (Model KC100, Kimberly Clark, Irving, Texas); one ANSI/AAMI PB70 Level 2 gown (N0NLV200, Medline, Mundelein, IL); one ANSI/AAMI PB70 Level 3 gown (Model ICP-Reorder#5050YFC, ICP Medical, St. Louis, MO); and one prototype gown, which is a candidate for ANSI/AAMI PB70 Level 4 (Reference #: 68–0013754-BS, LYG Bronson Nonwoven Product Co. Ltd, China). Four coveralls were tested, including a Proshield (Model 1, DuPont, Richmond, Virginia); a Tyvek (Classic Plus, Model CHA5, DuPont, Richmond, Virginia); a Microgard (Model 2000 Ts+, Microgard, United Kingdom); and a Tychem (Model QC, DuPont, Richmond, Virginia). The gowns and coveralls were randomly assigned to A-H. Swatches sufficiently larger than the exposure area of the test fluid were cut from randomly selected areas of each garment. The discontinuous regions of the fabrics consisted of zippers (for coveralls), tie-backs (for gowns), and seams (for both). The gown tie-backs were adhered with glue, the gown seams were heat-sealed, 3 of the 4 coveralls seams were sewn or serge sewn and one coverall’s (G) seam was taped. One (G) of the 4 coveralls had a taped storm-flap protecting the zipper area, while the other 3 were not covered or sealed.

The structure (solid volume fraction, fabric uniformity, fiber orientation, manufacturing and bonding process, basis weight, and thickness) and pore geometry of a fabric determine how air passes through it, which ultimately affect its air permeability and end-use.^[17] Relevant to the resistance against fluids for some of the fabrics in this study, there is a linear correlation between air permeability and water permeability of spunlaid heat bonded nonwoven fabrics.^[18] To determine the structural integrity and protective level of the four gowns tested in this study, which were each identified by the protective level reported by their manufacturers, and the 4 coveralls that were tested, air permeability was measured using a Frazier permeability tester (Model #FAP5385F4; Frazier Precision Instrument Company, Inc., Hagerstown, MD), according to ASTM D737 (Standard Test Method for Air Permeability of Textile Fabrics).^[19] Ten samples were randomly taken from continuous regions of the garments, and summarized by their mean (Table 1). Air permeability values of 3 of the 4 gowns and 3 of the 4 coveralls were zero with the other gown and coverall comparable to those found in the literature.^[20]

Table 1.

Air permeability of the gowns and coveralls, measured according to ASTM D737,^[19] N = 10.

Air Permeability (ft3/min/ft2)
A2	B	C	D	E	F	G	H
48.95	39.47	0.00	0.00	0.00	0.00	0.00	0.93

Test liquids

To cover the range of human bodily fluids,^[21,22] 2 preparations of bodily fluids with different surface tensions were selected for this study: (1) water (colored with 0.1% safranin-o, a basic red 2 biological stain; 71 dynes/cm); and (2) synthetic blood (42 dynes/cm; Johnson, Moen & Co. Inc., Cannon Falls, MN).^[7,16] The synthetic blood contained 1.00% direct red 081, 0.55% G110 ammonium salt-acrylic polymer, 0.005% ammonia, 98.444% water, and 0.001% other ingredients (trade secret). Surface tensions of the synthetic fluids were measured at room temperature using a DuNouy Precision Tensiometer (Model 70535, CSC Scientific Company, Inc., Fairfax, VA).

Apparatus and procedures for the test

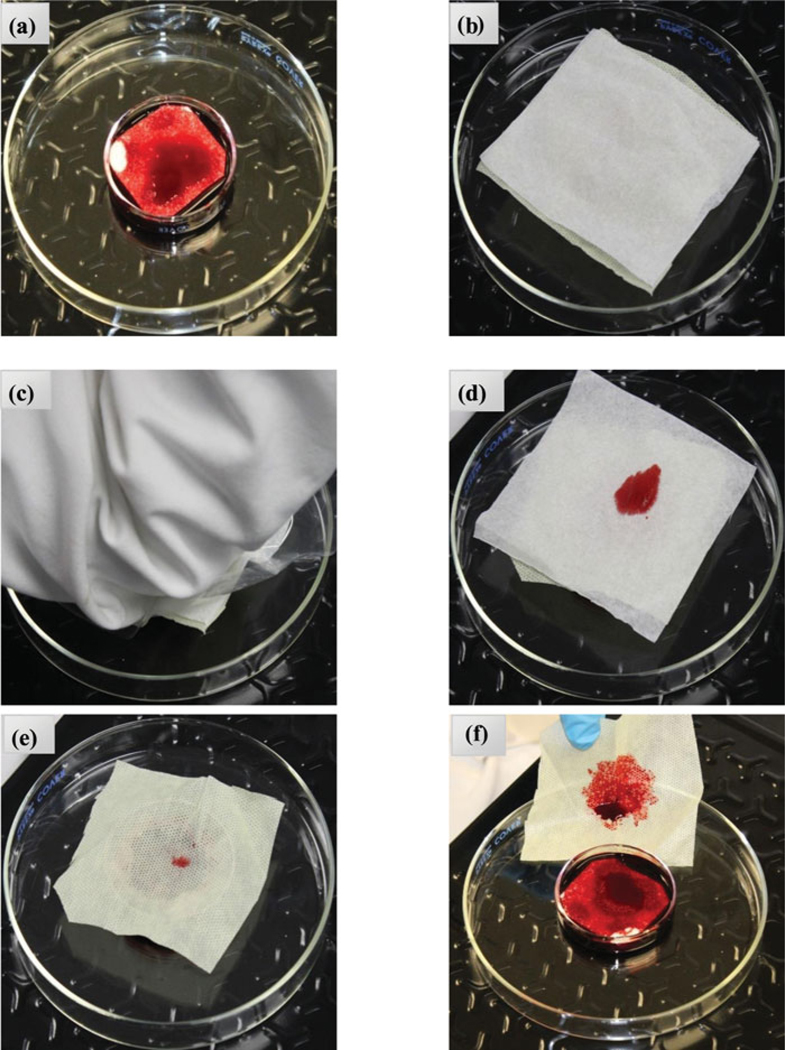
Figure 1 shows the ELT process. The test apparatus included a 2-inch diameter Petri dish, centered on a platform used to contain the test materials. It was set at the center of a digital bench scale in order to maintain consistent applied elbow pressure. A 1.75-in diameter, 0.25-in thick polyester foam pad with 90 pores/inch, with a compression ratio of 3:1 and free of surfactants and other additives,^[23] was placed into the Petri dish and supersaturated with the test fluid (Figure 1a). The exterior face of each garment swatch was layered over the foam pad. To serve as a blotter and facilitate visualization of fluid penetration through the sample swatch, the interior side of the swatch was covered with a layer of Kimwipe. A thin piece of clear plastic polyethylene was laid over the Kimwipe to prevent penetrated fluid from making contact with the elbow or personal clothing worn by the test operator (Figure 1b).

Figure 1.

ELT process for Gown A1 as an example, which had failed: (a) foam pad saturated with synthetic blood; (b) foam pad covered by “pre-test”fabric, which is then covered by the blotter; (c) elbow lean onto blotter with polyethylene to separate fluid from clothing of elbow; (d) “post-test”fabric, strike-through of fluid observed through blotter; (e) penetration side of fabric showing less fluid than blotter; and (f) side of fabric in direct contact with foam pad.

Two test operators performed the ELT to test the swatches: one with a heavier arm (44 PSI) and the other with a lighter arm (2 and 4 PSI) (Figure 1c), which is within the range reported as typical for exertion on surgical gowns during the pressing and leaning common in surgery.^[24] Additionally, the lower pressures also corresponded to those used in other standard penetration tests (e.g., ASTM 1671). To perform each test, the operator leaned their elbow on the top of the blotter for 10 sec, and removed their elbow for visual inspection of the blotter to observe fluid penetration. Hand weights were held by each operator to control applied pressure and enhance repeatability. The error for the higher pressure was 44 +/−1, and for the lower pressures, 4 +/− 0.2, 2+/0.2. The presence of fluid on the elbow side of the blotter (Figures 1d-f) was interpreted as failure (strike-through) of the fabric sample.

To determine the “lean” pressure of each test operator, in pounds per square inch (PSI), the elbow-lean weight from the test scale was divided by the elbow blot area. The elbow blot area was measured by each operator leaning directly onto a saturated pad and pressing on it also for 10 sec. The elbow blot area was calculated by transposing its irregular shape to a sheet of paper and normalizing this to that of a square cut from the same sheet of paper.

For a sample collection, three replicates were tested both for continuous and discontinuous regions. However, in most cases, 6 replicates were tested for the continuous regions of garments that did not have either 0% or 100% failure. Since the higher pressure would provide a significantly greater challenge,^[12] testing the lower pressures for the continuous regions that passed at the highest pressure was not conducted. In contrast, the continuous regions of garments that failed at the highest pressure (44 PSI) were tested at the less challenging lower pressures, 4 PSI down to 2 PSI. To more closely identify the weakest area of protection, the discontinuous regions of the garments that passed the continuous region testing, including ties, and taped and non-taped zippers and seams, were further evaluated at 2 PSI and 44 PSI. Unlike with the continuous regions, because of limited supplies during this studies’ quick response to the Ebola epidemic, for low pressure evaluation, the discontinuous regions were only tested at 4 PSI.

Data analysis

Visual observation of fluid on the blotter, regardless of how little, is considered a garment failure by the ELT method. This rating system is also used in other garment fluid challenge tests (e.g., ASTM F1670 and ASTM F1819).^[7,16] The amount of penetrated fluid varies with the fabric’s permeability, its specified level of protection, potential imperfections in its construction, its handling over time, the fluid’s surface tension and viscosity, and experimental errors, such as inevitable variations in the amount of fluid available in the foam pad during its use, the visual resolution of the experimentalist, etc. To provide a partially quantifiable level of failure, the blot spot size was used and visually rated as very small (v), small (s), medium (m), and high (h) (Figure 2), which is consistent with previous work used to semi-quantitatively measure fluid strike-through.^[25] To compare garment performance for a given applied pressure, garment region and fluid type, the cumulative blot spot size (CBSS) was calculated. CBSS is fundamentally computed by numerical assignment to very small (v), small (s), medium (m), and high (h) as 1,2, 3, and 4, respectively. For a given garment type, replicate blots vary in size. Thus, a cumulative approach is taken (a greater detailed of the calculations are presented in Appendix B).

Figure 2.

Blotter images of blood used to semi-quantitatively estimate amount of fluid strike-through, identified as: (a) very small (v); (b) small (s); (c) medium (m); and (d) high (h).

Statistical approach

Statistical differences between test groups were evaluated by comparison within and between the average CBSS ($\overline{\text{CBSS}}$) for each test parameter. It is estimated that the intrinsic variation of the blot size within and between statistically large enough populations of garment models would produce a normal distribution; this is because of the inherent variability within and between fabrics from their differences in permeability, composition and structure, as well as intrinsic experimental variation. Unfortunately, test materials were limited due to the then urgency of the response to the “Ebola crises” resulting in sample groups too small to provide an ideal normal distribution. However, the data is ordinal and was ranked in the order of CBSS. Thus, the Mann-Whitney U-Test (MWUT) (Microsoft Excel 2010), a rank-sum test for nonparametric data with a relatively low number of samples, was used to evaluate the differences between the sum of the ranks of the fabric samples with respect to applied elbow pressure, fluid type, and garment region. To identify normal distributions within the data set, the Shapiro-Wilk Test (Microsoft Excel 2010) was used.^[26–28]

Results and discussion

Resistance of continuous regions

Continuous regions as a group

The amount of failures by challenge classification (pressure, fluid, region), and by garment model (A-H), as determined by $\overline{\text{CBSS}}$, is summarized in Tables 2–4. As expected, higher failure rates were observed at a higher pressure. For example, the average failure rate for synthetic blood (combining data from all nine garments) at 44 PSI was 50% (i.e., 18/36) compared to 12.5% (i.e., 3/24) at 2 PSI (Table 2). Comparison by surface tension shows not much difference by the overall failure rate, with colored water (higher surface tension) failing at 52% (i.e., 17/33) at 44 PSI and 4% (i.e., 1/24) for 2 PSI (Table 2). However, the ELT has inherent variability within its methodology, and causational differences became more evident by incorporating the blot size for comparisons. Six pairs of fabric sample-sets were statistically tested, with respect to applied elbow pressure and fluid type, for differences in their $\overline{\text{CBSS}}$ (Table 4), with respect to applied elbow pressure and fluid type. Comparison between the rank sums using the Mann-Whitney U Test showed that a change of elbow pressure from 2 PSI to 44 PSI significantly increased the values of $\overline{\text{CBSS}}$ for both blood and water (p < 0.05), giving increased failure rates byafactorof4.4 for blood and21.5 for water. The pressure effect, however, was not statistically significant between 4 PSI and 44 PSI for blood or water, while the fluid effect (synthetic blood vs. colored water) was not significant at low or high pressure.

Table 2.

Failure rate for continuous regions of garments grouped by gowns (A1-D) and by coveralls (E-H). Fractions reference the number of samples that failed divided by the total number tested. The amount of fluid passage through garment is represented as a function of the blot size: very small (v), small (s), medium (m), and high (h) (see Figure 2), where v = 1, s = 2, m = 3, and h = 4^*.

ID	Synthetic Blood Failure Rate				Colored Water Failure Rate
	2 PSI	4 PSI	44 PSI	Total	2 PSI	4 PSI	44 PSI	Total
A1	3s(3/3)	1v1s1m(3/3)	1s2h(3/3)	9/9	1v(1/3)	1v2h(3/3)	2s1m(3/3)	7/9
A2	(0/3)	1s3m(4/6)	3m(3/3)	7/12	(0/3)	2s(2/6)	3m(3/3)	5/12
B	(0/6)	1s(1/3)	3m2h(5/6)	6/15	(0/6)	(0/3)	2s3m(5/6)	5/15
C	(0/3)	(0/3)	1s(1/6)	1/12	(0/3)	(0/3)	(0/6)	0/12
D#	**	(0/3)	(0/3)	0/6	**	(0/3)	(0/3)	0/6
E	**	(0/3)	(0/3)	0/6	**	(0/3)	(0/3)	0/6
F	(0/6)	1s(1/3)	3m(3/3)	4/12	(0/6)	2s(2/3)	2s1m(3/3)	5/12
G#	(0/3)	(0/3)	2v1s(3/6)	3/12	(0/3)	(0/3)	3m(3/3)	3/9
H#	**	(0/3)	(0/3)	0/6	**	(0/3)	(0/3)	0/6
$\overline{\text{CBSS}}$ *	1.0	1.72	4.4	30/90	0.16	1.67	4.28	25/87
Total	(3/24)	9/30	(18/36)		(1/24)	(7/30)	(17/33)

^#Manufacturers claimed garment passed ASTM F1671.

^*$\overline{\text{CBSS}}$ = average cumulative blot spot size = average of the total blots observed for each pressure of a given fluid and region (see Appendix B, Equation B1–3). For comparison purposes, the number of replicates are normalized to 3 for each garment tested. For example, the CBSS for A2 at 4 PSI is normalized from 11 at N = 6–5.5 for N = 3.

^**ELT not conducted at 2 because garments passed at higher pressure levels.

Table 4.

Comparison of the average cumulative blot spot size ($\overline{\text{CBSS}}$) (A, B) and ratio of $\overline{\text{CBSS}}$ (A/B) of each fabric sample as a function of pressure, fluid, and garment region. N represents the total number of garments applied to $\overline{\text{CBSS}}$ for the paired analysis.

Pressure effect*	${\overline{\text{CBSS}}}_{\text{A}}$ 44 PSI	NA 44 PSI	${\overline{\text{CBSS}}}_{\text{B}}$ 2 PSI	NB 2 PSI	A/B**
Blood c	4.4	9	1.0	6	4.4**
d	9.3	6	2.6	8	3.6**
c+d	12.3	6	1.5	5	8.2**
Water c	4.3	9	0.2	6	21.5**
d	8.3	6	3.7	8	2.2**
c+d	10.6	6	2.3	5	4.6**
	44 PSI	44 PSI	4 PSI	4 PSI
Blood c	4.3	9	1.7	9	2.5
Water c	4.4	9	1.7	9	2.6
Fluid Effect	Blood	Blood	Water	Water
2PSI c	1.0	6	0.2	6	5.0
d	2.6	8	3.7	8	0.7
c+d	1.5	5	2.3	5	0.7
4 PSI c	4.4	9	4.3	9	1.0
d	9.3	6	8.3	6	1.1
c+d	12.3	6	10.6	6	1.2
Region Effect	Disc.	Disc.	Cont.	Cont.
Blood 2 PSI	2.6	8	1.0	6	2.6**
44 PSI	9.3	6	4.4	9	2.1**
Water 2 PSI	3.7	8	0.2	6	18.5
44 PSI	8.3	6	4.3	9	1.9**

^*c (Cont.) = continuous, d (Disc.) = discontinuous, c+d = entire garment.

^**Mann-Whitney U Test of H₀ (p < 0.05): Pressure effect ($44\ngtr 2$), Fluid effect ($\text{b}\ngtr \text{W}$), and Region effect ($\text{d}\ngtr \text{c}$). Ratios in bold-italic had at least one variable with a Normal distribution by Shapiro-Wilk Test.

^****$\overline{\text{CBSS}}$ = average cumulative blot spot size

Continuous regions of individual garments

The number of replicates for each garment within a test challenge group was not sufficient to statistically compare effects within an individual garment model. However, for several cases, the trends and differences are apparent and have been evaluated. In comparison to the statistical evaluation of strike-through results of garments as a group, analysis of individual garment models elucidated greater differences between pressure and fluid type (Tables 2 and 5, Figures 3 and 4). Table 5 presents the rank order of the failure rate by garment model and exposure type with the outcome of each garment model computed as the sum of the CBSS failure rates by pressure (see Appendix B, Equation B2). Figure 3 presents CBSS, stacked by pressure (2, 4, and 44 PSI) for each garment, and Figure 4 shows the difference in strike-through between synthetic blood and colored water using the CBSS data from Table 5. Gowns C, B, A2, and A1, in this order, showed an increasing failure rate with increased applied elbow pressure. Both Gowns B and C passed all trials for both fluids at only the lowest pressure (2 PSI), while Gown C passed nearly all conditions, except for the synthetic blood at the highest pressure of 44 PSI. Gown A1 failed nearly all challenge conditions except for the colored water at the lowest applied pressure. Gown A2 passed all tests at 2 PSI, failed over half the tests at 4 PSI, and all the tests at 44 PSI. As expected, gowns with higher air permeability (Table 1), in terms of wearer comfort, offer a lower protection level to synthetic blood. Generally, there is a negative relationship between protection performance and air permeability.^[29] Although protective clothing made of impermeable materials tends to have increased discomfort levels, the ability to protect exposures from blood or bodily fluids that may contain Ebola virus would take priority when considering the trade-off between comfort and protection.

Table 5.

Rank order of failure rate, using CBSS, by garment model and fluid type, first-order rank by synthetic blood for continuous fabric regions and second-order ranked by synthetic blood for discontinuous fabric regions. A lower rank order corresponds to a lower level of strike-through. CBSS for each case is the sum of the CBSS by pressure (see Appendix B, Equation B2).

ID	Continuous (c)		Discontinuous (d)		Entire Garment (c+d)
	Blood	Water	Blood	Water	Blood	Water
D#	0**	0**	0	1	0	1
E	0**	0**	34	42	34	42
H#	0**	0**	39	41	39	41
C	1	0	18	19	19	19
G#	2	9	***	***	***	***
B	10.5	6.5	24	15	34.5	21.5
F	11	11	36	41	47	52
A2	14.5	11	***	***	***	***
A1	22	17	*	*	22	17
Total	61	54.5	153	159	214	213.5

^#Manufacturers claimed garment passed ASTM F1671.

^*Discontinuous regions of A1 not tested, because it had a high rate of failure for the continuous regions tested.

^**Since D, E, and H were not tested at 2 PSI at their continuous regions, for purposes of summing values for the 3 tested pressures, calculation of the cumulative blot area for these fabrics assumed that they would have pass at 2 PSI since they had convincingly passed at both 4 PSI and 44 PSI at their continuous regions.

^***A2 and G not tested at 44 PSI at the discontinuous regions: A2, because the continuous regions greatly failed at this pressure; G would have been tested, but there was a limited supply. Thus, unlike for D, E, and H, the CBSS could not be assumed.

Figure 3.

Cumulative blot area (amount of fluid strike-through) for a given pressure, calculated as the sum of the visually determined blot sizes of all replicates within a garment model (see Appendix B, Equation B1), and stacked graphically by pressure for a given region and fluid type.

Figure 4.

Difference between strike-through of synthetic blood and colored water, derived from the CBSS (see Appendix B, Equation B2), summed by pressure for each garment model, where only samples tested at all three pressures are plotted. Positive results show greater strike-through of synthetic blood and negative results favor colored water.

Three of the 9 garment models (Gown D, and Coveralls E and H) passed at all evaluated pressures and fluids, while the remaining 6 had a range of failures depending on the challenge condition. From the 9 garments tested, 3 make claims of passing ASTM F1671 or equivalent viral penetration tests by their manufacturers: Gown D and Coveralls G and H. As shown in Table V, a clear trend between passing ASTM F1671 and CBSS was not found. Gown D and Coverall H had no failures (i.e., CBSS = 0) in the continuous regions, while Coverall G which makes similar claims had some failures at the highest pressure level at 44 PSI. Conversely, Coverall E that does not make any claims of passing ASTM F1671 had no failures in the continuous regions (i.e., CBSS = 0). These findings could be attributed to the differences between the test methods and the fabrics tested. The third coverall (F) showed higher failure rates with increases in pressure: passing all trials for both fluids at 2 PSI; failing 1of3 times for blood and 2 of 3 times for water at 4 PSI, and 3 of 3 times for both fluids at 44 PSI. Interestingly, at different pressures, Coveralls F and G were the only models in which, depending on pressure, more failures were found for the colored water vs. synthetic blood, subtly for Coverall F at 4 PSI, and substantially for Coverall G at 44 PSI (Figures 3a, 3b, and 4a). As shown in Table 2, Coveralls F and G seemed to have converse responses in the synthetic blood (b) to colored water (w) failure ratio (b/w), with respect to pressure: at 4 PSI, b/w = [(1/3)/(2/3) = 50%] for Coverall F and no difference (0% failure rates for both) for Coverall G; and at 44 PSI, b/w = [(3/3)/(3/3) = 100%] for Coverall F and [(3/6)/(3/3) = 50%] for Coverall G, where for each term the numerator represents the number of failures and the denominator the sample number. However, when considering the same outcomes using the CBSS term (see Appendix B, Equation B2), the results are much different at the higher pressures, especially for Coverall G. For example, at 4 PSI, b/w (2/4) = 50% for Coverall F with no difference (9/9) for Coverall G, while at 44 PSI, b/w (9/7) = 128% for Coverall F, suggesting a slight favoring of blood penetration, which is in stark contrast to Coverall G, b/w (2/9) = 22%, which greatly shows a substantial favoring of colored water penetration. Evaluation by CBSS helps separate the values dimensionally, where the results (converted from a percent to a decimal) suggest that synthetic blood favored strike-through over colored water by a factor of 1.18 for Coverall F, which was completely opposite for Coverall G, in that the strike-through of colored water was about 4.5% (i.e., 1/22) times greater than blood. These results seem to suggest that at low pressure, colored water more easily penetrates through Coverall F, while the converse occurs at high pressure, with colored water much more easily penetrating Coverall G and synthetic blood slightly more easily penetrating Coverall F.

The differences in response to penetration by fluid type between Coveralls F and G may be in the composition of the fabric and/or their porosity. Both coveralls are constructed by different manufacturers using a polyethylene and/or polypropylene non-woven fiber structure, and are designed to allow water vapor (perspiration) to escape from the suit and to prevent saturation of liquids. The polypropylene and polyethylene in fabric fibers are classified as olefins and hydrophobic in nature.^[30] According to their manufacturers, these two coveralls are designed to be minimally porous to allow perspiration to vaporize through, while at the same time prevent liquid and particle penetration. Coverall G uses a polyethylene microporous film to allow for vapor transpiration and withstand saturation of liquids and penetration of particles less than 0.01 μm. Coverall F is composed of flash spun high density polyethylene, which offers an inherent barrier against particles down to 1.0 micron in size. Both models are also treated to have anti-static properties on their exterior surface according to the manufacturers’ reporting their passing the British anti-static test, EN 1149–5.^[31] This standard specifies the electrostatic requirements and test methods for electrostatic dissipative clothing to avoid incendiary discharges. Additionally, regarding this study and the potential effects on strike-through, it is important to note that the surfactants are used by industry to create antistatic properties to aid in the construction of fabrics and prevent these static discharges during the wearing of garments.^[32] Also, the wick effect by the surfactant contributes to its absorption of moisture, which also dries quickly as the relatively small amount disperses.^[33] The intrinsic surfactants may variably affect the garments to produce a lower surface tension in the colored water to make it behave more like the synthetic blood, while the smaller pore size of Coverall G may allow the colored water through more easily by wicking it through.

There are likely a few counteracting properties contributing to the overall penetration of fluid through these breathable water repellent fabrics. As noted, surface tension has been shown to be the primary cause of strike-through in comparison to other fluid properties, including viscosity,^[34] where the authors also reported that, by a hydrostatic biological fluid resistance test (a draft standard in 1993, similar in approach to ASTM F1670), a coverall comparable to Coverall F failed 25% of the time at 1 PSI (N = 5) and 100% at 2 PSI (N = 5), and by the ELT, 100% of the time (N = 3). Thus, Coverall F should not be expected to be impervious to bodily fluids under all conditions. The converse favoring of colored water for Coverall F at low pressure and for Coverall G at high pressure by the ELT in this study likely is affected by conflicting and complimentary physical properties set by the conditions of the test. For example, there is very little opposing resistance formed by the elbow being pressed against the thin foam material laid over a hard solid surface. Additionally, the elbow produces non-uniform forces across the garment. This likely results in a localized maximum pressure somewhere near the area of the elbow in greatest contact with the swatch. Unlike with the ASTM F1670 and AATCC 127 methods, which apply a relatively uniform hydrostatic force with only air resistance on the opposite side, the elbow force is more likely to both crush and displace the garment fibers against the opposing surface, potentially increasing spaces between the fiber structures, and ultimately allowing for greater permeability and penetration of liquids and particles. It is expected that fiber displacement would be greater at higher pressures. Since Coverall F is reported to only protect against 1 μm particles or greater, while Coverall G reports 0.01 μm, the 2 garments most likely have corresponding large and small pore sizes, ultimately contributing to proportional variations in strike-through. Additionally, the intrinsic surfactant in both garments may have a normalizing effect on the surface tension of water, potentially reducing it to being close to that of synthetic blood. From this, the properties of the fluid’s viscosity may become more important. Since surfactants cause a wicking effect, colored water may more easily pass through large pore fabrics (e.g., F) than small pore fabrics (e.g., G), while the fluids with greater viscosity (blood) may be relatively too thick to transport as easily. Thus, explaining why the colored water strike-through is greater than synthetic blood at low pressure for Coverall F; albeit, too small a sample size to be conclusive. However, as the greater elbow pressure of 44 PSI is applied, displacing the fibers and increasing the pore size of both coveralls, the wicking effect from the surfactant may become dominant in comparison to fabric resistance, especially for Coverall G, which has an accelerated penetration of colored water 4.5 times that of synthetic blood. It may be then assumed that for Coverall F the pore opening becomes so large that the viscosity of blood becomes less important than the wick effect, reducing its relative penetration compared to at 2 PSI. Further studies conducted as a function of time and a greater series of pressures may allow for this phenomenon to be tested. Finally, because a greater proportion of failures occur for both Coveralls F and G at the high pressure, the results are more robust for suggesting the causes of differences in fluid type effects on strike-through.

Resistance of discontinuous regions and whole garment

As with the continuous regions, the amount of failures by challenge classification (pressure, fluid, region), and by garment model (A-H), as determined by CBSS, are summarized for the discontinuous regions and the whole garment (Tables 3–5): Table 3 shows the raw failure rates by garment model; Table 4, statistical comparisons of $\overline{\text{CBSS}}$ by grouping the gowns with challenge type; and Table 5, a summary of $\overline{\text{CBSS}}$ for individual models, rank-ordered by the synthetic blood challenge for the blood results of the continuous regions, and 2nd ordered by the synthetic blood challenge for the discontinuous regions. Figure 3b presents the CBSS for discontinuous regions of individual garment models by synthetic blood challenge and Figure 3d is for colored water challenge. Figure 4 presents the difference in strike-through between synthetic blood and colored water, sorted by garment model for all regions. Except for Gown A1, which did not pass the continuous region, zipper and seams of the shoulder and sleeve areas of the remaining garments, were further evaluated. As shown in Table 3, similar to the continuous regions there was a general increase in failure rates at the higher pressure across all garments. For discontinuous regions, surface tension of the carrier liquid played a lesser role in the overall trends, as differences between the two types of simulated bodily fluids were more garment specific.

Table 3.

Failure rate for discontinuous regions of garments grouped by gowns (A2–D) and by coveralls (E–H). The number of samples that failed are divided by the total number tested. Numerator = number of failed samples; denominator = total number tested.

ID	Synthetic Blood					Colored Water
	2 PSI		44 PSI		Total Fails	2 PSI		44 PSI		Total Fails
	Tie	Sleeve	Tie	Sleeve		Tie	Sleeve	Tie	Sleeve
A2	1s	0	**	**		0	0	**	**	0/6
	Shoulder	Sleeve	Shoulder	Sleeve		Shoulder	Sleeve	Shoulder	Sleeve
B	1v	0	3h	1 m 2h	7/12	0	0	2 m 1h	1 s 1m	5/12
C	0	0	3m	3m	6/12	3s	0	3s	2 s 1m	9/12
D	0	0	0	0	0/12	0	0	1v/9	0	1/18
	Seam	Zip	Seam	Zip		Seam	Zip	Seam	Zip
E	1m	1 m 1h	3h	3h	9/12	1v 1s 1m	3h	3h	3h	12/12
F	1m	3m	3h	3h	10/12	1 s 1m	3h	3h	3h	11/12
G	0	0	**	**	0/6	0	0	**	**	0/6
H	1 s 2m	3m	2 m 1h	3h	12/12	2m	3h	1 m 2h	3h	11/12
$\overline{\text{CBSS}}$ *	2.68		9.25		54/84	3.69		8.33		51/84
total	(15/48)		(30/36)			(19/48)		(30/42)

^*$\overline{\text{CBSS}}$ = average cumulative blot spot size = average of the total blots observed for each pressure of a given fluid and region (see Appendix B, Equation B1–3). For comparison purposes, the number of replicates are normalized to 3 for each garment tested, and for each pressure and fluid type $\overline{\text{CBSS}}$ is derived by combining the paired discontinuous regions.

^**A2 and G not tested at 44 PSI at the discontinuous regions: A2, because the continuous regions greatly failed at this pressure; G would have been tested, but there was a limited supply. Thus, unlike for D, E, and H, the CBSS could not be assumed.

^***v, s, m, and h represent that blot spot sizes were visually rated as very small, small, medium, and high, respectively.

The heat-sealed seams of Gown D passed at both pressures for synthetic blood. For colored water, however, a tiny spot was observed on the blotter for 1 of 3 replicates of the shoulder seams for Gown D at high pressure. The results were opposite of what was postulated according to the surface tension (i.e., sample passing with the synthetic blood test should also pass when tested using colored water). Therefore, 6 more replicate measurements were further conducted and all passed the tests, resulting in a low failure rate of 11% (i.e., one with a very small spot out the nine replicate as shown in Table 3). If not from experimental error, this observation may suggest that the structures of the seams generally may not be as uniform as those of the continuous regions, and the protection levels may vary individually. Coverall G had taped seams; it was only evaluated at 44 PSI, since it passed all challenges at the lower pressures. At 44 PSI, no strike-through occurred for either synthetic blood or colored water.

The sleeve-seam of Gown C passed for both fluids at the low pressure, but the shoulder-seam only passed for the low pressure at the low surface tension of synthetic blood. Nearly all zippers for the tested garments failed except two cases being the garment model E zipper at low pressure for the synthetic blood. The results that seams of Gown C passed at the low pressure but failed at the high pressure indicate that penetration increases with increasing pressure, as demonstrated by other investigators.^[35]

The discontinuous regions and whole garment were statistically evaluated in the same manner that the continuous regions were (Table 4)—4 pairs of fabric sample-sets for the discontinuous regions and 8 pairs for the whole garments were tested with respect to effects of applied elbow pressure, fluid type and region, with differences evaluated by $\overline{\text{CBSS}}$ (Table 4). The Shapiro-Wilk Test showed that none of the distributions within the 4 pairs of 9 garments for the discontinuous regions were normally distributed (p > 0.05), while 1 pair (water at 44 PSI) for the whole garment was (p < 0.05). Comparison between the rank sums using the Mann-Whitney U Test showed that a change of elbow pressure from 2 PSI to 44 PSI significantly increased the values of $\overline{\text{CBSS}}$ for both blood and water (p < 0.05). Increased failure rates resulted for blood, at 3.5 times and 8.2 times for the discontinuous region and whole garment, respectively, and for water, at 2.3 times and 4.6 times, for the discontinuous region and whole garment, respectively Compared to the discontinuous regions, the continuous regions seemed to be most affected by the increase in pressure, possibly because the greater proportion of openings through the discontinuous regions offering less resistance at the lower pressure. The pressure effect, however, was not statistically significant for the fluid effect at both low and high pressure. Just as with the effect of pressure on strike-through, the region effect was statistically significant for synthetic blood and colored water at both 2 and 44 PSI (p < 0.05). This was clearly expected, especially since 7 of the 9 models did not have additional support for their seams.

Although the discontinuous regions generally failed more than the continuous regions, this was not the case for all garment models (Figures 3 and 4). For example, Garments D and G passed all but 1 test, likely because of their heat sealed and taped seams, respectively. Some of the models that passed the continuous regions, or only had a very small level of failure, failed substantially greater for synthetic blood and colored water in their discontinuous regions (e.g., C and H). In contrast, 2 that failed in the continuous region improved in the discontinuous region (A2 and G). The effect of fluid type on garment model by region is clearly shown in the plot of their differences (Figure 4), where synthetic blood dominated the strikethrough of the continuous regions of all gowns, while only for the discontinuous region of Gown B. Colored water had a slightly greater strike-through in the discontinuous regions of Gowns C and D, with a greater impact on strikethrough for 3 of 4 coveralls (E, F, and H), which failed in their discontinuous regions. Overall, only 1 garment model (Gown D) demonstrated nearly 100% barrier protection for the whole garment, with only 1 failure of 42 tests.

Summary and conclusions

• As an alternate test to the laboratory based AATCC, ISO, and ASTM standard tests, such as in urgent field operations where these may not be readily available, the ELT demonstrated the ability to offer a quick, visual, semi-quantitative assessment, and evaluation of the barrier performance of isolation gowns and coveralls.

• The ELT was observed to provide a convincing pass/fail outcome, albeit the results are limited because of the relatively low number of samples and that the test is highly variable due to the intrinsic error in the ability of the test operator to accurately and repeatability place the elbow in the correct location, and that the elbow does not have a uniform surface.

• Among the 9 protective garments tested, three of them (D, E, and H) passed all pressures and fluids in the continuous regions. For the discontinuous regions of these, the results suggest that the zippers were not protective, while the heat-sealed seams on Gown D provided protection on all but 1 sample. For garments whose continuous regions passed at low pressures, our results show that taped seams on Coverall G and heat-sealed seams of Gown C were protective.

• Because of the high failure rates in the seam areas of the coveralls, to ensure maximum protection, employers should be diligent in purchasing garments where the seams have been tested by the manufacturer to demonstrate sufficient barrier performance. Several seaming techniques (e.g., serged or sewn, bound, taped, double taped, and ultrasonically welded) are used in protective ensembles. Additional studies are needed to determine if one seaming technique is better than another.

• As hypothesized, for most garments, the failure rates of the garments were greatest at higher applied pressure, at lower fluid surface tension, and for discontinuous regions.

APPENDIX

APPENDIX A – STANDARD TESTS USED TO EVALUATE BARRIER EFFICACY

The barrier effectiveness of Level 1– 4 garments are determined by a separate set of conditions. Level 1 garments are determined by the American Association of Textile Chemists and Colorists (AATCC) 42 water resistance/impact penetration test, which determines the ability of a material to resist water penetration under spray impact. ^(A1) A volume of water is allowed to spray against a taut surface of a test specimen backed by a weighed blotter. The blotter is then reweighed to determine water penetration and the specimen is classified accordingly. For a garment to be considered Level 1, it must pass the AATCC 42 impaction test with less than 4.5g of water weighed on the blotter. Level 2 and Level 3 garments are gauged by both the AATCC 42 impact test and the AATCC 127 water resistance/hydrostatic pressure test. AATCC 127 determines the ability of a material to resist water penetration under constant contact with increasing pressure. ^(A2) One surface of the test specimen is subjected to a hydrostatic pressure, increasing at a constant rate, until three points of leakage appear on its other surface. The water may be applied from above or below the test specimen. For a garment to be considered Level 2, it must pass the AATCC 42 impaction test with less than 1.0g of water weighed on the blotter and pass the AATCC 127 hydrostatic test with a minimum of 20 cm-H₂O of applied pressure. For the respective tests, Level 3 is determined with no more than 1.0g on the blotter and a minimum of 50 cm-H₂O of applied pressure. For surgical and isolation gowns to be considered Level 4, they must pass the American Society for Testing and Materials (ASTM) 1671 test ^(A3), which uses the ASTM 1670 for pre-screening. ^(A4) ASTM 1670 also is used to determine the barrier effectiveness of surgical drapes. ASTM 1671 is a viral penetration test, which applies 2 PSI of pressure to a 60 mL viral broth against a fabric swatch in which a garment fails if a single virus is detected on the opposite side. ASTM 1670 uses the same apparatus as ASTM 1671, but with 2 PSI of pressure applied to 60 mL of a standardized synthetic blood. A garment is considered to have failed ASTM 1670 by visualization of a single drop of fluid.

APPENDIX B – CALCULATIONS OF THE CUMMULATIVE BLOT SPOT SIZE

As a partial “quantitative” numerical approach for the evaluation of strike-through effects by fluid type, garment region, and applied pressure, the blot spot sizes were assigned values as follows: v = 1, s = 2, m = 3, and h = 4. For comparison between garments (g) for a given pressure (p), region (r) and fluid (f), the cumulative blot spot size (CBSS) was calculated as:

$$\text{CBSS}(\text{g};\text{p},\text{r},\text{f})=(\text{Kv}+\text{Ks}+\text{Km}+\text{Kh})\text{g,}$$ (Eq. B1)

where

g = garment model (A1, A2, B, C, D, E, F, G, H);

p = pressure (2, 4, 44 PSI);

r = region “c” (continuous), “d” (discontinuous) and “c+d” (entire garment);

f = fluid type “b” (synthetic blood) and “w” (colored water); and

Kv, Ks, Km, and Kh = numbers of samples with observed blot with sizes of very small, small, medium, and high, respectively.

For example, hypothetically, for the case of triplicate testing of the continuous region of garment A tested against synthetic blood at 44 PSI, where the distribution of blot sizes were 1 small and 2 medium, the CBSS would be:

$$\text{CBSS}(\text{A};44,\text{c},\text{b})=0(1)+1(2)+2(3)+0(4)=8$$

To evaluate the effect of garment region on the strike-through of a given fluid for a single garment model, the sum of CBSS for the corresponding set of pressures would be:

$$\begin{gathered} \text{CBSS}{(\text{g};\text{r},\text{f})}_{\text{p}}=\sum {(\text{kv},\text{ks},\text{km},\text{kh})}_2+\sum {(\text{kv},\text{ks},\text{km},\text{kh})}_4+\sum {(\text{kv},\text{ks},\text{km},\text{kh})}_{44} \\ =\text{CBSS}{(\text{g};\text{r},\text{f})}_2+\text{CBSS}{(\text{g};\text{r},\text{f})}_4+\text{CBSS}{(\text{g};\text{f},\text{r})}_{44} \end{gathered}$$ (Eq. B2)

For example, assuming a CBSS of the continuous regions for garment A tested against synthetic blood to be 1 at 2 PSI, 3 at 4 PSI, and 8 at 44 PSI, and the discontinuous regions to be 0 at 2 PSI, 5 at 4 PSI and 12 at 44 PSI, then

$$\text{CBSS}{(\text{A};\text{c},\text{b})}_{2,4,44}=1+3+8=12$$

vs.

$$\text{CBSS}{(\text{A};\text{d},\text{b})}_{2,4,44}=0+5+12=17.$$

Thus, for this example, the discontinuous region of garment A tested against synthetic blood would have an overall higher failure rate as determined by its cumulative blot size of 17, in contrast to 12 for the continuous region. The cumulative blot size was used in this study to compare the effects of fluid type (corresponding to surface tension), region, and pressure on the overall average strike-through of fluid through protective garments. For this, the average CBSS ($\overline{\text{CBSS}}$) was determined by:

$$\begin{array}{l}{\overline{\text{CBSS}}}_{\text{g}}=\sum {[\text{CBSS}(\text{p},\text{r},\text{f})]}_{\text{g}}/\text{n}\\ =\left[\text{CBSS}{(\text{p},\text{r},\text{f})}_{\text{A}1}+\text{CBSS}{(\text{p},\text{r},\text{f})}_{\text{A}2}+\text{CBSS}{(\text{p},\text{r},\text{f})}_{\text{B}}+\dots \dots +\text{CBSS}{(\text{p},\text{r},\text{f})}_{\text{H}}\right]/\text{n,}\end{array}$$ (Eq. B3)

where n = the number of garment models tested under the given set of conditions = (≤ 9)

For example, the average CBSS of the continuous regions of 9 garment models, tested for strike-through of synthetic blood with an applied elbow pressure of 2 PSI, with their CBSS alternating between 1 and 0 would be:

$$\overline{\text{CBSS}}=[0+1+0+1+0+1+0+1+0]/9=4/9=0.44$$ (Eq. B4)