Adaptive behaviors and vaccination on curbing COVID-19 transmission: Modeling simulations in eight countries

Abstract

Current persistent outbreak of COVID-19 is triggering a series of collective responses to avoid infection. To further clarify the impact mechanism of adaptive protection behavior and vaccination, we developed a new transmission model via a delay differential system, which parameterized the roles of adaptive behaviors and vaccination, and allowed to simulate the dynamic infection process among people. By validating the model with surveillance data during March 2020 and October 2021 in America, India, South Africa, Philippines, Brazil, UK, Spain and Germany, we quantified the protection effect of adaptive behaviors by different forms of activity function. The modeling results indicated that (1) the adaptive activity function can be used as a good indicator for fitting the intervention outcome, which exhibited short-term awareness in these countries, and it could reduce the total human infections by 3.68, 26.16, 15.23, 4.23, 7.26, 1.65, 5.51 and 7.07 times, compared with the reporting; (2) for complete prevention, the average proportions of people with immunity should be larger than 90%, 92%, 86%, 71%, 92%, 84%, 82% and 76% with adaptive protection behaviors, or 91%, 97%, 94%, 77%, 92%, 88%, 85% and 90% without protection behaviors; and (3) the required proportion of humans being vaccinated is a sub-linear decreasing function of vaccine efficiency, with small heterogeneity in different countries. This manuscript was submitted as part of a theme issue on “Modelling COVID-19 and Preparedness for Future Pandemics”.

1. Introduction

The novel coronavirus (COVID-19) has become a worldwide pandemic and the infection number is keeping increasing (WHO, 2021). As of December 6, 2021, the total number of confirmed cases of COVID-19 in the world is larger than 265 million, with over 5.24 million deaths (WHO, 2021). COVID-19 is disrupting the global economic, political and social systems, which is posing comprehensive threats to population health around the world. To fight against COVID-19, people change their behaviors and are encouraged to take vaccination. Yet the combined effects of virus mutation, limited efficiency of vaccination and high infectivity are bringing great challenges to the prevention and control. Evaluating the effectiveness of intervention strategies and vaccination patterns is a urgent scientific issue.

Under the media coverage and government guidance, the persistent eruption of human infection in COVID-19 triggers a series of protection behaviors, in which people are forced/willing to wear masks, keep social distancing, wash hands frequently and take vaccination (Levin et al., 2021). For example, the US government strengthened border control and restricted incoming travelers since January 2020. After declaring a public health emergency in March, more drastic measures are implemented, including closing school, postponing/canceling big gathering, avoiding international travel, home quarantine. Wearing masks was encouraged in public since April, and mask mandate was enforced and then cancelled during 2021 and 2022. The non-pharmaceutical intervention (NPI) measure were gradually released Since Jun 2020. The UK government imposed stay-at-home order for 6 weeks during March and April, 2020, and many behavioral and social interventions were implemented sine then. From July 2021, UK moved to the final stage of easing restrictions. It was found that all countries have implemented or are implementing intervention strategies in varying degrees to combat COVID-19. These interventions mainly refers to NPIs, including mask wearing, adaptation or closure of school/business, travel restrictions, limits and restrictions on public and private gatherings (Levin et al., 2021). How to design optimized prevention and control measures (considering psychological factors (Brzezinski et al., 2021, Nowak et al., 2020, Petrocchi et al., 2020), behavioral changes (Teslya et al., 2020, Tang et al., 2021) and vaccination strategies (Matrajt et al., 2021, Moore et al., 2021, Chhibber et al., 2022, Han et al., 2021)) have attracted extensive attention recently. Recent studies indicated that (1) surgical masks can prevent the spread of droplets from infectious individuals (Leung et al., 2020); (2) maintaining social distance can reduce the risk of interpersonal communication associated with COVID-19 (Teslya et al., 2020, Anderson et al., 2020, Viner et al., 2020); (3) NPIs can alleviate infection intensity and slow or even contain the variants in COVID-19 (Zhao et al., 2022); and (4) cleaning, hygiene and hand washing can effectively keep away coronavirus (WHO, 2021). However, the estimated effectiveness of vaccination seems to be inconsistent (Moore et al., 2021, Chhibber et al., 2022, Han et al., 2021). Here we went a further step to combine the complex interplay between human protection behavior, vaccination and disease transmission, aiming at providing reasonable intervention strategies under different circumstances. We focused on the following key issues: (1) how to build dynamic equations to describe the interplay, so as to accurately describe the influence of adaptive protection behavior on the mutual checks and balances of the pandemic? (2) how to determine the optimal vaccination coverage, and integrate vaccination and NPI for disease prevention?

To tackle the above issues, we developed an ordinary differential system to simulate the transmission process with two routes (susceptible–exposed–infected–recovered or susceptible–immune), in which vaccination is reflected by shifting parts of susceptible people to those with immunity after a time delay, and adaptive protection behavior is considered by modifying the transmission strength. Here adaptive protection behavior represents the performance people conduct to avoid infections, in which its role is regulated by human awareness, and it is magnified when disease worsens and people become alarmed. Hence it can be taken as adaptive NPI activity. We then validated the model by Markov Chain Monte Carlo (MCMC) method to examine the spread patterns in eight countries with most reported cases (i.e., America, India, South Africa, Philippines, Brazil, UK, Spain and Germany). We finally revealed the influences of adaptive behaviors and vaccination by numerical analysis.

2. Method and materials

2.1. Study area and data

Our study focused on the COVID-19 infection in eight countries, that is the United States (America), India, South Africa, Philippines, Brazil, the United Kingdom (UK), Spain and Germany. The reason of choosing these countries lies in that they have reported the highest numbers of COVID-19 case in the world, and different intervention strategies they adopted can make good comparison. Their total population numbers are 3,267, 1,354, 57, 106, 210, 66, 82 and 46 million, respectively. These countries distribute in North/South America, Asia, Africa, and Europe.

The information of COVID-19 infections and vaccination reported as well as demography in the eight countries during Marth 2020 and October 2021 was used in this study. The cumulative daily numbers of clinical infections in each country were download from the Humanitarian Data Exchange (https://data.humdata.org/dataset/novel-coronavirus-2019-ncov-cases). The daily records of COVID-19 vaccinations and demography in these countries were extracted from the Our World in Data (https://ourworldindata.org/) and Bing surf.

2.2. Modeling framework

In view of the existing knowledge about the clinical progression of COVID-19 infection in humans, as well as the recently implemented control strategies, we developed a new COVID-19 transmission model by ordinary differential equations. The model is based on the following assumptions

• •People are divided into the epidemiologically relevant stages for COVID-19 transmission: susceptible ($S$), latent ($E$), preclinical infectious ($I_p$), subclinical infectious ($I_s$), clinical infectious ($I_c$), recovered ($R$) and immune due to vaccination ($V$). Here $I_p$ and $I_s$ are inapparent infections, in which $I_s$ results in few or no symptoms, and symptoms appear when people evolve from $I_p$ to $I_c$ (Davies et al., 2020). Unlike $I_c$, they are unlikely to be ascertained by syndromic surveillance (Davies et al., 2020). The sum of these classes equals the total population size, that is, $N=S+E+I_p+I_s+I_c+R+V$. The human population is assumed to be fully susceptible before the introduction of COVID-19 and is kept constant in size throughout the study period.
• •Newly infected individuals are generated by the standard mass action formulation. Susceptible people could be infected at rate $\lambda$ after effective contacts with those who are infectious ($I_p,I_s$ and $I_c$), and then become exposed (in latent state). After an incubation period $1/\eta$, they become either preclinically infectious (with probability $\kappa$) or subclinically infectious. Subclinical infections could not be easily found and treated, but they can self-recover after time $1/\gamma$. The preclinical infections appear symptoms after time $1/\delta$ and then enter clinical class. Clinical infections receive treatment and are cured through time $1/\omega$. After that, they acquire complete immunity upon recovery. It is assumed that the duration of subclinical infection is equal to the sum of duration of preclinical and clinical infection, i.e., $1/\gamma =1/\delta +1/\omega$.
• •
  During COVID-19 transmission, people usually modify their behavior and take preventative steps to reduce infection risk, such as wearing masks and reducing travel. Individuals’ self-protection awareness usually intensify as the cases increase, and then they will adopt stricter measure against infection. We called such performances as adaptive protection behaviors, which obviously can alleviate infectivity. Their influence weight on infectivity is quantified by variable $f$, which is a decreasing function of case number (Eksin et al., 2019). If the function $f$ depends on the cumulative (current) cases, it can be called “long-term (short-term) awareness”. The difference of these two kinds of functions are that people take protective measures according to the information of either total infections or current infection (Eksin et al., 2019). Accordingly, we propose the following functions to measure the impacts of people adaptive behavior on disease transmission

  $$f_1=e^{-k{I}_c},f_2=e^{-k(I_c+\varphi R)},f_3={\left(1-\frac{I_c}{N}\right)}^k,f_4={\left(1-\frac{I_c+\varphi R}{N}\right)}^k.$$ (2.1)

  Here $f_1$ and $f_3$ ($f_2$ and $f_4$) correspond to “short-term awareness” (“long-term awareness”). Function selection in each country is based on their performance in model fitting.
• •People can acquire immunity by vaccination, and then they remove from susceptible state to vaccinated state. Since vaccine potency survey showed that people reach protection usually after two weeks of their second injection (Baden et al., 2021), we introduce a time delay to account for the interval between the date that susceptible individual is vaccinated to the date that his/her immune system starts working. Moreover, given that all of the available COVID-19 vaccines cannot completely prevent infection, which may show 94.1% efficacy at preventing Covid-19 illness (Baden et al., 2021), we provide a vaccine protection rate to measure its effectiveness. Hence, at time $t$, this part of susceptible people $\vartheta \theta S(t-\tau )$ enters vaccinated class, where $\vartheta$, $\theta$ and $\tau$ represent vaccine protection rate, vaccination rate and immune delay, respectively.

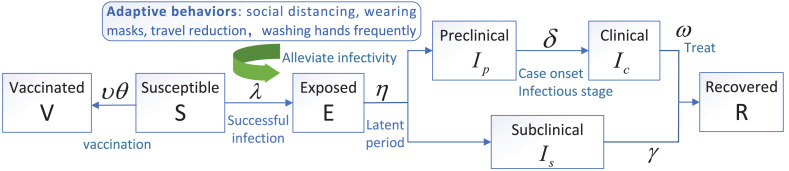
Accordingly, the essential features of the transmission process are depicted in Fig. 1. The governing equations for simulating the transmission dynamics of COVID-19 are illustrated as follows:

$$\left\{\begin{array}{c}\frac{dS\left(t\right)}{dt}=-\lambda f\frac{S\left(t\right)}{N}\left[I_p\left(t\right)+\alpha I_s\left(t\right)+\beta I_c\left(t\right)\right]-\vartheta \theta S(t-\tau ),\hfill \\ \frac{dE\left(t\right)}{dt}=\lambda f\frac{S\left(t\right)}{N}\left[I_p\left(t\right)+\alpha I_s\left(t\right)+\beta I_c\left(t\right)\right]-\eta E\left(t\right),\hfill \\ \frac{d{I}_p\left(t\right)}{dt}=\kappa \eta E\left(t\right)-\delta I_p\left(t\right),\hfill \\ \frac{d{I}_s\left(t\right)}{dt}=(1-\kappa )\eta E\left(t\right)-\gamma I_s\left(t\right),\hfill \\ \frac{d{I}_c\left(t\right)}{dt}=\delta I_p\left(t\right)-\omega I_c\left(t\right),\hfill \\ \frac{dR\left(t\right)}{dt}=\omega I_c\left(t\right)+\gamma I_s\left(t\right),\hfill \\ \frac{dV\left(t\right)}{dt}=\vartheta \theta S(t-\tau ).\hfill \end{array}\right)$$ (2.2)

The parameters are presented in Table 1.

Fig. 1.

Flow diagram of COVID-19 transmission among humans. Related parameters are defined in Table 1.

Table 1.

Description of model parameters, with time unit as day or per day.

Parameters	Definitions	Value	Source
$1/\eta$	Duration of incubation period	7.76	Qin et al. (2020)
$\lambda$	Dominant infection rate		fitting
$\kappa$	Proportion of the exposed evolving preclinical infections	0.82	Mizumoto et al. (2020)
$1/\delta$	Time span from illness onset to be treated	1.5	Kerkhov (2020)
$\vartheta$	Vaccine protection rate	0.94	Baden et al. (2021)
$\theta$	Vaccination rate	varied
$1/\omega$	Duration of treatment for symptomatic patients	19	Woodruff (2020)
$\alpha$	Relative infectivity of inapparent infections	1/3	Chen et al. (2020)
$\beta$	Relative infectivity during treatment	1	Chen et al. (2020)
$\tau$	Time from vaccination to vaccine works	14	Baden et al. (2021)

2.3. Model validation

We validated the proposed model by fitting the infection data in eight countries for inferring their transmission patterns. Here we used the MCMC algorithm to estimate the uncertain parameters (i.e., $\Phi =\text{(}\lambda ,k,\varphi ,E\left(0\right),I_p\left(0\right),I_c\left(0\right)$) in our model. The cumulative cases of reporting and modeling are separately denoted by vectors $I=(I_1,I_2,\dots ,I_m)$ and $\Lambda =({\Lambda }_1,{\Lambda }_2,\dots ,{\Lambda }_m)$, where $m=577$ is the study period. Their relationship can be written as $\Lambda =I+ϵ$, in which $\varepsilon \sim N(0,{\Sigma }_m)$ is the error matrix with a diagonal matrix of ${\Sigma }_m=diag({\sigma }_1^2,{\sigma }_2^2,\dots ,{\sigma }_m^2)$. Given the prior information of $\Phi$, the time series of $\Lambda$ is generated by running the model, and then the likelihood function is computed by:

$$P\left(\Lambda \right|\Phi )={\left(2\pi \right)}^{-m/2}|\Sigma {|}^{-1/2}ex{p}^{\frac{{(\Lambda -I)}^{\prime }(\Lambda -I)}{2\Sigma }}.$$

Since the parameters in $\Phi$ are conditionally independent, their joint posterior distribution can be written as:

$$P\left(\Lambda \right|\Phi )\propto {\Pi }_{t=1}^{m}P\left(\Lambda \right|\Phi )P\left(k\right)P\left(\varphi \right)P\left(\lambda \right)P\left(E\left(0\right)\right)P\left(I_p\left(0\right)\right)P\left(I_c\left(0\right)\right)$$ (2.3)

We implemented the MCMC algorithm as follows: (1) parameters in $\Phi$ were initialized based on their prior information; (2) the predictive cases were produced by running the model, and the posterior distribution $P\left(\Omega \right|Y)$ was estimated by (2.3); and (3) the values and distribution of $\Phi$ were updated through sampling, and the predictive cases were also updated by running the model with a new $\Phi$. In this case, the new $\Phi$ is accepted with the probability of

$$min\left(1,\frac{P\left({\Omega }^{\ast }\right|Y)Q\left(\Omega \right|{\Omega }^{\ast })}{P\left(\Omega \right|Y)Q\left({\Omega }^{\ast }\right|\Omega )}\right),$$

where the $Q\left({\Phi }^{\ast }\right|\Phi )$ was the adaptive proposal distribution. After 100,000 iterations, the posterior distributions of $\Phi$ were inferred from the final 70% iterations. We examined the performances of the model with different quantification of adaptive behavior, and selected the expression of function $f_i$ by the criterion of least fitting error $Er={\sum }_{t=1}^m{(I_t-{\Lambda }_t)}^2/N$. The above analysis was realized by employing the deSolve and FME packages in R language software.

To identify the contributions of parameters to the variability of model output, we performed global sensitivity analysis by using Latin Hypercube Sampling (LHS) and partial rank correlation coefficient (PRCC) technique for the input parameters against the simulated infections (Marino et al., 2008). We defined the baseline values of each parameter (see table S1 in Supplementary Information) based on their posterior distribution, and then conducted LHS sampling procedure, which yields 1000 non-overlapping equiprobable intervals for each parameter. Thus, LHS matrix was generated with 1000 rows for the number of simulation (simple size) and 8 columns corresponding to the number of varied parameters. After checking the monotonic relationship between input parameters and output infections, we plug each row of the LHS into the model and conduct simulation, yielding 1000 times series of human infections. Subsequently, we computed the PRCCs between each parameter and the cumulative infection size at each day, and then averaged them over time. Parameters with high absolute PRCC values close to 1 are said to be highly correlated with model output, in which those with negative (positive) PRCC values means that their increase can enlarge (reduce) infections (Marino et al., 2008).

After validating the proposed model, we quantified the transmission patterns of COVID-19 under different scenarios of vaccination and collective behaviors, by assigning the model parameters with different values.

3. Results

Since March 2020, COVID-19 disease began to spread in the studied countries, i.e., America, India, South Africa, Philippines, Brazil, UK, Spain and Germany (the following data are presented in this order), and the infection numbers kept rapidly increasing since then. As of December 2021, the attack rates in these countries were 14%, 3%, 5%, 2%, 10%, 12%, 11% and 5%, respectively.

Based on biological significance, the initial conditions of the model (2.2) were set to be nonnegative, and the right-hand side of the model ensures that its solutions will always stay in the set

$$\Omega =\{(S,E,I_p,I_s,I_c,R,V)\in R_{+}^7\mid 0\le S,E,I_p,I_s,I_c,R,V\le N\}.$$

The basic reproduction number, $R_0$, is one of the most important theoretical concepts in epidemiology, which can quantify infection potential (Van den Driessche and Watmough, 2002). $R_0$ is interpreted as the average number of secondary cases that are produced by a single primary case in a fully susceptible population (Van den Driessche and Watmough, 2002). We calculated the basic reproduction number $R_0$ by using the theory of next generation matrix, written as $R_0=\rho \left(F{V}^{-1}\right)$, where $F$ is the rate of occurring new infections, $V$ is the rate of transferring individuals outside the original group, and $\rho$ represents the spectral radius of matrix (Van den Driessche and Watmough, 2002). Direct calculation yields that

$$F=\left(\begin{array}{cccc}\hfill 0\hfill & \hfill \lambda f\hfill & \hfill \alpha \lambda f\hfill & \hfill \beta \lambda f\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),V=\left(\begin{array}{cccc}\hfill \eta \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -\kappa \eta \hfill & \hfill \delta \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill (\kappa -1)\eta \hfill & \hfill 0\hfill & \hfill \gamma \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\delta \hfill & \hfill 0\hfill & \hfill \omega \hfill \end{array}\right).$$

It follows from the characteristic equation of $F{V}^{-1}$ that the basic reproduction number is given by

$$R_0=\rho \left(F{V}^{-1}\right)=\frac{\lambda f\kappa \gamma \omega +\alpha \lambda f(1-\kappa )\delta \omega +\beta \lambda f\kappa \delta \gamma }{\delta \gamma \omega }.$$ (3.1)

The three components of $R_0$ are separately contributed by the infections in preclinical, subclinical, and clinical states. It is observed that $R_0$ has no connection with vaccination. Based on the fitting parameters (see in the last column of Table 2), the basic reproduction numbers in these countries were estimated at around $1.5\text{–}3$, with the minimum value (1.46) in the Philippines and the maximum value (3.02) in South Africa.

Table 2.

Behavioral function, parameter value and error of the best fitting results in eight countries.

Country	Function	$\lambda$	$k$	$\varphi$	Error	$R_0$
America	$f_3$	0.1021	57.579	–	5.505e＋12	2.27
India	$f_1$	0.1258	4.2895e−7	–	8.831e＋12	2.27
South Africa	$f_1$	0.1677	1.0217e−5	–	2.854e＋10	3.02
Philippines	$f_1$	0.0793	1.7474e−6	–	2.029e＋10	1.46
Brazil	$f_3$	0.1463	189.014	–	1.602e＋12	2.64
UK	$f_3$	0.0929	32.6316	–	4.888e＋11	1.68
Spain	$f_4$	0.1078	94.4445	1.3667e−6	7.325e＋10	1.94
Germany	$f_2$	0.0965	1.2878e−6	0.033334	1.869e＋10	1.74

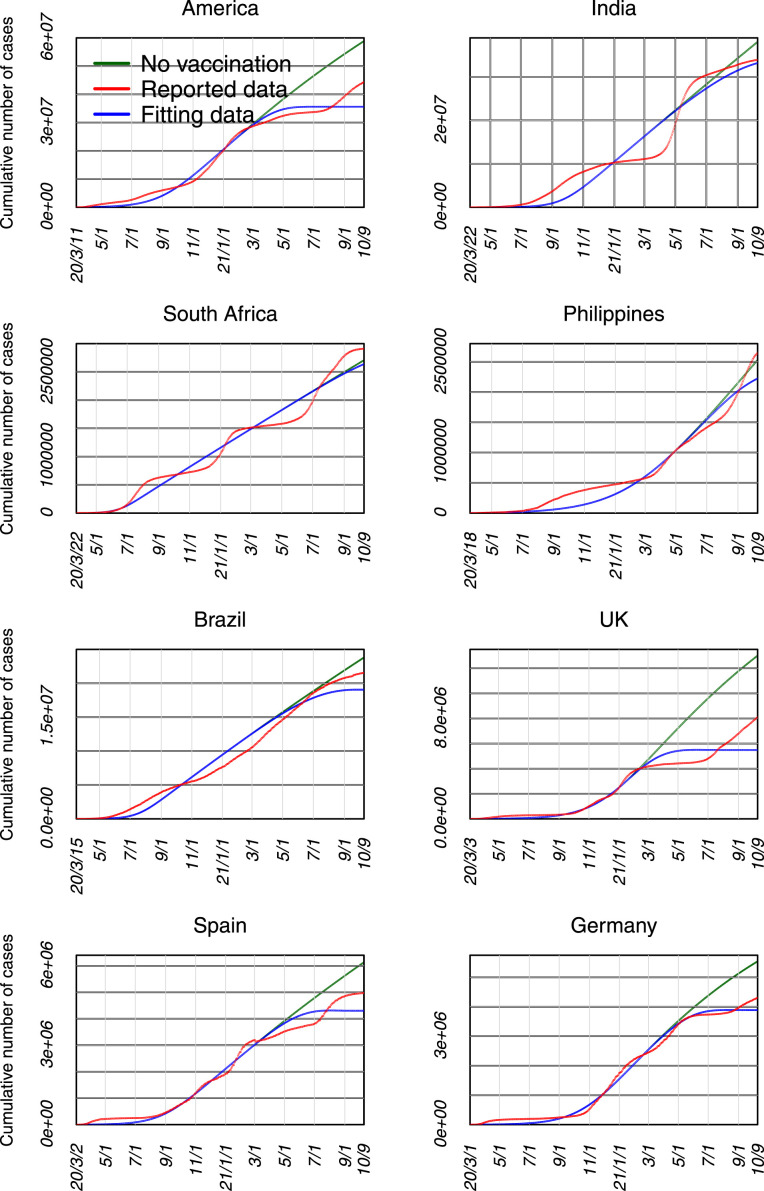
The fitting results are shown in Table 2, Figs. 2, 4 and S1. It is found that the estimated parameters enable to draw a good fitting capacity of reported cases in these countries, in which the model accounts for larger than 91% of variation in daily data. It is estimated that the infection rate $\lambda$ is between 0.08 and 0.17, and most people in these countries (except Spain and Germany) mainly exhibited short-term protective behaviors.

Fig. 2.

The fitting results of the COVID-19 cases in eight countries.

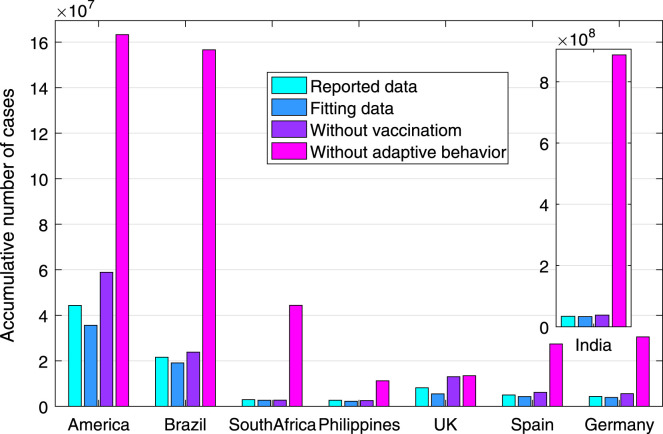
Fig. 4.

The number of cumulative cases as of October 9, 2021, in eight countries in different scenarios.

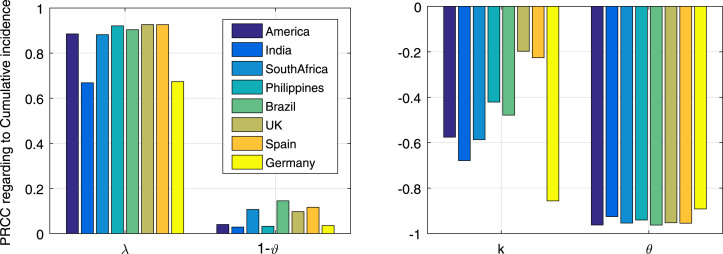
The results of sensitivity analysis are shown in Fig. 3. It is observed that the most sensitive parameters are vaccination rate ($\theta$), infection rate ($\lambda$) and behavior parameter ($k$), followed by vaccine protection rate ($\vartheta$). While the initial conditions and long-term behavior parameter ($\varphi$) have no significant effect on model output. Specifically, the vaccination (infection) rate has overwhelming negative (positive) relation with case number, and such correlation is consistent in all these countries. The behavior parameter in Germany is more sensitive in determining the modeling infection.

Fig. 3.

Sensitivity of model parameters to the cumulative cases as indicated by PRCC values, in which only parameters with small P-values ($<0.05$) are shown.

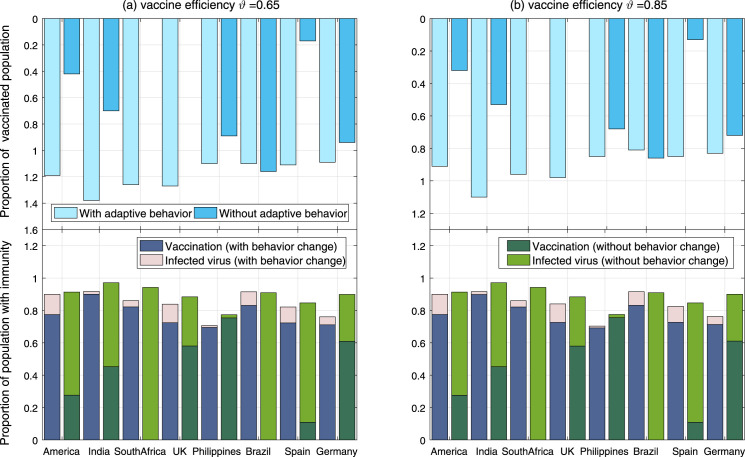
Fig. 4 shows the total infection number with the vaccination and adaptive protective behaviors that have already been adopted in these countries. It is observed that if without adaptive behaviors, the total number of human infections (as of October 9, 2021) in America, India, South Africa, Philippines, Brazil, the United Kingdom, Spain and Germany could reach 163.29, 887.72, 44.34, 11.23, 156.64, 13.43, 27.42 and 30.49 million. These were 3.68, 26.16, 15.23, 4.23, 7.26, 1.65, 5.51 and 7.07 times of the reported cases. If without implementing vaccination, human infection number would increase by 65.33%, 14.72%, 2.56%, 13.78%, 4.95%, 137.07%, 42.57% and 42.60%, respectively. It is found that the protective efficacy of adaptive behavior (vaccination) is much more significant in India, South Africa and Brazil (UK and America).

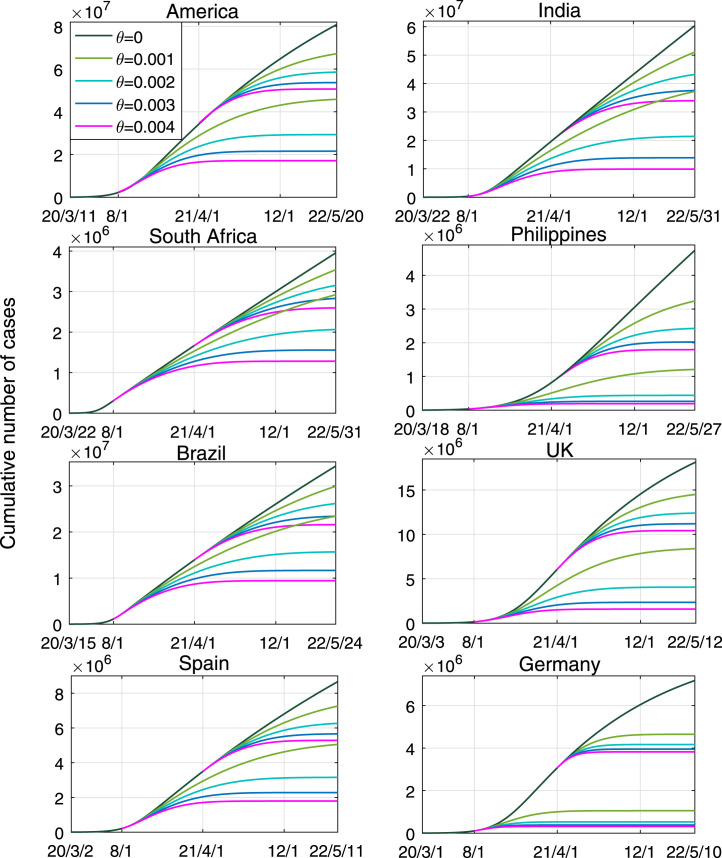
Fig. 5 shows the effects of different vaccination rates on curbing COVID-19 transmission in eight countries, in case of adaptive behaviors. It is observed that (1) if without vaccination, as of May 2022, the cumulative numbers in these countries would keep increasing and reach 80.84, 60.39, 3.96, 4.74, 34.31, 18.15, 8.67 and 7.18 million, respectively; (2) if the vaccination is carried out from August 2020, with $\theta =0.001$ (i.e., there are 0.1% susceptible individuals to be vaccinated every day), it would not stop the infection in these countries (except Germany), but after 21 months it can reduce total infections by 43.30%, 38.30%, 26.11%, 74.53%, 31.71%, 53.77%, 41.88% and 85.31% (compared to the situation without vaccination), respectively; (3) if the vaccination is implemented from August 2020 and is lasted for 12 months with $\theta =0.002$, it would stop the infection in America, India, Philippines, UK and Spain; and (4) if the vaccination rate $\theta$ is larger than 0.003, the infection in all these countries could be prevented after $3-10$ months. It is found that the vaccination takes effect more quickly in Germany, Philippines and UK.

Fig. 5.

Estimated prevalence of COVID-19 infections with different vaccination rate $\theta$. There are two timings for vaccination: from August 2020 or April 2021. The effective protection rate of the vaccine was $\vartheta =94.1\text{\%}$.

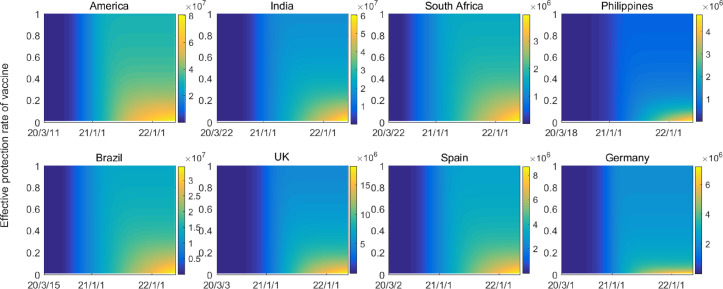
Fig. 6 shows the impacts of vaccine protection rates on disease evolution with daily vaccination rate $\theta =0.001$. It is observed that the increase of protection rate definitely yields less cases and slower transmission. However, it is impossible to prevent disease transmission in case of small protection rate of vaccine ($\vartheta <0.2$), no matter how long the vaccination is implemented. The epidemic situation in the Philippines and Germany could be controllable when $\vartheta \ge 0.2$, and in other countries it may need $\vartheta \ge 0.4$.

Fig. 6.

Estimated prevalence of COVID-19 infections with different effective protection rate of vaccination. The cumulative numbers of human cases are shown with vaccination from January 2021 and vaccination rate $\theta =0.001$.

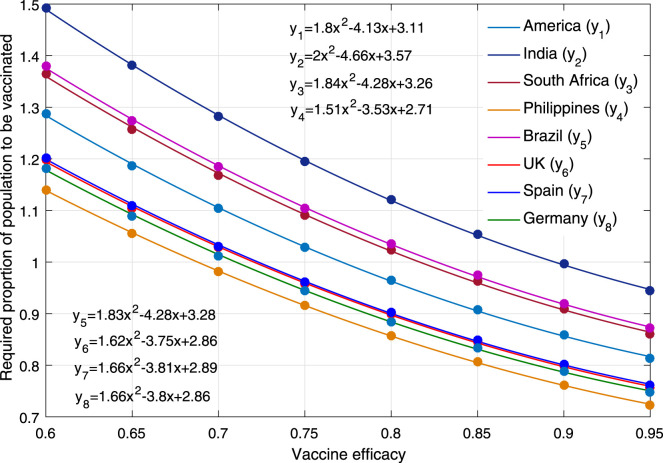
Fig. 7 and Table 3 show how many people should to be vaccinated or acquire immunity in case of different vaccine efficiency ($\vartheta$) and adaptive behaviors, for full control of COVID-19. It is observed that the proportion of population with immunity (denoted by $\varepsilon$) is roughly the same with different $\vartheta$ in each country. In case of adaptive behaviors, parameter $\varepsilon$ in these countries should be 90%, 92%, 86%, 71%, 92%, 84%, 82% and 76%, respectively. If without adaptive behaviors, parameter $\varepsilon$ is a little larger, especially in South Africa and Germany. When vaccine efficiency is $\vartheta =0.65$ and the population has adaptive behavior, the proportions of vaccinated population in these countries should be 119%, 138%, 126%, 106%, 127%, 110%, 111% and 109%, respectively. These data larger than 100% means that some of them have to be vaccinated twice. When vaccine efficiency increases to $\vartheta =0.85$, the above proportions drop to 91%, 105%, 96%, 81%, 98%, 85%, 85% and 83%, respectively. As shown in Fig. 8, it is further observed a sub-linear decrease of vaccination proportion (denoted by $\xi$) as the vaccine efficiency $\vartheta$ increases. Their relationship can be written as quadratic function by regression method, in which $\xi$ is taken the biggest value in India and the smallest value in the Philippines.

Fig. 7.

Required proportion of human population that is vaccinated or has immunity in case of different vaccine efficiency and collective behaviors. The simulation time is from March 2020 to October 2021, with vaccination starting from January 2021. The evaluation standard is that the number of new cases in October 2021 will not exceed 100.

Table 3.

Requirements for vaccination rate and number of vaccinations (million) in eight countries under different protection rates. Group behavior has self-protection consciousness. X (Y) represents the proportion (number) of population to be vaccinated.

	$\vartheta$	60%	65%	70%	75%	80%	85%	90%	95%
America	X	1.29	1.19	1.10	1.03	0.96	0.91	0.86	0.81
	Y	42.07	38.78	36.06	33.59	31.52	29.69	28.05	27.00
India	X	1.49	1.38	1.28	1.20	1.12	1.05	0.99	0.94
	Y	202.54	187.05	173.64	161.99	151.85	142.59	134.95	127.93
South Africa	X	1.36	1.26	1.17	1.09	1.02	0.96	0.91	0.86
	Y	7.83	7.22	6.71	6.26	5.87	5.53	5.22	4.94
Philippines	X	1.14	1.06	0.98	0.92	0.86	0.81	0.76	0.72
	Y	12.21	11.32	10.50	9.80	9.17	8.63	8.15	7.74
Brazil	X	1.38	1.27	1.18	1.10	1.04	0.98	0.92	0.87
	Y	29.13	26.89	24.99	23.30	21.86	20.58	19.42	18.40
UK	X	1.20	1.10	1.03	0.96	0.90	0.85	0.80	0.76
	Y	7.98	7.35	6.85	6.38	5.99	5.63	5.32	5.04
Spain	X	1.20	1.11	1.03	0.96	0.90	0.85	0.80	0.76
	Y	5.58	5.15	4.78	4.46	4.19	3.94	3.72	3.53
Germany	X	1.18	1.09	1.01	0.95	0.88	0.83	0.79	0.75
	Y	9.72	8.97	8.33	7.78	7.28	6.86	6.48	6.16

Fig. 8.

Relationship between vaccine efficiency and the proportion of human population to be vaccinated for completely preventing COVID-19.

4. Discussion

We have developed a delay differential system to simulate COVID-19 evolution dynamics. We evaluated the roles of adaptive protection behaviors and vaccination situations in curbing COVID-19 infections, by focusing on recent outbreaks in eight countries with most reported cases.

Our model is in accordance with deterministic and compartmental principle, which captures the intrinsic rules of people’s transition across different states. In this model, we measured vaccination by shifting people from susceptible state to immune state. Such tackling technique is similar to existing studies (Moore et al., 2021, Han et al., 2021). Other studies also considered that vaccination can potentially reduce the probability of developing COVID-19 symptoms upon infection and the infectiousness of vaccinated individuals (Matrajt et al., 2021). Here we added a time delay to account for the duration between vaccination and immunity production. Moreover, we quantified the influence of protective behaviors by inserting an activity function $f$ into the infectivity, in which $f$ is a non-linear decreasing expression of infection scale. Since $f$ has time-space heterogeneity and there is no standard reference, inspired by existing studies (Eksin et al., 2019, Xiao et al., 2015), we proposed four formulas of $f$ and chose the specific one according to fitting goodness. The protection behavior can be viewed as adaptive NPI performance. Knowing that adopted intervention would modify the transmission parameters, most existing studies modeled it by a time-varied infectivity (i.e., a piecewise function of time), in which intervention can reduce the infectivity (Tang et al., 2021, Bertuzzo et al., 2020). In such case, more uncertain parameters are needed, which may produce extra fitting difficulty. Here we measured the intervention by activity function $f$ with less uncertain parameters and obtained good fitting, indicating the reliability of our model.

By validating the proposed model to fit the surveillance data in eight countries by MCMC algorithm, we clarified the influencing mechanism of adaptive behavior and vaccination, which offers the following insights for guiding COVID-19 control.

First, the adaptive protection behaviors play a significant role in preventing human infection of COVID-19. It should be noted that all these countries have implemented similar NPI measures from early 2020, and gradually reduced interventions since 2021 to different levels. Our results indicated that if without adaptive behaviors, the total infection in these countries could be 3.68, 26.16, 15.23, 4.23, 7.26, 1.65, 5.51 and 7.07 times as large as reported. Our estimation of NPI outcome is consistent with existing research (Teslya et al., 2020, Tang et al., 2021, Shabat et al., 2021). Hence it is very necessary to maintain media publicity and government guidance during epidemic transmission. Changing adaptive protection behavior may lead to second explosive outbreak. Yet we estimated that the protection yields the feature of short-term response in many countries, which is only dependent on current infections. More comprehensive protection behaviors could results in less cases.

Second, the pattern of vaccination with different efficiency in alleviating COVID-19 infection is further clarified. Promoting vaccination and enhancing vaccine efficiency can quickly and efficiently suppress human infection. To obtain herd immunity, all people should be vaccinated if vaccine efficiency is less than 70%. The average proportions of people with immunity in these countries should be larger than 84% with adaptive protection behaviors or 89% without protection behaviors. Hence no matter how non-pharmaceutical intervention is implemented, collective immunity must reach a high level for disease prevention. Existing studies also claimed that dynamic allocation of vaccines could be a key factor in reducing COVID-19 burden (Matrajt et al., 2021, Chhibber et al., 2022, Han et al., 2021). Moreover, we found that vaccination rate is heavily dependent on vaccine efficiency. That is similar to recent work (Matrajt et al., 2021), in which they indicated that optimal allocation of vaccine vitally depends on the single-dose efficacy (Matrajt et al., 2021). We further clarified the relationship between vaccination rate and vaccine efficiency by quadratic polynomials (see Fig. 8).

Our paper has the following limitations: (1) as an average reflection of collective transmission pattern, the model with fixed parameters is based on deterministic compartmental principle, and the stochastic features originated from parameter diversity and individual difference were not considered. (2) the adaptive behavior function and model parameters could not entirely capture the diversity and heterogeneity of human behaviors and disease transmission in space and time; and (3) our model did not take into account all potential factors (such as virus variant, reinfection, age composition, birth and death), and our analysis relied on fitting results, which may yield certain deviation from reality. It should be noted that reinfection has been detected in some case reports (Ren et al., 2022), and some studies took this into account by using SEIRS model framework (Krueger et al., 2022). Base on current limited information of reinfection (i.e., small reinfection rate, and large duration between the first infection and reinfection), it seems that reinfection has little influence on the transmission process simulated by our model (see Figure S2). Another reason could be the short time of our simulation. Moreover, the vaccination coverage level in our study is usually larger than the $R_0$-dependent threshold (i.e., $(1-1/R_0)/\vartheta$). There are two indicators accounting for this, that is, (1) modeling framework: our model considered the time lag between vaccination and immune response, and it involved a nonlinear function to match the effects of human protection behaviors, which played a big role in preventing human infections, but this function became zero when linearizing the model in calculating the next generation matrix; and (2) computation method: the criteria to judge disease elimination in our simulation is that the number of new cases in October 2021 will not exceed 100, which certainly require more vaccination coverage to achieve this criteria in such short time.

In summary, we have constructed an epidemic model for identifying the transmission patterns of COVID-19 in eight countries, with essential impacts of adaptive protection activity and vaccination. We concluded that people behavior and vaccination rate/efficiency are always the key elements that shape the complex occurrence mode and its future trends. People protection behaviors can hold back and prevent infection (particularly in early stage), but vaccination is still the best strategy in the long run.

CRediT authorship contribution statement

Zhaowan Li: Methodology, Validation, Visualization, Data curation, Writing – original draft. Jianguo Zhao: Validation, Data curation, Writing – review & editing. Yuhao Zhou: Software, Investigation, Writing – review & editing. Lina Tian: Data curation, Visualization. Qihuai Liu: Methodology, Resources, Funding acquisition. Huaiping Zhu: Conceptualization, Project administration, Writing – review & editing. Guanghu Zhu: Conceptualization, Methodology, Resources, Funding acquisition, Supervision, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the Supplementary material related to this article.

MMC S1

Fitting results, parameter distributions used in sensitivity analysis, and simulation with reinfection.