Abstract
We explored the impacts of a mathematics prerequisite on student success in Introductory Biology, focusing on students historically underserved in science, technology, engineering, and mathematics (STEM). Specifically, we studied Introductory Biology student outcomes 5 years before and 6 years after adding the prerequisite. Students who had not previously passed Intermediate Algebra had a 54.91% chance of passing Introductory Biology, compared with a 69.25% chance for students who had passed this math course. Furthermore, we found a disproportionate benefit of passing the math course for Pell Grant recipients. When considering pre- versus post-prerequisite terms of Introductory Biology, we found pass rates were significantly higher after the mathematics prerequisite was required, but grades were not. After the mathematics prerequisite, enrollments in Introductory Biology temporarily decreased in comparison to a similar chemistry course and the college’s overall enrollments, a potential cost to students. Pell Grant recipients and women took Introductory Biology at the same rate as before, and contrary to our hypothesis, we saw the proportion of persons excluded due to ethnicity or race (PEER) students enrolled in Introductory Biology was higher after the implementation. This study provides a model for assessing prerequisites in a local context and contributes evidence that mathematical prerequisites can benefit students.
INTRODUCTION
Prerequisites, although commonplace across college curricula, are controversial due to a variety of costs and benefits to students. At their best, prerequisite courses (called “prereqs” hereafter) aim to give students the highest likelihood of success in courses by ensuring students are prepared to maximize learning. At their worst, prereqs represent additional hoops for students to jump through en route to their academic and career goals, ones that may block them from completing their desired academic paths. The obstacles that prereqs represent to students vary but may include an increase in the number of courses required or adding additional terms to their degree completion (Boatman and Long, 2018; Ngo and Melguizo, 2020). Prereqs might also increase the total cost of the degree and work against financial aid time limits, hindering degree completion. Economically disadvantaged students might be particularly affected, as they are already less likely to complete their academic pathways compared with wealthier students (Paulsen and John, 2002). Because the benefits may be great but the costs of prereqs can also be high, Shaffer et al. (2016) encouraged thoughtful consideration of prereqs before implementation and rigorous assessment in a local context (e.g., at each institution) to determine whether their benefits outweigh their costs.
There is no clear consensus from the science, technology, engineering, and mathematics (STEM) education literature that prereqs result in benefits for students such as promoting student success in subsequent courses or better preparing students for content and rigor of future courses. The limited research addressing potential benefits provides contradictory results (Sato et al., 2017). A few studies, mostly focused on bachelor’s degree programs, support the position that prereqs positively impact student success. For example, when the University of South Florida began enforcing prereqs in their upper-division biology courses, failure rates (grades “D” and “F”) dropped by 18%, and withdrawal rates dropped by 21% (McCoy and Pierce, 2004). In a different analysis, medical students who completed undergraduate anatomy courses earned higher grades in similar courses in medical school (Forester et al., 2002). However, a greater number of studies show a negligible impact of prereq courses on content familiarity in a subsequent course. For example, using familiarity scales and student perceptions of learning, several studies found that material from various biology prereqs was only sometimes retained and useful in subsequent biology courses (Shaffer et al., 2016, 2018; Sato et al., 2017). In a pathophysiology course, there was no difference in course grades between students who completed the prereq and those who did not (Pieronek, 1991). Finally, there was no difference in course grades between biochemistry students who did or did not take the prereq organic chemistry class (Wright et al., 2009). In our review of the literature, we found no published studies assessing the effects of a mathematics prerequisite for an introductory biology course.
Although there is mixed evidence of the benefits of prereqs to students, there are important concerns about costs, particularly when we consider the costs through an equity lens. In addition to potentially wasting students’ time and money, prereqs might disproportionately impact students who are and have been historically underserved in STEM. These students are more likely to experience barriers such as stereotype threat (Beasley and Fischer, 2012), a lower sense of belonging (Trujillo and Tanner, 2014), and a weaker science identity (Hazari et al., 2013). A prereq may amplify those experiences and may also serve as a barrier to progress in the major. These barriers may have complex and unexpected intersections; for example, a student who already has a lower sense of belonging in biology and experiences stereotype threat in math classes may interpret the existence of a math prereq as a signal that they do not belong in this major. Therefore, to assess the implementation of a prereq equitably, it is critical that these intersecting barriers be explored.
A potential costly impact of prereqs from a diversity and equity standpoint is the assumption that they work through “elimination of weak students” (Marcal and Roberts, 2000). This gatekeeper mentality, viewing prereqs as rites of passage that filter out students who are unprepared for future courses in the discipline, relies on inaccurate assumptions about students who are filtered out. Historically, the gatekeeper mindset assumes that the students who are “weeded out” of these courses are those who did not truly want to be there or lacked the skills or motivation for success. However, evidence shows that these courses disproportionately weed out historically underserved students instead (Harris et al., 2020; Thompson, 2021). Gatekeeping may be harmful to overall numbers of STEM graduates and disproportionately harmful to students from currently and historically marginalized groups, eliminating students who might have otherwise successfully completed a major.
The assessment of prereq course effectiveness in the context of community colleges is of particular importance because of the key role community colleges play in higher education. Community college students enter via open enrollment, which results in a student population with a wide variety of academic backgrounds. Prereq courses may therefore be particularly beneficial for student success in community colleges to ensure a common academic foundation. On the other hand, the gatekeeping nature of prereqs might be exacerbated in these contexts. Community college students are more diverse than students in 4-year colleges and universities across many demographic variables, including socioeconomic status, first-generation status, and race/ethnicity (www.aacc.nche.edu/research-trends/fast-facts). Given the student diversity in community colleges, the costs and benefits of a prereq may be amplified; thus, understanding the ramifications of requiring a prereq in a community college setting are of particular importance. Because community colleges host nearly half of all undergraduate students yet publish fewer than 1–3% of the studies in the biology education literature (Schinske et al., 2017; Lo et al., 2019), studies of the impacts of prereqs on students taking biology at community colleges are needed.
In this retrospective study, we explored the impacts of implementing a prereq for Introductory Biology (Intro Bio) through the lens of potential benefits to student success and potential costs, with a particular focus on students historically and currently underserved in STEM. The stakes of implementing a prereq course are particularly high if the cost of that prereq leads to exclusion of a diverse pool of future scientists and further contributes to systemic biases. Given the potential for financial, temporal, and social costs, prereqs must be studied closely and considered with skepticism before and after implementation to ensure they provide benefits with minimal costs. In an attempt to address the very low passing rate in Intro Bio—sometimes below 60%—faculty at the community college where this study was conducted reviewed student data and chose to implement a mathematics prereq. We use this opportunity to answer three questions about the costs and benefits of this prereq. RQ1: Did students who passed Intermediate Algebra (before it was required) earn higher grades in and/or pass Intro Bio at a higher rate? In a post hoc attempt to determine whether the prereq was justified, we compared two groups of students before implementation of the prereq: those who had passed or tested out of (abbreviated as “passed” for ease of reading hereafter) Intermediate Algebra (Int Algebra) and those who had not. RQ2: Are pass rates and course grades in Intro Bio higher after students were required to have passed the prereq? We examined changes in student success before and after implementation of the prereq. RQ3: Did implementation of the math prereq negatively affect students? To assess unintended costs of implementing the prereq, we compared student enrollment and demographics before and after implementation of the prereq.
METHODS
Institutional Context
This study was conducted at a very large open-enrollment community college on the West Coast (Carnegie Foundation for the Advancement of Teaching, 2011). At the time of this study, the college used placement tests for student placement in math, reading, and writing classes. Students come from a wide variety of backgrounds, including academic career level (homeschool, pre–high school diploma, dual credits, start-and-stop enrollment, and postbaccalaureate STEM credit toward professional school applications). While the list of demographic variables that may impact student success in a community college Intro Bio course is long, we focused on several that are common and well documented in the literature: persons excluded due to ethnicity or race (PEERs), first-generation college students (FGN), Pell Grant recipients, and women.
Course Context
The four-credit course, Intro Bio, is the first in a yearlong sequence designed for students intending to transfer to 4-year universities who will major in biology or a closely related discipline. Course content includes cellular biology, evolution, genetics, and metabolism, and a laboratory component is included. Quantitative biology skills include graphing, proportional reasoning, probability, and basic exponents.
Preliminary research into potential variables affecting Intro Bio pass rates and grades was conducted in Fall 2011 (unpublished data). Passing was considered a grade of 1.7 (equivalent to a “C−”) and above. In response to low midterm assessment scores, an analysis by instructors in 2011 identified student background in mathematics as correlated with academic achievement. Previous analysis of self-reported chemistry background among Intro Bio students indicated it was a poor predictor of student success in Intro Bio.
In 2012, Int Algebra was implemented as a prereq for Intro Bio with the intention of improving pass rates and course grades. Int Algebra or higher was chosen because it is the prereq for the Introductory Chemistry (Intro Chem) course at the college and is required for a majority of the programs/majors that Intro Bio students pursue. Thus, most students who take Intro Bio also need to pass Int Algebra; the prereq did not add a course to most students’ requirements, but rather affected the order in which courses need to be taken. Content in Int Algebra includes polynomials, coordinate graphing, rational and radical equations, and quadratic functions. Mathematical skills used in Intro Bio, such as graphing, graph interpretation, and proportional reasoning, are learning outcomes or placement test topics for math courses lower than Int Algebra. Probability, used in calculating simple genetic outcomes, is not a learning outcome until classes that come after Int Algebra.
Comparison Groups
RQ1: Did Students Who Passed Int Algebra before Taking Intro Bio (before It Was Required) Earn Higher Grades in and/or Pass Intro Bio at a Higher Rate?
Before implementation of the prereq, two groups of Intro Bio students existed (groups 1a and 1b): those who had passed Int Algebra before enrolling in Intro Bio and those who had not. We compared the course outcomes of these students when pursuing the answer to RQ1 (Table 1).
TABLE 1.
Comparison groups and outcomes measured for each of the three research questions in our study
| Research questions | Comparison groups | Outcomea | Results |
|---|---|---|---|
| RQ1: Did students who passed Int Algebra (before it was required) earn higher grades and/or pass Intro Bio at a higher rate? | Preimplementation only (2008–2012)
|
|
Figure 1 Table 3 |
| RQ2: Are pass rates and course grades in Intro Bio higher after students were required to have passed the prereq? |
|
|
Table 4 |
|
|||
|
|||
| RQ3: Did implementation of the math prereq negatively affect students? | Preimplementation (2008–2012) vs. postimplementation (2013–2018)
|
|
Figures 2 and 3Tables 5 and 6 |
aAll outcomes were disaggregated by student identity, including PEER, FGN, Pell Grant recipient, and binary gender.
RQ2: Are Pass Rates and Course Grades in Intro Bio Higher after Students Were Required to Have Passed the Prereq?
To answer RQ2, we made three comparisons (Table 1). First, we compared student outcomes (Intro Bio course grade and probability of passing Intro Bio) for all students pre-prereq and all students post-prereq (groups 1 and 2). We expected that, after implementation of the prereq, students would have higher course grades and higher probability of passing Intro Bio. Next, we compared students who did pass Int Algebra before taking Intro Bio pre-prereq with all students post-prereq (groups 1a and 2). We expected that there should be no difference between students who did pass Int Algebra pre-prereq and all students post-prereq (because after the prereq was implemented, all students would have passed Int Algebra). Finally, we compared student outcomes for students who did not pass Int Algebra before taking Intro Bio pre-prereq with outcomes for all students post-prereq (groups 1b and 2). We expected that, after implementation of the prereq, students should have higher course grades and higher probability of passing Intro Bio than students who did not pass the prereq before it was implemented.
RQ3: Did Implementation of the Prereq Negatively Affect Students?
Enrollment and demographics at the college were changing during the time of this study, thus we could not simply compare enrollment and demographics of Intro Bio before and after implementation of the prereq. The college experienced a steep increase in enrollment in 2011, followed by a steep decline related to local economic conditions. Thus, we used enrollment in Intro Chem, a course that is unlikely to be impacted by a prereq for Intro Bio, as a direct comparison that controls for background changes unlikely to be impacted by the prereq (Table 1). Intro Chem is a five-credit course and the first in a yearlong general chemistry series designed for students intending to transfer who will major in chemistry, biology, or a closely related discipline. For simplicity, we only considered enrollment in Intro Bio and Intro Chem in the Fall quarter.
Data Collection
Deidentified records were collected from 1416 community college students enrolled in Intro Bio in academic years 2008 through 2018, which began in Fall 2007 and ended in Spring 2018. This represented a period of 5 years immediately before the implementation of the prereq and the 6 years immediately following the implementation of the prereq. See Table 2 for a summary of student demographic data.
TABLE 2.
Total enrollment, student demographic variables, and pass rates for Intro Bio students, Fall 2007 to Fall 2017 (academic years 2008–2018; N = 1416 students)
| Academic yeara | Total enrollment N (no. sect.b) | Student demographics | ||||
|---|---|---|---|---|---|---|
| Female % | First generation % | Pell Grant recipient % | PEER % | Passed Intro Bioc % | ||
| 2008 | 117 (4) | 58 | 38 | 37 | 15 | 68 |
| 2009 | 126 (4) | 53 | 46 | 34 | 12 | 72 |
| 2010 | 168 (5) | 53 | 49 | 43 | 9 | 67 |
| 2011 | 155 (5) | 57 | 51 | 47 | 10 | 66 |
| 2012 | 156 (5) | 51 | 57 | 49 | 12 | 57 |
| 2013 | 132 (5) | 55 | 52 | 48 | 17 | 72 |
| 2014 | 95 (4) | 54 | 48 | 39 | 26 | 82 |
| 2015 | 104 (4) | 44 | 47 | 40 | 16 | 80 |
| 2016 | 102 (4) | 55 | 51 | 32 | 22 | 75 |
| 2017 | 137 (5) | 53 | 52 | 44 | 28 | 82 |
| 2018 | 124 (5) | 53 | 51 | 41 | 27 | 73 |
Dashed line indicates prereq implementation.
bno. sect = number of course sections offered in a given year.
Passed Intro Bio = course grade of “C−” or better
Student records used for this study included grades in each of the aforementioned classes, overall grade point average (GPA), and demographic attributes. A data management plan and IRB oversight (proposal no. 188 at Pacific Lutheran University) were completed to ensure responsible handling of student records.
Statistical Analysis
We tested our hypotheses by fitting multilevel regression models and identified the best-fitting model using model selection. Our outcome variables had different distributions, so for each, we fit a different kind of regression model (Theobald et al., 2019). For course grade and total enrollment, we fit linear regression models. For probability of passing, we fit logistic regression models. For enrollment composition (e.g., what proportion of total enrollment was PEER students), we fit binomial regression models.
We tested our hypotheses within a backward model selection framework. In all cases, we had a priori hypotheses including disproportionate effects of the math prerequisite on students from currently and historically underserved groups in STEM (Table 1 and Supplemental Table S1). Thus, we had a set of plausible candidate models and sought to make inferences using the best-fitting model (Burnham and Anderson, 2002). Note that we only ever fit models that included one demographic variable. While this strategy precludes testing hypotheses about students with intersectional identities, we felt this was the best approach given our total sample size.
Our backward model selection process involved two-steps. First, we identified the best random effect structure, allowing the intercept of our grouping variable to vary, not the slope. Second, we singularly removed fixed variables until the best-fitting, simplest, most parsimonious model was identified (Zuur et al., 2009). We used Akaike information criterion, with a small sample size correction (AICc) to compare models, favoring the simpler model with the lowest AICc. Models with AICc values within two units were considered identical, and the simpler model was preferred (Burnham and Anderson, 2002). Information criteria used to select all best-fitting models (exclusive of models that select the best random effect structure) are shown in Supplemental Table S1.
We used multilevel models (also known as hierarchical models, but as our grouping variables were not all hierarchical, we prefer the term “multilevel models,” in line with Gelman and Hill, 2007) to account for the nonindependence of our observations (Theobald, 2018). Starting with the most complex model that included an interaction between prereq implementation (before or after) and student demographics, we fit a multilevel model that included a varying intercept (hereafter random effect) for year, section, instructor, all combinations, or no random effect at all. We only tested varying intercept models, because we did not have an a priori reason to suspect that a prereq would have a different effect on any of those factors.
Once the appropriate multilevel structure (i.e., random effect structure) was identified, we fit separate models testing disproportionate effects of the prereq on students from singular demographic groups, because our sample size did not warrant testing for intersectional effects or controlling for one demographic characteristic while controlling for another. To select the best model, we singularly removed fixed effects, starting with the interaction, until the simplest, most parsimonious model was identified. We report parameter estimates as well as SEs from best-fitting models. Note that interpreting p values and t values from models after model selection is not wise, because model selection is more likely to return models with “significant” values; thus, in the one place we report p values, they are for corroboration only. We fit multilevel models using the lme4 package (Bates et al., 2015) in R v. 4.0.5 (R Core Team, 2021).
RESULTS
RQ1: Did Students Who Passed Int Algebra before Enrolling in Intro Bio (before It Was Required) Earn Higher Grades in and/or Pass Intro Bio at a Higher Rate?
To explore whether instituting a math prereq could help students in Introductory Biology, we looked at the time period before the Int Algebra prereq was implemented (2008–2012) and compared student outcomes for students who did and did not pass Int Algebra before taking Intro Bio. Figure 1A shows the range of cumulative GPAs of students entering Intro Bio disaggregated by whether or not they had passed Int Algebra (before implementing the prereq). Even though students with higher cumulative GPAs were more likely to pass Int Algebra, there were students from across the cumulative GPA distribution who did not pass Int Algebra. In these analyses, students without prior GPA (n = 104), without Pell information (n = 3), or without PEER information (n = 38) were removed from the corresponding analysis.
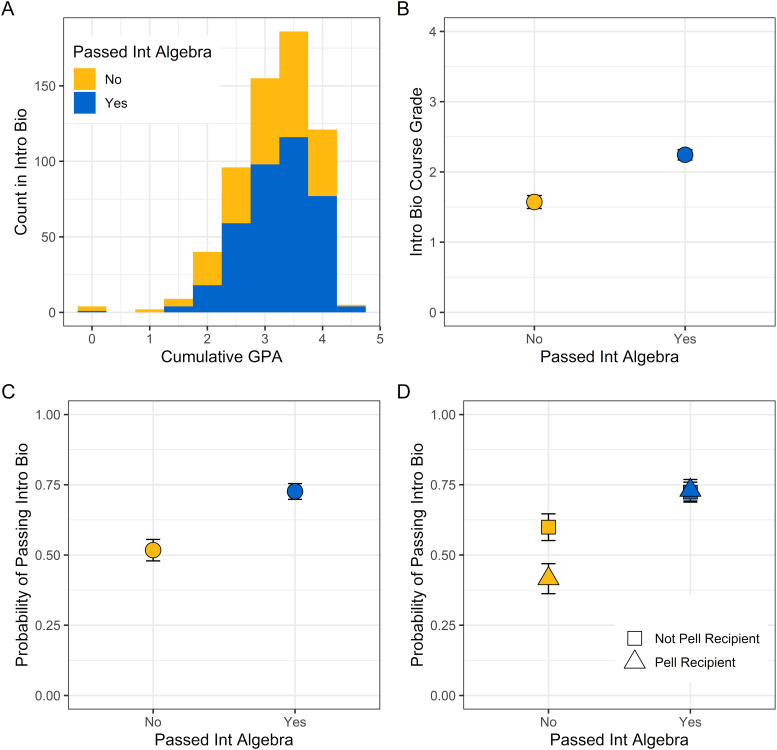
FIGURE 1.
Would a math prereq help students? Looking only at students who took Intro Bio before the Int Algebra prereq was instituted in 2013, students who completed or tested out of Int Algebra or a higher level of mathematics before taking Intro Bio earned higher course grades (4 = “A”, 0 = “F” or “W”) in Intro Bio than students who did not (B) and had a higher probability of passing Intro Bio (C). There was a disproportionate benefit of completing or testing out of Int Algebra before taking Intro Bio for Pell Grant recipients (D). Note: In D, there is no difference in the probability of passing Intro Bio between Pell recipients and non–Pell Grant recipients who both passed Int Algebra; thus the two data points for Pell Grant recipients and non–Pell Grant recipients who passed Int Algebra overlap. (B–D) Modeled results of the best-fitting model, not controlling for prior college GPA. Bars are standard error around the estimated mean. See Table 3 for quantitative results.
We found that students who passed Int Algebra before taking Intro Bio earned higher course grades in Intro Bio on average (Figure 1B and Table 3, columns 1 and 2) and had a higher probability of passing Intro Bio (Figure 1C and Table 3, columns 3 and 4) compared with students who did not pass Int Algebra before taking Intro Bio. These results are qualitatively similar with and without controlling for prior college GPA. Controlling for prior college GPA removes 104 students from the complete data set, and these students are likely first-year students who have not previously taken any college courses. We were initially leery of this potential bias, but the results are robust (reported in Table 3). For a student with an average GPA who had passed Int Algebra, our model predicted a grade increase of roughly 0.5 in the course GPA (Figure 1B and Table 3). This translates to approximately a difference in grade from about a “C” to a “B−”. Students who had previously passed Int Algebra had a 69.25% chance of passing Intro Bio compared with a 54.91% chance of passing for those who had not completed this mathematics course (Figure 1C and Table 3).
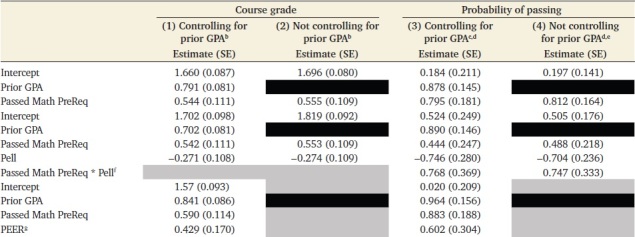
TABLE 3.
Quantitative effects of passing the Int Algebra before taking Intro Bio on course grade in Intro Bio (columns 1, 2) and the probability of passing Intro Bio (columns 3, 4), controlling for prior college GPA (columns 1, 3) or not controlling for prior college GPA (2, 4)a
|
aTable reports estimate with standard error of the estimate reported in parentheses. (Note that backward model selection was performed using AICc to identify the best-fitting model, so p values are not reported, nor should they be interpreted; Burnham and Anderson, 2002; Theobald, 2018.) See Supplemental Table S1 for a complete list of all the models that were tested and the results of model selection. For clarity, black fill indicates that variables were not tested in the model shown and gray fill indicates that variables were not retained in the final model.
bModels do not include random effects; tested varying intercepts (and constant slopes) for Year, Section, Instructor, and all combinations.
cModel includes a varying intercept for instructor; tested varying intercepts for Year, Section, Instructor, and all combinations.
dEffects reported as logodds. Passing was considered a grade of 1.7 (equivalent to a “C−”) and above.
eModel includes a varying intercept for Section; tested varying intercepts for Year, Section, Instructor, and all combinations.
fThe Pell*Prereq interaction was never retained in the final models for course grade but was retained in final models for probability of passing.
gPEER status was never retained in final models that did not control for prior GPA, so it is not reported here.
Furthermore, there was a disproportionate benefit of passing Int Algebra for students who were Pell Grant recipients. Specifically, our model retained an interaction between Pell Grant recipient status and passing Int Algebra, showing that Pell recipients who passed Int Algebra were equally as likely as non–Pell recipients to pass Intro Bio, whereas Pell recipients who did not pass Int Algebra were disproportionately less likely to pass Intro Bio than their non–Pell Recipient peers (Figure 1D and Table 3, columns 3 and 4). Passing or testing out of Int Algebra before taking Intro Bio disproportionately benefited Pell Grant recipients, whose probability of passing without Int Algebra was below 50% and nearly 75% if they had Int Algebra. There were no disproportionate effects of the math prereq on course grade for students from PEER groups, Pell Grant recipients, FGN students, or women. These effects were qualitatively identical when controlling for prior college GPA or not (Table 3, odd columns vs. even columns).
RQ2: Are Pass Rates and Course Grades in Introductory Biology Higher after Students Were Required to Have Passed the Prereq?
To assess the impact of the prereq after it was implemented, we looked at student outcomes (course grades and probability of passing) across three comparisons:
All students before the prereq was implemented compared with all students after the prereq was implemented.
Students who passed Int Algebra before the prereq was implemented compared with all students after the prereq was implemented.
Students who did not pass Int Algebra before the prereq was implemented compared with all students after the prereq was implemented.
Counter to our prediction, when comparing all students in the pre- and postimplementation groups, there was no difference in grades, but consistent with our predictions, there was a significant improvement in pass rates (Table 4). Furthermore, consistent with our prediction, there was no difference in course grade or the probability of passing Intro Bio between students who did pass Int Algebra before the prereq was implemented and all students after the prereq was implemented (Table 4, middle column). Finally, consistent with our prediction, students after the prereq was implemented had higher course grades and higher probability of passing Intro Bio than students who did not pass the Int Algebra before the prereq was implemented (Table 4, final column).
TABLE 4.
Student outcomes before and after implementation of the math prerequisitea
| All students prediction: after prereq > before prereq | Did pass Math pre vs. all post 2013 Prediction: after prereq = before prereq | Did not pass Math pre vs. all post 2013 Prediction: after prereq > before prereq | |
|---|---|---|---|
| Grade in Intro Bio | |||
| After Prereq (ref: before prereq) | 0.124 (0.089) p = 0.163 | −0.0574 (0.097) p = 0.552 | 0.483 (0.112) p = 1.7e−5 |
| ΔAICcb | 3.196 | 4.559 | −11.346 |
| Probability of Passing Intro Bio | |||
| After Prereq (ref: before prereq) | 0.462 (0.163) p = 0.0047 | 0.145 (0.194) p = 0.452 | 1.047 (0.200) p = 1.67e−7 |
| ΔAICcb | −5.583 | 1.469 | −21.491 |
aStudent outcomes were more favorable after the implementation of the math prereq. Estimates of effects are on a linear 4.0 scale (Grade in Intro Bio) or on the logodds scale (Probability of Passing). Standard error of the estimate shown in parenthesis, boldface indicates significance to a <0.05. Boldface and p values shown for corroboration with backward selection and change in AICc. (Note that backward model selection was performed using AICc to identify best-fitting model, so p values should not be interpreted; Burnham and Anderson, 2002; Theobald, 2018.)
bΔAICc comparing the model with and without an indicator for before/after implementation of the prereq (with – without, so negative values indicate that the model with the before/after indicator has superior fit); all models control for prior GPA and include a varying intercept for instructor.
RQ3: Did Implementing a Math Prereq Negatively Affect Students?
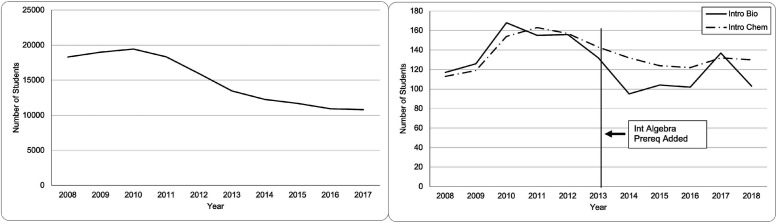
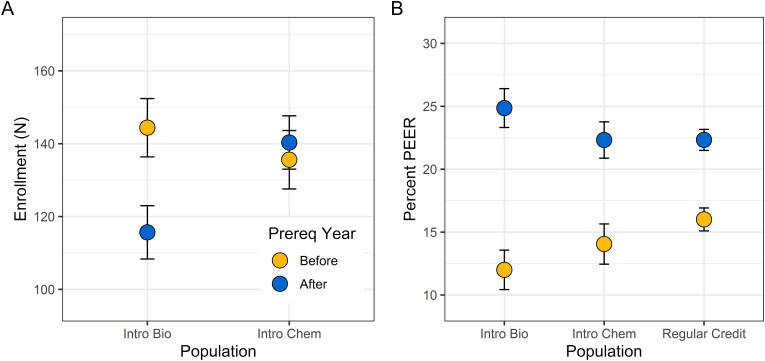
We predicted that enrollments in Intro Bio would be negatively affected, because before implementation of the prereq, an average of 39.1% (SD = 2.07%) of students per year would not have been able to enroll because they had not passed Int Algebra. After implementation of the Int Algebra prereq, enrollment in Intro Bio declined disproportionally compared with enrollment in Intro Chem (Figures 2 and 3A, and Tables 5 and 6). We also examined the extent to which students from historically and currently marginalized groups (including PEER students, FGN students, Pell recipients, and women) might be affected by the prereq course and found no negative effects on enrollments. In fact, students from PEER groups made up a larger proportion of the student body in Intro Bio across the six years after the implementation of the prereq; this increase was larger in Intro Bio than it was in Intro Chem or the college overall (Figures 2B and 3B and Table 6). The total number of students enrolled in Intro Bio and the college overall was lower after the prereq was introduced, and this reduced enrollment was not observed in Intro Chem in the same time period (Table 6). The proportion of enrolled students who were PEER students was higher for all three populations (Intro Bio, Intro Chem, and the college) after the prereq was instituted (Table 6). This increase in proportion of PEER students from pre to post was largest in Intro Bio (Table 6). Taken together, in our community college setting, implementing a math prereq for Introductory Biology improved student grades and pass rates in Introductory Biology without disproportionately negatively impacting students from historically and currently marginalized groups in STEM.
FIGURE 2.
Enrollment trends comparing the whole college (left) with Intro Bio and Intro Chem (right). Whole-college data are for students registered for credit and Intro Bio and Intro Chem data include Fall term only.
FIGURE 3.
What are the unintended consequences of the math prereq? Compared with enrollment in Intro Chem, there is a decline in enrollment in Intro Bio after implementation of the prereq (A). Counterintuitively, despite a decrease in enrollment in Intro Bio and an overall increase in the percent of PEER students at the college over this time period (Regular Credit), there is a disproportionate increase in the percentage of PEER students in Intro Bio after the implementation of the prereq (B). Data in B are for Fall quarters for Intro Bio and Intro Chem, and all quarters for the whole college.
TABLE 5.
Enrollment before and after the implementation of the math prerequisite: mean and SD (in parentheses) of Fall quarter (Intro Bio and Intro Chem) and annual (whole-college) total enrollment, percent PEER students and percent Pell Grant recipients of total enrollment, averaged over the years before the prereq was instituted (2008–2012) and after the prereq was instituted (2013–2018) shown for Intro Biology, Intro Chem, and whole college
| Mean N (SD) | Mean % PEER (SD) | Mean % Pell (SD) | |
|---|---|---|---|
| Intro Bio | |||
| Before | 144 (19.7) | 12.4 (2.30) | 42.0 (6.40) |
| After | 116 (16.2) | 24.8 (5.19) | 40.7 (5.35) |
| Intro Chem | |||
| Before | 136 (14.9) | 14.0 (2.92) | 41.4 (8.38) |
| After | 140 (14.7) | 22.3 (3.83) | 41.8 (6.43) |
| College | |||
| Before | 17,072 (2249) | 16.0 (2.12) | 43.8 (10.6) |
| After | 13,761 (2619) | 22.3 (1.97) | 42.7 (7.06) |
TABLE 6.
Relationship between student enrollment and math prerequisitea
| A. Total number of studentsb | B. Proportion PEER of total enrolledc | |
|---|---|---|
| Intercept | 115.667 (7.316) | 24.859 (1.547) |
| Before Prereq (ref: After Prereq) | 28.733 (10.825) | −12.859 (2.203) |
| Intro Chem (ref: Intro Bio) | 24.667 (6.872) | −2.539 (1.766) |
| Whole College (ref: Intro Bio) | −2.530 (1.313) | |
| Before Prereq: Intro Chem | −33.467 (10.193) | 4.589 (2.552) |
| Before Prereq: Whole College | 6.536 (1.839) |
aQuantitative effects showing the correlation between total number of students enrolled in Intro Bio and Intro Chem before and after the prereq was instituted (A) and the correlation between proportion of the student population who identify as PEER students in Intro Bio, Intro Chem, and the College (B). Gray cells indicate that this contrast was not made. Effects from best-fitting multilevel linear, which include varying intercept for year. Standard error of the estimate reported in parentheses. (Note that backward model selection was performed using AICc to identify the best-fitting model so p values are not reported, nor should they be interpreted; Burnham and Anderson, 2002; Theobald, 2018.)
bThe total number of students enrolled in Intro Bio was lower after the prereq was instituted, and this negative effect was not observed in Intro Chem across the same time period.
cThe proportion of enrolled students who were PEER students was higher for all three populations (Intro Bio, Intro Chem, and the college) after the prereq was instituted. This increase in proportion PEER students from pre to post was largest in Intro Bio.
DISCUSSION
This study is the first we know of to show benefits of a prerequisite college math course on student success in Intro Bio, but it is not the first to observe math course effects on academic success in other contexts. For example, completion of advanced mathematics in high school was a greater predictor of student success in introductory business courses than prior course work in economics or accounting (Alcock et al., 2008). In other studies, a combination of mathematics and English was linked to success in an accounting class (McCarron and Burstein, 2017), and ACT math scores predicted success in computer science classes (Butcher and Muth, 1985). This “mathematics effect” (McCarron and Burstein, 2017) is not universal, however. Studies of chemistry student success and math prerequisites are mixed. One study found that a math prereq did not correlate to success in a chemistry course (Wilson, 1994), while an open-enrollment university found a math prereq did correlate to greater student retention and success in chemistry (Donovan and Wheland, 2009). Additionally, a statistics prereq had no meaningful impact of achievement in a follow-up research course for nursing students (Grace and D’Aoust, 2006). Given these mixed results in the literature of a “math effect,” it is notable that we saw a benefit to students and that Pell Grant recipients particularly benefited in terms of probability of passing the class.
Although these results are encouraging, the reason for the positive effect we report remains unknown. The learning outcomes for Int Algebra do not correspond to any specific mathematics skill used in the Intro Bio curriculum, thus a direct benefit of the prereq cannot be presumed. That said, there are many possible indirect benefits of Int Algebra for Intro Biology. For example, quantitative skills used by students working through population growth equations or simply additional number sense that is gained from Int Algebra. In addition to possible indirect effects of math on biology, students with more experience in college might have greater success; this could play out in Intro Bio if the prereq forces students to gain more college experience before enrolling. The benefit of college experience may be enhanced in the context of community colleges, which are open-enrollment institutions that attract a broad diversity of students with varying academic preparations. More investigation into the possibilities of indirect benefits and/or the benefits of additional time in college are warranted. Some guiding questions include: Are there skills learned in Int Algebra that transfer easily to quantitative content in biology? Do students build strong study habits in the math course that specifically prepare them to succeed in Introductory Biology? Do students who experience math course success become more likely to succeed in other STEM courses due to increased confidence, the development of a growth mindset, or a stronger sense of belonging (Canning et al., 2021)? If it is not a matter of specific mathematical skills preparing students for Intro Biology success, it may be a matter of conditional reasoning skills (Attridge and Inglis, 2013). Conditional reasoning allows a thinker to understand statements such as “if x, then y.” These skills are developed by mathematics course work and may benefit Introductory Biology students (Attridge and Inglis, 2013). Addressing such questions may lead to more targeted interventions than a prereq, which could work to improve student success in Intro Bio (e.g., a modular skills unit at the beginning of Intro Bio or changes to advising recommendations).
Our model supported most of our predictions: Implementation of the math prereq led to higher pass rates overall, and students who took Intro Bio after implementation of the math prereq had higher grades than those who took Intro Bio before implementation of the prereq without having taken Int Algebra (Table 4). We did not find indications of grade inflation in Intro Bio over this time, and students who had taken Int Algebra before Intro Bio before implementation of the prereq had similar pass rates and grades in Intro Bio compared with students who took biology after implementation of the prereq (Table 4). One prediction was not supported: Course grades did not improve when we compared all students before with all students after implementation (Table 4). This may in part be due to the fact that withdrawals, which count against the pass rate, are not included in grade averages, allowing grade averages to remain similar despite different pass rates. Another possibility may be that grading—even when grades are not based on a curve—is very often relative to who is in the class. Intro Bio grades at this college are not scaled such that there is a fixed median but rather assigned based on points earned. Nonetheless, which students are in the class influences the overall shape of the grade distribution.
The decrease in DFW rates (i.e., the number of students who earn a “D” or an “F” or withdraw from the class) after implementation of the prereq is a clear benefit to students: Improvements in both grade point average and probability of passing the class (i.e., earning credits) may be of personal significance for students and important for their future academic goals, including toward transfer to 4-year colleges and acceptance in professional schools. A recent study of achievement gaps in introductory chemistry found that historically and currently marginalized groups in STEM who earn a grade of “C−”or lower are less likely than well-represented students to persist in the chemistry major, but underserved students with a “C” or above are more likely to persist (Harris et al., 2020). This shift in grade from a “C−” to a “C” seems to move students into a “hyperpersistent zone” or a level of success that makes underserved students more likely to continue in the major. If the prereq better prepares students to pass Intro Bio the first time they take it, this might have a similar impact on student success in the long run, though it would be difficult to track posttransfer from the community college context. At a minimum, reduced DFW rates directly reduce the financial and time costs of a degree by avoiding situations in which courses need to be repeated.
Although the benefits of the prereq were clear, we were concerned about potential unintended costs to students, particularly those from historically and currently marginalized groups in STEM. We were relieved to detect no decrease in enrollment percentages of students from these groups. Instead, we measured a relative increase in PEER students’ enrollment in Intro Bio after implementation of the math prereq when compared with enrollments in a comparable STEM introductory sequence course (General Chemistry) and the college’s enrollment as a whole (Figure 3). We also saw a larger positive impact of Int Algebra for Pell Grant recipients when we compared students who had passed Int Algebra with students who had not passed before the prerequisite implementation (Figure 1D). Finally, when we assessed changes in enrollment postimplementation, Intro Bio decreased on average more than Intro Chem but less than the college overall, and the timing of enrollment changes in Intro Bio was not closely associated with the implementation of the prereq (Figures 2 and 3A and Tables 5 and 6). Enrollment is sensitive to many variables not included in our study, though we cannot rule out the impact of prereq implementation. Overall, the results shown here support the continued use of the math prereq with regularly scheduled re-evaluation to monitor for reduced positive or new negative impacts on student success.
One of the major unintended costs that remains a concern is the potential that Int Algebra is acting as gatekeeping course, shifting the barrier from Intro Bio to an earlier course. The question of whether the barrier has shifted to an earlier course is one that is extremely difficult to answer directly. Our study did not have access to students who might have enrolled in Intro Bio but did not due to the prereq. Indirectly, however, we have evidence of congruence between the enrollment of the college overall and the enrollments of Intro Bio and Intro Chem (Figure 2), suggesting that implementation of the prereq did not cause a reduction in enrollment in Intro Bio, as would be expected if the prereq simply shifted the barrier to success from Intro Bio to Int Algebra. Additionally, Int Algebra is a required course in the mathematics pathway for most majors that include Intro Bio, so it would be a necessary course whether or not it served as a prerequisite for Intro Bio, minimizing the potential cost of the prerequisite to the order of courses rather than the addition of a course.
How will state and national changes to developmental course offerings impact prerequisites in Introductory Biology courses? To date, our community college still offers developmental course work for students placing below college-level mathematics, reading, and writing skills. The California Acceleration Project and state law banning nontransferable courses at universities by 2018 and community colleges by 2019 (Colvin, 2020) is a way to reduce costs to students and increase student degree completion. But if the results of this study are broadly applicable, such policies may discourage the local use of math as a prereq for introductory STEM courses and may actually have negative impacts on students by making them less likely to pass introductory courses in their major, thus costing them time and money and discouraging them from pursuing STEM degrees. Research supports using multiple measures for community college math placement, because when placement is based solely on test scores, students may be placed as many as three levels below their previously completed high school math course work (Ngo and Melguizo, 2016), costing them additional time and money. The use of a mathematics course as a prerequisite for Intro Bio requires re-evaluation when changes to mathematics course availability and mathematics placement processes occur.
Limitations and Future Studies
Although our results support the use of a math prereq for Introductory Biology in the context of this open-enrollment community college, these results cannot address the costs and benefits of widespread implementation of a math prereq. In agreement with Shaffer et al. (2016), we maintain that each institutional context is unique and requires assessment of the impacts of prereqs on both student success and demographic composition. For example, in some colleges and universities, all incoming students have had the equivalent of intermediate/college algebra in high school, and thus a similar math prereq would likely have little to no impact on student success in subsequent courses. Furthermore, the potential costs and benefits of a prereq may differ substantially among institutions due to differences in degree tracts, funding models, and student bodies.
There are also potential costs of prereqs that cannot be addressed in the current study. The implementation of a math prereq may have caused some students to delay their enrollment in Introductory Biology by up to a year, or more if multiple attempts were needed to complete the prereq, thereby increasing their time in school and the financial costs of their education, both of which may be barriers to their long-term completion of their educational goals. Longitudinal studies and student surveys of experiences could uncover hidden costs that we are unable to see in this retrospective analysis.
Importantly, the institution studied here changed significantly during the course of this time period. Community college enrollments are particularly sensitive to economic conditions, and student populations vary with job availability (Foote and Grosz, 2020), and we see impacts of the 2008 economic recession and the years following in enrollments during the course of this study. Finally, student demographic data-collection methods change over time, and our college currently does not track factors like the numbers of gender nonbinary students, the population of postbaccalaureate students, or other populations of students who may be currently underserved.
This study assessed the implementation of one prereq math course for one community college Introductory Biology course. Addressing similar questions at other community colleges and universities over different time periods would inform the broader applicability and usefulness of math prereqs. It would also be interesting to consider why the math prereq works in this context. Is a lack of quantitative reasoning skills a barrier for success in the Introductory Biology course? Why did Int Algebra disproportionately benefit Pell Grant recipients before implementation of the prereq? Answering these questions could lead to better understanding of when a prereq is most useful and when another intervention may be better suited to support student success in Introductory Biology.
Supplementary Material
Acknowledgments
We thank the Community College Biology Instructor Network to Support Inquiry Into Teaching and Education Scholarship (CC Bio INSITES - NSF award no. 1730130) for their mentorship. This project was supported in part by CC Bio INSITES network. Special thanks to Lisa Corwin and Jeff Schinske for organizing CC Bio INSITES and to the Howard Hughes Medical Institute for meeting services.
REFERENCES
- Alcock, J., Cockcroft, S., Finn, F. (2008). Quantifying the advantage of secondary mathematics study for accounting and finance undergraduates. Accounting & Finance, 48(5), 697–718. [Google Scholar]
- Attridge, N., Inglis, M. (2013). Advanced mathematical study and the development of conditional reasoning skills. PLoS ONE, 8(7), e69399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bates, D., Mächler, M., Bolker, B., Walker, S. (2015). Fitting linear mixed-effects models using lme4. Journal of Statistical Software, 67(1), 1–48. doi: 10.18637/jss.v067.i01 [Google Scholar]
- Beasley, M. A., Fischer, M. J. (2012). Why they leave: The impact of stereotype threat on the attrition of women and minorities from science, math and engineering majors. Social Psychology of Education, 15(4), 427–448. [Google Scholar]
- Boatman, A., Long, B. T. (2018). Does remediation work for all students? How the effects of postsecondary remedial and developmental courses vary by level of academic preparation. Educational Evaluation and Policy Analysis, 40(1), 29–58. [Google Scholar]
- Burnham, K. P., Anderson, D. R. (2002). A practical information-theoretic approach. In: Model selection and multimodel inference (2nd ed.). New York: Springer. [Google Scholar]
- Butcher, D. F., Muth, W. A. (1985). Predicting performance in an introductory computer science course. Communications of the ACM, 28(3), 263–268. [Google Scholar]
- Canning, E. A., Ozier, E., Williams, H. E., AlRasheed, R., Murphy, M. C. (2021, August). Professors who signal a fixed mindset about ability undermine women’s performance in STEM. Social Psychological and Personality Science, 13(5), 927–937. [Google Scholar]
- Carnegie Foundation for the Advancement of Teaching. (2011). The Carnegie Classification of Institutions of Higher Education (2010 ed.) Menlo Park, CA. [Google Scholar]
- Colvin, R. L. (2020). (rep.). The math problem: Removing the math barrier to college completion. National University and National Laboratory for Education Transformation. Retrieved September 9, 2021, from https://www.luminafoundation.org/resource/the-math-problem/ [Google Scholar]
- Donovan, W. J., Wheland, E. R. (2009). Comparisons of success and retention in a general chemistry course before and after the adoption of a mathematics prerequisite. School Science and Mathematics, 109(7), 371–382. [Google Scholar]
- Foote, A., Grosz, M. (2020). The effect of local labor market downturns on postsecondary enrollment and program choice. Education Finance and Policy, 15(4), 593–622. [Google Scholar]
- Forester, J. P., McWhorter, D. L., Cole, M. S. (2002). The relationship between premedical coursework in gross anatomy and histology and medical school performance in gross anatomy and histology. Clinical Anatomy, 15(2), 160–164. [DOI] [PubMed] [Google Scholar]
- Gelman, A., Hill, J. (2007). Data analysis using regression and multilevel/hierarchical models. Cambridge, UK: Cambridge University Press. [Google Scholar]
- Grace, J. T., D’Aoust, R. (2006). Evidence-based program requirements: Evaluation of statistics as a required course. Nursing Education Perspectives, 27(1), 28–33. [PubMed] [Google Scholar]
- Harris, R. B., Mack, M. R., Bryant, J., Theobald, E. J., Freeman, S. (2020). Reducing achievement gaps in undergraduate general chemistry could lift underrepresented students into a “hyperpersistent zone.” Science Advances, 6(24), eaaz5687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hazari, Z., Sadler, P. M., Sonnert, G. (2013). The science identity of college students: Exploring the intersection of gender, race, and ethnicity. Journal of College Science Teaching, 42(5), 82–91. [Google Scholar]
- Lo, S. M., Gardner, G. E., Reid, J., Napoleon-Fanis, V., Carroll, P., Smith, E., & Sato, B. K. (2019). Prevailing questions and methodologies in biology education research: A longitudinal analysis of research in CBE—Life Sciences Education and at the Society for the Advancement of Biology Education Research. CBE—Life Sciences Education, 18(1), ar9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marcal, L., Roberts, W. W. (2000). Computer literacy requirements and student performance in business communications. Journal of Education for Business, 75(5), 253–257. [Google Scholar]
- McCarron, K. B., Burstein, A. N. (2017). The importance of mathematics as a prerequisite to introductory financial accounting. Community College Journal of Research and Practice, 41(9), 543–550. [Google Scholar]
- McCoy, E. D., Pierce, S. K. (2004). The function of course prerequisites in biology. Herndon, VA: American Institute of Biological Sciences. [Google Scholar]
- Ngo, F., Melguizo, T. (2016). How can placement policy improve math remediation outcomes? Evidence from experimentation in community colleges. Educational Evaluation and Policy Analysis, 38(1), 171–196. [Google Scholar]
- Ngo, F., Melguizo, T. (2020). The equity cost of inter-sector math misalignment: Racial and ethnic disparities in community college student outcomes (Brief III). USC Pullias Center for Higher Education. [Google Scholar]
- Paulsen, M. B., John, E. P. S. (2002). Social class and college costs: Examining the financial nexus between college choice and persistence. Journal of Higher Education, 73(2), 189–236. [Google Scholar]
- Pieronek, J. F. (1991). Relationship between the successful completion of advanced coursework and knowledge of required prerequisites for the returning registered nurse in a baccalaureate nursing program (Doctoral dissertation). Detroit, MI: Wayne State University. [Google Scholar]
- R Core Team. (2021). R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/ [Google Scholar]
- Sato, B. K., Lee, A. K., Alam, U., Dang, J. V., Dacanay, S. J., Morgado, P., & Sandholtz, J. H. (2017). What’s in a prerequisite? A mixed-methods approach to identifying the impact of a prerequisite course. CBE—Life Sciences Education, 16(1), ar16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaffer, J. F., Dang, J. V., Lee, A. K., Dacanay, S. J., Alam, U., Wong, H. Y., & Sato, B. K. (2016). A Familiar(ity) Problem: Assessing the Impact of Prerequisites and Content Familiarity on Student Learning. PLOS ONE, 11(1), e0148051. 10.1371/journal.pone.0148051 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaffer, J. F., Schriner, S. E., Loudon, C., Dacanay, S. J., Alam, U., Dang, J. V., & Sato, B. K. (2018). The impact of physiology prerequisites on future anatomy and physiology courses. HAPS Educator, 22(3), 199–207. [Google Scholar]
- Schinske, J. N., Balke, V. L., Bangera, M. G., Bonney, K. M., Brownell, S. E., Carter, R. S., & Corwin, L. A. (2017). Broadening participation in biology education research: Engaging community college students and faculty. CBE—Life Sciences Education, 16(2), mr1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theobald, E. (2018). Students are rarely independent: When, why, and how to use random effects in discipline-based education research. CBE—Life Sciences Education, 17(3), rm2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theobald, E. J., Aikens, M., Eddy, S., Jordt, H. (2019). Beyond linear regression: A reference for analyzing common data types in discipline based education research. Physical Review Physics Education Research, 15(2), 020110. [Google Scholar]
- Thompson, M. E. (2021). Grade expectations: The role of first-year grades in predicting the pursuit of STEM majors for first-and continuing-generation students. Journal of Higher Education, 92(6), 961–985. [Google Scholar]
- Trujillo, G., Tanner, K. D. (2014). Considering the role of affect in learning: Monitoring students’ self-efficacy, sense of belonging, and science identity. CBE—Life Sciences Education, 13(1), 6–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson, C. E. (1994). Comparison of final course grades in introductory college chemistry with or without math prerequisite. Washington, DC: Nova Southeastern University. [Google Scholar]
- Wright, R., Cotner, S., Winkel, A. (2009). Minimal impact of organic chemistry prerequisite on student performance in introductory biochemistry. CBE—Life Sciences Education, 8(1), 44–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuur, A., Ieno, E. N., Walker, N., Saveliev, A. A., Smith, G. M. (2009). Mixed effects models and extensions in ecology with R. New York: Springer Science & Business Media. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.