Basal bodies bend in response to ciliary forces

Abstract

Motile cilia beat with an asymmetric waveform consisting of a power stroke that generates a propulsive force and a recovery stroke that returns the cilium back to the start. Cilia are anchored to the cell cortex by basal bodies (BBs) that are directly coupled to the ciliary doublet microtubules (MTs). We find that, consistent with ciliary forces imposing on BBs, bending patterns in BB triplet MTs are responsive to ciliary beating. BB bending varies as environmental conditions change the ciliary waveform. Bending occurs where striated fibers (SFs) attach to BBs and mutants with short SFs that fail to connect to adjacent BBs exhibit abnormal BB bending, supporting a model in which SFs couple ciliary forces between BBs. Finally, loss of the BB stability protein Poc1, which helps interconnect BB triplet MTs, prevents the normal distributed BB and ciliary bending patterns. Collectively, BBs experience ciliary forces and manage mechanical coupling of these forces to their surrounding cellular architecture for normal ciliary beating.

INTRODUCTION

Ciliary beating is utilized by microorganisms and epithelia to move fluid for cell motility and the clearance and circulation of biological fluids (Bustamante-Marin and Ostrowski, 2017; Bayless et al., 2019). Motile cilia comprise axoneme scaffolds of nine doublet (A-B) microtubules (MTs) radially arranged around a central pair of singlet MTs. Doublet MTs slide and bend by the coordinated activities of axonemal dynein motors, nexin links, and radial spokes (RSs) (Viswanadha et al., 2017). Concerted axonemal bending promotes an asymmetric waveform that drives directed fluid flow and exerts asymmetric mechanical forces to the cell.

Computer models of ciliary and flagellar beating indicate that the ciliary forces needed to bend axonemes dominate over viscous drag forces generated by cilium–fluid interactions (Brokaw, 1985, 2009). Thus, the major forces acting upon cilia are created by the activities of cilia themselves. Axonemal dynein MT motors are anchored to A tubules of the ciliary doublet MTs, and the motor domain extends to the B tubules of adjacent doublet MTs. Dynein activation slides doublet MTs relative to each other (Brokaw, 1965; Satir, 1967; Summers and Gibbons, 1971; Sale and Satir, 1977; Riedel-Kruse et al., 2007). Doublet MT sliding is resisted by nexin links between adjacent doublet MTs, thereby promoting axonemal bending. The cyclic axonemal trajectory consists of a power stroke, which generates directed fluid flow, and a recovery stroke, which resets the cycle. Several models propose that the asymmetric ciliary waveform is established by asymmetric dynein activation, which spatially and temporally regulates doublet MT sliding of 25–100 nm along the axoneme (Lindemann, 1994; Woolley and Bozkurt, 1995; Vernon and Woolley, 2004; Riedel-Kruse et al., 2007; Satir et al., 2014; Lesich et al., 2016; Lin and Nicastro, 2018). The sliding control model hypothesizes that the mechanical properties of the axoneme base can modulate the forces that are transmitted along the axoneme (Woolley and Bozkurt, 1995; Vernon and Woolley, 2004; Riedel-Kruse et al., 2007). Flagellar doublet sliding at the axoneme base, so-called basal sliding, imposes mechanical forces on the outer dense fibers associated with the axoneme MTs and the connecting piece (Vernon and Woolley, 2002, 2004). Resistance to basal sliding through variance in asymmetric elastic compliance and deformation of the connecting piece or basal region modulates flagellar beating (Goldstein, 1981; Vernon and Woolley, 2002, 2004; Lindemann and Mitchell, 2007; Lindemann and Lesich, 2016; Riedel-Kruse et al., 2007; Lesich et al., 2016). Less is understood about how basal sliding forces in cilia at the cell cortex impact the canonical basal body (BB) structure. It is suggested that the BB at the ciliary base may experience and resist ciliary forces (Warner and Satir, 1974; Vernon and Woolley, 2004). How axonemal forces are transmitted, resisted, and regulated at the ciliary base remains poorly understood.

Cilia are anchored to promote the transmission of axonemal forces to the cell for both cell motility and epithelial fluid flow. Motile cilia are nucleated, positioned, and anchored to the cell cortex by BBs. BBs comprise nine triplet MTs (A-B-C), where the A-B tubules of BBs are continuous with the axoneme’s A-B tubules. The cartwheel (CW) at the BB proximal end comprises a central hub and spokes that connect to the proximal end of the BB triplet MTs. Bld10, a protein that establishes CW-triplet MT connections, stabilizes BBs against ciliary forces (Bayless et al., 2012, 2016). The nine BB triplet MTs are linked to each other by connections with neighboring triplet MTs (A-C linkers and the helical inner scaffold) (Meehl et al., 2016; Li et al., 2019; Le Guennec et al., 2020). Poc1 is a helical inner scaffold protein, and loss of Poc1 disrupts A-C linker positioning and spacing (Meehl et al., 2016; Li et al., 2019; Le Guennec et al., 2020). Loss of Poc1 also causes ciliary beating–dependent BB instability and the asymmetric disassembly of specific triplet MTs relative to the axis of the ciliary power stroke (Pearson et al., 2009; Meehl et al., 2016). This suggests that the asymmetric forces produced by beating cilia are resisted by BBs. Consistent with this, both BB proteins and MT posttranslational modifications (PTMs) that stabilize BBs localize asymmetrically to BBs relative to the direction of the power stroke (Bobinnec et al., 1998; Bayless et al., 2016; Basquin et al., 2019). BBs are considered structurally rigid because of the many linkages within the BB ultrastructure (triplet MTs, CW, helical inner scaffold, A-C linkers), the presence of stabilizing MT PTMs, and the lack of ciliary dynein (Bayless et al., 2015; Tassin et al., 2015). However, sperm that lack conserved BB structures (CWs and A-C linkers), deform at the connecting piece, and produce sperm head translocations during flagellar beating (Vernon and Woolley, 2004; Lindemann and Mitchell, 2007; Khanal et al., 2021), consistent with axonemal basal sliding force transmission to the sperm head (Vernon and Woolley, 2004; Lesich et al., 2016; Fishman et al., 2018; Khanal et al., 2021). While BBs are stabilized against ciliary forces and suggested to deform (Warner and Satir, 1974), it is unclear how forces from cilia are transmitted to BBs and how BBs respond.

Cilia and BBs are attached to the surrounding cortical cytoskeleton and plasma membrane by BB-appendage structures (Werner et al., 2011; Kunimoto et al., 2012; Chien et al., 2013; Turk et al., 2015; Herawati et al., 2016; Mahuzier et al., 2018; Junker et al., 2019; Nabi et al., 2019; Soh et al., 2020). These structures help establish and maintain the position of BBs and motile cilia. Moreover, BB-appendage structures and the surrounding cytoskeletal network resist the ciliary forces and/or shear forces from ciliary beating and fluid movement (Mitchell et al., 2007; Marshall and Kintner, 2008; Chien et al., 2013; Mahuzier et al., 2018). Tetrahymena thermophila BBs possess three BB-appendage structures—two MT bundles facing the cell posterior and right (when viewed from above) and one striated fiber (SF) facing the cell anterior (Allen, 1967). While all BB-appendages appear to be important for BB organization, SFs, which contact their neighboring BB’s posterior MT bundle, elongate in response to elevated ciliary forces and gain attachments to the cell cortical cytoskeleton (Galati et al., 2014; Soh et al., 2020). This was suggested to further anchor BBs to resist the elevated ciliary forces and demonstrates that SFs are responsive to forces from cilia. Moreover, mammalian and Caenorhabditis elegans rootlet structures, analogous to Tetrahymena SFs, are required for ciliary base stability (Yang et al., 2005; Mohan et al., 2013). When the Tetrahymena SF length is reduced, BBs and cilia disorganize in a ciliary force–dependent manner (Jerka-Dziadosz et al., 1995; Galati et al., 2014; Soh et al., 2020). Interconnections between neighboring BBs through their SFs are thought to regulate ciliary beating through intracellular coupling (Wan and Goldstein, 2016; Soh et al., 2020). The inherent asymmetries within T. thermophila ciliary units (cilium, BB, and BB-appendages) and the asymmetry of their beat stroke would suggest that they establish mechanisms for transmitting and resisting asymmetric mechanical forces from cilia to the BB and cell cortex.

Cilia, BBs, and BB-appendages experience mechanical forces produced by motile cilia. We show that the triplet MTs of BBs bend coincident with cilia bending during the beat stroke. BB bending is focused to the triplet MTs adjacent to the SF connection. Environmental temperature alters BB bending patterns coincident with changes to the ciliary waveform and SF connectivity to neighboring BBs and the cell cortex. BB bending is no longer focused on the SF connection when SF length and inter-BB connections are reduced. Furthermore, the BB stability protein Poc1 helps propagate normal bending patterns through the BB. This suggests that BBs physically transmit forces from beating cilia into the cell and that the structural properties of BBs and BB-appendages chaperone force transmission.

RESULTS

Basal bodies bend during ciliary beating

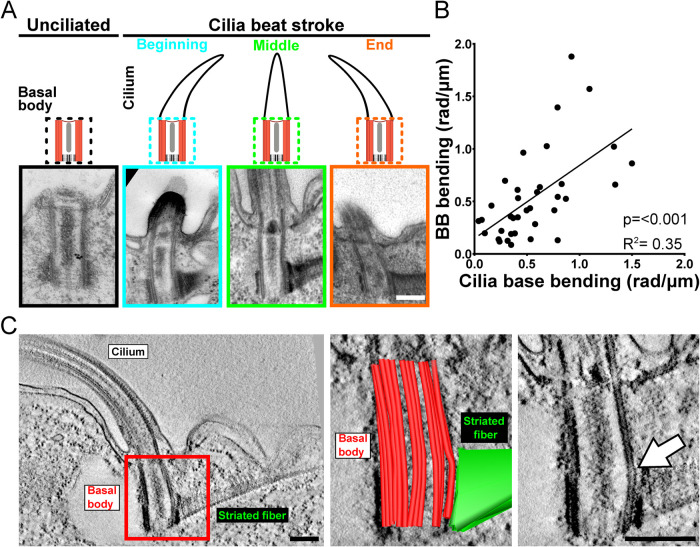
Axonemal doublet MTs are continuous with the A-B MTs of BBs, providing a direct link between ciliary sliding forces and BBs (Supplemental Figure S1A; Warner and Satir, 1974). To test whether forces produced by axonemal dynein sliding affect the canonical BB architecture, swimming T. thermophila cells were fixed using high-pressure freezing and freeze substitution (HPF-FS) to catch beating cilia and BBs in their dynamic states. Thin-section EM images and three-dimensional (3D) EM tomography of BBs were visualized relative to cilia at different positions in their beat stroke. Both methods show BB triplet MTs bend in response to ciliary beating while unciliated BBs do not bend (Figure 1A and Supplemental Figure S1B; Allen, 1967, 1969). The BB MTs’ bend is concave relative to the cell anterior at the beginning of the power stroke (negative curvature) and convex at the end of the power stroke (positive curvature). At the midpoint of the ciliary power stroke, when doublet MTs are not displaced relative to their neighbors, BBs are straighter. Consistent with BB bending as a direct response to ciliary beating, the magnitude of BB bending corresponds with that of the bending cilium (Figure 1B). The primary site of BB bending is near the junction connecting BBs to the SF (Figure 1C). SFs are oriented toward the cell’s anterior, opposite the direction of the ciliary power stroke. Thus, BB bending is asymmetric and maximal at the site of BB connection to the SF that anchors BBs to neighboring BBs and to the cell cortex. SFs may therefore transmit the asymmetric forces produced by cilia into the cell cortex.

FIGURE 1:

BBs bend consistent with ciliary bending. (A) Thin (80 nm)-section EM images of T. thermophila BBs show triplet MT bending at 37°C. Schematic and representative images of cilia and BB position. Unciliated BB triplet MTs are straight. Conversely, ciliated BB triplet MTs bend corresponding to the direction of the ciliary bending. (B) Increased cilia bending correlates with increasing BB bending (p < 0.001, R² = 0.35). The absolute maximum BB bending (rad/μm; y-axis) is measured relative to absolute maximum ciliary bending (rad/μm; x-axis) at the proximal end (Supplemental Figure S1C). n = 37 BBs. (C) Representative 3D EM tomography image of a BB and cilium at the end of the power stroke. Left panel displays cilium, BB, and SF. Middle image is a single-slice view of a model overlay of the BB triplet MTs (red) and SF (green) using 3D modeling. Right image displays single-slice view without the model. White arrow denotes the bending triplet MTs. Scale bars, 200 nm.

Patterns of isolated triplet MT curvature relative to cilia position in the beat stroke

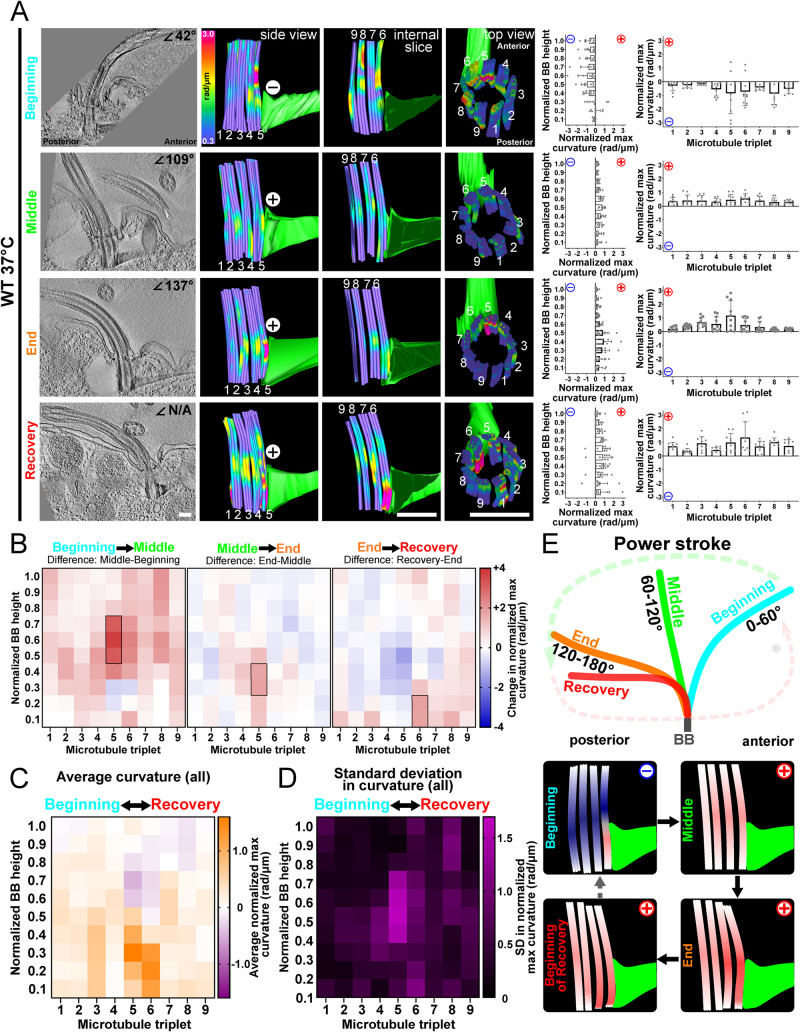
The ciliary beat stroke of T. thermophila consists of a power stroke moving in the anterior to posterior direction and then a counterclockwise recovery stroke in which the cilium travels parallel to the cell surface in preparation for the next power stroke (viewed from above the cell; Wood et al., 2007). The bending or curvature of BBs relative to the ciliary power stroke at 37°C was analyzed to test when forces are transmitted to specific triplet MTs within BBs. EM sections of tomograms were scanned to identify ciliated BBs in the medial region of cells. BB bending differs in amplitude and location depending on the cilium’s position in the power stroke. At the power stroke beginning (0–60°), BBs bend in the same direction as their cilium (Figure 2A and Supplemental Figure S2). The bending is negative (concave curvature relative to cell’s anterior–posterior axes) within the triplet MTs and is greatest (max = 3.6 rad/µm) at triplet MTs 5 and 6. Triplet MTs 5 and 6 connect to the SF, and the observed bending in these triplet MTs occurs just above the SF attachment. In the middle of the power stroke (61–120°), when the cilium is relatively straight, BBs display less curvature. The curvature is positive (convex curvature relative to the cell’s anterior–posterior axes) and distributed around the medial region of the triplet MTs. At the end of the power stroke (121–180°), the cilium is pointed toward the cell’s posterior and the BB bends in the same direction. The positive bending is again focused on the anterior triplet MTs 5 and 6 (max = 2.5 rad/µm) adjacent to the SF. At the beginning of the recovery stroke or the end of the power stroke, BB bending is focused on anterior triplet MT 6 (max = 3.3 rad/µm). Thus, the individual BB triplet MTs bend with distinct patterns relative to the ciliary position in the power stroke. This bending pattern is focused asymmetrically to triplet MTs 5 and 6 that attach to the SF.

FIGURE 2:

BB bending is consistent with ciliary beat stroke position. (A) BB triplet MTs display unique bending patterns relative to cilia beat stroke position. Left panels are 8.6 nm max-projected images of EM tomograms. Middle panels are model views (side, internal slice, and top views) of corresponding BBs. Curvature of the triplet MTs where cold colors (blue) indicate low curvature and warm colors indicate high curvature (red). Graphs represent the normalized maximum BB curvature for the BB proximal to distal axis (left) and for each triplet MT (right). The maximum value for each bin (1/10th the length of the BB) along the BB proximal-distal axis is normalized by subtracting the lowest maximum value of all bins in each BB. Each graph represents the means and SDs of normalized maximum values for each proximal to distal bin (left) or each triplet MT (right) for a single BB, with 27 tubules averaged into nine triplet MTs. (B) Differences in BB bending through the ciliary beat cycle. In the first half of the power stroke, BB bending increases in the positive direction in the middle of triplet MT 5 (left heatmap). In the second half of the power stroke, BB bending increases in the positive direction at the base of triplet MT 5 (middle heatmap). In the transition from the power stroke to the recovery stroke, BB bending is observed at the base of triplet MTs 6–8 where bending becomes more positive (right heatmap). Black boxes denote >75% difference from other bins (p > 0.05). Blue (negative) and red (positive) indicate the direction of curvature relative to the cell’s anterior–posterior axis. (C) Average BB bending at all ciliary positions is greatest at triplet MTs 5 and 6. Heatmap indicates the average of normalized maximum curvature values from the four BBs in A. Purple indicates negative bending, and orange indicates positive bending. The greatest positive and negative bending occurs in triplet MTs 5 and 6, indicating that these triplet MTs experience the greatest structural deformations. (D) Heatmap indicates the SD in the normalized maximum curvature values from the four BBs in A. The greatest SD to BB bending occurs in the middle and at the base of triplet MTs 4–6. Magenta indicates high SD. (E) Schematic models represent cilia and BBs through the power stroke (beginning, middle, and end) and the onset of the recovery stroke. Scale bar, 200 nm.

To understand the dynamic BB changes, BB bending during the ciliary power stroke was quantified and differences were visualized as heatmaps depicting each triplet MT along the BB axis. Because it is difficult to capture cilia and BBs at precisely the same point in the ciliary beat stroke, each model analyzed for the dynamic distribution of BB bending is based on a single BB. Averages of three BBs for each condition near the end of the power stroke and/or the start of the recovery stroke are presented in the supplemental figures. Between the beginning and the middle of the power stroke, the primary curvature change is in the middle-anterior region of the BB that switches from a negative bending direction to a positive one (Figure 2, A and B, and Supplemental Figure S2A). Between the middle and the end of the power stroke, the positive curvature moves downward to the proximal end of triplet MT 5. Averaging the three BBs with cilia near the end of the ciliary power stroke showed a similar bending pattern (Supplemental Figure S2B). Between the end of the power stroke and the beginning of the recovery stroke, the positive curvature shifts to triplet MTs 6–8. When BB bending patterns from all four BBs shown in Figure 2A are combined and averaged for each bin, the greatest curvature occurs in the medial (negative curvature) and basal (positive curvature) regions of triplet MTs 5 and 6 (Figure 2C). The SD of the described maximum curvature indicates which regions of the BB undergo the greatest changes during the ciliary beat stroke. The greatest SD occurs in the medial and proximal regions of triplet MTs 4–6 (Figure 2D). These regions therefore undergo the most physical deformation in triplet MT bending. We posit that these regions must be stabilized to maintain the structural integrity of BBs. Overall, this supports a model for BBs experiencing and absorbing mechanical forces through triplet MT bending (Figure 2E). Furthermore, prominent BB bending is adjacent to the SF (triplet MTs 5 and 6) and the transverse MTs (triplet MT 4), supporting a model in which SFs and the transverse MTs also experience ciliary forces from BBs and transmit them to neighboring BBs and to the cell cortex.

Computer simulation of BB bending in response to ciliary beating

We next tested whether the BB bending patterns observed in our 3D EM tomography studies would be recapitulated in a computational model of ciliary beating that includes the BB. A computational (finite-element) model of the cilium, BB, SF, BB-appendage MTs, and cell cortex was generated in the commercial simulation software COMSOL Multiphysics (COMSOL Multiphysics v. 5.6; www.comsol.com; COMSOL AB, Stockholm, Sweden) using the Beam interface within the Structural Mechanics module (Figure 3 and Supplemental Figure S3). All MT filaments including axonemal doublet MTs and BB triplet MTs are modeled as slender (Euler–Bernoulli) beams. The central pair MTs are modeled as a single beam with a preferential bending direction. Viscous drag is applied using resistive force coefficients (Gray and Hancock, 1955; Bayly et al., 2011). This model uses asymmetric activation of dynein on one side of the axoneme (doublet MTs 5–9) to model the power stroke. RSs in this model are flexible enough to allow sliding between doublet MTs and the central pair, but do not support sliding at their attachment points. To avoid undesired structural nonlinearities and ensure convergence of the simulation, relative sliding between adjacent doublet MTs was limited by reducing the maximum distributed dynein force to 125 pN/μm; deformations were scaled to account for effects of larger forces (see Materials and Methods). This analysis predicts a maximum sliding amplitude at the ciliary tip between doublet MTs 6 and 7 of 151 nm (Table 1). At the base of the cilium, maximum sliding amplitudes of ∼25 nm occurred between doublet MTs 2 and 3. While a rigorous comparison of these sliding amplitudes to experimental data is beyond the scope of the current work, these results show that interfilament sliding occurs in the model at amplitudes comparable to experimental measures. Further computational model details are provided in Materials and Methods.

FIGURE 3:

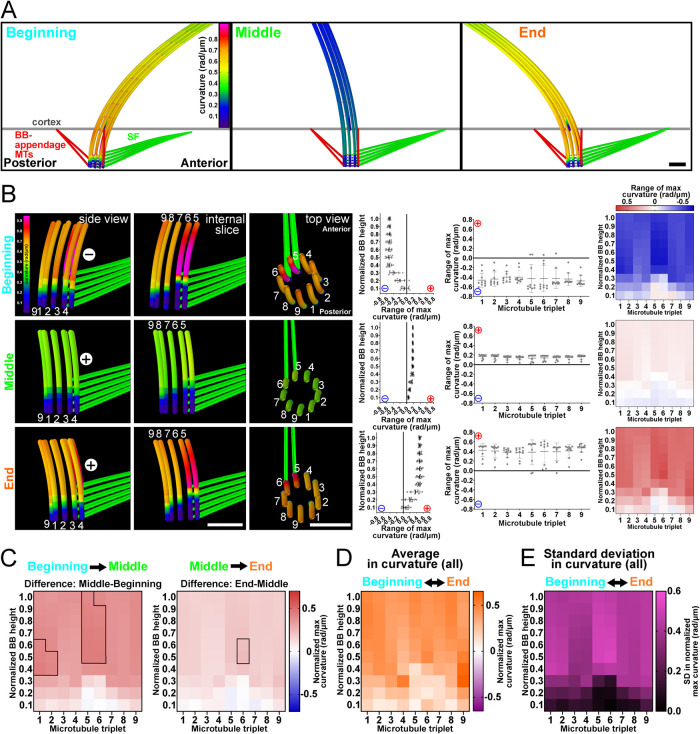
Computer model of BB bending relative to ciliary bending. (A) Computational model depicting the cilium, BB, SF, and BB-appendage MTs during the ciliary power stroke to determine the parameters required to simulate BB bending. (B) Computational modeling can approximately replicate BB bending profiles observed in the EM tomograms. Bending occurs at triplet MTs 5 and 6. Left panels are model views (side, internal, and top) of BB triplet MTs. Colors indicate curvature of the modeled triplet MTs where cold colors (blue) indicate low curvature and warm colors (red) indicate high curvature. Graphs show BB curvature for the BB proximal to distal axis (left) and for each triplet MT (right) as quantified in Figure 2. Left heatmap describes the bending amplitude and direction for each representative modeled BB. (C) BB bending changes with ciliary power stroke position. BB bending becomes more positive in the middle of triplet MTs 1 and 2 and middle/top of triplet MTs 5 and 6 in the first half of the power stroke (left heatmap). BB bending becomes more positive in the middle of triplet MT 6 in the second half of the power stroke (right heatmap). Black boxes denote >75% difference from other bins (p > 0.05). Blue (negative) and red (positive) colors indicate the direction of curvature relative to the cell’s anterior–posterior axis. (D) Average BB bending of all ciliary positions. (E) Heatmap indicates the SD in the maximum curvature values from computer modeled BBs. The largest SD occurs at triplet MTs 5 and 6. Magenta indicates high SD. Scale bar, 200 nm.

TABLE 1:

Model parameters and MT sliding quantification in computational model.

Parameter	Description	Value	References or comment
EI	Flexural rigidity per doublet	73 pN·μm2	Okuno and Brokaw, 1979; Pelle et al., 2009; Xu et al., 2016
kN	Interdoublet normal stiffness	105 pN/μm2	Yagi and Kamiya, 1995; Minoura et al., 1999; Xu et al., 2016
kN_RS	RS normal stiffness	105 pN/μm2	Found to sufficiently maintain axoneme cross-section shape without convergence issues
kT_RS	RS shear stiffness	100 pN/μm2	Estimate found to allow sufficient range of motion
kN_AC	AC-linker normal stiffness	106 pN/μm2	Estimate found to give triplet separation and curvature independence consistent with data
kT_AC	AC-linker shear stiffness	105 pN/μm2	Estimate found to give triplet translocations consistent with data
cN, cT	Normal, tangent resistive force coefficient	(3, 1.5) × 10–3 pN·s/μm2	Gray and Hancock, 1955; Bayly et al., 2011
kCortex	Cortical attachment stiffness per filament	11 pN/μm	Estimate found to allow BB bending consistent with data
Lc	Cilium length	5.6 μm	Akella et al., 2010; Junker et al., 2021
Lbb	BB length	500 nm	Allen, 1969
L_SF	SF horizontal length	1.2 μm	Soh et al., 2020
L_pcMT	Postciliary MT horizontal length	500 nm	This study
L_tMT	Transverse MT horizontal length	187 nm	This study
L_AC	Axial length of AC-linkers	150 nm	Meehl et al., 2016
L_CW	Axial length of CW	75 nm	Meehl et al., 2016
r	Axoneme radius	100 nm	Nicastro et al., 2006; Lindemann and Mitchell, 2007
P	Distributed dynein force	500 pN/μm	Shingyoji et al., 1998
T	Period of oscillation	40 ms	Soh et al., 2022
pLag	Phase lag between adjascent BBs	3 ms	Soh et al., 2022

	Maximum relative sliding (nm) for MT pair:
	1–2	2–3	3–4	4–5	5–6	6–7	7–8	8–9	9–1
Cilium tip	136	147	106	8	109	151	137	61	62
Cilium base	19	25	21	6	12	21	21	12	7
Base - 10× less stiff AC-linker	23	29	23	8	12	25	24	12	11
Difference from WT	21%	14%	10%	33%	0%	19%	14%	0%	57%

Computational model parameters and data for the relative sliding between adjacent MTs at tip and base of modeled cilium and BB. For relative sliding values, row 3 gives relative sliding at the cilium base when the model is perturbed by reducing AC linker stiffness by a factor of 10. Row 4 gives the percent difference in sliding magnitudes at the base of the cilium in the perturbed model.

The BB is anchored to the cell cortex by several attachments: 1) the distal end of the BB is linked to the cortex, 2) postciliary MTs link the proximal end of BB triplet MT 9 to the cell cortex, 3) transverse MTs link the proximal end of BB triplet MT 4 to the cell cortex, and 4) the SF links triplet MTs 5 and 6 to the cell cortex. All of these structures are required for BB anchorage to resist ciliary forces (Supplemental Videos 1–8). Detachment of the SF from the cell cortex in the model led to a sixfold increase in BB front-to-back rocking (periodic rotation in the direction of the predicted cell anterior–posterior axis) and an 11-fold increase in side-to-side rocking, as well as an average 25% reduction to maximum BB bending in triplet MTs 5 and 6 ( Table 2). However, removal of the SF attachment places an additional burden on the remaining accessory structures and the triplet MTs they are attached to. Maximum bending in triplet MT 4 increased by 30%, and maximum bending in triplet MT 9 increased by 85%. Detachment of the postciliary MTs at the cell cortex led to a complex rocking motion with a threefold increase in BB front-to-back rocking and a fivefold increase in side-to-side rocking, as well as an average 10% increase in maximum bending in triplet MTs 5 and 6. Detachment of the transverse MTs at the cell cortex led to no significant increase in the amplitude of front-to-back rocking but a sixfold increase in side-to-side rocking. Maximum curvature in triplet MT 9 increased 18% at the end of the cycle.

TABLE 3:

EM tomography sample sizes for identification and final modeling for each experimental condition.

	Sample sizes for genotype and temperature
	WT at 37°C	WT at 30°C	disA1-1 at 30°C	poc1Δ at 30°C
EM grids	3	2	1	1
Cells screened	150	100	100	100
Cells acquired	7	14	5	15
BBs acquired	10	15	8	15
BBs modeled	6	9	3	3

TABLE 2:

Perturbations to computational model.

	Rocking (°)		Maximum bending beginning/end (rad/μm)
Perturbation	Front-back	Side-side	Triplet MT 4	Triplet MT 5	Triplet MT 6	Triplet MT 9
None	6.9	6.0	–0.78/0.70	–1.06/0.90	–0.97/0.92	–0.76/0.73
SF detachment	43.0	66.0	–1.01/0.70	–0.74/0.74	–0.69/0.70	–1.41/1.28
pcMT detachment	22.0	32.0	–0.77/0.72	–1.14/1.03	–1.05/1.00	–0.76/0.72
tMT detachment	7.6	35.0	–0.77/0.70	–1.10/0.91	–0.92/0.92	–0.74/0.86
10× less stiff A-C linkers	14.6	8.8	–0.77/1.06	–1.42/1.23	–1.27/1.17	–0.95/1.06

Quantification of BB rocking and bending at the beginning and the end of the ciliary beat stroke when structural elements are perturbed by detachment in the computational model.

Movie S1.

Download video file ^{(906.8KB, mov)}

Baseline side. Side view of a computational model representing 37°C T. thermophila BB and ciliary movements (Figure 3 and S3).

Movie S2.

Download video file ^{(542.9KB, mov)}

Baseline top. Top view of a computational model representing 37°C T. thermophila BB and ciliary movements (Figure 3 and S3).

Movie S3.

Download video file ^{(1.4MB, mov)}

No SF connection side. Side view of a computational model representing 37°C T. thermophila BB and ciliary movements when SF connections to the anterior BB and the cell cortex are lost (Figure 3 and S3).

Movie S4.

Download video file ^{(1.2MB, mov)}

No SF connection top. Top view of a computational model representing 37°C T. thermophila BB and ciliary movements when SF connections to the anterior BB and the cell cortex are lost (Figure 3 and S3).

Movie S5.

Download video file ^{(1.4MB, mov)}

No pcMT side. Side view of a computational model representing 37°C T. thermophila BB and ciliary movements when pcMTs are lost (Figure 3 and S3).

Movie S6.

Download video file ^{(1.5MB, mov)}

No pcMT top. Top view of a computational model representing 37°C T. thermophila BB and ciliary movements when pcMTs are lost (Figure 3 and S3).

Movie S7.

Download video file ^{(1.4MB, mov)}

No tMT side. Side view of a computational model representing 37°C T. thermophila BB and ciliary movements when tMTs are lost (Figure 3 and S3).

Movie S8.

Download video file ^{(1.4MB, mov)}

No tMT top. Top view of a computational model representing 37°C T. thermophila BB and ciliary movements when tMTs are lost (Figure 3 and S3).

In all cases, removing one of the three BB anchoring structures led to increased bending and twisting in the remaining two. These three structures are analogous to a three-legged stool, as the loss of any one component leads to increases in rocking about the axis defined by the remaining two cortical attachments. Baseline rocking measurements in the computational model (measured at the BB base) show maximum amplitude of 6.9° of front-to-back rocking and 6° of side-to-side rocking. This equates to a predicted displacement of 59 nm. All rocking data are given as the angle swept by a vector tangent to the proximal end of the BB. Experimental rocking data are difficult to obtain due to the lack of a consistent reference against which to measure BB angles.

Consistent with the experimental results in Figure 2, the BB bends coincident with the cilium’s position in the beat cycle (Figure 3, A and B, and Supplemental Figure S3; Supplemental Videos 1 and 2). At the beginning of the power stroke the BB bends negatively, in the middle it is relatively straight, and at the end bending is positive (Figure 3B). At both the beginning and the end of the power stroke, the bending is focused to the medial region of triplet MTs 5 and 6, adjacent to the SF (Supplemental Figure S3). The predominant differences between the beginning, middle, and end of the power strokes are also focused on triplet MTs 5 and 6 (Figure 3C). This is evident by the highest SD of BB curvature at triplet MTs 5 and 6 (Figure 3, D and E). The BB bending direction and the focus of bending to triplet MTs 5 and 6 is consistent with the experimental EM tomography data (Figure 2 and Supplemental Figure S3A). The principal difference between BBs in the computational model compared with experimental EM tomograms is in the degree to which BB bending is focused at triplet MTs 5 and 6 at the BB–SF interface. BB bending at triplet MTs 5 and 6 in the EM tomograms is elevated and less distributed across the other triplet MTs when compared with the computational model (Figures 2 and 3). This suggests that additional BB structural elements and/or events may be required in the model. For example, the SF may exert additional forces to the BB absent from this model, or the helical inner scaffold, missing from this model, may be important to create the deformed shape (see below). Differences may also result from the limited bending amplitudes the current computational model can achieve. Despite these differences, the computational simulation supports our hypothesis that axoneme sliding forces can produce the bending patterns in BBs found in our EM tomography. Moreover, this bending is focused to the site of connection between BB triplet MTs 5 and 6 and the SF.

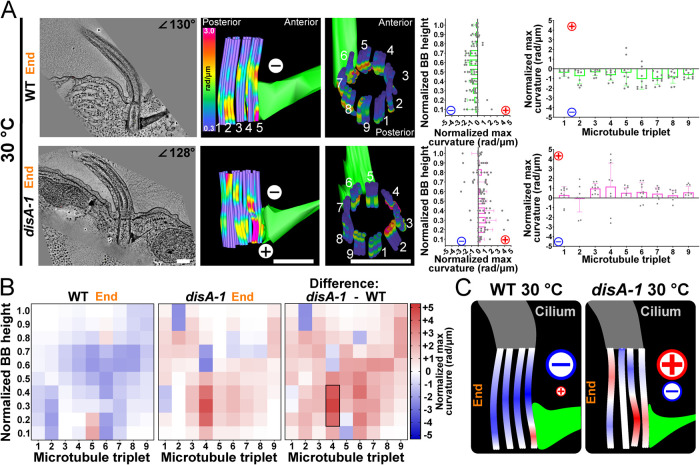
Environmental temperature reverses the direction of BB bending

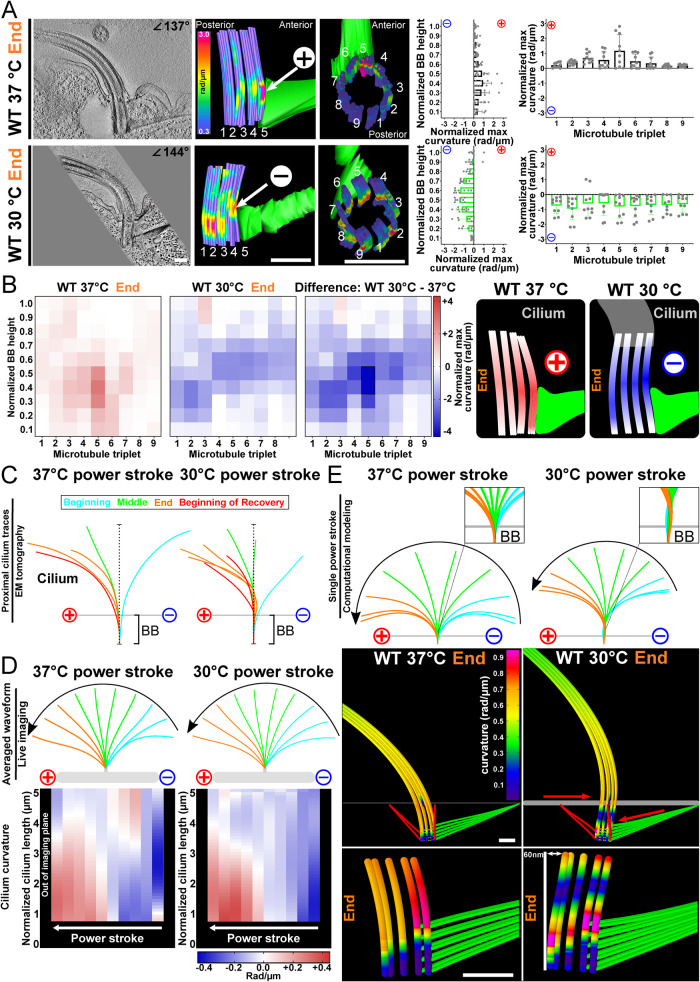
Ciliary forces and cell motility rates can be reduced by decreasing the environmental temperature of culture conditions (Goto et al., 1982; Galati et al., 2014). To test whether altered ciliary forces change BB bending, we reduced the cellular growth temperature from 37 to 30°C. Surprisingly, BBs at 30°C have a greater maximum curvature across triplet MTs when compared with that at 37°C (2.8-fold increase; Figure 4, A and B). Moreover, the direction of BB curvature at the end of the power stroke is reversed at 30°C (negative) compared with 37°C (positive). At 30°C, BB bending is focused to the medial region of the BB as opposed to the proximal end at 37°C (Figure 4, A and B). The greater overall BB bending at 30°C is accompanied by a distribution of the bending to triplet MTs around the entire BB (Figure 4, A and B; Supplemental Figures S2A and S4A). However, focused bending on triplet MTs 5 and 6 still occurs just above the BB’s attachment to the SF (Figure 4A). These results remain consistent across multiple BBs at different phases of the ciliary beat stroke (Figure 4A; Supplemental Figures S2 and S4). Thus, the distribution and the directionality of BB curvature changes when ciliary forces are reduced with decreased temperature and asymmetric forces are more equally distributed across triplet MTs.

FIGURE 4:

Temperature impacts BB bending patterns and ciliary waveform. (A) The direction of BB bending at the end of the power stroke changes at 30°C compared with 37°C. Scale bar, 200 nm. Middle panels are model views (side and top) of BB triplet MTs from corresponding EM tomogram. Arrows denote high curvature. Cold colors (blue) indicate low curvature, and warm colors (red) indicate high curvature. Graphs show BB curvature for the BB proximal to distal axis (left) and for each triplet MT (right) as in Figure 2. (B) Heatmaps show the location and direction differences in curvature between 37 and 30°C BBs at the end of the power stroke. The greatest difference occurs in the medial region of triplet MTs 2–5 and 7. The blue (negative) and red (positive) colors indicate the direction of curvature relative to the cell’s anterior–posterior axis. Schematic model represents BB bending differences between BBs 37 and 30°C at the end of the ciliary power stroke. Black box denotes >75% difference from other bins (p > 0.05). (C) Cilia at 30°C, compared with 37°C, are more bent at the proximal region of the cilium at the end of the power stroke. Colors denote the position of the cilium in the power stroke. Traces from EM tomograms include the BB and the proximal approximately 1 µm of the cilium. (D) Cilia at 30°C are more curved than cilia at 37°C from 1 µm (the nearest to the BB that can be imaged) to 2.5 µm from the BB as observed in live cell imaging throughout the power stroke. Average ciliary curvature is displayed as colored lines. Heatmaps of cilia curvature show that 30°C cilia curvature is greatest in the proximal regions of cilia at the beginning and end of the power stroke. The blue (negative) and red (positive) colors indicate the direction of ciliary curvature relative to the cell’s anterior–posterior axis. (E) Computer-simulated BB bending can recapitulate negative bending and ciliary waveform by the addition of a posteriorly oriented force on the SF attachment and an anteriorly oriented force on the cortex attachment resulting in a 60 nm relative displacement along the anterior–posterior axis. This model predicts forces from coupled BBs and from forces transmitted through the SF from neighboring cilia. The resulting shear and rotation of the BB reorient the cilium at its base with respect to the 37°C model (note clockwise rotation of the 30°C cilium).

Because BB bending was increased and in the opposite direction when ciliary forces were reduced by lowering the temperature, we asked whether the ciliary waveform was different between these conditions. Using live cell differential interference contrast (DIC) microscopy at high frame rates, we visualized ciliary beating of immobilized T. thermophila cells at different environmental temperatures. Immobilization of T. thermophila cells was performed via a magnetism-based approach (Soh et al., 2022). Consistent with an elevated T. thermophila swim speed at higher temperatures, the cilium beat frequency (CBF) at 37°C was approximately 10% faster than the CBF at 30°C. Quantification of cilia curvature revealed that the ciliary waveforms are different when T. thermophila cells are cultured at 30°C as opposed to 37°C (Figure 4, C and D). At 30°C, the magnitude of cilia bending increases. The increased bending is most prominent at the proximal end of the cilium (closest to the BB) at the beginning and the end of the power stroke. This is also observed when three BBs near the end of the power stroke are averaged to measure consistent changes between BBs (Supplemental Figure S4, B–D). Therefore, bending patterns of BBs and their cilia are altered based on the cell’s environmental response to temperature.

That BB bending and cilia waveforms change when temperatures are lowered was unexpected. To gain insight into how this may occur, computational models were utilized to determine conditions that recapitulate similar BB bending patterns. The wild-type (WT) power stroke at 30°C exhibits a greater degree of “counterbend” (a reversal of the ciliary curvature at the distal end of the cilium) as compared with the 37°C power stroke (Figure 4, C and D). To test whether the the ciliary counterbend could be responsible for the reversal of curvature in the BB at 30°C, we created counterbends in the cilium by two different methods. The dynein activation model relies on asymmetric activation of dynein on one side of the axoneme. First, the dynein activation model was altered by replacing the longitudinally uniform, temporally varying activation pattern with a sinusoidal spatial activation pattern (with an amplitude 250 pN/μm and wavelength 7.5 μm) that propagates distally to create the beat stroke. While this change creates a counterbend in the cilium, it does not reverse the bending of the BB. Second, an increased shear stiffness was applied at the distal end of the cilium by stiffening the distal array of RSs to the stiffness of the doublets. This created a counterbend in the cilium but reduced the overall beating amplitude and did not reverse bending in the BB. None of the tested manipulations of the axoneme produced BB bending consistent with the negative BB bending observed at the end of the power stroke in our experimental results. This suggests that the changes to the ciliary waveform are not responsible for the changes to the BB bending pattern that we observe at 30°C.

SFs are shorter and have fewer cortical cytoskeleton attachments when cells are grown at 30°C compared with 37°C (Galati et al., 2014; Soh et al., 2020). The mechanical and structural properties of SFs therefore change at lower temperatures and may allow the SF more freedom to transmit forces to the BB. We hypothesized that force transmission (from neighboring BBs) through the SF onto the BB could produce the bending patterns observed in the EM tomography. To test this in the computational model, a translational force was exerted on the distal end of the SF such that it would transmit into the BB (Figure 4E and Supplemental Videos 9 and 10). This represents a force transmitted from the anterior BB through its postciliary MTs (pcMTs) to the connected SF (Allen, 1969; Soh et al., 2020). A force in the opposite direction was applied to the BB distal end attached to the cell cortex, representing force transmitted from the posterior BB SF to the pcMTs. Adjacent Tetrahymena cilia in the cell medial region beat with a temporal delay, whereby the posteriorly positioned cilium is approximately 3 ms ahead in its beat cycle (Soh et al., 2022). To account for this temporal delay, the applied forces were coordinated with the ciliary beat cycle. Thus, the force that is exerted by the anterior BB is a function of its cilium’s position during the power stroke, which is 3 ms behind in its beat cycle relative to its posterior cilium neighbor. The combination of these forces resulted in a 60 nm relative translation of the distal end relative to the proximal end of the BB during the power stroke (Figure 4E). A force amplitude of 900 pN (estimated 3600 pN at large deformation) was required to create the BB counterbend that has a comparable magnitude to those observed in EM tomography results. This magnitude is comparable to the total shear force produced between two adjacent doublet MTs if all the dynein arms generate ∼2 pN each.

Movie S9.

Download video file ^{(1.4MB, mov)}

30° C model side. Side view of a computational model representing 30°C T. thermophila BB and ciliary movements when forces are produced through the SF and cell cortex (Figures 3, 4, and S3).

Movie S10.

Download video file ^{(1.1MB, mov)}

30° C model top. Top view of a computational model representing 30°C T. thermophila BB and ciliary movements when forces are produced through the SF and cell cortex (Figures 3, 4, and S3).

Indeed, imposing this force through the SF produced a negative bending pattern of the BB similar to that observed by EM tomography (Figure 4E). Furthermore, this generated a counterbend at the ciliary base suggesting that it is possible for intracellular SF forces to alter ciliary power strokes through BB bending and force transmission to the cilium (Figure 4E). This suggests a model in which changes to BB bending upon environmental temperature change, occurs through altered force transmission by SFs. While much remains to be understood about these forces, they may be responsible for propagating mechanical coupling of neighboring BBs and impacting the ciliary waveform. These results highlight the importance of SFs in promoting cilia and BB dynamics.

SFs focus BB bending to triplet MTs 5 and 6

BB bending concentrates at the site of connection between BBs and SFs, suggesting that SFs are a focal point where ciliary forces are imposed upon BBs. To test whether SFs are responsible for focused BB bending through their attachments to neighboring BBs, we quantified BB bending in a T. thermophila genetic mutant with short SFs that lose connections with neighboring BBs (disA-1; Jerka-Dziadosz et al., 1995; Galati et al., 2014; Soh et al., 2020). BB bending was compared between WT and disA-1 cells at 30°C with cilia at matching positions at the end of the power stroke. Unlike WT BBs, disA-1 BBs had increased levels of triplet MT curvature in both positive and negative directions within the same BB (Figure 5). This bending or buckling is distributed throughout BBs without focused bending at triplet MTs 5 and 6, as observed in WT BBs (Figure 5 and Supplemental Figure S5). BB bending is observed at other triplet MTs (e.g., triplet MT 4) that are not connected to SFs but are linked to the transverse MTs (Figure 5B and Supplemental Figure S5, D–F). Additionally, WT BBs at 30°C bend primarily in the BB’s medial region while disA-1 BBs bend throughout the BB length (Figure 5, A and B). Thus, SF length or connectivity to neighboring BBs and the cell cortex is important for focused bending of the medial region of BB triplet MTs 5 and 6 that normally connect to SFs.

FIGURE 5:

SFs focus bending within the BB. (A) The direction and location of BB bending at the end of the power stroke changes in disA-1 mutants that have short SFs and are disconnected from neighboring BBs and the cell cortex. The graphs represent the means and SDs of normalized maximum values for each proximal to distal bin (left graph) or each triplet MT (right graph) as in Figure 2. (B) SF connections promote consistent negative bending focused at triplet MTs 5 and 6. Left heatmap shows a 30°C WT BB curvature. The middle heatmap shows a 30°C disA-1 BB curvature. Right heatmap quantifies the difference in triplet MT bending between WT and disA-1 BB curvature, where the greatest difference is in the elevated positive bending in triplet MT 4. Black box denotes >75% difference from other bins (p > 0.05). (C) Schematic model showing that SF connections are important for negative BB curvature and focused bending at triplet MTs 5 and 6. disA-1 BBs exhibit both positive and negative curvature, with positive curvature predominating across the BB. Scale bar, 200 nm.

A major difference between WT and disA-1 BB bending at 30°C is that disA-1 BB bending is mostly positive while WT BB bending is mostly negative (Figure 5B). This demonstrates experimentally that SFs at 30°C promote negative bending in BBs at the end of the power stroke as disA-1 mutant cell SFs are disconnected from neighboring BBs and therefore weaken force transmission between BBs. The lack of negative bending in disA-1 BBs is consistent with our computational simulation that reproduced negative bending in WT BBs by the addition of forces transmitted through SFs (Figure 4E). We hypothesize that SF linkages to the anterior BB allow for physical coupling between neighboring BBs that regulate BB bending and ciliary beating. Importantly, BBs in disA-1 cells do not display WT 37°C BB bending patterns as focal bending at the medial-proximal regions of triplet MTs 5 and 6 was not observed. Moreover, when the SF is detached in the computer simulations, we observe a similar result. The mean curvatures over the entire BB at the end of the beat stroke are similar between the two models (approximately 0.4 rad/μm). However, the maximum curvature in triplet MTs 5 and 6 in the baseline model is 0.92 rad/μm but exhibits a 20% reduction in the detached SF model (0.74 rad/μm). Removal of the SF led to an increase in curvature in triplet MT 9 from 0.73 in the baseline model to 1.28 rad/μm in the detached SF model. Triplet MT 9 attaches to the pcMTs that link to the cell cortex, and this suggests that a balance between anchorage structures is important for BB bending. This indicates that SF length and connectivity to neighboring BBs and/or the cell cortex is important for transmission of ciliary forces through triplet MTs 5 and 6. We predict that this asymmetric force transmission toward the regions of the BB that face the cell anterior is utilized for coordinated ciliary beating and ciliary waveform modulation.

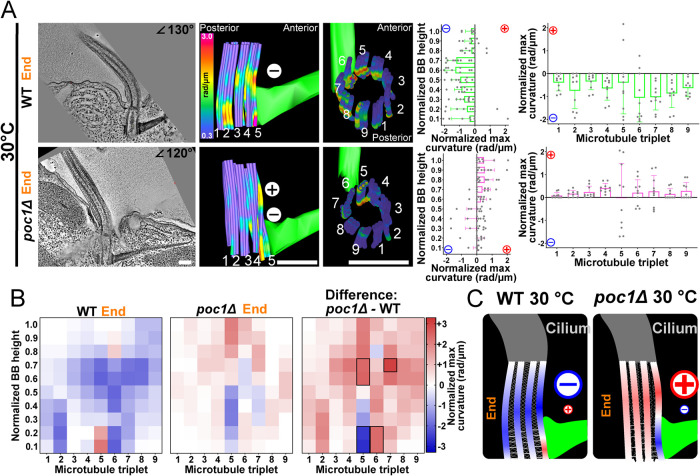
Poc1 is required for dissipating forces in BB bending to neighboring triplet MTs

BB triplet MTs are laterally interconnected by structures including the A-C linkers and the helical inner scaffold (Meehl et al., 2016; Li et al., 2019; Le Guennec et al., 2020). The Poc1 protein resides at the BB helical inner scaffold and is enriched at the proximal region of BBs (Pearson et al., 2009; Bayless et al., 2016; Meehl et al., 2016; Le Guennec et al., 2020). When Poc1 is lost, A-C linker distribution is disrupted, triplet MTs 1 and 2 facing the cell posterior preferentially disassemble, and BB instability increases with increasing ciliary force (Pearson et al., 2009; Bayless et al., 2016; Meehl et al., 2016). To test whether BB triplet MT interconnectivity is important for normal BB bending, we quantified triplet MT bending in WT and poc1Δ BBs at 30°C. In contrast to WT BBs, poc1Δ BBs exhibit isolated regions of both positive and negative triplet MT bending within the same BB, particularly on triplet MT 5 (Figure 6A and Supplemental Figure S6). Curvature in WT BBs at 30°C is distributed across multiple triplet MTs. Importantly, this was not observed in poc1Δ BBs (Figure 6A and Supplemental Figure S6). poc1Δ BB bending is specifically enriched at triplet MT 5, which exhibits a higher degree of curvature in both the positive and negative directions (Figure 6, A and B). In addition, the overall direction of poc1Δ BB bending is positive as compared with the negative bending in WT BBs at 30°C (Figure 6B). In the poc1Δ, negative bending is limited to triplet MT 5 and is absent in neighboring triplets. This suggests that forces from SFs are received by triplet MT 5 but are not effectively dissipated to neighboring triplet MTs in poc1Δ cells. These data support a model where Poc1, by promoting linkage between neighboring triplet MTs, is important for the distribution of forces between triplet MTs (Figure 6C; Li et al., 2019).

FIGURE 6:

Poc1 distributes coordinated BB bending. (A) The direction and location of BB bending at the end of the power stroke changes in poc1Δ at 30°C. Middle panels are model views (side and top) of BB triplet MTs from the corresponding EM tomogram. The graphs represent the means and SDs of normalized maximum values for each proximal to distal bin (left graph) or each triplet MT (right graph) as in Figure 2. (B) poc1Δ BBs show both positive and negative bending focused on triplet MT 5. Left heatmap shows 30°C WT BB curvature. Middle heatmap shows 30°C poc1Δ BB. Right heatmap quantifies the difference between WT and poc1Δ BBs. The greatest difference occurs in triplet MTs 5–7, which display curvature in opposing directions Blue (negative) and red (positive) colors indicate the direction of curvature relative to the cell’s anterior–posterior axis. Black boxes denote >75% difference from other bins (p > 0.05). (C) Schematic model of triplet MT connections as important for BB bending patterns. poc1Δ BBs have high positive and negative curvature on triplet MT 5 that is not effectively propagated across the BB. Scale bars, 200 μm.

poc1Δ BBs can also exhibit highly variable curvature in triplet MTs 1, 7, 8, and 9 (Supplemental Figure S6, D and E). This region of high variability corresponds to the triplet MTs that face the cell posterior and specifically disassemble when experiencing ciliary forces in poc1Δ cells (Supplemental Figure S6, G and H; Meehl et al., 2016). We suggest that the elevated and variable curvature in these triplet MTs contributes to BB instability in poc1Δ cells. This elevated and variable triplet MT curvature may be due to defective transmission of ciliary forces between triplet MTs resulting in local focal bending events that cannot be redistributed to neighboring triplet MTs. It remains unclear why posterior-facing triplet MTs more unstable when our studies suggest that most bending occurs at triplet MT 5. It could be that attachment to the SF stabilizes triplet MT 5, whereas variable bending in posterior-facing triplet MTs 1, 2, 8, and 9 lacks supporting protection and leads to their instability, breakage, and loss. To capture triplet MT disassembly event intermediates, we performed thin-section EM of chemically fixed poc1Δ cells at high temperature to escalate BB disassembly. As found previously, we observed weak triplet MT breakage near the middle of the BB, but this appears to be a transient event that is difficult to capture in our fixed-cell EM analyses (Supplemental Figure S6, G–I; Pearson et al., 2009). In summary, triplet MT interconnectivity contributed by the helical inner scaffold and/or the A-C linkers produce consistent and distributed BB bending patterns and likely act to distribute forces from both cilia and SFs (Figure 6C).

Improved simulation using triplet MT connections and SF forces

To simulate the effect of Poc1 loss on BBs, the stiffness of the A-C linkers in the model was reduced by an order of magnitude. This led to an increase in BB rocking concentrated in the front-to-back direction (Table 2), an increase in the maximum curvature in triplet MTs connected to external structures (triplet MTs 4, 5, 6, and 9), and a relative decrease in the maximum curvature of triplet MTs not connected to external structures (Table 2). Interestingly, the average interdoublet shearing at the transition zone increased by ∼20% when the A-C linker stiffness was reduced in the model, indicating an increase in BB triplet MT shearing (Table 1).

Because Poc1 also localizes to the helical inner scaffold, we next included a predicted helical inner scaffold into the model (Le Guennec et al., 2020). The overall dimensions of the modeled helical inner scaffold (155 nm diameter and extending 150–450 nm from the base of the BB) were based on the structure obtained for Paramecium tetraurelia BBs (Le Guennec et al., 2020). The helical inner scaffold was parameterized by assigning it an elastic modulus of ∼1 GPa and varying the diameter of the beams from 2 to 16 nm. At small diameters (2 nm), the helical inner scaffold had a minimal effect on the overall BB bending, but as the diameters were increased, overall BB bending decreased. Thus, the helical inner scaffold has a stabilizing effect on BBs.

We hypothesized that the helical inner scaffold may account for some of the observed differences between the EM tomography and the computer model, including the concentration of the medial bend at the end of the power stroke that was observed in the EM tomography (Figure 2A). In contrast, the computer model exhibited a more evenly distributed bend (Figure 3B). Indeed, in the model at low-to-moderate helical inner scaffold stiffness, the helical inner scaffold suppresses curvature in the distal region of triplet MTs 5 and 6, while having a minimal impact on the curvature of those triplets adjacent to the SF (Supplemental Figure S3D). However, we were not able to completely recreate the medial-to-distal diminishing average curvature observed in the EM tomography. A possible explanation for these differences is material nonlinearities not accounted for in the model. Regions of elevated curvature adjacent to the SF in triplet MTs 5 and 6 in the model may lead to increased nonlinear local bending (“kinking”) that more closely resembles the EM tomography.

Though the 37°C model captures many aspects of the deformations observed by EM tomography, as noted above, differences remain (Supplemental Figure S3A). Significantly, the average BB curvature at 37°C decreases from the medial to the distal region, thereby concentrating medial curvature at the end of the power stroke (Figure 2A). In the model, the average curvature remains nearly constant. In our initial model (Figure 3), the SF at 37°C is longer and attaches to the cell cortex, causing it to be a stationary structure, whereas the shorter SF at 30°C is detached from the cell cortex and is therefore able to transmit motion and force between the adjacent BBs that the SF couples. However, to determine whether SF pushing and/or pulling forces could be responsible for differences between the model and the data, we modulated the phase and magnitude of the periodic force applied to the SF attachment point. If the SF force transmission is reversed in phase from the 30°C model—pulling on the BB during the power stroke and pushing on the BB during the recovery stroke—it magnifies the curvature of the medial region of the BB (with a twofold increase in triplet MTs 5 and 6; Supplemental Figure S3D). The overall effect of this is that the average curvature is elevated in the medial region. However, the distal curvatures are not as low as those observed in the EM tomography.

To attempt to reduce distal curvatures in the model, the reverse SF force was applied to the model including the helical inner scaffold. Though adding the helical inner scaffold did reduce curvature in the distal region, it did not reduce the average curvature in that region to below the levels of curvature in the proximal region, as observed in the EM tomography (Figure 2A). The helical inner scaffold in this case has the additional effect of transmitting the elevated curvature adjacent to the SF in triplet MTs 5 and 6 to triplet MTs 7 and 8, which was not observed in the EM tomography. Thus, additional modeling parameters are required to resolve the bending observed in the EM tomography.

DISCUSSION

Here we illustrate how BBs receive and transmit mechanical forces imposed by beating cilia and propose a model in which transmission of those forces is a determinant of the ciliary waveform and plays a role in coordinating ciliary beating. Evidence for each part of this model is discussed below.

Flagellar and ciliary basal deformation

Previously, BBs were thought to be rigid and stable structures. However, studies in mammalian and urchin sperm have shown how basal sliding forces are propagated to the base of the axoneme. Sperm flagella, doublet MTs link to the connecting piece at the base of the cilium via outer dense fibers. Sliding forces then impose both compressive and tensile forces upon the connecting piece, thereby creating deformations and changes to the position of the sperm head. Moreover, changes to force resistance by the basal domain are proposed to impact flagellar beating by controlling switching in beating direction and changes to the waveform. Thus, basal sliding forces both are imposed upon the base of the flagellum and tune flagellar activities. A key question is whether the connecting piece at the sperm flagellum and the BB at the cilium share similar activities in limiting basal sliding and controlling ciliary beating (Warner and Satir, 1974; Vernon and Woolley, 2004; Riedel-Kruse et al., 2007).

Our studies show that BBs experience basal sliding forces that bend triplet MTs experiencing compression. The observed bending patterns require attachments to SFs that, along with postciliary MTs and transverse MTs, anchor BBs and cilia to each other and to the cell cortex. Changes to SF anchorage and movement may be responsible for changes to the ciliary waveform. This is consistent with intracellular coupling found for Tetrahymena cilia and Chlamydomonas flagella (Quaranta et al., 2015; Wan and Goldstein, 2016; Soh et al., 2022). Moreover, linkages within the BBs support resistance to basal sliding forces, as predicted by Vernon and Woolley (2004). Using a poc1Δ mutant strain, we observed that disruption of intra-BB linkages prevents the distribution of BB sliding forces between neighboring triplet MTs, compromising the stability of BBs as they resist basal sliding forces. These linkages may be in the form of A-C linkers and/or the helical inner scaffold (Li et al., 2012; Meehl et al., 2016; Le Guennec et al., 2020). Our data demonstrate that BBs are deformed by ciliary sliding forces and these deformations are modulated by both intra- and inter-BB stability factors, namely Poc1, which affects connections between triplet MTs and the SF that extends from the BB toward the BB directly anterior in the ciliary row.

Conservation of BB triplet MT bending

Motile cilia are present across all eukaryotic lineages (Cavalier-Smith, 2002; Carvalho-Santos et al., 2011; Hodges et al., 2012). Force transmission from motile cilia to BBs is likely conserved. We hypothesize that organisms with cilia and BB-appendages similar to those of T. thermophila also exhibit analogous BB bending patterns. Upon reinspection of published EM images, we find BB bending in T. thermophila to be apparent in previous publications (Figure 1 and Supplemental Figure S1; Allen, 1967, 1969). Triplet MT bending is also observed across several subphyla or classes of ciliate BBs (Allen, 2007; Gogendeau et al., 2020). Additionally, BB triplet MTs of algae, such as Chlamydomonas, bend (Sloboda and Rosenbaum, 2007). The bending of vertebrate multiciliary arrays is less evident, possibly because of rotational triplet MT bending (Anderson, 1972).

While BB and BB-appendage structures of vertebrate multiciliary arrays have differences from single-celled organisms, we suspect that BB curvature will similarly be focused at junctions between BBs and BB-appendage structures. For example, BB bending may focus on connection sites between BB triplet MTs and the basal foot that nucleates the MTs for BB orientation and interconnection. BB rootlets may also serve as a hinge point in BB bending. In mice, rootlets in multiciliated epithelia are SFs at the base of BBs that may distribute or restrict BB bending to the proximal ends of BBs as found in T. thermophila. In Xenopus, striated rootlets extend from the BB base and fan out to contact actin filaments from posterior BB neighbors (Werner et al., 2011). Moreover, mammalian and C. elegans rootlet structures are required for ciliary base stability (Yang et al., 2005; Mohan et al., 2013). Thus, the position, orientation, and interactions of BB-appendage structures at the cell cortex may influence the transmission of forces to and from neighboring cilia. We suspect that the BB bending patterns will differ between organisms based on the structures of the BBs, the BB-appendages, and the waveforms of the cilia. Importantly, we predict that the focused site of triplet MT bending will occur on the BB side that is opposite the direction of fluid flow as that is the site of sliding compression when cilia are at the end of their power stroke. For flagella that have relatively symmetric waveforms, connecting piece deformations or BB bending is expected to similarly occur in the plane of the ciliary beat stroke most prominently near BB-appendages (Avidor-Reiss and Turner, 2019; Khanal et al., 2021; Lindemann and Lesich, 2021). Thus, BBs and their associated structures adapt to the ciliary waveform and environment in which they beat to maximize effective cell motility and fluid flow.

Response of BB bending, ciliary waveform, and SFs to environmental change

BB bending and ciliary waveform adjust with an environmental change to temperature (Rikmenspoel, 1984; Teff et al., 2008; Geyer et al., 2022). Both BB bending patterns and ciliary bending waveforms are different when comparing cells at 37 and 30°C (Figure 4, C and D). While the BB bending pattern at 37°C can nearly be computationally modeled utilizing the forces of the ciliary bend alone, the inverse bending observed at 30°C could not be recapitulated by changing the cilia bending waveform itself. SFs decrease in length at lower temperatures and lose anchorage sites to the cell cortex while maintaining connections to the postciliary MTs of the anterior BB (Galati et al., 2014; Soh et al., 2020). This may allow the SF more freedom of motion to transmit mechanical forces from the anterior BB. Using computer modeling, we show that pushing forces imposed on BBs by SFs can reverse the direction of BB bending (Figure 4E). The negative bending in these BBs also propagates to the cilium. The cilium bending in the computer model increases at the end of the power stroke, particularly at its proximal or basal region, and this is consistent with bending changes observed in live imaging of beating cilia (Figure 4, C and D). Therefore, changes to ciliary waveforms associated with changing environmental conditions may well be produced through changing intracellular force transmission through SFs and altered deformations of BBs.

T. thermophila disA-1 mutants with defective SFs provide further insight into how force transmission through BBs and SFs can impact the ciliary waveform. disA-1 mutants do not have known ciliary defects, yet they display altered ciliary waveforms compared with control cilia (Soh et al., 2022). Without a fully functional SF, the BB counterbend at 30°C is abolished (Figure 5) and could account for the altered ciliary waveform. This is consistent with computer models proposing that the mechanical properties of BBs and coupling between BBs can regulate ciliary waveform (Riedel-Kruse et al., 2007; Lesich et al., 2016; Lindemann and Lesich, 2016; Guo et al., 2021).

SFs connect BBs and ciliary units

Taken together, a model comes into focus: SFs point anteriorly and contact the posterior-facing postciliary MT bundle from the anterior BB and also contact the nearby cortical cytoskeleton (this study; [Soh et al., 2020]). Thus, forces from anterior BBs and cilia could be transmitted to neighboring BBs through the physical connections between postciliary MT bundles and SFs. These physical connections are hypothesized to provide a means of intracellular physical coupling to regulate the synchrony between beating cilia. We propose that changes to BB bending and ciliary waveform are achieved through force transmission from adjacent ciliary units through postciliary MT bundles and SFs. At 30°C, SFs shorten and lose connections with the cortical cytoskeleton adjacent to the anterior BBs (Soh et al., 2020). If this connection of SFs to the cortical cytoskeleton acts to ground ciliary forces, then loss of this secondary connection could increase force transmission between postciliary MTs and SFs of adjacent BBs and cilia. We suggest that this creates a route for the increased transmission of ciliary forces between adjacent ciliary units. Increasing the forces transmitted between the two ciliary units could explain the increase in overall BB bending and the directional inversion in the BB bend when comparing BBs at 37°C to those at 30°C. Thus, force transmission between ciliary units is modulated by the length and connectivity of SFs (and possibly postciliary MTs). In turn, this impacts BB bending patterns. This intracellular coupling between adjacent BBs and cilia might also provide a means for regulating ciliary beating and metachronal synchrony. Further studies are required to capture the precise dynamics for how pushing and pulling forces may be produced between neighboring BBs using SFs and how this might be controlled. We propose that cells modulate ciliary waveforms (e.g., in response to environmental temperature changes) by altering BB bending through the tuning of force transmission from one ciliary unit through the pcMT SF connection to its posterior neighbor. In this model, the SF is of particular importance as it is the component that modulates how much force is received by the BB from its anterior neighbor.

In summary, this study demonstrates that BBs bend in response to forces from beating cilia. Asymmetric forces from beating cilia are transmitted into the cell through BB bending and focused on the BB triplet MTs that connect to SFs. Both cilia waveform and BB bending are responsive to temperature changes, and these differences can be explained by SF force transmission altering BB bending patterns. Both the length and connectivity of SFs and the doublet MT interconnections are important for normal BB bending patterns. Together, we propose a model where cilia, BBs, and BB-appendages interact through the transmission of mechanical forces for ciliary beating and directed fluid flow.

MATERIALS AND METHODS

Request a protocol through Bio-protocol.

Tetrahymena strains and culture

Tetrahymena thermophila cells B2086, SB1969, disA-1, and poc1Δ were obtained from the Tetrahymena Stock Center (https://tetrahymena.vet.cornell.edu/index.php). T. thermophila strains were cultured in 2% SPP media (2% protease peptone, 0.1% yeast extract, 0.2% glucose, and 0.003% Fe-EDTA) at 30°C unless otherwise indicated. Cells collected for analysis were grown to mid–log phase (approximately 3 × 10⁵ cells/ml). Cell counts were determined using a Coulter Counter Z1 (Beckman Coulter). The forces from ciliary beating were manipulated by altering temperature (Galati et al., 2014). For temperature shift experiments, cells were transferred into fresh SPP media and incubated for 24 h at the specified temperatures.

Electron microscopy and tomography

Cells were prepared for electron microscopy (EM) and tomography as previously described (Meehl et al., 2009; Giddings et al., 2010). Cells were gently spun in 2% SPP that contains 15% dextran (molecular weight 9000–11,000; Sigma-Aldrich) and 5% bovine serum albumin. Cells were concentrated and transferred to a sample holder and high-pressure frozen using a Wohlwend Compact 02 high-pressure freezer (Technotrade International). After low-temperature freeze substitution in 0.25% glutaraldehyde and 0.1% uranyl acetate in acetone, cells were slowly infiltrated with Lowicryl HM20 resin. Serial thick (250–300 nm) sections were cut using a Leica UCT ultramicrotome. The serial sections were collected on Formvar-coated copper slot grids and poststained with 2% aqueous uranyl acetate for 4 min followed by Reynold’s lead citrate for 3 min.

For each condition in this study, 100–150 BBs were screened in 5–15 cells (Table 3). BBs in the beginning, middle, or end of the power stroke were analyzed. Where tomograms were acquired, BB triplet MTs were modeled in three dimensions, and their curvature was quantified (Figure 2 and Supplemental Figure S2). Dual-axis tilt series (−60 to +60°) of Tetrahymena cells were collected on a Tecnai F30 intermediate voltage electron microscope (ThermoFisher). Images were acquired using the SerialEM acquisition program with a Gatan CCD camera at 1.2 or 1.5 nm/pixel (Mastronarde, 2005). Serial section tomograms of Tetrahymena cortical structures were generated using the IMOD software package (Kremer et al., 1996; Mastronarde, 1997; Giddings et al., 2010). Tomograms were reconstructed and modeled using the IMOD software package (bio3d.colorado.edu/imod/).

3D tomographic modeling and quantification

3D models of BBs were generated using the IMOD software package (Kremer et al., 1996; Mastronarde, 1997; Giddings et al., 2010). Using tomograms from tilt series, BBs were oriented in 3D space to obtain top-down views (looking down the cylinder of the BB). BB MTs were modeled as open contours in five-slice max-projected z-stacks by picking five and six points along each of the MTs. MTs were identified as hollow, circular electron densities with diameters of approximately 25 nm. In the event that the exact MT location was difficult to discern, crescent-shaped electron densities and relative location were used to define the MT location. The relative MT locations were informed by the known conserved triplet MT structure. No events deviating from the conserved structure were observed except in poc1 mutant BBs when triplet MTs were occasionally missing (Supplemental Figure S6, F and G). IMOD drawing tool’s Smooth Contours function was used to smoothen modeled MTs by adding 10× intermediate points (50–60 total points). The smooth tensile fraction was 0.5 pixels, and smooth point distance was 5 pixels, points were added in equal distribution regardless of Z-step, and originally selected contour points were locked in place before smoothening. These points were then manually confirmed to be within the boundaries of the MTs in the tomograms. After smoothing modeled MTs, the curvature was quantified using the imodcurvature function. Imodcurvature calculates curvature based on circle fitting to surrounding points over a length of 110 pixels (63 nm). For points near the end of the contour, the fit is to half of that length on the side away from the end and to whatever length is available on the side toward the end. This calculation was performed serially for every point with two flanking points. The curvature values calculated by imodcurvature are also directly applied as a heatmap on the modeled MTs in IMOD. BB curvature is binned as a 10 × 9 array, whereby curvature values along the length of a BB were split into 10 bins and the nine triplet MTs were split into 9 bins, before averaging. The dynamic range of curvatures in all models is 0.3 rad/µm (dark purple) to 3.0 rad/µm (magenta). The maximum curvature values used in all quantifications were obtained by taking the maximum values from normalized bins equal to 1/10th the length of the MT for each MT in the BB. Normalization was conducted by subtracting the average lowest maximum values from each triplet MT in the BB. Triplet averages (nine triplet MTs) of these maximum values were then calculated for each corresponding bin in each triplet MT. Averaging based on triplet MTs is consistent with visual representations of MTs in IMOD, and curvature does not change based on MT identity (A, B, C tubule: unpublished data). BB curvature values were represented as 10 × 9 heatmap arrays (10 bins long, nine triplet MTs wide). 3D models of SFs were made in IMOD from side views of BBs. SFs were projected longitudinally and modeled as closed contours every three z-slices to generate a meshed model.

These EM tomogram modeling methods were analyzed for reproducibility through independent modeling. The same BB (Figure 2) was independently modeled by two of this article’s authors, A. Junker and A. Soh (Supplemental Figure S1F). The curvature amounts and patterns were consistent between the two independent models, where most curvature was found near the base-middle of triplet MTs 5 and 6. The only statistically significant difference (p < 0.05) was in triplet MT 1. This difference is located at a region of low curvature and does not impact the overall pattern of curvature found in the BB.

Computational modeling

The computational (finite-element) model of the cilium, BB, and BB-appendage structures was created in COMSOL Multiphysics using the Beam interface within the Structural Mechanics module (COMSOL Multiphysics v. 5.6; www.comsol.com; COMSOL AB, Stockholm, Sweden). All MT filaments including axonemal doublet MTs and BB triplet MTs were modeled as slender (Euler–Bernoulli) beams with linear elastic material properties. The central pair MTs were modeled as a single beam with an increased area moment of inertia about the non–power stroke transverse bending axis (to model the effect of two coupled MT singlets). All beam connections are modeled as fixed. Viscous drag was applied to the central pair using resistive force coefficients (Gray and Hancock, 1955; Bayly et al., 2011).

RSs were modeled using beam elements: 30 circular arrays of nine radially oriented beams were linearly patterned along the length of the model of the axoneme. Each beam represents the effects of multiple RSs as the actual number of RSs in the axoneme is much greater than the number of spokes in the model. Estimates for RS shear and normal stiffness were used to calculate flexural and axial rigidity for these beams. Spoke connections were modeled as fixed joints at the central and outer filaments. Though the spoke connections themselves do not slide, compliance of the spokes allows relative sliding of the axial filaments.

Nexin-dynein regulatory complex (N-DRC) linkers were modeled using extrusion coupling operators within COMSOL, which make it possible to model interdoublet stiffness as an applied-force function of relative displacement. The effect of this modeling is a continuous elastic connection between adjacent doublets that creates normal stiffness but not shear stiffness at small deformations.

In the BB, AC-linkers and the proximal CW structure were modeled using a longitudinally oriented linear pattern of representative beams. BB accessory structures such as the SF, pcMT, and transverse MT (tMT) were modeled as beams. Axial and flexural rigidity for these elements was calculated based on estimates of the physical properties of these structures. The helical inner structure was modeled as an array of nonagons with vertices located on a 155 nm circle. This array was patterned along the BB axis 150–450 nm from the base of the BB. Vertices of each nonagon were connected along the BB axis and to the neighboring MT triplets by beam elements. As with other structures represented in this model, the individual beam elements represent the overall effect of the biological structures and are not intended to be an accurate geometric reproduction. All interbeam end connections were modeled as fixed joints.

Connections between the modeled structure and structures external to the model, such as the cellular cortex and other BBs, were modeled using the spring foundation constraint. This allows elastic connections (with translational and rotational spring constants) to fixed points representing other cellular structures. In cases where those external structures were modeled as being in motion, the foundation attachment point was given a time-dependent prescribed displacement. Forces applied to the SF tip and cortical attachments were applied in this way.

Beam elements in COMSOL use cubic shape functions for displacements. Large deformations in beam structures are obtained through a combination of element-level deformations as well as rigid body translations and rotations of linear beam elements. The beam mesh was therefore refined along the BB triplet MTs to ensure that deformations of individual elements were small. Mesh refinement studies were used to confirm convergence of curvature values in the BB triplet MTs in test studies. Meshing of RSs was restricted to one element per spoke to reduce undesirable behavior such as buckling of spokes, which will prevent convergence of the solution.

Dynein forces were modeled as distributed axial forces that remain tangentially applied to doublets under time-dependent deformation (follower loads). Every base-ward force on one doublet must be balanced by a tip-ward force on the adjacent incrementally numbered doublet. This ensures that the net internal forces are balanced. Additionally, a distributed moment must be applied to counteract the force pair and keep internally produced moments in balance (Hines and Blum, 1983; Brokaw, 1985; Xu et al., 2016). For simplicity of modeling, dynein force was prescribed using a “switching” model in which dynein arrays on the power stroke (doublet MTs 5–9) and on the recovery stroke (doublet MTs 9–4) sides of the beat plane are alternately activated (with uniform force along the length of the axoneme) to produce the power and recovery strokes (Sale and Satir, 1977; Satir and Matsuoka, 1989). In most cases, this was applied using a sinusoidal function of time where dynein motors on the power stroke side of the axoneme activate in proportion to the positive regions of the sine wave and dynein motors on the recovery stroke side activate in proportion to the negative regions of the sine wave. In some specific studies, a prescribed spatiotemporally propagating activation pattern was used to drive the system.

Time-dependent studies were solved using backward differentiation formula (BDF) time stepping with a relative error tolerance of 10^–3. Fully coupled nonlinear equations were solved using Newton’s method with automatic damping. Geometrically nonlinear effects were included in the solution. Inertial effects were considered negligible and not included in the solution.

This model of the axoneme (like all models) has limitations. RSs likely slide along the central pair, and N-DRC links may slide along doublets, but sliding at joints is challenging to simulate, and is not included in the current finite-element model. Instead, deformations of spokes and links are limited by keeping dynein forces low, maintaining deformations in a regime where RS beams and N-DRC couplings do not become taut. Triplet MT stiffnesses were kept the same as doublet stiffnesses to increase curvature at lower dynein forces. For visualization and direct comparison with EM data, deformations and extracted curvature values were amplified fourfold.

A key objective was to accurately model how dynein forces drive ciliary beating; however, some compromises were necessary to limit the complexity of the model. First, dynein activation was prescribed along the length of the cilium, without modeling any specific theory of ciliary beat generation (of which none is yet generally accepted). Second, at large deformations, approximations in the model become increasingly inaccurate. For example, the moments associated with dynein forces acting across the axoneme diameter are oriented about an axis perpendicular to the dominant plane of beating and do not reorient with out-of-plane deformation of the axoneme. This leads to internal moment imbalances at large deformations. Additionally, at the discretization level (mesh size) used to generate model results, internal moments from interdoublet links (modeled by “extrusion coupling” in the finite-element model) do not balance. This effect approximately doubles the applied moment at maximum dynein load, which increases the bending of the cilium for a given level of dynein activity. Increasing the mesh resolution resolves the moment imbalance but prevents the model from converging. Finally, applied dynein forces are tangent to individual filaments, which leads to an applied force imbalance when loaded filaments become nonparallel (a maximum imbalance of 1.8 pN was calculated, which is a fraction of a percent relative to a total interdoublet force of 700 pN).

Despite these imperfections of the model, it recapitulates many aspects of observed BB deformation and serves as a useful tool for gaining insight into the physical BB-cilium system and understanding the roles individual components (SF, AC-linkers, pcMT, tMT) serve in stabilizing the BB against forces transmitted from the cilium.

Interfilament sliding in computational model

Interdoublet sliding between doublets n and n + 1 was evaluated by first calculating the position vector, δ(s), from a point on doublet MT n to a point the same distance, s, along the length of doublet MT n + 1 and then projecting that position vector onto the tangent vector, t(s), of doublet n using the dot product: Δ(s) = δ(s)⋅t(s). As noted above, sliding between filaments (doublets and central pair) is permitted by elastic compliance of spokes and links; sliding at attachment points was not modeled. To avoid undesired structural nonlinearities that prevent convergence of the simulation, relative sliding between adjacent doublet MTs was limited by keeping the maximum distributed dynein force low: <125 pN/µm. Realistic model behavior, expected to be obtained at fourfold-higher dynein forces, was obtained by scaling deformations by a factor of four. Maximum sliding amplitude at the tip of the small-deformation model was 38 nm between doublet MTs 6 and 7. To obtain the predicted sliding at deformations comparable to those observed, this amplitude was multiplied by four to obtain the predicted maximum relative sliding amplitude of 151 nm between triplet MTs 6 and 7 (Table 1).

Computational model parameters

An additional challenge of the computer simulation is the estimation of the physical properties of the nanoscale structures present in the cilium and accessory structures. In cases where experimentally obtained estimates of properties were available, they were used in the model as either fixed estimates or plausible ranges. These included axoneme flexural rigidity, dynein force, N-DRC stiffness, and resistive force coefficients for a cilium in water, as well as parameters such as beat period and posterior–anterior phase lag (Table 1; Supplemental Figure S3).

Where experimental estimates of parameter values were not available, ballpark estimates were made based on the size, shape, and estimated material properties of structures. Simulation parameter sweeps were run to determine sensitivity of the model to the parameters and to bring the overall model behavior in-line with observed behavior. Initially, this parameter estimation and refinement was run on a 2D version of the model for rapid iteration before building the more complex 3D model.

Live cell imaging of cilia beating

Using a magnetism-based strategy, T. thermophila cells were immobilized and their cilia were imaged via fast time-lapse DIC microscopy (Soh et al., 2022). Briefly, cells were fed with iron particles (Sigma-Aldrich) that were suspended in SPP media. Next, cells were immobilized inside microfluidics chambers using bar magnets that are positioned along the chamber. All experiments were performed at the respective temperatures (30 and 37°C) using a microscope stage incubator (Pathology Devices). Imaging was performed using an inverted wide-field microscope (Ti Eclipse; Nikon). A 60× Plan Apochromat (NA 1.4) objective lens (Nikon) was used. 2D movies were acquired using a scientific complementary metal-oxide semiconductor camera (Zyla; Andor Technology) at approximately 650 frames per second.

Cilia waveform and curvature analyses were focused on the cilium power stroke axis using a previously described approach (Bottier et al., 2019). Briefly, consecutive movie frames of cilia were manually traced and fitted with a 2nd-order polynomial line function. Owing to reduced contrast at the cilium base, analysis was performed on the distal 4.5 µm of all tracked cilia. Curvature along the cilium length was quantified. Curvature extrapolation was applied for both ends of all traced cilia. To ensure that the curvature of each cilium is uniformly weighted, each cilium was tracked for six beat cycles. Cilia waveform and curvature were obtained by averaging across nine cilia. All cilia were aligned along the same axis based on the relative of the anterior BB’s position.

Data representation and graphing

Red–blue heatmaps indicate differences in BB bending between different parts of the ciliary power stroke. The location, level, and direction of the normalized average in maximum curvature are determined by the axis and colors. The location of bending is indicated by the axis, y-axis indicates relative proximal distal height on BBs broken into 10 bins (normalized BB height, one bin = 1/10th the height of a BB), and x-axis indicates the triplet (1–9). The colors blue and red indicate the direction of curvature relative to the cell’s anterior–posterior axis (axis of the ciliary power stroke). Blue indicates negative bending = bending toward the cell anterior; red indicates positive bending = bending toward the cell posterior. Colored lines and bars on all dot plots indicate the mean and SD, respectively (Supplemental Figures S2 and S4–S6). Dots represent individual measurements; light gray lines indicate the location of zero.

Quantification and statistical analyses

All experimental data sets represent a minimum of three BB regions or triplet MTs. Comparisons between genotypes or conditions include only analyses from completely modeled BB with cilia in the same part of the beat stroke (beginning, middle, end, recovery) with no visible damage (Table 3). Statistical tests were run in Prism8 (GraphPad Software). A Shapiro–Wilk normality test was performed to assess for normal distribution. Normally distributed continuous data sets were analyzed using an unpaired, two-tailed Student’s t test. Non–normally distributed data sets were analyzed using the Mann–Whitney test. F tests were used to determine variance. This includes heatmaps of BB bending in which the normalized maximum values of each triplet in each proximal-distal bin were compared between two BBs. All p values are numerically presented. Analyses between curvature values in proximal-distal or lateral (triplet MTs) axes (Supplemental Figures S2 and S4–-S6) were compared against other triplet MTs of the same BB. One-way analyses of variance were performed on normally distributed data. Wilcoxon rank sum tests were performed to obtain p values on non–normally distributed data. All p values are numerically presented. Statistical significance in the variances between triplet MTs was tested using Bartlett’s test. Power statistics was performed to ensure ample sample size for the comparison between cilium curvature obtained from live imaging. A 5% margin of error and 95% confidence level were applied. Colored lines and bars on all dot plots indicate the mean and SD, respectively.

Abbreviations used:

BB

basal body

CW

cartwheel

EM

electron microscopy

MT

microtubule

PTM

posttranslational modification

SF

striated fiber.