Deep-learning-augmented computational miniature mesoscope

Abstract

Fluorescence microscopy is essential to study biological structures and dynamics. However, existing systems suffer from a trade-off between field of view (FOV), resolution, and system complexity, and thus cannot fulfill the emerging need for miniaturized platforms providing micron-scale resolution across centimeter-scale FOVs. To overcome this challenge, we developed a computational miniature mesoscope (CM²) that exploits a computational imaging strategy to enable single-shot, 3D high-resolution imaging across a wide FOV in a miniaturized platform. Here, we present CM² V2, which significantly advances both the hardware and computation. We complement the 3 × 3 microlens array with a hybrid emission filter that improves the imaging contrast by 5×, and design a 3D-printed free-form collimator for the LED illuminator that improves the excitation efficiency by 3×. To enable high-resolution reconstruction across a large volume, we develop an accurate and efficient 3D linear shift-variant (LSV) model to characterize spatially varying aberrations. We then train a multimodule deep learning model called CM²Net, using only the 3D-LSV simulator. We quantify the detection performance and localization accuracy of CM²Net to reconstruct fluorescent emitters under different conditions in simulation. We then show that CM²Net generalizes well to experiments and achieves accurate 3D reconstruction across a ~7-mm FOV and 800-μm depth, and provides ~6-μm lateral and ~25-μm axial resolution. This provides an ~8× better axial resolution and ~1400× faster speed compared to the previous model-based algorithm. We anticipate this simple, low-cost computational miniature imaging system will be useful for many large-scale 3D fluorescence imaging applications.

1. INTRODUCTION

Fluorescence microscopy is indispensable to study biological structures and dynamics [1]. However, the emerging need for compact, lightweight platforms achieving micron-scale resolution across centimeter-scale fields of view (FOVs) has created two new challenges. The first challenge is to overcome the barrier of large-scale imaging while preserving the resolution [2]. Recently developed tabletop systems [3,4] have enabled multiscale measurements with sufficient resolution; however, they are complex and bulky. The second challenge is to perform large-scale imaging in a compact, lightweight platform. Miniaturized fluorescence microscopes (i.e., miniscopes) [5] have enabled neural imaging in freely moving animals. However, most of the miniscopes rely on a gradient index (GRIN) objective lens [5] that limits the FOVs to <1 mm². Wide FOV miniscopes have recently been developed by replacing the GRIN with a compound lens [6,7], but at the cost of degraded resolution and increased size, weight, and system complexity. In general, fundamental physical limits preclude meeting the joint requirements of FOV, resolution, and miniaturization using conventional optics.

Computational imaging techniques have unique capabilities that overcome the limitations of conventional optics by jointly designing optics and algorithms. Light field microscopy (LFM) [8] and related technologies [9,10], achieve single-shot, high-resolution 3D fluorescence imaging [11,12]. LFM works by attaching a microlens array (MLA) to an existing microscope to collect both spatial and angular information, which enables the reconstruction of the 3D fluorescence from a single shot. Although miniaturized LFMs [13,14] enable single-shot 3D imaging on modified miniscope platforms, the FOV is limited by the GRIN lens. Lensless imaging is another computational imaging technique for single-shot 3D imaging, where a mask [15] or a diffuser (random microlens array) [16,17] is placed directly in front of a CMOS. However, the removal of focusing optics imposes penalties to the measurement’s contrast and SNR [4], severely limiting the sensitivity for imaging weak fluorescent signals [4].

We recently developed a computational miniature mesoscope (CM²) [18] that aims to overcome all the key limitations of FOV: resolution, contrast, SNR, and the size and weight in existing miniature fluorescence imaging systems. The CM² combines the merits of both LFM and lensless designs. It places a 3 × 3 MLA directly in front of a CMOS sensor for imaging, like the lensless design. This approach ensures compactness and is lightweight while further exploiting the microlens’s focusing power to provide high image contrast. The CM² captures an image with multiple views, which enables robust recovery of 3D fluorescence in a single shot, like the LFM. Previously, we demonstrated CM² V1 that achieved 3D fluorescence imaging in a 7 × 8 mm² FOV with 7-μm lateral and 200-μm axial resolution [18]. CM² V1 is the first standalone computational miniature fluorescence microscope with an integrated illumination module. Using a four-LED array in an oblique epi-illumination geometry, CM² V1 can uniformly illuminate a 1 − CM² FOV and achieves a ~24% light efficiency. In this work, we significantly advance the CM² technology and introduce CM² V2, which integrates innovations in both hardware and computation to address limitations in light efficiency, image contrast, reconstruction quality, and speed, as summarized in Fig. 1.

Fig. 1.

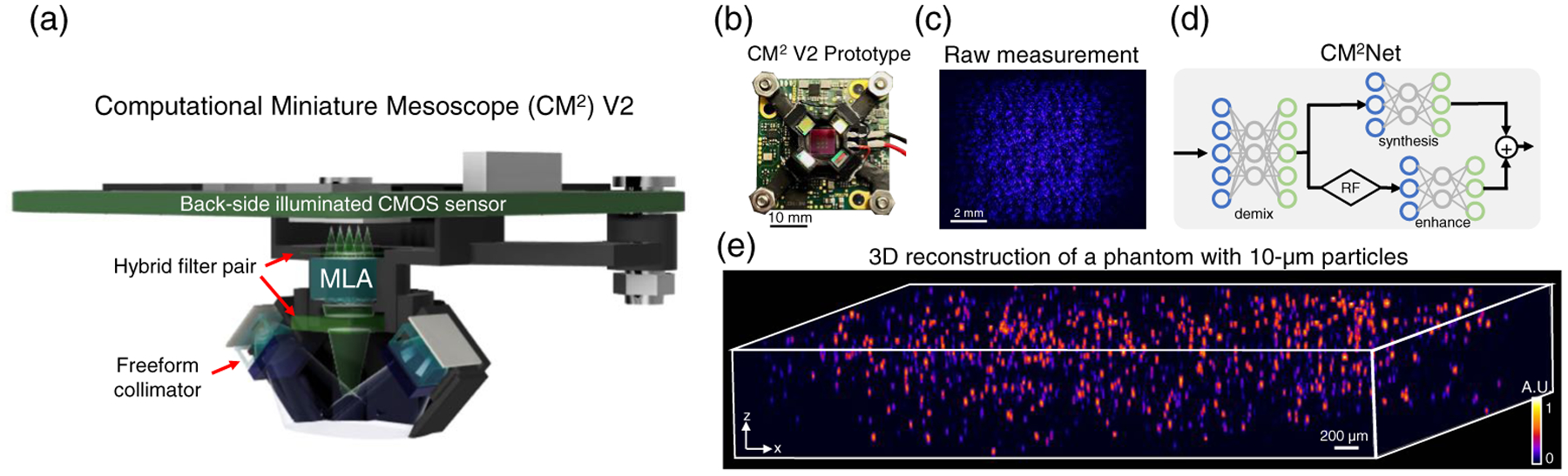
Overview of the computational miniature mesoscope (CM²) V2. (a) CM² V2 hardware platform features miniature LED illuminators for high-efficiency excitation, hybrid filters for spectral leakage rejection, and a BSI CMOS sensor for high-SNR measurement. (b) Photo of the assembled CM² V2 prototype. (c) Example CM² measurement from a volume consisting of 10-μm fluorescent beads. (d) CM²Net combines view demixing (demix), view synthesis (synthesis) and light-field refocusing (RF) enhancement (enhance) modules to achieve high-resolution, fast, and artifact-free 3D reconstruction. (e) CM²Net reconstruction from the measurement in (c), spanning a 7 mm FOV and 800-μm depth range.

On the hardware, we present updates that significantly improve the image contrast and light efficiency. First, we complement the 3 × 3 MLA with a hybrid emission filter [19], as shown in Fig. 1(a), that suppresses the spectral leakage suffered by the V1 system. Second, we design and 3D-print a miniature free-form LED collimator, as shown in Fig. 1(a), that is lightweight and improves the excitation efficiency while preserving the compactness. This new illuminator achieves ~80% efficiency, a ~3× improvement over the V1 design, and provides a confined uniform illumination with an up to 75 mW excitation power across an 8 mm diameter FOV. Built around a backside illuminated (BSI) CMOS, as shown in Figs. 1(a) and 1(b), CM² V2 achieves a 5× improvement in image contrast and captures high-SNR measurements in various experimental conditions, as shown in Fig. 1(c).

For the computation, we present a deep learning model, termed CM²Net, to achieve high-quality 3D reconstruction across a wide FOV with significantly improved axial resolution and reconstruction speed. Deep learning has recently emerged as the state of the art to solve many inverse problems in imaging [20]. Deep learning techniques, for example, have been developed for LFM to achieve high-resolution 3D reconstruction [21,22]. To devise a robust and accurate model, we consider several key features in the image formation of CM². The measurement contains light field information in 3 × 3 overlapped views, and the system is 3D linear shift-variant (LSV) [18]. CM²Net solves the single-shot 3D reconstruction problem using three functional modules, as shown in Fig. 1(d). The “view demixing” module separates the single measurement into 3 × 3 nonoverlapping views by exploiting the distinct aberration features from the array point spread functions (PSFs). The “view-synthesis” module and the “light field refocusing enhancement” module jointly perform high-resolution 3D reconstruction across a wide FOV using complementary information.

To incorporate the 3D-LSV information into the trained CM²Net, we develop an accurate and efficient 3D-LSV forward model to synthesize CM² measurements. Our 3D-LSV model is based on a low-rank approximation using a small number of experimentally calibrated PSFs taken on a sparse 3D grid. A key difference between our 3D-LSV model and the depth-wise LSV model [14] is the reduced model complexity by a global decomposition and the resulting shared basis PSFs. We show that the added axial interpolation in our 3D model achieves “axial super-resolution” beyond the large axial step used in the PSF calibration. We generate all the training data using this 3D-LSV simulator to train CM²Net, which bypasses the need to physically acquire a large-scale training data set in our experiments.

We first quantitatively evaluate CM²Net’s performance to reconstruct 3D fluorescent emitters in simulation. Our results demonstrate that CM²Net is robust to variations in the imaging FOV and fluorescent emitter’s size, intensity, 3D location, and seeding density. Our ablation studies show that the view-demixing module significantly reduces the false positive rates in the reconstruction, and that the reconstruction module, consisting of the view-synthesis-net and light field refocusing enhancement-net, learns complementary information and enables accurate 3D reconstructions across a wide FOV. We quantify the CM²Net’s detection performance and localization accuracy on fluorescent emitters with seeding densities and SNRs approximately matching in vivo cortex-wide, one-photon calcium imaging across ~7 mm FOVs. CM²Net achieves an averaged recall and precision of 0.7 and 0.94, respectively, that is comparable to the state-of-the-art deep-learning-based neuron detection pipeline [23]. It achieves an averaged lateral and axial rms localization error (RMSE) of 4.17 μm and 11.2 μm, respectively, indicating close to a singlevoxel localization accuracy. We further perform numerical studies to show that the trained CM²Net generalizes well to complex neural structures, including sparsely and densely labeled neurons across the entire mouse cortex and brain vessel networks.

We show that the 3D-LSV simulator-trained CM²Net generalizes well to experiments, and an example reconstruction on 10-μm beads is shown in Fig. 1(e). We demonstrate CM²Net’s robustness to variations in the emitter’s local contrast and SNR on mixed 10-μm and 15-μm beads. Notably, CM²Net enhances the axial resolution to ~25 μm—~8 × better than the model-based reconstruction. The 3D reconstructions are validated against tabletop widefield measurements. The reconstruction quality is quantitatively evaluated and shown to have a nearly uniform detection performance across the whole FOV with few incorrect detections. In addition, CM²Net reduces the reconstruction time to <4 s for a volume spanning a 7 mm FOV and an 0.8 mm depth on a standard 8 GB GPU, which is a ~1400 × faster speed and a ~19 × less memory cost than the model-based algorithm.

We believe our contribution is, to the best of our knowledge, a novel deep-learning-augmented computational miniaturized microscope that achieves single-shot high-resolution (~6-μm lateral and ~25-μm axial resolution) 3D fluorescence imaging across a mesoscale FOV. Built using off-the-shelf and 3D-printed components, we expect this simple, low-cost miniature system will be useful in a wide range of large-scale 3D fluorescence imaging and neural recording applications.

2. METHODS

A. CM² V2 Hardware Platform

CM² V2 is a stand-alone miniature fluorescence microscope built with off-the-shelf and 3D-printed components, as illustrated in Figs. 1(a) and 2(a). It mainly consists of two parts, including a newly designed illumination module and an upgraded imaging module. Compared to the V1 platform, the V2 platform features free-form LED collimators that improve the illumination efficiency by ~3 ×, and a hybrid emission filter design that improves the image contrast by ~5 ×.

Fig. 2.

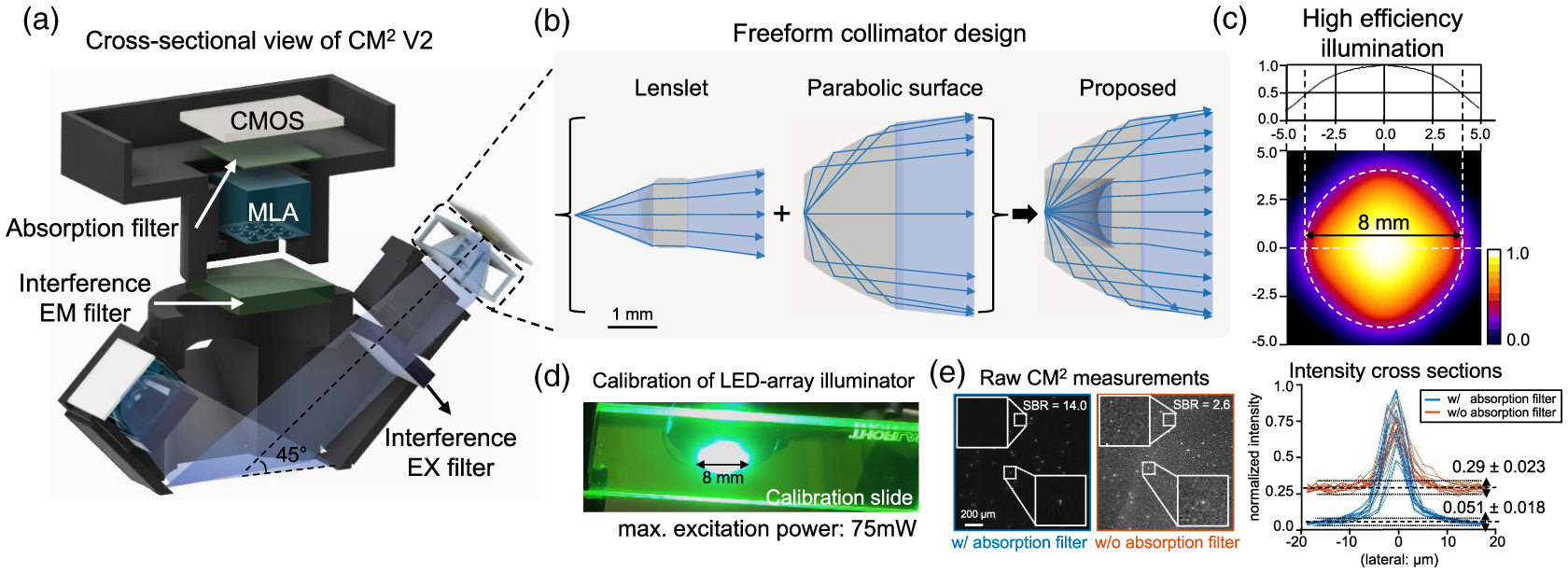
CM² V2 hardware platform. (a) A cross-sectional view of the CM² V2 platform. The platform incorporates an MLA, free-form illuminators, a hybrid interference-absorption emission filter pair, and a BSI CMOS sensor. (b) The free-form LED collimator combines a singlet and a TIR parabolic surface. (c) Zemax simulation of the four-LED array demonstrates high-efficiency, uniform excitation onto a confined 8 mm circular region. (d) Experimental validation of the illumination module. (e) The hybrid emission filter pair improves the raw measurement’s SBR by > 5× (sample: 10-μm fluorescent beads in clear resin). Intensity profiles taken from several fluorescent beads show the SBR improvement by the hybrid filter design.

For the illumination module, our design goal is to achieve a ~50 mW total excitation power across a centimeter-scale FOV, which is sufficient for one-photon widefield calcium imaging in mouse brains [4]. In addition, the illumination module must be highly efficient without incurring an excessive heat burden. Our solution incorporates a compact, lightweight free-form collimator in-between the surface-mounted LED (LXML-PB01-0040, Lumileds) and the excitation filter (no. 470, Chroma Technology). The collimator is based on a refraction-reflection, free-form design [24]. It consists of an inner refractive lenslet and an outer parabolic reflective surface, as shown in Fig. 2(b). The lenslet collimates the light within a ~52-deg conical angle. The parabolic surface satisfies the total internal reflection (TIR) condition and collimates the light emitted at high angles. The LED is placed around the shared focal point of the lenslet and the parabolic refractor. Each collimator is ~4 × 4 × 1 mm³ in size, weighs ~0.03 grams, and is 3D printed with clear resin (printed on Formlabs Form 2, no. RS-F2-GPCL-04). The design achieves an efficiency of ~80% in a Zemax simulation, which considers the finite-sized LED emitter, broadband LED emission spectrum, and angle-dependent transmission spectrum of the excitation filter.

The entire illumination module consists of four LED illuminators placed symmetrically around the imaging module. After performing an optimization in Zemax, the LED illuminator is placed ~6.7 mm away from the imging optical axis and tilted by ~45 deg to direct the light toward the central FOV. The Zemax simulation shows that this design provides a nearly uniform illumination confined in an 8 mm circle, as shown in Fig. 2(c). The experimental validation on a green fluorescence calibration slide (no. FSK2, Thorlabs) closely matches the simulation, as shown in Fig. 2(d). The total excitation power is measured to be up to 75 mW (at a maximum driving current of 350 mA) at a ~470 nm excitation wavelength.

The imaging module is built around an off-the-shelf 3 × 3 MLA (no. 630, Fresnel Technologies Inc.) to form a finite-conjugate imaging geometry with ~0.57 magnification. The lateral resolution is primarily limited by the NA of a single microlens, which is ~6 μm measured experimentally (see Supplement 1). We incorporate an interference-absorption emission filter pair to improve the signal-to-background ratio (SBR) in the raw measurement. An interference filter (no. 535/50, Chroma Technology) is placed in front of the MLA. An additional long-pass absorption filter (Wratten color filter no. 12, Edmund Optics) is placed after the MLA to suppress the leakage light. The emission spectra of the emission and absorption filters are optimized for the green fluorescence, as detailed in Supplement 1. Compared to measurement of only the interference filter, this hybrid filter design improves the SBR by >5× on a phantom consisting of 10-μm fluorescence beads, as shownin Fig. 2(e). This improvement makes the new CM² V2 platform more robust in low-light fluorescence imaging conditions.

The CM² V2 is built around a backside-illuminated (BSI) CMOS sensor (IMX178LLJ, IDS Imaging), which gives a 4.15 μm effective pixel size. The dome-shaped. 3D-printed housing (printed on Formlabs Form 2, black resin, no. RS-F2-GPBK-04) provides mechanical support and light shielding. The size and weight of CM² V2 is only limited by the CMOS sensor. The CM² V2 prototype is ~36 × 36 × 15 mm³ in size, including the commercial CMOS PCB board. The custom parts excluding the PCB are ~20 × 20 × 13 mm³ in size and weigh only ~2.5 grams.

B. 3D LSV Model of the CM²

Our goal is to build an accurate, efficient 3D LSV model to describe the CM² image formation. Using the synthetic data simulated from this model, we will later train the proposed CM²Net to perform 3D reconstruction. In this section, we describe a sparse PSF calibration procedure and a low-rank. approximation-based 3D-LSV model. First, to calibrate the spatially varying PSFs, we scan a 5-μm point source on a three-axis translation stage. The point source is scanned across an 8 mm × 8 mm × 1 mm volume with steps of 1 mm laterally and 100 μm axially, which yields a stack of 9 × 9 × 11 calibrated PSFs, as illustrated in Fig. 3(a). Several examples of calibrated PSFs are shown in Fig. 3(b), which highlight the following key features of the CM² image formation. At a given lateral position, the off-axis foci shift laterally with the depth, akin to the light field. At a given depth, the PSFs are still shift variant because of the spatially varying aberrations from the microlenses and the missing side foci at large, off-axis locations (when the lateral location >1.7 mm) [18]. As a result, a 3D-LSV forward model is necessary to fully characterize the CM² 3D PSF. Unfortunately, scanning the point source on the entire dense grid at our desired 3D resolution (4.15 μm × 4.15 μm × 10 μm) across the targeted imaging volume (~8 mm × 8 mm × 1 mm) would require ~370 million PSF measurements, which is impractical. Next, we describe a computational procedure to address this challenge.

Fig. 3.

3D LSV model of the CM². (a) Illustration of the sparse PSF calibration process. A point source is scanned through the 8 × 8 × 1 mm³ imaging volume with a 1 mm lateral and 100-μm axial steps, generating in-total 891 calibrated PSFs. (b) Example preprocessed calibrated PSFs. The shift variance in 3D is clearly visible. (c) Results of the low-rank decomposition. Rows 1–2: Computed basis PSFs and coefficient volumes, respectively, from the decomposition on the calibrated PSFs. Row 3: 3D-interpolated coefficient volumes. (d) A total of 64 basis PSFs are chosen for our 3D-LSV model that yields a small 0.025 normalized mean squared error (MSE). (e) Validation of the simulated PSF using our 3D-LSV model at an unseen location. The error between the numerically simulated and experimentally measured PSFs is small, as quantified by the pixel-wise absolute error.

We develop a low-rank, approximation-based 3D-LSV model to simulate the CM² measurement in four steps:

1. We denote the sparsely calibrated PSFs as H(u, v; x, y, z), where (u, v) are the pixel coordinates of the PSF image, and (x, y, z) is the 3D location of the point source. In total, the calibrated PSF set contains N = 891 images. Note that the effect of the PSF calibration grid is studied in Supplement 1. Each raw PSF image contains ~6.4M pixels, which is too large to be directly operated on for the low-rank decomposition. To address this issue, we develop a memory-efficient scheme by exploiting the highly confined foci in the PSF image. We remove most of the dark regions in the images and then align the cropped foci. The alignment step essentially compensates for the depth-dependent lateral shift in the off-axis foci. We denote this “compressed” and aligned PSF calibration set as H_c(u′, v′; x, y, z), where (u′, v′) are the new pixel coordinates after cropping and alignment.

2. We approximate the N calibrated PSFs by a rank-K singular value decomposition (SVD) using

   $$H\left(u^{\prime },v^{\prime };x,y,z\right)\approx \sum _{i=1}^K{M}^i(x,y,z)H_b^i\left(u^{\prime },v^{\prime }\right),$$ (1)

   where $H_b^i\left(u^{\prime },v^{\prime }\right)$, {i = 1, …, K } denotes the i^th basis PSF and Mⁱ(x, y, z) is the corresponding coefficient volume. Equation (1) approximates the set of calibrated PSFs as a linear combination of K basis PSFs. The first five basis PSFs and coefficient volumes are shown in the first two rows in Fig. 3(c). We choose K = 64 that has a small ~2.5% approximation error on the calibration set, which is shown in Fig. 3(d). The choice of K incurs a trade-off between the model accuracy and computational cost. In addition, this low-rank approximation also helps suppress noise in the raw PSF measurements. More details can be found in Supplement 1.

3. To obtain the coefficient volumes at any uncalibrated 3D location, we perform 3D bilinear interpolation from the sparse calibration grid to the dense reconstruction grid. This procedure relies on the assumption that the PSFs are slowly varying in 3D [25], which means that: 1) The basis PSFs can be accurately estimated from a sparse set of PSF measurements, and 2) The decomposition coefficients are smooth in 3D. The interpolated coefficient volumes for the first five basis PSFs are shown in the third row in Fig. 3(c).

4. The final 3D-LSV model is computed by K weighted 2D depth-wise convolutions in the lateral dimension ⊛_u,v, followed by a summation along the axial dimension z:

   $$g(u,v)=\sum _z\sum _{i=1}^K\left[M^i(u,v,z)O(u,v,z)\right]{⊛}_{u,v}{H}_b^i(u,v,z).$$ (2)

Here, O(u, v, z) is the 3D fluorescence distribution of the object. Both the basis PSF $H_b^i(u,v,z)$ and coefficient volume Mⁱ(u, v, z) have been placed back to the original sensor pixel coordinates by accounting for the expected lateral shift at each depth z. The pixel coordinates (u, v) in the image and the object space coordinates (x, y) are related by the magnification M by u = Mx, v = My.

More details on this 3D-LSV model can be found in Supplement 1.

C. CM²Net Design

To enable fast and accurate 3D reconstruction from a CM² measurement, we implement a modular deep learning model called CM²Net to incorporate the key feature of the CM² physical model. Each CM² image contains 3 × 3 multiplexed views to capture projection information about the 3D object [18]. This multiview geometry introduces two challenges to the network design. First, the image features needed for 3D reconstruction are nonlocal, instead they are separated by a few thousand pixels. To fully capture the nonlocal information requires a sufficiently large receptive field, which is not easily achieved by a standard convolutional neural network. Second, the view-multiplexing requires the network not only to reconstruct 3D information, but also to remove crosstalk artifacts. To address these challenges, CM²Net combines three modules to break the highly ill-posed inverse problem into three simpler tasks, including view demixing, view synthesis, and a light field refocusing enhancement, as illustrated in Fig. 4.

Fig. 4.

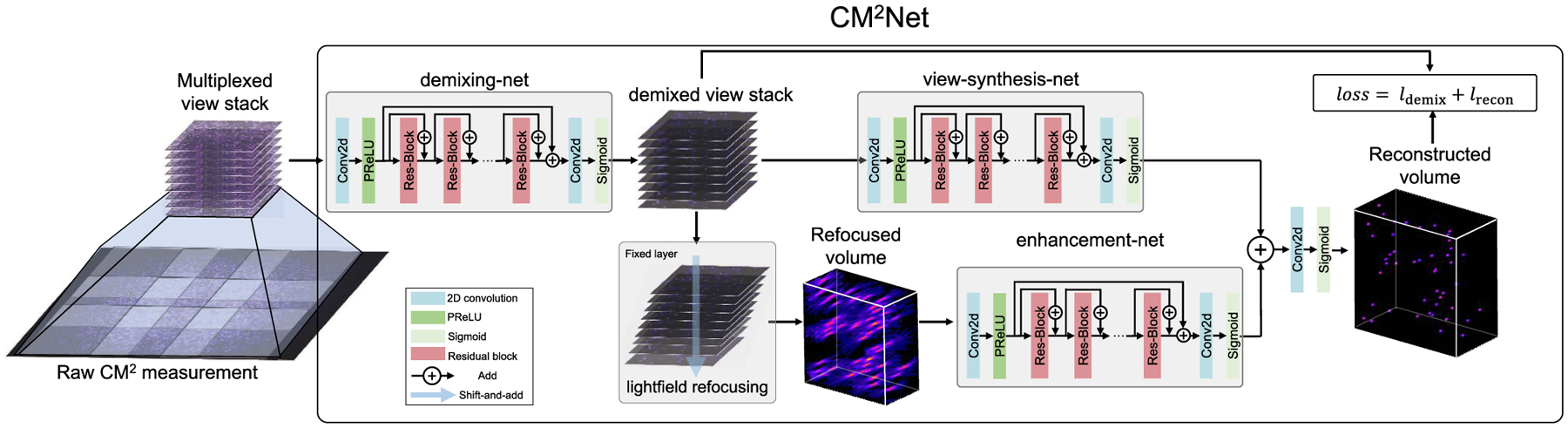
CM²Net structure. The raw CM² measurement is first preprocessed to form a multiplexed view stack. The demixing-net removes the crosstalk artifact and outputs the demixed view stack by learning view-dependent aberrations. The demixed view stack is processed by the “shift-and-add” light field refocusing algorithm to form a geometrically refocused volume. The enhancement-net branch removes the refocusing artifacts and enhances the reconstructed 3D resolution. The view-synthesis-net branch directly processes the demixed views to perform the 3D reconstruction. The sum of the output from the two branches is further processed to form the final reconstruction. CM²Net is trained with a mixed loss function combining the demixing and reconstruction losses.

The first module, view “demixing-net,” demultiplexes a CM² image into nine demixed views, each corresponding to the image captured by a single microlens without crosstalk from the other microlenses. To perform this task, demixing-net synthesizes the information contained in the entire CM² measurement. To facilitate this process, we first construct a view stack by cropping and view-aligning nine patches from the raw measurement based on the chief ray of each microlens, as shown in Fig. 4. This input view stack contains multiplexed information, which demixing-net seeks to demultiplex. The ground truth output is the demixed view stack containing nine crosstalk-free images, which is made possible on simulated training data using our 3D-LSV model. Our results show that this task can be accurately performed by using the distinctive aberration features from different microlenses. In Supplement 1, we further perform an ablation study on demixing-net and highlight that it significantly reduces the false positives in the reconstructions.

The demixed view stack is akin to a 3 × 3 view light field measurement, which is processed by two reconstruction branches. The first branch is “view-synthesis-net,” which directly performs the 3D reconstruction based on disparity information in the views, as inspired by the deep-learning-enhanced LFM [22]. The second branch explicitly incorporates the geometrical optics model of the light field. The demixed views are first processed by the light field refocusing algorithm [26] to generate a refocused volume, and then are fed into “enhancement-net” to remove any artifacts and enhance the reconstructed resolution. The refocused volume already provided most of the 3D object information, but suffers from three artifacts, including severe axial elongation due to limited angular coverage, boundary artifacts from the “shift-and-add” operation, and missing object features at the peripheral FOV regions due to inexact view matching between the 3 × 3 MLA. To achieve the best performance, the outputs from the two branches are summed and further processed to yield the final 3D reconstruction. To highlight the effectiveness of this design, we conduct ablation studies and visualize the respective activation maps of the two branches in Supplement 1. Our results show that the light field refocusing enhancement-net achieves a high-quality reconstruction at the central FOV region, and the view-synthesis-net improves the performance at the peripheral FOV regions. Together, the two reconstruction branches use complementary information to achieve high-resolution reconstruction across a wide FOV.

Overall, CM²Net is trained entirely on simulated data from our 3D-LSV model. The loss function combines a demixing loss and a reconstruction loss loss = α₁l_demix + α₂l_rec, which promotes, respectively, the fidelity of the demixed views and the 3D reconstruction results. For both loss components, we use binary cross entropy (BCE) since it promotes sparse reconstructions [27], which are defined by $\text{BCE}\left(y,\widehat{y}\right)={\sum }_i{y}_i\text{log}\left({\widehat{y}}_i\right)+\left(1-y_i\right)\text{log}\left(1-{\widehat{y}}_i\right)$. The summation is over all the voxels indexed by i, and y and $\widehat{y}$ denote, respectively, the ground truth and the reconstructed intensity The weights of the two loss functions (α₁, α₂) are set to be (1, 1) after performing hyperparameter tuning, which concluded that the demixing and reconstruction losses have equal importance.

CM²Net is implemented in Python 3.7 with TensorFlow 2.3. The multiple subnetworks are trained together in an “end-to-end” fashion on an Nvidia P100 GPU (16 GB) with a batch size of 2. We use Adam optimizer with an adaptive learning rate schedule. The initial learning rate is 10⁻⁴ and automatically decreases by a factor of 0.9 after the loss on a small validation set (~400 patches) plateaus for two consecutive epochs. The training takes ~48 h to complete. Additional implementation details are provided in Supplement 1.

D. Synthetic Training Data Generation

We generate a large-scale training dataset for CM²Net based on the 3D-LSV model [Eq. (2)] from a set of synthetic volumes. The FOV of each synthetic volume follows a uniform random distribution between 6.5 mm and 7.5 mm, U [6.5 mm, 7.5 mm]. The degree of view multiplexing is determined by the FOV [18]. For FOV < 2.7 mm, no view multiplexing is present. As the FOV increases, the overlap between neighboring views increases approximately quadratically. At the largest FOV = 7.5 mm, ~64% of overlap is present. The depth range is fixed at 800 μm. The volumes are sampled at 4.15 μm laterally (matching the effective pixel size of CM² V2) and 10 μm axially (10× higher sampling than the physical scanning step size).

We randomly place spherical emitters into the volumes by the following steps. Due to the large sampling grid size, we first generate each ground-truth emitter on a 5× finer grid (0.83 μm × 0.83 μm × 2 μm). Next, we perform 5 × 5 × 5 average binning to make the ground-truth volume have the same grid size as the final reconstruction. The emitter’s diameter follows a uniform random distribution U [8 μm, 20 μm], which approximately matches the typical size of neuronal cell bodies. The emitter’s intensity is set by the surface area; i.e., proportional to the diameter squared, which matches our experimental measurements. The size range used in our data leads to a 6.25× intensity variation range. To further vary the emitter’s intensity at a given size, a random scaling factor following a uniform distribution U [0.8, 1.2] is added, which approximately matches the contrast from one-photon fluorescence microscopes on calcium indicators [28]. The emitter density in each volume follows a uniform random distribution U [10,100] (number of emitters/mm²), which simulates different fluorescence labeling densities used in cortex-wide neuronal imaging applications [3,4].

We first generate noise-free measurements using the 3D-LSV model. We then add realistic levels of mixed Gaussian and Poisson noise. The parameters for the additive Gaussian noise (normalized mean = 0.048, standard deviation = 0.017) are estimated by multiple dark measurements taken with the same acquisition parameters as the real experiments (30 ms exposure time, 40 dB gain). The Poisson noise is added by estimating the expected photon budget (~500 peak number of photons and a unit effective gain) in typical widefield one-photon imaging [4]. To train the view demixing-net, we generate the ground-truth nonoverlapping views using the same 3D-LSV model with the single microlens PSF.

After synthesizing the measurements, we crop the overlapped views (1920 × 1920 pixels) based on the chief ray location of each microlens at the in-focus image plane. Next, we stack the nine cropped views to form a 1920 × 1920 × 9 multichannel input to CM²Net. Finally, CM²Net is trained on 9700 uniformly cropped patches (320 × 320 pixels) from 270 synthetic objects.

3. RESULTS

A. 3D-LSV Simulator Enables Accurate 3D Reconstruction Across a Wide FOV

To demonstrate that our 3D-LSV model is essential to achieve accurate 3D reconstruction across a wide FOV, we compare two CM²Net models trained with two different forward models. The first network, termed LSV-CM²Net, is trained by our 3D-LSV model. The second network, termed LSI-CM²Net, is trained by our previous depth-wise LSI model [18], which assumes the on-axis PSF is invariant at each depth. We also benchmark the network reconstructions against the depth-wise LSI model-based deconvolution algorithm [18].

The 3D reconstructions on a cylindrical volume (~7-mm diameter, 0.8-mm depth) from LSV-CM²Net, LSI-CM²Net, and a model-based deconvolution are shown, respectively, in Figs. 5(a)–5(c). In each figure, we overlay the reconstruction (in red) onto the ground truth (in green) and visualize the XY and XZ maximum intensity projections (MIP). When the reconstruction matches with the ground truth (i.e., true positives), the overlayed region appears in yellow. When the reconstruction misses certain particles (i.e., false negatives), the region appears in green. When the reconstruction creates false particles (i.e., false positives) or suffers from axial elongations, the region appears in red. By visual inspection, LSV-CM²Net can accurately reconstruct the entire 7 mm FOV throughout the 0.8-mm depth range, as highlighted by the three zoomed-in regions of the XZ MIPs taken from the central and two peripheral regions. In contrast, the LSI-CM²Net suffers from severe artifacts, especially beyond the central 3 mm diameter region. The model-based reconstruction matches well with the ground truth across the entire volume, but suffers from severe axial elongations [18].

Fig. 5.

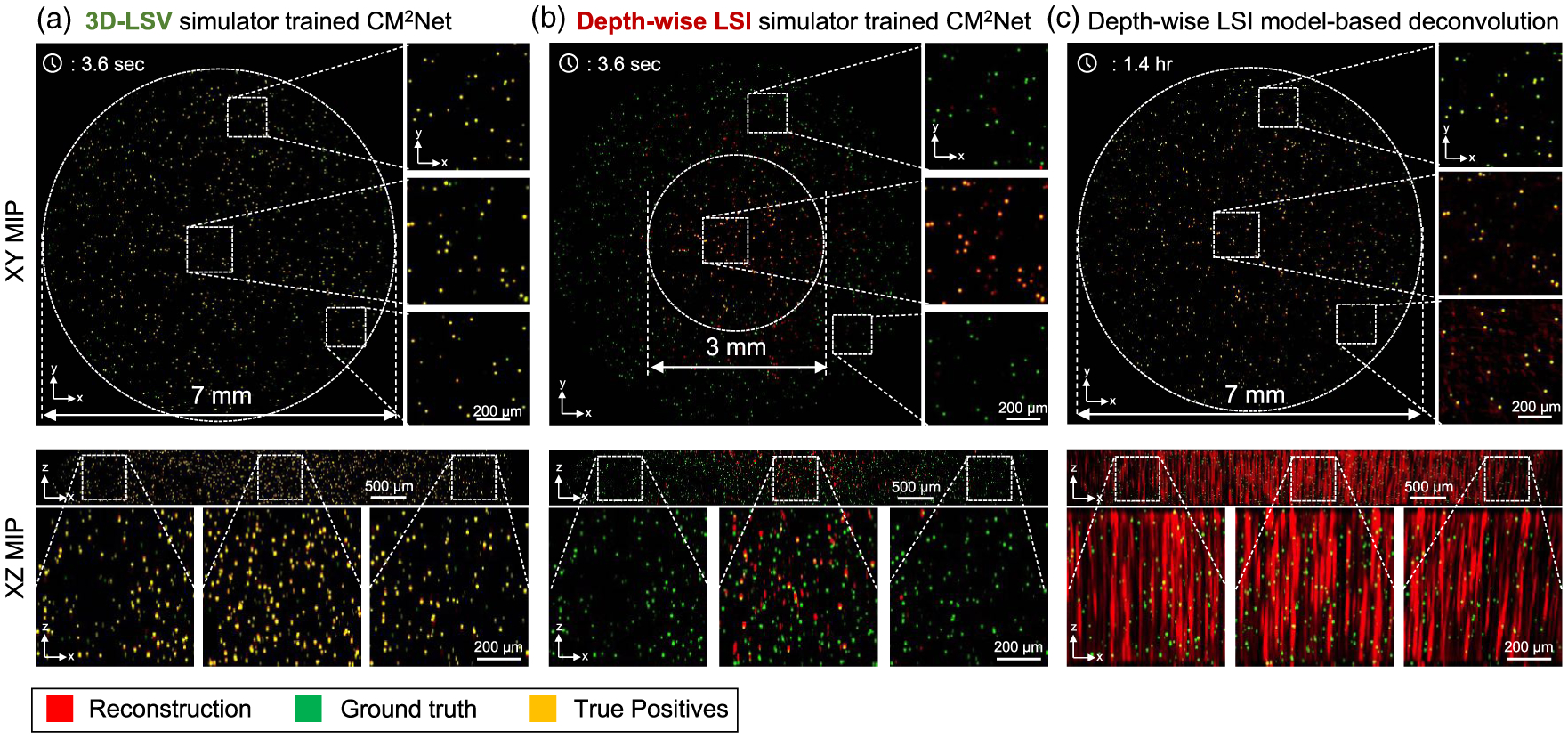
3D-LSV simulator enables wide-FOV, high-resolution 3D reconstruction. Reconstructions from (a) LSV-CM²Net trained with the 3D-LSV simulator, (b) LSI-CM²Net trained with the depth-wise LSI simulator, and (c) depth-wise LSI model-based deconvolution. LSV-CM²Net provides accurate and high 3D resolution reconstruction across the entire volume. LSI-CM²Net suffers from many false negatives. The model-based deconvolution suffers from severe axial elongations. In all figures, the positive z-axis points at the direction towards the CM² system.

A major improvement of CM²Net over the model-based deconvolution is the significantly reduced axial elongation, as also shown in our experiments in Section 3.C. In addition, CM²Net dramatically reduces the reconstruction time and memory burden. To perform the large-scale reconstruction in Fig. 5 (~230 million voxels), the model-based method requires ~1.4 h and ~150-GB RAM. In contrast, CM²Net takes only ~3.6 s on an entry-level GPU (Nvidia RTX 2070, 8 GB RAM), which is a ~1400 × increase in speed and a~19 ×reduction in memory cost.

To demonstrate the potential applications of CM²Net to reconstruct complex brain structures, we perform simulation studies on imaging 3D neuronal populations and mouse brain vessels in Supplement 1. Our results on neuronal imaging show that CM²Net can achieve high reconstruction performance on both sparsely (20 neurons/mm²) labeled and densely (100 neurons/mm²) labeled neuronal populations across a cortex-wide (7.5 × 6.6 mm) FOV and is robust to the complex brain geometry. Our results on a mouse blood vessel network highlight a few key properties of the particle-dataset trained CM²Net. First, the view-demixing module can perform reliable demultiplexing on axially overlapping small vessels. The demixing results highly match with the ground truth, demonstrating that the demixing network is robust to overlapping views from continuous objects, even though it is trained entirely on sparse fluorescent beads. Second, the light field refocused volume on demixed views can correctly resolve complex 3D geometry, which lays the foundation for the final 3D reconstruction. Third, the reconstruction module can correctly reconstruct the vessel network, albeit with discontinuity artifacts. We attribute the artifacts to the sparsity constraint implicitly enforced by the particle-dataset trained CM²Net on the 3D reconstruction. Overall, CM²Net can provide high-quality reconstruction on brain vasculature across a wide (6 × 4 mm) FOV and can resolve the complex 3D geometry.

B. Quantitative Analysis of CM²Net Performance

We quantitatively show that the trained CM²Net can provide high-quality reconstruction and is robust to variations in the emitter’s lateral location (FOV), seeding density, depth, size, and intensity in simulation. To perform the evaluation, we simulate a testing set consisting of 180 volumes that uniformly fall in nine density ranges [10:10:100] (number of emitters/mm²). The data synthesis procedure follows the procedure in Section 2.D.

We quantify the detection capability of CM²Net using recall, precision, F1 score, and the Jaccard index. Recall measures the sensitivity/detection rate by the ratio between the correctly reconstructed and the actual total number of emitters. Precision measures the specificity by the ratio between the correctly reconstructed and the total reconstructed number of emitters. The F1-score and Jaccard index combine these two complementary metrics. In addition, we quantify the 3D localization accuracy by a lateral and an axial rms localization error (RMSE) [29]. A global threshold needed to binarize the reconstructed volume when computing the metrics is set by maximizing the F1 score on the testing set [23]. More details on the quantitative metrics are provided in Supplement 1. We compute the statistics of each metric at a given condition (e.g., a lateral location), when all other parameters (e.g., emitter’s depth, density, size) are randomized.

First, the performance at different lateral locations are evaluated in Fig. 6(a). We aggregate the emitters into seven bins [0 mm: 0.5 mm: 3.5 mm] (distance from the center) and compute the statistics. The averaged precision and recall (blue) remain >0.93 and >0.68 when the distance is <3 mm (i.e., FOV < 6 mm). Precision and recall reduce, respectively, to ~0.85 and ~0.37 when the distance is ~3.5 mm (FOV = 7 mm). Lateral/axial RMSE (orange) is less than 5 μm/15 μm within the 6 mm FOV and degrade to 8.7 μm/21 μm at the edge. The standard deviation (the error bar) increases with the distance, indicating that the reconstruction is more consistent at the central FOV. To better visualize the detection performance, we calculate recall and precision maps in Fig. 6(a) and the details are provided in Supplement 1. The precision map shows that CM²Net provides nearly isotropic, high specificity within the 7 mm FOV. The recall map shows that CM²Net provides a high detection rate in the central 6 mm FOV, and degrades at the outer regions.

Fig. 6.

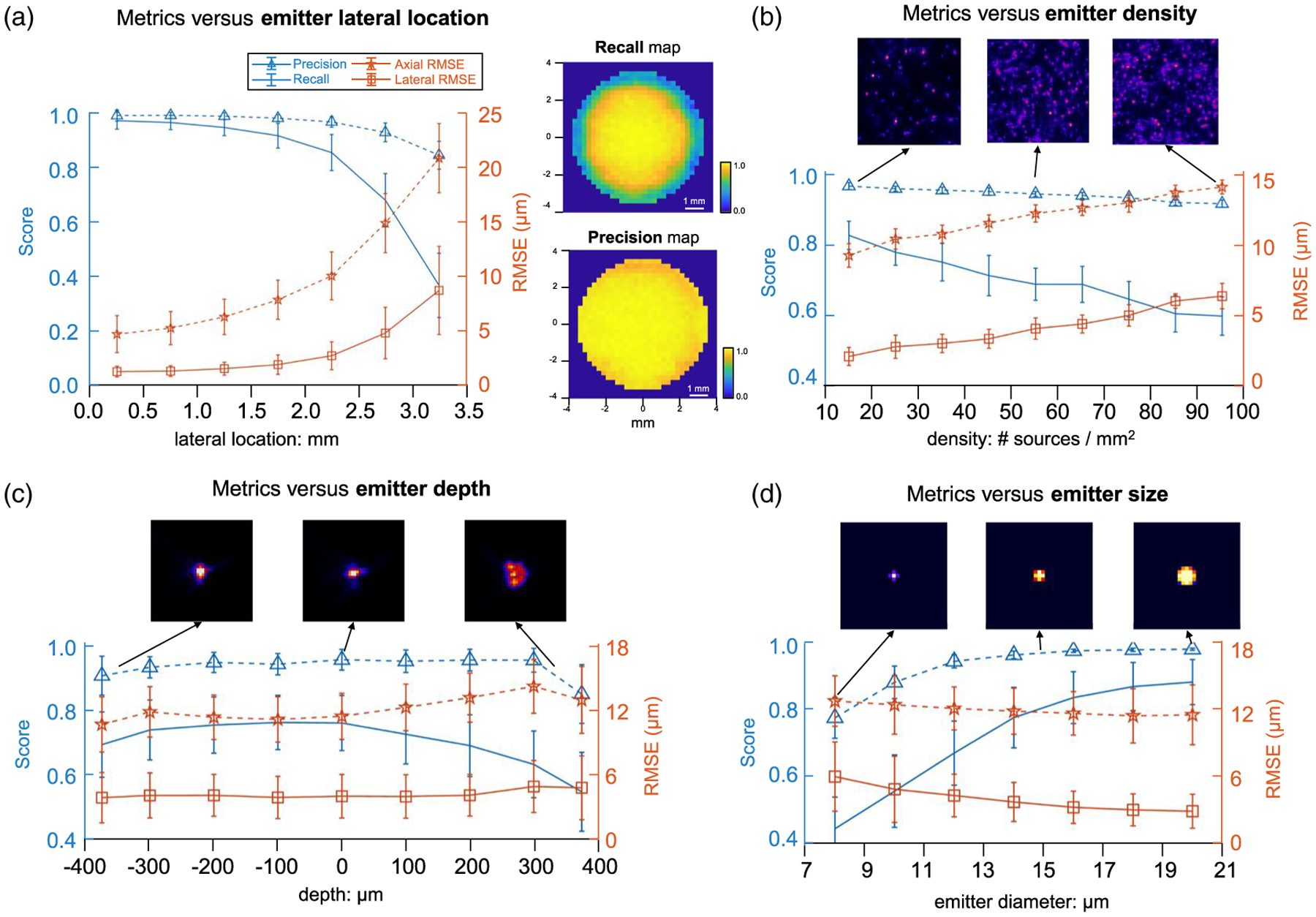
Quantitative evaluation of CM²Net in simulation. Detection performance quantified by recall and precision (blue) and localization accuracy by lateral and axial RMSE (orange) when varying the emitter’s (a) lateral location, (b) seeding density, (c) depth, and (d) size. (a) CM²Net achieves precision > ~ 0.85 for a lateral location <3.5 mm (FOVs < 7 mm). Recall drops from 0.97 at the central FOV to 0.35 near the edge. Lateral/axial RMSE increases from 1.24 μm/4.7 μm at the central FOV to 8.7 μm/21 μm near the edge. The recall and precision maps (250 μm patch size) show nearly isotropic, high-detection performance across the central 6 mm FOV. (b) Precision is >0.92 for all emitter densities. Recall decreases from ~0.83 at the lowest density to ~0.61 at the highest density. Lateral/axial RMSE degrades linearly from 2 μm/9.3 μm at 10 emitters/mm² to 6.4 μm/14 μm at 100 emitters/mm². Three example image patches are shown to visualize the density variations. (c) Precision is >0.85 throughout the depth, and recall is >0.7 within the [−400 μm, 200 μm] depth range and drops to ~0.54 at 400μm. Lateral/axial RMSE is <5 μm/14 μm for all depths. The foci from the central microlens at −400 μm, 0 μm, and 400 μm are shown in the top panel to visualize the depth-dependent aberrations. (d) Precision is >0.9 and the recall is >0.71 for the emitter’s diameter >11 μm. Lateral/axial RMSE decreases almost linearly from 5.9 μm/12.7 μm for 8 μm emitters to 2.8 μm/11.5 μm for 20 μm emitters. Both the detection rate and localization accuracy degrade for smaller emitters since the local SNR and emitter’s intensity scales with the diameter squared. The top panel shows examples of reconstructed emitters of diameters 8,14, and 20 μm.

To understand the origin of the degradation in the peripheral FOV, we perform ablation studies by feeding the CM²Net’s reconstruction module with the ground truth demixed views (see Supplement 1). The results show consistently high recall (>0.89) for the entire 7 mm FOV, showing the robustness of the reconstruction module. This implies that the degraded recall is due to imperfect view-demixing at the outer FOV regions. To further diagnose the system, we compare the intensity distribution of the point source for PSF calibration and the recall map, and find qualitative correspondence. We hypothesize that the training of view-demixing net is affected by the rapid intensity fall-off (~85% drop at the 7 mm FOV edge) of the imperfect point source.

We evaluate the metrics for different emitter densities in nine bins: [10: 10: 100] (emitters/mm²) in Fig. 6(b). As expected, both the precision and recall decrease, whereas both lateral and axial RMSEs increase with the density. Precision remains >0.92 for all emitter densities, indicating very few false positives in the reconstruction, despite the large (10× span) density variations. Recall decreases approximately linearly from ~0.83 at 10 emitters/mm² to ~0.61 at 100 emitters/mm². The lateral/axial RMSE increases approximately linearly from 2 μm/9.3 μm at the lowest density to 6.4 μm/14 μm at the highest density. This means that, as the density increases, CM²Net suffers from more false negatives and lower localization accuracy.

We evaluate the metrics for different emitter depths in nine bins: [−400 μm, −350 μm), [−350 μm: 100 μm: 350 μm), [350 μm, 400 μm] in Fig. 6(c). The smaller bin size in the first and last bins are due to the limited depth range used in the study. Precision is consistently >0.85 for the entire range. Recall is >0.7 within [−400 μm, 200 μm], and gradually decreases to ~0.54 at 400 μm. To explain the decrease in the recall at these large defocus depths, we visualize the on-axis PSF and show that it degrades more severely as the source moves closer to the MLA. This results in lower SNRs in the measurement, which leads to more false negatives. Lateral/axial RMSE is <5 μm/14μm for all depths, and degrades only slightly in a large defocus. The slight drops in the first and last bins are attributed to the smaller sample size (in combination with the smaller bin size and fewer true positives), which introduces errors in the statistics. We observe that the minimum RMSE is centered around the 100 μm bin, which suggests that there may be a slight defocus between our nominal and the actual focal plane. Overall, the RMSE analysis shows that the 3D localization is generally robust to defocus within the 800 μm depth range.

Finally, we quantify the metrics for different emitter diameters in seven bins: [7 μm: 2 μm: 21 μm]. For diameters ranging from 11–20 μm, the precision is >0.9 and the recall is >0.71. As the diameter decreases, both the precision and recall drop approximately linearly to, respectively, 0.55 and 0.48 for 8 μm emitters,. The lateral/axial RMSE decreases from 5.9 μm/12.7 μm for 8 μm emitters to 2.8 μm/11.5 μm for 20 μm emitters. We attribute the worse performance for smaller emitters to two factors. First, since the emitter’s intensity is proportional to the size squared, the SNR rapidly decreases as the size reduces. Second, due to the coarse sampling in the reconstruction, the number of voxels for each emitter is <5 when the diameter is <11 μm, as shown in the top panel of Fig. 6(d).

The averaged precision and recall for the entire testing set is, respectively, ~0.7 and ~0.94, which is comparable to the state-of-the-art deep learning neuron detection algorithm [23]. The averaged lateral and axial RMSEs are, respectively, 4.17 μm and 11.2 μm, which is close to the reconstruction grid size (lateral 4.15 μm and axial 10 μm) and indicates that the localization accuracy is close to one voxel. This study establishes that CM²Net can detect emitters with few “hallucinated” sources (an average ~4% false positive rate) and high detection rates (an average ~30% false-negative rate) with good localization accuracy in a broad range of conditions.

C. CM²Net Achieves High 3D Resolution, Wide-FOV Reconstruction in Experiments

We demonstrate that the generalization capability of simulator-trained CM²Net enables high 3D resolution reconstruction in experiments with high detection performance.

We first image a cylindrical volume embedded with 10 μm green-fluorescent beads. The details about the sample preparation and experimental setup are provided in Supplement 1. The phantom is estimated to have 10–20 emitters/mm². First, to remove the nonuniform background and match the intensity statistics with the simulation data, we preprocess the raw experimental measurements with histogram matching. Next, we manually cropped nine views to input to CM²Net for the 3D reconstruction. Supplement 1 provides additional details.

The CM²Net reconstruction is shown in Fig. 7(a) and is validated against wide-field measurements from a standard tabletop epifluorescence microscope in Fig. 7(b). First, we validate the full FOV reconstruction by comparing the XY MIPs of the reconstruction and the wide-field z stack from a 2×, 0.1 NA objective. To further assess the reconstruction at a greater resolution, two zoomed-in XY MIPs of the reconstruction from the central and edge of the FOV are compared to the high-resolution z stack from a 20×, 0.4 NA objective. A visual inspection shows that the reconstruction matches well to the wide-field measurements. The reconstruction quality maintains at the peripheral FOV regions, which is a marked improvement over our previous model-based reconstruction [18].

Fig. 7.

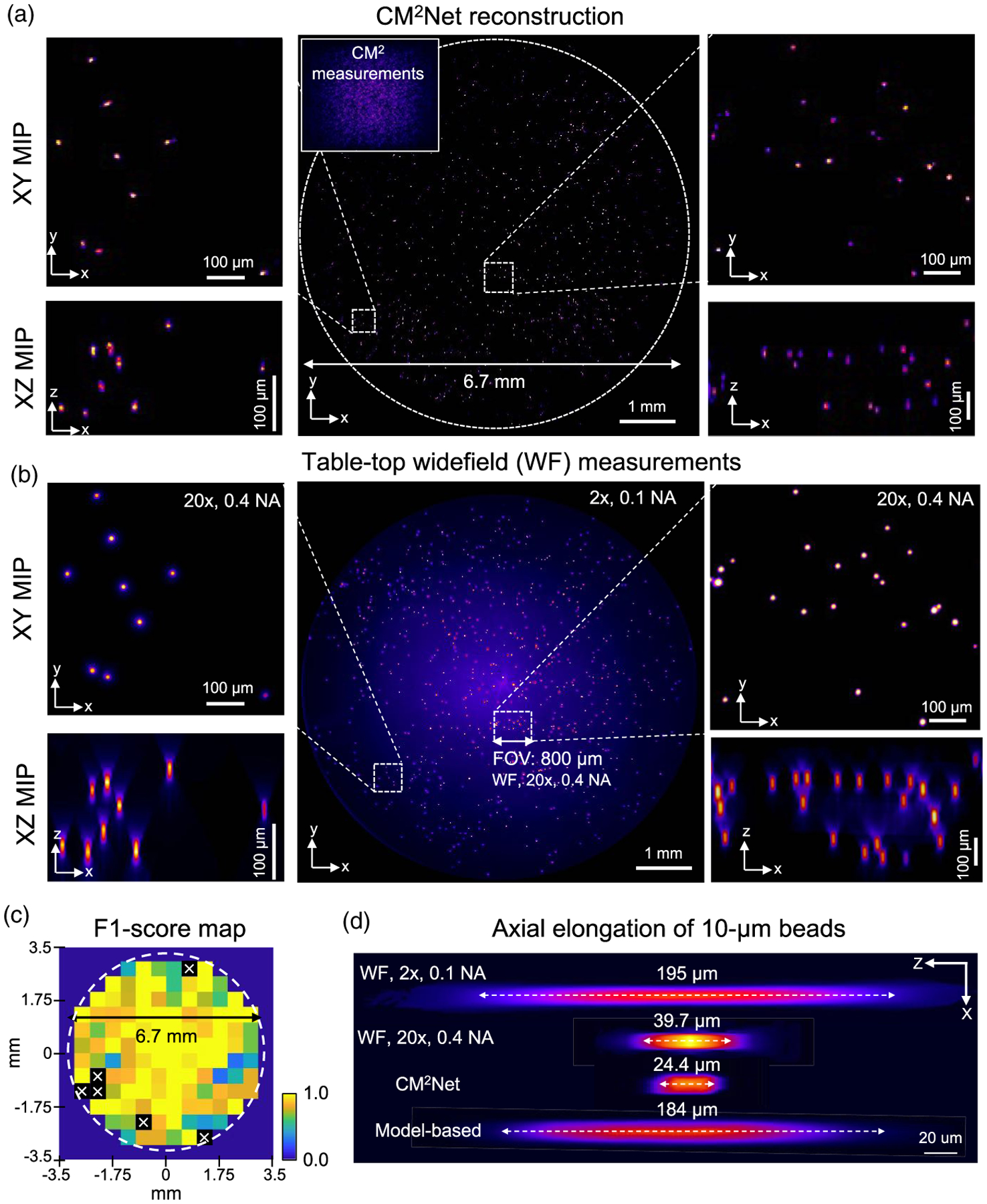
CM²Net achieves high 3D resolution reconstruction across a wide FOV in an experiment. (a) Visualization of the CM²Net reconstruction. Measurement shown in the inset (sample: 10 μm fluorescent beads in a cylindrical volume with ~6.7-mm diameter and ~0.5-mm depth). (b) Validation using 2×, 0.1 NA, and 20×, 0.4 NA objective lenses on a wide-field (WF) microscope. CM²Net provide high-quality reconstruction across the 6.7 mm FOV as validated by the 2× measurement. Both lateral and axial reconstructions are in good agreement with the high-resolution 20× measurement. (c) F1 score map computed by comparing the XY MIPs of CM²Net reconstruction and WF 2× measurement (500 μm patch size). “x” marks the F1 score = 0, resulting from either the WF measurement or CM²Net reconstruction is empty. (d) The axial elongations are 195 μm, 184 μm, 39.7 μm, and 24.4 μm for, respectively, WF 2×, model-based deconvolution, WF 20×, and CM²Net reconstruction.

A major goal we aim to achieve using CM² is 3D high-resolution imaging across a wide FOV. To highlight this capability, we compare the FOV achieved by CM² V2 (~7 mm) with the 2× objective (~8 mm) and 20× objective (~800 μm), which is marked in Figs. 7(a) and 7(b). Representative axial profiles of the 10 μm beads reconstructed by the CM²Net, model-based deconvolution, and 2× and 20× wide-field measurements are compared in Fig. 7(d). CM²Net achieves an axial elongation of ~24 μm, which is ~8 × better than the model-based deconvolution (~184 μm) and outperforms the 20×, 0.4 NA measurement (~39.7 μm).

To quantify the detection performance, we compute the recall, precision, and F1 score by comparing the XY MIPs of the CM²Net reconstruction and wide-field 2× measurement. CM²Net achieves recall ~0.78 and precision ~0.80. In comparison, the recall and precision in the simulation at the corresponding density are, respectively, ~0.83 and ~0.97. The simulator-trained CM²Net degrades slightly in an experiment, with a ~5% higher false negative rate and ~17% higher false-positive rate. We attribute the reduced performance to the undesired extra views in the experimental measurements. See the analysis in Supplement 1.

To quantify spatially variations in performance, we construct the recall and precision maps in Supplement 1. The recall in most regions is >0.75, indicating <25% false-negative rates. The precision is >0.8, except for a few patches with <2 beads, indicating only a few false positives in the reconstruction. In Fig. 7(c), we show that the F1 score map generally achieves a high value of >0.75. An overlay between the full FOV reconstruction and the wide-field 2× measurement is shown in Supplement 1 to provide further visual inspections.

This experiment shows that CM²Net provides high 3D resolution reconstruction across a wide FOV with high sensitivity and precision. The 24 μm axial elongation achieved by CM²Net is ~4 × better than the 100 μm axial spacing in the PSF calibration. This shows that the axial interpolation in our 3D-LSV model is effective to achieve axial super resolution in real experiments. Both the recall and precision agree with the simulation, validating that the 3D-LSV simulator-trained CM²Net can generalize well to experimental measurements.

D. Experimental Demonstration on Mixed-size Fluorescent Beads

Fluorescent emitters with different sizes and brightness result in different local contrast and SNRs in the CM² measurement [18]. This is an important consideration as we develop CM² toward realistic biological applications. To demonstrate this capability, we conduct proof-of-concept experiments on mixed-size fluorescent beads. Our result shows that CM²Net can robustly handle such sample variations in real experiments.

We image a cylindrical volume (diameter ~6.5 mm, depth ~0.8 mm) embedded with mixed 10 μm and 15 μm beads, and provide more details in Supplement 1. The phantom is estimated to have 10–20 emitters/mm². In the CM² measurements, the 15 μm beads are ~2.2× brighter than the 10 μm beads, matching with their surface area ratio and our synthetic data model in Sec. 2.4. The CM²Net reconstruction is shown in Fig. 8(a). The 3D reconstruction is validated against wide-field measurements in Fig. 8(b). First, we assess the full-FOV reconstruction by comparing the XY MIPs of the CM²Net reconstruction and the 2× z stack measurement. We further compare two zoomed-in regions from the center and corner FOVs with the high-resolution 20× z stack measurement. By visual inspection, CM²Net reliably reconstructs both 10 μm and 15 μm beads. The XZ MIPs of the CM²Net 3D reconstruction are in good agreement with the 20× z stack measurements. The axial confinement on both 10 μm and 15 μm beads by CM²Net are better than the 20× measurements.

Fig. 8.

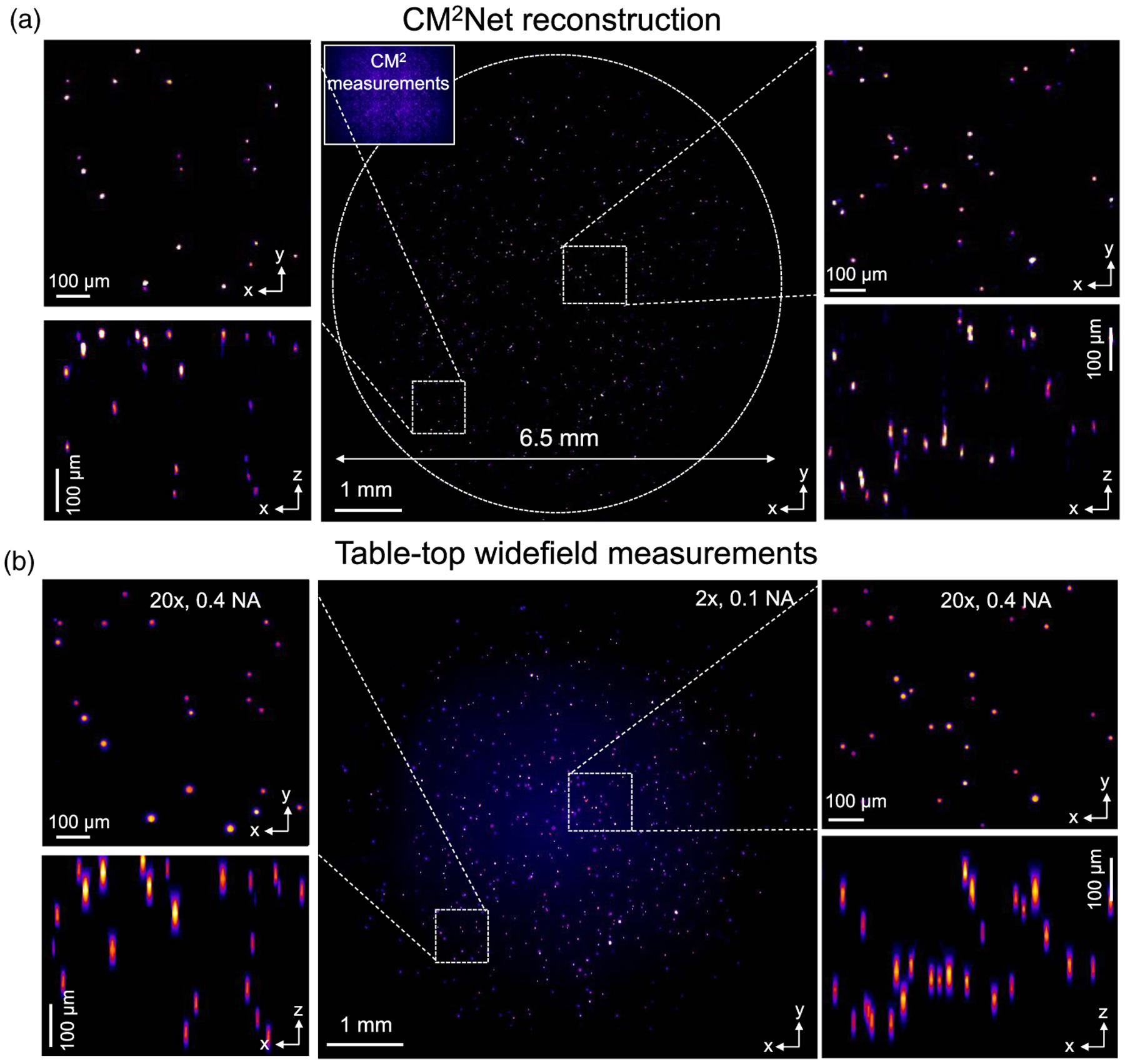
Experiment on mixed fluorescent beads. (a) Visualization of the CM²Net reconstruction. The CM² measurement shown as the inset. (b) Validation measurements from wide-field 2×, 0.1 NA, and 20×, 0.4 NA objectives (sample: mixed 102 μm and 15 μm fluorescent beads in a cylindrical volume with ~6.5-mm diameter and ~0.8-mm depth). The CM²Net full FOV reconstruction is in good agreement with the 2× measurement. The lateral and axial reconstructions are validated by the high-resolution 20× measurement in both the central and peripheral FOV regions.

To quantitatively assess the CM²Net reconstruction, we compute recall, precision, and F1 score maps in Supplement 1 by comparing the XY MIPs from the CM²Net reconstruction and wide-field 2× measurement. CM²Net achieves an averaged recall ~0.73 and precision ~0.84 across the 6.5 mm FOV. Compared to the mono 10 μm bead experiment, we attribute the slightly decreased recall to the greater intensity and SNR variations. We attribute the increased precision to the reduced FOV and less contamination from the extra views, and provide an analysis in Supplement 1. An overlay between the full FOV reconstruction and the 2× measurement is shown in Supplement 1 to provide further visual inspections. The results show that CM²Net is robust to the emitter size and intensity variations in the experiment.

This experiment again highlights the wide FOV and high-resolution 3D imaging capability of CM² V2. Our training data containing randomized emitter sizes and intensities are effective to make CM²Net robust to experimental variations. As a result, CM²Net can provide high-quality 3D reconstruction with good sensitivity and precision on mixed-size emitters that have large differences in the feature size and local SNR.

4. CONCLUSION

In summary, we have presented what we believe, to the best of our knowledge, a new computational miniature mesoscope (CM²) system, which is a deep learning-augmented miniaturized microscope for single-shot, 3D high-resolution fluorescence imaging. The system reconstructs emitters across a ~7-mm FOV and an 800 μm depth with high sensitivity and precision, and achieves ~6-μm lateral and ~25-μm axial resolution.

The main hardware advancement in CM² V2 includes a novel 3D-printed free-form illuminator that increases the excitation efficiency by ~3 ×. Each 3D-printed LED collimator can provide up to 80% light efficiency, but weighs only 0.03 grams. It is low cost and rapidly fabricated on a tabletop 3D printer. In addition, we adapted a hybrid emission filter design that suppresses the excitation leakage and improves the measurement SBR by more than 5×.

The computational advancement includes three main parts. First, we developed an accurate and computationally efficient 3D-LSV forward model that characterizses the spatially varying PSFs across the large (CM² × mm scale) imaging volume supported by the CM². Second, we developed a multimodule CM²Net that achieves robust, high-resolution 3D reconstruction from a single-shot CM² measurement. Third, using the 3D-LSV simulator to generate the entire training dataset, CM²Net provides high detection sensitivity and precision and good localization accuracy on fluorescent emitters across a wide FOV and they generalize well to experiments. In addition, our numerical studies show that CM²Net can achieve high reconstruction performance on both neuronal populations and vascular structures across a cortex-wide FOV and is robust to the complex mouse brain geometry.

Our demonstration on the utility of free-form optics fabricated by 3D printing may be a fruitful area for future research, especially for miniature microscopes and other miniature optical devices. In recent years, free-form optics has emerged as the ideal solution to bypass many limitations in conventional optics, such as compactness and imaging performance [30]. At the same time, nonconventional optics has been enabled by novel 3D printing processes, such as micro-optics [14,31], diffractive optics [32], and volume optics [32]. We envision that 3D-printed free-form optics can be incorporated into future CM² platforms to enhance the imaging capabilities of these platforms.

The CM² V2 platform is built on a backside illuminated (BSI) CMOS sensor, which significantly improves the measurement’s SNR and dynamic range over a conventional CMOS sensor in the V1 platform. The size and weight of the CM² V2 prototype is limited by the availability of a miniature BSI CMOS sensor. However, we do not anticipate this to be a major roadblock for future development, thanks to the recent development of the MiniFAST [33] BSI CMOS-based miniscope. With further advancement on the high-speed data transmission and high pixel-count BSI CMOS sensor platform, we expect CM² can be further miniaturized to be suitable for wearable in vivo neural recordings on mice and other small animals.

We believe our 3D-LSV model is essential to achieve high 3D resolution reconstruction across a large imaging volume. A notable result we have demonstrated is that the axial resolution is not limited by the axial step used for the 3D PSF calibration. This allowed us to bypass the large data requirement in the alternative depth-wise LSV framework [14,16,21] and to perform data-efficient PSF calibrations across a centimeter-scale FOV and millimeter-scale depth range. We expect that the same sparse 3D PSF calibration, low-rank decomposition, and 3D interpolation procedure are applicable to other computational 3D microscopy techniques, such as LFM and lensless imaging. In addition, it may be possible to develop hybrid 3D PSF calibration procedures by combining physical measurements and numerical modeling to further improve model accuracy, as recently shown in high-resolution LFM imaging [34,35].

Our CM²Net incorporates both the view-multiplexing and light field information in the CM² image formation. We have shown that the view-demixing module significantly suppresses the false positives in the 3D reconstruction. The simulator-training scheme was essential to enable the training of the view-demixing subnetwork. This highlights several key advantages of simulator-based training over experiment-based training schemes. It not only forgoes the laborious physical data collection process, but also enables access to novel data pairs that are impractical to collect experimentally. The reconstruction module combining the light field refocusing enhancement and view-synthesis branches is able to learn complementary information from the demixed views to create highly accurate 3D reconstructions, which makes it readily applicable to other LFM modalities.

Our numerical study on brain vasculature reconstruction indicates that the emitter-dataset trained CM²Net implicitly enforces a sparsity constraint to the 3D reconstruction that produces discontinuity artifacts. We trained CM²Net on individual emitters since our targeted application is to image neurons labeled with genetically encoded calcium indicators in mouse brains [36]. To better adapt CM²Net to other complex structures such as blood vessels, one can perform transfer learning on a dataset tuned to a specific application. Conveniently, our 3D-LSV simulator is directly applicable to generate non-emitter data, as shown in our study.

An outstanding challenge to expand the utility of CM² is tissue scattering [18]. There are several promising solutions we envision that are applicable to CM², such as the miniature structured illumination technique [37] and scattering-incorporated 3D reconstruction frameworks [38,39], which will be investigated in our future work.

Data availability.

The CM² V2 hardware, the CM²Net implementation, and the pretrained model are available at [40].