Modeling noncanonical RNA base pairs by coarse-grained IsRNA2 model

Abstract

Noncanonical base pairs contribute crucially to the three-dimensional architecture of large RNA molecules; however, how to accurate model them remains an open challenge in RNA 3D structure prediction. Here we reported a promising coarse-grained IsRNA2 model to predict noncanonical base pairs in large RNAs through molecular dynamics simulations. By introducing a five-bead per nucleotide coarse-grained representation to reserve the three interacting edges of nucleobases, IsRNA2 accurately models various base pairing interactions, including both canonical and noncanonical base pairs. A benchmark test indicated that IsRNA2 achieves a comparable performance to the atomic model in de novo modeling of noncanonical RNA structures. In addition, IsRNA2 was able to refine the 3D structure predictions for large RNAs in RNA-Puzzles challenges. Finally, the graphics processing unit (GPU) acceleration was introduced to speed up the sampling efficiency in IsRNA2 for very large RNA molecules. Therefore, the coarse-grained IsRNA2 model reported here offers a reliable approach to predict structures and dynamics of large RNAs.

Graphical Abstract

Introduction

The accurate determination of the three-dimensional (3D) structure of RNA molecules is crucial for a better understanding of their various biological functions^1-3, including carrying genetic information, regulating gene expression, performing enzymatic activity and so on. However, experimental determination of the atomic structures of RNA molecules through X-ray crystallography, NMR, or cryo-electron microscopy remains a very challenging task, requiring a substantial amount of time and technical resources. Thus, there is a huge gap between the number of known RNA sequences^4,5 and the number of atomic RNA 3D structures available in the Protein Data Bank (PDB)⁶. As a result, various computational approaches have been developed to complement experiments for RNA 3D structure determination^7-10.

Similar to computational protein structure prediction, different strategies have been adopted to predict the RNA 3D structures⁹, such as homologous modeling¹¹, templated-based approach^12-15, fragment assembly^16-18, and physics-based methodology^19-23. Among them, the coarse-grained (CG) model is particularly attractive for RNA structure prediction and folding simulations²⁴, as it can largely improve the efficiency of conformational space sampling, especially for large RNA molecules. In recent years, different CG models of various representations of the nucleotides have been developed to predict RNA 3D structures and to study RNA folding behaviors, with or without the aid of experimental data^9,24. For instance, through simplifying the nucleotides into three beads, iFoldRNA¹⁹ and its variations^25-26 used discrete molecular dynamics (MD) simulations to predict 3D structures for small to medium-sized RNA molecules, with the aid of hydroxyl radical probing data²⁵ and sparse NMR constraints²⁶. The multilevel representation CG model, SimRNA²³, employed a statistical potential and Monte Carlo method to study the structural and dynamical properties of RNAs up to 190 nucleotides (nts), with the secondary structure and/or additional long-range contact information combined in particular. More recently, we developed an iterative simulated reference state approach to model correlated interactions in RNA folding (IsRNA) and to accurately parameterize the energy functions in the CG model²⁷. Subsequently, through MD simulations, a large-scale benchmark test on RNA 3D structure prediction indicated that the updated IsRNA1 (version 1; as compared to version 0 IsRNA) model can provide improved performance for relatively large RNAs of complicated topologies, such as large stem-loop structures and structures containing long-range tertiary interactions²⁸. Moreover, combined with experimental data, the IsRNA/IsRNA1 model was able to elucidate the folding pathway of an RNA pseudoknot²⁹, to model the loop composition effect in RNA folding stability³⁰, and to characterize binding features of an RNA aptamer to its targeted protein³¹.

As demonstrated by the RNA-Puzzles^32-35, a Critical Assessment of Protein Structure Prediction (CASP)³⁶-like collective evaluation of RNA 3D structure predictions, an accurate description of noncanonical base pairing interactions constitutes the important bottleneck in RNA 3D structure modeling and still remains as an open challenge. Though many methods have enabled predictions for Watson-Crick (WC) base pairs and native-like global folds, the true positive rate for the prediction of noncanonical base pairs is only ~20% or lower, aside from previously solved templates that happen to recur in new challenge^34-35. Compared to WC base pairing interactions, the noncanonical base pairs are more variable and have abundant covariation rules as they also involve the base’s sugar and Hoogsteen edges^37-38. These interactions have caused significant challenge for ab initio predictions of noncanonical base pairing interactions, even with the additional constraints from chemical probing data^34,39. However, noncanonical base pairs contribute crucially to RNA 3D structures and are central to the 3D architecture of folded RNA molecules⁴⁰. Without realization of these noncanonical interactions, it is hard to explain evolutionary data, difficult to predict molecular partners, or almost impossible to be prospectively tested by compensatory mutagenesis via RNA computational modeling. In some pioneering works, Das and coworkers have proposed an all-atom refinement based on atomic energy functions⁴¹ (FARFAR) and enhanced conformational sampling methods, including enumerative stepwise assembly⁴² and stepwise Monte Carlo method with a unique add-and-delete move set⁴³, to predict noncanonical RNA motifs at atomic resolution. Recently, deep learning-based methods have been developed to better describe the noncanonical base pairs for structure refinement⁴⁴ and assessment⁴⁵. Despite their success, all these methods demand huge computational resources and are thus less suitable for modeling large RNA molecules. Therefore, it is desired to balance the efficiency and accuracy in the CG model to appropriately describe noncanonical base pairs in RNA molecules.

The previous benchmark test²⁸ has shown that IsRNA1 CG model failed to recover some noncanonical base pairs in large RNAs, especially for the multi-way junctions. One reason is that the 2-bead CG representation for pyrimidine bases in previous IsRNA1 model could not fully capture noncanonical base pairing interactions such as the difference among base’s WC, sugar, and Hoogsteen edges³⁷. Hence, through systematic analyses of various noncanonical base pairs, we here developed an updated CG model, named IsRNA2 (version 2), to better account for noncanonical base pairing interactions in large RNAs. In this updated IsRNA2 model, both the purine and pyrimidine bases are represented by three CG beads and the WC, Hoogsten, and sugar edges of bases are sufficiently preserved. After reparameterization of the energy functions through the iterative simulated reference state approach²⁷, the ability of the updated IsRNA2 model in simulating noncanonical motifs was tested. Then, the IsRNA2 model was used to refine our previous predictions in the RNA-Puzzles challenges. Moreover, apart from the multi-thread central processing unit (CPU) parallel calculations, we also developed the graphics processing unit (GPU) acceleration for IsRNA2, which significantly improved the simulation speed. Overall, the updated IsRNA2 is a promising CG model to study the folding dynamics and predict the 3D structures of large RNA molecules.

Simulation model and method

CG representation of RNA nucleotide.

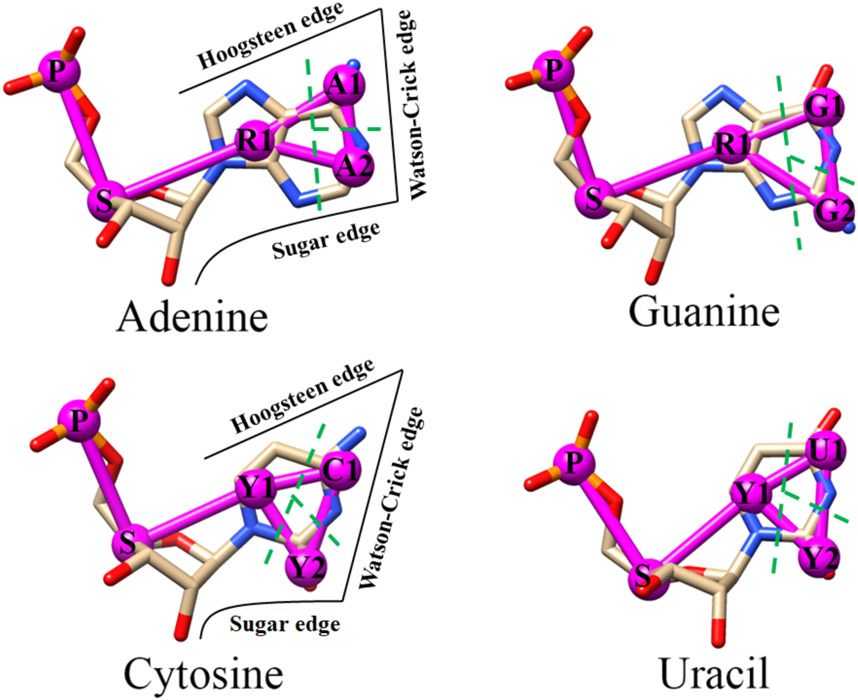
Same as the previous IsRNA, IsRNA1 versions^27-28, the backbone of RNA is represented by two CG beads P and S located at atoms P and C4’, which define the phosphate group and the ribose sugar ring, respectively. However, for the base moiety, the updated IsRNA2 model uses three CG beads for both purines and pyrimidines (see Figure 1). To reduce the overall degree of freedoms, the nucleotides adenine and guanine share a common CG bead R1, and the cytosine and uracil share two common CG beads Y1 and Y2. All the base’s CG beads are positioned at the center-of-mass of the grouped heavy atoms. Compared to the previous IsRNA/IsRNA1 models (ten CG beads in total), the current IsRNA2 model introduces eleven unique types of CG beads to better describe both the canonical and noncanonical base pairing interactions in RNA molecules. Then, the topology file of RNA is more complicated in IsRNA2 and it requires moderately more computational resources relative to IsRNA1. The properties of those eleven CG beads are summarized in Table 1.

Figure 1.

Atomistic and coarse-grained representation of the four nucleotides in RNA molecule. The atomistic models are displayed as sticks with heavy atoms phosphorus, oxygen, carbon, and nitrogen colored by orange, red, gray, and blue, respectively. The coarse-grained representations in IsRNA2 are indicated by magenta bead-spring model, wherein the phosphate group and sugar ring are represented by bead P and S, respectively, and each base is coarse-graining into three different beads. The related base moiety for each coarse-grained bead is divided by the green dashed line. Base’s Watson-Crick, sugar, and Hoogsteen edges³⁷ for purine and pyrimidine are identified in the left plane.

Table 1.

Properties of eleven types of coarse-grained beads in the updated IsRNA2 model.

CG bead	Mass (amu)	Diameter (Å)	Grouped heavy atoms
P	94.97	3.7	P, OP1, OP2, O5’, O3’
S	92.05	3.1	C5’, C4’, O4’, C3’, C2’, O2’, C1’
R1	78.05	3.2	N9, C8, N7, C5, C4, N3
A1	26.02	2.5	C6, N6
A2	26.02	2.7	C2, N1
G1	42.02	2.7	C6, O6, N1
G2	26.02	2.7	C2, N2
Y1	38.03	3.1	N1, C5, C6
Y2	28.01	2.9	C2, O2
C1	40.03	2.5	N3, C4, N4
U1	42.02	2.7	N3, C4, O4

Updated CG force field in IsRNA2.

Generally, the force field in the updated IsRNA2 model can be written as

$$E_{total}=E_{bond}(b)+E_{angle}(\theta )+E_{torsion}(\varphi )+E_{bp}(r,\theta ,\varphi )+E_{pair}(r)$$ (1)

Same as our previous models^27-28, the bond stretching energy E_bond (b) and bond angle bending energy E_angle (θ) have a form of harmonic function plus a Gaussian term, and the torsion angle energy E_torsion(φ) is in a quadruple Fourier form; see Supporting Information (SI) for details. The base pair energy E_bp(r, θ, φ) is used to restrain the predefined secondary structure and is defined as

$$E_{bp}(r,\theta ,\varphi )=E_{bond}(r_1)+E_{bond}(r_2)+E_{angle}(\theta )+{\sum }_{i=1}^5{E}_{torsion}({\varphi }_i)$$ (2)

Here E_bond, E_angle, and E_torsion share the identical formulas for those in Eq. 1 and the definitions of the structural parameters (r₁, r₂, θ, and φ_i) for all the three canonical base pairs are listed in Table 2. Only the canonical base pairs (GC, AU, and GU) are restrained by the energy E_bp (r, θ, φ) through the whole work.

Table 2.

Structural parameters for secondary structure constrains used in Eq. 2.

Base pair	r 1	r 2	θ	φ 1	φ 2	φ 3	φ 4	φ 5
GC	G1-C1	G2-Y2	G2-Y2-C1	R1-G1-G2-Y2	G1-G2-Y2-C1	G2-Y2-C1-Y1	R1-G1-C1-Y1	R1-G2-Y2-Y1
AU	A1-U1	A2-Y2	A2-Y2-U1	R1-A1-A2-Y2	A1-A2-Y2-U1	A2-Y2-U1-Y1	R1-A1-U1-Y1	R1-A2-Y2-Y1
GU	G1-U1	G1-Y2	R1-G1-U1	R1-G2-G1-Y2	G2-G1-Y2-U1	G1-Y2-U1-Y1	R1-G1-U1-Y1	---

To enable GPU acceleration in the LAMMPS platform⁴⁶, the pairwise interaction E_pair (r), which describes the base-base stacking, noncanonical base pairing, base-backbone and backbone-backbone interactions, is modified as

$$\begin{gathered} E_{pair}(r)=\epsilon {\left(\frac{\sigma }{r}\right)}^9+D_0\left[e^{-2\alpha (r-r_0)}-2e^{-\alpha (r-r_0)}\right]+\frac{H_1}{\sqrt{2\pi }{\sigma }_1}{e}^{-\frac{(r-r_1{)}^2}{2{\sigma }_1^2}}+\frac{H_2}{\sqrt{2\pi }{\sigma }_2}{e}^{-\frac{(r-r_2{)}^2}{2{\sigma }_2^2}},r< \\ {r}_{cut} \end{gathered}$$ (3)

The first term with ε = 0.5 kcal/mol and σ = (σ_i, + σ_j)/2 (σ_i is the diameter of CG bead i) accounts for excluded volume interaction, which is similar with the energy term E_LJ(r) in the previous IsRNA/IsRNA1 models^27-28. The second Morse term describes the overall profile of the pairwise interaction and the following two Gaussian terms are used to fix the major local minimums. For different CG bead pairs, the cutoff distance r_cut varies from 6.9 to 13.5Å.

The iterative simulated reference state approach²⁷ was used to parameterize the CG force field for IsRNA2. In our previous studies²⁷, this iterative simulated approach has been demonstrated to account for the correlated interactions between different structural degrees of freedoms as well as the effects from inherent chain connectivity and excluded volume, which has resulted in a reasonably accurate CG force field. Here, a simulated dataset contained 70 structures with size 26~188 nts and considerable noncanonical base pairs was used. In each step of the iterative simulated reference state calculation, after relaxation of the native structures, a total of 35,000 snapshots were generated from MD simulation trajectories to deduce the energy parameters. We followed the identical procedure given in our previous work²⁸ to sequentially parameterize energy functions in the new IsRNA2 model. We noted that no explicit artificial bias toward the native structures was introduced in the determination of energy functions of IsRNA2 through iterative simulated reference state approach²⁷. Thus, the potential bias problem in the following test tests can be neglected. See SI Table S1-S4 for all the energy parameters obtained for IsRNA2 model.

Simulation details.

The MD simulations with the new IsRNA2 model were implemented in the modified LAMMPS software⁴⁶, and the Langevin dynamics (NVT ensemble) with integration timestep Δt = 1fs was performed. For RNA 3D structure prediction or refinement, replica-exchange MD (REMD) simulations with ten replicas possessed temperatures from 200K to 425K were run to enhance the sampling efficiency in the 3D conformational space. The simulation time for each replica is 50ns and three duplicated runs with different initial structures (if available) were performed. Thus, the total simulation time for a prediction/refinement is 1.5μs (3 duplicated run*10 replica*50 ns). After sufficient relaxation, the structure snapshots were collected from the last 25ns simulations in the interval of 50ps. To obtain the predicted structures, the top 10% structures with lowest potential energies from the collected snapshots (5,000 snapshots in total) were clustered based on pairwise root-mean-square deviations (RMSDs). The detailed process and choice of the cutoff RMSD threshold for the clustering can be found in our previous study²⁸. The centroid structures of the top clusters (ranked by their sizes) provide the top predicted 3D structures. Similar to that in the IsRNA, IsRNA1 versions^27-28, a built-in single-nucleotide fragment matching algorithm was developed to recover the all-atom model from the five-bead CG representation. Finally, an atomic energy minimization was employed to reduce the possible atomic distortion and clash in the predictions.

Results and Discussions

Representation of noncanonical base pairs.

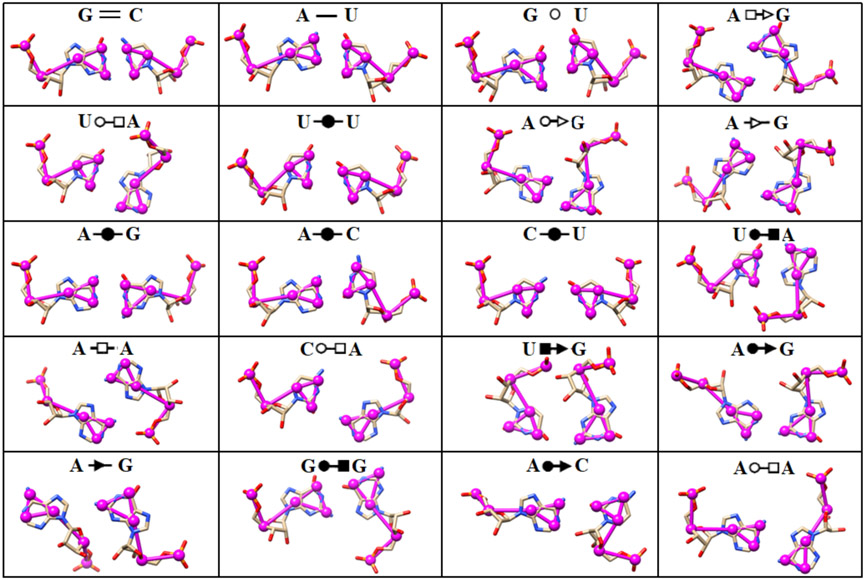
Noncanonical base pairs mediate specific interactions to stabilize the 3D architecture of various RNA motifs⁴⁰, including junction topology, kink turn, tetraloop-receptor motif, triple-stranded structure, quadruplex structure, and so on. Apart from the WC edge presented in the canonical interactions, noncanonical base pairs also involve one or two of the other two sides of the nucleobase: Hoogsteen and sugar edges^37-38. Thus, to accurately predict noncanonical base pairing interactions using coarse-grained representations, a fundamental step is to preserve the essential properties of those three edges of nucleobase. However, this pivotal point was missed due to the two-bead representation of pyrimidines in previous IsRNA and IsRNA1 models. And benchmark test for RNA 3D structure prediction by IsRNA1 indicated that some loop segments or even the full configuration, such as for the multi-way junctions, misfolded in the simulations²⁸. Therefore, following the previous classification of RNA base pairs³⁷, we here introduced a new three-bead CG representation for the base moieties of four types of nucleotides. As shown in Figure 1, in this three-bead representation, the newly updated IsRNA2 model preserves the essential features of the base’s WC, Hoogsteen, and sugar edges, which enables appropriate descriptions of various noncanonical base pairing interactions. For the top 20 most occurred base pairs in the Representative Sets of RNA 3D Structures⁴⁷ (release 3.115), which contain both the canonical and noncanonical base pairs and cover nearly all the types of interactive base edges and cis-/trans-conformations, IsRNA2 could provide a specific set of distances between particular bead pairs for each case (see Figure 2). If necessary, a set of particular angles and torsions can also be introduced to describe certain base pairing interactions. Overall, the new five-bead CG representation for each nucleotide in IsRNA2 model provides a good starting point to accurately predict noncanonical base pairing interactions in RNA motifs.

Figure 2.

Representations of 20 most occurred base pairing interactions in the IsRNA2 model. Both the canonical (the first three types) and noncanonical (the remaining) base pairs are annotated in the LW form³⁷. : GC cis Watson-Crick, : AU cis Watson-Crick, : GU wobble, : trans Hoogsteen/Sugar edge, : trans Watson-Crick/Hoogsteen, : cis Watson-Crick/Watson-Crick, : trans Watson-Crick/Sugar edge, : trans Sugar edge/Sugar edge, : cis Watson-Crick/Hoogsteen, : trans Hoogsteen/Hoogsteen, : cis Hoogsteen/Sugar edge, : cis Watson-Crick/Sugar edge, : cis Sugar edge/Sugar edge.

De novo prediction of noncanonical RNA structures.

To test the capability of modeling noncanonical base pairing interactions, IsRNA2 was used to predict 3D structure on a benchmark set of 23 RNA noncanonical motifs derived from a previous study⁴¹. Those noncanonical structures were observed in high-resolution crystallographic models of important RNA molecules and contain various common RNA motifs, such as tetraloop, kink-turn, hook-turn, 3-way junction, pseudoknot, and so on. As shown in Table 3, those RNA motifs involve one or more segments and their sizes vary from 6 to 50 nts. Here, we mainly focused on the conformations of noncanonical regions. Thus, to improve the efficiency and accuracy of conformation sampling, two canonical base pairs immediately adjacent to the motifs at each end are constrained as boundary conditions through Eq. 2. Similar to our previous study, the template-based algorithms Vfold3D^12,48/VfoldLA^18,49 were used to generate three initial 3D structures, if available, for REMD simulations in IsRNA2 and finally five candidate predictions were provided.

Table 3.

Comparison of de novo modeling of noncanonical RNA motifs with IsRNA2, IsRNA1, and FARFAR model. The best performance over three models with lowest all heavy-atom RMSD is boldfaced for each case.

No.	Motif name (PDB id)	Sizea	IsRNA2			IsRNA1			FARFARe
			Rankb	RMSDc	INFd	rank	RMSD	INF	rank	RMSD
1	Rev response element high-affinity site (1csl)	6+7	1	2.72	0.77	2	2.88	0.67	2	3.95
2	Fragment with A-C pairs, SRP helix VI (1d4r)	6+6	3	0.65	0.90	1	1.00	0.97	1	1.83
3	Fragment with G-G and G-A base pairs, SRP helix VI (1d4r)	8+8	1	1.87	0.78	1	2.41	0.76	3	3.27
4	UUCG tetraloop (1f7y)	8	1	2.60	0.71	1	2.77	0.67	1	1.12
5	Kink-turn motif (1jj2)	7+10	2	9.05	0.52	4	8.55	0.62	2	8.85
6	Helix with A-C base pairs (1kd5)	8+8	2	2.73	0.79	2	2.45	0.73	2	2.45
7	SRP domain IV (1lnt)	8+8	4	1.56	0.76	2	2.89	0.75	4	1.54
8	Hook-turn motif (1mhk)	5+6	3	3.58	0.64	4	4.99	0.46	5	2.56
9	GAGA tetraloop from sarcin-ricin loop (1q9a)	6	2	0.74	0.91	3	1.15	0.61	1	0.82
10	Loop 8, A-type RNase P (1u9s)	9	2	3.08	0.80	1	4.45	0.67	5	1.38
11	Pentaloop from conserved region of SARS (1xjr)	9	5	2.57	0.59	2	3.70	0.56	3	1.10
12	L3, thiamine pyrophosphate riboswitch (2gdi)	9	5	2.09	0.74	1	3.05	0.56	4	2.00
13	Active site, hammerhead ribozyme (2oeu)	11+7+5	4	7.67	0.65	2	6.88	0.60	4	8.64
14	Stem C internal loop, L1 ligase (2oiu)	8+8	2	1.87	0.78	5	5.68	0.43	1	2.24
15	J4a-4b region, metal-sensing riboswitch (2qbz)	9+9	5	1.46	0.82	2	3.29	0.77	3	3.71
16	P1-L3, SAM-II riboswitch (2qwy)	50	2	3.94	0.62	2	9.82	0.51	5	7.40
17	J4/5 from P4-P6 domain, Tetrahymena thermophila ribozyme (2r8s)	7+6	3	1.54	0.90	4	2.98	0.72	1	1.76
18	J5-5a hinge, P4-P6 domain, Tetrahymena ribozyme (2r8s)	10+9	5	9.35	0.55	2	9.95	0.65	3	9.99
19	Pseudoknot, domain III, CPV internal ribosome entry site (3b31)	12+8	1	3.77	0.85	5	3.15	0.91	4	3.55
20	G-A base pair (157d)	5+5	4	0.86	0.92	3	0.88	0.96	1	1.19
21	Helix with U-C base pairs (255d)	6+6	1	1.38	0.87	1	1.30	0.85	2	2.10
22	Loop E motif, 5S RNA (354d)	11+11	1	2.57	0.62	5	7.25	0.58	2	1.64
23	Pre-catalytic conformation, hammerhead ribozyme (359d)	11+8+6	2	5.34	0.66	2	7.14	0.71	5	8.44
	average		2.65	3.17	0.75	2.48	4.29	0.68	2.78	3.54

^aFor RNA motif contained multiple chains, the size (number of nucleotides) for each chain is separated by “+”.

^bThe rank of the best prediction from the top five clusters.

^cLowest all-heavy-atom root-mean-square deviation (in Å) for the best prediction from the top five clusters.

^dINF is the interaction network fidelity⁵⁹ for all the canonical and noncanonical base-pairing and base-stacking interactions.

^eSince the original predictions of FARFAR are unavailable, the INFs for FARFAR are absent here.

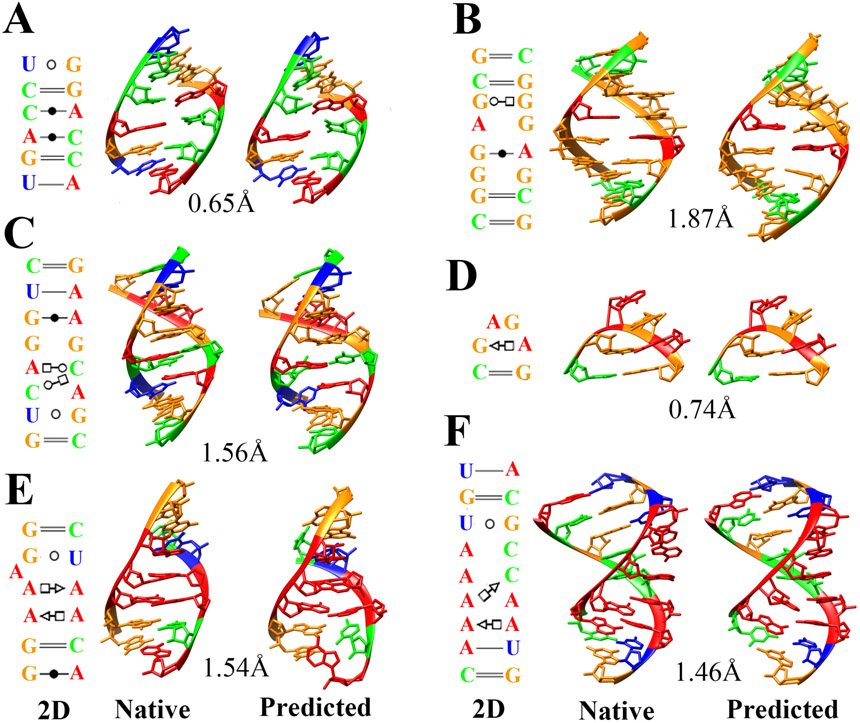
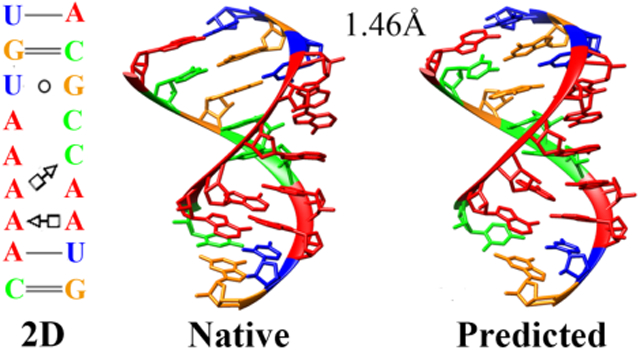
For 15 of the 23 noncanonical motifs, IsRNA2 provided at least one of five predictions with less than 3.0 Å all-heavy-atom RMSD to the experimentally determined structure (see Table 3). Among them, the best predicted 3D structures for 9 cases reached atomic accuracy (RMSD < 2.0 Å) and nearly all the native noncanonical base pairs were recovered, including not only the nucleotides but also the base edges in the noncanonical contact, when the fluctuations in base pairing interactions are neglected. Our current study cases incorporated those widely adopted RNA motifs, such as fragments with A-C, G-G, and G-A base pairs⁵⁰, Escherichia coli SRP domain⁵¹, GAGA tetraloop from sarcin/ricin domain⁵², J4/5 from P4-P6 domain, Tetrahymena thermophila ribozyme⁵³, and so on (see Fig. 3). However, IsRNA2 failed to predict the near-native 3D structures (RMSD < 5.0 Å) for 4 motifs (see Table 3), including the three-way junctions in the active site⁵⁶ and pre-catalytic conformation of hammerhead ribozymes⁵⁷, which may be caused by the insufficient sampling of conformational space under the current simulation conditions. Another possibility is that the current energy functions of IsRNA2 could not well capture the particularly sharp turns of the backbone, such as for the kink-turn motif⁵⁸ and J5-5a hinge in the P4-P6 domain of Tetrahymena ribozyme⁵³. To fix those problems in future, incorporation of experimental information, such as the NMR data^26,39, into the simulation as constraints is promising.

Figure 3.

3D structure modeling for several noncanonical RNA motifs with IsRNA2 model. (A) Fragment with A-C pairs, SRP helix VI⁵⁰ (PDB id: 1d4r, row 2 in Table 3), (B) fragment with G-G and G-A base pairs, SRP helix VI⁵⁰ (PDB id: 1d4r, row 3 in Table 3), (C) Escherichia coli SRP domain IV⁵¹ (PDB id: 1lnt, row 7 in Table 3), (D) GAGA tetraloop from sarcin/ricin domain⁵² (PDB id: 1q9a, row 9 in Table 3), (E) J4/5 from P4-P6 domain, Tetrahymena thermophila ribozyme⁵³ (PDB id: 2r8s, row 17 in Table 3), and (F) J4a-4b region, metal-sensing riboswitch⁵⁴ (PDB id: 2qbz, row 15 in Table 3). Adenine, guanine, cytosine, and uracil are colored by red, orange, green, and blue, respectively. The 2D structure (left column) is extracted from the native structure (middle column) by the program DSSR⁵⁵. The predicted 3D structure (right column) is from the top five clusters with lowest RMSD. The all heavy-atom RMSDs for those predictions are also given.

Additionally, we compared the performance of IsRNA2 on 3D structure prediction with two other models and the results were summarized in Table 3. Compared with the previous IsRNA1 model²⁸, because of the clear definition of three base interacting edges in the updated CG representation, IsRNA2 provided better predictions (smaller RMSDs) for 18 of 23 noncanonical structures. Moreover, the average RMSD over all the tested structures decreased from 4.29 Å (IsRNA1) to 3.17 Å (IsRNA2) and the average interaction network fidelity⁵⁹ (INF) increased from 0.68 (IsRNA1) to 0.75 (IsRNA2). Ideally, an INF of 1.0 means that the predicted structure perfectly reproduces the interaction networks in the native structure. These results demonstrated the importance of definition of base interacting edges (WC, Hoogsteen, and sugar edges) in CG representation for accurate modeling of noncanonical base pairs. When compared to the atomic FARFAR model⁴¹, which uses fragment assembly drawn from a crystallographic model and a full-atom energy function, the CG IsRNA2 model could still obtain better predictions (smaller RMSDs) for 13 noncanonical structures and slightly lower the average RMSD from 3.54 Å (FARFAR) to 3.17 Å (IsRNA2); See Table 3. Additionally, for the benchmark set of 23 noncanonical RNA structures, the numbers of best predictions (lowest RMSD) provided by IsRNA2, FARFAR, and IsRNA1 are 11, 8, and 5 (a case shares the identical RMSD with FARFAR), respectively. Overall, the updated IsRNA2 CG model demonstrated comparable or better performance than the previous atomic model in de novo modeling of noncanonical RNA motifs.

Refinement of RNA 3D structure predictions in RNA-Puzzles.

As a CASP-like blind assessment of RNA 3D structure prediction, the RNA-Puzzles (http://www.rnapuzzles.org/) provides a platform for the evaluation of cutting-edge RNA structure prediction algorithms and the results of four rounds of challenges have been published^32-35. To further verify the improvement of IsRNA2 on 3D structure prediction for large RNA molecules, we used IsRNA2 model to refine the predictions submitted by our group (Chen group) in the previous RNA-Puzzles challenges. With the top 3 models (if available) with lowest RMSDs submitted by Chen group as the initial structures and the secondary structure (canonical base pairs) extracted from the native structure as constraints (Eq. 2), 50 ns (each replica) REMD simulations were run to refine the 3D predictions. However, same as the previous work²⁸, only a short 1.5 ns REMD simulation was run for the multi-way junctions to avoid large conformation changes. Finally, top five predictions from the centroid structures of clusters were obtained.

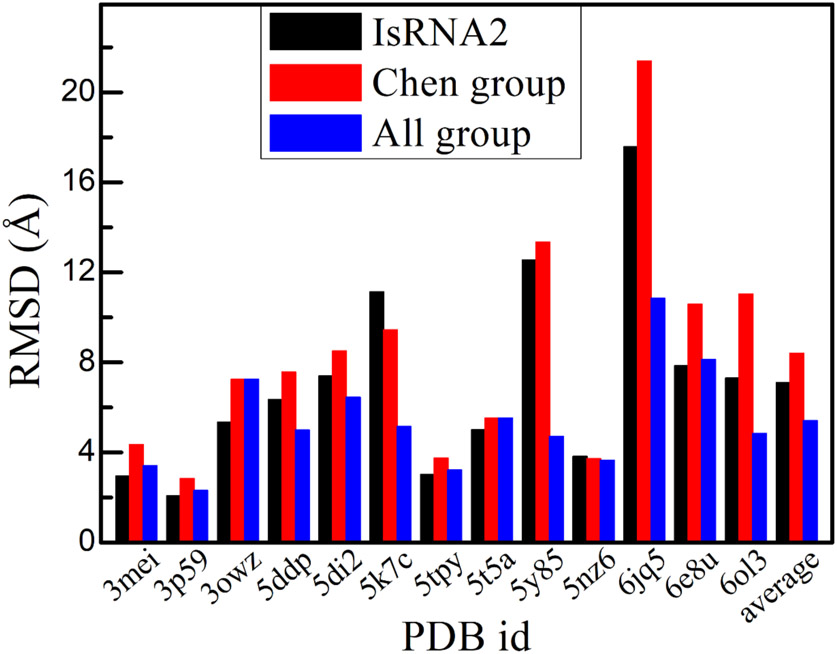
Here, the predictions for 13 challenges in RNA-Puzzles have been refined by IsRNA2 model. Those 13 challenges include ribozyme, riboswitch, virus-associated RNA, and RNA aptamer, with their sizes varying from 37 to 112 nts. Moreover, the structural topologies of those challenges cover stem-loop, multi-way junction, pseudoknot, and structure contained tertiary interaction. As shown in Fig. 4, out of the 13 selected challenges, the lowest RMSDs of five predictions for 11 cases decreased after refinement using IsRNA2, indicating that the IsRNA2 model could indeed further refine the initial submissions from Chen group. For instance, for the glycine riboswitch⁶⁰ (PDB id: 3owz, puzzle #3), Mango-III fluorogenic aptamer⁶¹ (PDB id: 6e8u, puzzle #23), and an adenovirus virus-associated RNA⁶² (PDB id: 6ol3, puzzle #24), the lowest RMSDs of the best predictions decreased from 7.24, 10.59, and 11.03 Å (initial predictions by Chen group) to 5.34, 7.85, and 7.30 Å (refined by IsRNA2), respectively. Only one of the remaining two challenges had a larger RMSD than the previous prediction (PDB id: 5k7c, puzzle #17), while the other case remained nearly unchanged (PDB id: 5nz6, puzzle #21). The average RMSD over the total 13 challenges decreased from 8.40 Å (Chen group) to 7.10 Å (IsRNA2). Furthermore, for 6 of 13 challenges, refinement by IsRNA2 model can obtain even better predictions than the best models from the submissions of all groups (see Fig. 4), such as for the regulatory motif from the thymidylate synthase mRNA⁶³ (PDB id: 3mei, puzzle #1), the glycine riboswitch⁶⁰ (PDB id: 3owz, puzzle #3), and the twister sister ribozyme⁶⁴ (PDB id: 5t5a, puzzle #19). Therefore, IsRNA2 model might be a powerful tool to refine the 3D structures predicted by other programs, for instance, the template-based Vfold3D¹²/VfoldLA¹⁸ model.

Figure 4.

Refinement of 3D structures predicted by Chen group in the RNA-Puzzles challenges through IsRNA2 model. Lowest RMSDs for the models from the predictions after refinement by IsRNA2 (“IsRNA2”) are shown. For comparison, the best prediction from initial submissions by Chen group (“Chen group”) and that from all group (“All group”, including Chen group) are also given for each case.

Furthermore, we compared the performance of IsRNA2 on model refinement with two recent methods, namely FARFAR2⁶⁵ and RNA-BRiQ⁴⁴ Based on the previous Rosetta’s FARFAR algorithm, FARFAR2 integrated RNA-Puzzle-inspired innovations with updated fragment libraries and helix modeling and could recover native-like structures more accurate than models submitted during the RNA-Puzzles trials⁶⁵. RNA-BRiQ combined a high-resolution knowledge-based potential (BRiQ) with a nucleobase-centric sampling algorithm to provide a robust improvement in refining near-native RNA models⁴⁴. As shown in Table 4, for 11 announced RNA-Puzzles challenges, IsRNA2, FARFAR2, and RNA-BRiQ provide best predictions (over those three methods) for 5, 1, and 6 (one case is identical to IsRNA2) cases, respectively. We noted that the sizes of the candidate pool to select the optimal prediction model for IsRNA2, FARFAR2, and RNA-BRiQ are 5, 10, and 20, respectively. Overall, despite the recent advancements by FARFAR2 and RNA-BRiQ algorithms, IsRNA2 is a competitive method in RNA model refinement.

Table 4.

Comparison of model refinement for RNA-Puzzles challenges with IsRNA2, FARFAR2, and RNA-BRiQ. The best prediction over those three models with lowest all heavy-atom RMSD is boldfaced for each challenge.

Puzzle (PDB)	Length (nt)	RNA	RMSD (Å)
			IsRNA2a	FARFAR2b	RNA-BRiQc
1 (3mei)	46	thymidylate synthase motif	2.94	2.50	1.97
2 (3p59)	100	nanosquare	2.06	2.71	2.06
3 (3owz)	84	glycine riboswitch	5.34	12.41	6.53
14b(5ddp)	61	Gln riboswitch (bound)	6.35	6.88	6.14
15 (5di2)	68	hammerhead ribozyme	7.40	5.98	6.78
17 (5k7c)	58	pistol ribozyme	11.13	6.69	5.68
18 (5tpy)	71	Zika xrRNA	3.02	5.02	3.47
19 (5t5a)	62	twister sister ribozyme	5.01	5.16	6.97
20 (5y85)	68	twister sister ribozyme	12.55	4.03	3.54
21 (5nz6)	41	guanidinium-In riboswitch	3.82	6.04	3.83
24 (6ol3)	112	adenovirus virus-associated RNA	7.30	7.68	5.53

^aLowest RMSD of top 5 predictions.

^bBest of 10 low-energy clusters, data collected from Ref 65.

^cLowest energy model within 20 refinement models, data collected from Ref 44.

GPU acceleration for large RNA molecules.

For large RNA molecules with size > 100 nts, the sufficient sampling in conformational space is challenging even at CG representation due to their huge number of available conformations. On the other hand, GPUs have become popular as accelerators in high-performance computing due to their impressive floating-point capabilities, high memory bandwidth, and low electrical power requirement. For instance, numerous MD codes have been developed to utilize GPUs to gain impressive speedups^66-71. Thus, based on the “GPU” package⁷² in the LAMMPS MD software⁴⁶, we have embedded and compiled the related source codes for the modified pairwise energy function in Eq. 3 to enable GPU acceleration in the IsRNA2 model. In this way, we expected the sampling speed for large RNAs to be largely improved.

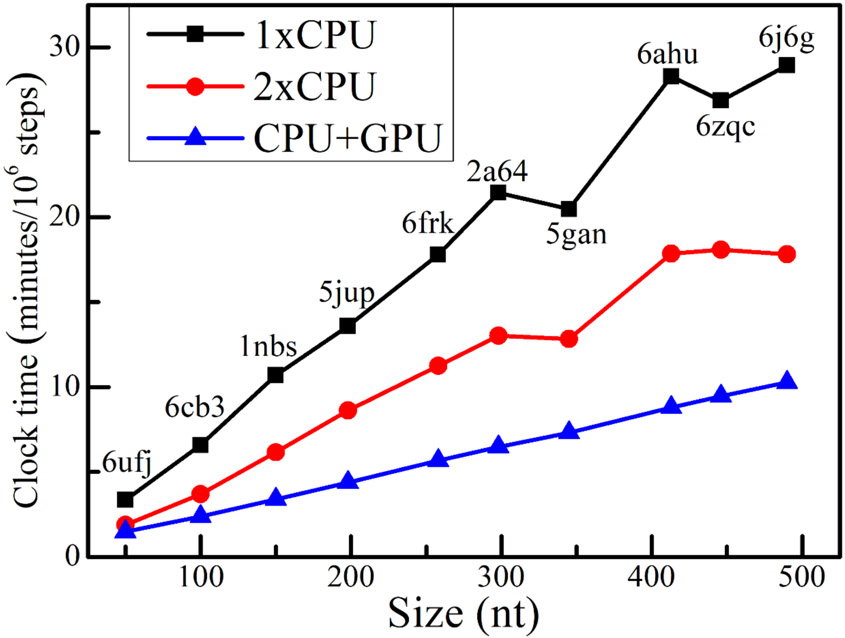
The performance of GPU acceleration was tested on 10 RNAs with sizes from 50 to 490 nts. With the native 3D structure as initial state and the secondary structure extracted from the native structure as constraints, a 1 ns MD simulation (10⁶ steps with integration timestep Δt = 1fs) was run on the Intel(R) Core(TM) i9-9900K 3.6GHz CPU and the GeForce RTX 2080 Ti GPU. The wall-clock time was collected and recorded. For comparison, the clock time of one single CPU thread run and two CPU threads parallel run were both reported. As shown in Fig. 5, for a bacterial ribonuclease P RNA⁷³ (PDB id: 2a64, 298 nts) and the human Ribonuclease P Holoenzyme⁷⁴ (PDB id: 6ahu, 413 nts), the clock time on a single CPU thread are 21.4 and 28.3 minutes, respectively, and they decrease to 6.5 and 8.8 minutes when the GPU accelerator (one CPU thread plus a GPU card) was employed, which indicates an about 3.2-fold speedup for GPU acceleration. When compared to the parallel run on two CPU threads, the GPU acceleration could also gain an about 2.0-fold speedup for the those two RNAs. Moreover, we noted a perfect linear relationship between the clock time and the size of RNA molecule for the GPU acceleration. Overall, these results demonstrated that the CG IsRNA2 model plus GPU accelerators can be a powerful platform to study large RNA molecules.

Figure 5.

Benchmark test for accelerating simulations in IsRNA2 through parallel central processing unit (CPU) threads and graphics processing unit (GPU) computing. For RNA molecules with different sizes (PDB ids are labeled), performances were tested on single CPU thread (1xCPU), two CPU threads (2xCPU), and GPU accelerator (CPU+GPU). The tested CPU is Intel(R) Core(TM) i9-9900K 3.6GHz and GPU is GeForce RTX 2080 Ti.

Conclusion

Noncanonical base pairs play a pivotal role in stabilizing RNA 3D structures⁴⁰, especially for large RNAs, and pose one of the most challenging bottlenecks for current RNA 3D structure prediction^34-35. On the other hand, CG models are promising and sometimes more suitable approaches, compared to atomistic models, in studying the dynamics of large RNAs due to reduced degrees of freedom and smoother free energy landscape and hence more efficient conformational sampling⁷⁵. Here, based on our previous efforts in RNA CG modeling^27-28, we developed an updated IsRNA2 (version 2) model to study the noncanonical base pairing interactions in large RNA molecules. By introducing a five-bead CG representation for both purine and pyrimidine nucleotides, the updated IsRNA2 model preserves the definition of three interacting edges of bases, namely WC, Hoogsteen and sugar edges, and captures the fundamental elements to accurately describe various base pairing interactions, including both canonical and noncanonical base pairs. After re-parameterizing the energy functions through the iterative simulated reference state approach, the IsRNA2 was used to de novo model noncanonical RNA motifs and refine 3D structure predictions in RNA-Puzzles challenges. For 15 out of 23 tested noncanonical RNA structures, IsRNA2 achieved a near atomic-resolution (RMSD < 3.0 Å) prediction and recovered most of the native noncanonical base pairs. With significantly improved accuracy, benchmarks also indicated that IsRNA2 is able to achieve a comparable performance to the atomic model in de novo modeling of noncanonical RNA structures. To further confirm the ability of IsRNA2 in modeling noncanonical base pairs, an additional benchmark test on more noncanonical motifs, such as those from Rosetta-SWM method⁴³, is needed in future. Furthermore, out of 13 selected challenges in RNA-Puzzles, 3D structure predictions for 11 cases were obviously refined by simulations in IsRNA2. For some challenges, IsRNA2 can provide even better models than the previous best submissions. Finally, the GPU acceleration was introduced in IsRNA2 model to boost the sampling speed, with a ~ 3.2-fold speedup for very large RNA molecules. In all, the reported IsRNA2 is a promising coarse-grained model to study the noncanonical base pairs in large RNA molecules.