A network medicine approach for identifying diagnostic and prognostic biomarkers and exploring drug repurposing in human cancer

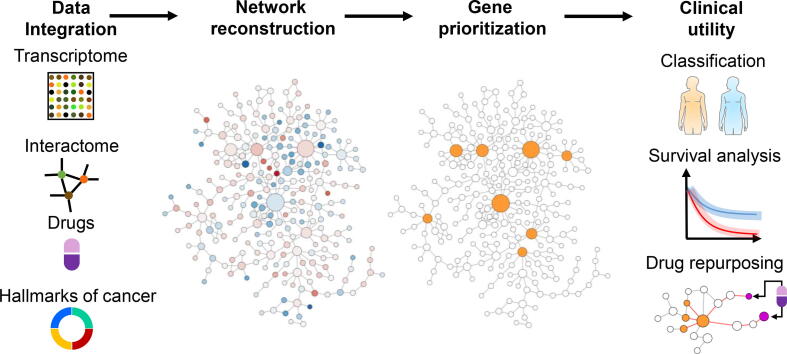
Graphical abstract

Highlights

• •We developed and applied an integrative network medicine approach to identify novel biomarkers and explore drug repurposing in 18 cancer types.
• •The approach uses a network-based method to prioritize genes in cancer-specific networks reconstructed using transcriptome and interactome data.
• •Genes with aberrant expression and strong regulatory impact on other dysregulated genes are prioritized and regarded as cancer genes and show diagnostic and prognostic potential.
• •We developed a network-proximity method to perform drug repurposing and shortlisted dozens of drugs that are repurposable for the identified cancer genes.
• •The study demonstrates the ability of the network medicine approach to refine our biological understanding of cancer diagnosis and prognosis and potentially improve clinical outcomes.

Abstract

Cancer is a heterogeneous disease mainly driven by abnormal gene perturbations in regulatory networks. Therefore, it is appealing to identify the common and specific perturbed genes from multiple cancer networks. We developed an integrative network medicine approach to identify novel biomarkers and investigate drug repurposing across cancer types. We used a network-based method to prioritize genes in cancer-specific networks reconstructed using human transcriptome and interactome data. The prioritized genes show extensive perturbation and strong regulatory interaction with other highly perturbed genes, suggesting their vital contribution to tumorigenesis and tumor progression, and are therefore regarded as cancer genes. The cancer genes detected show remarkable performances in discriminating tumors from normal tissues and predicting survival times of cancer patients. Finally, we developed a network proximity approach to systematically screen drugs and identified dozens of candidates with repurposable potential in several cancer types. Taken together, we demonstrated the power of the network medicine approach to identify novel biomarkers and repurposable drugs in multiple cancer types. We have also made the data and code freely accessible to ensure reproducibility and reusability of the developed computational workflow.

1. Introduction

Tumorigenesis and tumor progression are linked to abnormal expression of genes [1]. These genes’ expression is too low or too high and therefore not regulated properly in cancer cells. Identification of such dysregulated cancer genes in cancer networks is important to characterize their regulatory role and help establish novel therapies. The easy access to annotated human genomics and interactome data allows for reconstruction of cancer-specific networks, making network-based characterization of cancer genes possible. Public repositories widely used by the community include The Cancer Genome Atlas (TCGA) [2] and Genomics Evidence Neoplasia Information Exchange (GENIE) [3] for genomics data and Reactome [4] and OmniPath [5] for interatcome data. However, there has been a lack of systematic approaches to investigate cancer genes across multiple cancer types and evaluate their clinical utility.

Network medicine approaches have been widely used to identify biomarkers for cancer subtype classification [6] and prognostic assessment [7] and to shortlist drug-repurposing candidates for cancer [8]. Owing to the natural ability of network-based approaches to integrate and interpret human genomics and interactome data, they are much more powerful than approaches that examine and analyze only genes with aberrant expression to identify tumor-specific molecular mechanisms, candidate targets and repositioned drugs for personalized treatment [9]. For instance, by integrating protein interactome with cancer genomics data, Zhang et al. identified dozens of subnetworks linked with prognosis across four cancer types. The authors used the subnetworks to develop prognostic models that can predict the survival of individual cancer patients [10]. Woo et al. developed a regulatory network-based approach that uses dysregulated gene expression profiles and molecular interactions following compounds perturbation to identify both direct targets and downstream proteins of drugs [11]. On the other hand, network-based gene prioritization has been remarkably useful to identify genes that are involved in cancer progression and correlated with clinical traits [12]. State-of-the-art gene prioritization algorithms include those based on network propagation that imitates transmission of information in networks [6], [13], network embedding that converts nodes to vectors and preserves the structure of the network [14], [15], and seed association that links seed genes (i.e. oncogenes) with candidate genes using defined rules [13]. For example, Leiserson et al. developed a pan-cancer network approach which combines a diffusion-based method and TCGA data to identify subnetworks and protein complexes perturbed by genes with somatic mutations [16]. The approach showed advances in detecting genes with rare mutations in cancer. Another important application for network medicine approaches is drug repurposing [17], [18]. In this case, drugs designed and approved for other diseases like infections show abilities to treat given (sub)-types of cancer. As a result, one can shorten the path towards clinical approval and accelerate application in targeted cancer therapy. Furthermore, in personalized treatment, drug repurposing is especially valuable for patients showing resistance to available therapies. Hence, one can integrate individual patients’ genomics data with network analysis to identify repurposable drugs for precision medicine [19]. Altogether, all these evidence demonstrate the ability of network-based methods to maximize the use of complex biomedical data for the identification of genes with potential clinical utility.

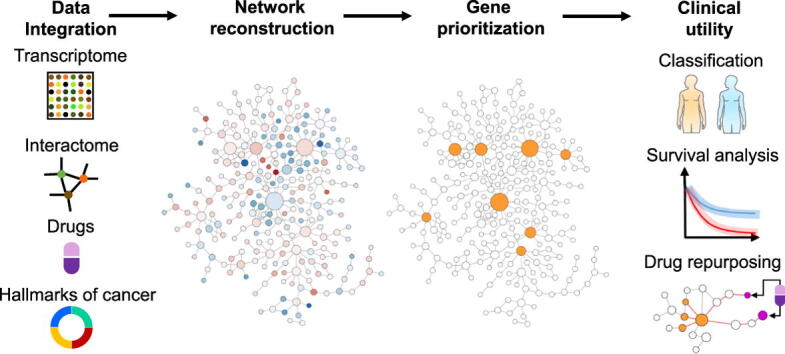
We presented an integrative network medicine approach to identify biomarkers and explore drug repurposing across cancer types (Fig. 1). We used a network-based method to prioritize genes in cancer-specific networks reconstructed using human interactome and transcriptome data. The top-ranking genes regarded as cancer genes because they show high expression fold-changes and have strong interactions with other highly perturbed genes. We further performed systematic analyses to evaluate the clinical utility of the cancer genes in cancer diagnosis and prognosis. Compared to the genes with the most dysregulated expression levels, the cancer genes identified by our method show improved performance in classifying tumor samples from normal tissues and predicting patients’ survival. Finally, we used a network proximity approach to perform drug repurposing. We shortlisted dozens of drug-repurposing candidates in several cancer types and elaborated on the molecular mechanisms through which they regulate the cancer genes. Our study demonstrates a network medicine approach that is useful for refining our biological understanding of cancer diagnosis and prognosis and potentially improving clinical outcomes.

Fig. 1.

Workflow of the study. The network medicine approach integrates human transcriptome and interactome data to reconstruct cancer-specific networks. A network topology-oriented scoring model is employed to prioritize genes in the networks. The potential clinical utility of identified genes is evaluated through tumor stratification, survival analysis, and drug repurposing. The detailed computational workflow is shown in Figure S1.

2. Methods and Materials

2.1. The network medicine approach

We developed a network medicine approach that integrates data analysis and network biology methods to conduct systematic, quantitative, and reproducible research. The approach contains several modules that are described in detail in the rest of this section. Figure S1 shows a flowchart of the computational methods used for analysis.

2.2. Gene expression data and differential gene expression analysis

We downloaded and used expression data from the Xena platform [20]. The platform contains tumor samples and their corresponding normal tissue samples for 33 cancer types. The raw data include 10,530 tumor and normal samples from TCGA [2] and 7,845 normal tissue samples from the Genotype-Tissue Expression (GTEx) project [21]. The raw FASTQ files were processed using a common RNA sequencing pipeline to eliminate batch effects from different computational processing. The pipeline re-aligned the fragments to the human reference genome (hg38) and quantified gene expression using the Kallisto [22] and RSEM tools [23]. We converted the Ensembl identifiers of genes into HGNC gene symbols and obtained a matrix of gene expression data with 18,375 samples for 33 cancer types. For the sake of data consistency and minimizing the effect of unbalance sample sizes [24], we removed 15 cancer types that do not have normal tissue samples from either TCGA or GTEX or have less than 20 normal tissue samples in total. This resulted in 18 cancer types with for the follow-up differential gene expression analysis. To increase confidence that the selected genes for differential expression analysis are expressed in both tumor and normal samples, we kept genes whose expression greater than zero in at least 20 tumor samples and 20 normal samples. Subsequently, we used the gene expression data of the 18 cancer types to identify differentially expressed genes (Table 1). We performed the analysis using the DESeq2 package in R [25]. Genes with an adjusted p-value smaller than 0.05 (computed using the Benjamini-Hochberg method) were regarded as significantly differentially expressed genes. To ensure that the selected significantly differentially expressed genes have biologically meaningful effect size [26], we used genes with an absolute log2 fold-change of at least 2 for subsequent analysis (Table S1).

Table 1.

Statistics of employed cancer data and networks. The table shows 18 cancer types and their corresponding tumor and normal samples from TCGA and GTEx. The last four columns show the number of genes used for differential expression analysis after filtering genes with low expression, the number of identified significantly differentially expressed genes, the number of nodes and edges of the corresponding cancer networks.

Cancer type	Tumor	Normal	# of genes	# of DEGs	# of nodes	# of edges
Bladder Urothelial Carcinoma (BLCA)	407	28	23,174	2,132	456	907
Breast Invasive Carcinoma (BRCA)	1,099	291	37,459	4,205	560	1,052
Colon Adenocarcinoma (COAD)	288	348	34,942	5,599	818	1,737
Esophageal Carcinoma (ESCA)	182	286	35,643	4,386	424	629
Kidney Chromophobe (KICH)	66	53	27,329	3,835	513	879
Kidney Renal Clear Cell Carcinoma (KIRC)	530	100	32,172	3,091	361	515
Kidney Renal Papillary Cell Carcinoma (KIRP)	288	60	29,511	2,756	344	550
Liver Hepatocellular Carcinoma (LIHC)	369	160	30,888	2,801	299	545
Lung Adenocarcinoma (LUAD)	513	347	37,018	4,642	610	1,082
Lung Squamous Cell Carcinoma (LUSC)	498	338	36,847	6,729	985	2,128
Pancreatic Adenocarcinoma (PAAD)	179	171	31,694	4,916	857	1,855
Prostate Adenocarcinoma (PRAD)	495	151	34,594	2,616	126	127
Rectum Adenocarcinoma (READ)	92	317	30,498	5,684	876	1,882
Skin Cutaneous Melanoma (SKCM)	468	557	36,487	9,223	1,270	2,781
Stomach Adenocarcinoma (STAD)	413	211	35,056	3,613	428	740
Thyroid Carcinoma (THCA)	512	338	36,496	3,958	274	401
Thymoma (THYM)	119	339	30,167	10,197	2,294	7,830
Uterine Corpus Endometrial Carcinoma (UCEC)	180	101	31,163	6,687	1,153	2,707

2.3. Gene set enrichment analysis

Gene set enrichment analysis helped us interpret the biological function of differentially expressed genes by comparing the distribution of expression statistics of genes of a biological pathway or term to randomly selected gene sets with the same size and derived from the same gene expression dataset [27]. We used MsigDB hallmark gene sets [28] and tested their expression statistic (i.e., log2 fold-change of gene expression divided by standard deviation) on the whole expression profile of a cancer type (Table S2). Terms with an adjusted p-value smaller than 0.05 (computed using the Benjamini-Hochberg method) were considered statistically significant, and each has an enrichment score that quantifies the degree of dysregulated expression in the associated genes. In other words, a high positive or negative score means the genes of a term are more likely to lie at the extremes of the gene expression statistic ordered from the highest to the lowest. We performed the analyses using the R package clusterProfiler [29].

2.4. Reconstruction of cancer-specific networks

We downloaded 135,435 molecular interactions from the OmniPath database that aggregates data from over 100 sources [5]. The database contains protein–protein and gene regulatory interactions, enzyme-substrate relationships, protein complexes, and intercellular communication. We kept only experimentally validated interactions for network reconstruction. In addition, we transformed microRNA names in the database to corresponding gene symbols from the HGNC database [30]. As a result, we obtained a directional generic network with 11,831 genes and 75,303 interactions. The interaction types include stimulation and inhibition. For undirected interactions without specification of interaction types, we assumed the interactions are bi-directional and thus added an entry to complement the missing interaction.

We reconstructed cancer-specific networks using the significantly differentially expressed genes identified for each cancer type to extract interaction information from the generic network (Table S3). Specifically, we took only interactions in which both interacting molecules are significantly differentially expressed genes. In addition, we computed Pearson correlation coefficients for each interaction based on the expression levels of the interacting genes and kept only those consistent with the interaction types. That means that a stimulatory interaction has a positive Pearson correlation coefficient and an inhibitory interaction a negative one. For undirected interactions, we assigned Pearson correlation coefficients as their edge weights.

2.5. Gene prioritization

We made use of the guilt-by-association principle to prioritize genes in cancer-specific networks. We assumed that important genes in tumor have high expression perturbation (indicated by log2 fold-change) and many interactions (indicated by node degree). The importance of genes were characterized by their node weights (absolute log2 fold-change multiplied by node degree). Furthermore, if such a highly perturbed and densely connected gene has short distances to other genes with high weights, its importance increases. The distance between genes was characterized by Pearson correlation coefficients with the formula -log10(|p| + c) and used as edge weights. The constant c = 1e-6 in the equation avoids the appearance of infinite values and is negligible compared to impactful correlations. A high correlation between two genes indicates a strong interaction between them and is transformed into a short distance in the network. We normalized node and edge weights using their maximum values, constraining them to the range [0, 1]. Then, we used the weights to calculate gene scores (S_i) using the following equation [31]

$$S_i(d)=\frac{2}{n\overline{p}}\sum _j(p_j-\overline{p})I(D^g\left(i,j\right)\le d)$$

where n is the total number of nodes in the network, p_j is the weight of node j and $\overline{p}$ is the average weight of all nodes in the network g. $I(D^g\left(i,j\right)\le d)$ is an identity function, equaling 1 if node i and node j are within distance d and 0 otherwise. The distance d increases from zero to the maximum distance between node i and other nodes in the network. This results in a curve that starts from the weight of node i when d equals 0 and ends at 0 when d reaches its maximum value, and the area under the curve is used to score the node in the network. A high score translates into a high ranking of a gene (Table S4). The analysis was performed using the R package SANTA [31].

2.6. Random forest classification of tumor and normal samples

We used a wrapper method to choose top-ranking genes based on their scores [32] and trained the random forest classifiers to distinguish between tumor and normal samples. We used random forest as it has demonstrated to be the top-performing algorithm in solving classification problems [33]. Besides, combining feature selection with random forest showed superior performance than other classifiers using different real-life datasets [34]. The number of chosen genes was constrained in the range [3], [9]. This strategy ensures as few as possible genes are selected to avoid model overfitting [35] and to facilitate clinical applications that favor biomarkers with less genes [36], [37]. The classifier with the best performance determined the optimal number of genes for each cancer type. For comparison, we trained a random forest classifier for each cancer type using the same number of significantly differentially expressed genes ranked by expression fold-change, and the selected genes are not restricted to be included in the cancer-specific interaction networks. We evaluated model performances using F1 score, Matthews correlation coefficient (MCC), and the receiver operating characteristic (ROC) curve. Specifically, the metrics were computed using confusion matrixes that contain four entries – true positive (TP), true negative (TN), false-positive (FP), and false-negative (FN). Sensitivity ($\frac{\mathit{TP}}{\mathit{TP}+FN}$) measures the proportion of tumor samples correctly determined as positive samples and specificity ($\frac{\mathit{TN}}{\mathit{FP}+TN}$) measures the proportion of normal samples correctly determined as negative samples. F1 score ($\frac{2\bullet precision\bullet recall}{\mathit{precision}+recall}$) combines both recall (i.e., sensitivity) and precision ($\frac{\mathit{TP}}{\mathit{TP}+FP}$) to measure a classifier’s accuracy. Precision represents the ratio of correct predictions of tumor samples to the total predicted tumor samples. MCC ($\frac{\mathit{TP}\times TN-FP\times FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}$) is a balanced metric and takes TP, FP, TN, and FN into account. MCC is recommended when the number of positive and negative samples is imbalanced [38], [39]. For instance, BLCA contains 407 tumor samples and 28 normal samples. The value of MCC is in the range [-1, 1], where 1 indicates a perfect classifier that can correctly distinguish tumor and normal samples, 0 indicates that the performance of a classifier is equal to random guessing, and −1 indicates that the model prediction is completely inconsistent with the observation. A ROC curve shows the performance of a classifier at all classification thresholds and has two parameters true positive rate (i.e., sensitivity) and true false positive rate (i.e., 1 - specificity). The area under ROC (AUC) can systematically evaluate the performance of a classifier for different combinations of the two parameters [40], and its value ranges from 0 to 1, with a value closer to 1 indicating that a classifier can better classify tumor and normal samples. For each cancer type, we developed two classifiers using the 10-fold cross-validation approach and compared the classifiers using the values of AUC, MCC, and F1 score. We performed the analysis using the R package randomForest [41].

2.7. Survival analysis

We downloaded the clinical information of cancer patients from the Xena platform. The data includes patients’ survival statuses and survival times after being diagnosed with cancer. For individual genes, we divided cancer patients into high-expression and low-expression groups using the median expression of genes. We performed two-sided log-rank tests to compare the survival curves (i.e., Kaplan-Meier curves) between the two groups [42]. We further examined the densities of the log-rank tests’ p-values computed for different numbers of top-ranked genes (n = 10, 20, 50, and 100) selected by the network method or expression fold-change and performed the Fisher-Pitman permutation test to show whether or not the difference between the two methods is significant (p-value ≤ 0.05).

Furthermore, we performed multivariate Cox regression with the ridge penalty [43] to calculate the risk scores for patients using top-ranking genes identified by the network method or expression fold-change. We chose the penalty parameter (λ) at its optimal value to obtain the coefficients (β) of the Cox model and used the model to compute patients’ risk scores. We performed the analyses using raw gene expression, z-score of gene expression, and minimum–maximum normalization of gene expression. Based on the median of the risk scores, we divided the tumor patients into high-risk and low-risk groups and performed two-sided log-rank tests to compare the survival curves between the two groups. The three methods showed similar performances in predicting patients’ survival rates. We developed and analyzed the Cox model using the R package glmnet [44] and drew Kaplan-Meier plots using the R package survival [45].

Moreover, we used a time-dependent ROC curve to estimate the changing of the time period in determining the ability of the selected gene sets in predicting patients’ survival status (alive or dead) [46]. For performing such analysis, we used the risk score of patients computed by the Cox model. Then, we adjusted the threshold for the risk score and the time point to calculate sensitivity and specificity for drawing the ROC curve. We used the R package timeROC [47] to draw the time-dependent ROC curves at 3, 5, and 10 years. The time-dependent AUC was used to compare the prognostic performance of the gene sets obtained using the network method or expression fold-change.

2.8. Network-based drug repurposing

We used a list that collected high-quality physical drug-target interactions on FDA-approved or clinically investigational drugs. The list was created using three drug-target databases (i.e., DrugBank, the Therapeutic Target Database, and the PharmGKB database) and refined by four metrics accounting for binding affinities between drugs and proteins (i.e., inhibition constant, dissociation constant, median effective concentration, or median inhibitory concentration) [48]. The list contained 4,428 FDA-approved or clinically investigational drugs and 2,256 unique human protein targets. We further annotated the list with the information that specifies FDA-approved drugs for specific cancers. The information was gathered from the NCI website (Table S7).

We used a network proximity method to identify repurposable drugs for cancer genes in each cancer type. Specifically, the method calculated the distance between drug targets (i.e., genes from the annotated drug-target interaction list; Table S7) and cancer genes (i.e., gene sets selected by the network method and used for sample classification in different cancer types; Table S4). Compared to random gene sets with the same size as the cancer gene set, a significantly shorter distance between drug targets and the cancer gene set implied the repurposing potential of drug candidates. We developed a method by considering the regulatory direction and strength between drug targets and cancer genes. Such modification allowed us to identify repurposable candidates that exert effects on cancer genes based on weighted distances. Only the drugs whose targets are upstream of the cancer gene set were considered effective. Specifically, the method requires three inputs - the largest fully connected subnetwork of a cancer-specific network, a set of drug targets included in the subnetwork, and a set of cancer genes included in the subnetwork. We computed the distance between the two gene sets in a network using the following equation

$$d_{\mathit{CT}}=\frac{1}{n_T\bullet n_C}\sum _{t∊T}\sum _{c∊C}wd(t,c)$$

where C and T denote the cancer gene set and the drug target set, respectively; n_<T,C> denotes the size of the respective gene sets; and wd(t, c) denotes the weighted shortest distance between a drug target t and a cancer gene c. While computing distances between genes, we set the distance of gene pairs not connected by a directed path to twice the network diameter. Next, from the subnetwork we generated a set of random genes C’ with the same size as the cancer gene set and computed $d_{C^{\prime }T}$. We repeated this step 1000 times and obtained the mean and standard deviation of $d_{C^{\prime }T}$. Then, we calculated the z-score (i.e., $\frac{d_{\mathit{CT}}-\overline{d_{C^{\prime }T}}}{\sigma (d_{C^{\prime }T})}$) for all drug candidates and derived corresponding p-values using the permutation test results. Drugs with z-score ≤ −1.5 and p-values ≤ 0.05 were considered repurposable due to significantly proximal drug-gene associations in the cancer-specific networks. To evaluate the toxicity of the identified repurposable drugs on non-cancer tissues, we defined a normal gene set that contains the same number of genes as the cancer gene set for each cancer type. The normal genes are ranked by a score that is the multiplication of the average expression of the gene in the normal tissue with the gene’s node degree in the network. Then, we used the same equation to compute the distance between the drug targets and the normal genes ($d_{\mathit{NT}}$) and compared it with the corresponding $d_{\mathit{CT}}$.

3. Results

3.1. Transcriptome analysis reveals distinct gene expression profiles of 18 cancer types

We used transcriptome data of 33 cancer types from the Xena platform including normal samples from TCGA and GTEx and re-processed them using our computational pipeline to remove batch effects (see Materials and Methods). The inclusion of data from GTEx alleviated the imbalanced number of tumor and normal samples in TCGA. We kept 18 of 33 cancer types that contain adequate sample sizes for both tumor and normal tissues to carry out follow-up analyses (see Materials and Methods; Table 1). First, we performed differential gene expression analysis to identify genes with aberrant expression in the 18 cancer types. The data showed that the significantly differentially expressed genes with absolute log2 fold-change of at least 2 could partially distinguish tumor samples from normal samples (Figures S2 and S3).

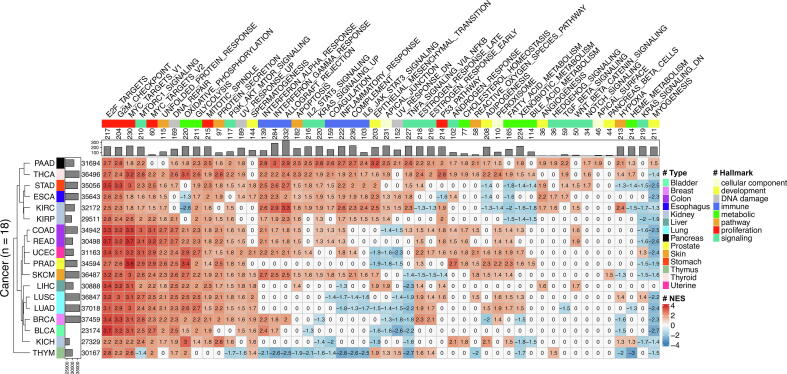
Then, we performed gene set enrichment analysis using a hallmark collection to interpret the biological function of the identified differentially expressed genes in the 18 cancer types (see Materials and Methods). The collection contains 50 gene sets that are good representations of cancer hallmarks [49], [49], [50] and have been designed to reduce redundancy and produce more robust enrichment analysis results. The identified differentially expressed genes of most cancer types were enriched in terms associated with cell proliferation (e.g., mitotic spindle assembly and G2/M checkpoint in cell cycle progression), DNA repair, PI3K signaling, and glycolysis (Fig. 2). Some cancer hallmarks were only associated with specific cancers. For example, TGF beta signaling and Notch signaling were associated with four and three out of 18 cancer types, respectively. Of note, cancers originating from similar organs or tissues were more likely to be clustered together (i.e., COAD and READ from the colon, LUSC and LUAD from the lung, and KIRC and KIRP from the kidney) in terms of the hallmarks for which their genes are enriched. Above all, the results implied that the identified differentially expressed genes are cancer specific, and therefore it will be interesting to investigate their role in cancer regulatory networks.

Fig. 2.

Gene set enrichment analysis on differentially expressed genes in different cancer types. The heat map shows the enrichment of differentially expressed genes from 18 cancer types (in rows) in 50 hallmark gene sets of cancer (in columns). On the heat map, grids with color and number are normalized enrichment scores (red: positive score; blue: negative score) for significantly enriched cancer hallmarks, while white grids with zeros represent absence of significance. The bar plot on the left shows the total number of identified genes in different cancer types. In the bar plot, the minimum value of the x-axis is 23,174 that is the number of genes identified in BLCA. The cancer types are annotated by colors based on tissue of origin, and they are clustered by a dendrogram computed using Euclidean distance with the average linkage algorithm. The bar plot on the top shows the total number of genes in the cancer hallmarks. The cancer hallmarks are annotated by colors based on their functional categories.

3.2. Gene prioritization in cancer-specific networks

The naturally ubiquitous, pleiotropic, and concerted gene regulation makes it challenging to quantify the importance of individual genes in tumors. We applied a network-based method that integrates gene expression profiles and gene interaction information to rank genes in cancer-specific networks. First, we reconstructed a generic network from experimentally validated molecular interactions (see Materials and Methods). The network was directional and composed of 11,831 genes with 75,303 interactions. Second, we integrated the network with the identified differentially expressed genes for each cancer type to create cancer-specific gene regulatory networks. The size of the cancer-specific networks varied from hundreds to thousands of genes and molecular interactions (Table 1 and Figure S4). The node degrees of the networks followed a power-law distribution (Figure S5), meaning the majority of genes have only a few connections to other genes, whereas some genes are connected to many other genes in the network. This scale-free property is widely found in biological networks [51], and most of biological networks have weakly scale free structures [52]. We then used a network method that considers gene expression and topological information to score genes (see Materials and Methods), and the scores were used to rank genes in the cancer networks according to their importance. This method allowed us to prioritize genes that are significantly differentially expressed and have high connectivity as well as strong regulatory effects on other dysregulated and densely connected genes in the cancer networks. Previously, we have used the method to identify microRNAs for improving the effectiveness of cancer immunotherapy [53]. Biologically, the identified genes in cancer networks could be functionally important and potentially linked to tumorigenesis and metastasis [49], [54], [55], therefore having potential as prognostic markers and therapeutic targets for cancer.

3.3. Prioritized genes show potential as diagnostic and prognostic biomarkers

We further investigated the usefulness of genes prioritized by the network method in discriminating between tumor and normal samples and compared their performance with top-ranking genes based on expression fold-change of the whole transcriptome. For each cancer type, we trained a random forest classifier using different numbers of network genes, chose the one with the best performance, and compared it with a classifier trained with the same number of expression-based genes (see Materials and Methods). The classifiers’ performances were evaluated by AUC, MCC, and F1 score using a 10-fold cross-validation approach. The results showed that small sets of fewer than 10 genes hold considerable discriminative power for each cancer type (Table 2). In terms of AUC values, the top-scoring genes ranked by the network method showed better performances than genes with the highest fold-change in 12 cancer types, in which BLCA, BRCA, LIHC, LUAD, and PRAD show the largest increase in AUC values ranging from 0.052 to 0.189. For the other six cancer types, the performance is slightly worse but the maximum reduction of AUC values is less than 0.03. Similar results were seen in other metrics such as MCC and F1 score. Likewise, the gene sets prioritized by the network method showed better discrimination in the hierarchical clustering of the samples in most cancer types (Figure S6). In comparison to pan-cancer marker genes that were identified to classify different cancer types of TCGA from normal tissues, the genes identified by the network method showed comparable performances (Table S5). Furthermore, network topology analysis showed that these genes play a crucial role through direct interacting with many other genes and regulating the information flow in the cancer-specific networks (Figure S7).

Table 2.

Performance of distinguishing between normal and tumor samples. The columns from left to right are cancer type, the number of genes used for training the random forest classifiers, and the performance metrics AUC, MMC, and F1 score. For each metric, the scores of a classifier trained using top-scoring network-derived genes (network) or genes with the highest fold-change in expression (log2fc) and their differences are shown. Asterisks indicate increases of at least 0.05 in AUC values.

Cancer type	# of gene	AUC			MCC			F1 score
		network	log2fc	diff.	network	log2fc	diff.	network	log2fc	diff.
BLCA	3	0.841	0.652	0.189*	0.725	0.371	0.354	0.984	0.969	0.015
BRCA	9	0.954	0.902	0.052*	0.914	0.816	0.098	0.982	0.962	0.020
COAD	6	0.995	0.998	−0.003	0.990	0.997	−0.007	0.994	0.998	−0.004
ESCA	8	0.959	0.981	−0.022	0.918	0.961	−0.043	0.949	0.976	−0.027
KICH	8	0.976	0.966	0.010	0.958	0.937	0.021	0.980	0.970	0.010
KIRC	9	0.959	0.967	−0.008	0.943	0.946	−0.003	0.991	0.991	0.000
KIRP	9	0.953	0.982	−0.029	0.923	0.972	−0.049	0.987	0.995	−0.008
LIHC	9	0.909	0.754	0.155*	0.819	0.564	0.255	0.944	0.880	0.064
LUAD	6	0.979	0.846	0.133*	0.961	0.685	0.276	0.984	0.862	0.122
LUSC	9	0.990	0.968	0.022	0.978	0.935	0.043	0.991	0.973	0.018
PAAD	5	0.977	0.964	0.013	0.956	0.929	0.027	0.978	0.964	0.014
PRAD	8	0.914	0.823	0.091*	0.862	0.728	0.134	0.969	0.942	0.027
READ	4	0.984	0.988	−0.004	0.974	0.971	0.003	0.979	0.977	0.002
SKCM	9	0.997	0.969	0.028	0.995	0.938	0.057	0.997	0.966	0.031
STAD	8	0.970	0.968	0.002	0.936	0.936	0.000	0.978	0.978	0.000
THCA	9	0.977	0.939	0.038	0.957	0.878	0.079	0.983	0.951	0.032
THYM	5	0.996	0.997	−0.001	0.988	0.989	−0.001	0.991	0.992	−0.001
UCEC	9	0.979	0.972	0.007	0.964	0.951	0.013	0.987	0.982	0.005

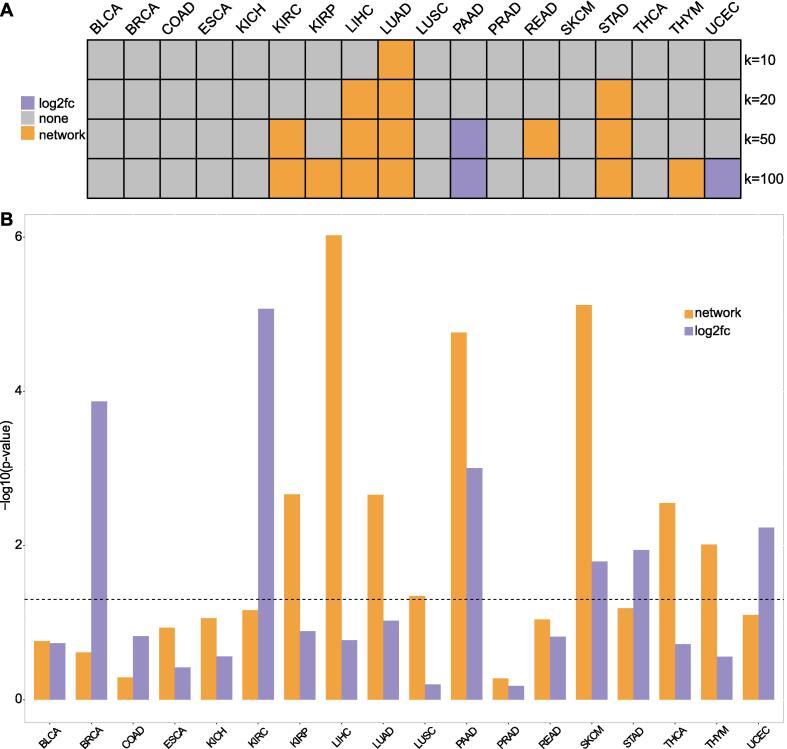
Next, we investigated the performance of genes prioritized by the network method in a retroactive prognostic prediction of cancer patients. For each cancer type, we performed survival analyses using the top genes ranked by network scores or expression fold-change. These genes were used in the top-performing classifiers. Specifically, we divided the tumor patients into two halves using individual genes, calculated p-values of the survival curves for each gene, and drew the density plot of the p-values (see Materials and Methods). Then, we compared the density plots to see which gene set is better at predicting the survival of tumor patients. The results showed that when the number of selected genes is 10, the performances of both gene sets are not significantly different except LUAD (Fig. 3A). Because the p-value distribution of the top-scoring genes of LUAD is more right-tailed (Figure S8), the network-derived genes have more power to discriminate the survival of the tumor patients than the top aberrantly expressed genes. With increasing number of genes (i.e., 20, 50, and 100), the network-derived genes outperformed the others in six cancer types but showed weaker performance in PAAD and UCEC (Fig. 3A and Figure S8).

Fig. 3.

Survival analysis. (A) The heat map shows comparisons of survival analysis using individual genes. For each cancer type, we compared the density plot of p-values of survival analyses using top k (i.e., 10, 20, 50, and 100) genes ranked by the network method (network) or fold-changes in expression (log2fc). The grid colors show which gene selection method led to better performance in predicting the survival time of tumor patients. The gray grids mean there was no significant difference. The p-value density plots can be found in Figure S8. (B) We compared prognostic abilities of combined genes that are derived from the network method (network) or fold-changes in expression (log2fc). The log-rank test p-values for differentiating high-risk and low-risk patients are shown. The grey dashed line indicates the value of 0.05, and p-values smaller than 0.05 is regarded as statistically significant. The corresponding survival curves can be found in Figure S9. The detailed information of the Cox models can be found in Table S6.

In the next step, we used multiple instead of individual genes to retroactively predict patient survival. We used the top genes ranked by the network method or by expression fold-change, with the number of genes equal to the optimal number found in the random forest models for each cancer type. The selected genes were used to develop the Cox models that compute an individual gene’s contribution to patient risk by fitting to observed survival times (see Materials and Methods). The models’ coefficients were used to compute patients’ risk scores and the scores were used to stratify the patients into high-risk and low-risk groups. Subsequently, we compared the survival of patients in the two groups.

The genes identified by the network method showed better performances in predicting patients’ survival than the expression-based genes. Specifically, the network-derived genes showed significant survival differences of high-risk and low-risk groups in eight cancer types while the other genes did in six (Figure S9). The network-derived genes showed better performances (i.e., smaller p-values) in 8 of 11 cancer types in which the high-risk group has a significantly poorer overall survival than the low-risk group (Fig. 3B). In addition, the time-dependent ROC analysis showed that the network-derived genes increase AUC in 12, 13, and 12 cancer types for predicting 3-, 5-, and 10-year overall survival of patients, respectively (Table 3).

Table 3.

Performance of predicting patients’ survival times. The columns from left to right are cancer type, the number of genes used for training the model, and AUC values for 3-, 5-, and 10-year overall survival of patients. For each AUC, it shows the score of the model trained using top-scoring gene sets (network) or the gene set with the highest fold-change in expression (log2fc), and differences in their scores.

Cancer type	# of gene	3 year AUC			5 year AUC			10 year AUC
		network	log2fc	diff.	network	log2fc	diff.	network	log2fc	diff.
BLCA	3	0.539	0.583	−0.044	0.568	0.570	−0.002	0.571	0.382	0.189
BRCA	9	0.604	0.646	−0.042	0.560	0.628	−0.069	0.471	0.596	−0.125
COAD	6	0.522	0.540	−0.018	0.529	0.539	−0.010	0.614	0.484	0.130
ESCA	8	0.721	0.554	0.167	0.805	0.768	0.038	0.531	0.870	−0.339
KICH	8	0.630	0.548	0.082	0.683	0.560	0.123	0.824	0.693	0.131
KIRC	9	0.541	0.567	−0.026	0.574	0.608	−0.034	0.643	0.618	0.026
KIRP	9	0.735	0.601	0.134	0.683	0.586	0.097	0.732	0.356	0.376
LIHC	9	0.705	0.540	0.165	0.722	0.534	0.188	0.146	0.048	0.098
LUAD	6	0.585	0.517	0.069	0.640	0.558	0.081	0.668	0.547	0.121
LUSC	9	0.605	0.526	0.079	0.573	0.540	0.033	0.454	0.410	0.044
PAAD	5	0.788	0.732	0.056	0.888	0.678	0.210	NA	NA	NA
PRAD	8	0.697	0.512	0.185	0.583	0.547	0.036	0.338	0.630	−0.291
READ	4	0.681	0.525	0.155	0.672	0.603	0.069	0.662	0.601	0.061
SKCM	9	0.627	0.589	0.039	0.654	0.608	0.047	0.631	0.585	0.046
STAD	8	0.543	0.553	−0.010	0.509	0.570	−0.061	0.322	0.787	−0.465
THCA	9	0.675	0.634	0.041	0.794	0.752	0.042	0.904	0.775	0.129
THYM	5	0.918	0.601	0.316	0.964	0.730	0.234	0.711	0.756	−0.045
UCEC	9	0.670	0.697	−0.027	0.760	0.654	0.106	0.951	0.587	0.364

Taken together, the genes prioritized by the network method show promising performance in classification of tumor and normal samples and predicting patients’ survival times, suggesting their potential as diagnostic and prognostic biomarkers in cancer.

3.4. Network-based drug repurposing

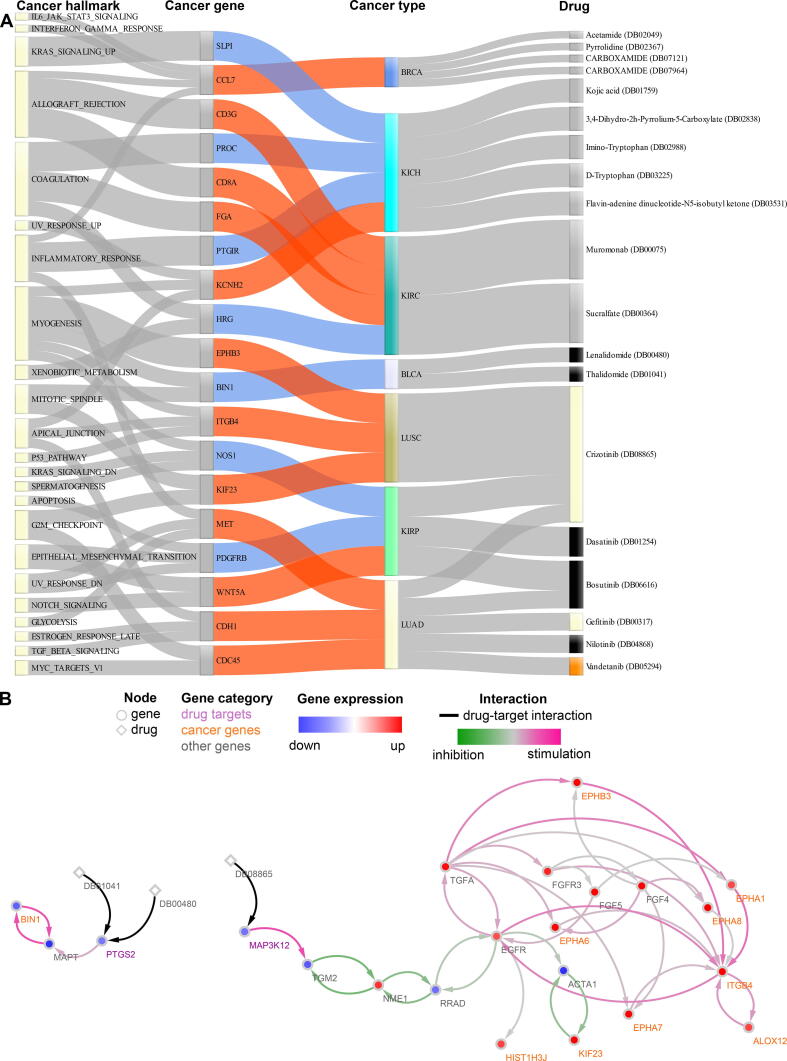
Using a network-based ranking, we prioritized genes that have high expression perturbation and strong regulatory effects on other dysregulated genes. The prioritized genes can be regarded as cancer genes, as genes with aberrant expression and strong regulatory impacts play vital roles in cancer pathogenesis [56], progression [57], [58], and resistance to anticancer therapies [59]. Therefore, it is interesting to identify drugs that directly or indirectly regulate cancer genes. Toward this goal, we developed a network proximity approach to systematically screen FDA-approved or clinically investigational drugs. The approach computed the distances between drug targets and the identified cancer genes in the corresponding directional cancer-specific networks, and the drug candidates with significantly short distances to the cancer genes were regarded as effective (see Materials and Methods). Such kind of approaches has also been applied to repurpose drugs for COVID19 [60] and Alzheimer’s disease [61]. As a result, we identified 19 drugs that potentially affect cancer genes in seven cancer types (Fig. 4A). Eight of the 19 drugs are FDA-approved cancer medications, and the others are non-cancer drugs. Furthermore, we evaluated the perturbing effects of the identified drugs on the cancer genes and its normal counterpart (see Materials and Methods). The data showed that, in the cancer networks, the distance from the drug targets to cancer genes is shorter than to normal genes, suggesting the perturbation effect of the drugs is less toxic to non-cancer tissues (Figure S10). Of note, in contrast to other drug repurposing methods that predict direct drug-molecule interactions, our model focuses on identifying efficacious drug candidates located at the upstream of the identified cancer genes in networks and therefore cannot provide analytic validation [62], such as sensitivity, specificity, and AUC, for the predictions. Hence, in the following, we show the predictive indications of the known eight cancer drugs and the mechanisms through which they can regulate the identified cancer genes in the same or different cancer types.

Fig. 4.

Drug repurposing analysis. (A) The Sankey diagram shows the connections between drugs and their potential targets. The left-most column are hallmarks of cancer identified in gene set enrichment analysis and their containing genes (Fig. 2). The two middle columns show significantly differentially expressed genes (the second column) and their expression change (red: upregulation; blue: downregulation) in corresponding cancer types (the third column). The last column lists identified drugs that can be repurposed in the connected cancer types. The colors in this column indicate different drug categories: FDA-approved for one of the 18 cancer types (color matching cancer color in the third column), FDA-approved for other cancer types (black), and non-cancer medicine (grey). For instance, crizotinib and gefitinib are yellow because they are approved drugs for LUAD. Vandetanib is orange because it is an approved drug for THCA, for which we have not identified any repurposable drug candidates. The complete results for drug repurposing can be found in Table S8. (B) The networks show the shortest paths between the repurposed drugs and cancer genes in BLCA (left) and LUSC (right). The paths were derived from the cancer-specific networks. Drugs and genes are shown in diamonds and circles, respectively. The node colors visualize the log2 fold-change of gene expression (red: upregulation; blue: downregulation). The label colors represent different categories of genes: drug target genes (purple), cancer genes (orange), and other genes (grey) on the shortest path between drug targets and cancer genes. The edge colors indicate the regulatory type between genes (pink: stimulation; green: inhibition), and drug-gene interactions are shown in black. DB00480: lenalidomide; DB01041: thalidomide; DB08865: crizotinib.

Lenalidomide and thalidomide are medications used in multiple myeloma, and our results showed that both drugs potentially affect BIN1 in bladder urothelial carcinoma (BLCA). The expression of BIN1 is attenuated in many human malignancies, and its loss can promote immune escape by tumor cells [63], [64]. Mechanistically, we predicted that both compounds regulate BIN1 by targeting PTGS2 that can affect the expression of the cancer gene through interactions with MAPT (Fig. 4B left). Crizotinib is a receptor tyrosine kinase inhibitor used to treat metastatic non-small cell lung cancer. In lung squamous cell carcinoma (LUSC), we predicted that crizotinib affects nine cancer genes through targeting MAP3K12 and its downstream pathway (Fig. 4B right). Three (i.e., ITGB4, EPHB3, and KIF23) of the cancer genes play a role in regulating hallmarks of cancer. Specifically, ITGB4 can promote cell invasion and epithelial-mesenchymal transition in hepatocellular carcinoma [65]. EPHB3 is overexpressed in non-small-cell lung cancer and promotes tumor metastasis by enhancing cell survival and migration [66]. The overexpression of KIF23 is found in several cancers and can promote tumor growth in primary lung cancer patients [67]. In kidney renal papillary cell carcinoma (KIRP), we predicted that crizotinib, dasatinib, and bosutinib are effective and can regulate genes such as NOS1, PDGERB, and WNT5A. The expression of NOS1 correlates with the pathological grading and the malignant potential of renal tumors [68]. PDGERB regulates angiogenesis in clear cell renal cell carcinoma and reduces renal tumor cell growth and progression [69]. WNT5A is a non-canonical Wnt-ligand gene involved in kidney development and is associated with kidney tumor development [70]. The three compounds target genes located upstream of the cancer genes in the KIRP network (Figure S11A). For lung adenocarcinoma (LUAD), we identified five repurposable cancer drugs (i.e., crizotinib, bosutinib, gefitinib, nilotinib, and vandetanib) for cancer genes with known roles, including MET, CDH1, and CDC45. MET has established oncogenic properties and is involved in cell proliferation, survival, and migration [71]. CDH1 plays a discrepant role in cancer, and it acts as a tumor suppressor in some tumors but promotes tumor progression and metastasis in others [72]. CDC45 is an oncogene in non-small cell lung cancer, and its knockdown can inhibit tumor cell proliferation both in vitro and in vivo [73]. From a mechanistic point of view, these compounds can potentially interact with the upstream genes of the cancer genes in the LUAD network and therefore achieve the repurposable effects (Figure S11B).

Furthermore, we used the genomics of drug sensitivity in cancer (GDSC) database to analyze cancer cell lines’ sensitivity to the identified repurposable cancer drugs. The database is the largest public resource that stores responses to almost 300 anticancer drugs across more than 1,000 cancer cell lines [74]. The data showed that for BLCA (Figure S12), all 18 corresponding cell lines are not sensitive to lenalidomide as they require a half maximal inhibitory concentration (IC50) value greater than the maximum drug screening concentration; For LUSC (Figure S12), 5 in 13 cell lines are sensitive to crizotinib as their IC50 values are smaller than the maximum drug screening concentration; For KIRP, the database does not contain the corresponding data; For LUAD (Figure S12), the ranking of the drugs based on the number of sensitive cell lines is crizotinib (23 in 62), gefitinib (15 in 62), bosutinib (3 in 61), and nilotinib (2 in 62). These results demonstrated the potential of the identified repurposable drugs to be effective in target cancers.

Taken together, we demonstrated the power of the network-based method for identifying repurposable drug candidates and depicting the corresponding molecular mechanisms through which the drugs can take effects. The identified candidates contain cancer and non-cancer drugs. We have focused on discussing the former because of their high clinical relevance, and the latter imply the novelty of our results. In addition, proving that the predictions are clinically justifiable requires biological validation, and such experiments could be designed and performed through collaboration with experimentalists and clinicians in the future.

4. Discussion and conclusions

We present a network medicine approach to search for diagnostic and prognostic biomarkers and predict new indications for existing drugs in cancer. The approach integrates human transcriptome and interactome data through network modeling that identifies cancer genes with aberrant expression and strong regulatory impacts in cancer-specific networks. The automated workflow also helps us reveal pertinent biomedical context for evaluating the clinical utility of the identified cancer genes. Moreover, we identified drug-repurposing candidates that potentially regulate the cancer genes. Although we developed this network medicine approach for cancer, its framework is equally applicable to other human diseases and any biological study that aims to understand gene networks with a systematic approach and analyze their emergent properties.

The rapid production of and easy access to transcriptome and interactome data have created an unprecedented opportunity to study cancer. However, complex multidimensional biomedical data pose many challenges in data analysis. Therefore, we integrated transcriptome and interactome data to reconstruct specific cancer networks and analyzed differentially expressed genes at the network level. The reconstructed networks contain annotated molecular interactions that are experimentally validated, hence reducing false positives and facilitating the mining and interpretation of data for specific cancer types. In addition, reconstructing such networks in an automated manner is much faster than using networks that are manually constructed and curated from literature [75] and not available for most cancer types considered in this study. Ultimately, automatic and manual curation of networks can be combined.

Furthermore, we performed network modeling on our cancer networks to prioritize genes and identify biomarkers for clinical applications. Network-based methods are widely used by the community to improve our understanding of tumorigenesis and tumor progression [76], [77] and also to elucidate compound mechanism of action [78]. Prominent studies include integrating tumor genome data with protein interaction networks to identify AKT2 and TFDP2 as driver genes in lung adenocarcinomas [79] and a combination of a disease network with deep learning to identify prognostic biomarkers for melanoma [7]. Besides, many gene prioritization algorithms have been developed to identify crucial genes using different types of biological networks, such as protein interaction networks and gene-disease association networks [80]. For instance, the NetICS algorithm is a graph diffusion-based method for prioritizing cancer genes by integrating multi-omics data on a directed protein interaction network [81]. The network embedding algorithm Node2Vec considers features of genes and preserves their neighbor genes to perform gene prioritization [82]. A recent study showed that the performance of gene prioritization algorithms is disease-dependent and is affected by network topologies shaped by the interactome annotated in databases [83]. For algorithms based on the guilt-by-association principle, it is most likely that the identified genes with priority are associated with important genes found in the literature [83]. The algorithm we used utilizes the guilt-by-association principle and prioritizes genes with highly perturbed expression and strong regulatory impacts on other genes in cancer. The top-ranking genes showed superior performances in diagnosis and prognosis of cancer compared to genes with the most dysregulated expression, indicating their potential clinical utility.

Over the last 15 years, researchers have made great efforts to develop drug repurposing methods, from early statistics-based chemoinformatics approaches [84] to recent ones using artificial intelligence [85], [86], [87] and network-based methods [88], [89]. These computational methods have been demonstrated to be effective but some limitations remain. First, it is difficult to compare their predictive powers because different datasets were used to develop those algorithms and there is a lack of standard benchmark datasets. Second, supervised methods are trained on datasets that do not contain high-quality negative sample data for drug-target interactions. Third, there is no systematic validation of the predictions by experiments. Also, a recent study has shown that no single drug repurposing algorithm offers consistently reliable outcomes across datasets [90]. A possible solution is to develop an ensemble model that aggregates predictions from all algorithms to increase overall accuracy. Here, we performed network-based drug repurposing on the identified cancer genes that have high expression perturbation and are in close vicinity to other highly perturbed genes. The developed algorithm makes use of edge weights to quantify regulatory strength between genes and ranks drugs based on network proximity in cancer networks. It results in repurposable drug candidates that may, via interacting with upstream genes, regulate the identified cancer genes that are biologically important due to the high degree of interactions with other genes and strong influence on the information flow in the cancer-specific networks. It is also worth mentioning that our results are restricted to the drug-target interaction list for identifying target genes and the database for reconstructing the cancer-specific networks. Different criteria for filtering the drug-target interactions and interactome data from other resources could affect our drug repurposing results.

In conclusion, we describe a network medicine approach as a reusable, robust framework for automated and integrated analysis of transcriptome and interactome data to identify biomarkers and cancer genes. The approach also incorporates all the prerequisites for reproducible research. Specifically, data, code, and results of the study are archived together following the FAIR principle [91]. Hence, it directly addresses some of the major challenges in the rigorous and data-driven selection of clinically actionable cancer genes. We expect that other biomedical researchers will be encouraged to use this approach for their future work.

CRediT authorship contribution statement

Le Zhang: Investigation, Validation, Project administration, Resources, Writing - review & editing. Shiwei Fan: Data curation, Software, Visualization, Writing – review & editing. Julio Vera: Project administration, Resources, Funding acquisition, Writing – review & editing. Xin Lai: Funding acquisition, Investigation, Validation, Conceptualization, Formal analysis, Methodology, Data curation, Project administration, Resources, Software, Visualization, Supervision, Writing - original draft, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: