Producing ratio measures of effect with quantitative microbial risk assessment

Abstract

Estimating the risk of infections or other outcomes incident to pathogen exposure is a primary goal of quantitative microbial risk assessment (QMRA). Such estimates are useful to predict population-level risks, to evaluate exposures based on normative or tolerable risk guidelines, and to interpret the likely public health relevance of microbial measurements in environmental media. To evaluate alternative control measures (interventions), ratio estimates of effect (e.g., odds and risk ratios) are needed that are more broadly interpretable in the health sciences and consistent with convention in epidemiology. In this paper, we propose a general method for estimating widely used ratio measures of effect derived from stochastic QMRA approaches, including the generation of appropriate confidence intervals. Such QMRA-derived ratios can be used as a basis for evaluating interventions via hypothesis testing and for inclusion in systematic reviews and meta-analyses in a form consistent with risk estimation approaches commonly used in epidemiology.

1. INTRODUCTION

Quantitative microbial risk assessment (QMRA) is a mechanistic framework for estimating the risk of health-related outcomes (infection, illness, death) using inputs of microbial measurements (hazard identification), exposure assessment, and dose-response relationships for specific pathogens. Its advantages and limitations are well understood (Haas, 2015, 2020). As the method has gained prominence among environmental microbiologists, environmental engineers, and infectious disease modelers, it has not been well integrated with epidemiology and the broader health sciences literature. Partly this is attributable to the siloed nature of research communities and methods. QMRA is a relatively recent arrival to the field of risk estimation, with roots outside more traditional health sciences. But it is also due to the disparate terminology used for conceptual framing – ratio measures are common in epidemiology and point estimates or ranges of estimated risk are typical in QMRA. In infectious disease epidemiology, the evaluation of interventions to control infections typically requires effect measure estimates that compare risk or odds across two or more groups (e.g., an intervention group and a reference or control group), expressed as a ratio, with formal group comparisons made via hypothesis testing. Common forms of these measures include risk ratios and odds ratios, which then form the basis for inclusion in meta-analyses for the calculation of pooled estimates of effect across individual studies. Randomized, controlled trials (RCTs) and other experimental study designs estimating effects of interventions use such measures, and they are broadly interpretable in the health sciences.

Epidemiology uses experimental design of controlled trials to infer causality: the effect that can be causally attributable to an intervention, by comparing risk between or across groups. In QMRA, causality is implicit in the framework because models produce risk estimates as a function of an assumed mechanistic causal chain. That chain starts with estimating microbial hazards in environmental media, followed by assumed or measured exposure to a calculated dose over some time period, and the use of a dose-response relationship to estimate the risk of infection or illness based on the number of infectious pathogens ingested. Ideally, traditional epidemiological and mechanistic risk assessment approaches are highly complementary, offering methods with different assumptions, strengths, and limitations. The gold standard for health research is the RCT, which, if done well, can support a high degree of causal inference. But RCTs are expensive, often lack formative work on pathogen exposures, and biological samples from subjects may be difficult to obtain or process. Direct measures of exposures may not be possible, and many interventions of interest (e.g., piped drinking water or a sanitation network) may not lend themselves to straightforward randomization or blinding. QMRA is a mechanistic approach that can be rapidly deployed at a fraction of the cost of an RCT, and experiments can be done in silica allowing for experimental designs and methods that would not be feasible in the real world. However, QMRA requires many assumptions, some more reasonable than others, and few studies have attempted to “ground truth” model predictions (Bouwknegt, Knol, van der Sluijs, & Evers, 2014; T. Burch, 2019; Evers & Bouwknegt, 2016; Mara, Sleigh, Blumenthal, & Carr, 2007; Soller et al., 2016) via direct comparison with epidemiological estimates. QMRA, interpreted alongside epidemiological studies, offers opportunities to better investigate the validity of the underlying assumptions.

The output of a QMRA model is an estimated probability of infection or disease, ideally accompanied by some confidence interval that captures the uncertainty of the estimate as a function of the model assumptions and/or input data. Risk estimates can be compared to a normative standard or some a priori level of tolerable risk (U.S Environmental Protection Agency (EPA), 2012), and can be used to estimate control measures (e.g., water treatment) required to meet these targets (T. R. Burch et al., 2021; Schijven et al., 2019). But, QMRA studies that are experimental – comparing across groups to produce ratio measures that directly compare estimates of risk in separate groups – are rare (J. Brown & Clasen, 2012; Enger, Nelson, Clasen, Rose, & Eisenberg, 2012). New approaches capable of producing estimates of effect with appropriate confidence intervals that are interpretable to others working in adjacent fields including epidemiology are required. In addition, these approaches can better facilitate hypothesis testing incorporating uncertainty, an essential element of the scientific process.

Herein we propose a method to estimate odds ratios (OR) and risk ratios (RR, also known as relative risk) from QMRA studies that compare estimates of infection or illness across exposure groups (e.g., between control and intervention arms in a trial). These QMRA-derived ratio measures can then be compared alongside estimates produced via standard epidemiological methods, with appropriate caveats specific to the methods used to produce them. We demonstrate this approach by estimating the impact of two hypothetical interventions compared to control groups: (1) the effect of drinking stored water from an intermittent tap on Cryptosporidium parvum infection risk in rural Cambodia relative to consumption of stored rain water; (2) the effect of apartment style housing construction on Giardia duodeanlis infection risk attributable to soil ingestion relative to existing housing in a low income informal settlement.

2. METHODS

2.1. Ratio measures in epidemiology

Causal models in epidemiology typically require, at minimum, an exposure or independent variable and an outcome or dependent variable, with the exposure variable hypothesized to impact the outcome variable via a pre-defined causal relationship. In experimental study design using an a priori group assignment to define some exposure, the primary independent variable may be the study arm (in intention-to-treat analyses) and the results for a quantitative outcome measure may be the dependent variable. The quantitative relationship between exposure and outcome variables are frequently estimated via measures of effect. For example, a ratio measure of effect could be estimated for consumption of water from different sources (independent variable) and Cryptosporidium parvum detected in stool (dependent variable), which we will examine later in one of our hypothetical examples. Two common ratio measures of effect are the OR and the RR. These measures, which can be produced using regression analyses, may be used to estimate and compare intervention effects on the relative probabilities of outcomes occurring across groups.

2.2. Conceptual basis for ratio measures via QMRA

QMRA is a rapidly evolving approach to risk estimation. While no definitive standards exist for study design, model construction, or reporting of results, and methods vary widely in the literature, the output of QMRA models is generally some expression of risk in probabilistic terms as a function of microbial measurements in environmental media and a range of either measured or assumed values that describe the associated exposure to that media and dose-response relationships. Typically, models produce an estimate of risk for an outcome like infection or disease between zero and one over some duration of exposure. In stochastic models, the output comprises many estimates of the risk (e.g., 1,000 or 10,000), which are often made via Monte Carlo techniques. Summary statistics are frequently used to report results, including the median, mean, or geometric mean. These point estimates may be reported alongside other point estimates at different quantiles (e.g., the 10^th and 90^th percentiles) to communicate a range of plausible estimates, or density plots may be used to illustrate some distribution of estimates. An example calculation for an infection across n days of exposure using an estimated daily probability of infection is then:

$$P_{\mathit{\text{inf}},n}=1-{\Pi }_i^n\left(1-P_{\mathit{\text{inf}},\mathit{\text{daily}},i}\right)\mathit{\text{where n}}=\mathit{\text{number of days of exposure}}$$ Equation 1.

QMRA can also use risk estimation for inter-group comparisons, for example the potential risk reduction attributable to water treatment versus a referent or control group lacking this intervention (A. W. Bivins et al., 2017; Elliott, Taylor-Edmonds, & Andrews, 2019). Each group under comparison requires output from separate stochastic models, premised on their respective exposures, and the two could then be compared on the basis of each group’s risk of the outcome over a defined period, including as a ratio of point estimates. Quantitative comparisons of such risk estimates can reveal differences across groups and may inform intervention selection to manage risks.

Hypothesis testing of QMRA estimates of risk using conventional methods, however, requires not only point estimates of risk but also precision statistics that convey their uncertainty and variability given the variability and uncertainty in the underlying data. While the calculation of a ratio of between group point estimates to produce RRs or ORs is straightforward, calculation of confidence intervals is not because the precision of the central tendency estimates may be influenced by decisions taken by the QMRA modeler. Critically, the modeler can pre-specify the number of output (dependent variable) estimates (e.g., Monte Carlo draws) in stochastic models and can parameterize probability distributions of input variables (independent) informed by – but typically not strictly constrained by – empirical data. Confidence intervals around mean or median estimates can be manipulated by selecting high numbers of model outputs or by specifying artificially precise probability distribution functions around sensitive input variables. In epidemiology, computed confidence intervals around ratio measures are a function of variance and model assumptions in the outcome and are inversely proportional to sample size (Gordis, 2014; Wasserstein, Schirm, & Lazar, 2019), typically yielding more precise estimates of effect where sample sizes are large because the variance of the sampling distribution of the mean is inversely proportional to the square root of the sample size. This is appropriate as conclusions derived from large datasets are assumed to be more robust than from small studies: chance variability in outcome measures is accounted for by inclusion of sufficiently large numbers of subjects drawn from a population. Sample size calculations to compute the required number of observations for hypothesis testing are standard in epidemiology and one of the primary considerations in designing trials (Hayes & Bennett, 1999).

In QMRA, no external constraints, such as experimental sample size, provide clear direction for calculating confidence intervals in ratio measures, because estimates of risk are not based on a defined number of observable subjects. Instead, we propose tying confidence interval estimation of QMRA-calculated ratio measures to the empirical unit of observation (i.e., microbial count data in environmental media), including its calculated variance alongside distributional assumptions. Such an approach necessarily ties the confidence interval to the sample size of the primary empirical data used to generate estimates of risk via QMRA, with the width of the confidence interval inversely proportional to the input data sample size. As such, output from modeled risk estimates generated from large datasets – incorporating variability of microbial count data over time and space and therefore potentially more representative of pathogen hazards – would be conveyed alongside an indicator of the reliability of the point estimate. Necessarily this method would communicate to the interpreter of the QMRA output some indication of the statistical robustness of the estimates. Other sources of uncertainty in QMRA-generated risk estimates, such as uncertainty with respect to dose-response relationships, would apply equally across all groups under comparison as intrinsic model variability and would therefore “factor out” in ratio measures.

2.3. Hypothetical Example 1: Piped Water Improvements

Achieving universal, consistent access to drinking water that is free of microbial and chemical contamination is an aim expressed in the United Nations Sustainable Development Goal Six (United Nations Children’s Fund (UNICEF) and World Health Organization, 2019). In Example 1, we present a hypothetical RCT that upgraded a household’s drinking water source from rainwater to an intermittent piped water connection. Households in the intervention group – equally distributed among 10 rural villages – in this this hypothetical example received the new piped water connection while households in the control group, which were equally distributed among 10 separate rural villages, did not. This example typifies a scenario where the decrease in dose ingested, which is the product of the concentration and volume, is caused by a decrease in pathogen concentration and not the quantity of the environmental media (i.e., water) ingested.

To demonstrate the potential for comparison of QMRA with an epidemiological trial, we assume stools from 300 individuals in each arm were evaluated 12 months following the piped water intervention for gut carriage of Cryptosporidium parvum as an indicator of exposure (J. Brown & Cumming, 2019). Further, we assume that 12-months post-intervention 11% (n=34/300) of participants in the control arm tested positive for Cryptosporidium parvum carriage while 5.5% (17/300) of intervention participants tested positive based on Sow et al. 2016 (Sow et al., 2016).

We estimated annual risk of infection by Cryptosporidium parvum from consumption of drinking water with QMRA populated with data from the literature. Empirical data for culturable E. coli in stored rainwater (n=1,166) and stored piped water (n=142), were taken from Brown et al. 2008 (J. M. Brown et al., 2008) and Shaheed et al. 2014 (Shaheed, Orgill, Montgomery, et al., 2014; Shaheed, Orgill, Ratana, et al., 2014), respectively (Table I). Then, we transformed CFUs of E. coli into Cryptosporidium parvum oocysts using a stochastic ratio observed in sewage (Medema et al., 2000), because we are unaware of direct measurements of Cryptosporidium parvum in stored rainwater. Next, we calculated the dose by multiplying this pathogen concentration by an assumed value for daily per capita consumption of water from a standard reference (US EPA, 2019). We then determined daily risk of infection using the dose response relationship from Messner et al. 2001 (Messner et al., 2001). We repeated this stochastic process 365 times – to simulate a daily probability of infection over the 12-month period of the hypothetical trial – for each microbial measurement, and then produced an annual risk of infection (Eqn. 1, Fig. 1). As 365 independent draws are far less than the 10,000 iterations often used in stochastic QMRA, we repeated the process of estimating the annual risk of infection 100 times and selected the median annual risk of infection corresponding to each microbial measurement as the outcome variable in hypothesis testing.

Table I.

Model Parameters for Example 1

Model Parameter	Value	Reference
CFUs E. coli per liter	Fixed for each measurement Intervention: n = 142 Control: n = 1,166	Brown et al. 2008(J. M. Brown, Proum, & Sobsey, 2008) Shaheed et al. 2014(Shaheed, Orgill, Montgomery, Jeuland, & Brown, 2014; Shaheed, Orgill, Ratana, et al., 2014)
Ratio of CFUs E. coli to viable Cryptosporidium parvum oocysts	LN(−15.8, 2.1)	Medema et al. 2000(Medema, Ketelaars, & Hoogenboezem, 2000)
Stored Drinking Water Consumption for Adults (liters/day)	U(1,2)	US EPA 2019(US EPA, 2019)
Cryptosporidium parvum dose response parameter (k)	LN(−2.9, 1.9)	Messner et al. 2001(Messner, Chappell, & Okhuysen, 2001)

^aNote: LN denotes lognormal distribution (mean, standard deviation). U denotes uniform distribution (minimum, maximum). Distribution parameters correspond to the inputs used for the rlnorm and runif functions in R.

Figure 1.

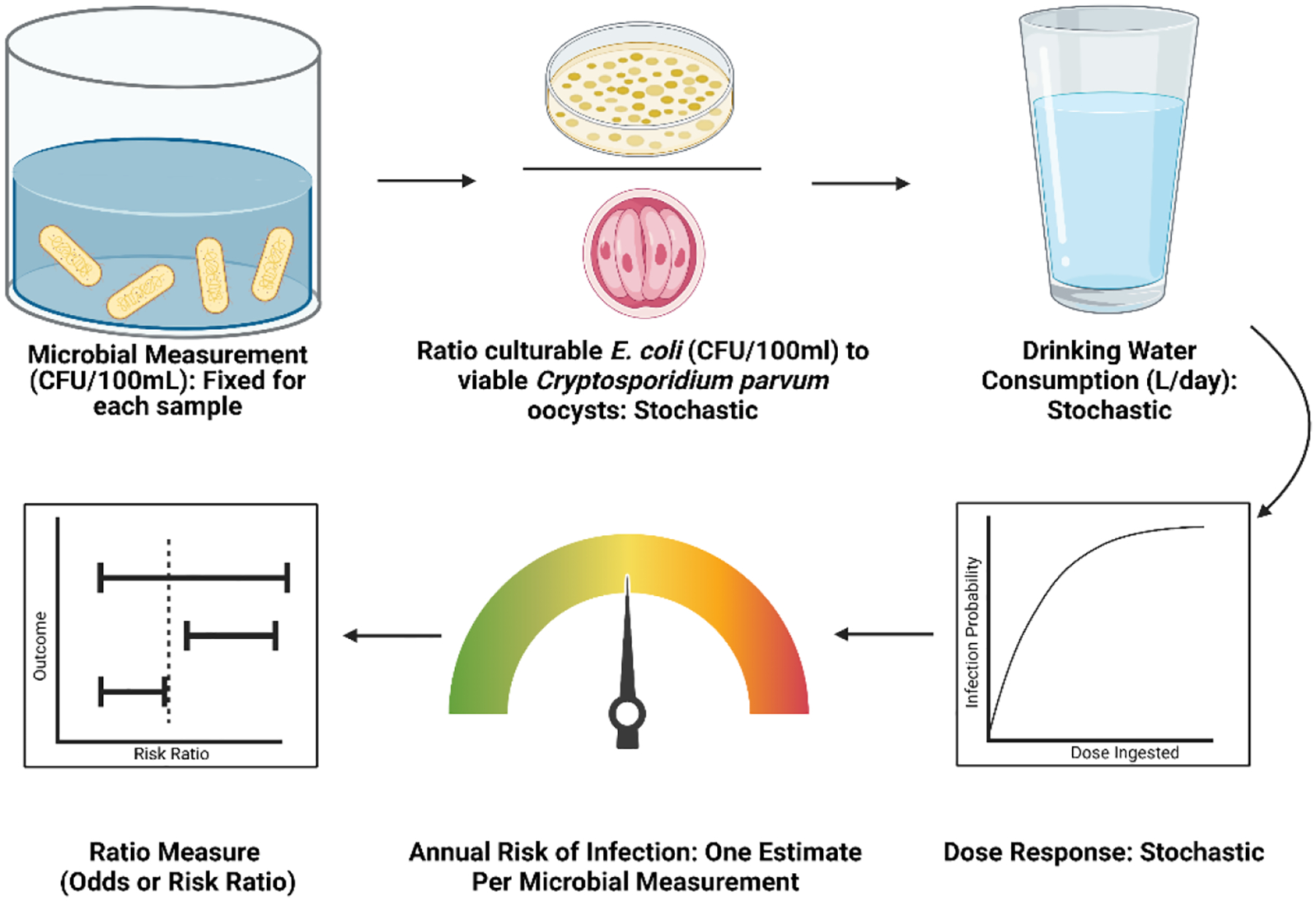
QMRA Model Workflow for Example 1

2.4. Hypothetical Example 2: Housing Improvements

Evidence suggests that housing improvements, including hardscape flooring, may reduce infection with enteric pathogens (Benjamin-Chung et al., 2021; Cattaneo, Galiani, Gertler, Martinez, & Titiunik, 2009). In Example 2 we present a hypothetical RCT where researchers wanted to evaluate the impact of housing improvements on infection by Giardia duodenalis among children living in informal neighborhoods. Intervention households received apartment complex style housing, while control households continued living in existing housing. Unlike Example 1, we assume that the housing intervention had no impact on the concentration of Giardia duodenalis in soil, but instead reduced the dose of pathogens ingested by decreasing the daily quantity of soil ingested.

Like in Example 1, we assume stools from 300 children, ages 12–23 months, in each arm were evaluated 12 months following the intervention for gut carriage of Giardia duodenalis as an indicator of exposure (J. Brown & Cumming, 2019) (Table II). We also assume – based on Knee et al. 2018 (Knee et al., 2018) – that 12-months post-intervention half (n=150/300) of children in the control arm tested positive for Giardia duodenalis carriage while one-third (100/300) of intervention children tested positive.

Table II.

Model Parameters for Example 2

Model Parameter	Valuea	Reference
Giardia duodenalis gene copies / gram dry soil	Fixed for each measurement Intervention: n = 90 Control: n = 90	Capone et al. 2021(Capone, Bivins, et al., 2021)
Ratio of viable Giardia duodenalis cysts	LN(−6.2, 2.4)	Capone et al. 2021(Capone, Bivins, et al., 2021)
Soil ingestion for children 12–23 months old (unimproved housing)	LN(−1.5, 0.69)	Kwong et al. 2019(Kwong et al., 2021)
Soil ingestion for children 12–23 months old (improved housing)	LN(−3.4, 0.68)	US EPA 2019(US EPA, 2019)
Giardia duodenalis dose response parameter (k)	LN(−3.9, 0.30)	Rose et al. 1991(Rose, Haas, & Regli, 1991)

^aNote: LN denotes lognormal distribution (mean, standard deviation). U denotes uniform distribution (minimum, maximum). Distribution parameters correspond to the inputs used for the rlnorm functions in R.

In a previous study, we used QMRA to estimate the annual risk of infection by Giardia duodenalis among young children living in a low income informal settlement (Capone, Bivins, et al., 2021). Because we lacked site-specific soil ingestion data, we modelled two exposure scenarios. For one model scenario we used parameters from the U.S. EPA Exposure Factors Handbook Chapter 5 (2017 update) (US EPA National Center for Environmental Assessment, 2017). This is a low-ingestion scenario pertinent to children in a high-income country living in housing that offers substantial protection from environmental exposures. In the second scenario we used parameters from Kwong et al. 2019 (Kwong et al., 2021), representing a high-ingestion scenario that may be common in low-income countries where housing is less robust, and play and contact with soil is likely to be more common among children. For our hypothetical RCT we used the Kwong et al. 2019 ingestion estimates for the control group because it best represents an exposure scenario for children living in sub-standard housing in a low-income country, while we used the U.S. EPA 2017 ingestion estimates for the intervention group because it better represents potential exposures in a setting with improved apartment-style housing. The QMRA model we developed for this analysis used the exact same parameters as Capone et al. 2021, except we did not treat the concentration of Giardia duodenalis gene copies as a stochastic parameter. Instead, we input each microbial measurement into a stochastic model to generate 365 estimates of daily risk, which we used to calculate an annual infection risk estimate (Eqn. 1). Then we repeated this process 100 times and used the median annual risk of infection linked to each individual microbial measurement as the outcome variable for hypothesis testing (Fig. 2). The resulting dataset consisted of 180 pairs of annual risks of infection and microbial count data.

Figure 2.

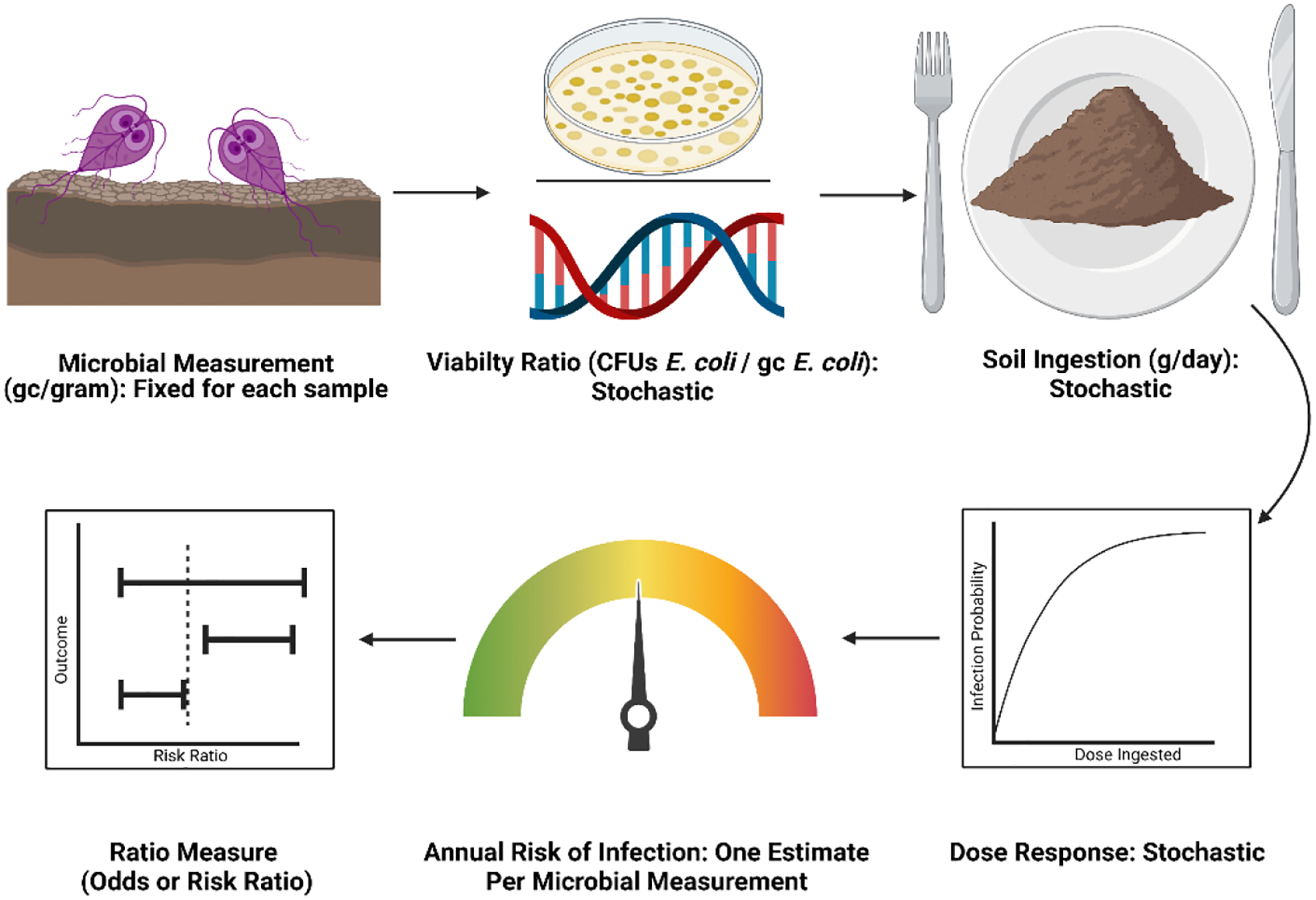
QMRA model workflow for Example 2

2.5. Regression Modelling

We used generalized estimating equations (GEE) (Halekoh, Højsgaard, & Yan, 2006) to calculate ORs by fitting unadjusted logistic regression models and fit unadjusted Poisson regression models to calculate RRs to estimate the association between water source or housing (independent variable) and QMRA estimated annual risk of infection by either Cryptosporidium parvum or Giardia duodenalis (dependent variable), respectively, in R version 4.0.4 (R Foundation for Statistical Computing, Vienna, Austria). Both models included robust standard errors and an exchangeable correlation structure. For Example 1 we accounted for clustering at the village level. With this approach the variance in the 95% confidence interval around each point estimate was directly linked to the empirical sample size because we calculated an individual infection risk from each microbial measurement. We also fit separate models for each example to assess the impact of the trial arm (independent variable) on the hypothetical results from the stool-based pathogen detection (dependent variable) using the same methods. The R code we used is publicly available (DOI: 10.17605/OSF.IO/JWZY9)(Capone, 2022).

2.6. Power Analysis

Power analysis is critical to a priori establish what samples size is needed to achieve a normative probability – typically 80% – of detecting an effect that exists. If the sample size is too small, a research project will lack the precision to provide statistically meaningful conclusions. While if the sample size is too large, then the project may waste time and resources. We used the WebPower (Zhang, Mai, Yang, & Zhang, 2018) package in R to demonstrate the inverse relationship between sample size and model variance. Input parameters for effect size were taken from the Poisson regression model outputs with a statistical power β = 0.80, significance level α = 0.05, and X = 1 was input for the population distribution of the predictor (Zhang et al., 2018).

3. RESULTS

3.1. Piped Water Upgrades

Using a traditional epidemiologic approach, we estimated that a hypothetical upgrade from rainwater to intermittent piped drinking water reduced the odds of stool-based Cryptosporidium parvum detection by approximately half (OR = 0.47, 95% CI: [0.26, 0.86]) and the risk by half (RR=0.50, 95% CI: [0.29, 0.88]) (Table III). Using QMRA, we estimated that the median annual risk of infection by Cryptosporidium parvum for adults in the intervention group was 1.5% (10^th percentile = 0.07%, 90^th Percentile = 59%) and in the control group was 59% (10^th percentile = 7.2%, 90^th Percentile = >99%). Using regression analysis, we found the hypothetical piped water intervention reduced the odds (OR = 0.14, 95% CI: [0.10, 0.19]) and risk (RR = 0.26, 95% CI: [0.20, 0.35]) of QMRA modelled infection by Cryptosporidium parvum compared to the control group.

Table III.

Results of a hypothetical RCT of piped drinking water

Epidemiology effect ratios
Exposure Variable	Reference	OR (95% CI)	RR (95% CI)
Stored piped water	Stored rainwater	0.47 (0.26, 0.86)	0.50 (0.29, 0.88)
QMRA-derived effect ratios
Stored piped water	Stored rainwater	0.14 (0.10, 0.19)	0.26 (0.20, 0.35)

3.2. Housing Improvements

We estimated that, by traditional epidemiology measures based on stool testing, our hypothetical housing intervention reduced the odds of stool-based Giardia duodenalis detection by half (OR = 0.50, 95% CI: [0.36, 0.70]) and the risk of detection by one-third (RR=0.67, 95% CI: [0.55, 0.81]) (Table IV). Like Capone et al. 2021, we estimated, via QMRA, the median annual risk of infection by Giardia duodenalis for children 12–23 months old in the intervention group was 5.4% (10^th percentile = 5.1%, 90^th percentile = 78%; parameters from U.S. EPA 2017) and was 17% (10^th perentile = 15%, 90^th percentile = >99%) in the control group (parameters from Kwong et al. 2019). Using regression analysis, we estimated the hypothetical housing intervention reduced the odds (OR = 0.44, 95% CI: [0.29, 0.68]) and risk (RR = 0.58, 95% CI: [0.43, 0.78]) of infection by Giardia duodenalis from soil ingestion.

Table IV.

Results of a hypothetical RCT of improved housing

Epidemiology effect ratios
Exposure Variable	Reference	OR (95% CI)	RR (95% CI)
Improved housing	Unimproved	0.50 (0.36, 0.70)	0.67 (0.55, 0.81)
QMRA-derived effect ratios
Improved housing	Unimproved	0.44 (0.29, 0.68)	0.58 (0.43, 0.78)

3.3. Power Calculation

We observed that increasing environmental media and stool sample sizes were inversely proportional to the power to detect an effect (Fig. 3). In Example 1, which was predicated on the magnitude change in E. coli in drinking water, we found that 120 water samples were needed per arm to achieve 80% power. In Example 2, which was dependent on the reduction in soil ingestion, we found 80 soil samples were needed per trial arm. In addition, using the hypothetical results from participant stools, we found 102 stool samples were needed per arm to achieve 80% power for Giardia duodenalis and 230 for Cryptosporidium parvum.

Figure 3.

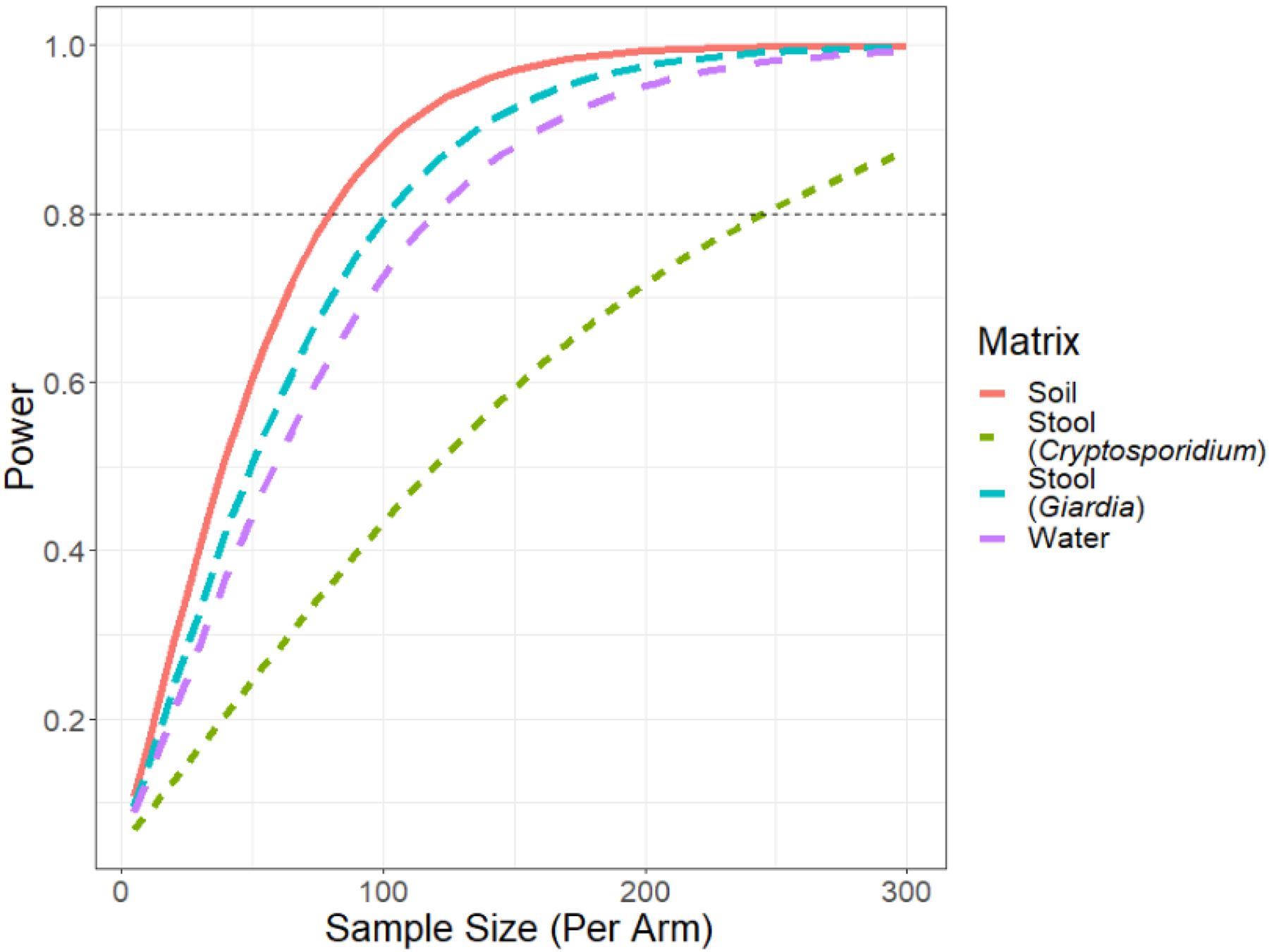
Power across sample sizes based on estimated effects from regression models

4. DISCUSSION

As a relatively recent arrival to the health sciences, it is incumbent on QMRA and its practitioners to learn to speak the language of epidemiology if broad relevance as a complementary approach is to be realized. Beyond the calculation of point estimates for ratio measures, confidence intervals informed by real world constraints and variability of empirical measurement are needed for robust hypothesis testing and to convey uncertainty in the model outputs. We demonstrated an approach that connects the outcome of stochastic QMRA with the ratio measures of effect commonly used in epidemiology. Similar experimental study designs using QMRA to evaluate relative risks across groups can help identify and prioritize control measures which deliver reductions in risk.

The number and volume of samples needed to accurately describe the distribution of pathogens in an environmental matrix is debated. While ratio measures can be produced using the output of a QMRA model based on any number of samples, confidence intervals must be constrained to transparently describe the uncertainty of the ratio measure. In epidemiological trials, group assignment is based on exposure, and in QMRA comparison groups are frequently stratified by exposure (e.g., microbial count data or ingestion parameter). This suggests it is appropriate to tie our approach (i.e., hypothesis testing) to the microbial sample size, and by doing so, we encourage gathering more microbial data that will increase confidence in the results. On the other hand, “engineered” confidence intervals may create the appearance of precision, which biases results towards an effect in studies that compare across groups by making confidence intervals artificially narrow. Certainly, a QMRA that is based on spatially and temporally rich microbial observation offers more confidence in its estimate than one based on a single or handful of samples. For studies planning to calculate ratio measures of effect using QMRA, power calculations present a useful tool to make informed decisions about study size.

The rapid development of new and easy to use methods – including PCR, culture techniques, genomic sequencing, and low-cost sensors – offer the opportunity to collect more microbial data and develop a more sophisticated understanding of how pathogens move through the environment and infect new hosts. These methods enable the rapid and low-cost generation of data which can be input into to QMRA models. Applications of QMRA models include standalone QMRA experiments, formative work, and explanatory models. Standalone models are those that would be difficult or impossible to conduct for ethical, financial, or logistical reasons. Example standalone QMRA experiments include those focusing on vulnerable populations who may not be accessible for ethical reasons or for rare pathogen exposures (e.g. Bacillus anthracis during a bioterrorist attack). Other standalone QMRA models could be used to support risk-based standards, choose between different technologies, set treatment targets, and inform management strategies. Formative research is used to plan intervention programs. Inherent to QMRA is the development of a complete chain of events that leads to exposure to an infectious microorganism, which requires consideration of potential exposure variables of interest. This process, alongside a sensitivity analysis, may indicate points of control and inform points of interest for data collection. By including QMRA in formative work researchers would gain a more explicit understanding of the causal chain that leads to infection, which can be under appreciated in traditional epidemiological frameworks. Risk prototyping via less resource intensive QMRA could allow proposed control measures to “fail faster”, which would enable an epidemiological study to be designed around the most promising intervention. Finally, QMRA can be used in an explanatory capacity and provide additional insight into the findings of epidemiological studies.

Epidemiological studies, such as RCTs, attempt to establish a causal link between an exposure and disease. However, many pathogens shed by humans, including in feces and aerosols, are transported into the environment before reception by a new host. While epidemiological studies can demonstrate a causal relationship between an exposure and an outcome, they often do not consider the fate and transport phenomena, or the human behavior, that compose the causal chain upstream of exposure and the dose response relationship downstream. QMRA models, on the other hand, account for the causal chain both upstream and downstream from exposures. In addition, epidemiological approaches are often not practical for low dose exposures because the number of samples needed for sufficient study power may be cost-prohibitive. In these instances, QMRA may be preferred because it would require fewer resources.

A common criticism of QMRA is the large number of assumptions that are required in models, and the uncertainty for key variables including microbial counts or density from typically sparse data, dose-response relationships derived in one context and applied in another, and the relationships between infection and the development of symptomatic disease. Methods for handling uncertainty have evolved rapidly in the field, with stochastic methods now common for generating confidence intervals around estimates of central tendency. An observation proffered by many practitioners is that a strength of QMRA is that comparisons across groups allow for considering and evaluating alternative control strategies, because such direct comparisons using the same assumptions can show relative differences even if point estimates may be highly uncertain. The same benefits would also apply to the calculation of ratio measures by factoring out common assumptions across groups – meaning that the same assumptions are made in the both the numerator and denominator such that they effectively reduce to one – including assumptions that may be little more than educated guesses. This “factoring out” of assumptions is functionally analogous to non-differential misclassification (Grimes & Schulz, 2002) in epidemiological studies. Non-differential misclassification is an equivalent misclassification of the exposure independent of the health outcome, or the health outcome independent of the exposure. This increases the similarity between the two groups and may bias the observed effect towards the null. Provided that assumptions are transparent and considered alongside point estimates in model output – best practice in QMRA reporting – readers can interpret the relative strengths and complementarity with similar ratio measures produced in epidemiological studies and consider whether and under what circumstances direct comparisons can be made. QMRA, alongside epidemiological studies, offers opportunities to investigate these assumptions by direct comparison with epidemiological outcomes.

In Example 1 we modeled a hypothetical RCT that evaluated upgrading households’ source of drinking water from rainwater to a piped connection with intermittent flow. We assumed that the intervention had no impact on the quantity of water consumed but resulted in an improvement in drinking water quality. We estimated that the hypothetical intervention reduced the odds and risk of stool-based Cryptosporidium parvum detection and the QMRA modelled annual risk infection by Cryptosporidium parvum. As infection with an enteric pathogen is upstream of diarrhea on the causal chain (J. Brown & Cumming, 2019; Wagner & Lanoix, 1958), this hypothetical example is corroborated by the findings of a 2020 systematic review, which found higher fecal indicator bacteria concentrations in drinking water were associated with increased odds of diarrhea (Goddard et al., 2020). Although, measures of fecal indicator bacteria – which we used as the empirical data in Example 1 – are an imperfect indicator of the presence and concentration of enteric pathogens, especially protozoan parasites, in drinking water (A. Bivins et al., 2020; McFeters, Bissonnette, Jezeski, Thomson, & Stuart, 1974; Murphy et al., 2017).

In Example 2 we modeled a hypothetical housing intervention where children’s exposure to soil was reduced in the intervention arm compared to the control group. While the soil ingestion parameter was the only difference between trial arms in this theoretical example, presumably such a transformative intervention would also include sanitation improvements and could also result in lower pathogen concentrations in soil relative the control group. We estimated that hypothetical intervention reduced the odds and risk of stool-based Giardia duodenalis detection and the modelled annual risk infection by Giardia duodenalis. No study has evaluated such substantial improvements in housing on Giardia duodenalis carriage by children, but multiple studies have examined the association between carriage and the presence of hardscape flooring. Hardscape flooring was associated with reduced odds of Giardia duodenalis carriage in Argentina (OR=0.28) (Basualdo et al., 2007) and a reduced prevalence in Kenya (aPR=0.78) and Bangladesh (aPR=0.82) (Benjamin-Chung et al., 2021). No association between flooring and Giardia duodenalis carriage was observed in Timor Leste (Campbell et al., 2016), though infrequent detection (13%) resulted in low power. The intervention we modelled, although hypothetical, represented more substantial housing improvements than to flooring alone. We estimated these substantial housing improvements would have a similar, and potentially greater, protective effect size than found while evaluating hardscape flooring alone. The plausibility of this biological gradient offers credence to our approach. If our theoretical results were produced in a real world trial, the results would be complementary to these epidemiological studies by offering potential causal evidence that housing improvements reduce soil ingestion, which may result in a reduced risk of infection by Giardia duodenalis and other pathogens in fecally contaminated soils (Baker et al., 2018; Capone, Berendes, et al., 2021; Fuhrmeister et al., 2020).

In addition to odds and risk ratios, other ratio measures including the incidence rate ratio (IRR) and risk differences (RD) are frequently used in epidemiological studies. Closely related to the risk ratio, the numerator of the incidence rate ratio (IRR) is the number of events in the intervention group divided by the person-time at risk and the denominator is the number of events in the reference group divided by the person-time at risk. The requirement of person-time in the calculation makes the IRR mathematically more complex than OR or RR. Calculating an IRR is possible from QMRA but would require additional assumptions, including the duration of infection or illness, and the duration of immunity prior to previously infected persons re-entering the susceptible pool.

Meta-analyses are used to pool estimates of effect for like interventions on comparable outcome measures across multiple epidemiolocal trials, ideally resulting in robust estimates of intervention effects that account for variability between trial settings and populations. Such methods are useful in positing likely generalizable effects from individual trials whose external validity may be unknown. Ratio measures generated from QMRA produce comparable estimates in a form that could be suitable for inclusion alongside or comparison with pooled estimates of effect from epidemiological meta-analyses, provided that the differences in methodologies are transparently articulated. The use of inverse-variance weighting in meta-analysis could also be used in estimating pooled estimates of effect across multiple QMRA trials, again making use of appropriately constrained uncertainty statistics following from the methods we describe here.

There are several limitations and challenges to our proposed approach. QMRA models often focus on a single pathogen and transmission route, whereas epidemiological studies may account for multiple pathogens and pathways relevant to a single disease endpoint, such as diarrhea. That is, QMRA modeling approaches may exclude elements outside of a well-defined system of assumed causal relationships, and epidemiological trials under real world conditions cannot make use of a similar set of simplifying assumptions; the two methods may generally have discordant levels of complexity. It is then plausible that an experimental QMRA model focusing on a single exposure route may estimate an effect, but in actuality, exposures through other routes may reduce or negate the observed effect (Briscoe, 1984). Likewise, infections are modelled on a pathogen-by-pathogen basis and disease states may be difficult to compare between epidemiological studies with unknown etiology and QMRA with assumed or modeled etiology. In addition, our approach uses the risk of infection or illness, and does not take into account multiple events. This suggests QMRA may underestimate the true effect of an intervention where repeated infection or illness is common. Combining QMRA with infectious disease transmission models such as SIR-type models (Kermack & McKendrick, 1927) may be one way to overcome this limitation by allowing for more sophisticated modeling approaches that can better represent real-world scenarios of interest. Collecting microbial samples cross-sectionally is useful for rapid QMRA, however, there may be important temporal and spatial differences in microbial counts especially between exposure groups. This suggests that microbial data is needed across the space and time of the modeled scenario. Well-designed spatial and temporal sampling will improve confidence in modelled estimates but could limit the rapid deployment of such methods. Finally, there are fundamental limitations in quantitative estimation of microbial count data that introduce uncertainty in QMRA modeling. Among these are constraints on limits of detection (LOD) and the methodological challenges associated with handling non-detects in samples (Canales, Wilson, Pearce-Walker, Verhougstraete, & Reynolds, 2018; Stokdyk, Firnstahl, Spencer, Burch, & Borchardt, 2016). Some pathogens, including many viruses (Center for Advancing Microbial Risk Assessment, 2015), have a high probability of causing infection even at extremely low doses. When the LOD of an assay is substantially above a pathogen’s median infectious dose, the modelled risk of infection or illness may quickly approach 100%. When this occurs for both groups, ratio measures generated by QMRA may not be informative.

Ratio measures generated from stochastic QMRA offer the microbial risk assessment community a path forward to begin speaking a common language with epidemiology and the broader health sciences. Studies that produce appropriately constrained ratio measures as estimates of effects for interventions can be complementary to other approaches to effect estimation and offer advantages in terms of speed, reduced logistical burdens, and lower cost than traditional human subjects research. QMRA and epidemiology offer valuable evidence that increases our understanding of the causal pathways that result in infection and illness. Integrating the two produces a complementary approach with the potential to benefit both fields.