A comparison of different methods for the first-in-pediatric dose selection

Abstract

Background and Aim:

To conduct a pediatric clinical trial, it is important to optimize pediatric dose as accurately as possible. This is mainly because due to ethical reasons, children cannot be given several doses to evaluate pharmacokinetics, safety, and efficacy of a drug.

Methods:

In this study, several simple methods to project a first-in-pediatric dose to initiate a clinical trial were evaluated. These methods were as follows:(1) Weight-based pediatric dose prediction (allometric scaling), (2) Salisbury rule (weight-based method), and (3) pediatric dose prediction based on predicted clearance. These methods were compared with the dose given to children in clinical practice. The methods were also compared with whole-body physiologically based pharmacokinetic (PBPK) model (n = 11). A ±30% prediction error (predicted vs. observed) was considered acceptable.

Results:

There were 27 drugs with 113 observations (different age groups from preterm neonates to adolescents). At least, ≤30% prediction error in pediatric dose projection was noted for more than 70% observations. The predictive performance of all the proposed methods was comparable with the whole-body PBPK.

Conclusions:

The proposed methods are simple and accurate and can be developed on a spreadsheet in a very short period of time.

Relevance for Patients:

The study provides an estimate of first-in-pediatric dose by simple methods to initiate pediatric clinical trials. Especially, Salisbury rule is based on body weight and is very simple and works fairly well in children >30 kg body weight and can be even used in clinical settings.

1. Introduction

Dosing of drugs in children requires a thorough consideration as there are physiological and biochemical differences between children and adults. Unlike first-in-adult dose, where the primary concern is the safety (not necessarily efficacy), in children, both safety and efficacy are the concerns because for ethical reasons children can only be dosed when they need medicine for an underlying disease [1,2].

Drug development for pediatrics is important because pediatric diseases may differ from those of adults in terms of etiology, mechanisms, clinical or biological features, and the course of disease. Some diseases only occur in children and some adverse events of drugs also only occur in children due to their different stages of growth and maturation [1,2]. The pharmacokinetics and pharmacodynamics of drugs, in most instances, are different in children than adults [1,2].

Ignoring the principles of pediatric pharmacology can have serious consequences. Gray baby syndrome and kernicterus following chloramphenicol [3] and sulfisoxazole [4] administration to children, respectively, are well known examples of serious side effects of these drugs when the developmental pharmacology in the pediatric population was ignored.

The studies with chloramphenicol led to the recognition that there are differences in drug metabolism among different age groups and the dose must be adjusted in children based on the ontogeny and not necessarily on body weight. Therefore, it is necessary to understand and recognize the impact of developmental processes in children. It is now well recognized that age and the disease state(s) can alter the pharmacokinetics and pharmacodynamics of a drug, as a result, adjustment in dosing regimen in children as compared to the adults is essential [2]. It should also be recognized that the etiology and course of disease may be different in children from adults. Hence, not only age but the nature of disease should also be taken into account for designing a suitable dosing regimen in children.

In pediatric drug development, the selection of first-in-children dose is very important. Before administering a drug to pediatric population, generally, the pharmacokinetic information and a safe and efficacious dose in adult population are known which can be used to select first-in-children dose. Over the years, empirical models such as pharmacometric modeling and simulation, allometric scaling, and physiologically based pharmacokinetic (PBPK) models have been suggested to select the first-in-children dose [2,5-9]. These models (with the exception of allometric scaling) are complex and time consuming and the acceptable criteria is generally within 2-fold prediction error. The acceptable 2-fold prediction error is too high for pediatric dosing. However, with these models, most of the time prediction error remains <2-fold [2,8-9].

Several simple pediatric dosing rules have been described in the literature. These rules are described below:

Clark’s rule (2–17 years), Clark’s surface area rule, Young’s rule, Webster’s rule, Fried’s rule, and Shirkey’s BSA recommendation [10,11]. These widely known rules were criticized by many experts in the field. For example, Munzenberger and McKercher [12] evaluated the performance of several pediatric dosing rules with the actual doses administered to pediatric patients. The authors’ overall conclusion was that these pediatric dosing rules, although simple, were unreliable.

The objectives of this study were to evaluate the predictive performance of the Salisbury rule to predict dose of drugs in children and compare the predictive power of Salisbury rule with other models as described below.

1. Weight-based pediatric dose prediction (allometric scaling)

2. Salisbury rule (weight-based method) [10]

3. Pediatric dose prediction based on predicted clearance (allometric scaling)

4. Comparison of the predictive performance of the aforementioned three models with the whole-body PBPK model.

2. Methods

From the literature, age, body weight, and clearance values for 27 drugs were obtained for adults and children [13-87] (Table 1). The proposed actual doses of these drugs were obtained from the FDA package insert, Drugs.com, and from the studies where a particular dose was given to an age group. The models used in this study were previously developed and validated from external data [2,8-10,83,88-92]. In this study, these models were used to predict dose in children (from preterm neonates to adolescents).

Table 1. Adult dose and clearance values used in the analysis of different methods for pediatric dose selection.

Drugs	References
Azithromycin (IV), adult dose=500 mg; adult CL=868 mL/min	[13-15]
Azithromycin (oral), adult dose=500 mg; adult CL=3206 mL/min	[15-17]
Linezolid, adult dose=600 mg; adult CL=138 mL/min	[18-19]
Oseltamivir (oral) adult dose=1500 mg; adult CL=670 mL/min	[20-21]
Famotidine IV, adult dose=20 mg; adult CL=455 mL/min	[22-25]
Fluconazole, adult dose=400 mg; adult CL=16.1 mL/hr	[26]
Cisapride (oral), adult dose=10 mg; adult CL=561 mL/min	[27-28]
Valsartan (oral), adult dose=80 mg; adult CL=133 mL/min	[29-30]
Alfentanil (IV), adult dose=1050 mcg; adult CL=350 mL/min	[31-35]
Levofloxacin, adult dose=500 mg IV; adult CL=175 mL/min	[36-37]
Theophylline, adult dose=28 mg/hr infusion; adult CL=45 mL/min	[38-45]
Topiramate oral, adult dose=400 mg/day; adult CL=33 mL/min (without inducers), adult CL=51 mL/min (with inducers)	[46-48]
Tapentadol (oral), adult dose=7 mg; adult CL=800 mL/min	[49-50]
Gentamicin (IV), adult dose=120 mg; adult CL=90 mL/min	[51-52]
Sufentanil (IV), adult dose=560 µg; ADULT CL=815 mL/min	[53-54]
Vancomycin (IV), adult dose=1000 mg; adult CL=90 mL/min	[55-57]
Ceftazidime (IV), adult dose=1000 mg; adult CL=115 mL/min	[58-60]
Drugs included in the PBPK comparison
Moxifloxacin (IV), adult dose=400 mg; adult CL=170 mL/min	[61-63]
Mefloquine (oral), adult dose=250 mg; adult CL=30 mL/min	[64-66]
Nilotinib (oral), adult dose=400 mg; adult CL=483 mL/min	[67-68]
Radiprodil (IV), adult dose=15 mg; adult CL=267 mL/min	[69]
Dolutegravir (oral), adult dose=50 mg twice daily; adult CL=17 mL/min	[70-71]
Oxycodone (IV), adult dose=7 mg; adult CL=800 mL/min	[72-75]
Lorazepam (IV), adult dose=2 mg; adult CL=75 mL/min	[76-79]
Lisinopril (oral), adult dose=20 mg; adult CL=435 mL/min	[80-82]
Midazolam (IV), adult dose=5 mg; adult CL=363 mL/min	[83-85]
Remdesivir (IV), adult dose=200 mg; adult CL=758 mL/min	[86-87]
Hydroxychloroquine (oral) adult dose=400 mg; adult CL=575 mL/min	[87]

IV: Intravenous, PBPK: Physiologically based pharmacokinetic

2.1. Method 1: Weight-based pediatric dose prediction

In general, pediatric dose is recommended based on per kg body weight (derived from adult dose and body weight). This approach assumes that there is a linear relationship between body weight and dose, irrespective of age. Considering that, body weight based on dosing across the age groups may not be a linear process, two allometric exponents were used to predict pediatric dose of drugs. One exponent was theoretical exponent 0.75 and the other exponent was 0.9. Just for the comparison purposes, a linear process or exponent 1.0 was also used [2,8,9,83].

The theoretical exponent 0.75 is not suitable across all age groups especially, in younger children, generally 2 years or younger [2]. Amiddle ground strategy was taken to choose an exponent to predict pediatric dose. The mid-point between 0.75 and 1.0 is 0.87 and it was rounded to 0.9. Hence, besides 0.75 and 1.0, exponent 0.9 was selected to predict pediatric dose using either body weight or predicted clearance. The exponent 0.9 was advocated in pediatric dose selection in some previous publications [2,8,9,83]. The pediatric dose across different age groups was predicted by the following equations:

Where, the “adult dose” is the adult dose of a given drug, W_C is the weight (in kilograms) of a child, and 70 (in kilograms) is the weight of an adult standardized to 70 kg.

The predicted dose was compared with the observed dose. The observed dose(s) were obtained (depending on the availability) from the package inserts of the FDA, Drugs.com, and also from the studies in which children of certain age were given certain doses.

2.2. Method 2. Salisbury rule (weight-based method)

2.2.1. This method was proposed by Lack and Stuart-Taylor and is as follows [10]

2.2.2. Modified Salisbury rule (weight-based method)

After the analysis of the data, it was noted that the predicted doses of drugs are systematically much higher than the observed dose in the neonates (preterm and term neonates). Therefore, to reduce the overestimation of the dose, a factor 1.7 rather than 2 was used to predict the dose in preterm and term neonates.

Since the dose of drugs in preterm and term neonates was over-predicted, the objective was to reduce the factor of 2 to a factor which is <2 which can reduce the overestimation of the doses. Factor 1.7 was obtained using theoretical exponent 0.75 and the proposed factor 2 by Lack and Stuart-Taylor for children <30 kg body weight (2^0.75) = 1.68, and was rounded to 1.7. This method was developed based on the observations noted in this study about neonates. This method was then used to evaluate the predictive performance of Salisbury rule in the neonates as a revised factor in the neonates.

2.3. Method 3: Pediatric dose prediction based on predicted clearance

Clearance was predicted in the children using allometry and then the pediatric dose was predicted according to the methods described below.

2.3.1. Age-dependent allometric exponent model (ADE) for the prediction of pediatric clearance

In this method, different allometric exponents were used for different age groups and clearance was predicted in a given age group according to Equation 4. This model was developed previously and validated by external data [2,83,88-92].

Where the “adult clearance” is the adult clearance of a given drug, W_C is the weight of a child, and W₇₀ is the weight of an adult standardized to 70 kg.

Exponent “b” in Equation 4 is age dependent. The age-dependent exponents as described previously for small molecules [2,83,88-92] are 1.2, 1.1, 1.0, and 0.9, and 0.75 for preterm neonates (0–3 months), term neonates (0–3 months), >3 months-2 years, >2–5 years, and >5 years, respectively. The exponents selected in the ADE model are based from previous experience, observation, and data analysis [2,83,88-92].

The pediatric doses across different age groups were predicted by the following equations:

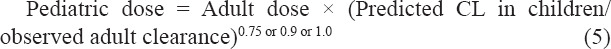
2.4. Comparison between whole-body PBPK modeling and the proposed methods

From the literature, 11 PBPK studies were randomly selected in which pediatric dose of drugs ranging from neonates to adolescents was predicted using PBPK models. It should be noted that the PBPK models were not developed in this study rather obtained from the literature and then compared the predicted dose from PBPK models with the predicted dose with the proposed methods. Although, there are a lot of PBPK models to predict pharmacokinetic parameters, there are not many studies with pediatric dose prediction. The basic principle of pediatric dose prediction from PBPK model is matching the exposure of a drug between adults and children and 11 such studies were considered appropriate for comparison purpose.

2.5. Statistical analysis

Percent prediction error between the observed and predicted dose was calculated according to the following equation:

Percent prediction error of ≤30% or ≤25% or ≤20% on either side of 100% (+ or −) was considered reasonably accurate prediction of the pediatric dose. Prediction error of +>30% and −>30% was considered overestimation or underestimation of the observed dose, respectively.

3. Results

The results of this study are summarized below. It should be noted that the predicted dose was a single value and was compared with a single observed value. In real-life situation, for many drugs, there will be a dose range in a given age group and this may minimize the prediction error noted in this study. Furthermore, for some drugs, in clinical practice, the observed dose used in this study may differ from the dose given to children due to the difference in the response. Considering these facts, a 30% prediction error by the proposed models was considered acceptable for the first-in-pediatric dose selection to initiate a clinical trial. In Table 1, adult dose and clearance values used in the analysis are provided.

3.1. Weight-based pediatric dose prediction

In this analysis of 27 drugs, there were 113 observations across the age groups. The results of the analysis are shown in Table 2. The predicted doses for 113 observations from exponent 0.75 and 0.9 were 60% and 84% within 30% prediction error and 47% and 63% within 20% prediction error (Table 2). The prediction error of +>30% (overestimation of the dose) was 39% and 5% by exponent 0.75 and 0.9, respectively. The prediction error of −<30% (underestimation of the dose) was 1% and 11% by exponent 0.75 and 0.9, respectively (Table 2). A slightly better result was obtained by exponent 0.9 than exponent 1.0 (linear scaling). Both these exponents’ predictive power was far superior than exponent 0.75. Exponent 0.75 overestimated (+>30%) the dose for 39% observations whereas exponent 1.0 underestimated (−>30%) 19% observations. Exponent 0.9 was more balanced both in terms of overestimation (5%) or underestimation (11%) of the observed dose than exponents 0.75 or 1.0. The underestimation of pediatric dose by linear scaling or 1.0 and overestimation by 0.75 indicate that these two exponents are not always suitable for first-in-pediatric dose selection. It should be, however, noted that from safety perspective, a lower dose is more acceptable than a higher dose.

Table 2. Prediction of dose based on body weights.

Percent error	>Neonates (n=84)			Preterm and term neonates (n=29)			Total (n=113)
	EXP 0.75, n (%)	EXP 0.90, n (%)	EXP 1.0, n (%)	EXP 0.75, n (%)	EXP 0.90, n (%)	EXP 1.0, n (%)	EXP 0.75, n (%)	EXP 0.90, n (%)	EXP 1.0, n (%)
30 (0.70–1.30)	63 (75.0)	74 (88.1)	69 (82.1)	5 (17.2)	21 (72.4)	22 (75.9)	68 (60.2)	95 (84.1)	91 (80.6)
25 (0.75–1.25)	52 (61.9)	67 (79.8)	54 (64.3)	4 (13.8)	14 (48.3)	18 (62.1)	56 (49.6)	81 (71.7)	72 (63.7)
20 (0.80–1.20)	49 (58.3)	60 (71.4)	47 (55.9)	4 (13.8)	11 (37.9)	18 (62.1)	53 (46.9)	71 (62.8)	65 (57.5)
>130 (>1.3)	20 (23.8)	0	0	24 (82.8)	6 (20.7)	1 (3.5)	44 (38.9)	6 (5.3)	1 (1.0)
<70 (<0.7)	1 (1.2)	10 (11.9)	15 (17.9)	0 (0.0)	2 (6.9)	6 (20.7)	1 (1.2)	12 (10.6)	21 (18.6)

There were 29 observations for preterm and term neonates in this study. From exponent 0.75 and 0.9, there were 17% and 72% observations within 30% prediction error, respectively (Table 2). The prediction error of +>30% was for 83% and 21% observations by exponent 0.75 and 0.9, respectively. The prediction error −>30% was 0% and 7% observations by exponent 0.75 and 0.9, respectively. Exponent 1.0 provided the best results in preterm and term neonates but 21% observations were with −>30% (underestimation) (Table 2).

Overall, a more accurate prediction of dose in pediatrics (across all age groups) was noted using exponent 0.9 than 0.75 or 1.0. Overall, exponent 0.9 was slightly better than exponent 1.0, and for all practical purposes, there may not be any difference in pediatric dose prediction from these two exponents. The exponent 0.75 substantially overpredicted the dose in preterm and term neonates.

3.2. Salisbury rule

2A: Out of 113 observations, there were 72% and 59% observations within 30% and 20% prediction error, respectively (Table 3), with the multiplication factor 2. The prediction error of +>30% and −>30% was 22% and 6%, respectively (Table 3).

Table 3. Prediction of dose based on Salisbury rule.

Percent error	<30 kg (n=89) (Factor 2), n (%)	>30 kg (n=24) (Wt+30), n (%)	Total (n=113), n (%)
30 (0.70–1.30)	58 (65.2)	23 (95.8)	81 (71.7)
25 (0.75–1.25)	54 (60.7)	21 (87.5)	75 (66.4)
20 (0.80–1.20)	48 (53.9)	19 (79.1)	67 (59.3)
>130 (>1.3)	25 (28.1)	0	25 (22.1)
<70 (<0.7)	6 (6.7)	1 (4.2)	7 (6.2)

There were 89 and 24 observations for children <30 kg and >30 kg, respectively. There were 64% and 96% observations within 30% prediction error for <30 kg and >30 kg, respectively. There were 55% and 86% observations within 20% prediction error for <30 kg and >30 kg, respectively. The prediction error of +>30% and −<30% was 28% and 7%, respectively, for children <30 kg and 0% and 4%, respectively, and for children ≥30 kg. The results indicated that the Salisbury rule predicted dose much more accurately in children weighing ≥30 kg than the children weighing <30 kg (Table 3).

2B: Children <30 kg body weight were divided into two groups. There were 60 observations with <30 kg excluding preterm and term neonates (Table 4). There were 29 observations for neonates. Using “2” as a multiplication factor as proposed by Salisbury rule for children <30 kg (excluding neonates), there were 75% and 62% observations within 30% and 20% prediction error, respectively (Table 4). The prediction error of +>30% and −<30% was 23% and 2%, respectively (Table 4). When factor ‘2’ as a multiplication factor was used in neonates, there were 41% and 38% observations within 30% and 20% prediction error, respectively. The prediction error of +>30% and -<30% was 41% and 17%, respectively (Table 4). The application of factor 1.7 in the neonates led to substantial improvement in the prediction of dose in the neonates. There were 79% and 69% observations within 30% and 20% prediction error, respectively. The prediction error of +>30% and −<30% was 7% and 14%, respectively (Table 4). The combination of factor 2 and 1.7 in children <30 kg substantially improved the prediction of dose in this weight group (Table 4). For 89 observations, there were 76% (from 64% for factor 2) and 64% (from 54% from factor 2) observations within 30% and 20% prediction error, respectively.

Table 4. Prediction of dose based on Salisbury rule (<30 kg) (different multiplication factors).

Percent error	<30 kg (n=60)*	Preterm and term neonates (n=29)		Total (n=89)
	Factor 2, n (%)	Factor 2, n (%)	Factor 1.7, n (%)	Factor 2, n (%)	Factor 1.7, n (%)
30 (0.70–1.30)	45 (75.0)	12 (41.4)	23 (79.3)	57 (64.0)	68 (76.4)
25 (0.75–1.25)	43 (71.7)	11 (37.9)	20 (69.0)	54 (60.7)	63 (70.8)
20 (0.80–1.20)	37 (61.7)	11 (37.9)	20 (69.0)	48 (53.9)	57 (64.0)
>130 (>1.3)	14 (23.3)	12 (41.4)	2 (6.9)	26 (29.2)	16 (17.0)
<70 (<0.7)	1 (1.7)	5 (17.2)	4 (13.8)	6 (6.7)	5 (5.6)

^*Not neonates and based on Factor 2

The results of the study indicated that the Salisbury rule predicts the pediatric dose fairly accurately. The proposed multiplication factor 1.7 rather than 2 substantially increased the dose prediction accuracy in the neonates (Table 4).

3.3. Pediatric dose prediction based on predicted clearance

In this approach, clearances of drugs were first predicted by the ADE model (n = 87). There were 26 observations for which observed CL values were not available. Out of 87 observations, 92% observations were within 2-fold prediction error and 86% were within 0.5–1.5 prediction error (Table 5). There was 0 (0%) and 8 (9%) observations with >2-fold and <0.5-fold prediction error, respectively.

Table 5. Predicted clearance of drugs as a function of prediction error ratio.

Error (ratio)	ADE
	Preterm and term neonates (n=27), n (%)	>Neonates (n=60), n (%)	Total (n=87), n (%)
0.5–2	23 (85.2)	57 (95.0)	80 (92.0)
0.5–1.5	20 (74.1)	55 (91.7)	75 (86.2)
0.7–1.3	14 (51.9)	40 (66.7)	54 (62.1)
>2	0	0	0
<0.5	5 (18.5)	3 (5.0)	8 (9.2)

ADE: Age-dependent exponent

In children who were not neonates (n = 60), 95% and 92% observations were within 0.5–2-fold and 0.5–1.5-fold fold prediction error, respectively. For the term and preterm neonates, out of 27 observations, 85% observations were within 2-fold prediction error and 74% were within 0.5–1.5 prediction error. No observation was >2-fold prediction error (the highest predicted/observed ratio was 1.64). Overall, the ADE approach provided a fairly accurate estimate of clearance values across the age groups (preterm neonates to adolescents). The current observation reconciles very well with the previous observations with the ADE model [87-89].

Based on the predicted clearances of drugs, pediatric doses of drugs were predicted. Three different exponents (0.75, 0.90, and 1.0) were used (these same exponents were used for body weights). The reason for using these three different exponents was that the dose and clearance relationship may not be always linear. Exponent 0.75 is a theoretical exponent and exponent 0.90 was selected as described in the method section for weight-based dose prediction and exponent 1.0 indicates a linear relationship.

The results of this analysis are summarized in Table 6. Since the predicted clearance was used in the dose selection, all 113 observations were used for pediatric dose prediction. Out of 113 observations, the predicted dose by exponent 0.75, 0.90, and 1.0 was within 30% and 20% prediction error for 62%, 79%, and 65% observations, respectively, and 47%, 53%, and 50% observations, respectively (Table 6). The prediction errors of +>30% and ->30% by exponent 0.75, 0.90, and 1.0 were 34%, 5%, and 1% observations, respectively, and 4%, 16%, and 34%, observations, respectively. The best results were obtained from exponent which was 0.90 and the worst as expected by the theoretical exponent 0.75. The theoretical exponent 0.75 (among all three exponents) not only provided the worst results in terms of 20% and 30% prediction error but overpredicted the dose for more than one-third of the observations. On the other hand, exponent 1.0 underpredicted the dose by one-third of the observations (Table 6). A balanced approach was obtained by exponent 0.90.

Table 6. Prediction of pediatric dose based on predicted clearance.

Percent error	>Neonates (n=84)			Preterm and term neonates (n=29)			Total (n=113)
	Exp 0.75 n (%)	Exp 0.90 n (%)	Exp 1.0 n (%)	Exp 0.75 n (%)	Exp 0.90 n (%)	Exp 1.0 n (%)	Exp 0.75 n (%)	Exp 0.90 n (%)	Exp 1.0 n (%)
30 (0.70–1.30)	58 (69.0)	72 (85.7)	67 (79.8)	12 (41.4)	17 (58.6)	6 (20.7)	70 (61.9)	89 (78.8)	73 (64.6)
25 (0.75–1.25)	50 (59.5)	64 (76.2)	57 (67.9)	9 (31.0)	12 (41.4)	5 (17.2)	59 (52.2)	76 (67.3)	62 (54.9)
20 (0.80–1.20)	46 (54.8)	53 (63.1)	53 (63.1)	7 (24.1)	7 (24.1)	3 (10.3)	53 (46.9)	60 (53.1)	56 (49.6)
>130 (>1.3)	25 (29.8)	4 (4.8)	1 (1.2)	13 (44.8)	2 (6.9)	0	38 (33.6)	6 (5.3)	1 (0.9)
<70 (<0.7)	1 (1.2)	8 (9.5)	16 (19.0)	4 (13.8)	10 (34.5)	23 (79.3)	5 (4.4)	18 (15.9)	39 (34.5)

For the preterm and term neonates (n = 29), the predicted dose by exponent 0.75, 0.90, and 1.0 was within 30% and 20% prediction error for 41%, 59%, and 21% and 24%, 24%, and 10% observations, respectively (Table 6). The prediction errors of +>30% and −<30% by exponent 0.75, 0.90, and 1.0 were 45%, 7%, and 0% and 14%, 35%, and 79%, respectively. In terms of 30% and prediction error, exponent 0.90 provided better results in the neonates than exponents 0.75 and 1.0. However, exponent 0.75 substantially overestimated (+>30%) the predicted dose and exponent 1.0 substantially underestimated (−>30%) the predicted dose. Exponent 1.0 provided the worst results in terms of underprediction as well as overall prediction of dose in the neonates (Table 6). The analysis indicates that using the predicted clearance of a drug, the predicted dose in preterm and term neonates can be incorrect even though the predicted clearance in 74% neonates was within 0.5–1.5 prediction error. The probability of lower or higher dose than an optimal dose is quite high.

In children who were not neonates (n = 84), the predicted dose by exponent 0.75, 0.90, and 1.0 was within 30% and 20% prediction error for 69%, 86%, and 80% and 55%, 63%, and 63% observations, respectively (Table 6). The prediction errors of +>30% and ->30%% by exponent 0.75, 0.90, and 1.0 were 30%, 5%, and 1% and 1%, 10%, and 19%, respectively (Table 6). In this age group, both exponents 0.9 and 1.0 predicted the dose fairly well.

Overall, the dose prediction in children by exponent 0.9 across the age groups (from neonates to adolescents) was reasonably accurate (79%) (Table 6).

3.4. Comparison between whole-body PBPK modeling and the proposed methods for the pediatric dose projection

The results of the analysis are shown in Table 7. Based on the comparison from 11 drugs, there is no indication that the PBPK model provides any better dose projection in pediatrics than the proposed methods. The other models are not only simpler than PBPK model but remain as robust and accurate as the PBPK model.

Table 7. A comparison between whole-body physiologically based pharmacokinetic and the proposed methods for the pediatric dose projection.

Drugs/age	PBPK	Weight based			Salisbury	Clearance based
		0.75	0.90	1.0		0.75	0.90	1.0
Moxifloxacin (IV), dose in mg/kg
>0.25–<2 years	9–10	9	7	6	8	9	7	6
≥2–<6 years	7–8	8	7	6	8	11	9	8
≥6–≤14 years	5–6	7	6	6	8	8	8	7
Mefloquine (IV), total dose in mg
0.25–<2 years	62.5	56	41	34	48	58	43	36
National guidelines suggest a dose range of 32.5–62.5 mg
Nilotinib (oral)
2–<6 years	230 mg/m2	265	244	231	224	225	201	186
6–12 years	230 mg/m2	248	238	231	216	206	190	180
12–<18 years	230 mg/m2	238	234	231	216	202	193	186
Radiprodil (oral)*, dose in mg/kg b.i.d, observed pediatric dose is not known. The dose was compared with PBPK dose projection. Adult dose=30 mg, adult CL=6 L/h from Johnson et al. (PBPK manuscript)
1 year	0.1	0.34	0.26	0.21	0.30	0.34	0.26	0.21
6 months	0.21	0.39	0.27	0.21	0.30	0.39	0.27	0.21
7 months	0.21	0.37	0.27	0.21	0.30	0.37	0.27	0.21
Dolutegravir (oral), total dose in mg
0–28 days	2–5	5.8	3.8	2.9	4.0	4.2	2.6	1.9
Oxycodone (IV), dose in mg/kg
Neonates	0.07	0.21	0.14	0.10	0.14	0.17	0.10	0.07
Toddler (1–2 years)	0.12	0.16	0.12	0.10	0.14	0.16	0.12	0.10
Preschool (4–5 years)	0.12	0.14	0.11	0.10	0.14	0.15	0.13	0.11
School age (5–12)	0.12	0.12	0.11	0.10	0.13	0.14	0.13	0.12
Adolescents	0.10	0.11	0.10	0.10	0.11	0.11	0.11	0.11
Lorazepam (IV), dose in mg/kg
Neonates (0 day old)	0.0037	0.061	0.039	0.028	0.040	0.025	0.013	0.0085
1 month old	0.0077	0.058	0.038	0.028	0.040	0.025	0.014	0.0091
Lisinopril (oral)
Infants to toddlers	1–2.5 mg	3.9	2.8	2.3	3.2	3.9	2.8	2.3
Midazolam (IV), total dose in mg (0.1 mg/kg) in children, adult dose=5 mg/kg
Preterm	0.21	0.45	0.28	0.20	0.24	0.26	0.15	0.10
Term	0.28	0.52	0.33	0.24	0.29	0.40	0.24	0.17
Remdesivir (based on body weight of 3 and 35 kg), observed dose is not known; the dose was compared with PBPK dose projection of 5 mg/kg in children (reference 86)
Preterm (3 kg)	15	19	12	9	10	15	9	6
Young (35 kg)	175	119	107	100	130	136	125	119
Hydroxychloroquine, observed dose is not known; the dose was compared with PBPK dose projection of 6 mg/kg in children
5 kg	30	55	37	29	34	46	30	22
15 kg	90	126	100	86	120	126	100	86
35 kg	210	238	214	200	260	271	251	238

^*Radiprodil: PBPK projected dose of 0.21 mg/kg/b.i.d. was based at 60% RO response. PBPK: Physiologically based pharmacokinetic, RO: Receptor occupancy, IV: Intravenous

The dose of radiprodil was projected by PBPK and allometry [69]. The PBPK model was based on an adult total dose of 30 mg. The clinical trial of radiprodil in pediatrics was terminated (according to manuscript “due to feasibility”); hence, clinical trial-based dose of radiprodil in children is not known. The PBPK model projected dose for three children age ranging from 6 months to 1 year (body weight from 6.15 to 11.5 kg). The projected dose in two children by PBPK model was same as an adult dose on per kg body weight basis (0.21 mg/kg b.i.d.). The authors also used exponent 0.75 (termed as allometry) to project dose in three children and concluded that “allometry” overpredicted radiprodil dose in children by a big margin. The projected dose by exponent 0.75 was 0.75 mg/kg (mean projected dose in three children). There are several caveats with the authors’ conclusions. The mean projected dose using exponent 0.75 is indeed 0.75 mg/kg but if this dose is given b.i.d, then the mean dose should be equal to 0.37 mg/kg b.i.d. (like PBPK dose projection). The authors used exponent 0.75 and claimed that they used allometry. Exponent 0.75 is neither the definition of allometry nor allometry is defined by any particular number or exponent. The allometric exponents widely vary and are data dependent [2,88-91,93,94]. It is now well established that the application of exponent 0.75 results in substantially higher projected clearance or dose in younger children [2,88-91,93,94]. Exponent 0.75 is not applicable in radiprodil study. For dose projection, an exponent 0.9 was proposed previously [2,8,9,83] and was used in this study. The authors had not only incorrectly applied allometry but also made an assumption that the projected dose by PBPK is absolutely correct and if a clinical trial is conducted, then the clinical trial will also project an exact dose of 0.21 mg/kg b.i.d. radiprodil as the most optimum dose in children. In Table 7, the projected dose of radiprodil in children by different methods is shown. At least, four out of six methods projected radiprodil dose in children close to the dose projected by PBPK for two children.

Lutz et al. [86] projected remdesivir dose by PBPK model. The authors correctly noted that “In children <20 kg, there is a notable deviation between PBPK and allometry predictions with greater separation at lower weights.” The reason for this was the application of exponent 0.75 on CL (allometry is not defined by exponent 0.75 and the authors claim that they applied allometry in their analysis was incorrect). Exponent 0.75 simply does not work for the younger children either for the prediction of CL or dose. The application of ADE would have substantially reduced this separation at lower weights. It is also true that allometry does not take into account enzyme ontogeny in very young children (<2 years) and changes in metabolite formation clearance but using the ADE-based exponents will reduce this separation at the lower weights or very young age [88-90,94].

In Table 7, I have compared the dose projection of remdesivir by PBPK with different methods proposed in this study. Two different body weights (3 and 35 kg) were used in the analysis. Based on 5 mg/kg remdesivir dose projected by PBPK, all proposed models underpredicted (range 43% [by exponent 1]–22% [by Salisbury rule]) remdesivir dose for 35 kg body weight. For 3 kg body weight, remdesivir dose projection by the proposed models had mixed results (27% higher [exponent 0.75] and 60% lower [exponent 1.0 CL-based] when compared with PBPK). However, in the absence of observed clinical dose, it is difficult to judge the accuracy of the projected dose either by PBPK or proposed models.

The oxycodone dose across the age groups is generally 0.1 mg/kg. The FDA package insert of oxycodone does not provide any dosing information for <11 years of age. However, in the literature, it appears that from the neonates to adults, a widely accepted oxycodone dose is 0.1 mg/kg [72-75]. Based on the PBPK modeling, Zheng et al. [72] proposed intravenous oxycodone dose from newborn to adults. According to the authors, the newborn should receive 0.07 mg/kg rather than 0.1 mg/kg oxycodone IV dose, whereas toddlers, preschool, and school-age children should receive 0.12 mg/kg oxycodone IV dose, and a dose of 0.1 mg/kg dose should be given to adolescents and adults. These proposed doses of oxycodone by the PBPK model across the age is not far from the dose of 0.1 mg/kg oxycodone dose generally given to subjects (neonates to adults). Furthermore, the dose of a drug is also adjusted based on the response of a patient. The IV oxycodone dose by different methods proposed in this study reconciles very well with the PBPK model as well as oxycodone dose given in clinical settings (Table 7).

For lorazepam, based on PBPK analysis, Maharaj et al. [76] suggested a dose of 0.0037 mg/kg in newborn (age 0 day) and 0.0077 mg/kg dose in 1-month-old children. These PBPK-based dosing recommendations in neonates (0 day old and 0-1 month old) substantially differed from the doses used in the literature and the FDA package insert (0.05–0.1 mg/kg) [76-79]. The adult dose of lorazepam for anxiety is 0.044 mg/kg. In this study, the analysis, based on different methods, indicated a dose ranging from 0.0085 to 0.061 mg/kg and 0.0091 to 0.058 mg/kg for the newborn (0 day old) and 0-1 month old, respectively (Table 7). Only the clinical trials will confirm if the proposed dose of lorazepam by the PBPK modeling or other methods are correct in the newborn and 0-1-month-old children.

With the exception of lorazepam, the doses of drugs projected by different proposed methods in this study reconciled very well with the doses projected by PBPK. The proposed methods in this report are simpler than the PBPK model yet in their predictive performance are as accurate and robust as PBPK models.

4. Discussion

Based on the PK information available from adults, especially, from exposure or clearance, it is possible to predict a pediatric dose to initiate a first-in-children clinical trial. This study is an attempt to develop simple models to predict the pediatric dose to initiate a pediatric clinical trial.

Although several simple models as described previously (introduction section) are available for the selection of pediatric dose, these methods are not considered optimum. Due to the shortcomings of these simple models, complex empirical models such as statistics-based pharmacometric and PBPK models were developed and it is widely believed that these models somehow provide accurate dose (acceptable prediction error is 2-fold) prediction to children. On the other hand, one should recognize that the models do provide approximation of a desirable objective and from this perspective are useful. It is, however, not necessary that the models should be complex rather simple models are highly desirable and can be as robust and accurate as the complex models.

In this analysis, three different categories (20%, 25%, and 30%) were chosen to describe the prediction accuracy of the doses in the pediatric population. These numbers although are somewhat arbitrary but have some practical value. Even after a well-controlled clinical trial, the recommended dose will have some variability in response and adverse effect. For example, a 50 mg recommended dose in a clinical trial may be optimum at 40 mg or 60 mg dose. Furthermore, intersubject variability in dose response also leads to variability. Considering these factors in the recommendation of a dose to a patient population, a 20–30% prediction error in dosing was considered by different models a good prediction. The proposed models in this study are to initiate pediatric clinical trials with a reasonably accurate first dose.

In an era of ‘Fit for Purpose,’ it becomes very important that different models and as simple as possible be explored to attain certain objectives. This notion has led to explore several simple models for the pediatric dose prediction to initiate pediatric clinical trials. These simple models can be developed on a spreadsheet in a very short period of time [83,88-91,92,95,96].

Weight (Clark’s rule) or age-based (Young’s rule) dosing is simple and attractive but neither of the methods is accurate for pediatric dose prediction [12]. In this analysis, it was noted that weight-based dosing does provide a good prediction of pediatric dosing if an allometric exponent of 0.90 is used (rather than a linear function). Almost 84% pediatric dose was within ≤30% prediction error across all age groups. In preterm and term neonates, almost 72% predicted dose was within ≤30% prediction error. The theoretical exponent 0.75 performed poorly in the neonates (Table 2). The linear extrapolation of dose from adults to children also performed well. In neonates, almost 76% pediatric dose was within ≤30% prediction error. It should be, however, noted that there were many drugs whose recommended dose was based on linear extrapolation from adult dose. In other words, no clinical trials were conducted to determine an optimum dose in children, especially in the neonates.

Exponent 0.90 is a compromise between exponent 0.75 and 1.0. Exponent 0.9 is as arbitrary exponent as 0.75 but provided more accurate results than exponent 0.75. There is no great scientific logic behind using exponent 0.90 and the use of a fixed allometric exponent has also no scientific basis [94]. However, almost 84% and 79% observations within <30% prediction error indicate that exponent 0.90 is an acceptable exponent and is better than 0.75 to predict pediatric dose using body weight or predicted clearance.

Allometric exponents widely vary and reliance and assumptions based on a single allometric exponent can lead to serious errors [94]. There are, however, situations when data are not available to estimate an allometric exponent, and then in this case, there is no choice but to use a fixed exponent. In this report, exponent 0.90 was found to be a suitable exponent for the pediatric dose prediction but it was also obvious that not necessarily for each and every drug and across all age groups exponent 0.90 would always provide the best results. For example, 84% pediatric dose was within ≤30% prediction error across all age groups indicating that 16% predicted pediatric dose did not meet the targeted prediction error but uncertainty is the nature of all empirical models.

Salisbury rule, which is based on body weight, performed very well across the two weight groups (72% observations with ≤30% prediction error), especially when body weight was >30 kg (96% observations with ≤30% prediction error) (Table 3). In preterm and term neonates, using multiplication factor 2 (since the body weight is <30 kg), only 41% observations had prediction error with ≤30%. Almost 41% observations were +>30% prediction error (overprediction). To reduce the overprediction of dose, in the neonates, a multiplication factor 1.7 was introduced which led to substantial improvement in the dose prediction of neonates (79% observations with ≤30% prediction error with 2 observations +>30%) (Table 3). The combination of factor 2 and 1.7 in children ≤30 kg led to a substantial improvement in the dose prediction in children ≤30 kg (from 64% to 76%). It should be noted that overprediction of dose in preterm and term neonates by Salisbury rule will be for the dose which was directly extrapolated from adults on per kg body weight. In general, the prediction error is around 40%.

Salisbury rule is not widely used but it seems that it has a great potential in predicting the pediatric dose. In children who are >30 kg body weight (approximately 10 years of age), the method provides excellent results. In neonates and may be in children >5 and <15 kg, some modification in the multiplication factor may be needed. The models with the allometric exponent of 0.9 on body weight and the modified Salisbury rule indicate that body weight can be used to predict the pediatric dose with confidence to initiate a pediatric clinical trial or can be used in a clinical setting. The modified Salisbury rule is very simple and robust. The results of the analysis in this study indicate that Salisbury rule should be further explored since this approach appears to be very simple and robust for pediatric dosing.

In this analysis, predicted clearance was also used for the prediction of pediatric dose. Using the ADE, the predicted clearance of drugs was within 2-fold prediction error for 92% subjects (Table 5).

To predict the dose from the predicted clearance, three exponents (0.75, 0.9, and 1) were used (Table 6). Exponent 0.75 provided the worst result and the best result was obtained by exponent 0.9. Exponent 0.75 overpredicted (+>30% prediction error) the dose across the age groups in 34% (n = 113) of subjects and by 45% (n = 29) in the preterm and term neonates. On the other hand, exponent 0.9 underpredicted (−>30% prediction error) the dose across the age groups in 16% (n = 113) of subjects and by 35% (n = 29) in the preterm and term neonates.

The overall dose prediction within ≤30% prediction error by exponent 0.9, Salisbury rule, and by predicted clearance was 84.1%, 80.5%, and 78.8%, respectively, indicating comparable dose prediction. However, in preterm and term neonates, the prediction accuracy differed. A ≤30% prediction error in dose by exponent 0.9, Salisbury rule, and by predicted clearance was 72.4%, 79.3% (using factor 1.7), and 58.6%, respectively. The low accuracy in dose prediction by predicted clearance in the neonates was despite the fact that the predicted clearance in preterm and term neonates was fairly accurate with 85% and 74% prediction error within 0.5–2-fold, and 0.5–1.5-fold, respectively.

In the literature, PBPK has been suggested as a modeling approach for the prediction of PK parameters as well as dose selection in children from adults. A whole-body PBPK model is widely used for this purpose but it has been now well established that a whole-body PBPK model is unnecessary and a minimal PBPK model can be used and provides as accurate and robust results as whole-body PBPK [97-100,98-103]. A minimal PBPK model indicates that rather than using all body organs and many physiological parameters, few organs and one or two physiological parameters can provide similar results as a whole-body PBPK model [97-100,98-103]. One such example is a recent study [103] in which total and renal clearances of drugs in subjects with renal impairment (mild, moderate, and severe) were predicted by just using creatinine clearance. A comparison with whole-body PBPK indicated that the simple creatinine clearance-based model was as robust and accurate as the PBPK model. Similarly, it has been shown that the clearances of drugs can be predicted across the age groups using allometry (ADE model) as accurately as the whole-body PBPK [83,88,92]. Allometry can also be used in drug-drug interaction studies. In a recent study, it was shown that using age-dependent allometry, clearance in children following drug-drug interaction studies can be predicted using adult clearance from adult drug-drug interaction studies [96]. In the study, the prediction error of drug clearance following drug-drug interaction studies in children ranged from 4% to 67%. Fifty-seven percent and ninety percent observations had a prediction error ≤30% and ≤50%, respectively. The results of the DDI study belie the assertion of Johnson and Ke in a recent publication [104] that “Allometric methods alone would not apply in assessing DDI changes with age and the likely effect on dose.”

In this study, pediatric dose predicted by the whole-body PBPK was compared (n = 11) by the simple models evaluated in this study and it was found that the predictive power of PBPK and simple models was comparable (Table 7). A comparison with whole-body PBPK and the proposed models indicated that these simple models were as robust as PBPK model. There is no advantage of using a complex PBPK model over a simple method which is as robust as a complex PBPK model. The simple models in this study belie the notion that a whole-body PBPK model with many physiological parameters and numerous body organs is needed to achieve certain objectives and other simple models are insufficient or inaccurate.

5. Conclusions

In this report, several simple methods to predict first-in-pediatric dose to initiate a pediatric clinical trial were evaluated. The methods are simple and can be used on a spreadsheet in a very short period of time. These simple models are robust and fairly accurate. From this study, it seems that weight can be used to predict first-in-pediatric dose with accuracy. Salisbury rule with modified factor (1.7 rather than 2 in neonates) and children >30 kg body weight provided accurate results and is robust. This method is not widely used but is very simple and accurate. This method can also be used in clinical settings (hospitals for pediatric dosing). The Salisbury rule with more data should be evaluated and implemented due to its accuracy and simplicity.

Complexity does not necessarily provide accuracy over simplicity. The models are inherently erratic and complexity will not necessarily improve the predictive performance of a given model. According to George Box, since all models are wrong the scientist cannot obtain a “correct” one by excessive elaboration. On the contrary, following William of Occam, he should seek an economical description of natural phenomena [105].

In a recent article, Deyme et al. [106] highlighted the usefulness and practical values of simple models. The authors wrote “Conversely, such simple models are the most likely to reach bedside application because of their simplicity. It is critical to balance the pros and cons of each strategy for precision medicine in real-world settings. Models should rather be built in the perspective of future practical application. Indeed, for an efficient in silico-to-bedside transposition, we believe that the more complex is a phenomenon, the simpler should be the mathematical model describing it.”

In a practical world, simple models are far more attractive than complex models and the search and efforts should be focused on simple models rather than complex and unnecessary elaborative models which provide no practical advantage over simple models. The regulatory agencies round the globe should recognize the importance of simple models and encourage simple models over unnecessarily complex models. Simple models are scientifically and economically highly desirable and there is no reason not to use them and promote them.

Funding

No fund was received from any source for this study.

Conflicts of Interest

There are no conflicts of interest for this work.