Elective surgery scheduling under uncertainty in demand for intensive care unit and inpatient beds during epidemic outbreaks

Abstract

Amid the epidemic outbreaks such as COVID-19, a large number of patients occupy inpatient and intensive care unit (ICU) beds, thereby making the availability of beds uncertain and scarce. Thus, elective surgery scheduling not only needs to deal with the uncertainty of the surgery duration and length of stay in the ward, but also the uncertainty in demand for ICU and inpatient beds. We model this surgery scheduling problem with uncertainty and propose an effective algorithm that minimizes the operating room overtime cost, bed shortage cost, and patient waiting cost. Our model is developed using fuzzy sets whereas the proposed algorithm is based on the differential evolution algorithm and heuristic rules. We set up experiments based on data and expert experience respectively. A comparison between the fuzzy model and the crisp (non-fuzzy) model proves the usefulness of the fuzzy model when the data is not sufficient or available. We further compare the proposed model and algorithm with several extant models and algorithms, and demonstrate the computational efficacy, robustness, and adaptability of the proposed framework.

1. Introduction

Elective surgeries contribute to a substantial portion of hospital revenue and healthcare systems have faced an unprecedented financial crisis by delaying elective surgeries due to the COVID-19 pandemic (Best et al., 2020, Kliff, 2020). Uncertainty is one of the most critical factors leading to the delay of elective surgery, and the COVID-19 pandemic aggravates this uncertainty. For example, surgery duration has increased significantly and become more unpredictable in the COVID-19 era as surgical teams have to wear additional personal protective equipment before surgery and there is a postoperative disinfection procedure in operating rooms. In addition, the deterioration of the patient’s condition, caused by a delay in surgery, increases the uncertainty of surgery duration (SD), length of the stay in the ward (LOSW), length of the stay in the intensive care unit (LOSI), and intensive care unit demand (ICD) of elective patients (Dai, Wang, & Shi, 2022). In addition to demand, the supply of beds for elective patients became uncertain because they can be preempted by non-elective patients at any time. For example, COVID-19 patients occupy most intensive care unit (ICU) beds and nursing staff, and their daily demand is uncertain, resulting in the shortage and uncertainty of ICU bed capacity available to elective patients (ICC).1

There are many methods to deal with uncertainty, and stochastic optimization is considered to be one of the widely used methods. Stochastic optimization assumes that uncertain parameters follow a known distribution or fitted distribution of actual data (Bovim et al., 2020, Zhang et al., 2019). However, it is difficult to accurately know the distribution in practice (Shehadeh, 2022). In addition, based on our interviews,2 sometimes the hospital administrators do not have sufficient data. In particular, the historical data cannot reflect the increase in SD, LOSW, and LOSI caused by the COVID-19 pandemic, and there is no data about ICC and ICD. Fuzzy optimization can reduce the dependence on data by making use of expert knowledge. At present, it has been widely used in various fields, including project selection (Singh, Rathi, Antony, & Garza-Reyes, 2022) and supply chain management (Cao et al., 2021, Gabriel et al., 2021). Considering these scenarios with inadequate data, we propose a fuzzy scheduling method based on expert estimation. The surgeon team estimate SD, LOSW, LOSI, ICD, and ICC based on their experience and the patient’s condition.

As far as we know, there is no accurate method to solve a fuzzy model directly. Most studies first transform the fuzzy model into a non-fuzzy model and then use solvers or heuristic algorithms to solve the problem as shown in Fig. 1 (Abdullah and Abdolrazzagh-Nezhad, 2014, Gonzalez-Rodriguez et al., 2008). However, the transformation process may lead to the loss of decision information. Therefore, we propose a transformation process to reduce the loss of decision information and improve the performance of the fuzzy model. On the other hand, for large-scale problems, accurate methods are often difficult to solve the model in an acceptable time because surgical scheduling is a complex combinatorial optimization problem. Therefore, we propose a hybrid heuristic algorithm to solve the transformation model for large-scale problems.

Fig. 1.

Surgery scheduling problem and optimization framework.

Concisely, this paper considers the scheduling of elective surgeries with uncertainty. We capture the uncertainty in SD, LOSW, LOSI, ICC, and ICD using fuzzy numbers and sets. We develop a fuzzy model to deal with the uncertainty and insufficient data caused by the COVID-19 pandemic. To solve the fuzzy model, we first transform the fuzzy model into a tractable mixed-integer programming (MIP) model, and then propose a hybrid heuristic algorithm for the large-scale problems to reduce the solving time. The experiment shows that the fuzzy model based on expert experience can effectively deal with scheduling problems with insufficient data. In addition, the proposed model has excellent adaptability to the uncertainty caused by the COVID-19 pandemic. Finally, the experience also proves that the transformation model that is easy to solve can provide an accurate solution for small-scale problems. At the same time, the proposed hybrid heuristic algorithm can obtain a satisfactory solution in a reasonable time for large-scale problems.

In summary, our contributions are as follows. First, we use expert knowledge to deal with insufficient data on SD, LOSW, LOSI, ICC, and ICD by using fuzzy numbers and fuzzy sets. Second, we model a surgery scheduling problem with uncertainty incorporating the challenges brought by COVID-19. Third, we present an approach to solve the proposed fuzzy model. Specifically, we first transform the fuzzy model into a tractable mixed-integer programming (MIP) model and then propose a hybrid heuristic algorithm for the large-scale problems to reduce the solving time.

The remainder of this paper is organized as follows. Following the literature review in Section 2, we developed a fuzzy model in Section 3 and solve it in Section 4. Computational experiments are provided in Section 5. Section 6 concludes the paper with discussions and remarks.

2. Related literature

We review the related literature on elective surgery scheduling in this section. Our thorough survey3 clearly indicated that there are only a handful of studies that focus on surgery ‘scheduling’ problems within a framework that facilitates uncertainty and scarcity driven by epidemic outbreaks such as COVID-19. Nevertheless, many researchers focus on the impact of the COVID-19 epidemic on elective surgeries (cf. Best et al., 2020, Beninato et al., 2022, Nguyen et al., 2022, Norris et al., 2021) and demonstrate the impact of the COVID-19 epidemic on surgical scheduling, in general, and elective surgeries, in particular. The COVID-19 pandemic has impacted the scheduling of elective surgeries in the following ways: First, historical data is simply unavailable to produce reasonable forecasts for scheduling; for example, complicated preoperative preparation procedures, postoperative disinfection, and reduction in the number of staff have led to changes in the distribution of surgery duration, and/or the mean and variance of the surgery duration. Secondly, the availability of ICU and inpatient beds has become uncertain and scarce due to increased and highly volatile emergency COVID-19 demand. While the extant literature mainly identifies these characteristics, we focus on modeling and solving the resulting problems. The following subsections respectively discuss the surgery scheduling literature and uncertainty therein.

2.1. Surgery scheduling

Surgical suites typically operate following either an open or block scheduling policy (Freeman et al., 2016, Miao and Wang, 2021). The open scheduling policy means that a surgeon can choose any working day to process a case. In addition, for the block scheduling policy, surgeon or surgeon groups are assigned to a period during which they can schedule their surgical cases. These time blocks are owned by surgeons and reserved in advance. Even if some time blocks are not used, they cannot be released during the planning period. Since patients in the same block must be scheduled for surgery on the same day, this may not be conducive to the flexible allocation and full utilization of ICU beds and inpatient beds, so we adopted an open scheduling policy.

Since the upstream stage consists of more expensive resources of hospitals, most studies focus on improving the utilization of upstream resources. For example, Li et al. (2016) propose a rescheduling method to improve the utilization of related resources in the OR. Batun et al. (2011) consider OR as a bottleneck resource and propose a stochastic mixed-integer programming model to minimize the total expected cost. Similarly, Roshanaei et al. (2017) consider the scarcity of OR and suggest a joint operation scheduling method based on multiple hospitals. These studies usually treat different hospital units in isolation. In contrast, our research treats surgery scheduling as a coordinated process between the upstream and downstream. Specifically, we consider the utilization efficiency of OR and the availability of ICU and ward.

Surgery scheduling under limited downstream resources has also been investigated. For example, Min and Yih (2010) propose a stochastic mixed-integer programming model for the shortage of downstream surgical intensive care unit (SICU) beds. Zhang et al. (2019) study a two-level optimization model considering the capacity limitation of the downstream SICU for the problem of elective surgery planning in a single department. These studies attempt to address the adverse effects of ICU capacity constraints on upstream OR utilization, whereas our study also highlights the importance of wards.

To compare the existing work on surgery scheduling and to highlight our contribution, we have summarized the relevant literature in Table 1 . Generally, the focus of research has been on the OR unit, while only several researchers have incorporated the ICU and ward and studied all three at the same time. Moreover, the objectives of surgical scheduling have varied across operating room overtime, patient waiting for costs, and extra ICU beds.

Table 1.

Related literature on surgery scheduling.

Paper	Objective function	Focused unit	Planning horizon
Denton et al., (2010)	OR overtime cost, OR open cost	OR	Intra-day
Lee and Yih (2014)	Completion time, waiting time	OR, Post-anesthesia CU	Intra-day
Min and Yih (2010)	Patient costs, expected overtime costs	OR, SICU	Intra-day
Gul et al. (2015)	Expected OR overtime, waiting and cancellation costs	OR	week
Jebali and Diabat (2015)	Patient-related cost, expected OR Utilization cost, penalty cost for exceeding ICU capacity	OR, ICU	Intra-day
Freeman et al. (2016)	The surgery revenue, costs for overtime and tardiness	OR	Intra-day
Neyshabouri and Berg (2017)	Cost of patient priority and waiting time, overtime cost, cost of lack of SICU capacity	OR, ICU	week
Kumar et al. (2018)	The LOSI of scheduled patients, the LOSI of canceled patients	OR, ICU	week
Eun et al. (2019)	Patient health condition and total overtime	OR	Intra-day
Behmanesh and Zandieh (2019)	Makespan and the unscheduled surgical cases	OR	Intra-day
Zhang et al. (2019)	Waiting cost, surgery cost, overuse of ORs, inadequate SICU beds and OR open cost	OR, ICU	week
Wang et al. (2019)	Operational costs, including the fixed costs for Opening ORs and the expected penalty costs of overtime	OR	Intra-day
Bovim et al. (2020)	Number of patients scheduled, cancellations, and resting in wards not designated	OR, Ward	week
Wang et al. (2020)	The expected value of average recovery completion time for all patients	OR	Intra-day
This paper	Waiting cost, OR overtime cost, extra ICU bed, extra inpatient bed	OR, ICU, Ward	week

Note: Different studies have used different terms for beds that exceed the capacity of the ICU. Commonly used terms include the exceeding ICU capacity, lack of SICU capacity, the extra beds acquired in the ward, and inadequate SICU beds. We use the term ‘extra’ ICU bed and ‘extra’ inpatient bed.

2.2. Uncertainty in surgery scheduling

The uncertainty in the scheduling of elective surgery mainly includes the SD, LOSI, LOSW, ICD, and ICC. The upstream stage mainly involves surgery duration, which can be subdivided into a pre-operative holding unit (PHU) duration, surgery duration, and post-anesthesia care unit (PACU) duration. Most of the scheduling studies focus on the uncertainty of surgery duration, as shown in Table 2 below. For example, Eun et al. (2019) use a stochastic mixed-integer program to optimize the assignment of surgeries. Furthermore, Neyshabouri and Berg, 2017, Schiele et al., 2021, and Zhang et al. (2019) consider the uncertainty of SD and LOSI. Only very few studies incorporate the uncertainty of LOSW (cf. Bovim et al., 2020, Schiele et al., 2021). As seen in Table 2, none of the existing studies consider the uncertainty of ICU demand and capacity. This is because, under normal circumstances, hospitals have sufficient ICU beds reserved for elective surgeries, thereby the uncertainties therein do not play a major role in scheduling decisions. However, when a large number of ICU beds are occupied by emergency patients (due to unprecedented events such as the COVID-19 pandemic), the availability of ICU beds becomes limited and uncertain. Thus, the hospital can no longer reserve ICU beds for each elective surgery patient, and it has to carefully consider the need for ICU beds for elective patients. In addition, since ICU beds are shared by elective and emergency patients, the uncertainty in available ICU capacity becomes very critical in this case.

Table 2.

Related literature on surgery scheduling considering uncertain factors.

Literature	SD	LOSI	LOSW	ICD	ICC	Method
Denton et al. (2010)	✓	✕	✕	✕	✕	RO
Min and Yih (2010)	✓	✓	✕	✕	✕	SO
Lee and Yih (2014)	✓	✕	✕	✕	✕	FO
Gul et al. (2015)	✓	✕	✕	✕	✕	SO
Jebali and Diabat (2015)	✓	✓	✕	✕	✕	SO
Freeman et al. (2016)	✓	✕	✕	✕	✕	SO
Neyshabouri and Berg (2017)	✓	✓	✕	✕	✕	RO
Kumar et al. (2018)	✕	✓	✕	✕	✕	SO
Eun et al. (2019)	✓	✕	✕	✕	✕	SO
Behmanesh and Zandieh (2019)	✓	✕	✕	✕	✕	FO
Zhang et al. (2019)	✓	✓	✕	✕	✕	SO
Wang et al. (2019)	✓	✕	✕	✕	✕	RO
Bovim et al. (2020)	✓	✕	✓	✕	✕	SO
Zhang et al. (2020)	✓	✓	✕	✕	✕	SO
Wang et al. (2020)	✓	✕	✕	✕	✕	FO
This paper	✓	✓	✓	✓	✓	FO

Note: SO - Stochastic Optimization, RO - Robust Optimization. FO - Fuzzy Optimization.

There exist other stochastic, robust, and fuzzy optimization models that deal with the uncertainty of surgery scheduling. For example, Kumar et al. (2018) propose a stochastic mixed-integer programming model to capture the uncertainty of LOSI when downstream capacity is limited. Min and Yih (2010) establish a stochastic compensation model and apply the sample average approximation algorithm to solve it. These authors apply stochastic optimization, and they need to assume that distributions of the parameters are known. In contrast, our model does not need to make such assumptions as we rely on expert opinion; thus, our model does not depend on historical data.

Denton et al. (2010) compare stochastic optimization (SO) and robust optimization (RO) models for the uncertainty of surgery duration. Their results show that RO performs better in situations where information about parameter distribution is limited. Neyshabouri and Berg (2017) employ a two-stage RO model to deal with the uncertainty in LOSI and LOSW. While we employ a fuzzy model to address the inadequacy of data in this paper, robust optimization has also been employed in the literature (Denton et al., 2010, Neyshabouri and Berg, 2017, Wang et al., 2019). However, for our surgery scheduling problem, since each surgery operation has a unique complexity and features, surgeons need to make a specific judgment and estimate for each patient based on their own experience, knowledge, and patient's physical condition(Chung et al., 2022, Moreno and Blanco, 2018); for example, the SD for cataract surgery was significantly influenced by anesthesia type, surgeon grade, high case complexity, pupil size, pupil expander use/type, CTR use, and intraoperative complications(Nderitu & Ursell, 2019). Thus, each estimate by the surgeons is not an exact value but a fuzzy interval with some uncertainty, which is difficult to describe by the uncertain sets in robust optimization. These models apply RO, which is suitable for situations with limited parameter distribution information. In comparison, we obtain the uncertain parameters from expert estimates that reflect the heterogeneity of patients, thereby reducing the complexity of the model. Thus far, there is limited literature on surgery scheduling with fuzzy theory. For example, Lee and Yih (2014) study a fuzzy model with the uncertainty of PACU duration. Behmanesh and Zandieh (2019) use a fuzzy optimization model based on multi-objective for the uncertainty of PHU time, SD, and PACU time. These studies focus on the intra-day surgery scheduling and highlight the uncertainty of the upstream (i.e., SD). In contrast, we consider the uncertainty in SD, LOSW, and ICD, and use a multi-day scheduling scheme.

3. Fuzzy surgery scheduling model with uncertain

In order to clearly represent the modeling process, we first developed a crisp surgery scheduling model by assuming that the surgical scheduling environment is certain. In Section 3.2, we further developed a fuzzy model considering the uncertainty of the scheduling environment, i.e., fuzziness.

3.1. The crisp surgery scheduling model

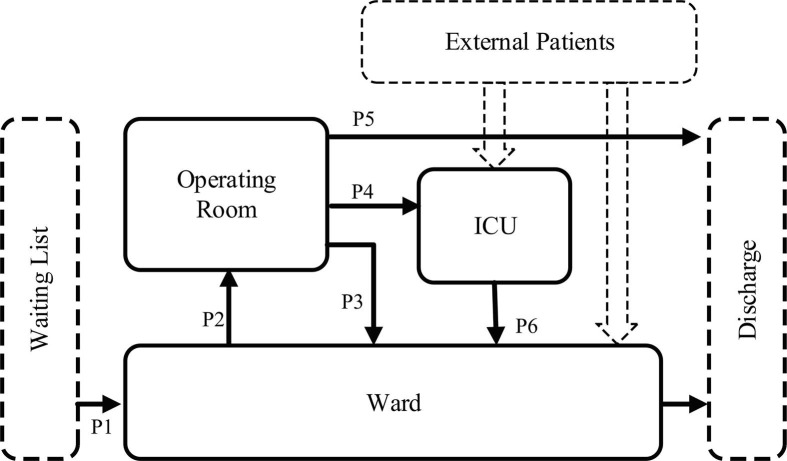
In this subsection, we present a crisp (non-fuzzy) model (CM) for our elective surgery scheduling problem. The goal is to schedule patients optimally for the surgery when the capacity of the OR, ICU, and ward are all limited. Before each planning horizon (week), all patients stay on a waiting list and the hospital needs to optimally4 select some patients from this list for treatment due to the capacity limit; the remaining patients will be considered during the next planning stage, i.e., in the subsequent week. Following the standard surgical practice, we assume that each patient is pre-assigned to a surgery team based on his/her primary surgeon and current needs, and this information is available at the time of the patient selection. Also, every patient has a latest surgery date before which his/her surgery must be completed. Therefore, patients are heterogeneous in terms of the surgery time requirement. Note that, whenever the capacity is limited, some patients may decide to leave the waiting list and look for another hospital, if they can’t get a timely appointment. After surgery, some patients will be discharged directly, some patients will enter the ICU, and the remaining patients will enter the ward to recover until they are discharged. Fig. 2 below illustrates the flow of patients during the surgery procedure. It should be observed that ICU and ward can admit patients externally and thus, the ICU capacity is shared among the patients from the OR and the direct ICU inpatients whereas the ward capacity is shared among the patients from OR, ICU, and the direct inpatients. As we discussed earlier, during epidemic outbreaks such as COVID-19, the external demand for ICU and ward beds increases rapidly. Therefore, the analysis of the problem under stringent ICU and ward capacities would be of particular interest in this study.

Fig. 2.

The flow of patients during the surgery procedure.

We now turn attention to the key determinants of our cost minimization objective function in the formulation. Unlike emergency surgeries, elective surgeries are less sensitive to the date of surgery. Nevertheless, due to health risks associated with waiting, elective surgeries can’t be postponed indefinitely. Therefore, our objective function incorporates the patients’ waiting cost for surgery. Waiting costs refer to the health risks and loss of satisfaction caused by waiting, which can be described as a loss of patient and social productivity due to treatment delays (Gerchak et al., 1996, Ayvaz-Cavdaroglu and Huh, 2010). However, choosing too many patients for surgery to reduce patient waiting times often results in OR overtime and overload of the ward which is costly. Thus, there exists an interesting tradeoff between the waiting cost and OR overtime and bed shortage costs. Consequently, our objective of this paper is to jointly reduce patient waiting costs, OR overtime costs, and both ICU and inpatient bed shortage costs by aptly scheduling elective surgeries.

To present the formulation of our problem, we first introduce the following notations in Table 3 .

Table 3.

Notation for indices, parameters, and decision variables.

Indices
$i$	Patient index; $i=1,2,3,...,N$, where $N$ indicates the number of elective surgeries on the waiting list.
$s$	Surgeon index; $s=1,2,3,...,S$, where $S$ indicates the number of surgeons.
$j$	OR index; $j=1,2,3,...,J$, where $J$ indicates the number of ORs.
$d$	Surgery date index; $d=1,2,3,...,D/D^{\text{'}}$, where $D$ indicates the number of days in the current planning horizon, and $D^{\text{'}}$ is a dummy day to accommodate excessive demand.
$e$	Date index of discharge from ward; $e=1,2,3,...,D,...,D+Q^W$, where $Q^W$ indicates the maximum LOSW of patients in Ward.
$r$	Date index of patient leave ICU; $r=1,2,3,...,D,...,D+Q^U$, where $Q^U$ indicates the maximum LOSI of patients in ICU.
Parameters
$H^A$	Index set of surgery date; $H^A=\left\{1,2,3,...,D^{\text{'}}\right\}$.
$H^E$	Index set of discharge date; $H^E=\left\{1,2,3,...,D,...,D+Q^W\right\}$.
$H^U$	Index set of the date that a patient leaves ICU; $H^U=\left\{1,2,3,...,D,...,D+Q^U\right\}$.
$H^I$	Index set of patients; $H^I=\left\{1,2,3,...,N\right\}.$
$B^W$	Number of available inpatient beds at the beginning of the current planning horizon.
$B^U$	Number of available ICU beds at the beginning of the current planning horizon.
$u_j^O$	Unit overtime cost per operating room $O{R}_j$.
$u^W$	Unit cost per an optional extra inpatient bed.
$u^U$	Unit cost per extra ICU bed.
$u_i^T$	Unit waiting cost of patient $i$.
$M^O$	Upper-bound for daily overtime hours of each OR.
$M^B$	Upper-bound on extra inpatient beds for each day.
$M^U$	Upper-bound on extra ICU beds for each day.
${\left\{Y_{\mathit{is}}\right\}}_{N\times S}$	Surgeon-patient matrix, $Y_{\mathit{is}}=1$, if the surgeon $s$ is the attending surgeon of patient $i$; otherwise $Y_{\mathit{is}}=0$.
$Z_i$	Type of patient; $Z_i$= 1 if a patient is an inpatient; otherwise $Z_i$ = 0.
${\left\{{\beta }_{\mathit{sd}}\right\}}_{S\times D}$	Availability of surgical team; ${\beta }_{\mathit{sd}}$= 1 if surgeon $s$ is available on day $d$, and otherwise ${\beta }_{\mathit{sd}}$ = 0.
$T_{\mathit{dj}}$	Open duration of operation room $O{R}_j$ on day $d$.
$L_i^S$	Surgery duration (SD) of patient $i$.
$L_i^W$	Length of stay in the ward (LOSW) of patient $i$.
$L_i^U$	Length of stay in ICU (LOSI) of patient $i$.
$D_i^U$	Type of patient; $D_i^U=1$ if a patient is admitted to ICU after surgery; otherwise $D_i^U=0$.
$R_d^U$	The number of released ICU beds on day $d$.
$R_d^W$	Number of released inpatient beds on day $d$.
$K_{\mathit{sd}}$	Maximum working time of surgeons $s$ on day $d$.
$\mathit{Du}{e}_i$	The latest date of the surgery of patient $i$. To keep the patient healthy, each patient has a due date by which the operation must be completed. The due date reflects the heterogeneity in the relative urgency and severity of the patient's condition.
$W_i^B$	Total waiting days of patient $i$ before the beginning of the current planning horizon.
$\theta$	Penalty coefficient of waiting time for patients deferred to the next planning horizon.
Decision Variables
$X_{\mathit{idj}}^s$	Binary variable; $X_{\mathit{idj}}^s$= 1, if patient $i$ is assigned to $O{R}_j$, surgeon $s$, on day $d$; otherwise $X_{\mathit{idj}}^s$ = 0.
$N_{\mathit{ie}}$	Binary variable; $N_{\mathit{ie}}$= 1, if patient $i$ is discharged from the ward on day $e$; otherwise $N_{\mathit{ie}}$ = 0.
$N_{\mathit{ir}}^U$	Binary variable; $N_{\mathit{ir}}^U$ = 1, if patient $i$ is discharged from ICU on day $r$; otherwise $N_{\mathit{ir}}^U$ = 0.
${\mathrm{\Delta }}_{\mathit{dj}}^O$	Total overtime of the $O{R}_j$ on day $d$.
${\mathrm{\Delta }}_d^W$	The number of extra beds in the ward used on day $d$
${\mathrm{\Delta }}_d^U$	The number of extra ICU beds used on day $d$.
${\mathrm{\Delta }}_i^T$	Total waiting days of patient $i$.

Note: The superscripts of all parameters are only used to distinguish symbols and have no specific meaning.

Some model parameters, such as the patient and attending surgeon team match ${\left\{Y_{\mathit{is}}\right\}}_{N\times S}$, the surgeon's working date ${\left\{{\beta }_{\mathit{sd}}\right\}}_{S\times D}$, the latest operation date ${\mathit{Due}}_i$ for each patient, and the surgical patient's demand for an inpatient bed $Z_i$, are known. In addition, some parameters such as $M^O$, $M^B$, $K_{\mathit{sd}}$, $W_i^B$, and $\theta$ are usually set by decision-makers. Finally, we refer to a bed in the ward as the inpatient bed, and a bed in the ICU as the ICU bed; the two are collectively called ‘bed’.

With these notations, we can formulate our joint scheduling problem with cost minimizing objective as follows:

$$\text{Min}\sum _{i=1}^N{u}_i^T{\mathrm{\Delta }}_i^T\text{+}\sum _{d=1}^D\sum _{j=1}^J{u}_j^O{\mathrm{\Delta }}_{\mathit{dj}}^O\text{+}\sum _{d=1}^D{u}_{}^W{\mathrm{\Delta }}_d^W+\sum _{d=1}^D{u}_{}^U{\mathrm{\Delta }}_d^U$$ (1)

The first term in the objective function (1) represents the patients’ waiting cost whereas the second, third, and fourth terms respectively represent the overtime cost of the OR, and the costs of the extra inpatient and ICU beds. As we have defined in Table 3, corresponding $u$ in each cost term of the objective function represents the unit cost associated with the respective decision variable.

Next, we introduce related sets of constraints and their interpretations.

$$\begin{array}{c}{\mathrm{\Delta }}_i^T=\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{H}_d^A{X}_{\mathit{idj}}^s+W_i^B\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s\hfill \\ +\theta ·D·\left(1-\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s\right),\forall i,\hfill \end{array}$$ (2)

$${\mathrm{\Delta }}_{\mathit{dj}}^O⩾\sum _{i=1}^N\sum _{s=1}^S{L}_i^S{X}_{\mathit{idj}}^s-T_{\mathit{dj}},\forall j,\forall d,$$ (3)

$${\mathrm{\Delta }}_{\mathit{dj}}^O⩾0,\forall j,\forall d,$$ (4)

$${\mathrm{\Delta }}_{\mathit{dj}}^O⩽M^O,\forall j,\forall d.$$ (5)

Equation (2) represents the waiting time of each patient. In particular, this constraint includes the waiting time of the current planning horizon as well as the waiting time before the start of the planning horizon. Among the patients with the same waiting unit cost, the patient with a long waiting time gets the priority. Due to the limited capacity of the hospital, not all patients on the waiting list can be served in the current planning horizon, and thus, the surgeries of some patients will be postponed to the next planning horizon; the third term on the right-hand side of Equation (2) captures the postponement penalty cost associated with these postponed patients. Since the total overtime of $O{R}_j$ on day $d$ should be non-negative, bounded, and larger than or equal to the excessive usage of the OR over the regular opening duration, we need constraints (2), (3), (4). Observe that, in our objective function (1), the second term on OR overtime can be represented as ${\sum }_{d=1}^D{\sum }_{j=1}^J{u}_j^O\mathit{max}\left\{{\sum }_{i=1}^N{\sum }_{s=1}^S{L}_i^S{X}_{\mathit{idj}}^s-T_{\mathit{dj}},0\right\}$ without the constraints (2), (3). However, the introduction of an auxiliary variable ${\mathrm{\Delta }}_{\mathit{dj}}^O$ gives us a linear model. The same remark applies for ${\mathrm{\Delta }}_d^W$ and ${\mathrm{\Delta }}_d^U$ in the model. Nevertheless, in the fuzzy model in Section 3.2, we will use the original form with $\mathit{max}(x,0)$ for convenience.

$$\left[\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{H}_d^A{X}_{\mathit{idj}}^s+L_i^U\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s\right]D_i^U·Z_i^{}=\sum _{r=1}^{D+Q^U}{H}_e^E{N}_{\mathit{ir}}^U,\forall i,$$ (6)

$$\sum _{r=1}^{D+Q^U}{N}_{\mathit{ir}}^U⩽1,\forall i,$$ (7)

$$\left[\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{H}_d^A{X}_{\mathit{idj}}^s+\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s\left(L_i^W·\left(1-D_i^U\right)+D_i^U\right)\right]Z_i^{}=\sum _{e=1}^{D+Q^W}{H}_e^E{N}_{\mathit{ie}},\forall i,$$ (8)

$$\sum _{e=1}^{D+Q^W}{N}_{\mathit{ie}}⩽1,\forall i.$$ (9)

The discharge day of an ICU patient can be calculated by adding LOSI to the operation day; Equations (5), (6) serve this purpose. Equations (7), (8) calculate the patient’s expected discharge date, which is the initial date of operation plus the number of days in the hospital.5 For patients who enter the ICU before the current planning horizon, if they leave the ICU during the current horizon, they will directly enter the ward. If a patient does not leave the hospital in the current planning horizon, then that patient will still be assigned to a bed in the next planning horizon until the discharge date. For patients scheduled in the current planning horizon, the day of leaving the ICU and the ward can be estimated based on their LOSI and LOSW. While variables $N_{\mathit{ie}}$ and $N_{\mathit{ir}}^U$ can be viewed as redundant variables, these variables not only help to understand the model, but also help the computations of the number of patients discharged each day.

$$\begin{array}{c}\sum _{d^{\prime }=1}^d\sum _{i=1}^N\sum _{j=1}^J\sum _{s=1}^S{Z}_i^{}{X}_{i{d}^{\prime }j}^s-\sum _{e=1}^d\sum _{i=1}^N{N}_{\mathit{ie}}^{}-B^W-\sum _{d^{\prime }=1}^d{R}_{d^{\prime }}^W+\sum _{d^{\prime }=1}^d{R}_{d^{\prime }}^U\hfill \\ +\sum _{r=1}^d\sum _{i=1}^N{N}_{\mathit{ir}}^U⩽{\mathrm{\Delta }}_d^W,\forall d,\hfill \end{array}$$ (10)

$${\mathrm{\Delta }}_d^W⩾0,\forall d,$$ (11)

$${\mathrm{\Delta }}_d^W⩽M^B,\forall d.$$ (12)

Constraints (9), (10), (11) handle the extra inpatient beds. The patients who enter the ward include patients leaving the operating room (see process P3 in Fig. 2), as well as patients who enter the ICU and then leave the ICU in the current planning horizon (process P6 in Fig. 2), and also include patients who enter the ICU before current planning horizon and leave the ICU in the current planning horizon. The patients leaving the ward include those who entered the ward during the current horizon and those before. Constraints (12) assure that the shortage of inpatient beds per day is less than an upper bound.

$$\sum _{i=1}^I\sum _{j=1}^J\sum _{d^{\prime }=1}^d\sum _{s=1}^S{X}_{i{d}^{\prime }j}^s{D}_i^U-B^U-\sum _{d^{\prime }=1}^d{R}_{d^{\prime }}^U-\sum _{r=1}^d\sum _{i=1}^N{N}_{\mathit{ir}}^U⩽{\mathrm{\Delta }}_d^U,\forall d,$$ (13)

$${\mathrm{\Delta }}_d^U⩾0,\forall d,$$ (14)

$${\mathrm{\Delta }}_d^U⩽M^U,\forall d.$$ (15)

Equations (12), (13), (14) represent extra ICU beds, i.e., the number of beds beyond the capacity. The availability of ICU beds includes the initially available ICU beds and the released ICU beds. These released ICU beds refer to patients who entered the ICU before the current decision period and left the ICU during the current decision period. Constraints (15) assure that the shortage of ICU beds per day is less than an upper limit.

$$\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s⩽\sum _{s=1}^S{\beta }_{\mathit{sd}}^{},\forall i,$$ (16)

$$\sum _{j=1}^J\sum _{i=1}^N{X}_{\mathit{idj}}^s{L}_i^S{\beta }_{\mathit{sd}}⩽K_{\mathit{sd}},\forall s,\forall d,$$ (17)

$$\sum _{d=1}^{D{\text{ue}}_i}\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s=1,\forall i,$$ (18)

$$\sum _{d=1}^{D^{\prime }}\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s=1,\forall i,$$ (19)

$$\sum _{d=1}^{D^{\prime }}\sum _{j=1}^J{X}_{\mathit{idj}}^s=Y_{\mathit{is}},\forall i,s.$$ (20)

In order to guarantee the availability of the assigned surgeon for each patient on the day of surgery, we have added the constraint (16). Constraints (17) respectively ensure that the daily working hours of the surgical team. Since patients must be admitted before their latest surgery date and each patient can only be assigned/discharged once, we employ constraints (17), (18). Constraint (19) ensures that unplanned patients in the current planning horizon will be assigned to a dummy date, meaning that some patients are postponed to the next planning horizon due to capacity constraints. Constraint (20) indicates that each patient is assigned to one surgeon only.

Although the solutions to the above scheduling problem would provide the directions on the type of patients that deserves a priority in admission, which OR should be assigned to these patients, the optimal time for surgeries, etc., we present a more robust version (with uncertainty) of the above deterministic problem next.

3.2. Fuzzy model

In Section 3.1, we assume that the surgical scheduling environment is certain, but in fact, the surgical scheduling environment is fuzzy. Therefore, in this subsection, we express the parameters in the surgical scheduling model as fuzzy numbers and fuzzy sets. Specifically, in the crisp model, we assume that all parameters, such as SD, LOSW, LOSI, ICD, and ICC, are known. In practice, decision-makers cannot obtain this information in advance. Although hospitals have historical data on SD, LOSW, and ICD, each patient presents a unique case with different characteristics and ICD dynamics changes due to external factors. For example, the demand for ICU beds has surged and become very uncertain due to the COVID-19 pandemic. In this subsection, we propose an approach based on expert estimates to handle the uncertainties. We represent uncertain parameters as fuzzy sets and fuzzy numbers. One of the key advantages of the fuzzy model is that the parameters can be determined either from expert estimates or a small amount of data (Yao and Lin, 2002). Section 3.2 introduces the fuzzy representation of uncertain parameters and presents a comprehensive description of the fuzzy model. The literature on decision-making in the fuzzy environment is rich(Bastos et al., 2019, Bellman and Zadeh, 1970).

Fuzzy models have been widely employed in hospital environments. In particular, triangular fuzzy numbers (TFNs) have been used for uncertain parameters in surgery scheduling studies (cf. Lee and Yih, 2014, Behmanesh and Zandieh, 2019; Wang et al., 2022). Similarly, we employ TFNs to capture uncertainty in our model (The definition of triangle fuzzy number can be seen in Appendix C.2). Specifically, we represent the patients’ SD by the TFN, ${\stackrel{\sim }{L}}_i^S=(L_i^{S_l},L_i^{S_m},L_i^{S_r})$, where $L_i^{S_l}$, $L_i^{S_m}$, and $L_i^{S_r}$ respectively denote the most optimistic, plausible, and pessimistic values of surgery duration of patient $i$; see Fig. 3 . Also, LOSI and LOSW can be represented by fuzzy numbers ${\stackrel{\sim }{L}}_i^W=(L_i^{W_l},L_i^{W_m},L_i^{W_r})$ and ${\stackrel{\sim }{L}}_i^U=(L_i^{U_l},L_i^{U_m},L_i^{U_r})$. It should be noted that we denote fuzzy numbers using ‘tilde’ throughout this paper.

Fig. 3.

Patients’ SD represented as a triangular fuzzy number ${\stackrel{\sim }{L}}_i^S$.

Since some patients have entered the ward (or ICU) before the current planning horizon and may leave the ward (or ICU) in the current planning horizon, it is necessary to estimate the ICU or inpatient beds that may be released in the current planning horizon. Specifically, the number of released ICU beds on day $d$ can be expressed as a TFN, ${\stackrel{\sim }{R}}_d^U$, and the number of released inpatient beds on day $d$ can be expressed as ${\stackrel{\sim }{R}}_d^W$. For patients whose discharge date exceeds the planned period, the hospital needs to evaluate the possibility of leaving the ward (or ICU) at the beginning of the next decision-making period. This approach ensures the adaptability of the model for highly uncertain environments with smaller decision-making periods.

Usually, hospitals cannot directly observe the patient’s type, $D_i^U$. However, hospitals can form a fuzzy set $\stackrel{\sim }{F}$ through expert estimation and then derive $D_i^U$ using a transformation of $\stackrel{\sim }{F}$. Specifically, experts (or surgeons) can assess whether each patient needs an ICU bed after the surgery and establish a fuzzy set $\stackrel{\sim }{F}$ after evaluating the current condition and the entire medical history of the patients. Let $P=\left\{p_1,p_2,\cdots ,p_n\right\}$ be a set of elective patients on the waiting list. Then, the fuzzy set of patients entering the ICU after surgery is as follows:

$$\stackrel{\sim }{F}=\left\{\left(p_1,{\mu }_1\right),\left(p_2,{\mu }_2\right),...,\left(p_k,{\mu }_k\right),...,\left(p_n,{\mu }_n\right)\right\}$$

where ${\mu }_k$ is the membership degree of the patient $p_k$ belonging to $\stackrel{\sim }{F}$, and ${\mu }_k\in [0,1]$. The membership degree indicates the degree to which each element in the set belongs to the set6 and Bellman and Zadeh (1970) proposed this idea in their seminal paper; please see Appendix C.1 for a complete definition. In this paper, the fuzzy set $\stackrel{\sim }{F}$ reflects the attending surgeon's uncertainty about whether a patient needs ICU care after a surgery.

Nevertheless, hospital managers still need to convert fuzzy sets into definite sets according to their attitudes toward risks in order to create surgical schedules. Specifically, let $A=F_{\lambda }$ denote the $\lambda$-cut set of $\stackrel{\sim }{F}$, where $\lambda$-cut set of a fuzzy number $\stackrel{\sim }{F}$ is defined as $F_{\lambda }=\left\{x\in \mathrm{\Omega }|{\mu }_{\stackrel{\sim }{F}}\ge \lambda \right\}$. Here, $\lambda$ represents the risk coefficient of the decision-maker's assessment of ICU needs. Then, the decision-maker gets a definite set $A$ of ICU requirements which determines $D_i^U$ through the following relationships:

$$\sum _{i=1}^N{H}_i^I{D}_i^U\text{=}{A}_v,\forall v=1,2,...,|A|,$$

$$D_i^U⩽1,\forall i.$$

Based on the crisp model and the operation rules of triangular fuzzy numbers,7 we can establish the fuzzy model (FM) below. Note that constraints (23), (28), and (29) jointly represent constraints (2), (3), (4), (9), (10), (11), and (12), (13), (14) in the original formulation, respectively.

$$\text{Min}\sum _{i=1}^N{u}_i^T{\mathrm{\Delta }}_i^T\text{+}\sum _{d=1}^D\sum _{j=1}^J{u}_j^O{\stackrel{\sim }{\mathrm{\Delta }}}_{\mathit{dj}}^O\text{+}\sum _{d=1}^D{u}^W{\stackrel{\sim }{\mathrm{\Delta }}}_d^W+\sum _{d=1}^D{u}^U{\stackrel{\sim }{\mathrm{\Delta }}}_d^U$$ (21)

Subject to:

$$\begin{array}{c}{\mathrm{\Delta }}_i^T=\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{H}_d^A{X}_{\mathit{idj}}^s+W_i^B\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s\hfill \\ +\theta ·D·\left(1-\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s\right),\forall i,\hfill \end{array}$$ (22)

$${\stackrel{\sim }{\mathrm{\Delta }}}_{\mathit{dj}}^O=\max \left\{\sum _{i=1}^N\sum _{s=1}^S{X}_{\mathit{idj}}^s{\stackrel{\sim }{L}}_i^S-T_{\mathit{dj}},0\right\}⩽M^O,\forall j,\forall d,$$ (23)

$$\left[\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s{H}_d^A+{\stackrel{\sim }{L}}_i^U\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s\right]D_i^U·Z_i^{}=\sum _{r=1}^{D+Q^U}{H}_e^E{N}_{\mathit{ir}}^U,\forall i,$$ (24)

$$\sum _{r=1}^{D+Q^U}{N}_{\mathit{ir}}^U⩽1,\forall i,$$ (25)

$$\left[\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s{H}_d^A+\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s\left({\stackrel{\sim }{L}}_i^W·\left(1-D_i^U\right)+D_i^U\right)\right]Z_i^{}=\sum _{e=1}^{D+Q^W}{H}_e^E{N}_{\mathit{ie}},\forall i,$$ (26)

$$\sum _{e=1}^{D+Q^W}{N}_{\mathit{ie}}⩽1,\forall i,$$ (27)

$${\stackrel{\sim }{\mathrm{\Delta }}}_d^W=\max \left\{\sum _{d^{\prime }=1}^d\sum _{i=1}^N\sum _{j=1}^J\sum _{s=1}^S{Z}_i^{}{X}_{i{d}^{\prime }j}^s-\sum _{e=1}^d\sum _{i=1}^N{N}_{\mathit{ie}}^{}-{\stackrel{\sim }{B}}^W-\sum _{d^{\prime }=1}^d{\stackrel{\sim }{R}}_{d^{\prime }}^W+\sum _{d^{\prime }=1}^d{\stackrel{\sim }{R}}_{d^{\prime }}^U+\sum _{r=1}^d\sum _{i=1}^N{N}_{\mathit{ir}}^U,0\right\}⩽M^B\forall d,$$ (28)

$${\stackrel{\sim }{\mathrm{\Delta }}}_d^U=\max \left\{\sum _{i=1}^I\sum _{j=1}^J\sum _{d^{\prime }=1}^d\sum _{s=1}^S{X}_{i{d}^{\prime }j}^s{D}_i^U-\sum _{r=1}^d\sum _{i=1}^N{N}_{\mathit{ir}}^U-{\stackrel{\sim }{B}}^U-\sum _{d^{\prime }=1}^d{\stackrel{\sim }{R}}_{d^{\prime }}^U,0\right\}⩽M^U,\forall d,$$ (29)

$$\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s⩽\sum _{s=1}^S{\beta }_{\mathit{sd}}^{},\forall i,\forall d\text{=}1,...,D,$$ (30)

$$\sum _{j=1}^J\sum _{i=1}^N{X}_{\mathit{idj}}^s{\stackrel{\sim }{L}}_i^S{\beta }_{\mathit{sd}}⩽K_{\mathit{sd}},\forall s,\forall d\text{=}1,...,D,$$ (31)

$$\sum _{d=1}^{D{\text{ue}}_i}\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s=1,\forall i,$$ (32)

$$\sum _{d=1}^{D^{\prime }}\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s=1,\forall i,$$ (33)

$$\sum _{d=1}^{D^{\prime }}\sum _{j=1}^J{X}_{\mathit{idj}}^s=Y_{\mathit{is}},\forall i,s,$$ (34)

$$\sum _{i=1}^N{H}_i^I{D}_i^U\text{=}{A}_v,\forall v=1,2,...,|A|,$$ (35)

$$D_i^U⩽1,\forall i=1,2,...,N.$$ (36)

4. Solution approach

Given that the fuzzy model cannot be solved directly by a solver, we first transform the fuzzy model into a tractable mixed-integer programming (MIP) model, and then propose a hybrid heuristic algorithm for the large-scale problems to reduce the solving time. The solver can be applied to small-scale problems, such as small hospitals or single departments, because its solution process is stable, fast, and convenient. The hybrid heuristic algorithm can be applied to large-scale problems, such as large hospitals, because its solution can be achieved in an acceptable time. Specifically, since fuzzy models can’t be solved directly using commercially available solvers (e.g., AIMMS, CPLEX, Gurobi), we provide two approaches. In Section 4.1, we transform the fuzzy model (FM) into an equivalent crisp model (FECM) and use a solver (CPLEX) to solve it. This transformation is required as the fuzzy models cannot be easily converted to an equivalent MIP model that can be solved using a commercial solver such as CPLEX; moreover, this approach is also useful when employing general meta-heuristics such as GA and DE. In our second approach in Section 4.2, we provide a heuristic algorithm based on an evolutionary algorithm and employ the proposed algorithm to obtain a satisfactory solution in a short time. The advantage of the transformation approach is that the resulting FECM can be solved directly to get accurate results utilizing an existing solver. However, the solution time will increase exponentially with the solution scale as surgical scheduling is an NP-hard problem (Denton et al., 2010, Gul et al., 2015). In addition, the process of transforming the FM into a FECM increases the complexity of the model. Nevertheless, this approach works well when 1) the planning horizon is long, 2) the problem scale is not too large, and 3) the model solution time requirement is low and produces very accurate results. The heuristic approach overcomes most of the disadvantages of the first method. In particular, the heuristic approach suits scenarios where the problem is large in scale and time-sensitive. This approach can be very useful in highly uncertain environments as shorter planning horizons and faster solution times are essential in such environments in order to enhance the adaptability of the models.

4.1. Transformation of the fuzzy model

We employ a transformation method proposed by Jiménez et al.(2007) to transform FM into a FECM. In our approach, we first transform FM into a FECM and then further linearize it.

First, we define the transformation approach and provide some background information. Consider the following fuzzy model:

$$\text{Min}z={\stackrel{\sim }{c}}^{T}x$$

$$\text{subject}\text{to}x\in N(\stackrel{\sim }{A},\stackrel{\sim }{b})=\left\{x\in R^n\left|{\stackrel{\sim }{a}}_{i}x⩾{\stackrel{\sim }{b}}_i,i=1,2,...,m,x⩾0\right)\right\}$$

where $\stackrel{\sim }{c}=({\stackrel{\sim }{c}}_1,{\stackrel{\sim }{c}}_2,...,{\stackrel{\sim }{c}}_n)$, $\stackrel{\sim }{A}={\left[{\stackrel{\sim }{a}}_{\mathit{ij}}\right]}_{m\times n}$, $\stackrel{\sim }{b}=({\stackrel{\sim }{b}}_1,{\stackrel{\sim }{b}}_1,...,{\stackrel{\sim }{b}}_n)$ represent, respectively, fuzzy parameters involved in the objective function and constraints. Then, the equivalent crisp (non-fuzzy) model can be written as follows:

$$\text{Min}EV(\stackrel{\sim }{c})x$$

$$\text{subject}\text{to}[(1-\alpha )E_2^{a_i}+\alpha E_1^{a_i}]x⩾\alpha E_2^{b_i}+(1-\alpha )E_1^{b_i},i=1,2,...,m,x⩾0,\alpha \in [0,1]$$ (37)

where $\alpha$ represents the degree that, at least, all the constraints are satisfied; that is, $\alpha$ is the feasibility degree of a decision $x$; the expected value of a fuzzy number, $\mathit{EV}(\stackrel{\sim }{c})$, is the halfway point of its expected interval, $\mathit{EI}(\stackrel{\sim }{c})$ (Heilpern, 1992). Specifically, we have

$$\mathit{EV}({\stackrel{\sim }{c}}_i)=\frac{E_1^{c_i}+E_2^{c_i}}{2}$$ (38)

$$\mathit{EI}({\stackrel{\sim }{c}}_i)=\left[E_1^{c_i},E_2^{c_i}\right]$$ (39)

where ${\stackrel{\sim }{c}}_i=\left(c_i^l,c_i^m,c_i^r\right)$,$E_1^{c_i}=\frac{1}{2}\left(c_i^l+c_i^m\right)$ and$E_2^{c_i}=\frac{1}{2}\left(c_i^m+c_i^r\right)$.

When (37) is a less than or equal ($\le$) type constraint, the crisp constraint can be written as follows:

$$[(1-\alpha )E_1^{a_i}+\alpha E_2^{a_i}]x⩽\alpha E_1^{b_i}+(1-\alpha )E_2^{b_i},i=1,2,...,m,x⩾0,\alpha \in [0,1]$$

Using the above specifications, the fuzzy model (FM) in Section 3.2 can be transformed into the FECM below; note that constraints in Equations (22), (25), (27), (30), and (31), (32), (33), (34), (35) are crisp (non-fuzzy) constraints, and therefore, we don’t have to transform them. Thus, we don’t repeat those constraints here.

$$\begin{array}{c}\text{Min}\sum _{i=1}^N{u}_i^T{\mathrm{\Delta }}_i^T\text{+}\sum _{d=1}^D\sum _{j=1}^J{u}_j^{O}EV\left({\stackrel{\sim }{\mathrm{\Delta }}}_{\mathit{dj}}^O\right)\hfill \\ +\sum _{d=1}^D{u}_{}^{W}EV\left({\stackrel{\sim }{\mathrm{\Delta }}}_d^W\right)+\sum _{d=1}^D{u}_{}^{U}EV\left({\stackrel{\sim }{\mathrm{\Delta }}}_d^U\right)\hfill \end{array}$$ (40)

subject to:

$$EV\left({\stackrel{\sim }{\mathrm{\Delta }}}_{\mathit{dj}}^O\right)=EV\left(\max \left\{\sum _{i=1}^N\sum _{s=1}^S{X}_{\mathit{idj}}^s{\stackrel{\sim }{L}}_i^S-T_{\mathit{dj}},0\right\}\right),\forall j,\forall d,$$ (41)

$$\sum _{i=1}^N\sum _{s=1}^S{X}_{\mathit{idj}}^s\left[\left(1-\alpha \right)\frac{L_i^{S_l}+L_i^{S_m}}{2}+\alpha \frac{L_i^{S_m}+L_i^{S_r}}{2}\right]-T_{\mathit{dj}}⩽M^O,\forall j,\forall d,$$ (42)

$$\left[\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s{H}_d^A+\left[\frac{1}{2}\frac{L_i^{U_l}+L_i^{U_m}}{2}+\frac{1}{2}\frac{L_i^{U_m}+L_i^{U_r}}{2}\right]\sum _{d=1}^D\sum _{j=1}^J{X}_{\mathit{idj}}\right]D_i^U·Z_i^{}=\sum _{r=1}^{D+Q^U}{H}_e^E{N}_{\mathit{ir}}^U,\forall i,$$ (43)

$$\begin{array}{c}\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{X}_{idj}^s{Z}_i^{}{H}_d^A\hfill \\ +\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{X}_{idj}^s{Z}_i^{}\left[\left[\frac{1}{2}\frac{L_i^{W_l}+L_i^{W_m}}{2}+\frac{1}{2}\frac{L_i^{W_m}+L_i^{W_r}}{2}\right]·\left(1-D_i^U\right)+D_i^U\right]\hfill \\ =\sum _{e=1}^{D+Q^W}{H}_e^E{N}_{ie},\forall i,\hfill \end{array}$$ (44)

$$EV\left({\stackrel{\sim }{\mathrm{\Delta }}}_d^W\right)=EV\left(\max \left\{\sum _{d^{\prime }=1}^d\sum _{i=1}^N\sum _{j=1}^J\sum _{s=1}^S{Z}_i^{}{X}_{i{d}^{\prime }j}^s-\sum _{e=1}^d\sum _{i=1}^N{N}_{\mathit{ie}}^{}-{\stackrel{\sim }{B}}^W-\sum _{d^{\prime }=1}^d{\stackrel{\sim }{R}}_{d^{\prime }}^W+\sum _{d^{\prime }=1}^d{\stackrel{\sim }{R}}_{d^{\prime }}^U+\sum _{r=1}^d\sum _{i=1}^N{N}_{\mathit{ir}}^U,0\right\}\right),\forall d,$$ (45)

$$\begin{gathered} \begin{array}{c}\sum _{d^{\text{'}}=1}^d\sum _{i=1}^N\sum _{j=1}^J\sum _{s=1}^S{Z}_i^{}{X}_{i{d}^{\text{'}}j}^s-\sum _{e=1}^d\sum _{i=1}^N{N}_{ie}^{}\\ \end{array} \\ -\left[\alpha \frac{B^{W_l}+B^{W_m}}{2}+\left(1-\alpha \right)\frac{B^{W_m}+B_{}^{W_r}}{2}\right] \\ -\sum _{d^{\text{'}}=1}^d\left[\alpha \frac{R_{d^{\text{'}}}^{W_l}+R_{d^{\text{'}}}^{W_m}}{2}+\left(1-\alpha \right)\frac{R_{d^{\text{'}}}^{W_m}+R_{d^{\text{'}}}^{W_r}}{2}\right] \\ +\sum _{d^{\text{'}}=1}^d\left[\left(1-\alpha \right)\frac{R_{d^{\text{'}}}^{U_l}+R_{d^{\text{'}}}^{U_m}}{2}+\alpha \frac{R_{d^{\text{'}}}^{U_m}+R_{d^{\text{'}}}^{U_r}}{2}\right]+\sum _{r=1}^d\sum _{i=1}^N{N}_{ir}^U⩽M^B,\forall d, \end{gathered}$$ (46)

$$EV\left({\stackrel{\sim }{\mathrm{\Delta }}}_d^U\right)=EV\left(\max \left\{\sum _{i=1}^I\sum _{j=1}^J\sum _{d^{\prime }=1}^d\sum _{s=1}^S{X}_{i{d}^{\prime }j}^s{D}_i^U-\sum _{r=1}^d\sum _{i=1}^N{N}_{\mathit{ir}}^U-{\stackrel{\sim }{B}}^U-\sum _{d^{\prime }=1}^d{\stackrel{\sim }{R}}_{d^{\prime }}^U,0\right\}\right),\forall d,$$ (47)

$$\begin{array}{c}\sum _{i=1}^I\sum _{j=1}^J\sum _{d^{\text{'}}=1}^d\sum _{s=1}^S{X}_{i{d}^{\text{'}}j}^s{D}_i^U-\sum _{r=1}^d\sum _{i=1}^N{N}_{\mathit{ir}}^U\\ -\left[\alpha \frac{B^{U_l}+B^{U_m}}{2}+\left(1-\alpha \right)\frac{B^{U_m}+B^{U_r}}{2}\right]\\ -\sum _{d^{\text{'}}=1}^d\left[\alpha \frac{R_{d^{\text{'}}}^{U_l}+R_{d^{\text{'}}}^{U_m}}{2}+\left(1-\alpha \right)\frac{R_{d^{\text{'}}}^{U_m}+R_{d^{\text{'}}}^{U_r}}{2}\right]⩽M^U,\forall d,\end{array}$$ (48)

$$\sum _{j=1}^J\sum _{i=1}^N\sum _{s=1}^S{X}_{\mathit{idj}}^s\left[\left(1-\alpha \right)\frac{L_i^{S_l}+L_i^{S_m}}{2}+\alpha \frac{L_i^{S_m}+L_i^{S_r}}{2}\right]{\beta }_{\mathit{sd}}⩽K_{\mathit{sd}},\forall s,\forall d.$$ (49)

In our formulation above, the objective and several constraints are not linear as the terms with $\mathit{EV}(·)$ are not linear. For example, $\mathit{EV}({\stackrel{\sim }{\mathrm{\Delta }}}_{\mathit{dj}}^O)$ given in Equation (41) is not linear. In order to linearize this, we introduce a crisp auxiliary variable ${\mathrm{\Phi }}_{\mathit{dj}}^O$, and change the related constraints as follows:

$${\mathrm{\Phi }}_{\mathit{dj}}^O⩾\sum _{i=1}^N\sum _{s=1}^S{X}_{\mathit{idj}}^s{\stackrel{\sim }{L}}_i^S-T_{\mathit{dj}},\forall j,\forall d,$$ (50)

$${\mathrm{\Phi }}_{\mathit{dj}}^O⩾0,\forall j,\forall d.$$

Then, we also have that $EV\left({\stackrel{\sim }{\mathrm{\Delta }}}_{\mathit{dj}}^O\right)=EV\left({\mathrm{\Phi }}_{\mathit{dj}}^O\right)={\mathrm{\Phi }}_{\mathit{dj}}^O,\forall j,\forall d$. Moreover, constraint (50) can be expressed as:

$${\mathrm{\Phi }}_{\mathit{dj}}^O⩾\sum _{i=1}^N\sum _{s=1}^S{X}_{\mathit{idj}}^s\left[\left(1-\alpha \right)\frac{L_i^{S_l}+L_i^{S_m}}{2}+\alpha \frac{L_i^{S_m}+L_i^{S_r}}{2}\right]-T_{\mathit{dj}},\forall j,\forall d.$$

Similarly, we can introduce crisp auxiliary variables ${\mathrm{\Phi }}_d^W$ and ${\mathrm{\Phi }}_d^U$ to linearize Equations (43), (45).

$$\begin{array}{c}{\mathrm{\Phi }}_d^W⩾\sum _{d^{\text{'}}=1}^d\sum _{i=1}^N\sum _{j=1}^J\sum _{s=1}^S{Z}_i^{}{X}_{i{d}^{\text{'}}j}^s-\sum _{e=1}^d\sum _{i=1}^N{N}_{\mathit{ie}}^{}\\ -\left[\alpha \frac{B^{W_l}+B^{W_m}}{2}+\left(1-\alpha \right)\frac{B^{W_m}+B^{W_r}}{2}\right]\\ -\sum _{d^{\text{'}}=1}^d\left[\alpha \frac{R_{d^{\text{'}}}^{W_l}+R_{d^{\text{'}}}^{W_m}}{2}+\left(1-\alpha \right)\frac{R_{d^{\text{'}}}^{W_m}+R_{d^{\text{'}}}^{W_r}}{2}\right]\\ +\sum _{d^{\text{'}}=1}^d\left[\left(1-\alpha \right)\frac{R_{d^{\text{'}}}^{U_l}+R_{d^{\text{'}}}^{U_m}}{2}+\alpha \frac{R_{d^{\text{'}}}^{U_m}+R_{d^{\text{'}}}^{U_r}}{2}\right]+\sum _{r=1}^d\sum _{i=1}^N{N}_{ir}^U,\forall d,\end{array}$$

$${\mathrm{\Phi }}_d^W⩾0,\forall d,$$

$$\begin{array}{c}{\mathrm{\Phi }}_d^U⩾\sum _{i=1}^I\sum _{j=1}^J\sum _{d^{\text{'}}=1}^d\sum _{s=1}^S{X}_{i{d}^{\text{'}}j}^s{D}_i^U-\sum _{r=1}^d\sum _{i=1}^N{N}_{\mathit{ir}}^U\\ -\left[\alpha \frac{B^{U_l}+B^{U_m}}{2}+\left(1-\alpha \right)\frac{B^{U_m}+B^{U_r}}{2}\right]\\ -\sum _{d^{\text{'}}=1}^d\left[\alpha \frac{R_{d^{\text{'}}}^{U_l}+R_{d^{\text{'}}}^{U_m}}{2}+\left(1-\alpha \right)\frac{R_{d^{\text{'}}}^{U_m}+R_{d^{\text{'}}}^{U_r}}{2}\right],\forall d,\end{array}$$

$${\mathrm{\Phi }}_d^U⩾0,\forall d.$$

A complete formulation of FECM after linearization is provided in Appendix D.

4.2. DE-OR algorithm

We propose a heuristic rule called OR-heuristic and combine it with the Differential Evolution (DE) algorithm to obtain a hybrid genetic algorithm which we call the ‘DE-OR’ algorithm.

4.2.1. Framework of DE-OR

Code: The chromosome $I$ consists of two substrings $\gamma$ and $\beta$, that represent the patient's OR allocation and surgery date allocation, i.e.,

$$I=\left(\begin{array}{c}\gamma \\ \beta \end{array}\right)=\left(\begin{array}{c}{o}_1,...,o_N\\ d_1,...,d_N,d_{N\text{+ 1}}\end{array}\right)$$

where $d_{N\text{+1}}$ is a dummy date, indicating that the patient has not been selected for surgery in the current decision period. For example, the OR of patient 1 is $o_1$, and the operation date of patient 5 is $d_5$.

Population Initialization: To improve the efficiency of the algorithm, we need to generate as many feasible solutions as possible. Here, we adopt a semi-random method based on heuristic rules. Specifically, we develop an OR-heuristic and then use it to generate the substring $\gamma$ of the chromosome $I$. A semi-random method is used to produce the substring $\beta$, taking into account the latest start date of the patient and the availability of the surgeon on a given day. The specific process is detailed in Algorithm 1.

Algorithm 1:Population Initialization
Input The latest date of the patient's operation $H$, the available date of the attending surgeon $P$, planning horizon $T$.  $m\leftarrow 0$  While $m$ not in $P$ do
for each $h\in H$ do   if $h\le T$ then    $m\leftarrow rand\left(1,h\right)$   else    $m\leftarrow rand\left(1,T+1\right)$
$n=OR\_heuristic(m)$
Output $[m,n]$

Fitness Function: Fitness function is defined as

$$H(s)=\left\{\begin{array}{cc}O(s),& \text{if}s\text{is feasible,}\\ C,& \text{otherwise,}\end{array}\right)$$

where $O(s)$ is the objective function and $C$ is a constraint penalty.

Crossover and Mutation: The algorithm generates the substring $\beta$ based on crossover and mutation, then generates $\gamma$ based on the OR-heuristic and $\beta$. The ‘crossover and mutation’ process is not completely random since we ensure that the feasible solution is still a feasible solution after each operation.

Population Diversification: We remove duplicate individuals from the population after each iteration, and then use Algorithm 1 to regenerate it.

More details on algorithms similar to the one above can be found in Storn and Price (1997).

4.2.2. OR-heuristic

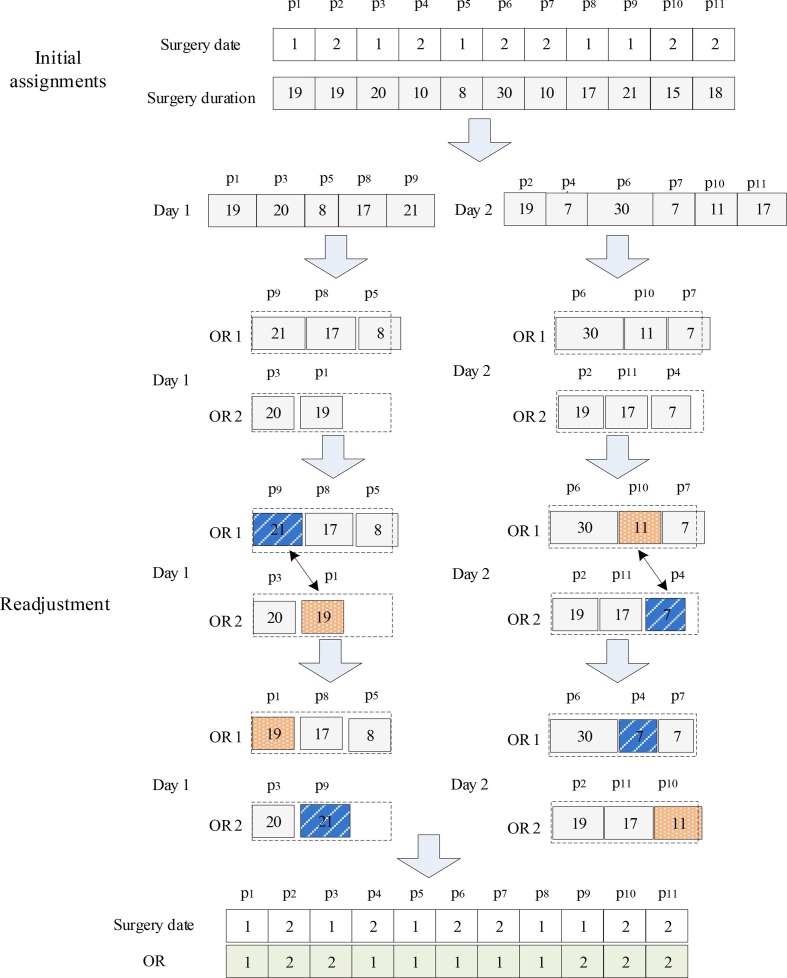
The algorithm includes an assignment operator and an adjust operator. To illustrate the process of the algorithm, we first present an example with 11 patients, 2 ORs with a maximum individual capacity of 45; see Fig. 4

Fig. 4.

Heuristics for OR allocation.

Assignment Operator: In the first step, the operator groups the patients according to the admission date, i.e., Day 1 and Day 2. For each group, the operator sorts the patients in descending order according to the surgery duration. Each patient is inserted sequentially into the freest OR until all patients obtain their OR; here, the patients are assigned to the OR with the highest availability first.

Adjust Operator: For each day, the operator calculates the surgery duration of each OR, and then selects the OR with the largest overtime (OR1 for Day 1) and the OR with the idlest time (OR2 for Day 1). Since the capacity of each OR is 45 units of time, the operator can calculate the timeout of OR1, which is $46-45=1$, and the idle time of OR2, which is $45-39=6$. The patient with the shortest surgery duration in OR2 is $p1$, and its surgery duration is 19. Using this, a threshold $L=19+1+6$ will be calculated. In the interval $[19,L]$, select the patient $p9$ with the largest surgery duration. Finally, exchange the ORs of patients $p1$ and $p9$. Repeat the above process until the patients on other days are also treated.

The algorithm process of OR assignment is summarized below.

Algorithm 2:$OR\_Assignment$
Input patient set $P$, patient's surgery duration $S$, patient's surgery date $D$, planning horizon $T$, operation room set R,   $\mathit{Pr}$, patients belonging to the operating room r   The $P$ is divided into sub-sets $P^1$, $P^2$, $P^{T+1}$, according to the surgery date $D$.   for $l\leftarrow 1$ to $T+1$ do    $P^l$ ← Sort in descending order ($P^l$)    for each $p\in P^l$ do     for each $r\in R$ do      $C_r$ ← Calculate the remaining capacity of operation room r     $r\leftarrow argmax\left(C_r\right)$     $O_p\leftarrow r$     $C_r\leftarrow C_r-S_p$    If $min\left(C_r\right)<0$ and $max\left(C_r\right)>0$ then     $r^{\mathit{min}}\leftarrow argmin\left(C_r\right)$     $r^{\mathit{max}}\leftarrow argmax\left(C_r\right)$     $p^m$ ← Find the patient with the smallest surgery time in $P^{r^{\mathit{max}}}$     $Y\leftarrow \left|min\left(C_r\right)\right|+max\left(C_r\right)+S_{p^m}$     $P^Y$ ← Patients whose surgery duration in $P^{r^{\mathit{min}}}$ is less than the threshold Y     $p^n$ ← The patient with the longest surgery duration in PY     L←$O_{p^n}$     $O_{p^n}$←$O_{p^m}$     $O_{p^m}$ ← L
Output $O$

We present several computational experiments to illustrate the efficacy of the DE-OR algorithm in the next section.

5. Computational experiments

For the contributions mentioned in this paper, we have carried out the verification one by one in the experimental part. The first part is the effectiveness of the fuzzy model, the second part is the verification of the proposed methods for resource shortage and uncertainty in the COVID-19 environment, and the last part is the effectiveness of the transformation method and heuristic algorithm. Specifically, in this section, we design three sets of experiments. First, the robustness and adaptability of the fuzzy model are tested in the first experiment when the data is limited, and the parameter distributions are unknown. The second experiment studies the adaptability of the fuzzy model for extreme circumstances with resource shortages and uncertain capacities such as COVID-19 environment. At last, the experiment is designed to verify the efficacy of the hybrid (DE-OR) algorithm and FECM.

Experimental Design:

Our experiments are designed using two decision-making environments in terms of the availability of data and information on underlying parameter distributions. In the first environment, it is assumed that neither data nor information on the underlying parameter distribution is available. We call this the ‘no decision-making information (No-Info)’ environment. The second environment assumes either data or information on the underlying parameter distribution is available. Thus, we call this the ‘given decision-making information (Given-Info)’ environment. Fig. 5 below depicts the two decision-making environments and data generation processes under each approach.

Fig. 5.

No-Info and Given-Info decision-making environments.

For the No-Info environment, it is required to obtain fuzzy numbers through expert (surgeon) estimates in order to solve the fuzzy model. However, since fuzzy data is not readily available, Behmanesh and Zandieh (2019) replicate the surgeon’s process of generating fuzzy data (by using crisp data) and generate fuzzy processing times $\left(t-u,t,t+u\right)$, where $u$ and $v$ were randomly approximated between intervals of 1 % to 30 % of the deterministic duration $\left(t\right)$. This approach has also been employed and validated recently by Wang et al. (2020), and thereby, we also adopt the same approach in this paper. In the Given-Info environment, since either fuzzy data or the underlying parameter distribution is available, we can simply utilize the fuzzy model or available stochastic optimization models to solve the problem. In particular, our numerical experiment adopts the data configuration proposed by Min and Yih (2010), where surgical patients are considered under 9 groups, namely, ENT, OBGYN, ORTHO, NEURO, GEN, OPHTH, VASCULAR, CARDIAC, and UROLOGY. Table B.1 in Appendix B provides a summary of descriptive statistics for these 9 groups. Moreover, to test the performance of the model, we divide the history records into two subsets. The first subset is called the training set, which serves as the input to the model, and the second subset is called the test set, which is used for performance evaluation. Finally, our algorithm was programmed in Python, and executed on a 3.7 GHz Intel Core i7 CPU computer with 16 GB memory using solver CPLEX within the Python docplex package for the MIP model.

Regarding the impact of the number of operations on the model, we tested the performance under different numbers of operating rooms. Although we assume operating rooms are homogeneous for simplicity, our model can be adapted to situations with different operating room types. Since the surgeons have different skills or experience, the same operation could have different surgery duration under different surgeons; therefore, we express the surgery duration of each patient as a different fuzzy number. Moreover, it is assumed that the ratio of surgeons to patients is 1:4. In addition, since the priority of the patient is related to the patient’s condition, we set different unit waiting costs to capture this important heterogeneity in our model; nevertheless, within each class and feasible range, waiting costs are generated randomly between two bounds. The differences in the surgical needs are reflected in the matching of patients and surgeons, as well as differences in surgery duration. We consider non-elective surgery as an external uncertainty and express it as a fuzzy number based on expert experience. Moreover, we do not consider temporary cancellations of patients as cancellations are rare.

Different studies in the literature have set the unit overtime cost according to the actual operating conditions of the related hospital. For example, Gul et al. (2015) set the operation unit overtime cost to $13/min. The main part of the downstream hospitalization cost is the cost of care. Izady and Israa (2021) use the cost of human resources to represent the cost of care. Following their approach, considering the human resource cost of the actual hospital, we set the bed shortage cost to $100. It may not be possible to know the true value of the patient waiting cost as it is highly dependent on individuals. In this study, based on the information that we gathered during our interviews with the hospital officials, we set the unit waiting cost of patients to be a randomly generated number between $70 to $80. Several other studies have employed similar estimates in the literature; for example, Gul et al. (2015) regard waiting costs as a punishment and employ a spectrum of daily waiting costs between two bounds.8 Table 4 summarizes our model parameters.

Table 4.

Model parameters.

Planning horizon ($D$)	one week
Unit overtime cost per operating room ($u_j^O$).	$Rand\left(10,16\right)$
Unit cost per optional extra inpatient bed ($u^W$).	100
Unit cost per optional extra ICU bed ($u^U$).	500
Unit waiting cost of patient $i$ ($u_i^T$).	$Rand\left(70,80\right)$
Upper-bound for daily overtime hours of each OR ($M^O$).	3 h
Upper-bound on extra inpatient beds for each day ($M^B$).	2
Upper-bound on extra ICU beds for each day ($M^U$).	2
Open duration of ${\mathit{OR}}_j$ on day $d$ ($T_{\mathit{dj}}$).	8 h
Maximum working time of surgeons $s$ on day $d$ ($K_{\mathit{sd}}$).	11 h
The latest date of the surgery of patient $i$ (${\mathit{Due}}_i$).	$Rand\left(1,2D\right)$
Total waiting days of patient $i$ before the beginning of the current planning horizon ($W_i^B$).	$Rand\left(0,D\right)$
Penalty coefficient of waiting time for patients deferred to the next planning horizon ($\theta$).	1–10
The feasibility of decision vector ($\alpha$).	0.6
Risk coefficient of the decision-maker's assessment of ICU needs ($\lambda$).	0.6

Note: For $a<b$, $Rand\left(a,b\right)$ denotes a randomly generated number from the uniform distribution over $(a,b)$.

5.1. Robustness and adaptability of the fuzzy model

Mulvey et al. (1995) describe robustness as the robustness of the model as well as the solution. A robust model should be less sensitive against modifications while the number of violated constraints should be minimized under a more robust solution; a model that possesses both of these characteristics can be thought of as an adaptable model. This notion of robustness has also been employed in Gorissen et al. (2015) as a performance measure of robustness. Therefore, we use the following formulas to describe the performance and robustness of our model:

$$\mathit{ob}:=\frac{1}{N}\times \sum _{n=1}^{N}o{b}_n;$$

$$\mathit{cons}:=\frac{1}{N}\times \sum _{n=1}^N\mathit{consnu}{m}_n,$$

where $n$ is the problem index in the simulation experiment, $o{b}_n$ is the objective value under the solution in the simulation experiment, and ${\mathit{consnum}}_n$ represents the number of times wherein the current scheduling solution exceeds the maximum capacity limit in the simulation environment. For example, consider a scheduling plan derived from the model for a 5-day working schedule with 2 operating rooms. For this plan, if a realization in the simulation environment produces OR overtime numbers of {190, 170, 160, 120, 170, 150, 120, 110, 130, 170}, then the number of times the OR capacity exceeds the limit ($M^O=180$) is 1. When the number of extra inpatient beds per day is $\{0,3,1,2,3\}$, the number of times it exceeds the capacity limit ($M^B=2$) is 2. Moreover, if the number of extra ICU beds per day is given by {$1,1,0,2,3\}$, then the number of times it exceeds the capacity limit ($M^U=2$) is 1. Thus, the total number of violations is ${\mathit{consnum}}_n=1+2+1=4$. Consequently, $\mathit{cons}$ reflects the adaptability of the solution scheme and represents the robustness of the model.

We next evaluate the performance and robustness of the fuzzy model by comparing it with several crisp (non-fuzzy) models. Following Lee et al. (2014), we set the modal point (MODE), center (CNE), lower bound (LS), and upper bound (US) of the support set of a TFN as the parameter values of the crisp models as shown in Fig. 6 . In Fig. 6, $m$ represents the degree of membership, and $x$ represents the elements in the TFN. It must be noted that all the models are solved using the DE-OR algorithm since it is suitable for both the fuzzy and crisp models.

Fig. 6.

Parameters of the crisp models.

As shown in Table 5 and Fig. 7 , not only FECM method consistently produces the lowest ob values but also generates very robust solutions as indicated by cons. While US is the only model that outperforms the FECM model in terms of ‘cons’, this model produces inferior ob values to the FECM model. Consequently, the scheduling scheme of FECM can adapt to an uncertain environment with high accuracy.

Table 5.

Simulation results of different models.

Problem	NP	LS		US		CNE		MODE		FECM
		ob	cons	ob	cons	ob	cons	ob	cons	ob	cons
1	18	9680	3.40	36,837	0.72	14,657	0.72	14,980	0.57	19,746	0.35
2	40	181,099	54.48	65,611	0.00	37,389	0.76	36,751	0.75	23,786	0.04
3	40	156,040	19.32	64,729	0.00	37,031	0.86	36,616	0.86	24,190	0.12
4	40	149,329	6.98	71,244	0.00	37,218	1.10	36,413	1.10	27,142	0.28
5	48	220,909	80.69	101,706	0.00	48,174	2.50	47,067	1.00	45,891	0.46
6	48	197,943	50.64	99,693	0.00	45,787	0.87	46,570	0.92	44,902	0.62
7	70	282,255	36.08	161,099	0.00	66,490	2.21	65,218	15.96	73,562	3.64
8	70	321,212	217.06	148,628	0.00	64,339	1.24	67,221	1.88	61,376	1.03
9	80	376,338	582.96	146,433	0.00	78,151	2.26	80,024	12.22	53,096	1.18
10	80	320,126	216.28	141,464	0.00	77,179	9.32	74,284	1.42	53,523	3.72
11	90	421,228	180.66	194,405	0.00	92,297	3.65	87,300	2.02	80,405	0.82
12	90	392,636	177.58	184,652	0.00	93,593	3.00	89,831	2.37	76,180	0.80
13	100	417,802	85.32	174,112	0.00	98,398	2.06	101,064	4.04	72,653	1.52
14	100	408,013	62.93	171,656	0.24	101,501	2.10	103,263	3.60	73,222	3.02
15	110	413,234	178.20	166,377	0.00	108,109	28.16	109,685	24.94	70,319	0.80
16	110	415,357	211.67	161,410	0.00	104,783	6.71	102,108	7.26	67,775	4.14
17	120	454,517	108.00	212,156	0.02	122,262	7.80	125,478	5.06	84,835	2.42
18	120	480,787	192.48	201,256	0.00	126,226	3.50	126,174	6.75	86,661	3.22
19	150	532,588	100.98	281,970	0.02	158,976	7.42	155,041	7.68	121,713	4.96
20	150	482,209	87.21	176,132	0.02	147,631	19.94	154,943	12.49	89,149	0.57
Average		331,665	132.65	148,078	0.05	83,010	5.31	83,002	5.64	62,506	1.69

Fig. 7.

Simulation results of different models.

Stochastic optimization is a widely proven method that can effectively deal with uncertain environments. To prove the applicability of the fuzzy model, we compare it with the classical stochastic model. In addition, the comparison is to show that the fuzzy model can deal with the surgery schedule problems in environment both with data and without data. We compare the performance of the fuzzy model with a well-known stochastic model (SM) proposed by Min and Yih (2010) in this subsection. Min and Yih (2010) use the sample average approximation (SAA) to solve their model. For fairness of comparison, we only consider the uncertainty in SD, LOSW, and LOSI, while all other parameters are assumed to be known. Moreover, to highlight the benefits of the fuzzy model, we select small-scale problems in our experiments. Finally, note that an SM requires an environment with known data while the fuzzy model requires fuzzy data. Thus, we use the given data to generate fuzzy data by representing the patients’ SD, LOSW, and LOSI as TFN ${\stackrel{\sim }{L}}_i^{(.)}=(L_i^{{(.)}_l},L_i^{{(.)}_m},L_i^{{(.)}_r})$, where $L_i^{{(.)}_l}$, $L_i^{{(.)}_m}$, and $L_i^{{(.)}_r}$ respectively represent the lowest value, mean value, and maximum value of the respective parameter distribution.

As shown in Table 6 , the crisp model (CM) has relatively higher ob and cons, indicating that the CM solution leads to higher costs and the CM does not adapt to uncertain environments easily. While the SM is very robust and associated with smaller objective values for some test problems, when the number of patients exceeds a certain threshold, the solution can be very long under the SM. Moreover, we observe that the performance of FECM and SM are similar although the solution time under FECM is much shorter than that under SM. Finally, as the sample size increases, both the SAA-based SM and the FECM usually cannot produce optimal results within a reasonable time frame whereas the DE-OR-based FECM (FECM-I) method produces a satisfactory solution in a quick time.

Table 6.

Comparison of CM, SM and FECM.

Problem	NP	CM				SM				FECM				FECM-I
		ob	cons	T		ob	cons	T		ob	cons	T		ob	cons	T
1	16	12,995	0.21	0.11		9197	0.17	200		9253	2.24	0.12		8980	0.01	173
2	18	12,240	0.18	0.08		8246	0.02	137		8118	0.01	0.08		8007	0	170
3	20	12,142	0.15	0.23		9518	0.04	454		9835	0.1	0.11		9386	0.01	176
4	25	20,846	0.22	0.45		15,163	0.03	>36 k		14,868	0.02	0.5		14,783	0.02	181
5	30	25,340	2.63	0.14		14,523	0.21	>36 k		14,726	0.07	1.84		15,094	0.03	188
6	35	36,783	0.73	2.47		23,806	0.15	>36 k		22,164	0.06	8.55		21,049	0.04	195
7	40	37,949	0.8	>36 k		25,267	0.17	>36 k		24,335	0.04	>36 k		24,752	0.08	199
8	48	60,732	1.81	>36 k		84,733	0.03	>36 k		55,285	1.3	>36 k		61,390	3.81	212
9	60	61,629	1.26	>36 k		44,509	0.28	>36 k		41,819	0.26	>36 k		42,734	0.9	311

Note: CM and FECM are solved by CPLEX; SM is solved by SAA; FECM-I is the model FECM solved by DE-OR.

According to the above experimental results, the adaptability of the fuzzy model to the uncertain environment is not much different from that of the stochastic optimization model. In comparison with the stochastic optimization model, the fuzzy model has a lower solution time complexity and requires a shorter solution time, thereby increasing the responsiveness of the model in an uncertain environment. Finally, it must be reiterated that fuzzy models are mainly suitable for uncertain environments with unknown parameter distributions. One of the main advantages of the fuzzy approach over stochastic programming is that the uncertain parameters do not have to follow any statistical distribution.

5.2. Adaptability of the fuzzy model for uncertainty during COVID-19 pandemic

In an uncertain environment, not only the patient’s SD, LOSW, and LOSI are uncertain, but also the available resources are highly uncertain. In particular, amid the pandemic outbreaks such as COVID-19, ICU resources become scarce. In this subsection, we focus on the adaptability of models when ICC and ICD are uncertain. To reduce the interference of the uncertainty of SD, LOSW, and LOSI in our findings, it is assumed that these parameters are given. Moreover, two separate sets of experiments are designed to study the effects due to uncertainty in each ICD and ICC. Specifically, Experiments 1 and 2 respectively consider the uncertainty in ICC and ICD while keeping the other component fixed.

In Experiment 1, we select the traditional ICU bed assessment policy for comparison, where the decision-makers use a certain percentage of surgical patients as the estimated number of patients who need ICU care after the surgery; these percentages are denoted by RT in Table 7 . Moreover, we set $\mathit{NP}=70$ and $\mathit{NR}=4$. For the estimation of the capacity parameters of the fuzzy model, we use the following three levels: $L1=(6,12,15)$, $L2=(16,20,30)$, and $L3=(30,35,40)$. In the experiment, different from the input data of the model earlier, the simulation data simulates the ICC when the actual plan is executed, whereas the earlier model estimates ICC before the plan is implemented. For our simulation data, ICC is randomly generated from the support of the fuzzy number (between LS and US) in the simulation environment; thus, we denote it by S $B$, and consider the following three value ranges: $S1=[6,15]$, $S2=[16,30]$, and $S3=[30,40]$. The results of the experiment are given in Table 7 below, where $B^U$ represents the estimated number of available ICU beds in CM, ${\stackrel{\sim }{B}}^U$ represents the estimated fuzzy number of available ICU beds in FECM, WC denotes the waiting cost of all patients, IC denotes the extra ICU bed cost of all patients, and TC is calculated by adding WC and IC. WC and IC are the sub-objectives of the proposed model. We chose these evaluation criteria since the uncertainty of ICC and ICD mainly affects the admission, i.e., patient waiting time and extra ICU bed demand.

Table 7.

Performance of FECM and CM under the uncertainty in ICC.

$\mathit{RT}$	$B^U$	${\stackrel{\sim }{B}}^U$	$\mathit{SB}$	CM				FECM
				WC	IC	TC		WC	IC	TC
0.1	7	L1	S1	33,700	745	34,445		32,940	821	33,761
0.1	7	L2	S2	35,000	0	35,000		28,500	0	28,605
0.1	7	L3	S3	34,040	0	34,040		27,500	0	27,515
0.3	21	L1	S1	27,640	10,914	38,599		32,940	3030	35,970
0.3	21	L2	S2	31,320	0	31,380		31,860	0	31,905
0.3	21	L3	S3	27,940	0	28,000		28,220	0	28,220
0.5	35	L1	S1	29,040	9286	38,431		35,280	855	36,135
0.5	35	L2	S2	27,680	0	27,695		28,240	0	28,240
0.5	35	L3	S3	29,900	0	29,900		30,380	0	30,380
0.7	49	L1	S1	30,900	3014	34,064		36,680	203	36,883
0.7	49	L2	S2	29,300	2	29,302		29,860	0	29,860
0.7	49	L3	S3	27,640	0	27,640		28,280	0	28,280
0.9	63	L1	S1	29,480	3155	32,725		34,860	67	34,927
0.9	63	L2	S2	28,500	0	28,710		28,880	0	28,880
0.9	63	L3	S3	30,020	0	30,155		30,000	0	30,000

Firstly, it is evident from our experiment that pessimistic ICC estimates by hospital managers can lead to a reduction in the number of scheduled elective surgeries, and thereby reduce or eliminate the cost of extra ICU beds; e.g., RT = 0.1, SB = S3, WC = 34,040, and IC = 0 in Table 7. In contrast, more optimistic estimates by the managers can lead to a higher number of scheduled surgeries; while this can reduce the patient waiting costs, it will lead to a serious shortage of ICU beds and increase the cost therein, e.g., RT = 0.9, SB = S1, WC = 29,480, and IC = 3155.

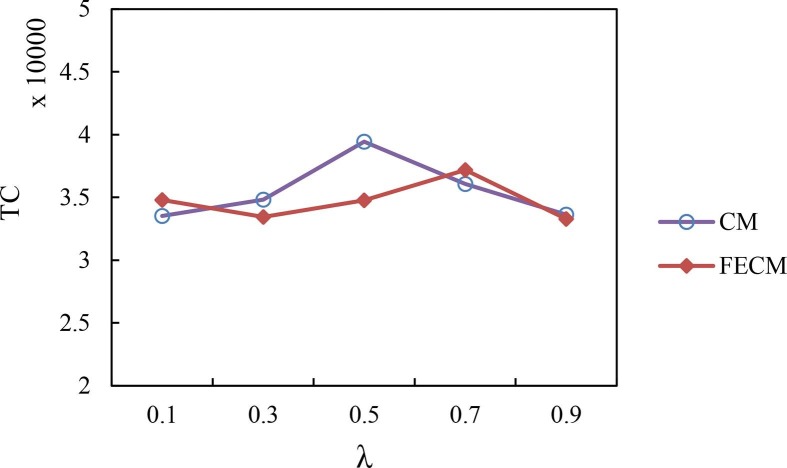
Fig. 8 compares the FECM method with the CM under small (S1), medium (S2), and large (S3) scale scenarios. As seen in Fig. 8, when the value of RT is small, i.e., approximately lower than 0.3, FECM clearly dominates CM while it is mostly very comparable with CM for other values of RT. Note that when RT > 0.3, the cost of CM and FECM looks similar because we have not calculated the fixed cost of beds. In fact, when RT > 0.3, the CM model needs to reserve a large number of bed resources, which is difficult to achieve in the resource shortage environment.

Fig. 8.

The total cost under models FECM and CM.

In Experiment 2, the ICD for CM is a randomly generated 0–1 sequence. Specifically, we first generate a random set ‘$\mathit{SS}$’ between [0,1]. For each element of $\mathit{SS}$, if it is greater than $\lambda$, then it is rounded up to 1, otherwise, it is rounded down to 0, then we get 0–1 set $S$. The ICD of the fuzzy model is crisp set $S$. The simulations are then carried forward using $\mathit{SS}=SS\ast (1\pm 0.3)$ in each step. Finally, the $\lambda$ defined in Section 3.2 represents the decision maker's assessment of ICD in FECM.

Fig. 9 and Table 8 depict $\mathit{TC}$, $\mathit{IC}$, and $\mathit{WC}$ as functions of $\lambda$. As seen in Fig. 9, when the hospital managers are more pessimistic as characterized by a smaller value of $\lambda$, it is less likely to exceed the ICU capacity. At the same time, the patients’ waiting costs are higher as expected. Interestingly, the total cost stays flat as a function of $\lambda$; thus, the model is not affected by the risk preference of the decision-maker and can be considered fairly robust. In addition, we found that only when the decision-maker is extremely conservative or extremely optimistic, FECM performs slightly worse than CM. Thus, our results suggest that a more moderate approach might be the best approach with fuzzy data.

Fig. 9.

Costs as a function of the preference coefficient ($\lambda$) of the decision-maker.

Table 8.

Performance of FECM and CM under the ICD uncertainty.

$\lambda$	CM			FECM
	WC	IC	TC	WC	IC	TC
0.1	29,400	4107	33,507	34,100	692	34,792
0.3	31,080	3746	34,826	33,280	164	33,444
0.5	32,620	6827	39,447	33,400	1363	34,763
0.7	32,100	3961	36,061	31,880	5292	37,172
0.9	30,560	3072	33,632	30,160	3132	33,292

5.3. Efficacy of the solution methods

In this section, we conduct extensive numerical experiments to demonstrate the efficacy of the transformation method and heuristic algorithm for the elective surgery scheduling problem.

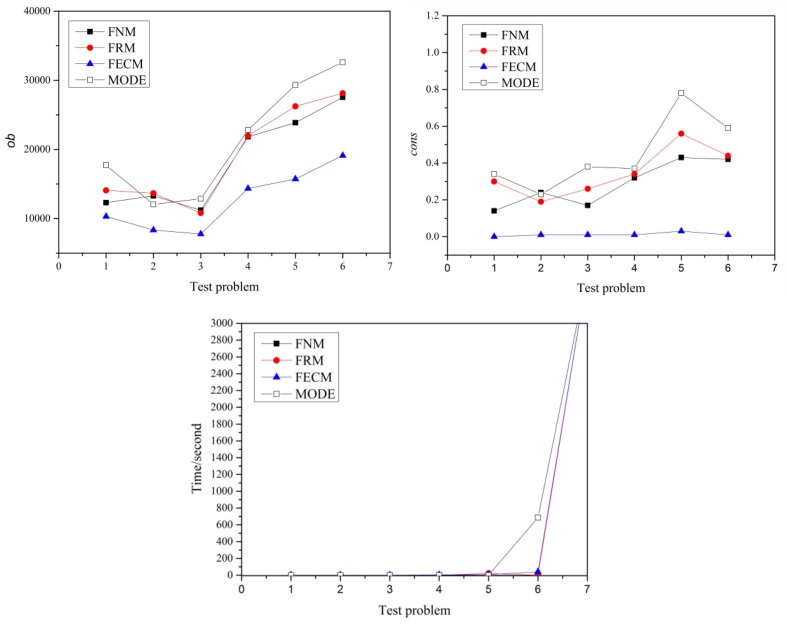
To further demonstrate the effectiveness of the transformation method, we compare the proposed crisp model (FECM) with other models by the same solver to avoid interference from the heuristic algorithm. We select Rodriguez’s and Niu’s models (Abdullah and Abdolrazzagh-Nezhad, 2014, Niu et al., 2008), two transformation models (named FRM and FNM in this paper), as our comparison models. In addition, the model MODE is also a comparison model. The experimental results are shown in Fig. 10 . For small-scale test problems 1–6, all the models can be solved within 800 s, but for large-scale problem 7, the solution times of all the models increase exponentially. Therefore, there is no significant difference in computational complexity between FECM and FRM, MODE for small-scale problems. On the other hand, FECM has a lower $\mathit{ob}$ and $\mathit{cons}$, indicating that it has better environmental adaptability. In addition, we found that the $\mathit{cons}$ of FECM are stable and do not change with the increase of the problem size, which shows that it has excellent robustness. On the contrary, MODE, FRM and FNM fluctuate considerably.

Fig. 10.

The comparison of model FECM and other transformation models.

The model MODE is a simplification of the fuzzy model according to fuzzy theory. For example, without loss of generality, the surgery duration of the fuzzy model is ${\stackrel{\sim }{L}}_i^S=(L_i^{S_l},L_i^{S_m},L_i^{S_r})$, while that of MODE is $L_i^{S_m}$ by assuming $L_i^{S_l}=L_i^{S_m}=L_i^{S_r}$. Therefore, the complexity of MODE is less than that of the fuzzy model. The experimental results show that there is no significant difference in the computational complexity between MODE and FECM, which indirectly proves that the complexity of FECM is not greater than that of the original fuzzy model.

For DE-OR algorithm, we have selected the following representative algorithms for comparison:

• •CPLEX: CPLEX optimization software package can be used to solve integer linear programming models CM and FECM and obtain accurate solutions for small-scale problems. However, this process could be time-consuming and may not produce optimal solutions for large-scale problems (Zhou, Geng, Jiang, & Wang, 2018)
• •GA: This is a standard genetic algorithm (Bonabeau et al., 1999), except that it uses the same initial population method as in DE-OR (to generate many feasible solutions); all other algorithms use the classic tournament selection, two-point crossover, and insertion mutation.
• •PSO-GA:Niu et al. (2008) proposed this hybrid particle swarm PSO-GA algorithm to solve the job-shop scheduling problem. Considering the similarity between surgery scheduling and job shop scheduling, we applied it to our problem for comparison.
• •DE: This is a standard Differential Evolution algorithm (Storn and Price, 1997), except that it uses the same initial population method as in DE-OR (to generate many feasible solutions).
• •FDE: This is an improved Differential Evolution algorithm (Tsafarakis, Zervoudakis, Andronikidis, & Altsitsiadis, 2020).
• •GA-VNS: This is a hybrid algorithm based on GA and variable neighborhood search (Wang et al., 2021).

Relative Percentage Deviation (RPD) has been used as a general performance indicator to evaluate the optimization effect of the algorithm. Since each algorithm needs $n$ runs, following Wang et al. (2018), we use the Average Relative Percentage Deviation (ARPD) defined below as the performance evaluation indicator:

$$\mathit{ARPD}=\frac{1}{n}\sum _{l=1}^n\frac{R_l^k-R_{\mathit{best}}}{R_{\mathit{best}}}\times 100$$

where $R_k$ represents the objective value of algorithm $k$, $R_{\mathit{best}}$ represents the objective value of the optimal solution, and $n$ represents the number of runs.

In our experiment, test problems 1–6 consider small-scale cases whereas problems 7–13 focus on large-scale cases. Table 9 and Fig. 11 present our experimental results for the small-scale cases, where NP, BU, BW, and NR respectively represent the number of the patients, the available number of ICU beds, the available number of inpatient beds, and the number of ORs; T and OB respectively denote the time to convergence in seconds and objective function value. In this case, CPLEX produces the optimal results ($R_{\mathit{best}}$) and thus, we can calculate the ARPD under each algorithm. As we noted above, one contribution of this study is to transform the fuzzy model into a simpler MIP model that can be handled directly using the commercial solver CPLEX, and this approach is also useful when employing general meta-heuristics such as GA and DE. As can be seen from Table 9, for small scales, our model can be solved quickly via CPLEX. In comparison, the meta-heuristic algorithm shows better stability. Moreover, compared with the classical heuristic algorithms GA, DE, and PSO-GA, the accuracy and speed of DE-OR are exceptional. By comparing the values of ‘ARPD’ and ‘T’ in Table 9 and Fig. 11, it is easily seen that the proposed DE-OR algorithm outperforms both classical heuristic algorithms GA and DE as well as the hybrid PSO-GA algorithm based on particle swarm and genetic algorithm. It should also be noted that the DE-OR algorithm produces solutions relatively quickly compared to PSO-GA, GA, and DE algorithms.

Table 9.

Comparison of experiment results under different algorithms (Small-scale case).

Problem	NP	BU	BW	NR	CPLEX		PSO-GA		GA		DE		DE-OR
					OB	T	ARPD	T	ARPD	T	ARPD	T	ARPD	T
1	18	1	6	2	13,075	0.16	0.38	291	22.56	309	22.56	289	0	281
2	40	4	40	2	13,901	12	4.86	333	6.29	370	4.55	334	0.89	324
3	40	4	35	2	13,950	2	7.81	336	4.3	372	3.76	334	1.19	324
4	40	4	30	2	14,025	8	6.95	336	4.91	371	4.81	335	2.14	324
5	48	4	45	2	18,375	323	5.25	348	5.27	387	5.14	349	1.77	340
6	48	4	40	2	18,551	2450	7.75	349	6.39	387	5.12	349	1.88	340

Fig. 11.

Comparison of experiment results under different algorithms (Small-scale case).

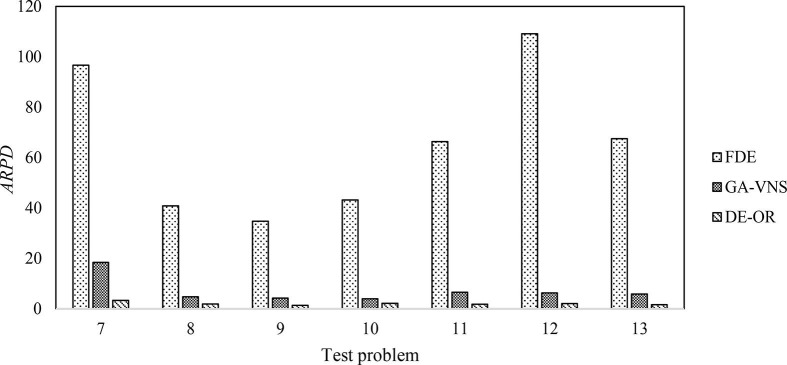
In order to minimize the selection bias in our comparison, we chose the most advanced ones such as FDE and GA-VNS. Furthermore, to prove the effectiveness of the algorithm in large-scale scenarios, we set up large-scale test cases. For the large-scale cases, CPLEX does not converge to the optimal solution in a reasonable amount of time even after increasing the value of the relative MIP gap tolerance to 0.1 (see values of ‘T’ under CPLEX in Table 10 ). Note that DE-OR has a significant advantage over solver (CPLEX) in terms of solution time when the problem scale is large and there is a shortage of resources such as ICU and inpatient beds (BU and BW). As we can see, the solution time in the CPLEX solver easily exceeds 10 h and this is not acceptable for a time-sensitive process such as surgery scheduling. In contrast, the DE-OR algorithm produces a satisfactory solution within 0–0.3 h even for large-scale cases. Finally, as shown in Fig. 12 , the DE-OR algorithm clearly dominates all other algorithms by producing a higher value for the ARPD.

Table 10.

Comparison of experiment results under different algorithms (Large-scale case). *Note: The test probems 7–13 are executed using 0.2, 0.11, 0, 0.14, 0.23, 0.19, and 0.33, respectively, as the value of the relative MIP gap tolerance.

Problem	NP	BU	BW	NR	CPLEX				FDE		GA-VNS		DE-OR
					OB		T*		ARPD	T	ARPD	T	ARPD	T
7	70	7	65	3	28,900		>36 k		96.64	732	18.43	616	3.3	548
8	70	7	55	3	28,868		>36 k		40.85	749	4.72	614	1.89	560
9	80	8	70	4	28,725		>36 k		34.73	891	4.18	715	1.31	669
10	80	8	60	4	28,575		>36 k		43.18	875	3.94	705	2.1	650
11	90	9	80	4	33,075		>36 k		66.29	1048	6.55	866	1.81	781
12	90	9	70	4	33,375		>36 k		109.13	1036	6.25	863	2.02	776
13	100	10	70	5	37,425		>36 k		67.46	1334	5.81	1102	1.6	981

Fig. 12.

Comparison of experiment results under different algorithms (Large-scale case).

6. Discussion and concluding remarks

We have studied the scheduling problem of elective surgeries as an uncertain system where the downstream includes both the ICU and ward. The proposed DE-OR algorithm is proven to be computationally efficient and more effective than the existing algorithms for the research problem in this paper. For example, the DE-OR algorithm outperforms both classical heuristic algorithms GA and DE as well as the hybrid PSO-GA algorithm based on particle swarm and genetic algorithms; moreover, when the problem scale is large and there is a shortage of resources such as ICU and inpatient beds, the DE-OR algorithm clearly dominates popular algorithms of CPLEX in terms of the solution time. The robustness and adaptability of the proposed fuzzy model and its solution via the algorithm DE-OR is shown to be superior to extant crisp heuristic methods such as modal point (MODE), center (CNE), lower bound (LS), upper bound (US). We have further shown that the solution time under FECM is much shorter than that under the SAA-based SM although the performance of FECM and SM are similar; moreover, our experiments show that while both the SAA-based SM and the FECM take a very long time to produce optimal results as the sample size increases, the optimal solution to the proposed FECM method can be computed relatively quickly using the DE-OR algorithm. Finally, we have also demonstrated the adaptability of the fuzzy model to scenarios with uncertainty in ICU demand and capacity as well as shortages in resources amid the pandemic such as COVID-19. The fuzzy method is based on expert experience and inference to describe the uncertain information of the surgical process. This method can be very useful when scheduling with uncertainties if historical data is insufficient or the existing medical environment undergoes major changes. Moreover, when an environment changes rapidly and the dynamic of the associated processes switches regimes, historical data can no longer predict future trends, and fuzzy models can be a solution for such scenarios.

In practical application, the solution time by the solver may be too long for large-scale problems. To make up for the defect of this practical application, we propose the algorithm DE-OR for our research problem, which can meet some environments with high requirements on scheduling time. The performance of the algorithm (DE-OR) is compared with different heuristic algorithms, yet DE-OR is highly customized for the specific model in the paper. Our future research will focus on the algorithm in more detail to further assess its superiority.

We have considered the initial state at the beginning of each planning horizon such as the initial waiting time of the patient and the availability of inpatient and ICU beds at the beginning and during a planning horizon. Thus, our formulation also facilitates replanning as the problem can be reformulated at any time for a given set of initial conditions. However, when the disturbances of the initial schedule get too large, the replanning problem needs a more rigorous treatment. While modeling the replanning horizon problem is beyond the scope of this paper, it will be an interesting and challenging problem for future research. Moreover, it should be noted that the hospital profit analysis may also include other costs such as the cost of empty wards and the cost of patients, surgeons, staff, operating room, etc. Although we have focused on fulfilling the patients’ surgery requirements while avoiding the risk of overloading due to insufficient resources, it will be interesting to see how one can incorporate other financial performance measures associated with surgeries in this setting as future research.

7. Data Availability

The datasets generated during and/or analyzed during the current study are available from the online materials alongside with this article.

CRediT authorship contribution statement

Zongli Dai: Investigation, Methodology, Software, Visualization, Writing – original draft. Sandun Perera: Investigation, Supervision, Writing – review & editing. Jian-Jun Wang: Conceptualization, Methodology, Funding acquisition, Project administration, Resources, Supervision, Writing – review & editing. Sachin Kumar Mangla: Writing – review & editing. Guo Li: Methodology, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A.

See Table A1

Table A1.

List of Abbreviations and Acronyms.

DE	Differential Evolution
DE-OR	Hybrid Genetic (algorithm)
FM	Fuzzy model
CM	Crisp(non-fuzzy) model
FECM	Equivalent crisp(non-fuzzy) model
ICU	Intensive Care Unit
SD	Surgery Duration
ICD	ICU Demands
ICC	Available ICU capacity
LOSI	Length of Stay (in ICU)
LOSW	Length of Stay (in the ward)
LS	Lower Bound (crisp model)
US	Upper bound (crisp model)
CNE	Center (crisp model)
MODE	Modal Point (crisp model)
OR	Operating Room
PACU	Post-Anesthesia Care Unit
PHU	Pre-operative Holding Unit
RO	Robust Optimization
SO	Stochastic Optimization
TFN	Triangular Fuzzy Number

Appendix B.

See Table B.1

Table B1.

The structure of test problems.

Surgical group	SD (minute)		LOSI (day)		LOSW (day)		Observations
	Mean	Standard deviation	Mean	Standard deviation	Mean	Standard deviation
ENT	74	37	0.1	0.1	3	1	788
OBGYN	86	40	2	2	2	2	342
ORTHO	107	44	1.5	1.5	1	2	859
NEURO	160	77	2	2	2	2	186
GEN	93	49	0.05	0.05	3	1	817
OPHTH	38	19	0.05	0.05	4	1	110
VASCULAR	120	61	3.5	3.5	5	2	303
CARDIAC	240	103	2	2	2	2	90
UROLOGY	64	52	0.8	0.8	6	1	198

Note:Min and Yih (2010) also generated SD and LOSI data using this approach.

Appendix C.1. Definition of a fuzzy set

Let $U$ be a classical set of objects, called the universe, whose generic elements are denoted by $x$, i.e., $U=\left\{x\right\}$. A fuzzy set $A$ in $U$ is characterized by a membership function ${\mu }_A(x)$, which associates each element in $U$ with a real number in $[0,1]$. A fuzzy set $A$is usually denoted by the set of pairs

$$A=\left\{\left(x,{\mu }_A\left(x\right)\right),x\in U\right\}$$

For example, for an ordinary set $A$,

$${\mu }_A\left(x\right)=\left\{\begin{array}{c}1,ifx\in A\\ 0,ifx\notin A\end{array}\right\}$$

When $U$ is a finite set such that $U=\left\{x_1,x_2,\cdots ,x_m\right\}$, a fuzzy set $A$ in $U$ can be represented as

$$A=\sum _{i=1}^n{x}_i/{\mu }_A\left(x_i\right)$$

Note that symbols ‘$\mathrm{\Sigma }$’ and symbol ‘/’ are not traditional summation and division symbols here.

Appendix C.2. Definition of triangle fuzzy number

If $T=\left(a^L,a^M,a^R\right)$, where $0\text{<}{a}^L⩽a^M⩽a^R$, T is called a triangular fuzzy number, and its membership function can be expressed as:

$${\mu }_A(x)=\left\{\begin{array}{cc}\frac{x-a^L}{a^M-a^L},& \text{if}{a}^L<x<a^M\\ \frac{x-a^R}{a^M-a^R},& \text{if}{a}^M<x<a^R\\ 0,& \text{otherwise}& \end{array}\right)$$

Appendix D.

$$\text{Min}\sum _{i=1}^N{u}_i^T{\mathrm{\Delta }}_i^T\text{+}\sum _{d=1}^D\sum _{j=1}^J{u}_j^O{\mathrm{\Phi }}_{\mathit{dj}}^O\text{+}\sum _{d=1}^D{u}_{}^W{\mathrm{\Phi }}_d^W+\sum _{d=1}^D{u}_{}^U{\mathrm{\Phi }}_d^U,$$

$${\mathrm{\Delta }}_i^T=\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{H}_d^A{X}_{\mathit{idj}}^s\text{+}{W}_i^B\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s+\theta ·D·\left(1-\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s\right)\text{,}\forall i,$$

$${\mathrm{\Phi }}_{\mathit{dj}}^O⩾\sum _{i=1}^N\sum _{s=1}^S{X}_{\mathit{idj}}^s\left[\left(1-\alpha \right)\frac{L_i^{S_l}+L_i^{S_m}}{2}+\alpha \frac{L_i^{S_m}+L_i^{S_r}}{2}\right]-T_{\mathit{dj}},\forall j,\forall d,$$

$${\mathrm{\Phi }}_{\mathit{dj}}^O⩾0,\forall j,\forall d,$$

$${\mathrm{\Phi }}_{\mathit{dj}}^O⩽M^O,\forall j,\forall d,$$

$$\left[\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s{H}_d^A+\left[\frac{1}{2}\frac{L_i^{U_l}+L_i^{U_m}}{2}+\frac{1}{2}\frac{L_i^{U_m}+L_i^{U_r}}{2}\right]\sum _{d=1}^D\sum _{j=1}^J{X}_{\mathit{idj}}\right]D_i^U·Z_i^{}=\sum _{r=1}^{D+Q^U}{H}_e^E{N}_{\mathit{ir}}^U,\forall i,$$

$$\sum _{r=1}^{D+Q^U}{N}_{\mathit{ir}}^U⩽1,\forall i,$$

$$\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s{Z}_i^{}{H}_d^A+\sum _{d=1}^D\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s{Z}_i^{}\left[\left[\frac{1}{2}\frac{L_i^{W_l}+L_i^{W_m}}{2}+\frac{1}{2}\frac{L_i^{W_m}+L_i^{W_r}}{2}\right]·\left(1-D_i^U\right)+D_i^U\right]=\sum _{e=1}^{D+Q^W}{H}_e^E{N}_{\mathit{ie}},\forall i,$$

$$\sum _{e=1}^{D+Q^W}{N}_{\mathit{ie}}⩽1,\forall i,$$

$$\begin{array}{c}{\mathrm{\Phi }}_d^W⩾\sum _{d^{\prime }=1}^d\sum _{i=1}^N\sum _{j=1}^J\sum _{s=1}^S{Z}_i^{}{X}_{i{d}^{\prime }j}^s-\sum _{e=1}^d\sum _{i=1}^N{N}_{\mathit{ie}}^{}-\left[\alpha \frac{B^{W_l}+B^{W_m}}{2}+\left(1-\alpha \right)\frac{B^{W_m}+B^{W_r}}{2}\right]-\sum _{d^{\prime }=1}^d\left[\alpha \frac{R_{d^{\prime }}^{W_l}+R_{d^{\prime }}^{W_m}}{2}+\left(1-\alpha \right)\frac{R_{d^{\prime }}^{W_m}+R_{d^{\prime }}^{W_r}}{2}\right]\hfill \\ +\sum _{d^{\prime }=1}^d\left[\left(1-\alpha \right)\frac{R_{d^{\prime }}^{U_l}+R_{d^{\prime }}^{U_m}}{2}+\alpha \frac{R_{d^{\prime }}^{U_m}+R_{d^{\prime }}^{U_r}}{2}\right]+\sum _{r=1}^d\sum _{i=1}^N{N}_{\mathit{ir}}^U,\forall d,\hfill \end{array}$$

$${\mathrm{\Phi }}_d^W⩾0,\forall d,$$

$${\mathrm{\Phi }}_d^W⩽M^B,\forall d,$$

$$\begin{array}{c}{\mathrm{\Phi }}_d^U⩾\sum _{i=1}^I\sum _{j=1}^J\sum _{d^{\prime }=1}^d\sum _{s=1}^S{X}_{i{d}^{\prime }j}^s{D}_i^U-\sum _{r=1}^d\sum _{i=1}^N{N}_{\mathit{ir}}^U-\left[\alpha \frac{B^{U_l}+B^{U_m}}{2}+\left(1-\alpha \right)\frac{B^{U_m}+B^{U_r}}{2}\right]\\ -\sum _{d^{\prime }=1}^d\left[\alpha \frac{R_{d^{\prime }}^{U_l}+R_{d^{\prime }}^{U_m}}{2}+\left(1-\alpha \right)\frac{R_{d^{\prime }}^{U_m}+R_{d^{\prime }}^{U_r}}{2}\right],\forall d,\end{array}$$

$${\mathrm{\Phi }}_d^U⩾0,\forall d,$$

$${\mathrm{\Phi }}_d^U⩽M^U,\forall d,$$

$$\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s⩽\sum _{s=1}^S{\beta }_{\mathit{sd}}^{},\forall i,\forall d,$$

$$\sum _{j=1}^J\sum _{i=1}^N\sum _{s=1}^S{X}_{\mathit{idj}}^s\left[\left(1-\alpha \right)\frac{L_i^{S_l}+L_i^{S_m}}{2}+\alpha \frac{L_i^{S_m}+L_i^{S_r}}{2}\right]{\beta }_{\mathit{sd}}⩽K_{\mathit{sd}},\forall s,\forall d,$$

$$\sum _{d=1}^{D{\text{ue}}_i}\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s=1,\forall i,$$

$$\sum _{d=1}^{D^{\prime }}\sum _{j=1}^J\sum _{s=1}^S{X}_{\mathit{idj}}^s=1,\forall i,$$

$$\sum _{d=1}^{D^{\prime }}\sum _{j=1}^J{X}_{\mathit{idj}}^s=Y_{\mathit{is}},\forall i,s,$$

$$\sum _{i=1}^N{H}_i^I{D}_i^U\text{=}{A}_v,\forall v=1,2,...,|A|,$$

$$D_i^U⩽1,\forall i.$$

Appendix F. Supplementary material

The following are the Supplementary data to this article:

Data availability

Data will be made available on request.