Abstract
What happens in the brain when we learn? Ever since the foundational work of Cajal, the field has made numerous discoveries as to how experience could change the structure and function of individual synapses. However, more recent advances have highlighted the need for understanding learning in terms of complex interactions between populations of neurons and synapses. How should one think about learning at such a macroscopic level? Here, we develop a conceptual framework to bridge the gap between the different scales at which learning operates––from synapses to neurons to behavior. Using this framework, we explore principles that guide sensorimotor learning across these scales, and set the stage for future experimental and theoretical work in the field.
Keywords: Neural population, sensorimotor learning, state space framework, neural plasticity, dimensionality, internal models
Toward a network perspective on biological learning
From infancy to adulthood, humans learn a staggeringly wide repertoire of behaviors. The secret to this remarkable capacity lies in how experience taps into the reservoir of computations that billions of interconnected cells in the brain can perform. Yet, understanding the logic behind learning in neural systems remains a formidable challenge in neuroscience.
The problem of learning has been largely framed through a bottom-up view that focuses on local plasticity mechanisms at the level of individual synapses. The idea that experience changes individual synapses originated in the work of Ramón y Cajal [1], was refined by models of Hebb [2], and found its earliest experimental evidence in animal studies of habituation, sensitization and classical conditioning [3–5]. This perspective has had a major impact on experimental and theoretical work. In experiments, it has led to an extensive body of knowledge about molecular mechanisms of synaptic plasticity [6], such as long-term potentiation [7] and spike-time dependent plasticity [8]. In theoretical work, it has led to the development of idealized learning rules [9,10] by which artificial neural networks learn associations and implement sophisticated input-output functions [11,12].
The allure of this bottom-up approach is that it has the potential to explain the causal path from individual synapses to neural activity to behavior. However, learning is an intrinsically multi-scale problem, which involves coordinated changes across millions of neurons and billions of synapses that collectively control behavior [13]. Therefore, it is essential to complement the classical microscopic characterization of plasticity mechanisms with a macroscopic perspective to shed light on the principles that coordinate changes across populations of synapses and between synapses and neurons. While there is a rich body of theoretical work on studying learning at such a macroscopic level [11,14–18], there is room for a wider adoption of this perspective for the analysis and interpretation of experimental data.
Why is this shift in perspective necessary to make progress on the question of learning? Consider, for instance, trying to explain the breadth of timescales at which learning can advance. We learn to operate a new coffee machine within seconds, we master a new clapping game over minutes, and we learn to bike over hours to days. How should one think about these timescales from the perspective of individual synapses? Are there distinct cellular mechanisms for each timescale? If so, how does the brain ‘know’ which ones to engage in a given context? Do all forms of learning even require synapses to change? With these open questions in mind, we think that the scope of research on the neurobiology of learning has to move toward network-level principles that more directly intersect with behavior. In this Opinion article, we use a state space framework to formulate the problem of learning across scales, from behavior to neurons to synaptic connections, and explore the computational principles that may guide learning at a macroscopic level [19–24]. Our hope is to highlight the value of using the state space framework for investigating principles of learning in biological systems, and to enrich ongoing conversations between theorists and experimentalists on this problem [25,26].
A state space framework to study sensorimotor learning
Consider a simple sensorimotor task of reaching for an apple. To do so, our brain must first transform the complex patterns of light impinging on our eyes (i.e., raw sensory input) to relevant latent sensory variables (see Glossary) such as the location and size of the apple. Latent sensory variables, in turn, should inform behaviorally-relevant latent motor variables such as which hand to use and how far to reach. Finally, the latent motor variables must drive the necessary patterns of muscle activations (i.e., final motor output) that let us interact with the environment.
For learning to occur, the process described above must operate as a closed loop; that is, the system has to sense the consequences of its actions and when necessary, make judicious internal adjustments. Where should learning tap into this multistage system? Early sensory stages (e.g., seeing objects) and late motor stages (e.g., moving limbs) serve a vast array of tasks, and are thus likely to have been optimized on a much longer timescale by evolution and/or development to perform general-purpose computations [27]. Here, we focus on the effects of learning on the intermediate stages, where computations over latent variables enable flexible adjustments of sensorimotor behaviors to different contexts and goals.
Converging evidence from animal studies suggest that task-relevant latent variables are represented by coordinated patterns of activity across large numbers of neurons that interact through even larger numbers of synapses [28–31]. In this view, learning must be considered as occurring through large-scale changes within a network of neurons and synapses. A useful conceptual framework to adopt this perspective is the state space framework [14,15,32,33]. A state space is a general multi-dimensional coordinate frame that jointly represents multiple variables in a system. A network of neurons can be characterized in terms of two complementary state spaces, the weight space and the activity space (Figure 1, Key Figure).
Figure 1. A state space framework to study sensorimotor learning at a network level.
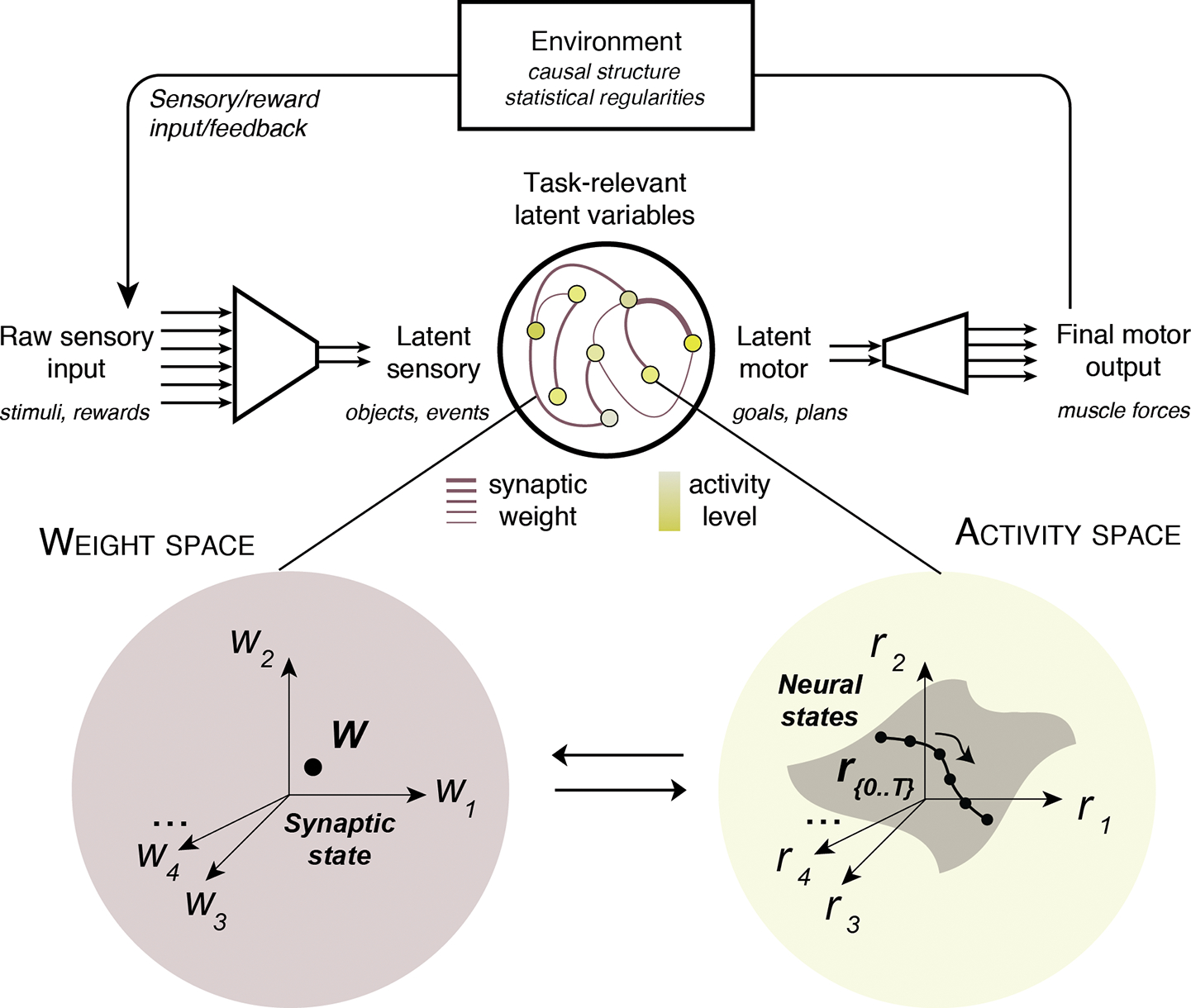
Sensorimotor tasks involve closed-loop interactions between the agent and the environment. The agent’s nervous system converts raw sensory inputs from the environment (e.g., sound waves entering the ear) into meaningful latent sensory variables (e.g., instructions). The agent has to use the latent sensory variables to compute task-relevant latent motor variables (e.g., a planned course of action) to control the final motor output (e.g., contracting the quadriceps). Finally, the agent senses the consequences of its actions based on environmental feedback (e.g., rewards, sensory outcomes). The agent’s sensorimotor system, depicted as a network of interacting neurons (middle), can be described at different scales in two interrelated state spaces. In the weight space (bottom left), each dimension (w1, w2, …) represents the strength of a synaptic connection between a pair of neurons in the network. A point in this space (i.e., synaptic state, w) defines the entire connectivity structure of the network. In the activity space (bottom right), each dimension (r1, r2, …) represents the activity of a single neuron in the network. A point in this space (i.e., neural state, r) jointly represents the activity of all the neurons in the network, and a collection of neural states (r{0,…,T}) depicts the changes in population activity over time. Both spaces are tightly connected: for instance, the synaptic state dictates the states that can be “visited” in the activity space under the current connectivity (‘neural manifold’ in grey).
The weight space is composed of multiple dimensions that represent the strength of individual synaptic connections between neurons. As such, a point in the weight space (i.e., synaptic state) corresponds to a set of synaptic weights which characterizes the synaptic architecture of the network. By contrast, the activity space is composed of multiple dimensions that correspond to the activity level of individual neurons. A point in the activity space (i.e., neural state) corresponds to a specific pattern of activity across the population at a given time point. A neural trajectory reflects the time-varying population dynamics in the activity space, and a neural manifold represents all the neural states that the network can reach for a given synaptic state [22,34,35]. Often, not all dimensions of the state space are explored during a given task, and the neural manifold usually occupies only a limited region of the space (subspace).
The weight space and the activity space are intimately related. On the one hand, the synaptic state in the weight space constrains neural trajectories in the activity space. This is because synaptic connections directly influence the activity patterns that a network of interconnected neurons can generate (e.g., if two neurons are directly connected, their activity will covary). On the other hand, the possible neural states occupied in the activity space can also constrain how the synaptic state evolves in the weight space, particularly during learning. This is exemplified by the well-known activity-dependent Hebbian plasticity rule (‘neurons that fire together wire together’).
The state space perspective provides an intuitive approach to understanding the network-level effects of learning: learning becomes the process of exploring and navigating different dimensions of the weight and/or activity space in search of a solution that ultimately leads to the desired behavioral outcome. It also provides a systematic way of interrogating the origins of the various timescales of learning observed in behavior. For instance, fast learning should be the result of an efficient search within these two state spaces. In the subsequent sections, we delve deeper into the general principles that might govern learning-dependent changes in the weight and activity spaces, and describe ways in which the search in these spaces might be facilitated during learning.
Learning in the weight space
Let us first consider the problem of learning in the weight space. In this space, the learning objective is to find a synaptic state that will allow the network to generate the desired behavior. What makes learning in the weight space challenging is the curse of dimensionality. Since even a small neural network in the brain can have millions of plastic synapses, achieving a desired behavior demands searching for a solution in an exceedingly large weight space. How does the brain solve this problem?
To address this question, experimental work has mainly focused on specific plasticity rules at the level of single synapses without regard to the collective changes that occur within a network of interconnected neurons, although progress is being made in that direction [13,24,36]. Therefore, it is unclear how synaptic plasticity mechanisms such as long-term potentiation [7], and spike-time dependent plasticity [8] guide the exploration in the weight space across a population of synapses.
To formalize the problem, let us depict moment-by-moment changes in the synaptic state within the weight space by a vector, ΔW (Figure 2, center). ΔW can be expressed in terms of a function, f, that we refer to as the learning policy. Within this framework, the effectiveness of a learning policy can be characterized in terms of the degree to which ΔW is chosen judiciously. The simplest learning policy is one that chooses ΔW randomly. This so-called random-walk strategy is highly inefficient and may never find a desirable solution. Therefore, it seems highly unlikely that such random walks would play a significant role in support of task-relevant learning.
Figure 2. General strategies for learning in the weight space.
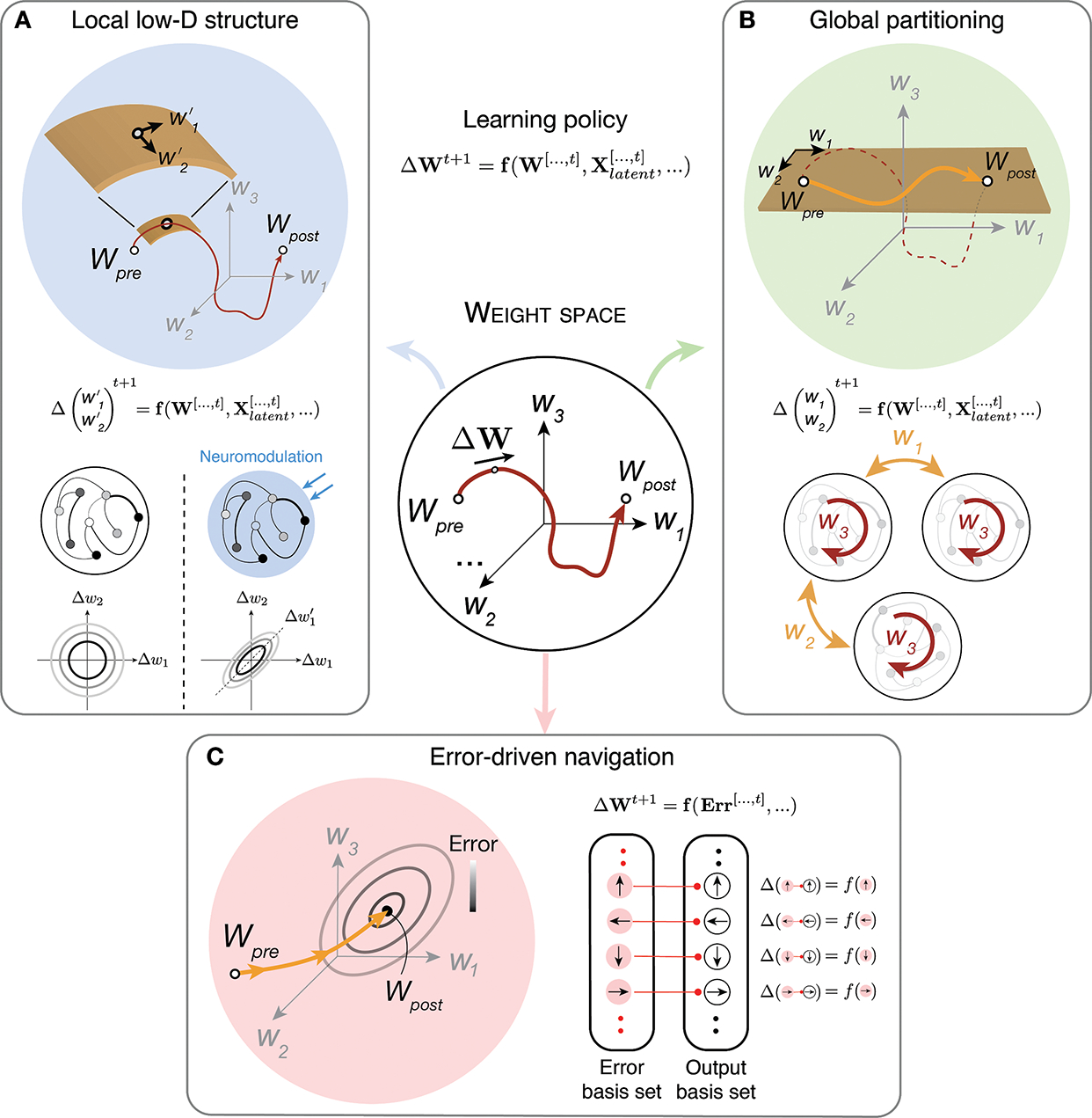
Synaptic learning in a network of neurons can be construed as a trajectory in the weight space (center; dark-red line from Wpre to Wpost). The instantaneous change in synaptic weight (ΔW) is governed by a ‘learning policy’ (top-middle equation), which is a function of the synaptic state history (W[…,t]), the latent sensory and motor state history (Xlatent[…,t]), and other task-irrelevant constraints. (A) The left box illustrates how a suitable learning policy could expedite learning by constraining synaptic changes to a manifold (left panel; dark orange curved plane) whose intrinsic dimensionality (e.g., a 2D plane [w′1, w′2]) is lower than that of the full weight space. This dimensionality reduction can be induced through neuromodulation or other physiological factors. In its simplest form, the dimensionality reduction can manifest itself as correlated changes across synaptic weights (left: baseline, right: under neuromodulation; ellipses illustrate positively correlated changes for two synaptic weights). (B) The right box illustrates how learning could be expedited by partitioning the weight space to lower-dimensional subspaces (light orange arrow over the dark orange plane composed of w1 and w2). This form of dimensionality reduction can be imposed by anatomical constraints. For example, the brain could take advantage of the hierarchical architecture of the sensorimotor system, and start the search within the low-dimensional subspace spanned by inter-areal connections (orange arrows with w1 and w2) before exploring the subspace associated intra-areal connections (dark-red arrow with w3). (C) Finally, the bottom panel illustrates a learning policy that makes explicit use of errors (Err[…,t]) to drive the synaptic state in an error-reducing direction (orange arrow; ellipses: iso-error contours; grayscale: colormap for error). This strategy can be implemented if the neurons that drive behavioral output (‘output basis set’) receive direct input (arrows within red circles) from another set of neurons (‘error basis set’) that are tuned to errors. When there is direct correspondence between these two sets of neurons, the errors can be reduced by weakening the synapses associated with active error-tuned neurons (i.e., activity-dependent plasticity).
At the other extreme are learning policies that choose ΔW optimally; that is, in the direction that maximally reduces behavioral errors. Doing so would require every synapse in the system to have direct information about behavioral errors (Figure 2C). This strategy is exemplified by the backpropagation algorithm used for training artificial neural networks [37,38] in which each synapse in the system is adjusted in the direction that would decrease the overall error. Ongoing research is exploring the possibility that the brain implements this algorithm, but the biological plausibility of this approach is debated since there are no known mechanisms for broadcasting behavioral errors to the entire system [25,39,40].
One possibility for implementing error-based synaptic learning is for the relevant brain circuits to possess a basis set for representing errors and use dedicated synapses to counter those errors. Certain lines of evidence support this possibility. For example, the cerebellum is thought to harbor such a basis set for sensorimotor errors and suitable plasticity mechanisms to reduce those errors [41–44], although the mechanistic origins of this process are the subject of active research [45].
In the absence of some form of error-based learning, the high dimensionality of the weight space would make synaptic learning extremely challenging. We envision three interrelated factors that could effectively reduce the dimensionality. First, physiological constraints could reduce the dimensionality of the learning policy. To explore the impact of such constraints, let us start by the general assumption that ΔW may depend on past neural states in the activity space (Xlatent[…,t], Figure 2, center). While we remain agnostic to the exact form of this dependence, we note that activity-dependent plasticity mechanisms such as various forms of Hebbian learning are widespread and well documented [6–8,36,46]. As we noted previously, mounting evidence suggests that task-relevant neural activity patterns supporting sensorimotor behavior are correlated and constrained to relatively low-dimensional manifolds [28–31,34]. Accordingly, ΔW associated with activity-dependent synaptic changes may be similarly low-dimensional (Figure 2A). Neuromodulatory mechanisms may also play a role in this form of dimensionality reduction [47,48]. For example, global dopamine release may act to coordinate plasticity across populations of synapses [49]. In other words, even though plasticity mechanisms operate locally and can be high-dimensional, correlated activity patterns across neurons and common neuromodulatory drive may induce correlations between synaptic changes. This view predicts the existence of ‘synaptic modes’ reminiscent of the ‘neural modes’ that have been observed in population dynamics in the activity space [34]. Accordingly, we think that one fruitful avenue of research is to characterize the structure of putative synaptic manifolds and characterize the learning policies that drive changes over those manifolds. This will inevitably require shifting the view of the experimentalist toward examining synaptic changes as part of a global, coordinated process. Progress in this direction will also require the advent of disruptive technologies that allow researchers to track the synaptic state of a network in vivo during learning.
Second, anatomical constraints that divide synapses into subpopulations can act to partition the weight space into lower-dimensional subspaces (Figure 2B). Partitioning the weight space could facilitate the search in different ways. For example, it would automatically reduce the dimensionality of the learning policy in each subspace. Learning could be further expedited if learning policies that operate at different timescales [46,50] take advantage of anatomically-defined hierarchies in the sensorimotor system. For example, in the cortex, learning could proceed through a cascade of adjustments starting from relatively sparse and low-dimensional inter-areal connections, and move progressively down the hierarchy to intra-areal microcircuits. Consistent with this idea, inter-areal connectivity patterns in cortico-cortical communications are often much sparser (lower-dimensional) than their intra-areal counterparts [51–53]. Moreover, recurrent interactions with other lower-dimensional subcortical nuclei such as the thalamus [54,55] could further contribute to the partitioning of the weight space.
Third, it seems unlikely that all plastic changes within the weight space play a role in task-relevant computations (i.e., support behavior). Indeed, theoretical considerations suggest that only a fraction of synaptic changes are directly responsible for task learning [56–58]. Other changes may be more important for homeostasis or other non-specific aspects of physiology. This possibility could further reduce the effective dimensionality during learning. Finally, recent analysis of task-optimized artificial neural networks suggest that the large dimensionality of weight space relative to task structure may somewhat counterintuitively facilitate learning by providing alternative solutions that can be reached from random initial conditions using low-dimensional synaptic subspaces [59].
Learning in the activity space
So far, we have focused on the weight space as the main substrate for learning. However, as we noted before, efficient learning in the weight space is challenging because synaptic states are two steps away from behavior; they control patterns of activity in the activity space, which ultimately control behavior. Therefore, adjustments in the weight space, especially those that are exploratory and not error-based, are unlikely to support rapid learning capacities that we possess––for example, adjusting movements to the tempo of a beat [60].
This raises an intriguing question; can the nervous system learn by making adjustments directly to the activity space without changing the synaptic state? At first glance, this seems implausible; how can a network of neurons behave differently if not for some change in connectivity? Recent theoretical and experimental work points toward one intriguing solution [28,29,61–64]. Although connectivity dictates the full range of behaviors a network can possibly generate, the specific activity patterns the network generates in a given context can be controlled by the inputs the network receives from other brain areas [Box 1]. The question therefore, is whether the system can generate suitable inputs to drive neural states toward the new desired state in the activity space without any change in network connectivity.
Box 1. Controlling neural activity via inputs or intrinsic connectivity.
To control the behavior of a network of neurons (e.g., during learning), two strategies can be used: first, synaptic connections between the neurons can change through plasticity to allow the network to modify its activity (Figure IB, bottom). Alternatively, the network may receive external inputs (e.g., from other parts of the brain) to alter its activity without changing the connectivity (Figure IB, top).
We use a curling analogy to illustrate how these two control strategies differ. In curling, the goal is to throw a sliding stone on a sheet of ice so that it stops as close to a target as possible. The trajectory of the stone depends on two parameters that are under control. First, throwing the stone more vigorously can make it slide further along the track (Figure IA, top). Second, sweeping the ice ahead of the stone’s path can heat up the surface and decrease friction forces to make the stone slide further (Figure IA, bottom). Giving the stone a larger impulse reflects a change in the input to the system, while modifying the ice properties is analogous to refining the intrinsic connectivity of the system.
The state space framework provides a concise explanation for these two learning strategies. Modifying the intrinsic connectivity corresponds to changing the synaptic state in the weight space. This in turn reshapes the neural manifold in the activity space, allowing the new desired state to be reached (Figure IB, bottom). The input-control strategy, in contrast, directly drives the neural state toward the desired state in the activity space (Figure IB, top). These two strategies offer varying degrees of flexibility for learning. Learning in the activity space via inputs is highly effective (as it does not require synaptic changes) but is limited in that target states must lie within the pre-existing neural manifold. By contrast, learning in the weight space requires (slower) synaptic changes, but can accommodate potentially any state in the activity space.
Figure I.
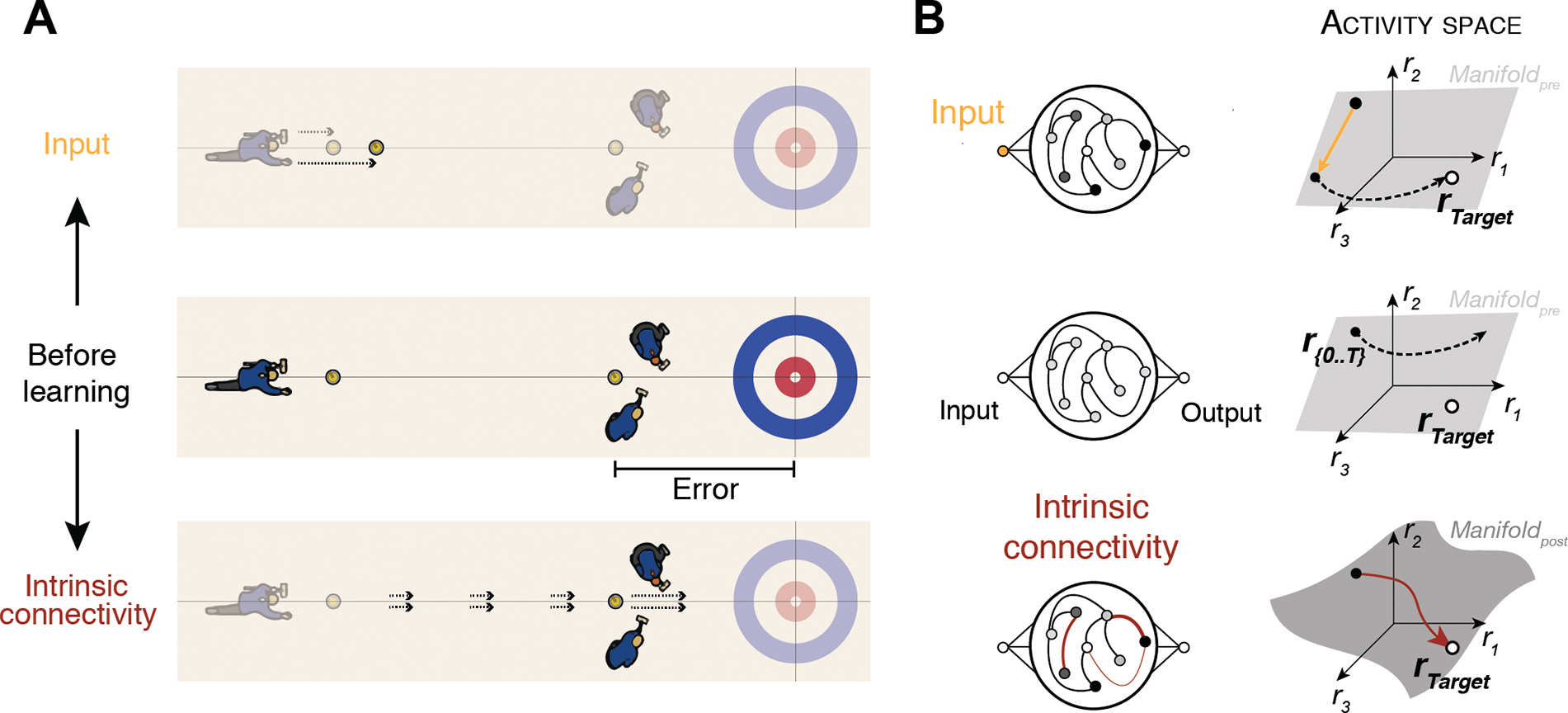
Curling analogy to illustrate control strategies in the state space framework.
How could the brain internally generate such ‘corrective’ inputs? Although this remains an open question [65], one possibility is that the brain relies on predictive signals to self-generate internal inputs from the feedback it receives. This learning strategy, originally formalized in the language of control theory [66], requires a few critical computational ingredients (Figure 3). First, the system needs to determine whether the sensory feedback signals an error. To do so, the system must have an internal model that predicts the expected sensory input based on what was intended. Second, the system must have a mechanism to quantify any discrepancy between the prediction and the observed outcome; that is, it must compute a prediction error (PE). Third, the system must be able to integrate and maintain PEs across trials to accommodate incremental learning. Finally, the system must convert the cumulative PE to a suitable input for making error-reducing adjustments to the neural states.
Figure 3. Feedback-driven learning within the activity space.
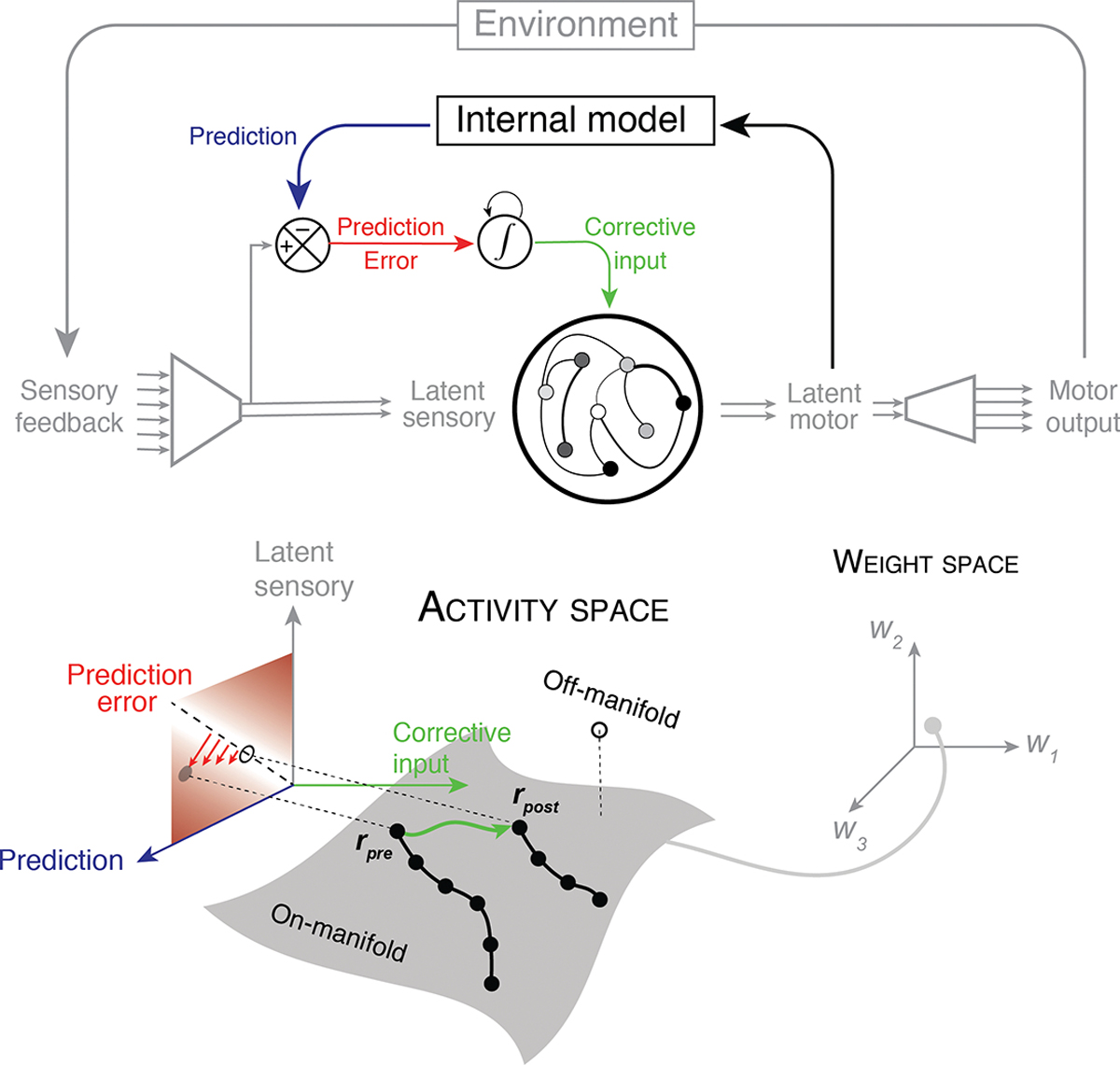
To allow learning to take place directly in the activity space (i.e., without changing the synaptic state), the agent may rely on an internal model of the environment (top) to internally generate corrective inputs in the face of systematic errors. The internal model uses the latent motor variables to predict latent sensory inputs (blue). The mismatch between the predicted and the actual latent sensory inputs yield a prediction error (red). Because this error is typically short-lived (e.g., reward is only available at the end of a trial), the error needs to be stored and accumulated (integrated) over time. This signal serves as an internally-generated corrective input (green) that drives the system in the direction that minimizes the prediction error. The bottom panel illustrates the logic of this error-reducing mechanism in the activity space. When the latent sensory feedback (gray arrow) and the predicted state (blue arrow) mismatch (red arrows away from the diagonal dashed line), the network generates a suitable corrective input (green arrow) that drives the system from its state prior to learning (rpre) to the desired state after learning (rpost). This strategy is viable only when the desired state is within the network’s pre-existing neural manifold (on-manifold: grey), which is determined by the network’s connectivity (bottom right: gray circle in weight space). Note that this is because the internal model exists outside the network of interest and induces learning only through corrective inputs to the network, not through changes in the intrinsic connectivity. If the desired state lies outside this manifold (off-manifold: open circle), feedback-driven learning will not be effective at reducing errors, and slower learning schemes based on changes in the weight space may be required.
Mounting behavioral and physiological evidence suggests that the sensorimotor system may have all the necessary ingredients to implement such error-driven learning in the activity space: the nervous system predicts the sensory consequences of self-generated movements [67] and motor plans [68], computes PE [69], relies on PE for rapid learning [41,68,70], integrates errors over trials [71–74] and generates suitable inputs for learning [20,21].
A final key requirement in this learning scheme is that the internally-generated corrective input must be aligned with the error signal generated externally by the environment. There is currently no experimental evidence for whether and how the nervous system generates such alignment. However, this requirement can be verified in future studies based on two specific predictions it makes about the geometry of the learning trajectory in the activity space (Figure 3). First, it predicts that the neural activity patterns observed throughout the learning process are confined to the pre-existing neural manifold. This is because the internal model exerts its influence through corrective inputs which can only move the system to states that are accessible without any change in connectivity. Second, it predicts that externally-controlled errors systematically drive the activity state along an error-reducing direction in the activity space; that is, the exploration within the pre-existing manifold should be directed – not random.
The degree to which these requirements are satisfied would undoubtedly depend on the nature of the task, the agent’s expertise, and the type of error that has to be corrected. For example, for an inexperienced agent, the task-relevant manifold in the activity space may not be fully formed, in which case the target neural state may be out of reach. That is, the internal model has not yet been learned and the target state therefore cannot be reached via corrective inputs. Under these conditions, the system may need to revert back to a slower learning scheme through adjustments of the synaptic state in the weight space. Similarly, when the environment undergoes complex changes that are beyond what the neural manifold can accommodate, the only option might be a slower exploration in the weight space (e.g., to learn the internal model).
The interplay between learning in the activity space and weight space may explain the different timescales of learning in a wide range of sensorimotor behaviors [75–77] including those that involve a Brain-Computer-Interface [22,78,79]. Moreover, it is conceivable that weight-based learning may systematically follow activity-based learning when errors are persistent. Indeed, corrective inputs may be transferred to changes in weights [80,81] for long-term storage [55], e.g., to optimize the dynamic range of neurons initially driven by the inputs.
Concluding remarks and future perspectives
Sensorimotor learning has been the topic of intensive research for several decades, with a particularly rich body of work at the behavioral level [82,83]. Most neurophysiological studies, however, have focused on how the nervous system performs sensorimotor tasks after learning is complete (but see [19–22,70,78,79,84]). There is consequently a gap in our understanding of how learning happens in the brain. Recent advances in large-scale neural recordings provide an exciting opportunity to address this question and characterize the neurobiological underpinnings of learning. Yet, making progress in that direction will require significant technical, experimental, and theoretical advances (see Outstanding Questions). In particular, a common language is needed for describing large-scale changes that occur within populations of neurons and synapses during learning.
Outstanding questions.
What computational demands require learning within the weight space versus the activity space?
What are the behavioral signatures of learning within the weight space versus the activity space?
What are the structural properties of synaptic/activity manifolds that characterize learning trajectories in the weight/activity space?
What anatomical and physiological constraints determine the structural properties of synaptic/activity manifolds?
How does the structure and dimensionality of synaptic/activity manifolds determine learning speed?
What is the space of functions that characterize learning policies over synaptic manifolds?
How are the key computational ingredients of learning in the activity space (internal models, prediction errors, integration, corrective input) implemented neurobiologically?
How are various learning mechanisms across the weight and activity spaces distributed within different neural systems in the brain?
How does learning in the weight space and activity space interact?
At what spatiotemporal resolution does one need to measure synaptic and activity states to understand learning at a macroscopic level, and what methodologies could help achieve this goal?
In this Opinion article, we build upon a state space framework previously developed to study multi-dimensional systems [14,15,33] and recently extended to study the dynamics of populations of neurons [85–87]. In this framework, we highlight how the problem of sensorimotor learning can be envisaged as the process of attaining a desired state in two multi-dimensional spaces, one for synaptic weights, and one for neural activities. We suggest that the broad behavioral timescales of sensorimotor learning may be explained by the complex interplay between these two state spaces. Notably, this framework has already been useful in linking behavior to activity patterns across populations of neurons—for example, in visual object recognition [88], context-dependent decision making [89], and motor planning and control [29,90]. Here we described ways in which the same approach could be extended to the question of learning and lead to testable predictions about the principles that guide or constrain learning across scales. We believe this framework could facilitate the dialogue between theorists and experimentalists when studying learning at a large-scale network level.
One crucial step in making progress toward a macroscopic understanding of learning is to develop transformative new technologies to measure large-scale changes in synaptic weights in vivo. This is a formidable task [36,91], although recent technical advances in imaging have allowed for monitoring up to thousands of synapses across multiple cortices during learning [13,92–94]. These tools are a prerequisite to assessing the structure of learning in the weight space and testing critical predictions of weight-based learning models [56–58]. As we have highlighted, the dimensionality of the search in the weight space may play a critical role in rapid forms of learning often observed in behavior.
Aside from technological breakthroughs, richer theoretical approaches are needed to infer the computational principles and algorithms that govern learning in the nervous system. Specifically, learning rules that have been proposed at the level of single synapses need to be scaled up to account for coordinated changes in weights across populations of synapses in the form of a learning policy. Moreover, theory-driven experimental work will have to address the question of how such macroscopic learning policies can emerge from low-level cellular processes and local plasticity mechanisms [95]. By providing a framework that bridges these different scales, from synapses to neurons to behavior, we hope to set the stage for integrating future experimental and theoretical efforts toward a more comprehensive understanding of learning.
Highlights.
Experimental work on the neural basis of learning has largely focused on single neurons and synapses, yet behavior depends on coordinated interactions between large populations of neurons and synapses.
A state space framework has been developed to study dynamics of multi-dimensional systems but has not yet been widely adopted to study signatures of learning in neural activity and synaptic weights at a population level.
Recent studies have successfully used the state space approach to link behavior to the geometry and structure of neural dynamics.
We propose a broader application of the state space framework for understanding learning in terms of coordinated changes across populations of synapses and neurons.
The state space framework provides an account of the various timescales of learning, and enables an understanding of the computational principles of learning at a macroscopic level.
Acknowledgement
H.S. is supported by the Center for Sensorimotor Neural Engineering. N.M. is supported by a MathWorks Engineering Fellowship and a Whitaker Health Sciences Fund Fellowship. R.R. is supported by the Helen Hay Whitney Foundation. M.J. is supported by NIH (NINDS-NS078127), the Sloan Foundation, the Klingenstein Foundation, the Simons Foundation, the McKnight Foundation, the Center for Sensorimotor Neural Engineering, and the McGovern Institute.
Glossary
- activity space
a state space in which each dimension represents the activity level of individual neurons in a network.
- backpropagation
a supervised learning algorithm that adjusts individual synaptic weights throughout a neural network in a direction that reduces error at the output of the network.
- dimensionality
the number of variables needed to specify the state of a system.
- error basis set
a population of neurons whose activity profile is tuned to different error values so that any error would activate a small subset of neurons.
- internal model
a process that simulates the causal structure of the environment and predicts the consequences of acting upon the environment.
- latent variable
variables that are not directly observable but may be inferred from other observable variables.
- learning policy
a function that specifies the dependencies of synaptic changes in the weight space.
- neural manifold
a region of the activity space that corresponds to a constrained collection of neural activity patterns.
- prediction error
the difference between actual and predicted outcomes of an action.
- state space
a multi-dimensional coordinate frame that represents all the relevant variables in a system.
- synaptic manifold
a region in the weight space that corresponds to a constrained collection of synaptic states.
- weight space
a state space in which each dimension represents the strength of individual synaptic connections between neurons in a network.
References
- 1.Cajal S.R. y. (1894) La fine structure des centres nerveux. The Croonian Lecture. Proc. R. Soc. Lond. 55, 444–468 [Google Scholar]
- 2.Hebb DO (1949) The organization of behavior; a neuropsychological theory, Wiley. [Google Scholar]
- 3.Spencer WA et al. (1966) Decrement of ventral root electrotonus and intracellularly recorded PSPs produced by iterated cutaneous afferent volleys. J. Neurophysiol. 29, 253–274 [DOI] [PubMed] [Google Scholar]
- 4.McCormick DA et al. (1982) Initial localization of the memory trace for a basic form of learning. Proc. Natl. Acad. Sci. U. S. A. 79, 2731–2735 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kandel ER and Tauc L (1965) Mechanism of heterosynaptic facilitation in the giant cell of the abdominal ganglion of Aplysia depilans. J. Physiol. 181, 28–47 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mayford M et al. (2012) Synapses and memory storage. Cold Spring Harb. Perspect. Biol. 4, [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Nicoll RA (2017) A Brief History of Long-Term Potentiation. Neuron 93, 281–290 [DOI] [PubMed] [Google Scholar]
- 8.Bi GQ and Poo MM (1998) Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 18, 10464–10472 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Oja E (1982) A simplified neuron model as a principal component analyzer. J. Math. Biol. 15, 267–273 [DOI] [PubMed] [Google Scholar]
- 10.Bienenstock EL et al. (1982) Theory for the development of neuron selectivity: orientation specificity and binocular interaction in visual cortex. J. Neurosci. 2, 32–48 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dayan P and Abbott LF (2001) Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems, MIT Press. [Google Scholar]
- 12.Hopfield JJ (1982) Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. U. S. A. 79, 2554–2558 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Roth RH et al. (2020) Cortical Synaptic AMPA Receptor Plasticity during Motor Learning. Neuron 105, 895–908.e5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Izhikevich EM (2007) Dynamical Systems in Neuroscience, MIT Press. [Google Scholar]
- 15.Gerstner W et al. (2014) Neuronal Dynamics: From Single Neurons to Networks and Models of Cognition, Cambridge University Press. [Google Scholar]
- 16.Vogels TP et al. (2005) Neural network dynamics. Annu. Rev. Neurosci. 28, 357–376 [DOI] [PubMed] [Google Scholar]
- 17.Rabinovich MI et al. (2006) Dynamical principles in neuroscience. Rev. Mod. Phys. 78, 1213–1265 [Google Scholar]
- 18.Buonomano DV and Maass W (2009) State-dependent computations: spatiotemporal processing in cortical networks. Nat. Rev. Neurosci. 10, 113–125 [DOI] [PubMed] [Google Scholar]
- 19.Ni AM et al. (2018) Learning and attention reveal a general relationship between population activity and behavior. Science 359, 463–465 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Perich MG et al. (2018) A Neural Population Mechanism For Rapid Learning. Neuron 100, 964–976.e7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Vyas S et al. (2018) Neural Population Dynamics Underlying Motor Learning Transfer. Neuron 97, 1177–1186.e3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sadtler PT et al. (2014) Neural constraints on learning. Nature 512, 423–426 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Herzfeld DJ et al. (2015) Encoding of action by the Purkinje cells of the cerebellum. Nature 526, 439–442 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dempsey C et al. (2019) Generalization of learned responses in the mormyrid electrosensory lobe. Elife 8, [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Richards BA et al. (2019) A deep learning framework for neuroscience. Nat. Neurosci. 22, 1761–1770 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kriegeskorte N and Douglas PK (2018) Cognitive computational neuroscience. Nat. Neurosci. 21, 1148–1160 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zador AM (2019) A critique of pure learning and what artificial neural networks can learn from animal brains. Nat. Commun. 10, 3770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Remington ED et al. (2018) A Dynamical Systems Perspective on Flexible Motor Timing. Trends Cogn. Sci. 22, 938–952 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Vyas S et al. (2020) Computation through neural population dynamics. Annu. Rev. Neurosci. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Saxena S and Cunningham JP (2019) Towards the neural population doctrine. Curr. Opin. Neurobiol. 55, 103–111 [DOI] [PubMed] [Google Scholar]
- 31.Sussillo D (2014) Neural circuits as computational dynamical systems. Curr. Opin. Neurobiol. 25, 156–163 [DOI] [PubMed] [Google Scholar]
- 32.Churchland PS and Sejnowski TJ (2016) The Computational Brain, MIT Press. [Google Scholar]
- 33.Strogatz SH (2018) Nonlinear Dynamics and Chaos with Student Solutions Manual: With Applications to Physics, Biology, Chemistry, and Engineering, Second Edition, CRC Press. [Google Scholar]
- 34.Gallego JA et al. (2017) Neural Manifolds for the Control of Movement. Neuron 94, 978–984 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chung S et al. (2018) Classification and Geometry of General Perceptual Manifolds. Phys. Rev. X 8, 031003 [Google Scholar]
- 36.Humeau Y and Choquet D (2019) The next generation of approaches to investigate the link between synaptic plasticity and learning. Nat. Neurosci. 22, 1536–1543 [DOI] [PubMed] [Google Scholar]
- 37.Werbos PJ (1990) Backpropagation through time: what it does and how to do it. Proc. IEEE 78, 1550–1560 [Google Scholar]
- 38.Rumelhart DE et al. Learning representations by back-propagating errors., Nature, 323. (1986), 533–536 [Google Scholar]
- 39.Lillicrap TP et al. (2020) Backpropagation and the brain. Nat. Rev. Neurosci. DOI: 10.1038/s41583-020-0277-3 [DOI] [PubMed] [Google Scholar]
- 40.Whittington JCR and Bogacz R (2019) Theories of Error Back-Propagation in the Brain. Trends Cogn. Sci. 23, 235–250 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Herzfeld DJ et al. (2015) Encoding of action by the Purkinje cells of the cerebellum. Nature 526, 439–442 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Suvrathan A et al. (2016) Timing Rules for Synaptic Plasticity Matched to Behavioral Function. Neuron 92, 959–967 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Narain D et al. (2018) A cerebellar mechanism for learning prior distributions of time intervals. Nat. Commun. 9, 469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kennedy A et al. (2014) A temporal basis for predicting the sensory consequences of motor commands in an electric fish. Nat. Neurosci. 17, 416–422 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Johansson F et al. (2014) Memory trace and timing mechanism localized to cerebellar Purkinje cells. Proc. Natl. Acad. Sci. U. S. A. 111, 14930–14934 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zenke F et al. (2017) The temporal paradox of Hebbian learning and homeostatic plasticity. Curr. Opin. Neurobiol. 43, 166–176 [DOI] [PubMed] [Google Scholar]
- 47.Marder E et al. (2014) Neuromodulation of circuits with variable parameters: single neurons and small circuits reveal principles of state-dependent and robust neuromodulation. Annu. Rev. Neurosci. 37, 329–346 [DOI] [PubMed] [Google Scholar]
- 48.Nadim F and Bucher D (2014) Neuromodulation of neurons and synapses. Curr. Opin. Neurobiol. 29, 48–56 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Roelfsema PR and Holtmaat A (2018) Control of synaptic plasticity in deep cortical networks. Nat. Rev. Neurosci. 19, 166–180 [DOI] [PubMed] [Google Scholar]
- 50.Raymond JL and Medina JF (2018) Computational Principles of Supervised Learning in the Cerebellum. Annu. Rev. Neurosci. 41, 233–253 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Markov NT et al. (2013) Cortical high-density counterstream architectures. Science 342, 1238406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Semedo JD et al. (2019) Cortical Areas Interact through a Communication Subspace. Neuron 102, 249–259.e4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Michaels JA et al. 25-Feb-(2020), A modular neural network model of grasp movement generation., bioRxiv, 742189 [Google Scholar]
- 54.Halassa MM and Sherman SM (2019) Thalamocortical Circuit Motifs: A General Framework. Neuron 103, 762–770 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Athalye VR et al. (2020) Neural reinforcement: re-entering and refining neural dynamics leading to desirable outcomes. Curr. Opin. Neurobiol. 60, 145–154 [DOI] [PubMed] [Google Scholar]
- 56.Raman DV and O’Leary T 19-Aug-(2020), Optimal synaptic dynamics for memory maintenance in the presence of noise., bioRxiv, 2020.08.19.257220 [Google Scholar]
- 57.Litwin-Kumar A et al. (2017) Optimal Degrees of Synaptic Connectivity. Neuron 93, 1153–1164.e7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Gilson M et al. (2009) Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks. I. Input selectivity--strengthening correlated input pathways. Biol. Cybern. 101, 81–102 [DOI] [PubMed] [Google Scholar]
- 59.Dubreuil A et al. (2020) The interplay between randomness and structure during learning in RNNs. Adv. Neural Inf. Process. Syst at <https://papers.nips.cc/paper/2020/hash/9ac1382fd8fc4b631594aa135d16ad75-Abstract.html> [Google Scholar]
- 60.Egger SW et al. (2020) A neural circuit model for human sensorimotor timing. Nat. Commun. 11, 3933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Remington ED et al. (2018) Flexible Sensorimotor Computations through Rapid Reconfiguration of Cortical Dynamics. Neuron 98, 1005–1019.e5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Shenoy KV et al. (2013) Cortical control of arm movements: a dynamical systems perspective. Annu. Rev. Neurosci. 36, 337–359 [DOI] [PubMed] [Google Scholar]
- 63.Wang J et al. (2018) Flexible timing by temporal scaling of cortical responses. Nat. Neurosci. 21, 102–110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Sauerbrei BA et al. (2020) Cortical pattern generation during dexterous movement is input-driven. Nature 577, 386–391 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Botvinick M et al. (2019) Reinforcement Learning, Fast and Slow. Trends Cogn. Sci. 23, 408–422 [DOI] [PubMed] [Google Scholar]
- 66.Jordan MI and Rumelhart DE (1992) Forward Models: Supervised Learning with a Distal Teacher. Cogn. Sci. 16, 307–354 [Google Scholar]
- 67.Wolpert DM et al. (1995) An internal model for sensorimotor integration. Science 269, 1880–1882 [DOI] [PubMed] [Google Scholar]
- 68.Egger SW et al. (2019) Internal models of sensorimotor integration regulate cortical dynamics. Nat. Neurosci. 22, 1871–1882 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Cullen KE and Brooks JX (2015) Neural correlates of sensory prediction errors in monkeys: evidence for internal models of voluntary self-motion in the cerebellum. Cerebellum 14, 31–34 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Brooks JX et al. (2015) Learning to expect the unexpected: rapid updating in primate cerebellum during voluntary self-motion. Nat. Neurosci. 18, 1310–1317 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Sarafyazd M and Jazayeri M (2019) Hierarchical reasoning by neural circuits in the frontal cortex. Science 364, [DOI] [PubMed] [Google Scholar]
- 72.Purcell BA and Kiani R (2016) Hierarchical decision processes that operate over distinct timescales underlie choice and changes in strategy. Proc. Natl. Acad. Sci. U. S. A. 113, E4531–40 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Zylberberg A et al. (2018) Counterfactual Reasoning Underlies the Learning of Priors in Decision Making. Neuron 99, 1083–1097.e6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Herzfeld DJ et al. (2014) A memory of errors in sensorimotor learning. Science 345, 1349–1353 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Verstynen T and Sabes PN (2011) How each movement changes the next: an experimental and theoretical study of fast adaptive priors in reaching. J. Neurosci. 31, 10050–10059 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Smith MA et al. (2006) Interacting adaptive processes with different timescales underlie short-term motor learning. PLoS Biol. 4, e179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Braun DA et al. (2009) Motor task variation induces structural learning. Curr. Biol. 19, 352–357 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Golub MD et al. (2018) Learning by neural reassociation. Nat. Neurosci. 21, 607–616 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Oby ER et al. (2019) New neural activity patterns emerge with long-term learning. Proc. Natl. Acad. Sci. U. S. A. 116, 15210–15215 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Abbott LF et al. (2016) Building functional networks of spiking model neurons. Nat. Neurosci. 19, 350–355 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Denève S et al. (2017) The Brain as an Efficient and Robust Adaptive Learner. Neuron 94, 969–977 [DOI] [PubMed] [Google Scholar]
- 82.Shadmehr R et al. (2010) Error correction, sensory prediction, and adaptation in motor control. Annu. Rev. Neurosci. 33, 89–108 [DOI] [PubMed] [Google Scholar]
- 83.Wolpert DM et al. (2011) Principles of sensorimotor learning. Nat. Rev. Neurosci. 12, 739–751 [DOI] [PubMed] [Google Scholar]
- 84.Law C-T and Gold JI (2008) Neural correlates of perceptual learning in a sensory-motor, but not a sensory, cortical area. Nat. Neurosci. 11, 505–513 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Fetz EE (1992) Are movement parameters recognizably coded in the activity of single neurons? Behav. Brain Sci. 15, 679–690 [Google Scholar]
- 86.Scott SH (2008) Inconvenient truths about neural processing in primary motor cortex. J. Physiol. 586, 1217–1224 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Churchland MM and Shenoy KV (2007) Temporal complexity and heterogeneity of single-neuron activity in premotor and motor cortex. J. Neurophysiol. 97, 4235–4257 [DOI] [PubMed] [Google Scholar]
- 88.DiCarlo JJ et al. (2012) How does the brain solve visual object recognition? Neuron 73, 415–434 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Mante V et al. (2013) Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature 503, 78–84 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Sohn H et al. (2019) Bayesian Computation through Cortical Latent Dynamics. Neuron 103, 934–947.e5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Marblestone AH et al. (2016) Toward an Integration of Deep Learning and Neuroscience. Front. Comput. Neurosci. 10, 94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Pfeiffer T et al. (2018) Chronic 2P-STED imaging reveals high turnover of dendritic spines in the hippocampus in vivo. Elife 7, [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Hayashi-Takagi A et al. (2015) Labelling and optical erasure of synaptic memory traces in the motor cortex. Nature 525, 333–338 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Loewenstein Y et al. (2015) Predicting the Dynamics of Network Connectivity in the Neocortex. J. Neurosci. 35, 12535–12544 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Magee JC and Grienberger C (2020) Synaptic Plasticity Forms and Functions. Annu. Rev. Neurosci. DOI: 10.1146/annurev-neuro-090919-022842 [DOI] [PubMed] [Google Scholar]


