Abstract
When COVID-19 suddenly broke out, the epidemic areas are short of basic emergency relief which need to be transported from surrounding areas. To make transportation both time-efficient and cost-effective, we consider a multimodal hub-and-spoke transportation network for emergency relief schedules. Firstly, we establish a mixed integer nonlinear programming (MINLP) model considering multi-type emergency relief and multimodal transportation. The model is a bi-objective one that aims at minimizing both transportation time consumption and transportation costs. Due to its NP-hardness, devising an efficient algorithm to cope with such a problem is challenging. This study thus employs and redesigns Grey Wolf Optimizer (GWO) to tackle it. To benchmark our algorithm, a real-world case is tested with three solution methods which include other two state-of-the-art meta-heuristics. Results indicate that the customized GWO can solve such a problem in a reasonable time with higher accuracy. The research could provide significant practical management insights for related government departments and transportation companies on designing an effective transportation network for emergency relief schedules when faced with the unexpected COVID-19 pandemic.
Keywords: COVID-19 pandemic, Emergency relief schedules, Multimodal hub-and-spoke transportation network, Bi-objective MINLP model, Customized Grey Wolf Optimizer, Meta-heuristics
1. Introduction
The COVID-19 virus, characterized with fast-speed spread, easy infection and long-time duration among people, has been described as a pandemic by the World Health Organization (WHO) [1]. Data published by WHO as of November 9, 2020, informed that the epidemic has spread to more than 210 countries [2]. Due to the suddenness of COVID-19 pandemic outbreak, the epidemic districts and their adjacent areas are always caught unprepared [3]. The local reserve of basic materials is usually not sufficient when COVID-19 suddenly comes [4].
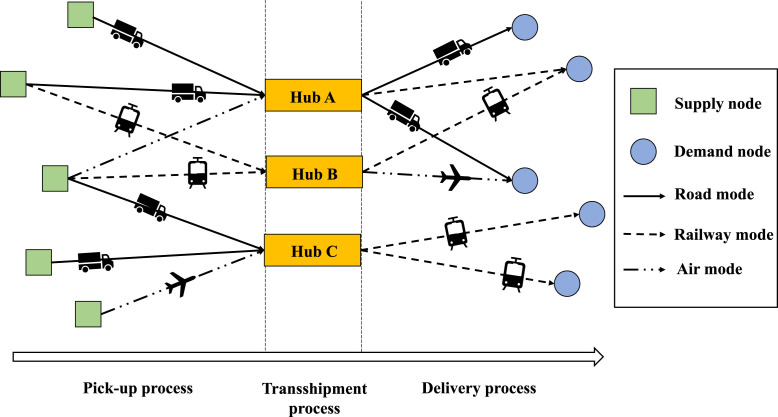
In such situation, people in disaster areas are in shortage of multi-type relief, such as basic living materials (food) and personal medical protection equipment (mask). Therefore, the scheduling of food and mask from other areas with adequate inventory for aid is of great importance. An optimal transportation network for food and mask scheduling depends on proper network structures. The hub-and-spoke structure is well-used in a comprehensive transportation network with scale of economies [5], [6], [7], [8]. In a hub-and-spoke transportation network, freights are firstly picked up from supply nodes and transited to proper hubs functioned as huge transshipment centers. After sorting, labeling and packaging operations inside hubs, such freights are then delivered to demand nodes (shown in Fig. 1). In the hub-and-spoke emergency relief transportation network, different types of relief may have particular transportation requirements. For instance, medical products are urgent relief with high value which should be transported within a relative short time. In reality, they are usually transported by air mode. Generally, different transportation modes have their specific advantages in aspects with capacity, unit freight and transportation time. Therefore, not only the scheduling of multi-type relief, but also multimodal transportation should be taken into considerations in the hub-and-spoke transportation network for satisfying various transportation requirements.
Fig. 1.
The structure of hub-and-spoke transportation network.
As is known for all, time is life, particularly faced with such cruel pandemic. The time efficiency of basic living supplies transition should always be taken in the first place. While considering transportation time consuming, the transportation cost should not be ignored since the economic expenditure is tighter than usual. Thus a proper transportation network for transporting emergency relief with both time efficiency and economic superiority is of essential necessity. Namely, in this research, minimizing both transportation time and transportation cost of the hub-and-spoke network should be considered.
Undoubtedly, the problem becomes much more complicated when we take all the mentioned aspects (multi-type relief, multimodal transportation, minimize both transportation time and transportation cost) into account. Based on considerations of two objectives mentioned in last paragraph, such a complex problem can be formulated as a bi-objective mixed integer nonlinear programming (MINLP) model which could not be directly solved by an MIP solver [9], [10]. In addition, due to its NP-hardness, the problem cannot be solved optimally by exact algorithms within a reasonable computational time, particularly for large-scale instances [11]. Therefore, it is essential to design efficient meta-heuristic approach to solve such problems. Among the existing meta-heuristic algorithms, Grey Wolf Optimizer (GWO) is a population-based nature-inspired algorithm recently proposed by Mirjalili in 2014 [12]. It simulates the social behavior of grey wolf for hunting prey which is a swarm intelligence algorithm based on leadership hierarchy. The application of GWO has been greatly active in the literature and related engineering fields [13], [14], [15], [16], [17], [18]. In this study, customized GWO is designed to cope with problems in pickup (from supply nodes to hubs) and delivery processes (from hubs to demand nodes) within a hub-and-spoke transportation network. To validate the correctness of model and the proposed algorithm, a real-world case is introduced for tests. Two other state-of-the-art algorithms: Firefly Algorithm (FA) [19] and Particle Swarm Optimization (PSO) [20] are also presented to make comparisons with customized GWO for algorithm efficiency verification.
From the aspects of transportation network design, tailored model establishment, customized GWO algorithm design, and important management insights for related authorities, the main contributions of this study are concluded and given as follows:
-
•
We are dedicated to designing and optimizing a comprehensive emergency relief supply transportation network with hub-and-spoke structure with high efficiency. In the network, multi-type relief and multimodal transportation are both considered.
-
•
A bi-objective MINLP model is established for the specific network which considers not only transportation time consumption but also transportation cost. In reality, transportation time consuming has greater priority than transportation cost with higher weights in the calculation.
-
•
To solve the model with efficiency, a customized GWO is designed and applied to solve a real-world case. The other two heuristic approaches are then introduced to make comparisons. The experimental results validate the superiorities of customized GWO.
-
•
The research can provide practical management insights for both related government departments and transportation companies. For government departments, the effective transportation network provides basic safeguards for medical aid and life order guarantee. For transportation companies undertaking transportation tasks, this study will guarantee both transportation capacities and economic benefits.
The remainder of the paper is organized as follows. In Section 2, a literature review of existing researches for solving emergency relies supply transportation problem and current applications for routing problems solved by GWO are given. In Section 3, we establish a bi-objective MINLP model minimizing both transportation time and cost to optimize the whole emergency relief transportation network. The basic GWO and customized GWO are presented in details in Section 4. In Section 5, to benchmark our algorithm, a real-world case are tested with three solution methods which include other two state-of-the-art heuristics. From the industrial case, practical management insights are summarized in Section 6. Finally, conclusion is given in Section 7.
2. Literature review
In this study, we aim at designing an efficient transportation network for emergency relief under COVID-19 pandemic. To effectively solve such a complex problem, a tailored GWO was designed. As a newly proposed meta-heuristic algorithm, GWO has wide applications in routing problems. Therefore, in this section, we first summarize typical emergency relief transportation research. Subsequently, the classical research on solving routing problems with GWO are reviewed and summarized.
2.1. Researches on emergency relief transportation
The emergency relief transportation, also called as emergency relief logistics, has long been researched by related scholars. Pettit et al. [21] present a refined model for logistics requirements in emergency conditions. The model takes the existing military and non-military response models into consideration. Sheu [22] presents a hybrid fuzzy clustering-optimization approach for emergency relief logistics in the crucial rescue period. Two recursive mechanisms containing disaster-affected area grouping and relief co-distribution are involved in a three-layer emergency logistics co-distribution framework. Numerical experiments are conducted based on earthquake disaster occurring in Taiwan and the corresponding results validate the superiority of the proposed method. Lei [23] proposes a novel decision support system for relief logistics in natural disasters. Capacity limitations, priority of commodities and dynamic demand requirements are considered in the system. An interactive solution approach is then introduced for solving dynamic and goal programming model. Altay [24] gives a detailed presentation about existing modeling approaches that relate to disaster relief. Also, some challenging directions that cannot be easily incorporated into mathematical models have also been presented. Customer service is then considered in the international emergency relief chains by Oloruntoba and Gray [25]. Inspired by the immune system, Hu [26] models container multimodal transportation emergency relief system as an affinity network. To solve such problem, an integer linear programming model is then proposed. Afterwards, the simulation results of case studies verify the promising effects of model. It is known that humanitarian relief logistics is one of the most important elements of emergency relief logistics management. For reality, Ali et al. [27] develop a multi-objective robust stochastic programming approach for disaster emergency relief logistics under uncertainty. It is worth mentioning that the uncertain parameters contain demand uncertainty, supplies uncertainty and procurement and transportation cost uncertainty. Malek and Moghaddam [28] present a bi-objective mixed integer mathematical model for Humanitarian Relief Logistics (HRL) which determines optimal warehouse locations, emergency relief amounts of warehouse, and transportation plans. Then a Reservation Level Tchebycheff Procedure (RLTP) method is proposed to solve the bi-objective model. Liu et al. [29] propose a stochastic model for post-disaster relief logistics considering the particular environmental conditions after a catastrophic earthquake in mountainous areas. A robust optimization approach is introduced to tackle with uncertainties of the proposed stochastic model. Considering the post-disaster road network repair work scheduling and relief logistics, Li and Teo [30] establish a multi-period bi-level programming model for the problem. To work it out, a maximum relative satisfaction degree based steady-state parallel genetic algorithm is proposed. From the new aspect of minimizing the late arrival of relief vehicles, Davoodi and Goli [31] proposed an integrated model for relief operations in critical situations. It is worth mentioning that the covering tour approach is applied for vehicle routing part in the model which can speed up the disaster logistics system systems. To work out the model, a hybrid benders decomposition and variable neighborhood search approach is designed and introduced whose applications in the case study are proved to be highly efficient. Boostani et al. [32] present a three-level relief chain problem in pre- and postdisaster duration. The objective functions contain three aspects: (1) minimizing total costs of the humanitarian relief supply chain, (2) maximizing the social welfare and (3) minimizing the environmental impacts. A multi-objective mixed integer stochastic programming model is established to decide facility locations, procurement and resource allocation.
2.2. Applications for GWO solving routing problems
The applications of GWO for solving routing problems are in a quite few amount. While there are still some researchers dedicated to introducing GWO to solving complex routing problems. A ‘K-GWO’ algorithm is designed by [33] combining GWO with the traditional K-means clustering algorithm to solve CVRP. The results tested on benchmark datasets validate the efficiency of ‘K-GWO’. A new technique to solve TSP based on standard GWO is proposed and verified among several numerical experiments [34]. Furthermore, swap operator and swap sequence are also considered to adapt GWO for TSP. A novel D-GWO [35] is recently presented for solving symmetric TSP, with which 2-opt algorithm also is combined. D-GWO is then verified by comparing the results with several hybrid algorithms among 17 instances from TSPLIB. More researches related to GWO and its applications can be found in [36]. Although GWO is a relative fresh algorithm compared with other classical ones, its superiorities on solving routing problems can be clearly observed from related researches. In this study, while enhancing the solution efficiency, we continue employing and redesigning a customized GWO for solving such emergency relief supply routing problem under COVID-19 pandemic.
3. Model establishment
In this section, we first present a formal description of the multi-type relief and multimodal transportation network design problem. Some necessary assumptions and notations are given in details subsequently. We then introduce a tailored bi-objective mixed integer linear programming (MILP) model established for the specific problem.
3.1. Problem description
Basic living and medical emergency relief (like food and mask) in the epidemic areas are always in critical shortage status at the initial stage of COVID-19 pandemic outbreak [3], [4]. Thus filling the basic supply shortage as soon as possible by scheduling emergency relief from other nearer regions is of great significance. While transportation cost should also be taken into considerations even though transportation time is more prioritized. Taking fully consideration of improving transportation time efficiency and minimizing transportation cost, a bi-objective MINLP model with reasonable constraints is proposed.
In reality, emergency supplies come in all directions from other regions functioned with sufficient material storage and relative optimal distance [37]. However, it would easily lead to high time consuming and cost waste if all the supply areas connect directly to each demand region. Thus hub-and-spoke transportation network is adopted in this research due to scale of economies. In the designed hub-and-spoke network, different transportation modes are also introduced since particular transportation mode has its own characteristics which caters for the specific transportation requirements. For instance, railway mode has advantages in freight volumes and unit transportation cost, but it cannot guarantee transportation time. While air mode is quite the contrary.
Based on what has mentioned above, a multi-type relief and multimodal transportation network with hub-and-spoke structure is designed in this study. Given supply and demand nodes, candidate hub nodes, demand quantities and other related parameters, the following terms can be determined:
-
•
which hub(s) is/are selected
-
•
which supply nodes and demand nodes are allocated to hub(s)
-
•
which transportation modes are selected to deliver the specific type of relief supplies
-
•
how many particular-type supplies are transported en-route
3.2. Assumptions and notations
For convenience to establish tailored model, some necessary assumptions and notations need to be given here. The assumptions are listed as bellows and notation explanations are given in Table 1.
-
•
The reserve in supply nodes are comprised of original reserve, social donation and other supply channels.
-
•
All the candidate hubs are established ones whose construction cost will not be reconsidered.
-
•
The areas where hubs are located have already been sufficiently supplied and do not need extra relief from supply nodes.
-
•
The direct connections between hubs are not allowed.
Table 1.
Notations explanation.
| Set | |
|---|---|
| I | The set of supply nodes, i I |
| O | The set of candidate hubs, o O |
| J | The set of demand nodes, j J |
| K | The set of transportation modes, k K |
| W | The set of emergency relief types, w W |
| Parameter | |
| The unit weight of the w-type emergency relief | |
| The transportation time of the w-type emergency relief picked up by the k-type vehicle from supply node to hub | |
| The transportation time of the w-type emergency relief delivered by the k-type vehicle from hub to demand node | |
| The transshipment time of the w-type emergency relief at hub | |
| The maximum capacity of the k-type vehicle | |
| The unit transportation cost of the w-type emergency relief picked up by the k-type vehicle from supply node to hub | |
| The unit transportation cost of the w-type emergency relief delivered by the k-type vehicle from hub to demand node | |
| The transshipment cost of the w-type emergency relief at hub | |
| The distance between supply node and hub when emergency relief is picked up by the k-type vehicle | |
| The distance between hub and demand node when emergency relief is delivered by the k-type vehicle | |
| The reserve of the w-type emergency relief at supply node | |
| The maximum capacity of hub | |
| The demand of the w-type emergency relief at demand node | |
| The maximum available vehicle number transported from supply node to hub | |
| The maximum available vehicle number transported from hub to demand node | |
| The minimum demand ratio of the w-type emergency relief at demand node | |
| Decision variables | |
| is 1 if the w-type emergency relief is transported by the k-type vehicle from supply node to hub , is 0 otherwise | |
| is 1 if the w-type emergency relief is transported by the k-type vehicle from hub to demand node , is 0 otherwise | |
| is 1 if node o is selected to be a hub, is 0 otherwise | |
| The amount of the w-type emergency relief picked up by the k-type vehicle from supply node to hub | |
| The amount of the w-type emergency relief delivered by the k-type vehicle from hub to demand node | |
3.3. Mathematical model
Based on problem assumptions and necessary notation explanations, the model for emergency relief hub-and-spoke transportation network under COVID-19 pandemic can be detailed given in this subsection.
3.3.1. Objective function
Objective function contains two parts: (1) minimizing transportation time and (2) minimizing the total transportation cost.
COVID-19 pandemic is undoubtedly a serious emergency event and the pandemic will rapidly expand as time passes for the sake of high-infectious characteristics and COVID-19 variant [37], [38]. To some extent, time is life. Therefore, the scheduling of emergency relief should always take transportation time efficiency as the first place. The transportation time contains three parts: transportation time from supply nodes to hubs, transshipment time inside hubs and transportation time from hubs to corresponding demand nodes (Eq. (1)).
| (1) |
Secondly, the consideration of transportation cost should also be taken after transportation time consuming. Once the transportation started from supply nodes, corresponding transportation cost will generate. Particularly, more urgent the supplies are, more expensive the transportation cost will be. It can be explained that the most urgent relief will be transported by air mode to assure the time efficiency whose transportation cost is much more higher than that of other modes (road and railway mode). As is known to all that the economy is rather tense during the COVID-19 pandemic due to distribution of regular social work and life. Therefore, optimizing total transportation cost should also be considered as the second objective which contains three aspects: Transportation cost from supply node to hub, transshipment cost in hub and transportation cost from hub to demand node (Eq. (2)).
| (2) |
3.3.2. Constraints
Reasonable constraints are essential components of a model since they can restrict the model and make the solutions accurate. Firstly, the hub location and allocation should be constrained as follows:
For hub nodes, each hub node can be connected with more than one supply nodes:
| (3) |
For demand nodes, each demand node can be served by more than one hub:
| (4) |
Only if the hub is established and selected can the arcs between supply nodes and hub (or between hub and demand nodes) exist
| (5) |
| (6) |
Each supply node has their own reserve limitation, the amount of relief supplies transported from the supply nodes should not exceed the corresponding reserve limitation. Similarly, each hub has its own capacity limitation for the specific relief, the amount of relief arrived and shortly stored at hubs should be within the limitation respectively:
| (7) |
| (8) |
The flow balance principal should always be obey, that is, the amount of relief flowing into the hub equals to the amount flowing out of the hub whatever the types:
| (9) |
The demand requirements should be satisfied as much as possible. In fact, the emergency relief may not be quite adequate when COVID-19 pandemic suddenly breaks out, but the minimum demand must be fulfilled:
| (10) |
| (11) |
For the transportation modes, the relief supplies with specific type can only be delivered by one transportation mode on the corresponding arc:
| (12) |
| (13) |
The available vehicle number of each transportation mode is different at each supply node and hub. The vehicles put into use should not exceed the corresponding transport capacity of each node:
| (14) |
| (15) |
All the decision variables domains are defined as follows:
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
4. Meta-heuristic approach
In this section, we first give a brief introduction to basic GWO. Subsequently, our customized GWO is described at length in four parts: construction stage, fitness calculation, improvement stage, and the customized GWO. To make it a clear and vivid readership, we finally depict the whole model solution framework.
4.1. Basic GWO
Grey Wolf Optimizer (GWO) is a population-based meta-heuristics algorithm inspired by the hunting and social behavior of the grey wolf pack. Grey wolf maintains a hierarchy of their society. Specifically, represents the leader wolf, represents the second-hierarchy wolf and is the third-hierarchy wolf. The rest wolves are called . Tracking, pursuing, and attacking are the main phases of grey wolf hunting. For vivid readership, detailed introduction of basic GWO is presented in Algorithm 1.
In order to model the social hierarchy of grey wolves, the first three best wolves (, , ) will instruct other wolves rushing to the target. The rest wolves () always update their locations according to , and .
In the process of hunting, encircling action can be defined as following:
| (21) |
| (22) |
where t indicates the current iteration, and are coefficient vectors, is the position vector of the prey, and indicates the position vector of a grey wolf.
The vectors and are calculated as follows:
| (23) |
| (24) |
where components of are linearly decreased from 2 to 0 over the course of iterations and , are random vectors in [0,1].
Each wolf uses the potential of , and wolves in hunting strategy as they are best in pack. The wolves update their position with the help of , and as follows:
| (25) |
| (26) |
where , and are the approximated positions of , and wolves. represents the updated position of wolf.
4.2. Customized GWO
The model given in Section 3 is a nonlinear one which could not be directly solved by MIP solver. In addition, due to its NP-hardness, the model cannot be solved optimally by exact algorithms within a reasonable computational time particularly for large-scale instances. Therefore, we design a meta-heuristic approach based on GWO structure. The proposed algorithm is comprised of two stages: construction stage and improvement stage. In construction stage, some initial operations are conducted and respective constraints are checked for validation. In improvement stage, we design a HD move strategy to update GWO solutions.
Our model can be simply described as Fig. 2. As is shown in Fig. 2, the designed transportation network is divided into three processes: (1) pickup process (from supply nodes to hubs), (2) transshipment process (transshipment operations inside hubs) and (3) delivery process (from hubs to demand nodes). The transportation planning of pickup process shares the same logic with that of delivery process. Thus we only introduce detailed solutions of pickup process. The solutions of delivery process can be obtained according to the same method used in pickup process. Now we proceed to design and introduce customized GWO for solving transportation problems in pickup process.
Fig. 2.
The diagram of the proposed transportation network.
4.2.1. Construction stage
In construction stage, we firstly initialize the pickup amount of food and mask. Specifically, initialize and generate a transportation-amount matrix with the scale of . For instance, if the number of supply nodes and hubs is both two, then we generate a 2 × 2 matrix formed as [[A1, A2], [B1, B2]]. During construction of transportation-amount matrix, it should be guaranteed that the sum of A1 and A2 is no more than the reserve of current first supply node. Similarly, the total of B1 and B2 should not exceed the reserve of current second supply node. Each item in the matrix represents detailed supply amount which is always non-negative. For instance, A1 denotes the transportation quantity from the first supply node to the first hub. Two sets of transportation-amount matrices are generated to represent the transportation amount of food and mask respectively. According to the model described in Section 3.3, constraint examinations should be conducted to initial transportation-amount matrices. Here, only the constraint related to hub capacity need to be checked. Take the first hub (hub1) for example, the current capacity of hub1 is the sum of A1 and B1, then we need to check whether the current capacity is within the limitation of hub1’s capacity. If all the capacity constraints of hubs are satisfied, then a transportation-amount matrix [[A1, A2], [B1, B2]] is successfully obtained. The initialization operations for transportation amounts then end up. Otherwise, regenerate transportation-amount matrix until all the hub constraints are satisfied.
Two matrices of transportation amount for food and mask could be obtained based on steps mentioned above. For the two transportation-amount matrices, we need to generate two respective transportation-mode matrices. For instance, given ‘road mode = 1, railway mode 2 and air mode 3’, the transportation-mode matrix can be initialized as [[2, 3], [1, 2]]. Then it can be described as: railway mode is selected to transit freights from the first supply node to the first hub. We generate transportation-mode matrices respectively against food and mask. Thus two specific transportation-mode matrices are obtained. Now we proceed to check constraints of vehicle number in each supply node. Namely, it should be examined that whether the available vehicle number can cater for current vehicle demand based on above-mentioned transportation mode. If the constraints are violated, then we regenerate transportation-mode matrices until the vehicle number constraints are satisfied.
Finally, we obtain a solution of pickup process which contains transportation-amount matrices of food and mask (, ) and corresponding matrices of transportation mode (, ). In summary, an initial solution of customized GWO will be formed as (, , , ).
4.2.2. Fitness calculation
Each solution can be regarded as a wolf in GWO structure. After construction stage, qualified wolves are obtained. Then we proceed to calculate the fitness of each wolf according to Eq. (27):
| (27) |
where is the whole time consuming and denotes the total transportation cost for one solution. and of pickup process can be calculated respectively by the first item of Eqs. (1), (2). and are particular weights of transportation time and transportation cost. The sum of and equals to 1 whereas is set to be more than 0.5 due to the priority of time efficiency under COVID-19 pandemic. It is worth mentioning that the solutions obtained will be better when and . and are obtained by ordering the time and transportation cost among all the solutions.
4.2.3. Improvement stage
According to the fitness calculation, the first three optimal solutions are selected to be , , wolf mentioned in basic GWO. In our proposed algorithm, improvement part is focus on enhancing transportation modes, that is, the value within and .
In improvement stage, Hamming distance (HD) concept [39] is introduced to update each ordinary wolf. In informatics, between two strings with equal length, the number of different characters in the corresponding positions is called hamming distance. For instance, the two binary strings [0 1 0 1] and [1 0 1 1], the first, second and third place are different between and , then HD is 3. Now we define the transportation-mode matrix needed to improve as and the target transportation-mode matrix is (matrix in , or ). Then, the moving distance of attracted by is defined as follows (Eq. (28)), that is, the random number between 0 and HD. New solutions are obtained after such HD move, as shown in Algorithm 2. After each HD move, we need to examine the constraints of vehicle number. If the new transportation mode cannot cater for the vehicle number, we will keep the original one. Otherwise, update current transportation mode.
| (28) |
4.2.4. The customized GWO
The design of customized GWO is given in Algorithm 2. At first, we initialize the transportation amount of food and mask by the methods introduced in Section 4.2.1, after which initial transportation-amount solutions and are obtained. Then, based on the and , we proceed to get transportation-mode solutions and . A wolf in customized GWO is defined as (, , , ).
In Algorithm 3, for the and , there are ten different transportation modes and being constructed respectively. Thus we form a wolf population with ten wolves. Afterwards, improvement stage introduced in Section 4.2.3 is conducted to update the wolf population. We firstly calculate fitness of wolf groups and then select the first three wolves with minimum fitness as , and . Carrying out HD move to enhance and for obtaining better results. Continually repeat the above steps until it reaches iteration time settings. Finally we output wolf (, , , ) as the solution of customized GWO where and are the optimal transportation mode against and via customized GWO.
4.3. The whole model solution framework
The whole model solution framework is given in Algorithm 4. As is mentioned above, the transportation process contains three parts: pickup process, transshipment process and delivery process. Firstly, we conduct customized GWO (Algorithm 3) to the pickup process. Solutions of pickup process are then obtained which contain transportation amount of food and mask ( and ) and their respective transportation mode ( and ) from supply nodes to hubs. Secondly, calculate transshipment time and cost of food and mask in transshipment process. After that, we proceed to solve delivery process using Algorithm 3 since the solution logic is the same of both pickup and delivery process. Solutions of delivery process can also be obtained which are comprised of transportation amount of food and mask, and their respective transportation mode from hubs to demand nodes. Above all, we get solutions of pickup process, transshipment process and delivery process. According to solutions of each process, the model transportation time consuming and transportation cost can be calculated respectively by Eqs. (1), (2). Whilst solving the model, repeat the above solving process until iteration time reaches. Meanwhile, the number of results are obtained, from which we choose the result with minimum as the final output result. By conducting the Algorithm 4, solutions of pickup process, transshipment process and delivery process are finally obtained which also give answers to Section 3.1.
5. Numerical experiments and analysis
In this section, we conduct the customized GWO to solve a real-world case of Hubei Province in China. To verify the efficiency of proposed algorithm, FA [19] and PSO [20] are also conducted and compared with customized GWO. The proposed algorithm is coded in Python and computational tests are performed on the computer with Intel(R) Core (TM) i7-5200U, CPU 2.20 GHz with 8 GB RAM. For statistical reliability, all the conducted algorithms take the same 20 independent runs.
5.1. Data collection
We use the real-life case of emergency relief (food and mask) transportation under COVID-19 pandemic in Hubei Province. The whole transportation network contains five supply nodes (Shijiazhuang, Xian, Chengdu, Guiyang and Nanning), three candidate hubs (Wuhan, Ezhou and Xiantao) and five demand nodes (Xiaogan, Huanggang, Huangshi, Tianmen and Xianning). The geographical locations of 13 nodes are shown in Fig. 3. The data comes from Gaode map, related offices and communities in Hubei province. It includes GIS (shown in Fig. 3) and parameter-related data (shown in Table 2). In Table 2, the food and mask amount are presented in the form of ‘(food-amount/ton,mask-amount/unit)’.
Fig. 3.
The geographical locations of 13 nodes.
Table 2.
Information of supply, hub capacity and demand.
| Supply |
Hub capacity |
Demand |
|||
| Shijiazhuang | (3000,1700k) | Wuhan | (15000,10000k) | Xiaogan | (4900,1000k) |
| Xian | (3800,1500k) | Ezhou | (8000,8000k) | Huanggang | (6300,2100k) |
| Chengdu | (5650,1500k) | Xiantao | (9000,8500k) | Huangshi | (2500,1900k) |
| Guiyang | (2650,1400k) | Tianmen | (1300,810k) | ||
| Nanning | (1900,1000k) | Xianing | (2000,2000k) | ||
5.2. Result of real-world case
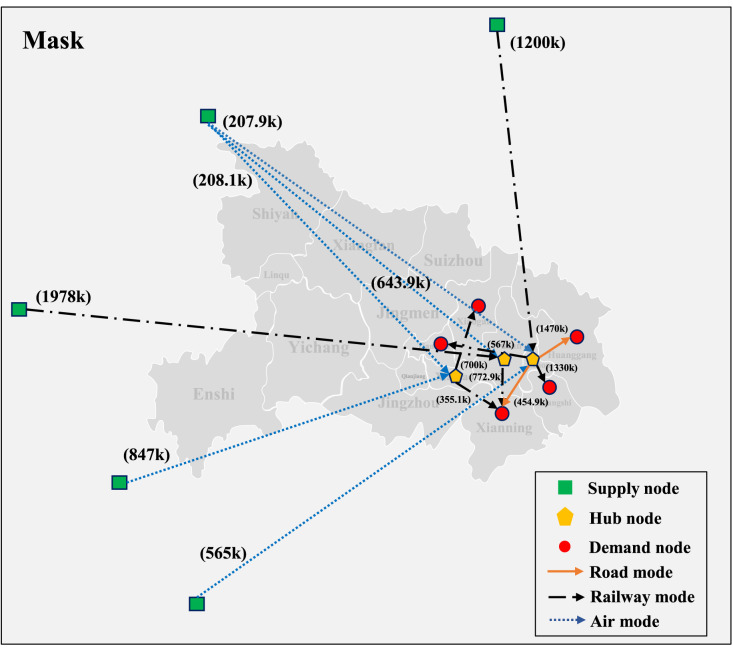
Fig. 4 and Fig. 5 visualize the results of food and mask transportation in the hub-and-spoke network solving by customized GWO. The more detailed route results are listed in Table 3 and Table 4. In two tables, pickup or delivery amount and transportation mode are given in the form of ‘(amount, transportation mode)’ whereas 1 represents road mode, 2 represents railway mode and 3 represents air mode. In addition, respective transportation time consuming cost and transportation cost of food and mask are given in Table 5.
Fig. 4.
The transportation network of food.
Fig. 5.
The transportation network of mask.
Table 3.
Pickup and delivery processes of food transportation.
| Process | Supply/Demand nodes | Hub nodes |
||
|---|---|---|---|---|
| Wuhan | Enzhou | Xiantao | ||
| Pickup | Shijiazhuang | (0,0) | (2600,2) | (0,0) |
| Xian | (3400,2) | (0,0) | (0,0) | |
| Chengdu | (0,0) | (214,2) | (5036,2) | |
| Guiyang | (2250,2) | (0,0) | (0,0) | |
| Nanning | (1500,2) | (0,0) | (0,0) | |
| Delivery | Xiaogan | (0,0) | (0,0) | (4126,2) |
| Huanggang | (6300,2) | (0,0) | (0,0) | |
| Huangshi | (0,0) | (1750,2) | (0,0) | |
| Tianmen | (0,0) | (0,0) | (910,2) | |
| Xianning | (850,2) | (1064,2) | (0,0) | |
Table 4.
Pickup and delivery processes of mask transportation.
| Process | Supply/Demand nodes | Hub nodes |
||
|---|---|---|---|---|
| Wuhan | Enzhou | Xiantao | ||
| Pickup | Shijiazhuang | (0,0) | (1200k,2) | (0,0) |
| Xian | (207.9k,3) | (643.9k,3) | (208.1k,3) | |
| Chengdu | (0,0) | (1978k,2) | (0,0) | |
| Guiyang | (0,0) | (0,0) | (847k,3) | |
| Nanning | (565k,3) | (0,0) | (0,0) | |
| Delivery | Xiaogan | (0,0) | (0,0) | (700k,2) |
| Huanggang | (0,0) | (1470k,1) | (0,0) | |
| Huangshi | (0,0) | (1330k,2) | (0,0) | |
| Tianmen | (0,0) | (567k,2) | (0,0) | |
| Xianning | (772.9k,2) | (454.9k,1) | (355.1k,2) | |
Table 5.
Time cost and transportation cost of real-world case.
| Relief supplies | Time cost (h) |
Transportation cost (CNY) |
||||
|---|---|---|---|---|---|---|
| Pickup | Transshipment | Delivery | Pickup | Transshipment | Delivery | |
| Food | 131.00 | 65.60 | 9.73 | 2906644.16 | 7287850.00 | 191696.00 |
| Mask | 82.97 | 10.40 | 36.83 | 3626481.24 | 1959192.42 | 77730.53 |
| Total cost | 336.53 | 16049594.34 | ||||
5.3. Comparative analysis of numerical results
To further verify the efficiency of proposed algorithm, comparisons with FA [19] and PSO [20] are conducted to solve the same case. The reason for choosing PSO and FA is that they both belong to Swarm Intelligent algorithm and they exhibit great performances on solving such combinatorial problems. The comparative results are given in Table 6 which are the best ones obtained by respective algorithms in 20 runs. From the table, it can be concluded that customized GWO makes better performance on solving the problem within a reasonable time. It is worth mentioning that running time of customized GWO is not the best, but it is in a reasonable range.
Table 6.
Comparisons among Customized GWO, FA and PSO.
| Algorithm | Cost |
Running time (s) | |
|---|---|---|---|
| Time cost (h) | Transportation cost (CNY) | ||
| Customized GWO | 336.53 | 16049594.34 | 27.32 |
| FA | 374.80 | 16276706.55 | 29.13 |
| PSO | 433.79 | 17057410.01 | 26.55 |
6. Management insights from the industrial case
As a sudden and fast-spread disease, COVID-19 pandemic caught related epidemic areas unawares. In the real-world case given in Section 5, when COVID-19 pandemic seriously breaks out, residents in epidemic areas need to stop working and keep themselves stay at home. Thus the production and economic activities in epidemic areas need to be suspended for weeks or even months until the epidemic is basically controlled. However, during this closure period, residents’ normal medical protection equipment and basic daily necessities need to be guaranteed in quantity and quality. Local reserves are often difficult to cover basic needs, so emergency supplies need to be transported from neighboring regions with sufficient supplies. For the epidemic areas, transportation time for basic emergency relief is in the first place since time means life. Besides, transportation is accompanied by a cost. Therefore, on the basis of meeting the transportation time and demand, the economy of transportation also needs to be considered. Therefore, in this study, we make efforts to design a practically time-efficient and cost-effective transportation network when faced with COVID-19. The results of the real-world case prove the efficiency of our methods and can provide significantly practical suggestions for related authorities. From such an industrial case, some practical management insights can be extracted and concluded for related government departments and transportation companies that undertake transportation tasks.
For relevant government departments, when COVID-19 pandemic suddenly broke out, it is of paramount importance to quickly control COVID-19 pandemic situation and ensure the stability of residents’ living order during the epidemic. The first aspect needing to consider is the isolation and medical measures for infected people and the medical protection for other residents, which requires timely transportation and guarantee of medical materials. The good living order of residents is based on enough food, so the basic food demand must be satisfied, which requires the timely guarantee of basic living materials. Therefore, the transportation network designed in this study is important for delivering necessary materials on time and on-demand, which also provides the basic safeguard of management for relevant government departments.
For related transportation companies which undertake such important transportation tasks, what they need to consider is transportation capacity and economic benefits. First of all, the transportation means (trucks, trains, and airplanes) should be sufficiently used and the transportation capacity should not exceed the limited standard, which requires that the balance between demand and capacity should be fully considered when designing the transportation network. In addition, transportation companies have economic costs. Minimizing total transportation cost on the basis of meeting transportation capacity is also an essential aspect of company operation. Therefore, the transportation network designed in this study also takes the transportation cost into account. In a word, the method proposed in our study can minimize the transportation cost for transportation company meanwhile catering to the transportation capacity, which has certain practical significance for related companies undertaking transportation tasks.
7. Conclusion
COVID-19 pandemic, a world-wide hazard disease, has spread over 210 countries with unbelievable speed. The suddenness of COVID-19 outbreak will lead to great shortage of basic living materials and medical protection products in the disaster-affected areas. Therefore, it is urgent to schedule aided materials from other nearer districts to injured areas. In this study, we make efforts to design a comprehensive multimodal transportation network with hub-and-spoke structure for transporting food and mask. Considering both transportation time efficiency and transportation cost, a bi-objective MINLP model is established. Due to its nonlinearity, related MIP solver cannot directly cope with it. In addition, as a NP-hard problem, it cannot be solved by exact algorithms with efficiency as the problem scales expand. Therefore, to solve such complex problem with efficiency, a meta-heuristic algorithm called customized GWO is designed and proposed in detail. Two stages are contained in proposed algorithm. In construction stage, transportation amount and transportation mode are well initialized. In improvement stage, HD move concept is introduced to further enhance solution accuracy. Taking the actual cases of Hubei Province as research background, the model is verified with real-world example. To prove that customized GWO is a promising approximation method to solve such problem, its performance is compared with other two state-of-the-art algorithms. The simulation results support the fact that our proposed algorithm can solve such problem with higher accuracy within a reasonable time.
The research has strong practical guiding significance for emergency relief supply transportation network design under COVID-19 pandemic. And some important management insights can be extracted and summarized for related government departments and transportation companies. For related government departments, this study can provide basic safeguards for medical aid and life order guarantee. For transportation companies undertaking transportation tasks, this study will guarantee both transportation capacities and economic benefits.
CRediT authorship contribution statement
Chi Li: Conceptualization, Programming, Validation. Peixiu Han: Conceptualization, Visualization, Writing – original draft. Min Zhou: Responsible for gathering information. Ming Gu: Writing – review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Remuzzi A., Remuzzi G. COVID-19 and Italy: What next? Lancet. 2020;395(10231):1225–1228. doi: 10.1016/S0140-6736(20)30627-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Alkan N., Kahraman C. Evaluation of government strategies against COVID-19 pandemic using Q-rung orthopair fuzzy TOPSIS method. Appl. Soft Comput. 2021;110 doi: 10.1016/j.asoc.2021.107653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Organisation for Economic Co-operation and Development N. OECD Publishing; 2020. The Face Mask Global Value Chain in the COVID-19 Outbreak: Evidence and Policy Lessons. [Google Scholar]
- 4.Bauchner H., Fontanarosa P.B., Livingston E.H. Conserving supply of personal protective equipment—A call for ideas. JAMA. 2020;323(19):1911. doi: 10.1001/jama.2020.4770. [DOI] [PubMed] [Google Scholar]
- 5.Cunha C.B., Silva M.R. A genetic algorithm for the problem of configuring a hub-and-spoke network for a LTL trucking company in Brazil. European J. Oper. Res. 2007;179(3):747–758. [Google Scholar]
- 6.Meng Q., Wang X. Intermodal hub-and-spoke network design: Incorporating multiple stakeholders and multi-type containers. Transp. Res. B. 2011;45(4):724–742. [Google Scholar]
- 7.Jeong S.-J., Lee C.-G., Bookbinder J.H. The European freight railway system as a hub-and-spoke network. Transp. Res. A. 2007;41(6):523–536. [Google Scholar]
- 8.Aykin T. Lagrangian relaxation based approaches to capacitated hub-and-spoke network design problem. European J. Oper. Res. 1994;79(3):501–523. [Google Scholar]
- 9.Kokash N. 2005. An introduction to heuristic algorithms; pp. 1–8. Department of Informatics and Telecommunications. [Google Scholar]
- 10.Žerovnik J. Heuristics for NP-hard optimization problems: Simpler is better!? Logist. Sustain. Transp. 2015;6(1):1–10. [Google Scholar]
- 11.Martí R., Reinelt G. Exact and Heuristic Methods in Combinatorial Optimization. 2022. Heuristic methods; pp. 27–57. [Google Scholar]
- 12.Mirjalili S., Mirjalili S.M., Lewis A. Grey wolf optimizer. Adv. Eng. Softw. 2014;69:46–61. [Google Scholar]
- 13.Nadimi-Shahraki M., Taghian S., Mirjalili S. An improved Grey Wolf Optimizer for solving engineering problems. Expert Syst. Appl. 2021;166 [Google Scholar]
- 14.Banaie-Dezfouli M., Nadimi-Shahraki M.H., Beheshti Z. R-GWO: Representative-based Grey Wolf Optimizer for solving engineering problems. Appl. Soft Comput. 2021;106 [Google Scholar]
- 15.Ghalambaz M., Yengejeh R.J., Davami A.H. Building energy optimization using Grey Wolf Optimizer (GWO) Case Stud. Therm. Eng. 2021;27 [Google Scholar]
- 16.Seyyedabbasi A., Kiani F. I-GWO and Ex-GWO: Improved algorithms of the Grey Wolf Optimizer to solve global optimization problems. Eng. Comput. 2021;37(1):509–532. [Google Scholar]
- 17.Goli A., Zare H.K., Tavakkoli-Moghaddam R., Sadeghieh A. 2019. An improved artificial intelligence based on gray wolf optimization and cultural algorithm to predict demand for dairy products: A case study. [DOI] [PubMed] [Google Scholar]
- 18.Rezk H., Arfaoui J., Gomaa M.R. Optimal parameter estimation of solar PV panel based on hybrid particle swarm and grey wolf optimization algorithms. Int. J. Interact. Multimed. Artif. Intell. 2021 [Google Scholar]
- 19.Altabeeb A.M., Mohsen A.M., Ghallab A. An improved hybrid firefly algorithm for capacitated vehicle routing problem. Appl. Soft Comput. 2019;84 [Google Scholar]
- 20.Ai T.J., Kachitvichyanukul V. Particle swarm optimization and two solution representations for solving the capacitated vehicle routing problem. Comput. Ind. Eng. 2009;56(1):380–387. [Google Scholar]
- 21.Pettit S.J., Beresford A.K. Emergency relief logistics: An evaluation of military, non-military and composite response models. Int. J. Logist.: Res. Appl. 2005;8(4):313–331. [Google Scholar]
- 22.Sheu J.-B. An emergency logistics distribution approach for quick response to urgent relief demand in disasters. Transp. Res. E: Logist. Transp. Rev. 2007;43(6):687–709. [Google Scholar]
- 23.Lei F. 2007 IEEE International Conference on Grey Systems and Intelligent Services. IEEE; 2007. Dynamic multi-objective emergency relief logistics: A decision support system framework; pp. 779–783. [Google Scholar]
- 24.Altay N. Large-Scale Disasters: Prediction, Control, and Mitigation. 2008. Issues in disaster relief logistics; pp. 120–146. [Google Scholar]
- 25.Oloruntoba R., Gray R. Customer service in emergency relief chains. Int. J. Phys. Distrib. Logist. Manage. 2009 [Google Scholar]
- 26.Hu Z.-H. A container multimodal transportation scheduling approach based on immune affinity model for emergency relief. Expert Syst. Appl. 2011;38(3):2632–2639. [Google Scholar]
- 27.Bozorgi-Amiri A., Jabalameli M.S., Al-e Hashem S.M. A multi-objective robust stochastic programming model for disaster relief logistics under uncertainty. OR Spectrum. 2013;35(4):905–933. [Google Scholar]
- 28.Rezaei-Malek M., Tavakkoli-Moghaddam R. Robust humanitarian relief logistics network planning. Uncertain Supply Chain Manag. 2014;2(2):73–96. [Google Scholar]
- 29.Liu Y., Lei H., Zhang D., Wu Z. Robust optimization for relief logistics planning under uncertainties in demand and transportation time. Appl. Math. Model. 2018;55:262–280. [Google Scholar]
- 30.Li S., Teo K.L. Post-disaster multi-period road network repair: Work scheduling and relief logistics optimization. Ann. Oper. Res. 2019;283(1):1345–1385. [Google Scholar]
- 31.Davoodi S.M.R., Goli A. An integrated disaster relief model based on covering tour using hybrid benders decomposition and variable neighborhood search: Application in the Iranian context. Comput. Ind. Eng. 2019;130:370–380. [Google Scholar]
- 32.Boostani A., Jolai F., Bozorgi-Amiri A. Designing a sustainable humanitarian relief logistics model in pre-and postdisaster management. Int. J. Sustain. Transp. 2020:1–17. [Google Scholar]
- 33.Korayem L., Khorsid M., Kassem S. Using grey wolf algorithm to solve the capacitated vehicle routing problem. IOP Conf. Ser.: Mater. Sci. Eng. 2015;83(1) [Google Scholar]
- 34.Sopto D.S., Ayon S.I., Akhand M., Siddique N. Modified grey wolf optimization to solve traveling salesman problem. 2018 International Conference on Innovation in Engineering and Technology; ICIET; IEEE; 2018. pp. 1–4. [Google Scholar]
- 35.Panwar K., Deep K. Discrete Grey Wolf Optimizer for symmetric travelling salesman problem. Appl. Soft Comput. 2021;105 [Google Scholar]
- 36.Faris H., Aljarah I., Al-Betar M.A., Mirjalili S. Grey Wolf Optimizer: A review of recent variants and applications. Neural Comput. Appl. 2018;30(2):413–435. [Google Scholar]
- 37.Tirkolaee E.B., Goli A., Ghasemi P., Goodarzian F. Designing a sustainable closed-loop supply chain network of face masks during the COVID-19 pandemic: Pareto-based algorithms. J. Clean. Prod. 2022;333 doi: 10.1016/j.jclepro.2021.130056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Dur-e Ahmad M., Imran M. Transmission dynamics model of coronavirus COVID-19 for the outbreak in most affected countries of the world. Int. J. Interact. Multimed. Artif. Intell. 2020 [Google Scholar]
- 39.M. Norouzi, D.J. Fleet, R.R. Salakhutdinov, Hamming distance metric learning, in: Advances in Neural Information Processing Systems, 2012, pp. 1061–1069.