Local circuit amplification of spatial selectivity in the hippocampus

Abstract

Local circuit architecture facilitates the emergence of feature selectivity in the cerebral cortex¹. In the hippocampus, it remains unknown whether local computations supported by specific connectivity motifs² regulate the spatial receptive fields of pyramidal cells³. Here we developed an in vivo electroporation method for monosynaptic retrograde tracing⁴ and optogenetics manipulation at single-cell resolution to interrogate the dynamic interaction of place cells with their microcircuitry during navigation. We found a local circuit mechanism in CA1 whereby the spatial tuning of an individual place cell can propagate to a functionally recurrent subnetwork⁵ to which it belongs. The emergence of place fields in individual neurons led to the development of inverse selectivity in a subset of their presynaptic interneurons, and recruited functionally coupled place cells at that location. Thus, the spatial selectivity of single CA1 neurons is amplified through local circuit plasticity to enable effective multi-neuronal representations that can flexibly scale environmental features locally without degrading the feedforward input structure.

Hippocampal functions that support memory and navigation⁶ are traditionally investigated at the level of feature selectivity in single place cells⁷ or circuit-level representations such as cognitive maps⁸, which leaves a major disconnect between these levels of implementation. Mesoscale circuit motifs that emerge from small numbers of functionally arranged excitatory principal cells and inhibitory interneurons are posited to bridge the gap between single-cell operations and macroscopic cognitive functions^9,10. Indeed, manipulation of individual cells has been shown to elicit detectable effects on circuit dynamics and ultimately behaviour¹¹, exemplifying the importance of understanding how single neurons are embedded within multicellular ensembles to perform specific functions¹². In the hippocampus, the functional organization of identified local circuits has been largely unexplored. In the traditional view of hippocampal area CA1, spatial tuning emerges in a subset of pyramidal cells on the basis of their feedforward inputs¹³, and thus, it remains unknown whether CA1 can also flexibly regulate spatial selectivity through local computations. This major knowledge gap stems from difficulties in accessing synaptically coupled microcircuits in vivo, and in unambiguously restricting optogenetic manipulations to individual neurons, particularly within the dense structure of the pyramidal cell layer. Here we leveraged single-cell labelling, tracing and optogenetics manipulations to uncover the mesoscale determinants of CA1 circuit functions.

Single-cell retrograde tracing in CA1

We first adapted a single-cell electroporation approach^4,9 and applied it to the mouse dorsal hippocampus to genetically label neurons in vivo and perform monosynaptic rabies (RABV) tracing¹⁴ from single CA1 starter pyramidal cells (Fig 1a). An individual neuron was electroporated with three plasmids: the RABV-TVA receptor, the glycoprotein (G) and a fluorescent protein (Venus) (Fig. 1b). Two days after electroporation, an envelope-A (EnvA) coated, G-deleted N2C tdTomato-RABV¹⁴ was injected in the vicinity of the starter cell (Fig. 1c). After 10–14 days, tdTomato-expressing presynaptic neurons could be seen throughout the hippocampus (Fig. 1c-e, Extended Data Fig. 1, Supplementary Table 1). Our quantification of the connectivity within CA1 revealed that 90.7 ± 0.02% (mean ± s.d.) of the local inputs to a starter pyramidal cell were inhibitory interneurons (Extended Data Fig. 1).

Fig. 1 ∣. In vivo single-cell electroporation and monosynaptic rabies tracing in hippocampal region CA1.

a, Schematic of in vivo two-photon (2p)-guided electroporation in a CA1 starter pyramidal cell (PC). DG, dentate gyrus; SO, stratum oriens; SP, stratum pyramidale; SR, stratum radiatum. b, Time lapse of electroporation (top) and expression (bottom). c, Schematic of retrograde tracing. d, Light-sheet image showing presynaptic neurons (red) and the starter neuron in CA1 (green). D, dorsal axis; M, medial axis; P, posterior axis. e, Distribution (mean ± s.e.m.) of presynaptic neurons (n = 6 mice) in the hippocampus. Two-way ANOVA (region × hemisphere), interaction, P = 0.079. Post-hoc Tukey’s tests: CA1 × CA2, P = 0.037; CA1 × CA3, P = 0.001; CA2 × CA3, P < 10⁻¹⁰; ipsilateral (ipsi.) × contralateral (contra.), P < 10⁻¹⁰ (adjusted for multiple comparisons). f, Experimental timeline for imaging and labelling interneurons presynaptic to a starter PC. g, Expression of the calcium indicator GCaMP is restricted to inhibitory interneurons using a VGAT-Cre driver line. h, One starter PC is electroporated with GCaMP and genes for the modified RABV. i, Z-stack projection after two-photon imaging, before (left) and after (right) RABV injection. j, During imaging, mice run on a treadmill for randomly delivered water rewards. The identity of each recorded interneuron is assessed on the basis of rabies tdTomato expression 14–21 days after data collection. Scale bars, 50 μm (all images).

We next sought to interrogate the functional coupling of individual place cells with their local presynaptic partners using this method. Given the larger number of local inhibitory connections, we examined whether spatial tuning in a starter pyramidal cell could vary with the level of inhibition provided by its presynaptic interneurons (Fig. 1f). To do so, we expressed a genetically encoded Ca²⁺ indicator (GcaMP7) in all inhibitory interneurons using the VGAT-Cre driver line (Fig. 1g). In the same mouse, we electroporated a starter pyramidal cell with to express the receptor TVA, the RABV-G, GCaMP and mRuby3 acting as a static marker (Fig. 1h). The mice were trained to run on a linear treadmill enriched with sensory cues¹⁵, and we then performed two-photon imaging of the starter cell and local interneurons using large-scale volumetric methods¹⁶ (Fig. 1i). Injection of the tdTomato-RABV was subsequent to two-photon imaging to prevent potential toxicity confounds inherent to RABV (Fig. 1i). Thus, the identity of each interneuron (tdTomato-expressing presynaptic versus non-expressing unlabelled) was mapped retrospectively to its in vivo dynamics 14–21 days after RABV injection (Fig. 1j). In total, we recorded 19 starter pyramidal cells together with their respective presynaptic interneurons, which we will refer to as ‘network’ (Supplementary Table 2).

Inhibition during place field formation

We first parcelled each imaging session on the basis of the spatial response of the starter pyramidal cell. In 11 of the 19 networks, we recorded the spontaneous formation of a place field, defined by the sudden appearance of a large-amplitude Ca²⁺ transient and smaller repeated events in the following traversals¹⁷ (Extended Data Fig. 2a). The appearance of this first event did not coincide with a change in the activity levels of the presynaptic interneurons, as a global decrease in activity was not observed preceding the lap of formation (Extended Data Fig. 2b, c), nor was a local reconfiguration of their spatial response observed at that location (Extended Data Fig. 2d, e). To quantify the response on a cell-by-cell basis, we calculated the in-field selectivity (IFS) index, a measure for whether a given interneuron is more (IFS closer to 1) or less (IFS closer to −1) active within the starter’s place field than outside. Using this index, we assessed the change in activity around the place field location but did not detect significant changes during the formation lap, in the laps preceding the formation, or in those following it (Extended Data Fig. 2f, g). These results show that presynaptic inhibition stayed relatively constant during and immediately after the formation of a place field in their target pyramidal cell, arguing for a lack of major contribution from interneurons in this process.

Presynaptic inhibition is inversely tuned

We next examined whether the spatial activity of interneurons was different when the starter pyramidal cell had an already established place field. In 8 of the 19 networks, the activity of the starter cell was selective to a specific location on the belt (place cell) from the first lap of the session (Fig. 2a, b). The activity of the interneurons was high across the belt¹⁶ (Fig. 2a, b), but we observed that presynaptic interneurons had lower activity than the unlabelled ones during the traversal of the place field (Fig. 2a, b). The difference in activity between the two populations was indeed significantly different only in the close vicinity of the place field peak (Fig. 2c, d). To examine this effect on a cell-by-cell basis, we used the IFS index to quantify the degree of selectivity in each population. We found that presynaptic interneurons had significantly more negative IFS values (Fig. 2e), indicating that the overall decrease seen at the population level was not driven by a small number of interneurons with large negative responses. We computed an average IFS value for each network and observed the same effect (Fig. 2f, ‘data’). By contrast, the two populations were not significantly different when the IFS index was computed at a random location on the belt, irrespective of the location of the place field (Fig. 2f, ‘shuffled’), or when the starter cell was not spatially tuned (Extended Data Fig. 3a-d). These results demonstrate that presynaptic inhibition is lower during the traversal of a stable spatial receptive field, but not that of a newly formed one. In four of the eight networks analysed above, we recorded the formation of the field in a directly preceding session (Extended Data Fig. 3e, f), and found that the rest period between the two sessions induced a substantial reconfiguration that led to the negative tuning in the presynaptic interneurons (Extended Data Fig. 3g-j). Together, these results show that the emergence of a spatial receptive field in place cells triggers plastic reorganization in CA1 local circuits that ultimately leads to negative selectivity in their own presynaptic inhibitory ensemble.

Fig. 2 ∣. Interneurons presynaptic to a place cell exhibit inverse spatial selectivity.

a, Representative fluorescence traces of the starter PC and its presynaptic interneurons during navigation. b, Activity heat maps along the belt (x axis) as a function of laps (y axis). Blue outline, starter PC; orange outlines, presynaptic interneurons. c, Spatial tuning curves (mean ± s.e.m.) centred around the peak of the starter’s place field (n = 8 mice (8 networks)). Blue area with dashed lines represents the average place field size: 33.2 ± 3.8 cm (mean ± s.e.m.). d, Difference in activity (mean ± s.e.m.) between the presynaptic and unlabelled interneurons from b, and P value as a function of position (purple). Shaded purple area indicates P < 0.05 (paired t-test). e, IFS index for all presynaptic (orange; n = 152) and unlabelled (grey; n = 1,235) neurons (Kolmogorov–Smirnov two-sample test, P = 0.005). Negative IFS indicates negative selectivity in the starter’s place field. Inset: mean ± s.e.m. (t-test, P = 0.002). f, IFS values (mean±s.e.m.) for all eight networks (data; paired t-test, P = 0.001) and after shuffling the position (shuffled; paired t-test, P = 0.08) of the starter’s place field to recompute random IFS values (data versus shuffled for presynaptic, P = 0.023; unlabelled, P = 0.56, paired t-tests). NS, not significant.

Reorganization of interneuron dynamics

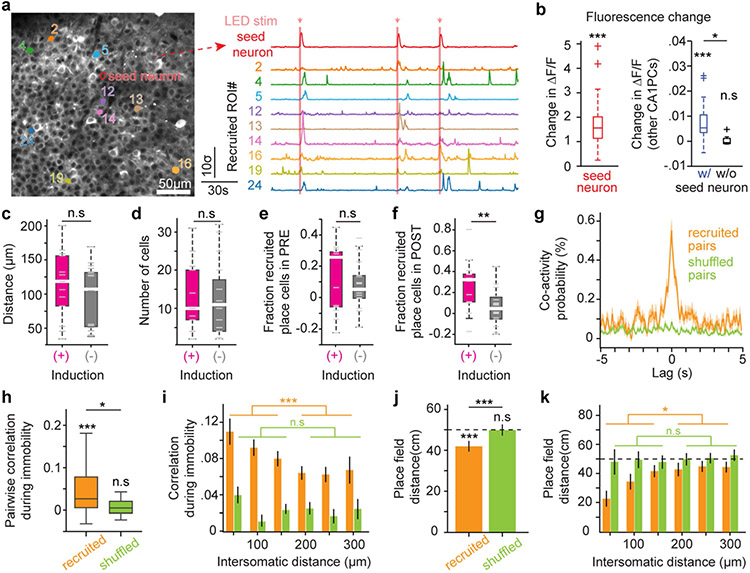
Thus far, we found that local circuit plasticity can promote correlative dynamics between single-cell representations and interneuron selectivity during navigation. It remains unknown, however, whether place cellscan individually generate such location-specific reconfigurations. To causally test this hypothesis, we developed an optogenetic approach to induce individual place fields at predetermined locations¹⁷, while longitudinally tracking the reorganization that this generates from an experimenter-defined time-zero (Supplementary Table 3). We electroporated a single pyramidal cell, referred to as seed neuron, with a red-shifted excitatory opsin (Fig. 3a) that we photostimulated¹⁸ at an arbitrary location (in a PRE session) to generate a place field that could last in post-stimulation laps after rest (POST session) in the home cage (7 successful sessions out of 14, n = 6 mice) (Fig. 3b). We used this procedure in VGAT-Cre mice to monitor how the controlled implantation of a place cell reconfigured interneuronal dynamics at this location (Fig. 3c). Consistent with previous reports¹⁹, the seed stimulations increased the activity of interneurons above baseline (Fig. 3d, Extended Data Fig. 4a, b), and without noticeable changes in behaviour (Extended Data Fig. 4c, d). When induction was successful (+), a subset of interneurons reconfigured their spatial response to develop inverse tuning around that location in the POST session (Fig. 3e, f). We quantified the degree of inverse selectivity on a cell-by-cell basis (Fig. 3g), and observed that the increase in activity in the induction laps in the PRE session correlated with how strongly anti-selective an interneuron would become in the POST session (Fig. 3h, Extended Data Fig. 4c, d). This reorganization pattern was not present when induction failed (−) or during laps immediately following photostimulation (Extended Data Fig. 5a-d), consistent with the development of inverse selectivity not directly following endogenous place field formation in our first set of experiments. Similarly, the induced location was not already biased with a higher fraction of negatively selective interneurons before induction (Extended Data Fig. 5e-g). Together, these results provide evidence that place field formation in an individual CA1 pyramidal cell can robustly promote plastic reorganization in local circuits.

Fig. 3 ∣. Optogenetic place field induction in single pyramidal cells reorganizes interneuron networks.

a, A single PC (seed) is electroporated with a red-shifted excitatory opsin and GCaMP. Optogenetics stimulations (LED) evoke large-amplitude responses. Scale bars, 15 μm. b, Repeated optogenetics stimulations can induce a lasting place field (+) (in magenta). Failed induction sessions (−) (in grey) are used as controls in the following analyses. Place fields were induced in a PRE session and recorded again in a POST session. c, Z-stack projection showing GCaMP7f-expressing interneurons (green) and the seed neuron (red). Scale bar, 50 μm. d, Photostimulation of the seed neuron during place field induction increases interneuron activity. e, Spatial tuning curve for all interneurons before (PRE) and after (POST) induction. Interneurons are ordered by their IFS, and centred around the induced location. A fraction of interneurons develops negative selectivity after successful inductions. f, Average IFS values (n = 7 for each condition from 6 mice). PRE versus POST for (−), P = 0.86; (+), P = 0.04 (Wilcoxon rank-sum tests). g, IFS values for all interneurons (n = 6 mice) show the development of negative selectivity after successful induction: (+), n = 1,208, P < 10⁻¹⁰; (−), n = 1,191, P = 0.24 (Wilcoxon signed rank-tests). (+) versus (−), P < 10⁻⁵ (Wilcoxon rank-sum test). h, On a cell-by-cell basis, the increased activity during induction laps in PRE correlates with negative selectivity in POST: (+), n = 792, P = 0.004; (−), n = 496, P = 0.86 (Pearson’s R). All box plots represent median (central line) and interquartile range (25th and 75th percentile); whiskers extend to the most-extreme data points (excluding outliers).

Pyramidal cells are functionally coupled

To further understand the extent to which a single pyramidal cell can influence the local circuitry, we next examined the effects exerted on the local pyramidal population. We induced seed neurons as described above (Fig. 3b) while performing large-scale population imaging (Fig. 4a). We observed that photostimulation of the seed neuron increased the number of Ca²⁺ events in other local pyramidal cells²⁰ (Fig. 4b, Extended Data Fig. 6a, b), which was not seen before any seed was electroporated in the brain, indicating that photostimulations alone cannot explain this effect (Fig. 4c). We found that the pyramidal cells that exhibited an increased response to photostimulations–referred to as recruited neurons (across sessions mean ± s.e.m.: 12.6 ± 1.6 neurons, Extended Data Fig. 6c-f)–were significantly more likely to be spatially tuned in the POST session (Fig. 4e). Notably, this quantification was restricted to the recruited neurons that were not already tuned in the PRE session, and this effect was seen only when induction was successful (Fig. 4e). In addition, the distribution of fields for these new place cells in the POST session had a higher density around the location where the seed pyramidal cell was induced in the PRE session (Fig. 4f, g, Extended Data Fig. 7). Together, these results show that the successful formation of a place field in an individual seed neuron can recruit a subset of pyramidal cells that will become spatially tuned at that location. Finally, we detected traces of this ensemble organization during periods of immobility and navigation before induction of the seed neuron, demonstrating the presence of already coupled pyramidal cells with distance-dependent like-to-like relationships (Extended Data Fig. 6g-k, Extended Data Fig. 4g-j). With such configuration, CA1 circuits can thus propagate spatial representations that originate in an individual neuron to a multicellular assembly, without biasing the global representation of the context at the population level (Extended Data Fig. 7).

Fig. 4 ∣. Recruitment of local pyramidal cells during place field induction is consistent with a subnetwork architecture.

a, Representative field of view with all CA1 PCs expressing GCaMP and one seed (red) electroporated with bReaChES-mRuby3. Scale bar, 50 μm. b, Photostimulations (arrows) drive the seed neuron and evoke somatic activity in other PCs. All of the following data were collected from 31 induction sessions (13 successful and 18 failures, n = 13 mice). c, Histogram of calcium transient onsets centred around optogenetic stimulations in time. Top, distribution for all seed neurons. Bottom, distribution for other PCs in the presence (blue) or absence (black) of an electroporated seed neuron (shaded area indicates bins in which P < 0.05, Fisher Z-test of proportions). d, Intersomatic distance to the seed neuron for PCs recruited by photostimulations (n = 405). e, Fraction of new spatially selective PCs in POST. Shuffled ID indicates a randomly chosen subset of neurons matching the number of recruited cells in a given session. POST (+), P = 0.003; POST (−), P = 0.4 (one-way ANOVAs, with post-hoc Tukey’s tests and P values adjusted for multiple comparisons: recruited versus non-recruited: P = 0.0093, recruited versus shuffled: P = 0.0058). Recruited (POST(+) versus POST(−)), P = 0.006 (Wilcoxon rank-sum test). f, Place fields of recruited PCs are more concentrated around the induced location in POST (+). g, Distribution of place field centroids from f. POST (+) versus POST (−), P = 0.006 (Kolmogorov–Smirnov two-sample test). Uniformity test for POST (+), n = 39, P = 0.019, and POST (−), n = 40, P = 0.30. h, Experimental findings can be explained by a computational model with subnetwork architecture. i, Model of de novo place field formation in a seed neuron with representative tuning curves at three different time points. Average activity from 40 simulated seeds. j, Left, emergence of a field has virtually no effect on neurons outside the subnetwork of the seeds. Right, within the subnetwork, the location is amplified by other PCs and interneurons become negatively selective. All box plots represent median (central line) and interquartile range (25th and 75th percentile); whiskers extend to the most-extreme data points (excluding outliers).

Subnetwork structure of the CA1 circuit

Finally, to investigate what structure and plasticity rules are necessary to support our experimental data, we developed a computational model of hippocampal region CA1 (Supplementary Table 4). First, we found that the dynamics we observed could not emerge out of single-cell interactions, such that a single seed pyramidal cell alone does not provide a strong enough input to induce interneuron reorganization (Extended Data Fig. 8a-d). We then introduced some degree of connection specificity through a subnetwork architecture, in which the seed neuron was part of an ensemble of other pyramidal cells and interneurons connected above chance level (Fig. 4h). The emergence of a place field in a seed pyramidal cell increased the response of its postsynaptic pyramidal partners mainly within the subnetwork (Fig. 4i, j, before field formation versus during field formation). When we introduced short-term synaptic depression at pyramidal-to-interneuron synapses¹⁹, this sequence of events deprived interneurons specifically within the subnetwork of their specific excitatory input at the target location (Fig. 4j, after field formation) and thus developed a selective decrease in their activity where the field was initially formed. Finally, the decreased level of inhibition in turn facilitates the amplification of this location by other pyramidal cells of the subnetwork (Extended Data Fig. 9a). This model is consistent with subnetwork of different sizes (Extended Data Fig. 8e-h), but the reciprocal coupling between pyramidal cells and interneurons within the subnetwork as well as specific pyramidal cell interconnectivity are necessary to recapitulate our observations (Extended Data Fig. 9b-e). An alternative model based on direct disinhibitory circuitry could not recapitulate our findings (Extended Data Fig. 10).

Discussion

Our results provide insights into the microcircuit mechanisms that underlie feature selectivity in CA1, and are consistent with a lack of a permissive role for disinhibition in place field formation²¹ but argue against spatially uniform inhibition during place field maintenance. Moreover, CA1 pyramidal cells do not operate as independent coding units. Rather, coordinated connectivity and plasticity between co-active pyramidal cells and associated inhibitory subnetworks enable feature-selective responses initiated in single cells to scale adaptively to multicellular assemblies. This local amplification could enable flexible and efficient encoding of behaviourally relevant environmental features locally within the CA1 region. Finally, our results suggest that CA1 pyramidal cells are more functionally coupled than previously considered. The nature of these connections may be monosynaptic²⁰, polysynaptic with non-random motifs²² or through gap junctions²³. Short-term synaptic plasticity of excitatory input and inhibitory output synapses of interneurons²⁴ could also contribute to the local circuit reorganization we describe. We speculate that such subnetwork structure may be optimized for providing CA1 with the ability to assign behavioural salience to CA3 representations through local circuit amplification, without compromising overall storage capacity or specificity.

The precise anatomical organization and fine-scale subnetwork connectivity that underlie the initial motif structure and govern its propagation are at present unknown. They can arise during development^25,26 or from experience-dependent structural plasticity²⁷. Furthermore, the gradual expression of local circuit reorganization suggests that an initial, rapid place field formation event¹⁷ in an individual or a few seed neurons can subsequently propagate through their associated subnetwork through slower and more-graded plasticity mechanisms. The precise loci and molecular mechanisms of neural plasticity^28,29 that underlie this local circuit amplification of feature selectivity remain to be determined.

Methods

Mice

All experiments were conducted in accordance with National Institutes of Health (NIH) guidelines and with the approval of the Columbia University Institutional Animal Care and Use Committee. Experiments were performed with healthy, 3-month-old heterozygous adult male and female VGAT-ires-Cre (Jackson Laboratory, 016962), VIP-ires-Cre (Jackson Laboratory, 031628), R26R-EYFP (Jackson Laboratory, 006148) crossed with VGAT-ires-Cre, or wild-type (Jackson Laboratory, 000664) mice on a C57BL/6J background. Mice were kept in the vivarium on a reversed 12-h light–dark cycle and were housed with 3–5 mice per cage (temperature, 22–23 °C; humidity, 40%).

Viruses

Cre-dependent recombinant adeno-associated virus (rAAV) expressing GCaMP7f under the control of the synapsin promoter (rAAV1-Syn-FLEX-GCaMP7f-WPRE-Sv40, Addgene 104492, titre: 1 × 10¹³ vg ml⁻¹) was used to express GCaMP7f in VGAT-expressing interneurons or VIP-expressing interneurons. For pyramidal cell (PC) imaging, we used a forward GCaMP6f-expressing AAV (Addgene 100833, titre: 1 × 10¹³ vg ml⁻¹).

Rabies virus production

EnvA-pseudotyped CVS-N2c rabies virus was produced essentially as described previously¹⁴. In brief, rabies virus was rescued by transfection of CVS-N2cΔG-tdTomato genomic plasmid, with mammalian expression plasmids for rabies virus genes P, L and M along with T7 RNA polymerase in Neuro2A cells. Six days after transfection, supernatant containing G-coated viral particles was collected and further amplified on Neuro2A cells stably expressing rabies G. After a further seven days the supernatant was collected, filtered and applied to Neuro2A cells stably expressing the EnvA glycoprotein. After washing to remove G-coated rabies virus, EnvA-coated virus was collected after seven days, filtered and concentrated by centrifugation. Viral titre was measured on HEK293 cells expressing the TVA receptor.

AAV injections and hippocampal window and headpost implant

For viral injections, 3–5-month-old mice were anaesthetized with isoflurane and placed into a stereotaxic apparatus. Meloxicam and bupivacaine were administered subcutaneously to minimize discomfort. After the skin was cut in the midline to expose the skull, the skull was levelled and a craniotomy was made over the right hippocampus using a drill. A sterile glass capillary loaded with rAAV was attached to a Nanoject syringe (Drummond Scientific) and slowly lowered into the right hippocampus. Dorsal CA1 was targeted at coordinates anteroposterior (AP) −2.2, mediolateral (ML) −1.75, dorsoventral (DV) −1.8, −1.6, −1.4, −1.2, −1 for interneuron imaging, and DV −1.2 and −1.0 mm for PC imaging, relative to Bregma, with 25 nl of virus injected at each DV location. After injection, the pipette was left in place for 5–10 min and slowly retracted from the brain. The skin was closed with several sutures and the mice were allowed to recover for four days before the window and headpost implant.

For CA1 window and headpost implant, the injected mice were anaesthetized with isoflurane and placed into the stereotaxic apparatus. After subcutaneous administration of meloxicam and bupivacaine, the skull was exposed and levelled, and a 3-mm craniotomy was made over the right hippocampus, centred on coordinates AP −2.2, ML −1.75 relative to Bregma. The dura overlying the cortex was removed, and the cortex overlying the hippocampus was slowly removed with negative pressure while the ice-cold cortex buffer was simultaneously applied. This process was performed until the white, horizontal fibres overlying CA1 became visible and any bleeding subsided. A stainless-steel cannula fitted with a glass window was inserted into the craniotomy and secured in place with Vetbond applied on the skull. Subsequently, dental cement was applied to the entire skull, and a headpost was affixed to the posterior skull with dental cement. The mice received a 1.0-ml subcutaneous injection of phosphate-buffered saline (PBS) and recovered in their home cage while heat was applied. The mice were monitored for three days post-operatively until behavioural training began.

Plasmid DNA

pCAG-TVA800-WT-HA was assembled by in-fusion cloning using Addgene plasmid 15778 (gift from E. Callaway). Notably, the HA-coding sequence was included in the primer sequences to allow for seamless HA insertion during fusion of the TVA-PCR product into the linearized XhoI/NotI pCAG vector backbone. pCAGGS-N2c(G) was a gift from T. Jessel, Addgene plasmid 73481. pCAG-GCaMP7s was assembled by in-fusion cloning using Addgene plasmid 104487 (gift from D. Kim) for PCR amplification as a template and inserted into NotI/XhoI sites of a pCAG-vector backbone according to the manufacturer’s instructions. pCAG-bReaChES-mRuby3 and pCAG-ChRmine-mScarlet were constructed through infusion cloning using pAAV-CaMKIIa-bReaChES-TS-mRuby3 and pAAV-CaMKIIa-ChRmine-TS-mScarlet as a PCR template (gifts from K. Deisseroth) into XhoI/NotI sites of a pCAG-vector backbone. The pCAG-Cre-mRuby fusion was constructed in a two-step infusion cloning process using pCAG-Cre (Addgene plasmid 13775, gift from C. Cepko) and pCAG-mRuby3 (Addgene plasmid 107744, gift from R. Larsen) as PCR templates to result in a Cre-mRuby fusion single ORF. The PCR products were inserted in frame XhoI/NotI restriction sites of a pCAG vector backbone.

Single-cell electroporation

Two-photon guided electroporation was adapted from previously described protocols⁴. Borosilicate glass pipettes (5–10 MΩ) were pulled (DMZ Zeitz-Puller) and filled with an intracellular solution (155 mM potassium gluconate, 10 mM HEPES, 10 mM KCl, 40 mM KOH, with 7.3 pH, 316 mOsm), Alexa Fluor 488 hydrazide (100 μM) and a cocktail of plasmid DNA. Plasmid concentration ranged between 50 and 150 ng μl⁻¹, without exceeding a total concentration of 300 ng μl⁻¹. Pipettes were positioned using a micromanipulator (Scientifica). Before entering the brain, a positive pressure (around 30 mBar) was applied. Pipettes were lowered in the brain until the resistance increased by 20%. At this point, electroporation was performed by applying electrical pulses. The pulses for the electroporation were powered using a stimulator (ISO-Flex), generated by a digitizer (Axon Digidata 1550B) and gated with a custom-made electronic circuit. Individual neurons were electroporated with a single pulse train at −5 V, 100 Hz, 0.5 ms pulse width, 1 s duration. The success of the electroporation was assessed by the spread of dye into the cell, and by subsequent removal of the pipette from the area without pulling the electroporated cell away. Protein expression was confirmed no less than 48 h after electroporation. Given the geometry of the brain and the design of our cannula, all electroporated neurons in CA1 resided in the intermediate portion of the proximo-distal axis. Similarly, all electroporated neurons were located in the deep portion of the PC layer (closer to stratum oriens) for technical reasons such as limiting the chance of clogging the pipette tip and preventing inadvertent electroporation of adjacent neurons.

Injection of rabies virus

After imaging data were collected, 0.25–0.5 μl of EnvA-N2cdG-tdTomato rabies virus (with a titre of 1 × 10⁸ infectious units per ml) was loaded in an approximately 3 MΩ pipette and injected near the site of electroporation. Expression of tdTomato became visible no less than 35 days after electroporation and was monitored daily for up to 21 days after injection.

Perfusion and tissue processing

After the completion of imaging experiments, mice were transcardially perfused with 40 ml of PBS (Thermo Fisher Scientific), followed by 40 ml of 4% paraformaldehyde (PFA, Electron Microscopy Sciences). Brains were stored overnight in 4% PFA at 4°C. The next day, the 4% PFA was removed and the brains were rinsed 3 × 5 min in PBS. Seventy-five-micrometre horizontal sections of the imaged hippocampus were cut on a vibrating microtome (Leica VT1200S) and washed 3 × 15 min in PBS. Subsequently, sections were permeabilized for 2 × 20 min in PBS with 0.3% Triton X-100 (Sigma-Aldrich). Blocking was then performed with 10% normal donkey serum (Jackson ImmunoResearch, 017-000-121) in PBST (PBS with 0.3% Triton X-100) for 45 min. The sections were then incubated in a PBS solution containing primary antibodies (see below for antibody information and dilutions) for one hour at room temperature, followed by two days at 4 °C. After two days, the primary antibody solution was removed from the slices and the slices were washed 3 × 15 min in PBS to remove unbound primary antibodies. The slices were subsequently incubated in a PBS solution containing a mixture of appropriate secondary antibodies conjugated to fluorescent labels (see below for antibody information and dilutions) for 2 h at room temperature. The sections were then washed 5 × 15 min in PBS at room temperature. Finally, sections were mounted on glass slides in Fluoromount-G aqueous mounting medium (Thermo Fisher Scientific) and coverslipped. The slides were allowed to dry at 4 °C for at least one day before imaging using a confocal microscope (Nikon A1R). Confocal micrographs were analysed using ImageJ 2.0.0 (NIH).

Whole-brain clearing was performed with the iDISCO+ protocol. Mice were perfused as described above and the brains were fixed overnight in 4% PFA. The brains were then slowly dehydrated in a methanol and water series, incubated in a dichloromethane (DCM) and methanol mixture, bleached in 5% hydrogen peroxide in methanol, and slowly rehydrated in a methanol and water series. The brains were then washed in a Triton X solution and incubated in a permeabilization solution for two days and then in a blocking solution for two days. The samples were subsequently incubated in primary antibody solution for seven days, washed, incubated in secondary antibody solution for seven days and washed again. Finally, brains were dehydrated in a methanol and water series, incubated first in a DCM and methanol mixture and then in 100% DCM, and stored in dibenzyl ether until imaging. Imaging was performed with a light sheet microscope (Ultramicroscope II, Miltenyi Biotec) and analysed using Imaris 9.5 (Bitplane).

Immunohistochemistry

Signals from red fluorescent proteins were amplified using the primary antibody guinea pig anti-RFP diluted 1:500 (Synaptic Systems, 390 005) and the conjugated secondary antibody donkey anti-guinea pig Rhodamine Red undiluted (Jackson, 706-295-148, 137877). Signals from green fluorescent proteins were amplified using the primary antibody chicken anti-GFP diluted 1:500 (AbCam, ab13970, GR236651-17) and the conjugated secondary antibody donkey anti-chicken Alexa 488 undiluted (Jackson, 703-545-155, 138498).

Two-photon imaging

Imaging was conducted using a two-photon 8-kHz resonant scanner (Bruker) with a piezoelectric crystal coupled to the objective as described previously¹⁸ or an AOD microscope (ATLAS, Femtonics) as described previously¹⁶. The objective was a Nikon 16× NIR water immersion, 0.8 NA, 3.0 mm working distance. The excitation laser was 920 nm (50–100 mW, Coherent). For some structural images in red, the laser was tuned to 960 nm or performed with a 1,070-nm fiber laser (Fidelity). Red (tdTomato or mRuby3) and green (GCaMP7f) channels were separated by emission cubes. Images were acquired at 1×, 1.5× or 2× digital zoom, with 512 × 512 pixels. For multiplane imaging, the piezo was programmed to sequentially settle at 5 to 6 z-depths, separated by 25 to 35 μm, and to wait at each plane for 15 ms before acquiring the image. This wait time was necessary to avoid motion artifacts due to the vibrations involved with the fast plane jumps. When the piezo reverses direction, the distance travelled between the last plane and the first plane (nearly 200 μm) was however too high to acquire a stable image, and thus the first plane was always discarded for analysis. Ultimately, all settings were adjusted to keep the frame rate above 5 Hz.

Optogenetics and place field induction

All optogenetic experiments were performed on Bruker microscopes. A dichroic mirror was used to allow red light to pass through into the brain, and green light to be reflected into the photomultiplier tube (PMT). The stimulation was performed with an ultrafast and high-power collimated LED, at 625 nm (Prizmatix, 625 nm). It was triggered using an Arduino that gated the inverse photostimulation signal of the Pockels cell, which turns off briefly between mirror turnaround, as well as when the piezo reverses direction. The average power of the LED was 35–70 mW measured under the objective. This approach allowed us to protect our PMTs from the high-intensity illumination but still take advantage of the fast, full-frame resonant galvo scanning without losing any frames during photostimulation.

For place field induction, a pulse of light of 1–1.5 s duration was delivered at a location randomly chosen on the belt for 4–6 laps, to recapitulate the procedure used in previous in vivo patch experiments^17,21 The location of the stimulation was moved to another random location on different PRE–POST imaging sessions.

Behavioural training

After recovery from surgery, mice were handled for several days and habituated to head-fixation. Mice were subsequently water-restricted to 85–90% of their original weight and trained to run on a single-fabric, cue-free belt. Mice were trained to lick and receive water rewards (water was delivered in response to tongue contact with a capacitive sensor) at random locations along the belt. As performance improved, the number of rewards delivered on each lap decreased. After several days of training on this cue-free belt, the mice were trained on a 2-m-long, cue-rich belt for randomly delivered water rewards. The belt consisted of three joined fabric ribbons and included some combination of the following tactile cues: coloured pom poms, velcro, glue gun spikes, pink foam strips and silver glitter masking tape.

Data acquisition and preprocessing

Imaging was started after mice could run approximately 10 laps in 10 min (usually after 7–10 days of total training). The mice were imaged for 10–15 min, twice per day separated by a 1-h interval, and for 1 to 3 days, depending on brain stability and behavioural performance. All analysis codes were written in Python 2.7. Preprocessing steps such as motion correction and region of interest (ROI) segmentation were performed as described previously^16,18 using the SIMA package³⁰ (v.1.3.2). Fluorescence was extracted from each ROI using the FISSA³¹ package (v.0.6.1) to correct for neuropil contamination, using eight patches of 50% the area of the ROI, and α = 0.1 for sparseness regularizer. For the resulting raw fluorescence trace of each interneuron, a baseline F was calculated by taking the first percentile in a rolling window of 30 s and a ΔF/F trace was calculated as previously described¹⁶. Relative fluorescence changes in CA1 PCs (ΔF/F) were computed with a baseline calculation method adapted from previous studies¹⁸, with uniform smoothing window t1 = 3 s and baseline size t2 = 60 s. For CA1 PCs, we then detected statistically significant calcium transients as described previously¹⁸.

Spatial tuning curves

For PCs, we used a previously described method¹⁸. In brief, calcium transient onsets during running bouts of at least 1 s in duration were used to calculate the spatial information of the cell. Transients were randomly shuffled to different times during the running events, and the spatial information was recalculated. One thousand iterations were performed to create a null distribution for spatial information, and the cell was considered to be a place cell if its spatial information was above the 95th percentile of the null distribution. The belt was evenly divided into 100 spatial bins, and the place field was calculated from its transient rate map over these bins. The rate map was the number of transients in a given spatial bin normalized by the occupancy of the mouse in that spatial bin, which was then smoothed with a Gaussian kernel (s = 3 spatial bins). To detect individual place fields, each local maximum of the smoothed rate map was fitted with a Gaussian curve centred at that location. For each smoothed rate map, the place fields in which the associated Gaussian was smaller than 50% of the largest Gaussian (by measuring the total area under the curve) were discarded. The remaining Gaussians were considered place fields.

For interneurons, the calcium fluorescence trace was used to approximate the firing activity over time, as previously described¹⁶. To calculate a spatial tuning curve for each interneuron, the treadmill was divided into 100 bins. For each bin, we calculated the average ΔF/F from frames where the mouse was in locomotion (velocity greater than 5 cm s⁻¹) and smoothed the resulting trace with a Gaussian kernel (σ = 3 bins) to obtain the spatial tuning curve.

Determination of the spatial selectivity of the starter cell

Nineteen mice were used for the analysis of the relationship between the activity of a starter PC and its presynaptic interneurons. Mice were imaged during two or three sessions and the data was separated on the basis of the spatial selectivity of the starter neuron, reported in Supplementary Table 2. In the case in which the spatial selectivity was identical on multiple sessions (which occurred only when the neuron was inactive), the first recorded session was used for analysis. The analysis of the development of negative tuning was performed for the mice in which spontaneous field formation was recorded and followed by a session in which the field was stable from the first lap and active at the same location. In some mice, a stable field in the starter neuron was observed at a given location, but then disappeared in the following session and ultimately a new field formed at the different location. In this case, the mice were not included for this analysis.

IFS index

Negative selectivity in interneurons was assessed by the IFS index, defined as the difference over the sum of the average activity inside the field of the single CA1 PC and outside. Negative values indicate that the activity is higher outside the place field than inside, and positive values indicate higher activity within the place field. This index better represented the raw data than correlation of the tuning curves of the interneurons and starter cells, because interneuron activity can have wider or smaller through activity than the place field of the starter cell (see Fig. 2a). The same IFS window of 30 cm, centred around the peak of the place field and which corresponds to the mean place field width of all cells, was kept throughout all analyses in both the rabies tracing and optogenetics induction datasets.

Identification of recruited CA1 pyramidal cells

To determine which CA1 neuron was recruited by the photostimulation of the starter cell during place field induction, we used three distinct criteria. First, we defined the time during which photostimulation increased the density of calcium transients in the PCs above chance level. For a given brain, we repeated the place field induction protocol in the absence of a starter neuron (before electroporation) to estimate the baseline of transient density around photostimulation onset times. Then, we tested for each time point (in bins of 0.25 s) the difference of transient proportion with and without a starter neuron. The first criterion for a recruited neuron was to have a transient in the statistically significant time window when transient density is higher than chance. The second criterion was based on the activity of the recruited neurons. To be identified, the average activity during laps of photostimulation needed to be higher than the average activity in laps preceding induction, for the location where the starters were induced. Third, to make sure that our identification did not pick already spatially selective recruited cells at that given location, any recruited neuron that matched the first two criteria but had a significant place field at the induced location was excluded for the analyses.

Probability of co-activity during immobility

To look at the time lag between neuron co-firing, we first generated a binarized trace for each neuron, in which all the frames were assigned the value 0, or 1 at the detected calcium onsets. For each neuron pair, we then calculated the cross-correlation by jittering the binarized traces between −2 and 2 seconds with one another. The co-activity probability was then taken as the sum of all the cross-correlograms divided by the number of pairs in total.

Network modelling

Model architecture.

Activity of neurons in the network is simulated by the following dynamic equations:

$$\begin{gathered} \tau \mathrm{d}{\mathbf{r}}_{\mathrm{E}}∕\mathrm{d}t=-{\mathbf{r}}_{\mathrm{E}}+\Phi (W_{\text{EE}}{\mathbf{r}}_{\mathrm{E}}+W_{\text{EI}}{\mathbf{r}}_{\mathrm{I}}+s_{\mathrm{E}}) \\ \tau \mathrm{d}{\mathbf{r}}_{\mathrm{I}}∕\mathrm{d}t=-{\mathbf{r}}_{\mathrm{E}}+\Phi (W_{\text{IE}}{\mathbf{r}}_{\mathrm{E}}+W_{\text{II}}{\mathbf{r}}_{\mathrm{I}}+s_{\mathrm{I}}) \end{gathered}$$ (1)

where r_E and r_I are the vectors of firing rates of N_E excitatory (E) and N_I inhibitory (I) neurons, respectively, and W is the matrix of connection weights, including connections between E to E (W_EE), E to I (W_IE), I to E (W_EI) and I to I (W_II) neurons. τ is the effective time constant of the network integration, and Φ(.) denotes the activation function of the network, which we assume to be a linear rectified function: Φ(I) = 0 for I < 0; Φ(I) = 1, for I≥0.

The external input to E and I neurons is represented by s_E and s_I The input to neuron i is described by, s_i=w_i^f(s_i^b+s_i^m), where w_i^f is the feedforward weight (drawn from a uniform distribution between [0.5, 1] for E and [0.2, 0.3] for I neurons). s_i^b=1+ζ is the baseline input independent of the location of the mouse (with ζ drawn from a uniform distribution between [−0.5, 0.5]), and s_i^m denotes the modulation of input based on the location:

$$s_i^{\mathrm{m}}=m_i\text{exp}(\gamma \cos [2\pi (x(t)-x_i^{\ast })∕L])∕\text{exp}(\gamma )$$ (2)

Here, x(t) is the position of the mouse at time t, and $x_i^{\ast }$ is the preferred spatial position of neuron i. The position of the mouse is obtained as x(t) = Vt, where V is the velocity. L = 2m is the total length of the circular belt, and we assume that the mouse runs at a constant velocity, V=2m min⁻¹. The preferred position of neurons $x_i^{\ast }$ is uniformly spread between [0, L), for both E and I neurons. The degree of spatial modulation of the response is determined by the modulation factor m (drawn from a uniform distribution between [0, 1] for E and [0, 0.1] for I neurons), and the sharpness of the spatial response profile is given by the exponent γ = 10.

Neurons are connected together with random connectivity. Connection from neuron j to neurons i, c_ij, is drawn from a binomial distribution with probability ϵ (c_ij = 1, that is, there is a connection, with probability ϵ; c_ij = 0, that is, there is no connection, with probability 1 – ϵ). E–E pairs are connected sparsely, with a connection probability of 10% (ϵ_EE = 0.1). Other connection types are more densely established, with a connection probability of 50% (ϵ_EI = ϵ_IE = ϵ_II = 0.5). On top of the random connectivity, the starter cell (the kth neuron, with k chosen randomly from [1, N_E]) in which the place field is induced (either spontaneously or by optical induction) is assumed to be part of a subnetwork. It comprises N_s E and I neurons (with neuron IDs: [k – N_s/2, k + N_s/2)). The E–E and E–I (E→I and I→E) connectivity between these neurons are elevated to 100% (ϵ_s = 1). Self-connections are not allowed throughout. If there is a connection from neuron j to neuron i (c_ij = 1), the weight of their connection, w_ij, is in turn drawn from a uniform distribution between [0, J], for E→{E, I}, and [−J, 0], for I→{E, I} synapses. J = 0.075.

We first stimulate the activity of the network before induction from equation (1). We refer to the activity of neurons obtained in this stage as r_B. The starter cell is forced to be untuned at this stage by allowing m_k = 0. Then, an extra input, s_I, is injected into the starter cell:

$$s_{\mathrm{I}}=\text{exp}(\gamma \cos [2\pi (x(t)-x_k^{\ast })∕L])∕\text{exp}(\gamma )$$ (3)

during the induction. We refer to the activity of neurons as a result of induction as r_I. Successful induction is modelled by the establishment of this tuned input in subsequent stages. The changes in the activity of neurons resulting from induction, δr=r_I–r_B, governs the plasticity in the network, which is modelled in two stages. First, connections between the starter cell and the rest of E neurons undergo synaptic potentiation according to the following rule:

$$\Delta w_{jk}^{\mathrm{p}}=\langle \delta r_k\delta r_j\rangle$$ (4)

where ⟨.⟩ denotes the temporal average. The weights are updated according to: w_jk ← w_jk + η_pΔw_jk^p, for the existing synaptic connections (c_jk = 1), with η_p denoting the rate of synaptic potentiation. The activity of the network with the updated weight (simulated according to equation (1), r_p, then guides the next stage of plasticity which is governed by depression of E→I synapses according to:

$$\Delta w_{ij}^{\mathrm{d}}=-\langle \delta r_i\delta r_j\rangle$$ (5)

where j counts over E and i over I neurons. δr describes the change in activity after potentiation stage relative to the baseline firing rates: δr=r_P–r_B. We update the network weights according to: w_ij ← w_ij + η_dΔw_ij^d, for the existing synaptic connections (c_ij = 1), with η_d denoting the rate of synaptic depression. If the weight of an E→I connection becomes negative after an update, it is set to zero. η_p = 100 and η_d = 5.

The activity of the network is simulated (equation (1)) with the final updated weights (equations (4) and (5)) to obtain the final responses. Network activity is simulated before, during and after induction for N_L = 10 laps (each lap lasting for T_L = L/V = 60 s), and the weights are updated based on the average activity across all laps. We simulated the activity of 40 different starter cells and their presynaptic inhibitory networks to obtain the results in Fig. 2. To expedite simulations, some experiments are performed with an increased velocity of V_s = 20 m min⁻¹; we made sure that this does not change the results. Default parameters of the simulations are described in Supplementary Table 4.

Anti-tuning in presynaptic interneurons argues for specific connectivity.

Our experimental results showed that negative tuning emerged specifically in the presynaptic pool of interneurons, and was absent in randomly sampled inhibitory populations. In the absence of subnetworks, with no specific connectivity between E and I neurons, the starter cell would be randomly connected to its presynaptic pool of interneurons. If any bias existed in the presynaptic pool of the starter cell, it would also be present in randomly chosen pools of interneurons, and hence it cannot be selective to presynaptic interneurons. Note that, even if the starter cell induces an anti-tuning specifically in its postsynaptic pool of interneurons, this bias would not be reflectedin its respective presynaptic pool of interneurons, unless pre- or postsynaptic interneurons form a reciprocally connected subnetwork with the starter cell. This reasoning was verified in our simulations, in which network models with only random connectivity did not show an emergence of anti-tuning selective to presynaptic interneurons. The generation of inverse selectivity in the presynaptic partners in silico can alternatively be achieved by specific connectivity in disinhibitory circuits. In this scenario, place field formation in the starter cell can increase the activity of interneuron-specific interneurons (INT1) with specific contacts to the presynaptic ensemble (INT2) (Extended Data Fig. 10). We implemented one such model and found that plasticity of E-to-I synapses can potentiate the disinhibitory motif (PC-to-INT1-to-INT2-to-PC), leading to the emergence of negative selectivity in a presynaptic pool of interneurons (INT2). However, in this configuration, INT2s that developed inverse selectivity were suppressed from the beginning at the preferred location of the starter PC (Extended Data Fig. 10), which would not be consistent with our previous results (Fig. 3g). Moreover, INT1s received stronger inputs from the starter PC as a result of PC-to-INT1 potentiation and thus developed a strong positive tuning (Extended Data Fig. 10). We would therefore expect to observe a significant increase in the activity of a subpopulation of IN1s responsible for disinhibition. We tested this hypothesis by performing place field induction in VIP-Cre mice, known to genetically label interneurons specializing in the disinhibitory control of PCs. In this set of experiments, we did not find significant differences between successful (+) and failed (−) induction sessions, nor did we observe that VIP neurons increased their selectivity at the induced location (Extended Data Fig. 10), ruling out their potential involvement in the circuit mechanisms that generate anti-selectivity.

Anti-tuning in presynaptic interneurons argues for collective dynamics.

Our network simulations also revealed that anti-selectivity in presynaptic interneurons do not emerge in network structures without specific E-E connectivity. This suggests that collective interaction of PC–PC subnetworks is involved in the generation of anti-tuning, and that single-cell interactions may not provide an explanation for the emergence of anti-selectivity. To understand this better, we developed a model with only a single starter PC (Extended Data Fig. 8), which represents the extreme case of single-cell interaction with interneurons. Numerical simulation of such a model revealed that anti-tuning cannot emerge as a result of depressive mechanisms in a structure with specific connectivity of a single cell and interneurons. Stronger depression of E–I synapses only diminished the tuning of presynaptic interneurons at the induced location, but did not lead to a negative tuning. Intuitively, this can be understood in terms of the reorganizations of weights between the starter PC and interneurons. Following induction of the place field in the starter PC, a depressive mechanism can decrease the weight of E→I synapses to interneurons with similar selectivity (denoted by red in Extended Data Fig. 8a). However, no matter how weak, the connection will still confer a net positive change in tuning towards the induced location at the postsynaptic interneuron, under the assumption that the starter PC was not tuned before the induction. On the other hand, (relative) potentiation of weights between the starter PC and interneurons tuned to other locations (denoted by blue in Extended Data Fig. 8a) would only increase the in-field selectivity of interneurons, on average. Thus, anti-Hebbian plasticity mechanisms are not able to generate anti-selectivity in interneurons if only applied at the single-cell level.

This reasoning can be presented more formally by the following mathematical argument. Suppose that an untuned cell with a baseline activity of r₀ at all locations changes its response and becomes selective to location x*:

$$r=r_0(1+\cos (2\pi (x-x^{\ast })∕L)$$

The activity of the postsynaptic interneurons before induction is given by wr₀, where w is the weight of E→I connection before induction. After induction, the activity of postsynaptic interneurons changes to αw r₀(1 + cos(2π (x–x*)/L), where αw is the weight after induction, with α>1 and α<1 describing synaptic potentiation and depression of E→I connections, respectively. The change in the activity of postsynaptic interneurons can therefore be written as:

$$\delta r_{\mathrm{I}}=\alpha w{r}_0(1+\cos (2\pi (x-x^{\ast })∕L)-w{r}_0$$

The untuned component of the change in the activity of inhibitory neurons can be written as:

$$\langle \delta r_{\mathrm{I}}\rangle =(\alpha -1)w{r}_0$$

where ⟨.⟩ denotes the average across space. The tuned component of the change (spatial modulation, denoted by ⟨⟨.⟨⟨) can, in turn, be described as:

$$\langle \langle \delta r_{\mathrm{I}}\rangle \rangle =\alpha w\cos (2\pi (x-x^{\ast })∕L)$$

For α>1 (synaptic potentiation) both the untuned and tuned components increase.

For α<1 (synaptic depression), the untuned component becomes negative:

$$\langle \delta r_{\mathrm{I}}\rangle =(\alpha -1)w{r}_0<0;for\alpha <1$$

However, the tuned component would only become weaker, but still remain positive, as a result of synaptic depression:

$$\langle \langle \delta r_{\mathrm{I}}\rangle \rangle =\alpha w\cos (2\pi (x-x^{\ast })∕L)>0;for\alpha <1$$

Therefore, in this set-up, it is not possible to obtain negative tuning as a result of synaptic depression of connections between a single PC and its post- or presynaptic interneurons.

Limitations of the model.

First, our model does not account for an initial bias in the presynaptic pool of interneurons, before induction, for PCs that successfully formed a place field. In fact, in our model we saw the opposite bias: in the E–I subnetwork, there was a positive bias towards the location of the place field, as I neurons receive input from E neurons with similar selectivity. Second, in our modelling, while we assumed that synaptic plasticity changes connection weights as a result of response changes after induction, similar plasticity mechanisms can be at play even before induction, in the ‘baseline’ state of the network. Such mechanisms can guide the process of induction towards starter cells belonging to the subnetwork, and explain why induction succeeds in some cells and why it fails in others. Third, the plasticity mechanisms in our model are prone to instability. Potentiation of E–E synapses can lead to unstable modes of activity in the network, if it is not controlled beyond a certain point. Depression of E–I weights, too, deprives the network of potent recruitment of inhibition, which is necessary for its stability, especially following the initial excitatory potentiation. Homeostasis mechanisms, which control the firing rate of neurons, or E-I potentiation may contribute to this stability.

Calculation of transsynaptic labelling efficacy in local CA1 pyramidal cells.

Anatomical studies³² have provided a quantitative estimate that CA1 PCs make about 200 synapses on local CA1 PC targets. Historically, these connections have been practically ignored in the field because this estimated connection probability (200 out of about 150,000 CA1 PCs ipsilaterally: around 0.13%) is lower than the approximately 1% collaterals in CA3²². However, we can calculate, based on our data, that the local PC–PC contacts may be higher than 200. To do so, we can use the transsynaptic efficacy at the CA3–CA1 synapses of around 0.5% derived from about 130 CA3 cells labelled divided by 28,000 ± 8,200 known CA3 synapses on CA1 PCs³². Assuming the same RABV labelling efficacy for the putative local PC contacts in CA1, we thus estimate that at most 1–3 presynaptic CA1 PCs (that is, around 0.5% of the previously estimated 200 presynaptic CA1 PCs targeting the starter postsynaptic cell) would be expected to be labelled. Given our anatomical data, we find on average 11 presynaptic CA1 PCs labelled by the RABV. If we use the same efficacy as the CA3–CA1 synapses, this would imply an order of magnitude more connections (around 2,000 PCs converging to 1 starter PC). Alternatively, it is possible that the labelling efficacy for local CA1 PCs contacts is higher compared to the more distant CA3 presynaptic cells.

Statistics and reproducibility

All statistical tests are two-sided. No adjustments were made for multiple comparisons except for ANOVAs with difference among groups deemed statistically significant (P < 0.05). In these case, Tukey’s test was used post hoc and P values were adjusted for multiple comparisons and always indicated in the legends where appropriate. For comparisons between two populations, t-tests were applied if the data points followed a normal distribution (confirmed using the Kolmogorov–Smirnov test). To analyse data that were not normally distributed, the non-parametric Wilcoxon rank-sum test (for unpaired samples) and Wilcoxon signed-rank test (for paired samples) were used.

Box plots always represent median and interquartile range (IQR, 25th to 75th percentile) and whiskers extend to cover the distribution without outliers (defined as points above 1.5 IQR below or above the box edges). Bar plots always represent mean and s.e.m unless specified otherwise.

Representative in vivo images as well as histological experiments were repeated independently in different mice with similar results for Fig. 1b, d (n = 6), Fig. 1i (n = 19), Fig. 3c (n = 6) and Fig. 4a (n = 13), and Extended Data Fig. 1a-g (n = 6), Extended Data Fig. 1l (n = 4), Extended Data Fig. 6a (n = 13) and Extended Data Fig. 10e (n = 4).

Extended Data

Extended Data Fig. 1 ∣. Anatomical location of presynaptic neurons targeting a single CA1 pyramidal cell.

See Supplementary Table 1. a, Representative coronal slice of the dorsal CA1 hippocampus with the starter pyramidal cell expressing the fluorophore Venus (green), TVA receptor and glycoprotein G, after electroporation. b, Coronal slice of the hippocampus 14 days after rabies injection. Neurons in red expressing tdTomato are presynaptic to the starter cell. c–e, Presynaptic neurons can be found in the entorhinal cortex, medial septum and supramammillary nucleus (a to d, blue is DAPI) f, In vivo two-photon images of a starter neuron (green) and presynaptic neurons (red). g, Post hoc immunohistochemistry labelling of the same tissue reveals that the HA tag fused with the TVA receptor is uniquely expressed in the starter neuron, indicating that rabies tracing is restricted to this individual cell. Scale bars are 50μm. h, Lateral distribution of the presynaptic interneurons (red) and unlabelled interneurons (grey) calculated on in vivo two-photon Z-stacks (n = 7 mice). Coordinates (0, 0) indicate the location of the starter neuron. i, Same, but for depth distributions. S.O: stratum oriens, S.P: stratum pyramidale, S.R: stratum radiatum. j, Strategy to generate VGAT-EYFP mice in which EYFP is expressed in all inhibitory interneurons. k, Schematic of the experiment. A starter cell is electroporated in a VGAT-EYFP mouse, followed by injection of a RABV-tdTomato. As a result, presynaptic interneurons will co-express EYFP and tdTomato and presynaptic pyramidal cells will express only tdTomato. l, Representative confocal images of the starter cell (left), presynaptic and unlabelled interneurons (middle) and presynaptic pyramidal cells (right). Scale bars are 50μm. m, Quantification for 4 mice across the ipsilateral CA1.

Extended Data Fig. 2 ∣. Spontaneous place field formation is not associated with a detectable decrease in the level of presynaptic inhibition.

See Supplementary Table 2. a, Representative trace of the starter neuron’s fluorescence activity during navigation. The first transient (pink) corresponds to the spontaneous formation of a place field, as shown in the fluorescence heat map (bottom). Fluorescence amplitude of the calcium transient during field formation is significantly higher than all other subsequent events (n = 11 mice, paired t-test, P = 0.008). b, Lap-average (n = 11 networks) activity (mean ± s.e.m.) of the presynaptic (red) and unlabelled (grey) interneurons centred around the onset lap of field formation (starter, blue) from. c, Inhibition levels in both populations remained relatively constant before and after formation. All groups n = 11, One-way ANOVAs: starter, P = 0.0004 (post hoc Tukey’s tests with P-values adjusted for multiple comparisons: all P<0.05); presynaptic: P = 0.32; unlabelled P = 0.68 d, Average tuning curve (mean ± s.e.m., all n = 11 networks) centred around the starter’s place field for the presynaptic and unlabelled interneurons at three different time points during field formation, showing no immediate spatial reconfiguration of their responses. e, Same analysis using population-vector correlation before and at lap formation onset for the presynaptic interneurons. f, Distribution of in-field selectivity index (IFS) for presynaptic interneurons before and during the lap of field formation, showing no change in spatial selectivity at the field’s location (n=199 from 11 mice). g, Distribution of the IFS difference (n = 199 from 11 mice) compared to a shuffle distribution in which the location of the starter’s place field is randomized on the belt.

Extended Data Fig. 3 ∣. Presynaptic interneuron spatial responses are not spatially selective when the starter is inactive and do not immediately reconfigure after spontaneous field formation.

See Supplementary Table 2. a, Normalized average tuning curves of the starter neurons (blue), their presynaptic partners (red) and unlabelled interneurons (grey), centred around the middle of treadmill. Thick line represents the average for n = 14 mice and shaded area the s.e.m. b, Box plots of IFS values for all 14 mice, averaged at the network level (paired t-test, P = 0.32). c, In-field selectivity (IFS) index for all presynaptic (n = 223) and unlabelled (n = 1730) interneurons from n = 14 mice, P = 0.19 (Kolmogorov-Smirnov two sample test). Negative IFS indicates negative selectivity in the starter’s place field. Insets (mean ± s.e.m.), P = 0.42 (t-test). d, IFS values were computed in b and c for a virtual place field in the middle of the treadmill. Here, each point represents the t-test’s P-values for IFS values of presynaptic vs. unlabelled interneurons while iteratively moving the location of the virtual field along the belt and recomputing the IFS at each location. This analysis shows that there is no difference in spatial selectivity anywhere on the belt when the starter cell has no place field. e, Experimental timeline: mice were imaged twice a day. Between each imaging session, they were allowed to rest in their home cage for one hour (also see Methods). In n = 4 mice, we tracked the spontaneous emergence of a place field in the starter neuron and its persistence in a later session. f, Representative heat map activity for a starter cell as a function of lap (y-axis) and position (x-axis) on the belt. Field creation occurred in the first session of the day at lap 4 (white arrow) and persisted after rest in a later session at the same location. g, Session-average tuning curve for the starter cell shown in f and 6 of its presynaptic interneurons, reconfiguring their response and developing anti-selectivity around the starter’s place field (dashed line) in the later session. h, Cell-by-cell correlation coefficients between the spatial response in the first session when the field emerged (creation) and a later session (stable) for the presynaptic (n=81) and unlabelled (n=267) neurons from 4 mice, P = 0.04 (unpaired t-test). i, Same analysis but for network averages (n = 4 mice), P = 0.26 (Paired t-test pre. vs unlab). j, Difference between the presynaptic and unlabelled interneurons average activity centred around the starter’s place field (grey), for both creation (top) and stable field session (bottom). In purple, P-values between the two distributions as a function of position on the belt. Purple shaded area indicates positions where P<0.05. Notice the dip in activity in the stable session indicating the development of anti-selectivity in the presynaptic ensemble when the starter cell has an already established place field. All box plots represent median (central line) and interquartile range (25th and 75th percentile); whiskers extend to the most-extreme data points (excluding outliers).

Extended Data Fig. 4 ∣. Photostimulation of a single pyramidal cell increases interneuron activity.

a, Left: Peri-stimulus time histogram (mean ± s.e.m.) centred around the onset of the LED stimulations for all interneurons (green, n = 2613 from 6 mice) and a shuffle trace in which LED onsets were randomly shuffled in time in each session (grey, same n). Right: Quantification of increased activity (data, P < 10⁻¹⁰; shuffle, P = 0.12, one-sample t-tests). Data vs shuffle, P<10⁻¹⁰ (paired t-test). b, Same analysis as a but all traces are averaged (n = 14 sessions in 6 mice, mean ± s.e.m.) for a given session (data, P=0.002; shuffle, P=0.23, one-sample t-tests). Data vs shuffle, P=0.003 (paired t-test). c, Difference in IFS between the PRE and POST session as a function of increased ΔF/F during optogenetics stimulations ((+), n=1208, P<10⁻⁷; (−), n=1157, P=0.12; Pearson’s R, n = 6 mice). d, Same as c but for the IFS in PRE only ((+), n=1208, P=0.00012; (−), n=1190, P=0.15; Pearson’s R, n = 6 mice). e, Mice velocity (mean ± s.e.m.) centred around LED stimulations during place field induction, separated by whether induction was successful (magenta, n = 15 sessions) or failed (grey, n = 13 sessions) from 10 mice (VGAT-Cre and VIP-Cre). Notice that mice slightly slow down during light presentation (1-1.5s stimulations) but continue running at relatively constant and high speeds. f, Difference in speed before and after LED stimulations from e for each condition. (+), P=0.53; (−), P=0.85 (one-sample t-tests). (+) vs (−), P=0.75 (t-test). g, Three-dimensional representation of all recorded interneurons (n=1208 from 6 mice) for successful inductions (+) plotted as a function of their distance in situ to the seed neuron (centred at x, y, z = 0, 0, 0). Both colour code and circle size indicate the change in IFS between PRE and POST sessions. h, Projection of g onto the Z-axis (depth) shows no distance-dependent relationship (n=1208 from 6 mice, P=0.29, Pearson’s R). i, Projection of g onto the X-Y axes. j, Euclidean distance (X–Y) to the seed neuron as a function of change in IFS shows significant relationship (n=1208 from 6 mice, P=0.012, Pearson’s R). Red bins represent the running IFS average value along the XY distance. All box plots represent median (central line) and interquartile range (25th and 75th percentile); whiskers extend to the most-extreme data points (excluding outliers).

Extended Data Fig. 5 ∣. No immediate spatial reconfiguration of interneurons after place field induction.

a, Average spatial tuning curve for all interneurons (n = 6 mice) for the laps before place field induction (pre-stim laps), directly following induction (post-stim laps) and in POST following successful (magenta) or failed (grey) inductions. Interneurons are ordered by their IFS, and centred around the induced location for each condition. b, IFS values on a cell-by-cell basis, showing that interneurons do not become immediately negatively selective at the induced location following successful induction. Top, comparison of IFS in pre-stim laps vs. post-stim laps for successful (+) and failed (−) inductions. (−), P = 0.81; (+), P = 0.06 (Wilcoxon signed rank-tests). (−) vs (+), P = 0.07 (Wilcoxon rank-sum test). Bottom, comparison between post-stim laps and POST session (1 h after rest). (−), P = 0.24; (+), P < 10⁻¹⁰ (Wilcoxon signed rank-tests). (−) vs (+): P < 10⁻¹⁰ (Wilcoxon rank-sum test). For top and bottom, interneurons recorded in all three sessions: n = 1190 for (+) and n = 1208 for (−) from 6 mice. c, 2D histogram of interneurons’ IFS in pre-stim laps and POST session (same n as b). (+), P < 10⁻¹⁰ ; (−), P < 10⁻¹⁰ (Pearson’s R). d, Average IFS values at the session level (n = 7 for each condition from 6 mice) before, immediately after and in the POST induction session. (−), all P > 0.05 (paired t-tests). (+), prestim vs POST, P = 0.04; all others P > 0.05 (paired t-tests). e, Fraction across 6 mice of negatively selective interneurons (IFS < 0) before induction and in the POST session. POST(+) vs prestim(+), P = 0.0003 ; POST(+) vs prestim(−), P = 0.0003 ; POST(+) vs POST(−), P<10⁻⁵ (Fisher’s exact tests). f, Difference in fraction of negatively selective interneurons (mean ± s.e.m.) between prestim and POST for each session (n = 7 for each condition from 6 mice). (+) vs (−), P = 0.028 (t-test). g, Overall fraction of negatively selective interneurons in prestim (top) and POST (bottom) sessions for successful (magenta) and failed (grey) inductions across 6 mice (same n as e), calculated as a function of position on the belt and not only at the location where the seed neuron is induced (corresponding to position 0 here). All box plots represent median (central line) and interquartile range (25th and 75th percentile); whiskers extend to the most-extreme data points (excluding outliers).

Extended Data Fig. 6 ∣. Photostimulation of a starter neuron entrains activity in other surrounding pyramidal cells.

a, Representative field of view with one starter pyramidal cell (red) electroporated with bReaChES and GCaMP expressed in all PCs. Optogenetic stimulations (arrows) drive activity in the starter neuron and evoke calcium events in other surrounding pyramidal cells. b, Quantification of increased fluorescence (post minus pre) for each photostimulation of the seed neuron (left, red, n = 31 sessions, P<10⁻¹⁰, t-test) and all other pyramidal cells (right) in 13 mice. The presence of a seed neuron with an excitatory opsin recruits other PCs above chance level. With seed (blue), n = 31 sessions, P<10⁻⁵; without seed (black), n = 8 sessions, P=0.59 (t-tests). With vs without seed, P = 0.013 (t-test). c, Intersomatic distance between recruited PCs and the starter neuron for successful (magenta, n = 13 sessions) and failed inductions (grey, n = 18 session), P = 0.19 (t-test) from 13 mice. d, Number of recruited pyramidal cells for each condition, P = 0.36 (Wilcoxon rank-sum test), same n as c. e, Fraction of recruited pyramidal cells that were place cells in the PRE session before photoinduction, minus the rate of place cells detected in the other non-recruited cells, for each session, P = 0.28 (Wilcoxon rank-sum test), same n as c. f, Fraction of recruited pyramidal cells that are place cells in the POST session after photoinduction, minus the rate of place cells detected in the other non-recruited cells for each session, P = 0.005 (Wilcoxon rank-sum test), same n as c. g, During immobility and before the seed neuron was induced, the recruited neurons are more likely to spontaneously co-fire (see Methods) than what would be expected by chance – here calculated by selecting an equivalent number of random pairs of neurons (n = 2205 pairs from 13 mice with neurons with at least 1 transient, mean ± s.e.m.). h, Similar to g, pairwise correlation of activity traces averaged for each session (n = 28 containing bouts of immobility before induction, from 13 mice) during immobility before seed induction. Recruited, P=0.0003; Shuffled, P=0.10 (t-tests). Recruited vs shuffled, P = 0.027 (t-test). i, This like-to-like relationship among recruited cells is more pronounced for neurons the intersomatic distances of which (mean ± s.e.m.) are within 150μm of one another (n=2402 pairs from 13 mice). Same assembly pairs, P=0.0008; Shuffled pairs, P=0.83 (t-tests). j, Pairwise distance (mean ± s.e.m.) of place field centroids for recruited and shuffled neurons (n = 494 pairs from 13 mice) during navigation in laps preceding induction. Chance level is represented by a dashed line: Recruited, P<10⁻⁵; Shuffled, P = 0.89 (t-tests). Recruited vs shuffled, P<10⁻⁵ (t-test). k, Similar to i, this effect is more pronounced for closer neurons (mean ± s.e.m.). Same assembly pairs, P=0.048; Shuffled pairs, P=0.40 (t-tests), same n as j. All box plots represent median (central line) and interquartile range (25th and 75th percentile); whiskers extend to the most-extreme data points (excluding outliers).

Extended Data Fig. 7 ∣. Place field induction in an individual neuron does not influence the global representation of the environment.

a, Representative examples of five sessions (from 5 distinct mice) showing the location of the place field of recruited neurons that became place cells from PRE to POST, for each condition (POST+: successful induction in the seed neuron, POST-: failed induction). Position 0 represents the location where the seed neuron was induced in PRE. b, Left: Heat maps representing the activity for all recruited cells as a function of position on the belt, centred around the induced location. Photoinduction (labelled ‘during stim’) drives a large increase in activity in the recruited cells, which was not present before induction (left, ‘before stim’). Right: distribution of the peaks of the spatial responses before (n = 243) and during (n = 306) photoinduction from 13 mice (P < 10⁻¹⁰, two-sample Kolmogorov-Smirnov test). During, P < 10⁻¹⁰; before, P = 0.19 (Kolmogorov-Smirnov uniformity tests). c, Left: Place field distribution of all the non-recruited place cells in the POST session for each condition. Right: Distribution of place field peaks from 13 mice (P = 0.13, two-sample Kolmogorov-Smirnov test). (+) (n = 1175), P = 0.67; (−) (n = 1177), P = 0.26 (Kolmogorov-Smirnov uniformity tests). d, Left: Place field distribution of non-recruited cells which formed a field in the POST session (not place cells in PRE but place cells in POST), for each condition from 13 mice. Right: Distribution of place field peaks (P = 0.12, two-sample Kolmogorov-Smirnov test). (+) (n = 856), P = 0. 34; (−) (n = 904), P = 0.10 (Kolmogorov-Smirnov uniformity tests).

Extended Data Fig. 8 ∣. Computational network model with single neurons and preferential connectivity cannot explain inverse selectivity in presynaptic interneurons.

a, Model with a single seed pyramidal cell. For all following analyses, the structure and parameters of the network is similar to Fig. 4 with the same number of seed neurons (n = 40). Specifically, the seed neuron has both random and specific connectivity with interneurons, with the same Ns (number of units within the subnetwork). b, Right: average activity of interneurons from the subnetwork of the starter cell (subnet.) and from the rest of the network (rand.). Right: in-field selectivity (IFS, mean ± s.e.m.) for interneurons presynaptic (n=2322) to the starter cell (presyn., n = 2322) and others (rand., n = 1696). c, Same as b (mean ± s.e.m.), when there is no depression between the starter cell and interneurons (d=0; n = 2301 presyn.; n = 1699 rand.). d, Same as b (mean ± s.e.m.), for stronger depression rate of synapses (d=50; n = 2283 presyn.; n = 1717 rand.). e–h, Simulation of the network model with different sizes of the pyramidal cell-interneuron subnetwork (Ns). Other parameters are the same as in Extended Data Fig. 9, which is copied here in f for comparison. e, IFS values (mean ± s.e.m.) for 10 pyramidal cells and 10 interneurons (Ns = 10; n = 4436 presyn.; n = 3564 rand.). f, IFS values (mean ± s.e.m.) for Ns = 15 (n = 4611 presyn.; n = 3389 rand.). g, IFS values (mean ± s.e.m.) for Ns = 20 (n = 4843 presyn.; n = 3157 rand.). h, IFS values (mean ± s.e.m.) for Ns = 25 (n = 5064 presyn.; n = 2936 rand.). The results are robust to change of the parameter, especially larger subnetworks lead to more prominent presence of the anti-tuning in presynaptic inhibition. Smaller subnetworks make the detection of anti-tuning difficult, although the effect is still observable in the average activity.

Extended Data Fig. 9 ∣. Computational model with subnetwork structure with different connectivity motifs.

a, Spatial tuning of all pyramidal cells (left) and interneurons (right) in the networks from 40 simulations (similar in the following b–e), sorted according to their in-field selectivity (IFS). Position is expressed relative to the location of place formation in the starter cells, respectively. b, Left: Average activity of interneurons within the subnetwork (subnet.) and from outside (rand.) as a function of position. Right: IFS (mean ± s.e.m.) for interneurons presynaptic to starter cells (presyn., n = 2335) and others (rand., n = 1789). The results are shown for the full model (Fig. 4) with pyramidal cell-interneuron subnetwork structure (illustrated on the top). c, Same as b (mean ± s.e.m.) for network structures with random connectivity and without the specific connectivity structure of the starter-cell-interneuron subnetwork (n = 1964 presyn.; n = 2043 rand.). d, Same as b (mean ± s.e.m.) without the specific connectivity of starter-PCs, while starter-interneurons preserve their specific connectivity (n = 2339 presyn.; n = 1669 rand.). e, Schematic illustration of the reorganization of activity and network interactions following field formation. The starter cell elevates the activity of pyramidal cells and interneurons within the subnetwork at its selective location (left), which is followed by depression of pyramidal cells-to-interneurons connections, leading to the diminished activity of interneurons within the subnetwork at that location (right).

Extended Data Fig. 10 ∣. Alternative model with direct disinhibitory circuitry.

a, Top: schematic of the circuit before field formation. A starter pyramidal cell (PC) contacts two interneuron entities (INT1 and INT2) with excitatory connections. INT1 (interneuron-selective interneuron such as VIP) exerts static inhibition onto INT2, which projects back to PC. Bottom: in this model, formation of a field in the starter PC drives INT1s and INT2s, but a stronger connectivity with INT1 leads to the depression of INT2 responses. b, Evolution of neuronal activity of the starter PC (left), INT1 (middle) and INT2 (right) following place field formation of the PC on lap 1. c, Average tuning curves before field formation (initial), during the formation (middle) and after field has formed (final), showing that INT2 ultimately exhibits negative tuning at that field location. d, Evolution of the synaptic weights as a function of time (laps) during the process of field formation. This model has experimentally testable predictions that we performed. e, To do so, we performed calcium imaging in VIP-Cre mice, known to genetically label a subset of interneuron-specific interneurons (INT1) and single-cell electroporation in an individual PC (seed) to perform place field induction. Left: schematic of the experiment. Right: In vivo two-photon image of GCaMP-expressing VIP interneurons (green) and a single CA1 PC expressing GCaMP and bReaChES (red). Scale bar is 50μm. f, PSTH (mean ± s.e.m.) centred at the onset of the LED photostimulation for all VIP interneurons and a shuffle trace in which LED onset was randomly chosen during the imaging session (n = 6 sessions in 4 mice). g, Box plots representing the increased activity following LED stimulation. Data, P=0.18; Shuff., P=0.30 (t-tests). Data vs Shuff, P=0.8 (t-test). The lack of increased activity during photostimulation goes against the prediction of our model that field formation should elevate responses in the INT1 population. h, Distribution of in-field selectivity (IFS) at the induced location for all VIP interneurons before photoinduction (PRE, n = 774), and after successful (POST(+), magenta, n = 439) and failed (POST(−), grey, n = 353) inductions. Data from n = 14 sessions in 4 mice. All P > 0.05 (unpaired t-tests). The lack of development of positive selectivity is not consistent with our model (see c). i, Average spatial tuning curve for all interneurons for the laps before place field induction (PRE), and in the POST session following successful (magenta) or failed (grey) inductions. Interneurons are ordered by their IFS, and centred around the induced location for each condition. j, Box plots representing IFS values for all VIP-positive interneurons (same n as h). PRE vs POST(−), P = 0.43; PRE vs POST(+), P = 0.37 (t-tests). All box plots represent median (central line) and interquartile range (25th and 75th percentile); whiskers extend to the most-extreme data points (excluding outliers).

Data availability

All data are available from the corresponding authors upon reasonable request. Source data are provided with this paper.

Code availability

All custom codes are available from the corresponding authors upon reasonable request.