Validation of Monte Carlo multithreading TOpas 3.6 software in order to simulate the 6 MV Elekta Synergy MLCi2 platform linac

Abstract

Background

Monte Carlo simulation is generally appreciated as an extraordinary technique to investigate particle physics processes and interactions in nuclear medicine and Radiation Therapy. The present task validates a new methodology of Monte Carlo simulation based on the Multithreading technique to reduce CPU time to simulate a 6 MV photon beam provided by the Elekta Synergy MLCi2 platform medical linear accelerator treatment head utilizing TOpas version 3.6 Monte Carlo software and the Slurm Marwan cluster.

Materials and methods

The simulation includes the linear accelerator (LINAC) major components. Calculations are performed for the photon beam with several treatment field sizes varying from 3 × 3 to 10 × 10 cm² at a 100 cm of distance from the source to the surface of the IBA dosimetry water box. The simulation was wholly approved by comparison with experimental distributions. To evaluate simulation accuracy, gamma index formalism for (2%/2mm) and (3%/2mm) criteria, Distance To Agreement DTA, and the estimator standard error ɛ and ɛ_max are used.

Results

Good agreement between simulations and measurements was observed for depth doses and lateral dose profiles, respectively. The gamma index comparisons also highlighted this agreement; more than 97% of the points for all simulations satisfy the quality assurance criteria of (2%/2mm). Regarding calculation performance, the event processing speed is faster using Gate-[mp] compared to TOpas-[mt] mode when running the identical simulation code for both.

Conclusions

Consequently, according to the achieved results, the proposed methodology shows the first validation of TOpas in radiotherapy linacs simulations and a reduction in calculation time, capping simulation accuracy as much as possible. For this reason, this software is recommended to be serviceable for Treatment Planning Systems (TPS) purposes.

Introduction

For a couple of decades, Monte Carlo simulations for radiation transport have been primarily employed for dosimetry and medical purposes as an alternative to analytical calculations. Highly accurate results are achieved with these methods thanks to the powerful grid computing resources [1–3]. TOpas is high-level C++ open-source (for students and researchers) software produced by the international TOpas collaboration [4, 5]. The initial focus was applied to hadron-therapy simulations but was later extended to include the modalities of treatments. TOpas receives all the physics models developed on the Geant4 generic MC simulation toolkit [6–8]. It gives users the ability to integrate specific components to handle complex geometries and sources and extract the relevant information efficiently from the simulation. All these features participated in the evolution of TOpas use for extended applications. In its recent versions, TOpas plays a crucial role in designing new medical machines to optimize treatment protocols and dose calculations for hadrontherapy. The goal is to use the MC TOpas code to calculate the dose distributions applying to a radiotherapy modality of treatment in a water phantom, keeping the accuracy of results within 2%. Accordingly, this paper is organized as follows; the Elekta Synergy MLCi2 platform accelerator is modeled, where all steps used in our simulation strategy are fully described. Moreover, in the third section, we show the results obtained and discuss the impact on calculation time of our simulation methodology based on the multithreading mode. Also, we offer the comparison of simulated (using Monte Carlo codes: Gate and TOpas) and experimental PDD’s and dose profile distributions using the SLURM-cluster. Finally, in the fourth section, conclusions are drawn from this work.

Materials and methods

Experimental data

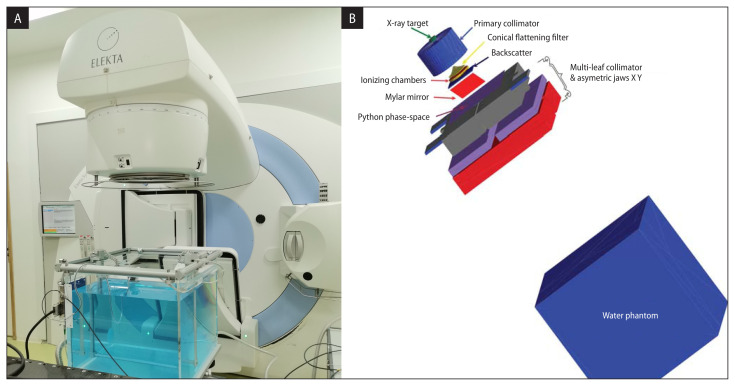
The energy photon beam (X 6 MV) was used in this study, with a reference dose rate of 400 UM/min, delivered by the Elekta Synergy MLCi2 platform linac (Fig. 1A). Also, our dosimetry calculation was carried out according to AAPM’s TG-51 protocol [9]. The experiment data were obtained utilizing a cylindrical ionization chamber, type Scanditronix Wellhofer CC13 having an active volume of 0.13 cm³ installed over a motorized guide in a resistance temperature detector of IBA Blue Phantom [10].

Figure 1.

The composition of system geometry employed in the simulation of Elekta Synergy MLCi2, using TOpas version 3.6 and Gate version 9.0

Monte Carlo codes

TOpas version 3.6

The TOpas code (“TOol for PArticle Simulation”) version 3.6 was used to simulate particle interactions with matter, a phantom of water in this case. The program is based on Geant4 (Geometry and Tracking), and it uses the same physics processes, models, and interaction cross-sections. Previous studies have confirmed perfect compatibility between the code and the experimental data regarding hadrontherapy and brachytherapy [11–12]. Nevertheless, TOpas is not yet approved in the simulations of linac heads used in radiotherapy treatment.

Gate version 9.0

GATE (Geant4 Application for Tomographic Emission) is an advanced open-source software (last version 9.0) developed by the international Open-GATE collaboration, dedicated to numerical simulations in medical imaging and radiotherapy [13, 14]. This version of GATE is based on the Geant4 toolkit version 10.6. Further, GEANT4 manages the kernel that simulates the interactions between particles and matter, and GATE provides additional high-level features to facilitate the design of GEANT4-based simulations [15].

Elekta Synergy MLCi2 linac geometry

Based on detailed information cited in the usually advanced papers published; we simulated the head linac using TOpas version 3.6 [16–18]. What is more, Figure 1B displays the global variant structure of our technique that can be applied to simulate the linear accelerator and the water phantom considered in this study. Simulation components are shown in Figure 1B and can be summarized as follows:

• X-ray target: generates bremsstrahlung X-rays using a thin tungsten and rhenium disk with a radius of 2.7 mm and a thickness of roughly 0.89 mm. The remaining primary electrons are absorbed in a copper absorber disk with a thickness of approximately 10 mm and a radius of 10 mm;

• primary collimator: it was made of tungsten alloy, about 101 mm in height, located at 67.15 mm just below the target. This component was used for two reasons, the first was to collimate the photons in the direction of the treatment field; and the other was to reduce the leakage radiation outside the field area;

• flattening filter: made of a mixture of manganese, carbon, iron, phosphor, and nickel, about 32.05 mm in height including the cylindrical base, located at 141.5 mm just below the primary collimator. A precisely specified surface configuration is attached (combining cones with various radiuses) to the lower end of the primary collimator and gives regular radiation intensity distribution across fields;

• ionizing chambers: made of polarizing mylar films, aluminum and ceramic motherboards, separated by spacers made of air, located at 170 mm just below the flattening filter. Designated for beam monitoring of photon and electron radiation production;

• backscatter plate: composed of aluminum, about 4 mm in height, and located at 184.5 mm just below the ionizing chambers. This component is fixed to eliminate unnecessary backscattered emissions from the system of collimation;

• mylar mirror: constructed of a thin mylar material. This segment is located at 225.1 mm under the dose ionizing chambers on the beam focal axis to facilitate patient setup and show the location and shape of the radiation beam;

• multi-leaf collimator MLC: made of tungsten alloy, about 10 and 77 mm in thickness and height, respectively, located just below the Phase Space position (280 mm), used for precise treatment and the most accurate conformal beam shaping for treatments;

• secondary collimators X, Y: are made of tungsten alloy and have about 100 mm of thickness. They are used to minimize the inter-leaf leakage and set the treatment field’s overall size;

• phantom: box of water with a size of 480 × 480 × 410 mm³ similar to the Iba blue water phantom located at a source surface distance of 100 cm from the target.

Dose calculation efficiency applying SBS

The decrease of simulation time for radiotherapy applications is a complex task according to the simulation efficiency. In this investigation, the SBS tool was used to reduce the simulation time. The SBS was selective in the direction criterion angle of 20 degrees, which is superior to the primary collimator’s size opening angle. For this reason, the photon output rate, defined as the number of photons reaching the squared area of the water phantom at an SSD = 100 cm for a fixed number of primary electrons, is compared with and without the SBS tool. The MC codes record the randomly deposited dose along the length of the photon step inside the phantom, wherever each hit is stored in the corresponding voxel; this displays the basic element needed to calculate dose distribution in a water box “dosel”. Nevertheless, if the step is longer than the dosel dimension, the dose will be recorded in a dosel ‘d’ selected randomly, which may influence the simulation efficiency. The statistical uncertainty in a dosel was determined with [19, 20]:

$${\sigma }_i=\sqrt{\frac{1}{N-1}\left(\frac{{\mathrm{\Sigma }}_{i=1}^N{X}_i^2}{N}-{\left(\frac{{\mathrm{\Sigma }}_{i=1}^N{X}_i}{N}\right)}^2\right)}$$ (1)

Where σ_i is an estimate of the mean dose’s standard error in dosel \i” and N is the number of primary histories. Further, the recorded relative statistical uncertainty corresponds to the ratio of σ_i to the quantity of the dose scored in the dosel \i”. The statistical uncertainty of the simulation is measured as proposed [19, 20]:

$${\sigma }_d=\sqrt{\frac{1}{N_D}\sum _{i=1}^{N_D}\left(\frac{{\sigma }_i}{D_i}\right)}$$ (2)

Where σ_d describes the statistical simulation uncertainty, N_D is the number of dosels receiving a dose higher than 50% of the maximal dose. Finally, the whole simulation efficiency ζ_s is described in terms of the SBS tool, taking into account the simulation time T and the statistical simulation uncertainty σ_d, where:

$${\zeta }_s=T^{-1}\times {\left(\frac{1}{N_D}\sqrt{\sum _{i=1}^{N_D}\left(\frac{{\sigma }_i}{D_i}\right)}\right)}^{-2}$$ (3)

Calculation performance

Monte Carlo simulations are CPU-heavy tasks. For this reason, the construction of the geometry has been done on a workstation with the following specifications: a 40-core Xeon Silver boosting up to 2.2 GHz, 64 GB of DDR4 RAM, and 2 TB of fast storage. Moreover, the calculations have been done on HPC cluster computing (Slurm “Simple Linux Utility for Resource Management”-CNRST Team Morocco) [21, 22] composed of 19 nodes managed by the CNRST Team and offers the following capacities: 760 cores (68 TFlops), 5.2 TB of memory, 108 TB of storage, and 2 GPU cards. A test was conducted on TOpas and Gate to investigate the efficiency of the TOpas multi-threaded and the rated efficiency of Multiprocessing Gate Jobs (M.G.J) calculations compared to the classical TOpas and GATE sequential calculations, by counting the events rate or the number of particles processed per unit time while keeping the simulation parameters the same for both tests. Later, an investigation was conducted by studying the event rate processing regarding the number of primary particles to figure out the most optimal parallel calculations running simultaneously.

Results

Simulation efficiency

The simulation efficiency and the photon output rate are evaluated by performing two full simulations with and without the SBS tool. And that’s by using the electron beam parameters of mean energy of 6.7 MeV and a spot spatial FWHM of 3 mm. As recommended in the literature [25], the FWHM energy is fixed at 3% of the mean energy (0.207 MeV). Results are summarized in Table 1.

Table 1.

The photon output rate increase using the bremsstrahlung splitting tool, compared to a reference simulation performed without it

Simulation MC	Primaries	Time (second)	Collected photons	Photon output rate	Output rate f(T) (particles.s−1)
Without B.S	106	275.6	2581	2.581 × 10−3	9.365
With B.S	106	3982.37	5850939	5.85	1469.21

Energy fluence spectra inside linac components

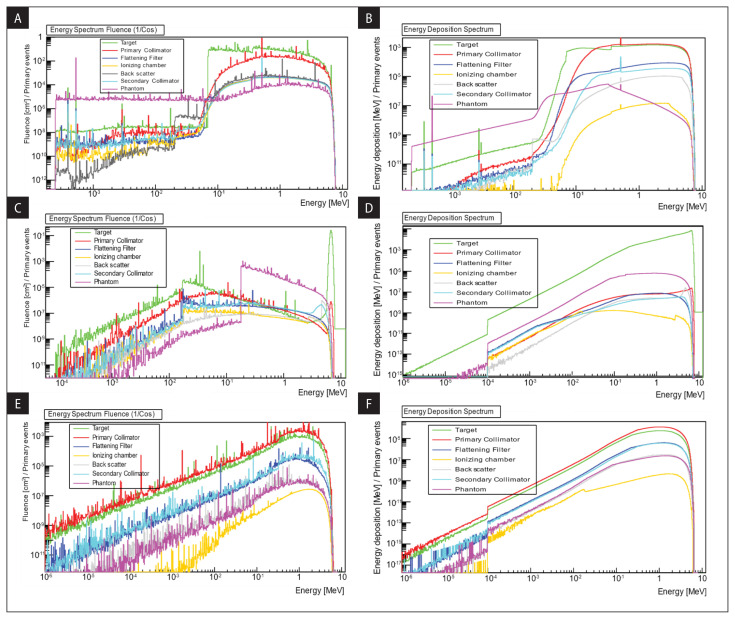
Figure 2 shows the fluence differential in energy corrected by [1/cos(ϕ)] and the energy deposition differential in energy scored using the GetTotalEnergyDeposit() tool for photons, electrons, and positrons. Where ϕ is the angle of the particle entering the studied volume, this works only for volumes perpendicular to the z-direction. No correction for cos(ϕ) = 0 is applied.

Figure 2.

Energy spectra of photons, electrons, and positrons at selected components in the linac and generated by an X-ray beam Elekta Synergy MLCi2 platform. AB. Photon fluence; CD. Electron fluence; EF. Positron fluence

Linac head validation

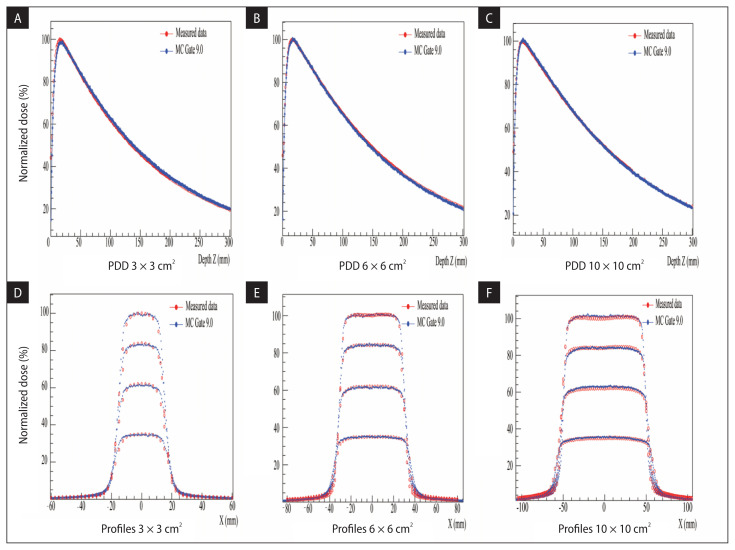
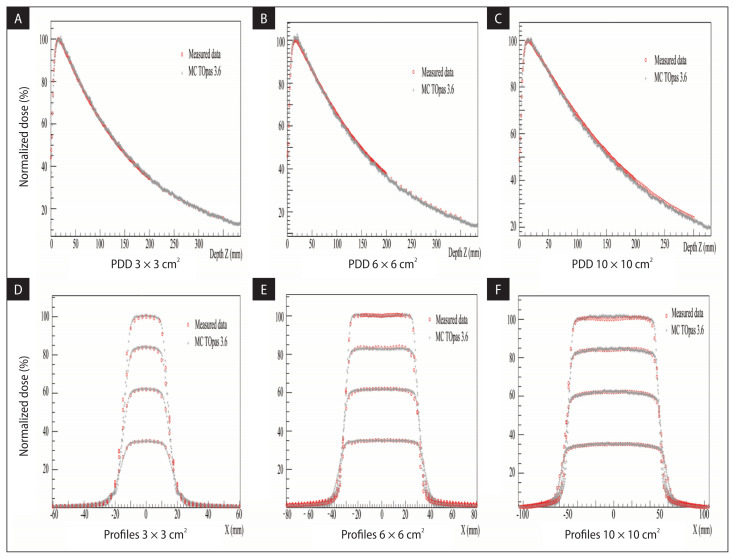
A two-dimensional gamma index analysis is performed to evaluate the capability of TOpas version 3.6 compared to Gate version 9.0 in dose distributions calculated in a water phantom. The analysis results for four regular irradiation fields are summarized in Table 3, Figures 3 and 4, respectively. In Figures 3 and 4, we show PDD’s dose distribution and normalized cross profiles for the same field at 1.5, 5, 10, and 20 cm of depth for experimental and simulated calculations applying TOpas and Gate, respectively. Table 3 summarizes several dosage metrics results used to compare the Topas MC simulation with the experiment dose distributions for the photon beam Elekta Synergy MLCi2 linac. To begin with, the global gamma index and DTA will tend to exhibit inaccuracies in higher dose gradient zones, with passing rates restricted to 2% and 2 mm, respectively. On the other hand, the local (ɛ) gamma index and the global gamma index normalized to the maximum value of the observed data (ɛ_max) analyses are utilized to highlight failures in high and low dosage gradients.

Table 3.

Comparison of the simulated PDDs and cross profiles with the experimental ones for the square field sizes ranging from 3×3 to 10×10 cm² using Gate-[Mp] and TOpas-[Mt] MC software

	MC simulation using Gate-[M-P] version 9.0				MC simulation using TOpas-[M-T] version 3.6
	ɛ	ɛ max	γ (2%/2mm)	DTA [mm]	ɛ	ɛ max	γ (2%/2mm)	DTA [mm]
Field size 3 × 3 cm 2
PDD	9.25 × 10−5	1.82 × 10−5	99.5935	0.25	1.37 × 10−3	8.014 × 10−4	99.0783	0.25
1.5 cm	9.174 × 10−3	1.995 × 10−3	100	0.25	9.861 × 10−3	1.76 × 10−3	97.9592	0.125
5 cm	1.05 × 10−2	2.941 × 10−3	98.2906	0.125	9.65 × 10−3	1.83 × 10−3	98	0.125
10 cm	6.905 × 10−3	1.946 × 10−4	99.1525	0.25	8.857 × 10−3	1.58 × 10−3	97.9	0.25
20 cm	7.102 × 10−3	1.464 × 10−3	99.1540	0.25	5.306 × 10−3	1 × 10−3	96	0
Field size 6 × 6 cm 2
PDD	1.07 × 10−3	2.32 × 10−5	99.187	0.125	1.332 × 10−3	8.182 × 10−4	99.83	0.25
1.5 cm	4.38 × 10−3	6.86 × 10−4	98.2456	0.125	5.726 × 10−3	1.996 × 10−3	97.3684	0.125
5 cm	6.22 × 10−3	1.11 × 10−3	100	0.25	6.439 × 10−3	1.233 × 10−3	96.9231	0.125
10 cm	3.69 × 10−3	7.15 × 10−3	100	0.25	6.939 × 10−3	1.356 × 10−3	97	0.125
20 cm	4.53 × 10−3	1.13 × 10−3	100	0.05	3.393 × 10−3	1.327 × 10−3	95.8462	0.02
Field size 10 × 10 cm 2
PDD	9.42 × 10−4	6.15 × 10−4	99.537	0.25	1.163 × 10−3	6.709 × 10−4	99.5868	0
1.5 cm	4.3 × 10−3	9.18 × 10−4	100	0.2	5.208 × 10−3	1.147 × 10−3	97.6471	0.025
5 cm	5.03 × 10−3	8.74 × 10−4	99.1736	0.125	3.406 × 10−3	4.03 × 10−4	100	0.125
10 cm	4.28 × 10−3	1.00 × 10−3	99.1597	0.125	3.581 × 10−3	8.163 × 10−4	99.1597	0.125
20 cm	2.82 × 10−3	1.03 × 10−3	100	0.2	2.689 × 10−3	8.82 × 10−3	100	0.1

Figure 3.

Dose distribution comparison between MC Gate version 9.0 and experiment data provided by Elekta Synergy MLCi2 platform

Figure 4.

Dose distribution comparison between MC TOpas version 3.6 and experiment data provided by Elekta Synergy MLCi2 platform

Calculation performance

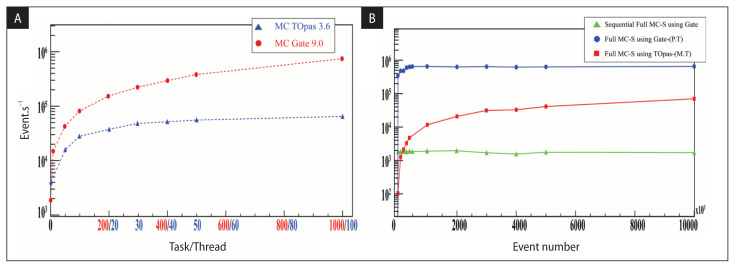
Figure 5A displays that the number of events simulated per unit time improved immediately in terms of the number of tasks utilized for Gate (Multiprocessing) and threads for TOpas MC simulation. The curve distribution exhibits the highest rate reached at 1000 tasks applying Gate MC code.

Figure 5.

The processing speed of TOpas-[mt] Vs. Gate-[mp]. A. Calculation speed in terms of thread-task number; B. Calculation speed of both sequential and multithreaded mode in terms of the total number of events for 100 threads

Discussion

Multiple simulations are run to adjust the mean energy of the primary electron beam, with an energy range of 5 to 7 MeV and a growth step of 0.1 MeV. The delivered doses are then compared to reference measurements. As a consequence, the mean electron energy of 6.7 MeV was determined to be the best fit for this Elekta Synergy MLCi2 model simulation. This mean value is greater than that found in the literature [24–26]. However, this mean value is close to that of 6.5 MeV provided by other simulations based on the manufacturer’s detailed specifications of the accelerator’s head components. The photon output rate and the output rate in the function of time are significantly higher, where the SBS tool is used. Further, according to the results given in Table 2. The simulation efficiency is found to be 2.181 times higher when implementing the SBS tool. To summarize, the simulation efficiency depends on both the photon output rate and the uncertainty of distribution dose within the water phantom. The SBS tool presents an ideal fit for this study because it improves the photon output rate without affecting the distribution dose uncertainty.

Table 2.

Computed simulation efficiency with and without SBS

	Time [min]	σD	ζs
Without B.S	1200	2.89 × 10−1	9.97 × 10−3
With B.S	1200	1.35 × 10−1	× 10−3

According to Figure 2. For most of the beam, the large amount of the photons is primary, i.e., they were only created in the target before reaching the rest of the linac segments. The Elekta Synergy MLCi2 6 MV beam has a significant number of scattered photons. The scattered photons are grouped into three major components: those last scattered from the primary collimator, the flattening filter, or the field-defining jaws (MLC and Jaws). These results are in good agreement with the results obtained by Sheikh-Bagheri [27]. Figure 2 also shows the simulated fluence spectra for contaminant electrons and positrons created by linac components and reaching a water phantom at a Source Surface Distance equal to 100 cm. The immediate drop in the fluence corrected by the energy deposition of very low-energy of contaminant radiation is due to the cut-off kinetic energy for the transport of electrons and positrons.

According to Figures 3 and 4, it can be achieved that the PDD and the cross profiles of the MC simulation applying TOpas and Gate (blue and gray curves) are very well matched with the measured data (red curve).

One can notice that depth and cross profile doses are in excellent agreement with measurements applying Gate MC code. The deviation amongst measurement and Gate MC simulation is discovered to be less than 1% using standard mean error ɛ. The simulation’s accuracy is confirmed by applying Distance To Agreement DTA and gamma index criterion, where 98% of the points have a gamma (2%/2 mm) < 1 and a DTA less than 0.5 mm. According to Table 3, the same reason is matched regarding TOpas MC code. The significant deviation of simulation accuracy occurred for the calculated profiles at depth 20 cm, with 95.8462% of the points having a gamma (2%/2 mm) < 1 for the 6 × 6 cm² radiation field. This deviation occurs in the penumbra regions and it may be due to the lower statistics of particles at this depth that significantly increase the error.

Furthermore, the comparison diagram of Figure 5B proves that speed processing is reasonably constant in terms of the total number of events simulated for both Multitasking for Gate or Multi-threading for TOpas and full sequential simulation.

Conclusion

In this work, we validated the new version of Monte Carlo TOpas 3.6 software in order to simulate linear accelerator Elekta Synergy MLCi2 dose distributions. Extensive dose distribution evaluation using the index formalism was performed for four regular squared fields of different sizes. Dose calculations were made utilizing TOpas-[multithreading] and Gate-[multiprocessing] Monte Carlo codes. They were running in the cluster computing technique (Slurm — CNRST Team Morocco). Experimental dose data for comparison were measured in an IBA water phantom and determined based on monthly quality assurance (QA) measurements without extra smoothing. The index analysis for (2%/2 mm) displays a satisfying criterion is passing 99% and 97% for Gate and TOpas MC simulations, respectively. In concerns to dose calculation performance, the use of Gate-[mp] significantly increases the event simulation speed compared to TOpas-[mt]. Ultimately, these preliminary results demonstrate that Topas can be applied for radiation therapy applications. Further, to prove that TOpas can be serviceable for treatment planning (TPS) purposes, other validations must be achieved with different energies, complex MLC fields, and dynamic IMRT irradiation fields.