New dose-response model and SARS-CoV-2 quanta emission rates for calculating the long-range airborne infection risk

Abstract

Predictive models for airborne infection risk have been extensively used during the pandemic, but there is yet still no consensus on a common approach, which may create misinterpretation of results among public health experts and engineers designing building ventilation. In this study we applied the latest data on viral load, aerosol droplet sizes and removal mechanisms to improve the Wells Riley model by introducing the following novelties i) a new model to calculate the total volume of respiratory fluid exhaled per unit time ii) developing a novel viral dose-based generation rate model for dehydrated droplets after expiration iii) deriving a novel quanta-RNA relationship for various strains of SARS-CoV-2 iv) proposing a method to account for the incomplete mixing conditions. These new approaches considerably changed previous estimates and allowed to determine more accurate average quanta emission rates including omicron variant. These quanta values for the original strain of 0.13 and 3.8 quanta/h for breathing and speaking and the virus variant multipliers may be used for simple hand calculations of probability of infection or with developed model operating with six size ranges of aerosol droplets to calculate the effect of ventilation and other removal mechanisms. The model developed is made available as an open-source tool.

1. Introduction

SARS-CoV-2 is spread by exposure to respiratory fluids carrying the infectious virus [1]. The virus-carrying respiratory droplets and aerosols can be produced through all expiratory activities including breathing, talking, coughing, and sneezing from both symptomatic and asymptomatic individuals [1]. These infectious aerosols and droplets may come into direct contact with susceptible individuals by inhalation from the surrounding air or indirect contact when the susceptible individual touches a surface contaminated by infectious respiratory fluid [2]. Although disputed at the start of the pandemic, the evidence for direct airborne transmission of SARS-CoV-2 has grown as the pandemic progressed [[3], [4], [5]]. It is now widely accepted that airborne transmission of SARS CoV-2 may be the leading cause of super-spreading events that are recognized as the pandemic's primary drivers [6]. Once recognized as the main route of COVID-19 spread, identifying the relative importance of different engineering controls targeting the spread of COVID-19 in indoor environments requires accurate prediction of the transmission risk. In this context, there is a need for predictive risk assessment tools for better understanding when planning effective strategies to minimize risks associated with airborne transmission.

The concept behind the mathematical tools used so far for modeling airborne transmission risk is based on coupling dose-response models with a box model containing a source and sink of contaminants. The infection risk inside the box can be modeled either using i) a simplified approach by analytically solving the conservation of mass equations for the contaminants under quasi-ideal and quasi-uniform assumptions/conditions (not considering the airflow dynamics inside the box) ii) a complex approach by numerically solving full conservation of mass and energy equations of the airflow dynamics and contaminant transport using numerical solvers, i.e., computational fluid dynamics (CFD). Whilst the latter generates more accurate predictions it requires an experienced user with expertise in using CFD tools. The computationally demanding CFD modeling approach is also limited by a time-consuming simulation process, taking a long time to run even in small indoor spaces. Hence, CFD models are neither easily applied to new rooms nor suited for rapid simulations, which may be essential for fast-evolving pandemic conditions. In addition, in comparison to the complex approach, the simplified approach can be implemented in the form of open-access digital tools that are straightforward, fast, and simple to use for epidemiologists, virologists, immunologists, and other public health experts without previous background expertise on airborne transmission risk modeling.

Although extensively used during the pandemic, there is yet still no consensus on a universal simplified approach, which may create misinterpretation of results, confusion among public health experts, etc. In this context, a short history described through mathematical development of the dose-response model coupled is presented in the next chapter.

2. Modeling background

In general, the dose-response models predict the probability of an infection or illness of a proportion of the susceptible population when exposed to a given dose, i.e. number of viral copies of a specific respiratory virus. These models are based on two principles: the estimation of the intake dose of the infectious agent and the estimation of the probability of infection under a given intake dose.

The two most commonly used dose-response models for calculating the infection risk of respiratory viruses are the exponential and beta-Poisson models [7]. Both models assume a random distribution of the number of copies in the exposed medium (ambient air) described by the Poisson probability distribution. If the exposed medium (ambient air) contains a known mean number of n viral copies, the probability that the susceptible person would ingest exactly m number of viral copies (per hour) would equal:

$$P\left(m;n\right)=e^{-n}\bullet \frac{n^m}{m!}$$ (1)

The number of viral copies k that will survive from the ingested copies m and cause an infection will depend on the survival probability p (%) of a single viral copy that differs depending on the host susceptibility, i.e. each host may have an equal or different probability of getting infected from the same number of viral copies. The probability P that exactly k number of m ingested viral copies will survive the host response and cause infection is determined by the binomial probability distribution:

$$P\left(k;m,p\right)=\left(\begin{array}{l}m\\ k\end{array}\right)\bullet p^k\bullet {\left(1-p\right)}^{m-k}$$ (2)

The exponential model assumes that each host has an equal probability of getting infected from a single viral copy defined as: $=\frac{1}{v}$ ; where v (−) is defined as the number of ingested viral copies that will cause an infection, i.e. the infectious dose (ID). So, the total infection probability defined by the exponential model is calculated according to the following transformations:

$$P\left(k;m,n,p\right)=\sum _{m=k}^{\infty }\left\{\left(\begin{array}{l}m\\ k\end{array}\right)\bullet p^k\bullet {\left(1-p\right)}^{m-k}\right\}\bullet \left\{e^{-n}\bullet \frac{n^m}{m!}\right\}=\sum _{m=k}^{\infty }\frac{m!}{\left(m-k\right)!\bullet k!}\bullet p^k\bullet {\left(1-p\right)}^{m-k}\bullet e^{-n}\bullet \frac{n^m}{m!}\bullet \frac{n^k}{n^k}\Rightarrow P\left(k;m,n,p\right)=\frac{{\left(np\right)}^k\bullet e^{-n}}{k!}\bullet \sum _{m=k}^{\infty }\frac{{\left((1-p\right)\bullet n)}^{m-k}}{\left(m-k\right)!}=\frac{{\left(np\right)}^k\bullet e^{-n}}{k!}\bullet e^{\left(1-p\right)\bullet n}$$ (3)

The probability that at least one viral copy will be ingested is valid for all $k>0$:

$$P\left(1\le k<\infty \right)=1-P\left(0\right)=1-e^{-p\bullet n}$$ (4)

In summary, given known parameters in both the exponential or the beta-Poisson dose-response model as well as the mean number of n viral copies in the exposed ambient air allows the calculation of the airborne transmission risk. To simplify the infection risk models by avoiding the use of parameters, Riley et al. [8] implemented Wells's concept of one quantum [9], which is defined as the number of inhaled infectious virus-laden aerosols n = v required to infect at least 63.21% percent of the susceptible persons defined through the exponential model:

$$P=1-e^{-p\bullet n}=1-e^{-\frac{1}{v}\bullet v}=1-e^{-1}=63.21\%$$ (5)

Under the assumption that the number of airborne quanta is constant in the ambient air, one may express the exponential dose-response model by using the total number N of inhaled quanta (each quanta containing v number of viral copies) as:

$$P=1-e^{-p\bullet n}=1-e^{-\mathit{N}\bullet \frac{1}{v}\bullet v}=1-e^{-\mathit{N}}$$ (6)

Riley et al. [9] further expanded the exponential dose-response model by assuming that if the quanta-carrying aerosols are evenly distributed in a ventilated room with a quanta concentration $n\left(t\right)\left[\frac{quanta}{m^3}\right]$ , the total amount of quanta inhaled $n$ in the room under steady-state conditions ($\frac{dn\left(t\right)}{dt}=0)$ for an exposure time t equals:

$$N=IR\bullet {\int }_0^{t}n\left(t\right)dt=IR\bullet n\bullet t$$ (7)

Further assuming that the only source of quanta is through exhalation from $I$ number of infected persons with an average quanta production rate of $q$, the quanta concentration $\mathit{n}$ in the room under steady-state conditions ($\frac{dn\left(t\right)}{dt}=0)$ becomes:

$$V\bullet \frac{dn\left(t\right)}{dt}=S-Q\bullet n\left(t\right)=>n=\frac{S}{Q}=\frac{I\bullet q}{Q}$$ (8)

then infection risk probability can be expressed in the following form:

$$P=1-e^{-\mathit{N}}=1-e^{-IR\bullet n\bullet t}=1-e^{-\frac{I\bullet IR\bullet q\bullet t}{Q}}$$ (9)

Equation (9) is known as the classical/conservative form of the Wells-Riley equation.

However, this original version assumed steady-state conditions, i.e. constant concentration of aerosolized quanta in the surrounding air. Gammaitoni and Nucci [10] introduced a model capable of incorporating non–steady-state quanta concentrations by solving equation (8) for $\frac{dn\left(t\right)}{dt}\ne 0$ . Given known initial quanta concentrations $n_0$ and known removal mechanisms $\sum \lambda$ allows evaluating the amount of quanta concentration in an indoor environment at any time interval:

$$V\bullet \frac{dn\left(t\right)}{dt}=S-V\bullet n\left(t\right)\bullet \sum \lambda =>n\left(t\right)={n_0\bullet e}^{-\sum \lambda \bullet t}+\frac{S}{V\bullet \sum \lambda }\bullet \left(1-e^{-\sum \lambda \bullet t}\right)$$ (10)

However, as in the original Wells-Riley model, the Gammaitoni and Nucci model [10] also considered the ventilation rate as the only removal/sink term in the equation. Therefore, the equation has been upgraded in later models to incorporate other removal mechanisms and control measures that can affect the infection risk, i.e., the biological decay of the airborne pathogen [11] and deposition loss of the infectious particles due to gravitational settling [12] but also the optional removal mechanisms such as ultraviolet radiation and supply air filtration in the case of a recirculating ventilation system [[13], [13]]. However, the input processing of these removal mechanisms may be troublesome: the data unavailability of the biological decay rates for certain viruses and the data uncertainty for the deposition rates due to the broad spectrum of both the amount and size ranges of the aerosol-carrying particles may misestimate the infection risk calculation. In addition, the input values of the source term described by the average quanta production rate have so far been based on quite limited literature data and vary not only on the type of disease for different viruses but also on the original epidemiological case study for the same virus type. Furthermore, the classical Wells Riley model is limited to fully and ideally air mixing in a single zone. Consequently, the airborne infection risk could be under-or overestimated.

These issues remained unsolved until the recent COVID-19 pandemic. As no standardized WR model exists, airborne transmission risk studies used different variations of the WR model; most often the conservative WR model with only the ventilation rate as the removal mechanism. Such simplification may not only misestimate the infection risk calculation but also miscalculate the potential effects of all existing removal mechanisms besides ventilation and their susceptibility to indoor environmental parameters. The specific objective of this study is to improve the classical WR-model by resolving the specific issues: i) develop an aerosol and droplet production rate model from the source, I.e. infected person for different expiratory modes and virus variants ii) expand the classical model with all potential removal mechanisms iii) propose a method to account for the incomplete mixing conditions. To reach these specific objectives, we decided to perform a comprehensive review of all the Wells-Riley models that have been used to model the infection risk in research studies published after the start of the pandemic in early 2020. By resolving the specific issues, the overall aim of this study is to develop and propose an advanced Wells Riley model for future and retrospective indoor infection risk assessments.

3. Methodology

The Medline database was searched for all original articles modeling the airborne transmission risk using the Wells-Riley model. A comprehensive list of search terms, i.e. “Wells-Riley model”, “airborne transmission risk ”, and “infection risk model”, was used, including Medical Subject Headings (MeSH). The search was limited to English-language articles published after 01.01.2020. The last search was conducted on 24^th August 2022. Finally, 21 articles [[13], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26], [27], [28], [29], [30], [31], [32], [33], [34]] were considered eligible for inclusion in the present review study. Data from the included studies were extracted using a predesigned spreadsheet. From each study, the following data were extracted: source details, authors, year of publication, whether the WR model was solved for a steady/non-steady state, whether fully mixing conditions were assumed or not, types of removal mechanisms, and information on source modeling regarding quanta emission rate including the droplet production rate.

3.1. Source: Quanta emission rate

The quanta emission rate was reported to be calculated as either directly estimated from previous epidemiological studies or derived from the volume emission rate, viral load, and quanta-response relationship.

3.1.1. Directly estimated from epidemiological studies for previous species of coronaviruses

This method was used in four risk assessment studies published during the pandemic and has also been used before the pandemic for assessment risk calculations for other respiratory viruses.

This method is not new and has been used before the current pandemic to estimate the quanta emission for other infectious respiratory viruses including measles [8], tuberculosis [10], and influenza [37]. The method was used by six studies when estimating the quanta emission rate for SARS-CoV-2 [15,21,23,24,29,32,35,36]. The method is based on fitting the quanta emission rate $S$ in equation (10) for a derived steady-state value of quanta concentration in air $n$ that was back-calculated from the infection risk equation (9) $P$ reported in previous outbreaks of SARS-CoV-2:

$$P=1-e^{-IR\bullet n\bullet t}=>n=-\frac{\ln \left(1-P\right)}{IR\bullet t}$$ (11)

The source is then back-calculated from equation (7):

$$S=-\frac{\sum \lambda \bullet \left(\frac{\ln \left(1-P\right)}{IR\bullet t}+{n_0\bullet e}^{-\frac{\sum \lambda }{V}\bullet t}\right)}{1-e^{-\frac{\sum \lambda }{V}\bullet t}}$$ (12)

This method requires considerable input information from the observed outbreaks, and additional building system details such as the amount of recirculated air, filter efficiency, ventilation rates, on rates, space volume, and exposure time of infected persons but also additional building system details such as the amount of recirculated air, filter efficiency, etc. With insufficient input details, the uncertainty risk may be too large for the quanta estimation rate S to be used for both future and retrospective infection risk assessments.

3.1.2. Derived from the droplet volume emission rate $\left(\frac{ml}{h}\right)$, the viral load ($\frac{RNA}{ml}$) and the quanta-response relationship $\left(\frac{quanta}{RNA}\right)$

This is a novel methodology for calculating the quanta emission rate that was reported in 15 studies [13,14,[16], [17], [18], [19], [20],[25], [26], [27], [28],30,31,34] and can be summarized in the following expression:

$$S=c_v\bullet c_i\bullet V_{exh}$$ (13)

$c_v$ – viral load in the respiratory tract $\left[\frac{RNA}{mL}\right]$

$c_i$ – the quanta-response relationship is defined as the ratio between one infectious quantum and the infectious dose expressed in viral copies, i.e. the number of viral RNA copies required to infect at least 63.21% of susceptible persons, $\left[\frac{quanta}{RNA}\right]$

$V_{exh}-$ the total volume of respiratory fluid exhaled per unit time, $\left[\frac{ml}{h}\right]$

3.1.2.1. Respiratory aerosol and droplet volume emission rate models

Three original methods/equations have so far been used to calculate $V_{exh}$:

• a)The method by Buonnano et al. [17].

$$V_{exh}=IR\bullet \sum _{i=1}^4\left(N_{i,j}\bullet V_i\right)$$ (14)

$IR$- breathing rate $\left[\frac{m^3}{h}\right]$

$V_i$– the spherical volume of a single droplet in the ith bin $\left[mL\right]$

$N_{i,j}$- Droplet number concentration in the ith bin of four aerosol droplet diameters during four different expiratory activities ($j$) as measured by Morawska et al. [36] $\left[\frac{particles}{{cm}^3}\right]$ as presented in Table S1 of supplementary materials.

A similar approach was used by Aganovic et al. for speaking. The size distribution (Table S2) for speaking is determined experimentally by the works of Morawska et al. [38] for droplet aerosols $\le$ 2 $\mu m$ and Chao et al. [39] for respiratory droplets $\ge$ 2 $\mu m$ [38]. However, instead of using the spherical volume of a single droplet, they used the following expression to calculate the total volume from a size bin:

$$V_i\left(D\right)=\frac{\pi \bullet \left({D_{\mathit{max}}}^4-{D_{\mathit{min}}}^4\right)}{24\bullet \left(D_{\mathit{max}}-D_{\mathit{min}}\right)}$$ (15)

where $D_{\mathit{max}}$ and $D_{\mathit{min}}$ denote the bin's lower and upper diameter values, according to Nicas [40].

• b)The method by Schjiven et al. [15].

Schjiven et al. [[13], [13]] developed two equations for calculating $V_{br}$ depending on the type of expiratory activity:

• i)Breathing

The total volume of aerosol droplets exhaled per hour of breathing was calculated as:

$$V_{breath}=60\bullet {10}^{N\left({\mu }_{br},{\sigma }_{br}\right)}\bullet {10}^{-12}\bullet \frac{\pi }{6}\bullet \sum _{i=1}^6\left(d_i^3\bullet {10}^{N\left({\mu }_i,{\sigma }_i\right)}\right)$$ (16)

$N\left({\mu }_{br},{\sigma }_{br}\right)$ – lognormal distribution of the breathing rate as measured by Fabian et al. [39] $\left[\frac{L}{\mathit{min}}\right]$ with mean ${\mu }_{br}={\mathit{log}}_{10}\left(6.8\right)$ and standard deviation (SD) ${\sigma }_{br}=0.05$

$d_i$– droplet diameter in the ith bin of six aerosol droplet diameters as measured by Fabian et al. [41] $\left[mL\right]$

$N\left({\mu }_i,{\sigma }_i\right)$ – lognormal distribution of the concentration of $d_i\left[\frac{particles}{\mathit{min}}\right]$ with mean ${\mu }_i$ and SD ${\sigma }_i$ for each bin given in Table S3.

• ii)Speaking and singing

According to Schjiven et al. [[13], [13]], the total volume of aerosol droplets exhaled per hour of speaking and singing was calculated by summing $n_{sp,si}$ samples of volumes of each aerosol diameter from the aerosol diameter data set $d\left(\mu \mathrm{m}\right)$ as follows:

$$V_{sp,si}=3\bullet {10}^{-12}\bullet n_{sp,si}\bullet \frac{\pi }{6}\bullet \sum _{i=1}^{k_{sp,si}}{d}_i^3$$ (17)

$d_i$– droplet diameter in the ith bin of $k_{sp}=13$ and $k_{sp}=5$ aerosol droplet diameters for loud-voiced counting [42] and singing [43] as in Table S4.

$n_{sp,si}$ - lognormal distribution of expelled aerosol d droplets calculated based on mean ${\mu }_{sp}=2.2$ and standard deviation ${\sigma }_{sp}=0.29$ from measured data during speaking [44] and ${\mu }_{si}=5.0$ and ${\sigma }_{si}=0.28$ for singing [43]:

$$n_{sp,si}={10}^{N\left({\mu }_{sp,si},{\sigma }_{sp,si}\right)}+0.5$$ (18)

• c)The method by Nordsiek et al. [16].

Instead of using measured data on droplet concentration in different size distributions, the model developed by Nordsiek et al. [14] utilized probability density functions (pdfs) of the droplet diameter. These functions were obtained using the tri-modal lognormal distribution derived by Johnson et al. [45]. The model is known as the bronchiolar-laryngeal-oral (B-L-O) tri-modal model, as it considers droplet production associated with three distinct modes: one occurring in the lower respiratory tract, another in the larynx, and a third in the upper respiratory tract and oral cavity, respectively. The number concentration of droplets of size k produced in each of the modes is given as a sum over each mode i [45]:

$$\frac{d{Cn}_k}{{d\log }_{10}{d}_p}=\ln \left(10\right)\bullet \sum _{i=1}^3\left[\left(\frac{{Cn}_i}{\sqrt{2\bullet \pi }\bullet \ln \left(GSDi\right)}\right)\bullet e^{\left(-\frac{{\left(\ln d_p-\ln {CMD}_i\right)}^2}{2\bullet {\left(\ln {GSD}_i\right))}^2}\right)}\right]$$ (19)

The model parameters for dehydrated aerosols produced during speaking [43] are presented in Table S5.

The notation $\frac{d{Cn}_k}{{d\log }_{10}{d}_p}$ represents the number concentration in each bin of particle diameters ($d{Cn}_k$) normalized by a bin width (k to k+1) that is constant in log space, i.e. ${d\log }_{10}{d}_p$ = $\log \left(\frac{d_{p,k+1}}{d_{p,k}}\right)$, where k represents a discretization of the dp space. The volume of particles of a given diameter is represented as a concentration $\left[\frac{{\mu m}^3}{{cm}^3}\right]$ , assuming all particles are spherical, is given by:

$$V_{exh}=IR\bullet d{Cn}_k\bullet \frac{\pi \bullet d_{p,k}^3}{6}$$ (20)

All three methods presented in a), b) and c) are compared to corresponding experimental data measurements for breathing, speaking, and singing as measured by Fleischer [46] as presented in Table 1 . Both volume droplet emission rate models by Bunonano et al. [16], and Schjiven et al. [[13], [13]] showed relatively good agreement with the data measurements by Fleishcer et al. [46] for both fine aerosols $\le 5\mu$ m and both fine and coarse aerosols $\le 20$ $\mu$ m. The volume emission rate measured by Fleischer et al. [46] for singing was within the range of volume rates generated by the model by Schjiven et al. model [[13], [13]] for singing. The model output by Nordsiek et al. underestimated the volume emission by speaking.

Table 1.

Comparison of droplet volume emission rate models for different expiratory activities against experimental data.

	Size range Ddry ($\mu$ m)	Breathing $V_{br}$$\left[\frac{pL}{h}\right]$	Speaking $V_{sp}$$\left[\frac{pL}{h}\right]$	Singing $V_{si}$$\left[\frac{pL}{h}\right]$
Model
Bunonano et al. [16]	$\le 5.5$	157	748	–
Schjiven et al. [[13], [13]]	$\le 20$	132a (0–54000)	1080a (0–54000)	12900a (930–123000)
Nordsiek et al. [14]	$\le 20$	–	142	–
Experimental data
Fleischer et al. [446]	$\le 5$	332	1289	6487
	$\le 20$	332	1390	10963

^amean (min-max) computed after running 10 000 Monte Carlo samples.

Based on these observations, we decide to introduce a new model for breathing, singing, and speaking similarly to Bunonano et al. [16] as follows:

$$V_{exh}=3600\bullet {10}^6\bullet \sum _{i=1}^6{P}_{i,br,sp,si}\bullet V_i\left(D\right)$$ (21)

$P_i$- particle emission rate $\left[\frac{particles}{s}\right]$ in the ith bin of six aerosol droplet diameters during three different expiratory activities ($br,sp,si$) as measured by Fleischer et al. [46] and presented in Table S6 of supplementary materials. $V_i\left(D\right)$ is the total volume from each size bin as calculated in equation (15).

3.1.2.2. Viral load $c_v$$\left[\frac{RNA}{mL}\right]$

The viral load in respiratory aerosol reflects the virion concentration in the fluid where the particles originate. The infected respiratory droplets may originate through sputum expelled from the lower respiratory tract (the trachea, the bronchi and bronchioles, and the alveoli) or the saliva generated in the upper respiratory tract (nasal cavity, throat/pharynx, or voice box/larynx). The respiratory droplets emitted by breathing are generated in the lower respiratory tract while the droplets produced by speaking are generated in the upper respiratory tract [47]. The amount of RNA gene copies emitted by an infected person depends both on the volumetric flow rate exhaled per unit time and the viral load at the origin of production (upper or lower respiratory tract) and so the total amount of RNA gene copies expelled will differ for different expiratory activities, such as speaking and breathing. When released from either the lower or upper respiratory tract (assumed to have ∼100% RH), droplets experience rapid evaporation and shrinkage upon encountering the unsaturated ambient air. Depending on the relative humidity value, the initial size of a hydrated respiratory droplet (∼100% RH) can be 2–3 times larger than the dehydrated droplet [48].

Therefore, the evaporation process may have a significant effect on the total calculated volume of the droplets and consequently on the number of viral RNA copies contained in dehydrated fine aerosols $\le$ 5 $\mu$ m as the data used for $c_v$ $\left[\frac{RNA}{mL}\right]$ is based on the viral load reported directly from respiratory tract samples (sputum or saliva). The studies utilizing the quanta emission rate based on viral load have so far used the initial viral load reported in sputum or saliva, assuming that the initial proportionality $\frac{RNA}{mL}$ accounts even after evaporation. However, this is not the case as shown by a recent study [49] that measured viral RNA in different-sized respiratory aerosols emitted by infected patients. It found that aerosols $\le$ 5 $\mu$ m contained more viral copies than aerosols $\ge$ 5 $\mu$ m so that 93% and 54% of the viral load in this study was detected in aerosols $\le$ 5 $\mu$ m for talking and breathing, respectively. Thus, it is crucial to calculate the viral copies $c_{v,\left(D_{dry}\le 5\mu \mathrm{m}\right)}$ contained in fine dehydrated aerosols. This may be done using the following procedure based on the balance equation of RNA copies, i.e. RNA copies are not affected by the short evaporation process and stay constant before and after evaporation that lasts some time $\Delta t_{evap}$:

$$c_{v,0}\bullet V_{exh,0}\bullet \Delta t_{evap}=c_{v,dry}\bullet V_{exh,dry}\bullet \Delta t_{evap}=>c_{v,0}\bullet \frac{\pi }{6}\bullet \sum _{i=1}^n{{n_{i,0}\bullet d}_{i,0}}^3=c_{v,dry}\bullet \frac{\pi }{6}\bullet \sum _{i=1}^n{{n_{i,dry}\bullet d}_{dry}}^3$$ (22)

The number of droplets in each size bin will remain the same before and after evaporation, i.e. $n_{i,0}=n_{i,eq}$ and if we now use the shrinkage factor for evaporation due to dehumidification of the initial hydrated droplet from Table S9 so that ${d_{i,eq}\approx 0.4\bullet d}_{i,0}$ , we can further write that:

$$c_{v,0}\bullet \sum _{i=1}^n{\left(\frac{d_{dry}}{0.4}\right)}^3=c_{v,dry}\bullet \sum _{i=1}^n{d_{dry}}^3=>c_{v,dry}=15.6\bullet c_{v,0}$$ (23)

The total number of RNA copies expelled during some time interval $\Delta t$ can be expressed as:

$$c_{v,dry}\bullet V_{exh,dry}\bullet \Delta t=c_{v,dry\left(\le 5\mu \mathrm{m}\right)}\bullet V_{exh,dry\left(\le 5\mu \mathrm{m}\right)}\bullet \Delta t+c_{v,dry\left(\ge 5\mu \mathrm{m}\right)}\bullet V_{exh,dry\left(\ge 5\mu \mathrm{m}\right)}\bullet \Delta t$$ (24)

Based on the viral loads in fine and coarse aerosols reported in Ref. [49] the viral load contained in dehydrated respiratory aerosols $\le$ 5 $\mu$ m $\left[\frac{RNA}{mL}\right]$ for breathing, speaking and singing can be calculated as:

$$c_{v,breath,dry\left(\le 5\mu \mathrm{m}\right)}\bullet V_{breath,dry\left(\le 5\mu \mathrm{m}\right)}=0.54\bullet c_{v,dry}\bullet V_{breath,dry}$$ (25)

$$c_{v,speak,dry\left(\le 5\mu \mathrm{m}\right)}\bullet V_{speak,dry\left(\le 5\mu \mathrm{m}\right)}=0.93\bullet c_{v,dry}\bullet V_{speak,dry}$$ (26)

$$c_{v,sing,dry\left(\le 5\mu \mathrm{m}\right)}\bullet V_{sing,dry\left(\le 5\mu \mathrm{m}\right)}=0.83\bullet c_{v,dry}\bullet V_{sing,dry}$$ (27)

Using (23) we get:

$$c_{v,breath,dry\left(\le 5\mu \mathrm{m}\right)}=8.4\bullet c_{v,0}\bullet \frac{V_{breath,dry}}{V_{breath,dry\left(\le 5\mu \mathrm{m}\right)}}$$ (28)

$$c_{v,speak,dry\left(\le 5\mu \mathrm{m}\right)}=14.5\bullet c_{v,0}\bullet \frac{V_{speak,dry}}{V_{speak,dry\left(\le 5\mu \mathrm{m}\right)}}$$ (29)

$$c_{v,sing,dry\left(\le 5\mu \mathrm{m}\right)}=13.0\bullet c_{v,0}\bullet \frac{V_{sing,dry}}{V_{sing,dry\left(\le 5\mu \mathrm{m}\right)}}$$ (30)

Where $V_{breath,dry}$ , $V_{speak,dry}$ and $V_{sing,dry}$ $\left[\frac{mL}{h}\right]$ are the total volumetric flowrates of all dehydrated respiratory aerosols and droplets exhaled by breathing, speaking, and singing respectively, while $V_{breath,dry\left(\le 5\mu \mathrm{m}\right)}$ , $V_{speak,dry\left(\le 5\mu \mathrm{m}\right)}$ and $V_{sing,dry\left(\le 5\mu \mathrm{m}\right)}$ are the volumetric flow rate of only dehydrated respiratory aerosols $\le$ 5 $\mu$ m in size. The correlation $\frac{V_{breath,eq}}{V_{breath,eq\left(\le 5\mu \mathrm{m}\right)}}=1.04$ was found using equation (16). Finally:

$$c_{v,breath,eq\left(\le 5\mu \mathrm{m}\right)}=8.7\bullet c_{v,0}$$ (31)

Similarly, the expression for the viral load in dehydrated aerosols for speaking and singing was derived using equation (17) respectively:

$$c_{v,speak,eq\left(\le 5\mu \mathrm{m}\right)}=78.7\bullet c_{v,0}$$ (32)

$$c_{v,sing,dry\left(\le 5\mu \mathrm{m}\right)}=26.0\bullet c_{v,0}$$ (33)

3.1.2.3. The quanta-RNA relationship $c_i$ ($\frac{quanta}{RNA})$

In absence of data for SARS-CoV-2, most infection risk models [14,[16], [17], [18],20,[25], [26], [27],30,31] at the start of the pandemic relied on the exponential dose-response relationship derived for the SARS-CoV virus by Watanabe et al. [50] as $c_i=\frac{1}{410}\frac{quanta}{RNA}$. This dose-response model was based on data for several viruses besides SARS-CoV, including human coronavirus HcoV229, murine hepatitis virus (MHV), swine virus (HEV), and brouchitis IBV for both animal and human hosts. Schjiven et al. estimated based on the data for a Dutch variant of SARS-CoV-2 that 1440 copies result in an infection, and this quanta response relationship was used in the other three studies [18,28,34]. This estimation was based on the data for a beta variant of SARS-CoV-2 (B.1.351) 3.13 · 10⁹ RNA/mL that allegedly matched 5.62 · 10⁷ TCID₅₀, i.e. ${1TCID}_{50}\approx$ 56 RNA copies. Unfortunately, no research data or reference was provided supporting this relationship. As the pandemic progressed new dose-response model emerged. Most recently, Miura et al. [51] derived the following dose response for HCoV-229E based on human challenge data:

$$P\left(n\right)=1-\left(0.17\bullet e^{-4.2{\bullet 10}^{-9}\bullet n}+\left(1-0.17\right)\bullet e^{-k\bullet n}\right)$$ (34)

So far only one dose-response research study has been performed for SARS-CoV-2 [52] for which 18/34 (52%) young adults were infected after being intranasal inoculated with 10 TCID₅₀ doses of a pre-alpha variant. For $k=-0.1$ => $P\left(10\right)=52\%$. Therefore as $P\left(14\right)=63.2\%$ we will define 14 TCID₅₀ as equal to 1 quanta. Sender et al. [53] analyzed human challenge data reported for a wild pre-alpha variant and concluded a relationship of ${1TCID}_{50}\approx {10}^{4}RNA$ copies, or $1quanta=14\bullet {10}^4$ RNA copies. Based on the quanta-RNA relationship for the original Wuhan strain, we derived also the quanta-RNA for several successive strains as shown in Table 2 .

Table 2.

Estimated quanta-RNA relationship for various strains of SARS-CoV-2.

Strain of SARS-CoV-2	Infectivity compared to variant in the previous row	${\mathit{c}}_{\mathit{i}}\left(\frac{quanta}{RNA}\right)$	Virus variant quanta multiplier (−)
Original (Wuhan)	–	14000	1.0
Alpha (B.1.1.7)	+90% [54]	7400	1.9
Delta (B 1.617.2)	+150% [55]	5000	2.8
Omicron (B.1.1.529)	+420% [56]	1200	11.7

When comparing the quanta-emission rates (quanta/h) to the previous model by Buonanno et al. [16], there are differences are more than tenfold even for the same expiratory activities and viral load, as shown in Table 3 . This significant difference is due to the difference between the values used to describe quanta-RNA relationship $c_i$. Buonanno et al. [16] used ${\mathrm{c}}_{\mathrm{i}}$ = 2 ⋅10⁻² $\left(\frac{quanta}{RNA}\right)$, based on data for SARS-CoV-1. In other words, Buonanno et al. [16] assumed that it would be needed to ingest at least 200 viral copies to infect at least 63.2% of the susceptible population, compared to our derived values of 14 000 viral copies of the original SARS-CoV-2 strain to cause infection.

Table 3.

Average quanta emission rates (quanta/h) for SARS-CoV-2 original strain.

Activity	Buonanno et al. [16] a Viral load 107 RNA/mL	This study Viral load 107 RNA/mL	This study Viral load 108 RNA/mL
Breathing	0.72	0.01	0.13
Speaking	9.7	0.38	3.8
Singing	62	0.90	9.0

^aIn the case of Buonanno we refer to 66th percentile values. In our study, in the case of a viral load of 10⁷ RNA/mL and 10⁸ RNA/mL we refer to 35th and 56% percentile values, respectively.

We have opted only for selecting representative quanta values depending on the purpose, as the viral load is a parameter with large variation. If the purpose is to model some event with a super spreader, extremely high values are to be used. In our application, we are interested in adequate ventilation in shared indoor spaces. In such a case, the aim is not to eliminate, but reduce the infection risk: an infectious person should infect no more than one person during the infectious period – therefore median values of the viral load are justified to use.

3.2. Sinks: Removal mechanisms

Altogether nine potential removal mechanisms were identified in the studies using the Wells-Riley model: ventilation ${\lambda }_{vent}$ [[13], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26], [27], [28], [29], [30], [31], [32], [33], [34], [35], [36]], deposition ${\lambda }_{dep}$ [[14], [15], [16], [17], [18],[20], [21], [22], [23], [24], [25], [26], [27], [28],[31], [32], [33], [34]], viral inactivation by relative humidity ${\lambda }_{RH}$ [[13], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26], [27], [28], [29],[31], [32], [33], [34]], portable air cleaner ${\lambda }_{PAC}$ [22,27,35,36], inactivation by ultraviolet germicidal irradiation of the recirculated air from the ventilation system or portable air cleaners ${\lambda }_{UVGI}$ [21,22,27,32], respiratory tract absorption rate ${\lambda }_{resp}$ [13,14,18,28,34], filtration of portable air cleaner or recirculated air ${\eta }_{filt-rec}$ [15,27,29,36], filtration by use of a face mask ${\eta }_{fm}$ [14,22,27,35]. The following sections present an overview of the removal mechanisms.

3.2.1. Ventilation ${\lambda }_{vent}$

Ventilation ${\mathit{\lambda }}_{\mathit{v}\mathit{e}\mathit{n}\mathit{t}}$ is the only removal mechanism included in the original Wells-Riley model, and thus in all following WR versions considered. Although not all buildings have installed mechanical ventilation systems, there is always an infiltration rate due to air leakage through the building envelope ranging from 0.6 to 3 ACH depending on standards [57].

Its removal rate is dependent on the good mixing assumption of the WR model, for which the airborne quanta is assumed to be equal across the space considered. It is the type of ventilation system that defines the airflow distribution, and hence the mixing conditions.

So far, there have been two modeling approaches [25,34] that have tried to account for the mixing conditions in the WR model. Both utilize the concept of ventilation efficiency $\epsilon$ [58] defined as:

$$\epsilon =\frac{n_{exh}\left(t\right)-n_{\mathit{sup}}\left(t\right)}{n\left(t\right)-n_{\mathit{sup}}\left(t\right)}$$ (35)

$n\left(t\right)$ – quanta concentration in the indoor environment at the time (t), $\frac{quanta}{m^3}$

$n_{\mathit{sup}}\left(t\right)$ – quanta concentration in the supply/outdoor at the time (t), $\frac{quanta}{m^3}$

$n_{exh}\left(t\right)$ – quanta concentration in the exhaust at the time (t), $\frac{quanta}{m^3}$

The ventilation efficiency can be simplified in case of no recirculation of ventilated air and as there is no airborne virus in outdoor air $n_{\mathit{sup}}\left(t\right)=0=>\epsilon =\frac{n_{exh}\left(t\right)}{n\left(t\right)}$ . The following two methods are presented below:

• a)The method by Shen et al. [25].

Expanding equation (10):

$$V\bullet \frac{dn\left(t\right)}{dt}=S-V\bullet n\left(t\right)\bullet \sum \lambda =S+Q_{vent}\bullet n_{\mathit{sup}}\left(t\right)-Q_{vent}\bullet n_{exh}\left(t\right)-V\bullet n\left(t\right)\bullet \sum {\lambda }_{rest}$$ (36)

Where ${\lambda }_{rest}=\sum \lambda -{\lambda }_{vent}$ are all the removal mechanisms excluding ventilation only. Further as $n_{\mathit{sup}}\left(t\right)=0$, ${\lambda }_{vent}=\frac{Q_{vent}}{V}$ and inserting $\epsilon =\frac{n_{exh}\left(t\right)}{n\left(t\right)}$ one gets:

$$V\bullet \frac{dn\left(t\right)}{dt}=S-Q_{vent}\bullet \epsilon \bullet n\left(t\right)-n\left(t\right)\bullet \sum {\lambda }_{rest}=S-V\bullet n\left(t\right)\bullet \epsilon {\bullet \lambda }_{vent}-V\bullet n\left(t\right)\bullet \sum {\lambda }_{rest}=s-V\bullet n\left(t\right)\bullet \left(\sum {\lambda }_{rest}+\epsilon {\bullet \lambda }_{vent}\right)$$ (37)

And the solution for transient conditions is then:

$$n\left(t\right)={n_0\bullet e}^{-\left(\sum {\lambda }_{rest}+\epsilon {\bullet \lambda }_{vent}\right)\bullet t}+\frac{S}{V\bullet \left(\sum {\lambda }_{rest}+\epsilon {\bullet \lambda }_{vent}\right)}\bullet \left(1-e^{-\left(\sum {\lambda }_{rest}+\epsilon {\bullet \lambda }_{vent}\right)\bullet t}\right)$$ (38)

• b)The method by Aganovic et al. [34].

The method proposed by Aganovic et al. [34] is based on dividing the indoor space into two zones to depict incomplete mixing. This concept has been introduced for airborne contaminants by Sandberg [58] and the model has shown to have good agreements with tracer gas measurements. Fig. 1 shows a schematic presentation of a two-zone exposure model of the imperfect room mixing loosely based on the two-zone models for imperfect mixing used earlier in literature [59,60]. In the exposure model, the space under consideration is divided horizontally into two perfectly mixed zones with uniform quanta concentrations in each zone $n_i\left(t\right)$ and $n_j\left(t\right)$: the occupied zone i reaching $h_{occup.}=1.8m$ above the floor and the rest is the unoccupied zone $n_j\left(t\right)$.

Fig. 1.

Schematic representation of a simplified two-zone exposure model [34].

The quanta balance for the lower occupied zone i can be expressed in the following form:

$$V_i\bullet \frac{d{n}_i\left(t\right)}{dt}=S+\beta \bullet Q{\bullet n}_j\left(t\right)-\beta \bullet Q{\bullet n}_i\left(t\right)-\sum {\lambda }_{i,rest}\bullet n_i\left(t\right){\bullet V}_i$$ (39)

$$V_j\bullet \frac{d{n}_j\left(t\right)}{dt}=Q\bullet n_{j,\mathit{sup}}-Q\bullet n_j\left(t\right)+\beta \bullet Q{\bullet n}_i\left(t\right)-\beta \bullet Q{\bullet n}_j\left(t\right)-\sum {\lambda }_{j,rest}\bullet n_j\left(t\right){\bullet V}_j$$ (40)

Where $\sum {\lambda }_{i,rest}$ and $\sum {\lambda }_{j,rest}$ are the rest of the sum of removal mechanisms except for ventilation in rooms $i$ and $j$ respectively. The volume of the occupied zone can be expressed as $V_i=\frac{1.8}{H}\bullet V$, where H is the height of the space, while the volume of the unoccupied zone is $V_j=\left(1-\frac{1.8}{H}\right)\bullet V$. As for infectious airborne contaminants $n_{\mathit{sup}}\approx 0$ it is possible to derive the expression for the mixing factor $\beta$ as a function of the contaminant removal effectiveness for steady state conditions $\epsilon =\frac{n_j}{n_i}\text{:}$

$$\beta =\frac{\epsilon }{1-\epsilon }\bullet \frac{Q\bullet H+\left(k+D\right)\bullet \left(H-1.8\right)\bullet V}{Q\bullet H}$$ (41)

The differential equations for the change in the quanta concentrations in zones i and j, i.e. the pair of equations (39), (40) for incomplete/imperfect mixing ventilation can be written in the following forms:

$$\frac{d{n}_i\left(t\right)}{dt}=A_1\bullet n_i\left(t\right)+{B_1\bullet n}_j\left(t\right)+C_1$$ (42)

$$\frac{d{n}_j\left(t\right)}{dt}=A_2{\bullet n}_i\left(t\right)+B_2\bullet n_j\left(t\right)+C_2$$ (43)

Where the constant coefficients A ₁,A ₂,B ₁,B ₂, C ₁ and C ₂ for the ventilation systems are presented in Table S7. The unique solutions to this set of first-order differential equations (42), (43):

$$n_i\left(t\right)=K_1\bullet \left(\frac{r_1}{A_2}\bullet e^{r_1\bullet t}-\frac{B_2}{A_2}\bullet e^{r_1\bullet t}\right)+K_2\bullet \left(\frac{r_2}{A_2}\bullet e^{r_2\bullet t}-\frac{B_2}{A_2}\bullet e^{r_2\bullet t}\right)-\frac{B_2}{A_2}\bullet \frac{C_1\bullet A_2-C_2\bullet A_1}{A_1\bullet B_2-A_2\bullet B_1}-\frac{C_2}{A_2}$$ (44)

$$n_j\left(t\right)=K_1\bullet e^{r_1\bullet t}+K_2\bullet e^{r_2\bullet t}+\frac{C_1\bullet A_2-C_2\bullet A_1}{A_1\bullet B_2-A_2\bullet B_1}$$ (45)

Where $r_1=\frac{A_1+B_2+\sqrt{{\left(A_1+B_2\right)}^2-4\bullet \left(A_1\bullet B_2-A_2\bullet B_1\right)}}{2}$ and $r_2=\frac{A_1+B_2-\sqrt{{\left(A_1+B_2\right)}^2-4\bullet \left(A_1\bullet B_2-A_2\bullet B_1\right)}}{2}$

The coefficients $K_2$ and $K_1$ can be calculated using initial conditions $n_i\left(0\right)=0$ and $n_j\left(0\right)=0$:

$$K_2=\frac{\left(C_1\bullet A_2-C_2\bullet A_1\right)\bullet \left(r_1-B_2\right)+C_1\bullet B_2-C_2\bullet B_1}{\left(r_2-r_1\right)\bullet \left(A_1\bullet B_2-A_2\bullet B_1\right)}$$ (46)

$$K_1=-K_2-\frac{C_1\bullet A_2-C_2\bullet A_1}{A_1\bullet B_2-A_2\bullet B_1}$$ (47)

3.2.2. Virus inactivation by relative humidity ${\lambda }_{RH}$ at the ambient temperature of 20–25 $°C$

Ambient temperature and humidity strongly affect the inactivation rates of enveloped viruses, including SARS-CoV-2 [61]. To characterize the impact of relative humidity on the inactivation rate ${\lambda }_{RH}$ for SARS-CoV-2 in aerosols, data on the aerosolized virus survival times at different relative humidities were obtained from experimental studies performed at indoor air temperatures 20–25 $°C$ [[62], [63], [64]]. The reported values for virus nebulized in artificial saliva, and for virus cultivated in the standard tissue culture medium are presented in Table S8. Previous studies have shown that the viral inactivation rates at different RH values for other enveloped viruses strongly depend on the complex composition of the respiratory droplet. While the exact salt to protein ratio is hard to identify, it has been assumed based on previous studies that the ratio is 1:1. The inactivation rates ${\lambda }_{RH}$ reported in Table S7 are shown for two distinct saliva/dry solutes compositions: an artificial medium-dry solute composition of 13.1 g/L salts and 3.6 g/L (3.6:1.0) proteins and a culture medium-dry solution composition consisting of 17.1 g/L salts and 6.8 g/L proteins (2.5:1.0). Therefore it is difficult to recommend whether values reported for artificial media or standard medium to be used separately [28] or to merge the values and use the mean [18].

3.2.3. The deposition rate ${\lambda }_{dep}$

The deposition rate of virus-carrying aerosols and droplets is determined by the settling or terminal velocity, which itself is dependent on droplet size. When released from the respiratory tract (assumed to have ∼99.5% RH), droplets experience rapid evaporation and shrinkage upon encountering the unsaturated ambient atmosphere. The dependence of the dry equilibrium size of an aqueous droplet (D_dry) containing dry solutes on RH can be derived from the separate solute volume additivity (SS-VA) model for multi-component particles by Mikhailov et al. [48]. For the sake of brevity, the equations are not repeated here. All the equations can be found in a recent study by Aganovic et al. [28] on the relationship between indoor RH and infection risk using the Wells-Riley model. The $D_{dry}/D_0$ ratios calculated according to the SS-VA model for the respiratory droplet initial size range of $0.3-10.0\mu \mathrm{m}$ are presented in Table S9 ratios The impact of RH on the size of dehydrated droplets with an initial size of 5 μm of different compositions (protein to salt ratios) as derived from the SS-VA model is shown in Fig. 2 .

Fig. 2.

The impact of RH on D_dry with an initial size of 5 μm of different compositions (protein to salt ratios) at an indoor air temperature range 20–25 °C.

The deposition rate ${\mathit{\lambda }}_{\mathit{d}\mathit{e}\mathit{p}}$ of a virus-laden droplet can be expressed as follows:

$${\mathit{\lambda }}_{\mathit{d}\mathit{e}\mathit{p}}=\frac{v_s}{H_{person}}$$ (48)

$H_{person}$ – the average height of the infected person(s), $m$

The gravitational settling velocity of the droplets $v_s$ and $\frac{m}{s}$ can be determined from the following:

$$v_s=\sum _{i=1}^n\frac{C_c\bullet {\rho }_d\bullet D_{eq,i}^2\bullet g}{18\bullet \mu }$$ (49)

$g$ – gravitational acceleration, $\frac{m}{s^2}$

${\rho }_d$ – density of droplets, $\frac{kg}{m^3}$

$\mu$ – viscosity of air, $\frac{g}{cm\bullet s}$

D_eq,i – mean droplet equilibrium diameter for n = 6 size bins (Table S6), $m$

$C_c-$ Cunningham Slip correction factor (−) and can be determined by the existing empirical expression [65]:

$$C_c=1+\frac{{\lambda }_g}{D_{eq}}\bullet \left(2.51+0.80\bullet e^{\frac{-0.55\bullet D_{eq}}{{\lambda }_g}}\right)$$ (50)

${\lambda }_g-$ mean free path $\left(\mu \mathrm{m}\right)$

3.2.4. Virus inactivation by ultraviolet germicidal irradiation (UVGI) ${\lambda }_{UVGI-R}$ of the recirculated air from the ventilation system or portable air cleaners

The virus-carrying aerosols can also be inactivated by ultraviolet germicidal irradiation (UVGI) zones in ducts or filters of the recirculation ducts and air cleaners that are placed in the space and can be calculated as:

$${{\lambda }_{UVGI-R}=\eta }_{UVGI}\bullet \left(Q_{rec}or{Q}_{PAC}\right)=1-e^{-k\bullet I_r\bullet {\tau }_r}$$ (51)

In both cases, the median virus inactivation efficiency ${\eta }_{UVGI}$ $[-]$ can be computed from expected flow rates according to the same principle [66]:

$${\eta }_{UVGI}=1-e^{-k\bullet I_r\bullet {\tau }_r}$$ (52)

$k$ – UVGI inactivation constant (obtained from experimental data) $\left[\frac{{cm}^2\bullet m}{W^{-1}\bullet s^{-1}}\right]$

$I_r$- inactivation rate constant $\left[\frac{\mu W}{{cm}^2}\right]$

$$I_r=\frac{P_r}{A_{r,50}\bullet L_r}$$ (53)

$P_r-$ the power of the UVGI device $\left[W\right]$

${\tau }_r-$ residence time of room air passing through UVGI $\left[s\right]$

$${\tau }_r=\frac{L_r}{v_r}$$ (54)

$L_r-$ length of the UVC device $\left[m\right]$

$v_r-$ velocity at the cross-section of the recirculation duct or the PAC fan

3.2.5. Inactivation – upper room UVGI removal factor ${\lambda }_{UVGI-UP}$

The second type of inactivation focused on in this model is upper room UVGI. A sufficient dosage of UV radiation will inactivate viruses (by photochemical disruption of viral RNA upon absorbing UV photons). Upper room applications of this technology make use of UV radiation generating lamp sources (low/medium pressure mercury vapor lamps or UV-C - LEDs), either wall mounted or suspended from the ceiling, to irradiate upper air zones of individual spaces while shielding the lower occupied zones from harmful UV radiation.

According to Harmon and Lau [22] the removal rate due to upper room UVGI is calculated as:

$${\lambda }_{UVGI-UP}=I_{r-UP}\bullet Z_{UP}$$ (55)

$Z_{UP}$- upper room susceptibility constant $\left[\frac{m^2}{J}\right]$ ($Z_{UP}\approx 0.377\frac{m^2}{J}$) [67]

$I_{r-UP}$ – upper room average irradiance $\left[\frac{\mu W}{{cm}^2}\right]$ ($I_{r-UP}\le 0.2\frac{\mu W}{{cm}^2}-$ supper permissible limit of irradiance at eye height [68])

3.2.6. The respiratory tract absorption rate, ${\lambda }_{resp}$

The respiratory tract absorption rate, ${\mathit{\lambda }}_{\mathit{r}\mathit{e}\mathit{s}\mathit{p}}$ is a function of droplet diameter and tidal volume size [69] and can be calculated according to the following equation:

$$\zeta =N\bullet \frac{k\bullet IR}{V}$$ (56)

IR is the inhalation rate of the exposed subject (which was assumed to be the inhalation rate for resting and standing averaged) at 0.52 $\frac{m^3}{h}$ , and $k$ (−) is a function of droplet diameter and tidal volume, the volume of air inhaled per breath [70]. We will use $k=0.54$ as in Ref. [69].

3.2.7. Portable air cleaners ${\lambda }_{PAC}$

Portable air cleaners (PAC) may be helpful for spaces with inadequate ventilation or when increased ventilation with outdoor air is not possible without compromising thermal comfort (temperature or humidity). PAC systems are mobile ventilation units that are commonly equipped with high-efficiency particulate air (HEPA) filters that capture at least 99.97% of particles of the maximum penetrating size (i.e., 0.3 μm in diameter). Under the assumption of fully mixing conditions, the removal rate of a HEPA-equipped PAC can be calculated as:

$${\lambda }_{PAC}=\frac{Q_{PAC}}{V}$$ (57)

$Q_{PAC}$ - clean air delivery rate (CADR) of a PAC unit $\left[\frac{m^3}{h}\right]$

$V$ - room volume $\left[m^3\right]$

3.2.8. Filtration of recirculated air ${\lambda }_{filt}$

For building HVAC systems the particle removal efficiency of filters is rated by the minimum efficiency reporting values (MERVs). MERVs rating standard specifies the filtration efficiency for three different ranges of particle sizes that follow a rating system with values ranging from 1 on the low end up to 16 (Table S10).

The removal rate of a recirculating air filter can be calculated as:

$${{\lambda }_{filt}=\eta }_{filt}\bullet Q_{rec}$$ (58)

To incorporate different removal efficiencies for different droplet size distributions, the quanta concentration equation (10) can be adjusted in the following manner:

$$n\left(t\right)={n_0\bullet e}^{-\left(\sum {\lambda }_{rest}+\sum _i^n{\eta }_{filt,i}\bullet Q_{rec}\right)}+\frac{S}{V\bullet \left(\sum {\lambda }_{rest}+\sum _i^n{\eta }_{filt,i}\bullet Q_{rec}\right)}\bullet \left(1-e^{-\left(\sum {\lambda }_{rest}+\sum _i^n{\eta }_{filt,i}\bullet Q_{rec}\right)\bullet t}\right)$$ (59)

Where $\sum {\lambda }_{rest}$ are the rest of the removal mechanisms except for filtration by recirculated air and

${\eta }_{filter,i}$ – filter efficiency for different size bins according to Table S10., $[\%]$

3.2.9. Filtration by face masks ${\eta }_{fm}$

Face masks provide air filtration of the virus-carrying aerosols and droplets in the surrounding air. The particle-size weighted removal efficiencies of different masks can be estimated based on the assumed infectious particle size distribution [25] (Table S11). The facemask removal efficiency is included in source rate $S$ in the following manner:

$$S=c_v\bullet c_i\bullet 3600\bullet {10}^6\bullet \sum _{i=1}^6{P}_{i,br,sp,si}\bullet V_i\left(D\right)\bullet \left({1-\eta }_{mask,i}\right)$$

${\eta }_{mask,i}$ – efficiency for different size bins according to Table S11., $[\%]$

4. Results and discussion

To assess the relative impact of different modes of sources and removal mechanisms on the airborne transmission risk, a simple case study was investigated with the same dimension characteristics and number of persons present for each case considered. The simple scenario consisted of a classroom with an area of 64 m² and 3 m height with one infected and twenty susceptible persons present. As only long-distance airborne transmission risk is considered all the persons were distanced 1.5 m, as shown in Fig. 3 . The time exposure considered was 60 min. The indoor temperature was in the range of 20–25 $°C$.

Fig. 3.

The layout of the classroom case scenario considered.

4.1. The impact of the source characteristics

The impact of four different source production characteristics was assessed for the case scenario conditions described. Only outdoor supplied mechanical ventilation was considered; i.e. no recirculation or use of PAC systems. Neither the infected nor the susceptible person wore a facemask.

Fig. 4 indicates the importance of considering the input characteristics of expiratory modes, type of SARS-CoV-2 variants, amount of viral load in the infected person, and the number of persons infected. For the particular classroom case scenario, the infection risk of long-distance airborne transmission after 180 min may be up to 40 times higher when the infected person is singing compared to breathing, and two times higher compared the case when the person is speaking (Fig. 4 a)). The calculated high infection risk for singing is supported by several previous singing-related COVID-19 outbreaks: the karaoke-related outbreaks in bars in Sapporo and Otaru (Japan) [71], the indoor choir rehearsals in Whir au Val (France) [72], Amsterdam (The Netherlands) [73] and Skagit County (USA) [74]. As the pandemic progressed, new and more infectious variants of SARS-CoV-2 emerged. Their impact on the infection risk was estimated as shown in Fig. 3 b). If again considering the exposure time after 180 min, the infection risk for the latest variant of Omicron is up to 8 times higher for identical indoor conditions compared to the original Wuhan strain that initiated the pandemic. The last two scenarios were considered for an infected person with a viral load of ${10}^8\frac{RNA}{mL}$, which is close to the median viral load reported in a recent study [75] in non-vaccinated (median ${10}^{8.1}\frac{RNA}{mL}$) and vaccinated people (median ${10}^{7.8}\frac{RNA}{mL}$). W while the infection risk for the Omicron variant at a viral load of ${10}^8\frac{RNA}{mL}$ is relatively high at $\sim$ 23% after 180 min, a tenfold increase in the viral load (${10}^8\frac{RNA}{mL})$ would result in an infection of most probably all of the 20 susceptible persons (P $\sim$ 96%) from long-airborne transmission by virus-laden aerosols $\le 5\mu m$ in size (Fig. 3 c)). Though a rarity, viral loads $>{10}^9\frac{RNA}{mL}$ have been reported [[76], [77], [78]], and considering our predicted infection simulations are probably the main drivers of super-spreading events in poorly ventilated conditions. The impact of more persons being infected than a single one is shown in Fig. 4 d).

Fig. 4.

The impact of quanta generation characteristics on the airborne infection risk: a) impact of expiratory modes (breathing, speaking, and singing) b) the impact of SARS-CoV-2 variants (speaking only) c) impact of viral load (speaking only) d) impact of the number of persons infected (speaking only).

Fig. 4. The impact of removal mechanisms on the airborne infection risk: a) ventilation rate b) filtration efficiency in case of recalculated air c) face mask d) upper room UVGI radiation.

4.2. The impact of removal mechanisms

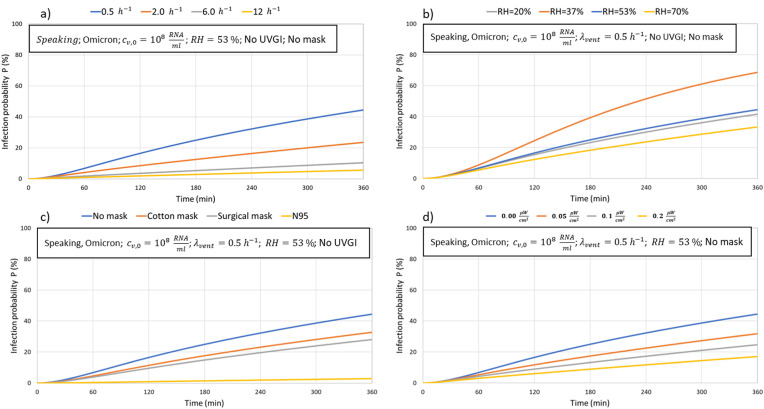
Fig. 5 compares four different removal mechanisms for the same setup conditions, amount of viral load in the infected person, expiratory mode (speaking), and virus variant (Omicron). The baseline scenario is shown in blue color in poorly ventilated conditions (0.5 ACH), RH = 53%, and no use of a face mask.

Fig. 5.

The impact of removal mechanisms on the airborne infection risk: a) ventilation rate b) filtration efficiency in case of recalculated air c) face mask d) upper room UVGI radiation.

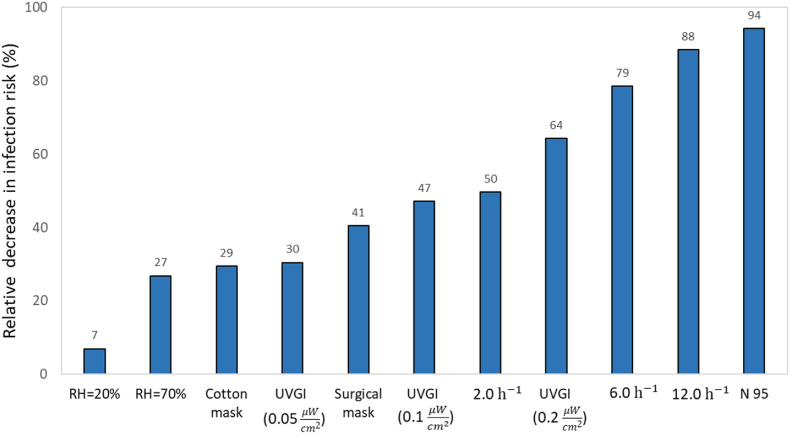
It is clear, that except for relative humidity, it is possible to reduce the infection risk below 10% with ventilation (6 and 12 ACH), face mask (N 95), or upper room UVGI (0.2 $\frac{\mu W}{{cm}^2}$) after 3 h of exposure compared to the baseline infection risk of 23%. High ventilation rates of 6 and 12 ACH and a highly efficient N 95 mask reduce the infection risk below 5% after 180 min. On the other hand, controlling relative humidity may decrease the infection risk slightly by reducing it to 20% or by increasing it to 70%. However, both of these RH values or on the end of the range allowed by leading standards for indoor air quality [79,80]. The next Fig. 6 shows the relative effect of applying the different removal mechanisms for the baseline scenarios for reducing the infection risk after 180 min.

Fig. 6.

The relative decrease in long distance-airborne infection risk after 180 min by applying different measures compared to the baseline scenario (no mask, no UVGI, ventilation rate = 0.5 h⁻¹, RH = 53%).

4.2.1. The impact of ventilation efficiency

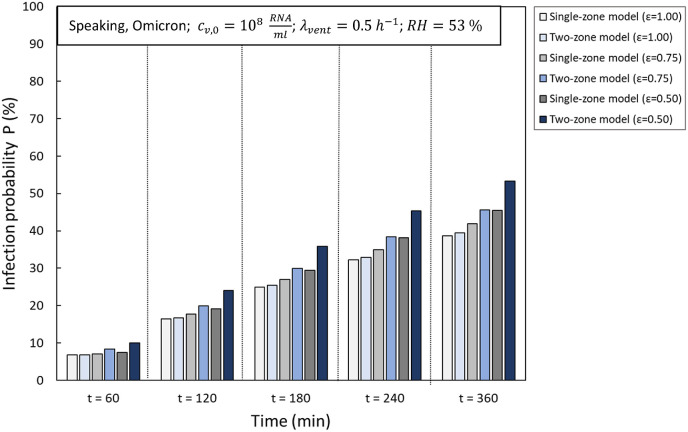
The single-zone (equation (38)) and two-zone model (equation (44) and (45)) were compared for three different $\epsilon$ (0.50, 0.75, and 1.00) values lower than 1, as the two-zone model for incomplete mixing ventilation is limited to $\epsilon <1\text{.}$ Fig. 7 . Shows that for a low ventilation rate (0.5 h⁻¹), the single-zone model underestimates the infection risk and this difference increases as the ventilation efficiency become lower. After 360 min, the maximum relative difference for the baseline scenario at 0.5 h⁻¹ is up to 15% at $\epsilon =$ 0.5 and up to 8% at $\epsilon =$ 0.75.

Fig. 7.

The impact of ventilation efficiency on the infection risk generated by a single-zone and two-zone model at a relatively low ventilation rate (0.5 h⁻¹).

While the relative difference between a lower ventilation rate and lower ventilation efficiency $\epsilon$ value is relatively high to be ignored (>5%), the maximum relative difference at higher ventilation rates (6.0 h⁻¹) is around 2% for $\epsilon =$ 0.75 and up to 5% for $\epsilon =$ 0.5 after 360 min of exposure (see Fig. 8 ).

Fig. 8.

The impact of ventilation efficiency on the infection risk generated by a single-zone and two-zone model at a relatively high ventilation rate (6 h⁻¹).

So low relative differences between the results obtained by the single- and two-zone models imply that the single-zone model may be used without losing significantly on accuracy and a relatively high ventilation rate (>6 h⁻¹). The impact of a variety of ventilation efficiency values to $0.5<\epsilon <1.5$ on the infection risk at 6 h⁻¹ are shown in Fig. 9 . This implies the importance of a possible misestimation of the infection risk for completely mixing conditions ($\epsilon =1$) at higher ventilation rates.

Fig. 9.

The impact of increased ventilation efficiency on the infection risk at a relatively high ventilation rate (6 h⁻¹) generated by the single-zone model.

5. Limitations

The model is still subject to several limitations. Unfortunately, the validation of the generated model against previous outbreaks is still not possible due to missing considerable input information from the observed events, and additional building system details such as the viral load of the infected person, expiratory modes (speaking or singing event), ventilation rates, space volume, and exposure time of infected persons but also additional building system details such as the amount of recirculated air, filter efficiency, etc. With insufficient input details, any validation process is futile. Future outbreak reports should include this information for validated retrospective infection risk assessments. Another major limitation is that model is only limited to long-airborne transmission risk assessment (>1.0-m social distance). Short-range airborne transmission may not be dealt with due to the main assumption that once released the droplets are instantaneously mixed evenly in every point of the room environment. This may be impossible to overcome by using the conventional dose-response approach based on quanta balances of open black boxes. Other limitations that may not be solved without using either expensive CFD simulations or on-site experimental measurements involve the inclusion of convective flows within the space, the impact of the activity and movement of occupants, and the change of pace and mode of expiration (breathing vs. talking). Hence future work should try to capture the physical processes as much as possible but also try to develop and run the dynamic models to arrive at realistic estimates.

6. Conclusions

This study reviewed the airborne infection models based on the Wells-Riley concept of quanta to provide the most suitable model for both retrospective and future long-distance airborne risk assessment. The model presented in this study presents an extended and improved Well-Riley model as a result of compiling and comparing all source and sink/removal terms reported during the COVID-19 pandemic. The used approaches for calculating the source and sink mechanisms published during the recent pandemic were reviewed and new data was utilized to characterize the viral load and removal mechanisms. Based on identifying unresolved issues for each sink and source term we improved the classical WR model by introducing the following novelties i) developing a new model to calculate the total volume of respiratory fluid exhaled per unit time ii) developing a novel viral dose-based generation rate model for dehydrated droplets after expiration iii) deriving a novel quanta-RNA relationship for various strains of SARS-CoV-2 iv) proposing a method to account for the incomplete mixing conditions. We show that the quanta emission rate reported in previous studies were overestimated even by factor 10 because of using data and assumptions being based on SARS-CoV-1. Recent studies have confirmed medium viral load for both vaccinated and unvaccinated persons about 10⁸ RNA copies in mL for the alpha and delta strains allowing to determine new average quanta emission rates including omicron variant. These quanta values for original strain of 0.13 and 3.8 quanta/h for breathing and speaking and the virus variant multipliers determined in this study may be used for simple hand calculations of probability of infection or to be used with developed model operating with six size ranges of aerosol droplets to calculate the effect of ventilation and other removal mechanisms. Overall, our new model allows for changing more than four source input parameters (expiratory mode, virus variant, viral load, and several infected persons) as well as six potential removal mechanisms by ventilation, viral inactivation by relative humidity, ventilation by using a portable air cleaner, inactivation by UVGI of the recirculated air from the ventilation system or portable air cleaners, upper room UVGI filtration of portable air cleaner or recirculated air and the filtration by use of a face mask. In addition, the model introduces the concept of ventilation efficiency for evaluating incomplete mixing conditions. By resolving these specific issues, an advanced and integrated Wells-Riley model was developed, tested, and recommended for future and retrospective indoor infection risk assessments. The model developed is made available as an open-source interactive computational tool.

CRediT authorship contribution statement

Amar Aganovic: Writing – original draft, Methodology, Formal analysis, Conceptualization. Guangyu Cao: Writing – review & editing, Conceptualization. Jarek Kurnitski: Writing – review & editing, Conceptualization. Pawel Wargocki: Writing – review & editing, Conceptualization.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the Supplementary data to this article:

Data availability

Data will be made available on request.