Particle-based model of mechanosensory contractility kit assembly

Abstract

Cell shape change processes, such as proliferation, polarization, migration, and cancer metastasis, rely on a dynamic network of macromolecules. The proper function of this network enables mechanosensation, the ability of cells to sense and respond to mechanical cues. Myosin II and cortexillin I, critical elements of the cellular mechanosensory machinery, preassemble in the cytoplasm of Dictyostelium cells into complexes that we have termed contractility kits (CKs). Two IQGAP proteins then differentially regulate the mechanoresponsiveness of the cortexillin I-myosin II elements within CKs. To investigate the mechanism of CK self-assembly and gain insight into possible molecular means for IQGAP regulation, we developed a coarse-grained excluded volume molecular model in which all protein polymers are represented by nm-sized spheres connected by spring-like links. The model is parameterized using experimentally measured parameters acquired through fluorescence cross-correlation spectroscopy and fluorescence correlation spectroscopy, which describe the interaction affinities and diffusion coefficients for individual molecular components, and which have also been validated via several orthogonal methods. Simulations of wild-type and null-mutant conditions implied that the temporal order of assembly of these kits is dominated by myosin II dimer formation and that IQGAP proteins mediate cluster growth. In addition, our simulations predicted the existence of “ambiguous” CKs that incorporate both classes of IQGAPs, and we confirmed this experimentally using fluorescence cross-correlation spectroscopy. The model serves to describe the formation of the CKs and how their assembly enables and regulates mechanosensation at the molecular level.

Significance

To survive, cells must sense and respond to mechanical stimuli. Experiments have demonstrated that macromolecular assemblies, termed contractility kits, are preassembled, and used by cells to respond to these mechanical signals. The precise mechanism of assembly, however, is unknown. In this work we use stochastic, spatial simulations to determine the means of assembly of these kits. The simulations show that the temporal order of assembly of these kits is dominated by myosin II dimer formation. Moreover, simulations predict the existence of a previously unknown type of kit. In vivo experiments were then performed and confirmed this prediction. This work elucidates the mechanism by which an important component of the cell’s mechanosensory machinery is formed.

Introduction

To survive in dynamic environments, cells must sense internal and external cues and respond to those changes. They achieve this through a meshwork of macromolecules that act as sensors and actuators, allowing cells to detect and react to biochemical and mechanical stimuli, apply forces, and undergo shape changes. This meshwork of macromolecules, which we refer to as the mechanobiome, allows cells to carry out mechanosensation, affecting cell characteristics such as elasticity and viscoelasticity, and enabling the execution of basic cellular processes. Investigating cellular mechanosensitivity and the mechanobiome at the molecular scale allows us to gain further insight into the molecular details enabling basic processes, such as proliferation, polarization, and cancer cell migration and metastasis.

In Dictyostelium cells, myosin II and cortexillin I are critical elements of the mechanobiome, with myosin II acting to stiffen the cell cortex and generate a contractile response to mechanical stress, while the actin cross-linker cortexillin I cross-links actin filaments and anchors them to the plasma membrane (1,2,3). Myosin II and cortexillin I have been discovered to be codependent in their ability to generate a mechanical response (4,5) and preassemble into complexes, which we refer to as contractility kits (CKs), in the cytoplasm before the reception of a mechanical stimulus. These kits are hypothesized to be the means by which mechanosensitive contractile proteins arrive at the cortex through diffusion. Then, if their arrival at the cortex is associated with additional inputs, such as a mechanical stress, the kits may be unpackaged so that the proteins may be incorporated into larger-scale cytoskeletal structures, building additional cortical cytoskeleton.

Other critical subunits in the CKs are the IQGAP proteins, particularly IQGAP1 and IQGAP2 (6). IQGAP1 serves as a negative regulator of the CKs, inhibiting the ability of myosin II and cortexillin I to accumulate in the cell cortex in response to applied mechanical stresses. IQGAP2, on the other hand, alleviates IQGAP1’s inhibition. When both IQGAPs are removed via genetic deletion, myosin II and cortexillin I can again accumulate in response to mechanical stress (6). Overall, the IQGAPs help provide a set point for mechanical stress sensing and responsiveness.

By being preassembled, the CKs poise the cell for a quick response to any encountered signal (2). Despite the extent of previous studies on cellular mechanosensing (7), much remains unknown about how the individual elements of the cortical network interact and regulate each other to mediate mechanosensation at the molecular scale, particularly regarding the CKs. The overarching goal of this research is to decipher the mechanisms of cytoskeletal systems that enable mechanosensation and shape change processes, particularly how mechanoresponsive myosin II-cortexillin I units enable mechanosensation in the context of CKs through the development of predictive computational models. To this end, we have constructed a coarse-grained excluded volume molecular model to investigate the self-assembly process of these kits in the absence of mechanical stress and gain further insight into how these kits may enable and regulate mechanosensation at a cellular scale.

Methods

Coarse-grained molecular modeling

To create a coarse-grained excluded volume molecular model of CK self-assembly, we used the software SpringSaLaD (8). In SpringSaLaD, molecules are represented as nm-sized domains connected by spring-like links, we thus refer to this model as a coarse-grained molecular model (as opposed to an atomistic model). Each domain is given a radius and diffusion coefficient in μm² s⁻¹ and can be specified to undergo transition, allosteric, and bimolecular reactions. Simulations in SpringSaLaD are based upon implementation of the Erban-Chapman algorithm (9). Alternative particle-based reaction-diffusion simulation techniques are based upon Green’s functions methods (10). For the readers interested in further details of the particle-based reaction-diffusion simulation methods, we refer them to (9,10,11,12,13).

Below we describe the various components included in the model, their coarse grain description, and the various binding and allosteric reactions involved. A schematic of the various molecules is provided in Fig. 1 A; details of the various domains are given in Table 1, and Table 2 lists the relevant reactions.

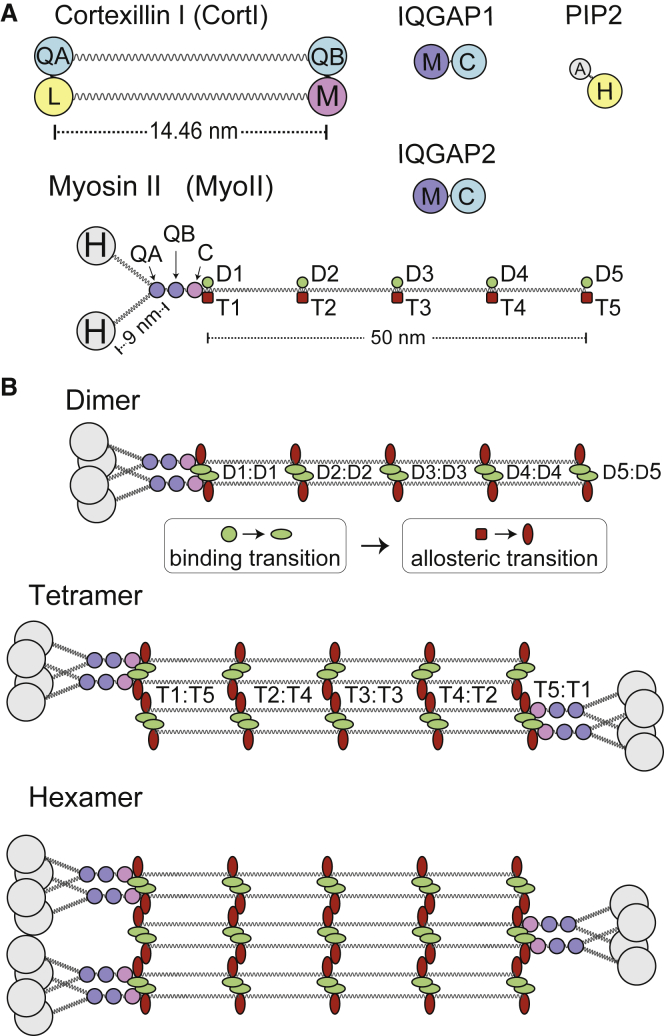
Figure 1.

Coarse-grained description of the molecular components in the model. (A) In SpringSaLaD, each molecule is described by constituent domains. The size and diffusion coefficient of each domain is found in Table 1, which also lists the binding partners of the various domains. (B) This shows how small-scale myosin II bipolar thick filament assembly proceeds. Parallel binding of two functional monomers through the dimerization domains (MyoII_D1-MyoII_D5) induces a change in the state of these domains and a corresponding allosteric transformation in the tetramerization domains (MyoII_T1-MyoII_T5). In this new state, dimers come together by antiparallel binding (MyoII_T1 in one dimer to MyoII_T5 in the other, etc.) to form a tetramer. The addition of further dimers can occur and lead to hexamers or higher-order assemblies. To see this figure in color, go online.

Table 1.

Molecule coarse graining

Molecule	Components	No.	Label	Binding partner(s)	Radius (nm)	D (μm2/s)	PDB
Cortexillin I	IQGAP binding	1	CortIQA	IQGAP1C, IQGAP2C	1.0	23.2	1D7M
	IQGAP binding	1	CortIQB	IQGAP1C	1.0	23.2
	lipid binding	1	CortIL	PIP2H	1.0	23.2
	myosin binding	1	CortIM	MyoIIC	1.0	23.2
	coiled-coil length				14.46
Myosin II	head	2	MyoIIH	none	2.5	14.55	3BZ7
	IQGAP binding	1	MyoIIQA	IQGAP1M, IQGAP2M	1.0	14.55
	IQGAP binding	1	MyoIIQB	IQGAP1M	1.0	14.55
	cortexillin binding	1	MyoIIC	CortIM	1.0	14.55
	tail dimerization	5	MyoIID1-D5	MyoIID1-D5	0.7	14.55
	tail tetramerization	5	MyoIIT1-T5	MyoIIT5-T1	0.7	14.55
IQGAP1	myosin binding	1	IQGAP1M	MyoIIQA, MyoIIQB	1.225	9.6
	cortexillin binding	1	IQGAP1C	CortIQA, CortIQB	1.225	9.6
IQGAP2	myosin binding	1	IQGAP2M	MyoIIQA	1.225	9.6	5CJP
	cortexillin binding	1	IQGAP2C	CortIQA	1.225	9.6	5CJP
PIP2	anchor	1	PIP2A	membrane	0.3	1.0
	headgroup	1	PIP2H	CortIL	0.5	1.0

Biochemical species are described through individual components that are joined by spring-like links. The table specifies the size and number of the various constitutive components. The labels serve to indicate their position in Fig. 1A as well as in the various reactions of Table 2. Also indicated are the domains and their potential binding partners. Diffusion coefficients for given domains were computed using the Rouse diffusion relationship as in Fig. 2B. Wherever available, the PDB codes represent structures of protein domains, for which the radius of gyration or length was measured as a form of estimating the radius or length assigned to the corresponding coarse-grained protein domain.

Table 2.

Reactions implemented in the coarse-grained model of CK assembly

			Reaction pair
Binding reactions
CortIQA + IQGAP1C	⇌	IQGAP1:CortI
CortIQA + IQGAP2C	⇌	IQGAP2:CortI	A1f, A1r
CortIQB + IQGAP1C	⇌	CortI:IQGAP1
CortIL+ PIP2H	⇌	CortI:PIP2
CortIM + MyoIIC	⇌	CortI:MyoII
MyoIIQA + IQGAP1M	⇌	IQGAP1:MyoII
MyoIIQA + IQGAP2M	⇌	IQGAP2:MyoII	B1f, B1r
MyoIIQB + IQGAP1M	⇌	IQGAP1:MyoII
MyoIIDk + MyoIIDk, $\mathit{k}=1,\dots ,5$	⇌	(MyoIIdimer)Dk	C1f, C1r
(MyoIIdimer)Tk + (MyoIIdimer)Tm, $\mathit{k}+\mathit{m}=6$	⇌	(MyoIItetramer)Tk,m
(MyoIItetramer)Tk + (MyoIIdimer)Tm, $\mathit{k}+\mathit{m}=6$	⇌	(MyoIIhexamer)Tk,m

Transition reactions
A1f:	→ IQGAP2:CortI	(CortIQA)-state0 → (CortIQA)-allosteric_reg	A2f
B1f:	→ IQGAP2:MyoII	(MyoIIQA)-state0 → (MyoIIQA)-allosteric_reg	B2f
C1f:	→ (MyoIIdimer)Dk	((MyoIIdimer)Dk)-state0 → ((MyoIIdimer)Dk)-tetra	C2f
A1r:	← IQGAP2:CortI	(CortIQA)-allosteric_reg → (CortIQA)-state0	A2r
B1r:	← IQGAP2:MyoII	(MyoIIQA)-allosteric_reg → (MyoIIQA)-state0	B2r
C1r:	← (MyoIIdimer)Dk	((MyoIIdimer)Dk)-tetra → ((MyoIIdimer)Dk)-state0	C2r
Allosteric reactions
A2f:	(CortIQA)-allosteric_reg	(CortIQB)-state0 → (CortIQB)-allosteric_reg
B2f:	(MyoIIQA)-allosteric_reg	(MyoIIQB)-state0 → (MyoIIQB)-allosteric_reg
C2f:	((MyoIIdimer)Dk)-tetra	((MyoIIdimer)Tk)-state0 → ((MyoIIdimer)Tk)-tetra
A2r:	(CortIQA)-state0	(CortIQB)-allosteric_reg → (CortIQB)-state0
B2r:	(MyoIIQA)-state0	(MyoIIQB)-allosteric_reg → (MyoIIQB)-state0
C2r:	((MyoIIdimer)Dk)-state0	((MyoIIdimer)Tk)-tetra → ((MyoIIdimer)Tk)-state0

Bimolecular binding reactions occur between specified pairs of domains (Table 1 and Fig. 1A). Myosin II dimerization occurs between five pairs of domains along the myosin II tail, while tetramerization occurs between five pairs of tetramerization domains also along the tail, given that the molecule has already formed a parallel dimer (Fig. 1B). The table lists only the bimolecular entities formed, but higher-order ensembles are formed when further domains bind. Transition reactions specify a binding-dependent change in the state of a particular domain. Allosteric reactions specify a change in the state of a particular domain, given that there has been a change in the state of the indicated allosteric site. The reaction pair column indicates the dependency of transition and allosteric reactions on given binding reactions. For example, binding of CortI_QA with IQGAP2_C leads to the transition reaction, A1f, which then leads to an allosteric transition, A2f, in the CortI_QB domain. The reverse unbinding reactions similarly cause a sequential change in states; e.g., A1r triggers A2r, which then leads to an allosteric reaction. Dependencies for transition and allosteric reactions are also listed on the left-hand side of the described reactions.

Cortexillin I

Cortexillin I is composed of two globular N-terminal calponin homology (CH) domains, followed by 18 continuous heptad repeats that dimerize to form a parallel two-stranded coiled coil, and two globular C-terminal actin/PIP2 binding domains (14). The functional unit of cortexillin is thus an obligate coiled-coil dimer. Within our model, we consider this coiled-coil dimer to be a single cortexillin I molecule (functional monomer) (Fig. 1 A; Table 1). Our coarse-grained cortexillin I monomer thus contains a total of four globular domains, each with a diameter of 2 nm, corresponding to the CH domains and C-terminal actin-binding domains, connected by two parallel springs 14.46 nm long representing the coiled-coil rod domain of cortexillin I (3,14). The size of cortexillin I globular domains was estimated by subtracting the length of the coiled coil (PDB: 1D7M) from the length of the total protein (3,14). In our model, binding of proteins to cortexillin occurs at these four globular domains. IQGAP binding occurs at sites CortI_QA and CortI_QB, located at opposite sides of the molecule (Fig. 1 A). Cortexillin I-lipid binding takes place between cortexillin’s lipid binding domain (CortI_L) and the lipid head domain (PIP2_H, described below). Cortexillin I-myosin II binding occurs at the cortexillin I myosin-binding domain (CortI_M). To restrict IQGAP binding to cortexillin I, such that the observed stoichiometric ratios are maintained, IQGAPs have been modeled to have a relationship of allosteric competitive inhibition. In SpringSaLaD, allosteric changes are specified via binding-dependent transition reactions that are coupled to subsequent allosteric reactions (Table 2) (8). In this model, we assume that cortexillin I has two IQGAP-binding sites and that the primary binding site (CortI_QA) is available to both IQGAPs, while the second (CortI_QB) is only available to IQGAP1. Thus, both IQGAPs compete for the cortexillin I primary binding site. The binding of IQGAP2 to CortI_QA causes a binding-dependent transition reaction that changes the state of this domain from state0 (basal) to the allosteric_reg state. If CortI_QA is in the allosteric_reg state, then the secondary site undergoes an allosteric state change (modeled through an allosteric reaction) from state0 to the allosteric_reg state, which inhibits binding of an IQGAP1 molecule to CortI_QB, thus maintaining IQGAP stoichiometry.

IQGAPs

IQGAPs are scaffolding proteins, known to regulate cytoskeletal dynamics and shape changes. In mammals, IQGAP proteins contain a total of five domains: a calponin-homology domain, an IQ domain, a WW domain, a GAP-related domain (GRD) domain, and a RasGAP-related C-terminus (RGCT) domain (15). However, the Dictyostelium versions only contain the GRD and RGCT domains (15,16,17). We have assumed that IQGAP1 is analogous in size to IQGAP2 and have used an available structure of human IQGAP2 (PDB: 5CJP) to measure the radius of gyration of the molecule, which we have used as a reference for the total molecular radius given during our model’s IQGAP coarse graining. In this model, we represent IQGAPs as globular proteins composed of two spherical domains each: one myosin II-binding domain (IQGAP1_M and IQGAP2_M, respectively) and one cortexillin I-binding domain (IQGAP1_C and IQGAP2_C, respectively) each with a radius of 1.225 nm, leading to a total protein lateral diameter of ∼5 nm (Fig. 1 A).

Myosin II

In the present model, we consider a myosin molecule to be a hexameric myosin II monomer (functional monomer). Each nonmuscle myosin II hexameric monomer is composed of two myosin II heavy chains, two essential light chains (ELCs), and two regulatory light chains (RLCs) (18). Each myosin heavy chain is composed of an N-terminal head domain, a neck region that binds one ELC and one RLC, followed by a long alpha helix that forms the coiled-coil rod domain of the tail (19). We thus modeled our coarse-grained myosin II molecule to have two head domains (MyoII_H), each with a radius of 2.5 nm (Table 1; PDB: 3BZ7), and a tail region composed of dimerization (MyoII_D1-MyoII_D5) and tetramerization domains (MyoII_T1-MyoII_T5) (Fig. 1 A). The number of domains for the myosin tail was selected based upon reference (20), where five patches of highly clustered positive and negative charge regions were hypothesized to mediate the contacts that allow for dimerization and tetramerization, leading to BTF formation. These dimerization and tetramerization domains were assumed to have an approximate radius of 0.7 nm (Table 1). Although the actual myosin II coiled coil is 190 nm long, we used a shortened version that is 50 nm long to make the coarse-grained simulation of this self-assembly system feasible, thus making the total end-to-end length ∼60 nm (Fig. 1 A).

IQGAP-myosin II binding happens at the myosin IQGAP-binding domains: MyoII_QA (primary) and MyoII_QB (secondary). As there are currently no data on IQGAP-myosin stoichiometry, we assumed a 2:1 IQGAP1:myosin II stoichiometry and a 1:1 IQGAP2:myosin stoichiometry, analogous to cortexillin I. Also, similarly to cortexillin I, we have implemented a relationship of allosteric competitive inhibition between the IQGAPs, once again enforced through the implementation of coupled transition and allosteric reactions in the same manner as described for cortexillin I above. Myosin II-cortexillin I binding occurs at the myosin MyoII_C domain (Fig. 1 A).

Myosin functional monomers can form parallel dimers via binding of equally numbered dimerization domains (i.e., MyoII_D1 of one monomer binds to MyoII_D1 of the other, etc.; see Fig. 1 B). Myosin tetramerization domains can only undergo the tetramerization reaction creating the initial bipolar filament when the molecules have formed parallel dimers. We incorporated this tetramerization within our SpringSaLaD model via a binding-dependent transition reaction. The binding of dimerization domains causes a change from the basal state0 to the tetramerization_state (Table 2). This state change in the dimerization domains induces an allosteric state change (specified through an allosteric reaction) in the corresponding tetramerization domains (i.e., MyoII_D1 induces a change in MyoII_T1) from state0 to tetramerization_state. When in this latter state, two dimers are able to tetramerize via antiparallel binding of the tetramerization domains in a subsequent binding reaction (i.e., MyoII_T1 of one monomer to MyoII_T5 of the other, etc.) (Table 2). k_off rate constants for dimerization and tetramerization reactions were obtained as explained in supporting derivation 1.

PIP2

Lipid bilayers are typically ∼3–4 nm thick, thus a monolayer can range from 1.5 to 2 nm in thickness (21). In the model, we included membrane-bound lipid molecules that can diffuse two-dimensionally along a plane. These PIP2 lipids are represented as membrane-bound molecules with an anchor (PIP2_A) and head (PIP2_H) domain. Cortexillin I binding occurs at the PIP2_H domain. We have attributed the PIP2 lipid heads in our model a radius of 0.5 nm such that they are visible within simulation movies (Video S1). The anchor domain has a radius of 0.3 nm. This leads to a total monolayer thickness of 1.6 nm. Lipid binding is only allowed on the monolayer side facing the inner portion of the simulation box, where other proteins can diffuse in three dimensions.

Video S1. Representative simulation movie of CK assembly

Cortexillin I molecules are shown in cyan, while IQGAP1 and IQGAP2 molecules are shown in yellow and purple, respectively. Myosin II hexameric monomers are shown as having magenta head domains, with pink and green tail regions. Frame rate utilized was three frames per second (dt_image = 10.6 s). Simulations were run in a (200 nm)³ box at the concentrations detailed in Table 3.

SpringSaLaD requires that rate constants be input into the simulation software for all bimolecular binding, transition, and allosteric reactions (8). In the case of bimolecular binding reactions, $k_{\text{on}}$ and $k_{\text{off}}$ rate constants are parameters that must be input into the simulation software and give rise to an effective interaction affinity ($K_D=k_{\text{off}}/k_{\text{on}}$). Experiments performed by Kothari et al. (1) provided effective interaction affinities for all bimolecular protein-protein interactions considered in this model. However, the specific rate constants for these protein-protein binding reactions have not been measured experimentally. We assumed a forward bimolecular reaction rate ($k_{\text{on}}$) of 2 μM⁻¹s ⁻¹ (22) and solved for the reverse rate constants ($k_{\text{off}}$) corresponding to each binding reaction using $k_{\text{off}}=K_D\times k_{\text{on}}$ (Table S1). A sensitivity analysis was carried out to determine how $k_{\text{on}}$ affected assembly dynamics and confirmed that the steady-state (arrived at t = 1.5 s) fraction bound for each protein pair was not affected (Figs. S1 and S2; Table S2).

IQGAP1 binds cortexillin I with a 2:1 stoichiometric ratio, while IQGAP2 binds cortexillin I with a 1:1 stoichiometric ratio (1). To restrict IQGAP binding to cortexillin I, such that the observed stoichiometric ratios are maintained, IQGAPs have been modeled to have a relationship of allosteric competitive inhibition as described in the cortexillin I and myosin II sections above. In this model, we assume that cortexillin I has two IQGAP-binding sites and that the primary binding site is available to both IQGAPs, while the second is only available to IQGAP1. Thus, both IQGAPs compete for the cortexillin I primary binding site (“competitive inhibition”). The allostery lies in the fact that, if IQGAP2 binds to the primary binding site, then IQGAP1 cannot bind to the secondary binding site. A sensitivity analysis was also conducted, observing the effect of this assumed stoichiometry on CK IQGAP1:IQGAP2 ratio (Fig. S1).

All transition and allosteric reactions in the model were assumed to have reaction rates of 1000 s⁻¹ ($k_{\text{on}}=k_{\text{off}}=1000{\text{ s}}^{-1}$), resulting in a fast occurrence in comparison with the rates of the specified binding reactions. Molecule concentrations in model simulations were chosen to approximate the biological concentrations measured by Kothari et al. (1) (Table 3). The cortexillin I-PIP2 binding reaction was assumed to have a $K_D$ of 1μM ($k_{\text{on}}$ = 1828 μM⁻¹ s⁻¹, $k_{\text{off}}$ = 1828 s⁻¹) since the affinity of the interaction has not been measured experimentally.

Table 3.

Molecular concentrations implemented in coarse-grained simulations of CK assembly

Molecule	Concentration (μM)
Cortexillin I	3.53
IQGAP1	3.74
IQGAP2	5.19
PIP2	33.1
Myosin II	3.74

Protein concentrations are based upon FCS measurements (1). Molecular concentrations were maintained constant in all simulations of CK self-assembly.

Model assumptions and limitations

Our motivation is to use a computational model to gain insight into the mechanism by which CKs assemble. While there is considerable experimental information available regarding some of the interactions, several assumptions need to be made. As explained above, the relationship between IQGAPs is hypothesized to be one of allosteric competitive inhibition and is modeled as such.

In these simulations, the binding location for IQGAP-myosin II interactions is modeled to occur between the tail and head domains, although structures of these bound complexes have not been discerned. For IQGAP-cortexillin interactions, we assumed binding to occur at the CH domains of cortexillin I (structures of these bound complexes have also not been discerned). An inherent limitation of this modeling approach is that protein molecules are depicted at the level of nm-sized spheres representing protein domains, joined by spring-like links, therefore the level of structural detail is limited and residue-level contacts are not included, but rather binding interactions are represented at the level of domain contacts between proteins.

We also assumed that the IQGAP1:myosin II binding stoichiometry is 2:1, but the stoichiometry of this interaction has not been experimentally measured. We have therefore assumed that the stoichiometry of IQGAP1:myosin II is analogous to that of IQGAP1:cortexillin I. We conducted an analysis of CK cluster IQGAP ratios where binding of IQGAP1 to the secondary site in myosin II has been disabled (thus making the IQGAP1:myosin II stoichiometry in the model 1:1). The analysis revealed some minor differences in the IQGAP1:IQGAP2 ratios of the clusters (Fig. S1). When comparing the original model (exhibiting 2:1 IQGAP1:myosin II binding stoichiometry) to the 1:1 IQGAP1:myosin II stoichiometry model, the 2:1 IQGAP1:IQGAP2 ratio in ambiguous CKs decreased from 59 to 36%, while the 1:1 IQGAP1:IQGAP2 ratio increased from 7 to 36%. We note that these percentages are calculated relative to the total number of ambiguous clusters. These results show a slight shift in the relative distributions of IQGAPs within the clusters stemming from the change in stoichiometry between IQGAP1:myosin II; however, no significant change in the number of clusters or average cluster size was observed. Sensitivity analysis was also conducted on the $k_{\text{on}}$ rates (Figs. S2 and S3; Table S2).

Mean-squared displacement diffusion coefficient analysis

To validate molecular diffusion coefficients implemented in SpringSaLaD, polymers of various lengths, ranging from one monomeric unit (monomer) up to 20-mer, were constructed. Each monomeric unit consisted of a 2.8 nm radius sphere and a diffusion coefficient of 25 μm² s⁻¹. Simulations were run at a volume fraction (the fraction of total volume occupied by all molecules) less than or equal to $\phi =\left(V_{\text{mol}}N\right)/V_{\text{box}}={10}^{-5}$ , where $V_{\text{mol}}$ represents the excluded volume occupied by the molecule(s) represented in the simulation and $V_{\text{box}}$ represents the total volume of the simulation box, thus allowing us to consider this a system of noninteracting particles. The squared deviation was calculated for each individual molecule in the simulation using the initial center of mass as reference via: $d^2={\left(x_0-x_i\right)}^2+{\left(y_0-y_i\right)}^2+{\left(z_0-z_i\right)}^2$, where ($x_0,y_0,z_0)$ is the center of mass for the molecule at $t=0$ and ($x_i,y_i,z_i)$ is the center of mass at time $t=i$. To obtain the diffusion coefficients, we first calculated the mean-squared displacement (MSD) of the center of mass for each individual molecule along a single trajectory. We then averaged the squared displacements over all the trajectories of this molecule type to obtain the MSD ($r^2$) as a function of time and then carried out a nonlinear least-squares fit to Einstein’s formula for three-dimensional (3D) diffusion, $⟨r^2⟩=6Dt$. This MSD analysis procedure was also used to corroborate that the CK component proteins modeled in SpringSaLaD were complying with experimentally measured diffusion coefficients (Table S3).

Fractional saturation analysis

To validate intermolecular interaction affinities implemented in SpringSaLaD, two simple monomeric molecules (A and B) were considered, each with a radius of 2.8 nm and a diffusion coefficient of 25 μm² s⁻¹. The molecules undergo a simple bimolecular binding reaction $A+B\leftrightharpoons C$ with forward and reverse rate constants $k_{\text{on}}=2$ μM⁻¹ s⁻¹ and $k_{\text{off}}=1$ s⁻¹, respectively, resulting in a $K_D=0.5$ μM. A fractional saturation curve was then constructed using this model by running ten replicate simulations at various B ligand concentrations (0.2–25 μM) while keeping the A concentration constant (3.5 μM; equal to 17 molecules within the simulation volume). Simulations were run in a cube of 200 nm on each side for 250 ms of simulation time with a time step of 10 ns ($dt$ = 10⁻⁸ s) and data acquisition time step of 0.1 ms ($d{t}_{\text{data}}$ = 10⁻⁴ s). For each simulation, the total fraction of A bound by B was calculated and used to compute the average total fraction of A bound at each B concentration, along with the standard deviation. The total fraction of A bound was obtained using the Site Property Counter provided by SpringSaLaD, which indicates the number of bound A molecules, and dividing by the total number of A molecules added into the simulation. The average fractional saturation data was then fit to a model for a bimolecular binding reaction with 1:1 stoichiometry given by:

$$\begin{array}{l}\theta =\frac{A_{tot}+B_{tot}+K_D-\sqrt{{\left(A_{tot}+B_{tot}+K_D\right)}^2-4A_{tot}{B}_{tot}}}{2A_{tot}}\hfill \end{array}$$ (1)

using nonlinear least-squares fit. This fractional saturation procedure was also implemented to ensure that CK component proteins modeled in SpringSaLaD were complying with experimentally measured effective interaction affinities (Table S4).

Computational fluorescence correlation and fluorescence cross correlation analysis

To recreate fluorescence correlation (FCS) computationally, an effective volume of (100 nm)³ at the center of the simulation box (centered around zero) was selected and center-of-mass calculations were carried out for all molecules at each time point in the simulation. This allowed us to track the concentration fluctuations for the various molecule types as they diffused in and out of the effective volume. We computed the corresponding proportional fluorescence fluctuations using $\delta F\left(t\right)=\int \eta W\left(r\right)\delta \left(C\left(r,t\right)\right)dV$, where $W\left(r\right)$ describes the spatial distribution of the emitted light, which we assumed to be a 3D Gaussian illumination fluorescence profile, $\eta$ is the photon count rate, and $dV$ indicates integration over the effective volume. A photon count rate $\eta$ of 125 MHz was used, in accordance with experiments (1). The function $\delta \left(C\left(r,t\right)\right)=⟨C⟩-C(r,t)$ describes the concentration fluctuations from the temporal average. Using the fluorescence fluctuation data for each molecule type, we computed the normalized autocorrelation of the emulated fluorescence signal as $G\left(t\right)=\frac{⟨\delta F\left(t\right)\delta F\left(t+\tau \right)⟩}{{⟨F\left(t\right)⟩}^2}$. We then fit the computationally emulated fluorescence autocorrelation data to the integrated form of the autocorrelation function for single-species 3D diffusion $\left(t\right)=\frac{1}{N}{\left(1+\frac{1}{{\tau }_D}\right)}^{-1}{\left(1+\frac{1}{{\omega }^2{\tau }_D}\right)}^{-1/2}$ , where $N$ represents the concentration of molecules, $\omega$ is the structural parameter (ratio of axial and lateral beam widths), and ${\tau }_D$ is the diffusion time (23). A structural parameter of $\omega =1$ was used for all computations (24). Fitting the fluorescence autocorrelation data to the integrated autocorrelation function for single-species 3D diffusion allowed us to extract the diffusion time for that particular molecule (or for diffusing CKs), from which we then calculated the diffusion coefficient for such a molecule using the relationship ${\tau }_D=\frac{z_0^2}{6D}$ , where $z_0$ represents the axial beam width parameter, set at 100 nm in all simulations.

Using this same fluorescence emulation procedure, we also computed the cross correlation between the fluorescence signals describing two distinct molecules to recreate fluorescence cross correlation spectroscopy (FCCS) computationally and gain information about effective interaction affinities between two pairs of molecules within clusters. In this case, we computed the normalized cross correlation of the emulated fluorescence signals as $G_x\left(t\right)=\frac{\delta F_1\left(t\right)\delta F_2\left(t+\tau \right)}{F{\left(t\right)}_1{F}_2\left(t\right)}$, where $\delta F_1$ and $\delta F_2$ represent the fluorescence fluctuations of the first and second molecules, respectively. We then computed an effective interaction affinity through the relationship:

$$\begin{array}{l}{K}_D=\frac{G_x}{N_{A}V{G}_a{G}_b}\left(\frac{G_a}{G_x}-1\right)\left(\frac{G_b}{G_x}-1\right)\hfill \end{array}$$ (2)

where $G_x$ represents the zero lag-time value for the cross correlation of the two fluorescence signals, $G_a$ represents the zero lag-time value for the autocorrelation of the first fluorescence signal molecule, $G_b$ is the zero lag-time value of the autocorrelation for the second molecule’s fluorescence signal, $N_A$ is Avogadro’s number, and V = (100 nm)³ is the effective volume (1).

CK identification and classification algorithm

We developed an algorithm to quantify the clusters that can be identified as CKs to characterize their composition and track their localization (cytoplasmic versus membrane bound). Here, to be considered a CK, a cluster must contain at least one myosin II, one cortexillin I, and one IQGAP molecule (1). Once identified, CKs were then classified into nonmechanoresponsive (containing IQGAP1 only), mechanoresponsive (containing IQGAP2 only), or ambiguous (containing both IQGAPs). In the case of classifying clusters observed in an iqgap1/2 null scenario, clusters were considered CKs if they had at least one myosin II and one cortexillin I molecule. Averages were obtained from various independent replicates. The total size of CKs at each time point was determined by the number of components as identified by the SpringSaLaD Cluster Tracker tool. CKs that contained at least one PIP2 molecule were considered membrane bound, as this lipid is restricted to the membrane; otherwise, they were considered cytoplasmic. CKs were identified out of a total number of clusters in the simulation using the Cluster Tracker tool provided by SpringSaLaD, which outputs the total number of clusters composed of molecules bound via intermolecular links.

Computation of simulations and analysis

All simulations were performed with SpringSaLaD, using $dt={10}^{-8}$ s and $d{t}_{spring}={10}^{-9}$ s (8). Simulations used for FCS and FCCS analysis were performed using a $d{t}_{data}={10}^{-5}$ s and $d{t}_{image}={10}^{-5}$ s and run for a total of 1.5–2 s of simulation time. Simulations used for CK classification and cluster composition analysis were run for a total 150 ms or 1.5 s of simulation time using $d{t}_{data}=d{t}_{image}={10}^{-2}$. Simulations used for generating representative images of kits were run for a total of 150 ms of simulation time using $d{t}_{data}=d{t}_{image}={10}^{-3}$ s. All analyses of simulation data were carried out using Python and Python libraries, including Numpy, Math, Pandas, and Seaborn.

A Kruskal-Wallis test was used to determine whether a statistically significant difference existed among groups. A Kruskal-Wallis test yielding a statistically significant difference (p < 0.05) was followed by a post-hoc Mann-Whitney-Wilcoxon test.

Cell culture and in vivo FCCS

FCCS experiments were performed with an instrument setup as described previously (1). Transformed Dictyostelium discoideum cells of the KAx3 background were cultured in Hans’ enriched HL-5 medium (1.4× HL-5 medium with 8% FM, penicillin, and streptomycin) containing 15 μg/mL G418 and 40 μg/mL hygromycin (25). Cells were seeded on Lab-Tek II 8-chamber German coverglass system at ∼50–70% confluency and allowed to adhere. Afterward, cells were imaged using a Zeiss AxioObserver with 780-Quasar confocal module microscope, equipped with a C-Apochromat 40× (NA 1.2) water objective. Rhodamine 6G (100 nM) was used for Z-plane determination, laser power calibration, and pinhole alignment. Cells with high fluorescence signal intensity were not selected for measurement to avoid fluorophore saturation. Fluorescence intensity data of two fluorophores are fitted to a single-component 3D diffusion model with a triplet-state component. The in vivo $K_{\text{D}}$ values were calculated using Eq. 2 with $G_a$ and $G_b$ the autocorrelations for mCherry and GFP, respectively, and $G_x$ the cross correlation of two fluorophores.

Results

Validation of diffusion and binding

To elucidate the mechanisms of CK self-assembly at the molecular level, we constructed a coarse-grained excluded volume model using SpringSaLaD (Methods). Although diffusion coefficients are measured experimentally on a complete protein (26), diffusion coefficients in SpringSaLaD are specified for each domain in a protein (Table 1). Thus, to determine which coefficients to specify for the individual domains in our model, we simulated the diffusion of simple polymers of varying lengths ranging from a single monomer unit to 20-mer. Twenty-five polymers were placed in a (500 nm)³ cube, yielding an equivalent concentration of 0.332 μM, and diffusion was simulated for 10 μs. The relatively large simulation environment was chosen to minimize interactions between polymers. The center of mass of each molecule was computed and used to calculate the MSD for each molecule (across 6 simulations for a total of 150 polymers) with reference to the initial position (Methods).

As expected, plotting the average MSD against time revealed a decrease in slope with increasing polymer size (increasing number of monomeric units), which in turn corresponds to a decrease in diffusion coefficient with increasing polymer size (Fig. 2 A). The polymers followed a Rouse-like diffusion relationship (27) in which the diffusion coefficient of the overall polymer is inversely proportional to the number of monomeric units in the polymer and directly proportional to the diffusion coefficient of the monomer ($D_{\text{poly}}=D_{\text{mono}}/N$; Fig. 2 B). This relationship was used to determine the necessary diffusion values for individual coarse-grained protein domains in the CK model to reproduce experimentally measured diffusion coefficients (Table 1).

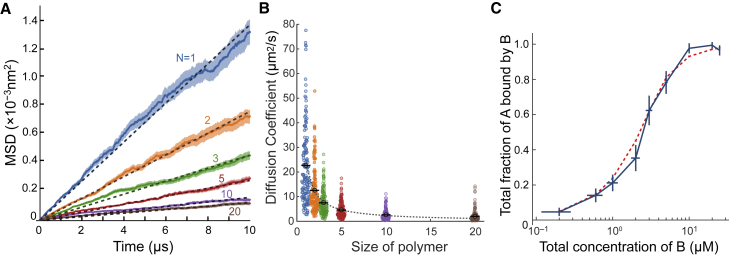
Figure 2.

Diffusion and bimolecular interaction affinities in SpringSaLaD. (A) Mean-squared displacement (MSD) of flexible polymers versus time. Six replicates of 10 μs simulations were run for polymers of different sizes, ranging from a single monomer unit to 20 monomer units. Solid lines represent the MSD obtained from six replicate simulations run in a box (500 nm)³ at a concentration of 0.332 μM (25 molecules per simulation). Shaded regions represent standard deviation of the MSD of all averaged particles. Dotted lines represent fits to Einstein’s diffusion relationship for three-dimensional diffusion. (B) Distribution of diffusion coefficients for each polymer size. Each colored dot represents the diffusion coefficient obtained for a single polymer as in (A). The gray circles are the average diffusion coefficient for that particular size of polymer. The dotted line represents the Rouse-like polymer diffusion relationship ($D_{\text{poly}}=D_{\text{mono}}/N$). (C) Fractional saturation curve for A + B $\rightleftharpoons$ C. The blue solid line represents the average total fraction of A molecules bound by B obtained by averaging results from 10 replicate simulations run at each concentration of B ligand. Error bars on the blue curve represent standard deviation. The red curve represents the result obtained from fitting a fractional saturation curve for a 1:1 stoichiometric ratio relationship, as depicted in Eq. 1. To see this figure in color, go online.

Effective interaction affinities for reactions in SpringSaLaD were validated via fractional saturation analysis (28). Fractional saturation analysis is a technique commonly implemented to measure binding affinity between an enzyme or protein of interest and a known ligand that binds to that molecule. In this procedure, the fraction of enzyme or molecule bound is calculated under varying ligand concentrations and used to construct a curve displaying the fraction of protein or enzyme bound versus added ligand. Ten replicate simulations were run at varying B ligand concentrations (0.2–25 μM) while keeping the A concentration at a constant 3.5 μM. The simulation data were then fit to a fractional saturation for a bimolecular binding reaction with 1:1 stoichiometry (Eq. 1, Fig. 2 C). The $K_D$ obtained from this fit was 0.604 μM, with a ${\chi }^2$ goodness of fit value of 0.0231 and a p value of 0.9999, indicating that no significant difference exists between the simulation data and the fitted model equation. Thus, these results indicate that SpringSaLaD effectively reproduces experimentally measured bimolecular interaction affinities.

Simulating CK formation

Having validated the diffusion and binding terms, we turned to creating a model of the CK elements and simulating their formation. Coarse-grained molecules were represented in terms of nm-sized spherical domains connected by spring-like links (Methods; Tables 1 and 2; Figs. 1 and 3). Once the detailed model was constructed, CK assembly parameters were extracted, specifically diffusion coefficients for individual molecules and clusters and effective bimolecular interaction affinities within clusters. To this end, we used a computational implementation of FCS (23,29,30,31) and FCCS (24,29,31) (Fig. 4, A and B). By computationally emulating FCCS, we were able to reproduce the median and mean values for many of the bimolecular interactions that lead to CK self-assembly (Fig. 4 C; Table S5). The computational FCS procedure was applied to simulations of individual molecules diffusing within a box (Table S3), as well as simulations of CK self-assembly, to obtain average estimates for diffusion coefficients of individual molecules and CKs, respectively. Overall, the median diffusion coefficients for CKs ranged from ∼0.4 to ∼0.8 μM⁻¹ s ⁻¹ (Fig. 4 D), depending upon the distribution of the molecule type that was tracked within the clusters, as well as varying cluster sizes. Taking this into account, we next investigated CK cluster composition and localization.

Figure 3.

Snapshots of contractility kit (CK) elements and their formation in silico. (A) Coarse-grained CK elements. Myosin II dimerization domains are shown in green (right-hand side), while tetramerization domains are shown on the left-hand side of the myosin tail in pink. All cortexillin domains are shown in cyan. IQGAP1 and IQGAP2 are shown in purple and yellow, respectively. The size of the various domains is given in Table 1 and illustrated in Fig. 1A. (B–D) Representative snapshots of CK assembly during simulation. Membrane-bound CKs (PIP2 head domain is in red) can be seen in (B and D). CKs are observed to assemble within the cytoplasmic area (C, this simulation is done in a rectangular box with large z-dimension). In (D), three CKs are circled. The bottom right CK is membrane bound; the other two are cytosolic. Time lapse of a representative simulation is available in Video S1. To see this figure in color, go online.

Figure 4.

CK FCS and FCCS measurements. (A) Computational FCS autocorrelation data versus time for CK clusters containing cortexillin I. Representative autocorrelation data produced from a single simulation tracking cortexillin I in CK clusters. (B) Computational FCCS cross correlation data versus time for cortexillin I-IQGAP1 and cortexillin I-IQGAP2 interactions. Representative cross correlation data were produced from a single simulation tracking cortexillin I-IQGAP interactions within clusters. (C) Protein-protein binding effective interaction affinities were obtained by performing computational FCCS and tracking molecule-type pairs within clusters. Data for (C and D) were obtained from 11 replicate simulations in the presence of a 200 × 200 nm² membrane containing 33 μM PIP₂ for 1.5 s. (D) Cluster diffusion coefficients were obtained by performing computational FCS and tracking individual molecule types, thus providing an estimate for median and average diffusion coefficients for clusters containing that particular molecule type. Red bars represent the median, and the boxes mark the 25^th and 75^th percentiles in (C and D). To see this figure in color, go online.

Simulations predict and experiments confirm the existence of ambiguous CKs

Having confirmed that the model recreates the experimentally measured parameters, we sought to determine how clusters are formed. In simulations of the complete system, the cluster number and size reached a steady state within 1 s of simulation time (Fig. 5 A). At steady state, we detected an average of 6.13 ± 0.78 CKs (mean ± SD), having an average size of 11.4 ± 1.9 component molecules at steady state (t = 1.45 s). Approximately half of the identified CKs seen in the simulations contained both IQGAP proteins (Fig. 5 B). We define these complexes that contain both IQGAPs as “ambiguous CKs” given that they contain both positive and negative regulatory IQGAPs.

Figure 5.

CK formation. (A) Average CK size (blue) and number (green) versus time. The solid lines represent averages while the shaded regions are the standard deviation (n = 8 simulations). (B) The solid black line represents the average number of ambiguous CKs versus time; black-shaded region represents the standard deviation (n = 6 simulations). (C) Frequency of molecule counts. The total number and compositions of CKs were calculated at the last time point of each replicate simulation. Frequency distributions of each CK component were thus calculated before reaching steady state (150 ms; orange bars) and at steady state (1.5 s, blue bars). (D) Ambiguous cluster IQGAP1/IQGAP2 ratio. Six replicate simulations were run in a (200 nm)³ cube for 1.5 s and 150 ms, respectively. The total number of ambiguous clusters at the last time point of the simulation was identified for each replicate, and the IQGAP1/IQGAP2 ratio was computed for each of these. For each distinct ratio identified, the percentage of ambiguous clusters displaying that ratio was computed out of the total ambiguous clusters observed across all six replicates (for both 150 ms and 1.5 s, respectively). (E) In vivo FCCS experiment testing the interaction between IQGAP1 and IQGAP2. Representative examples of cross correlation data versus time-lag for cells expressing mCh-IQGAP2 and GFP-IQGAP1, cells expressing fused mCh-GFP (positive control), and cells expressing unfused mCh and GFP (negative control), respectively (one experiment). The red solid line represents the fit to the 3D single-species diffusion-integrated cross correlation function, which is used to extract effective $K_D$ values for each experiment. (F) FCCS-derived mCh-IQGAP2, GFP-IQGAP1 effective $K_D$. The first column shows the distribution of effective $K_D$ values observed for the mCherry, GFP-negative control, having an average effective $K_D$ of 6.98 ± 5.36 μM (mean ± SD; median: 5.19 μM). Similarly, the second and third columns display the distributions of effective $K_D$ values obtained for the positive control of fused mCherry-GFP ($K_D$ of 1.54 ± 0.83 μM; median: 1.52 μM) and for the interaction between IQGAP1 and IQGAP2 ($K_D$ of 2.75 ± 1.78 μM, median: 1.99 μM), respectively. p values were derived from Kruskal-Wallis followed by a Mann-Whitney-Wilcoxon post-hoc test (p values for the post-hoc test shown in the figure). Red bars represent the median, and the boxes mark the 25^th and 75^th percentiles. To see this figure in color, go online.

We next assessed the temporal order of assembly of CKs (Video S1) and CK composition by constructing frequency distributions of each CK component before and after steady state was reached, in other words, at 150 ms and 1.5 s, respectively (Fig. 5 C). Comparing the frequency distributions of each protein before and at steady state, we observed that the steady-state cortexillin I, IQGAP1, IQGAP2, and myosin II distributions broadened and were noticeably skewed. We also noted that, at steady state, the myosin II distribution had peaks only at even numbers due to the dimer-addition mechanism of bipolar filament assembly. Overall, the IQGAP1 distribution had larger peaks at even numbers, reflecting the imposed myosin dimer addition and the 2:1 stoichiometry of IQGAP:cortexillin I binding.

To investigate the composition of the ambiguous CKs, we calculated the IQGAP1/IQGAP2 ratios for all ambiguous CKs and determined how frequently each IQGAP ratio was observed (Fig. 5 D). This frequency was used to compute what percentage of all identified ambiguous CKs exhibited each particular ratio. When comparing the pre-steady-state (150 ms) and steady-state IQGAP ratio compositions we observed an approximately twofold increase in the observed percentage of complexes that have a 2:1 IQGAP1:IQGAP2 ratio. This increase was accompanied by an approximately 50% decrease in the complexes with equal numbers, and approximately 75% decrease in the 1:2 IQGAP1:IQGAP2 ratios within ambiguous CKs. Collectively, these shifts in relative fractions of IQGAP ratios within ambiguous CKs result from the respective binding stoichiometries as the stochastic system tends toward chemical equilibrium.

The model and simulations predict the existence of ambiguous clusters. To test this prediction, we performed FCCS experiments of mCherry-IQGAP2 interacting with GFP-IQGAP1 in Dictyostelium cells and, indeed, we detected IQGAP1-IQGAP2 interactions in living cells (Fig. 5, E and F). The observed average effective $K_D$ for the IQGAP1-IQGAP2 interaction was 2.75 ± 1.78 μM (mean ± SD; median: 1.99 μM). As a negative control, we measured the interaction between free mCherry and GFP proteins, which had an average effective $K_D$ of 6.98 ± 5.36 μM (median: 5.19 μM). For a positive control, we used a construct in which mCherry and GFP fluorophores were chemically bound via a protein linker, which had an average effective $K_D$ of 1.54 ± 0.83 μM (median: 1.52 μM). These values are statistically significant, confirming the in vivo interaction between the two IQGAPs and the existence of the ambiguous clusters in cells. Statistical significance was corroborated via a Kruskal-Wallis test of statistical significance, followed by a post-hoc Mann-Whitney-Wilcoxon test.

Geometry affects the location of CK formation

We observed that during simulations carried out in a cube in SpringSaLaD a large proportion of CKs localized to the membrane. To determine whether this was a result of the surface area to volume ratio of our simulation box, we carried out and analyzed simulations in boxes of various dimensions (Fig. 6). When simulating CK assembly in a cubic box ([200 nm]³, high surface area-to-volume [S.A./Vol] ratio = 0.005 nm⁻¹), which has a relatively high S.A./Vol. ratio (Fig. 6 A), we saw kits initially forming in roughly equal numbers between the membrane and cytoplasm. However, as the system settled into a steady state, the majority of observed CKs were membrane bound. Decreasing the S.A./Vol. ratio approximately fourfold (Fig. 6 B, S.A./Vol = 0.00125 nm⁻¹) greatly increased the average initial number of cytoplasmic CKs. Nevertheless, this number peaked at around 200 ms, after which we see the distribution of membrane and cytoplasmic CKs shift to approximately equal numbers. Overall, the number of membrane bound CKs continued increasing throughout the beginning of the simulation, suggesting that CKs are primarily formed in the cytoplasm and can then bind, as a formed kit, to the membrane.

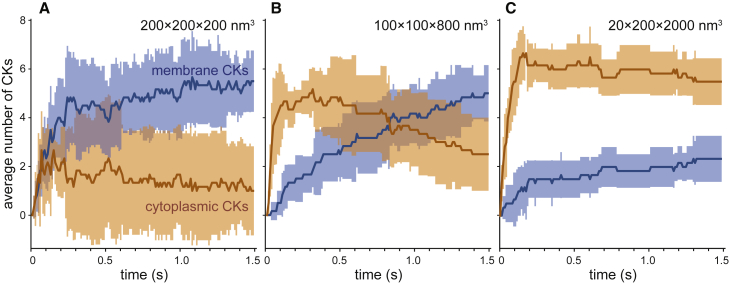
Figure 6.

Effect of surface area to volume ratio on CK localization. Simulations under varying spatial dimensions. Orange and blue markers represent the average number of total cytoplasmic and membrane CKs identified, respectively, from six replicate simulations. Shaded regions represent standard deviation. The volume of each simulation box was maintained at a constant 8 × 10⁶ nm³. Spatial dimensions of the simulation box were: 200 × 200 × 200 nm³ (A), 100 × 100 × 800 nm³ (B), and 20 × 200 × 2000 nm³ (C). To see this figure in color, go online.

Finally, we considered a large, rectangular simulation box with a low S.A./Vol ratio (0.0005 nm⁻¹), which is likely to be the most biologically relevant (Fig. 6 C). In this case, the membrane versus cytoplasmic CK distribution was inverse to that seen in the cube. Most of the kits formed in the cytoplasm, and the number of kits reached a maximum at approximately 200 ms, after which the system approached a steady state. Although some CKs translocated to the membrane, the majority remained cytoplasmic. Thus, by selecting the adequate spatial parameters, we can recapitulate the experimental observation that CKs form and primarily diffuse in the cytoplasm (1).

CK formation in mutant cells

Having recreated CK assembly in a wild-type (WT) scenario, we next investigated the role of individual molecules by performing a variety of “null-mutant” simulations of CK assembly (Fig. 7). From these simulations, intermolecular interaction affinities between CK components were quantified via computational FCCS analysis (Fig. 7, A–C). CK diffusion coefficients were computed via computational FCS analysis (Fig. 7, D–F), and count distributions of various CK components were quantified (Fig. 7, G–I).

Figure 7.

Null-mutant CK FCS/FCCS. The average and median cluster diffusion coefficients and effective $K_D$ values were obtained from replicate simulations (for each null-mutant condition) of CK self-assembly in the presence of a 200 × 200 nm membrane containing 33 μM PIP2. All simulations were run in a 200 × 200 × 200 nm cube for 1.5 s. (A–C) Cluster protein-protein interaction $K_D$ values for WT, iqgap1, iqgap2, and iqgap1/2 null simulations. Protein-protein binding effective interaction affinities were obtained by performing computational FCCS and tracking molecule-type pairs within clusters. (D–F) Cluster diffusion coefficients for the various simulations. Cluster diffusion coefficients were obtained by performing computational FCS and tracking individual molecule types (cortexillin I (D), myosin II (E), and IQGAPs (F)), thus providing an estimate for median and average diffusion coefficients for clusters containing that particular molecule type. (G–H) Dot plot frequency distributions displaying the frequency of molecule type (cortexillin I (G), myosin II (H), and IQGAPs (I)) counts within CKs observed at steady state ($t=1.5$ s). Statistical tests for the data in (A–F) were derived from Kruskal-Wallis followed by a Mann-Whitney-Wilcoxon post-hoc test, as compared with the corresponding WT simulation condition. p values are reported in Tables S6 and S7. Red lines are medians, boxes represent 25^th and 75^th percentiles. To see this figure in color, go online.

We first considered the role of IQGAP1 through iqgap1 null simulations. When compared with WT simulations, in these simulations we saw ∼6- to 8-fold increases in the apparent affinity of the interactions between cortexillin I:IQGAP2 (Fig. 7 A; 0.337 ± 0.160 vs 0.043 ± 0.013 μM; mean ± SD also below) and myosin II:IQGAP2 (Fig. 7 B; 0.304 ± 0.106 vs 0.053 ± 0.010 μM). Similar simulations in which IQGAP2 was eliminated showed an approximately ∼2- to 3-fold increases in affinity of the cortexillin I:IQGAP1 (Fig. 7 A; 0.134 ± 0.071 vs 0.042 ± 0.011 μM) and myosin II:IQGAP1 interactions (Fig. 7 B; 0.172 ± 0.089 vs 0.081 ± 0.029 μM).

CKs containing only IQGAP1 or IQGAP2 (single mutants) showed no significant decrease in average diffusion coefficients when compared with WT simulations (Fig. 7, D–F). Finally, we performed iqgap1/iqgap2 double null simulations in which both IQGAPs were eliminated from the CK self-assembly simulation. In these simulations, the CK diffusion coefficients increased, particularly for cortexillin I (Fig. 7 D; WT: 0.52 ± 0.096 μm²/s to iqgap1/2: 0.86 ± 0.16 μm²/s) and myosin II (Fig. 7 E, 0.400 ± 0.086 μm²/s vs 0.604 ± 0.092 μm²/s), suggesting a possible decrease in CK size. Eliminating both IQGAPs had a small, but statistically significant effect on the observed cortexillin I-myosin II interaction affinity (Fig. 7 C, ranging from 0.067 ± 0.018 to 0.12 ± 0.034 μM). The direct bimolecular interaction between cortexillin I and myosin II is independent of IQGAP binding; however, the generation of larger macromolecular complexes gave rise to effective higher affinity interactions as measured through computational FCCS.

The computational FCS analysis of the null-mutant simulations suggested the presence of smaller CKs, and this led us to examine the composition of CKs under all three null-mutant conditions (Figs. 7, G–I and S5). We observed a shift upward in the IQGAP1 distribution in iqgap2 null simulations, with increasing frequency counts concentrated between two and six IQGAP1 molecules and no clusters with zero IQGAP1 molecules (Fig. 7 I). An analogous shift upward was observed in the IQGAP2 distribution within the iqgap1 scenario, suggesting that the IQGAP proteins can complementarily substitute each other’s role in cluster growth. The increased binding of the remaining IQGAP protein within the single null-mutant scenario is an effect of the allosteric competitive inhibition enforced between IQGAPs. Looking at the cortexillin I (Fig. 7 G) and myosin II (Fig. 7 H) count distributions, we observed a slight narrowing of the distributions in the iqgap1 and iqgap2 scenarios, which was even more pronounced in the iqgap1/2 condition. We also note that no myosin II hexamers were formed within CKs and that a larger fraction of clusters contained only one or two cortexillin I molecules in the absence of one or both IQGAPs (Fig. 7 H). Overall, this suggests that CKs lacking IQGAPs tend to be smaller than those formed in the WT simulation condition and that IQGAPs likely help mediate cluster growth.

Finally, using our CK identification algorithm (Methods) we calculated the average number of CKs and the average CK size versus time in iqgap1/2 simulations (Fig. S5) and observed that while the number of CKs was comparable with that of WT, the average size of the CKs in the double-mutant scenario was approximately half of that observed in the WT simulations (Fig. 5 A).

Discussion

The recent discovery of CKs suggests that cells preassemble the machinery needed to respond quickly to mechanical stresses. These kits consist of mechanoresponsive proteins myosin II and cortexillin I, but also contain IQGAP scaffolding proteins that regulate their assembly and possible localization. CKs are believed to poise the cell for a swift response to mechanical stress by delivering mechanosensitive contractile proteins that can be incorporated into larger-scale cytoskeletal structures (such as BTFs) upon a diffusional encounter with the cortex. Because the molecular details behind the formation of these kits are challenging to observe experimentally, mathematical modeling provides an excellent tool for probing the dynamics of CK formation and how these may preassemble. Here, we have developed a predictive coarse-grained in silico molecular model of CK assembly that allows us to study the interactions of the constituents at a molecular level. We validated the model by successfully recapitulating in silico several in vivo experiments and compared the model outputs with experimentally measured parameters, including molecular diffusion coefficients and bimolecular interaction affinities between CK components in WT and mutant scenarios.

In our simulations, we observed CKs form, grow, and move to and from the membrane. Our simulations showed that, as observed experimentally, CKs primarily assemble in the cytoplasm and, after assembly, they can move and bind to the membrane. This effect was particularly apparent in environments where we lowered the S.A./Vol. ratio to a ratio that is more likely to be representative of the cellular environment. Our simulations suggest that myosin II and cortexillin I elements form the core of the kits; in particular, myosin II dimers provide initial binding sites for other CK proteins. The kits then continue to grow through the fusion of independent clusters, which is primarily mediated via myosin tetramer and small-scale myosin hexamer (BTF₆) formation, but particularly via IQGAP binding, which can serve to recruit additional myosin II and cortexillin I elements to a growing cluster.

Unexpectedly, our simulations suggested the existence of previously unknown ambiguous clusters that contain both IQGAPs. In fact, simulations suggested that this was the largest group consisting of nearly 50% of all kits. We tested this prediction in vivo using FCCS measurements and confirmed the interactions between IQGAP1 and IQGAP2. The existence of ambiguous kits offers new ideas about how the formation and distribution of CKs may be regulated inside the cell. If CKs existed only in isolated forms of either nonmechanoresponsive CKs containing only IQGAP1 and mechanoresponsive CKs containing only IQGAP2, the cell could regulate the mechanoresponsiveness setpoint partly by adjusting the relative concentration of two IQGAPs in the cytoplasm. In fact, in our single IQGAP null-mutant simulations, we observed an increase in apparent affinity and binding of the remaining IQGAP. The presence of ambiguous kits with both IQGAPs suggests that the regulation and recruitment of CKs to sites of stress could achieve a higher level of tunability and robustness. For example, the formation of larger ambiguous clusters, containing more mechanoresponsive myosin II and cortexillin I elements, could lead to increased delivery of these contractile elements and thus potentially a larger mechanoresponsiveness. Having a variety of versions with different ratios of IQGAP1 versus IQGAP2 may then help set the sensitivity of the system and allow subsets of CKs to be more readily poised to elicit mechanoresponsive accumulation versus programmed cortex assembly.

The role of the two IQGAPs in mechanosensation is complementary. Whereas cells that have only IQGAP2 are highly mechanoresponsive, those that have only IQGAP1 are not (6). Moreover, the double mutants are also mechanoresponsive, suggesting that IQGAP1 serves as an inhibitor of cortexillin I and myosin II, and part of the role of IQGAP2 is to alleviate IQGAP1’s inhibition (1,6). In our simulations, we probed the effect of these two IQGAP proteins by considering null-mutant simulations. Our results show that, in the double null-mutant, CKs tend to be smaller (Figs. 6, S3, and S4), suggesting that IQGAPs help generate larger CKs by providing additional binding sites to mediate cluster fusion.

While the CK concept has only been shown experimentally in Dictyostelium cells, we suspect that the concepts will likely hold in other cell types, even if the specific binding partners are different. Some suggestions of this likelihood are already present. For example, ACTN4 was recently found to associate with nonmuscle myosin IIA (NMIIA) (32). Another mammalian protein, anillin, is highly analogous to cortexillin I in its role in tethering the actin network to the plasma membrane during cytokinesis, and anillin can bind directly to NMII (33). Furthermore, we found that anillin is similarly mechanoresponsive in dividing mammalian cells (34).

Mammalian cells also express IQGAP proteins. These proteins include CH domains, multiple IQ repeats, and a WW domain, in addition to the GRD domain and the RGCT domain. The Dictyostelium IQGAP proteins only share homology through the GRD and RGCT regions. In our work, we have found that the IQGAPs (IQGAP1 and IQGAP2) provide control over the mechanoresponsiveness of the contractility machinery and are part of the CK system. It would not be a big surprise if the IQGAPs provide a similar role in mammalian and other cell types. In fission yeast, for example, an IQGAP protein (Rng2) helps localize myosin II to the contractile ring independently of actin filaments (35). Other modes of NMII regulation are also essential for mechanoresponsiveness. Unlike mammalian NMIIs, Dictyostelium myosin II does not form a 10S structure, although it can form fold-back structures within the tail region that do not involve the light chains (36, 37). These fold-back structures are not essential for regulating bipolar filament assembly, however (20). Like mammalian NMII, light-chain phosphorylation does lead to activation of the motor domain. However, this light-chain phosphorylation is nonessential for many biological activities as a nonphosphorylatable RLC-complemented RLC (mlcR) null is still able to form myosin II bipolar filaments, complete cytokinesis, undergo motility, and perform development (36). But, in this nonphosphorylatable RLC-complemented mlcR mutant, myosin II cannot undergo a mechanoresponsive accumulation (4). Thus, light-chain phosphorylation does provide a critical regulatory function that allows myosin II to be mechanoresponsive.

In Dictyostelium and mammalian nonmuscle cells, heavy-chain phosphorylation directly controls the ability of myosin II to assemble into bipolar thick filaments. Heavy-chain phosphorylation sets the fraction of myosin II that is assembled in the cell and controls myosin II assembly dynamics. Because myosin II serves as both the sensor and actuator of this mechanoresponsiveness, heavy-chain phosphorylation sets the setpoint, establishing how mechanoresponsive a particular cell type can be—enough myosin II must be assembled in the cortex to sense the stress with enough free CK pool available to respond (38). Through our prior modeling work, we created mathematical models that account for the role of heavy-chain phosphorylation in mediating myosin II mechanoresponsiveness (5,38,39).

Our simulations have allowed us to complement the information that has been obtained from in vivo experiments, giving us a deeper look at what constitutes the nucleus of these kits and how they form and grow. Our simulations also help confirm the experimental observations about where the kits form. In the future, the model can be expanded to include other CK components (1). We would also like to explore further other avenues for CK regulation, including the role of myosin II heavy-chain phosphorylation by myosin heavy-chain kinases. Heavy-chain phosphorylated myosin II’s could be included in the CKs, resulting in assembly incompetent CKs that cannot incorporate into large-scale cytoskeletal structures, such as BTFs, or incorporate less efficiently (1,20). We also aim to further explore how CKs are incorporated into large-scale cytoskeletal structures by constructing a cell-scale model of CK assembly and incorporating these phenomena.

Author contributions

P.A.I. and A.I.P.-R. designed research with consultations from D.N.R. A.I.P.-R. (computational) and L.T.S.N. (experimental) performed research and analyzed the respective data. P.A.I. and A.I.P.-R. drafted the paper with contributions and editing from L.T.S.N. and D.N.R.

Editor: Dimitrios Vavylonis.