Abstract
Refractometry is important for characterizing optical performance of materials. Refractive index can quickly be assessed using critical angle or thin film techniques. However, these methods only assess the material surface. Measurement of bulk refractive index is performed by measuring the refracted angle of a transmitted beam, but requires precision sample geometry. The method presented here avoids costly sample preparation by measuring the sample geometry and refracted angle simultaneously using reflections from the front and back surfaces of a wedge of material. The method is demonstrated for polydimethylsiloxane (PDMS) prepared under a range of curing conditions and no significant dependence was observed. Spectral dependence is characterized and Sellmeier coefficients are reported.
PDMS is a widely used polymer with applications in photonics and microfluidics [1–9]. It can be easily cured under many conditions into a solid that is optically clear in the visible and NIR wavelengths [10]. The use of PDMS as a lens material has been a growing area of interest due to its high refractive index, ability to be easily shaped at large and small scales, and low cost to manufacture [5]. Despite the growing range of applications, there has been only limited characterization of the refractive index of PDMS, which is often reported as a single value with no dispersion information or dependence on curing conditions.
Measurements made by Schneider et al and Cai et al are noteworthy since they included spectral characterization, however these measurements employed Abbe refractometry in the former, and ellipsometry of spin-coated thin film in the latter [11, 12]. These methods measure the index at the surface, which may be a significant limitation because it has been observed that PDMS refractive index can vary at the surface compared to the bulk value[13]. To characterize bulk refractive index of PDMS, a novel measurement geometry was developed by the authors and compared to Abbe refractometry of PDMS samples cured under a range of temperatures and curing agent concentrations. The method requires only low-cost components, is self-normalized, and does not require precise sample preparation, making it useful for measurement of other cured polymers.
Refractometry or measurement of refractive index is generally performed in one of three ways: i) measurement of critical angle as with an Abbe refractometer, ii) ellipsometry, or iii) measurement of transmitted angle from a prism of the material to be characterized. The Abbe refractometer is most common and works with liquids or solids with a single flat surface [14, 15]. While easy to use and accurate to the fourth decimal place, Abbe refractometers only probe the surface of the material, making it difficult to assess an inhomogeneous material [11, 16]. Ellipsometry is another common method of assessing refractive index in thin films and has been used to measure PDMS [12, 17–19]. Ellipsometry provides a more complete characterizations of the material including birefringence and absorption, but requires a uniform thin film, typically spin coated, and therefore again only assesses the refractive index near a surface. It has been observed that the refractive index of PDMS may be altered near the surface [13]. This could bias a surface based measurement, and so a measurement of bulk refractive index is also needed. Other methods have been demonstrated, including prism coupling and fiber optic refractometers. Placing a sample of material against a prism of known index and detecting evanescent wave modes from critical angle illumination is a high-precision method with access to spectral properties [20]. Fiber optic refractometers use etched fibers or fiber Bragg gratings which immersed in the test media are capable of high-precision refractive index measurements [21–23]. Both of these types of methods offer precision to the fourth decimal place but require precision prisms, moving components, or use long wavelengths (unless harmonic detection frequencies are used) [20, 21, 23]. The instrument developed here is intended to offer third decimal place precision with no moving or precision parts.
Bulk refractive index is generally based on measuring the angle of a transmitted beam refracted through a wedge or prism made of the material to be measured. The Hilger-Chance refractometer can be used to measure liquid samples by placing the liquid in a prism shaped cavity formed with high precision glass prisms of well characterized material [24]. A similar approach can be used for solids, but requires polishing of the sample on two surfaces and precise measurement of the wedge angle. Automated measurement of liquids was demonstrated by incorporating a lens and camera to measure the angle of the transmitted beam in a Hilger-Chance refractometer [25]. In the method presented here by the authors, an additional modification enables automatic measurement of the wedge angle at the same time as the measurement of refracted angle to avoid the need for precise fabrication of each sample. This reflective Hilger-Chance (RHC) refractometer allows for a self referenced measurement of the sample wedge angle and the sample refractive index.
1. METHODS
A. PDMS Sample Preparation
PDMS elastomer (Sylgard 184) was mixed with its curing agent (CA) using a magnetic stir bar and then degassed in a vacuum desiccator. A glass wedge was constructed with an internal angle of approximately 1° and filled with the desired PDMS mixture and cured. Wedges are constructed from 1 mm thick glass slides that are held at a 1° angle and adhered with a UV epoxy. The resulting wedge cavity was at least 1 mm thick and was filled with liquid samples for curing. Curing temperatures ranged from 60° C to 85° C for 1 hour followed by 48 hours at room-temperature to ensure a total cure. Samples were cured using 6.67%, 10%, or 20% curing agent by mass. PDMS refractive index was measured and compared to measurements from an Abbe refractometer (WY1A, Scientific Instruments & Optical Sales, Brisbane, Australia).
B. Reflective Hilger-Chance Refractometer
The RHC refractometer geometry, shown in Figure 1, enables simultaneous measurement of the wedge angle of the sample as well as the refracted angle due to the sample refractive index. The instrument is low-cost and composed solely of the source, a collimating lens, beamsplitter, Fourier lens, and camera. The sample is placed in a wedge shaped cell formed by two glass slides cemented together at a small angle. The top slide is smaller than the bottom and assembled such that the bottom slide extends beyond the top slide as in 1. Samples are injected into the wedge cavity where surface tension keeps them in place until measurement or curing. Although low-cost laser diodes spanning the spectral range of interest could be used, our measurements made use of a tunable white light laser. An acousto-optical tunable filter (AOTF) selects a wavelength from the supercontinuum source and is coupled to the single mode fiber (S405-XP, Thorlabs). Light from a single mode fiber was collimated with a 20mm focal length lens, LC (10x Olympus PLAN achromat objective), to a beam spot 4 mm in diameter. Collimated light illuminates the wedge as well as the exposed top surface of the bottom slide to produce three reflections: T from the top surface (air-glass interface), E directly from the exposed surface of the bottom support slide (air-glass interface), and S from the bottom slide which refracts out of the sample (sample-glass interface). The reflections return at an angle which is imaged into lateral separation by a Fourier lens, LF (Thorlabs AC254–100-A), onto an image sensor (Thorlabs DCC3240N). The angle is determined from the focal length f of LF and separation between reflected spots. Spots were located with sub-pixel accuracy using weighted centroid (MATLAB regionprops from the image processing toolbox). From these measured angles, the wedge angle and the refractive index of the sample can be calculated through application of Snell’s law.
Fig. 1.
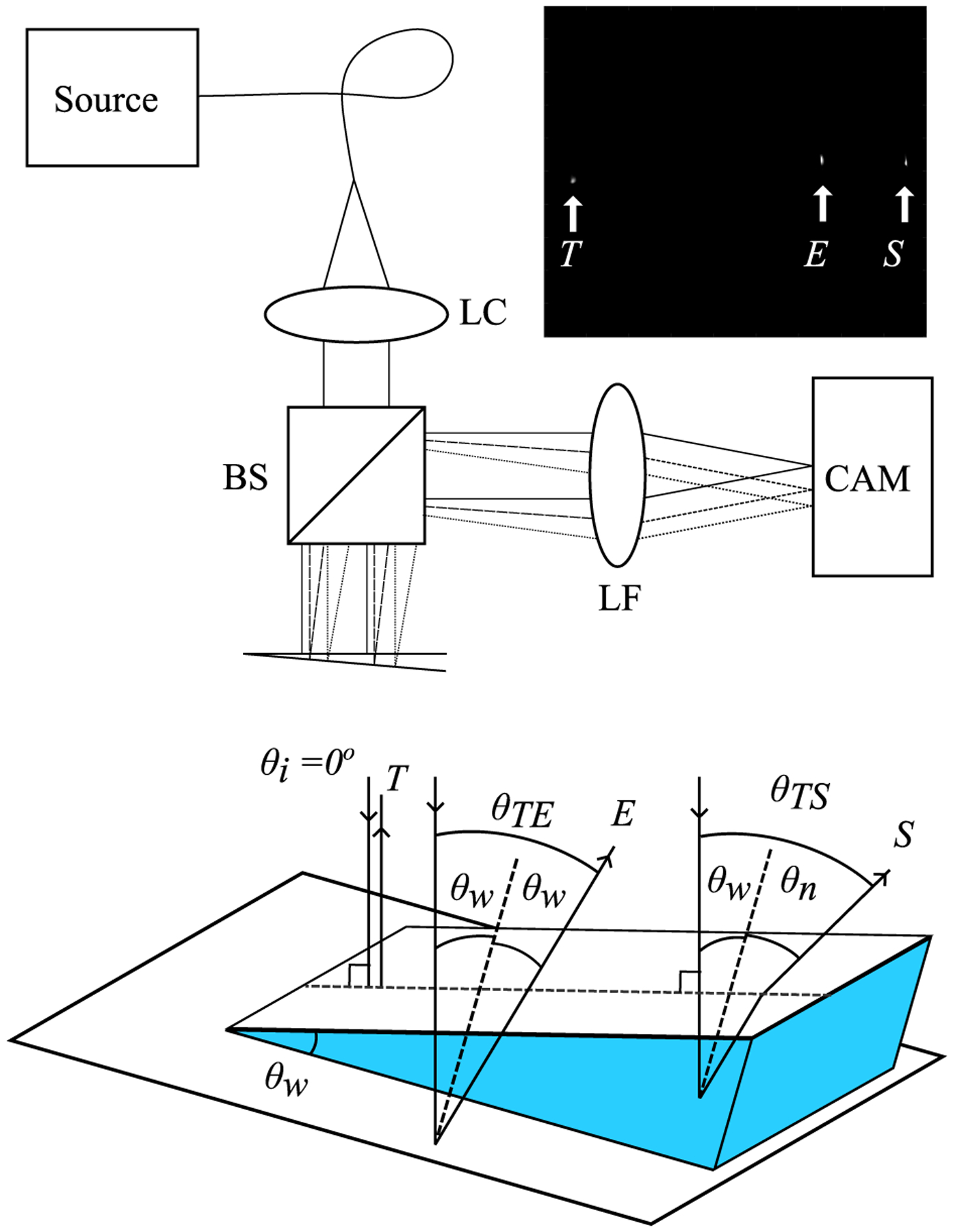
Top: optical layout. In-set: sample image showing relative position of reflections where T is the reflection from the top surface of the wedge, E is the reflection coming directly from the exposed bottom slide, and point S is the reflection from the bottom surface which refracts out of the sample. Bottom: detailed view of sample.
C. Refractive Index Calculation
A measure of the wedge angle, θw, is provided by the angle, θTE, between reflections from the top of the wedge, T, and the exposed bottom slide, E. The ray that transmits through the sample and refracts out with an additional angle, θn, provides the refractive index of the material by measuring its total angle, θTS, and applying Snell’s law using Equation 1.
| (1) |
There is a dependence of the relative reflection angle from the sample, θn, on the angle of incidence, θi, onto the wedge (see Equation 2), but the solution is simplified when θi = 0° and is normal to the top of the wedge as shown in Figure 1. In this case, there is no refraction upon entering the sample, and the internal reflected angle from the bottom slide is equal to twice the wedge angle. A simple application of Snell’s law gives θTS. The angle of the wedge is calculated as half of the reflection angle θTE. Normal incidence can be achieved by first determining the location on the camera of a retroreflection from a corner cube or an Enhanced Backscattering (EBS) peak from a diffusely scattering sample as described below. Once the retroreflection location is determined, the wedge is simply tilted to align spot T to this location on the camera.
| (2) |
D. Error Analysis
There are several potential sources of error for the RHC geometry including: non-normal incidence on the wedge, spot location, inaccurate lens focal length, poor collimation, poor surface flatness of the glass slides, and surface contamination of the lower slide causing spurious reflections.
When the incident light is not normal to the top surface, the refracted angle, θTS, has a dependence on the incident angle that is not measured but is described by Eq. 2. The sample refractive index, nsmp, contains error on the order of 1 × 10−4 when approximately 0.044 mrad of incident angle are introduced. However, this error can be minimized by aligning spot T on the camera to the location of a retroreflection using either a corner cube, or the peak from Enhanced Backscattering. The error in index resulting from this dependence was calculated as 1 × 10−4 for 0.015 mrad corresponding to the specified tolerance of the beam deviation for the cornercube (Thorlabs PS975M). Interestingly, since the EBS peak acts like phase conjugation, the peak is always located in the retroreflection direction [26]. The EBS peak can be observed by holding a highly scattering material such as paper, dried white paint, or a white reflectance standard at the sample position and moving it slightly to average out speckle. This offers a secondary method of locating the retroreflection angle that is low-cost and does not require high-tolerance components.
Determining spot location presents another source of error. When a 100 mm Fourier lens is used, each pixel on the camera represents to 0.053 mrad of angle corresponding to a refractive index increment of ≈ 3 × 10−3. Weighted centroid provides sub-pixel localization of the spots and improve accuracy.
Converting centroid distances to angle depends on the focal length of the lens, which has a tolerance and varies as a function of wavelength due to chromatic aberration. The lens used here has a focal length tolerance of ±1 mm and chromatic shift of ±0.15 mm. However, an error of 5 mm on a f =100 mm lens only produces an error in refractive index of < ±10−4, indicating that this geometry is insensitive to focal length error for a well-collimated beam.
Error in collimation of the beam has two effects. First, if the beam has slight convergence or divergence, when the Fourier lens is focused to produce sharp spots on the camera, spots can translate with focus and the effect is similar to the focal length error described above. This error is eliminated when the sample is placed at the front focal plane of the Fourier lens as in a telecentric imaging system. Second, imperfectly collimated rays span a range of angles that could be treated as uncertainty. However, symmetry in this error on either side of the beam center results in a centroid that is still centered on the correct location along the line of spots. Reflections T and S will have the same angular separation as for ideal collimation. Reflection E is produced from a different part of the beam and collimation error can translate this spot orthoganal to the line . Indeed, E was observed as far as 10 pixels off the line , which corresponds to ≈ 0.5 mrad of collimation error. However, when this point was projected onto , the difference in calculated wedge angle θw compared to that found from simple centroid distance was 3.5 × 10−3 mrad and resulting in a mean change of refractive index of approximately 3 × 10−4. To minimize collimation error, LC was focused using a shear plate interferometer.
While the remaining sources of error due to poor surface flatness of the glass slides or surface contamination could be addressed by using higher quality precision slide, this would offset one of the advantages of the method, which is low cost and simple material preparation. In practice, these sources of error were easy to identify because they produce distorted and aberrated spots, and so data with poor spot quality can simply be discarded.
2. RESULTS
Using water and glycerol for validation, the RHC refractometer was used to measure refractive index and dispersion at room temperature (21°C − 23°C). Values were found to match the literature to within the standard deviation of the measurement as shown in Figure 2 and a stable fit of Sellmeier coefficients for two terms was obtained as shown in Table 1. These data indicate the instrument is able to accurately measure refractive index of liquid samples.
Fig. 2.
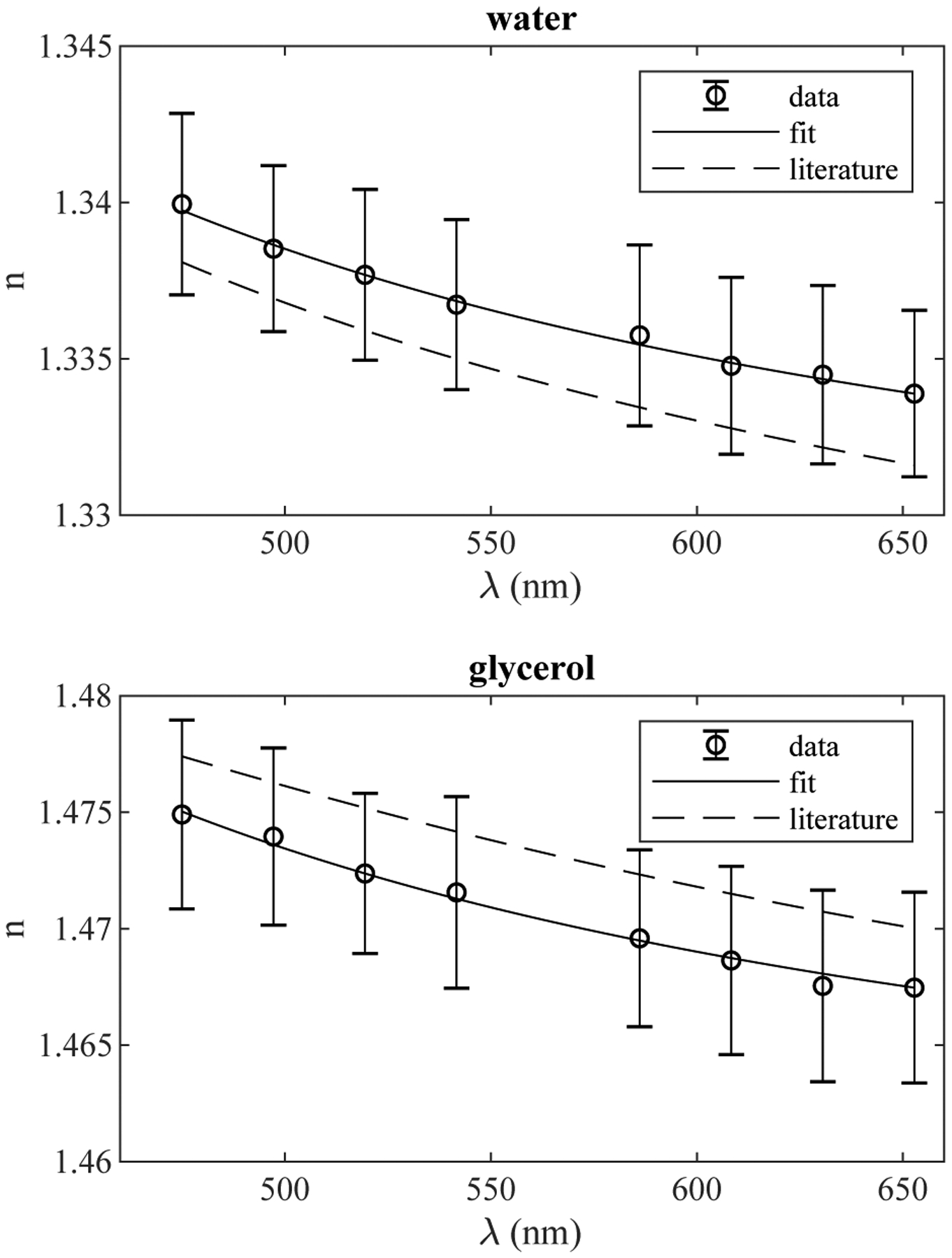
Refractive index of water and glycerol standards as a function of wavelength. Data points are a mean of 5 replicate measurements with error bars indicating standard deviation.
Table 1.
Mean refractive index (nD) values with standard deviation and two terms of Sellmeier coefficients fit to RHC data.
| nD Abbe | nD RHC | B 1 | B 2 | C 1 | C 2 | R 2 | |
|---|---|---|---|---|---|---|---|
| Water | 1.3342 ± 0.0003 | 1.3358 ± 0.0029 | 0.5616 | 0.2011 | 5269 | 1.943 × 104 | 0.9943 |
| Glycerol | 1.4753 ± 0.0005 | 1.4696 ± 0.0038 | 1.144 | 0.0186 | 6770 | 1.197 × 106 | 0.9930 |
| PDMS Uncured | 1.4103 ± 0.0001 | 1.4024 ± 0.0023 | 0.9369 | 0.0514 | 1.080 × 104 | 9.943 × 107 | 0.9975 |
| Curing Agent | 1.4018 ± 0.0003 | 1.3950 ± 0.0028 | 0.9220 | 0.0981 | 1.021 × 104 | 1.163 × 107 | 0.9941 |
| PDMS Cured | 1.4119 ± 0.0013 | 1.4157 ± 0.0075 | 0.9660 | 0.3528 | 1.124 × 104 | 9.243 × 107 | 0.9986 |
Samples were prepared by placing degassed PDMS into glass wedges and curing. For each condition, a second sample was cured on an open glass slide and peeled off for measurement on the Abbe refractometer at room temperature. Samples were cured at 6 different temperatures for each of 3 curing agent concentrations for a total of 18 conditions. Each sample was measured at 5 different locations and at 8 wavelengths for each location. The mean wedge angle was found to be 0.917° with a standard deviation of 0.160°. To assess any dependence on cure temperature, the 5 replicate measurements at 586 nm of each of the 3 curing agent concentrations was pooled for 15 total measurements at each cure temperature and shown in Figure 3 along with measurements from the Abbe refractometer. Least squares fit of the data indicate no significant trend with cure temperature (R2 = 0.039 for RHC, and R2 = 0.229 for Abbe). Similarly, the dependence on curing agent concentration was evaluated by pooling the 5 measurements for each of the 6 cure temperatures for a total of 30 measurements of a given curing agent concentration. Again, the results showed no significant trend (R2 = 0.050 for RHC, and R2 = 0.338 for Abbe).
Fig. 3.
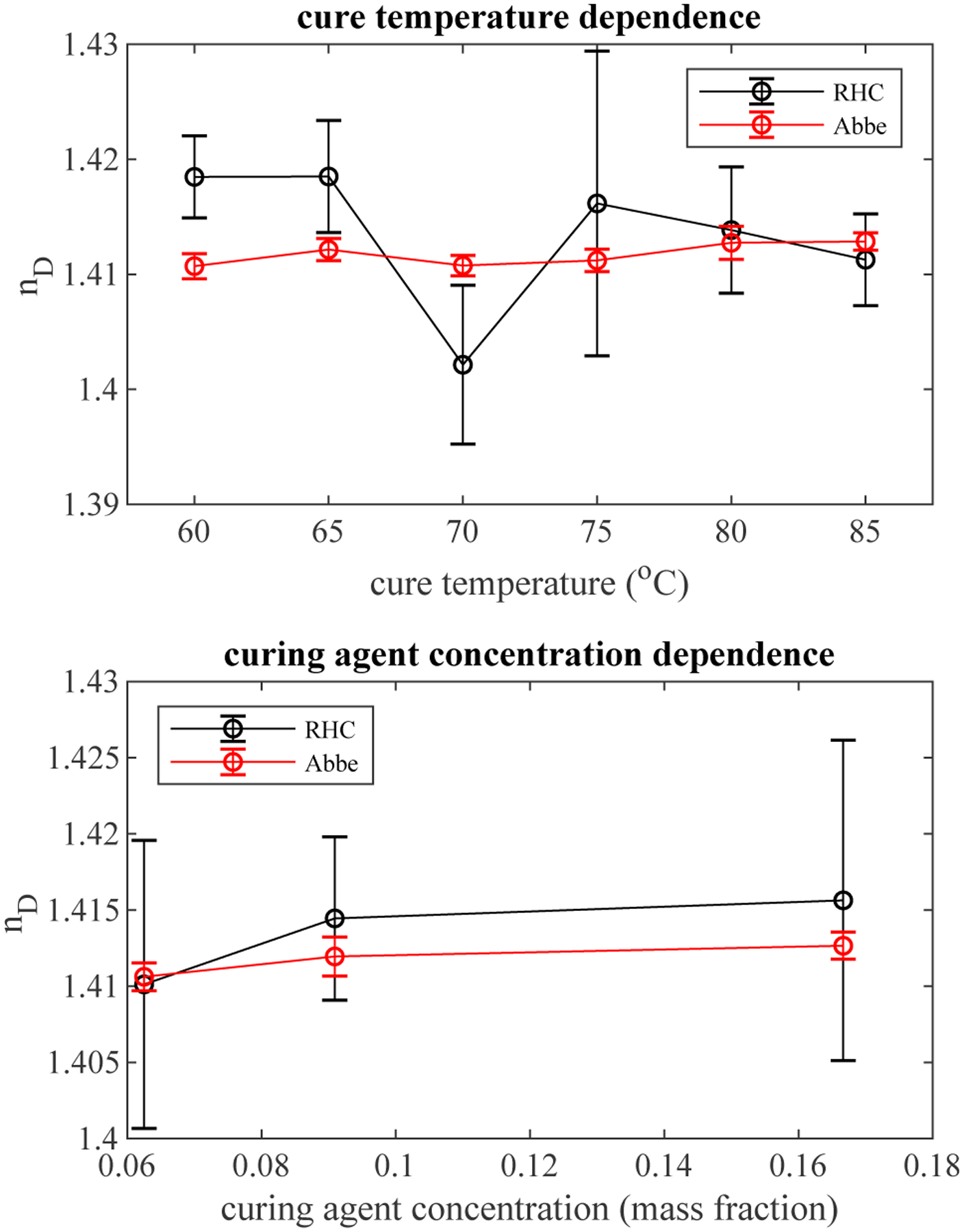
Refractive index of PDMS as a function of cure temperature (above) and curing agent concentration (below). Data points are a mean with error bars representing standard deviation. For cure temperature, 3 samples with 5 measurements each were pooled. For curing agent, 5 measurements of 6 samples made at each curing agent concentration were pooled.
Since no dependence on curing agent concentration or cure temperature was found, measurements were pooled for each wavelength to determine dispersion, which is usually modeled by the Sellmeier equation given in Equation 3.
| (3) |
Sellmeier coefficients for both cured and uncured PDMS were determined and agreed well with a single coefficient found by Schneider, et al [11]. Least squares fitting was used to determine Sellmeier coefficients (see Table 1) using constraints on the C coefficients suggested by literature [27]. The C coefficients should correspond to absorption bands of the material on either side of the visible spectrum and the B coefficients provide weighting to these terms. It was found that the NIR and IR terms contributed relatively little to the dispersion and the UV absorption of PDMS is not well-characterized. In the case of both fitting methods, Sellmeier terms were determined for both cured and uncured PDMS with sufficiently good fits (R2 > 0.99) and are shown in 4.
Fig. 4.
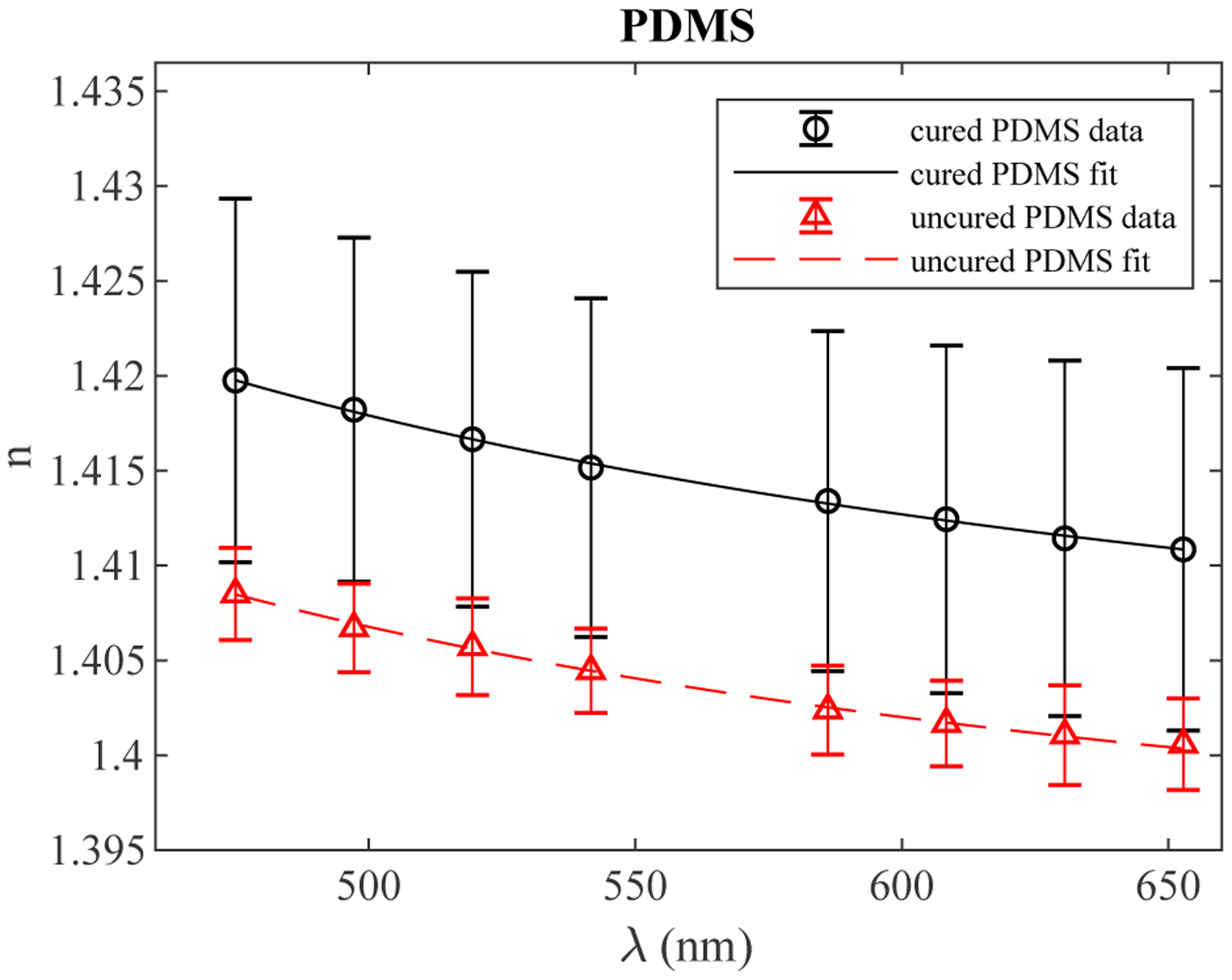
Refractive index of PDMS in its cured and uncured states as a function of wavelength. Data points are a mean with standard deviation. For cured PDMS there are 90 measurements (5 replicate measurements of 18 samples) and for uncured PDMS there are 5 measurements.
3. DISCUSSION AND CONCLUSIONS
The Hilger-Chance refractometer measures bulk refractive index by measuring the angle of a ray refracted by a prism of material with precisely known wedge angle and application of Snell’s law. The RHC refractometer method presented here enables measurement of this refracted ray angle in reflection while simultaneously providing a precise measure of the wedge angle. The self-referenced measure of sample wedge angle provides a simple, low-cost method for determining refractive index to 3 decimal places without requiring high precision prism fabrication. The RHC method can be employed at different wavelengths to measure dispersion. While dispersion was measured using an available tunable white light laser for convenience, low-cost laser diodes could be used to minimize cost. If simplicity and low-cost were not a priority, the accuracy of the method could be further improved by using higher precision optically flat glass in constructing the wedge, and improving the collimation method. This instrument is capable of measuring the refractive index of any optically transmissive material that can be retained in the wedge through either surface tension or curing. The measurement error of cured PDMS was dominated by sample to sample variation, as shown by the much larger standard deviation for cured PDMS compared to uncured PDMS or glycerol and water measurements. This method complements surface measurements obtained using Abbe refractometry or ellipsometry for samples that have inhomogeneous refractive index. Dispersion of PDMS was determined and fitted Sellmeier coefficients were reported.
FUNDING INFORMATION
This work was supported by the National Science Foundation (NSF) (1240416), National Cancer Institute (NCI) of the National Institutes of Health (NIH) (5R01CA183101), and by the Retina Research Foundation Edwin and Dorothy Gamewell Professorship.
REFERENCES
- 1.Chang-Yen DA, Eich RK, and Gale BK, “A monolithic pdms waveguide system fabricated using soft-lithography techniques,” J. Light. Technol 23, 2088–2093 (2005). [Google Scholar]
- 2.Kopetz S, Cai D, Rabe E, and Neyer A, “Pdms-based optical waveguide layer for integration in electrical-optical circuit boards,” AEU - Int. J. Electron. Commun 61, 163–167 (2007). [Google Scholar]
- 3.Mao X, Lin S-CS, Lapsley MI, Shi J, Juluri BK, and Huang TJ, “Tunable liquid gradient refractive index (l-grin) lens with two degrees of freedom,” Lab on a Chip 9, 2050–2058 (2009). [DOI] [PubMed] [Google Scholar]
- 4.Camou S, Fujita H, and Fujii T, “Pdms 2d optical lens integrated with microfluidic channels: Principle and characterization,” Lab on a Chip 3, 40–45 (2003). [DOI] [PubMed] [Google Scholar]
- 5.Lee WM, Upadhya A, Reece PJ, and Phan TG, “Fabricating low cost and high performance elastomer lenses using hanging droplets,” Biomed. Opt. Express 5, 1626–1635 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.International Society for Optics and Photonics, Fabrication and characterization of silicone-based tissue phantoms with tunable optical properties in the visible and near infrared domain, vol. 6870. [Google Scholar]
- 7.Hidayat R, Gomulya W, Pitriana P, Irmansyah R, Miranti R, Herman H, Hidayat S, Fitrilawati F, Fujii A, and Ozaki M, “Siloxane based organic-inorganic hybrid polymers and their applications for nanostructured optical/photonic components,” ITB J. Eng. Sci 44 B, 207–219 (2012). [Google Scholar]
- 8.Polynkin P, Polynkin A, Peyghambarian N, and Mansuripur M, “Evanescent field-based optical fiber sensing device for measuring the refractive index of liquids in microfluidic channels,” Opt. Lett 30, 1273–1275 (2005). [DOI] [PubMed] [Google Scholar]
- 9.Seo J and Lee LP, “Disposable integrated microfluidics with self-aligned planar microlenses,” Sensors Actuators, B: Chem. 99, 615–622 (2004). [Google Scholar]
- 10.Cai D, Neyer A, Kuckuk R, and Heise HM, “Raman, mid-infrared, near-infrared and ultraviolet-visible spectroscopy of pdms silicone rubber for characterization of polymer optical waveguide materials,” J. Mol. Struct 976, 274–281 (2010). [Google Scholar]
- 11.Schneider F, Draheim J, Kamberger R, and Wallrabe U, “Process and material properties of polydimethylsiloxane (pdms) for optical mems,” Sensors Actuators, A: Phys. 151, 95–99 (2009). [Google Scholar]
- 12.Cai Z, Qiu W, Shao G, and Wang W, “A new fabrication method for all-pdms waveguides,” Sensors Actuators, A: Phys. 204, 44–47 (2013). [Google Scholar]
- 13.Martinček I, Turek I, and Tarjányi N, “Effect of boundary on refractive index of pdms,” Opt. Mater. Express 4, 1997 (2014). [Google Scholar]
- 14.Rheims J, Köser J, and Wriedt T, “Refractive-index measurements in the near-ir using an abbe refractometer,” Meas. Sci. Technol 8, 601–605 (1997). [Google Scholar]
- 15.Herrmann PP, “Determination of thickness, refractive index, and dispersion of waveguiding thin films with an abbe refractometer,” Appl. Opt 19, 3261 (1980). [DOI] [PubMed] [Google Scholar]
- 16.Barnes J, Dreher M, Plett K, Brown RS, Crudden CM, and Loock HP, “Chemical sensor based on a long-period fibre grating modified by a functionalized polydimethylsiloxane coating,” Analyst. 133, 1541–1549 (2008). [DOI] [PubMed] [Google Scholar]
- 17.McCrackin F, Passaglia E, Stromberg R, and Steinberg H, “Treasure of the past vii: Measurement of the thickness and refractive index of very thin films and the optical properties of surfaces by ellipsometry,” J. Res. Natl. Inst. Standards Technol 106, 589 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Motakef S, Suratwala T, Roncome RL, Boulton JM, Teowee G, and Uhlmann DR, “Processing and optical properties of inorganic-organic hybrids (polycerams). ii. pdms-based waveguides,” J. Non-Crystalline Solids 178, 37–43 (1994). [Google Scholar]
- 19.Schnyder B, Lippert T, Kötz R, Wokaun A, Graubner VM, and Nuyken O, “Uv-irradiation induced modification of pdms films investigated by xps and spectroscopic ellipsometry,” Surf. Sci 532–535, 1067–1071 (2003). [Google Scholar]
- 20.Prajzler V, Nekvindova P, Spirkova J, and Novotny M, “The evaluation of the refractive indices of bulk and thick polydimethylsiloxane and polydimethyl-diphenylsiloxane elastomers by the prism coupling technique,” J. Mater. Sci. Mater. Electron 28, 7951–7961 (2017). [Google Scholar]
- 21.Jorgenson R and Yee S, “A fiber-optic chemical sensor based on surface plasmon resonance,” Sensors Actuators B: Chem. 12, 213–220 (1993). [Google Scholar]
- 22.Wu D, Zhao Y, and Li J, “Pcf taper-based mach–zehnder interferometer for refractive index sensing in a pdms detection cell,” Sensors Actuators B: Chem. 213, 1–4 (2015). [Google Scholar]
- 23.Liang W, Huang Y, Xu Y, Lee RK, and Yariv A, “Highly sensitive fiber bragg grating refractive index sensors,” Appl. physics letters 86, 151122 (2005). [Google Scholar]
- 24.Hughes J, “A new precision refractometer,” J. Sci. Instruments 18, 234 (1941). [Google Scholar]
- 25.Pixton BM and Greivenkamp JE, “Automated measurement of the refractive index of fluids,” Appl. optics 47, 1504–1509 (2008). [DOI] [PubMed] [Google Scholar]
- 26.Rogers JD, Stoyneva V, Turzhitsky V, Mutyal NN, Pradhan P, Çapoğlu IR, and Backman V, “Alternate formulation of enhanced backscattering as phase conjugation and diffraction: derivation and experimental observation,” Opt. express 19, 11922–11931 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tatian B, “Fitting refractive-index data with the sellmeier dispersion formula,” Appl. Opt 23, 4477 (1984). [DOI] [PubMed] [Google Scholar]


