Abstract
In addition to the role that our visual system plays in determining what we are seeing right now, visual computations contribute in important ways to predicting what we will see next. While the role of memory in creating future predictions is often overlooked, efficient predictive computation requires the use of information about the past to estimate future events. In this article, we introduce a framework for understanding the relationship between memory and visual prediction and review the two classes of mechanisms that the visual system relies on to create future predictions. We also discuss the principles that define the mapping from predictive computations to predictive mechanisms and how downstream brain areas interpret the predictive signals computed by the visual system.
Keywords: vision, prediction, memory
MEMORY AND PREDICTION ARE INTIMATELY LINKED BUT SELDOM INVESTIGATED TOGETHER
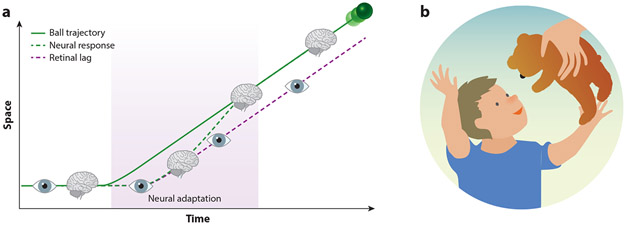
Our ability to predict future visual events is essential to our survival on a multitude of timescales. One important shorter-timescale goal of prediction is to overcome sensory and motor lags so we can fluidly interact with the world. Lags from the retina alone mean that, if we were to use our unprocessed information from photoreceptors in the retina to determine the position of an object moving at 100 kph, then we would be off by more than a meter (Figure 1a). Thankfully, lag compensation starts as early as the retina (Berry et al. 1999) and progresses through to the motor system so that we can accurately capture objects, with our foveas or with our limbs. Another important goal of prediction is to anticipate visual inputs, both to signal inputs that are novel and to indicate when something unexpected happens (Figure 1b). Novelty and prediction error signals are thought to play a crucial role in efficient learning by driving curiosity-driven exploration (Gottlieb & Oudeyer 2018, Ranganath & Rainer 2003). While these examples span a range of timescales and involve different mechanisms and brain areas, they each rely on predictive computations implemented within the visual system.
Figure 1.
Examples of prediction. (a) Catching a ball. Shown is the lag between the estimated position of a fast-moving ball attributed to the latency of processing in the retina (purple dashed) relative to its actual position (green). Lag compensation in both the eye and the brain allows us to accurately estimate ball position. (b) Novelty. Curiosity-based exploration is crucial for efficient learning.
Prediction is about the future (“What will you see next?”) and, at first glance, might have seemingly little to do with the past. However, central to predictive computation is the use of the past to estimate the future. Some have even proposed that our ability to remember exists for the sole purpose of making future predictions about the quality of the options laid out before us (Schacter et al. 2007). While considerable evidence suggests that computations supporting both visual memory and visual prediction are implemented by the visual system, confusion exists around when and how visual memory and visual prediction are related. For example, at higher stages of visual processing such as inferotemporal (IT) cortex, neurons respond with increases in firing rate both when an image has never been seen before (Li et al. 1993, Meyer & Rust 2018, Xiang & Brown 1998), a form of memory, and when viewing a violation of an extensively familiar learned image sequence (Meyer & Olson 2011, Meyer et al. 2014, Schwiedrzik & Freiwald 2017), a form of prediction. How are these and other examples of memory and prediction related to one another? Similarly, insofar as prediction requires memory, we know that the brain employs multiple memory mechanisms and that memories can be integrated with incoming visual information via both feedforward and feedback processing. Do existing examples of prediction and memory fall into model classes, and if so, what do the different members of these classes have in common? Examples of predictive computation in the visual system also span the entire hierarchy, from the retina to IT cortex. Are the mechanisms that support computations at different levels similar or distinct? Finally, what insights can be gained from the more abstract, theoretical descriptions (centered around information capacity and coding efficiency) about the constraints that memory imposes on prediction?
A FRAMEWORK LINKING VISUAL MEMORY AND FUTURE VISUAL PREDICTION
Prediction can mean many different things; we focus in this review on the predictive computation of future visual events (also called forecasting) as opposed to inference of the current visual input under conditions of ambiguity (for reviews, see Bastos et al. 2012, de Lange et al. 2018, Lee & Mumford 2003). The two differ insofar as the introduction of the element of time into future prediction imposes a unique set of computational and mechanistic demands, particularly on memory systems. We also focus on predictability confined to the domain of the external visual world as opposed to predictable visual changes that follow from an organism’s eye or body movement (for a review, see Keller & Mrsic-Flogel 2018).
A Theoretical Framework for Memory and Prediction
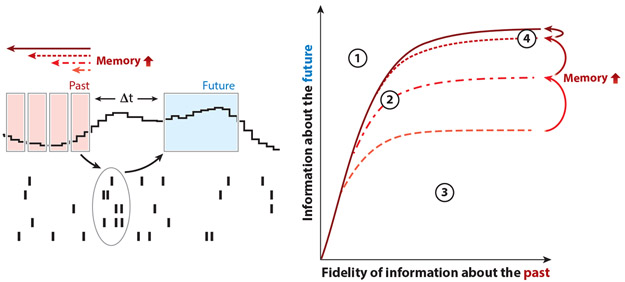
To dissect the role of remembering the past and predicting the future quantitatively, these two demands on the system must be put on equal footing. Before exploring the mechanistic underpinnings of memory, adaptation, or prediction, we first ask what kinds of trade-offs between memory and prediction the brain has to juggle. One of the cleanest normative frameworks for weaving together computational constraints and goals comes from information theory. Specifically, the information bottleneck approach (Bialek et al. 2001, Marzen & DeDeo 2017, Still 2014, Tishby et al. 2000) (Figure 2) allows us to answer questions such as how much the visual system needs to remember about the past to predict the future as well as possible. This question, in essence, describes what matters to the organism—the future visual input—as well as what helps it compute that—the past visual input. The information bottleneck method also specifies how each of the three elements required for creating future visual predictions interact. First, prediction exploits and is bounded by the temporal correlations in the external world. To make a prediction, the brain needs to remember its past and current sensory inputs, up to the relevant correlation times in the environment, and extrapolate those into future predictions. In other words, the future can only be predicted to the degree to which it is predictable. Second, prediction is limited by the amount of information that has been retained about the past stimulus. This can be thought of as the fidelity of memory. Some events in the past are predictive of future events (i.e., are temporally correlated with the future), whereas others are not, and the ability of a system to optimally predict the future requires it to distinguish between these two and preferentially retain predictive information. Third, prediction is constrained by the duration of the memory of the past, in addition to the fidelity of its representation. More explicitly, the timescale along which a system can predict the future is limited by the timescale along which it remembers the past, up to the longest correlation times in the external world, after which longer memory cannot further enhance prediction (Figure 2). While a system can represent future predictions explicitly, it need not necessarily do so; rather, future predictions can be computed implicitly and transformed into signals indicating violations of these predictions that are often referred to as prediction errors or surprise signals in the predictive coding literature (Bastos et al. 2012, Friston 2005, Hosoya et al. 2005, Mlynarski & Hermundstad 2018, Rao & Ballard 1999, Srinivasan et al. 1982). As detailed below, this framework clarifies the role that memory plays in making different types of predictions.
Figure 2.
The information bottleneck technique links optimal prediction and memory. The information bottleneck technique is a method for computing the maximal amount of information that a compressed signal, like the brain’s code for the visual stimulus, can carry about a relevant variable in the original input. Within our prediction framework, that relevant feature is the future stimulus. In the diagram, the input is the past stimulus measured within a window of time preceding the neural response (past), and the relevant variable is the future stimulus (future) starting at some time in the future, Δt. For a particular Δt, we can trace out the maximal amount of information that a neural population could possibly carry about the future stimulus given how much information that population encoded about the past stimulus. There are several notable regions in this information plane spanned by the past and future information (left). First (①), there is an inaccessible region: You cannot know more about the future than about the past; i.e., there is no fortune-telling. The brain’s code can occupy any other region in the plane. Second (②), sitting near the bound means that the neural code contains the maximal amount of predictive information possible for a given level of fidelity of past information. Third (③), neural responses that reflect information about the past but fall away from the bound are not optimized for prediction as a consequence of encoding unpredictable parts of the input stimulus. Fourth (④), the saturation point, reflecting the maximal information that you can glean about the future, is set by the correlation structure in the stimulus. It is important to note that memories of the past can, themselves, be faulty. The x axis in the bottleneck plots reflects precisely that fidelity. For a system with a given memory time window, neural systems can be so noisy that they carry no information about the past stimulus (the origin). Conversely, they could represent the past stimulus with high precision (e.g., with finer and finer stimulus resolution, moving outward along the x axis). Increasing the timescale for memory of the past can improve prediction, up to the limits set by the longest correlation times in the stimulus itself (e.g., dashed versus solid lines). In this example, expanding the length of the past stimulus history saturates after the memory of the past is expanded to four blocks of time in the past.
Novelty as a Violation of Persistence
In the simplest case, visual memory and visual prediction are one and the same. That is, visual familiarity can be envisioned as the prediction that things will persist, or equivalently, that the current state of the visual world will continue. Novelty, in turn, can be envisioned as a violation of that prediction, thereby linking the higher firing rate responses of visual neurons to the concept of surprise or prediction errors. In the theoretical framework described above, memory about the past can be compressed into an estimate of the current state of the system because no expected changes need to be computed.
Predicting Change by Extrapolating Memories of Recent Events
Types of future prediction that are more complex than persistence require extrapolation of a memory of recent events into future predictions. The simplest examples include predictions that visual events will continue to change in the same way that they did in the last sampled epoch. That extrapolated trajectory of the visual scene might be linear for the simplest of models (i.e., a constant rate of change), and it could include learned local associations, as in tasks that involve learning temporal sequences of images. Extrapolation is required for prediction when things change in time, such as when objects move. More complex forms of extrapolation capture and combine longer-timescale and, potentially, higher-order nonlinear correlations between the past and the future.
HOW DOES THE VISUAL SYSTEM COMPUTE FUTURE PREDICTIONS?
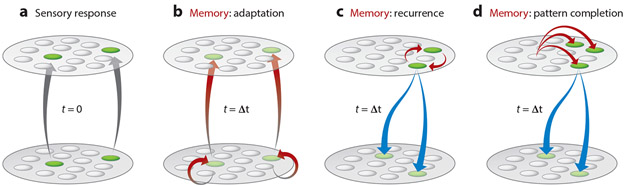
As described above, two distinct forms of information about the past contribute to future predictions: learned information about the temporal structure of the world (where learned can refer to evolution, development, or adult experience) and memories of recent stimulus events that can be extrapolated into the future. A predictive system also requires the machinery to combine these to make future predictions. Where and how are these learning, memory, and prediction components thought to be instantiated by the visual system? In this section, we review the literature, organized by two classes of neural mechanisms. The first (Figure 3b) is an exclusively feedforward architecture that stores memories of recent stimulus history via simple memory mechanisms such as adaptation and gap-junction coupling. This variant has been linked to the computation of novelty in cortex (Bogacz & Brown 2003, Li et al. 1993, Meyer & Rust 2018, Vogels 2016, Xiang & Brown 1998), as well as the computation of nontrivial forms of predictive change in the retina (Berry & Schwartz 2011, Gollisch & Meister 2010, Hosoya et al. 2005, Srinivasan et al. 1982). The second architecture (Figure 3c-d) lies at the heart of some of the most prominent models of predictive coding in cortex (Bastos et al. 2012, Friston 2005, Lee & Mumford 2003, Rao & Ballard 1999) and differs from the first class in two notable ways. First, it incorporates feedback machinery to compute predictions and/or surprise. Second, it incorporates more sophisticated memory mechanisms, such as recurrence and hippocampal pattern completion.
Figure 3.
Computational proposals for prediction and memory. (a) A depiction of the initial, sensory-evoked response (gray arrows and green circles) at the first time point (t = 0). All other panels depict the processing that happens at the next time point (t = Δt) for three different models of prediction. (b) A predictive architecture in which memories of recent stimulus history are stored via adaptation (red arrows), which can take the form of gain adaptation (bottom layer, lighter green circles) or adaptation of the feedforward synapses that connect the layers. In this class of model, connectivity is exclusively feedforward. (c) A predictive architecture in which memories of recent stimulus history are maintained via persistent, recurrent activity (red arrows) and extrapolation of recent events into future predictions happens via feedback (blue arrows). (d) A predictive architecture that extrapolates the current sensory input forward in time using hippocampal pattern completion and integrates this information with incoming sensory signals via feedback (blue arrows).
PREDICTIONS COMPUTED BY FEEDFORWARD PROCESSING AND SIMPLE MEMORY MECHANISMS
Visual Novelty
In the case of persistence, prediction is an automatic consequence of memory insofar as adaptation produces a reduced stimulus-evoked response to the same input when it is repeated, and the enhanced response to novel (or not recently viewed) images can in principle be interpreted by the brain as a prediction error or surprise signal. At higher stages of visual processing, such as IT, these visually specific reductions in firing rate with familiarity can last several minutes or even hours following a single viewing of an image (Li et al. 1993, Meyer & Rust 2018, Xiang & Brown 1998), a phenomenon called repetition suppression. While repetition suppression is found at all stages of visual processing (e.g., the retina to IT), it increases in its magnitude as well as its duration across the visual cortical hierarchy (Kohn 2007, Li et al. 1993, Meyer & Rust 2018, Xiang & Brown 1998, Zhou et al. 2018). Intriguingly, IT repetition suppression acts in a highly stimulus-specific fashion that is much more narrowly tuned for complex images than the stimulus-evoked response (Sawamura et al. 2006). These results imply that cortical repetition suppression could be a form of memory that supports highly specific visual predictions of persistence over nontrivial timescales. Indeed, one recent study evaluated the behavioral relevance of repetition suppression over timescales of minutes and found that it was well aligned with behavioral reports of remembering and forgetting (Meyer & Rust 2018). Together, these results suggest that the abstract and conceptual concept of novelty likely is represented via a relatively well-characterized signal: repetition suppression.
Where does repetition suppression come from? Feedforward, adaptation-like mechanisms clearly contribute to repetition suppression (Vogels 2016) (Figure 3b). The degree to which feedback mechanisms also contribute has been the focus of some debate. For example, while visual novelty is also reflected in structures that lie downstream from visual cortex, such as the hippocampus (Jutras & Buffalo 2010, Sakon & Suzuki 2019, Xiang & Brown 1998), it is unclear whether this reflects memory storage within the hippocampus itself or novelty signals inherited from memory storage in earlier cortical brain areas. In one class of theoretical predictive coding proposals, a component of cortical repetition suppression is in fact hypothesized to reflect higher-level expectations that are integrated via feedback (Friston 2005). This hypothesis has been tested most extensively in experiments where the probability of occurrence of different classes of visual stimuli (e.g., faces, fruits) is manipulated, thereby changing the expectation about what is most likely to appear, under the assumption that expectations are represented beyond visual cortex. Human functional magnetic resonance imaging (fMRI) studies have verified that repetition suppression is indeed stronger for expected events (Summerfield et al. 2008), although the effect appears to be restricted to highly familiar objects such as faces and letters presented in familiar fonts (Grotheer & Kovacs 2014, Kovacs et al. 2013), and it is reported to be reflected in the human but not monkey visual cortex (Kaliukhovich & Vogels 2011, Vinken et al. 2018). Added support of the hypothesis that some component of cortical repetition suppression is fed back from the medial temporal lobe comes from investigation of one human patient with medial temporal lobe damage, in which cortical repetition suppression was reduced relative to controls under task conditions that required attending to novel images (Kim et al. 2020). These results tie into a broader literature that links visual novelty and visual attention with processing in the hippocampus (Aly & Turk-Browne 2016, 2017).
Retinal Reversal Response
The role of feedforward adaptation in shaping predictive persistence, as described above, is conceptually straightforward. More remarkable is the fact that the brain can and does use feedforward mechanisms to compute violations of predictive change or surprise (for reviews, see Gollisch & Meister 2010; Hosoya et al. 2005; Kastner & Baccus 2013, 2014; Srinivasan et al. 1982; Warket al. 2009; Weber & Fairhall 2019; Weber et al. 2019). The reversal response observed both in mouse and salamander retinas is an example of such a surprise signal. In contrast to smooth motion, which activates a temporally progressive pattern of responses across the retina, a steadily moving object that abruptly reverses course activates a volley of synchronized spikes approximately 150 ms after the reversal (Schwartz et al. 2007). These signals could be used to reliably detect the occurrence of stimulus motion direction changes from the activity of small retinal populations (Schwartz et al. 2007). Notably, important properties of the reversal response cannot be captured by simple linear–nonlinear models, including the fact that synchronized spiking across cells results in a fixed latency in the reversal response regardless of the location of the reversal within a cell’s receptive field (Schwartz et al. 2007). However, extensions that incorporate adaptive gain mechanisms can replicate this phenomenon (Chen et al. 2014). In this adaptive cascade model, the synchronized volley of spikes after a motion reversal results from the interaction of nonlinear summation and adaptive gain in the inputs to the retinal output cells (the bipolar cells), as well as adaptive gain in the retinal output cells (the ganglion cells) themselves. Thus, the reversal response incorporates gain-adaptation-mediated memory mechanisms to compute surprise.
Optimal Prediction of Tethered Brownian Motion
Because many things happen in the visual world, and only some of them are causally related to what will happen next, the most sophisticated forms of prediction must discriminate these input sources to create accurate and efficient predictions. A predictive system capable of complex extrapolation can be envisioned as having a model of the correlation structure of the visual world that dissects predictable from nonpredictable inputs to enable this filtering process. Evidence that the retina does this includes a study that incorporated the information bottleneck approach (Figure 2) to demonstrate that the population response of the salamander retina filters away the unpredictable past to retain stimulus information that correlates best with the future (Palmer et al. 2015, Salisbury & Palmer 2016). In these experiments, a dark bar on a gray background moves as if receiving random velocity kicks, while being tethered to the center of the display screen by a restoring force and subject to damping proportional to its velocity. The resultant system is a stochastically driven, damped harmonic oscillator, or equivalently, tethered Brownian motion. The random kicks are unpredictable, while two timescales of predictable motion (drag and the restoring force) interact to produce relatively complex trajectories. The consequence of the dissection of this motion information into its predictable and nonpredictable parts is a retinal population that is optimally predictive of the future position and velocity of the moving bar (Palmer et al. 2015) and instantiates a form of slow-feature analysis (Chalk et al. 2018, Palmer et al. 2015). While the circuit mechanisms supporting this form of optimal prediction in the retina remain unclear, feedback from higher visual areas is excluded by the anatomical isolation of the circuit. Similarly, while processing within the retina itself is largely feedforward, a small fraction of its connectivity involves feedback [including connections from horizontal cells to photoreceptors (Drinnenberg et al. 2018, Jackman et al. 2011, Thoreson et al. 2008), as well as from inhibitory amacrine cells to bipolar cells (Chávez et al. 2010, Dong & Werblin 1998), the latter of which is sometimes called lateral inhibition]. Because no evidence exists to date to suggest links between these feedback connections and the predictive computation described in this section, we default to the simplifying assumption that this processing is feedforward; however, we highlight that this is an open question for future research.
Flash Lag Effect
Another example of a type of predictive change that has been largely linked to feedforward mechanisms is the flash lag effect (FLE): a visual illusion in which a flashed and a moving object that are presented at the same location appear as if they were displaced in a manner consistent with extrapolation of the moving object ahead of the flashed one (Anstis 2007, Eagleman & Sejnowski 2000, Hazelhoff & Wiersma 1924, Kanai et al. 2004, Khoei et al. 2017, Nijhawan 2002, Sheth et al. 2000). Like retinal motion anticipation, the FLE is an example of extrapolation that forecasts an object’s future position according to its current velocity and may support the brain’s ability to compensate for sensory lags in the visual system. Experiments revealed that the flash lag effect can largely be attributed to mechanisms that likely originate in the retina (Nijhawan 2002, Patel et al. 2000, Subramaniyan et al. 2018), although one form of the FLE has been demonstrated to be exclusively binocular and thus must arise via cortical mechanisms (Nieman et al. 2006). New evidence suggests that the more standard, monocular form of the FLE arises from longer response latencies to flashed as compared to moving stimuli (Subramaniyan et al. 2018), adding weight to the argument that the FLE is implemented via feedforward mechanisms in the visual system. Similar to other forms of predictive computation in the retina, the FLE has been hypothesized to arise from retinal adaptation (Sheth et al. 2000). Differential latencies to flashed versus moving stimuli may also have their origins in gap-junction coupling between direction-selective ganglion cells, as is observed in the mouse retina (Trenholm et al. 2013). In this case, the memory arises from the buildup of inputs from a small number of nearby, gap-junction-coupled direction-selective ganglion cells. Finally, while some have posited that more cognitive, feedback mechanisms are responsible for the illusion (Eagleman & Sejnowski 2000, Lopez-Moliner & Linares 2006, Shioiri et al. 2010), mounting experimental evidence points toward predominantly feedforward mechanisms (Patel et al. 2000, Subramaniyan et al. 2018).
In summary, while the computational requirements for predicting change are more extensive than those for predicting novelty insofar as they require extrapolation of recent stimulus events into future predictions, the brain appears to use similar types of mechanisms, including feedforward processing and adaptation (Figure 3b), to compute both novelty (in cortex) and predictive change (in the retina). Beyond the retina, the computation of predictive change has largely been attributed to feedback mechanisms and more sophisticated forms of memory (detailed below). However, the illustration by the retina of the power of feedforward, hierarchical stacks of adaptation for computing predictive change, coupled with the hierarchical organization of visual cortex (e.g., V1 > V2 > V4 > IT), leads one to naturally wonder whether this same mechanism has been vastly underappreciated in computing predictive change in cortex.
PREDICTIONS COMPUTED VIA FEEDBACK AND MORE SOPHISTICATED FORMS OF MEMORY
In contrast to the feedforward models presented above, classic predictive coding proposals posit a role for feedback in computing predictions. The idea at the core of these feedback models is that any predictable output from a neuron should be subtracted so that only deviations from expectations, or surprises, are transmitted forward through the visual hierarchy (Friston 2005, Jehee & Ballard 2009, Lee & Mumford 2003, Rao & Ballard 1999, Srinivasan et al. 1982). In these models, temporal correlations (or predictions) are stored at higher stages and are used to quell predicted responses at earlier stages through feedback inhibition (Heeger 2017; Jehee & Ballard 2009; Kiebel et al. 2008; Lotter et al. 2017; Rao & Ballard 1997, 1999; Wacongne et al. 2012). Predictive coding descriptions that incorporate feedback also typically incorporate memory mechanisms that are more sophisticated than adaptation, including persistent activity maintained by recurrent connectivity (Heeger 2017, Lotter et al. 2017) (Figure 3c) or hippocampal pattern completion (Hindy et al. 2016) (Figure 3d).
The clearest evidence of a role for feedback in computing predictive change includes the adept ability of humans and other animals to learn the statistical regularities of visual image sequences artificially crafted by an experimenter from images that are otherwise unrelated (e.g., image A followed by image B, image C followed by image D, etc.). In tasks like this, the detection of sequence violations requires predictive extrapolation in a manner akin to motion extrapolation in that the current state completely specifies the next state. Following repeated exposure to two-image sequences through passive viewing, primate IT neurons respond with considerably higher firing rates (20–50%) to sequence violations relative to their responses to the intact sequence, and neural signatures of this type of prediction error or surprise signal can be detected for sequence violations set in place hundreds of milliseconds previously (Meyer & Olson 2011, Meyer et al. 2014, Schwiedrzik & Freiwald 2017).
By design, these experimentally configured image sequences must be learned during adulthood, and the evidence suggests that these sequences are stored in the medial temporal lobe structures that are broadly associated with learning. For example, following repeated passive viewing of a sequence of fractal patterns, neurons in a highly visual structure that receives its primary feedforward input from IT, perirhinal cortex, begin to respond with increasing similarity to neighboring images in the temporal sequence (Miyashita 1988). Likewise, representational similarity for temporally related sequence pairs measured by human fMRI increases in perirhinal cortex as well as other medial temporal lobe structures, including parahippocampal cortex and the hippocampus (Schapiro et al. 2012). Moreover, one human patient with bilateral medial temporal lobe damage was demonstrated to be impaired at learning image sequences (Schapiro et al. 2014). Examination of the prediction error signal within visual cortex also supports the notion that at least some component of this signal originates via feedback: Within an early stage of the primate visual face patch hierarchy, violations to learned temporal sequences produce prediction error signals that are initially tuned to changes in low-level visual features such as view but later become tuned for violations of higher-order properties such as identity (Schwiedrzik & Freiwald 2017). This study provides the strongest support to date that predictive computation about the future incorporates feedback.
Together, these results suggest that learned image sequences are stored in the medial temporal lobe and that the computation of prediction errors in visual cortex incorporates feedback from higher brain areas. In the case of learned image sequences, the mechanisms may include a process known as hippocampal pattern completion. The general idea behind pattern completion is that the experience of one component of a memory reactivates a pattern of activation that reflects the entire experience (Cohen & Eichenbaum 1993, Marr 1971) (Figure 3d). Hints that hippocampal pattern completion may also be involved in predictions of learned sequences come from a study in which human subjects were trained to learn sequences of images, actions, and outcomes that took the form of visual images (Hindy et al. 2016). The sequences could be decoded from fMRI patterns in the hippocampus but not those in early visual cortex, and hippocampal activity early in a trial was predictive of information in visual cortex at a later time in the trial. These results are consistent with the notion that sequence information is likely fed back from the hippocampus to visual cortex.
In summary, several lines of evidence support a role for feedback in computing one type of predictive change in cortex: adult learned image sequences. In contrast to computational models that store memories of recent stimulus history via recurrent connectivity and persistence (Figure 3c), there are indications that, in this case, the memory process may be pattern completion in the hippocampus (Figure 3d). Thus far, investigations of predictive change in the visual system have largely been limited to scenarios in which prediction happens over the course of a few hundreds of milliseconds and where one state completely specifies the next. An important focus of future research will be to determine the cortical mechanisms involved in visual prediction along longer timescales and with the introduction of the more complex, probabilistic dependencies found in the natural world.
WHAT PRINCIPLES ORGANIZE PREDICTIVE COMPUTATION IN THE VISUAL SYSTEM?
Throughout the examples above, it is clear that prediction in the visual system cannot be organized neatly according to obvious grouping principles such as brain area or prediction type (Table 1). The evidence against grouping by brain area includes a central role for feedforward, adaptation mechanisms in both the retina and cortex. The evidence against organizing by prediction type includes the fact that the brain uses similar underlying neural mechanisms (adaptation and feedforward processing) to support multiple types of prediction, including novelty and, in the retina, sophisticated forms of predictive change. However, there are some indications of the principles that may be in play: All of the examples presented above can be parsed into universal predictions that follow from natural image statistics (persistence, motion extrapolation, the retinal reversal response, the optimal prediction in the retina to tethered Brownian motion, and the flash-lag effect) versus individual predictions that follow from adult experience (the probability of familiar object occurrence and configured image sequences). Others have also pointed out the conceptual distinction between perceptual versus learned or mnemonic expectations (Hawkins & Blakeslee 2004, Hindy et al. 2016, Koster-Hale & Saxe 2013). Without exception, when applied to the examples above, this parsing maps to differences in neural mechanism (Table 1), with the former supported by simple, adaptation memory mechanisms and feedforward architectures (Figure 3b) and the latter supported by memories that are stored at higher stages and fed back to visual cortex (Figure 3c-d; see also the Future Issues).
Table 1.
Examples of visual prediction
| Example | Type of prediction |
Brain area | How input correlations are learned |
How memories of recent history are stored |
Extrapolation mechanism |
|---|---|---|---|---|---|
| Examples that are thought to rely on feedforward processing and simple memory mechanisms | |||||
| Novelty (Kaliukhovich & Vogels 2011, Li et al. 1993, Meyer & Rust 2018, Xiang & Brown 1998) | Predictive persistence | Retina and cortex | Evolution and/or development | Adaptation | Feedforward |
| Reversal response (Chen et al. 2014, Schwartz et al. 2007) | Predictive change | Retina | Evolution and/or development | Adaptation | Feedforward |
| Tethered Brownian motion (Palmer et al. 2015, Salisbury & Palmer 2016) | Predictive change | Retina | Evolution and/or development | Adaptation | Feedforward |
| Flash lag effect (Anstis 2007, Eagleman & Sejnowski 2000, Hazelhoff & Wiersma 1924, Khoei et al. 2017, Lopez-Moliner & Linares 2006, Nieman et al. 2006, Nijhawan 2002, Patel et al. 2000, Sheth et al. 2000, Shioiri et al. 2010, Subramaniyan et al. 2018, Trenholm et al. 2013) | Predictive change | Retina and V1 | Evolution and/or development | Adaptation, gap-junction coupling | Feedforward |
| Examples that are thought to involve feedback processing and more sophisticated forms of memory | |||||
| Novelty with expectation (Grotheer & Kovacs 2014, Kovacs et al. 2013, Summerfield et al. 2008) | Predictive persistence | Human visual cortex | Learning in adulthood | Unknown | Feedback |
| Configured image sequences (Hindy et al. 2016, Meyer & Olson 2011, Meyer et al. 2014, Schwiedrzik & Freiwald 2017) | Predictive change | High-level visual cortex (e.g., IT) | Learning in adulthood | Hippocampal pattern completion | Feedback |
The two classes of examples in this table cannot be parsed by the type of prediction or brain area, but they do align with the distinction between the times when the input correlations are learned (during evolution and development versus in adulthood, respectively). Abbreviation: IT, inferotemporal.
FUTURE ISSUES.
What principles organize predictive computation in the visual system? There are indications that predictive mechanisms may map to universal predictions that follow from natural image statistics versus individual predictions that follow from adult experience (Table 1), but to determine whether this or some other principle organizes predictive computation, more examples are needed.
Is the visual system efficiently encoding the past to make future predictions? New experiments are needed to test this thoroughly in a wider variety of organisms and at different processing stages in the brain. To answer this question in any visual area, one has to present stimuli that have both predictable and nonpredictable components. Only by presenting the brain with a mixture of information types can you really know whether a neural ensemble specifically encodes more about the future input than it does about potentially nonpredictive features, like object texture.
What does the brain do with the increased firing rate responses implicated in both novelty and surprise? Whether all types of prediction (novelty, sequence violations, and other forms of surprise) are extracted from higher stages of the visual system via a common decoding scheme that alerts the brain whenever something unpredicted happens, as opposed to separate channels for each type of prediction, remains unknown. Similarly, future investigations will be needed to determine the downstream brain areas that decode this information, as well as exactly what higher cognitive processes are triggered during fast, efficient visual prediction.
WHAT DOES THE BRAIN DO WITH THE INCREASED FIRING RATE RESPONSES IMPLICATED IN BOTH NOVELTY AND SURPRISE?
The evidence presented above suggests that, while responses in IT to novel images and image sequence violations are computed via markedly different mechanisms, they produce qualitatively similar firing rate increases (relative to familiar images and predictable sequences, respectively). What role might these firing rate increases play in activating processes downstream? In the case of novelty, the decreases in firing rate that follow from stimulus repetition have been hypothesized to be the memory signal that drives explicit behavioral reports of remembering whether an image has been viewed before (Bogacz & Brown 2003, Desimone 1996, Li et al. 1993, Xiang & Brown 1998), where the mapping of IT neural signals onto behavioral reports can be accomplished via variants of a total-spike-count, linear-decoding scheme (Meyer & Rust 2018). This idea can be generalized to one in which the magnitude of the IT population response reflects not only image familiarity, but also more broadly the predictability of the incoming visual input, thereby triggering downstream processes by any type of prediction error. At higher stages of visual processing, the enhanced response to novel and/or unexpected visual input may be used to drive curiosity-based exploration for efficient learning (Gottlieb & Oudeyer 2018, Ranganath & Rainer 2003) in a manner analogous to how visual novelty has been employed in recent machine learning approaches (e.g., Bellemare et al. 2016, Houthooft et al. 2016, Pathak et al. 2017, Stadie et al. 2015). These enhanced responses may also trigger changes to downstream cognitive processes, including internal models of the current external context (Gold & Stocker 2017; see also the Future Issues).
CONCLUDING REMARKS
While memory and future prediction are intimately bound together, they have classically been studied in isolation. In this review, we highlight emerging work describing how they are connected, ranging from new theoretical insights to their shared neural mechanisms. In comparison to our understanding of how the brain determines what we are looking at right now, our understanding of how our brains remember the past and predict the future is still in its infancy. At the same time, there is excitement in the field centered around collaborative interactions between theory and experiment and modern approaches that allow for the unprecedented monitoring and manipulation of neural activity in organisms performing visual memory and prediction tasks. By merging these techniques to examine visual prediction and memory in concert, we can discover new organizing principles in neural coding that bridge brain areas and behavioral contexts, from the retina to higher-order cortical areas and from short- to longer-term glimpses into the future.
SUMMARY POINTS.
New developments in information theory, and specifically the information bottleneck method (Figure 2), provide both a conceptual framework and a quantitative account of how visual memory constrains the ability to predict future visual events. Recent work demonstrates how the information bottleneck method can be used to define the maximal amount of future visual information that a system can predict and compare a system (like the retina) against this benchmark to evaluate its optimality (Palmer et al. 2015, Salisbury & Palmer 2016).
One class of models associated with future visual predictive computation relies on an exclusively feedforward architecture that stores memories of recent stimulus history via simple memory mechanisms such as adaptation and gap-junction coupling. These mechanisms have been linked to the computation of novelty in cortex (Bogacz & Brown 2003, Li et al. 1993, Meyer & Rust 2018, Vogels 2016, Xiang & Brown 1998), as well as the computation of nontrivial forms of predictive change in the retina (Berry & Schwartz 2011, Gollisch & Meister 2010, Hosoya et al. 2005, Srinivasan et al. 1982). Recent work supports the behavioral relevance of putative visual novelty and memory signals, reflected as repetition suppression in high-level visual cortex (Meyer & Rust 2018).
A second class of models of future visual predictive computation incorporates feedback and lies at the heart of some of the most prominent models of predictive coding in cortex (Bastos et al. 2012, Friston 2005, Lee & Mumford 2003, Rao & Ballard 1999). Recent work demonstrates empirical support of the feedback proposal (Schwiedrzik & Freiwald 2017), as well as implicating memory mechanisms in the medial temporal lobe (Schapiro et al. 2012, 2014), including hippocampal pattern completion (Hindy et al. 2016).
The principles that map the three predictive components (learned temporal structure of the world, memories of recent events, and future extrapolation) onto these two classes of models cannot be organized by obvious grouping principles such as brain area or prediction type (Table 1).
ACKNOWLEDGMENTS
Julia Kuhl contributed Figures 1 and 3. This work was supported by the National Eye Institute of the National Institutes of Health (award R01EY020851 to N.C.R. and R01EB026943 to S.E.P.), the National Science Foundation (CAREER award 1265480 to N.C.R. and CAREER award 1652617 to S.E.P.), and the Simons Foundation (Simons Collaboration on the Global Brain award 543033 to N.C.R.). This work was also supported in part by the National Science Foundation, through the Center for the Physics of Biological Function (PHY-1734030).
CITATION DIVERSITY STATEMENT
Recent work in several fields of science has identified a bias in citation practices such that papers from women and other minorities are under-cited relative to the number of such papers in the field (Caplar et al. 2017, Dworkin et al. 2020, Maliniak et al. 2013). In this review, we sought to proactively consider choosing references that reflect the diversity of the field in thought, form of contribution, gender, and other factors (Zurn et al. 2020). To quantify the gender diversity of our citations, we obtained the predicted gender of the first and last author of each reference by using databases that store the probability of a name being carried by a man or a woman (Zhou et al. 2020). By this measure (after excluding self-citations to the first and last authors of this review), our references contain 5.7% woman(first)/woman(last), 6.8% man/woman, 13.6% woman/man and 73.9% man/man. Expected proportions estimated from five top neuroscience journals, as reported by Dworkin et al. (2020), are 6.7% woman/woman, 9.4% man/woman, 25.5% woman/man, and 58.4% man/man; however, we note that proportions are expected to be lower in computational neuroscience. We look forward to future work that could help us to better understand how to support equitable practices in science.
Footnotes
DISCLOSURE STATEMENT
The authors are not aware of any affiliations, memberships, funding, or financial holdings that might be perceived as affecting the objectivity of this review.
LITERATURE CITED
- Aly M, Turk-Browne NB. 2016. Attention promotes episodic encoding by stabilizing hippocampal representations. PNAS 113:E420–29 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aly M, Turk-Browne NB. 2017. How hippocampal memory shapes, and is shaped by, attention. In The Hippocampus from Cells to Systems: Structure, Connectivity, and Functional Contributions to Memory and Flexible Cognition, ed. Hannula DE, Duff MC, pp. 369–403. Berlin: Springer [Google Scholar]
- Anstis S 2007. The flash-lag effect during illusory chopstick rotation. Perception 36:1043–48 [DOI] [PubMed] [Google Scholar]
- Bastos AM, Usrey WM, Adams RA, Mangun GR, Fries P, Friston KJ. 2012. Canonical microcircuits for predictive coding. Neuron 76:695–711 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bellemare MG, Srinivasan S, Ostrovski G, Schaul T, Saxton D, Munos R. 2016. Unifying count-based exploration and intrinsic motivation. In Advances in Neural Information Processing Systems 29 (NIPS 2016), ed. D Lee, Sugiyama M, Luxburg U, Guyon I, Garnett R, pp. 1471–79. N.p.: NeurIPS [Google Scholar]
- Berry MJ II, Brivanlou IH, Jordan TA, Meister M. 1999. Anticipation of moving stimuli by the retina. Nature 398:334–38 [DOI] [PubMed] [Google Scholar]
- Berry MJ II, Schwartz G. 2011. The retina as embodying predictions about the visual world. In Predictions in the Brain: Using Our Past to Generate a Future, ed. Bar M, pp. 295–310. Oxford, UK: Oxford Univ. Press [Google Scholar]
- Bialek W, Nemenman I, Tishby N. 2001. Predictability, complexity, and learning. Neural Comput. 13:2409–63 [DOI] [PubMed] [Google Scholar]
- Bogacz R, Brown MW. 2003. Comparison of computational models of familiarity discrimination in the perirhinal cortex. Hippocampus 13:494–524 [DOI] [PubMed] [Google Scholar]
- Caplar N, Tacchella S, Birrer S. 2017. Quantitative evaluation of gender bias in astronomical publications from citation counts. Nat. Astron 1:0141 [Google Scholar]
- Chalk M, Marre O, Tkačik G. 2018. Toward a unified theory of efficient, predictive, and sparse coding. PNAS 115:186–91 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chávez AE, Grimes WN, Diamond JS. 2010. Mechanisms underlying lateral GABAergic feedback onto rod bipolar cells in rat retina. J. Neurosci 30:2330–39 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen EY, Chou J, Park J, Schwartz G, Berry MJ. 2014. The neural circuit mechanisms underlying the retinal response to motion reversal. J. Neurosci 34:15557–75 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen NJ, Eichenbaum H. 1993. Memory, Amnesia, and the Hippocampal System. Cambridge, MA: MIT Press [Google Scholar]
- de Lange FP, Heilbron M, Kok P. 2018. How do expectations shape perception? Trends Cogn. Sci 22:764–79 [DOI] [PubMed] [Google Scholar]
- Desimone R 1996. Neural mechanisms for visual memory and their role in attention. PNAS 93:13494–99 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong C-J, Werblin FS. 1998. Temporal contrast enhancement via GABAC feedback at bipolar terminals in the tiger salamander retina. J. Neurophysiol 79:2171–80 [DOI] [PubMed] [Google Scholar]
- Drinnenberg A, Franke F, Morikawa RK, Jüttner J, Hillier D, et al. 2018. How diverse retinal functions arise from feedback at the first visual synapse. Neuron 99:117–34.e11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dworkin JD, Linn KA, Teich EG, Zurn P, Shinohara RT, Bassett DS. 2020. The extent and drivers of gender imbalance in neuroscience reference lists. Nat. Neurosci 23:918–26 [DOI] [PubMed] [Google Scholar]
- Eagleman DM, Sejnowski TJ. 2000. Motion integration and postdiction in visual awareness. Science 287:2036–38. [DOI] [PubMed] [Google Scholar]
- Friston K 2005. A theory of cortical responses. Philos. Trans. R. Soc. Lond. B 360:815–36 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gold JI, Stocker AA. 2017. Visual decision-making in an uncertain and dynamic world. Annu. Rev. Vis. Sci 3:227–50 [DOI] [PubMed] [Google Scholar]
- Gollisch T, Meister M. 2010. Eye smarter than scientists believed: neural computations in circuits of the retina. Neuron 65:150–64 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gottlieb J, Oudeyer PY. 2018. Towards a neuroscience of active sampling and curiosity. Nat. Rev. Neurosci 19:758–70 [DOI] [PubMed] [Google Scholar]
- Grotheer M, Kovacs G. 2014. Repetition probability effects depend on prior experiences. J. Neurosci 34:6640–46 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hawkins J, Blakeslee S. 2004. On Intelligence. New York: Times Books [Google Scholar]
- Hazelhoff FF, Wiersma H. 1924. Die Wahrnehmungszeit. [The sensation time.] Z. Psychol 96:171–88 [Google Scholar]
- Heeger DJ. 2017. Theory of cortical function. PNAS 114:1773–82 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hindy NC, Ng FY, Turk-Browne NB. 2016. Linking pattern completion in the hippocampus to predictive coding in visual cortex. Nat. Neurosci 19:665–67 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hosoya T, Baccus SA, Meister M. 2005. Dynamic predictive coding by the retina. Nature 436:71–77 [DOI] [PubMed] [Google Scholar]
- Houthooft R, Chen X, Duan Y, Schulman J, De Turck F, Abbeel P. 2016. VIME: variational information maximizing exploration. In Advances in Neural Information Processing Systems 29 (NIPS 2016), ed. Lee D, Sugiyama M, Luxburg U, Guyon I, Garnett R, pp. 1109–17. N.p.: NeurIPS [Google Scholar]
- Jackman SL, Babai N, Chambers JJ, Thoreson WB, Kramer RH. 2011. A positive feedback synapse from retinal horizontal cells to cone photoreceptors. PLOS Biol. 9:e1001057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jehee JF, Ballard DH. 2009. Predictive feedback can account for biphasic responses in the lateral geniculate nucleus. PLOS Comput. Biol 5:e1000373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jutras MJ, Buffalo EA. 2010. Recognition memory signals in the macaque hippocampus. PNAS 107:401–6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaliukhovich DA, Vogels R. 2011. Stimulus repetition probability does not affect repetition suppression in macaque inferior temporal cortex. Cereb. Cortex 21:1547–58 [DOI] [PubMed] [Google Scholar]
- Kanai R, Sheth BR, Shimojo S. 2004. Stopping the motion and sleuthing the flash-lag effect: spatial uncertainty is the key to perceptual mislocalization. Vis. Res 44:2605–19 [DOI] [PubMed] [Google Scholar]
- Kastner DB, Baccus SA. 2013. Spatial segregation of adaptation and predictive sensitization in retinal ganglion cells. Neuron 79:541–54 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kastner DB, Baccus SA. 2014. Insights from the retina into the diverse and general computations of adaptation, detection, and prediction. Curr. Opin. Neurobiol 25:63–69 [DOI] [PubMed] [Google Scholar]
- Keller GB, Mrsic-Flogel TD. 2018. Predictive processing: a canonical cortical computation. Neuron 100:424–35 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khoei MA, Masson GS, Perrinet LU. 2017. The flash-lag effect as a motion-based predictive shift. PLOS Comput. Biol 13:e1005068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiebel SJ, Daunizeau J, Friston KJ. 2008. A hierarchy of time-scales and the brain. PLOS Comput. Biol 4:e1000209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim JG, Gregory E, Landau B, McCloskey M, Turk-Browne NB, Kastner S. 2020. Functions of ventral visual cortex after bilateral medial temporal lobe damage. Prog. Neurobiol 191:101819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohn A 2007. Visual adaptation: physiology, mechanisms, and functional benefits. J. Neurophysiol 97:3155–64 [DOI] [PubMed] [Google Scholar]
- Koster-Hale J, Saxe R. 2013. Theory of mind: a neural prediction problem. Neuron 79:836–48 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kovacs G, Kaiser D, Kaliukhovich DA, Vidnyanszky Z, Vogels R. 2013. Repetition probability does not affect fMRI repetition suppression for objects. J. Neurosci 33:9805–12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee TS, Mumford D. 2003.Hierarchical Bayesian inference in the visual cortex. J. Opt. Soc. Am. A 20:1434–48 [DOI] [PubMed] [Google Scholar]
- Li L, Miller EK, Desimone R. 1993. The representation of stimulus familiarity in anterior inferior temporal cortex. J. Neurophysiol 69:1918–29 [DOI] [PubMed] [Google Scholar]
- Lopez-Moliner J, Linares D. 2006. The flash-lag effect is reduced when the flash is perceived as a sensory consequence of our action. Vis. Res 46:2122–29 [DOI] [PubMed] [Google Scholar]
- Lotter W, Kreiman G, Cox DD. 2017. Deep predictive coding networks for video prediction and unsupervised learning. Paper presented at 5th International Conference on Learning Representations (ICLR), Toulon, France, Apr. 24–26 [Google Scholar]
- Maliniak D, Powers R,Walter BF. 2013.The gender citation gap in international relations. Int. Organ 67:889–922 [Google Scholar]
- Marr D 1971. Simple memory: a theory for archicortex. Philos. Trans. R. Soc. Lond. B 262:23–81 [DOI] [PubMed] [Google Scholar]
- Marzen SE, DeDeo S. 2017. The evolution of lossy compression. J. R. Soc. Interface 14:0166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer T, Olson CR. 2011. Statistical learning of visual transitions in monkey inferotemporal cortex. PNAS 108:19401–6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer T, Ramachandran S, Olson CR. 2014. Statistical learning of serial visual transitions by neurons in monkey inferotemporal cortex. J. Neurosci 34:9332–37 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer T, Rust NC. 2018. Single-exposure visual memory judgments are reflected in inferotemporal cortex. eLife 7:e32259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miyashita Y 1988. Neuronal correlate of visual associative long-term memory in the primate temporal cortex. Nature 335:817–20 [DOI] [PubMed] [Google Scholar]
- Mlynarski WF, Hermundstad AM. 2018. Adaptive coding for dynamic sensory inference. eLife 7:e32055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nieman D, Nijhawan R, Khurana B, Shimojo S. 2006. Cyclopean flash-lag illusion. Vis. Res 46:3909–14 [DOI] [PubMed] [Google Scholar]
- Nijhawan R 2002. Neural delays, visual motion and the flash-lag effect. Trends Cogn. Sci 6:387–93 [DOI] [PubMed] [Google Scholar]
- Palmer SE, Marre O, Berry MJ II, Bialek W 2015. Predictive information in a sensory population. PNAS 112:6908–13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patel SS, Ogmen H, Bedell HE, Sampath V. 2000. Flash-lag effect: differential latency, not postdiction. Science 290:1051. [DOI] [PubMed] [Google Scholar]
- Pathak D, Agrawal P, Efros AA, Darrell T. 2017. Curiosity-driven exploration by self-supervised prediction. In ICML ’7: Proceedings of the 34th International Conference on Machine Learning, pp. 2778–87. NewYork: Assoc. Comput. Mach. [Google Scholar]
- Ranganath C, Rainer G. 2003. Neural mechanisms for detecting and remembering novel events. Nat. Rev. Neurosci 4:193–202 [DOI] [PubMed] [Google Scholar]
- Rao RP, Ballard DH. 1997. Dynamic model of visual recognition predicts neural response properties in the visual cortex. Neural Comput. 9:721–63 [DOI] [PubMed] [Google Scholar]
- Rao RP, Ballard DH. 1999. Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nat. Neurosci 2:79–87 [DOI] [PubMed] [Google Scholar]
- Sakon JJ, Suzuki WA. 2019. A neural signature of pattern separation in the monkey hippocampus. PNAS 116:9634–43 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salisbury JM, Palmer SE. 2016. Optimal prediction in the retina and natural motion statistics. J. Stat. Phys 162:1309–23 [Google Scholar]
- Sawamura H, Orban GA, Vogels R. 2006. Selectivity of neuronal adaptation does not match response selectivity: a single-cell study of the fMRI adaptation paradigm. Neuron 49:307–18 [DOI] [PubMed] [Google Scholar]
- Schacter DL, Addis DR, Buckner RL. 2007. Remembering the past to imagine the future: the prospective brain. Nat. Rev. Neurosci 8:657–61 [DOI] [PubMed] [Google Scholar]
- Schapiro AC, Gregory E, Landau B, McCloskey M, Turk-Browne NB. 2014. The necessity of the medial temporal lobe for statistical learning. J. Cogn. Neurosci 26:1736–47 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schapiro AC, Kustner LV, Turk-Browne NB. 2012. Shaping of object representations in the human medial temporal lobe based on temporal regularities. Curr. Biol 22:1622–27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz G, Taylor S, Fisher C, Harris R, Berry MJ II. 2007. Synchronized firing among retinal ganglion cells signals motion reversal. Neuron 55:958–69 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwiedrzik CM, Freiwald WA. 2017. High-level prediction signals in a low-level area of the macaque face-processing hierarchy. Neuron 96:89–97.e4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheth BR, Nijhawan R, Shimojo S. 2000. Changing objects lead briefly flashed ones. Nat. Neurosci 3:489–95 [DOI] [PubMed] [Google Scholar]
- Shioiri S, Yamamoto K, Oshida H, Matsubara K, Yaguchi H. 2010. Measuring attention using flash-lag effect. J. Vis 10:10. [DOI] [PubMed] [Google Scholar]
- Srinivasan MV, Laughlin SB, Dubs A. 1982. Predictive coding: a fresh view of inhibition in the retina. Proc. R. Soc. Lond. B 216:427–59 [DOI] [PubMed] [Google Scholar]
- Stadie BC, Levine S, Abbeel P. 2015. Incentivizing exploration in reinforcement learning with deep predictive models. arXiv:1507.00814 [cs.AI] [Google Scholar]
- Still S 2014. Information bottleneck approach to predictive inference. Entropy 16:968–89 [Google Scholar]
- Subramaniyan M, Ecker AS, Patel SS, Cotton RJ, Bethge M,et al. 2018. Faster processing of moving compared with flashed bars in awake macaque V1 provides a neural correlate of the flash lag illusion. J. Neurophysiol 120:2430–52 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Summerfield C, Trittschuh EH, Monti JM, Mesulam MM, Egner T. 2008. Neural repetition suppression reflects fulfilled perceptual expectations. Nat. Neurosci 11:1004–6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thoreson WB, Babai N, Bartoletti TM. 2008. Feedback from horizontal cells to rod photoreceptors in vertebrate retina. J. Neurosci 28:5691–95 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tishby N, Pereira FC, Bialek W. 2000. The information bottleneck method. arXiv:physics/0004057 [physics.data-an] [Google Scholar]
- Trenholm S, Schwab DJ, Balasubramanian V, Awatramani GB. 2013. Lag normalization in an electrically coupled neural network. Nat. Neurosci 16:154–56 [DOI] [PubMed] [Google Scholar]
- Vinken K, Op de Beeck HP, Vogels R. 2018. Face repetition probability does not affect repetition suppression in macaque inferotemporal cortex. J. Neurosci 38:7492–504 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogels R 2016. Sources of adaptation of inferior temporal cortical responses. Cortex 80:185–95 [DOI] [PubMed] [Google Scholar]
- Wacongne C, Changeux J-P, Dehaene S. 2012. A neuronal model of predictive coding accounting for the mismatch negativity. J. Neurosci 32:3665–78 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wark B, Fairhall A, Rieke F. 2009. Timescales of inference in visual adaptation. Neuron 61:750–61 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber AI, Fairhall AL. 2019. The role of adaptation in neural coding. Curr. Opin. Neurobiol 58:135–40 [DOI] [PubMed] [Google Scholar]
- Weber AI, Krishnamurthy K, Fairhall AL. 2019. Coding principles in adaptation. Annu. Rev. Vis. Sci 5:427–49 [DOI] [PubMed] [Google Scholar]
- Xiang JZ, Brown MW. 1998. Differential neuronal encoding of novelty, familiarity and recency in regions of the anterior temporal lobe. Neuropharmacology 37:657–76 [DOI] [PubMed] [Google Scholar]
- Zhou D, Cornblath EJ, Stiso J, Teich EG, Dworkin JD. 2020. Gender diversity statement and code notebook v1.0. Software. https://zenodo.org/record/3672110#.YAHAV-hKhjV [Google Scholar]
- Zhou J, Benson NC, Kay KN, Winawer J. 2018. Compressive temporal summation in human visual cortex. J. Neurosci 38:691–709 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zurn P, Bassett DS, Rust NC. 2020. The Citation Diversity Statement: a practice of transparency, a way of life. Trends Cogn. Sci 24:669–72 [DOI] [PubMed] [Google Scholar]