Abstract
The brain shows a topographical hierarchy along the lines of lower- and higher-order networks. The exact temporal dynamics characterization of this lower-higher-order topography at rest and its impact on task states remains unclear, though. Using 2 functional magnetic resonance imaging data sets, we investigate lower- and higher-order networks in terms of the signal compressibility, operationalized by Lempel–Ziv complexity (LZC). As we assume that this degree of complexity is related to the slow–fast frequency balance, we also compute the median frequency (MF), an estimation of frequency distribution. We demonstrate (i) topographical differences at rest between higher- and lower-order networks, showing lower LZC and MF in the former; (ii) task-related and task-specific changes in LZC and MF in both lower- and higher-order networks; (iii) hierarchical relationship between LZC and MF, as MF at rest correlates with LZC rest–task change along the lines of lower- and higher-order networks; and (iv) causal and nonlinear relation between LZC at rest and LZC during task, with MF at rest acting as mediator. Together, results show that the topographical hierarchy of lower- and higher-order networks converges with their temporal hierarchy, with these neural dynamics at rest shaping their range of complexity during task states in a nonlinear way.
Keywords: core-periphery organization, lower-higher-order network topography, neural complexity, slow–fast frequency balance, spatiotemporal neuroscience
Introduction
The brain exhibits an elaborate intrinsic topography along the lines of lower- and higher-order networks. Lower-order networks (i.e. sensory networks) are distinguished from higher-order networks (i.e. default-mode network [DMN], executive network, and others), with both lower- and higher-order networks standing at opposite ends of the spatial hierarchy (Cole et al. 2013, 2016; Margulies et al. 2016; Huntenburg et al. 2018). Recently, studies demonstrate that such a spatial hierarchy converges with a corresponding temporal hierarchy of intrinsic neural timescales (INTs) (Cole et al. 2014, 2016; Margulies et al. 2016; Huntenburg et al. 2018; Murphy et al. 2018; Gutierrez-Barragan et al. 2019; Wang et al. 2019; Ito et al. 2020; Raut et al. 2020; Golesorkhi, Gomez-Pilar, Tumati, et al. 2021a). This leaves open whether this hierarchy is featured by a particular temporal dynamic, like the slow–fast frequency balance in their power spectral density (PSD). The main goal of our paper is to address this gap in our knowledge by focusing on the intrinsic temporal dynamics of the various lower- and higher-order regions/networks and how that shapes their information processing during rest and task states.
The temporal dynamic of a region’s neural activity is related to information processing as manifest in the regularity/irregularity balance of the signal (Akdemir Akar et al. 2015). This signal randomness or degree of signal compressibility can well be measured by Lempel–Ziv complexity (LZC) (Abásolo et al. 2006; Akdemir Akar et al. 2015; Bai et al. 2015; Ibáñez-Molina et al. 2015). LZC measures the number of distinct patterns in a binary sequence, namely the degree incompressibility of a signal (Lempel and Ziv 1976; Aboy et al. 2006; Boly et al. 2015). It reflects the number of bits required to reconstruct a signal (Lempel and Ziv 1976) (see the validity of LZC in functional magnetic resonance imaging [fMRI]; Deshpande et al. 2006; Schabus et al. 2007; Boly et al. 2015; Hudetz et al. 2016; Varley et al. 2020), as well as in other imaging modalities including MEG, EEG, and spike train analysis (Szczepański et al. 2003; Abasolo et al. 2007; Gómez et al. 2009; Fernández et al. 2011; Luo et al. 2013; Bachmann et al. 2018; Baria et al. 2018; Ibáñez-Molina et al. 2018; Mateos et al. 2018). Low LZC values indicate high degree of signal compressibility entailing high signal regularity, i.e. low compressibility, as one would, for instance, expect when slower frequencies are predominant. Conversely, high LZC values reflect low degrees of signal compression, indexing low signal regularity which may predominate in regions with faster frequencies. This relationship, although expected, is far from obvious, since high-frequency oscillations in a regular way, such as a sine wave, should give low LZC values.
In view of this hypothesized relationship and due to the fact that temporal dynamics is manifest in the PSD, we are interested on computing the median frequency (MF) (Schwilden et al. 1985; Schwender et al. 1996; McDonald et al. 1999; Bachiller et al. 2015; Verrusio et al. 2015; Huang et al. 2018). MF summarizes the spectral distribution of a given signal, providing a measure of the frequency balance which, in the case of fMRI, covers the frequency range of 0.01–0.1 Hz. In essence, MF is the frequency at which the power spectrum is divided into 2 regions with equal area (Poza et al. 2007). In other words, it estimates the “center of mass” of the spectral distribution, with the advantage of being little affected by random noise (Chiang et al. 2018). Therefore, lower values in MF indicate a higher dominance of the slower frequencies in the power spectrum, while higher MF values are related to a higher dominance of the faster frequencies (Schwilden et al. 1985; Schwender et al. 1996; McDonald et al. 1999; Bachiller et al. 2015; Verrusio et al. 2015). Given that MF (or a related measure like mean frequency) has been successfully employed in fMRI (Huang et al. 2018), it is ideally suited to measure the temporal dynamics of lower- and higher-order networks.
Together, LZC and MF allow insight into the intraregional temporal dynamics and complexity of information, i.e. signal compressibility of lower- and higher-order networks (see Fig. 1 for general overview), which are key in shaping the even more basic topography of core (higher-order networks) and periphery (lower-order networks (Margulies et al. 2016, Golesorkhi, Gomez-Pilar, Tumati, et al. 2021a; Golesorkhi, Gomez-Pilar, Zilio, et al. 2021b; Wolff et al. 2022). For that purpose, we rely on the 7T fMRI data set of the Human Connectome Project (HCP), while using the 3T fMRI HCP for replication (see Supplementary Material).
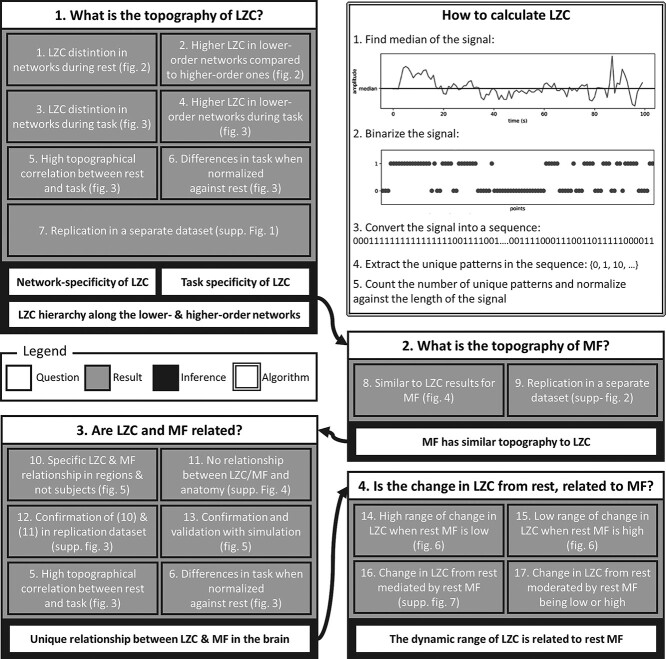
Fig. 1.
Schema of the paper. Each box is one of the questions being investigated in this work. Each box is divided into 3 parts: a question (white), several analyses (grey), and one or more inferences (black). The white box contains an overall view of how LZC is calculated.
Specific aims and hypotheses
The first specific aim is to investigate temporal dynamics of lower- and higher-order networks in the resting state by measuring signal compressibility (LZC) and frequency balance (MF). We pursue the following hypothesis. As most likely related to their continuous exposure to high loads of chaotic external information input (Chaudhuri et al. 2015; Gollo et al. 2015, 2017; Margulies et al. 2016; Huntenburg et al. 2018), lower-order regions like sensory networks and multimodal sensory regions may show high LZC, reflecting higher signal compressibility, as well as higher MF, indexing a shift towards faster frequencies. On the contrary, higher-order regions/networks, i.e. DMN, frontoparietal network (FPN), language network, and dorsal attention network, do not receive such direct information input, but only indirectly through its “filtering” by the lower-order networks (Gollo et al. 2015, 2017; Margulies et al. 2016; Golesorkhi, Gomez-Pilar, Zilio, et al. 2021b). For that reason, we expect lower LZC, and slow-frequency dominated PSD, i.e. low MF, in the higher-order networks.
The second specific aim is to investigate changes in LZC and MF during different task states including a movie and a retinotopy task (as provided by 7T HCP). Since task states produce disturbances in the neuronal signal in the resting state (Luo et al. 2013; Boly et al. 2015; Baria et al. 2018; Pappas et al. 2019; Varley et al. 2020), we expect an increase in signal compressibility, i.e. higher LZC, along with a shift of the spectral distribution towards faster frequencies, i.e. higher MF during the transition from rest to task. Moreover, given the differential nature of the 2 tasks, we expect differences between them, i.e. task-specific changes of LZC and MF in lower- and higher-order networks (Luo et al. 2013; Boly et al. 2015; Baria et al. 2018; Pappas et al. 2019; Varley et al. 2020).
The third specific aim consists of linking the 2 aspects of temporal dynamics: signal compressibility, i.e. LZC, and frequency balance, i.e. MF. Given that we assume both LZC and MF follow the spatial hierarchy of lower- and higher-order networks in first 2 hypotheses, we now expect that rest–task changes in signal compressibility (LZC) are related to the spectral distribution of lower- and higher-order networks, i.e. resting-state MF. To establish the LZC–MF relationship, we calculate different correlations, as well as a mediation model to delve in the causal relation between them. Furthermore, we conduct various simulation models applying different kinds (pink, white, etc.) and levels of noise to demonstrate that the LZC–MF relationship is specifically related to the brain’s topography rather than noise.
Materials and methods
Experimental design
Data were selected from HCP’s 7T dataset (rather than HCP 3T) to achieve a high signal-to-noise ratio (and to have more fine-grained resolution), which is especially relevant for properly capturing temporospatial dynamics. Other reasons for choosing the 7T data were the longer and more continuous scanning during task states. We used HCP 3T resting-state data for validation purposes; in contrast, we did not use the task data of the 3T dataset because of their short block design, which makes proper measurement of the dynamics with our measures impossible.
From the data of 1,200 subjects released in HCP-1200 (Van Essen et al. 2013), 146 of them had completed the full 7T imaging protocol of the HCP without any imaging quality issues. A total of 14 fMRI runs (time repetition [TR] = 1 s), including 4 resting state (REST), 4 movie watching (MOVIE), and 6 retinotopy (RET), of these participants were used in this study. Full details on data acquisition and preprocessing are provided in separate articles (Glasser et al. 2013; Thanh Vu et al. 2017). In each MOVIE run, subjects had to watch a movie of approximately 15 min consisting of several clips separated by 20-s rest periods. Different clips were used in different runs (details are available at HCP S1200 Release Reference). For RET, stimuli were constructed by creating slowly moving apertures and placing a dynamic colorful texture within the apertures (check ref. Benson et al. 2018 for details).
Preprocessed data were downloaded from the HCP database at https://db.humanconnectome.org. The preprocessing pipeline includes registration to MNI space, alignment for motion, fieldmap correction, FIX denoising, and MSMAll group registration. Full details of all the steps are available in the study of Glasser et al. (2013) and Salimi-Khorshidi et al. (2014).
Data processing and statistical analysis
All steps of the data processing were performed with in-house scripts written in Python programming language using numpy, scipy, cifti, joblib, matplotlib, and seaborn libraries. The source code is freely available at www.georgnorthoff.com/code/. For brain map visualization purposes, wb_view (part of Connectome Workbench software) was used.
All statistical analyses were performed in the statsmodel library (Seabold and Perktold 2010) in Python and R v.3.6, and all P-values were corrected for multiple comparisons using the false discovery rate (FDR) method. The Student’s t-test was used to measure the statistical differences between lower- and higher-order networks. Moreover, analysis of variance (ANOVA) was used to investigate the difference between the networks during each condition. All the statistical tests were accompanied by their nonparametric counterparts in the Supplementary Result section.
Template and network definition
The preprocessed data were high-pass filtered at 0.01 to both maintain the full frequency spectrum of the data (Craig et al. 2018) and remove noise. After that, signals were averaged over brain voxels defined in the template provided by Ji et al. (2019) to get 1 fMRI signal per region per subject per run. The template contains 717 regions categorized into 12 networks of visual1, visual2, auditory, somatomotor, posterior multimodal, ventral multimodal, orbito-affective, dorsal attention, language, cingulo-opercular, frontoparietal, and default mode. To investigate our lower-order versus higher-order hypothesis, we also divided the regions into lower-order and higher-order networks (HON). Lower-order networks included the regions in the visual1, visual2, auditory, somatomotor, posterior multimodal, ventral multimodal, and orbito-affective networks. Regions inside dorsal attention, language, cingulo-opercular, frontoparietal, and DMNs were put under the higher-order networks category.
Calculation of LZC
To calculate the LZC (Fig. 1 white box), each signal was converted into a binary sequence. Previous studies (Nagarajan 2002; Aboy et al. 2006) suggest that the median of the signal’s amplitude is a good candidate to use as a binarization threshold. After binarizing each region’s signal and converting it to a string sequence, the Lempel–Ziv algorithm (Lempel and Ziv 1976) was used to compute LZC. As earlier studies have pointed out, LZC is dependent on the length of the sequence, thus a normalization factor (more info in Aboy et al. 2006) was used to remove that effect. LZC processing is illustrated in Fig. 1A.
Calculation of MF
MF was measured by first calculating the PSD of each region’s signal. PSD was calculated using the Welch algorithm (Welch 1967) with a Hanning window implemented in the Scipy package of Python programming language. The MF was calculated from the PSD as the frequency which divides the area under the curve (AUC) of PSD into 2 halves (Fig. 4A).
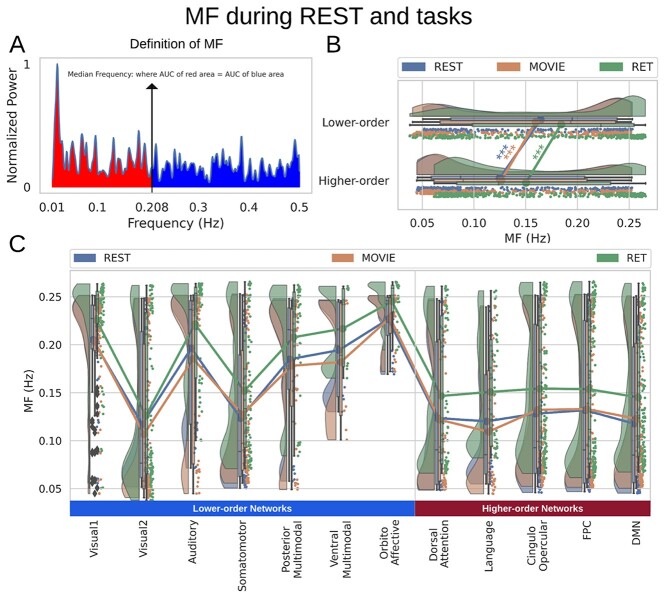
Fig. 4.
MF during both resting and task states. Points in the rain clouds represent regions. Stars represent the significance level 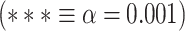 . A) A power spectrum of a sample signal. MF is calculated as the frequency at which the AUC of power up to that frequency (red area) is equal to AUC beyond that point (blue area). B) Similar to LZC, MF is significantly higher in lower-order networks compared to higher-order ones. C) MF is also significantly different among the 12 networks during both resting and task states.
. A) A power spectrum of a sample signal. MF is calculated as the frequency at which the AUC of power up to that frequency (red area) is equal to AUC beyond that point (blue area). B) Similar to LZC, MF is significantly higher in lower-order networks compared to higher-order ones. C) MF is also significantly different among the 12 networks during both resting and task states.
Resting and task state topographical calculations
The values of both measurements (i.e. LZC and MF) were first calculated for each of the 14 fMRI runs and then averaged over the runs in all 3 conditions (REST, MOVIE, and RET). After that, based on the requirements of each analysis, the values were either averaged over the lower- and higher-order division or the 12 aforementioned networks. The lower-order category was compared to the higher-order using Student’s t-test over regions.
Rest–task similarity
The similarity between resting and task states was addressed using spatial and regional correlations. The spatial correlation was calculated as a single Pearson correlation coefficient between resting and a task condition (e.g. REST vs. MOVIE) over brain regions after averaging over subjects (thus creating a single brain per condition). The regional correlation was used to measure the regional similarity between resting and task states. This correlation was calculated for each region across subjects between a pair of conditions (e.g. LZC during REST and MF during REST).
Percentage of change from resting state
The difference between resting and task states was calculated as a percentage of change per region per subject. Each region’s REST and task (e.g. MOVIE) values were put in the 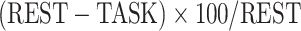 formula to both measure the change from resting to task state and normalize against rest at the same time. Then, for each subject, the percentage of change values was either averaged over the 12 networks or along the lower- and higher-order divisions. The difference between lower- and higher-order networks and the difference among the networks were statistically tested using the Student’s t-test and ANOVA methods.
formula to both measure the change from resting to task state and normalize against rest at the same time. Then, for each subject, the percentage of change values was either averaged over the 12 networks or along the lower- and higher-order divisions. The difference between lower- and higher-order networks and the difference among the networks were statistically tested using the Student’s t-test and ANOVA methods.
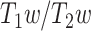 map
map
The ratio of T1- to T2-weighted images is suggested to provide a noninvasive neuroimaging proxy of anatomical hierarchy in the primate cortex (Burt et al. 2018). So, we used it to investigate whether the relationship between LZC and MF is anatomically based. A cortical map containing the 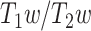 was provided with the HCP dataset. The map was MSMAll registered and bias field-corrected. We parcellated the map into the regions/networks of our template by averaging the
was provided with the HCP dataset. The map was MSMAll registered and bias field-corrected. We parcellated the map into the regions/networks of our template by averaging the  values of voxels into different regions.
values of voxels into different regions.
Simulation of motion’s effect on LZC
The effect of motion and ways to mitigate it is well established in fMRI literature (Glasser et al. 2013; Jo et al. 2013; Power et al. 2014; Liu 2016; Thanh Vu et al. 2017). The approach used in the current paper, that is averaging voxels to get one time series per region, further eliminates any local shifts on voxels that might cause from head motion. To go one step further, we simulated the effect of motion on LZC. For that purpose, 5,000 pink noise signals with the same duration of the fMRI data (900 time points) were generated. Then, 1%, 2%, 5%, and 10% of time points were randomly chosen as time points with motion. A random number between −4 and 4 was added to those time points to simulate the effect of motion, that is a similar range of the typical motion noise. For comparison purposes, LZC and MF were calculated before and after the addition of “noise.” Results can be found at Supplementary Results. Briefly, we found that even with very high number of perturbed time points (10%), the change in LZC was only about 0.05. Furthermore, Spearman correlation coefficient between LZC and MF was practically the same between no motion and different amounts of motion. These results together show that with effective care to motion artifacts, LZC can be used safely with fMRI data.
LZC–MF simulation
The relationship between LZC and MF was explored using simulated signals. 35,000 pseudo-aleatory signals within 7 different categories (5,000 each, see Supplementary Fig. 5 for a sample signal in each category) were simulated to investigate whether the LZC–MF relationship is nonlinear or not and whether the relationship is specific to the brain. The 7 categories were (i) pink noise, (ii) white noise, (iii) sine wave, and linear combinations of (iv) pink and white noises, (v) pink noise and sine wave, (vi) white noise and sine wave, and (vii) pink noise, white noise, and sine wave.
The weights of the signals’ linear combinations were chosen randomly. All random values were chosen from a uniform distribution and were controlled to produce signals in the same frequency range of our original data (0.01–0.5 Hz). Pink noise was chosen to model the scale-free behavior (He et al. 2010), white noise for pure randomness, and sine wave for oscillation. The MF and LZC were calculated for each signal and used to further investigate the relationship between the 2 measurements and validate LZC calculations in fMRI data.
Calculation of LZC-ratio
To further validate the relationship between MF and LZC we used amplitude adjusted Fourier transform (AAFT) method. This method was used to generate surrogate fMRI time series through phase shuffling of the original fMRI signals under the constraint of preserving the spectral power profile (Schreiber and Schmitz 2000). First, for each region’s signal, a new time series was generated using AAFT. Then, LZC of the surrogate signal was calculated (surrogate LZC). Finally, LZC-ratio was calculated as the ratio of our original LZC values to their corresponding surrogate LZC values: 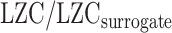 .
.
Change in LZC from REST and MF-REST mediation model
To investigate the relationship between MF during resting state (MF-REST) and the change in LZC task from resting state, a mediation analysis was performed using the mediation library in R. Two separate models were created for the 2 task conditions. Each model consisted of MF-REST as the mediator, LZC during REST as the independent variable (IV) and LZC during a task condition as the dependent variable (DV). After running the model and observing the indirect effects of IV on DV, the significance of that effect was tested using bootstrapping procedures (Hayes 2009; Tingley et al. 2014). Unstandardized indirect effects were computed for each of 1,000 bootstrapped samples, and the 95% confidence interval was computed by determining the indirect effects at the 2.5th and 97.5th percentiles.
Change in LZC from REST and MF-REST moderation model
To further investigate the relationship between the change in LZC from REST and MF-REST, regions were divided into 2 categories based on their MF-REST values. The median of MF-REST was used as the threshold and the regions with lower (higher) MF-REST than the median were put into the low (high) MF-REST category. The median was used to balance the 2 categories. A new binary variable (Z) was created for each region’s MF-REST category (0 = low MF-REST and 1 = high MF-REST). Z was injected in a linear regression model as a moderator: 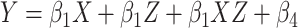 . In the linear regression equation, Y is LZC during a task condition, X is LZC during resting state, and Z is the binary value of MF during resting state.
. In the linear regression equation, Y is LZC during a task condition, X is LZC during resting state, and Z is the binary value of MF during resting state.
Results
The main aim of this article is to investigate the temporal dynamics of the spatial hierarchy of lower- higher-order networks (see Fig. 1 for an overview of our guiding questions and their results). Using the 7T of HCP, fMRI signals of 146 subjects during resting and 2 different task states were parcellated into 717 brain regions defined in the template provided by (Ji et al. 2019; Pappas et al. 2019). These regions were divided into 12 networks of visual1, visual2, auditory, somatomotor, posterior multimodal, ventral multimodal, orbito-affective, dorsal attention, language, cingulo-opercular, frontoparietal, and default. These networks, in turn, were divided into 2 categories of lower- and higher-order regions. Regions in visual1, visual2, auditory, somatomotor, posterior multimodal, ventral multimodal, and orbito-affective networks were classified as lower-order networks while the remaining networks were regarded as higher-order networks (Cole et al. 2013, 2014, 2016; Margulies et al. 2016; Huntenburg et al. 2018; Murphy et al. 2018; Gutierrez-Barragan et al. 2019; Wang et al. 2019; Ito et al. 2020; Raut et al. 2020).
To operationalize and measure intraregional signal compressibility, i.e. regularity/irregularity, we used LZC. LZC is algorithmically defined as the number of different patterns in a binary sequence indexing the signal complexity (the white box of Fig. 1 shows how LZC is calculated). LZC is formally defined as an index of how much a signal can be compressed, and in other words, it measures the diversity of the patterns that are present in a signal, i.e. higher LZC is associated with lower compressibility and higher irregularity (Aboy et al. 2006; Schartner et al. 2017). The amplitude of regional signals was individually binarized using its median as a robust threshold (Nagarajan 2002; Aboy et al. 2006) and then fed into the LZC algorithm yielding a single LZC value per region of a subject during a specific condition (resting or task state). LZC is complemented by a measure of the frequency balance, namely MF, which measures the balance of slow–fast frequencies of PSD, that is its shift towards slower (low MF) or faster (high MF) frequencies. All the subsequent statistical tests were also validated with their nonparametric counterparts.
Preprocessed 7T fMRI data (TR = 1) were downloaded from the HCP WU-Minn HCP 1200 subjects data release and then high-pass filtered at 0.01 Hz (more detail about the data release is provided in the Section 2). The data include resting state (REST, 16 min), and 2 task states of movie watching (MOVIE, 15 min) and retinotopy (RET, 5 min). Finally, we used the 3T fMRI data of the HCP for replicating our findings.
The topography of LZC during the resting state
Our first question is to investigate the spatial distribution of LZC in the resting state (see below for simulation on the validity of LZC measurement in fMRI). After averaging across subjects, the regional distribution of LZC values (Fig. 2A) suggested a specific spatial pattern of LZC. To investigate that, we used the 12 predefined networks (Fig. 2B) and divided the LZC values into them (Fig. 2C). This revealed different LZC patterns among the networks. Performing 1-way ANOVA over the 12 networks across regions showed significant  differences among them
differences among them  .
.
Fig. 2.
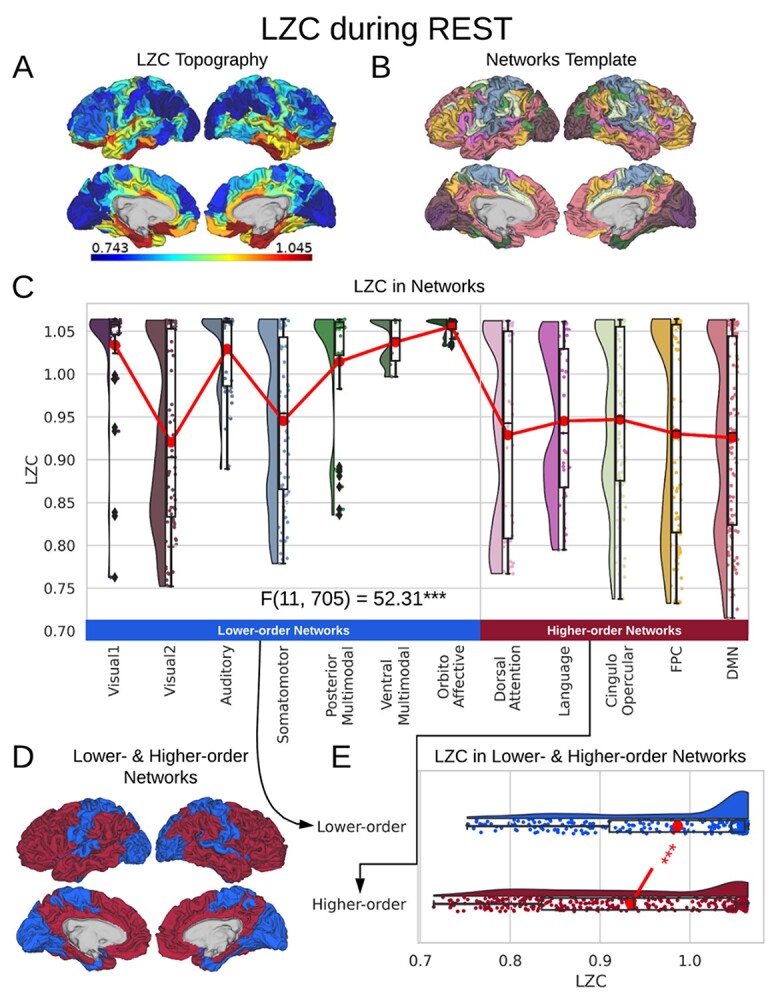
LZC during the resting state. Rainclouds represent regions. A) Spatial distribution of LZC during REST condition. LZC is calculated for a region after binarizing its blood oxygenation level-dependent (BOLD) signal’s amplitude using the median as a threshold. B) Brain map of the 12 networks defined in the study of Ji et al. (2019). Colors represent different networks. C) Distribution of LZC values in different networks. Colors are the same as in B. Higher-order networks show lower LZC compared to lower-order ones. One-way ANOVA showed a significant 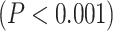 difference among all networks
difference among all networks 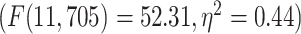 . D) Brain map representing lower- and higher-order categories. E) LZC during resting state along the lower- and higher-order categories. The Student’s t-test shows lower-order regions have significantly higher LZC compared to higher-order ones
. D) Brain map representing lower- and higher-order categories. E) LZC during resting state along the lower- and higher-order categories. The Student’s t-test shows lower-order regions have significantly higher LZC compared to higher-order ones 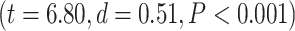 . Stars represent the significance level
. Stars represent the significance level 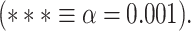
Significant differences in LZC values among networks paved the way to further investigate the topography of LZC along the lines of lower- and higher-order categories (Fig. 2D). Again, the resting-state LZC was averaged across subjects and then compared between lower- and higher-order regions (Fig. 2E). Student’s t-test (with the Cohen’s d for the effect size) showed a significant 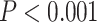 difference between the 2 types of networks
difference between the 2 types of networks 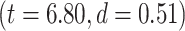 , with the lower-order having higher LZC compared to the higher-order category. Together, these results show clear topographical differences in the spatial distribution of LZC (These results were also replicated in our 3T replication dataset in Supplementary Fig. 1). Given that lower- and higher-order networks are known to process different kinds and degree of information (Zhang et al. 2018), our result of LZC following these topographical differences support the assumption that LZC reflects this differences.
, with the lower-order having higher LZC compared to the higher-order category. Together, these results show clear topographical differences in the spatial distribution of LZC (These results were also replicated in our 3T replication dataset in Supplementary Fig. 1). Given that lower- and higher-order networks are known to process different kinds and degree of information (Zhang et al. 2018), our result of LZC following these topographical differences support the assumption that LZC reflects this differences.
The topography of LZC during task states
Spatial distribution of LZC was investigated during the 2 tasks of movie-watching (MOVIE) and retinotopy (RET) in 3 different ways: analysis of absolute values, spatial correlations, and analysis of percentage changes, i.e. rest–task difference. The 2 tasks have different complexity and temporal structure; 1 containing rich stimuli of movie clips viewed in long intervals and 1 containing very simple retinotopic stimuli viewed in short intervals. The different input structure of the 2 tasks suggests that they should impact the information processing in lower- and higher-order networks in different ways.
Similar to the resting state analysis, LZC values were calculated for lower- and higher-order networks (Fig. 3A) and their difference was statistically tested across regions. First, a 2-way ANOVA with network order (2 levels: lower vs. higher) and task condition (2 levels: MOVIE vs. RET) as factors was conducted on the LZC values over the regions. The model showed significant 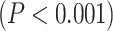 effect of network order on LZC
effect of network order on LZC 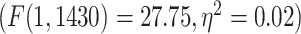 . Further analysis using Student’s t-test for each task condition confirmed that lower-order networks have significantly higher LZC compared to higher-order ones in both MOVIE
. Further analysis using Student’s t-test for each task condition confirmed that lower-order networks have significantly higher LZC compared to higher-order ones in both MOVIE 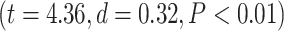 and RET
and RET 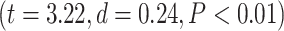 .
.
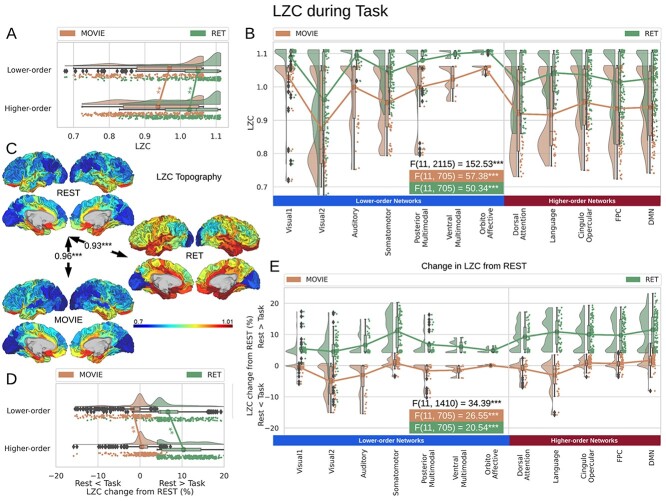
Fig. 3.
LZC during the task states. Points in the rain plots represent regions. A) LZC during MOVIE and RET for lower- and higher-order networks. The paired Student’s t-test between lower- and higher-order networks is significant with 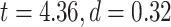 for MOVIE and
for MOVIE and 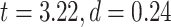 for RET. B) LZC during the 2-task conditions for the 12 networks. Three separate ANOVA models (1 over the whole data, 1 for only the MOVIE, and 1 for only the RET data) showed significant differences among the networks. C) Spatial distribution of LZC during REST, MOVIE, and RET conditions alongside their corrected spatial correlation coefficients. The correlation is calculated over the regions to show the spatial similarity between resting and task states. D) Change in LZC from REST to both task conditions for lower- and higher-order networks. Similar to task state results, the change was also significantly different between the 2 categories. E) Change in LZC from REST to MOVIE and RET is also significantly different among the 12 networks. Stars represent the significance level
for RET. B) LZC during the 2-task conditions for the 12 networks. Three separate ANOVA models (1 over the whole data, 1 for only the MOVIE, and 1 for only the RET data) showed significant differences among the networks. C) Spatial distribution of LZC during REST, MOVIE, and RET conditions alongside their corrected spatial correlation coefficients. The correlation is calculated over the regions to show the spatial similarity between resting and task states. D) Change in LZC from REST to both task conditions for lower- and higher-order networks. Similar to task state results, the change was also significantly different between the 2 categories. E) Change in LZC from REST to MOVIE and RET is also significantly different among the 12 networks. Stars represent the significance level 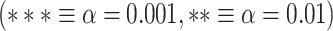 .
.
Moreover, dividing the LZC values into the 12 networks (Fig. 3B) and conducting similar 2-way ANOVA (factors: networks with 12 levels and task with 2 levels) on them also showed significant 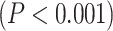 effect of network on LZC values
effect of network on LZC values 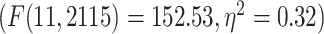 . Next, 2 separate 1-way ANOVAs were designed to further test the effect of network on LZC in each task. Both models showed significant
. Next, 2 separate 1-way ANOVAs were designed to further test the effect of network on LZC in each task. Both models showed significant 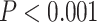 differences among the networks in LZC values (MOVIE:
differences among the networks in LZC values (MOVIE: 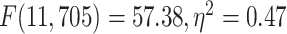 ; RET:
; RET: 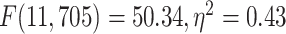 ).
).
The differences in LZC between lower- and higher-order categories and also among the networks in the tasks were analogous to the previous resting-state results, suggesting that the topography of LZC during task states was similar to the resting state. To test this hypothesis, we, in a second analysis, calculated the spatial correlation between the resting state (REST) and each task condition (MOVIE and RET, Fig. 3C). For each pair of conditions, LZC values were first averaged across subjects yielding a pair of LZC maps, then the 2 maps were correlated over regions, using Pearson correlation, yielding a single correlation value. The result showed significantly high correlation coefficients for both MOVIE 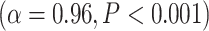 and RET
and RET 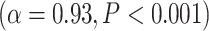 . These data further support the assumption that the resting-state LZC topography is preserved during the 2 tasks.
. These data further support the assumption that the resting-state LZC topography is preserved during the 2 tasks.
Despite the fact that resting-state LZC topography was similar in resting and task states, we nevertheless observed increases and decreases in LZC during the 2 task states. Therefore, in a third step, we calculated the percent of LZC change from resting state for each region. For each task, the regional LZC values were subtracted from and then divided by their corresponding resting state values 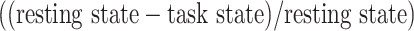 , thus normalizing the task state against the resting state, i.e. rest–task difference. We applied the statistical models we applied during the task states also to rest–task differences, i.e. to their percentage change values. Two-way ANOVA with network order (lower vs. higher) and task condition (MOVIE vs. RET) showed significant
, thus normalizing the task state against the resting state, i.e. rest–task difference. We applied the statistical models we applied during the task states also to rest–task differences, i.e. to their percentage change values. Two-way ANOVA with network order (lower vs. higher) and task condition (MOVIE vs. RET) showed significant 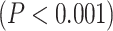 effect of network order on the percentage of change
effect of network order on the percentage of change 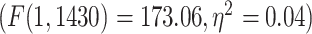 , and further Student’s t-test showed higher percentage of change in higher-order networks compared to lower-order ones in both MOVIE
, and further Student’s t-test showed higher percentage of change in higher-order networks compared to lower-order ones in both MOVIE 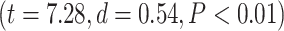 and RET
and RET 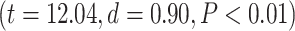 . On the network level, similar to task analysis, significant effect of network in a 2-way ANOVA model (network and condition)
. On the network level, similar to task analysis, significant effect of network in a 2-way ANOVA model (network and condition) 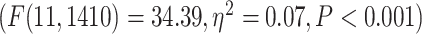 was followed by significant differences among the networks in 2 separate 1-way ANOVAs for MOVIE
was followed by significant differences among the networks in 2 separate 1-way ANOVAs for MOVIE 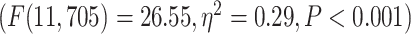 and RET
and RET 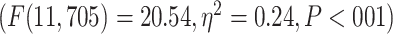 .
.
Although percentage of LZC change was statistically different between lower- and higher-order categories (Fig. 3D), and over the 12 networks (Fig. 3E), it presented distinctive results for the 2 tasks. In the MOVIE, positive values (decrease in LZC from REST to MOVIE) were observed in visual, auditory, and language networks. In contrast, LZC values were prominently increased from REST to our second task, i.e. RET (negative percentage of change), in all networks. Taken together, LZC topography during rest along the lines of lower- and higher-order networks is largely preserved during and thus carried over to the different task states. Additionally, one can nevertheless observe task-related changes in LZC once task is subtracted from rest; these concerned LZC differences between lower- and higher-order networks during the tasks. Hence, task-related LZC changes seem to loosely reflect the different input structures of our 2 tasks.
Temporal dynamics: MF in rest and task states
To link the LZC in resting and task states to the other aspect of temporal dynamics, i.e. frequency balance, we characterized the distribution of their PSD using the MF. MF is defined as the frequency which divides the area under the PSD into 2 halves. It was chosen to provide a summary measure of the distribution of low versus high frequencies in the PSD in a given frequency range (Fig. 4A, see also Methods for the details).
Calculating MF over different brain networks revealed a topographical distribution analogous to the one of LZC (Fig. 4B and C). Student’s t-test showed significantly 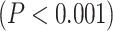 higher MF in lower-order networks compared to higher-order ones in both resting
higher MF in lower-order networks compared to higher-order ones in both resting 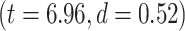 and task states (MOVIE:
and task states (MOVIE: 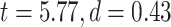 ; RET:
; RET: 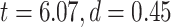 ). Furthermore, tested with 1-way ANOVA, the topographical distribution was also significantly
). Furthermore, tested with 1-way ANOVA, the topographical distribution was also significantly 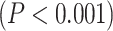 different among the 12 networks (REST:
different among the 12 networks (REST: 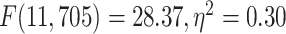 ; MOVIE:
; MOVIE: 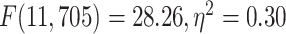 ; RET:
; RET: 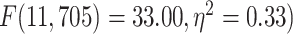 . These results are also replicated in the 3T dataset (Supplementary Fig. 2). Together, these results show that the topographical differentiation of lower- and higher-order networks also holds on frequency grounds, namely based on the PSD as measured by MF.
. These results are also replicated in the 3T dataset (Supplementary Fig. 2). Together, these results show that the topographical differentiation of lower- and higher-order networks also holds on frequency grounds, namely based on the PSD as measured by MF.
Empirical data: the relationship between MF and LZC
The similarity in the topographical distribution of MF and LZC raises the question of their relationship. Specifically, it allows us to address how intraregional temporal balance is related to signal compressibility. This was addressed in 4 steps. First, for each condition (REST, MOVIE, or RET), we calculated the regional correlation between MF and LZC. Regional correlation is calculated per region across subjects as the Pearson correlation between MF and LZC values (Fig. 5A). P-values were corrected for multiple comparisons using the FDR method at 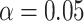 , while nonsignificant coefficients were ignored. This revealed a variety of correlation values for the LZC–MF relationship across the wide range of 0.43–0.88 across the different regions. Given such a wide range of correlation values, we assumed that topographical differences strongly shape the MF–LZC relationship; this was addressed in subsequent analyses.
, while nonsignificant coefficients were ignored. This revealed a variety of correlation values for the LZC–MF relationship across the wide range of 0.43–0.88 across the different regions. Given such a wide range of correlation values, we assumed that topographical differences strongly shape the MF–LZC relationship; this was addressed in subsequent analyses.
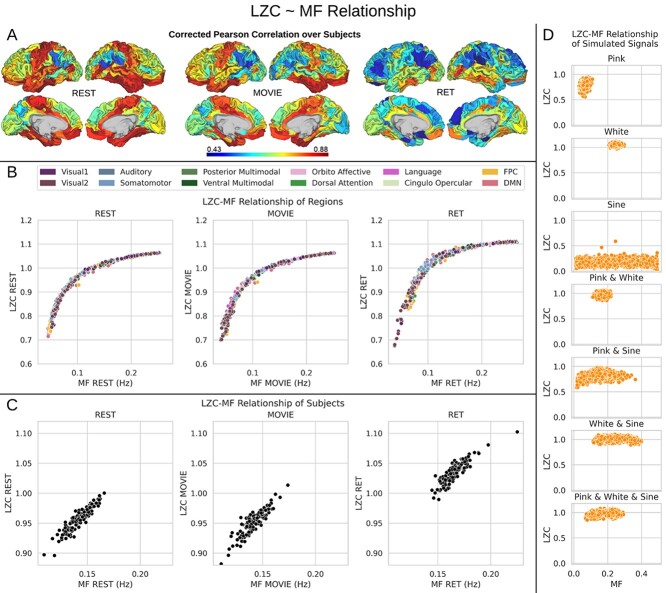
Fig. 5.
The relationship between MF and LZC. A) Regional Pearson correlation between MF and LZC or the 3 conditions of REST, MOVIE, and RET. P-values are corrected using the FDR method at 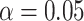 . The wide range of correlation values (0.43–0.88) suggests that topographical differences affect the MF–LZC relationship. B) Regional scatter plots of MF–LZC relationship for the 3 conditions. Each point is a region averaged over subjects, and the colors show the regions belonging to specific networks. All plots show LZC as a nonlinear function of MF. C) Scatter plots of MF–LZC relationship for different subjects in the 3 conditions. Each point is a subject averaged over regions. The nonlinear relationship can no longer be observed. D) Simulation of the MF–LZC relationship with 7 different types of signals. Each plot shows the distribution of LZC as a function of MF for 5,000 simulated signals. The nonlinear relationship cannot be observed in the simulated signals, suggesting that it is unique to the brain signal.
. The wide range of correlation values (0.43–0.88) suggests that topographical differences affect the MF–LZC relationship. B) Regional scatter plots of MF–LZC relationship for the 3 conditions. Each point is a region averaged over subjects, and the colors show the regions belonging to specific networks. All plots show LZC as a nonlinear function of MF. C) Scatter plots of MF–LZC relationship for different subjects in the 3 conditions. Each point is a subject averaged over regions. The nonlinear relationship can no longer be observed. D) Simulation of the MF–LZC relationship with 7 different types of signals. Each plot shows the distribution of LZC as a function of MF for 5,000 simulated signals. The nonlinear relationship cannot be observed in the simulated signals, suggesting that it is unique to the brain signal.
In the second step, the LZC–MF relationship was explored in more detail by looking at their values in different brain regions. First, both LZC and MF values were averaged over subjects and then each region’s LZC value was plotted against its corresponding MF value (Fig. 5B). This suggested a nonlinear regime between MF and LZC over brain regions across all 3 conditions. Specifically, we observed that regions with lower MF in rest exhibit largely different LZC values in both rest and task, whereas regions with higher MF in rest no longer showed marked LZC differences in both rest and task. Together, this amounts to a nonlinear relationship in the topography of MF and LZC with high and low MF exerting differential impacts on LZC (also replicated in 3T dataset in Supplementary Fig. 3).
We tested whether this nonlinear relationship is specifically related to the topographical distribution of LZC and MF (topographical relationship) rather than interindividual differences between subjects (Step 3). To do so, LZC and MF values were averaged over all regions leaving a pair of LZC and MF values per subject (subject-based relationship). This revealed a relationship different from the topographical one, suggesting a linear trend for the subject-based relationship of LZC and MF: the higher the MF in a specific individual (across all its regions), the higher its LZC (across all its regions, Fig. 5C). One caveat is that the range of value for the calculation of interindividual LZC–MF relationship is lower than the one in our regional topographic LZC–MF; for that reason, we cannot fully exclude potential nonlinear regime in interindividual MF–LZC relationship.
As the fourth step, the LZC–MF relationship was further explored by using the brain’s 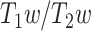 values (see Methods) to test whether it is structurally based.
values (see Methods) to test whether it is structurally based. 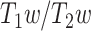 is suggested to provide a noninvasive proxy of anatomical hierarchy in primate cortex (Burt et al. 2018). For both LZC and MF, each region’s values were averaged over subjects and then the regional distribution was plotted as functions of
is suggested to provide a noninvasive proxy of anatomical hierarchy in primate cortex (Burt et al. 2018). For both LZC and MF, each region’s values were averaged over subjects and then the regional distribution was plotted as functions of 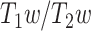 values (Supplementary Fig. 4A for LZC and B for MF). This also failed to show here the observed topographical relationship between LZC and MF on functional grounds. That suggests the nonlinear relationship of MF and LZC to hold independent of their underlying anatomical relationship; we thus assume that the nonlinear topographical LZC–MF relationship is primarily driven by the topographical distribution of intraregional frequency balance, i.e. MF, rather than being based on structural anatomical grounds (also replicated in 3T dataset in Supplementary Fig. 3).
values (Supplementary Fig. 4A for LZC and B for MF). This also failed to show here the observed topographical relationship between LZC and MF on functional grounds. That suggests the nonlinear relationship of MF and LZC to hold independent of their underlying anatomical relationship; we thus assume that the nonlinear topographical LZC–MF relationship is primarily driven by the topographical distribution of intraregional frequency balance, i.e. MF, rather than being based on structural anatomical grounds (also replicated in 3T dataset in Supplementary Fig. 3).
Simulation: the relationship between MF and LZC using synthetic data
As a final confirmatory analysis to show the truly topographical nature of the nonlinear MF–LZC relationship, we decided to perform a simulation analysis using synthetic data. Seven different categories of pseudo-aleatory signals, that is without any topographical distribution, were simulated in the same frequency range (0.01–0.5) as our data with the same sampling rate. We generated different kinds of signals including pink noise, white noise, sine wave, and their linear combinations (e.g. white and pink noises or white noise and sine wave). Each signal type or category contained 5,000 signals (total of 35,000, see Supplementary Fig. 5 for a sample signal in each category) with different combinations of power set randomly in the same ranges as the real signals.
Pink noise was utilized to simulate scale-freeness (He et al. 2010), sine wave for oscillatory component, and white noise for pure randomness. The parameters for each signal and the weights for their linear combinations used random values chosen from uniform distributions to bound the signals in the predefined frequency range of our real data. Calculating LZC and MF on these signals and plotting them against each other (Fig. 5D) showed no specific relationship between the 2 measurements. These results, thus, suggest that the nonlinear relationship between LZC and MF is related specifically to the topographical distribution in different brain regions. These results also provide evidence for the possible dissociation between LZC and MF, as their correlation is different depending on the signals assessed even in the same range of values. Moreover, validating our use of LZC in fMRI, our simulation shows that LZC is not measuring noise in the BOLD signal of fMRI, but its level of compressibility.
Empirical data: the relationship between LZC task-related change from resting state and MF during resting state—the dynamic range of LZC
Is the change of LZC from rest to task in specific regions dependent upon the slow–fast frequency balance of the PSD, i.e. MF, of that particular region? If rest MF mediates LZC rest–task differences, one would strongly assume that the PSD (MF) processes changes in signal compressibility (LZC) during the transition from resting to task state. This mediation hypothesis is based on the assumption that previous studies showed a relationship between the PSD distribution (as indexed by spectral entropy) and the change in connectivity strength from rest to task states (Gomez-Pilar et al. 2018). Could the distribution of PSD also be influencing the change in compressibility of the neural signal? We, therefore, investigated how the degree of change in LZC from resting to task state is related to the power spectrum during rest (MF-REST). The “change” values of all regions were plotted against their corresponding MF values during rest (MF-REST) for both task conditions (Fig. 6A). Careful consideration of these plots alongside a mediation analysis of LZC with MF as a mediator (see Fig. 6B) strongly suggests that there is a relationship of MF-REST with the rest–task changes or differences of LZC.
Fig. 6.
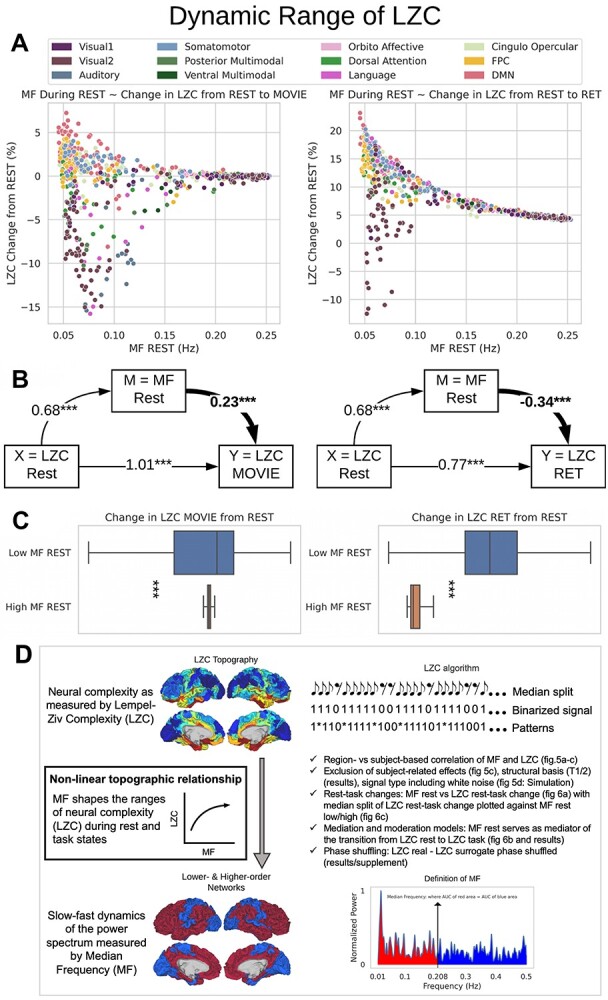
The relationship between MF during REST and the change in LZC from REST to TASK. A) The scatter plot of MF-REST (x-axis) versus the change in LZC (y-axis) from REST to MOVIE (left) and RET (right). The plots indicate a decrease in the range of the “change” as a function of MF-REST. B) Mediation model to investigate the role of MF-REST in the change in LZC from resting to task state. LZC-REST is used as the independent variable and the model investigates whether the effect of LZC-REST on LZC-MOVIE (left) or LZC-RET (right) as the dependent variable is mediated by MF-REST. The bootstrapped model showed significant partial mediation through MF-REST. C) Box plots showing the range of the “change” values for low-MF and high-MF during REST. MF-REST was median-split into low and high categories. Statistics were conducted using Student’s t-test over subjects. For each subject, a range of LZC change was calculated in low and high MF categories. For both conditions (MOVIE and RET), the range of LZC change in low-MF is significantly wider than high-MF. Stars represent the significance level  . D) Nonlinear topographic relationship of slow–fast dynamics and neural complexity.
. D) Nonlinear topographic relationship of slow–fast dynamics and neural complexity.
Following that, we decided to conduct a median-split of the MF-REST values across brain regions. That served the purpose of calculating the LZC rest–task “change” values in dependence on low MF-REST and high MF-REST, respectively. Plotting both categories with box plots (Fig. 6C) revealed a large difference in the range of change in LZC values (i.e. the range of change in LZC from resting to task states) between low and high MF-REST categories. To test whether this difference is significant or not, the “change” values of each subject were divided into 2 categories of low and high MF-REST. Then, the significant 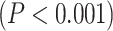 difference between the 2 was confirmed by Student’s t-test over subjects (MOVIE:
difference between the 2 was confirmed by Student’s t-test over subjects (MOVIE: 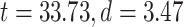 ; RET:
; RET: 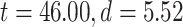 ).
).
Moreover, to further validate the previous results, we calculated LZC-ratio (see below) using AAFT method. AAFT generates surrogate time series through phase-shuffling of the original signals under the constraint of preserving the spectral power profile (Schreiber and Schmitz 2000). LZC-ratio was calculated as 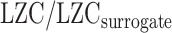 , in which LZC is the original LZC value for each region, and
, in which LZC is the original LZC value for each region, and 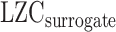 is the LZC of the time series generated using AAFT for the same region. We repeated the previous analysis (Fig. 6) using LZC-ratio instead of LZC (Supplementary Fig. 6), which revealed similar results, thus further confirming the dynamic range of LZC. These data suggest that the range of LZC rest–task change values in low MF-REST regions is significantly higher than in high MF-REST regions. The fact that this preserved during the subtraction of the phase shuffled surrogate LZC from the real LZC suggests a key role for phase-related mechanisms in mediating the nonlinear topographic impact of slow–fast frequency MF on complexity, i.e. LZC.
is the LZC of the time series generated using AAFT for the same region. We repeated the previous analysis (Fig. 6) using LZC-ratio instead of LZC (Supplementary Fig. 6), which revealed similar results, thus further confirming the dynamic range of LZC. These data suggest that the range of LZC rest–task change values in low MF-REST regions is significantly higher than in high MF-REST regions. The fact that this preserved during the subtraction of the phase shuffled surrogate LZC from the real LZC suggests a key role for phase-related mechanisms in mediating the nonlinear topographic impact of slow–fast frequency MF on complexity, i.e. LZC.
Together, these results suggest that the range in which the region’s LZC can change from rest to task is associated with the same region’s level of MF-REST (low or high). Therefore, we speak of a dynamic range of LZC, which we hypothesize to be related to the PSD of the region as indexed by MF: low rest MF indexing stronger power in slower frequencies yields a large dynamic range of LZC, i.e. a wide range of rest–task differences among its regions. While high rest MF indexing relatively stronger faster frequency power is related to small a dynamic range of LZC, i.e. narrow range of rest–task differences among its regions.
To further test the dynamic range of LZC, we incorporated a moderation model to see if MF-REST being low or high can moderate the relation between LZC during rest and task states. A binary moderator variable (Z) for MF-REST being low (Z = 0) or high (Z = 1) was defined. Then, the effect of LZC-REST and Z was explored on LZC during the 2 task conditions using linear regression (see Methods for details). The model showed significant moderation of the LZC rest–task relationship with MF-REST being low or high. For MOVIE, the effect of the moderator was 0.08 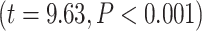 . Likewise, for RET, the effect of the moderator was 0.42
. Likewise, for RET, the effect of the moderator was 0.42 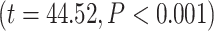 . In other words, our moderation analysis suggests that the effect of LZC during REST on LZC during MOVIE (or RET) is moderated by the level of MF during REST.
. In other words, our moderation analysis suggests that the effect of LZC during REST on LZC during MOVIE (or RET) is moderated by the level of MF during REST.
Taken together, these results show strong evidence for the relationship of MF and LZC to operate in a nonlinear topographical way (see Fig. 6D). The level of MF in a region’s resting state drives its propensity for the degree of change in its degree of signal compressibility (LZC) during the transition from resting to task state. Regions with low rest MF (indicating strong power in the slow frequency ranges) can yield a larger LZC rest–task change than regions with high MF. Thereby, the slow frequency ranges of resting-state MF seem to foster larger dynamic ranges in the regions’ signal compressibility. Therefore, the topographical distribution of slow and fast frequencies (indexing the hierarchical lower- and higher-order regions’ temporal dynamic) relates to the degree to which they can change their signal compressibility (LZC) during the transition from rest to task (Fig. 6D).
Replication with 3T data
Topographical resting-state LZC/MF of 3T data
3T resting-state data were analyzed using the same procedure as our 7T data (Supplementary Fig. 1 for LZC and Supplementary Fig. 2 for MF). The difference between lower- and higher-order networks was statistically tested with Student’s t-test between the 2 across regions which showed that both LZC and MF are significantly 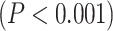 higher (LZC:
higher (LZC: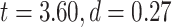 ; MF:
; MF: 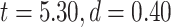 ) in lower-order networks compared to higher-order ones. Furthermore, MF and LZC were also significantly
) in lower-order networks compared to higher-order ones. Furthermore, MF and LZC were also significantly 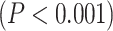 different among the 12 networks tested with 1-way ANOVA (LZC:
different among the 12 networks tested with 1-way ANOVA (LZC: 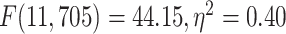 ; MF:
; MF: 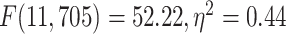 ). These results validate our original topographical findings.
). These results validate our original topographical findings.
The relation between LZC and MF in 3T data
As another confirmatory analysis, the relationship between MF and LZC was investigated in resting-state 3T data. Like before, first the 2 measurements were correlated with each other using Pearson methods (Supplementary Fig. 3A). Moreover, LZC was plotted as a function of MF both for each region (Supplementary Fig. 3B left) and for each subject (Supplementary Fig. 3B right). The nonlinear relationship over the brain regions was again observed in the 3T data. Both regional (averaged over subjects) LZC and MF were separately plotted as functions of 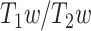 values, which did not show any specific nonlinear relationship (Supplementary Fig. 3C). Taken together, these results replicate our findings on the relationship of LZC with MF.
values, which did not show any specific nonlinear relationship (Supplementary Fig. 3C). Taken together, these results replicate our findings on the relationship of LZC with MF.
Discussion
We here investigate the intra-regional temporal dynamic of lower- and higher-order networks in resting and task state fMRI. Our main findings in both main (7T HCP) and replication (3T HCP) data sets are as follows: (i) significantly different resting-state LZC and MF in lower- and higher-order networks with the latter showing lower values in both LZC and MF; (ii) task-related and task-specific LZC and MF changes during different tasks in lower- and higher-order networks; (iii) nonlinear topographical relationship of LZC and MF with regions showing lower rest MF values being related to lower resting-state LZC and larger capacity for task–rest changes in LZC in especially higher-order network regions; and (iv) relation between LZC at rest and LZC during task, where frequency balance (MF) is acting as mediator. Together, these findings provide evidence that the spatial topographical hierarchy of lower- and higher-order networks is related to a corresponding hierarchy in their temporal dynamic.
Topographical differences in temporal dynamics of lower- and higher-order networks
We show different degrees of LZC in different networks during the resting state. Higher-order networks like the DMN, FPN, language, and dorsal attention exhibit lower values of LZC in the resting state. In contrast, lower-order networks like sensory networks, orbito-affective, and multimodal show high LZC values. Importantly, we demonstrate analogous findings in frequency balance, i.e. MF, that, like LZC, follow the hierarchy of lower- and higher-order networks during both rest and task states. This suggests that the signal is more regular and more chaotic, i.e. lower LZC, in higher-order networks than in lower-order networks. That reverberates upon and is in line with the larger topographical distinction of core (higher-order networks) and periphery (lower-order networks) (Margulies et al. 2016, Golesorkhi, Gomez-Pilar, Tumati, et al. 2021a; Golesorkhi, Gomez-Pilar, Zilio, et al. 2021b; Wolff et al. 2022).
Our findings complement previous results that show analogous differences between lower- and higher-order networks. Spatially, reflecting regions of the periphery, lower-order networks are more locally connected while higher-order networks, constituting the core, are more globally connected throughout the whole brain. This led, recently, to the so-called core–periphery organization (Margulies et al. 2016; Huntenburg et al. 2018): Lower-order unimodal networks like sensory networks are at the periphery while higher-order transmodal networks like DMN and FPN constitute the core as they are connected throughout the whole brain. Recent data suggest such core–periphery organization to be mirrored also in the brain’s temporal organization as its INTs are shorter in the lower-order networks, i.e. the periphery, and longer in the higher-order networks, i.e. the core (Kiebel et al. 2008; Chaudhuri et al. 2015; Gollo et al. 2015, 2017; Murray et al. 2015; Baldassano et al. 2017).
Our data extend these findings by showing that lower- and higher-order networks exhibit different temporal dynamics with low signal compressibility and high signal compressibility dominating, respectively. The differential role of lower- and higher-order regions in information processing is further supported by our results in task states. We observed network- and task-specific changes during the 2 tasks relative to the resting state. Together, extending previous findings (Boly et al. 2015), the observed task–rest differences in LZC and MF further support the assumption of task- and network-specific changes and, more generally, the key role of temporal dynamic during the transition from rest to task states.
Signal compressibility (LZC) is shaped by frequency balance (MF)
Is signal compressibility (LZC) related to frequency balance (MF) along the lines of lower- and higher-order networks? We saw a similar topographical pattern in LZC and MF. This suggests a close relationship between LZC and MF, meaning that the intraregional PSD (MF) may mediate their signal compressibility (LZC). Probing this assumption, we tested various correlations, simulations, and mediation models.
Spatial correlation confirmed such a close relationship; however, regional LZC–MF correlation revealed quite a variety of different degrees in their correlation within the different regions. Such a wide variety of LZC–MF correlations across different regions suggests a differential relationship of regions. This was confirmed by subsequent analyses. We obtained a nonlinear topographical pattern in the LZC–MF relationship in both rest and task states. Regions with low MF at rest showed lower rest LZC and more differentiation in their respective LZC rest–task changes than those regions exhibiting high rest MF. We could further demonstrate that such nonlinear relationship is related specifically to the topographical distribution of low and high MF values rather than being associated with interindividual differences, anatomical differences in 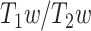 of the different regions, or some other kinds of LZC–MF relationship independent of their topographical distribution (as tested for in simulation).
of the different regions, or some other kinds of LZC–MF relationship independent of their topographical distribution (as tested for in simulation).
Further, we observe that the MF is related to the range of possible LZC rest–task changes. Regions with low MF values during rest show much larger changes in their rest–task LZC values than those with high MF (see Supplementary Results). Hence, MF in rest seems to modulate the capacity for change in LZC during the transition from rest to task: regions with low MF and thus more power in the slower frequency ranges have a higher likelihood of exhibiting larger changes in their signal complexity, i.e. increases or decreases, during the transition from rest to task states. Hence, it is the temporal dynamics of the different regions’ resting state rather than the regions themselves (independent of their dynamics) that is related to the topographical distribution of LZC during rest and task.
How can frequency balance (MF) during rest modulate and shape signal compressibility (LZC) during task? Low values in MF reflect stronger power in the infraslow frequency fluctuations which can be characterized by extremely long-cycle durations. These long-cycle durations are assumed to be ideal for summing and pooling different stimuli occurring at different points in time such that their respective information is processed and thus lumped together (He and Raichle 2009; Li et al. 2014; Northoff 2014, 2017; Himberger et al. 2018). Such summing and pooling may thus enable higher degrees of integration of temporally distinct stimuli (Himberger et al. 2018; Golesorkhi, Gomez-Pilar, Zilio, et al. 2021b). That, in turn, leads to less chaotic signal dynamics with lower LZC values. One would consequently expect that regions showing lower values in MF should also exhibit lower LZC values, which is exactly what we observed in our data.
This supposed modulation of the LZC–MF relationship by the pooling and summing of stimuli through cycle duration may also account for the observed differences in the rest–task changes of the LZC in regions with low and high rest MF. Given the inverse relationship between power and frequency, i.e. the scale-freeness of the brain oscillations (He et al. 2010), if a region shows low MF, the power of its long-cycle duration is stronger than that of a region with higher rest MF. That may allow the low rest MF region to pool, sum, and ultimately integrate more external stimuli during task states (Himberger et al. 2018) than a region with high rest MF. This, in turn, changes the range of that region’s signal complexity and thus its LZC to a large degree. This stands in contrast to a high rest MF region that, due to its lower power of its shorter cycle durations, cannot pool and sum as many external stimuli and consequently cannot exhibit a large range of LZC values from rest to task. That remains to be tested in future modeling studies though.
Limitations
There are a few considerations that should be considered in this study. First, task unspecificity should also be replicated using different tasks in different modalities and domains; however, concerning our metrics, we included 2 tasks with completely different complexity and temporal structure. The movie presents a continuous task while the retinotopy is an event-related trial-based discontinuous task. The inclusion of tasks with 2 different structures accounts for the recent suggestion (Huk et al. 2018) of considering and including tasks with different structures, i.e. continuous versus trial-based. Second, this study contains no behavioral measurement; but on the other hand, the tasks measured pure perception and stimulus processing with no interference of cognitive demands, thus no-report paradigms as distinguished from report paradigms (Tagliazucchi et al. 2014). The reliance on no-report paradigms allowed to isolate stimulus-related effects, i.e. movie and visual stimuli during retinotopy, as they are supposed to be related to, specifically, primary sensory networks like visual and auditory networks. Hence, the no-report paradigms are ideal to test the response of primary networks independent of any task-related confounds as in report paradigms. Third, the frequency of the retinotopic stimuli might impact the MF. Investigating this idea is beyond the scope of this work and is an interesting topic for further research. Fourth, we did not investigate functional connectivity here. The basic dynamics of the relationship of inter-regional functional connectivity to intraregional power spectra including MF as well as to time-dependent measures like LZC remains yet unclear, though. Given such methodological uncertainty, we refrained from linking our measures of MF and LZC to functional connectivity.
Conclusion
The brain exhibits spatial hierarchy along the lines of lower- and higher-order networks. Here we investigate whether the regions’ activities during rest and task states in such spatial hierarchy are shaped by a corresponding temporal hierarchy in their neural dynamics. We observe lower LZC indexing high degree of complexity, i.e. signal compressibility in higher-order network regions while lower-order network regions are characterized by lower degree of complexity, i.e. signal compressibility with higher LZC, during both rest and task states. Observing an analogous topography in MF, we demonstrate that resting-state MF levels are related to the degree of LZC rest–task changes in a nonlinear topographical way in especially higher-order networks. In conclusion, our findings demonstrate that the spatial hierarchy of lower- and higher-order network exhibits a more or less analogous complexity, i.e. signal compressibility and temporal slow–fast dynamics, with the latter shaping the former in a nonlinear topographical way. Above and beyond task-specific cognitive effects (as investigated in Cognitive Neuroscience), our findings demonstrate a more fundamental temporal-dynamic task-unspecific shaping of the higher-lower-order network topography during task-related activity as postulated in “Spatiotemporal Neuroscience” (Northoff et al. 2020a,b).
Supplementary Material
Contributor Information
Mehrshad Golesorkhi, School of Electrical Engineering and Computer Science, University of Ottawa, Ottawa ON K1Z 7K4, Canada; Mind, Brain Imaging and Neuroethics Research Unit, Institute of Mental Health, Royal Ottawa Mental Health Centre and University of Ottawa, Ottawa ON K1Z 7K4, Canada.
Javier Gomez-Pilar, Biomedical Engineering Group, University of Valladolid, Paseo de Belén, 15, Valladolid 47011, Spain; Centro de Investigación Biomédica en Red en Bioingeniería, Biomateriales y Nanomedicina (CIBER-BBN), Madrid 28029, Spain.
Yasir Çatal, Mind, Brain Imaging and Neuroethics Research Unit, Institute of Mental Health, Royal Ottawa Mental Health Centre and University of Ottawa, Ottawa ON K1Z 7K4, Canada.
Shankar Tumati, Mind, Brain Imaging and Neuroethics Research Unit, Institute of Mental Health, Royal Ottawa Mental Health Centre and University of Ottawa, Ottawa ON K1Z 7K4, Canada.
Mustapha C E Yagoub, School of Electrical Engineering and Computer Science, University of Ottawa, Ottawa ON K1Z 7K4, Canada.
Emanuel A Stamatakis, Division of Anaesthesia, School of Clinical Medicine, University of Cambridge, Cambridge CB1 0SP, United Kingdom.
Georg Northoff, Mind, Brain Imaging and Neuroethics Research Unit, Institute of Mental Health, Royal Ottawa Mental Health Centre and University of Ottawa, Ottawa ON K1Z 7K4, Canada; Centre for Cognition and Brain Disorders, Hangzhou Normal University, Hangzhou 311121, China; Mental Health Centre, Zhejiang University School of Medicine, Hangzhou, Zhejiang 310053, China.
Funding
This work was supported by EJLB-Michael Smith Foundation; Canadian Institutes of Health Research; Ministry of Science and Technology of China; National Key R&D Program of China (2016YFC1306700); Hope of Depression Foundation (HDRF); Start-Up Research Grant in Hangzhou Normal University and European Union’s Horizon 2020 Framework Program for Research; Innovation under the Specific Grant Agreement No. 785907 (Human Brain Project SGA2), and Canada-UK Artificial Intelligence (AI) Initiative “The self as agent-environment nexus: crossing disciplinary boundaries to help human selves and anticipate artificial selves” (ES/T01279X/1) (together with Karl J. Friston from the United Kingdom).
Conflict of interest statement
The authors declare no conflict of interest.
References
- Abásolo D, Hornero R, Gómez C, García M, López M. Analysis of EEG background activity in Alzheimer’s disease patients with Lempel-Ziv complexity and central tendency measure. Med Eng Phys. 2006:28:315–322. [DOI] [PubMed] [Google Scholar]
- Abasolo D, James CJ, Hornero R. 2007. Non-linear analysis of intracranial electroencephalogram recordings with approximate entropy and lempel-ziv complexity for epileptic seizure detection. In: Annual International Conference of the IEEE Engineering in Medicine and Biology - Proceedings. IEEE. p. 1953–1956. https://pdfs.semanticscholar.org/3a27/6417e5350e29cb6bf04ea5a4785601d5a215.pdf [DOI] [PubMed]
- Aboy M, Hornero R, Abásolo D, Álvarez D. Interpretation of the Lempel-Ziv complexity measure in the context of biomedical signal analysis. IEEE Trans Biomed Eng. 2006:53:2282–2288. [DOI] [PubMed] [Google Scholar]
- Akdemir Akar S, Kara S, Agambayev S, Bilgiç V. Nonlinear analysis of EEGs of patients with major depression during different emotional states. Comput Biol Med. 2015:67:49–60. [DOI] [PubMed] [Google Scholar]
- Bachiller A, Lubeiro A, Díez Á, Suazo V, Domínguez C, Blanco JA, Ayuso M, Hornero R, Poza J, Molina V. Decreased entropy modulation of EEG response to novelty and relevance in schizophrenia during a P300 task. Eur Arch Psychiatry Clin Neurosci. 2015:265:525–535. [DOI] [PubMed] [Google Scholar]
- Bachmann M, Päeske L, Kalev K, Aarma K, Lehtmets A, Ööpik P, Lass J, Hinrikus H. Methods for classifying depression in single channel EEG using linear and nonlinear signal analysis. Comput Methods Prog Biomed. 2018:155:11–17. [DOI] [PubMed] [Google Scholar]
- Bai Y, Liang Z, Li X. A permutation Lempel-Ziv complexity measure for EEG analysis. Biomed Signal Process Control. 2015:19:102–114. [Google Scholar]
- Baldassano C, Chen J, Zadbood A, Pillow JW, Hasson U, Norman KA. Discovering event structure in continuous narrative perception and memory. Neuron. 2017:95:709–721.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baria AT, Centeno MV, Ghantous ME, Chang PC, Procissi D, Apkarian AV. Bold temporal variability differentiates wakefulness from anesthesia-induced unconsciousness. J Neurophysiol. 2018:119:834–848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benson NC, Jamison KW, Arcaro MJ, Vu AT, Glasser MF, Coalson TS, Van Essen DC, Yacoub E, Ugurbil K, Winawer J, et al. . The Human Connectome Project 7 tesla retinotopy dataset: description and population receptive field analysis. J Vis. 2018:18:1–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boly M, Sasai S, Gosseries O, Oizumi M, Casali A, Massimini M, Tononi G. Stimulus set meaningfulness and neurophysiological differentiation: a functional magnetic resonance imaging study. PLoS One. 2015:10:e0125337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burt JB, Demirtaş M, Eckner WJ, Navejar NM, Ji JL, Martin WJ, Bernacchia A, Anticevic A, Murray JD. Hierarchy of transcriptomic specialization across human cortex captured by structural neuroimaging topography. Nat Neurosci. 2018:21(9):1251–1259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaudhuri R, Knoblauch K, Gariel MA, Kennedy H, Wang XJ. A large-scale circuit mechanism for hierarchical dynamical processing in the primate cortex. Neuron. 2015:88:419–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiang S, Vankov ER, Yeh HJ, Guindani M, Vannucci M, Haneef Z, Stern JM. Temporal and spectral characteristics of dynamic functional connectivity between resting-state networks reveal information beyond static connectivity. PLoS One. 2018:13:e0190220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole MW, Reynolds JR, Power JD, Repovs G, Anticevic A, Braver TS. Multi-task connectivity reveals flexible hubs for adaptive task control. Nat Neurosci. 2013:16:1348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole MW, Bassett DS, Power JD, Braver TS, Petersen SE. Intrinsic and task-evoked network architectures of the human brain. Neuron. 2014:83:238–251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole MW, Ito T, Bassett DS, Schultz DH. Activity flow over resting-state networks shapes cognitive task activations. Nat Neurosci. 2016:9(12):1718–1726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Craig MM, Manktelow AE, Sahakian BJ, Menon DK, Stamatakis EA. Spectral diversity in default mode network connectivity reflects behavioral state. J Cogn Neurosci. 2018:30(4):526–539. [DOI] [PubMed] [Google Scholar]
- Deshpande G, LaConte S, Peltier S, Hu X. Tissue specificity of nonlinear dynamics in baseline fMRI. Magn Reson Med. 2006:55:626–632. [DOI] [PubMed] [Google Scholar]
- Fernández A, Ríos-Lago M, Abásolo D, Hornero R, Álvarez-Linera J, Paul N, Maestú F, Ortiz T. The correlation between white-matter microstructure and the complexity of spontaneous brain activity: a diffusion tensor imaging-MEG study. NeuroImage. 2011:57:1300–1307. [DOI] [PubMed] [Google Scholar]
- Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR, et al. . The minimal preprocessing pipelines for the Human Connectome Project. NeuroImage. 2013:80:105–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golesorkhi M, Gomez-Pilar J, Tumati S, Fraser M, Northoff G. Temporal hierarchy of intrinsic neural timescales converges with spatial core-periphery organization. Commun Biol. 2021a:4:277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golesorkhi M, Gomez-Pilar J, Zilio F, Berberian N, Wolff A, Yagoub MCE, Northoff G. The brain and its time: intrinsic neural timescales are key for input processing. Commun Biol. 2021b:4:970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gollo LL, Zalesky A, Hutchison RM, Heuvel M, Breakspear M, Matthew Hutchison R, Heuvel M, Breakspear M. Dwelling quietly in the rich club: brain network determinants of slow cortical fluctuations. Philos Trans R Soc B Biol Sci. 2015:370:20140165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gollo LL, Roberts JA, Cocchi L. Mapping how local perturbations influence systems-level brain dynamics. NeuroImage. 2017:160:97–112. [DOI] [PubMed] [Google Scholar]
- Gómez C, Hornero R, Abásolo D, Fernández A, Escudero J. Analysis of MEG background activity in Alzheimer’s disease using nonlinear methods and ANFIS. Ann Biomed Eng. 2009:37:586–594. [DOI] [PubMed] [Google Scholar]
- Gomez-Pilar J, Luis-García R, Lubeiro A, Uribe N, Poza J, Núñez P, Ayuso M, Hornero R, Molina V. Deficits of entropy modulation in schizophrenia are predicted by functional connectivity strength in the theta band and structural clustering. NeuroImage Clin. 2018:18:382–389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutierrez-Barragan D, Basson MA, Panzeri S, Gozzi A. Infraslow state fluctuations govern spontaneous fMRI network dynamics. Curr Biol. 2019:29:2295–2306.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayes AF. Beyond Baron and Kenny: statistical mediation analysis in the new millennium. Commun Monogr. 2009:76(4):408–420. [Google Scholar]
- He BJ, Raichle ME. The fMRI signal, slow cortical potential and consciousness. Trends Cogn Sci. 2009:13:302–309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He BJ, Zempel JM, Snyder AZ, Raichle ME. The temporal structures and functional significance of scale-free brain activity. Neuron. 2010:66:353–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Himberger KD, Chien HY, Honey CJ. Principles of temporal processing across the cortical hierarchy. Neuroscience. 2018:389:161–174. [DOI] [PubMed] [Google Scholar]
- Huang Z, Liu X, Mashour GA, Hudetz AG. Timescales of intrinsic BOLD signal dynamics and functional connectivity in pharmacologic and neuropathologic states of unconsciousness. J Neurosci. 2018:38:2304–2317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudetz AG, Liu X, Pillay S, Boly M, Tononi G. Propofol anesthesia reduces Lempel-Ziv complexity of spontaneous brain activity in rats. Neurosci Lett. 2016:628:132–135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huk A, Bonnen K, He BJ. Beyond trial-based paradigms: continuous behavior, ongoing neural activity, and natural stimuli. J Neurosci. 2018:38:1920–1917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huntenburg JM, Bazin PL, Margulies DS. Large-scale gradients in human cortical organization. Trends Cogn Sci. 2018:22:21–31. [DOI] [PubMed] [Google Scholar]
- Ibáñez-Molina AJ, Iglesias-Parro S, Soriano MF, Aznarte JI. Multiscale Lempel-Ziv complexity for EEG measures. Clin Neurophysiol. 2015:126(3):541–548. [DOI] [PubMed] [Google Scholar]
- Ibáñez-Molina AJ, Lozano V, Soriano MF, Aznarte JI, Gómez-Ariza CJ, Bajo MT. EEG multiscale complexity in schizophrenia during picture naming. Front Physiol. 2018:9:1213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ito T, Hearne LJ, Cole MW. A cortical hierarchy of localized and distributed processes revealed via dissociation of task activations, connectivity changes, and intrinsic timescales. NeuroImage. 2020:221:117141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji JL, Spronk M, Kulkarni K, Repovš G, Anticevic A, Cole MW. Mapping the human brain’s cortical-subcortical functional network organization. NeuroImage. 2019:185:35–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jo HJ, Gotts SJ, Reynolds RC, Bandettini PA, Martin A, Cox RW, Saad ZS. Effective preprocessing procedures virtually eliminate distance-dependent motion artifacts in resting state FMRI. Im C-H, editor. J Appl Math. 2013:2013:935154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiebel SJ, Daunizeau J, Friston KJ. A hierarchy of time-scales and the brain. PLoS Comput Biol. 2008:4:e1000209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lempel A, Ziv J. On the complexity of finite sequences. IEEE Trans Inf Theory. 1976:22(1):75–81. [Google Scholar]
- Li Q, Hill Z, He BJ. Spatiotemporal dissociation of brain activity underlying subjective awareness, objective performance and confidence. J Neurosci. 2014:34(12):4382–4395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu TT. Noise contributions to the fMRI signal: an overview. NeuroImage. 2016:143:141–151. [DOI] [PubMed] [Google Scholar]
- Luo Q, Xu D, Roskos T, Stout J, Kull L, Cheng X, Whitson D, Boomgarden E, Gfeller J, Bucholz RD. Complexity analysis of resting state magnetoencephalography activity in traumatic brain injury patients. J Neurotrauma. 2013:30:1702–1709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Margulies DS, Ghosh SS, Goulas A, Falkiewicz M, Huntenburg JM, Langs G, Bezgin G, Eickhoff SB, Castellanos FX, Petrides M, et al. . Situating the default-mode network along a principal gradient of macroscale cortical organization. Proc Natl Acad Sci U S A. 2016:113:12574–12579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mateos DM, Guevara Erra R, Wennberg R, Perez Velazquez JL. Measures of entropy and complexity in altered states of consciousness. Cogn Neurodyn. 2018:12:73–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDonald T, Berkowitz R, Hoffman WE. Median EEG frequency is more sensitive to increases in sympathetic activity than bispectral index. J Neurosurg Anesthesiol. 1999:11:255–259. [DOI] [PubMed] [Google Scholar]
- Murphy C, Jefferies E, Rueschemeyer SA, Sormaz M, Wang H, ting, Margulies DS, Smallwood J.. Distant from input: evidence of regions within the default mode network supporting perceptually-decoupled and conceptually-guided cognition. NeuroImage. 2018:171:393–401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray RJ, Debbané M, Fox PT, Bzdok D, Eickhoff SB. Functional connectivity mapping of regions associated with self- and other-processing. Hum Brain Mapp. 2015:36:1304–1324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagarajan R. Quantifying physiological data with Lempel-Ziv complexity - certain issues. IEEE Trans Biomed Eng. 2002:49:1371–1373. [DOI] [PubMed] [Google Scholar]
- Northoff G. Unlocking the brain, volume 2: consciousness, 2013, Oxford University Press.
- Northoff G. “Paradox of slow frequencies” – are slow frequencies in upper cortical layers a neural predisposition of the level/state of consciousness (NPC)? Conscious Cogn. 2017:54:20–35. [DOI] [PubMed] [Google Scholar]
- Northoff G, Wainio-Theberge S, Evers K. Is temporo-spatial dynamics the “common currency” of brain and mind? In quest of “Spatiotemporal Neuroscience”. Phys Life Rev. 2020:33:34–54. [DOI] [PubMed] [Google Scholar]
- Northoff G, Wainio-Theberge S, Evers K. Spatiotemporal neuroscience--what is it and why we need it. Phys Life Rev. 2020b:33:78–87. [DOI] [PubMed] [Google Scholar]
- Pappas I, Adapa RM, Menon DK, Stamatakis EA. Brain network disintegration during sedation is mediated by the complexity of sparsely connected regions. NeuroImage. 2019:186:221–233. [DOI] [PubMed] [Google Scholar]
- Power JD, Mitra A, Laumann TO, Snyder AZ, Schlaggar BL, Petersen SE. Methods to detect, characterize, and remove motion artifact in resting state fMRI. NeuroImage. 2014:84:320–341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poza J, Hornero R, Abásolo D, Fernández A, García M. Extraction of spectral based measures from MEG background oscillations in Alzheimer’s disease. Med Eng Phys. 2007:29:1073–1083. [DOI] [PubMed] [Google Scholar]
- Raut RV, Mitra A, Marek S, Ortega M, Snyder AZ, Tanenbaum A, Laumann TO, Dosenbach NUF, Raichle ME. Organization of propagated intrinsic brain activity in individual humans. Cereb Cortex. 2020:30:1716–1734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salimi-Khorshidi G, Douaud G, Beckmann CF, Glasser MF, Griffanti L, Smith SM. Automatic denoising of functional MRI data: combining independent component analysis and hierarchical fusion of classifiers. NeuroImage. 2014:90:449–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schabus M, Dang-Vu TT, Albouy G, Balteau E, Boly M, Carrier J, Darsaud A, Degueldre C, Desseilles M, Gais S, et al. . Hemodynamic cerebral correlates of sleep spindles during human non-rapid eye movement sleep. Proc Natl Acad Sci. 2007:104:13164–13169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schartner MM, Carhart-Harris RL, Barrett AB, Seth AK, Muthukumaraswamy SD. Increased spontaneous MEG signal diversity for psychoactive doses of ketamine, LSD and psilocybin. Sci Rep. 2017:7(1):1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schreiber T, Schmitz A. Surrogate time series. Phys D Nonlinear Phenom. 2000:142(3-4):346–382. [Google Scholar]
- Schwender D, Daunderer M, Mulzer S, Klasing S, Finsterer U, Peter K. Spectral edge frequency of the electroencephalogram to monitor “depth” of anaesthesia with isoflurane or propofol. Br J Anaesth. 1996:77:179–184. [DOI] [PubMed] [Google Scholar]
- Schwilden H, Schuttler J, Stoeckel H. Quantitation of the EEG and pharmacodynamic modelling of hypnotic drugs: etomidate as an example. Eur J Anaesthesiol. 1985:2:121–131. [PubMed] [Google Scholar]
- Seabold S, Perktold J.. 2010. Statsmodels: econometric and statistical modeling with Python, Proceedings of the 9th Python in Science Conference.
- Szczepański J, Amigó JM, Wajnryb E, Sanchez-Vives MV. Application of Lempel-Ziv complexity to the analysis of neural discharges. Netw Comput Neural Syst. 2003:14:335–350. [PubMed] [Google Scholar]
- Tagliazucchi E, Carhart-Harris R, Leech R, Nutt D, Chialvo DR. Enhanced repertoire of brain dynamical states during the psychedelic experience. Hum Brain Mapp. 2014:35:5442–5456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thanh Vu A, Jamison K, Glasser MF, Smith SM, Coalson T, Moeller S, Auerbach EJ, Uğurbil K, Yacoub E. Tradeoffs in pushing the spatial resolution of fMRI for the 7T Human Connectome Project. NeuroImage. 2017:154:23–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tingley D, Yamamoto T, Hirose K, Keele L, Imai K. Mediation: R package for causal mediation analysis. J Stat Softw. 2014:59(5):1–38. [Google Scholar]
- Van Essen DC, Smith SM, Barch DM, Behrens TEJ, Yacoub E, Ugurbil K. The WU-Minn Human Connectome Project: an overview. NeuroImage. 2013:80:62–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varley TF, Luppi AI, Pappas I, Naci L, Adapa R, Owen AM, Menon DK, Stamatakis EA. Consciousness & brain functional complexity in propofol anaesthesia. Sci Rep. 2020:10:1018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verrusio W, Ettorre E, Vicenzini E, Vanacore N, Cacciafesta M, Mecarelli O. The Mozart effect: a quantitative EEG study. Conscious Cogn. 2015:35:150–155. [DOI] [PubMed] [Google Scholar]
- Wang P, Kong R, Kong X, Liégeois R, Orban C, Deco G, Van Den Heuvel MP, Yeo BTT. Inversion of a large-scale circuit model reveals a cortical hierarchy in the dynamic resting human brain. Trop Subtrop Agroecosyst. 2019:5(1):eaat7854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welch PD. The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans Audio Electroacoust. 1967:15:70–73. [Google Scholar]
- Wolff A, Berberian N, Golesorkhi M, Gomez-Pilar J, Zilio F, Northoff G. Intrinsic neural timescales: temporal integration and segregation. Trends in cognitive sciences. 2022:26(2):159–173. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Mao Z, Feng S, Liu X, Lan L, Zhang J, Yu X. Altered functional networks in long-term unilateral hearing loss: a connectome analysis. Brain Behav. 2018:8:e00912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zilio F, Gomez-Pilar J, Cao S, Zhang J, Zang D, Qi Z, Tan J, Hiromi T, Wu X, Fogel S, et al. . Are intrinsic neural timescales related to sensory processing? Evidence from abnormal behavioral states. NeuroImage. 2021:226:117579. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.