Abstract
This paper makes the first comparative assessment of the impacts of the first and second waves of the ongoing COVID-19 pandemic for the US stock market and its uncertainty. To this end, we investigate the dynamic conditional correlation and the asymmetric impacts of shocks on the correlation between the US and Chinese stock markets before and during the COVID-19 crisis. Furthermore, we analyze and compare the relationship between the COVID-19 pandemic and US returns and uncertainty during the first and second waves of the pandemic. First, we find that the dynamic correlation approach supports the presence of volatility spillovers (contagion effects) between the two stock markets, especially during the rapid spread phase of COVID-19 in the US. Second, the analysis of news impact correlation surfaces shows that the shocks to the US and Chinese markets have asymmetric effects on the correlation between the two markets. Finally, we find a persistent link between US returns, uncertainty, and the COVID-19 pandemic during the first and second waves of the outbreak. Our results prove that the pandemic has shown harmful consequences for financial markets in general and the US economy in particular.
Keywords: COVID-19 pandemic, Comparative assessment, First wave, Second wave, US stock market, Economic uncertainty
1. Introduction
The World Health Organization (WHO) declared the COVID-19 outbreak to be a global emergency on January 30, 2020. Nine months later, the COVID-19 pandemic had resulted in roughly 31.12 million confirmed cases and over 950,000 deaths (WHO, 2020). As a result, the governments of the world's largest countries have enforced border shutdowns, travel restrictions, and quarantine, thus sparking fear of an impending financial recession and economic crises.
The COVID-19 pandemic has also affected the world economy through the shutdown of financial market indices. The ensuing financial crisis is detectable in the behaviors of different stock market indices. In the United States (US), for example, the S&P 500, DJI Average, and Nasdaq index fell dramatically until the government secured the Coronavirus Aid, Relief, and Economic Security (CARES) Act, at which point the three indices rose by 7.3%,1 7.73%,2 and 7.33%,3 respectively. Moreover, the 10-year US Treasury Bond Yields have dropped to 0.67%.4 Several research papers have recently explored and confirmed the dramatic impact of the COVID-19 crisis on financial markets (see, e.g., Albulescu, 2020; Zaremba et al., 2020; Zhang et al., 2020; Corbet et al., 2020; Akhtaruzzaman et al., 2020; Ashraf, 2020; Sharif et al., 2020; Goodell, 2020).
The main purpose of this paper is twofold. First, we model volatility spillovers by examining the conditional correlations between the Chinese and US stock indices before and during the COVID-19 pandemic. Further, we examine the asymmetric impacts of shocks on the correlation between the two markets. To this end, we apply auto regressive moving average dynamic conditional correlation generalized autoregressive conditional heteroskedasticity (ARMA-DCC-GARCH(1,1)) and ARMA-asymmetric DCC-GARCH (ARMA-ADCC-GARCH(1,1)) models, which explicitly consider the leverage effect in financial markets. Second, we examine the persistence in the relationship between COVID-19 metrics (cases and deaths) and the US stock market and its uncertainty using the DCC process and the wavelet approach.
This paper contributes to the literature in two ways. First, we shed light on the spillover risk between the Chinese and US stock markets from January 5, 2011 to September 21, 2020, which period includes the COVID-19 pandemic period. Second, we investigate the persistence of the linkage between the global cumulative daily confirmed infection cases and deaths generated by COVID-19 and the US stock market, as well as US uncertainty5 during the first and the second waves of the COVID-19 pandemic (i.e., between January 13, 2020 and September 21, 2020).
Our findings suggest that the volatility spillover between the Chinese and US stock markets has been higher during the COVID-19 period compared to the pre-COVID-19 one. We also identify a long and persistent relationship between the US market and the global daily COVID-19 cases and deaths. This relationship includes various levels of US stock market uncertainty. Even after the general quarantine restrictions during the first COVID-19 wave were lifted, the correlation continued during the second wave. Consequently, our results confirm that the COVID-19 health crisis has had harmful consequences for financial markets and the macroeconomic conditions in the US. The pandemic's effect is especially pronounced with respect to increasing economic uncertainty. The main findings of this paper are thus confirming recent empirical results (Kurita and Managi, 2020; Katafuchi et al., 2020; Yoo and Managi, 2020).
The rest of the paper is organized as follows. In Section 2, we briefly review the related literature on the socioeconomic impacts of the COVID-19 crisis. Section 3 presents the empirical methodology and the data. We then discuss the results in Section 4. Finally, the robustness check of the main empirical results are presented in Section 5, while Section 6 concludes the paper.
2. Related literature: empirical findings
Focusing on recent publications on the financial and socioeconomic impacts of the COVID-19 pandemic, we review the related literature from two perspectives: (1) the transmission volatility during the COVID-19 crisis and (2) the relationship of COVID-19 metrics with stock market performance and economic uncertainty. Several recent studies investigate the financial and socioeconomic impacts of the COVID-19 crisis. For instance, Akhtaruzzaman et al. (2020) use the DCC approach to examine contagion transmission for both financial and nonfinancial firms between China and the G7 economies during the COVID-19 pandemic. They find that both financial and non-financial firms experience a significant increase in the conditional correlations between their stock returns. They also argue that the magnitude of the increase in these correlations is considerably higher for financial firms, indicating their important role in financial contagion transmission between China and the G7 countries. Finally, they show that the optimal hedge ratios increase significantly in most cases, which imply higher hedging costs during the COVID-19 crisis period. Corbet et al. (2020) indicate that, at the beginning of the 2020 COVID-19 pandemic, it came as no surprise that the Chinese markets acted as the epicenter of both physical and financial contagion. Furthermore, Corbet et al. (2021) show the existence of sharp, dynamic, and new correlations related to the term “corona.” Zhang et al. (2020) conclude that the rapid spread of COVID-19 has had dramatic impacts on financial markets worldwide, thus leading to a significant increase in global financial market risk and causing investors to suffer significant losses over a short period of time.
Concerning the impact of the pandemic on economic uncertainty, several studies show that the COVID-19 crisis has been characterized by high uncertainty levels affecting all major economies. For instance, Ashraf (2020) uses daily the number of COVID-19 confirmed cases and deaths and panel data analysis techniques to examine the stock market responses to the COVID-19 crisis. He shows that stock markets responded negatively to the growth in the number of confirmed cases, as stock market returns declined as the number of confirmed cases increased. Furthermore, stock markets reacted more proactively to the growth in the number of confirmed cases than to the one in the number of deaths.
Based on a wavelet-based approach, Sharif et al. (2020) use daily COVID-19 observations (i.e., number of cases in the US) to investigate the relationship between the recent spread of COVID-19, oil price volatility shocks, the stock market, geopolitical risks, and economic policy uncertainty in the US. They show that the effect of the COVID-19 pandemic on geopolitical risks is substantially higher compared to its impacts on US economic uncertainty. Additionally, Goodell (2020) highlights the possible impacts of COVID-19 on financial markets and institutions and Zaremba et al. (2020) explore the policy responses to the pandemic in 67 countries, demonstrating that non-pharmaceutical interventions significantly increased equity market volatility.
Albulescu (2020) uses ordinary least squares (OLS) regression to examine the impact of official announcements of COVID-19 new cases and the fatality ratio on the volatility of the US financial market. He considers both the global and US COVID-19 metrics, and demonstrate that the pandemic enhanced the realized volatility of the S&P 500 index. He also suggests that the prolonged nature of the COVID-19 pandemic is an important source of financial volatility and thus presents a challenge for risk management.
This brief literature review focuses on recent developments in the research on the socioeconomic impacts of the COVID-19 pandemic. The following section develops the empirical methodology used to investigate how these impacts manifest in financial markets and in terms of economic uncertainty.
3. Empirical methodology
3.1. Empirical model
Several empirical methods have been used to investigate the risk spillovers and estimate correlations between stock market returns. In this paper, we use the multivariate GARCH to model volatility and construct dynamic conditional correlations based on a rolling-window analysis. We chose to use restricted correlation models, such as DCC and ADCC due to their comparative advantages. Namely, they are designed to solve the problems encountered when using the Baba, Engle, Kraft, and Kroner (BEKK) and VECH models due to the presence of a large number of free parameters. The DCC and ADCC models are easier to estimate and are comparatively more robust. They are thus the most appropriate for examining the time-varying correlations between financial products and economic variables (Ciner et al., 2013).
Let be an n × 1 vector of the sample's asset returns and ARMA(1,1) a process in the mean equation for , where is conditional on the set of information and residuals, . The equation can be written as:
| (1) |
and the residuals can be modeled as:
| (2) |
is the conditional covariance matrix of and is an n × 1 identically and independently distributed vector of random errors. In the first step, we estimate the GARCH parameters and then we estimate the dynamic conditional correlations in the second step:
| (3) |
is the conditional covariance matrix, n × n, and is the conditional correlation matrix. is a diagonal matrix with time-varying standard deviations on the diagonal. and are determined as:
| (4) |
| (5) |
where h is the expression of the univariate GARCH models, which are used to derive the expression of h on the diagonal matrix (where H is a diagonal matrix). The GARCH(1,1) parameters of can be expressed by:
| (6) |
is a symmetric positive definite matrix, and can be written as follows:
| (7) |
is the n × n unconditional correlation matrix of the standardized residuals, . Parameters and are associated with the smoothing process and are used to construct DCCs. The DCC model means return to equilibrium if is less than unity () and positive. The correlation is estimated as follow:
| (8) |
We use an ADCC model because the DCC model fails to capture asymmetry effects:
| (9) |
The indicator function, , is equal to 1 if , and 0 otherwise. The dynamics of for the ADCC model are given as:
| (10) |
where A, B, and G are n × n parameter matrices and is a vector of zero-threshold standardized errors, which are equal to when below 0, and 0 otherwise. and are the unconditional matrices of and , respectively. To test these models and their relevance for our research question, we construct a daily dataset collected from different sources. The next sub-section presents the data and describes their proprieties.
3.2. Data
To perform empirical investigations, we used daily data from the US S&P 500 index, which measures the stock performance of the 500 large companies traded on the exchange, and on Chinese stocks from the CSI 300 index. We chose the CSI 300 index because it is a capitalization-weighted stock market index designed to replicate the performance of the top 300 stocks traded on the Shanghai and Shenzhen stock markets. It has also been frequently and commonly used as a representative index to measure the overall performance of the Chinese stock market (Chen et al., 2013). The CSI 300 prices are denominated in CNY while the S&P 500 ones are denominated in USD. We collected daily data for the S&P 500 index and the CSI 300 index from January 5, 2011 to September 21, 2020, meaning our sample period covers the COVID-19 crisis as well.
The choice of the starting date and the analysis period is justified by our research objective and supported by the availability of the data for both indices. Further, we assembled another dataset on the cumulative cases of COVID-19 infections and deaths, US stock market performance (S&P 500), VIX, and EPU. The VIX measures the volatility of the stock market (S&P 500) and represents the stock market's expectations of volatility over the next 30 days. Higher VIX values represent more uncertainty or fear in the market, while lower values indicate less market uncertainty.
The EPU is a new measure of uncertainty, developed by Baker et al. (2020), which is based on the frequency of newspaper references to the number and size of federal tax code provisions set to expire in future years; it also captures the disagreement among economic forecasters about policy relevant variables and economic policy uncertainty. The S&P 500 index data were collected from the Federal Reserve Bank of St. Louis and the CSI data from Yahoo Finance. The VIX was also obtained from Yahoo Finance. The US EPU index can be freely downloaded from the EPU website.6 Finally, we obtained data on the global cumulative daily COVID-19 cases and deaths from the WHO.
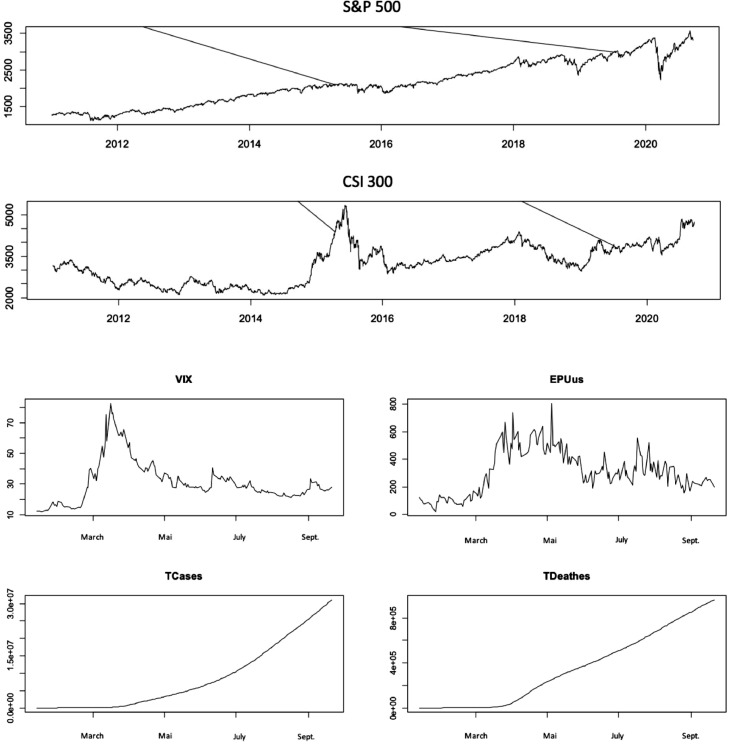
To perform a comparative assessment of the socioeconomic impacts between the first and second COVID-19 waves, we used a sample from January 13, 2020 to September 21, 2020. The different data series show different patterns as follows (see Fig. 1 ). The US and Chinese stock markets experienced a significant drop during the COVID-19 pandemic. By contrast, the two measures of US economic uncertainty (VIX and EPU) show a sharp rise around the start of the COVID-19 pandemic. The higher values represent more uncertainty or fear for both the S&P 500 and the overall economic situation, their rise coinciding with the rising numbers of COVID-19 infection cases and deaths globally.
Fig. 1.
Time series plots of daily series (financial markets indices, VIX, cases, and deaths).
Using these daily series, we calculated the daily returns as follows:
where is the daily closing price or settlement. The descriptive statistics for the S&P 500 and CSI 300 series are presented in Table 1 .
Table 1.
Descriptive statistics of the S&P 500 and CSI 300 daily data.
| S&P 500 | CSI 300 | |
|---|---|---|
| No. obs. | 2292 | 2292 |
| Min | −12.76522 | −9.15444 |
| Max | 8.96832 | 7.42630 |
| Range | 21.73354 | 16.58074 |
| Median | 0.06903 | 0.02373 |
| Mean | 0.04119 | 0.01703 |
| S.E. mean | 0.02360 | 0.03075 |
| Var. | 1.27646 | 2.16792 |
| Std. dev. | 1.12980 | 1.47239 |
| Coef. var. | 27.43135 | 86.48180 |
| JB | 31,000 | 2700 |
| Prob. | < 2e-16 | < 2e-16 |
| ARCH (12) | 910 | 260 |
| Prob. | < 2e-16 | < 2e-16 |
Note: S.E., Var, Coef. var., and Std. dev., stand for standard error, variance, coefficient of variance, and standard deviation. JB is the Jarque-Bera test with the null hypothesis of normality. ARCH is the autoregressive heteroskedasticity test. < 2e-16 indicates small p-values and the rejection of a null hypothesis at the 1% significance level.
The means of both stock returns (China and the US) both before and during the COVID-19 pandemic represent positive daily returns. The coefficients of variation indicate that the CSI 300 has a higher variability and the S&P 500 a lower variability. The S&P 500 also has a lower standard deviation. The Jarque-Bera and ARCH-LM test reveal normality and heteroskedasticity issues. The Jarque-Bera test reveals that each series is far from being normally distributed. The ARCH-LM(12) test show strong evidence of ARCH effects, meaning that all series exhibit strong clustering. Table 2 shows the descriptive statistics of the S&P 500, US EPU, VIX, and world cumulative daily COVID-19 cases and deaths for the first and second waves.
Table 2.
Descriptive statistics of daily data S&P 500, US EPU, VIX and COVID-19 cases/deaths.
| First wave of COVID-19 | |||||
|---|---|---|---|---|---|
| S&P 500 | EPU | VIX | Cases | Deaths | |
| Min | −12.76522 | −77.8809 | −26.6228 | 0.000 | 0.000 |
| Max | 8.96832 | 144.8161 | 38.2167 | 178.161 | 113.635 |
| Range | 21.73354 | 222.6970 | 64.8394 | 178.161 | 113.635 |
| Median | 0.18418 | −1.1564 | −1.2072 | 5.585 | 5.907 |
| Mean | −0.01693 | 0.9279 | 0.7322 | 11.546 | 12.775 |
| S.E. mean | 0.31413 | 3.1539 | 1.1193 | 2.217 | 2.060 |
| Var | 9.96637 | 1004.6517 | 126.5385 | 496.431 | 428.403 |
| Std. dev. | 3.15696 | 31.6962 | 11.2489 | 22.281 | 20.698 |
| Coef. var. | −186.49388 | 34.1587 | 15.3629 | 1.930 | 1.620 |
| JB | 54 | 61 | 45 | 5200 | 830 |
| Prob. | 2e-12 | 5e-14 | 2e-10 | < 2e-16 | < 2e-16 |
| ARCH (12) | 37 | 13 | 23 | 75 | 67 |
| Prob. | 2e-04 | 0.4 | 0.03 | 4e-11 | 1e-09 |
| Second wave of COVID-19 | |||||
| Min | −6.0753 | −63.1028 | −12.2421 | 0.8317 | 0.45687 |
| Max | 3.1015 | 58.6848 | 39.1709 | 7.3858 | 5.85851 |
| Range | 9.1768 | 121.7876 | 51.4130 | 6.5541 | 5.40164 |
| Median | 0.3590 | 0.5865 | −1.1041 | 1.8011 | 1.11765 |
| Mean | 0.1348 | −0.8796 | −0.1874 | 2.3205 | 1.48414 |
| S.E. mean | 0.1338 | 2.6225 | 0.7409 | 0.1555 | 0.09679 |
| Var. | 1.8088 | 694.6205 | 55.4387 | 2.4437 | 0.94613 |
| Std. dev. | 1.3449 | 26.3557 | 7.4457 | 1.5632 | 0.97269 |
| Coef. var. | 9.9763 | −29.9622 | −39.7228 | 0.6737 | 0.65539 |
| JB | 92 | 0.71 | 280 | 73 | 120 |
| Prob. | < 2e-16 | 0.7 | < 2e-16 | < 2e-16 | < 2e-16 |
| ARCH (12) | 6 | 11 | 1.2 | 53 | 61 |
| Prob. | 0.9 | 0.6 | 1 | 5e-07 | 2e-08 |
Note: S.E., Var., Coef. var., and Std. dev. stand for standard errors, variance, coefficient of variance, and standard deviation, respectively. JB is the Jarque-Bera test with the null hypothesis of normality. ARCH is the autoregressive heteroskedasticity test. < 2e-16 indicate the rejection of the null hypothesis at the 1% significance level.
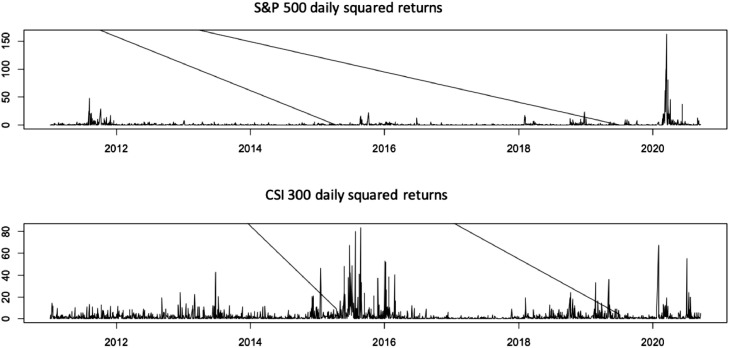
The time series graphs of returns squared (Fig. 2 ) show how volatility has changed for the S&P 500 and CSI 300 over time. Each series displays several periods of volatility clustering in the pre-COVID-19 period and during the COVID-19 pandemic. The effect is most pronounced for the S&P 500 during the pandemic.
Fig. 2.
Squared daily data plots.
4. Discussion of the empirical results
Our modeling strategy is to first estimate four different versions of the DCC and ADCC models. Each version includes a constant in the mean equation and a GARCH(1,1) variance equation. Adjustments were made to include an ARMA(1,1) () term in the mean equation and the distribution choice. The model selection criteria indicate that the best fit is the first version (A) of the DCC and ADCC models with the AR (1) and MA (1) terms in the mean equation estimated with a multivariate t distribution (see Table 3 ) for the S&P 500 and CSI 300. Consequently, both models are estimated with the AR(1) and MA(1) terms in the mean equation. To address the non-normality in the distribution of returns, the DCC and ADCC models are estimated with a multivariate t distribution.
Table 3.
Different specifications of the DCC and ADCC models.
| DCC | ||||
|---|---|---|---|---|
| A | B | C | D | |
| ARMA(1,1) | yes | no | yes | no |
| Distribution | MVT | MVT | MV NOR | MV NOR |
| No. obs. | 2292 | 2292 | 2292 | 2292 |
| Akaike | 5.6917 | 5.7011 | 5.8394 | 5.8500 |
| Bayes | 5.7468 | 5.7362 | 5.8870 | 5.8776 |
| Shibata | 5.6915 | 5.7010 | 5.8393 | 5.8500 |
| Hannan-Quinn | 5.7118 | 5.7139 | 5.8568 | 5.8601 |
| Likelihood | −6501 | −6519 | −6673 | −6693 |
| ADCC | ||||
| A | B | C | D | |
| ARMA(1,1) | yes | no | yes | no |
| Distribution | MVT | MVT | MV NOR | MV NOR |
| No. obs. | 2292 | 2292 | 2292 | 2292 |
| Akaike | 5.6674 | 5.6688 | 5.8158 | 5.8217 |
| Bayes | 5.7300 | 5.7114 | 5.8709 | 5.8567 |
| Shibata | 5.6672 | 5.6687 | 5.8156 | 5.8216 |
| Hannan-Quinn | 5.6903 | 5.6843 | 5.8359 | 5.8344 |
| Likelihood | −6470 | −6479 | −6643 | −6658 |
Note: This table presents the diagnostic statistics for each type of DCC and ADCC specification.
We model the ARMA-DCC-ADCC-GARCH process between the US (S&P 500) and Chinese stock markets (CSI 300). The results are presented in Table 4 . The lag order (1,1) is chosen by minimized information criteria (including the Akaike and the Schwarz information criteria) (Table 3). The results of the mean equation show that the coefficients on all return series are significant at the 10% level.
Table 4.
Estimation results for the ARMA-DCC-ADCC-GARCH process.
| DCC | ADCC | |||||||
|---|---|---|---|---|---|---|---|---|
| Coef. | S.E. | t-stat | Prob | Coef. | S.E. | t-stat | Prob | |
| 0.076282 | 0.005486 | 1.390e+01 | 0.00000 | 0.074262 | 0.012511 | 5.935825 | 0.000000 | |
| 0.959602 | 0.008604 | 1.115e+02 | 0.00000 | 0.763577 | 0.114258 | 6.682928 | 0.000000 | |
| −1.034701 | 0.000011 | −9.17e+04 | 0.00000 | −0.819141 | 0.116016 | −7.060620 | 0.000000 | |
| 0.027871 | 0.007215 | 3.860e+00 | 0.00012 | 0.030567 | 0.006465 | 4.727788 | 0.000002 | |
| 0.185074 | 0.028642 | 6.461e+00 | 0.00000 | 0.000436 | 0.017796 | 0.024515 | 0.980442 | |
| 0.808261 | 0.025064 | 3.228e+01 | 0.00000 | 0.824524 | 0.024022 | 34.323514 | 0.000000 | |
| 0.294672 | 0.051119 | 5.764436 | 0.000000 | |||||
| 4.497313 | 0.352616 | 1.275e+01 | 0.00000 | 4.709163 | 0.411914 | 11.432406 | 0.000000 | |
| 0.041053 | 0.021508 | 1.907e+00 | 0.05600 | 0.038547 | 0.021795 | 1.768637 | 0.076954 | |
| −0.851760 | 0.086278 | −9.83e+00 | 0.00000 | −0.85170 | 0.086537 | −9.834702 | 0.000000 | |
| 0.849592 | 0.087669 | 9.690e+00 | 0.00000 | 0.850468 | 0.087846 | 9.681397 | 0.000000 | |
| 0.013565 | 0.005676 | 2.390e+00 | 0.01648 | 0.015339 | 0.007077 | 2.167408 | 0.030204 | |
| 0.057572 | 0.010050 | 5.728e+00 | 0.00000 | 0.051603 | 0.010820 | 4.769331 | 0.000002 | |
| 0.939849 | 0.009696 | 9.693e+01 | 0.00000 | 0.937363 | 0.011737 | 79.861534 | 0.000000 | |
| 0.015100 | 0.018404 | 0.820452 | 0.411958 | |||||
| 4.440714 | 0.365139 | 1.216e+01 | 0.00000 | 4.407926 | 0.363746 | 12.118146 | 0.000000 | |
| a | 0.002567 | 0.001322 | 1.942e+00 | 0.05207 | 0.012249 | 0.014017 | 0.873901 | 0.382172 |
| 0.996613 | 0.002131 | 4.675e+02 | 0.00000 | 0.933156 | 0.166451 | 5.606178 | 0.000000 | |
| c | 0.000000 | 0.016984 | 0.000009 | 0.999993 | ||||
| 5.123312 | 0.297466 | 1.723e+01 | 0.00000 | 5.260955 | 0.329326 | 15.974936 | 0.000000 | |
| Akaike | 5.6917 | 5.6674 | ||||||
| Bayes | 5.7468 | 5.7300 | ||||||
| Shibata | 5.6915 | 5.6672 | ||||||
| H-Q | 5.7118 | 5.6903 | ||||||
| LL | −6501 | −6470 | ||||||
Notes: DCC and ADCC are estimated using a multivariate normal (MVNORM) distribution. All specifications include a constant and AR(1) and MA(1) terms in the mean equation.
The short-term persistence (α) is statistically significant for most variables under the two models. The estimated coefficient on long-term persistence (β) is statistically significant for each series, thus indicating the importance of long-term persistence. The sum of the coefficients for short-term and long-term persistence is less than unit. In each case, the short-term persistence is lower than the long-term one, which indicates that long-term volatility is more intense than short-term volatility. The statistical significance of short- and long-term persistence provides evidence of volatility clustering. We can also see volatility clustering for all variables in Fig. 2. The estimated asymmetric term (γ) is positive and statistically significant for the S&P 500. This means that the negative residuals for the S&P 500 tend to increase variance (conditional volatility) more than positive shocks of the same magnitude, while there is no statistically significant leverage effect for the Chinese market.
We then estimated the dynamic conditional correlation coefficients and the results are presented in Table 4. The estimated coefficients, a and , are positive and statistically significant at the 1% level in each of the two models (except for in the ADCC model). Their sum is below unity, which indicates that the DCCs return to equilibrium (i.e., are mean-reverting). We can conclude that the DCC models are reasonable and that the volatility of recent returns has a significant influence on the dynamic relationship between the S&P 500 stock market and all variables, as indicated by the considerable value of a. Nonetheless, the values of are all significant and close to 1 for each series, indicating that the dynamic relationships between the equity market and all other variables are long-term persistent. Our results confirm the long-term relationship between the US and Chinese stock markets.
For parameter Shape (λ), which represents the degrees of freedom, the S&P 500 has the highest estimated value. This means that the distribution of CSI 300 stocks has larger tails than the S&P 500 distribution. Shape is equal to the degrees of freedom when the number of degrees of freedom approaches infinity and the form of distribution t approaches that of a normal distribution. The information criteria show that the ADCC is the best fitting model.
4.1. Analysis of dynamic conditional correlations
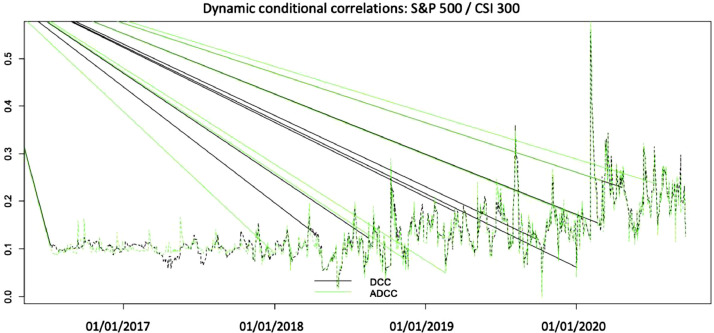
To construct dynamic conditional correlations between the US and Chinese stock markets that are one step ahead, we use rolling window analysis. The estimation window is fixed at 2292 observations and 1000 dynamic conditional correlations one step ahead are also produced. GARCH models are refitted every 20 observations. Considering that the relationship between the US and China changes over time, we explore the time-varying dynamic conditional correlation of the market pair before and during the COVID-19 pandemic. The results are presented in Fig. 3 .
Fig. 3.
Rolling one-step-ahead dynamic conditional correlations.
For comparison, we considered for the S&P 500/CSI 300 pair that the time-varying conditional correlations obtained from the DCC and ADCC models exhibit similar patterns. The results of the time-varying conditional correlations show that the conditional correlation between the two markets fluctuates greatly during the analysis period, meaning that investors adjust their portfolio structures frequently. That the dynamic conditional correlation among the market pair is positive and supports the presence of contagion effects, especially at the beginning of the third quarter of 2020 during the rapid increase in the number of COVID-19 cases in the US. Consequently, during the COVID-19 crisis, the risk spillover between the Chinese and US stock markets was strong. From Fig. 3, the dynamic correlations between the two markets under both models are higher during the COVID-19 period compared to the pre-COVID-19 one. In sum, the correlation between the S&P 500 and CSI 300 stock markets is time-varying and highly volatile, suggesting portfolio managers should change their portfolio structures over time.
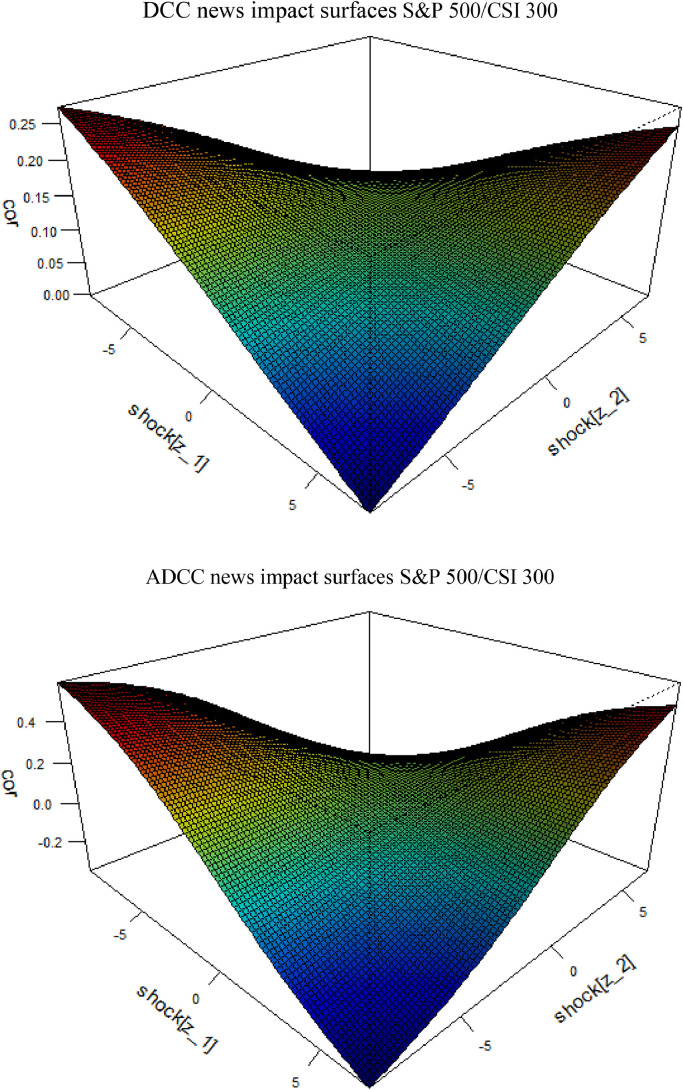
Moreover, we analyze the news impact correlation surfaces for each pair (see Fig. 4 ). We find that the news impact correlation surfaces of the DCC and ADCC models have similar shapes. For the S&P 500/CSI 300 pair, the results of the news impact correlation surfaces of the DCC or ADCC models show that the shocks to each stock market have asymmetric effects on the correlation between US and Chinese markets. Moreover, the shape of the news impact correlation surfaces produced from the DCC and ADCC models for each pair are convex.
Fig. 4.
News impact correlation surfaces between S&P 500 and CSI 300.
4.2. Persistence of linkage between the S&P 500, EPU, and VIX during the first and second COVID-19 waves
To produce a comparative assessment of the contagion effect between the second and first waves of the COVID-19 pandemic, we apply the DCC process to estimate the dynamic conditional correlation coefficients between the US stock market, the US EPU index, the VIX, and global cumulative daily COVID-19 cases and deaths (see Table 5 ). We estimate and compare the persistence of the correlation between the pair during the first and second waves of the COVID-19 pandemic.
Table 5.
DCC parameters between the US stock market, US uncertainty, and the COVID-19 pandemic.
| First wave of the COVID-19 pandemic | ||||||
|---|---|---|---|---|---|---|
| S&P 500/COVID-19 | VIX/COVID-19 | US EPU/COVID-19 | ||||
| Coef. | Prob. | Coef. | Prob. | Coef. | Prob. | |
| 0.144328 | 0.000004 | 0.144267 | 0.000016 | 0.161976 | 0.000001 | |
| 0.855672 | 0.000000 | 0.855733 | 0.000000 | 0.838024 | 0.000000 | |
| Second wave of the COVID-19 pandemic | ||||||
| S&P 500/COVID-19 | VIX/COVID-19 | US EPU/COVID-19 | ||||
| Coef. | Prob. | Coef. | Prob. | Coef. | Prob. | |
| 0.050281 | 0.000056 | 0.049712 | 0.000000 | 0.046179 | 0.000000 | |
| 0.939617 | 0.000000 | 0.941952 | 0.000000 | 0.925436 | 0.000000 | |
During the first and second waves of the COVID-19 pandemic, the estimated coefficients, and , are positive and statistically significant at the 1% level. Their sum is below 1, which indicates that the DCCs return to equilibrium (i.e., are mean-reverting). Consequently, we can conclude that the DCC models are reasonable and that the volatility of recent returns has a significant influence on the dynamic relationship between the S&P 500 stock market, the VIX, the US EPU index, and the global cumulative daily COVID-19 cases and deaths, which is indicated by the considerable value of coefficient . Nonetheless, the values of coefficient are all significant and close to 1 for each pair, indicating that the dynamic linkages between the US stock market, the two measures of US uncertainty, and the COVID-19 pandemic are long-term persistent.
Finally, our results confirm the long-term relationship between the US stock market, the VIX, the US EPU. and the global cumulative daily COVID-19 cases and deaths during the first and second waves of the pandemic. Even after the general quarantine restrictions were eased after the first wave, the correlation continued to persist during the second wave. We can conclude that the continued rise in COVID-19 infections and deaths during the first and second waves increased the uncertainty on the US stock market and the economic, with serious financial consequences. Our results confirm the recently published findings of Zhang et al. (2020).
5. Robustness check: wavelet analysis
We tested the robustness of the empirical results using the wavelet coherence method, namely focusing on the correlation between the financial and economic variables and the COVID-19 pandemic variables (i.e., total cases and deaths). The wavelet coherence technique identifies specific parts of the domain of time-frequency (see Grinsted et al., 2004), where unexpected and major variations happen in the co-movement patterns of the time series under observation. The equation of the coefficient of the adjusted wavelet coherence, as identified by Torrence and Compo (1998), is expressed as follows:
M is the smoothing mechanism. The value of the wavelet squared coherence ranges from 0 to 1 (0 ≤ ≤ 1).The range of the squared wavelet coherence coefficient shows the correlation degree. Indeed, when this coefficient is close to 0, it indicates the absence of correlation (no co-movement), and when it is close to 1, it indicates a higher correlation (higher co-movement) that can be considered a scale-specific squared correlation between series. The Monte Carlo method is used to examine the hypothetical allocation of the wavelet coherence. This approach allows us to examine the lead/lag relationship between two series, while avoiding the issue of the squared coherence not being able to distinguish the positive and negative relationships between two series.
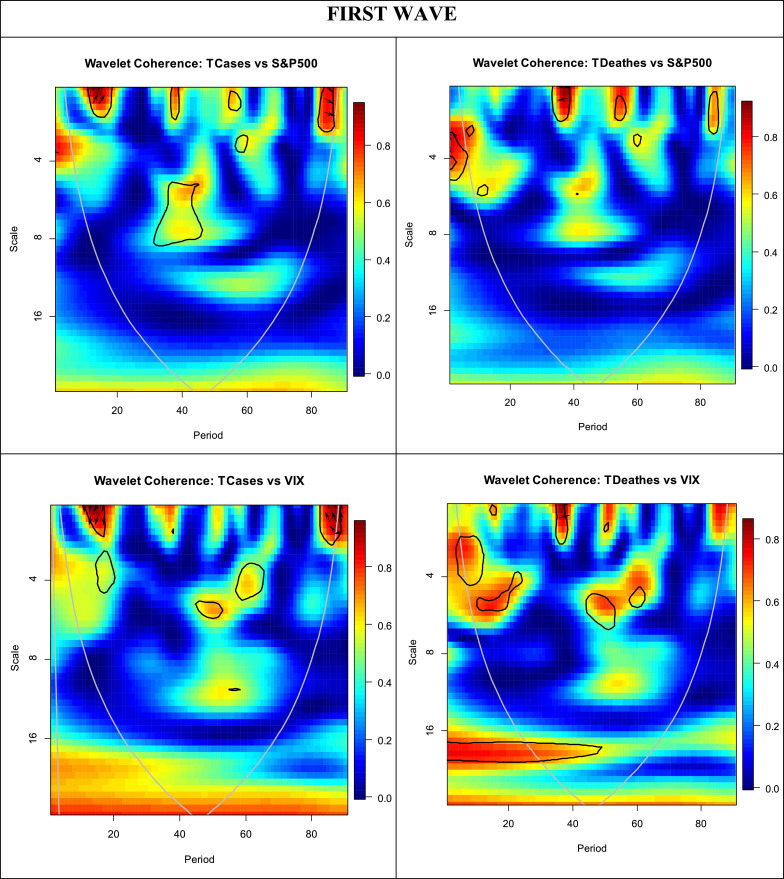
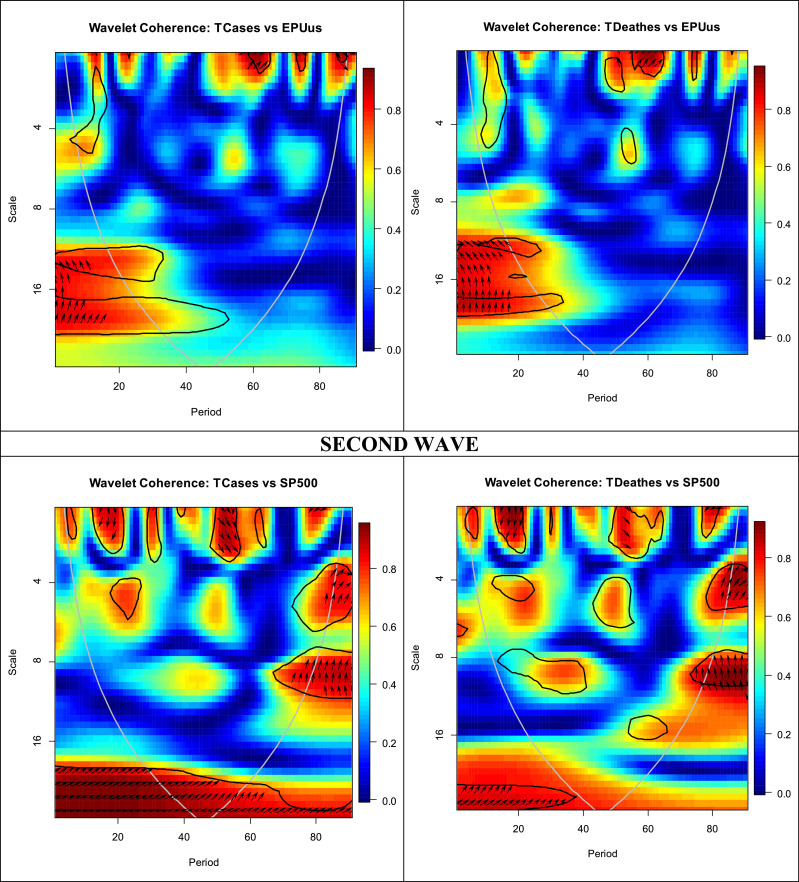
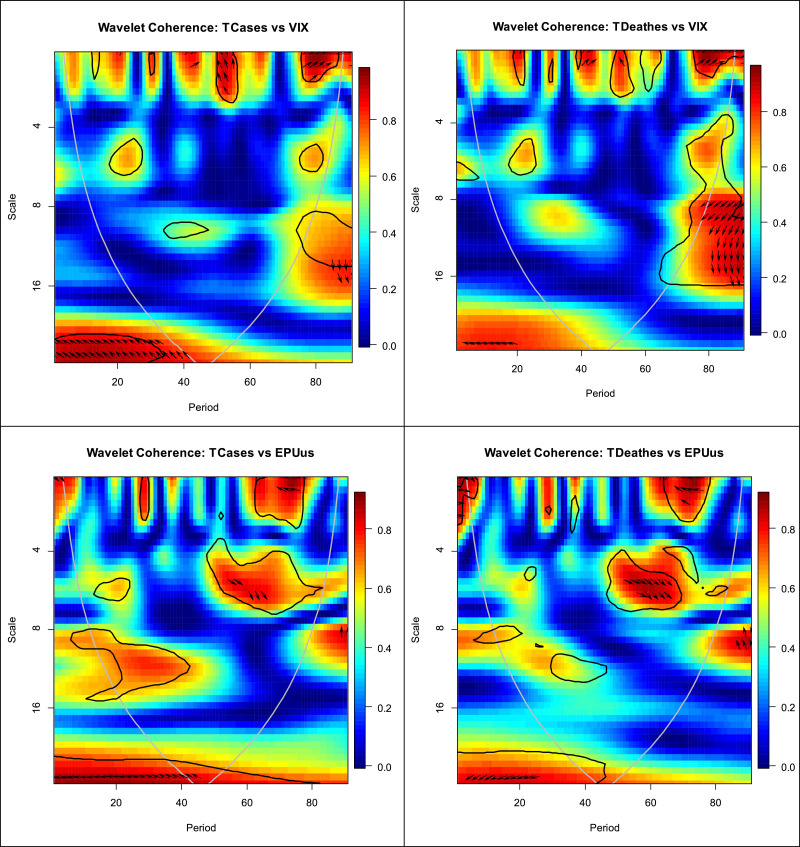
We applied wavelet coherence to test the correlation and interdependence between daily COVID-19 cases and deaths and US stock (S&P 500) and US uncertainty (VIX and EPU indexes). We estimated and compare the co-movement between each couple of variables during the first and second waves of the-19 pandemic and the wavelet coherence plots are presented in Fig. 5 . The plots represent the estimated wavelet coherence method and the relative phasing of the two series are shown by arrows. The black contour of the estimated plots is the 5% significance level, the red/warm colored region is the one with strong co-movement, whereas the blue/cold colored area represents regions with weak co-movements. The direction of arrows is the direction of the interdependence and causality relationships (Torrence and Webster, 1999; Tiwari, 2013; Yang et al., 2017; Pal and Mitra, 2019; Jiang and Yoon, 2020). When the arrow points to the right, the two variables are positively correlated and when it points to the left, the two variables are negatively correlated. The up-right and down-left (↗↙) arrows mean that the first variable leads the second, whereas the down-right and the up-left (↘↖) arrows indicate that the second variable leads the first. The up (↑) and down (↓) arrows imply that the variable is leading and lagging, respectively.
Fig. 5.
Wavelet coherence plots, couple-wise estimates during the first and second waves of the COVID-19 pandemic.
We start by analyzing the wavelet coherence between each couple of variables during the first wave of COVID-19 outbreak and identify many significant high degrees of co-movement. From Fig. 5, we detect the existence of many small islands that indicate a strong dependence at the beginning, the middle, and the end of the first wave period over short-run frequency bands.
The confirmed cases and S&P 500 couple shows strong dependence at the beginning of the first wave period over the 0–4-day frequency bands. The direction of the arrows is up-right (↗) which means that confirmed cases and the US stock market are positively correlated. The plots show another island of higher co-movement between this couple of variables at the end of the wave over the short run. Additionally, in observing the co-movement between cases/deaths and S&P 500, we detect many small islands of a higher degree of dependence. COVID-19 (confirmed cases and deaths) and VIX show several areas of higher coherence. Further, we detect a negative coherence, especially for the first couple at the beginning and the end of the wave over the short run (0–4-day frequency bands). The direction of the arrows is to the left, where the first island shows that confirmed cases lead the VIX (down-left ↙), while the second island shows the existence of an anti-cyclic relationship between infected cases and the VIX. We identify a positive dependence (up-right ↗) between deaths/cases and the VIX over the short run (2-day frequency). Finally, we detect many areas of a higher degree of positive and negative dependence between COVID-19 and the US EPU over the short run (0–2-day frequency bands) and long-run (12 to more than 16-day frequency bands). The direction of the arrows is up-right (↗), indicating that COVID-19 leads the US EPU, while the up-left arrows (↖) mean that there is an anti-cyclic effect between COVID-19 and US EPU.
During the second wave of the COVID-19 outbreak, as per Fig. 5, there is a more meaningful and significant degree of coherence between the COVID-19 pandemic and the US stock market and US uncertainty than during the first wave. We identify many large areas with high significant dependence over the short and long run during the second wave. For the COVID-19 and S&P 500 stock, the direction of the arrows is mostly up-right (↗), which means that this couple of variables is positively correlated, and COVID-19 is leading the co-movement. The direction of the arrows for the higher coherence island between COVID-19 and the VIX shows a positive and negative dependence over the short and long run and they point up-right and down-left (↗↙) and down-right and up-left (↘↖), which indicates that COVID-19 leads the VIX and there is an anti-cyclic effect between them. Finally, for the last two couple of variables, the direction of the arrows for strong co-movement areas is down-right and up-left (↘↖), which reveals an anti-cyclic effect between COVID-19 and the US EPU.
Our findings thus imply a higher co-movement between the COVID-19 pandemic and the US stock market and uncertainty during the first and second waves of the outbreak, while the degree of dependency is more pronounced during the second wave. The results of the wavelet coherence approach confirm and support the results in Table 5, which reveal the persistence of a linkage between the COVID-19 pandemic and the S&P 500, VIX, and EPU during the first and second waves of the pandemic. Therefore, using two different approaches, we tested and confirmed the robustness of our empirical findings.
6. Conclusions
First, our study sheds light on the effects of the COVID-19 pandemic on the risk spillover between the Chinese (CSI 300) and US (S&P 500) stock markets before and during the COVID-19 crisis period. from January 5, 2011 to September 21, 2020. We also studied the asymmetric effects of shocks on the correlation between the two markets. Second, we investigated the linkage between the S&P 500 stock market, as well as two US uncertainty indices (VIX and EPU), and the global cumulative daily COVID-19 cases and deaths during the first and second waves, from January 13, 2020 to September 21, 2020. To achieve our objectives, we applied multivariate GARCH models (DCC-GARCH and ADCC-GARCH), DCC process, and wavelet coherence. We found that the dynamic conditional correlations support the presence of contagion effects, especially during the rapid spread of COVID-19 in the US. The volatility spillover between the Chinese and US markets was higher during the COVID-19 pandemic than before it. The results of the news impact correlations show that the shocks in both markets have asymmetric impacts on the relationship between the US and China stock markets during our sample period, including during the COVID-19 pandemic.
We confirm the long-term relationship between the US stock market, the VIX, the US EPU, and the global cumulative daily COVID-19 cases and deaths during the first wave of the pandemic. Even after the general quarantine restrictions were eased following the first COVID-19 wave, the persistence of the correlation continued during the second wave. We confirmed these empirical results using the wavelet coherence methodology and showed that the continued increase in COVID-19 infections and deaths during the first and second waves increased the uncertainty of the US stock market and the overall economy, with serious financial consequences.
Authors' contributions
All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by [Mohamed Youssfi], [Younes Ben Zaied], [Nidhaleddine Ben Cheikh], [Béchir Ben Lahouel], and [Houssem Bouzgarrou]. The current revised version of the manuscript was written and approved by all authors.
Funding
Not applicable
Availability of data and material
Not applicable
Code availability
Not applicable
Declaration of Competing Interest
Not applicable.
Biographies
Mohamed YOUSSFI is currently a PhD candidate at the IHEC, University of Sousse Tunisia. His-research interests are econometric modeling, quantitative finance, and economic forecasting.
Younes BEN ZAIED is a professor of Finance at EDC Paris Business School. His-research interests include water demand management, environmental economics and policy, demand modeling for water, climate change impacts on agriculture and finance. His-work has appeared in Technological Forecasting and Social Change, Applied Economics, Annals of Operations Research, Journal of International Money and Finance, Finance Research Letters, Bankers, Markets & Investors, Climatic Change, Economics Bulletin, Environmental Modeling & Assessment, Environmental Economics, Journal of Quantitative Economics, etc.
Nidhaleddine BEN CHEIKH is a professor of Economics at ESSCA Paris school of management. His-research interests are: the study of the non-linear dynamics of exchange rate shocks, the impact of climate change on water resources and agricultural production, and the impact of oil price fluctuations linked to geopolitical tensions on Middle Eastern countries. In recent years he published several papers on refereed journals including Annals of Operations Research, Journal of International Money and Finance, Finance Research Letters, Bankers, Markets & Investors, Climatic Change, Environmental Modeling & Assessment, Environmental Economics, Economics Bulletin, etc.
Béchir BEN LAHOUEL is an associate professor of Management sciences at IPAG Business School Paris. His-research revolves primarily around the environmental management grounded in economic theory, input-output modeling, and social, human and environmental impact analysis. He published his work in refereed academic journals such as Technological Forecasting and Social Change, Journal of Cleaner Production, Finance Research Letters, Bankers, Markets and Investors, Environmental Economics and Policy Studies, Journal of Organizational Change Management, European Business Review, Corporate Governance, Question(s) de management, etc.
Houssem BOUZGARROU is an associate professor at the Institut Supérier de Gestion, University of Sousse Tunisia. His-research interests include the analysis of stocks volatility and performance, the economic growth before and after the financial crisis, the dynamic dependence between US indices and commodities prices. He published his work in refereed academic journals such as International Review of Financial Analysis, Research in International Business and Finance, International Journal of Monetary Economics and Finance, Bankers, Markets & Investors, Environmental economics, Journal of Asset Management.
Footnotes
This article belong to the special section on Social-Economic Impacts of Epidemic Diseases.
S&P 500 index: https://www.marketwatch.com/investing/index/spx
Dow Jones industrial average: https://www.marketwatch.com/investing/index/djia
NASDAQ composite index: https://www.marketwatch.com/investing/index/comp
10 year Treasury rate: https://ycharts.com/indicators/10_year_treasury_rate
We use the implied volatility index (VIX) and US Economic Policy Uncertainty Index (EPU).
Appendix
(Table A1 )
Table A1.
Unit root tests.
| ADF test | |||||
|---|---|---|---|---|---|
| Level | |||||
| S&P 500 | CSI 300 | EPUUS | VIX | ||
| With constant | t-Statistic Prob. |
−0.5786 0.8728 |
−1.1273 0.7071 |
−2.3883 0.1466 |
−2.3275 0.1646 |
| With constant & trend | t-Statistic Prob. |
−4.9020 0.0003 *** |
−2.5823 0.2886 |
−2.2894 0.4370 |
−2.4781 0.3386 |
| Without constant & trend | t-Statistic Prob. |
1.4614 0.9648 |
0.3655 0.7900 |
−0.9107 0.3205 |
−0.6460 0.4361 |
| First Difference | |||||
| d(S&P 500) | d(CSI 300) | d(EPUUS) | d(VIX) | ||
| With constant | t-Statistic Prob. |
−14.8412 0.0000 *** |
−45.7654 0.0001 *** |
−22.0476 0.0000 *** |
−5.8235 0.0000 *** |
| With constant & trend | t-Statistic Prob. |
−14.8441 0.0000 *** |
−45.7737 0.0000 *** |
−22.0308 0.0000 *** |
−5.8589 0.0000 *** |
| Without constant & trend | t-Statistic Prob. |
−14.7400 0.0000 *** |
−45.7679 0.0001 *** |
−22.1117 0.0000 *** |
−5.8335 0.0000 *** |
| PP test | |||||
| Level | |||||
| S&P 500 | CSI 300 | EPUUS | VIX | ||
| With constant | t-Statistic Prob. |
−0.5381 0.8813 |
−1.2645 0.6481 |
−3.3649 0.0136 ** |
−2.0998 0.2451 |
| With constant & trend | t-Statistic Prob. |
−4.8681 0.0003 *** |
−2.7379 0.2212 |
−3.3171 0.0670 * |
−2.2076 0.4819 |
| Without constant & trend | t-Statistic Prob. |
1.5614 0.9714 |
0.3104 0.7754 |
−1.0202 0.2759 |
−0.5347 0.4840 |
| First Difference | |||||
| d(S&P 500) | d(CSI 300) | d(EPUUS) | d(VIX) | ||
| With constant | t-Statistic Prob. |
−57.6733 0.0001 *** |
−45.7847 0.0001 *** |
−27.2469 0.0000 *** |
−18.0532 0.0000 *** |
| With constant & trend | t-Statistic Prob. |
−57.6693 0.0000 *** |
−45.7923 0.0000 *** |
−28.7578 0.0000 *** |
−18.3686 0.0000 *** |
| Without constant & trend | t-Statistic Prob. |
−57.6219 0.0001 *** |
−45.7896 0.0001 *** |
−27.2674 0.0000 *** |
−18.0897 0.0000 *** |
Notes: *, **, and *** denote significance at the 10%, 5%, and 1% levels, respectively; (no) means not significant.
References
- Akhtaruzzaman M., Boubaker S., Sensoy A. Financial contagion during COVID-19 crisis. Finance Res. Lett. 2020;38 doi: 10.1016/j.frl.2020.101604. 101604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albulescu C.T. COVID-19 and the United States financial markets’ volatility. Finance Res. Lett. 2020;38 doi: 10.1016/j.frl.2020.101699. 101699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashraf B.N. Stock markets’ reaction to COVID-19: cases or fatalities? Res. Int. Bus. Finance. 2020;54 doi: 10.1016/j.ribaf.2020.101249. 101249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker S.R., Farrokhnia R.A., Meyer S., Pagel M., Yannelis C. Consumption During the 2020 COVID-19 Pandemic. National Bureau of Economic Research; 2020. How does household spending respond to an epidemic? Working paper w26949. [Google Scholar]
- Chen H., Han Q., Li Y., Wu K. Does index futures trading reduce volatility in the Chinese stock market? A panel data evaluation approach. J. Futures Mark. 2013;33(12):1167–1190. [Google Scholar]
- Ciner C., Gurdgiev C., Lucey B. Hedges and safe havens: an examination of stocks, bonds, gold, oil and exchange rates. Internat. Rev. Finan. Anal. 2013;29:202–211. [Google Scholar]
- Corbet S., Larkin C., Lucey B. The contagion effects of the COVID-19 pandemic: evidence from gold and cryptocurrencies. Finance Res. Lett. 2020;35 doi: 10.1016/j.frl.2020.101554. 101554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbet S., Hou Y., HU Y., Lucey B., Oxley L. Aye Corona! The contagion effects of being named Corona during the COVID-19 pandemic. Finance Res. Lett. 2021;38 doi: 10.1016/j.frl.2020.101591. 101591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodell J.W. COVID-19 and finance: agendas for future research. Finance Res. Lett. 2020;35 doi: 10.1016/j.frl.2020.101512. 101512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grinsted A., Moore J.C., Jevrejeva S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004;11(5/6):561–566. [Google Scholar]
- Jiang Z., Yoon S.M. Dynamic co-movement between oil and stock markets in oil-importing and oil-exporting countries: two types of wavelet analysis. Energy Econ. 2020;90 104835. [Google Scholar]
- Katafuchi Y., Kurita K., Managi S. COVID-19 with stigma: theory and evidence from mobility data. Eco. Disaster. Clim. Change. 2020 doi: 10.1007/s41885-020-00077-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurita K., Managi S. University Library of Munich; Germany: 2020. COVID-19 and Stigma: Evolution of Self-restraint behavior, MPRA Paper. 104042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pal D., Mitra S.K. Oil price and automobile stock return co-movement: a wavelet coherence analysis. Econ. Modell. 2019;76:172–181. [Google Scholar]
- Sharif A., Aloui C., Yarovaya L. COVID-19 pandemic, oil prices, stock market, geopolitical risk and policy uncertainty nexus in the US economy: fresh evidence from the wavelet-based approach. Int. Rev. Financ. Anal. 2020;70 doi: 10.1016/j.irfa.2020.101496. 101496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tiwari A.K. Oil prices and the macroeconomy reconsideration for Germany: using continuous wavelet. Econ. Modell. 2013;30:636–642. [Google Scholar]
- Torrence C., Compo G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998;79(1):61–78. [Google Scholar]
- Torrence C., Webster P.J. Interdecadal changes in the ENSO–monsoon system. J. Clim. 1999;12(8):2679–2690. [Google Scholar]
- World Health Organization, Novel Coronavirus (2019-nCOV) Situation Report, 92, (2020). Retrieved From https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports.
- Yang L., Cai X.J., Hamori S. Does the crude oil price influence the exchange rates of oil-importing and oil-exporting countries differently? A wavelet coherence analysis. Int. Rev. Econ. Financ. 2017;49:536–547. [Google Scholar]
- Yoo S., Managi S. Global mortality benefits of COVID-19 action. Technol. Forecast. Soc. Change. 2020;160 doi: 10.1016/j.techfore.2020.120231. 120231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaremba A., Kizys R., Aharon D.Y., Demir E. Infected markets: novel coronavirus, government interventions, and stock return volatility around the globe. Finance Res. Lett. 2020;35 doi: 10.1016/j.frl.2020.101597. 101597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang D., Hu M., Ji Q. Financial markets under the global pandemic of COVID-19. Finance Res. Lett. 2020;36 doi: 10.1016/j.frl.2020.101528. 101528. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Not applicable