Abstract
Current theories on the conformation and dynamics of unknotted and non-concatenated ring polymers in melt conditions describe each ring as a tree-like double-folded object. While evidence from simulations supports this picture on a single ring level, other works show pairs of rings also thread each other, a feature overlooked in the tree theories. Here we reconcile this dichotomy using Monte Carlo simulations of the ring melts with different bending rigidities. We find that rings are double-folded (more strongly for stiffer rings) on and above the entanglement length scale, while the threadings are localized on smaller scales. The different theories disagree on the details of the tree structure, i.e., the fractal dimension of the backbone of the tree. In the stiffer melts we find an indication of a self-avoiding scaling of the backbone, while more flexible chains do not exhibit such a regime. Moreover, the theories commonly neglect threadings and assign different importance to the impact of the progressive constraint release (tube dilation) on single ring relaxation due to the motion of other rings. Despite that each threading creates only a small opening in the double-folded structure, the threading loops can be numerous and their length can exceed substantially the entanglement scale. We link the threading constraints to the divergence of the relaxation time of a ring, if the tube dilation is hindered by pinning a fraction of other rings in space. Current theories do not predict such divergence and predict faster than measured diffusion of rings, pointing at the relevance of the threading constraints in unpinned systems as well. Revision of the theories with explicit threading constraints might elucidate the validity of the conjectured existence of topological glass.
1. Introduction
Topological constraints emerging from the mutual uncrossability between distinct chain segments dominate the viscoelastic behavior of polymer systems in high-density (melt) conditions.1−3 In this context, of notable interest are those situations where polymers are prepared in a well-defined topological state which remains quenched as polymers diffuse and flow. The simplest example in this respect, and the central topic of the present work, is the case of melts of unknotted and non-concatenated ring polymers. People have been now studying this particular class of polymer solutions for several decades, from the theoretical4−27 as well as the experimental28−33 point of view. Researchers have shown that there exist intriguing conceptual connections between melts of ring polymers and, for instance, chromosomes34,35 and a polymer glass based on the nonlinear topology of the chains.36−39 Yet, because of the particular nature of the problem, many fundamental aspects concerning the physics of ring polymer melts remain poorly understood. At present in fact, physical theories taking exactly into account the constraint by means of suitably topological invariants40−44 remain mathematically hard, if not completely intractable, problems, and their applicability to the dense, many-chain systems is limited. Therefore, the various physical pictures that have been proposed so far4,5,7,15,19 introduce suitable approximations to deal with the constraint which make the problem more affordable but, inevitably, they require a supplement of validation, either from experiments or from numerical simulations.
In a series of landmark papers4,5,7 topological constraints have been approximated, in a mean-field fashion, as a lattice of infinitely thin impenetrable obstacles (see Figure 1); therefore, in avoiding concatenation, rings should protrude through them by double-folding on branched, tree-like conformations. As a consequence,13,18,24 rings form compact shapes whose mean linear size or gyration radius, ⟨Rg⟩, scales with the total contour length of the chain, L, as
| 1 |
for L larger than the characteristic and material-dependent45 contour length scale, Le, known as the entanglement length, and with dT, the tube diameter of the melt, equivalent to the average mesh distance of the array of topological obstacles.1−3 Many nontrivial predictions of the lattice-tree model—especially single-chain ones as, for instance, the scaling behavior of the rings (eq 1) or their monomer diffusion in the melt—appear in good agreement with brute-force dynamic simulations.6,8−10,16,20,24 Notably, the model has also helped cast a multiscale algorithm14 for generating ring melt conformations at negligible computational cost.
Figure 1.
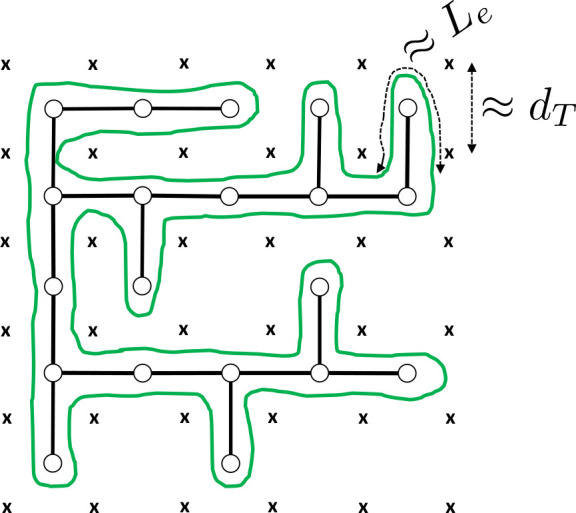
Schematic picture of a single ring polymer conformation
(green
line) in a melt which double-folds around its tree-like backbone.
The crosses (×) represent the lattice of topological obstacles
created by the surrounding rings in the melt. The lattice spacing
is on the order of the tube diameter dT, and the polymer contour length inside each unit
cell is 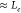 . Random displacements of the loops
protruding
from the mean path on the backbone of the branched structure (thick
black line) change the ring’s shape and dominate melt dynamics
at long time scales.7,16
. Random displacements of the loops
protruding
from the mean path on the backbone of the branched structure (thick
black line) change the ring’s shape and dominate melt dynamics
at long time scales.7,16
While seemingly accurate, the double-folding/branching model (Figure 1) dismisses22,23 the possibility of ring–ring interpenetrations (or, threadings) which instead—and without violating the
non-concatenation constraint!—have physical consequences which
become particularly evident when melts are driven out-of-equilibrium,
such as in an elongation flow26 or for
an induced asymmetry in the local monomer mobilities.39 Moreover, from a broader perspective it remains unclear
if the entanglement scales Le and dT (eq 1) are the only relevant
ones for melts of rings or if, and up to what extent, they are influenced
by the local bending rigidity or Kuhn length3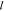 K of the chain.
In fact, the value of Le is measured from a linear melt (e.g., by primitive path analysis46) and the length scale is only assumed to be applicable for rings (with the same polymer model) as well,
although no direct method to find the value explicitly
from the rings is known. Some recent comparisons of crazing in linear
and ring glasses suggest47,48 that Le(rings)/Le(linear) ≈ 4, but its role in equilibrium
ring melts, as well as its connection to
K of the chain.
In fact, the value of Le is measured from a linear melt (e.g., by primitive path analysis46) and the length scale is only assumed to be applicable for rings (with the same polymer model) as well,
although no direct method to find the value explicitly
from the rings is known. Some recent comparisons of crazing in linear
and ring glasses suggest47,48 that Le(rings)/Le(linear) ≈ 4, but its role in equilibrium
ring melts, as well as its connection to 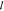 K, has not been
thoroughly investigated. All these aspects (double-folding/branching,
threadings, entanglement scales) are clearly all related to each other
and, yet, how they mutually influence each other remains poorly understood.
K, has not been
thoroughly investigated. All these aspects (double-folding/branching,
threadings, entanglement scales) are clearly all related to each other
and, yet, how they mutually influence each other remains poorly understood.
In order to address these questions, in this work we perform a
systematic investigation of the static and dynamic properties of melts
of unknotted and non-concatenated ring polymer conformations obtained
in large-scale computer simulations. To this purpose, we present first
a modified version of the kinetic Monte Carlo algorithm described
in refs (49) and (50) with the purpose of achieving
higher values of the polymer Kuhn length 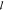 K: in doing
so, we built on the numerically efficient strategy originally devised
in ref (8), which allows
us to increase substantially the overlap between polymer chains and
to reach feasibly the asymptotic regime eq 1, with relatively moderate chain sizes and,
hence, computing times. Then, by employing established tools like
the polymer mean gyration radius and shape,51 contour length correlations8 and spatial
contacts,52 spanned surface,23 and minimal surface,17,53 alongside the motion of the melt for unperturbed conditions54 or after partial pinning37 of a given fraction of the polymer population, we find
out that rings are systematically threading each others via the formation
of locally double-folded structures on length scales below the tube
diameter dT. Additionally,
we show that the threading loops of contour length
K: in doing
so, we built on the numerically efficient strategy originally devised
in ref (8), which allows
us to increase substantially the overlap between polymer chains and
to reach feasibly the asymptotic regime eq 1, with relatively moderate chain sizes and,
hence, computing times. Then, by employing established tools like
the polymer mean gyration radius and shape,51 contour length correlations8 and spatial
contacts,52 spanned surface,23 and minimal surface,17,53 alongside the motion of the melt for unperturbed conditions54 or after partial pinning37 of a given fraction of the polymer population, we find
out that rings are systematically threading each others via the formation
of locally double-folded structures on length scales below the tube
diameter dT. Additionally,
we show that the threading loops of contour length 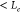 (which we name shallow
threadings) influence significantly many, nonuniversal, properties
of the rings.
(which we name shallow
threadings) influence significantly many, nonuniversal, properties
of the rings.
The paper is structured as follows. In Section 2, we present the notation employed in this work (Section 2.1) and summarize the main predictions for the structure (Section 2.2) and the dynamics (Section 2.3) of melts of rings according to various models with the emphasis on their lattice-tree features. In Section 3, we present and discuss our lattice polymer model and derive the relevant length and time scales of the polymer melts. In Section 4 we present the main results, for the structure (Section 4.1) and the dynamics (Section 4.2) of the rings. In these sections and in the final Section 5 we present and discuss how the tree-like models can be reconciled with the threading features. We also indicate measurements that can help to discriminate between the different models and discuss the common deficiency of all of them. Additional tables and figures are included in the Supporting Information (SI).
2. Ring Polymers in Melt: Theoretical Background
2.1. Entanglement Length and Time Units: Definitions and Notation
Single polymers in melt are made of a linear
sequence of monomer units with mean bond length = ⟨b⟩. The total number of monomers of each polymer
chain is = N and the polymer contour length is L = N⟨b⟩,
while we denote by 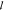 (≤L) the contour
length of a polymer subchain made of n ≡
(≤L) the contour
length of a polymer subchain made of n ≡ 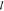 /⟨b⟩ ≤ N monomers.
/⟨b⟩ ≤ N monomers.
Topological
constraints (entanglements)
affect polymer conformations in the melt when the total contour length
of each chain, L, exceeds the characteristic entanglement
length scale Le. In general Le is a nontrivial function
of the chain bending stiffness or the Kuhn length, 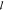 K, and the Kuhn
segment density, ρK, of the melt
(see eq 19 and ref (46)). Then, the mean gyration
radius of the polymer chain of contour length L = Le and Kuhn length
K, and the Kuhn
segment density, ρK, of the melt
(see eq 19 and ref (46)). Then, the mean gyration
radius of the polymer chain of contour length L = Le and Kuhn length 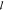 K,
K,
| 2 |
is of the order of the cross-sectional diameter of the tube-like region1−3 where the polymer is confined due to the presence of topological constraints. Unless otherwise said, we will express chain contour lengths L in units of the entanglement length Le and, to this purpose, we introduce the compact notations14,23
| 3 |
| 4 |
where Ne corresponds to the number of monomers Le/⟨b⟩
of an
entanglement length and Z and z are
the number of entanglements of the polymer chain and the polymer subchain
of contour lengths L and 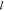 , respectively.55 Accordingly, variables such as the polymer mean-gyration
radius
⟨Rg⟩ or
the mean-magnetic radius ⟨Rm⟩ (see definitions eqs 20 and 21, respectively) are expressed
in units of the tube diameter dT (eq 2).
, respectively.55 Accordingly, variables such as the polymer mean-gyration
radius
⟨Rg⟩ or
the mean-magnetic radius ⟨Rm⟩ (see definitions eqs 20 and 21, respectively) are expressed
in units of the tube diameter dT (eq 2).
With respect to polymer dynamics, entanglements affect the motion
of the chains on time scales τ larger than a characteristic
time τe, known as the entanglement
time. τe is defined as
in ref (54); namely
it corresponds to the time scale where the monomer mean-square displacement g1(τ = τe) (eq 8) is 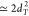 (eq 2). From now on, we adopt τe as
our main unit of time.
(eq 2). From now on, we adopt τe as
our main unit of time.
In Section 3.4, we present a detailed derivation of these quantities for the polymer melts considered in this work.
2.2. Ring Structure
According to the lattice-tree picture,4,5,7,13,14,16 ring conformations in the melt are the result of the balance between compression to avoid linking with other rings and swelling to avoid self-knotting. At the same time, this size competition can be viewed as a balance between double-folding (which minimizes threadings between chains) and random branching (which maximizes polymer entropy). As a consequence, a melt of rings can be mapped14 to an equivalent melt of randomly branching polymers or lattice trees with the same large-scale behavior (see Figure 1). In turn, this mapping can be employed to derive quantitative predictions13,18,24,56 for the scaling exponents describing the characteristic power-law behaviors as a function of L/Le ≡ Z ≳ 1 of the following observables:
- (i)
- (ii)
-
(iii)The mean ring size as a function of the mean path length:
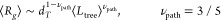
7
Equation 5 means that rings (i.e., the equivalent trees) behave like compact, space-filling objects, while eq 7 expresses the fact that linear paths follow self-avoiding walk statistics.13 Notice also that eq 7 follows directly from eqs 5 and 6; hence νpath = ν/ρ. While the model explains and quantifies the origin of branching and correctly predicts the measured exponent ν in the asymptotic limit, there have been no attempts so far to measure the exponents ρ or νpath in simulations directly (the backbone is not easily “visible” in the conformations). Moreover, the theory is based on scales above Ne and states explicitly16 that the branches might not be double-folded to the monomer scale. This means that the branches can open up to sizes about dT to allow for a branch of another ring to thread through. As we will show in Section 4.1, this is indeed the case.
Another very popular and accurate model is the so-called fractal loopy globule (FLG).19 The model is based on the conjecture that the ring structure arises from a constant (and equal to the Kavassalis–Noolandi number57) overlap parameter (number of segments/loops of a given length sharing a common volume) on all scales above Le in a self-similar manner. As a result, the exponent ν = 1/3 is practically postulated. As such, the ring structure, as loops on loops, is “somewhat analogous” to a randomly branched structure, where the loops of the FLG are viewed as the branches. The authors assert that the loops are not perfectly double-folded, but do not elaborate on the double-folded structure further, except that the number of loops/branches n(r) of size r per ring is n(r) ∼ r–3.
The difference of the FLG and the lattice-tree models, from the structural point of view, is in the branching statistics, manifested in the structure of the mean (primitive) path. [Note that here we use the terms primitive path and tree backbone interchangeably, because they have the same meaning for linear polymers: the shortest end-to-end path of the chain to which its contour can be contracted without crossing other chains. In rings, there are no ends, and therefore such equivalence is, to say the least, not clear. The tree backbone, governing the stretching and branching of the ring is a properly weighted average of all possible path lengths in the tree structure (see ref (16) for details), while the primitive path of the ring is measured in ref (19) with a method analogous, but not identical, to primitive path analysis.46] While in the lattice-tree model the scaling of the size of a segment of the ring with the corresponding primitive path is governed by the exponent νpath on scales above Ne (7), in the FLG the scaling is more complicated because it takes into account “tube dilation”. The tube dilation means freeing of the constraints imposed by the other surrounding segments due to their motion, hence effectively increasing the length scale between constraints, making it time-dependent Ne(t). In the FLG model, if the segment is shorter than Ne(t), its primitive path is just straight; hence the size of the segment scales linearly with the length. If the segment is longer than Ne(t), its size scales with the exponent ν = 1/3 equal to that of the whole ring. The analysis of the primitive paths in ref (19) reports that they do not observe the scaling of the size of the primitive path with its length with the exponent νpath = 3/5. Yet their analysis focuses on a rather flexible system only, and the reported dependence broadly and smoothly crosses over from the exponent 1 to 1/3 (hence visiting all the intermediate exponents). As we show below in Section 4.1, we find an indication of the exponent νpath = 3/5 in the stiff melts.
2.3. Ring Dynamics
As originally pointed out by Obukhov et al.,7 the branched structure induced by the topological obstacles (Figure 1) has direct implications for ring dynamics as well. Here, we limit ourselves to a schematic description of the physics of the process and to recapitulate the main results, without entering into a detailed derivation which, being far from trivial, the interested reader can find explained in detail in refs (7), (16), and (27).
In order to quantify chain dynamics, we introduce54 the monomer mean-square displacement
| 8 |
and the mean-square displacement of the ring center of mass
| 9 |
as a function of time τ. Then, three regimes can be identified. For time scales τ ≲ τe and length scales ≲ dT, monomer motion is not affected by entanglements, and we expect the characteristic Rouse-like3 behavior, g1(τ) ∼ τ1/2 and g3(τ) ∼ τ. On intermediate time scales τ ≳ τe, the motion of the ring is dominated by mass transport along the mean path on the tree-like backbone (Figure 1). Finally, for large time scales τ ≳ τr where τr ≈ τeZ2+ρ is the global relaxation time of the chain,16 the whole chain is simply diffusing, i.e., g1(τ) ∼ g3(τ) ∼ τ. The complete expressions for g1 and g3, up to numerical prefactors but including the coefficients for smooth crossovers,16 are given by
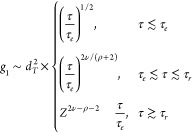 |
10 |
and
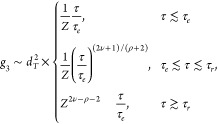 |
11 |
where the exponents ν and ρ appearing here are the same ones introduced in the scaling behaviors of the static quantities; see Section 2.2.
Finally, we introduce the monomer mean-square displacement in the frame of the chain center of mass:
| 12 |
It is not difficult to see that g2(τ)
≃ g1(τ) – g3(τ) and that 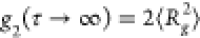 where
where 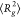 is the chain mean-square gyration radius
(see definition, eq 20). We adopt the appearance of a plateau in the large-time behavior
of g2 as the signature that our chains
have attained complete structural relaxation (see Figure S1 in the SI).
is the chain mean-square gyration radius
(see definition, eq 20). We adopt the appearance of a plateau in the large-time behavior
of g2 as the signature that our chains
have attained complete structural relaxation (see Figure S1 in the SI).
The FLG model19 takes into account the tube dilation, as mentioned in Section 2.1, but otherwise uses self-similar dynamics characteristics for other branched ring conformations as well. Therefore, as shown in ref (19), the predictions for the g1 of both models, the lattice-tree dynamics and the FLG, can be concisely written as
| 13 |
for times τe ≤ τ ≤ τr. The parameter θ governs the tube dilation: θ = 0 means no tube dilation as in the lattice-tree model, while θ = 1 means full tube dilation as in the FLG model. Note that in FLG, because of the full tube dilation the exponent νpath does not impact the dynamics. The exponents are 0.26 for the lattice-tree model and about 0.29 for FLG.
Interestingly both the FLG and the annealed lattice-tree model are very close in the predictions of the scaling of the monomer mean-squared displacements and other dynamical quantities,19 apart from the scaling of the diffusion coefficient with N. This is computed as D ∼ R2/τr, where the relaxation time τr involving the tube dilation can be written as
| 14 |
which gives
| 15 |
Although the exponent is difficult to measure accurately in simulations due to a need of very long runs, the theories underestimate the exponent obtained from the simulations10,19 as well as that from the experiments33 by 0.67 and 0.45 for the FLG and the lattice-tree model, respectively. As we show below in Section 4.2, the source of the discrepancy can be caused by the threadings.
3. Polymer Model and Numerical Methods
3.1. Melts of Rings: The Kinetic Monte Carlo Algorithm
We model classical solutions of ring polymers of variable Kuhn
length 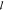 K and with excluded
volume interactions by adapting the kinetic Monte Carlo (kMC) algorithm
for elastic lattice polymers on the three-dimensional face-centered-cubic
(fcc) lattice introduced originally in refs (49) and (50) and employed later in
several studies on polymer melts.23,58,59 In the following we provide the main features of
the model, while we refer the reader to the mentioned literature for
more details.
K and with excluded
volume interactions by adapting the kinetic Monte Carlo (kMC) algorithm
for elastic lattice polymers on the three-dimensional face-centered-cubic
(fcc) lattice introduced originally in refs (49) and (50) and employed later in
several studies on polymer melts.23,58,59 In the following we provide the main features of
the model, while we refer the reader to the mentioned literature for
more details.
In the model, any two consecutive monomers along the chain sit either on nearest-neighbor lattice sites or on the same lattice site (with no more than two consecutive monomers occupying the same lattice site), while nonconsecutive monomers are never allowed to occupy the same lattice site due to excluded volume. By adopting the lattice distance a between fcc nearest-neighbor sites as our unit distance, the bond length b between nearest-neighbor monomers fluctuates between a and 0 (the latter case corresponding to a unit of stored length): for an average bond length = ⟨b⟩, a polymer chain with N bonds has then a total contour length L = N⟨b⟩ < Na. Thanks to this numerical “trick”, polymers are made effectively elastic.49
Ring polymers in the melt are asymptotically compact (eq 1), yet reaching this regime
requires
the simulation of very large rings, which, in turn, may imply prohibitively
long8,9,14 equilibration
times. In order to overcome this limitation and, yet, still achieve
substantial overlap between the different polymer chains for moderate
chain lengths and, hence, feasible simulation times, we adopt the
efficient strategy described in ref (8) and consider polymer chains which are locally
stiff, namely, polymers whose Kuhn length3 K is significantly
larger than the mean bond length ⟨b⟩.
To this purpose, we have complemented the chain Hamiltonian by introducing
the bending energy term:
K is significantly
larger than the mean bond length ⟨b⟩.
To this purpose, we have complemented the chain Hamiltonian by introducing
the bending energy term:
| 16 |
where κbend represents the
bending stiffness which determines 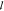 K (see Section 3.4), and
K (see Section 3.4), and 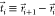 is the
oriented bond vector between monomers i and i + 1 having spatial coordinates
is the
oriented bond vector between monomers i and i + 1 having spatial coordinates 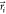 and
and 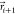 . [For ring polymers,
it is implicitly assumed
the periodic boundary condition along the chain N + 1 ≡ 1.] Importantly, since bond vectors are obviously ill-defined
when two monomers form a stored length, the sum in eq 16 is restricted to the effective bonds of the chains. By increasing κbend, the energy
term eq 16 makes polymers
stiffer.
. [For ring polymers,
it is implicitly assumed
the periodic boundary condition along the chain N + 1 ≡ 1.] Importantly, since bond vectors are obviously ill-defined
when two monomers form a stored length, the sum in eq 16 is restricted to the effective bonds of the chains. By increasing κbend, the energy
term eq 16 makes polymers
stiffer.
Then, the dynamic evolution of the melts proceeds according to the following Metropolis–Hastings-like60 criterion. One monomer is picked at random and displaced toward one of the nearest lattice sites. The move is accepted based on the energy term eq 16 and if, at the same time, both chain connectivity and excluded volume conditions are not violated: in particular, the latter condition is enforced by imposing that the destination lattice site is either empty or, at most, occupied by one and only one of the nearest-neighbor monomers along the chain. In practice, it is useful to make the following conceptual distinction concerning how this move effectively implements classical polymer dynamics.1−3 The selected monomer which is displaced toward an empty or a single-occupation site (or, a Rouse-like move) may, in general, change the local chain curvature and, hence, depend on the bending energy term eq 16. Conversely, a unit of stored length traveling along the chain (or, a reptation-like move) is not affected by the curvature because eq 16 is, again, strictly restricted to the effective bonds of the chains. Overall, as explained in detail in ref (50), the stored length method ensures that the algorithm remains efficient even when it is applied to the equilibration of very dense systems. The specific values for the acceptance rates as a function of the bending rigidity κbend are summarized in Table 1.
Table 1. Values of Physical Parameters Characterizing the Melts of Polymers Studied in This Papera.
| κbend | acc. rate | ⟨ cos θ⟩lin | ⟨ cos θ⟩ring | ⟨b⟩/a | lK/a | ρKlK3 | Le/a | Ne | dT/a | τe/τMC(×104) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.069 | 0.187 | 0.171 | 0.731 | 1.440 | 2.679 | 58.738 | 80.379 | 3.755 | 15.0 |
| 1 | 0.048 | 0.476 | 0.447 | 0.696 | 2.194 | 5.920 | 20.708 | 29.764 | 2.752 | 5.2 |
| 2 | 0.036 | 0.670 | 0.635 | 0.669 | 3.393 | 13.620 | 8.759 | 13.088 | 2.226 | 2.8 |
a is the unit
distance of the fcc lattice, and the monomer number per unit volume
is ρa3 ≃ 1.77 (Section 3.2). (i) κbend, bending stiffness parameter (eq 16); (ii) acceptance rate of the kMC algorithm;
(iii, iv) ⟨cos θ⟩lin/ring, mean
value of the cosine of the angle between two consecutive bonds along
the linear/ring polymer (eq 16); (v) ⟨b⟩, mean bond length;
(vi) 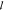 K, Kuhn length
(eq 18); (vii)
K, Kuhn length
(eq 18); (vii) 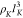 , number of Kuhn segments per Kuhn volume;61 (viii) Le, entanglement length (eq 19); (ix) Ne ≡ Le/⟨b⟩, number of bonds per entanglement length; (x)
, number of Kuhn segments per Kuhn volume;61 (viii) Le, entanglement length (eq 19); (ix) Ne ≡ Le/⟨b⟩, number of bonds per entanglement length; (x)  , diameter
of the effective tube confining
polymer chains in the melt; (xi) τe, entanglement time.
, diameter
of the effective tube confining
polymer chains in the melt; (xi) τe, entanglement time.
3.2. Melts of Rings: Simulation Details
We have studied bulk properties of dense solutions of M closed (ring) polymer chains made of N monomers or bonds per ring. By construction, rings are unknotted and non-concatenated. We simulate values
with
fixed total number of monomers = 40 000
(for computational convenience, the total number of monomers for N = 640 is slightly less). All these systems have been studied
for the bending stiffness parameters κbend = 0, 1,
2 (eq 16). In addition,
we have also simulated melts with 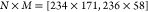 for κbend = 1 and
for κbend = 1 and 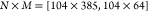 for κbend = 2: once rescaled
in terms of the corresponding entanglement units (see Section 3.4 and Table 1), these two setups have the same number
of entanglements per chain Z ≈ 8 of N = 640 with κbend = 0.
for κbend = 2: once rescaled
in terms of the corresponding entanglement units (see Section 3.4 and Table 1), these two setups have the same number
of entanglements per chain Z ≈ 8 of N = 640 with κbend = 0.
Bulk conditions
are implemented through the enforcement of periodic boundary conditions
in a simulation box of total volume 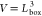 . Similarly to previous works,23,50,59 melt conditions correspond to
fixing the monomer number per fcc lattice site to (i)
. Similarly to previous works,23,50,59 melt conditions correspond to
fixing the monomer number per fcc lattice site to (i) 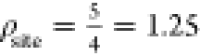 for N ≤ 320 and
(ii)
for N ≤ 320 and
(ii) 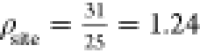 for N = 640, respectively,
since the volume occupied by the fcc lattice site is
for N = 640, respectively,
since the volume occupied by the fcc lattice site is 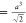 ,62 the monomer
number per unit volume is given by (i)
,62 the monomer
number per unit volume is given by (i) 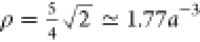 for N ≤ 320, and
(ii)
for N ≤ 320, and
(ii) 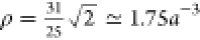 for N = 640. Accordingly,
we fix
for N = 640. Accordingly,
we fix 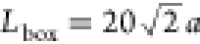 for all N’s.
for all N’s.
Finally, our typical runs amount to a minimum of 7 × 106 up to a maximum of 3 × 108 kMC time units where one kMC time unit τMC is = NM: these runs are long enough such that the considered polymers have attained proper structural relaxation (see Figure S1 in the SI).
3.3. A Closer Look at the Bending Stiffness
It is worth discussing in more detail the consequences of the energy term, eq 16.
On the fcc lattice, the angle θ between consecutive chain bonds is restricted to the five values 0°, 45°, 90°, 135°, and 180°. Otherwise, for ideal polymers (i.e., in the absence of the excluded volume interaction), the angles θi in eq 16 are obviously not correlated to each other. This implies that the distribution function Pideal(κbend; cos θ) of the variable cos θ follows the simple Boltzmann form:
| 17 |
where 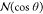 represents the total number of
lattice
states for two successive bonds with given cos θ and
represents the total number of
lattice
states for two successive bonds with given cos θ and  is the normalization
factor.
is the normalization
factor.
In polymer melts, excluded volume interactions induce an effective long-range coupling between bond vectors and the distribution function Pmelt(κbend; θ) is expected to deviate from eq 17: for instance, one can immediately see that the angle = 180° (i.e., cos θ = −1) is possible for ideal polymers but strictly forbidden in the presence of excluded volume interactions. The distributions Pmelt(κbend; θ) for the different κbend’s and in comparison to Pideal(κbend; θ) are given in Figure 2 (square-solid vs circle-dashed lines, respectively). Corresponding mean values ⟨cos θ⟩ for the different κbend’s and for open linear chains and closed rings are summarized in Table 1: the values for the two chain architectures are very similar, with differences in the range of a few percent.
Figure 2.
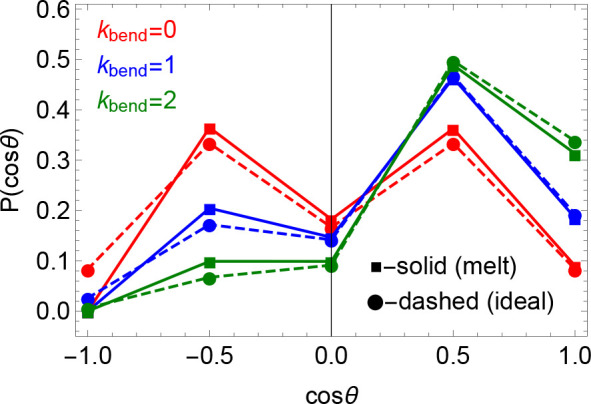
Distribution
functions 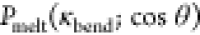 (square-solid lines) of the cosine of the
angle θ between consecutive bonds along the polymer chain in
ring melts for different values of the bending stiffness parameter
κbend. The curves are compared to the results for
ideal rings,
(square-solid lines) of the cosine of the
angle θ between consecutive bonds along the polymer chain in
ring melts for different values of the bending stiffness parameter
κbend. The curves are compared to the results for
ideal rings, 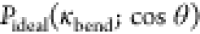 (eq 17, circle-dashed lines).
(eq 17, circle-dashed lines).
3.4. Polymer Length and Time Scales
We provide here a detailed derivation of the relevant length and time scales characterizing our polymer melts (they are summarized in Table 1). Since we work at fixed monomer density ρ (see Section 3.2), the values of these parameters depend only on the bending stiffness parameter κbend.
Average Bond Length, ⟨b⟩
We observe that ⟨b⟩ is slightly decreasing with κbend: arguably, this is the consequence of the progressive stiffening of the polymer fiber on the fcc lattice which privileges less kinked conformations through the reduction of the effective total contour length of the chain.
Kuhn Length, 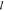 K
K
By
modulating the bending constant κbend, we can fine-tune
the flexibility of the polymers (eq 16). The latter is quantified in terms of the Kuhn length 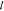 K, namely, the
unit of contour length beyond which the chain orientational order
is lost.2,3 For linear chains,
K, namely, the
unit of contour length beyond which the chain orientational order
is lost.2,3 For linear chains, 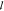 K is defined
by the relation2,3
K is defined
by the relation2,3
| 18 |
where ⟨R2(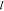 )⟩ is
the mean-square end-to-end
distance between any two monomers along the chain at monomer number
separation n or contour length separation
)⟩ is
the mean-square end-to-end
distance between any two monomers along the chain at monomer number
separation n or contour length separation 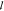 = n⟨b⟩. In order to determine
the Kuhn length of our polymer chains,
we have simulated melts of M = 125 linear chains
with N = 320 monomers per chain at the same monomer
density
= n⟨b⟩. In order to determine
the Kuhn length of our polymer chains,
we have simulated melts of M = 125 linear chains
with N = 320 monomers per chain at the same monomer
density 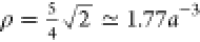 (Section 3.2) and for κbend = 0, 1,
2; then, after equilibration, we have computed numerically eq 18. As shown in Figure 3 (symbols), the chains
become increasingly stiffer with κbend as expected
by displaying, in particular, plateau-like regions for large
(Section 3.2) and for κbend = 0, 1,
2; then, after equilibration, we have computed numerically eq 18. As shown in Figure 3 (symbols), the chains
become increasingly stiffer with κbend as expected
by displaying, in particular, plateau-like regions for large 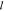 ’s.
In analogy to the procedure employed
in ref (59), the heights
of these plateaus, obtained by best fits to corresponding constants
on the common interval
’s.
In analogy to the procedure employed
in ref (59), the heights
of these plateaus, obtained by best fits to corresponding constants
on the common interval 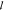 ∈ [150,
200] (Figure 3, dashed
lines) provide the values of the
corresponding
∈ [150,
200] (Figure 3, dashed
lines) provide the values of the
corresponding  K’s which
are used in this work (see Table 1).
K’s which
are used in this work (see Table 1).
Figure 3.
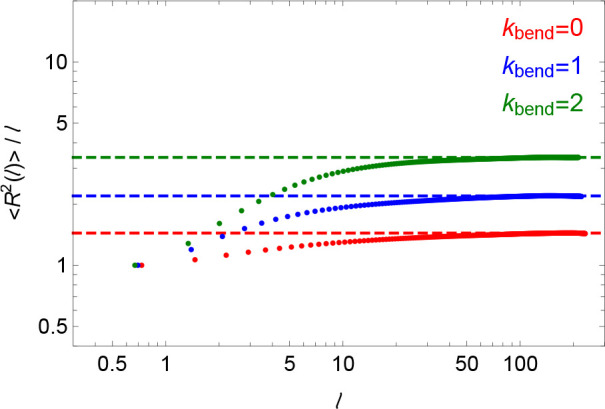
(Symbols) Ratios of the mean-square end-to-end distance,
⟨R2( )⟩/
)⟩/ , to the corresponding
monomer contour length
separation
, to the corresponding
monomer contour length
separation 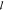 for linear
chains in the melt and for the
different bending stiffness parameters κbend (see
legend). (Dashed lines) Best fits of the plateau-like behaviors on
the contour length interval
for linear
chains in the melt and for the
different bending stiffness parameters κbend (see
legend). (Dashed lines) Best fits of the plateau-like behaviors on
the contour length interval 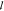 ∈ [150,
200] (see eq 18 and
the text for details).
∈ [150,
200] (see eq 18 and
the text for details).
Entanglement Length, Le, and Tube Diameter, dT
The entanglement
length Le marks the crossover
from entanglement-free to entanglement-dominated
effects in polymer melts. In general Le depends in a nontrivial57,63 manner on the microscopic details of the polymer melt, typically
the chain Kuhn length 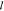 K and the monomer
density ρ. By combining packing arguments64 and primitive path analysis,46 Uchida et al.61 showed that Le can be expressed as a function of
K and the monomer
density ρ. By combining packing arguments64 and primitive path analysis,46 Uchida et al.61 showed that Le can be expressed as a function of 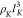 , the number of Kuhn segments in a Kuhn
volume at given Kuhn density
, the number of Kuhn segments in a Kuhn
volume at given Kuhn density 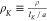 :
:
| 19 |
where the two power
laws account for the two
limits of loosely entangled melts (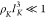 , exponent
= 2) and tightly entangled solutions (
, exponent
= 2) and tightly entangled solutions (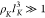 , exponent
= 2/5). By using eq 19, it is a simple exercise to extract Le/
, exponent
= 2/5). By using eq 19, it is a simple exercise to extract Le/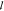 K and the corresponding
number of monomers per entanglement length, Ne ≡ Le/⟨b⟩. [Strictly speaking, eq 19 was derived for the
entanglement length of a melt of linear chains. Yet,
recent theoretical work12,14,23 on ring melts has demonstrated that the
same Le describes the correct
contour length where topological constraints affect ring behavior
and chains become manifestly crumpled.] We observe (Table 1) that Ne decreases by approximately 1 order of magnitude
by the apt fine-tuning of κbend. This means that
rings with the same contour length but stiffer will become increasingly
entangled.8 Finally, we use the definition eq 2:
K and the corresponding
number of monomers per entanglement length, Ne ≡ Le/⟨b⟩. [Strictly speaking, eq 19 was derived for the
entanglement length of a melt of linear chains. Yet,
recent theoretical work12,14,23 on ring melts has demonstrated that the
same Le describes the correct
contour length where topological constraints affect ring behavior
and chains become manifestly crumpled.] We observe (Table 1) that Ne decreases by approximately 1 order of magnitude
by the apt fine-tuning of κbend. This means that
rings with the same contour length but stiffer will become increasingly
entangled.8 Finally, we use the definition eq 2:
for computing the tube
diameters of polymers
of different bending stiffnesses. Notice (Table 1) that, by changing chain stiffness, dT moves from smaller to comparable
to 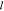 K, meaning that
we are effectively able to explore the mentioned crossover from loosely
to tightly entangled melts.
K, meaning that
we are effectively able to explore the mentioned crossover from loosely
to tightly entangled melts.
Entanglement Time, τe
The entanglement time τe marks
the onset to entanglement-related effects in polymer dynamics. As
anticipated in Section 2.1, τe is evaluated numerically
as 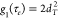 , where g1(τ)
is the monomer time mean-square displacement (eq 8) and dT is the tube diameter (eq 2). For consistency with the definitions for Le and dT, notice that g1(τ)
has been calculated on the same dynamic simulations of melts of linear chains used for calculating
, where g1(τ)
is the monomer time mean-square displacement (eq 8) and dT is the tube diameter (eq 2). For consistency with the definitions for Le and dT, notice that g1(τ)
has been calculated on the same dynamic simulations of melts of linear chains used for calculating 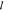 K.
K.
3.5. Computing the Ring Minimal Surface
The minimal surface spanned by a ring polymer was introduced17,53 as a quantitative tool for measuring the “exposed” area that each ring offers to its neighbors. In this section, we limit ourselves to summarize the salient numerical aspects of the procedure used to obtain the minimal surface; the interested reader will find a complete overview on minimal surfaces for melts of rings in the mentioned references and also in ref (22).
The search for the minimal surface of a ring polymer is based on a suitable minimization algorithm which works as the following. Essentially, the algorithm is based on successive iterations of triangulations evolving under surface tension by moving the free vertices: each triangle in the initial triangulation is made of two successive monomer positions and the center of the mass of the ring; then it is refined (by subdividing each edge into two edges, creating therefore four triangles out of one) and the surface area minimized by the surface tension flow with restructuring of the mesh. Finally, the algorithm stops when the relative surface area does not change by more than 0.1% over a few tens of additional steps of the minimization procedure. Similarly to the eye of a needle pierced by a thread, the single minimal surface of a given ring can be pierced or threaded by the other surrounding polymers in the melt: in particular, once the minimal surfaces of the rings in the melt are determined, it is possible to define in a precise and robust manner what amount of the total contour length of any given ring passes through the minimal surface of another ring.
4. Results
4.1. Ring Structure
In order to characterize ring structure, we consider the chain mean-square “gyration” radius,
| 20 |
where 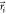 are the monomer coordinates and
are the monomer coordinates and 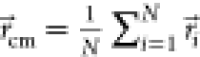 is the chain center of mass, and the mean-square
“magnetic” radius first introduced in ref (23) and defined as
is the chain center of mass, and the mean-square
“magnetic” radius first introduced in ref (23) and defined as
| 21 |
where, inspired by the analogy to the classical electrodynamics of the magnetic far field generated by a loop carrying a constant electric current,
| 22 |
is the (oriented) area enclosed by the ring.
Both quantities are an expression of the average (square) ring size,
yet they have different meaning: in particular, eq 21 was introduced to detect and quantify the
presence of open loops inside the ring. Numerical values of 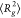 and
and 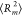 for melts of rings with different flexibilities
are summarized in Table S1 in the SI.
for melts of rings with different flexibilities
are summarized in Table S1 in the SI.
Figure 4 shows these
quantities, rescaled (filled symbols) by the corresponding tube diameters dT and as a function of the
total number of entanglement Z = L/Le; see Section 2.1 for details
and Table 1 for specific
values of dT and Le. For further comparison,
we have also included the results for 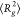 obtained from Monte Carlo simulations (bond-fluctuation
model) of melts of rings by Müller et al.8 (open symbols) and the universal curves (solid gray lines)
from the “hierarchical crumpling” method by Schram et
al.23 The excellent matching between these
old data sets and the present new data validates our methodology:
the average ring size covers the full crossover from Gaussian (∼ Z1) to compact (∼ Z2/3) behavior. This is particularly evident for the stiffest
rings (κbend = 2) whose reduced flexibility “helps”,
in agreement with Müller et al.,8 reaching the asymptotic behavior. The data for the mean-square magnetic
radius
obtained from Monte Carlo simulations (bond-fluctuation
model) of melts of rings by Müller et al.8 (open symbols) and the universal curves (solid gray lines)
from the “hierarchical crumpling” method by Schram et
al.23 The excellent matching between these
old data sets and the present new data validates our methodology:
the average ring size covers the full crossover from Gaussian (∼ Z1) to compact (∼ Z2/3) behavior. This is particularly evident for the stiffest
rings (κbend = 2) whose reduced flexibility “helps”,
in agreement with Müller et al.,8 reaching the asymptotic behavior. The data for the mean-square magnetic
radius 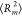 rescale equally well and, as noticed in
ref (23), with the
same large-Z behavior
rescale equally well and, as noticed in
ref (23), with the
same large-Z behavior 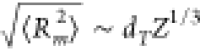 . However, a closer look at the ratio
. However, a closer look at the ratio 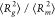 (see Figure S2 in the SI) reveals significant, albeit extremely slow (
(see Figure S2 in the SI) reveals significant, albeit extremely slow (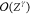 with γ ≈ 0.07), power-law
corrections which were not noticed in the previous
study:23 instead, a similar result was
already described in ref (8), where, however, the authors employed a different definition
for the area spanned by a ring which was based on the 2d projection of the chain onto a random direction.
with γ ≈ 0.07), power-law
corrections which were not noticed in the previous
study:23 instead, a similar result was
already described in ref (8), where, however, the authors employed a different definition
for the area spanned by a ring which was based on the 2d projection of the chain onto a random direction.
Figure 4.
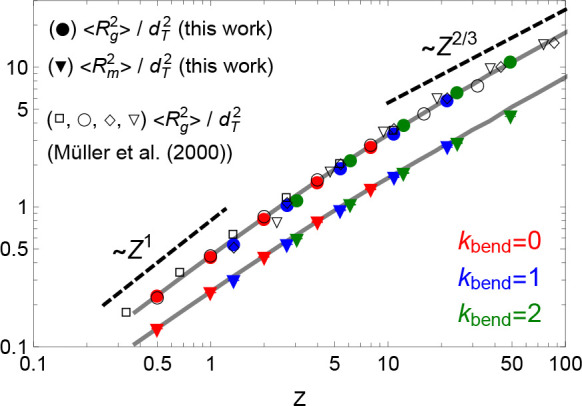
Scaling behavior of the
mean-square gyration radius, 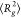 , and the mean-square magnetic radius,
, and the mean-square magnetic radius, 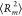 , of ring polymers as a function of the
total number of entanglements, Z = L/Le, of the chain. Error
bars are smaller than the symbols size. The empty symbols reproduce
the ring data by Müller et al.,8 with different symbols for the different Kuhn lengths used in that
work (by employing their notation: σ/κBT = 0 (□), 1 (○), 2 (◇),
3 (▽), from flexible to increasingly stiffer chains). The solid
gray lines are for the on-lattice rings on the fcc lattice studied
in ref (23).
, of ring polymers as a function of the
total number of entanglements, Z = L/Le, of the chain. Error
bars are smaller than the symbols size. The empty symbols reproduce
the ring data by Müller et al.,8 with different symbols for the different Kuhn lengths used in that
work (by employing their notation: σ/κBT = 0 (□), 1 (○), 2 (◇),
3 (▽), from flexible to increasingly stiffer chains). The solid
gray lines are for the on-lattice rings on the fcc lattice studied
in ref (23).
The universal behaviors of the two quantities 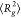 and
and 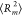 characterize the chain as a whole, yet,
in principle, there could be other length scales below Le which produce no effect on these quantities
but affect and become visible in others. We look then at the average
behavior of the ring minimal surface (hereafter, min S), a concept introduced17,22,53 to quantify the “exposed” area that each ring offers
to its neighbors (see Section 3.5 for technical details). Surprisingly, our data (collected
in Table S1 in the SI) demonstrate that
this is not the case (see Figure 5): in fact ⟨min S⟩ ∼ Z for the different flexibilities, in agreement with previous
results17 for off-lattice simulations,
but the three data sets—contrary to
characterize the chain as a whole, yet,
in principle, there could be other length scales below Le which produce no effect on these quantities
but affect and become visible in others. We look then at the average
behavior of the ring minimal surface (hereafter, min S), a concept introduced17,22,53 to quantify the “exposed” area that each ring offers
to its neighbors (see Section 3.5 for technical details). Surprisingly, our data (collected
in Table S1 in the SI) demonstrate that
this is not the case (see Figure 5): in fact ⟨min S⟩ ∼ Z for the different flexibilities, in agreement with previous
results17 for off-lattice simulations,
but the three data sets—contrary to 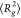 and
and 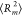 (Figure 4)—do not collapse onto each other after rescaling
in terms of entanglement units Z and
(Figure 4)—do not collapse onto each other after rescaling
in terms of entanglement units Z and 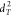 . Notice that
this finding—which
looks even more surprising given that both
. Notice that
this finding—which
looks even more surprising given that both 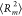 and ⟨min S⟩
are in the end two measures of the ring effective area—is robust
and independent of the triangulation resolution employed to calculate
the minimal surface of the rings (○ symbols vs × symbols
in Figure 5). Note
also that ⟨min S⟩ is normalized by
and ⟨min S⟩
are in the end two measures of the ring effective area—is robust
and independent of the triangulation resolution employed to calculate
the minimal surface of the rings (○ symbols vs × symbols
in Figure 5). Note
also that ⟨min S⟩ is normalized by 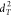 , which should
correct for the different
“elementary areas” due to different local structure
of the polymer model. [Note also that normalization by the other microscopic
length scale,
, which should
correct for the different
“elementary areas” due to different local structure
of the polymer model. [Note also that normalization by the other microscopic
length scale, 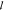 K, would not
imply a collapse either; in fact it would make it even worse as
K, would not
imply a collapse either; in fact it would make it even worse as  K grows with
κbend (see Table 1).]
K grows with
κbend (see Table 1).]
Figure 5.
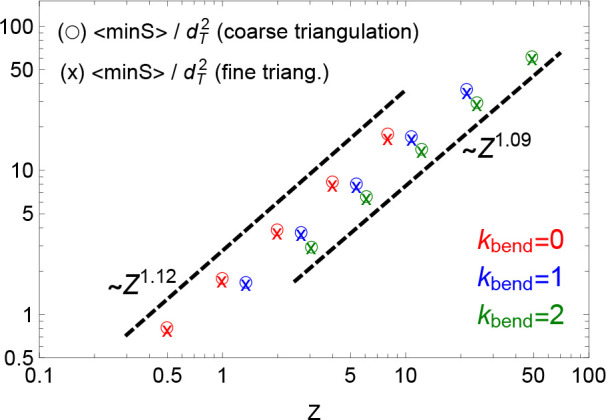
Mean minimal surface area, ⟨min S⟩, of ring polymers as a function of the total number of entanglements, Z, of the chain. The ○ and × symbols (see legend) are for the two chosen resolutions in the triangulation procedure at the basis of the calculation of the ring minimal surface (see Section 3.5 for details). For the higher resolution, we take two additional refining steps before the minimization procedure stops. Error bars are smaller than the symbols’ size. The power laws (dashed lines) correspond to best fits to the data.
What could be the physical
origin of this discrepancy? In an earlier
paper22 it was shown that the minimal surface
of each ring can be pierced (threaded) a certain number of times by
portions of surrounding rings, but that it is necessary to distinguish
carefully the contributions from chain contour lengths z = 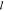 /Le ≲ 1 (shallow
threadings) from the
others. For each ring piercing the minimal surface of another ring,
we define22 the threading contour length
/Le ≲ 1 (shallow
threadings) from the
others. For each ring piercing the minimal surface of another ring,
we define22 the threading contour length 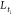 as the contour length portion of the ring
comprised between the two consecutive penetrations i-th and i + 1-th, which allow us to assign
as the contour length portion of the ring
comprised between the two consecutive penetrations i-th and i + 1-th, which allow us to assign 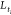 unambiguously to either
“side” of the other ring’s minimal surface. Based
on
unambiguously to either
“side” of the other ring’s minimal surface. Based
on 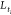 , we consider the following observables:
, we consider the following observables:
-
1.
The mean number of chain neighbors threaded by a single ring, ⟨nt⟩.
-
2.
The mean relative amount of contour length of a ring on one side of another ring’s minimal surface with respect to the other side:
| 23 |
where the so-called separation length,17,22
| 24 |
quantifies the total contour length of one of the two complementary portions (the other has contour length L – Lsep) obtained by the passage of the penetrating ring through the minimal surface of a penetrated ring: i.e., Q = 1 simply means that the penetrating ring is half split by the penetrated surface.
-
3.
The mean number of times any ring penetrates the minimal surface of any other ring, ⟨np⟩.
These
different quantities may be computed by taking into account
all possible threading segments or by excluding the shallow ones,
namely, as said, those whose contour lengths are shorter than the
entanglement length Le. Noticeably, in the first case there is no evidence for universal
collapse (Figure 6,
left-hand panels) in any of these quantities. On the contrary (Figure 6, right-hand panels),
universal collapse is observed after removing the contribution of
the short threading filaments: this points to the fact that the same
shallow threadings are responsible for the lack of universality observed
for ⟨min S⟩ (Figure 5). Assuming that each shallow threading contributes 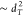 to the average ⟨min S⟩, their removal
restores universality almost completely (Figure S3 in the SI). To justify the assumption
that each threading does not contribute more than about
to the average ⟨min S⟩, their removal
restores universality almost completely (Figure S3 in the SI). To justify the assumption
that each threading does not contribute more than about 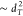 to the minimal surface, we measured the
mean distance ⟨d⟩ between two bonds
involved in the threading. We find that indeed ⟨d⟩ ≲ dT (see the values, the corresponding distribution functions, as well
as the discussion of the cases with more than two piercings in Figure S4 in the SI), which strongly supports
the fact that threadings occur on scales below the entanglement scale.
We still find some cases when ⟨d⟩ > dT, but these are exponentially
rare (see Figure S4 in the SI).
to the minimal surface, we measured the
mean distance ⟨d⟩ between two bonds
involved in the threading. We find that indeed ⟨d⟩ ≲ dT (see the values, the corresponding distribution functions, as well
as the discussion of the cases with more than two piercings in Figure S4 in the SI), which strongly supports
the fact that threadings occur on scales below the entanglement scale.
We still find some cases when ⟨d⟩ > dT, but these are exponentially
rare (see Figure S4 in the SI).
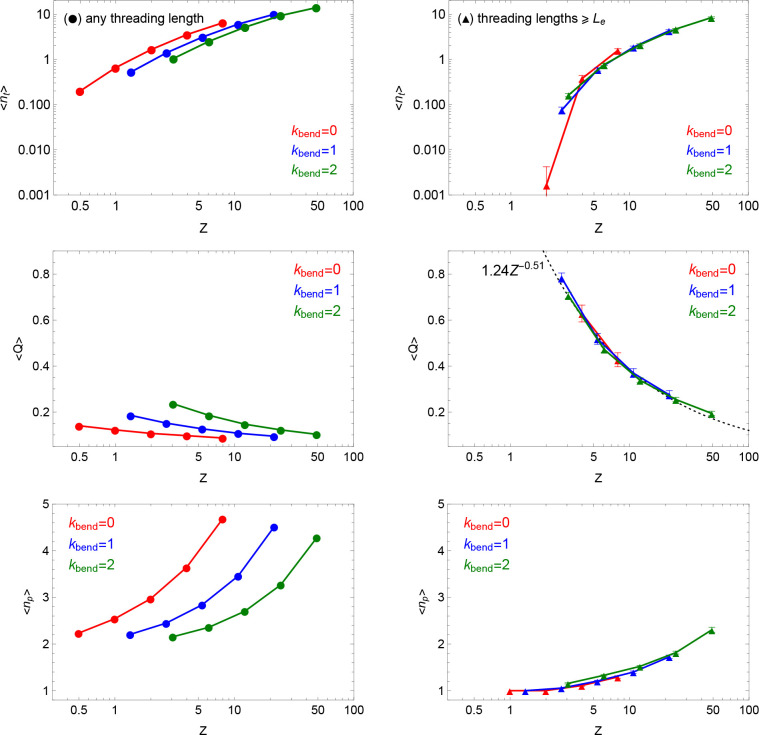
Figure 6.
Statistics of threadings by minimal surfaces as a function of the total number of entanglements, Z, of each ring in the melt. The data (circles) shown in the left-hand panels (respectively, (up-triangles) in the right-hand panels) have been obtained by including threading lengths Lt of any size (respectively, Lt ≥ Le). Error bars represent the error of the mean calculated from 100 uncorrelated snapshots. (Top) ⟨nt⟩: mean number of rings threaded by a single ring. (Middle) ⟨Q⟩: mean relative amount of contour length piercing one ring minimal surface side with respect to the other (eq 23). The dashed (black) line on the right-hand panel corresponds to the best fit to the data. (Bottom) ⟨np⟩: mean number of times a ring penetrates the minimal surface of any other single ring.
Additionally, restricting the discussion to the universal behaviors, we see that ⟨Q⟩ decreases with Z, i.e., less material enters the minimal surface of a ring. Yet, the mean number of times, ⟨np⟩, any ring penetrates the minimal surface of any other single ring increases: notice that these two apparent contradictory features can be easily reconciled by supposing that while retracting from each other (i.e., decreasing ⟨Q⟩), rings may at the same time pierce each other more frequently by the increased propensity to form branches at the entanglement scale. Overall, this agrees with the results by two of us (J.S., A.R.)22 for off-lattice dynamic simulations of melts of rings. [Notice, however, that in ref (22) we have reported the scaling behavior ⟨Q⟩ ∼ Z–0.31, distinct from the one measured here (⟨Q⟩∼ Z–0.51, see middle right panel in Figure 6). This apparent discrepancy is due to the fact that in ref (22) the mean value ⟨Q⟩ includes the contribution of the shallow threadings: in fact, their removal gives identical results to the ones of the present work (data not shown).]
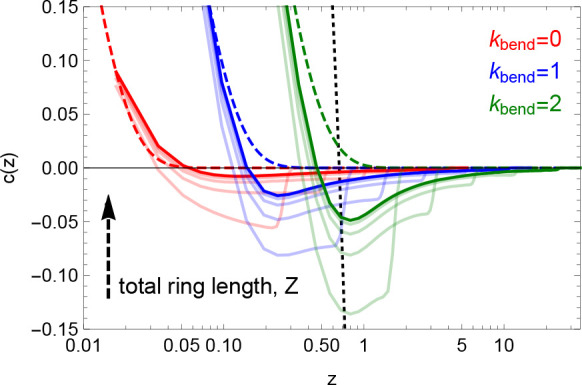
According to the lattice-tree model (Section 2.2), the contour length of each ring above the entanglement length Le should double-fold along a branched (i.e., tree-like) backbone. We seek now specific evidence of this peculiar organization. As the first of these signatures, we look at the bond-vector correlation function8,14,23
| 25 |
Contrary to the
known exponentially decaying behavior typical of
linear polymers (solid lines vs long-dashed lines in Figure 7) c(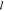 ) is manifestly
nonmonotonic, showing an
anticorrelation well whose minimum becomes more pronounced and locates
around z =
) is manifestly
nonmonotonic, showing an
anticorrelation well whose minimum becomes more pronounced and locates
around z = 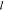 /Le ≈ 1 with the increasing of the
chain stiffness. By
using the function
/Le ≈ 1 with the increasing of the
chain stiffness. By
using the function 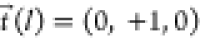 for 0
<
for 0
< 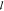 < Le and
< Le and 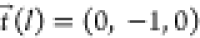 for Le <
for Le < 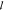 < 2Le as a toy model for an exactly
double-folded polymer filament
of contour length = 2Le, it is easy to see that c(z =
< 2Le as a toy model for an exactly
double-folded polymer filament
of contour length = 2Le, it is easy to see that c(z = 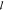 /Le) = (1–3/2z)/(1
– z/2) for 0 < z <
1 and c(z) = −1 for 1 ≤ z < 2,
i.e., c(
/Le) = (1–3/2z)/(1
– z/2) for 0 < z <
1 and c(z) = −1 for 1 ≤ z < 2,
i.e., c(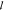 ) displays
an anticorrelation minimum at z = 1 or
) displays
an anticorrelation minimum at z = 1 or 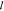 = Le (short-dashed line in Figure 7). A deep anticorrelation
well is particularly visible
in short rings (at a given κbend), while in larger
rings the effect is smoothed, arguably because thermal fluctuations
wash out such strong anticorrelations.
= Le (short-dashed line in Figure 7). A deep anticorrelation
well is particularly visible
in short rings (at a given κbend), while in larger
rings the effect is smoothed, arguably because thermal fluctuations
wash out such strong anticorrelations.
Figure 7.
Bond-vector orientation
correlation function, c(z) (eq 25), as a function of the
number of entanglements z = 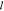 /Le along the chain. Lines of equal color
are for the same chain
stiffness (see legend), full colors are for the longest rings (N = 640), while lines in fainter colors are for chains of
shorter contour lengths (see arrow’s direction). The long-dashed
lines correspond to the exponential decay typical of linear polymers
with local stiffness, namely,
/Le along the chain. Lines of equal color
are for the same chain
stiffness (see legend), full colors are for the longest rings (N = 640), while lines in fainter colors are for chains of
shorter contour lengths (see arrow’s direction). The long-dashed
lines correspond to the exponential decay typical of linear polymers
with local stiffness, namely, 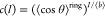 , where the values for ⟨ cos θ⟩ring are reported in Table 1. The short-dashed line is the analytical function
for an exactly double-folded polymer filament of contour length =
2Le (see the text for
details).
, where the values for ⟨ cos θ⟩ring are reported in Table 1. The short-dashed line is the analytical function
for an exactly double-folded polymer filament of contour length =
2Le (see the text for
details).
As a second signature,
we look at the mean contact probability,52 ⟨pc(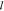 )⟩,
between two monomers at given
contour length separation
)⟩,
between two monomers at given
contour length separation 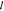 defined as
defined as
| 26 |
where Θ(x) is the usual Heaviside step function and the “contact distance” rc between two monomers is taken equal to one lattice unit, a.
Reducing finite ring size effects by plotting ⟨pc⟩ in terms of the variable24 ζ ≡ z(1 – z/Z), the data from the different rings (see Figure S5 in the SI) form three distinct curves according to their Kuhn length (Figure 8). Notably these curves display the asymptotic power-law behavior ∼ζ–γ with scaling exponent γ close to 1, as reported in the past.9,14,35 At the same time, the stiffer chains with κbend = 2 display a short, yet quite evident, leveling of the contact probability curves around z ≈ 1 (see arrow’s direction), which is clearly compatible with double-folding on the entanglement scale.
Figure 8.
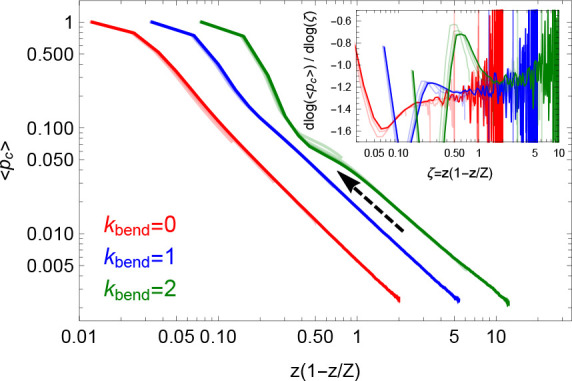
Mean contact
probabilities, ⟨pc(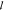 )⟩
(see eq 26), as a function
of the “effective”
ring contour length ζ ≡ z(1 – z/Z). The arrow points at the leveling
of the curves around z ≈ 1. Inset: local differential
exponent
)⟩
(see eq 26), as a function
of the “effective”
ring contour length ζ ≡ z(1 – z/Z). The arrow points at the leveling
of the curves around z ≈ 1. Inset: local differential
exponent 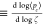 . Color code is as in Figure 7.
. Color code is as in Figure 7.
However, we show now that the most compelling evidence for
double-folding
comes from examining the average polymer shape. To
this purpose, we introduce the 3 × 3 symmetric gyration tensor 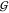 whose elements
are defined by
whose elements
are defined by
| 27 |
where ri,α with α = x, y, z are the Cartesian
components of the spatial
position of monomer i: the trace of the tensor 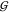 ,
, 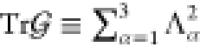 , is equal to
, is equal to 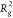 , and the
three ordered eigenvalues,
, and the
three ordered eigenvalues, 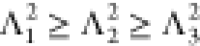 , quantify the spatial variations of the
polymer along the corresponding principal axes, i.e., the instantaneous
shape of the chain. Polymers are ellipsoidal on average,51 with mean values
, quantify the spatial variations of the
polymer along the corresponding principal axes, i.e., the instantaneous
shape of the chain. Polymers are ellipsoidal on average,51 with mean values 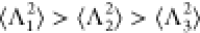 (see values in Table S1 in the SI): similarly to
(see values in Table S1 in the SI): similarly to 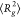 (Figure 4), we do expect a scaling curve for each
(Figure 4), we do expect a scaling curve for each 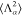 in universal units Z and dT and, for Z ≫ 1,
in universal units Z and dT and, for Z ≫ 1, 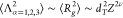 . In general
our data (see Figure S6 in the SI) reflect
well this trend, except for the
smallest mean eigenvalue
. In general
our data (see Figure S6 in the SI) reflect
well this trend, except for the
smallest mean eigenvalue 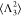 , which displays systematic deviations from
the asymptotic behavior which persist for chain sizes well above the
entanglement threshold Z ≈ 1. Interestingly,
these deviations are quantitatively consistent with
the scaling properties of rings being double-folded on an underlying
tree-like structure (Section 2.2): in fact, according to Figure S6 in the SI and for the given mean path length ⟨Ltree⟩ ∼ Zρ (eq 6)
of the “supporting” tree, we can write the expressions
, which displays systematic deviations from
the asymptotic behavior which persist for chain sizes well above the
entanglement threshold Z ≈ 1. Interestingly,
these deviations are quantitatively consistent with
the scaling properties of rings being double-folded on an underlying
tree-like structure (Section 2.2): in fact, according to Figure S6 in the SI and for the given mean path length ⟨Ltree⟩ ∼ Zρ (eq 6)
of the “supporting” tree, we can write the expressions
| 28 |
| 29 |
where the latter is equivalent to assuming local stiff behavior at small contour length separations. Equations 28 and 29 are just equivalent to
| 30 |
with νpath = 3/5 (eq 7). Our data
are well described
by eq 30 (see Figure 9) before the crossover
to the asymptotic regime, 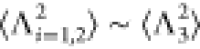 , finally takes place. Notice that the value
of νpath agrees well with that of the annealed tree
model.13 Note also that here we observe
the exponent clearly only for the stiffest system. This might explain
why the work19 that analyzed only simulations9 with low stiffness (roughly, between our κbend = 0 and κbend = 1 in terms of Le) reports that they do not
see νpath (there measured as the scaling of the chain primitive path with the contour length).
, finally takes place. Notice that the value
of νpath agrees well with that of the annealed tree
model.13 Note also that here we observe
the exponent clearly only for the stiffest system. This might explain
why the work19 that analyzed only simulations9 with low stiffness (roughly, between our κbend = 0 and κbend = 1 in terms of Le) reports that they do not
see νpath (there measured as the scaling of the chain primitive path with the contour length).
Figure 9.
Mean eigenvalues, 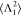 and
and 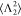 , of the gyration tensor eq 27 as a function of the smallest
eigenvalue
, of the gyration tensor eq 27 as a function of the smallest
eigenvalue 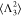 . The dashed lines are the predicted limits
of small and large length scales.
. The dashed lines are the predicted limits
of small and large length scales.
In conclusion, the universal scaling features
of the static quantities and the bond correlations reveal double-folded
tree-like structure on scales above Le, with indications 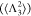 that
the trees are of the annealed tree
type.13 Conversely, the nonuniversal features (⟨min S⟩) and threading
analysis show that the trees are threaded on scales smaller than the
tube diameter dT, hence
reconciling the tree picture with that of the threaded conformations.
At the same time the “depth” of threadings can be (Figure 6) longer than Le, giving hints on its relevance
for the dynamic features. Therefore, in the next section we explore
the consequences of the double-folding and threadings on the dynamic
properties of the melts.
that
the trees are of the annealed tree
type.13 Conversely, the nonuniversal features (⟨min S⟩) and threading
analysis show that the trees are threaded on scales smaller than the
tube diameter dT, hence
reconciling the tree picture with that of the threaded conformations.
At the same time the “depth” of threadings can be (Figure 6) longer than Le, giving hints on its relevance
for the dynamic features. Therefore, in the next section we explore
the consequences of the double-folding and threadings on the dynamic
properties of the melts.
4.2. Ring Dynamics
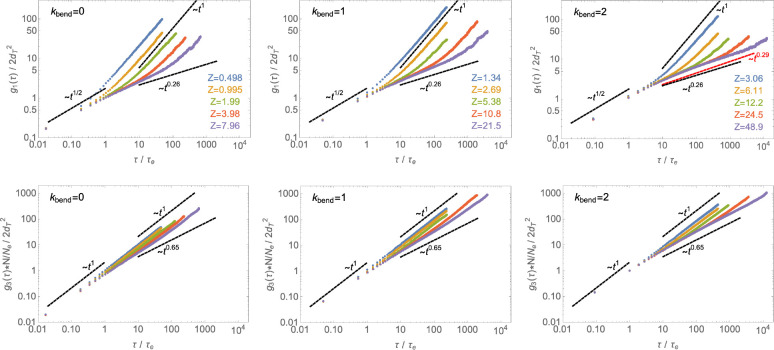
As briefly discussed in Section 2.3, the lattice-tree model predicts universal dynamic chain behavior for length scales ≳ dT and time scales ≳ τe. Recent numerical works employing off-lattice molecular dynamics simulations10 and lattice models27 agree well with these predictions. In order to compare the dynamic behavior of the present systems to the results of the lattice-tree model (namely, eqs 10 and 11) with ν = 1/3 (eq 5) and ρ = 5/9 (eq 6), we look then at the monomer mean-square displacement, g1(τ), and the center of mass mean-square displacement, g3(τ), and plot them in properly rescaled length and time units by using the values of the parameters dT and τe reported in Section 3.4. Figure 10 demonstrates the correctness of the rescaling procedure and, in line with previous works,10,27 the good agreement between our simulations (symbols) and the lattice-tree predictions (dashed black lines), in particular for melts of rings with κbend = 2 and Z ≈ 50. Notice though that our data also match well the predictions of the FLG model19 by Ge et al. (dashed red line in the top-right panel), since the two scaling exponents (0.29 vs 0.26, respectively) are within 10% of each other and, hence, beyond the present accuracy of our data.
Figure 10.
Monomer time mean-square displacement, g1(τ) (eq 8), and chain center of mass time mean-square displacement, g3(τ) (eq 9). Symbols of the same color are for the same number of monomers N, and the corresponding number of entanglements Z per chain is indicated in the legends. The dashed black lines correspond to the dynamic predictions of the lattice tree model, eqs 10 and 11 with ν = 1/3 (eq 5) and ρ = 5/9 (eq 6). The dashed red line in the top-right panel corresponds to the theoretical prediction of the FLG model19 by Ge et al.
We conclude now the paper by investigating the implications of threading and double-folding for ring dynamics. While slightly off-topic with respect to the main body of this work, we think nonetheless that the results we are going to discuss represent a valid complement to it.
The formation of topological links via threadings has been held responsible of the unique rheological properties of melts of rings as, for instance, the unusually strong extension-rate thickening of the viscosity in extensional flows.26 Notably, it was conjectured36 that inter-ring threadings should form a network of topological obstacles which, by percolating through the entire melt, should sensibly slow down the relaxation of the system, not dissimilar from what happens in those materials undergoing the glass transition. While direct proof of this topological glass is currently missing, recently Michieletto and others37,38 gave indirect evidence of this through the following numerical experiment: they froze (pinned) a certain fraction fp of rings in the melt and reported that the dynamics of the remaining ones is considerably reduced if not frozen at all. In corresponding melts of linear chains this effect is not seen, so they attributed the observed slowing down to the presence of threadings present in rings but absent in linear chains.
In the numerical experiments
discussed here, while double-folding
is “enhanced” (Section 4.1) by the chain local stiffness, long threadings,
with Lt > Le, which should be the ones
affecting
the dynamics of the system, are universal. At this level, it is unclear
what the impact of these features is on the dynamics and whether or
not they can be distinguished. To get some insight into this question,
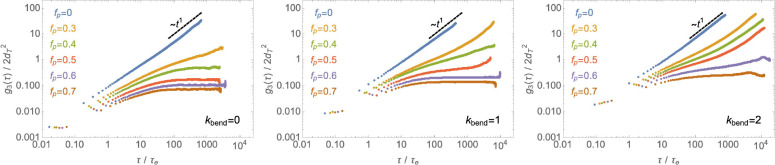
we have taken inspiration from the mentioned pinning numerical experiments37,38 and performed additional simulations of melts of rings for κbend = 0, 1, 2 with the same number of entanglements Z = 8 (to ensure the same large-scale behavior, see Figure 4) and for ring pinning
fractions fp from 0 (i.e.,
no pinning) to 70%. Then we monitored the mean-square displacement, g3(τ), of the center of mass of the nonpinned
rings. As shown in Figure 11, our results are consistent with the proposed picture: more
flexible rings (κbend = 0, left panel) which we have
interpreted as less double-folded are already completely frozen at fp ≃ 30–40%, while
the stiffer (and comparably more double-folded) rings (κbend = 2, right panel) require fp ≃ 60–70%. Importantly, these specific
fractions do not seem to depend on the finite size of our systems:
dynamic runs with smaller (and, arguably, more finite-size dependent)
systems give similar values for the freezing fractions (see Figure S7 in the SI). Finally, we see that this
is compatible with a network of percolating topological constraints.
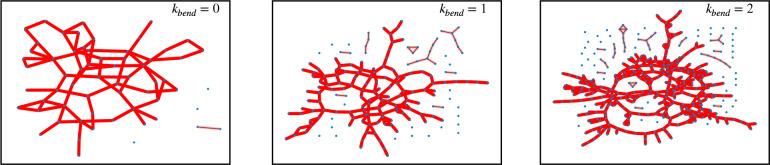
To this purpose, we represent the melts as networks where each node
corresponds to a ring, and we draw a link between two nodes (i.e.,
rings) whenever the minimal surface of one of the two rings is pierced
by a threading segment of the other ring of contour length Lt > Le (i.e., we neglect the shallow threadings).
A picture of these networks is shown in Figure 12: it is seen that, at increasing chain stiffness,
the fraction of rings globally connected through threadings sensibly
decreases with chain stiffness, from 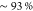 for κbend = 0 to
for κbend = 0 to 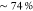 for κbend = 1 and κbend = 2; that is, the network
of threadings is percolating
less through the stiffer melts. [In principle, these percentages may
be affected by finite-size effects due to the limited number of chains
of our melts. Nonetheless, our conclusions should be fairly robust.]
Notice that this decrease corresponds roughly to the fractional amount
for κbend = 1 and κbend = 2; that is, the network
of threadings is percolating
less through the stiffer melts. [In principle, these percentages may
be affected by finite-size effects due to the limited number of chains
of our melts. Nonetheless, our conclusions should be fairly robust.]
Notice that this decrease corresponds roughly to the fractional amount 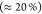 of rings which need to be additionally
pinned in the stiffer systems compared to κbend =
0 in order to get complete freezing (Figure 11). To summarize, flexible melts showing
higher propensity to shallow threadings (Figure 6) are more strongly affected by the pinning,
pointing to a possible dynamical role of the shallow threadings. In
contrast—yet consistent with the pinning fraction—the
deep threadings in flexible melts form more connected networks in
comparison to the stiffer melts, seemingly suggesting that these alone
are the relevant ones in the pinning experiment. The latter result
is however surprising, because the deep threadings were found to behave
universally for the systems with different stiffness (see Figure 6). We leave this
puzzle for future work.
of rings which need to be additionally
pinned in the stiffer systems compared to κbend =
0 in order to get complete freezing (Figure 11). To summarize, flexible melts showing
higher propensity to shallow threadings (Figure 6) are more strongly affected by the pinning,
pointing to a possible dynamical role of the shallow threadings. In
contrast—yet consistent with the pinning fraction—the
deep threadings in flexible melts form more connected networks in
comparison to the stiffer melts, seemingly suggesting that these alone
are the relevant ones in the pinning experiment. The latter result
is however surprising, because the deep threadings were found to behave
universally for the systems with different stiffness (see Figure 6). We leave this
puzzle for future work.
Figure 11.
Effects of random pinning on chain dynamics. Chain center of mass time mean-square displacement, g3(τ) (eq 9), at different pinning fractions, fp, and chain flexibilities, κbend (see legends). Results correspond to melts with the same number of entanglements, Z ≈ 8, per individual chain.
Figure 12.
Network representation of ring melts with the same number of entanglements, Z ≈ 8, per individual chain and for different chain flexibilities κbend (see legends). Each node of the network represents a given ring of the melt, and the bond between two nodes means that one of the two ring is threading the (minimal surface of the) other (see the discussion in Section 4.1). For constructing the networks, we have included threading lengths Lt > Le for which universal scaling behavior emerges (see Section 4.1).
Another view on the results of our pinning experiments shows that the threading constraints are a relevant physical feature that needs to be taken into account to refine models for the ring dynamics. As we mentioned (eq 14), the ring relaxation time with (θ = 1) or without (θ = 0) the tube dilation can be written19 as
Notably, the pinning of a large fraction fp of rings must stop the dilation, because the pinned chains around a mobile ring cannot move, hence impose constraints at all times. The plateau of the g3 that we observe indicates a divergence of the relaxation time, but the FLG as well as the lattice models give a finite prediction for the relaxation time even for inhibited dilation θ = 0. Indeed this is the consequence of neglecting of the threadings. Although the FLG model is built on the full tube dilation in the melt, and therefore, its comparison to the pinning with a limited dilation is problematic, its general formulation (eq 14) allows considering a partial (θ < 1) or no tube dilation. Last but not the least, even though both the lattice-tree and the FLG model underestimate the scaling exponent of the diffusion coefficient with N in comparison to simulations and experiment, a similar underestimation of the scaling exponent of the diffusion coefficient is found in linear melts when compared to a naïve reptation theory.2 The agreement between the theory and the experiment is restored when contour length fluctuations and tube dilation are incorporated. In the rings, the FLG model already includes the tube dilation, yet the prediction of the exponent does not agree with the experiment, which indicates that this is due to the neglect of the threadings. Another explanation of the discrepancy might be the correlation hole effect as indicated in ref (33). Whether this is independent of threadings remains to be elucidated.
5. Discussion and Conclusions
The conformational properties of unknotted and non-concatenated ring polymers in dense melts represent one of the remaining unsolved challenges in polymer physics. In this work, in particular, we have focused on which properties of the rings can be interpreted as signatures of the hypothesis proposed long ago4,5,7 that the polymer fiber double-folds around a branched (lattice-tree) path.
In this respect, global observables like
the polymer mean-square
gyration radius or the mean-square magnetic radius (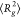 and
and 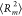 , Figure 4) are very useful for model validation but otherwise
offer little insight.
, Figure 4) are very useful for model validation but otherwise
offer little insight.
On the contrary, robust evidence for double-folding comes by exploiting the mean polymer shape (Figure 9). The three principal axes of the polymer are very different in size and, for relatively moderate polymer lengths, they are not at the same “point” of the crossover to asymptotic behavior: in particular, on the studied range where the largest and the smallest axes are not proportional to each other, we have shown that their functional relation is in quantitative agreement with the lattice-tree model. This argument is proposed here for the first time, and it could be useful to revise data relative to other polymer models at its light.
Additional signatures of double-folding
on polymer contour lengths z = 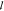 /Le ≲ 1 become manifested also in
the characteristic negative
well of the bond-vector orientation correlation function (Figure 7) and in the “softer”
slope of the mean contact probability ⟨pc(
/Le ≲ 1 become manifested also in
the characteristic negative
well of the bond-vector orientation correlation function (Figure 7) and in the “softer”
slope of the mean contact probability ⟨pc( )⟩ (Figure 8) displayed before
the asymptotic ∼
)⟩ (Figure 8) displayed before
the asymptotic ∼  –1 power-law behavior
effectively takes place. Intriguingly, the reported ⟨pc(
–1 power-law behavior
effectively takes place. Intriguingly, the reported ⟨pc( )⟩ for
chromatin fibers measured
in conformation capture experiments52 displays
the same systematic two-slope crossover65 for
)⟩ for
chromatin fibers measured
in conformation capture experiments52 displays
the same systematic two-slope crossover65 for 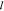 ≲ 105 base pairs, i.e.,
below the estimated34 entanglement length
of the chromatin fiber. Notice that, in this respect, the formulated
hypothesis that such a “shoulder” in the contact probability
derives from active loop-extrusion65 provides
a dynamic explanation about how (double-folded) loops can form; otherwise
it is not needed per se in order to explain the observed
trend in the contact probabilities.
≲ 105 base pairs, i.e.,
below the estimated34 entanglement length
of the chromatin fiber. Notice that, in this respect, the formulated
hypothesis that such a “shoulder” in the contact probability
derives from active loop-extrusion65 provides
a dynamic explanation about how (double-folded) loops can form; otherwise
it is not needed per se in order to explain the observed
trend in the contact probabilities.
Overall it is worth stressing that these features, that we interpret as manifestations of double-folding, can be made explicit only by introducing some (even if only moderate) bending penalty to the polymer elasticity.
Using minimal surfaces we confirm (Figure 5) that rings may reduce their threadable surfaces via double-folding on the entanglement scale and that the piercings of the minimal surface occur only on the scale below the entanglement tube radius. Yet, the threading loops can be numerous and their length can exceed the entanglement length, but these threading features (Figure 6 and Figure S3) evaluated on length scales larger than one entanglement length behave universally. The universal behavior shows the applicability and the relevance47 of the (linear) entanglement scale to ring polymer melts.
From the point of view of ring dynamics, we have reported that single monomer and global chain motions are in good agreement (Figure 10) with the theory stating that the dominant mode of relaxation is mass transport along the mean path of the underlying tree. Yet the threading constraints can cause divergence of the relaxation time if a fraction of rings is immobilized, a feature not predicted by the theories. Revisiting the theories to incorporate threading constraints explicitly might also help to clarify if the conjecture on the existence of topological glass in equilibrium is valid.
Acknowledgments
J.S. and A.R. acknowledge networking support by the COST Action CA17139 (EUTOPIA). The computational results presented have been achieved in part using the Vienna Scientific Cluster (VSC).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.macromol.2c01264.
Table of mean values of structural properties of ring polymers, monomer mean-square displacement g2 in the frame of the ring center of mass, ratios of mean-square gyration radius and mean-square magnetic radius, mean minimal surface after removing the contribution of shallow threadings, distribution functions of distances d between subsequent piercings, mean contact probabilities, mean-square eigenvalues of the gyration tensor, effect of random pinning on smaller melts (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- De Gennes P.-G.Scaling Concepts in Polymer Physics; Cornell University Press, 1979. [Google Scholar]
- Doi M.; Edwards S. F.. The Theory of Polymer Dynamics; Clarendon: Oxford, 1986. [Google Scholar]
- Rubinstein M.; Colby R. H.. Polymer Physics; Oxford University Press: New York, 2003. [Google Scholar]
- Khokhlov A. R.; Nechaev S. K. Polymer chain in an array of obstacles. Phys. Lett. A 1985, 112, 156–160. 10.1016/0375-9601(85)90678-4. [DOI] [Google Scholar]
- Rubinstein M. Dynamics of Ring Polymers in the Presence of Fixed Obstacles. Phys. Rev. Lett. 1986, 57, 3023–3026. 10.1103/PhysRevLett.57.3023. [DOI] [PubMed] [Google Scholar]
- Cates M. E.; Deutsch J. M. Conjectures on the statistics of ring polymers. J. Phys. (Paris) 1986, 47, 2121–2128. 10.1051/jphys:0198600470120212100. [DOI] [Google Scholar]
- Obukhov S. P.; Rubinstein M.; Duke T. Dynamics of a Ring Polymer in a Gel. Phys. Rev. Lett. 1994, 73, 1263–1266. 10.1103/PhysRevLett.73.1263. [DOI] [PubMed] [Google Scholar]
- Müller M.; Wittmer J. P.; Cates M. E. Topological effects in ring polymers. II. Influence of persistence length. Phys. Rev. E 2000, 61, 4078–4089. 10.1103/PhysRevE.61.4078. [DOI] [PubMed] [Google Scholar]
- Halverson J. D.; Lee W. B.; Grest G. S.; Grosberg A. Y.; Kremer K. Molecular dynamics simulation study of nonconcatenated ring polymers in a melt. I. Statics. J. Chem. Phys. 2011, 134, 204904. 10.1063/1.3587137. [DOI] [PubMed] [Google Scholar]
- Halverson J. D.; Lee W. B.; Grest G. S.; Grosberg A. Y.; Kremer K. Molecular dynamics simulation study of nonconcatenated ring polymers in a melt. II. Dynamics. J. Chem. Phys. 2011, 134, 204905. 10.1063/1.3587138. [DOI] [PubMed] [Google Scholar]
- Sakaue T. Ring Polymers in Melts and Solutions: Scaling and Crossover. Phys. Rev. Lett. 2011, 106, 167802. 10.1103/PhysRevLett.106.167802. [DOI] [PubMed] [Google Scholar]
- Halverson J. D.; Grest G. S.; Grosberg A. Y.; Kremer K. Rheology of Ring Polymer Melts: From Linear Contaminants to Ring-Linear Blends. Phys. Rev. Lett. 2012, 108, 038301. 10.1103/PhysRevLett.108.038301. [DOI] [PubMed] [Google Scholar]
- Grosberg A. Y. Annealed lattice animal model and Flory theory for the melt of non-concatenated rings: towards the physics of crumpling. Soft Matter 2014, 10, 560–565. 10.1039/C3SM52805G. [DOI] [PubMed] [Google Scholar]
- Rosa A.; Everaers R. Ring Polymers in the Melt State: The Physics of Crumpling. Phys. Rev. Lett. 2014, 112, 118302. 10.1103/PhysRevLett.112.118302. [DOI] [PubMed] [Google Scholar]
- Obukhov S.; Johner A.; Baschnagel J.; Meyer H.; Wittmer J. P. Melt of polymer rings: The decorated loop model. EPL (Europhysics Letters) 2014, 105, 48005. 10.1209/0295-5075/105/48005. [DOI] [Google Scholar]
- Smrek J.; Grosberg A. Y. Understanding the dynamics of rings in the melt in terms of the annealed tree model. J. Phys.: Condens. Matter 2015, 27, 064117. 10.1088/0953-8984/27/6/064117. [DOI] [PubMed] [Google Scholar]
- Smrek J.; Grosberg A. Y. Minimal Surfaces on Unconcatenated Polymer Rings in Melt. ACS Macro Lett. 2016, 5, 750–754. 10.1021/acsmacrolett.6b00289. [DOI] [PubMed] [Google Scholar]
- Rosa A.; Everaers R. Computer simulations of melts of randomly branching polymers. J. Chem. Phys. 2016, 145, 164906. 10.1063/1.4965827. [DOI] [PubMed] [Google Scholar]
- Ge T.; Panyukov S.; Rubinstein M. Self-Similar Conformations and Dynamics in Entangled Melts and Solutions of Nonconcatenated Ring Polymers. Macromolecules 2016, 49, 708–722. 10.1021/acs.macromol.5b02319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michieletto D. On the tree-like structure of rings in dense solutions. Soft Matter 2016, 12, 9485–9500. 10.1039/C6SM02168A. [DOI] [PubMed] [Google Scholar]
- Dell Z. E.; Schweizer K. S. Intermolecular structural correlations in model globular and unconcatenated ring polymer liquids. Soft Matter 2018, 14, 9132–9142. 10.1039/C8SM01722K. [DOI] [PubMed] [Google Scholar]
- Smrek J.; Kremer K.; Rosa A. Threading of Unconcatenated Ring Polymers at High Concentrations: Double-Folded vs Time-Equilibrated Structures. ACS Macro Lett. 2019, 8, 155–160. 10.1021/acsmacrolett.8b00828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schram R. D.; Rosa A.; Everaers R. Local loop opening in untangled ring polymer melts: a detailed “Feynman test” of models for the large scale structure. Soft Matter 2019, 15, 2418–2429. 10.1039/C8SM02587H. [DOI] [PubMed] [Google Scholar]
- Rosa A.; Everaers R. Conformational statistics of randomly branching double-folded ring polymers. Eur. Phys. J. E 2019, 42, 1–12. 10.1140/epje/i2019-11765-3. [DOI] [PubMed] [Google Scholar]
- Michieletto D.; Sakaue T. Dynamical Entanglement and Cooperative Dynamics in Entangled Solutions of Ring and Linear Polymers. ACS Macro Lett. 2021, 10, 129–134. 10.1021/acsmacrolett.0c00551. [DOI] [PubMed] [Google Scholar]
- O’Connor T. C.; Ge T.; Rubinstein M.; Grest G. S. Topological Linking Drives Anomalous Thickening of Ring Polymers in Weak Extensional Flows. Phys. Rev. Lett. 2020, 124, 027801. 10.1103/PhysRevLett.124.027801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghobadpour E.; Kolb M.; Ejtehadi M. R.; Everaers R. Monte Carlo simulation of a lattice model for the dynamics of randomly branching double-folded ring polymers. Phys. Rev. E 2021, 104, 014501. 10.1103/PhysRevE.104.014501. [DOI] [PubMed] [Google Scholar]
- Kapnistos M.; Lang M.; Vlassopoulos D.; Pyckhout-Hintzen W.; Richter D.; Cho D.; Chang T.; Rubinstein M. Unexpected power-law stress relaxation of entangled ring polymers. Nat. Mater. 2008, 7, 997–1002. 10.1038/nmat2292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pasquino R.; et al. Viscosity of Ring Polymer Melts. ACS Macro Lett. 2013, 2, 874–878. 10.1021/mz400344e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iwamoto T.; Doi Y.; Kinoshita K.; Ohta Y.; Takano A.; Takahashi Y.; Nagao M.; Matsushita Y. Conformations of Ring Polystyrenes in Bulk Studied by SANS. Macromolecules 2018, 51, 1539–1548. 10.1021/acs.macromol.7b02358. [DOI] [Google Scholar]
- Huang Q.; Ahn J.; Parisi D.; Chang T.; Hassager O.; Panyukov S.; Rubinstein M.; Vlassopoulos D. Unexpected Stretching of Entangled Ring Macromolecules. Phys. Rev. Lett. 2019, 122, 208001. 10.1103/PhysRevLett.122.208001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruteva M.; Allgaier J.; Monkenbusch M.; Porcar L.; Richter D. Self-Similar Polymer Ring Conformations Based on Elementary Loops: A Direct Observation by SANS. ACS Macro Lett. 2020, 9, 507–511. 10.1021/acsmacrolett.0c00190. [DOI] [PubMed] [Google Scholar]
- Kruteva M.; Monkenbusch M.; Allgaier J.; Holderer O.; Pasini S.; Hoffmann I.; Richter D. Self-Similar Dynamics of Large Polymer Rings: A Neutron Spin Echo Study. Phys. Rev. Lett. 2020, 125, 238004. 10.1103/PhysRevLett.125.238004. [DOI] [PubMed] [Google Scholar]
- Rosa A.; Everaers R. Structure and Dynamics of Interphase Chromosomes. Plos Comput. Biol. 2008, 4, e1000153 10.1371/journal.pcbi.1000153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halverson J. D.; Smrek J.; Kremer K.; Grosberg A. Y. From a melt of rings to chromosome territories: the role of topological constraints in genome folding. Rep. Prog. Phys. 2014, 77, 022601. 10.1088/0034-4885/77/2/022601. [DOI] [PubMed] [Google Scholar]
- Lo W.-C.; Turner M. S. The topological glass in ring polymers. EPL (Europhysics Letters) 2013, 102, 58005. 10.1209/0295-5075/102/58005. [DOI] [Google Scholar]
- Michieletto D.; Turner M. S. A topologically driven glass in ring polymers. Proc. Natl. Acad. Sci. U.S.A. 2016, 113, 5195–5200. 10.1073/pnas.1520665113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michieletto D.; Nahali N.; Rosa A. Glassiness and Heterogeneous Dynamics in Dense Solutions of Ring Polymers. Phys. Rev. Lett. 2017, 119, 197801. 10.1103/PhysRevLett.119.197801. [DOI] [PubMed] [Google Scholar]
- Smrek J.; Chubak I.; Likos C. N.; Kremer K. Active topological glass. Nat. Commun. 2020, 11, 26. 10.1038/s41467-019-13696-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brereton M. G.; Vilgis T. A.. The statistical mechanics of a melt of polymer rings. 1995, 28, 1149–1167. 10.1088/0305-4470/28/5/007 [DOI] [Google Scholar]
- David Moroz J.; Kamien R. D. Self-avoiding walks with writhe. Nuclear Physics B 1997, 506, 695–710. 10.1016/S0550-3213(97)00601-9. [DOI] [Google Scholar]
- Kholodenko A. L.; Vilgis T. A. Some geometrical and topological problems in polymer physics. Phys. Rep. 1998, 298, 251–370. 10.1016/S0370-1573(97)00081-1. [DOI] [Google Scholar]
- Kung W.; Kamien R. D. Topological constraints at the Theta-point: Closed loops at two loops. Europhysics Letters (EPL) 2003, 64, 323–329. 10.1209/epl/i2003-00177-6. [DOI] [Google Scholar]
- Ferrari F.; Paturej J.; Pia̧tek M.; Zhao Y. Knots, links, anyons and statistical mechanics of entangled polymer rings. Nuclear Physics B 2019, 945, 114673. 10.1016/j.nuclphysb.2019.114673. [DOI] [Google Scholar]
- Everaers R.; Karimi-Varzaneh H. A.; Fleck F.; Hojdis N.; Svaneborg C. Kremer–Grest Models for Commodity Polymer Melts: Linking Theory, Experiment, and Simulation at the Kuhn Scale. Macromolecules 2020, 53, 1901–1916. 10.1021/acs.macromol.9b02428. [DOI] [Google Scholar]
- Everaers R.; Sukumaran S. K.; Grest G. S.; Svaneborg C.; Sivasubramanian A.; Kremer K. Rheology and Microscopic Topology of Entangled Polymeric Liquids. Science 2004, 303, 823. 10.1126/science.1091215. [DOI] [PubMed] [Google Scholar]
- Wang J.; Ge T. Crazing Reveals an Entanglement Network in Glassy Ring Polymers. Macromolecules 2021, 54, 7500–7511. 10.1021/acs.macromol.1c01080. [DOI] [Google Scholar]
- Smrek J. Unraveling entanglement. Journal Club for Condensed Matter Physics 2022, 10.36471/JCCM_January_2022_03. [DOI] [Google Scholar]
- Hugouvieux V.; Axelos M. A. V.; Kolb M. Amphiphilic Multiblock Copolymers: From Intramolecular Pearl Necklace to Layered Structures. Macromolecules 2009, 42, 392–400. 10.1021/ma801337a. [DOI] [Google Scholar]
- Schram R. D.; Barkema G. T. Simulation of ring polymer melts with GPU acceleration. J. Comput. Phys. 2018, 363, 128–139. 10.1016/j.jcp.2018.02.027. [DOI] [Google Scholar]
- Bishop M.; Michels J. P. J. Scaling in threeâdimensional linear and ring polymers. J. Chem. Phys. 1986, 84, 444–446. 10.1063/1.450158. [DOI] [Google Scholar]
- Lieberman-Aiden E.; et al. Comprehensive Mapping of Long-Range Interactions Reveals Folding Principles of the Human Genome. Science 2009, 326, 289–293. 10.1126/science.1181369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lang M. Ring Conformations in Bidisperse Blends of Ring Polymers. Macromolecules 2013, 46, 1158–1166. 10.1021/ma301359b. [DOI] [Google Scholar]
- Kremer K.; Grest G. S. Dynamics of entangled linear polymer melts: A molecularâdynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. 10.1063/1.458541. [DOI] [Google Scholar]
- From eqs 3 and 4 we see
a further reason
of interest to study melts of rings by varying the Kuhn length
 K: if the prefactor
was stiffness-dependent, the universal scaling of all the quantities
in terms of the number of entanglements would not be expected.
K: if the prefactor
was stiffness-dependent, the universal scaling of all the quantities
in terms of the number of entanglements would not be expected. - Everaers R.; Grosberg A. Y.; Rubinstein M.; Rosa A. Flory theory of randomly branched polymers. Soft Matter 2017, 13, 1223–1234. 10.1039/C6SM02756C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kavassalis T. A.; Noolandi J. New View of Entanglements in Dense Polymer Systems. Phys. Rev. Lett. 1987, 59, 2674–2677. 10.1103/PhysRevLett.59.2674. [DOI] [PubMed] [Google Scholar]
- Olarte-Plata J. D.; Haddad N.; Vaillant C.; Jost D. The folding landscape of the epigenome. Physical Biology 2016, 13, 026001. 10.1088/1478-3975/13/2/026001. [DOI] [PubMed] [Google Scholar]
- Ubertini M. A.; Rosa A. Computer simulations of melts of ring polymers with nonconserved topology: A dynamic Monte Carlo lattice model. Phys. Rev. E 2021, 104, 054503. 10.1103/PhysRevE.104.054503. [DOI] [PubMed] [Google Scholar]
- Metropolis N.; Rosenbluth A. W.; Rosenbluth M. N.; Teller A. H.; Teller E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. 10.1063/1.1699114. [DOI] [Google Scholar]
- Uchida N.; Grest G. S.; Everaers R. Viscoelasticity and primitive path analysis of entangled polymer liquids: From F-actin to polyethylene. J. Chem. Phys. 2008, 128, 044902. 10.1063/1.2825597. [DOI] [PubMed] [Google Scholar]
- Ashcroft N. W.; Mermin N. D.. Solid State Physics; Saunders College Publishing: New York, 1976. [Google Scholar]
- Lin Y. H. Number of entanglement strands per cubed tube diameter, a fundamental aspect of topological universality in polymer viscoelasticity. Macromolecules 1987, 20, 3080–3083. 10.1021/ma00178a024. [DOI] [Google Scholar]
- Morse D. C. Viscoelasticity of tightly entangled solutions of semiflexible polymers. Phys. Rev. E 1998, 58, R1237–R1240. 10.1103/PhysRevE.58.R1237. [DOI] [PubMed] [Google Scholar]
- Fudenberg G.; Abdennur N.; Imakaev M.; Goloborodko A.; Mirny L. A. Emerging Evidence of Chromosome Folding by Loop Extrusion. Cold Spring Harb. Symp. Quant. Biol. 2017, 82, 45–55. 10.1101/sqb.2017.82.034710. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.