Abstract
Heterosis refers to the superior performance of a hybrid offspring over its two inbred parents. Although heterosis has been widely observed in agriculture, its molecular mechanism is not well studied. Recent advances in high-throughput genomic technologies such as RNA sequencing (RNA-seq) facilitate the investigation of heterosis at the gene expression level. However, it is challenging to identify genes exhibiting heterosis using RNA-seq data because high-dimension of hypotheses tests are conducted with limited sample size. Furthermore, detecting heterosis genes requires testing composite null hypotheses involving multiple mean expression levels instead of testing simple null hypotheses as in differential expression analysis. In this manuscript, we formulate a statistical model with parameters directly reflecting heterosis status, and develop a powerful test to detect heterosis genes. We employ a Bayesian framework where the RNA-seq count data are modeled through a Poisson-Gamma mixture with Dirichlet processes as priors for the distributions of the parameters of interest, the fold changes between each parent and the hybrid. Markov Chain Monte Carlo sampling with Gibbs algorithm is utilized to provide posterior inference to detect heterosis genes while controlling false discovery rate. Simulation results demonstrate that our proposed method outperformed other methods utilized to detect gene expression heterosis.
Keywords: Gene expression heterosis, RNA-seq, semi-parametric Bayesian, Dirichlet process, MCMC, Bayesian FDR
1. Introduction
Heterosis, also called hybrid vigor, describes the phenotypic improvement of a hybrid offspring over its two inbred parents. Heterosis was documented by [7] and has been widely utilized in growing agricultural crops, such as rice [30], to increase development rates and grain yields. In China, hybrid rice is estimated to be planted on more than 50% of the rice farmland, and produces 10–20% more than inbred varieties [6]. However, the mechanism of heterosis is not yet well studied [5].
Researchers have speculated that genes which are differentially expressed between hybrid offspring and its two inbred parents, or gene expression heterosis, might be responsible for phenotypic heterosis [14,27]. The recent development of high-throughput genomic technologies, such as microarray and RNA-sequencing (RNA-seq), allow researchers to measure the expression levels for tens of thousands of genes simultaneously. Then gene expression heterosis can be studied by comparing expression levels between the hybrid offspring and its two inbred parents for all expressed genes. More specifically, it is of particular interest to test for each gene if it exhibits high-parent heterosis (HPH), i.e. the mean expression level of the hybrid is greater than both parental means, or low-parent heterosis (LPH), i.e. the mean expression level of the hybrid is less than both parental means.
For both microarray and RNA-seq technologies, tens of thousands of genes are simultaneously measured for their expression levels. However, due to the high cost of such experiments, sample sizes are usually small. This introduces the ‘small n, large p’ problem, where n refers to the sample size and p refers to the number of variables (genes). The power for hypothesis testing in such settings is often low after adjusting for multiple testing errors. To utilize information from other genes, hierarchical models and Bayesian methods have been employed to borrow information across genes. These strategies have been established in differential expression analysis, such as the widely applied moderated-t test for microarray data [26] and baySeq [13] for RNA-seq data. Differential expression analysis aims to identify genes whose expression levels change across treatments or conditions. Hence, the null hypothesis is no change, and is a simple null case. However, for detecting HPH or LPH genes, the null hypotheses involve the mean expression levels for three conditions in a composite null. Therefore, the well-developed differential expression analysis methods are not directly applicable for the detection of heterosis genes.
Only a few methods have been proposed to detect gene expression heterosis. In 2014, Ji et al. [15] constructed an empirical Bayesian framework to detect gene expression heterosis with microarray data where gene expression measurements were modeled as continuous variables. They proposed a normal hierarchical model, which allows information to be borrowed across genes for estimating mean and variance parameters. They applied an empirical Bayes procedure to first estimate model hyperparameters, and then obtain the posterior distributions for gene-specific parameters, based on which heterosis is evaluated. Nowadays, RNA-seq technologies instead of microarray are widely applied for gene expression studies. Generally, RNA-seq count data are modeled with a negative binomial (NB) distribution [1,20]. Based on the work of [15], Niemi et al. [23] proposed an empirical Bayes approach for estimating gene expression heterosis with RNA-seq count data based on an NB hierarchical model in 2015, where heterosis was evaluated by comparing one model parameter with the absolute value of another model parameter. In 2019, Landau et al. [17] developed a general hierarchical model for RNA-seq count data and a fully Bayesian analysis with parallelized Markov Chain Monte Carlo (MCMC) algorithm to improve the computational efficiency. They also showed that the empirical Bayes approach can be an approximation of a fully Bayesian analysis if accurate hyperparameter estimates can be obtained. Both methods [17,23] are based on the assumption that gene-specific parameters are independent and arise from given parametric distributions. However, the distributions of parameters across all genes are not guaranteed to follow the assumed parametric distributions in practice. Empirical distributions of parameters could be irregular and vary between studies [18]. Therefore, under these circumstances, it is hard to model the empirical distribution across all genes with given parametric methods. In addition, both methods [17,23] did not assess the controlling of false discovery rate (FDR), which has been the choice of error criterion in RNA-seq data analysis, where tens of thousands of hypotheses tests are simultaneously conducted.
To avoid unrealistic parametric assumptions and to take FDR control into consideration, we propose to use nonparametric Bayesian methods. The Dirichlet process (DP) mixture model is one popular nonparametric Bayesian method, and such a modeling method has been used for differential expression analyses when comparing two different conditions. For instance, Do et al. [8] utilized DP mixtures to model the mean expression levels of genes for each of two conditions with microarray data in 2005. Liu et al. [18] chose DP mixtures for modeling the distribution of fold change parameters of a treatment condition with respect to a reference condition for RNA-seq data in 2015. In 2019, Bi and Liu [3] modified the base distribution of the DP prior used in [18], in order to guarantee that the model is invariant regardless of which treatment group is set to be the reference condition.
Building on the work of [18], we capture RNA-seq data with a Poisson-Gamma mixture that is equivalent to an NB model. We treat the hybrid offspring as the reference treatment, as heterosis status is determined by comparing the hybrid genotype with two parental lines. In addition, we parameterize our model so that we have model parameters corresponding to the fold changes between the mean expression levels of the hybrid offspring versus each parental line separately. We then construct a semi-parametric Bayesian approach and use posterior results for detection of gene expression heterosis while controlling FDR.
The rest of this manuscript is organized as follows. Section 2 introduces our proposed semi-parametric Bayesian approach and prior models, then applies the MCMC sampling scheme for posterior inference and FDR estimation. Section 3 provides an algorithm for improving computational efficiency grounded on a division of the data. In Section 4, we conduct several simulation studies with NB distributions and compare the results of our approach to the method in [23]. In Section 5, we analyze a real maize dataset and identify heterosis genes with our proposed method. Section 6 provides a summary and some discussion of our work.
2. Method
In this section, we first introduce our modeling framework, specify the prior models we adopted, then provide the MCMC sampling method for posterior inference and FDR estimation.
2.1. Model
We consider gene expression heterosis experiments that involve three genotypes: the hybrid offspring genotype, and the two parental inbred lines. Although the offspring genotype is generated by crossing the two parental lines, plants for the three genotypes are grown together in the same environment to provide samples for gene expression heterosis studies. Suppose that a completely randomized design with independent biological replicates for each genotype has been used for the gene expression heterosis experiments. For RNA-seq experiments with biological replicates in each treatment (genotype) group, the NB distribution has been commonly employed for modeling the RNA-seq count data [1,13,20]. Notice that the NB distribution has no conjugate prior and introduces computational difficulties in Bayesian hierarchical modeling. We re-parameterize the NB model with Poisson-Gamma mixtures that make Bayesian hierarchical modeling much easier.
Consider an RNA-seq heterosis experiment that measures G genes. Let denote the observation for gene g from biological replicate j of genotype i, where , i = 1, 2, 3, (i = 1 denotes hybrid offspring, i = 2 denotes parental line 1, and i = 3 denotes parental line 2), , and is the number of biological replicates in treatment i. Then count data can be modeled using a Poisson-Gamma mixture model as below,
where denotes a normalization factor accounting for nuisance technical effects such as sequencing depths across the replicates [1], is the conditional expression mean from replicate j in treatment i for gene g, denotes the shape parameter that corresponds to the reciprocal of the dispersion parameter in the NB model for gene g, refers to the rate parameter for hybrid offspring, the product of and is the rate parameter for parental line 1, and the product of and is for parental line 2. In fact, the marginal distribution of is NB with dispersion parameter and mean parameter , , and for the hybrid, parental line 1, and parental line 2, respectively. Note that the mean ratio of offspring over parental line 1 is , which is referred to as the fold change parameter between hybrid offspring versus parental line 1 for gene g. Similarly, denotes the fold change parameter between hybrid offspring versus parental line 2.
With our parameterization, HPH genes are genes with
| (1) |
Similarly, LPH genes are genes with
| (2) |
As shown in (1) and (2), under our unique parameterization for heterosis detection, conditions for HPH and LPH are expressed by comparing each of the two parameters with a constant instead of comparing three means with each other, which simplifies the problem. In addition, using the fold change parameters and make interpretation more straightforward.
2.2. Prior specification
Since our primary focus is the fold change parameters and , it is crucial to choose appropriate prior distributions for them. To provide maximal flexibility, we propose to use nonparametric Bayesian modeling with DP to model the prior distributions for and .
A DP is a family of stochastic processes whose realizations are probability distributions. In other words, a DP is a distribution over distributions. DP is specified by a base distribution and a positive real number M called the concentration parameter. For a given measurable set Ω, a random probability distribution F is drawn from a DP if for any measurable finite partition of Ω, denoted by , has Dirichlet distribution . We denote F as . The base distribution represents the mean of the process, while the concentration parameter illustrates how strong the discretization is.
Next we will utilize a DP for modeling the fold change parameters. Here we illustrate the DP modeling procedure for (fold change between hybrid offspring and parental line 1) as an example, the same procedure is applied to . Following [18], a mixture of a point mass at one and a Gamma distribution is used as the base distribution of the DP prior for . This can be written as
| (3) |
for gene g, , where is the proportion of equivalently expressed genes between the hybrid and parent 1, represents point mass at x. Throughout this manuscript, we set so that no prior preference is given to either differential expression or equivalent expression between hybrid offspring and parental line 1. We set the concentration parameter M = 1, a common choice in applications [8,12,16].
We assign an exponential distribution for the prior of , and a Gamma distribution for the prior of ,
| (4) |
| (5) |
where r, , and , are hyperparameters. Also, we set r = 0.01, , , , to have non-informative priors so that the inference for and primarily relies on the observed data. All priors for , , and are set to be independent. Because we apply nonparametric priors for the fold change parameters and parametric priors for other parameters, the method we propose is a semi-parametric Bayesian approach.
2.3. Markov Chain Monte Carlo simulation
With the priors specified, the posterior distributions can be derived via multiplying the priors by the likelihood function. We adopt an MCMC [29] based sampling method to draw samples from the posterior distribution. More specifically, we utilize the Gibbs algorithm to perform MCMC when conjugate priors are utilized.
In DP mixture modeling procedure, MCMC sampling methods are generally based on integrating F over its DP prior (3), where the sequence of 's follows a Pólya urn scheme [4,9], that is,
| (6) |
where is the vector after deleting .
Then, the most straightforward way to draw samples from our model is to update through iteratively. However, this approach is inefficient. Since in RNA-seq experiments, it is likely that many genes share the same or very similar , but this method cannot change for multiple genes simultaneously. A change to the for genes in such a group occurs with a low probability. Thus, converging to the posterior distribution may take a long time [21]. Due to this computational efficiency issue of the MCMC algorithm, configuration indicators are used here as in [18]. Suppose K is the number of distinct values in and let the distinct values be denoted by . Define as the configuration indicators by
Then, the prior model for is re-parameterized with and as below,
where and have independent priors and CRP stands for Chinese Restaurant Process, which is a random distribution with the full conditional distribution of written as
where is the number of unique values in after deleting , and is the number in who equal after deleting .
The MCMC sampling scheme uses Gibbs sampling algorithm to update each of the following parameters: (1) 's, (2) 's, (3) 's, (4) 's and (5) 's, where the update of 's and 's utilizes the configuration indicators as shown above.
The detailed derivations of the full conditionals for each parameter are provided in Web Appendix A. The posterior samples for both and are then used for further inference.
2.4. Bayesian FDR estimation
In gene expression heterosis studies, a massive number of hypotheses tests are conducted, each related to a gene. Therefore, the number of false significant results needs to be controlled for such multiple testing procedure. As in other genomic studies, we choose to control FDR, defined as the expected proportion of false positives among the discoveries [2], in RNA-seq data analysis. In a Bayesian framework, we are able to construct procedures for estimating FDR through Bayesian FDR [11,22] by using posterior probability.
Given gene g, , the posterior probability that this gene exhibits HPH is denoted by , while the posterior probability that the gene exhibits LPH is denoted by . and can be estimated as the proportion of posterior samples drawn from MCMC for gene g that satisfy the HPH or LPH conditions, i.e.
where N denotes the total number of posterior samples used for inference. We conclude the gene exhibits HPH or LPH when the estimated is less than a critical value , which can be chosen based on a desired level of FDR, γ,
where
Then the Bayesian FDR controlled at γ can be estimated by
3. Data division
The method we proposed is based on the MCMC sampling scheme that updates parameters iteratively among genes. Not surprisingly, such a procedure is quite time consuming, especially when the total number of genes is huge. In order to improve the computational efficiency, we consider a strategy that divides the raw dataset into several small datasets, applies our proposed method independently to the smaller datasets using parallel computing and then combines the posterior samples together for further inference. Assume we have G genes, and we randomly divide them into m groups, so that each group has an approximately equal number of genes. We assess our proposed method with and without this data division strategy in simulation studies.
4. Simulation studies
In this section, we carry out several simulation studies to evaluate our proposed semi-parametric approaches, SBA (without data division) and SBA_div (with data division), and compare them to the empirical Bayes method in [23] (eBayes_Laplace and eBayes_Normal, depending on the parametric prior assumption). Landau et al. [17] proposed a fully Bayesian analysis and also showed that their fully Bayesian method could be well approximated by the empirical Bayes method in [23]. In addition, the fully Bayesian method is more time consuming and requires more computational resources than the empirical Bayes method. Hence, we only include the empirical Bayes method [23] but not the fully Bayesian method [17] in our simulation studies. Converting RNA-seq count data into continuous data and applying the approach proposed in [15] is also an option, but Niemi et al. [23] have already demonstrated in their simulation studies that such approach had inferior performance to their method, thus we also omit the comparison with the method developed in [15].
To imitate the real RNA-seq data, gene-specific mean and dispersion parameters were estimated from a real maize dataset [28]. We conducted two simulation studies, A and B, which differed in how fold change parameters were simulated. For each simulation study, 32 datasets were generated independently, and test performance for each method under comparison was assessed by averaging results over the 32 datasets. Each dataset contained 3000 genes, 3 genotypes and 3 replicates per genotype, and was simulated based on NB models with estimated pairs of mean and dispersion parameters. For our SBA and SBA_div methods, posterior probabilities were estimated by 5000 posterior samples after 3000 iterations burn-in. Convergence was checked by Gelman-Rubin criteria [10].
4.1. Simulation A
We estimated the gene-specific mean from one treatment group in [28]'s maize dataset, as well as the dispersion parameters across two treatments. We randomly sampled 3000 out of 27,819 pairs of mean and dispersion parameters without replacement, to use as geometric means across three genotypes ( ) and dispersion parameters ( ) for gene . The RNA-seq count data for the hybrid offspring were generated from for gene g. Then, 1500 out of the 3000 genes were randomly selected, and for these genes were set to be 1, which means that count data for parental line 1 were also drawn from . The remaining 1500 genes were simulated to have fold change parameters set to be 0.125, 0.25, 4, or 8, thus we had 375 genes for each value of . Then RNA-seq count data for parental line 1 were drawn from . The count data for parental line 2 were generated similarly while was generated independently of . Note that such that the geometric mean of the hybrid and two parental lines is .
4.2. Simulation B
Similar to Simulation A, 3000 genes were drawn from , where pairs of and were sampled from the estimates from the same maize data. Again, 1500 out of 3000 genes were randomly selected to have fold changes between hybrid and parental line 1. For the remaining 1500 genes, we simulated from the following distribution,
The fold change parameters between the hybrid and parent 2, , were generated in the same way independently of .
4.3. Simulation results for detecting gene expression heterosis
Different normalization methods may affect the performance of the methods under comparison. To avoid the impact of different normalization methods, we set normalization factor for all methods in both simulation studies.
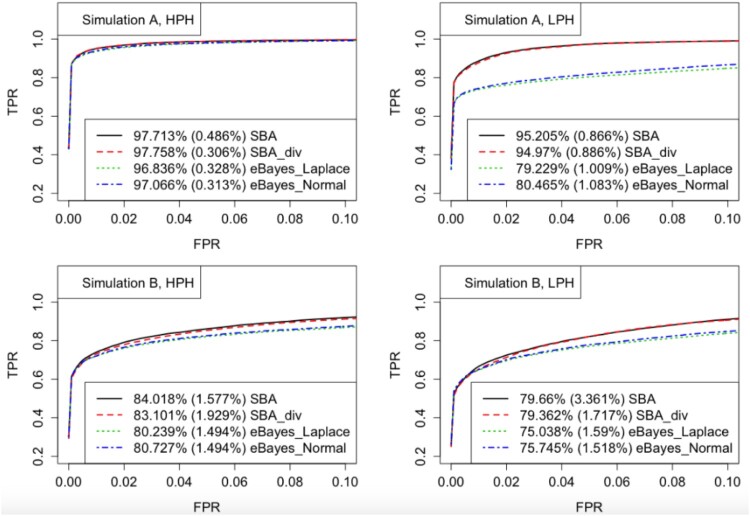
We first evaluate the performances of different methods with the receiver operating characteristic (ROC) curve, which is the plot of the true positive rate (TPR) against the false positive rate (FPR). For each simulated dataset, TPR and FPR were calculated by ranking heterosis genes via posterior probabilities. Then, given each FPR level, the average TPRs over 32 simulated datasets were calculated, leading to the ROC curves shown in Figure 1. We only plotted the ROC curves within the region where FPR is below 0.1, which is often of primary interest in practice. The partial area under curve (AUC) values were calculated as well, which is the proportion of the total area in the region where FPR is no larger than 0.1. The average AUC values and the standard deviations across simulated datasets are presented in the legends.
Figure 1.
ROC curves for Simulations A and B. Given each FPR level, the TPRs were averaged over 32 simulated datasets. The partial AUC values were calculated by averaging the percentages of the total area in the plotted region where FPR is below 0.1, and reported in the legends, with the standard deviations in parentheses.
As indicated in Figure 1, our proposed methods (SBA and SBA_div) generated higher ROC curves and greater AUC values than the empirical Bayes method proposed in [23], under both simulation settings A and B. To implement SBA_div, we randomly divided the 3000 genes into 5 groups, with 600 genes in each group, then applied our SBA method independently to the 5 groups. Therefore, Figure 1 demonstrates that our proposed methods outperformed the empirical Bayes method in terms of the ability to correctly ranking true heterosis genes.
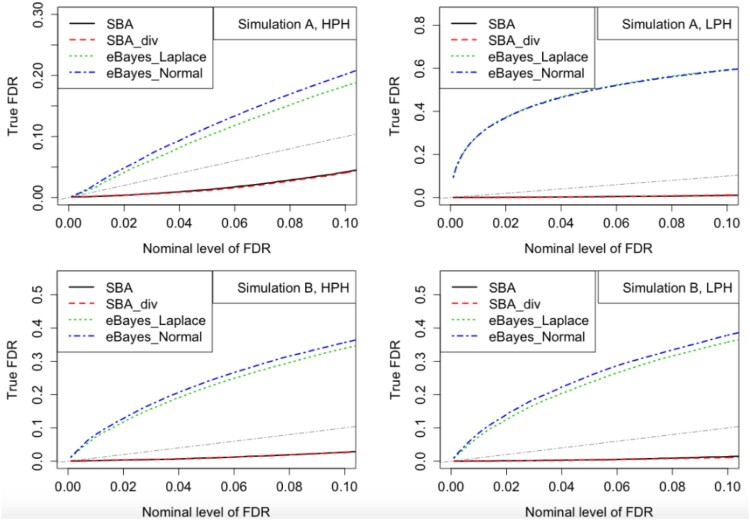
We also evaluated the FDR estimation method described in Subsection 2.4 using the posterior probabilities for each method. FDR plots for Simulations A and B are presented in Figure 2. Given each nominal level of FDR, the actual observed FDRs were estimated by averaging the proportion of false discoveries among declared heterosis genes across 32 simulated datasets. A well-performing method would control the FDR close to or below nominal level. As shown in Figure 2, our proposed methods (SBA and SBA_div) controlled FDR, while FDR was not controlled for the empirical Bayes method in [23].
Figure 2.
FDR plots for Simulations A and B. Given each nominal level of FDR, the actual observed FDRs were estimated by averaging the proportion of false discoveries among declared heterosis genes across 32 simulated datasets. The gray dash-dotted lines represent the Y = X line.
In Figure 2, the FDR curves for our proposed methods are below the Y = X line, indicating that our methods are conservative. For further study of the FDR control, we checked the actual FDR, the number of declared heterosis genes, and the number of truly declared heterosis genes for each nominal level of FDR. The results for HPH or LPH in Simulations A and B are presented in Table 1 and Web Tables 1-3 in Web Appendix B respectively. The empirical Bayes methods identified more true heterosis genes than our methods. However, they also generated many more false positives than desired and resulted in liberal actual FDR.
Table 1.
Results for HPH in Simulation A.
| Nominal level | Actual | Number of declared | Number of declared truly | Total number of | |
|---|---|---|---|---|---|
| of FDR | Method | FDR | heterosis genes | heterosis genes | heterosis genes |
| 0.01 | SBA | 0.0018 | 495 | 494 | 613 |
| SBA_div | 0.0021 | 494 | 493 | ||
| eBayes_Laplace | 0.0175 | 567 | 557 | ||
| eBayes_Normal | 0.0228 | 576 | 563 | ||
| 0.05 | SBA | 0.0129 | 562 | 555 | 613 |
| SBA_div | 0.0116 | 561 | 555 | ||
| eBayes_Laplace | 0.1004 | 657 | 591 | ||
| eBayes_Normal | 0.1145 | 672 | 595 | ||
| 0.1 | SBA | 0.0420 | 609 | 583 | 613 |
| SBA_div | 0.0405 | 607 | 583 | ||
| eBayes_Laplace | 0.1829 | 736 | 601 | ||
| eBayes_Normal | 0.2018 | 756 | 604 | ||
| 0.2 | SBA | 0.1305 | 694 | 603 | 613 |
| SBA_div | 0.1297 | 692 | 602 | ||
| eBayes_Laplace | 0.3150 | 889 | 609 | ||
| eBayes_Normal | 0.3352 | 917 | 610 |
Based on the simulation results, our proposed methods generated higher ROC curves compared with the empirical Bayes method in [23]. Furthermore, our methods controlled FDR, and hence provided a reliable list of genes exhibiting HPH or LPH at a desired level of FDR. All in all, our proposed methods worked better than the empirical Bayes method proposed in [23] under both simulation settings.
4.4. Number of groups
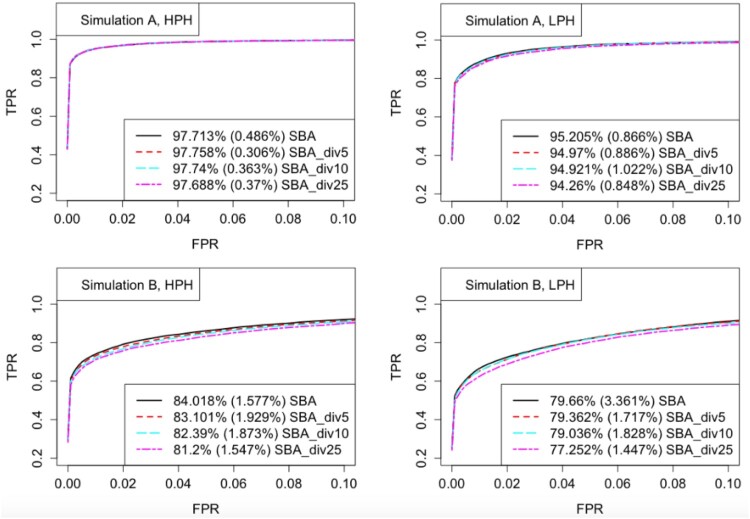
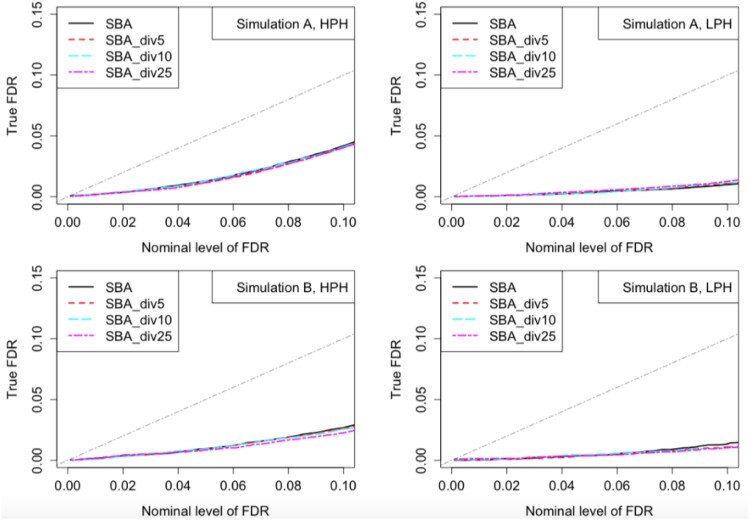
In this subsection, we studied how the SBA_div method works as the number of groups, m, varies. If we randomly divide the G = 3000 genes into m groups, , or 25, the ROC curves and FDR plots are shown in Figures 3 and 4. In Simulation A, the results based on different m's did not differ too much, indicating that we could choose a relatively large m to receive more computational efficiency. In Simulation B, smaller m led to slightly better results, which was as expected. All choices of divisions controlled FDR well across all simulation settings.
Figure 3.
ROC curves for different data divisions under Simulations A and B. Given each FPR level, the TPRs were averaged across the 32 simulated datasets. The partial AUC values were calculated by averaging the percentages of the total area in the plotted region where FPR is below 0.1, and reported in the legends, with the standard deviations in parentheses.
Figure 4.
FDR plots for different data divisions under Simulations A and B. Given each nominal level of FDR, the actual observed FDRs were estimated by averaging the proportion of false discoveries among declared heterosis genes across 32 simulated datasets. The gray dash-dotted lines represent the Y = X line.
4.5. Computational time
Table 2 provides the computational time needed for each method. The computational time for each simulation was calculated on a cluster node that was equipped with two 8-core 2.6GHz Intel Haswell E5-2640 v3 processors. Our SBA method with random division (SBA_div) and the empirical Bayes methods [23] (eBayes_Laplace and eBayes_Normal) could be parallelized to increase efficiency, and the parallelization was done across 16 cores. We could notice that the computational time based on the data division of our proposed method (SBA_div) was comparable to the empirical Bayes methods. As the number of divisions increased, the computational time decreased. However, as indicated in Figures 1 and 3, a larger number of divisions led to slightly worse results but was still better than the empirical Bayes methods.
Table 2.
Computational time needed for each method.
| Method | Simulation A | Simulation B |
|---|---|---|
| SBA | 90.6 mins | 163.1 mins |
| SBA_div5 | 45.2 mins | 56.5 mins |
| SBA_div5_parallel | 9.9 mins | 12.0 mins |
| SBA_div10 | 39.8 mins | 43.8 mins |
| SBA_div10_parallel | 4.6 mins | 5.3 mins |
| SBA_div25 | 37.0 mins | 39.1 mins |
| SBA_div25_parallel | 3.4 mins | 3.7 mins |
| eBayes_Laplace | 40.5 mins | 40.7 mins |
| eBayes_Laplace_parallel | 3.8 mins | 3.7 mins |
| eBayes_Normal | 39.8 mins | 39.7 mins |
| eBayes_Normal_parallel | 3.0 mins | 3.0 mins |
5. Real data analysis
We applied our proposed methods to a real RNA-seq heterosis dataset published by [24]. This data studies gene expression heterosis between parental lines, B73 and Mo17, and the hybrid genotype (B73×Mo17). We used the same criterion as in [23] to filter genes with low abundance. More specifically, we kept genes with an average count equal to or greater than one and with no more than two zero read counts within the four biological replicates for each genotype, and 28,943 genes were left for gene expression heterosis analysis.
Table 3 provides the number of heterosis genes detected by different methods when controlling FDR at 0.1 or 0.05. The eBayes_Laplace and eBayes_Normal methods detected more LPH genes than our proposed methods. However, based on our simulation results that FDR control was very liberal for the empirical Bayes methods, the list of declared heterosis genes may include more false positives than desired.
Table 3.
Number of heterosis genes detected when controlling FDR at different levels.
| Heterosis | FDR | SBA | SBA_div5 | SBA_div10 | SBA_div16 | eBayes_Laplace | eBayes_Normal |
|---|---|---|---|---|---|---|---|
| HPH | 0.1 | 27 | 31 | 30 | 30 | 28 | 35 |
| HPH | 0.05 | 12 | 13 | 12 | 14 | 8 | 9 |
| LPH | 0.1 | 7 | 9 | 6 | 10 | 75 | 82 |
| LPH | 0.05 | 0 | 4 | 0 | 4 | 23 | 12 |
Although the eBayes_Laplace and eBayes_Normal methods detected nearly the same number of HPH genes when controlling FDR at 0.1 or 0.05, the lists of HPH genes detected by the empirical Bayes method [23] were different from what our method identified. Venn diagrams of detected HPH and LPH genes when controlling at different FDR levels are presented in Web Figures 1–2 in Web Appendix C respectively. Again, the HPH genes detected from [23] might not be reliable due to their failure of FDR control based on our simulation results. Without knowing the true heterosis genes at the moment, more biological experiments are needed to validate these results.
6. Discussion
Gene expression heterosis has been hypothesized to help account for phenotypic heterosis, such as grain yields increment. Thus, identifying heterosis genes is a crucial issue, and may have a strong impact on biology and genetics. Existing methods for detecting gene expression heterosis with RNA-seq data require parametric assumptions [17,23]. We proposed a novel model within a semi-parametric Bayesian framework so that heterosis is directly modeled by our model parameters. We adopted an MCMC sampling scheme to provide posterior inference for detecting gene expression heterosis. Our method provides a more flexible way that avoids the dependence on parametric assumptions. From the simulation studies, we demonstrated that our proposed method outperformed the empirical Bayes method in [23], in terms of ranking heterosis genes and FDR control. Therefore, our method offers a reliable way to detect gene expression heterosis for RNA-seq experiments.
Throughout the process of building our semi-parametric Bayesian modeling framework, we considered the two inbred parents to be independent, and modeled the fold change parameters between the hybrid offspring and each parental line, and , separately. Consider parental line 1 as an example: we set the hybrid offspring as the reference condition, and modeled the distribution of gene-specific fold change parameters between the hybrid and parental line 1 using a DP prior. In a typical heterosis study containing two parents and one hybrid, the hybrid offspring is naturally selected as reference, thus fold changes and can be viewed as effects of each parental line on the hybrid. If there is biological knowledge that and may be correlated, the two parameters may be modeled jointly.
Our proposed model assumes that the hybrid offspring and two inbred parents share the same dispersion parameter, which aligns with popular methods for RNA-seq data analysis such as edgeR [20,25], DESeq [1] and DESeq2 [19]. Our method can be extended to a more flexible model that assumes different dispersion parameters for the hybrid offspring and two parental lines, where i = 1, 2, 3 denotes hybrid offspring, parental line 1, and parental line 2 respectively. Then the full conditional distributions for , , , and can be modified easily. However, adding more parameters would introduce additional steps in the MCMC sampling scheme and hence increase computational complexity.
The DP priors depend on the base distribution and the concentration parameter M. We used a mixture of two components as : a point mass at one and a Gamma distribution. The choice of the point mass component is due to the high frequency of estimated fold changes that lie in the small range around 1 based on real data. The choice of the Gamma distribution as the second component is because the Gamma distribution ensures conjugacy that facilitates computation. In the DP priors, the concentration parameter M is commonly chosen as M = 1 in applications [8]. We also checked the simulation results with various values of M ( 0.2, 0.5, 2, 5, 10 or 20), where the results remained nearly the same for different M.
We specified so that no prior preference is given to either differential expression or equivalent expression between hybrid offspring and either parental line. To investigate the robustness of setting under different simulation scenarios, we conducted more simulations by varying the proportion of genes having fold change 1 between hybrid offspring and each parental line. Simulation results (presented in Web Appendix D) show that using this prior of is robust under all settings. Our proposed methods (SBA and SBA_div) performed better than the empirical Bayes method in terms of both ROC curves and FDR control under all simulation scenarios.
Although our proposed semi-parametric Bayesian method provides a reliable approach for the detection of gene expression heterosis, computational complexity might be an issue. In order to improve the efficiency, we also provided an algorithm based on a division of the data. The choice of number of groups, m, is a trade-off between efficiency and accuracy. According to the simulation results, a larger number of divisions m led to lower accuracy, but still outperformed the current empirical Bayes methods with comparable computational time. Additional discussion about data division can be found in Web Appendix D.
When performing our proposed method on the real data, the heterosis genes detected with different number of divisions are not exactly the same. Part of the reason is due to the randomness of MCMC. If we run another MCMC using a different seed, the heterosis genes detected by the two MCMCs are not necessarily the same. In addition, whether the Markov chains are long enough to get accurate results could also be a potential problem. We checked the effective sample size for each gene. Genes that were detected to be heterosis genes by all numbers of divisions had effective sample sizes greater than genes that had different declared heterosis status by different numbers of divisions. So for those genes with a low effective sample size, we may need to run longer chains. Based on simulation checking, running the Markov chains longer do increase the percentage of overlapping genes, as expected. However, running longer chains is more time consuming. Therefore, it is also a trade-off between efficiency and accuracy, and we will let the users decide which one is more important for a practical application.
Supplementary Material
Acknowledgments
The authors would like to thank David Walker from Iowa State University for proofreading the manuscript.
Funding Statement
This research was partially supported by the National Institute of General Medical Sciences (NIGMS) of the National Institutes of Health and the joint National Science Foundation/NIGMS Mathematical Biology Program under Award Number R01GM109458, the Office of Science (BER), US Department of Energy (DE-SC0014395), and by the Iowa State University Plant Sciences Institute Scholars Program.
Disclosure statement
No potential conflict of interest was reported by the author(s).
References
- 1.Anders S. and Huber W., Differential expression analysis for sequence count data, Genome Biol. 11 (2010), p. R106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Benjamini Y. and Hochberg Y., Controlling the false discovery rate: a practical and powerful approach to multiple testing, J. R. Stat. Soc. B 57 (1995), pp. 289–300. [Google Scholar]
- 3.Bi R. and Liu P., A semi-parametric Bayesian approach, iSBA, for differential expression analysis of RNA-seq data, bioRxiv preprint (2019). Available at 10.1101/558270. [DOI] [PMC free article] [PubMed]
- 4.Blackwell D. and MacQueen B.J., Ferguson distributions via polya urn schemes, Ann. Stat. 1 (1973), pp. 353–355. [Google Scholar]
- 5.Chen Z.J., Genomic and epigenetic insights into the molecular bases of heterosis, Nat. Rev. Genet. 14 (2013), pp. 471–482. [DOI] [PubMed] [Google Scholar]
- 6.Cheng S.H., Zhuang J.Y., Fan Y.Y., Du J.H., and Cao L.Y., Progress in research and development on hybrid rice: a super-domesticate in China, Ann. Bot. 100 (2007), pp. 959–966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Darwin C.R., The Effects of Cross and Self Fertilization in the Vegetable Kingdom, Murray, London, 1876. [Google Scholar]
- 8.Do K.A., Muller P., and Tang F., A Bayesian mixture model for differential gene, J. R. Stat. Soc. Ser. C 54 (2005), pp. 627–644. [Google Scholar]
- 9.Escobar M.D., Estimating normal means with a Dirichlet process prior, J. Am. Stat. Assoc. 89 (1994), pp. 268–277. [Google Scholar]
- 10.Gelman A. and Rubin D.B., Inference from iterative simulation using multiple sequences, Stat. Sci. 7 (1992), pp. 457–472. [Google Scholar]
- 11.Genovese C. and Wasserman L., Bayesian and frequentist multiple testing, Bayesian Stat. 7 (2003), pp. 145–161. [Google Scholar]
- 12.Green P.J. and Richardson S., Modeling heterogeneity with and without the Dirichlet process, Scand. J. Stat. 28 (2001), pp. 355–375. [Google Scholar]
- 13.Hardcastle T.J. and Kelly K.A., Empirical Bayesian methods for identifying differential expression in sequence count data, BMC Bioinform. 11 (2010), Article 422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hubner N., Wallace C.A., Zimdahl H., Petretto E., Schulz H., Maciver F., Mueller M., Hummel O., Monti J., Zidek V., Musilova A., Kren V., Causton H., Game L., Born G., Schmidt S., Mller A., Cook S.A., Kurtz T.W., Whittaker J., Pravenec M., and Aitman T.J., Integrated transcriptional profiling and linkage analysis for identification of genes underlying disease, Nat. Genet. 37 (2005), pp. 243–253. [DOI] [PubMed] [Google Scholar]
- 15.Ji T., Liu P., and Nettleton D., Estimation and testing of gene expression heterosis, J. Agric. Biol. Environ. Stat. 19 (2014), pp. 319–337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kalli M., Griffin J., and Walker S., Slice sampling mixture models, Stat. Comput. 1 (2011), pp. 93–105. [Google Scholar]
- 17.Landau W., Niemi J., and Nettleton D., Fully Bayesian analysis of RNA-seq counts for the detection of gene expression heterosis, J. Am. Stat. Assoc. 114 (2019), pp. 610–621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Liu F., Wang C., and Liu P., A semi-parametric Bayesian approach for differential expression analysis of RNA-seq data, J. Agric. Biol. Environ. Stat. 20 (2015), pp. 555–576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Love M.I., Huber W., and Anders S., Moderated estimation of fold change and dispersion for RNA-Seq data with DESeq2, Genome Biol. 15 (2014), p. 550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.McCarthy D.J., Chen Y., and Smyth G.K., Differential expression analysis of multifactor RNA-Seq experiments with respect to biological variation, Nucl. Acids Res. 40 (2012), pp. 4288–4297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Neal R.M., Markov chain sampling methods for Dirichlet process mixture models, J. Comput. Graph Stat. 9 (2000), pp. 249–265. [Google Scholar]
- 22.Newton M.A., Noueiry A., Sarkar D., and Ahlquist P., Detecting differential gene expression with a semiparametric hierarchical mixture method, Biostatistics 5 (2004), pp. 155–176. [DOI] [PubMed] [Google Scholar]
- 23.Niemi J., Mittman E., Landau W., and Nettleton D., Empirical bayes analysis of RNA-seq data for detection of gene expression heterosis, J. Agric. Biol. Environ. Stat. 20 (2015), pp. 614–628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Paschold A., Jia Y., Marcon C., Lund S., Larson N.B., Yeh C-T., Ossowski S., Lanz C., Nettleton D., Schnable P.S., and Hochholdinger F., Complementation contributes to transcriptome complexity in maize (Zea mays L.) hybrids relative to their inbred parents, Genome Res. 22 (2012), pp. 2445–2454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Robinson M.D., McCarthy D.J., and Smyth G.K., edgeR: A bioconductor package for differential expression analysis of digital gene expression data, Bioinformatics 26 (2010), pp. 139–140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Smyth G.K., Linear models and empirical bayes methods for assessing differential expression in microarray experiments, Stat. Appl. Genet. Mol. Biol. 3 (2004), Article 3. [DOI] [PubMed] [Google Scholar]
- 27.Song R. and Messing J., Gene expression of a gene family in maize based on noncollinear haplotypes, Proc. Natl. Acad. Sci. USA 100 (2003), pp. 9055–9060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Tausta S.L., Li P., Si Y., Gandotra N., Liu P., Sun Q., Brutnell T.P., and Nelson T., Developmental dynamics of Kranz cell transcriptional specificity in maize leaf reveals early onset of C4-related processes, J. Exp. Bot. 65 (2014), pp. 3543–3555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tierney L., Markov Chains for exploring posterior distributions, Ann. Stat. 22 (1994), pp. 1701–1728. [Google Scholar]
- 30.Yu S., Li J., Xu C., Tan Y., Gao Y., Li X., Zhang Q., and Maroof M., Importance of Epistasis as the genetic basis of heterosis in an elite rice hybrid, Proc. Natl. Acad. Sci. 94 (1997), pp. 9226–9231. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.