Visitor arrivals forecasts amid COVID-19: A perspective from the Africa team

Abstract

COVID-19 disrupted international tourism worldwide, subsequently presenting forecasters with a challenging conundrum. In this competition, we predict international arrivals for 20 destinations in two phases: (i) Ex post forecasts pre-COVID; (ii) Ex ante forecasts during and after the pandemic up to end 2021. Our results show that univariate combined with cross-sectional hierarchical forecasting techniques (THieF-ETS) outperform multivariate models pre-COVID. Scenarios were developed based on judgemental adjustment of the THieF-ETS baseline forecasts. Analysts provided a regional view on the most likely path to normal, based on country-specific regulations, macroeconomic conditions, seasonal factors and vaccine development. Results show an average recovery of 58% compared to 2019 tourist arrivals in the 20 destinations under the medium scenario; severe, it is 34% and mild, 80%.

Introduction

The tourism industry has seen continuous growth over the past three decades, with worldwide tourism arrivals growing from 439 million tourists in 1990 (UNWTO, 2006) to 1.5 billion during 2019 (UNWTO, 2020a), representing an average annual growth rate of 4.3% per year. The growth has not always been smooth and events such as the financial crisis and subsequent recession have seen a decline in international tourism for the year 2009 in all regions (except Africa, UNWTO, 2010). Health pandemics, such as the 2003 outbreak of SARS, the 2009 bird flu, the 2012 MERS-CoV and the 2013–14 Ebola (Gössling et al., 2020) also had an influence on international tourism, although their influence remained regional and not widespread.

The novel coronavirus (COVID-19) is the first health pandemic in the modern era of travel that had a widespread impact on international travel. By August 2020 the highly contagious coronavirus, which was first identified in China's city of Wuhan, rapidly spread in the world with the exception of 12 countries (McCarthy, 2020). This pandemic has had a strong domino effect since all nations imposed travel restrictions to contain the spread of the virus, and by May 2020, 72% of all destinations locked their borders completely (UNWTO, 2020b). This has been followed by the adjournment or cancellation of major events, such as the Tokyo 2020 Olympic Games. As virus numbers started to decline, countries reopened their borders to international tourists, and by September 2020, 53% of destinations relaxed restrictions on international tourism (UNWTO, 2020c). However, several countries have also seen an explosion of new coronavirus cases in the second part of 2020, with more COVID-19 patients hospitalised than before initial lockdowns were imposed by the respective governments.

This rapid closure of borders and the subsequent standstill in international tourism present tourism forecasters with a challenging conundrum, which is exacerbated by the inability of scientists to forecast the spread and duration of the pandemic (Ioannidis et al., 2020). The main reasons why forecasts during this pandemic are inaccurate are the lack of historical data, which is a requirement in forecasting models, and a lack of understanding of the uncertainties involved during such pandemics (Pinson & Makridakis, 2020).

There is a rich literature available on forecasting tourism demand, with the first review of empirical research (Witt & Witt, 1995) identifying both time series and econometric models as popular methods, with less emphasis on qualitative methods. A subsequent review by Song and Li (2008) showed that artificial intelligence models became more common after the turn of the millennium, while Wu et al. (2017) identified combining forecasts and judgementally adjusting forecasts as some of the more recent trends in this field. However, most tourism forecasts assess time periods where there were no adverse events.

There are some exceptions; for example, Choe et al. (2020) used time series and econometric methods to forecast the loss in tourism to South Korea during the MERS outbreak, showing a quick recovery to model forecasts after the pandemic. During the Avian Flu and SARS outbreak, Asia experienced a steep decline in international tourism with the impact modelled ex post by Kuo et al. (2008). In addition, Mao et al. (2010) assessed the recovery patterns after the SARS pandemic and showed that it is location-specific, depending on the ability to restore normality and confidence. These authors all assess the impact of a pandemic after it has dissipated, but their research shed light on the difficulties to forecast tourism during a pandemic.

This competition challenged forecasters to predict international arrivals for 20 destinations (a total of 120 series to be forecasted as selected by the organisers of the competition) in two phases: (i) Stage 1 entails identifying the method that delivers the most accurate ex post forecasts of visitor arrivals pre-COVID; (ii) Stage 2 calls for ex ante forecasts of visitor arrivals since the onset of the pandemic up to the fourth quarter of 2021 using a baseline and three scenarios. According to the competition guidelines, the baseline assumes no COVID-19 using data up to the end of 2019 and the best performing model from the first stage (which we refer to as ‘under normal circumstances’), while the three scenarios should reflect mild, medium and severe COVID-19 impacts.

In stage 1 of this competition, we use an array of methods and combinations of methods, which significantly expand the current tourism forecasting literature. The methods range from univariate time series models, popular in tourism forecasting, to neural networks and machine learning, and expansions of the univariate models into multivariate versions. In this part of the competition, the benefits of applying temporal hierarchies in tourism forecasting become apparent. In the second stage, we resort to judgemental adjustment of model-based forecasts, given the uniqueness of the current pandemic and the uncertainties involved in forecasting during a pandemic. The proposed adjustment scheme and implementation are an innovation unique to this paper.

Modelling strategies

Data

Our objective is to forecast international visitor arrivals for 20 destination countries, from five origin countries, and at a total level, as selected by the competition organisers. The time series are quarterly and span a variable amount of time, ending in 2019Q4 or later. Table 1 provides a list of the destinations and origins (the total level is omitted from the table), together with the starting and ending quarter for each time series.

Table 1.

List of destination and origin countries/regions.

Destination	Start	End	Origins
USAa	1996Q1	2020Q1	Canada, China, Japan, Mexico, UK
Canada	1995Q1	2020Q1	China, France, Mexico, UK, USA
Chile	1998Q1	2019Q4	Argentina, Bolivia, Brazil, Peru, USA
Mexico	2005Q1	2019Q4	Brazil, Canada, Colombia, UK, USA
Czech Rep.c	2010Q1	2020Q1	Germany, Italy, Kingdom, Russia, United
UK	2000Q1	2020Q1	France, Germany, Ireland, Spain, USA
Finlandb	1995Q1	2020Q1	China, Germany, Russia, Sweden, UK
Swedenc	1995Q1	2020Q1	Denmark, Germany, Norway, UK, USA
Bulgaria	2008Q1	2020Q1	Germany, Greece, Romania, Russian, Turkey
Japan	1997Q1	2020Q2	China, Hong Kong, Korea, Taiwan, USA
Korea	1998Q1	2020Q2	China, Hong Kong, Japan, Taiwan, USA
Thailand	2000Q1	2020Q1	China, India, Korea, Laos, Malaysia
Singapore	1995Q1	2020Q2	Australia, China, India, Indonesia, Malaysia
Malaysia	1998Q1	2020Q1	Brunei, China, Indonesia, Singapore, Thailand
Indonesia	2002Q1	2019Q4	Australia, China, India, Malaysia, Singapore
Australia	1991Q1	2020Q2	Germany, Indonesia, Malaysia, New Zealand, UK
New Zealand	2002Q1	2020Q2	Australia, China, Germany, UK, USA
Tunisiab	2000Q1	2020Q1	Algeria, France, Germany, Libya, Russia
South Africab	1999Q1	2020Q1	Germany, Lesotho, Mozambique, UK, USA
Mauritiusb	2011Q1	2020Q1	France, Germany, United Kingdom, Reunion Island South Africa

^aChina starts 2007Q1; UK, Japan, and China end 2020Q2.

^bThe series for these countries are international tourist arrivals.

^cThe series for these countries are hotel nights.

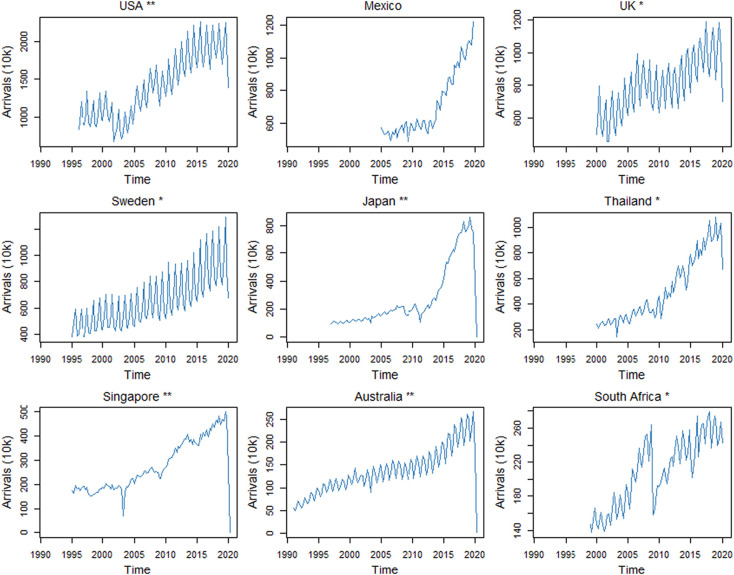
The time series are non-stationary exhibiting both stochastic trends and seasonality. Fig. 1 provides examples of total arrivals for selected destination countries. Bulgaria exhibits a strong outlier in 2018Q1, which was replaced by the expected value of an appropriate ETS model (see Phase 1 Section for model details).

Fig. 1.

Examples of total arrivals to nine destination countries; * signifies that there is data for 2020 Q1; ** signifies that 2020 Q2 data is available.

Furthermore, we make use of potential predictive variables. These are collected at an annual frequency from the International Monetary Fund's World Economic Outlook (IMF, 2020), including forecasts up to 2021. These series are transformed to quarterly series by replicating annual values four times as suggested by Nikolopoulos et al. (2011), who recommend the use of equal weights, over various weighting schemes.

We consider the following variables: (i) gross domestic product growth; (ii) purchasing power parity (PPP); and (iii) the implied PPP conversion rate. We use these variables from the origin, but also as a ratio between origin and destination, to show the relative purchasing power of tourists in each pair of countries/regions. For the resulting six variables, we consider up to three annual lags, to capture any dynamics in the perception of tourists (Athanasopoulos et al., 2011; Song & Witt, 2000). Given the limited sample size, we use the Akaike information criterion to allow the models to eliminate lags. If this is done, the sample is expanded accordingly to improve parameter estimation (see modelling details in Phase 1 Section).

The forecasting task is organised into two phases. The first focuses on the pre-Covid-19 period, exploring the business as usual scenario, and the second focuses on forecasting to end 2021, where model forecasts are enriched with judgemental information to account for the never observed before effects of the pandemic.

Phase 1

We implement a series of forecasting methods to produce forecasts. These can be grouped into two overall categories, i.e. univariate and multivariate. The former uses only past arrivals to predict the future, while the latter makes use of additional macro-economic indicators to model the pairwise variance of arrivals between countries.

Random walk and seasonal random walk

Given historical observations, y _t, t = 1, …, n, and n being the sample size of the time series at hand, we construct forecasts as:

$${\widehat{y}}_{t+h}=y_t$$

$${\widehat{y}}_{t+h}=\left\{\begin{array}{c}{y}_{t-s+h},h\le s\\ {\widehat{y}}_{t-s+h},h>s\end{array}\right)$$

respectively for the naïve and the seasonal random walk (SNaïve), where s is the seasonal period. As neither of the forecasts requires any estimation or modelling choices from the analyst, we consider these as benchmark forecasts. More complex forecasts are considered valuable only if they can predictively outperform these benchmarks.

Exponential smoothing

Exponential smoothing (ETS) models the time series as a collection of local level, slope, and seasonality components. Together with the error term, these components may interact additively or multiplicatively. Hyndman et al. (2002) embedded exponential smoothing in the state-space modelling framework, providing the statistical rationale for optimising model parameters and choosing between the 30 common variants of the model. We follow the same restrictions used by Kourentzes and Athanasopoulos (2019) to simplify the model form selection.

The exponential smoothing family of models is used widely in both academia and practice, due to its relatively good performance and transparency (Gardner Jr, 2006; Ord et al., 2017), and has also been shown to perform well in forecasting tourism arrivals (Athanasopoulos et al., 2011; Kourentzes & Athanasopoulos, 2019). We implement ETS using the forecast package (Hyndman et al., 2020) for R (R Core Team, 2020) that optimises model parameters and initial values by maximum likelihood estimation and chooses between the different models by minimising the Akaike information criterion (AIC) (Burnham & Anderson, 2004).

The state-space formulation of ETS can be extended to include explanatory variables (ETSx) in the observation equation (Hyndman et al., 2008). Variable selection becomes important, and we minimise the AIC to identify the best predictors.

Theta method

The theta method, proposed by Assimakopoulos and Nikolopoulos (2000), models the time series as a combination of a long-term slope and local variations after the data has been treated for seasonality. The method has been shown to perform very well (Makridakis & Hibon, 2000). Fiorucci et al. (2016) showed that the method can be generalised to state-space model, which again was shown to perform very competitively.

We rely on the tsutils package (Kourentzes, 2020) for R that automatically tests for trend and the need to de-seasonalise the time series. Seasonality is modelled as a stochastic process, in contrast to the original implementation (Assimakopoulos & Nikolopoulos, 2000) that used classical time series decomposition to extract seasonal indices.

Autoregressive integrated moving average

The autoregressive integrated moving average (ARIMA) family of models forecasts time series by modelling lags of the time series observations and errors to capture its various patterns. These may be seasonal, giving rise to seasonal ARIMA models. The identification of the order of the autoregressive and moving average processes requires the time series to be stationary (see Ord et al., 2017). To identify the appropriate ARIMA form, we follow the methodology by Hyndman and Khandakar (2007) available in the forecast package (Hyndman et al., 2020) for R.

Moreover, we implement ARIMA with explanatory variables in the format of a RegARIMA model, using a regression formulation for the explanatory variables with ARIMA errors. The identification of the model remains challenging and there is no widely established approach on how to resolve this. We follow a heuristic approach, where we first identify a well-performing univariate ARIMA. From this, we calculate the residuals, with which we build a stepwise regression with the explanatory variables, and eliminating superfluous terms by minimising the AIC. Once the best set of explanatory variables has been identified, we jointly estimate the complete regARIMA model (in he forecast package for R), allowing the ARIMA orders to be re-specified.

Neural networks and extreme learning machines

Two key advantages of neural networks are that they can flexibly model both linear and nonlinear interactions in time series, and that the exact functional form is captured by the network in a data-driven fashion (Ord et al., 2017). However, the training of the networks is demanding. This has led to their successful use in data-rich conditions, but less so when the data is sparse. Crone and Kourentzes (2010) showed that pre-filtering inputs to the network using a stepwise approach can benefit their performance for low-frequency data. To mitigate training issues and potential overfitting, it is recommended to train networks multiple times with random initialisations and subsequently construct an ensemble (Kourentzes, Barrow, & Crone, 2014). Given the low frequency that tourism arrivals are recorded in our dataset we opt to use multilayer perceptions (MLP), instead of deep-learning, as implemented in the nnfor package (Kourentzes, 2019) for R.

Extreme learning machines (ELMs) try to mitigate the complex optimisation that neural networks face. Instead of attempting to tune all weights in a network, they are left to their random initial values, except for weights in the output layer. This single layer can be easily optimised via ordinary least squares or equivalent approaches. ELMs have shown to be very efficient in training, particularly when data is limited (Huang et al., 2006). Here, we specify the inputs of the ELM as for MLP, and train the last layer using lasso regression (Tibshirani, 1996) to limit the potential for overfitting. We rely on the implementation in the nnfor package for R.

For both MLP and ELM we consider lags {1, 2, 3, 4, 8, 12, 16} allowing to capture both local and seasonal dynamics, and any modelling is done after the time series are made stationary. In addition, the networks are provided with 3 binary dummy variables that allow for the deterministic encoding of seasonality. We use 20 ensemble members that are combined using the median operator. Although both MLP and ELM can use explanatory variables, due to the relatively poor performance of their univariate counterparts, we omit these extensions.

Random forests

Random forest (RF) is a generalisation of decision trees. The principal idea is that instead of using a single decision tree to model the desired interaction, we use multiple small trees that work well when combined (Breiman, 2001). Crucially, each tree uses only a small number of potential inputs (usually one or two) chosen randomly. Therefore, these shallow trees are trivial to build, and there is a limited need for variable selection (Hastie et al., 2009).

For the generation of the RF, we rely on the implementation in the random forest package (Liaw & Wiener, 2002) for R. To use it, first, all the time series are made stationary and we input: (i) all lags from 1 to 8 periods; (ii) any of the seasonal lags 12 or 16 that are identified as useful using a stepwise selection, and (iii) seasonal dummy variables, which again are subject to a stepwise selection. These settings were identified after trials on a validation set. Finally, we use ensembles of 500 individual trees. The univariate RF is strongly outperformed by the ETS and ARIMA; we therefore do not consider extending them with explanatory variables.

Hierarchical forecasting

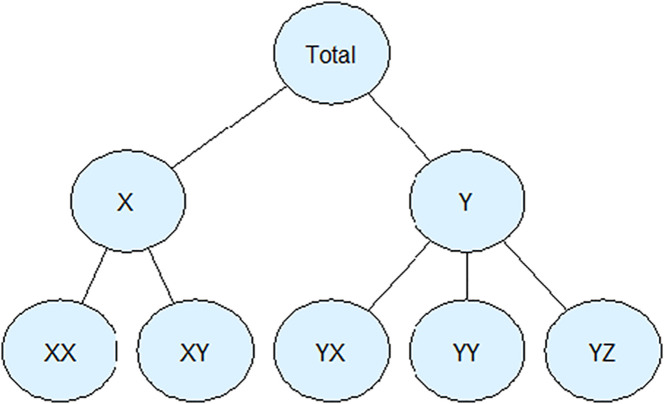
Tourism arrivals exhibit a hierarchical structure, where different categories of tourists, destination attributes, product types, or geographical divisions may add up to more aggregate scales. Therefore, a collection of time series that follows such an aggregation structure is referred to as a “hierarchical time series”. For example, arrivals in various cities, the wider region, or the country can be arranged in a hierarchy (Athanasopoulos et al., 2009), as in Fig. 2 . Nodes at a more disaggregate level sum up to observations at more aggregate nodes. In the example, Total = X + Y, X = XX + XY, and Y = YX + YY + YZ.

Fig. 2.

An example hierarchy of time series.

When these equality constraints are observed, the forecasts are coherent. However, typically, when forecasts are generated, they are incoherent. Therefore, the sum of the forecasted values from the disaggregate levels will not match up to forecasts at aggregate levels. This incoherency has both organisational and forecast accuracy implications. From a forecast accuracy perspective, if the forecasts were perfectly matching reality, then they would be coherent by definition. Any incoherency implies forecast errors and suggests that the forecasts can be improved further. We can reconcile the incoherent forecasts by adjusting them so that their aggregation constraints are not violated. This is the task of hierarchical forecasting (Athanasopoulos et al., 2009).

One of the most prominent approaches for forecast reconciliation is the MinT method (Wickramasuriya et al., 2019), which achieves this by constructing a weighted linear combination of the base forecasts at each node. This is done by

$${\tilde{\mathit{y}}}_t=\mathit{SG}{\widehat{\mathit{y}}}_{\mathit{t}}$$

where ${\widehat{\mathit{y}}}_{\mathit{t}}$ is a column vector containing all the base forecasts, ${\tilde{\mathit{y}}}_t$ is the equivalent for the reconciled coherent forecasts, S is the so-called ‘summing’ matrix that maps the hierarchy, and G contains the reconciliation weights that map the incoherent forecasts into coherent bottom-level forecasts. To obtain G, we use the in-sample forecast residuals and calculate their covariance using a shrinkage estimator, proposed by Schäfer and Strimmer (2005). Where the shrinkage estimator is insufficient, we use the overly simplified structural scaling (Athanasopoulos et al., 2017). The advantage of the structural scaling is that it requires no estimation, and therefore it is reliable, irrespective of the sample size or the dimensionality of the hierarchy. Hierarchical forecasting is independent of the forecasting methods used, which can differ freely among the various nodes of the hierarchy.

Temporal hierarchies

Athanasopoulos et al. (2017) proposed a temporal version of hierarchical forecasting, where the demarcations occur across time. For example, for quarterly time series, as is the case with our data, four quarters can be aggregated in a year. In this case, the hierarchical forecasts belong to different periods of the same time series.

The advantage of temporal hierarchies stems from the use of disaggregate and aggregate data to produce the final forecasts. As a time series is aggregated, high-frequency components, such as seasonality and shocks, are filtered, strengthening long-term components. This permits identifying appropriate models for a given time series multiple times, once at each temporal aggregation level. Their combination borrows strength from all specifications (Kourentzes, Petropoulos, & Trapero, 2014). Kourentzes and Athanasopoulos (2019) showed that temporal hierarchies applied to tourism arrivals can offer substantial benefits in accuracy, more so than their cross-sectional counterpart discussed above.

Implementation considerations

For each set of base forecasts, generated by the different forecasting approaches, we can generate cross-sectional hierarchical forecasts for each destination country. The hierarchy is formed by the lowest level containing the five origin countries, and the aggregate level containing the total arrivals to the destination country. These two levels will not be coherent, as the top level of the hierarchy includes arrivals from countries that are not included in the bottom level of the hierarchy. We overcome this limitation by constructing an artificial series that corresponds to arrivals from the rest of the world. Therefore, using the available historical observations, this time series is constructed as: Rest = Total – Σ(Origin countries in the dataset). This artificial time series is forecasted as well, and its predictions contribute to the hierarchical reconciliation.

Similarly, we can construct temporal hierarchy forecasts for each time series. We denote these by using the prefix ‘THieF-’. For the univariate forecasts, we consider THieF forecasts of the better performing models, giving us THieF-ETS, THieF-Theta, and THieF-ARIMA. For the models that make use of the explanatory variables, we construct two pairs of forecasts for ETSx and RegARIMA. Each pair considers two options to model the annual arrivals. In the first option, we use annual versions of the explanatory time series (THieF-ETSx and THieF-RegARIMA). In the second option, we use univariate forecasts (THieF-ETSxu and THieF-RegARIMAu). Although intuitively the first option is more appealing, we opt to include the second as well, since the time series at the annual temporal aggregation level become much shorter, making the identification and estimation of connections between variables much harder. THieF forecasts make use of the thief package (Hyndman & Kourentzes, 2018) for R.

As hierarchical forecasting adjusts forecasts to produce coherent ones, it is possible to end up with negative forecasts. Although this probability is typically minimal, it becomes significant after the onset of Covid-19 restrictions, when arrivals may be zero or close to zero. In that case, adjustment forecasts can become negative. To overcome this, we rely on the heuristic proposed by Kourentzes and Athanasopoulos (2021) that iteratively adjusts the reconciled forecasts until all predictions are non-negative.

Phase 2

A significant challenge in producing predictions for phase 2, which focuses on the years 2020–2021, is that we are facing an unprecedented disruption due to the Covid-19 pandemic. The challenge is two-fold. There is a lack of data on the effects of the pandemic on visitor arrivals. Furthermore, travel restrictions are primarily legislatively driven, and may not necessarily correlate with the diffusion of the pandemic in populations, as legislators consider multiple dimensions in their decision-making.

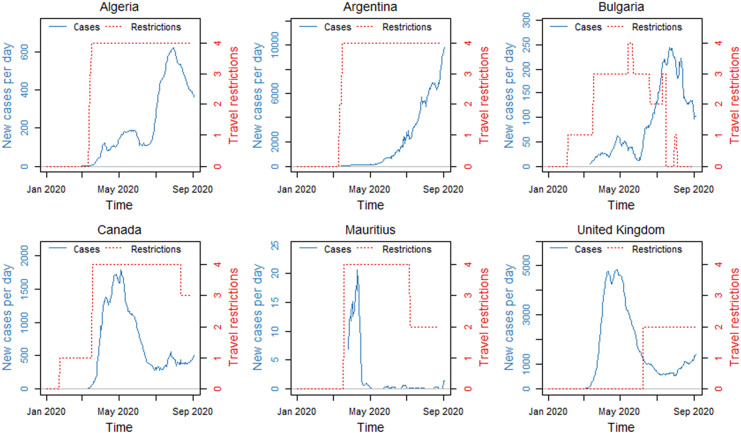
To overcome this, we propose a method of judgementally adjusting model-based forecasts from phase 1. Our dataset contains 48 countries/regions. The process started with a scrutiny of both the country/region-specific as well as global outlook. The country/region outlooks focused on Covid-19 evolution, type/level of government restrictions and actions, and foreign affairs approaches and type/level of international border limitations to arrivals. Information from the World Health Organization (WHO, 2020) was used to identify the countries' first COVID case, its peak day in terms of diagnosed cases, the cumulative cases, deaths, and the number of cases. Additionally, governments' responses were noted and visualised with the aid of the Coronavirus source data (Ritchie, 2020) as depicted for a sample of countries in Fig. 3 . At the global level, besides the macroeconomic data for model-building explained in Data Section, evidence on the development of a vaccine and the timeline of its introduction to the market (large scale) were collected, and seasonal differences between Northern Hemisphere and Southern Hemisphere were considered before embarking on judgemental predictions.

Fig. 3.

Visualisation of COVD-19 progression and travel restrictions imposed for selected countries (Source of Data: Ritchie, 2020).

In principle one can ask analysts to provide individual judgemental predictions for each pair of countries and each quarter in 2021, but it will amount to a daunting number of 9024 [(48²–48)x4] individual predictions from each analyst. This will impose a substantial mental load, degrading the quality of the forecasts (Miller et al., 2011). Instead, we simplify the task by grouping countries in wider regions. We construct such groups by taking into consideration geographical and climate proximity, which implicitly assumes cultural and risk perception similarities. We rely on coarse groupings to keep the mental load manageable. We conclude with eight regional groups, broadly matching continental demarcations (see Table 2 ). Each analyst was asked to submit their expectation of either 0 or 1 for travel between each pair of groups for five periods (2020Q4-2021Q4), matching the simplified states of unrestricted travelling (0) compared to restrictions to travel (1). An example of the task that the analysts were asked to complete is provided in Table 2.

Table 2.

Example of the expectations that were collected from the analysts.

Year/quarter		To
		Africa North	Africa South	America North	America South	Asia East	Asia West	Europe	Oceania
From	Africa North	0	0	1	1	0	0	1	1
	Africa South	0	0	1	1	0	0	1	1
	America North	1	0	0	0	1	0	1	1
	America South	1	0	0	0	1	0	1	1
	Asia East	0	0	1	0	0	0	1	0
	Asia West	1	0	1	0	0	0	1	0
	Europe	1	1	1	1	1	1	0	1
	Oceania	1	0	1	1	0	0	1	0

Moreover, recognising that a 0–1 binary classification may not accurately represent the expectations of experts for what ‘unrestricted travelling’ means, we asked participants to provide us with a percentage estimate of unrestricted travelling (0) compared to the baseline (model) scenario. Similarly, for the opposite case (where the analyst gives a value of 1), we do not expect this to be equal to zero arrivals. Instead, we can use observational data to obtain an estimate.

From Table 1, we observe that we have five countries with data in the period 2020Q2. Considering the five corresponding origin countries for each destination, the total aggregate arrivals, and the implied series with the rest of arrivals from the hierarchical structure, we can obtain 35 measurements of how arrivals were reduced over the baseline scenario, which are the forecasts generated from the forecasting approach selected above. For ‘restricted travel’, the calculation becomes $y_{2020Q2}/{\widehat{y}}_{2020Q2}$. Since we are averaging ratios, we use the geometric mean, which gives residual tourism traffic of just 0.24% of the baseline scenario.

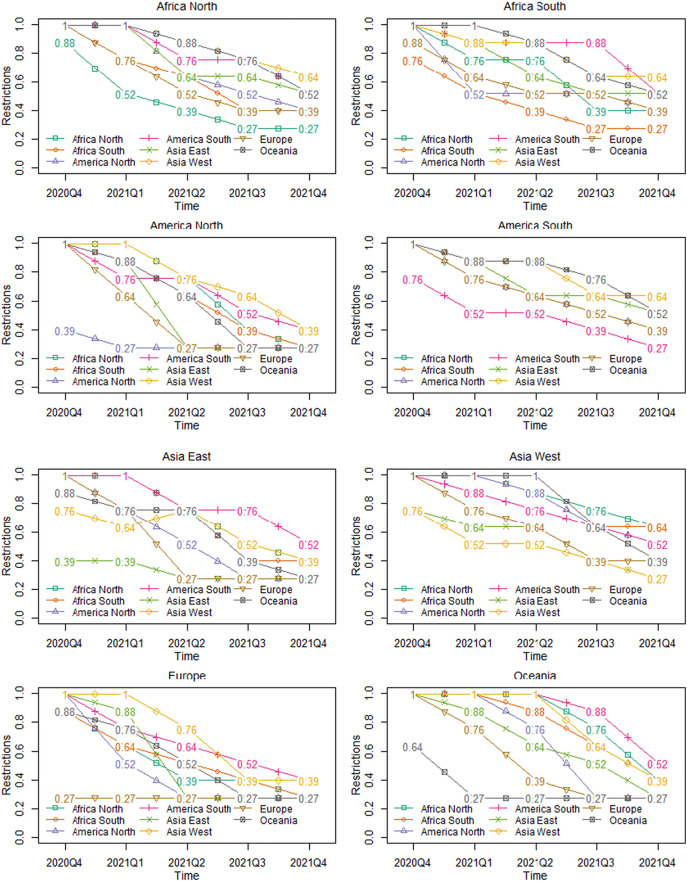
Judgemental forecasts are well known to suffer from biases, such as anchoring, recency, and reliance on readily available information (Gigerenzer & Todd, 1999; Kahneman, 2011). Naturally, as this research is conducted during the Covid-19 pandemic, such biases can become more acute. To mitigate this, we sourced sets of forecasts from different analysts, which we then combined (Petropoulos et al., 2018; Surowiecki, 2005). The combination mechanism is not critical, although removing human judgement from the combination is beneficial (Ferrell, 1985; Harvey & Harries, 2004). To this end, we use simple averaging, which further avoids the need to estimate combination weights, thereby reducing any variance in these and the method's complexity (Kourentzes et al., 2019). The resulting forecasts can take any value from 0 to 1, with in-between values capturing the lack of consensus and its strength. The resulting combined forecasts, as well as the adjustment of the lower bound to reflect the average judgement of the analysts on the discrepancy between arrivals in 2021Q4 compared to that of 2019Q4, are illustrated in Fig. 4 .1

Fig. 4.

Combined analyst forecasts for return to normal, per region.

To populate the values for 2020Q1 to 2020Q3, we followed a set of simple rules. For 2020Q1, all values were set to 1/3, reflecting the global onset of the pandemic in March 2020. This is mirrored in the travel restrictions imposed by different countries, which were mostly introduced in March (Ritchie, 2020). The second quarter of 2020 was set to 1 for all cases, reflecting observations at the time of writing. For 2020Q3, if a destination was in the northern hemisphere, we used the judgemental estimates for 2020Q4, and otherwise we set all values to 1. The last rule was introduced to reflect the summer period in the northern hemisphere, where we expect 2020Q3 to be no worse than 2020Q4, in this case opting to potentially err towards pessimism to reflect inertia of perceptions from 2020Q2.

To adjust the forecasts, given a model forecast ${\widehat{y}}_{\mathit{ijt}}$ between countries i and j at period t, and a combined judgement of potential travel disruptions ${\widehat{d}}_{\mathit{ijt}}$ (the combined judgemental expectations, with the adjusted min-max bounds, see Fig. 4), we construct the final forecast as:

$${\tilde{y}}_{\mathit{ijt}}={\widehat{y}}_{\mathit{ijt}}{w}_{\mathit{ijt}}$$

$$w_{\mathit{ijt}}=\left\{\begin{array}{c}\frac{{\alpha }^{\left(1-{\widehat{d}}_{\mathit{ijt}}\right)}-1}{\alpha -1},\alpha \ne 1\\ 1-{\widehat{d}}_{\mathit{ijt}},\alpha =1\end{array}\right)$$

where α is a scalar (0 < α) and the resulting 0 ≤ w _ijt ≤ 1, acting as a proportional reduction of the forecast between 0 and ${\widehat{y}}_{\mathit{ijt}}$ depending on the value of ${\widehat{d}}_{\mathit{ijt}}$. The value of α allows to set the steepness of adjustment, as illustrated in Fig. 5 . We consider three scenarios, medium, severe, and mild, with the respective values of α being 1, 10, and 0.1. The severe scenario introduces a slower recovery as ${\widehat{d}}_{\mathit{ijt}}\to 0$, while the mild assumes the opposite. The values of 0.1 and 10 ensure that the two scenarios are symmetric. This decision was based on an additional pair of negative and positive integers that the analysts were asked to provide denoting their pessimistic (severe) and optimistic (mild) projections for the speed of recovery, from which we elucidated their symmetric perception of risk for the two scenarios.

Fig. 5.

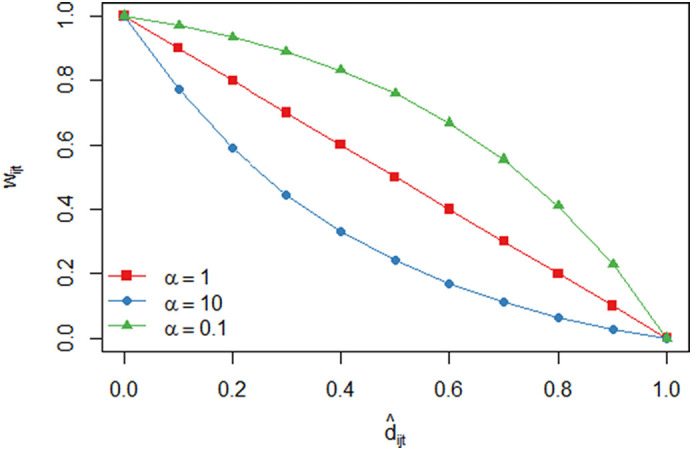
The resulting weights for the three different scenarios considered.

All adjustments are done considering pairs of countries. However, we are also generating forecasts for the total arrivals of a destination country. For these, we infer the weights as follows. From the UNWTO database (UNWTO, 2020d), we obtain historical annual arrivals for each destination country from all the available origins for years 2015 to 2018 where data were available at the time of collection. These were averaged and summed into the same eight groups for which we collected judgemental estimates and were subsequently forecasted for the years 2020 and 2021, using either single exponential smoothing or linear trend exponential smoothing. The model choice was done using AIC, corrected for sample size.

The resulting octuplet of weights is used to linearly combine the octuplet of judgemental expectations for a given target region for a specific quarter, providing a single weight to adjust the model forecasts. Repeating the process across all the quarters of interest, and selecting the weights for 2020 or 2021 accordingly, provide the appropriate vector for the total arrivals. Our approach has the advantage that we do not need to ask the experts to consider yet another series of expectations, especially when judgemental predictions of totals are known to suffer from subadditivity (Sprenger et al., 2011). When we use cross-sectional hierarchical forecasts, we use the same weights w _it to also adjust the artificially introduced series ‘Rest’.

Performance metric

To identify the best alternative forecasting approach for phases 1 and 2, we rely on selecting the best performing forecast on a validation set, for horizons of one to four quarters ahead. For phase 1, where the target is to predict the year 2019, we use the six preceding quarters as a validation set. For phase 2, we expand the validation set to include the year 2019. For the evaluation, we rely on a rolling origin scheme (Fildes & Petropoulos, 2015; Ord et al., 2017). At the first forecast origin, we specify and optimise the various forecasts and predict the next four quarters, recording their performance. Subsequently, we increase the in-sample by one quarter and re-specify and re-optimise the forecasts. We repeat the process until the validation set is exhausted.

We measure the performance using a seasonal variant of the mean absolute scaled error (MASE), where, for each forecast, we calculate the mean absolute error (MAE), and divide that by the in-sample MAE of the seasonal random to make it scale-independent, as in Athanasopoulos et al. (2011). To summarise MASE across time series we calculate the mean.

Results and discussion

Forecast selection results

Our findings for forecast selection in phases 1 and 2 are similar, and therefore for brevity, we only present the summarised relative MASE results for the phase 2 forecast selection. Table 3 provides the average MASE across all time-series, for the four forecast horizons of interest, for the base and the hierarchical forecasts. The best overall forecast for each horizon is highlighted in boldface. The results correspond to the validation set for this phase (2017Q3 to 2019Q4) that helps us identify the best method to use for generating the forecasts up until 2021Q4. The selection is done on the overall performance. These forecasts are then adjusted judgementally to produce the final predictions.

Table 3.

Average MASE for phase 2 forecast selection in the validation sample (2017Q3 to 2019Q4) across all countries.

Forecast	Base forecasts					Hierarchical forecasts
	t + 1	t + 2	t + 3	t + 4	Overall	t + 1	t + 2	t + 3	t + 4	Overall
Univariate
Naive	4.467	5.261	4.585	1.292	3.901	4.467	5.261	4.594	1.293	3.904
SNaive	1.589	1.589	1.637	1.292	1.527	1.590	1.590	1.638	1.293	1.528
ETS	1.348	1.479	1.600	1.329	1.439	1.350	1.485	1.596	1.323	1.439
Theta	1.309	1.463	1.622	1.415	1.452	1.304	1.461	1.623	1.410	1.450
ARIMA	1.296	1.465	1.650	1.399	1.453	1.291	1.461	1.647	1.401	1.450
MLP	1.498	1.810	2.031	1.832	1.793	1.540	1.833	2.072	1.863	1.827
ELM	1.409	1.640	1.800	1.562	1.603	1.402	1.635	1.791	1.544	1.593
RF	1.402	1.667	1.862	1.638	1.642	1.396	1.664	1.858	1.631	1.637
THieF-ETS	1.324	1.458	1.578	1.360	1.430	1.313	1.455	1.565	1.347	1.420
THieF-Theta	1.328	1.495	1.669	1.450	1.486	1.325	1.491	1.669	1.446	1.483
THieF-ARIMA	1.291	1.441	1.625	1.366	1.431	1.283	1.436	1.614	1.372	1.426
Multivariate
ETSx	1.378	1.550	1.691	1.391	1.503	1.379	1.544	1.685	1.373	1.495
regARIMA	1.463	1.741	2.122	1.865	1.798	1.441	1.725	2.116	1.856	1.785
THieF-ETSx	1.413	1.548	1.735	1.472	1.542	1.405	1.539	1.732	1.477	1.538
THieF-ETSxu	1.379	1.502	1.666	1.401	1.487	1.366	1.492	1.655	1.400	1.478
THieF-regARIMA	2.027	2.125	2.307	2.035	2.124	1.968	2.046	2.198	1.907	2.030
THieF-regARIMAu	1.445	1.659	1.943	1.675	1.681	1.468	1.659	1.937	1.673	1.684

We can observe a few clear patterns in the performance of the forecasting approaches. Standard univariate statistical approaches (ETS, Theta, ARIMA) perform well. Machine learning approaches, although they outperform the benchmark SNaïve, do not outperform the statistical forecasts. This can be partially explained by the quarterly sampling frequency of the time series, which limits both the sample size, disadvantaging machine learning approaches, and exhibiting relatively simple dynamics due to their quarterly nature, to the benefit of statistical forecasts. Comparing the univariate forecasts against predictions that make use of explanatory variables, we observe that the latter do not consistently add value, but are competitive to their univariate counterparts. We note that there are two limiting factors. The models are trained in periods of relative stability; therefore, univariate extrapolation can be very effective. Secondly, the explanatory variables are only updated at an annual level, which suggests that intra-annual variability is captured only univariately.

Using temporal aggregation (THieF- results) improves the performance of the univariate forecasts further, but seems to introduce issues when explanatory variables are used. We attribute this to challenges in the identification of the annual models with explanatory variables, which is further evidenced by the superior performance of the THieF-ETSxu and THieF-regARIMAu that uses univariate forecasts at the annual level, over their conventional counterparts (THieF-ETSx and THieF-regARIMA). Cross-sectional hierarchies provide marginal improvements in almost all cases and are deemed beneficial.

Our evaluation suggests that the best performing forecast is generated by the hierarchical THieF-ETS, which we use hereafter to construct the judgementally adjusted forecasts up until 2021Q4. This finding is in agreement with Kourentzes and Athanasopoulos (2019), who found that both temporal and cross-sectional hierarchies provide benefits to tourism forecasting.

Table 4 presents the forecasting performance of the various models for the phase 1 test period (2019Q1 to 2019Q4, considering four t + 1, three t + 2, two t + 3, and one t + 4 forecasts). We observe that in this sample the order of the performance of the forecasts somewhat changes. This is to be expected since it is a smaller sample. Again we find temporal hierarchy (THieF-) forecasts to perform best, with the THieF-ARIMA being more accurate than THieF-ETS for the 1-, 2-, and 4-quarter-ahead forecasts in 2019, while THieF-ETS remains the most accurate for the 3-quarter-ahead forecasts in 2019. In addition, the hierarchical THieF-ETS (our forecast choice from the selection procedure) remains more accurate than its non-hierarchical counterpart.

Table 4.

Average MASE for phase 1 test period (2019Q1 to 2019Q4) across all countries.

Forecast	Base forecasts					Hierarchical forecasts
	t + 1	t + 2	t + 3	t + 4	Overall	t + 1	t + 2	t + 3	t + 4	Overall
Univariate
Naive	4.105	4.831	4.548	1.272	3.689	4.105	4.831	4.548	1.272	3.689
SNaive	1.179	1.243	1.286	1.272	1.245	1.179	1.243	1.286	1.272	1.245
ETS	1.012	1.131	1.268	1.352	1.191	1.013	1.127	1.260	1.336	1.184
Theta	0.978	1.164	1.297	1.417	1.214	0.974	1.159	1.301	1.420	1.214
ARIMA	0.976	1.141	1.325	1.318	1.190	0.969	1.135	1.324	1.345	1.193
MLP	1.215	1.548	1.740	1.790	1.573	1.236	1.528	1.749	1.844	1.589
ELM	1.085	1.261	1.428	1.397	1.293	1.080	1.250	1.432	1.400	1.291
RF	1.116	1.324	1.526	1.533	1.375	1.117	1.325	1.529	1.537	1.377
THieF-ETS	0.968	1.125	1.260	1.411	1.191	0.965	1.119	1.238	1.369	1.173
THieF-Theta	0.993	1.208	1.345	1.482	1.257	0.996	1.202	1.347	1.488	1.258
THieF-ARIMA	0.955	1.114	1.276	1.279	1.156	0.955	1.110	1.269	1.311	1.161
Multivariate
ETSx	1.064	1.274	1.454	1.398	1.298	1.062	1.261	1.441	1.382	1.287
regARIMA	1.053	1.216	1.378	1.377	1.256	1.026	1.171	1.328	1.334	1.215
THieF-ETSx	1.097	1.291	1.539	1.509	1.359	1.092	1.273	1.526	1.490	1.345
THieF-ETSxu	1.046	1.259	1.472	1.480	1.314	1.035	1.235	1.448	1.438	1.289
THieF-regARIMA	1.828	1.914	1.862	1.840	1.861	1.762	1.825	1.724	1.655	1.742
THieF-regARIMAu	1.083	1.226	1.304	1.334	1.237	1.059	1.188	1.286	1.332	1.216

Patterns of recovery based on the scenarios

The expected recovery differs between the scenarios produced. Under the severe scenario, on average, the countries will recover only 34% of their total arrivals in 2021Q4 compared to 2019Q4; and under a mild scenario, the destinations will have recovered on average 80% of arrivals compared to 2019Q4. Table 5 summarises these results for the total arrivals series in all countries in the sample.

Table 5.

Predicted 2021 recovery rates of total visitor arrivals in 20 selected destinations.

Destination	Scenario 1 Severe	Scenario 2 Medium	Scenario 3 Mild
Australia	31%	56%	80%
Bulgaria	37%	60%	80%
Canada	41%	65%	83%
Chile	19%	39%	61%
Czech Republic	38%	63%	87%
Finland	36%	61%	83%
Indonesia	25%	49%	73%
Japan	45%	72%	92%
Korea	38%	63%	85%
Malaysia	38%	62%	81%
Mauritius	20%	42%	67%
Mexico	41%	65%	85%
New Zealand	28%	50%	72%
Singapore	36%	60%	82%
South Africa	31%	57%	80%
Sweden	35%	60%	83%
Thailand	35%	61%	84%
Tunisia	28%	53%	77%
UK	37%	63%	85%
USA	36%	58%	78%

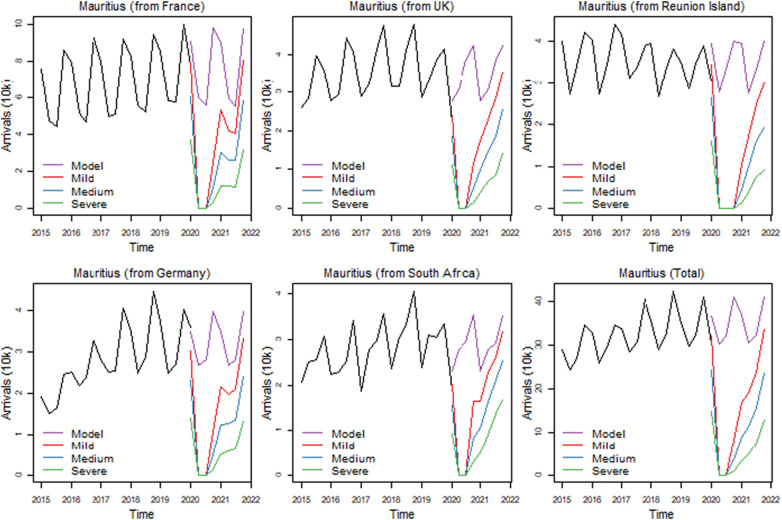
Within the group of 20 destinations, Chile and Mauritius will take longer to recover with only 19% and 20% recovery rates under the severe scenario and 61% and 67%, respectively, under the mild scenario. The slower rate for Chile may be accounted for the fact that countries such as Argentina, Bolivia and Brazil, which are among the key markets of Chile, are also suffering heavy tolls from the pandemic.

Mauritius (Fig. 6 ) on the other hand, has been labelled as a low-risk country by the centre for disease control. The country was very effective in controlling the spread of the disease locally. This was achieved by closing the borders to international travel for seven months starting March. However, on 25 July, an oil spill in the vicinity of the island attracted a considerable amount of negative publicity from the international media. Furthermore, the island is heavily reliant on long-haul markets and is known for its upmarket product, which is more likely to suffer in times of global economic crises. The additional costs in terms of money and time of the mandatory 14-day strict quarantine at a local hotel and PCR tests imposed on all international arrivals will be heavily detrimental to demand as it will substantially increase costs of an already fairly expensive destination. This can have a longer-term impact on demand and dampen recovery.

Fig. 6.

Scenario forecasts for Mauritius [graphs of countries not shown in the text can be found in the online resources].

Our forecasts suggest that intraregional travel will recover before interregional travel. It is mostly seen in the European and North American destinations. For example, at the start of the recovery, which is 2021Q1, for a destination like Mexico, it means that by this time, under the normal scenario, arrivals from Canada and the USA will be 69% and 67% of what is expected without the demand shock caused by the pandemic. However, this falls to 29% and 27% with respect to arrivals from the UK and Brazil respectively and to 17% from Columbia. The same trend is observed in Europe. For example, Sweden will have recovered at least 70% of expected arrivals from Germany, the UK, Norway and Denmark, but only 48% from the USA. Similarly, there is some evidence that this will also be the trends in Asian destinations, although the pattern is not as clear.

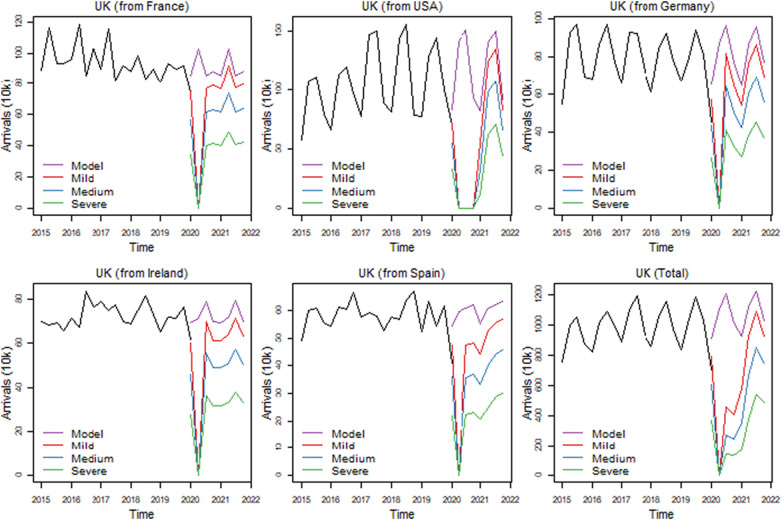
Compared to other countries in the sample, the graphs for the arrivals to the UK (Fig. 7 ) from its main source markets do not display a flat bottom. The only exception in the USA. This implies that recovery for travel from the European sources considered, has been almost immediate. Short haul travel to the UK is expected to start recovering from as early as 2020Q4. Arrivals from France, which is an important source, rise to 72% of expected arrivals for this period, followed by Ireland (70%), Germany (65%) and Spain (60%). Longer-haul travel will slowly start to recover from 2021Q1 reaching approximately 40% of what will normally be expected from the USA for that period. On 3 July, the government announced a travel corridor, which exempted British citizens, residents and tourists from certain countries from the 14 days of quarantine imposed. It may explain why arrivals from 2020 Spain and the USA, which are not included in the exemption, are expected to take longer to recover.

Fig. 7.

Scenario forecasts for the UK.

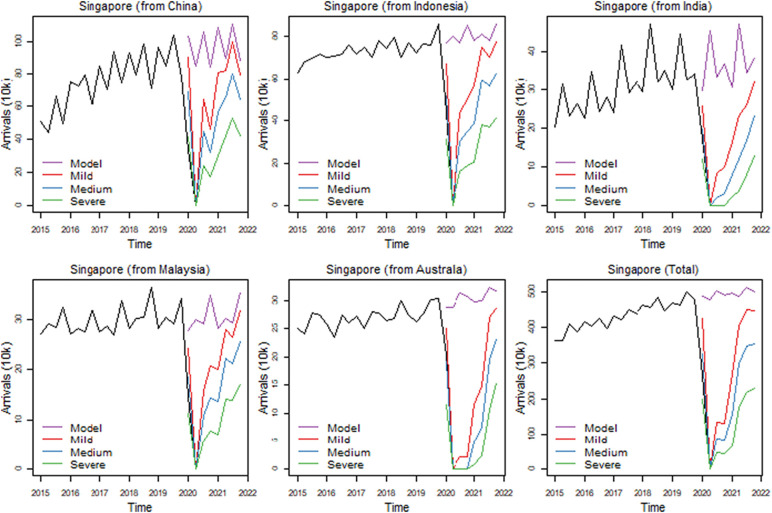
Singapore (Fig. 8 ) is relatively less affected by the pandemic and the recovery depends to some extent on bilateral agreements with and measures taken by the home country. From 23 March 2020, Singapore closed its borders to all short-term tourists to date, but special arrangements have been implemented that allow short-term arrivals from regional markets such as Australia, China and Malaysia.

Fig. 8.

Scenario forecasts for Singapore.

At the beginning of 2021Q2, arrivals to Singapore from China, Indonesia, and Malaysia will be at 51%, 40% and 42%, respectively, while on the other hand, arrivals from India and Australia will be at only 8% and 15%, respectively. Flights to and from Australia are severely restricted and other strong measures on outbound travel have been imposed by the government of Australia. This situation in Australia is not expected to change in the near future and this affects the recovery process significantly, hence the lower number for Australia in 2021Q2. By 2021Q4, however, Singapore will be receiving 73% of expected arrivals from Australia, but only 61% of arrivals from India due to the strict measures imposed by the government of Singapore on arrivals from India where cases of infections with Covid-19 continue to rise at a much higher rate.

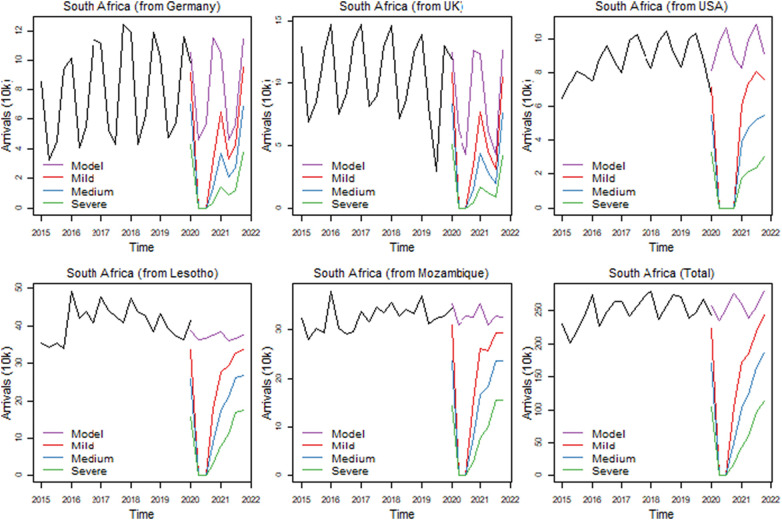
In the sample of countries under study, the bottom time for the majority of countries is 2020Q2, except for New Zealand, Australia, Chile, South Africa and Mauritius, where this happens one quarter later. In the case of South Africa (Fig. 9 ), the Minster for Tourism announced that the decision to open borders depends not only on the situation locally, but on the source markets as well, and that borders are expected to reopen in 2020Q4.

Fig. 9.

Scenario forecasts for South Africa.

The recovery pattern predicted is in many ways as discussed above. Short-haul travel from neighbouring countries such as Lesotho and Mozambique is predicted to reach 58% and 60% by 2021Q2 and 71% and 72% by 2021Q4. On the other hand, the longer-distance travel from Germany, the UK and the USA will be 45%, 46% and 47% of predicted travel, respectively, by 2021Q2 and these figures rise to 60% by 2021Q4. The country is expected to have recovered up to 80% of total international arrivals under the mild scenario.

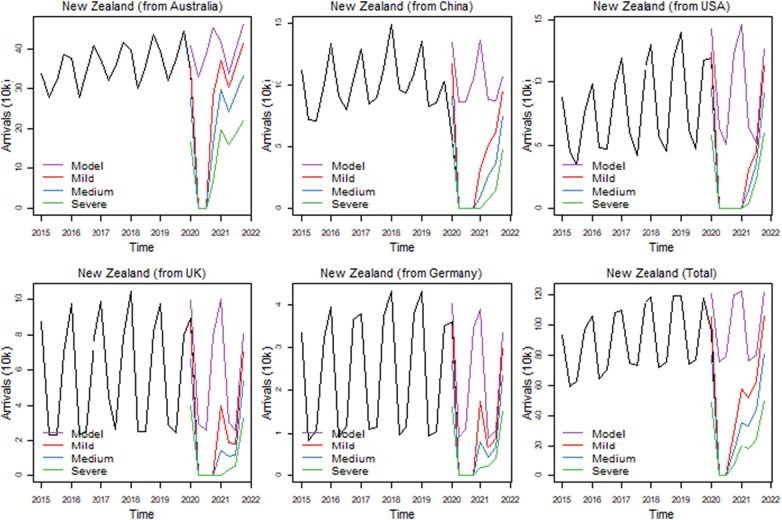
Similar trends are observed in New Zealand (Fig. 10 ). The three scenarios predict a significant drop in total visitor arrivals in New Zealand over the period 2020Q4-2021Q4 compared to the number of international tourists over the period 2019Q1–2019Q4. Specifically, the gaps between the expected trends of visitor arrivals under the three scenarios are predicted to be the highest during the 2020Q4 period, ranging from a 76.6% drop in international visitor arrivals compared to 2019Q4 under the mild scenario to a 94.6% decrease under the severe one. Contrary to most countries that are currently trying to manage COVID-19 by allowing it to be in their communities after the initial containment measures, the New Zealand government has no intention to allow COVID-19 to be in the community. Since the beginning of the COVID-19 pandemic and travel restrictions, only New Zealanders and New Zealand permanent residents have been allowed to enter the country. Given the pace at which COVID-19 infection rates are currently rising across the globe, it is reasonable to assume that New Zealand will continue to have one of the world's tightest border controls until the virus dies out or a vaccine is widely in use.

Fig. 10.

Scenario forecasts for New Zealand.

Overall, the negative impact of COVID-19 on total visitor arrivals in New Zealand is expected to start decelerating from the first trimester of 2021 and within approximately 12 months our model predicts that by 2021Q4, these gaps between visitor arrivals in 2019Q4 and the ones under the three scenarios will be reduced to 10.6% (mild), 31.6% (medium) and 58.6% (severe). Even when travel restrictions are progressively lifted on a case-by-case basis, given the potential for reinfection, international tourists will remain less likely to visit long-haul destinations, such as New Zealand, due to fear of COVID-19 and because their home countries might be still facing economic recessions due to the economic consequences of the ongoing COVID-19 pandemic.

On this basis, it is realistic to assume that during the period 2021Q1–2021Q3, New Zealand will remain virtually out of reach to a large number of international tourists from other regions, with an improvement over the last trimester of 2021 when the summer season starts in New Zealand. The losses of visitor arrivals from Australia in 2021 are expected to be lower than from other source markets such as China, Germany, the UK and USA. These observations are similar to the previous destinations discussed above, which show that intraregional travel is most likely to recover faster than interregional travel. In the meantime, the tourism industry will focus on domestic tourists, with Tourism New Zealand (2020) predicting that there will be an increase in domestic tourism of more than 100% during 2021.

Conclusion

In the modern era of international tourism, the COVID-19 pandemic is unlike any other crisis experienced, affecting all countries worldwide and leading to a widespread closure of borders never experienced before. The tourism industry was brought to a standstill and the repercussions of border closures, declines in economic growth rates and the subsequent changes in consumer behaviour will leave a lasting effect on the industry.

In this forecasting competition, we found that univariate forecasting techniques, combined with cross-sectional hierarchical outperform multivariate models under ‘normal’ circumstances. The THieF-ETS model was therefore also used to generate baseline forecasts for 2020 and 2021. To produce the scenarios and adjust the model forecasts, we resorted to judgemental techniques. Since governments imposed restrictions on travel, analysts provided a regional view on the relaxation of restrictions, with the arithmetic average feeding into the models. These views were based on country-specific regulations, macroeconomic conditions, seasonal factors and vaccine development.

Our recommended forecasts are generated from a univariate model, which may be contrary to the expectation that using macroeconomic indicators or perhaps forecasts of the spread of the pandemic can improve the forecasts. However, in our view, this reflects the uncertainty pertaining to forecasts of the economy and the pandemic, which are certainly true at the time of writing. One would expect that, in hindsight, once the explanatory variables are observed, they would also carry predictive power for the visitor arrivals.

Our most likely (medium) scenario shows that during 2021, tourism to the 20 destinations may recover on average to 58% of 2019 (pre-COVID) levels, over all destinations. Pessimistically, under the severe scenario, recovery will only be an average of 34% and optimistically (the mild scenario), 80% compared to 2019 visitor arrivals. We expect regional travel to lead the recovery and destinations that are highly reliant on intercontinental tourism may therefore experience longer recovery times.

This holds important managerial and policy implications, since the speed of recovery is dependent on policy actions that should be aimed at restoring confidence and adjusting to the new circumstances. The research by Mao et al. (2010) on recovery after the SARS outbreak clearly shows that not all countries have the same recovery rates, with some countries falling into a hysteresis with slower recovery. In the current pandemic, our outlook and results are driven by views on the successful development and distribution of a vaccine as the main driver of confidence. During previous pandemics, recovery was relatively quick after the threat has been eliminated. Countries with a good vaccine policy should therefore benefit from restoring confidence; although this should be augmented by programmes and promotions to inform travellers of the precautions taken for their safety. Governments of many destinations are currently debating on the introduction of a ‘vaccination passport’ to allow entry from abroad. Zeng et al. (2005) also show that countries with good external relations with origin countries tend to recover quicker after a pandemic, highlighting the importance of international policy and local stability in tourism recovery. Since it is expected that regional travel will recover before intercontinental tourism, marketing efforts should firstly aim at attracting local and regional travellers, with border policies also reflecting this.

This paper makes several contributions; firstly, methodologically it shows that exponential smoothing techniques still outperform many of the newer data-driven techniques (such as neural networks) in tourism demand forecasting under ‘normal circumstances’; secondly, the usefulness of using temporal hierarchies in improving forecasting accuracy is also evident from this research; thirdly, we propose a unique scheme for judgemental adjustment of model-based forecasts that can be applied in adverse circumstances, such as the current pandemic, which addresses the shortcomings of model-based forecasts during uncertainty. No other tourism forecasting research study has attempted to forecast tourism demand during a pandemic, since the previous pandemics were both regionally concentrated and relatively short in duration. Given the immense uncertainty during times of pandemics and the failure of model-based forecasts to deliver accurate forecasts in such circumstances, this research offers an alternative view on the application of judgemental adjustment to develop scenario forecasts.

Our research is not without limitations, since this is a very uncertain time and forecasting during a pandemic is prone to all the uncertainties that accompany the coronavirus. Given the task of forecasting visitor arrivals from five different destinations to 20 countries worldwide, the approach taken in this research is understanding the regional context rather than country-specific context. Although regional specialists have added value, the origin-destination-specific context could be enhanced in future research. Since the research forms part of a forecasting competition, the focus is more on exploring various methods and developing tourism forecasting techniques during times of pandemics, than an analysis of the pandemic in a specific country. At the time of forecast little information were available on the possibility of mutations in the virus leading to new strains. The new strains that have emerged since then have resulted in much stricter controls and lockdown in many countries, leading to temporary closures of international borders. However, the roll out of vaccines against the virus have successfully started in a few of the main tourism generating markets. Both factors are likely to affect travel. Our approach was further guided by the limited research available on the impact of pandemics on tourism demand and is one of the first attempts to forecast the possible recovery of tourism before this health pandemic has been resolved.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.