Abstract
The tumor size ratio (TSR), time‐to‐tumor growth (TTG), and tumor growth rate (kG) are frequently suggested as model‐based predictors of overall survival (OS) for different types of tumors. When the tumor metrics are applied in forecasting of the outcome for individual patients at an early stage, the tumor data might be sparse resulting in imprecise prediction. This simulation study aimed to investigate how the tumor follow‐up data and estimation approaches influence the accuracy in the tumor size metrics and the predicted hazard of death for individual patients. Longitudinal tumor size and OS data were simulated using tumor growth inhibition and Weibull distribution models, respectively. Based on the model and increasing measurement durations, the accuracy (defined as 80–125% of the simulated “true” value) in individual metrics and hazard was computed. TSR week 6 (TSRw6) accuracy was adequate for 91% of the patients when tumor size was measured up to 12 weeks. For TTG and kG metrics, the highest accuracy observed was lower (43 and 77%, respectively) and occurred later (42 and 60 weeks, respectively). The simultaneous (joint) and sequential estimation approaches resulted in similar accuracies, however, in general, the sequential approach where individual tumor size parameters are fixed, demonstrated inferior estimation properties. The TSRw6 and the model‐predicted tumor time course (absolute or relative change) had better forecasting properties than TTG or kG. The population pharmacokinetic (PK) parameters and data approach performed similarly or better than the simultaneous approach and had a better accuracy in estimating individuals' hazard of death than the individual PK parameters method.
Study Highlights.
WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?
Developed population models have potential to predict tumor response and hazard of death in a new patient at an early stage, facilitating early clinical judgments and interventions.
WHAT QUESTION DID THIS STUDY ADDRESS?
Typically, all available tumor size (TS) measurements within a patient are used in model development and for identifying the “optimal” TS metric predicting overall survival. When the tumor metrics are applied in forecasting the outcome for individual patients at an early stage, the tumor data might be sparse resulting in imprecise prediction. This simulation study aimed to investigate how the tumor follow‐up data and estimation approaches influence the accuracy in the TS metrics and the predicted hazard of death for individual patients.
WHAT THIS STUDY ADDS TO OUR KNOWLEDGE?
TSR week 6 (TSRw6) accuracy was adequate for 91% of the patients when TS was measured up to 12 weeks. For time‐to‐tumor growth (TTG) and tumor growth rate (kG) metrics, the highest accuracy observed was lower (43 and 77%, respectively) and occurred later (42 and 60 weeks, respectively). The choice of analysis method had relatively little influence on the accuracy of the estimated hazard ratio.
HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?
This simulation study concludes that for early prediction of treatment outcome for an individual patient, TSRw6 or tumor time course is a more promising metric than TTG or kG. The simultaneous (joint) and sequential estimation approaches resulted in similar accuracies, however, in general, the sequential approach where individual TS parameters are fixed, demonstrated inferior estimation properties.
INTRODUCTION
Population modeling has increasingly been applied to evaluate longitudinal tumor size (TS) data and to investigate TS metrics as predictors of long‐term clinical end points, such as overall survival (OS) or progression free survival. 1 , 2 These models have potential to predict tumor response in a new patient at an early stage, facilitating early clinical judgments and interventions. If response is low, the model can be applied to determine dose modifications predicted to maximize the efficacy. Moreover, in line with the strive for model‐informed drug discovery and development, 3 the models developed based on information gathered during phase I/II trials are used to predict the efficacy and clinical outcomes of phase III trials, thereby assisting “go, no‐go” decisions. 3 , 4
The tumor size ratio (TSR), 5 , 6 , 7 , 8 , 9 , 10 the time to tumor growth (TTG), 10 , 11 , 12 , 13 , 14 or the estimated tumor growth rate constant (kG) 10 , 15 , 16 have been identified as predictors of OS in various cancer types. Typically, all available TS measurements within a patient are used in model development and for identifying the “optimal” TS metric predicting OS. The tumor follow‐up or the number of TS measurements per patient depends on many factors, like response to drug, adverse effects, and mortality. Thus, the available TS measurements can be as sparse as one or two in addition to baseline. When the data are sparse and contain limited information, the individual parameter estimates may not deviate from the population mean, leading to shrinkage 17 of parameter estimates. Consequently, the individual parameter estimates might shrink toward the typical value when models are applied at an early stage after initiation of therapy. Shrinkage in parameter estimates can lead to biased tumor metrics of an individual, influencing the evaluation of predictors of survival 18 as well as the prediction of hazard for an individual patient.
A TS model, built on longitudinal data, can be linked to time to event models of OS by different estimation approaches, similar to when pharmacokinetic (PK) models are associated with pharmacodynamic (PD) models. 19 Estimation of both tumor and OS specific model parameters at the same time can be achieved in the simultaneous (SIM) approach using a joint tumor‐OS model. The SIM estimation allows the survival data to influence the tumor model fit and account for uncertainties in the data. The SIM approach is increasingly been suggested and proposed to be superior to individual PK parameters (IPPs). However, the population PK parameters and data (PPP&D) approach, shown to have good estimation properties for PK‐PD models have rarely been considered. In sequential approaches, the tumor model is developed first and the developed tumor model is linked to the OS model using one of the sequential methods. The two most commonly applied sequential methods are IPP and PPP&D. In IPP, the empirical Bayes estimates (EBEs) from the tumor model are used in the OS model. The EBEs rely, however, on the richness of individuals' data and can be sensitive to parameter shrinkage 18 (i.e., when individual data are sparse, the individual estimates rely more on the population estimates and the variance of the EBEs becomes lower than the estimated variance parameter). Consequently, the values of model‐derived metrics can be affected, leading to biased parameter estimates of the survival model. This problem is partially addressed in PPP&D. In the PPP&D approach for tumor‐OS modeling, the population parameters (typical values and estimated between‐subject variability) of the developed tumor model are fixed, but the individual tumor size data are kept as dependent variables when the OS model parameters are estimated. SIM and sequential approaches might influence the quantification of the tumor size metric‐survival relationship and this may affect the forecasting of survival for a new individual. We will here use the same abbreviations (PPP&D and IPP), although here it is a PD parameter (TS) rather than PK that drives the outcome variable OS.
This study aims to investigate how the sparseness of available TS data may influence the accuracy in prediction of different TS metrics and how different estimation approaches influence the metrics' value in predicting the hazard of death for an individual patient.
METHODS
Simulation of data
Tumor size data
TS data for 1000 subjects were simulated using a simplified tumor growth inhibition model for bevacizumab plus chemotherapy in colorectal cancer 12 (Table 1), at baseline (time = 0), and at 6, 12, 18, 24, 36, 48, 60, 72, 84, and 96 weeks after treatment initiation. Two different tumor follow‐up conditions were considered, (i) with dropout from tumor measurements forced after the first measurement with ε 20% increase from the tumor nadir, mimicking Response Evaluation Criteria in Solid Tumors (RECIST) criteria for progression in sum of longest diameter (SLD), 20 and (ii) without dropout where none of the patients were allowed to drop out during the 96‐week study period. In addition, the advantage of a pretreatment scan (4 weeks before start of treatment) was explored in scenario (i) for kG.
TABLE 1.
Tumor size model parameters used in the simulation 12
| Parameter | Description (unit) | Estimate | IIV |
|---|---|---|---|
| kG | Tumor growth rate (week−1) | 0.00583 | 1.06 |
| KDE | Tumor growth inhibition rate (week−1) | 0.0498 | 0.63 |
| λ | Exponential decrease in tumor growth inhibition rate (week−1) | 0.0866 | 0.63 |
| Baseline | Tumor baseline SLD (cm) | 9.67 | 0.71 |
| Additive residual error | Unexplained variability (cm) | 0.98 | ‐ |
Abbreviations: IIV, interindividual variability; SLD, sum of longest diameter.
The TSR calculated at week 6 (TSRw6), TTG‐derived based on tumor model parameters, and the simulated value of kG were considered as the “true” value of the metrics for each simulated individual. The “true” metrics for a typical individual were 0.739, 24.8 weeks−1 and 0.00583 weeks−1 for each metric, respectively.
Survival data
OS data for 1000 individuals were simulated using a Weibull distribution 12 characterizing the increase in hazard over time and a relationship to one of the three tumor metrics, as described in Equation 1.
| (1) |
where, λ and α denote the scale and shape parameters, respectively, t is time, and β is the coefficient related to the tumor metric (TM). For kG, the value in log domain was applied as the predictor in the survival model. Weibull parameters and β (β TTG = −0.0417) were available from the published model. 12 For the other metrics, the mean β value that was estimated from 1000 simulated survival data sets using the published model including a TTG‐relationship. Then, using the estimated β and Weibull parameters, survival data were simulated for each TM. In the mean β, values were 2.76, and 0.322 for TSRw6 and logkG, respectively. For each individual, the “true” relative hazard ratio (rHR i ) was derived as a ratio between the individual hazard ratio (calculated from the individuals' TM and the related coefficient value, i.e., ) and the typical hazard ratio (calculated from population median TM value and the related coefficient value, ).
To further evaluate the forecasting ability of models, additional OS data sets were simulated using the time‐varying predictors absolute TS (TS[t], β = 0.497) and tumor change from baseline (relTS[t], β = 0.731).
Accuracy calculations
The accuracy of TS metrics and estimated rHR was defined as percentage deviation from the “true” value. The acceptable accuracy for a patient was set to 80–125% of the “true” value (Equation 2), which is the same threshold as used for acceptance in bioequivalence studies. In addition to accuracy, shrinkage 17 of the estimated TS metric was calculated on the variance scale 18 (Equation 3).
| (2) |
| (3) |
The study was divided into three parts (Figure 1): (1) the accuracies of forecasted values of TSRw6, kG, and TTG were investigated; (2) the accuracies of forecasted values of the hazard in the OS models were evaluated and SIM and sequential estimation approaches were compared, and (3) the accuracy of forecasted survival probabilities was assessed.
Bayesian estimation of TS metrics: The Bayesian forecasting utility, prospective evaluation (proseval) in PsN, 21 was applied to investigate the accuracy of the predicted TS metrics. The proseval function estimates individual parameters based on the original model without re‐estimation of parameters (MAXEVAL = 0 in NONMEM) using a successive increase in the number of (simulated) tumor size observations. The proseval derived tumor metrics were compared to the “true” tumor metric for each simulated individual.
Accuracy of estimated hazard and impact of estimation approach on TS‐OS model: In this evaluation, the parameter related to the tumor metric in the hazard (HZ) function (i.e., β in Equation 1) was allowed to be re‐estimated for TSRw6, kG, and TTG using the simulated TS‐OS data sets. The parameter estimate was consequently dependent on the values of the model‐derived tumor metric that had been estimated based on a varying number of TS measurements and follow‐up times. For each individual, the rHR was calculated using the estimated β parameter and the individual's derived tumor metric (i.e., ), and the accuracy was calculated as the percentage deviation from the individual's “true” rHR for the metric. The SIM and sequential (IPP or PPP&D) estimation approaches were investigated for the re‐estimation of the hazard.
Forecasting events: The survival time for each patient was forecasted using tumor metrics derived based on varying amount of available tumor data (at landmark time, s) and “true” parameters from the simulation. In this scenario, in addition to TSRw6, kG, and TTG, TS(t), and relTS were also investigated. The different landmark times considered were 6, 12, 18, 24, and 36 weeks. For each patient, the cumulative survival probability from the start of the study was determined in different prediction time windows (t), by fitting the model (MAXEVAL = 0) using the available data. In these evaluations, t was 6, 12, 18, 24, and 36 weeks. The time‐dependent Brier score (BS) and time‐dependent area under the curve (AUC) were calculated (Equations 4 and 5). 22 , 23 , 24 The BS function developed by Blanche et al. 24 was applied in the computation of BS score and timeROC package in R for the time‐dependent AUC.
| (4) |
| (5) |
where is the cumulative survival probability, s is the landmark time (6, 12, 18, 24, or 36 weeks), and t is the prediction window for forecasting. The BS is calculated based on the events in the prediction window because direct comparison between metrics and landmark times is not possible. Hence, in the analysis, the calculated BS were scaled (sBS; Equation 6) to the base model values (Weibull function without predictors).
| (6) |
Simulation and estimation were carried out using the nonlinear mixed‐effects modeling software NONMEM (version 7.4). 25 The first‐order conditional estimation method with interaction was used for assessment of TS metrics and the Laplace method was used in the estimation of HZ of death. R (version 3.1) was used for data management and graphical analysis. Model development, evaluation, and the proseval tool were facilitated by Perl‐speaks‐NONMEM (PsN) toolkit (version 4.8), and Pirana (version 2.9.9). 26
FIGURE 1.
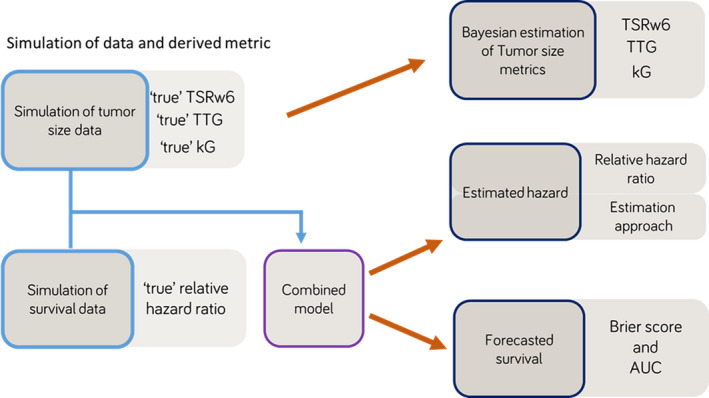
Project workflow: 1000 tumor size and survival data were simulated and during simulation “true” values of tumor metrics and hazard ratios were obtained. Using varying amount of tumor data, the accuracy of tumor metrics, estimated hazard, and forecasts were analyzed in three different steps. AUC, area under the curve; kG, tumor growth rate; TSRw6, tumor size ratio week 6; TTG, time‐to‐tumor growth
RESULTS
Simulated data
The medians (2.5th and 97.5th percentiles) of the 1000 simulated TSRw6, TTG, and kG, were 0.841 (0.468 and 1.09), 24.4 (−2.33 and 122) weeks, and −5.19 (−3.13 and −7.25; log scale, week−1), respectively, and the values were similar between different follow‐up scenarios. The median time of the last TS measurement was 36 (6 and 96) weeks.
Bayesian estimation of tumor size metrics
TSRw6: The accuracy of the TSRw6 metric was adequate for the majority of the individuals (>90%; Figure 2, blue lines, Figure S1). When measurements at baseline and at week 6 were available, about 91% of the individuals had acceptable TSRw6 accuracy with shrinkage of 40%. By adding the week 12 measurement, the accuracy increased to 94% and shrinkage reduced to 27%. The accuracy and shrinkage were little affected by the addition of later tumor measurements. With a stricter accuracy criterion of ±10% of “true” TSRw6, the accuracy was 70% for baseline plus week 6 measurement, which was improved to 77% by allowing a week 12 measurement. Dropout had little influence on the results (Figures 2 and S1).
FIGURE 2.
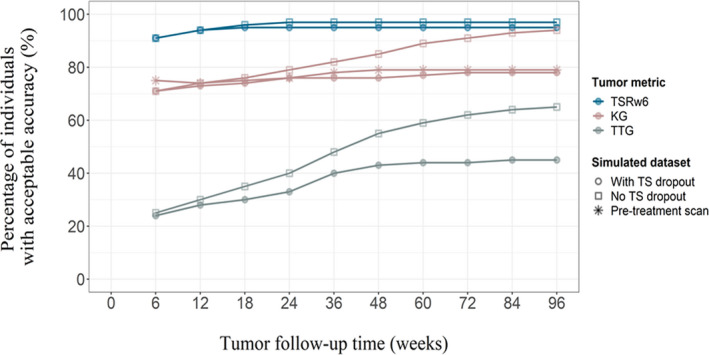
The percentage of individuals in the patient population with adequate accuracy of model‐predicted tumor metrics. The accuracy while assuming no dropout from tumor follow‐up (squares) and while considering dropout due to disease progression (20% increase from tumor nadir, circles) are shown for TSRw6 (blue), KG (rose) and TTG (gray). The effect of a pretreatment scan in predicting kG (red) due to disease progression is shown in stars. kG, tumor growth rate; TS, tumor size; TSRw6, tumor size ratio week 6; TTG, time‐to‐tumor growth
TTG: The accuracy of the TTG metric was, in general, low compared to the accuracy of TSRw6 (Figure 2, red lines, Figure S1). The accuracy of the model predicted that the TS metrics improved as the number of measurements increased. The percentage of individuals with acceptable deviation from the “true” TTG increased from 24% (shrinkage = 88%) when data up to week 12 was included to 43% (shrinkage = 68%) when TS data up to week 48 was included and dropout from TS measurements was considered in the simulations. The later observations (t ≥ week 48) affected the accuracy marginally. By applying a lenient accuracy criterion (±30%), the accuracy increased from 32% (week 12) to 53% (week 48). When no dropout from TS measurements was allowed (i.e., all measurements up to 96 weeks were used), the accuracy improved to 65% and the associated shrinkage was 44%.
kG: An adequate accuracy of the kG metric was observed for 71% of the population by allowing a week 6 measurement in addition to baseline (Figure 2, gray lines, Figure S1). The associated shrinkage was, however, as high as 85%. Addition of later observations improved the accuracy and the percentage of individuals with acceptable deviation from the “true” kG was 77% with a shrinkage of 60% when all TS measurements were used (i.e., 96 weeks of measurements) and dropout was allowed (Figure 2). When applying 10% as the criteria for acceptable accuracy, the percentage of the population with acceptable accuracy was 42% with 12 weeks of measurements and 50% with 96 weeks of measurements. When dropout was not allowed in the prediction of kG, the accuracy was increased to 94% (shrinkage = 43%) with all available data.
Addition of a pretreatment scan increased the number of individuals having acceptable accuracy and the shrinkage reduced. At week 6, 73% (shrinkage = 67%) of the populations' kG values were estimated accurately and, when all tumor measurements were used, the corresponding percentage was 79% (shrinkage = 58%).
Accuracy of estimated hazard and impact of estimation approach on TS‐OS model
Accuracy of estimated relative hazard ratio
The rHR calculated based on the estimated TSRw6 and βTSRw6 was associated with the highest accuracy. With one post baseline measurement, 77% of the individuals had acceptable accuracy when using TSRw6 as predictor; whereas with data until week 6, the accuracy was 20% for TTG and 56% for kG based rHR (Figure 3). With an additional week 12 measurement in TSRw6‐based analysis, the rHR was accurate for 85% of the individuals. However, to achieve maximum accuracy with TTG and kG metrics, a longer tumor follow‐up was required and it was only 46% and 62% of individuals, respectively, for TTG and kG. The results are shown in Figure 3 (lines connected with circled points).
FIGURE 3.
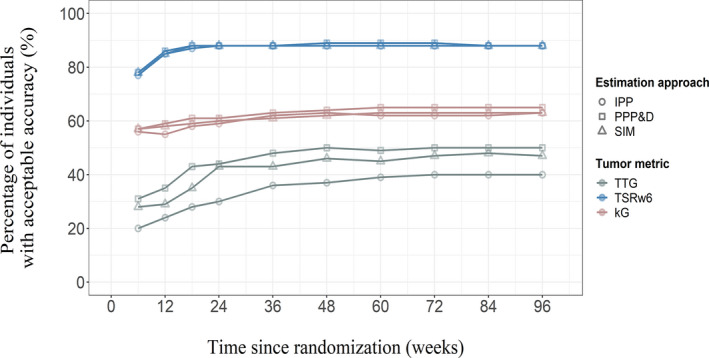
The percentage of individuals in the patient population with adequate accuracy of re‐estimated hazard ratio. The accuracy while using different metrics; TSRw6 (blue), kG (rose), and TTG (gray), TS(t) (red). The different estimation methods used were sequential (IPP‐round points, PPP&D‐square) and simultaneous (SIM‐triangle). IPP, individual PK parameters; kG, tumor growth rate; PPP&D, population pharmacokinetic parameters and data; SIM, simultaneous; TSRw6, tumor size ratio week 6; TS(t), absolute tumor size; TTG, time‐to‐tumor growth
Impact of the estimation approach on the estimated hazard ratios
TSRw6: When only week 0 and week 6 measurements were used, 77% (IPP) and 78% (PPP&D and SIM) of the individuals had an acceptable accuracy of the HR (Figure 3). By adding a week 12 measurement, the corresponding percentages increased to 85% (IPP and SIM), and 86% (PPP&D). The accuracy was only slightly improved by adding later observations. Accuracy percentages were 88% for all three approaches when all tumor data were used (Figure 3).
TTG: The percentage of the population with accurate HR was always lower than 50% despite inclusion of more tumor data or the chosen estimation approach (Figure 3). With baseline and week 6 data only, the accuracy was 20% (IPP), 31% (PPP&D), and 28% (SIM). The accuracy was highest at week 48; 51% for PPP&D, 46% for SIM, and 37% for IPP.
kG: When baseline and week 6 tumor data were used, the percentage of population with acceptable accuracy was 56% (IPP), 57% (PPP&D), and 58% (SIM). The accuracy was little affected by adding week 12 to week 24 measurements, whereas adding tumor data beyond week 24 increased the accuracy (median TTG was 24 weeks) and it was 62% (IPP), 65% (PPP&D), and 63% (SIM) when all tumor data were used (Figure 3).
Forecasting events
TSRw6: The sBS score with tumor data until week 6 was calculated as 0.21 (s = 6, t = 6 weeks), indicating that addition of TSRw6 as predictor of OS improved the forecasts for the prediction window of 6 weeks, compared to the model without the predictor. The accuracy in forecasts was little influenced by an increased prediction window, and for the prediction window week 36, sBS was 0.29. The calculated AUC was greater than 95% and the value was marginally affected by the prediction window. The additional tumor follow‐up data did not improve the forecasts any further (Figure 4).
FIGURE 4.
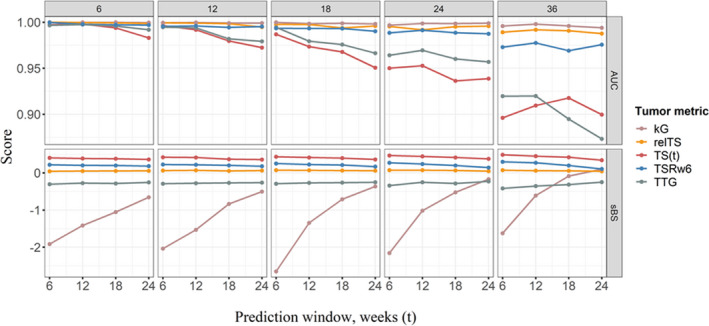
Scaled BS score (sBS) and AUC relating to forecasts of survival events based on tumor metric derived at landmark times 6, 12, 18, 24, and 36 weeks (columns) and for prediction windows 6, 12, 18, and 24 weeks (points). The tumor metrics; TSRw6 (blue), kG (rose), TTG (gray), TS(t) (red), and relTS (yellow). AUC, area under the curve; kG, tumor growth rate; relTS, tumor change from baseline; TS, tumor size; TSRw6, tumor size ratio week 6; TTG, time‐to‐tumor growth
TTG: The accuracy of forecasts based on TTG metric was poor for all the landmark times and prediction windows tested in the current study (Figure 4). The sBS values were less than zero, in other words, the model without TTG as predictor forecasted the events more accurately than the TTG based TS‐OS model. The AUC was greater than 95% for s = 6, 12, 18, and 24 weeks and the AUC was around 90% for s = 36 weeks.
kG: For a tumor follow‐up until week 36 and a prediction window of 24 weeks, the kG‐based OS forecast had better accuracy (sBS = 0.1) than the base model. However, the forecasts based on kG before week 36 did not show any improvement over application of a model without any predictors. The calculated AUC was greater than 95% for the landmark times investigated (Figure 4).
TS(t) and relTS: The time‐varying predictors TS(t) and relTS had better accuracy in forecasting events compared to the base model, in all different landmark times and prediction windows evaluated in the current study (Figure 4). TS(t) showed nearly a 10 times improvement in sBS (sBSTS(t) = 0.4 vs. sBSrelTS = 0.06) compared to relTS forecasts. The AUC values were above 95% for both metrics in all landmark times, except for TS(t) when s = 36 weeks, where the AUC was 90%.
DISCUSSION
In this study, the influence of the richness of TS data on the predictability of tumor metrics and hazard of death was investigated for a tumor size‐OS model. TSRw6 was a more accurately predicted metric, and predicted individuals' hazard of death better, compared to TTG or kG. The PPP&D method resulted in accuracies of hazard of death that were similar or improved (for TTG) to simultaneous estimation, and better than those from the commonly applied IPP estimation method.
The study results indicate that the model‐derived TSRw6 metric has potential for early prediction of the treatment effect because it was sufficient to have fewer tumor measurements for deriving the metric with adequate adequacy. The TSRw6 was associated with an acceptable shrinkage (<30%) and the effect of tumor follow‐up time (>week 6) had little influence on shrinkage in TSRw6, which is in line with the study results by Ribba et al. 18 Moreover, the TSRw6 metric demonstrated a reasonable accuracy for predicting hazard of death across all estimation methods. Addition of one extra measurement at week 12 in the prediction of TSRw6 improved the accuracy of the metric and estimated relative hazard. Therefore, it would be recommended to study patients for at least 12 weeks to make reasonable predictions of survival probability for an individual using the model‐derived TSRw6 metric. This metric may have potential to be applied in clinical practice to evaluate the therapy and model‐informed precision dosing for a patient.
In the study by Ribba et al. 18 the shrinkage of TTG was reported to be above 40% and similar results (shrinkage >50%) were found in the current study for IPP method. The high shrinkages of TTG mostly from kG shrinkages as it was high (>40%), whereas TSRw6 had a much better shrinkage (<30%). As expected, the accuracy of the TTG estimation improved when tumor data indicating that the nadir has passed was included. The analytical solution of TTG can conveniently provide an insight on time to progression, however, as the results demonstrated, the uncertainty in the prediction is high when TS is only measured every 6 weeks, and before TTG has occurred.
The shrinkage in kG was high (60%) when tumor dropout was considered, although the accuracy of kG improved with the addition of tumor data after disease progression (i.e., when the data contained more information on tumor regrowth). These results are in line with findings in a study by Murphy et al. 27 where the uncertainty of model‐estimated doubling time (derived from kG) was investigated in seven ordinary differential equation models of tumor growth (exponential, Mendelsohn, logistic, linear, surface, Gompertz, and Bertalanffy). Murphy et al. found that depending on the time of available tumor data (60 or 120 days), and presence or absence of a chemotherapy effect, the model‐derived doubling time of an individual's tumor could vary 6 to 12‐fold, depending on the choice of tumor model used in the model fitting. 27 Our results indicate that the estimated doubling time could range between a factor of 0.03 and 12.6 of the “true” doubling time, depending on the number of available tumor measurements for a given model. It should be noted that, in the current study, we have explored only one structural model and the results could vary with other tumor models. It could therefore be wise to be cautious in using model‐based kG when predicting OS. The current study emphasizes the importance of following the tumor size for at least 6–12 weeks after disease progression for more accurate estimation of individual kG values.
We also explored a simulation scenario where one tumor measurement was collected 4 weeks before initiation of therapy, reflecting a screening measurement in addition to a baseline measurement, which would enable gathering more information about the natural tumor growth rate. However, using the published parameters, 12 this addition resulted in only marginal improvement in the accuracy and the shrinkage associated with the parameter. The kG value used in the study (0.00583 week−1) 12 indicates a tumor doubling time of 119 weeks, and a tumor measurement 4 weeks prior to treatment may not inform the model sufficiently about tumor growth rate as anticipated. In fast growing tumors, an additional TS measurement may be more valuable.
In the present study, we compared SIM (“joint”) and sequential estimation approaches to understand how the choice of method can affect the accuracy of the estimated rHR. The SIM and PPP&D methods were found to perform equally good when connecting PK and PD models by Zhang et al 19 The IPP approach was demonstrated to be inferior 19 , 28 when parameters were associated with high shrinkage. PPP&D equaled or provided better results compared to the SIM method in several scenarios tested. From the current study results, we conclude that the PPP&D approach would be the preferred choice because it had shorter runtimes (7 min vs. 19 min) compared to the simultaneous approach and better accuracy than IPP. Moreover, it performed the best for TTG, although TTG was performing overall the worst. An alternative would be the ‘individual PK parameter estimates and their uncertanity’ method that has been demonstrated to have similar properties as PPP&D. 28
In clinical trials, usually the change in the SLD is used in the evaluation of treatment response. Moreover, often the dynamic changes are categorized into best overall response. This categorization of continuous tumor changes into categories will lead to loss of information. 29 To address the dynamic characteristics of the tumor, a model‐based approach has been recommended and, in the past decade, the approach has gained increasing popularity in drug development. 30 Established relationships also have, however, the potential to be used in clinical practice. The model‐derived individual maximum a posteriori parameter values could be applied in the predictions of the individuals' tumor metric and clinical outcome given an available model. 30 , 31 The current study demonstrated the accuracy of predictions of both the metrics and in the hazard of death. The TSRw6, TS(t) and relTS showed better forecasts of death events compared to TTG and kG, and the current study warrants a more cautious screening and interpretation of tumor metrics in population modeling of tumor‐OS and their applications.
The TS measurements were simulated in accordance with planned tumor data collection timepoints, as per original clinical trial protocol. However, in most clinical trials, the measurements are not collected at exact timepoints and this was not considered in the current study. The benefit of evaluating model‐predicted TSRw6 over observed TSRw6 was out of the scope for the current study. The model derived TSRw6 has the advantage that it can be estimated regardless of when the actual measurement was done, thereby allowing flexibility in the time of TS measurements. The kG parameter used in the current study (0.00583/week) corresponds to a slow growing tumor (~2.5 year doubling time). The absolute bias was similar for patients with kG values below and above the typical value of kG, although a kG less than the typical estimate was associated with under prediction, whereas a kG above the typical estimate was more often associated with overprediction. The TGI model, used in the simulations, has been used for different anticancer drug classes in various indications. 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 It should, however, be acknowledged that the actual accuracy values will depend on model structure and parameter values. This work suggests that before a tumor metric from a TGI model is used for forecasting, it would be advisable to explore its potential for obtaining satisfactory accuracy. Another assumption made in our simulation study is that all patients were enrolled at the same time (i.e., all patients had the possibility to be followed for 96 weeks). In addition, the dropout due to disease progression was only on the basis of 20% increase in TS from tumor nadir. In clinical trials, progression and subsequent dropout can, for example, also be due to new lesion appearance, drug intolerance, or loss of follow‐up due to other reasons. In the current study, a univariate analysis (i.e., the accuracy of one predictor), was evaluated at a time, however, in TS‐OS model development, multiple predictors are typically tested. If the approach used in such a multivariate TS‐OS analysis is IPP, shrinkage effects from multiple parameters could influence the results, which was not investigated in the current study.
CONCLUSIONS
This simulation study demonstrates that TSRw6 and the model‐predicted tumor time course (absolute or relative change) had better forecasting properties than TTG or kG for early prediction of treatment outcome for an individual patient, because fewer measurements are needed for adequate estimation of the metric. A week 12 measurement, in addition to baseline and a week 6 measurement, appears to be beneficial for estimating an individual's TSRw6. This study also highlights that the use kG or TTG could be problematic in evaluating early treatment response and predicting hazard of death for an individual patient. The PPP&D approach performed similarly or better than the simultaneous approach and had a better accuracy in estimating individuals' hazard of death than the IPP method.
AUTHOR CONTRIBUTIONS
S.M.K and L.E.F. wrote the manuscript, designed the research, and analyzed the data. S.M.K. performed the research.
FUNDING INFORMATION
This work was supported by the Swedish Cancer Society (Grant number: 20 1226 PjF).
CONFLICT OF INTEREST
The authors declared no competing interests for this work. As Deputy Editor‐in‐Chief of CPT: Pharmacometrics and Systems Pharmacology, Lena Friberg was not involved in the review or decision process for this paper.
Supporting information
Figure S1.
Appendix S1
Krishnan SM, Friberg LE. Bayesian forecasting of tumor size metrics and overall survival. CPT Pharmacometrics Syst Pharmacol. 2022;11:1604‐1613. doi: 10.1002/psp4.12869
REFERENCES
- 1. Bender BC, Schindler E, Friberg LE. Population pharmacokinetic‐pharmacodynamic modelling in oncology: a tool for predicting clinical response. Br J Clin Pharmacol. 2015;79:56‐71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Bruno R, Mercier F, Claret L. Evaluation of tumor size response metrics to predict survival in oncology clinical trials. Clin Pharmacol Ther. 2014;95:386‐393. [DOI] [PubMed] [Google Scholar]
- 3. Marshall SF et al. Good practices in model‐informed drug discovery and development: practice, application, and documentation. CPT Pharmacometrics Syst Pharmacol. 2016;5:93‐122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Sharma MR, Karrison TG, Jin Y, et al. Resampling phase III data to assess phase II Trial designs and endpoints. Clin Cancer Res. 2012;18:2309‐2315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Claret L, Gupta M, Han K, et al. Prediction of overall survival or progression free survival by disease control rate at week 8 is independent of ethnicity: Western versus Chinese patients with first‐line non‐small cell lung cancer treated with chemotherapy with or without bevacizumab. J Clin Pharmacol. 2014;54:253‐257. [DOI] [PubMed] [Google Scholar]
- 6. Claret L, Girard P, Hoff PM, et al. Model‐based prediction of phase III overall survival in colorectal cancer on the basis of phase II tumor dynamics. J Clin Oncol. 2009;27:4103‐4108. [DOI] [PubMed] [Google Scholar]
- 7. Claret L, Lu JF, Bruno R, Hsu CP, Hei YJ, Sun YN. Simulations using a drugdisease modeling framework and phase II data predict phase III survival outcome in first‐line nonsmall‐cell lung cancer. Clin Pharmacol Ther. 2012;92:631‐634. [DOI] [PubMed] [Google Scholar]
- 8. Bruno R, Lindbom L, Schaedeli Stark F, et al. Simulations to assess phase II noninferiority trials of different doses of capecitabine in combination with docetaxel for metastatic breast cancer. CPT Pharmacometrics Syst Pharmacol. 2012;1(12):e19. doi: 10.1038/psp.2012.20 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Mietlowski W et al. Survival prediction in everolimus‐treated patients with metastatic renal cell carcinoma incorporating tumor burden response in the RECORD‐1 Trial. Eur Urol. 2012;64:994‐1002. [DOI] [PubMed] [Google Scholar]
- 10. Bruno R, Bottino D, de Alwis DP, et al. Progress and opportunities to advance clinical cancer therapeutics using tumor dynamic models. Clin Cancer Res. 2019;1–9:1787‐1795. doi: 10.1158/1078-0432.ccr-19-0287 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Claret L, Bruno R, Lu JF, Sun YN, Hsu CP. Exploratory modeling and simulation to support development of motesanib in asian patients with non‐small cell lung cancer based on MONET1 study results. Clin Pharmacol Ther. 2014;95:446‐451. [DOI] [PubMed] [Google Scholar]
- 12. Claret L, Gupta M, Han K, et al. Evaluation of tumor‐size response metrics to predict overall survival in Western and Chinese patients with first‐line metastatic colorectal cancer. J Clin Oncol. 2013;31:2110‐2114. [DOI] [PubMed] [Google Scholar]
- 13. Han K, Claret L, Sandler A, das A, Jin J, Bruno R. Modeling and simulation of maintenance treatment in first‐line non‐small cell lung cancer with external validation. BMC Cancer. 2016;16:1‐9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Claret L, Mercier F, Houk BE, Milligan PA, Bruno R. Modeling and simulations relating overall survival to tumor growth inhibition in renal cell carcinoma patients. Cancer Chemother Pharmacol. 2015;76:567‐573. [DOI] [PubMed] [Google Scholar]
- 15. Quartino AL, Claret L, Li J, et al. Evaluation of tumor size metrics to predict survival in advanced gastric cancer. In PAGE 22 Abstr 2812. 2013. Accessed October 2, 2022. https://www.page‐meeting.org/?abstract=2812
- 16. Claret L et al. A model of overall survival predicts treatment outcomes with atezolizumab versus chemotherapy in non–small cell lung cancer based on early tumor kinetics. Clin. Cancer Res. 2018;24:3292 LP‐3298. [DOI] [PubMed] [Google Scholar]
- 17. Savic RM, Karlsson MO. Importance of shrinkage in empirical bayes estimates for diagnostics: problems and solutions. AAPS J. 2009;11:558‐569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Ribba B, Holford N, Mentré F. The use of model‐based tumor‐size metrics to predict survival. Clin Pharmacol Ther. 2014;96:133‐135. [DOI] [PubMed] [Google Scholar]
- 19. Zhang L, Beal SL, Sheiner LB. Simultaneous vs. sequential analysis for population PK/PD data II. Robustness of methods. J Pharmacokinet Pharmacodyn. 2003;30:405‐416. [DOI] [PubMed] [Google Scholar]
- 20. Eisenhauer EA, Therasse P, Bogaerts J, et al. New response evaluation criteria in solid tumours: Revised RECIST guideline (version 1.1). Eur J Cancer. 2009;45:228‐247. [DOI] [PubMed] [Google Scholar]
- 21. Nordgren R, Freiberga S, Ueckert S, Yngman G, Karlsson MO. PsN: an open source toolkit for non‐linear mixed effects modelling. 2016. Accessed October 2, 2022. https://uupharmacometrics.github.io/PsN/
- 22. Tardivon C, Desmée S, Kerioui M, et al. Association between tumor size kinetics and survival in urothelial carcinoma patients treated with atezolizumab: implication for patient's follow‐up. Clin Pharmacol Ther. 2019;106:810‐820. doi: 10.1002/cpt.1450 [DOI] [PubMed] [Google Scholar]
- 23. Desmée S, Mentré F, Veyrat‐Follet C, Guedj J. Nonlinear mixed‐effect models for prostate‐specific antigen kinetics and link with survival in the context of metastatic prostate cancer: a comparison by simulation of two‐stage and joint approaches. AAPS J. 2015;17:691‐699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Blanche P, Proust‐Lima C, Loubère L, Berr C, Dartigues JF, Jacqmin‐Gadda H. Quantifying and comparing dynamic predictive accuracy of joint models for longitudinal marker and time‐to‐event in presence of censoring and competing risks: comparing dynamic predictive accuracy of joint models. Biometrics. 2014;71:102‐113. [DOI] [PubMed] [Google Scholar]
- 25. Beal S, Sheiner L, Boeckmann A, Bauer R. NONMEM 7.4 users guides. ICON plc, Gaithersburg, MD, 1989–2018. Icon Development Solutions. 2018. https://nonmem.iconplc.com/nonmem743/guides [Google Scholar]
- 26. Keizer RJ, Karlsson MO, Hooker A. Modeling and simulation workbench for NONMEM: Tutorial on Pirana, PsN, and Xpose. CPT Pharmacometrics Syst Pharmacol. 2013;2(6):e50. doi: 10.1038/psp.2013.24 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Murphy H, Jaafari H, Dobrovolny HM. Differences in predictions of ODE models of tumor growth: a cautionary example. BMC Cancer. 2016;16:1‐10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Lacroix BD, Friberg LE, Karlsson MO. Evaluation of IPPSE, an alternative method for sequential population PKPD analysis. J Pharmacokinet Pharmacodyn. 2012;39:177‐193. [DOI] [PubMed] [Google Scholar]
- 29. Ratain MJ, Eckhardt SG. Phase II studies of modern drugs directed against new targets: if you are fazed, too, then resist RECIST. J Clin Oncol. 2004;22:4442‐4445. [DOI] [PubMed] [Google Scholar]
- 30. Keizer RJ, ter Heine R, Frymoyer A, Lesko LJ, Mangat R, Goswami S. Model‐informed precision dosing at the bedside: scientific challenges and opportunities. CPT Pharmacometrics Syst Pharmacol. 2018;7:785‐787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Desmée S, Mentré F, Veyrat‐Follet C, Sébastien B, Guedj J. Nonlinear joint models for individual dynamic prediction of risk of death using Hamiltonian Monte Carlo: Application to metastatic prostate cancer. BMC Med Res Methodol. 2017;17:1‐12. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1.
Appendix S1


