Abstract
The function of mammalian cells is largely influenced by their tissue microenvironment. Advances in spatial transcriptomics open the way for studying these important determinants of cellular function by enabling a transcriptome-wide evaluation of gene expression in situ. A critical limitation of the current technologies, however, is that their resolution is limited to niches (spots) of sizes well beyond that of a single cell, thus providing measurements for cell aggregates which may mask critical interactions between neighboring cells of different types. While joint analysis with single-cell RNA-sequencing (scRNA-seq) can be leveraged to alleviate this problem, current analyses are limited to a discrete view of cell type proportion inside every spot. This limitation becomes critical in the common case where, even within a cell type, there is a continuum of cell states that cannot be clearly demarcated but reflects important differences in the way cells function and interact with their surroundings. To address this, we developed Deconvolution of Spatial Transcriptomics profiles using Variational Inference (DestVI), a probabilistic method for multi-resolution analysis for spatial transcriptomics that explicitly models continuous variation within cell types. Using simulations, we demonstrate that DestVI is capable of providing higher resolution compared to the existing methods and that it can estimate gene expression by every cell type inside every spot. We then introduce an automated pipeline that uses DestVI for analysis of single tissue sections and comparison between tissues. We apply this pipeline to study immune crosstalk within lymph nodes following infection and explore the spatial organization of a mouse tumor model. In both cases, we demonstrate that DestVI can provide a high resolution and accurate spatial characterization of the cellular organization of these tissues, and that it is capable of identifying important cell-type-specific changes in gene expression - between different tissue regions or between conditions. DestVI is available as an open-source software package in the scvi-tools codebase (https://scvi-tools.org).
Introduction
Spatial transcriptomics opens up new opportunities to define the organization of cellular niches and crosstalk that modulate cellular function [1]. In particular, this emerging technology helped study the organization of complex tissues such as the mouse brain [2] and the human heart [3]. The research of human pathologies, such as the structure of tumors, is also an important avenue for spatial transcriptomics [4,5] since the tumor microenvironment consists of a rich milieu of cell types and states that are organized in different anatomical niches.
The landscape of experimental assays for performing spatial transcriptomics analyses of tissue sections is diverse, although all assays are data-rich and require automated and quantitative computational analyses. For example, methods based on fluorescence imaging (MERFISH [6], osmFISH [2,6], seqFISH [7]) have near single-transcript resolution. However, these methods rely on cell-segmentation algorithms [8,9]. Additionally, these studies are dependent on pre-selected marker genes and are not genome-wide and hence require imputation of the missing gene to avoid overlooking critical information [10–12]. On the other hand, pseudo-bulk spatial transcriptomic measurements (Slide-Seq [13,14], 10x Visium [15]) are appealing technologies as they provide measurements of the whole transcriptome, although the spatial resolution, in current versions, is limited to cell aggregates (10 microns for Slide-Seq and 55 microns for 10x Visium). Depending on the density of the tissue, a single bead spot of 10x Visium may have a large number of cells, emphasizing the need for deconvolution of spots to obtain a better resolution view of their cellular content.
To overcome this limitation of current leading genome-wide spatial transcriptomics experimental protocols, these datasets are often matched with a single cell RNA-sequencing (scRNA-seq) dataset from the same tissue. The convention for analyzing such pairs of datasets (as implemented by all existing pipelines, including NMFReg [14], RCTD [16], SPOTLight [17], Stereoscope [18], DSTG [19], and cell2location [20]) is to apply a two-step process. First, a dictionary of cell types is inferred from the scRNA-seq data; then, the proportion of each cell type within each spot is estimated using a linear model. This approach has had promising results, in particular when analyzing brain tissue sections in which the diversity of cellular composition is well captured by a discrete view of cell types [21].
However, the aforementioned methods are more challenging to apply in settings where there is no clear way to stratify cells into discrete types or subtypes. This is especially important when cells that belong to the same overall type (e.g., T helper cells) may carry different functions and span a continuum of states (e.g., following different inflammatory signals) [22]. As a way to resolve this fundamental conundrum of single-cell data analysis, current algorithms leave the user with the choice of setting the granularity in which the data is to be analyzed (i.e., number of clusters per broad cell type). However, there are some inherent trade-offs: deeper clustering of the scRNA-seq data provides more granular transcriptomic resolution but makes the deconvolution problem more difficult, and the results potentially less accurate.
In this manuscript, we propose a conceptually different framework. Instead of limiting the analysis to a discrete view of cell types, we propose to also model the variation within each cell type via continuous latent variables. Towards this end, we introduce DEconvolution of Spatial Transcriptomics profiles using Variational Inference (DestVI), a Bayesian model for multi-resolution deconvolution of cell types in spatial transcriptomics data. Much like existing deconvolution methods, DestVI takes as input a scRNA-seq dataset, with annotations and a spatial transcriptomics dataset. Unlike other methods, DestVI learns cell-type-specific profiles and continuous sub-cell-type variations using a conditional deep generative model [23] and recovers the cell-type frequency as well as a cell-type-specific snapshot of the average transcriptional state at every spot. We also propose a post-hoc analysis pipeline, based on auto-correlation and a spatially-aware version of PCA, to highlight the main axes of spatial variation and help guide the downstream analysis. Our pipeline also helps extract molecular signatures that characterize a given tissue section or different areas inside the same tissue using cell-type-specific differential expression.
We used simulations to benchmark DestVI against discrete deconvolution approaches applied to different levels of cell state granularity (i.e., number of clusters per cell type) and show that DestVI significantly outperforms every baseline in terms of imputation of cell-type-specific gene expression. We then showcase the broad usability of DestVI in two very different biological models using 10x Visium measurements. First, we applied DestVI to study the murine lymph node, which is a considerably structured and well-studied secondary lymphoid organ. We report the spatial organization of cell types in this organ at steady-state and study the effects of stimulation with pathogens [24]. DestVI accurately identifies the effects on the spatial and transcriptional organization of monocytes that are activated upon immunization and form immune response niches. We then proceeded to apply DestVI to a mouse tumor model. In this more complex tissue, DestVI delineates the spatial coordinates of main immune cells within the tumor microenvironment (TME). Furthermore, our spatial analysis identified a discrete sub-population of immunosuppressive macrophages, expressing an hypoxia activation signature, within the tumor core [25]. DestVI is implemented in the scvi-tools package [26], and readily available along with accompanying tutorials.
Results
Multi-resolution deconvolution of cell states in spatial transcriptomics data using DestVI
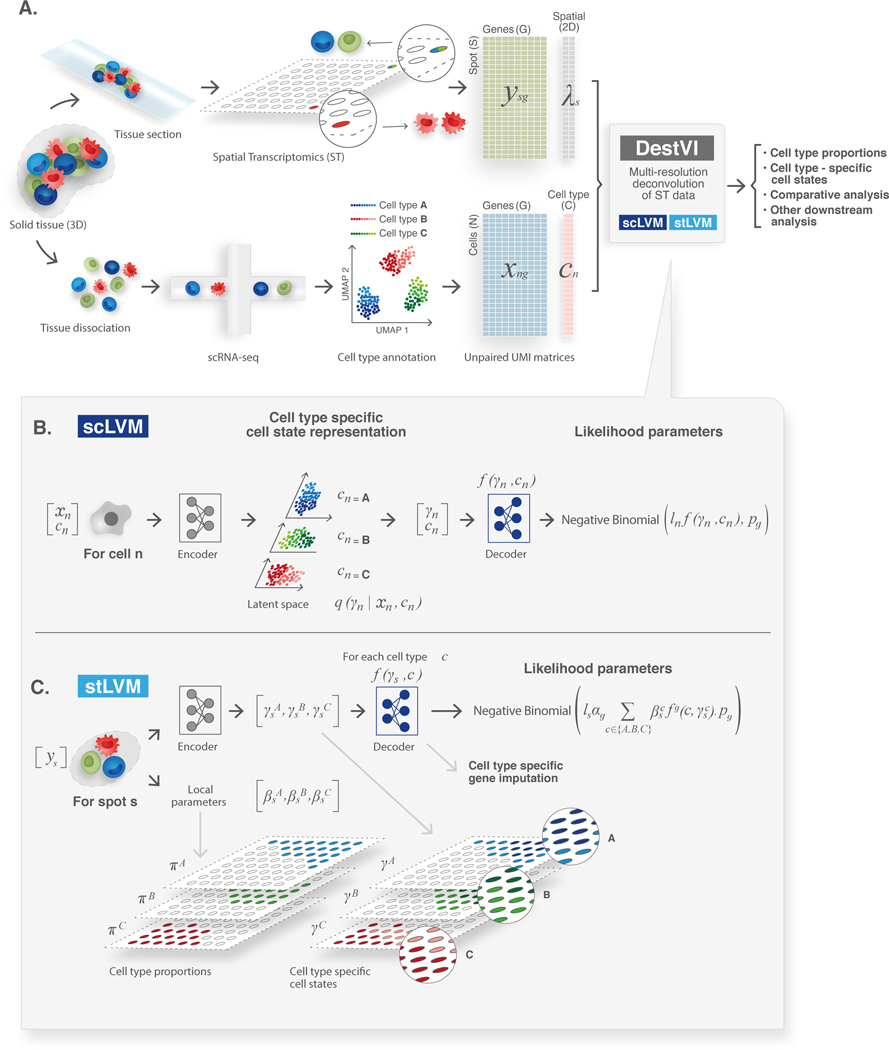
DestVI uses two different latent variable models (LVMs) [27] for delineating cell-type proportions as well as cell-type-specific continuous sub-states. The input for DestVI is a pair of transcriptomics datasets: a query spatial transcriptomics data as well as a reference scRNA-seq data from the same tissue (Figure 1). DestVI assumes that each cell in the reference dataset is annotated with a discrete cell-type label (Online Methods). The output of DestVI consists of two components: first, the expected proportion of cell types for every spot, and second, a continuous estimation of cell-state for every cell type in every spot, which represents an average state for cells of this type in the spot (Figure 1A). This spot-level information may then be used for downstream analysis and formulation of biological hypotheses (described later in this section).
Figure 1: Schematic representation of the ST analysis pipeline with DestVI.
(A) A ST analysis workflow relies on two data modalities, producing unpaired transcriptomic measurements, in the form of count matrices. The ST data measures the gene expression in a given spot , and its location . However, each spot may contain multiple cells. The single cell RNA-sequencing data measures the gene expression in a cell , but the spatial information is lost because of tissue dissociation. After annotation, we may associate each cell with a cell type . These matrices are the input to DestVI, composed of two latent variable models: the single-cell latent variable model (scLVM) and the ST latent variable model (stLVM). DestVI outputs a joint representation of the single-cell data, and the spatial data by estimating the proportion of every cell type in every spot, and projecting the expression of each spot onto cell-type-specific latent spaces. These inferred values may be used for performing downstream analysis such as cell-type-specific DE and comparative analyses of conditions. (B) Schematic of the scLVM. RNA counts and cell type information from the single cell RNA-sequencing data are jointly transformed by an encoder neural network into the parameters of the approximate posterior of , a low-dimensional representation of cell-type-specific cell state. Next, a decoder neural network maps samples from the approximate posterior of along with the cell type information to the parameters of a count distribution for every gene. The superscript notation denotes the -th entry of the vector . (C) Schematic of the stLVM. RNA counts from the ST data are transformed by an encoder neural network into the parameters of the cell-type-specific embeddings . Free parameters encode the abundance of cell type in spot , and may be normalized into CTP (Methods). The decoder from the scLVM model maps cell-type-specific embeddings to estimates of cell-type-specific gene expression. These values are summed across all cell types, weighted by the abundance parameters , to obtain the parameter approximating the gene expression of the spot. After training, the decoder may be used to perform cell-type-specific imputation of gene expression across all spots.
To model the reference scRNA-seq data, the first LVM (scLVM; Figure 1B) of DestVI posits that for each gene and cell the number of observed transcript, , follows a negative binomial distribution, which has been shown to represent the properties of RNA count data [28]. The distribution is parameterized as (), with mean and where is a gene specific parameter determining the mean-variance relationship at every spot. Parameter of the negative binomial depends on the type assigned to the cell (), its overall number of detected molecules (), and a low-dimensional latent vector (here 5 dimensions) which captures the variability within its respective cell type. A neural network maps and to the vector . The gene-specific parameter is optimized using variational Bayesian inference (Online Methods). scLVM is closely related to scVI, our previous work in scRNA-seq modeling strategies [29], although here we aim at capturing transcriptional variation that is cell-type specific. To fit scLVM, DestVI relies on amortized variational inference with deep neural networks [30]. After this procedure, we obtain for every cell a distribution that quantifies the cell state, as well as a measure of its uncertainty (Online Methods).
To model the spatial transcriptomics data, the second LVM (stLVM, Figure 1C) of DestVI posits that for each gene and each spot the number of observed transcripts also follows a negative binomial distribution (as in [18], [20]). The rate parameter of the distribution depends on latent factors that capture technical variation ( - the overall number of molecules detected in the spot and - a multiplicative factor to correct for gene-specific bias between spatial and scRNA-seq measurements) and biological variation, decomposed over cell types. The latter factors come at two levels: is a scalar proportional to the relative part of cells of type inside the spot, and is a low-dimensional vector that estimates the average state of these cells. To ensure this correspondence, stLVM uses the same decoder neural network trained by scLVM - a step that can be interpreted as transfer learning of cell state decoding - from scRNA-seq data to the spatial data. To facilitate the decoupling between the factors that are included in the stLVM model and to further facilitate consistency with the scRNA-seq measurements, we utilize an empirical prior for . This prior is based on the values of inferred for the scRNA-seq data from cell type [31]. To fit stLVM, DestVI relies on an amortized maximum a posteriori (MAP) inference scheme, in which the parameters for the cell-type proportions are kept as free, but the values are tied with a neural network (Online Methods). Finally, in our implementation, the actual cell-type proportions are obtained by normalizing (to sum to one).
DestVI outperforms competing methods for imputing cell-type-specific gene expression on semi-simulated data
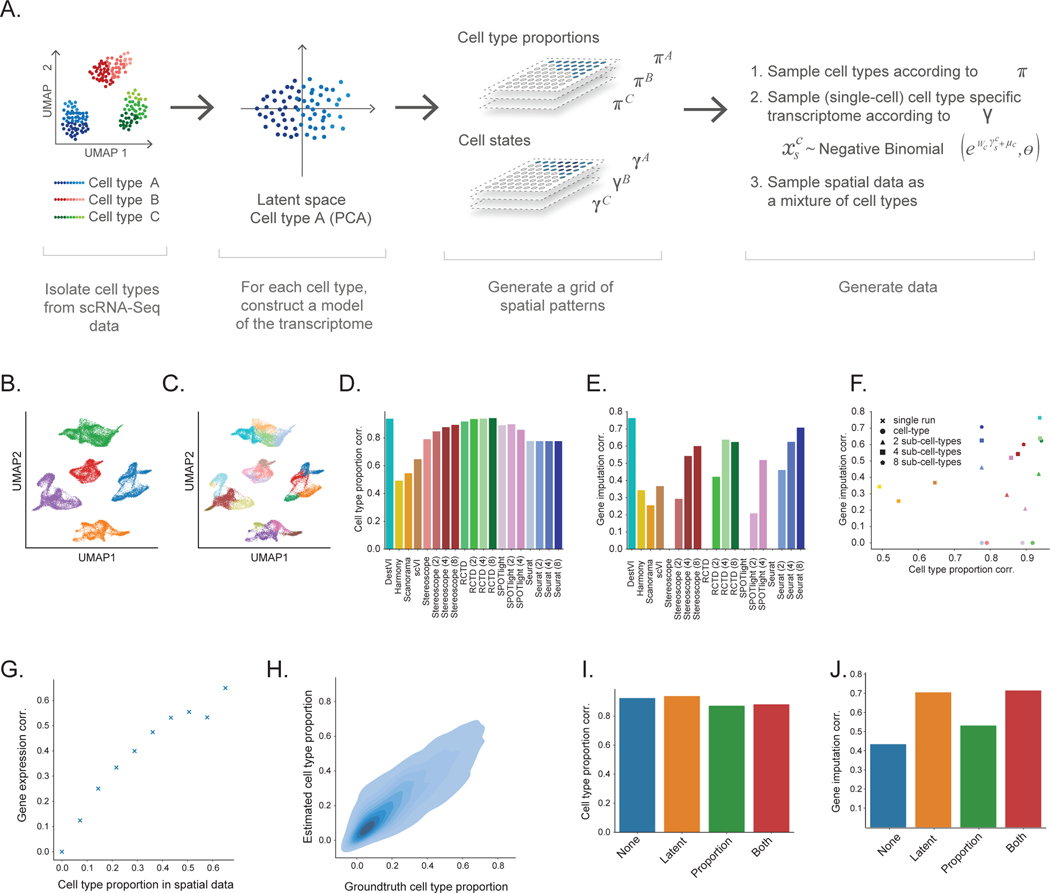
Most benchmarking analyses of deconvolution focus on the ability of a given algorithm to recapitulate the proportion of cell types in every spot. In this setting, it is natural to use a clustered dataset of scRNA-seq data and generate synthetic “spot” measurements by sampling cells from different clusters with a given ground truth proportion. However, to fully assess the performance of DestVI to infer continuous cell states in addition to cell-type proportions, we instead built a more nuanced simulation framework that also accounts for variability within cell types (Figure 2A, Online Methods). In this scheme, each spot is defined by a cell-type proportion, as well as the (continuous) state of cells in every type. To model the continuum of cell states, we construct a linear model for every cell type, with a negative binomial likelihood. The coefficients of these linear models are learned using sparse PCA on a cell-type-annotated scRNA-seq dataset. Using sparse PCA ensures that the simulation is based on a probabilistic model different from the one used in DestVI. We then generate a spatial dataset by sampling, for each spot, its cell-type proportion and the coefficients of the cell state representations. We ensure spatial dependency in this data, by sampling those variables from a Gaussian process. The resulting simulator therefore generates spatial transcriptomics measurements while providing ground truth about cell-type-specific gene expression patterns (Supplementary Figure 1).
Figure 2: Evaluating the performance on DestVI on simulations.
(A) Schematic view of the semi-simulation framework. For each cell type of a scRNA-seq dataset, we learned a continuous model of cell. We sampled spatially-relevant random vectors on a grid to encode the proportion of every cell type in every spot , as well as the cell-type-specific embeddings . Then, we feed those parameters into the learned continuous model to generate ST data (Methods). (B-C) Visualization of the single-cell data, and the cell state labels used for comparison to competing methods (UMAP embeddings of the single-cell data; 32,000 cells). (B) Cells are colored by cell type. (C) Cells are colored by the sub-cell types, obtained via hierarchical clustering (5 clusters). (D-F) Comparison of DestVI to competing algorithms, possibly applied to different clustering resolutions. Performance is not reported for cases that did not terminate by three hours (SPOTLight with 8 sub-clusters; Methods). (D) Spearman correlation of estimated CTP compared to ground truth for all methods. (E) Spearman correlation of estimated cell-type-specific gene expression compared to ground truth, for combinations of spot and cell type for which the proportion is > 0.4 for the parent cluster (not applicable to algorithms run at the coarsest level, as they do not provide cell type proportions at any sub cell type level). (F) Scatter plot of both metrics, that shows the tradeoff reached by all methods. Colors in this panel are in concordance with the ones from panel (E-F). (G-H) Follow-up stress tests for DestVI. (G) Accuracy of imputation, measured via Spearman correlation as a function of the cell-type proportion in a given spot. (H) Head-to-head comparison of estimated cell-type proportion against ground truth across all spots and cell types (8,000 combinations of spot and cell type). (I-J) Ablation studies for the amortization scheme used by DestVI. “None” stands for vanilla MAP inference. “Latent” and “Proportion” refer to only the inference of the latent variables, and only the cell type abundance being amortized with a neural network, respectively. “Both” refers to fully-amortized MAP inference. (I) Spearman correlation of estimated CTP compared to ground truth. (J) Spearman correlation of estimated cell-type-specific gene expression compared to ground truth.
We compared the performance of DestVI to a number of leading benchmark methods. First, we compared DestVI to discrete deconvolution approaches: RCTD [16], SPOTLight [17], Stereoscope [18], and Seurat [32]. We consider the performance of these methods when trained with different levels of sub-clustering (only for algorithms that completed in less than three hours; Figure 2B–C), where the lowest resolution of clustering corresponds to the original cell types, and every subsequent resolution further partitions each type into distinct states. As a sanity check, we inspected the biological variability of gene expression between each subcluster of the same parent cluster (assessed by selecting the top-2 differentially expressed genes between each of the 8 sub cell types and the rest within cell type 0 in scanpy; Supplementary Figure 2). Reassuringly, the DE genes between sub-clusters strongly overlap with the groundtruth variable genes within the parent cell type, as encoded by the sparsity pattern of the coefficient of the linear model (75% of the DE genes reflected expected biological variation in these simulations). Using this range of sub-clustering levels helped explore the tradeoff between the ability to predict cell-type-specific gene expression (additional sub-clustering should be better, up to a certain extent) to the ability to accurately infer cell-type proportions, considering that sub-clustering may interfere with the ability to predict the frequency of the parent cluster. We also benchmarked against a second set of methods: scVI [29], Harmony [33] and Scanorama [34], that can be used to match the spatial measurements to the scRNA-seq measurements via a common embedding. In these approaches, inferences about cell-type proportions or cell-type-specific gene expression are done using k-nearest neighbors imputation (Online Methods).
To evaluate the accuracy of cell-type proportion estimates, we calculated the Spearman correlation between the inferred and ground truth proportions, and reported the average over cell types. We only considered combinations of spot and cell type for which the proportion is sufficiently high (here > 0.4). We also assessed how well each algorithm captures the variation within cell types, by calculating the Spearman correlation between the inferred and ground truth cell-type specific gene expression in every spot (again, reporting the average over all cell types).
Considering the results of cell-type proportion estimation (Figure 2D), we find that the embedding methods have a generally lower performance compared to other methods, specifically designed for deconvolution. This has been already reported (e.g., [20]) and is expected, as these embedding methods (e.g., scVI) do not explicitly consider that spatial spots may include a mixture of cell types. In the deconvolution methods, we find that the impact of the clustering resolution on accuracy is different for different algorithms. For example, performance slightly increases for Stereoscope and RCTD, and slightly decreases for SPOTLight. Seurat has a stable performance across clustering resolutions. Finally, we find that DestVI compares favorably to the other methods, regardless of their sub-clustering resolution during training. Considering the results of cell-type-specific gene imputation (Figure 2E), we notice that overall the performance highly depends on the level of clustering (with the exception of DestVI, that is sub-clustering agnostic). At low sub-clustering resolution, the deconvolution methods have a lower performance compared to the embedding-based ones. At higher resolution (more than four clusters per cell type), the deconvolution methods outperform the embedding-based ones. However, two complications arise when adding more cell states. First, there is a computational burden to adding more cell states for deconvolution. For example, SPOTLight did not terminate after three hours with eight sub-clusters per cell type. Second, the performance is expected to plateau at some clustering level. For example, RCTD’s correlation did not improve using eight sub-clusters compared to four sub-clusters. Since it is hard in practice to estimate the number of sub-clusters, especially in this specific context of deconvolution, this makes the discrete deconvolution approaches less applicable for spatial analysis. DestVI outperforms all methods with this metric and the same results follow using Pearson correlation as well (Supplementary Figure 3).
While our benchmarking analysis thus far considered clustering at different resolutions, the methods we compared against did not take advantage of the hierarchical nature of those clusters (i.e., that each cell type is divided into several clusters). To explore the merit of including this information, we constructed an additional, simple two-step baseline to compare against. The first step consists in locating niches of particular cell types in the tissue, for example by applying a deconvolution method (using the coarsest level of clustering, with one cluster per cell type). Then, we classify the spot of the niche formed by the high-abundance region of the cell type (for every cell type) into sub-cluster identity (at the more granular resolution; 8 clusters per cell type). Briefly, the classifier is a random forest, learned per cell type on the single-cell data to match the transcriptome to one of the eight subclusters. It is applied to the raw counts of every spot of the niche in the spatial data. We report the accuracy of this approach, and compare it to the same classifier applied to the imputed values from DestVI (Supplementary Figure 4). On this benchmark, DestVI’s imputed values are more predictive and achieve higher classification accuracy.
Taken together, these results demonstrate that DestVI provides a compelling alternative to discrete deconvolution algorithms, especially when there are rich continuous patterns of transcriptional variation within cell types, as is the case for most biological models. Specifically, we observe that DestVI demonstrates robust performance in gene expression imputation while still adequately estimating cell-type proportions (Figure 2F). Of note, our analysis was limited to spots in which the cell type in question was sufficiently abundant. As expected, we observe that the ability of DestVI to predict cell-type-specific gene expression decreases in the case of low frequency (Figure 2G). We do observe, however, much less effect on the accuracy of cell-type proportion estimate (Figure 2H). DestVI can therefore provide an internal control for which spots can be taken into account when conducting a cell-type-specific analysis of gene expression or cell state. We leverage this property and propose an automated way of estimating a threshold for the minimal cell-type proportion that is required for such an analysis (Online Methods).
Finally, we also utilized the simulation to benchmark several variants of DestVI (Figure 2I–J). Specifically, we wanted to verify our design choice for the analysis of spatial data in which we keep the parameters for the cell-type proportion free but treat the parameters as a function of the input data (i.e., amortizing inference using an encoder neural network; Online Methods). Towards this end, we assessed the performance of several variants of DestVI, using an encoder neural network for the proportions, parameters , both of them, or none of them. Interestingly, we have noted that using a neural network for the proportions yields lower performance for cell-type proportion estimation compared to keeping free parameters (Figure 2I). Conversely, using a neural network for estimating the embedding variables yields much higher performance for gene expression imputation (Figure 2J). We attribute this phenomenon to the fact that there are many embedding variables to infer (dimension of latent space times number of cell types) per spot, and that using a neural network may regularize the solution as compared to using free parameters.
DestVI outperforms competing methods on a single-cell spatial transcriptomics dataset
Assessing DestVI with real data from technologies such as Visium or Slide-Seq is complicated by the lack of a clear ground truth on the composition of cell types inside every spot and their respective gene expression profiles. An opportunity to conduct such an analysis, however, is afforded by the sci-Space assay [35]. In contrast to other technologies, sci-Space provides transcriptional information that is at a resolution of a single-cell, while the spatial information is on a more coarse level (about 200 microns; i.e., coarser than Visium or Slide-Seq). In that case, we can treat each spatial position as a single 200-micron “spot” (summing the transcriptomes of all the included cells) and provide these as an input to DestVI and the other benchmark methods. At the same time, we still have access to the ground truth (cell type composition and cell type- specific gene expression) inside each of these 200-micron spots, thus allowing quantification of accuracy as in our simulation analysis (Online Methods). Using a dataset of mouse embryo cortex [35], we apply our full battery of tests from the simulation benchmarking, and report our results in Supplementary Figure 5. Overall, for all methods we inspected, the accuracy is lower than what observed in the simulation study (Figure 2). However, consistent with our simulations, we find that DestVI is still the top performing method in this more realistic test.
An automated analysis pipeline with DestVI
The resulting model enables several types of downstream analyses for drawing hypotheses on both the spatial structure of an individual sample as well as the differences amongst pairs of conditions. In the following, we propose a standard pipeline for analysis of a single sample. In the subsequent sections we demonstrate how to use this pipeline to gain insight from a simple sample (a single lymph node, or tumor section) and help guide comparative analysis between samples (between lymph node sections, or distinct areas of a tumor section). The pipeline consists of two parts. In the first part, we consider the data from a resolution of cell types. For each cell type we report its proportion in every spot, and then highlight cell types that tend to occur at specific niches (i.e., not uniformly distributed across the tissue), using Geary’s C autocorrelation statistic for the inferred proportions [36]. The second part of the pipeline facilitates a more in-depth view - looking at variability within cell types, thus going beyond the functionality that is available in current pipelines. We start by selecting, for each type, spots that have a sufficiently high proportion of cells of that type. We propose an automated way of estimating a cell-type-specific threshold for this procedure, but it may be also manually curated. We consider for each cell type different values of the threshold (taken on a grid), and calculate - the respective Geary’s statistics, accounting only for spots with proportion higher than . We then select our threshold to be the inflection point of the resulting curve (Online Methods). With this constrained view, our pipeline proceeds to report the main axes of variation in each cell type, using the spatial data. This analysis helps highlight and visualize the most dominant transcriptional programs in every cell type, as well as exploring their dependence on the cells’ locations. To this end, we developed a weighted PCA scheme that uses the inferred cell states (in the spatial data) and accounts for the inferred cell-type proportions as well as the spatial layout of the spots (following previous work on robust linear dimensionality reduction [37]; Online Methods). We also identify genes that are correlated with each weighted principal component and report enriched gene signatures (using EnrichR [38]) to help with their interpretation.
Our model also provides a natural way to estimate and evaluate the significance of differences between conditions, or between niches in the same tissue section. Specifically, for each cell type we can compare the extent to which cells of a given type tend to co-localize in specific niches, by comparing the respective Geary’s C statistics. On the gene level, we can identify cell-type-specific differential expression, comparing different conditions or different tissue areas. This analysis draws directly from our probabilistic representation of the data, which allows for uncertainty quantification and hypotheses testing (Online Methods).
DestVI identifies a spatially organized lymph node multicellular immune response following pathogen stimulation
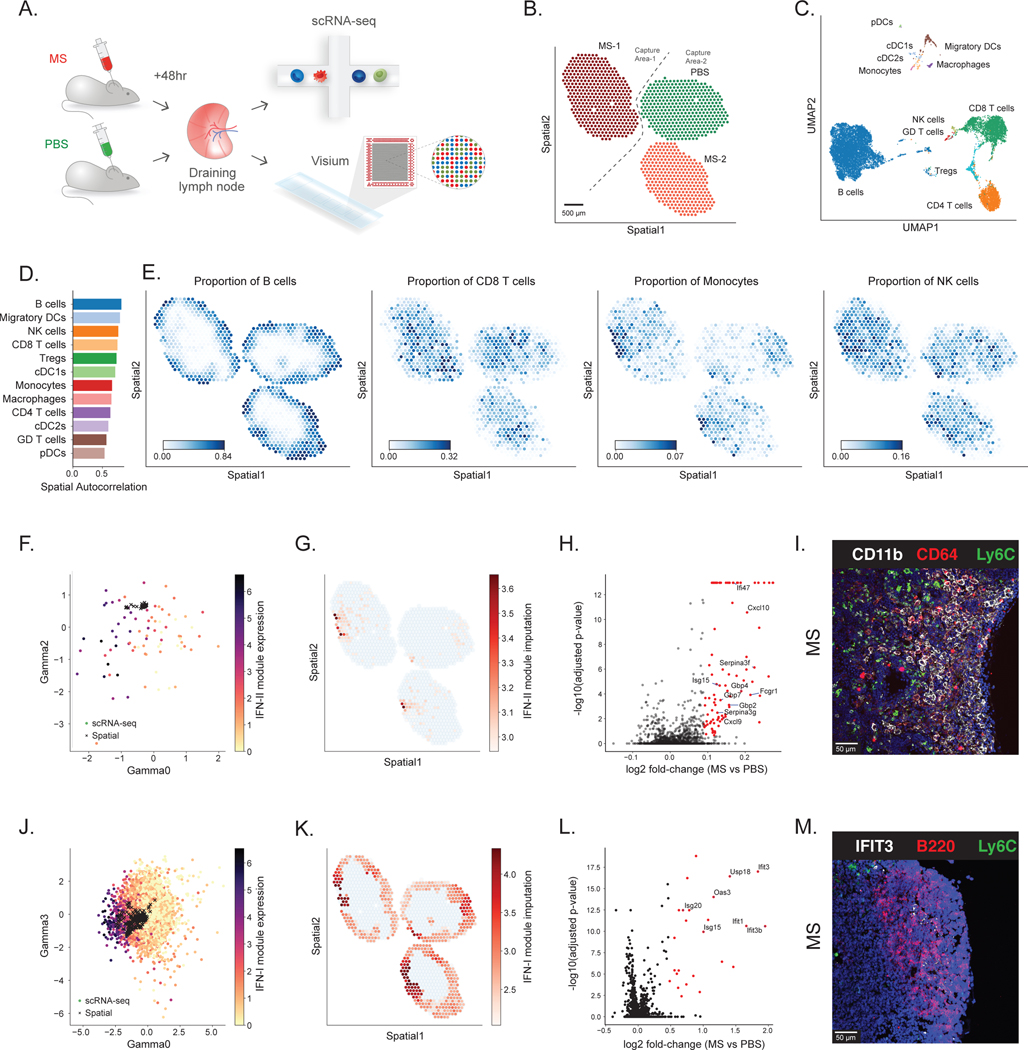
For a first application of DestVI, we aimed to study spatial pattern of antigen-specific immunity and profiled murine auricular lymph nodes following 48 hr stimulation by Mycobacterium smegmatis (MS), a gram-positive bacteria which induces a robust CD4+ T cell response characterized by IFN [24]. For spatial analysis, we used the Visium platform to profile four lymph node sections (two sections stimulated with MS and two sections from control (PBS) injections, processed on two capture areas of the same Visium slide). A matching single cell RNA-seq data set was also obtained for these conditions (Figure 3A; Online Methods).
Figure 3: Application of DestVI to the murine lymph nodes.
(A) Schematics of the experimental pipeline. We processed murine lymph nodes with ST (10x Visium) and single-cell RNA sequencing (10x Chromium) following 48 hr stimulation by Mycobacterium smegmatis (MS) compared with PBS control (two sections from each condition). (B) ST data (1,092 spots; only three sections passed the quality check) (Supplementary Methods). Sample MS-1 and samples PBS / MS-2 were processed on different capture areas of the same Visium gene expression slide. (C) UMAP projection of the scRNA-seq data (14,989 cells). (D) Spatial autocorrelation of the CTP. (E) Spatial distribution of CTP for B cells, CD8 T cells, Monocytes and NK cells, as inferred by DestVI. (F) Embedding of the monocytes (circles; 128 single-cells) alongside the monocytes-abundant spots (crosses; 79 spots). Single-cells are colored by expression of IFN-II genes identified by Hotspot (Fcgr1, Cxcl9 and Cxcl10; Supplementary Figures 12–14). (G) Imputation of monocyte-specific expression of the IFN-II marker genes for the monocytes-abundant spots of the spatial data (log-scale) (H) Monocyte-specific DE analysis between MS and PBS lymph nodes (2,000 genes; 79 spots; total 10,980 samples from the generative model). Red dots designate genes with statistical significance, according to our DE procedure (two-sided Kolmogorov-Smirnov test, adjusted for multiple testing using the Benjamini-Hochberg procedure; Methods). (I) Immunofluorescence imaging from a MS lymph node, staining for CD11b, CD64 and Ly6C in the interfollicular area (IFA). Scale bar, 50 μm. (J) Embedding of the B cells (circles, 8,359 single-cells) alongside the B-cells-abundant spots (crosses, 579 spots). Single-cells are colored by expression of the IFN-I genes identified by Hotspot (Ifit3, Ifit3b, Stat1, Ifit1, Usp18 and Isg15; Supplementary Figures 17–18). (K) Imputation of B cell-specific expression of the IFN-I gene module on the spatial data (log-scale), reported on B-cells-abundant spots. (L) B cell-specific DE analysis between MS and PBS lymph nodes (2,000 genes; 579 spots; 6,160 samples). Red dots designate genes with statistical significance, according to our DE procedure (two-sided Kolmogorov-Smirnov test, adjusted for multiple testing using the Benjamini-Hochberg procedure; Methods). (M) Immunofluorescence imaging from a MS lymph node, staining for IFIT3, B220 and Ly6C in B cell follicle near the inflammatory IFA. Scale bar, 50 μm.
After quality control, we noticed that the number of UMIs per spot in one of the control lymph nodes was significantly lower than the other sections, and discarded this sample from further analysis (Supplementary Figure 6). After spot filtering on the remaining lymph nodes; a total of 400, 369 and 323 spots for the MS-1, MS-2 and PBS lymph nodes were used for analysis with DestVI, respectively (Figure 3B; Online Methods). As a preliminary test for the validity of the information obtained from 10x Visium, we began with a clustering analysis of the raw data using scanpy (Supplementary Figure 7A). We noted the high reproducibility of clusters for the MS conditions, as well as marked differences between the MS- stimulated and control (PBS) tissue sections, characterized by several clusters (Supplementary Figure 7B). The matching single cell RNA-seq data yielded 14,989 cells after quality filtering (Online Methods; Supplementary Table 1). We annotated the scRNA-seq data by transferring cell type information from a publicly available murine lymph node dataset [39] with scANVI [40] and manually curating the annotation of rare cell types (Online Methods). We present this information in a two-dimensional plot of the annotated latent space (Figure 3C, Supplementary Figure 8), as embedded by scVI [29], and laid out by UMAP [41]. We observe a cellular MS specific response including changes in NK and monocytes abundance (Supplementary Figure 9), as previously reported [24].
We applied DestVI in order to explore for each cell type how infection-induced differences in transcriptional states may be associated with changes of spatial organization. The reports that are automatically generated by our analysis pipeline are provided in Supplementary Note 1. These reports helped guide our exploration of the data, and we summarize the resulting main findings in the remainder of this section. Using the first part of our automated pipeline, we began by exploring the spatial distribution of cells from each type (Figure 3D–E; Supplementary Figure 10). As expected, the first striking pattern is the organization of the lymph node sections into the B cell follicles (Cd79a; external area) and a T cell compartment (CD8; internal area) (Figure 3E; Supplementary Figure 11) [42,43]. Interestingly, we find that monocytes also tend to form spatially coherent niches, with a stronger extent of co-localization of the monocyte population in the stimulated lymph node compared to the control (comparing the Geary’s C values of their inferred proportions; Figure 3E; Supplementary Figure 12). This finding is consistent with our previous work, which showed that after immunization with MS, NK cells are recruited to the lymph nodes and produce IFN. This signaling axis further promotes the up-regulation of IFN signaling in monocytes [24]. The spatial data, further identified organized multicellular immune response niches, located between the B cell follicles as shown in Figure 3E and also referred to as the interfollicular area (IFA) [44].
We then explored the inferred spatial organization of cell states within every cell type, a unique feature of our pipeline compared to other algorithms for spatial analysis (Figure 3F–M). Interestingly, we find that the main axes of variation in the monocyte population (using our weighted PCA scheme to co-analyze both modalities) reflect cytokine and chemokine signaling cascades, as well as a robust interferon response (Supplementary Note 1). The importance of interferon signaling as a source of variation in the monocyte population is also apparent in the scRNA-seq data (Supplementary Figures 13–15). We find this through both unsupervised analysis (using Hotspot [45]) and by comparing gene expression of monocytes between MS- stimulated and control lymph nodes (Supplementary Figure 16).
Through joint analysis with DestVI, we can now further contextualize this variation with the location of the monocytes and their unique spatial niche in the lymph node. To this end, we first inspected our inferred low-dimensional representation of cell state and found that it indeed reflects co-variation in the expression of type-II interferon response genes (here, plotting the cells and spots in dimensions 0 and 2 of the 5- dimensional vector; colored by the sum of Fcgr1, Cxcl9 and Cxcl10; Figure 3F). Moving to the tissue coordinates, we found a clear localization of inferred monocyte-specific expression of IFN-II genes in the IFA (Figure 3G). Comparing the two conditions, this visualization suggests that the amount of expression of IFN-II genes in those constrained niches is markedly higher in the MS versus the control LN. In order to more formally identify the differences in expression of monocytes across the two conditions, we performed differential expression (using the values imputed by DestVI) and discovered a rich set of differentially expressed IFN-II response genes, some already used in our signature analysis (e.g., Fcgr1 and Cxcl9), but also other genes (Gpb2, Serpina3g and Ifi47) (Online Methods, Figure 3H, Supplementary Table 2, Supplementary Figure 15). This is consistent with previous findings, where under pathogen immunization monocytes or macrophages carrying antigens migrate to draining lymph nodes through afferent lymphatics to induce immune responses [46–50]. In order to verify this discovery using alternative spatial measurements, we performed immunofluorescence staining of LN from naive and MS treated mice, with CD64 (Fcgr1; a marker we identified with DestVI), CD11b and Ly6C. In line with the results identified by DestVI, we find a higher number of inflammatory monocytes in the MS treated LN localized to the IFA and the peripheral subcapsular sinus (SCS) (Figure 3I, Supplementary Figure 17).
Our results also point to functional heterogeneity within the B cell compartment, with a strong enrichment for type I interferon signaling in the first weighted principal component (Supplementary Note 1). As above, we find that this axis of variation is also captured in the scRNA-seq data (Supplementary Figures 18–20), and thus proceed to explore its spatial properties. First, we find that it is indeed captured by the joint latent representation of cells and spots (dimension 0 of the 5- dimensional vector; colored by Ifit1, Ifit3, Ifit3b, Stat1, Usp18 and Isg15; Figure 3J). We then use the B-cell specific gene expression estimates from DestVI to inspect the spatial organization of this signature (Figure 3K). Interestingly, the module appears to be expressed across all the lymph nodes, but at lower levels in the PBS LN compared to the MS LN. This observation is also supported by differential expression analysis, comparing B cells in the MS vs. the control tissues (Figure 3L, Supplementary Table 3, Supplementary Figure 20). In addition, we investigated the effect of tissue localization on B cells in the MS samples by comparing B cells in each interferon-enriched zone to B cells in the rest of the respective lymph node (Supplementary Table 4, Supplementary Figure 21). In both cases, we noticed a similar strong signature of type I interferon signaling. These observations were further validated by immunofluorescence staining for IFIT3, B220 and Ly6C (Online Methods). We identify IFIT3+B220+ cells on the MS sample in the B cell follicle near the inflammatory IFA (Figure 3M) but not in control samples (Supplementary Figure 22). Applying DestVI to spatial transcriptomics data, we therefore detected the unexpected finding of spatially-enriched interferon reaction in B cells.
In summary, the unique features of our analysis enable robust spatial characterization of cell types and states within naive and pathogen challenged lymph nodes. DestVI identifies a clear and specialized immune niche involving IFN signaling of different cell types, including monocytes and B cells activated by MS infected mice and localized to the peripheral subcapsular sinus and interfollicular area.
DestVI identifies a hypoxic population of macrophages within the tumor core
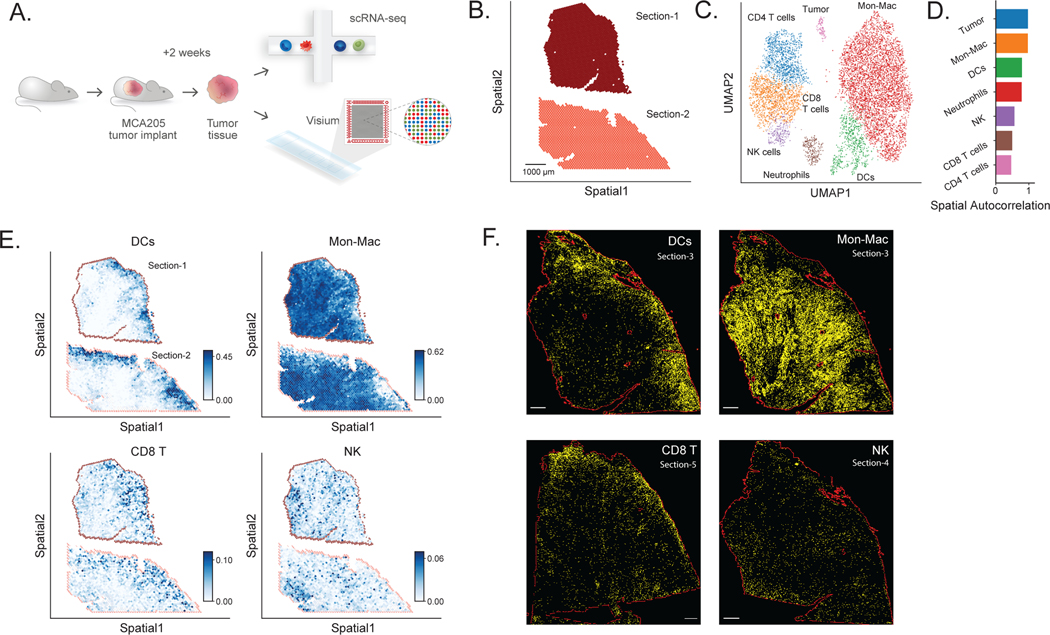
Whie the lymph node generally has a well characterized and reproducible cellular structure, we next applied DestVI for studying a more complex and less structured tissue. Towards this end, we spatially profiled a syngeneic mice tumor model (MCA205) using Visium. MCA205 was derived from 3-methylcholanthrene-induced fibrosarcoma in C57BL/6 mice. MCA205 is a weakly immunogenic fibrosarcoma-derived cell line which is a common model used to study the immune responses to tumors and for developing immunotherapies [51]. Knowledge about the spatial distribution of immune cells transcriptome in MCA205 may benefit drug assessments [52]. Fourteen days after intracutaneous transplantation of MCA205 tumor cells, we have characterized the tumor using scRNA-seq and Visium (Figure 4A; Supplementary Figure 23; Online Methods). A total of 2,125 spots (Section-1) and 1,902 spots (Section-2) were used for analysis with DestVI following quality metrics and filtering (Figure 4B). Along with the Visium data, we also collected cells from a separate MCA205 tumor for single-cell RNA sequencing. After processing and filtering, this dataset comprised a total of 8,051 immune cells and tumor cells (Online Methods; Supplementary Table 5).
Figure 4: Application of DestVI to a MCA205 tumor sample.
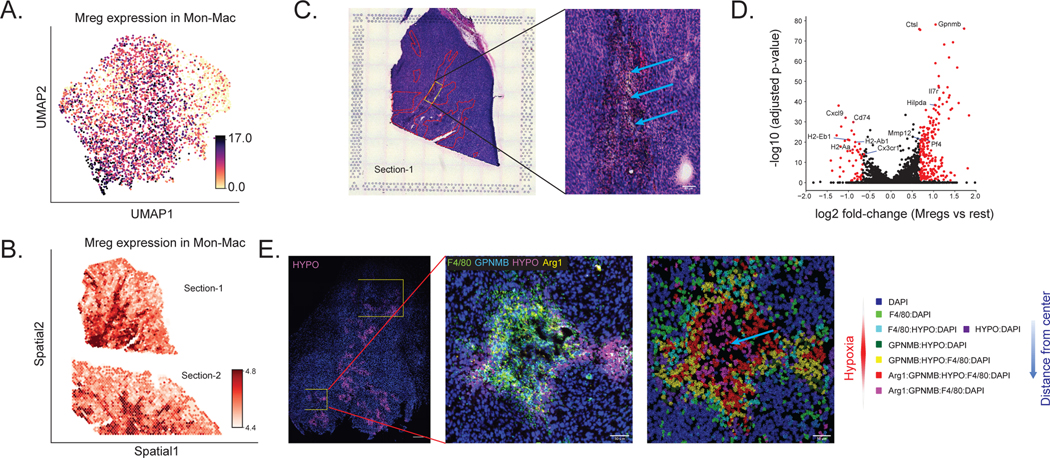
(A) Schematics of the experimental pipeline. We performed ST (10x Visium) and single-cell RNA sequencing (scRNA-seq, single-cell MARS-seq protocol) on MCA205 tumor that contains heterogeneous immune cell populations 14 days after intracutaneous transplantation into the wild-type mouse (two sections). (B) Visualization of the ST data for two MCA205 tumor sections, after quality control (4,027 spots). Scale bar, 1000 μm. The two sections were processed on the different capture areas of the same Visium gene expression slide. (C) UMAP projection of the scRNA-seq data (8,051 cells), embedded by scVI and manually annotated. (D) Spatial autocorrelation of the CTP for every cell type, computed using Hotspot. (E) Spatial distribution of CTP for DCs, monocytes and macrophages (Mon-Mac), CD8 T cells and NK cells. (F) Immunofluorescence imaging from neighboring tumor sections, using antibodies for MHCII+ cells showing for DCs (Section-3, +20 μm from Section-2), F4/80+MHCII− cells showing for Mon-Mac (Section-3, +20 μm from Section-2), TCRb+ cells showing for CD8 T cells (Section-5, +60 μm from Section-2) and NK1.1+ cells showing for NK cells (Section-4, +30 μm from Section-2). All scale bars denote 500 μm. Red solid lines indicate the section boundary. Right side is the MCA205 tumor marginal boundary. The staining marker positive cells are segmented and annotated using QuPath and showing yellow color here with changed brightness and contrast (Supplementary Methods).
We annotated the single cell RNA-seq data by labeling clusters of the latent space from scVI [29] based on marker genes from immune cells (Online Methods). We present this information in a two-dimensional plot of the annotated latent space (Figure 4C), laid out by UMAP [41]. We then explored the spatial distribution of these cell types and states using DestVI. After running DestVI, we applied our post-hoc interpretative pipeline (Online Methods) and reported the whole analysis in Supplementary Note 2. We first inspected the cell-type proportions of the major immune subsets (CD8 T cells, monocytes, macrophages, dendritic cells, and NK cells; Figure 4D–E; remaining cell types in Supplementary Figure 24). In order to validate those results, we performed immunofluorescence staining on three adjacent sections of the same tumor sample (Section-3, Section-4, Section-5; at distances 20, 30 and 60um respectively to Section-2; Supplementary Table 6). We observed that both types of T cells (CD4+, CD8+) were highly abundant on the boundary of the MCA205 tumor. We verified this observation by staining for T cell markers (TCRb) using immunofluorescence on Section-5 (Figure 4F) [53]. Quantification of this signal at different areas of the tissue showed strong correlation of the cell type density compared to the inferred values from the transcriptomics profiles (⍴ = 0.91; Online Methods; Supplementary Figure 25). We also observed that NK cells occupy very specific niches within the MCA205 tumor and tested this spatial property by staining for NK1.1 on Section-4 (Figure 4F). Notably, comparison of the two views (staining, Visium) is challenging because the NK cells occupy specific niches and not a broader region (like the T cells) and because the Visium section is truncated, thus missing NK-enriched areas (out of Visium fiducial frame). However, image quantification based on the intersecting tissue areas (staining, Visium) show a similar pattern of NK cells in DestVI and the immunofluorescence staining (⍴ = 0.94; Supplementary Figure 26). Antigen-presenting DCs also exhibited non-uniform spatial organization, with marked localization at the boundary of the MCA205 tumor (Figure 4D–E), a property we further tested by staining for the MHC-II marker which stains for DC on Section-3 (Figure 4F; ⍴ = 0.87; Supplementary Figure 27). Finally, we noted that monocytes and macrophages (jointly labeled as Mon-Mac in the scRNA-seq data; as there was no clear demarcation in latent space) were present broadly in the MCA205 tumor, with no specific pattern (Figure 4D–E), and we verified this by staining for F4/80 on Section-3 (Figure 4F, ⍴ = 0.75; Supplementary Figure 28). Together, these results suggest that DestVI is able to provide a precise and detailed view of the spatial organization of major immune subsets in the MCA205 tumor.
Since the Mon-Mac population did not have a specific spatial pattern (unlike DCs, NK cells and T cells), we hypothesized that the spatial coordinates may reflect different cell states within the Mon-Mac population. Indeed, using DestVI for analysis of spatial patterns within the Mon-Mac population reveals a stratification of this subset into spatial niches, each with a distinct expression signature (Supplementary Note 2). We therefore proceeded to an in depth analysis of the Mon-Mac populations.
We started by exploring the scRNA-seq data and, using Hotspot, identified several gene expression programs that distinguish different states within the Mon-Mac population (each represented by a different module of co-expressed genes; see Supplementary Figures 29–30). Five of these programs matched our previous findings in independent biological replicates of the same MCA205 tumor system [54]. More precisely, three of the detected modules of co-expressed genes pertain to general monocytes markers and help distinguish a Monocyte (Ace) gene expression program (defined by Ly6c2, Plac8, Ly6a, Ace, Ear2), a Monocyte-DC program characterized by MHC class II genes (H2-Aa, Cd74, H2-Ab1), and a Monocyte (IFN) program characterized by type I interferon signaling (Ifit1, Ifit2, Ifit3, and Isg15; Supplementary Figure 31B–D). Additional two modules define specific tumor-infiltrating myeloid suppressive cell populations [54]. The first module corresponds to tumor associated macrophages (TAM), expressing C1qa, C1qb, C1qc, Ms4a7 and Apoe (Supplementary Figure 31A). The second one corresponds to a regulatory myeloid (Mreg) population discovered previously [54], with expression of Trem2, Gpnmb, Mmp12, and Il7r, as well as markers of hypoxia - Hmox1, and Hilpda (Figure 4G).
To inspect the spatial distribution of these subpopulations, we used DestVI to infer the Mon-Mac specific expression of the corresponding gene modules in our Visium data (Figure 4H; The spatial distribution of other modules is displayed in Supplementary Figure 31E–H). We found that the tumor-infiltrating myeloid suppressive cells (Mreg and TAM) were mostly abundant in the inner layers of the MCA205 tumor, consistent with previous observations in human tumors [55] and murine models [54]. These myeloid cells, which were found to be Arg1+ in other studies (here, Arg1 was not detected in our sequencing data) are associated with poor antitumor response [56]. Interestingly, of the two tumor-infiltrating myeloid populations, we found a marked localization of the Mreg cells (Figure 4H; Supplementary Figure 32). To explore the meaning of this pattern, we first used DestVI to look for genes that are differentially expressed in the Mreg enriched areas vs. the rest of the tumor using, and identified markers consistent with our single-cell data, and our previous study, including Ctsl, Il7r and Hilpda [54] (Figure 4J, Supplementary Table 7). To understand the nature of this hypoxia niche, we overlapped the location of those cells onto the H&E staining (Figure 4I) and noticed that they strongly correspond to perinecrotic areas of the MCA205 tumor [57–59]. This observation is also consistent with previous work, as cells with similar phenotypes have been observed to congregate in hypoxic tissue niches (cancerous [60] and non-cancerous [61]).
We then proceeded to validate the localization of the Mreg cells with multiplexed immunofluorescence staining in additional MCA205 tumor samples (n=12) (Online Methods), measuring the abundance of macrophage and Mreg markers; F4/80, Arg1, GPNMB, as well as a specific probe for hypoxic regions (Hypoxyprobe; Online Methods). Image processing and quantification of these factors helped identify specific phenotypes of macrophages in the MCA205 tumor (results for a specific section in Figure 4K). The Hypoxyprobe positive staining (Hypoxia) helped identify a clear hypoxic pattern in the MCA205 tumor, for which necrotic core areas are consistently surrounded by the hypoxic probe labeled areas. Additional staining of F4/80, GPNMB and Arg1 showed that F4/80+GPNMB+HYPO+ cells and F4/80+GPNMB+Arg1+HYPO+ cells are enriched in hypoxic regions and in perinecrotic areas.
In summary, DestVI correctly maps cell types of immune cells onto the spot coordinates and identifies a clear and specialized niche involving metabolic changes in response to hypoxia within the macrophage population. Our further experimental validation also suggests that DestVI could be an reliable tool for exploring complex cell-type specific phenotypic changes in different tumor models under immunotherapy treatments.
Discussion
We introduce DestVI, a multi-resolution approach to deconvolution of spatial transcriptomics profiles using an auxiliary single-cell RNA sequencing dataset. Via simulations, we show that classical deconvolution approaches that are based on clustering the scRNA-seq data may be difficult to apply and miss important information in the case of marked variation within cell types. DestVI circumvents this problem by learning cell-type-specific latent variables on the scRNA-seq data, using a deep generative model, and mapping those latent variables onto the spatial data. Coupled to the automated pipeline we developed, DestVI is capable of interpretable analyses to compare the within-cell-type gene expression levels across different conditions, or different niches of the same tissue section.
Throughout this manuscript, we have employed a fixed set of hyperparameters for DestVI. For example, we used five latent variables for the cell-type-specific cell states , and two for the number of hidden layers in the decoder neural networks. The number of latent dimensions was originally motivated by the hypothesis that if ten dimensions were sufficient to discriminate cell types with scVI, then less should be enough to describe intra-cell-type variation. Importantly, excess dimensions could result in overfitting during the deconvolution step. Similarly, the number of hidden layers was defined by early work. We noticed that with a single hidden layer, cells from different types were not mixing in latent space. This may not be suitable as there may not be information shared across types (e.g., induction of interferon specific response genes). Similarly, too many layers could result in overfitting. We investigated the performance of variants of DestVI for other values of our hyperparameters, on our set of simulations from Figure 2 (Supplementary Figure 33). It appears that the performance of the method is overall stable with respect to the number of dimensions, and the number of hidden layers, although two hidden layers seems to significantly outperform other choices.
An important feature of our work is the ability to perform cell-type-specific differential expression in the spatial data. The methodology of differential expression analysis in this work has two steps. First, we generate gene expression profiles from a specific cell type in two sets of spots, using the point estimates of the cell-type-specific cell states provided by our MAP inference procedure (possibly sampling multiple times from the normalized mean of the negative binomial; refer to Online Methods). Second, we use these values for calculating the log-fold change, as well as for hypothesis testing via a two-sample Kolmogorov–Smirnov test, and correct for multiple hypothesis testing (Online Methods). Although this scheme is simple, and is helpful to identify molecular response in individual cell types, it has several limitations that we outline here. First, utilizing a frequentist test on samples from a generative model is not elegant and may cause inflation of significance levels. Indeed, a given gene in differential expression analysis may have a lower p-value when more samples are drawn from the generative model (the number of samples from the generative model is systematically reported in the figure legends). However, this may not be a desirable scenario because those samples are generated in-silico, and do not represent a new datapoint. A more principled approach, and a subject for future work, is to apply variational inference to estimate the uncertainty around the measurements. This uncertainty may then be incorporated in the hypothesis testing procedure, providing a fully-Bayesian treatment of the differential expression analysis, as in our previous work [62,63]. Second, the signal captured by our differential expression analysis is mainly restricted to cell state variations that are present in the single-cell RNA sequencing data. Indeed, the raw spatial data is used only to calculate local estimates (i.e., imputation per spot) of cell type specific state , but these estimates are then input to the scLVM decoder. As a consequence, our approach may perform poorly at identifying genes that are acting independently from other genes, but that have a high spatial coherence. A compelling avenue for successfully identifying such genes during differential expression with DestVI is to rely on a weighted average of the local parameters estimated by the generative model and the real data, instead of using only the imputed values. This idea was introduced in the context of scRNA-seq imputation by the SAVER-X method, in which an autoencoder alongside the high-dimensional expression data is used to perform accurate data imputation [64]. We are envisioning extensions of DestVI to also make use of the raw count data differential expression module.
Although deconvolution of spatial transcriptomics data has recently received considerable attention, none of the methods benchmarked in this manuscript (including DestVI) make explicit use of the spatial coordinates during inference (e.g., inference of cell type proportions in a given spot should be influenced by its nearby spot). A plethora of computational techniques, based on black-box inference techniques [65,66] for Gaussian processes [67] is likely to make this possible. However, the level of technical development to achieve this may not be reasonable, because the parameters studied in this work (cell-type abundance) may not be spatially smooth (e.g., neighboring spots may be very different) for some tissues, such as the tumor. Consequently, we developed a simpler modification of DestVI that takes into account enforces smoothness of the cell-type abundance parameters over the spatial coordinates with a spatially-aware penalization based on a quadratic cost (the scaling factor can be set via cross-validation, holding out parts of the transcriptome). This promotes neighboring spots to have similar cell-type abundance, and improves the results on the simulations (Supplementary Note 3).
As for applying classical deconvolution algorithms, several practical considerations are necessary for a successful analysis with DestVI, especially with respect to the preparation of the scRNA-seq data. Although general guidance appears in a recent review on integration of spatial transcriptomics and scRNA-seq data [68], we provide here supplementary advice that is more specific to DestVI. A first point for discussion pertains to the clustering of the scRNA-seq data. Similarly to classical deconvolution methods, and as described in [68], we carefully identified cell types based on a semi-supervised pipeline for the lymph node data, and an unsupervised pipeline for the tumor data. We checked those labels based on the expression of marker genes, and potentially corrected them by merging clusters. A natural question is what is the level of resolution for clustering that is most adapted to analysis with DestVI. Throughout the paper, we followed two basic principles. First, DestVI assumes that cells of a given type that co-exists in the same spot tend to have a similar state. Therefore, different cellular states of the same type that tend to co-localize should be annotated separately in the reference scRNA-seq data. Second, when there is no clear demarcation of cells into groups (as in the case with continuous sources of variation), the clustering problem tends to be difficult and ambiguous. Therefore, we purposely stop at a resolution where cells cannot be easily demarcated by clusters. These two basic principles help selecting a clustering that is most informative for using DestVI. A second important point pertains to the size of the single-cell data, and the number of cells per cluster. Existing algorithms set a hard threshold on the number of cells per cell type used for deconvolution. For example, the Stereoscope method filters out cell types with less than 25 cells. This number should be a lower bound for the application of DestVI as well, because the algorithm attempts to learn a full model of intra-cell type variation, instead of just estimating the average transcriptome of the cell type. However, we have demonstrated the performance of DestVI in accurately identifying the monocyte response to MS (Figure 3), with monocyte being a rare cell type (79 out of 14,952 cells; i.e., 0.52% of cells in the scRNA-seq dataset). Therefore, we would recommend having around 100 cells per type for analysis with DestVI. A last point for discussion pertains to the library size of the scRNA-seq data. For the lymph node data, the scRNA-seq data was collected using Chromium, and the median library size was 5,867 UMIs. The MCA205 tumor was profiled using MARS-Seq (median library size: 3,469 UMIs). In general, we suggest that users of DestVI prepare their single-cell RNA sequencing data according to power analysis tools [69].
Integrating spatial transcriptomics with single-cell RNA sequencing data is compelling, as it provides a way to increase the resolution of the former, while providing more insight about the variability that is observed in the latter. However, there are several sources of mismatch between the two modalities that may lead to decreased performance. A first source of mismatch, also mentioned in [68], consists in discrepancies of cell types captured by each assay. A general strategy we recommend is to always perform a new run of scRNA-seq data for deconvolution, but it is not always enough. For example, rare cell types may not be properly captured by scRNA-seq if not enough cells are sequenced. This is the case for the tumor data, in which most of the cells are tumor cells. To circumvent this issue, we used gating strategies for enriching a known panel of interesting immune cells.
A related question is the effect of missing cell types - namely cell types that are present in the spatial data but not in the reference scRNA-seq data or vice versa. To test this, we have added two additional cell types and studied the change of performance of several methods (DestVI, RCTD and Stereoscope), as in Figure 2. Then, we proceeded to remove one cell type from the scRNA-seq data only and to the spatial data only, separately (Online Methods). We assessed the performance of the methods on the remaining cell types (Supplementary Figure 34). On all those tests, the performance of every method does not vary much and DestVI performs as well or better than alternative methods. A second possible source of mismatch is the gene set used for deconvolution. As designed, DestVI (but also RCTD, Stereoscope, scVI and most other methods for data integration) rely on a common gene set between scRNA-seq and spatial transcriptomics. However, depending on the respective technologies used in either assay, there can be important discrepancies in gene capture, making it difficult for the intersection gene set to capture all the subtle variations in gene expression. A potentially promising and flexible approach would be to learn an embedding of the genes, for example using the embedded topic model [70], so that the method could handle missing genes in either assay.
Despite the conceptual advantage of modeling continuous transcriptomic variation within cell types, one might wonder its impact on the hypotheses described in this manuscript. In other words, could we have gained the same biological insights with classical deconvolution approaches? To answer this question, we focus on the interferon response from the monocytes population in MS versus PBS lymph nodes (Figure 3GH), as it was already characterized in our previous work [24]. We apply RCTD as well as Stereoscope to the same dataset, with different levels of resolution for the clustering of the single-cell data (2, 4 and 8 clusters per cell type). As an attempt to reproduce our results in Figure 3, we proceed to deconvolution, imputation of monocyte-specific gene expression, and then differential expression of MS versus PBS (Supplementary Figure 35 for RCTD, Supplementary Figure 36 for Stereoscope). Although both of RCTD and Stereoscope correctly identify the location of basic cell types (B cells, T cells and monocytes, Supplementary Figure 35ABC and 36ABC), the imputation of the monocyte-specific gene expression of IFN marker genes qualitatively show no difference between MS and PBS lymph nodes for every clustering resolution (Supplementary Figure 35DEF and 36DEF). Additionally, we applied a t-test to the normalized imputed gene expression for differential expression analysis between MS and PBS (Supplementary Figure 35GHI and 36GHI). For almost all combinations of levels of clustering for the scRNA-seq, and deconvolution methods, none of the markers identified in our previous scRNA-seq analysis (and DestVI) were differentially expressed. One notable exception is RCTD with 8 clusters per cell type that identifies one single marker (Cxcl10) out of the eleven. Enrichment analysis of those DE genes reveals a signal pertaining to immunity, but not associated with monocytes (IL2 and IL12 signalling). In order to provide a more quantitative analysis, we have assessed the correlation of the estimated log-fold changes to our previous differential expression analysis (Figure 3G of [24]). With respect to both of the Spearman and the Kendall correlation metrics, we show drastic improvement over the other methods (Supplementary Figure 37). All in all, those results suggest that only DestVI could have identified the interferon response in the monocytes between MS and PBS lymph nodes.
Both of the case studies described in this manuscript focus on spatial transcriptomics measurement captured by the commercial 10x Visium protocol. This technology has typically low spatial resolution (55 microns diameter per spot), compared to emerging technologies such as Slide-Seq v2 [13] (10 microns), HDST [71] (2 microns) and Seq-Scope [72], that can map RNA transcripts at the sub-micrometer resolution. With the development of such high-resolution spatial transcriptomics profiling methods, one might wonder about the utility of the DestVI pipeline for these new datasets. Notably, most of those high-resolution methods cannot guarantee perfect spatial delineation of single cells and for this reason can make data analysis challenging.
To illustrate this, we use a recent dataset of liver tissue profiled with the Seq-Scope technology. The transcriptomic data was aggregated at two different levels of resolution, each then analyzed with a classical pipeline of scRNA-seq data analysis. First, a segmentation algorithm is run on the H&E staining in order to define cell boundaries. This analysis is suitable to the study of hepatocyte zonation, but that delineation of individual cells does not capture other cell types such as endothelial cells or macrophages, that are much smaller than, and in between hepatocytes. Therefore, a second strategy was used by taking a fixed 10 microns size grid, treating each as a unit for downstream analysis with Seurat (Supplementary Figure 38A). It is important to note however, that each of these units does not necessarily correspond to one unique cell, and may include RNA captured from multiple cells. We therefore ran the DestVI pipeline on this form of the data, using the liver cells from the Tabula Muris Senis as scRNA-seq reference [73] (Online Methods). According to the original study, the tissue is mostly composed of hepatocytes (Supplementary Figure 38B). Similarly, the proportions of macrophages and endothelial suggests that the non-parenchymal cell populations are present in small and fragmented areas throughout the tissue (Supplementary Figure 38CD). However, DestVI estimated the non-parenchymal cell populations to be more abundant than originally estimated (Supplementary Figure 38E). Notably, the average estimates of proportion from DestVI (around 71% hepatocytes, 13% macrophages and 16% endothelial cells) better agree with the literature (around 60–70% hepatocytes, and even proportions of macrophages and endothelial cells) [74–76] compared to estimates with no deconvolution (95%, 2.5%, and 2.5%; using Seurat). This discrepancy suggests that deconvolution methods are able to provide more accurate information than a single-cell workflow. We therefore further inspected the distribution of cell type proportions predicted by DestVI. Focusing on macrophages, we found that a significant proportion of spots that had an expression of the Kupffer cell marker Clec4f were identified as including macrophages by DestVI and not by the no-deconvolution pipeline (Supplementary Figure 38F). Conversely, cells that did not include this marker and were not identified as macrophages by the no-deconvolution pipeline were also not called by DestVI, implying that DestVI increased the sensitivity of macrophage identification. Turning to hepatocytes, we used DestVI to explore how hepatocyte-specific gene expression pertains to liver zonation [77]. DestVI accurately recapitulates the difference between the central region and the portal region, without having to rely on a different segmentation of the tissue (Supplementary Figure 38GH). To further assess the performance of DestVI in this regime, we modified our simulation scheme to reduce the number of cell types per spot, and to reduce the library size of the spatial data (Online Methods). We apply DestVI, RCTD and Stereoscope on this new dataset (Supplementary Figure 39), and notice that DestVI still performs favorably.
Spatial transcriptomics is a promising approach for unravelling cell-cell interactions [78] and other forms of cellular communication and function in a tissue [79]. We expect that approaches such as DestVI will provide the necessary level of resolution and help further our understanding of the local signaling environments and how they impact cell functions and spatial cues, such as interaction between specific cellular subsets, chemical gradients and metabolic cross talk.
Online Methods
Model of single-cell RNA sequencing data
Assumption and model for the single-cell data (scLVM)
Let designate a cell in the scRNA-seq dataset. We assume that each cell is annotated with cell-type label , but those labels are broad enough such that the introduction of continuous covariates into the model helps explain additional variance in gene expression (i.e., within-cell-type variation). For example, represents a discrete cell type (e.g., B cells or CD8 T cells) while is a continuous vector summarizing a sub-cell state of interest (e.g., B cell activation, CD8 T cell exhaustion).
In the following, we assume that is observed (e.g., obtained via clustering) and that , however, is unobserved and treated as a latent variable. We posit the following generative model for our data:
where is the library size of cell is a two-layers neural network and is a -dimensional vector. takes as input the concatenation of the one-hot encoding of , as well as the scalar , and outputs a -dimensional vector. has a softplus non-linearity at its output to ensure positivity.
This generative model has significant overlap with our previous proposed method single-cell Variational Inference (scVI [29]), which is also a conditional deep generative model. On top of the conceptual difference that scVI conditions on the batch identifier, whereas scLVM conditions on the cell-type information, there are several technical points in which these two models differ. First, we use the standard parametrization for the negative binomial distribution: the number of successful independent and identical Bernoulli trials before failures are achieved, in which is the probability of failure of each Bernoulli trial. This is in contrast with scVI that relies on the mean-dispersion parameterization for the negative binomial distribution, and is necessary to make the definition of the spot gene expression level as the sum of contributions from individual cells correct (as emphasized in [18]). Furthermore, changes were required to the neural network architecture for the transfer learning to work adequately. Indeed, we found that using a decoder with randomness such as dropout [80] or with running parameters as in batch normalization [81] did not work, so we replaced those with layer normalization [82].
Variational inference
We use auto-encoding variational Bayes [30] to optimize the marginal conditional likelihood . We use a mean-field Gaussian variational distribution , parameterized by a two-layer neural network . This neural network takes as input the concatenation of the gene expression vector as well as the one-hot encoding of the cell-type label, and outputs the mean and the variance of the variational distribution for . We optimize the evidence lower bound:
where denotes the prior likelihood for . For this, we subsample the observations in mini-batches and we sample from the variational distribution using the reparameterization trick. Additionally, we reweight cells by their inverse cell-type proportion (capped with a minimal proportion of 5%). We have found this to be an effective method for learning a better representation of the lowly abundant cell types (e.g., monocytes in the lymph node).
Model of spatial transcriptomics data
Assumption for the spatial data
In the spatial data, we assume that the gene expression of each spot is the combination of multiple cells, each potentially being from different cell types. A standard modeling assumption is that a spot has for expression the sum of individual cells [16,18]. Similarly, let us assume each spot has cells, and that each cell in spot is generated from latent variables . We then have a distribution of gene expression:
with is a spot specific scaling factor and is a correction term for the difference in experimental assays. From the standard property of the rate-shape parameterization of the negative binomial distribution, the distribution of the total gene expression in spot and gene is:
We now assume that all the cells from a given cell type in a given spot must all be generated from the same covariate . Instead of determining the cell identity of all individual cells in the spot, we focus on determining the density into broad cell types, as well as the archetype of the sub-cell state, which is a simpler problem. More concretely, we assume that there cannot be both significantly different cell states of the same cell types within a radius of 50 microns (i.e., a spot).
Generative model
These points in mind, we parameterize the sum in the previous equation to be over cell types. We obtain the following generative process:
where and denote respectively the decoder network and the rate parameter of the negative binomial, transferred from scLVM. The gene-specific multiplicative factor explicitly controls for discrepancies between the technologies. Parameters are positive, and designate the abundance of every cell type in every spot. These parameters may be normalized per spot to return an estimate of the cell-type proportion. In our implementation, we also add a constant term that serves as an unknown cell-type, as in [18].
An important technical component of DestVI is the empirical prior we use for the per-spot per cell type latent variable. Indeed, the model is susceptible to factor technology discrepancies into the latent space instead of the multiplicative factor if an informative prior is not used and we noticed this pathological behavior with an isotropic normal prior. Consequently, we designed an empirical prior based on the single-cell data, for each cell type :
where designates a set of cells from cell type in the scRNA-seq dataset, and designates the variational distribution from the single-cell latent variable model. In another context, this prior over is referred to as a variational aggregated mixture of posteriors (VampPrior, [31]). However, the objective here is simply to use the points as a more informative prior for deconvolution, the VampPrior method seeks to learn a multi-modal, more complex prior in order to better fit the data.
MAP inference
We infer point estimates for random variables and for parameters using a penalized likelihood method. In addition to vanilla MAP inference, we introduced two key ideas that stabilized the performance of DestVI. First, we added to the likelihood a variance penalty for the parameter , calculated across all the genes. This strategy was applied previously by ZINB-WaVE to regularize estimates of dispersion parameters in their likelihood-based matrix factorization of single-cell data [83]. Second, compared to a standard deconvolution model that has exactly parameters per spot, stLVM has parameters and latent variables per spot, where denotes the dimension of the latent space learned by scLVM. In order to avoid overfitting, we therefore proposed to use a neural network to parameterize the latent variables as a function of the input data (as in auto-encoding variational Bayes). Namely, we proposed several variants of the algorithm in which either both, part of or none of and may be parameterized by neural networks. Intuitively, the use of a neural network for inference of may be helpful whenever there are shared transcriptomics profiles across cell types (such as inflammatory signals). In addition, we optionally incorporated a sparsity prior for the cell type abundance per spot for settings where we expect the presence of very few cell types per spot. This penalty is enforced for the high-resolution liver data analysis, as well as the Sci-Space data. Because we may not easily perform classical cross-validation in our inference scenario, we manually increased the regularization strength by a constant factor until the abundance was mostly zero for most cell types. These points in mind, the objective function to train this generative model is simply composed of (i) the negative binomial likelihood (ii) the likelihood of the empirical prior (iii) the variance penalization for and (iv; optionally) the sparsity prior for the cell type abundance.
Simulations and data generative process
The benchmarking of spatial deconvolution methods often relies on using a single-cell RNA sequencing dataset with cell-type annotation, and aggregating multiple cells into a pseudo-bulk using a ground truth proportion. The algorithms are then evaluated on the prediction of the cell-type proportions [18]. This approach is not entirely adequate to our setting, as we would like to assess imputation of cell-type-specific variations of the transcriptome that are lost when combining together random cells of a given cluster. Instead, we used a real dataset of scRNA-sequencing data to simulate paired spatial and single-cell transcriptomics data. This helps properly benchmark our method against existing deconvolution methods.
Learning cell-type-specific transcriptomic modules from single-cell data
We propose to build a simulation process for generating single-cell data, and learn its parameters from real data. Concretely, the goal is an algorithm for sampling gene expression counts of a single cell. We let the distribution that governs these counts be a function of the cell’s type , as well as a low-dimensional embedding . The intuition behind this design choice is to have clear differences of transcriptome from one cell type to another, but continuous variations of cellular states within a type. A similar approach was taken in the design of the Simsym simulator for scRNA-seq data [84].
As a model for the counts, we propose to map the low-dimensional embedding to the gene expression space using a negative binomial generalized linear model for every cell type :
where describes a cell type specific offset of gene expression, and is a linear map. This is a simplification of Simsym that relies on a Beta-Poisson likelihood model. However, the negative binomial has been shown to perform well in modeling scRNA-seq data [28,85]. We learned the parameters , and based on the lymph node scRNA-seq dataset of this manuscript. Out of all the cells, we kept five cell types: B cells, CD4 T cells, CD8 T cells, migratory DCs and Tregs. Those cell types were selected because they were the most abundant in the dataset.
Although approximate inference of these parameters is in principle possible, for example using maximum likelihood as in ZINB-WaVE [83], we wanted to enforce sparsity on the gene loading matrix motivated by the idea that only a subset of the genes contribute to the variation of gene expression within a unique cell type. Also, sparsity seemed necessary because for some cell types, the number of cells was much lower than the number of genes (e.g., around cells for the regulatory T cells and genes). Consequently, we learned patterns of transcriptomic variation within each cell type using a sparse PCA model, on log-normalized data [86]. The counts were normalized using scanpy [87] with a target count of 10,000 UMIs and the sparse PCA model was fit using sklearn [88], using four components and a Lagrange multiplier of 5 for the penalty. The output of this procedure is a cell-type-specific embedding for every cell , a mean expression profile for every cell type , and a dictionary of within cell-type transcriptomic variation . The dispersion parameter for every gene is estimated from the data using scVI [29].
Generating spatial maps of transcriptome
To build the spatial transcriptomics data, we first constructed a regular grid of dimension . Each spot (i.e., point on the grid) is associated with spatial coordinates . For the cell-type proportions , we built a covariance matrix based on the spatial coordinates:
where denotes the median distance between all pairs of points in the grid. The parameter controls the level of spatial smoothness of the stochastic process and is fixed to . This kernel matrix may be used to sample independent draws from a Gaussian process:
and interpret them as an energy to derive cell-type proportions at every spot:
where is a temperature parameter, set to . Large would correspond to all proportions to be equal to 20%, while small would tend to make the proportions binary. Regarding the embedding variables for every cell type , we treat them as independent draw from the same kernel.
For every spot , we sample a fixed number of cells . For every single-cell, we decide on its cell-type based on a draw from the categorical distribution parameterized by the proportions . We then use the previously introduced simulation model to generate the transcriptome of that cell (of cell type and embedding ). In our simulation, the scRNA-seq dataset has cells per spot. Finally, for every spot, we average the mean parameter of the negative binomial distribution across all cells and we sample from the same observation model.
Comparison to competing methods
Our major claim is that DestVI is able to infer cell-type proportions but also to detect within cell-type transcriptomic variations in the spatial transcriptomics data. Although cell-type proportion estimation methods are reasonably simple to benchmark based on simulations, there is more ambiguity with respect to the second task. We provide a robust evaluation of the performance of algorithms at identifying continuous cell states within each cell type, based on cell-type-specific gene expression imputation.
We therefore provided a slight modification of every algorithm so that it may be used to impute gene expression at a given cell type and a given spot . For example, DestVI directly performs this task by accessing the inferred variable and decoding as , which serves as an unnormalized gene expression. For algorithms based on embeddings and nearest-neighbors imputation (scVI, Harmony, Scanorama), we impute by calculating the average gene expression of the -nearest neighbors of the embedding of the spot restricted to the single-cell data of cell type only. Similarly, we estimate the proportion using the empirical proportion of cell types for the -nearest neighbors of the embeddings of the spot restricted to all the single-cell data. Finally, we also evaluate the performance of discrete deconvolution algorithms (Stereoscope, Seurat, RCTD and SPOTLight) for within cell-type gene expression. For this, we re-cluster the single-cell data for each cell type at several depths, using hierarchical clustering (2, 4 and 8 clusters per cell type). Then, we run the discrete deconvolution methods on the re-clustered data. We also calculate the mean gene expression for every cluster based on the single-cell data. Finally, we impute gene expression for cell type at spot by averaging the gene expression of every cluster in cell type , weighted by the conditional proportions of every cluster at the spot. Given these modifications, we evaluated the imputation based on correlation metrics (e.g., spearman correlation) across an oracle list of genes for each cell type. The list of genes for each cell type is given by the indices of the non-zero coefficients of the matrix , learned via sparse PCA. We have found that this selection of genes helps make the evaluation more robust.
Interestingly, SPOTLight did not terminate after three hours for the most granular clustering (8 clusters per cell type).
Preprocessing and benchmarking details for the sci-Space dataset
We obtained the data for the 14 sagittal sections derived from two embryonic day 14 (E14.0) mouse embryos (C57BL/6N) from the original publication. We preprocessed the data as per the cortex-specific analysis conducted in Figure 5 of the sci-Space manuscript. More precisely, we filtered for section 8, 9, 11, 13 and 14 and kept only the cells whose anatomical annotation was cortex. Within those cells, we filtered for the top four abundant cell types (8,186 neurons, 1,610 radial glias, 581 connective tissue progenitors and 507 endothelial cells) included in the original study. We additionally selected the top 4,000 highly variable genes using scanpy. We assembled the spatial dataset by summing the transcriptome of all cells that share the same spatial barcode. Additionally, we increased the complexity of the dataset in two ways. First, we lowered the sequencing depth by performing binomial subsampling at rate 0.1. Second, we enriched the data by adding spots generated in-silico from the individual cells of each spot, but with different proportions. In particular, we enriched for cell types other than neurons by a factor of 5, as the original dataset is dominated by spots with mostly neurons. For evaluation, we applied the benchmarking pipeline previously used with the simulations. The main difference is that it relies on a subset of genes with interesting zonation patterns (in the simulation, this is given by the sparsity pattern of the loading matrix from the PCA). For this, we took the intersection of the highly variable gene list and the list of genes highlighted in Figure 5 of the sci-Space paper.
Figure 5: DestVI identifies a hypoxic population of macrophages in the tumor core.
(A) Visualization of the hypoxia gene expression module on the Mon-Mac cells from the scRNA-seq data (4,400 cells), on the embedding from scVI (identified using Hotspot; see Supplementary Figures 28–29). (B) Imputation of gene expression for this module on the spatial dataset (log-scale), reported only on spots with high abundance of Mon-Mac (3,906 spots across the two sections). Imputation for other modules is shown in Supplementary Figure 30. (C) H&E stained histology of Section-1 (left), with overlapping Mreg identified regions from DestVI showing red polygons (as identified in Supplementary Figure 32). Blue arrows show the location of cells from the necrotic core. H&E stained histology showing a magnification of the necrotic core of the yellow frame in Section-1 (right). Scale bar, 55 μm. (D) Mon-Mac cell-specific DE analysis between the Mreg enriched areas and the rest of the tumor section (2,886 genes; 379 spots for the Mreg enriched area and 361 randomly sampled spots from the rest of the tumor; total of 2,220 samples from the generative model). Red dots designate genes with statistical significance, according to our DE procedure (two-sided Kolmogorov-Smirnov test, adjusted for multiple testing using the Benjamini-Hochberg procedure; Methods). (E) Representative image of the multiplexed immunofluorescence staining. (left) Hypoxic areas as identified by the Hypoxyprobe (HYPO) in a whole MCA205 tumor section. Two yellow frames show the hypoxic areas with necrotic cores. Scale bar, 500 μm. (middle) Magnification of a necrotic core with F4/80, Arg1, GPNMB, Hypoxyprobe (HYPO) and DAPI staining. Scale bar, 50 μm. (right) Annotation of different macrophages surrounding the necrotic core. Different colors shown in the legend bar show different staining combinations. Red spindle shows the extent of hypoxia. Blue arrow shows the location of cells from the necrotic core. Scale bar, 50 μm.
Automated pipeline for data exploration
Although DestVI may be used in a biologically informed setting, when practitioners are seeking for spatial relevance of specific transcriptomic modules in a given cell type (e.g., interferon type I response in B cells), we also designed a more agnostic pipeline to quickly explore, interpret and visualize the results of DestVI.
Spatially localized cell types
In this first step we simply calculate the auto-correlation index as reported by Hotspot [45] on the cell-type proportion for each individual cell type.
Selecting informative thresholds for cell-type proportions
We wanted to select the threshold based on the spatial information. Therefore, we chose a characteristic point of the auto-correlation curve, as a function of the thresholding. More precisely, for every cell type , we apply the hard-thresholding operator to the proportion vector at different levels (noted ). We take to be the empirical percentiles of the proportion across all spots. For each thresholded vector , we then calculate the auto-correlation metric from Hotspot [45] for all of those thresholded proportions. The result is a curve that may be interpolated using splines using the scipy.interpolate function from SciPy [89]. We then analytically differentiate the spline and look for an inflection point (null second derivative).
Finding main axes of variation in the combined data
Interpreting the cell-type-specific latent dimensions of DestVI may be challenging. We therefore present here a visualization technique that aims at summarizing the inferences. The major question we would like to solve here is the following: within a single cell type, which directions of vary spatially? In other words, we wish to find within cell-type and spatially-varying transcriptomic programs.
General matrix factorization methods (such as NMF, PCA or CCA) could be applied to find those important components. However, they present several crucial limitations: (i) the samples are not reweighted by the cell-type proportion. This is especially important because is inferred at every spot, even when is null, (ii) we are only interested in variations that are relevant with respect to the spatial coordinates .
To identify those, we focus on identifying the directions of that vary the most (as in PCA), but while enforcing some agreement with respect to the spatial location, and by taking into account the cell-type proportions. More precisely, let be a fixed cell type. We define first spatial PC of the space, noted , as the argument of the solution to the variational problem:
This problem, whether we are interested in a single or in several PCs, is tractable, as it may be formulated as an eigenvalue problem. We present this formulation below, providing a more succinct presentation than in [37]. We then explain in further details how this weighted PCA is related to a classical PCA. Interestingly, the previous optimization problem could be extended to find pairs of cell-type-specific transcriptional programs that are spatially co-activated (via a weighted CCA), but we leave this to future work.
Principal Component Analysis (PCA)
Let denote a dataset, in which each datapoint . The problem of finding the first principal component may be formulated as finding the direction of maximal variance in the data:
Laplacian-weighted PCA
We wish to incorporate sample-to-sample weights into this objective function, so that we can accordingly reweights pairs of observations according to a non-negative, symmetric dissimilarity matrix . From this matrix, we form the Laplacian matrix . A Laplacian matrix is a PSD matrix with zero-sum rows and columns. Then, relying on the the identity , in which and are iid copies of , we define the first weighted principal component as the solution of the following optimization problem:
We now argue that this optimization problem is no different than the original PCA formulation, and can be solved via eigenvalue decomposition. This is because the objective function from the weighted optimization problem is still the evaluation of a quadratic form:
Consequently, we can find the Laplacian weighted principal components via eigenvalue decomposition of the matrix . When the random variable is centered, and the dissimilarity matrix is trivial, we obtain . More importantly, it seems we can rotate the data and solve PCA on it.
Interpretation of the weighted PCA
For interpreting the spatially-weighted PCA for every cell type, we first project the cell-type-specific cell state of the spatial data as well as the scRNA-seq data onto the two weighted principal components. We then use a two-dimensional colormap to assign a color to the spots in the spatial data, according to the position of the (2D) projection of the cell-type-specific cell state. This is helpful to prioritize which cell type may have spatially consistent variations in cell states. To relate this to the functions of each axis of the PCs, we filter genes that are the most correlated with each PC (Pearson correlation) and we ran gene set enrichment analysis using EnrichR [37,38] for the top 50 genes.
A post-hoc recipe for differential expression with DestVI
Performing differential expression with a probabilistic model is always challenging, but is crucial for making robust scientific discoveries. In our previous work, we used a purely Bayesian approach to differential expression [62,63]. Because we apply MAP inference (and not fully-Bayesian inference) to DestVI, we instead developed a hybrid approach to differential expression, where we sample from the adequate generative distribution and then derive a p-value with a frequentist test. More precisely, for two bags of spots and , and a cell type , we operate as follows.
Characterizing cell-type-specific gene expression
We query the parameters of the generative distribution for that spot, but only for the contribution from cell type . We do this by embedding all the spots, and keeping only the latent variable for the cell type of interest and then querying the decoder network for this particular and cell type . This vector, along with , fully characterize the transcriptome of a fictitious cell of type in spot :
where is a fixed scalar equal to the average library size in the single-cell data.
Simulating cell-type-specific gene expression
Then, we sample multiple times per spot from the mean of the Poisson distribution underlying the negative binomial:
There are several considerations for sampling this way. First, as we underlined in our previous work for calculating gene correlations in totalVI, using the mean of the generative distribution provides all forms of biases. Second, sampling from the full negative binomial distribution introduces Poisson noise, and reduces sensitivity of the method. Sampling from the Gamma distribution is an intermediate, although post-hoc, solution. This step plays the role of denoising and is especially important when there are very few spots in the bags or , because we can generate more data points.
Hypothesis testing
For every spot in every bag, we generate between and independent samples of the random variables and apply a two-sample Kolmogorov–Smirnov test, and we correct for multiple testing using the Benjamini-Hochberg procedure [90]. Additionally, we tag genes as differentially expressed if two conditions are met: (i) the null hypothesis is rejected, after control of the FDR at level 0.05, and (ii) the log-fold change (LFC) is greater than a data-driven threshold, in absolute value. To calculate this threshold, we assume that a significant amount of LFCs will concentrate around zero (which correspond to the genes that are equally expressed), while DE genes will concentrate around other modes. Based on this assumption, we fit a three-component Gaussian Mixture Model (GMM) to the LFC, and keep the mean of the mode with largest absolute value, whose associated distributions should contain differentially expressed genes.
Experimental conditions and sample preparation
Mice
C57BL/6J mice were purchased from Harlan and housed in the Weizmann Institute of Science animal facility, under specific pathogen-free conditions. For consistency, female mice, 6–8 weeks of age, were used for all experiments. All mice were provided with normal chow and water ad libitum, and housed under a strict 12-hour light-dark cycle. All experimental protocols were approved by the Institutional Animal Care and Use Committee (IACUC).
Preparation of antigens
Inactivated Mycobacterium Smegmatis (MS) was prepared as previously reported in [24]. Simply M. smegmatis was grown in Luria-Bertani broth overnight at 37°C. Bacteria were washed thrice in PBS containing 0.05% Tween 80 and heat-killed at 75°C for 1 hour, then aliquoted into a useful size and stored at −80°C.
Immunizations
Mice were anesthetized and M. smegmatis was administered by intradermal injection into the ear pinna. PBS was injected into the ear pinna of control animals. The pathogen immunization dose is 4M CFU, according to our previous study [24]. The auricular lymph nodes were harvested 48 hours after immunization.
Tumor model
MCA205 fibrosarcoma cell lines were kindly provided by Sergio Quezada group at UCL cancer institute, London, UK. Cells were cultured in DMEM (41965–039) medium supplemented with 10% heat-inactivated FBS, 1mM sodium pyruvate, 2mM l-glutamine, 1% penicillin-streptomycin (Thermo Fisher Scientific). Cells were cultured in 100 mm tissue culture plates in an incubator with humidified air and 5% CO2 at 37°C. For establishment of solid tumors, 8 weeks, female mice were injected intradermally with 5 × 105 MCA205 tumor cells suspended in 100 μL PBS on their right flank. On day 14, tumor volume was measured using a caliper and prepared according to Visium spatial protocols of tissue preparation guide (CG000240).
RNA-sequencing and data processing
Single-cell RNA-Sequencing for the lymph node
To prepare single cell suspensions for scRNA-seq using 10x Genomics system, auricular LNs were digested in IMDM containing 100 μg/mL Liberase TL and 100 μg/mL DNase I (both from Roche, Germany) for 20 minutes at 37°C. Last 5 minutes of incubation, EDTA was added at a final concentration of 10 mM. Cells were collected, filtered through a 70 μm cell strainer, washed with PBS + 0.04% BSA for a final concentration of 1000 cells/μL.
Cellular suspension was immediately loaded onto Next GEM Chip G targeting ~5000 cells and then ran on a Chromium controller instrument (10x Genomics) to generate GEM emulsion. Single cell 3’ RNA-seq libraries were generated according to the manufacturer’s protocol using the v3.1 Next GEM dual index workflow. Final libraries were quantified using NEBNext Library Quant Kit for Illumina (NEB) and high sensitivity D1000 TapeStation (Agilent). Libraries were pooled and sequenced on an SP 100 cycles reagent kit on a NovaSeq6000 instrument (Illumina), aiming for ~ 50,000 reads per cell. Reads from raw FASTQ files were processed with Cell Ranger 4.0 and mapped to the mouse mm10–2020 reference (10x Genomics). No read depth normalization was applied when aggregating datasets.
Lymph node scRNA-seq data processing
Using Scanpy [87], we filtered out cells with less than 200 UMIs and genes expressed in less than 3 cells, as well as cells with more than 20% mitochondrial genes. We estimated doublet scores for all barcodes using Scrublet [91]. Because we did not expect any novel cell types in the data, we seeked to automatically annotate our samples based on publicly available murine lymph node scRNA-seq [39]. We therefore harmonized all the samples from both datasets using scVI [29], and transferred labels using scANVI [40]. For both algorithms, we filtered genes to match the highly variable genes from the dataset of [39]. After manual examination of the expression of marker genes (Supplementary Table 4 of [39]) and its adequation with the automated labels, we noticed some mislabeling inaccuracies on the rare cell types of the myeloid cluster. Consequently, we clustered the myeloid compartment with Louvain and curated the annotation, based not only on the automated annotation, but also the gene expression of the key marker genes. Finally, we also removed a cluster of doublets, as predicted by Scrublet. We recapitulate the number of cells for each cell type in Supplementary Table 1.
Single-cell RNA-Sequencing for the tumor
To prepare tumor infiltrating leukocytes single cell suspensions, the tumors underwent mechanical (gentle-MACSTM C tube, Miltenyi Biotec Inc., San Diego, CA) and enzymatic digestion (0.1mg/ml DNase type I (Roche), and 1mg/ml Collagenase IV (Worthington) in RPMI-1640) for 10 minutes at 37°C and repeat one more time. Cells then filtered through 100 μm cell strainer, washed with an ice cold sorting buffer, centrifuged (5 min, 4°C, 350g), and stained with fluorophores conjugated anti-mouse CD45 antibodies on ice 30 minutes to avoid light. After staining, cells were washed and resuspended in a cold washing buffer (0.5% BSA and 2 mM EDTA in PBS), filtered through a 70 μm cell strainer. Before sorting, cells were stained with DAPI (4’,6-Diamidino-2-Phenylindole, 0.5 μg/mL, ThermoFisher, D1306) to exclude dead/dying cells. Cell sorting was performed using a BD FACSAria Fusion flow cytometer (BD Biosciences), gating for CD45+ cells after exclusion of dead cells and doublets (Supplementary Figure 23). Single cells were sorted into 384-well plates and single cell RNA-seq libraries were generated using a modified version of the single cell MARS-seq protocol [92] [93]. In brief, mRNA from cells sorted into cell capture plates were barcoded, converted into cDNA and pooled using an automated pipeline. The pooled cDNA are then amplified and Illumina libraries are being generated. Final libraries were quantified using Qubit and high sensitivity D1000 TapeStation (Agilent). Libraries were pooled and sequenced an SP 100 cycles reagent kit on a NovaSeq6000 instrument (Illumina). Sequences were mapped to the mouse (mm10). Demultiplexing and filtering was performed as previously described [93], with the following adaptations: Mapping of reads was performed using HISAT (version 0.1.6); reads with multiple mapping positions were excluded. Reads were associated with genes if they were mapped to an exon, using the ensembl gene annotation database (embl release 90). Exons of different genes that shared a genomic position on the same strand were considered as a single gene with a concatenated gene symbol. The level of spurious unique molecular identifiers (UMIs) in the data were estimated by using statistics on empty MARS-seq wells, and excluded rare cases with estimated noise > 5% (median estimated noise over all experiments was 2%).
Tumor scRNA-seq data processing
Using Scanpy [87], we filtered out cells with less than 200 UMIs and genes expressed in less than 10 cells. We selected 4,000 highly variable genes using scanpy and reduced dimensionality of the data using scVI [29]. We applied leiden clustering and annotated the data based on marker genes (CD4 and Icos for CD4 T cells, Cd8a and Cd8b1 for CD8 T cells, Gzma and Prf1 for NK cells, C1qa and Ly6a for macrophages / monocytes, S100a8 for Neutrophils, H2-Ab1, H2-Eb1 and H2-Aa for DCs and Cd63 and Col3a1 for tumor cells. We recapitulate the number of cells for each cell type in Supplementary Table 5.
Visium data generation
Auricular LNs and the MCA205 tumor were prepared according to Visium spatial protocols of tissue preparation guide (10x Genomics). Firstly, freshly obtained tissue samples were snap frozen in liquid nitrogen, then embedded in chilled Optimal Cutting Temperature compound (OCT; Tissue-Tek) and frozen on dry ice, then stored at −80°C in a sealed container for later use. For Visium samples preparation, OCT-embedded tissue blocks were cut to 10 μm thick using a LEICA CM1950 machine and mounted on the Visium spatial gene expression slide. For gene expression samples, tissues were permeabilized for 18 minutes, based on tissue optimization time course experiments. Brightfield histology images were taken using a 10X objective (Plan APO, NA 0.25) on Leica DMI8 wide-field inverted microscope according to Visium spatial gene expression imaging guidelines (CG000241). Raw images were stitched together using Leica application suite X (LAS X) software and exported as TIFF/PNG files with low- and high-resolution settings.
Libraries were prepared according to the Visium spatial gene expression user guide (10x Genomics). Final libraries were quantified using NEBNext Library Quant Kit for Illumina (NEB) and high sensitivity D1000 TapeStation (Agilent). The number of reads required for sequencing was calculated taking into account the percentage of the tissue within each capture area (calculated using imageJ). Libraries were pooled according to the desired number of reads and sequenced on an SP 200 cycles reagent kit on a NovaSeq6000 instrument (Illumina).
Visium raw data processing
Raw FASTQ files and histology images were processed by sample with the Space Ranger software v1.2.1. For the lymph node, we calculated the quality control metrics using Scanpy [87] and noticed that one of the PBS samples was of low quality, as indicated by the number of UMIs per spot. We also filtered out spots with less than 4,000 UMIs and genes expressed in less than 10 spots. The number of spots after filtering was 1,092 across the remaining three lymph nodes. For the tumor data, we filtered out spots with more than 2% mitochondrial gene expression, spots with less than 10,000 UMIs and genes expressed in less than 10 spots.
Immunofluorescence
Tissues embedded in OCT for Visium were sliced to 10 μm thick sections using a LEICA CM1950 machine and mounted on SuperFrost Plus slides (Thermo Scientific). For visualization, sections were firstly fixed by 4% Formaldehyde solution in PBS diluted from 16% Formaldehyde (Thermo Scientific) 10 minutes at room temperature. Then sections were washed by PBS three times and blocked with a blocking buffer solution (5% donkey serum, 2% BSA, 0.2% Triton X-100) for 2 h at room temperature, and incubated with primary antibody at 4°C overnight. If secondary antibody is necessary, after three times PBST (0.02% Triton X-100) washes corresponding secondary antibody was incubated at room temperature 1 hour. After three times PBST washed, DAPI (4’,6-Diamidino-2-Phenylindole, 1 μg/mL, ThermoFisher, D1306) reagent was added for 10 min to detect cell nuclei. Sections were mounted with SlowFade Gold Antifade Mountant (Invitrogen, S36937) and sealed with cover-slips. Microscopic analysis was performed using a laser-scanning confocal microscope (Zeiss, LSM880). Images were acquired and processed with the same threshold settings using Imaris software (Bitplane). The primary antibodies used were: CD45 APC (1:100, 30-F11, eBioscience, 17–0451-82), CD11b Biotin (1:100, M1/70, Biolegend, 101204), CD11b PE (1:100, M1/70, eBioscience, 12–0112-83), CD64 PE (1:100, X54–5/7.1, Biolegend, 139303), Ly6C FITC (1:100, HK1.4, Biolegend, 128005), B220 (1:100, RA3–6B2, Biolegend, 103208), CD3 Biotin (1:100, 17A2, Biolegend, 100243), TCRb PE (1:100, H57–597, Biolegend, 109207), MHCII I-A/I-E FITC (1:100, M5/114.15.2, Biolegend, 107606), F4/80 APC (1:100, BM8, eBioscience, 17–4801-82), NK1.1 PE(1:100, PK136, eBioscience, 12–5941-63), CD31 APC (1:100, MEC13.3, Biolegend, 102509), IFIT3 polyclonal antibody (1:500, Proteintech, 15201–1-AP). Secondary antibody used were: Streptavidin APC (1:400, Biolegend, 405207), Goat anti-Rabbit IgG-heavy and light chain Antibody DyLight® 650 Conjugated (1:800, Bethyl, A120–101D5).
Multiplexed staining for MCA 205 tumor
Mice with MCA205 tumor were prepared as described above. To detect hypoxia in tumors, mice with MCA205 tumor 14 days were performed intraperitoneal injection with Hypoxyprobe™-1 solution at a dosage of 60 mg/kg, 1 h prior to sacrificing. MCA205 tumors were flash frozen in liquid nitrogen then embedded in OCT media (Tissue-Tek) on dry ice and stored at −80°C until use. Eppendorf Cell Imaging Dish (EP0030740017) were coated with 1mg/ml Poly-D-lysine hydrobromide (PDL, Sigma, P6407) for 5 minutes at room temperature. After three times rinsed with water and dried overnight. Cryosections were cut at 10 μm thickness using a LEICA CM1950 machine and mounted onto the center of the pretreated cell imaging dish. Sealed the cover with parafilm (Sigma, P7793) stored at −80°C until staining.
Before staining, frozen sections were incubated on a heat block set to 37°C for 1 minute. Sections were immediately fixed by 4% Formaldehyde solution in PBS diluted from 16% Formaldehyde (Thermo Scientific) 15 minutes at room temperature. Then sections were washed by PBS six times following permeabilized with 0.3% PBST (Triton X-100) for 15 minutes at room temperature. After six times PBS washes, sections were performed 4i staining protocol [94]. Briefly, one 4i cycle includes blocking, staining, imaging and elution. Whole three rounds 4i is manually handled without any microfluidic setup. First round stains CD31 APC (1:200, MEC13.3, Biolegend, 102509), CD11b FITC (1:200, M1/70, Biolegend, 101205), DAPI (1 μg/mL, ThermoFisher, D1306). Second round stains Arginase 1 (ARG1, 1:200, Novus, NB100–59740), secondary antibody DyLight 550 conjugated donkey anti-goat IgG heavy and light chain antibody (1:400, Bethyl, A50–101D3), pimonidazole antibody (Hypoxyprobe, 1:200, PAb2627AP), secondary antibody Cy2 conjugated AffiniPure donkey anti-rabbit IgG heavy and light chain antibody (1:200, Jackson ImmunoResearch, 711–225-152), DAPI (1 μg/mL, ThermoFisher, D1306). Third round stains F4/80 (1:100, Abcam, ab6640), secondary antibody DyLight 594 conjugated donkey anti-rat IgG heavy and light chain cross-adsorbed antibody (1:400, Bethyl, A110–337D4), GPNMB (1:200, Abcam, ab234529), secondary antibody Alexa Fluor 647 conjugated AffiniPure F(ab’)2 fragment donkey anti-rabbit IgG heavy and light chain antibody (1:400, Jackson ImmunoResearch, 711–606-152), DAPI (1 μg/mL, ThermoFisher, D1306). All stained sections were imaged by using a 25x/0.95 Water PlanApo objective in Andor Dragonfly spinning disk confocal on an inverted Leica DMi8 microscope. Images were acquired via Fusion with fields montage mode with 10% overlap, with a pixel resolution of 2048 × 2048 per tile with 16-bit pixel depth. The images were stitched automatically with precise mode in Fusion.
Image processing and quantification
For image analysis. First step is using Imaris 9.8.0 (Bitplane) to convert all Imaris image file images to OME-TIFF images. Then create a new projection in QuPath [95]. Put all the relevant images under the same projection. Choose the region of interest (ROI) and export this ROI as OME-TIFF and rename them. Fiji [96] will be used for image registration. First step is using the Bio-Formats plugin [97] to import all the images as hyperstack images. Concatenate all the images into a stack image. Use a modified plugin Linear Stack Alignment with SIFT MultiChannel (https://github.com/BIOP/ijp-siftalignmultichannel-ij2) which is based on Linear Stack Alignment with SIFT plugin [98] to align the images, using DAPI channel from each round staining with affine registration. The aligned stack image further changed to hyperstack images. Make a new projection for analysis of the aligned hyperstack images from Fiji in QuPath. The multiplexed images analysis is based on the QuPath multiplexed analysis process. The analyzed images could be exported as TIFF images and further use Fiji to add scale bars.
Extending simulations for assessing robustness to cell type mismatch
We added two additional cell types to our simulations, whose parameters was learnt from our lymph node scRNA-seq data using sPCA (as per previous simulations). To simulate a cell type missing from the single-cell data, we simply filtered all the cells from this cell type out post-hoc. To simulate a cell type missing from the spatial data, we cancelled all the contributions of that cell type to the transcriptome, inside of every spot.
Data preprocessing for the Seq-Scope liver analysis
We relied on publicly available single-cell RNA sequencing data from Tabula Muris Senis [73], filtering for the droplet-based liver tissue data. We annotated the data manually, based on scanpy and marker genes (Mup3 for hepatocytes, Clec4f for macrophages and Kdr for endothelial cells). We imported the spatial transcriptomics data at 10 microns resolution from the Seq-Scope paper [72], and annotated at the spot-level by Seurat.
Extending simulations for high-resolution data
In order to simulate high-resolution data, we have relied on the simulations with increased number of cell types (7) and lowered the temperature parameter from 1 to 0.5 (lowering from 5–6 to 2–3 the empirical number of cell types per spot). We have also decreased the library size of the spatial transcriptomics data to be 50% of the library size of the scRNA-seq data, via binomial downsampling.
Data Availability
The raw data discussed in this manuscript have been deposited in the National Center for Biotechnology Information’s Gene Expression Omnibus and are accessible through accession number GSE173778 (murine lymph node and tumor; spatial transcriptomics and scRNA-seq data). Processed sequencing data are available on our reproducibility repository (https://github.com/romain-lopez/DestVI-reproducibility).
Supplementary Material
Acknowledgements
We would like to acknowledge Adam Gayoso, Galen Xing and Justin Hong for their help integrating DestVI in the scvi-tools codebase. Thanks to Zoë Steier for providing guidance on the annotation of the lymph node single-cell data. We acknowledge Shalev Itzkovitz for his guidance on interpreting the liver results. We thank Efrat Davidson for the artwork. We are grateful for insightful conversations with Aviv Regev, Dana Pe’er, Quaid Morris, Alexis Battle, Assaf Weiner, Elior Rahmani and Matthew Jones.
Funding:
NY and RL were supported by the Chan Zuckerberg Biohub. I.A. is an Eden and Steven Romick Professorial Chair, supported by Merck KGaA, Darmstadt, Germany, the Chan Zuckerberg Initiative, the Howard Hughes Medical Institute International Scholar award, the European Research Council Consolidator Grant 724471-HemTree2.0, an SCA award of the Wolfson Foundation and Family Charitable Trust, the Thompson Family Foundation, a Melanoma Research Alliance Established Investigator Award (509044), the Israel Science Foundation (703/15), the Ernest and Bonnie Beutler Research Program for Excellence in Genomic Medicine, the Helen and Martin Kimmel award for innovative investigation, the NeuroMac DFG/Transregional Collaborative Research Center Grant, an International Progressive MS Alliance/NMSS PA-1604 08459, the ISF Israel Precision Medicine Program (IPMP) 607/20 grant and an Adelis Foundation grant.
Footnotes
Software Availability
The code to reproduce the results in this manuscript is available on the Github repository https://github.com/romain-lopez/DestVI-reproducibility and has been deposited to Zenodo https://doi.org/10.5281/zenodo.4685952. The reference implementation of DestVI, along with accompanying tutorials is available via the scvi-tools codebase at https://scvi-tools.org/.
Competing Interests Statement
N.Y. is an advisor and/or has equity in Cellarity, Celsius Therapeutics, and Rheos Medicine.
References
- 1.Wagner A, Regev A, Yosef N. Revealing the vectors of cellular identity with single-cell genomics. Nat Biotechnol. 2016;34: 1145–1160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Codeluppi S, Borm LE, Zeisel A, La Manno G, van Lunteren JA, Svensson CI, et al. Spatial organization of the somatosensory cortex revealed by osmFISH. Nat Methods. 2018;15. doi: 10.1038/s41592-018-0175-z [DOI] [PubMed] [Google Scholar]
- 3.Asp M, Salmén F, Ståhl PL, Vickovic S, Felldin U, Löfling M, et al. Spatial detection of fetal marker genes expressed at low level in adult human heart tissue. Sci Rep. 2017;7: 12941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hunter MV, Moncada R, Weiss JM, Yanai I, White RM. Spatial transcriptomics reveals the architecture of the tumor/microenvironment interface. Cold Spring Harbor Laboratory. 2020. p. 2020.11.05.368753. doi: 10.1101/2020.11.05.368753 [DOI] [Google Scholar]
- 5.Ji AL, Rubin AJ, Thrane K, Jiang S, Reynolds DL, Meyers RM, et al. Multimodal Analysis of Composition and Spatial Architecture in Human Squamous Cell Carcinoma. Cell. 2020;182: 1661–1662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chen KH, Boettiger AN, Moffitt JR, Wang S, Zhuang X. RNA imaging. Spatially resolved, highly multiplexed RNA profiling in single cells. Science. 2015;348: aaa6090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Eng CL, Lawson M, Zhu Q, Dries R, Koulena N, Takei Y, et al. Transcriptome-scale super-resolved imaging in tissues by RNA seqFISH. Nature. 2019;568. doi: 10.1038/s41586-019-1049-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Petukhov V, Soldatov RA, Khodosevich K, Kharchenko PV. Bayesian segmentation of spatially resolved transcriptomics data. Cold Spring Harbor Laboratory. 2020. p. 2020.10.05.326777. doi: 10.1101/2020.10.05.326777 [DOI] [Google Scholar]
- 9.Littman R, Hemminger Z, Foreman R, Arneson D, Zhang G, Gómez-Pinilla F, et al. JSTA: joint cell segmentation and cell type annotation for spatial transcriptomics. Cold Spring Harbor Laboratory. 2020. p. 2020.09.18.304147. doi: 10.1101/2020.09.18.304147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Biancalani T, Scalia G, Buffoni L, Avasthi R, Lu Z, Sanger A, et al. Deep learning and alignment of spatially-resolved whole transcriptomes of single cells in the mouse brain with Tangram. Cold Spring Harbor Laboratory. 2020. p. 2020.08.29.272831. doi: 10.1101/2020.08.29.272831 [DOI] [Google Scholar]
- 11.Abdelaal T, Mourragui S, Mahfouz A, Reinders MJT. SpaGE: Spatial Gene Enhancement using scRNA-seq. Nucleic Acids Res. 2020;48: e107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lopez R, Nazaret A, Langevin M, Samaran J, Regier J, Jordan MI, et al. A joint model of unpaired data from scRNA-seq and spatial transcriptomics for imputing missing gene expression measurements. arXiv [cs.LG]. 2019. Available: http://arxiv.org/abs/1905.02269 [Google Scholar]
- 13.Stickels RR, Murray E, Kumar P, Li J, Marshall JL, Di Bella DJ, et al. Highly sensitive spatial transcriptomics at near-cellular resolution with Slide-seqV2. Nat Biotechnol. 2020. doi: 10.1038/s41587-020-0739-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rodriques SG, Stickels RR, Goeva A, Martin CA, Murray E, Vanderburg CR, et al. Slide-seq: A scalable technology for measuring genome-wide expression at high spatial resolution. Science. 2019;363: 1463–1467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ståhl PL, Salmén F, Vickovic S, Lundmark A, Navarro JF, Magnusson J, et al. Visualization and analysis of gene expression in tissue sections by spatial transcriptomics. Science. 2016;353: 78–82. [DOI] [PubMed] [Google Scholar]
- 16.Cable DM, Murray E, Zou LS, Goeva A, Macosko EZ, Chen F, et al. Robust decomposition of cell type mixtures in spatial transcriptomics. Cold Spring Harbor Laboratory. 2020. p. 2020.05.07.082750. doi: 10.1101/2020.05.07.082750 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Elosua-Bayes M, Nieto P, Mereu E, Gut I, Heyn H. SPOTlight: seeded NMF regression to deconvolute spatial transcriptomics spots with single-cell transcriptomes. Nucleic Acids Res. 2021. doi: 10.1093/nar/gkab043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Andersson A, Bergenstråhle J, Asp M, Bergenstråhle L, Jurek A, Fernández Navarro J, et al. Single-cell and spatial transcriptomics enables probabilistic inference of cell type topography. Commun Biol. 2020;3: 565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Song Q, Su J. DSTG: deconvoluting spatial transcriptomics data through graph-based artificial intelligence. Brief Bioinform. 2021. doi: 10.1093/bib/bbaa414 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kleshchevnikov V, Shmatko A, Dann E, Aivazidis A, King HW, Li T, et al. Comprehensive mapping of tissue cell architecture via integrated single cell and spatial transcriptomics. Cold Spring Harbor Laboratory. 2020. p. 2020.11.15.378125. doi: 10.1101/2020.11.15.378125 [DOI] [Google Scholar]
- 21.Ortiz C, Navarro JF, Jurek A, Märtin A, Lundeberg J, Meletis K. Molecular atlas of the adult mouse brain. Science Advances. 2020;6: eabb3446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lähnemann D, Köster J, Szczurek E, McCarthy DJ, Hicks SC, Robinson MD, et al. Eleven grand challenges in single-cell data science. Genome Biol. 2020;21: 1–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lopez R, Gayoso A, Yosef N. Enhancing scientific discoveries in molecular biology with deep generative models. Mol Syst Biol. 2020;16: e9198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ronnie Blecher-Gonen. Single-Cell Analysis of Diverse Pathogen Responses Defines a Molecular Roadmap for Generating Antigen-Specific Immunity. Cell Systems. 2019;8: 109–121.e6. [DOI] [PubMed] [Google Scholar]
- 25.Kumar S, Sharife H, Kreisel T, Mogilevsky M, Bar-Lev L, Grunewald M, et al. Intra-Tumoral Metabolic Zonation and Resultant Phenotypic Diversification Are Dictated by Blood Vessel Proximity. Cell Metab. 2019;30: 201–211.e6. [DOI] [PubMed] [Google Scholar]
- 26.Gayoso A, Lopez R, Xing G, Boyeau P, Wu K, Jayasuriya M, et al. scvi-tools: a library for deep probabilistic analysis of single-cell omics data. bioRxiv. 2021. p. 2021.04.28.441833. doi: 10.1101/2021.04.28.441833 [DOI] [PubMed] [Google Scholar]
- 27.Blei DM. Build, Compute, Critique, Repeat: Data Analysis with Latent Variable Models. Annual Review of Statistics and Its Application. 2014. pp. 203–232. doi: 10.1146/annurev-statistics-022513-115657 [DOI] [Google Scholar]
- 28.Grün D, Kester L, van Oudenaarden A. Validation of noise models for single-cell transcriptomics. Nat Methods. 2014;11: 637–640. [DOI] [PubMed] [Google Scholar]
- 29.Lopez R, Regier J, Cole MB, Jordan MI, Yosef N. Deep generative modeling for single-cell transcriptomics. Nat Methods. 2018;15: 1053–1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kingma DP, Welling M. Auto-Encoding Variational Bayes. arXiv [stat.ML]. 2013. Available: http://arxiv.org/abs/1312.6114v10 [Google Scholar]
- 31.Tomczak JM, Welling M. VAE with a VampPrior. arXiv [cs.LG]. 2017. Available: http://arxiv.org/abs/1705.07120 [Google Scholar]
- 32.Stuart T, Butler A, Hoffman P, Hafemeister C, Papalexi E, Mauck WM 3rd, et al. Comprehensive Integration of Single-Cell Data. Cell. 2019;177: 1888–1902.e21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Korsunsky I, Millard N, Fan J, Slowikowski K, Zhang F, Wei K, et al. Fast, sensitive and accurate integration of single-cell data with Harmony. Nat Methods. 2019;16: 1289–1296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hie B, Bryson B, Berger B. Efficient integration of heterogeneous single-cell transcriptomes using Scanorama. Nat Biotechnol. 2019;37: 685–691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Srivatsan SR, Regier MC, Barkan E, Franks JM, Packer JS, Grosjean P, et al. Embryo-scale, single-cell spatial transcriptomics. Science. 2021;373: 111–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Geary RC. The Contiguity Ratio and Statistical Mapping. The Incorporated Statistician. 1954. p. 115. doi: 10.2307/2986645 [DOI] [Google Scholar]
- 37.Koren Y, Carmel L. Robust linear dimensionality reduction. IEEE Transactions on Visualization and Computer Graphics. 2004. pp. 459–470. doi: 10.1109/tvcg.2004.17 [DOI] [PubMed] [Google Scholar]
- 38.Chen EY, Tan CM, Kou Y, Duan Q, Wang Z, Meirelles GV, et al. Enrichr: interactive and collaborative HTML5 gene list enrichment analysis tool. BMC Bioinformatics. 2013;14: 128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Gayoso A, Steier Z, Lopez R, Regier J, Nazor KL, Streets A, et al. Joint probabilistic modeling of single-cell multi-omic data with totalVI. Nat Methods. 2021;18: 272–282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Xu C, Lopez R, Mehlman E, Regier J, Jordan MI, Yosef N. Probabilistic harmonization and annotation of single-cell transcriptomics data with deep generative models. Mol Syst Biol. 2021;17: e9620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.McInnes L, Healy J, Saul N, Großberger L. UMAP: Uniform Manifold Approximation and Projection. Journal of Open Source Software. 2018. p. 861. doi: 10.21105/joss.00861 [DOI] [Google Scholar]
- 42.Garraud O, Borhis G, Badr G, Degrelle S, Pozzetto B, Cognasse F, et al. Revisiting the B-cell compartment in mouse and humans: more than one B-cell subset exists in the marginal zone and beyond. BMC Immunol. 2012;13: 63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hampton HR, Chtanova T. The lymph node neutrophil. Semin Immunol. 2016;28: 129–136. [DOI] [PubMed] [Google Scholar]
- 44.Kastenmüller W, Torabi-Parizi P, Subramanian N, Lämmermann T, Germain RN. A spatially-organized multicellular innate immune response in lymph nodes limits systemic pathogen spread. Cell. 2012;150: 1235–1248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.DeTomaso D, Yosef N. Identifying Informative Gene Modules Across Modalities of Single Cell Genomics. Cold Spring Harbor Laboratory. 2020. p. 2020.02.06.937805. doi: 10.1101/2020.02.06.937805 [DOI] [Google Scholar]
- 46.Reynoso GV, Weisberg AS, Shannon JP, McManus DT, Shores L, Americo JL, et al. Lymph node conduits transport virions for rapid T cell activation. Nat Immunol. 2019;20: 602–612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Leal JM, Huang JY, Kohli K, Stoltzfus C, Lyons-Cohen MR, Olin BE, et al. Innate cell microenvironments in lymph nodes shape the generation of T cell responses during type I inflammation. Sci Immunol. 2021;6. doi: 10.1126/sciimmunol.abb9435 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Moran I, Grootveld AK, Nguyen A, Phan TG. Subcapsular Sinus Macrophages: The Seat of Innate and Adaptive Memory in Murine Lymph Nodes. Trends Immunol. 2019;40: 35–48. [DOI] [PubMed] [Google Scholar]
- 49.Coombes JL, Han S-J, van Rooijen N, Raulet DH, Robey EA. Infection-induced regulation of natural killer cells by macrophages and collagen at the lymph node subcapsular sinus. Cell Rep. 2012;2: 124–135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Jakubzick C, Gautier EL, Gibbings SL, Sojka DK, Schlitzer A, Johnson TE, et al. Minimal differentiation of classical monocytes as they survey steady-state tissues and transport antigen to lymph nodes. Immunity. 2013;39: 599–610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Wei S, Shreiner AB, Takeshita N, Chen L, Zou W, Chang AE. Tumor-induced immune suppression of in vivo effector T-cell priming is mediated by the B7-H1/PD-1 axis and transforming growth factor beta. Cancer Res. 2008;68: 5432–5438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Pfirschke C, Engblom C, Rickelt S, Cortez-Retamozo V, Garris C, Pucci F, et al. Immunogenic Chemotherapy Sensitizes Tumors to Checkpoint Blockade Therapy. Immunity. 2016;44: 343–354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Hatfield SM, Kjaergaard J, Lukashev D, Schreiber TH, Belikoff B, Abbott R, et al. Immunological mechanisms of the antitumor effects of supplemental oxygenation. Sci Transl Med. 2015;7: 277ra30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Katzenelenbogen Y, Sheban F, Yalin A, Yofe I, Svetlichnyy D, Jaitin DA, et al. Coupled scRNA-Seq and Intracellular Protein Activity Reveal an Immunosuppressive Role of TREM2 in Cancer. Cell. 2020;182: 872–885.e19. [DOI] [PubMed] [Google Scholar]
- 55.Massi D, Marconi C, Franchi A, Bianchini F, Paglierani M, Ketabchi S, et al. Arginine metabolism in tumor-associated macrophages in cutaneous malignant melanoma: evidence from human and experimental tumors. Hum Pathol. 2007;38: 1516–1525. [DOI] [PubMed] [Google Scholar]
- 56.Chang CI, Liao JC, Kuo L. Macrophage arginase promotes tumor cell growth and suppresses nitric oxide-mediated tumor cytotoxicity. Cancer Res. 2001;61: 1100–1106. [PubMed] [Google Scholar]
- 57.Steinberg JD, Raju A, Chandrasekharan P, Yang C-T, Khoo K, Abastado J-P, et al. Negative contrast Cerenkov luminescence imaging of blood vessels in a tumor mouse model using [68Ga]gallium chloride. EJNMMI Res. 2014;4: 15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Wippold FJ 2nd, Lämmle M, Anatelli F, Lennerz J, Perry A. Neuropathology for the neuroradiologist: palisades and pseudopalisades. AJNR Am J Neuroradiol. 2006;27: 2037–2041. [PMC free article] [PubMed] [Google Scholar]
- 59.Godet I, Shin YJ, Ju JA, Ye IC, Wang G, Gilkes DM. Fate-mapping post-hypoxic tumor cells reveals a ROS-resistant phenotype that promotes metastasis. Nat Commun. 2019;10: 4862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Carmona-Fontaine C, Deforet M, Akkari L, Thompson CB, Joyce JA, Xavier JB. Metabolic origins of spatial organization in the tumor microenvironment. Proc Natl Acad Sci U S A. 2017;114: 2934–2939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Duque-Correa MA, Kühl AA, Rodriguez PC, Zedler U, Schommer-Leitner S, Rao M, et al. Macrophage arginase-1 controls bacterial growth and pathology in hypoxic tuberculosis granulomas. Proc Natl Acad Sci U S A. 2014;111: E4024–E4032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Lopez R, Boyeau P, Yosef N, Jordan MI, Regier J. Decision-Making with Auto-Encoding Variational Bayes. 2020. Available: http://arxiv.org/abs/2002.07217 [Google Scholar]
- 63.Boyeau P, Lopez R, Regier J, Gayoso A, Jordan MI, Yosef N. Deep Generative Models for Detecting Differential Expression in Single Cells. bioRxiv. 2019. p. 794289. doi: 10.1101/794289 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Wang J, Agarwal D, Huang M, Hu G, Zhou Z, Ye C, et al. Data denoising with transfer learning in single-cell transcriptomics. Nat Methods. 2019;16: 875–878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Jazbec M, Ashman M, Fortuin V, Pearce M, Mandt S, Rätsch G. Scalable Gaussian Process Variational Autoencoders. arXiv [stat.ML]. 2020. Available: http://arxiv.org/abs/2010.13472 [Google Scholar]
- 66.Bonilla EV, Krauth K, Dezfouli A. Generic Inference in Latent Gaussian Process Models. J Mach Learn Res. 2019;20: 1–63. [Google Scholar]
- 67.Rasmussen CE. Gaussian Processes for Machine Learning. 2006. [Google Scholar]
- 68.Longo SK, Guo MG, Ji AL, Khavari PA. Integrating single-cell and spatial transcriptomics to elucidate intercellular tissue dynamics. Nat Rev Genet. 2021. doi: 10.1038/s41576-021-00370-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Schmid KT, Höllbacher B, Cruceanu C, Böttcher A, Lickert H, Binder EB, et al. scPower accelerates and optimizes the design of multi-sample single cell transcriptomic studies. Nat Commun. 2021;12: 6625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Dieng AB, Ruiz FJR, Blei DM. Topic Modeling in Embedding Spaces. Transactions of the Association for Computational Linguistics. 2020. pp. 439–453. doi: 10.1162/tacl_a_00325 [DOI] [Google Scholar]
- 71.Vickovic S, Eraslan G, Salmén F, Klughammer J, Stenbeck L, Schapiro D, et al. High-definition spatial transcriptomics for in situ tissue profiling. Nat Methods. 2019;16: 987–990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Cho C-S, Xi J, Si Y, Park S-R, Hsu J-E, Kim M, et al. Microscopic examination of spatial transcriptome using Seq-Scope. Cell. 2021;184: 3559–3572.e22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Tabula Muris Consortium. A single-cell transcriptomic atlas characterizes ageing tissues in the mouse. Nature. 2020;583: 590–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Robinson MW, Harmon C, O’Farrelly C. Liver immunology and its role in inflammation and homeostasis. Cellular & Molecular Immunology. 2016. pp. 267–276. doi: 10.1038/cmi.2016.3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Krenkel O, Tacke F. Liver macrophages in tissue homeostasis and disease. Nature Reviews Immunology. 2017. pp. 306–321. doi: 10.1038/nri.2017.11 [DOI] [PubMed] [Google Scholar]
- 76.Lopez BG, Tsai MS, Baratta JL, Longmuir KJ, Robertson RT. Characterization of Kupffer cells in livers of developing mice. Comp Hepatol. 2011;10: 2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Droin C, Kholtei JE, Bahar Halpern K, Hurni C, Rozenberg M, Muvkadi S, et al. Space-time logic of liver gene expression at sub-lobular scale. Nat Metab. 2021;3: 43–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Armingol E, Officer A, Harismendy O, Lewis NE. Deciphering cell-cell interactions and communication from gene expression. Nat Rev Genet. 2021;22: 71–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Yosef N, Regev A. Writ large: Genomic dissection of the effect of cellular environment on immune response. Science. 2016;354: 64–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J Mach Learn Res. 2014;15: 1929–1958. [Google Scholar]
- 81.Ioffe S, Szegedy C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv [cs.LG]. 2015. Available: http://arxiv.org/abs/1502.03167 [Google Scholar]
- 82.Ba JL, Kiros JR, Hinton GE. Layer Normalization. arXiv [stat.ML]. 2016. Available: http://arxiv.org/abs/1607.06450 [Google Scholar]
- 83.Risso D, Perraudeau F, Gribkova S, Dudoit S, Vert J-P. A general and flexible method for signal extraction from single-cell RNA-seq data. Nat Commun. 2018;9: 284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Zhang X, Xu C, Yosef N. Simulating multiple faceted variability in single cell RNA sequencing. Nat Commun. 2019;10: 2611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Choudhary S, Satija R. Comparison and evaluation of statistical error models for scRNA-seq. doi: 10.1101/2021.07.07.451498 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Zou H, Hastie T, Tibshirani R. Sparse Principal Component Analysis. J Comput Graph Stat. 2006;15: 265–286. [Google Scholar]
- 87.Wolf FA, Angerer P, Theis FJ. SCANPY: large-scale single-cell gene expression data analysis. Genome Biol. 2018;19: 15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, et al. Scikit-learn: Machine Learning in Python. J Mach Learn Res. 2011;12: 2825–2830. [Google Scholar]
- 89.Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, et al. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat Methods. 2020;17: 261–272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Benjamini Y, Hochberg Y. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. Journal of the Royal Statistical Society: Series B (Methodological). 1995. pp. 289–300. doi: 10.1111/j.2517-6161.1995.tb02031.x [DOI] [Google Scholar]
- 91.Wolock SL, Lopez R, Klein AM. Scrublet: Computational Identification of Cell Doublets in Single-Cell Transcriptomic Data. Cell Syst. 2019;8: 281–291.e9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Keren-Shaul H, Kenigsberg E, Jaitin DA, David E, Paul F, Tanay A, et al. MARS-seq2.0: an experimental and analytical pipeline for indexed sorting combined with single-cell RNA sequencing. Nat Protoc. 2019;14: 1841–1862. [DOI] [PubMed] [Google Scholar]
- 93.Jaitin DA, Kenigsberg E, Keren-Shaul H, Elefant N, Paul F, Zaretsky I, et al. Massively parallel single-cell RNA-seq for marker-free decomposition of tissues into cell types. Science. 2014;343: 776–779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Gut G, Herrmann MD, Pelkmans L. Multiplexed protein maps link subcellular organization to cellular states. Science. 2018;361. doi: 10.1126/science.aar7042 [DOI] [PubMed] [Google Scholar]
- 95.Bankhead P, Loughrey MB, Fernández JA, Dombrowski Y, McArt DG, Dunne PD, et al. QuPath: Open source software for digital pathology image analysis. Sci Rep. 2017;7: 16878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Schindelin J, Arganda-Carreras I, Frise E, Kaynig V, Longair M, Pietzsch T, et al. Fiji: an open-source platform for biological-image analysis. Nat Methods. 2012;9: 676–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Linkert M, Rueden CT, Allan C, Burel J-M, Moore W, Patterson A, et al. Metadata matters: access to image data in the real world. J Cell Biol. 2010;189: 777–782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Lowe DG. Distinctive Image Features from Scale-Invariant Keypoints. International Journal of Computer Vision. 2004. pp. 91–110. doi: 10.1023/b:visi.0000029664.99615.94 [DOI] [Google Scholar]
- 99.Svensson V, Teichmann SA, Stegle O. SpatialDE - Identification of spatially variable genes. bioRxiv. 2017. p. 143321. doi: 10.1101/143321 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Arnol D, Schapiro D, Bodenmiller B, Saez-Rodriguez J, Stegle O. Modeling Cell-Cell Interactions from Spatial Molecular Data with Spatial Variance Component Analysis. Cell Rep. 2019;29: 202–211.e6. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The raw data discussed in this manuscript have been deposited in the National Center for Biotechnology Information’s Gene Expression Omnibus and are accessible through accession number GSE173778 (murine lymph node and tumor; spatial transcriptomics and scRNA-seq data). Processed sequencing data are available on our reproducibility repository (https://github.com/romain-lopez/DestVI-reproducibility).