Green Closed-Loop Supply Chain Network Design During the Coronavirus (COVID-19) Pandemic: a Case Study in the Iranian Automotive Industry

Abstract

This paper presents a new mathematical model of the green closed-loop supply chain network (GCLSCN) during the COVID-19 pandemic. The suggested model can explain the trade-offs between environmental (minimizing CO₂ emissions) and economic (minimizing total costs) aspects during the COVID-19 outbreak. Considering the guidelines for hygiene during the outbreak helps us design a new sustainable hygiene supply chain (SC). This model is sensitive to the cost structure. The cost includes two parts: the normal cost without considering the coronavirus pandemic and the cost with considering coronavirus. The economic novelty aspect of this paper is the hygiene costs. It includes disinfection and sanitizer costs, personal protective equipment (PPE) costs, COVID-19 tests, education, medicines, vaccines, and vaccination costs. This paper presents a multi-objective mixed-integer programming (MOMIP) problem for designing a GCLSCN during the pandemic. The optimization procedure uses the scalarization approach, namely the weighted sum method (WSM). The computational optimization process is conducted through Lingo software. Due to the recency of the COVID-19 pandemic, there are still many research gaps. Our contributions to this research are as follows: (i) designed a model of the green supply chain (GSC) and showed the better trade-offs between economic and environmental aspects during the COVID-19 pandemic and lockdowns, (ii) designed the hygiene supply chain, (iii) proposed the new indicators of economic aspects during the COVID-19 outbreak, and (iv) have found the positive (reducing CO₂ emissions) and negative (increase in costs) impacts of COVID-19 and lockdowns. Therefore, this study designed a new hygiene model to fill this gap for the COVID-19 condition disaster. The findings of the proposed network illustrate the SC has become greener during the COVID-19 pandemic. The total cost of the network was increased during the COVID-19 pandemic, but the lockdowns had direct positive effects on emissions and air quality.

Introduction

It is possible to quickly transmit COVID-19 from one person to another [1]. As a result of pandemics, supply chains (SCs) worldwide can become chaotic [2]. Lockdown policies and reduced physical contact are among the basic principles of the World Health Organization (WHO) in the conflict over COVID-19 [3]. Closed-loop supply chains (CLSCs) provide an alternative logistical method for dealing with environmental destruction and resource scarcity. In CLSCs, materials are controlled, emissions and waste are reduced, and the production process is cost-effective. In a CLSC, the material can be stored to minimize the environmental impact of SC activities [4]. A green closed-loop supply chain network (GCLSCN) has been identified as an important issue given the growing attention paid to environmental problems [5]. COVID-19’s continuing outbreak also impacts emissions in fundamental ways [6]. The emergence of environmental protection, client awareness, desire, and the development of carbon policies have all made reducing CO₂ emissions one of the primary objectives of supply chain design (SCD) [7]. During the COVID-19 pandemic and intense lockdowns, China reported a 25% reduction in CO₂ emissions [8]. Virus infections can cause disease, so the best method is to prevent them [9]. Therefore, we have suggested the following hygiene protocols during the COVID-19 pandemic in SC:

1. In addition to the existing shower installations, all facilities must have water, soap, alcohol, hand sanitizer, tissues, and bins at the entry.

2. The personnel who engage in high-risk activities are assigned appropriate PPE, which may include medical masks, gloves, face shields, goggles, and gowns.

3. All cleaning staff should be trained and provided with the PPE suitable for the task.

4. Disposing of face masks and disposable tissues with closed bins hygienically.

5. Publishing brochures about personal hygiene instructions.

6. Wash your hands after sneezing or coughing, before caring for patients and preparing food, and after using the toilet, door buttons, bags, boot buttons, printers, keyboard and mouse, and tables.

7. Handwashing procedures: (A) Use soap (liquid if possible) and running water (warm if possible). (B) Rub your hands with soap and water on your nails, fingers, and wrists for 20–30 s. (C) Rinse your hands carefully. (D) If possible, dry your hands with a paper towel. (E) Turn off the faucet with a paper towel and open the bathroom door. (F) Dispose of paper towels in the trash/closed trash.

8. If your hands are not contaminated with dirt or dust, you can use a gel or an alcohol-based hand sanitizer when you are not near the bath.

9. If you need to cough or sneeze, cover your face with your elbow or use a disposable tissue and instantly dispose it in a closed container. Wear masks to protect yourself and others. (Surgical masks are suggested).

10. The Proper Procedure for Wearing Face Masks: (A) Wash your hands thoroughly before using the mask. (B) Make sure your nose and mouth are closed and correct openings or gaps between the face and mask. (C) Do not touch the face or mask without washing your hands or cleaning with an alcohol-based product. (D) When removing the face mask, clean your hands first. (E) Put your face mask in a basket/bag/container/bin and immediately clean your hands with soap and water or a hand cleanser.

11. Do not share your personal belongings with other persons.

12. Observe social distancing (keep 2 m apart from others).

13. Clean and disinfect the items and surfaces you are dealing with.

14. Avoid touching the money directly and replace cash payments with credit payments [10].1

15. Avoid unnecessary travel.

16. Avoid physical meetings and hold online meetings.

17. Reduce working hours as much as possible.

18. Allow employees to work from home and reduce the number of employees working (if it is possible).

19. Reduce the number of employees working from offices [11, 12].

By incorporating economic and environmental performance indicators into the green supply chain network design (GSCND), the mathematical model of this paper aims to increase SC’s efficiency. Therefore, this study designed a new and hygienic GSCND model focusing on CO₂ emissions. The model described above is considered to provide five types of facilities. The forward flow begins with the extraction of raw materials in supplier centers and consigning them to the factories for producing a new product. A new/remanufactured/refurbished product is transferred along the forward way to satisfy the customer’s needs. In river logistics, the returned products are collected from customers and shipped to the collection/distribution centers. The returned products are examined and classified as suitable for remanufacturing and refurbishing, which are sent to the factories and the recycling/landfill centers. This article’s novelty is presenting multi-objective mixed-integer programming (MOMIP) and COVID-19 pandemic issues in a CLSC framework.

Related Works and Contributions

The literature review section has divided the research into three groups. The first category deals with carbon policy in the SC, the second is the effect of COVID-19 limitations on CO₂ emissions, and the third is recent supply chain issues.

Carbon Policy in the SC

The role of the carbon tax in a SC is to encourage the producer and the retailer to reduce emissions [13]. Zeballos et al. [14] dealt with various shipping costs in connection with real needs in CLSC design. Mohammed et al. [15] consider producing, warehousing, disposing, and recycling emissions in the CLSC. Different carbon rates are applied in each country, year, and analysis. According to Australia’s environmental policy in 2015, Zakeri et al. [16] applied a tax rate for CO₂ emissions trading from SCD. At the same time, Fareeduddin et al. [17] mention how Australia’s tax rate affects the supply chain network design (SCND). Paksoy et al. [18] offer a model for SCN with a bi-objective (BO) function that considers transport costs, greenhouse gas (GHG) emissions, and fuel consumption. To control for CO₂ emissions during transportation, determine the maximum CO₂ emissions for each manufacturing and recycling final product. Martí et al. [19] mention CO₂ emissions, including raw materials, production, storage, and transportation. Optimization and emission reduction in SC were based on carbon tax [20]. This policy is generally defined as the upper bound of carbon emission and must be enforced. The common carbon cap policy has been considered in some research for the GSCND. Many authors set a limitation in the manufacture, warehousing, transportation, and recycling [15, 17, 19, 21–24]. Other scholars consider the periodic or global carbon cap on the GSCND [25–29]. Coordination and decision-making in SC consider cap and trade [30]. The main source of GHG emissions is raw materials, considered by Abdallah et al. [31]. Kannan et al. [32] mention emissions in open facilities and transportation based on backward logistics, which minimizes the CO₂ footprint. Transport emissions, raw materials, open facilities, manufacturing, distribution centers, and electricity consumption are all included in articles on cap and trade. Chaabane et al. [97] and Rezaee et al. present a linear programming (LP) model, which contacts the CO₂ of production and transportation with the production scale [,]. In the context of cap and trade, outsourcing issues should be considered in SC [24, 32–35, 35]. Green supply chain concerns CO₂ emissions for agricultural products [36]. Designing the GCLSCN model focuses on CO₂ emissions [37].

CO₂ Emissions During the COVID-19

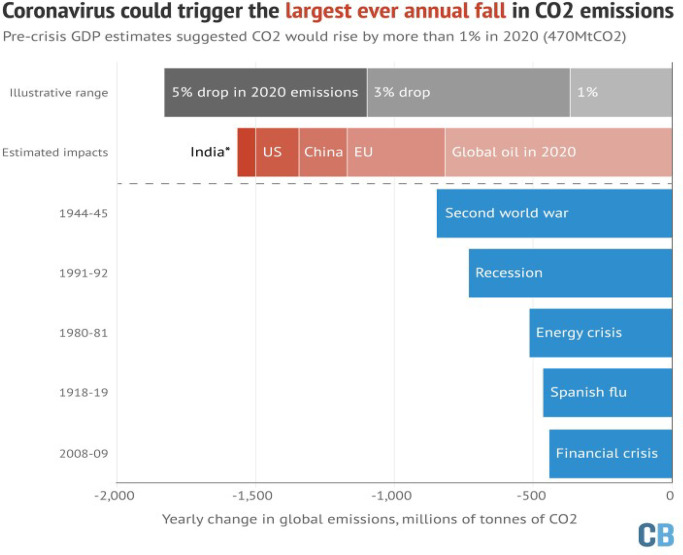
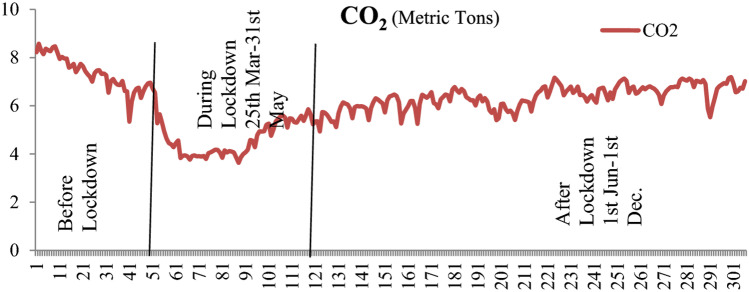
Information from the WHO demonstrates that GHG emissions rose to another record a couple of years ago. CO₂ emissions were higher in the last 5 years than in the previous 5 years [38]. It is assessed that the emissions from the world’s biggest carbon producer (China) over the last few days lowered by about 25% compared to the pre-COVID-19 outbreaks (nationalgeographic.com). The International Energy Agency (IEA) has anticipated that the CO₂ emission could fall by 8% during the lockdown days [39]. There is a possibility that emissions will fall by more than 5% in 2020, according to some estimates. It is the most significant yearly reduction so far [39]. Figure 1 analyzes the decrease in CO₂ emissions during the current outbreak with pandemics’ past significant events. The maximum reduction in CO₂ emissions during COVID-19 has been observed so far. In addition to reducing the spread of COVID-19, lockdowns also reduced human activity [40]. The new SC regarding hazardous gas emissions during the pandemic was proposed by Abbasi et al. [41]. As a result of the lockdown limitations, the amount of CO₂ released into the atmosphere has temporarily decreased [42]. During this pandemic, many emissions may be reduced due to the current lockdown condition since all major transportation activities have been stopped.

Fig. 1.

Change in the emission of CO₂ during the pandemic [8]

Recent Supply Chain Issues

Abbasi et al. [43] recently focused on designing sustainable recovery networks during the COVID-19 outbreak. Mosallanezhad et al. [44] developed a multi-objective (MO) metaheuristics approach for personal protection during the COVID-19 outbreak. Relief supply chain network during the COVID-19 pandemic and using the Internet of things (IoT) optimize the developed approaches [45]. In designing a model, the social aspect in CLSC was considered for the avocado industry [46]. A metaheuristic method for a dual-channel CLSCD was used in the tire industry under uncertainty [47]. Abdi et al. [48] developed a new stochastic model using stochastic programming for a closed-loop supply chain network (CLSCN). The metaheuristic method was also used for sugarcane supply chain network [49]. Ivanov and Das [50] concentrate on supply chain managers (SCMs) and SC resilience during COVID-19. A model for disruption risk is managing the SC during COVID-19 [51]. Rowan and Laffey [52] researched the shortage of SC for PPE during the COVID-19 pandemic. Ivanov [53] determined the future effect of the COVID-19 pandemic on the global supply chain, with a risk management approach. A sustainable blood supply chain considers social and environmental impacts [54]. Mosallanezhad et al. [55] designed a NP-hard model for the shrimp supply chain. Hobbs [56] researched on food supply chains and SC resilience during the COVID-19 outbreak. Ivanov and Dolgui [57] analyzed intertwined supply networks during COVID-19. Hajiaghaei-Keshteli and Fathollahi Fard [58] designed the sustainable closed-loop supply chain network (SCLSCN) design with discount supposition in the transportation costs. Free and Hecimovic [59] researched on supply and demand during and after COVID-19. Liao et al. [60] designed a CLSCN new mixed linear mathematical model for citrus fruit crates considering environmental and economic issues. Abdi et al. [61] designed and solved a new model using the metaheuristic green supply chain (GSC) method with simultaneous pickup and split delivery. Cheraghalipour et al. [62] suggested and solved a model with metaheuristic algorithms for the rice SC. Samadi et al. [63] developed a new model for discount supposition considering metaheuristic approaches. Illahi and Mir [64] researched the efficient logistics and SCM during and after COVID-19. Chouhan et al. [65] suggested a CLSCN for handling uncertain demands. Salehi-Amiri et al. [66] designed a SCLSCN for the walnut industry by using mixed-integer linear programming. Nandi et al. [67] used blockchain for redesigning SC during COVID-19. ‏Fasihi et al. [68] designed a fish CLSC by developing a BO mathematical model. Zahedi et al. [69] designed a CLSCN, considering multi-option transportation and multi-task sales agencies. The uncertainty of MO model for SC design considers reliability [70]. Fathollahi-Fard et al. [71] developed an objective model for a green home healthcare supply chain. The position of this research compared to that of previous research is shown in Table 1.

Table 1.

The recent research contribution of SC

Authors	Reference	Year	Focused CO2 emission	Focused hygienic cost	Focused closed-loop network	Focused COVID-19
Hajiaghaei-Keshteli and Fathollahi-Fard	[58]	2019			*
Samadi et al.	[63]	2020			*
Ivanov and Das	[50]	2020				*
Hobbs	[56]	2020				*
Liao et al.	[60]	2020	*		*
Rowan and Laffey	[52]	2020				*
Ivanov	[53]	2020				*
Chouhan et al.	[65]	2020			*
Ivanov and Dolgui	[57]	2020				*
Mosallanezhad et al.	[44]	2021				*
Zahedi et al.	[45]	2021				*
Fathollahi-Fard et al.	[47]	2021			*
Abdi et al.	[48]	2021			*
Chouhan et al.	[49]	2021			*
Shahed et al.	[51]	2021				*
Mousavi et al.	[54]	2021	*
Mosallanezhad et al.	[55]	2021			*
Free and Hecimovic	[59]	2021				*
Illahi and Mir	[64]	2021				*
Salehi-Amiri et al.	[66]	2021			*
Yachai et al.	[36]	2021	*
Kazancoglu et al.	[37]	2022	*		*
Nandi et al.	[67]	2021				*
Fasihi et al.	[68]	2021			*
Zahedi et al.	[45]	2021				*
Salehi-Amiri et al.	[46]	2022			*
Current research		2022	*	*	*	*

Research Gap and Innovation

Due to the recency of the COVID-19 pandemic, there are still many research gaps. The research papers in Table 1 have not simultaneously considered CO₂ emission, hygienic cost, and COVID-19 pandemic issues in the CLSC framework. In this paper, we develop concepts of GSCND. In summary, the suggested paper shows some concerns that cover the literature gaps, and innovation can be categorized as follows:

1. Designing a hygienic SC.

2. Designing a new GSC considering pandemics in two dimensions of sustainability:

   • Calculating COVID-19 hygiene costs in addition to the normal condition to develop economic aspects.
   • Developing the environmental aspects by considering the reduction of CO₂ emissions during the COVID-19 lockdowns.

3. In this paper, the distribution center is merged with the collection center to prevent physical contact with customers during the COVID-19 outbreak.

4. This paper presents a MOMIP model and COVID-19 pandemic issues in the CLSC framework.

Therefore, this study designed a new and hygienic GSC model to fill this gap in the COVID-19 disaster.

Mathematical Model

The GSC covers both aspects (economic and environmental) of sustainability. Recycling is an environmentally friendly process that can save costs and improve economic efficiency. CLSC integrates a forward supply chain (FSC) with a reverse supply chain (RSC). In this article, the distribution center (DC) is merged with the collection center (CC) during the COVID-19 pandemic for the following reasons: reducing building costs, reducing CO₂ emission, reducing environmental pollution, and preventing physical contact of customers (observance of social distancing). To increase the efficiency of SC, this mathematical model has been designed by incorporating economic and environmental performance indicators into the GSCND during the COVID-19 pandemic. In addition to a total cost measure to calculate all the monetary expenditure in a specific SC design and environmental and social efficiency that are measured indexes used in a mathematical modeling method, multi-objective optimization (MOO) is fulfilled to create the GSC. The model will allow us to achieve the best design of the SC, determining which facilities (suppliers–factories–distribution/collection centers–recycling/landfill centers) should be included in the network, recognizing the flows of units of product among different echelons. This research provides useful information to DMs for helpful information, judgments, and ultimately creating more sustainable decisions during the pandemic. The explanation of the suggested mathematical model for GSC design is delineated in four subsections: problem statement and assumptions, model components, formulation process, and multi-objective (MO) approach.

Problem Statement and Assumptions

The mathematical model described above is considered to provide five types of facilities:

• Suppliers (S),

• Production/Remanufacturing/Refurbishing centers (Factories) (F),

• Collection/Distribution centers (CDC),

• Customers (C),

• Recycling/landfill centers (RLC).

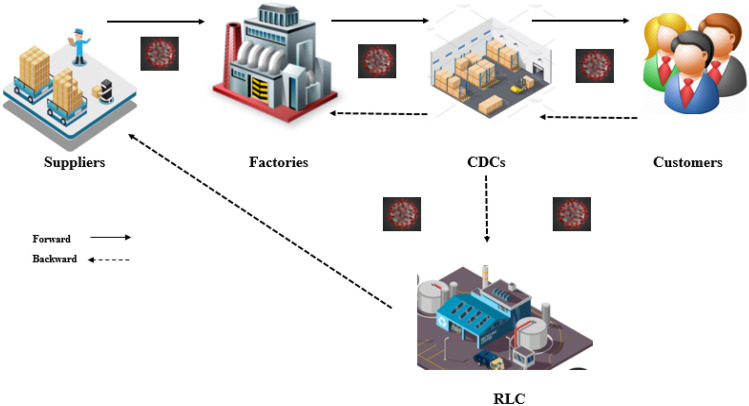
In the forward flow, raw materials are extracted in supplier centers and consigned to factories for manufacture. To satisfy customer needs, new/remanufactured/refurbished products are transferred through the forward supply chain (from factories to CDCs and from CDCs to customers). Customer-returned products are collected by the reverse supply chain (RSC) and shipped to the CDCs. Those products that qualify for remanufacturing and refurbishing are sent to factories, while those that do not are sent to RLCs for landfilling and recycling. According to its specifications, this product is considered end of life (EOL). Figure 2 shows the designed schematic of the problem.

Fig. 2.

The logistics networks between echelons are depicted

It is necessary to make certain assumptions to design a mathematical model:

• The COVID-19 outbreak is considered in the supply chain thoroughly.

• The cost of the model includes regular and hygienic.

• The DC is merged with the CC to observe social distancing during the COVID-19 pandemic.

• All customer demand was always satisfied during the COVID-19 pandemic and lockdowns with every factory through every CDC.

• It is assumed that a determined percentage of the total demand is disposed of.

• The COVID-19 hygiene protocol is followed for all returned products that enter RLCs for disposal.

• Customer demand and product returns are inevitable.

• The locations of Fs, CDCs, and RLCs are potential.

• The locations of suppliers and customers exist.

• There are several shipping alternatives for each connection (e.g., road/rail/air/sea).

• All shipping alternatives have unlimited capacities.

• Distances between network nodes should be feasible.

• The network consists of both forward and reverse flows (closed-loop).

Model Components

The SC model includes the sets, parameters, and variables described as follows: The sets S, F, I, B, and C contain the existing suppliers, the potential factories, the potential CDCs, the potential RLCs, and the existing customers, respectively. The sets TS, TF, TI, TC, and TB include the shipping options from suppliers, factories, CDCs, customers, and RLCs, respectively. The model’s parameters are technical parameters, economic parameters, and environmental parameters. Binary and non-negative, continuous decision variables are applied to implement the goals of the mathematical model, namely assign the GSC network and the number of units of products that flow through the network.

The hygiene costs for prevention and control of COVID-19 include the following:

• Disinfection costs,

• Hand sanitizer costs,

• The costs of PPE (Shield–Mask–Gown–Gloves)

• COVID-19 tests costs (Normal–Fast),

• COVID-19 education costs,

• The costs of COVID-19 medicines, vaccines, and vaccination [6, 72].

The following are positive impacts of COVID-19 and lockdown on the environment:

• Reducing CO₂ emissions and industrial activities

• Reducing CO₂ emissions and shipping activities

The negative impact of COVID-19 on the environment is as follows:

• Increased medical waste during the COVID-19 pandemic.

.       IncreasedPPE waste disposal increased during the COVID-19 pandemic (plastic waste–soil and water pollution) [73–79, 95].

Notations

In this section, notations for the mathematical model are explained (Tables 2, 3, 4, 5, and 6).

Table 2.

Indices

$s=\{1,2,...,S\}$	Set of fixed locations for suppliers,
$f=\{1,2,...,F\}$	Set of potential locations for factories,
$i=\{1,2,...,I\}$	Set of potential locations for CDCs,
$c=\{1,2,...,C\}$	Set of fixed locations for customers,
$b=\{1,2,...,B\}$	Set of potential locations for RLCs,
$ts=\{1,2,...,TS\}$	Set of shipping alternatives from suppliers,
$f=\{1,2,...,TF\}$	Set of shipping alternatives from factories,
$ti=\{1,2,...,TI\}$	Set of shipping alternatives from CDCs,
$tc=\{1,2,...,TC\}$	Set of shipping alternatives from customers,
$tb=\{1,2,...,TB\}$	Set of shipping alternatives from RLCs,

Table 3.

Technical parameters

$d_c$	The demand of customer c,
$M$	Maximum supplier extraction capacity,
$M_f$	Maximum factory production capacity,
$M_i$	Maximum CDC collection/distribution capacity,
$M_b$	Maximum RLC recycling/landfilling capacity,
$M{r}_f$	Maximum factory remanufacturing and refurbishing capacity,
$M{N}_{\text{dismantled}}$	Minimum percentage of the returned product to be remanufactured (unit),
$M{N}_{\text{disposed}}$	Minimum percentage of the returned product to be recycled and landfilled (unit),
${\gamma }_{\mathit{sf}}^{\mathit{ts}}$	Shipping rate from the supplier s to factory f with shipping alternative ts,
${\gamma }_{\mathit{fi}}^{\mathit{tf}}$	Shipping rate from factory f to CDC i with shipping alternative tf,
${\gamma }_{\mathit{if}}^{\mathit{ti}}$	Shipping rate from CDC i to factory f with shipping alternative ti,
${\gamma }_{\mathit{ic}}^{\mathit{ti}}$	Shipping rate from CDC i to customer c with shipping alternative ti,
${\gamma }_{\mathit{ci}}^{\mathit{tc}}$	Shipping rate from customer c to CDC i with shipping alternative tc,
${\gamma }_{\mathit{ib}}^{\mathit{ti}}$	Shipping rate from CDC i to RLC b with shipping alternative ti,
${\gamma }_{\mathit{bs}}^{\mathit{tb}}$	Shipping rate from RLC b to supplier s with shipping alternative tb,
${\delta }_{\mathit{sf}}$	Distance between supplier s and factory f,
${\delta }_{\mathit{fi}}$	Distance between factory f and CDC i,
${\delta }_{\mathit{if}}$	Distance between CDC i and factory f,
${\delta }_{\mathit{ic}}$	Distance between CDC i and customer c,
${\delta }_{\mathit{ci}}$	Distance between customer c and CDC i,
${\delta }_{\mathit{ib}}$	Distance between CDC i and RLC b,
${\delta }_{\mathit{bs}}$	Distance between RLC b and supplier s,

Table 4.

Economic parameters

$F_f$	Fixed cost for opening factory f during the COVID-19 pandemic,
$F_i$	Fixed cost for opening CDC i during the COVID-19 pandemic,
$F_b$	Fixed cost for opening RLC b during the COVID-19 pandemic,
$V_s$	The variable cost for extracting a unit of raw material from the supplier s,
$V_f$	The variable cost for producing a unit of product in the factory f,
$V_i$	The variable cost for distribution a unit of product in the CDC i,
$V{r}_i$	The variable cost for collecting, inspecting, consolidating, and sorting a unit of the returned product in the CDC i,
$V_b$	The variable cost for recycling and landfilling a unit of the returned product in RLC b,
$V{r}_f$	The variable cost for remanufacturing and refurbishing a unit of the returned product in the factory f,
$TC{O}_{\mathit{sf}}^{\mathit{ts}}$	The shipping cost of a unit of raw material from the supplier s to factory f with alternative shipping ts,
$TC{O}_{\mathit{fi}}^{\mathit{tf}}$	The shipping cost of a unit product from factory f to CDC i with alternative shipping tf,
$TC{O}_{\mathit{ic}}^{\mathit{ti}}$	The shipping cost of a unit of product from CDC i to customer c with alternative shipping ti,
$TC{O}_{\mathit{ci}}^{\mathit{ti}}$	The shipping cost of a unit of the returned product that is collected from customer c to CDC i with alternative shipping tc,
$TC{O}_{\mathit{if}}^{\mathit{ti}}$	The shipping cost of a unit of the returned product that is available for remanufacturing and refurbishing from CDC i to factory f with alternative shipping ti,
$TC{O}_{\mathit{ib}}^{\mathit{ti}}$	The shipping cost of a unit of returned product that is unsuitable for remanufacturing and refurbishing, from CDC i to RLC b with alternative shipping ti,
$TC{O}_{\mathit{bs}}^{\mathit{tb}}$	The shipping cost of a unit of recycled product from RLC b to supplier s with alternative shipping tb,
$H{V}_s$	The cost of COVID-19 prevention and control while extracting a unit of raw material from the supplier s,
$H{V}_f$	The cost of COVID-19 prevention and control during production of a unit of product in the factory f,
$H{V}_i$	The cost of COVID-19 prevention and control for distributing a unit of product from the CDC i,
$HV{r}_i$	The cost of COVID-19 prevention and control for collecting, inspecting consolidation, and sorting a unit of the returned product in the CDC i,
$H{V}_b$	The cost of COVID-19 prevention and control for recycling and landfilling a unit of the returned product in the RLC b,
$HV{r}_f$	The cost of COVID-19 prevention and control for remanufacturing and refurbishing a unit of the returned product in the factory f,
$HT{C}_{\mathit{sf}}^{\mathit{ts}}$	The cost of COVID-19 prevention and control during the shipping of a unit of raw material from the supplier s to factory f with alternative shipping ts,
$HT{C}_{\mathit{fi}}^{\mathit{tf}}$	The cost of COVID-19 prevention and control during the shipping of a unit of product from factory f to CDC i with alternative shipping tf,
$HT{C}_{\mathit{ic}}^{\mathit{ti}}$	The cost of COVID-19 prevention and control during the shipping of a unit of product from CDC i to customer c with alternative shipping ti,
$HT{C}_{\mathit{ci}}^{\mathit{tc}}$	The cost of COVID-19 prevention and control during the shipping of a unit of returned product from customer c to CDC i with alternative shipping tc,
$HT{C}_{\mathit{if}}^{\mathit{ti}}$	The cost of COVID-19 prevention and control during the shipping of a unit of the returned product that is available for remanufacturing and refurbishing from CDC i to factory f with alternative shipping ti,
$HT{C}_{\mathit{ib}}^{\mathit{ti}}$	The cost of COVID-19 prevention and control during the shipping of a unit of returned product that is unsuitable for remanufacturing and refurbishing from CDC i to RLC b with alternative shipping ti,
$HT{C}_{\mathit{bs}}^{\mathit{tb}}$	The cost of COVID-19 prevention and control during the shipping of a unit of recycled product from RLC b to supplier s with alternative shipping tb,

Table 5.

Environmental parameters

$e_s$	The rate of CO2 released to extract a unit of raw material in supplier s during the COVID-19 pandemic and lockdown days,
$e_f$	The rate of released CO2 to produce a unit of product in factory f during the COVID-19 pandemic and lockdown days,
$e_i$	The rate of CO2 released to handle and distribute 1 unit of product in the CDC i during the COVID-19 pandemic and lockdown days,
$e{r}_i$	The rate of CO2 released to collect, inspect, consolidate, and sort 1 unit of the returned product in the CDC i during the COVID-19 pandemic and lockdown days,
$e{r}_f$	The rate of CO2 released to remanufacture 1 unit of the returned product in the factory f during the COVID-19 pandemic and lockdown days,
$e{r}_b$	The rate of CO2 released to recycle and landfill 1 unit of the returned product in RLC b during the COVID-19 pandemic and lockdown days,
$ET{C}_{\mathit{sf}}^{\mathit{ts}}$	CO2 released by shipping alternative ts to send a unit of raw material from supplier s to factory f for a unit distance during the COVID-19 pandemic and lockdown days,
$ET{C}_{\mathit{fi}}^{\mathit{tf}}$	CO2 released by shipping alternative tf to send a unit of product from factory f to CDC i for a unit distance during the COVID-19 pandemic and lockdown days,
$ET{C}_{\mathit{ic}}^{\mathit{ti}}$	CO2 released by shipping alternative ti to send a unit of product from CDC i to customer c for a unit distance during the COVID-19 pandemic and lockdown days,
$ETC{R}_{\mathit{ci}}^{\mathit{tc}}$	CO2 released by shipping alternative tc to collect a unit of returned production from customer c to CDC i for a unit distance during the COVID-19 pandemic and lockdown days,
$ETC{R}_{\mathit{if}}^{\mathit{ti}}$	CO2 released by shipping alternative ti to send a unit of the returned product to be remanufactured from CDC i to factory f for a unit distance during the COVID-19 pandemic and lockdown days,
$ETC{R}_{\mathit{ib}}^{\mathit{ti}}$	CO2 released by shipping alternative ti to send a unit of returned production from CDC i to RLC b for a unit distance during the COVID-19 pandemic and lockdown days,
$ETC{R}_{\mathit{bs}}^{\mathit{tb}}$	CO2 released by shipping alternative tb to send a unit of returned production from RLC b to supplier s for a unit distance during the COVID-19 pandemic and lockdown days,

Table 6.

Variables

$x_f$	If factory f is open, equals 1; otherwise 0.
$x_i$	If CDC i is open, equals 1; otherwise 0.
$x_b$	If RLC b is open, equals 1; otherwise 0.
$Y_{\mathit{sf}}^{\mathit{ts}}$	Quantity of units of raw material sent from supplier s to factory f with shipping alternative ts,
$Y_{\mathit{fi}}^{\mathit{tf}}$	Quantity of units of product sent from factory f to CDC i with shipping alternative tf,
$Y_{\mathit{ic}}^{\mathit{ti}}$	Quantity of units of product sent from CDC i to customer c with shipping alternative ti,
$Y_{\mathit{ci}}^{\mathit{tc}}$	Quantity of units of returned product collected from customer c to CDC i with shipping alternative tc,
$Y_{\mathit{if}}^{\mathit{ti}}$	Quantity of units of returned product available for remanufacturing and refurbishing sent from CDC i to factory f with shipping alternative ti,
$Y_{\mathit{ib}}^{\mathit{ti}}$	Quantity of units of returned product unsuitable for remanufacturing and refurbishing sent from CDC i to RLC b with shipping option ti,
$Y_{\mathit{bs}}^{\mathit{tb}}$	Quantity of units of recycled product sent from RLC b to supplier s with shipping option tb,

Formulation Process

A mathematical optimization model consists of two parts: objective functions and constraints. The model’s objectives are to minimize costs (economic aspect) and CO₂ emissions (environmental aspect) during COVID-19 lockdown days. The bi-objective design of the network during the pandemic and lockdown periods is formulated as follows: The mathematical formulation of the objective functions is described in Eqs. (1)–(2), and the constraints of the mathematical model are given in Eqs. (3)–(18). The total cost is the summation of the total fixed cost (TF), the total variable cost (TV), the total hygiene cost (TH), and the total shipping cost (TS). The total emission of CO₂ is calculated by adding the total CO₂ due to working facilities (EM), such as extracting raw materials, producing, remanufacturing, refurbishing, recycling, and landfilling, and the total CO₂ due to shipping (ES). It is assumed that all emissions of CO₂ are in this model with the observance of hygienic protocol during the COVID-19 pandemic and lockdowns.

$$\mathrm{Min}{Z}_1=TF+TV+TH+TS$$ 1

$$TF=\sum _f{F}_f{x}_f+\sum _i{F}_i{x}_i+\sum _b{F}_b{x}_b$$ 1.1

$$\begin{array}{cc}\hfill TV=& \sum _s{V}_s\sum _f\sum _{\mathit{ts}}{Y}_{\mathit{sf}}^{\mathit{ts}}+\sum _f{V}_f\sum _i\sum _{\mathit{tf}}{Y}_{\mathit{fi}}^{\mathit{tf}}\hfill \\ \hfill & +\sum _i{V}_i\sum _c\sum _{\mathit{ti}}{Y}_{\mathit{ic}}^{\mathit{ti}}+\sum _{i}V{r}_i\sum _c\sum _{\mathit{tc}}{Y}_{\mathit{ci}}^{\mathit{tc}}\hfill \\ \hfill & +\sum _{f}V{r}_f\sum _i\sum _{\mathit{ti}}{Y}_{\mathit{if}}^{\mathit{ti}}+\sum _b{V}_b\sum _i\sum _{\mathit{ti}}{Y}_{\mathit{ib}}^{\mathit{ti}}\hfill \end{array}$$ 1.2

$$\begin{array}{c}TH=\sum _{s}H{V}_s\sum _f\sum _{\mathit{ts}}{Y}_{\mathit{sf}}^{\mathit{ts}}+\sum _{f}H{V}_f\sum _i\sum _{\mathit{tf}}{Y}_{\mathit{fi}}^{\mathit{tf}}+\sum _{i}H{V}_i\sum _c\sum _{\mathit{ti}}{Y}_{\mathit{ic}}^{\mathit{ti}}+\sum _{i}HV{r}_i\sum _c\sum _{\mathit{tc}}{Y}_{\mathit{ci}}^{\mathit{tc}}+\sum _{f}HV{r}_f\sum _i\sum _{\mathit{ti}}{Y}_{\mathit{if}}^{\mathit{ti}}+\sum _{b}H{V}_b\sum _i\sum _{\mathit{ti}}{Y}_{\mathit{ib}}^{\mathit{ti}}\\ +\sum _s\sum _f\sum _{\mathit{ts}}{\mathit{HTC}}_{\mathit{sf}}^{\mathit{ts}}{Y}_{\mathit{sf}}^{\mathit{ts}}+\sum _f\sum _i\sum _{\mathit{tf}}{\mathit{HTC}}_{\mathit{fi}}^{\mathit{tf}}{Y}_{\mathit{fi}}^{\mathit{tf}}+\sum _i\sum _c\sum _{\mathit{ti}}{\mathit{HTC}}_{\mathit{ic}}^{\mathit{ti}}{Y}_{\mathit{ic}}^{\mathit{tc}}+\sum _c\sum _i\sum _{\mathit{tc}}{\mathit{HTC}}_{\mathit{ci}}^{\mathit{tc}}{Y}_{\mathit{ci}}^{\mathit{tc}}+\sum _i\sum _f\sum _{\mathit{ti}}{\mathit{HTC}}_{\mathit{if}}^{\mathit{ti}}{Y}_{\mathit{if}}^{\mathit{ti}}\\ +\sum _i\sum _b\sum _{\mathit{ti}}{\mathit{HTC}}_{\mathit{ib}}^{\mathit{ti}}{Y}_{\mathit{ib}}^{\mathit{ti}}+\sum _b\sum _s\sum _{\mathit{tb}}{\mathit{HTC}}_{\mathit{bs}}^{\mathit{tb}}{Y}_{\mathit{bs}}^{\mathit{tb}}\end{array}$$ 1.3

$$\begin{array}{c}TS=\sum _s\sum _f\sum _{\mathit{ts}}{\mathit{TCO}}_{\mathit{sf}}^{\mathit{ts}}{Y}_{\mathit{sf}}^{\mathit{ts}}+\sum _f\sum _i\sum _{\mathit{tf}}{\mathit{TCO}}_{\mathit{fi}}^{\mathit{tf}}{Y}_{\mathit{fi}}^{\mathit{tf}}+\sum _i\sum _c\sum _{\mathit{ti}}{\mathit{TCO}}_{\mathit{ic}}^{\mathit{ti}}{Y}_{\mathit{ic}}^{\mathit{ti}}+\sum _c\sum _i\sum _{\mathit{tc}}{\mathit{TCO}}_{\mathit{ci}}^{\mathit{tc}}{Y}_{\mathit{ci}}^{\mathit{tc}}+\sum _i\sum _f\sum _{\mathit{ti}}{\mathit{TCO}}_{\mathit{if}}^{\mathit{ti}}{Y}_{\mathit{if}}^{\mathit{ti}}\\ +\sum _i\sum _b\sum _{\mathit{ti}}{\mathit{TCO}}_{\mathit{ib}}^{\mathit{ti}}{Y}_{\mathit{ib}}^{\mathit{ti}}+\sum _b\sum _s\sum _{\mathit{tb}}{\mathit{TCO}}_{\mathit{bs}}^{\mathit{tb}}{Y}_{\mathit{bs}}^{\mathit{tb}}\end{array}$$ 1.4

$$\mathrm{Min}{Z}_2=EM+ES$$ 2

$$EM=\sum _s{e}_s\sum _f\sum _{\mathit{ts}}{Y}_{\mathit{sf}}^{\mathit{ts}}+\sum _f{e}_f\sum _i\sum _{\mathit{tf}}{Y}_{\mathit{fi}}^{\mathit{tf}}+\sum _i{e}_i\sum _c\sum _{\mathit{ti}}{Y}_{\mathit{ic}}^{\mathit{ti}}+\sum _{i}e{r}_i\sum _c\sum _{\mathit{tc}}{Y}_{\mathit{ci}}^{\mathit{tc}}+\sum _{f}e{r}_f\sum _i\sum _{\mathit{ti}}{Y}_{\mathit{if}}^{\mathit{ti}}+\sum _{b}e{r}_b\sum _i\sum _{\mathit{ti}}{Y}_{\mathit{ib}}^{\mathit{ti}}$$ 2.1

$$\begin{array}{c}ES=\sum _s\sum _f\sum _{\mathit{ts}}{{\mathit{ETC}}_{\mathit{sf}}^{\mathit{ts}}Y}_{\mathit{sf}}^{\mathit{ts}}{\delta }_{\mathit{sf}}{\gamma }_{\mathit{sf}}^{\mathit{ts}}+\sum _f\sum _i\sum _{\mathit{tf}}{\mathit{ETC}}_{\mathit{fi}}^{\mathit{tf}}{Y}_{\mathit{fi}}^{\mathit{tf}}{\delta }_{\mathit{fi}}{\gamma }_{\mathit{fi}}^{\mathit{tf}}+\sum _i\sum _c\sum _{\mathit{ti}}{\mathit{ETC}}_{\mathit{ic}}^{\mathit{ti}}{Y}_{\mathit{ic}}^{\mathit{ti}}{\delta }_{\mathit{ic}}{\gamma }_{\mathit{ic}}^{\mathit{ti}}\\ +\sum _c\sum _i\sum _{\mathit{tc}}{\mathit{ETCR}}_{\mathit{ci}}^{\mathit{tc}}{Y}_{\mathit{ci}}^{\mathit{tc}}{{\delta }_{\mathit{ci}}\gamma }_{\mathit{ci}}^{\mathit{tc}}+\sum _i\sum _f\sum _{\mathit{ti}}{\mathit{ETCR}}_{\mathit{if}}^{\mathit{ti}}{Y}_{\mathit{if}}^{\mathit{ti}}{{\delta }_{\mathit{if}}\gamma }_{\mathit{if}}^{\mathit{ti}}+\sum _i\sum _b\sum _{\mathit{ti}}{\mathit{ETCR}}_{\mathit{ib}}^{\mathit{ti}}{Y}_{\mathit{ib}}^{\mathit{ti}}{{\delta }_{\mathit{ib}}\gamma }_{\mathit{ib}}^{\mathit{ti}}\\ +\sum _b\sum _s\sum _{\mathit{tb}}{\mathit{ETCR}}_{\mathit{bs}}^{\mathit{tb}}{Y}_{\mathit{bs}}^{\mathit{tb}}{\delta }_{\mathit{bs}}{\gamma }_{\mathit{bs}}^{\mathit{tb}}\end{array}$$ 2.2

Subject to:

$$\begin{array}{cc}\sum _{s\in S}\sum _{ts\in TS}{Y}_{\mathit{sf}}^{\mathit{ts}}\le M_f{x}_f& {}_{\forall f\in F}\end{array}$$ 3

Constraint (3) describes the total number of row material units that enter a factory from any suppliers via any transportation options which should be lower or equal to the maximum capacity of the respective factory.

$$\begin{array}{cc}\sum _{f\in F}\sum _{tf\in TF}{Y}_{\mathit{fi}}^{\mathit{tf}}\le M_{i}x{}_i& {}_{\forall i\in I}\end{array}$$ 4

Constraint (4) states that the total number of product units that enter a CDC from any factories via any transportation options should be lower or equal to the maximum capacity of the respective CDC.

$$\begin{array}{cc}\sum _{i\in I}\sum _{ti\in TI}{Y}_{\mathit{ib}}^{\mathit{ti}}\le M_{b}x{}_b& {}_{\forall b\in B}\end{array}$$ 5

Constraint (5) shows that the total number of returned product units to be recycled, incinerated, and landfilled collected from any customers to an RLC via any transportation options should be lower or equal to the maximum capacity of the respective RLC.

$$\begin{array}{cc}\sum _{i\in I}\sum _{ti\in TI}{Y}_{\mathit{if}}^{\mathit{ti}}\le M{r}_{f}x{}_f& {}_{\forall f\in F}\end{array}$$ 6

Constraint (6) presents the total number of returned product units shipped from a CDC to any factories via any transportation options which should be lower or equal to the respective factory’s maximum remanufacturing and refurbishing capacity.

$$\begin{array}{cc}\sum _{c\in C}\sum _{tc\in TC}{Y}_{\mathit{ci}}^{\mathit{tc}}\le M{r}_{i}x{}_i& {}_{\forall i\in I}\end{array}$$ 7

Constraint (7) describes the total number of returned product units shipped from a customer to any CDCs via any transportation options which should be lower or equal to the maximum collecting capacity of the respective CDC.

$$\begin{array}{cc}\sum _{i\in I}\sum _{tf\in TF}{Y}_{\mathit{fi}}^{\mathit{tf}}\le \sum _{f\in F}\sum _{ts\in TS}{Y}_{\mathit{sf}}^{\mathit{ts}}& {}_{\forall f\in F}\end{array}$$ 8

Constraint (8) explains that the total number of product units shipping from a factory to any CDCs via any transportation options should be lower or equal to the total number of raw material units shipping from a supplier to any factories.

$$\begin{array}{cc}\sum _{c\in C}\sum _{ti\in TI}{Y}_{\mathit{ic}}^{\mathit{ti}}\le \sum _{i\in I}\sum _{tf\in TF}{Y}_{\mathit{fi}}^{\mathit{tf}}& {}_{\forall i\in I}\end{array}$$ 9

Constraint (9) illustrates that the total number of product units shipping from a CDC to any customers via any transportation options should be lower or equal to the total number of products shipping from a factory to any CDCs.

$$\begin{array}{cc}\sum _{b\in B}\sum _{ti\in TI}{Y}_{\mathit{ib}}^{\mathit{ti}}\le \sum _{i\in I}\sum _{tf\in TF}{Y}_{\mathit{fi}}^{\mathit{tf}}& {}_{\forall i\in I}\end{array}$$ 10

Constraint (10) shows that the total number of product units shipping from a CDC to any RLCs via any transportation options should be lower or equal to the total number of products shipping from a factory to any CDCs.

$$\begin{array}{cc}\sum _{f\in F}\sum _{ti\in TI}{Y}_{\mathit{if}}^{\mathit{ti}}\le \sum _{i\in I}\sum _{tf\in TF}{Y}_{\mathit{fi}}^{\mathit{tf}}& {}_{\forall i\in I,\forall f\in F}\end{array}$$ 11

Constraint (11) describes that the total number of returned product units shipping from a CDC to any factories via any transportation options should be lower or equal to the total number of product units shipping from a factory to any CDCs.

$$\begin{array}{cc}\sum _{i\in I}\sum _{tc\in TC}{Y}_{\mathit{ci}}^{\mathit{tc}}\le \sum _{c\in C}\sum _{ti\in TI}{Y}_{\mathit{ic}}^{\mathit{ti}}& {}_{\forall i\in I,\forall c\in C}\end{array}$$ 12

Constraint (12) states that the total number of returned product units shipping from a customer to any CDCs via any transportation options should be lower or equal to the total number of product units shipping from a CDC to any customers.

$$\begin{array}{cc}{d}_c\le \sum _i\sum _{\mathit{ti}}{Y}_{\mathit{ic}}^{\mathit{ti}}& {}_{\forall c\in C}\end{array}$$ 13

Constraint (13) shows that the total number of product units distributed from any CDCs via any transportation options to satisfy a customer’s demand should be higher or equal to the respective demand of the customer.

$$\begin{array}{cc}\sum _c\sum _{\mathit{tc}}{Y}_{\mathit{ci}}^{\mathit{tc}}\le d_c& {}^{\forall c\in C}\end{array}$$ 14

Constraint (14) describes that the total number of returned product units collected from a customer to any CDCs via any transportation options should be lower than the respective customer demand.

$$\begin{array}{cc}M{N}_{\text{disposed}}·d_c\le \sum _i\sum _{\mathit{tc}}{Y}_{\mathit{ci}}^{\mathit{tc}}& {}^{\forall c\in C}\end{array}$$ 15

Constraint (15) states that the total number of product units to be recycled, incinerated, and landfilled sent to any RLCs via any transportation options from a customer should be higher or equal to the minimum percentage of restitution from the total number of demands of the respective customer.

$$\begin{array}{cc}\sum _{f\in F}\sum _{ti\in TI}{Y}_{\mathit{if}}^{\mathit{ti}}\ge M{N}_{\text{dismantled}}\sum _{c\in C}\sum _{ti\in TI}{Y}_{\mathit{ci}}^{\mathit{ti}}& {}^{\forall i\in I}\end{array}$$ 16

Constraint (16) shows that the total number of products units to be refurbished and remanufactured delivered to any factories from a CDC via any transportation options should be greater or equal to the minimum percentage of product units to be remanufactured from the total amount of units of returned product.

$$\begin{array}{cc}{Y}_{\mathit{sf}}^{\mathit{ts}},Y_{\mathit{fi}}^{\mathit{tf}},Y_{\mathit{ic}}^{\mathit{ti}},Y_{\mathit{ci}}^{\mathit{tc}},Y_{\mathit{if}}^{\mathit{ti}},Y_{\mathit{ib}}^{\mathit{ti}},Y_{\mathit{bs}}^{\mathit{tb}}\ge 0& {}_{\forall s\in S;\forall f\in F;\forall i\in I;\forall b\in B;\forall c\in C;\forall ts\in TS;\forall tf\in TF;\forall ti\in TI;\forall tb\in TB;\forall tc\in TC}\end{array}$$ 17

Constraint (17) describes the total number of raw materials, products, and returned products that flowed from a supplier to a factory via transportation options, a factory to a CDC via transportation options, a CDC to a customer center via transportation options, a customer center to a CDC via transportation options, and a CDC to a RLC and a factory via transportation options should be higher or equal to zero.

$$\begin{array}{cc}{X}_f,X_i,X_b\in \left\{0,,,1\right\}& {}_{\forall f\in F;\forall i\in I;\forall b\in B}\end{array}$$ 18

Constraint (18) explains the binary numbers used to describe the potential of facilities (Factories, CDCs, and RLCs).

Multi-objective optimization problem (MOOP) Approach

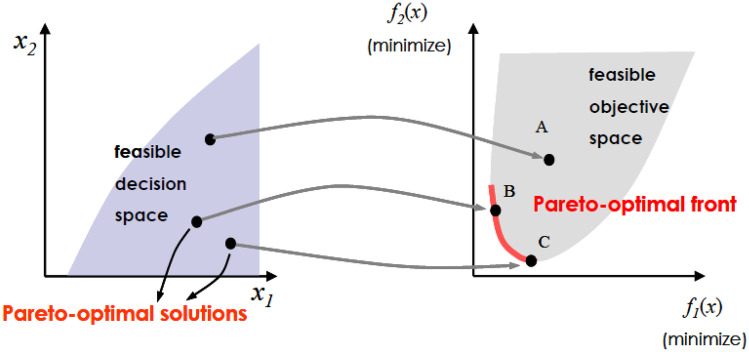
The multi-objective optimization problems (MOOPs) consist of two or more objective functions that must be minimized or maximized. A set of solutions defines the best trade-offs between competing objectives in a single-objective optimization problem (SOOP). Considering a set of solutions, the non-dominant solution set is the set of all solutions that the members of the solution group do not dominate. The non-dominant group of fully feasible decision space is called the Pareto-optimal set (POS). The boundary defined by the set of all mapped points in the POS is called the Pareto-optimal front (POF).

The aims of MOOP are as follows:

• To achieve a set of solutions as close to POF as possible.

• To achieve a set of solutions as diverse as possible [80].

Scalarization Methods

MOOP is traditionally solved by scalarization, which involves formulating a SOOP corresponding to the MOOP [81].

$$\mathrm{Min}(\mathrm{f}1(\times ),\cdots ,\mathrm{fp}(\times ))$$ 19

$$x\in X$$ 20

The weighted sum method (WSM) uses the vector of weights λ ∈ R^p ≥ as a parameter [81].

$$\mathrm{Min}\left({\sum }_{k=1}^p,{\lambda }_k,,f_k,(x)\right)$$ 21

$$x\in X$$ 22

An approach to managing WSM is to weigh each aspect and minimize the weighted sum of all elements. The main advantage of this approach is to model and solve MOP with SO methods [82]. Figure 3 illustrates the Pareto concept in more detail. The mathematical model for solving with two objective functions  (OFs) is shown in Sect. 3.4.2.

Fig. 3.

An illustration of the Pareto solutions [80]

WSM

$$\mathrm{Minimize}{w}_1{f}_1+w_2{f}_2$$

Subject to:

Eqs. (3) to (18)

Where w₁ ≥ 0 and w₂ ≥ 0 are weights such that w₁ + w₂ = 1, and f₁ and f₂ are the OFs.

Implementation and Evaluation

Case Study

The first cases of COVID-19 were confirmed in Iran on February 19, 2020. The model’s validity and the solution method’s functionality are assessed through the data for the considered case study. The Iranian automotive industry will become the most critical industry in Iran over the years. We are collecting data from the company’s SC. A real case study has evaluated the outcomes of the model. The accuracy of the created model and the solution method’s functionality are assessed through the data for the considered case study. At last, it should be referenced that the proposed model is a dependable and responsive closed-loop SCND model. Tables 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, and 19 show the required data for modeling.

Table 7.

Supplier’s data

Supplier’s locations (City)	Average variable cost before February 19, 2020 (Rials) (100,000 units)	Average variable and hygiene cost during the COVID-19 pandemic (February 19, 2020–June 26, 2021) (Rials), including: Disinfection and sanitizer costs + PPE costs + COVID-19 test cost + costs of COVID-19 education + Costs of COVID-19 vaccine (100,000 units)	Specific net CO2 emission before February 19, 2020 (kg CO2 per tonne of material)	Specific net CO2 emission during the COVID-19 pandemic (February 19, 2020–June 26, 2021) (kg CO2 per tonne of material)	Average CO2 emissions = average CO2 released $\times$ average distance $\times$ average shipping rates before February 19, 2020 (road/rail/air, tonnes)	Average CO2 emissions = average CO2 released $\times$ Average distance $\times$ Average shipping rates during the COVID-19 pandemic (February 19, 2020–June 26, 2021) (road/rail/air, tonnes)
Isfahan	11,000,000,000	13,000,000,000	486.7	470.2	7800	6905
Yazd	12,700,000,000	14,500,000,000	399.6	384.2	6500	6070
Tehran	18,000,000,000	19,200,000,000	376.0	369.2	8500	7605

Table 8.

Data of factories

Factory location (City)	Average fixed cost during the COVID-19 pandemic (February 19, 2020–June 26, 2021) (Rials)	Average variable cost before February 19, 2020 (Rials) (100,000 units)	Average variable and hygiene cost during the COVID-19 pandemic (February 19, 2020–June 26, 2021) (rials), including disinfection and sanitizer costs + PPE costs + COVID-19 test cost + costs of COVID-19 education + costs of COVID-19 vaccine (100,000 units)	Specific net CO2 emission before February 19, 2020 (kg CO2 per tonne of material)	Specific net CO2 emission during the COVID-19 pandemic (February 19, 2020–June 26, 2021) (kg CO2 per tonne of material)	Average CO22 emissions = average CO2 released $\times$ average distance $\times$ average shipping rates before February 19, 2020 (road/rail/air; tonnes)	Average CO2 emissions = average CO2 released $\times$ average distance $\times$ average shipping rates during the COVID-19 pandemic (February 19, 2020–June 26, 2021) (road/rail/air; tonnes)
Tehran	500,000,000,000	18,000,000,000	22,000,000,000	686.7	670.2	10,400	9880
Saveh	190,000,000,000	10,000,000,000	13,000,000,000	596.2	574.1	9600	8763
Kashan	350,000,000,000	14,000,000,000	17,000,000,000	476.0	469.2	8820	7900

Table 9.

Data of recycling/landfilling

Recycling/landfilling location (Tehran Province)	Average fixed cost during the COVID-19 pandemic (February 19, 2020–June 26, 2021) (rials)	Average variable cost before February 19, 2020 (rials) (100,000 units)	Average variable  and hygiene costs during the COVID-19 pandemic (February 19, 2020–June 26, 2021) (rials), including disinfection and sanitizer costs + PPE costs + COVID-19 test cost + costs of COVID-19 education + costs of COVID-19 vaccine (100,000 units)	Specific net CO2 emission before February 19, 2020 (kg CO2 per tonne of material)	Specific net CO2 emission during the COVID-19 pandemic (February 19, 2020–June 26, 2021) (kg CO2 per tonne of material)	Average CO2 emissions = average CO2 released $\times$ average distance $\times$ average shipping rates before February 19, 2020 (road/rail/air; tonnes)	CO2 emissions = average CO2 released $\times$ average distance $\times$ average shipping rates during the COVID-19 pandemic (February 19, 2020–June 26, 2021) (road/rail/air; tonnes)
Damavand	25,000,000,000	10,000,000,000	12,900,000,000	286.7	160.3	7300	6201
Km 17 Jade Makhsous	16,070,000,000	8,000,000,000	11,500,000,000	496.2	374.1	5690	4080
Tehran	32,000,000,000	12,000,000,000	13,400,000,000	576.0	469.8	9401	9000

Table 10.

Data of Saipa collection/distribution

Collection/Distribution locations (Tehran Province)	Average fixed cost during the COVID-19 pandemic (February 19, 2020–June 26, 2021) (rials)	Average variable cost before February 19, 2020 (rials) (100,000 units)	Average variable and hygiene costs during the COVID-19 pandemic (February 19, 2020–June 26, 2021) (rials), including disinfection and sanitizer costs + PPE costs + COVID-19 test cost + costs of COVID-19 education + costs of COVID-19 vaccine (100,000 units)	Specific net CO2 emission before February 19, 2020 (kg CO2 per tonne of material)	Specific net CO2 emission during the COVID-19 pandemic (February 19, 2020–June 26, 2021) (kg CO2 per tonne of material)	Average CO2 emissions = average CO2 released $\times$ average distance $\times$ average shipping rates before February 19, 2020 (road/rail/air; tonnes)	Average CO2 emissions = average CO2 released $\times$ average distance $\times$ average shipping rates during the COVID-19 pandemic (February 19, 2020–June 26, 2021) (road/rail/air; tonnes)
Damavand	40,000,000,000	8,000,000,000	10,000,000,000	296.7	100.9	5800	4905
Abali	99,000,000,000	19,000,000,000	22,000,000,000	200.0	180.0	3500	4100
Islamshahr	65,000,000,000	7,000,000,000	9,000,000,000	376.0	250.0	2500	3905
Baqershahr	45,000,000,000	2,000,000,000	4,000,000,000	586.7	400.1	1820	6002
Bumehen	99,000,000,000	3,000,000,000	3,800,000,000	396.2	301.3	7510	6040
Robat Karim	65,000,000,000	13,000,000,000	15,000,000,000	400.0	370.0	6506	7756
Pakdasht	48,000,000,000	4,500,000,000	9,500,000,000	776.4	676.4	5937	4999
Rudehen	99,000,000,000	15,000,000,000	17,000,000,000	296.7	201.7	6500	6020
Chahar Dangeh	65,000,000,000	4,000,000,000	8,000,000,000	200.0	187.0	8500	7805
Tehran	110,000,000,000	8,900,000,000	14,300,000,000	576.0	486.0	10,800	8999
Kahrizak	29,000,000,000	9,000,000,000	11,000,000,000	296.2	156.2	2200	1021
Lavasan	65,000,000,000	6,800,000,000	8,700,000,000	696.3	506.3	3570	2705
Pardis	40,000,000,000	10,000,000,000	12,000,000,000	340.0	300.0	5605	4936
Shahr-e Qods	99,000,000,000	12,000,000,000	14,600,000,000	390.0	376.5	7529	6001
Varamin	85,000,000,000	8,500,000,000	10,500,000,000	196.7	177.7	6692	6025
Fardis	70,000,000,000	5,600,000,000	7,700,000,000	220.0	179.0	5500	5009
Shahr-e Rey	49,000,000,000	11,000,000,000	14,000,000,000	479.0	379.8	4900	3000

Table 11.

Shipping costs

	Average unit shipping cost before February 19, 2020 (road/rail/air/sea) (Rials/Ton)	Average unit shipping cost during the COVID-19 pandemic (February 19, 2020–June 26, 2021) (road/rail/air) (Rials/Ton)
Tehran–Kashan	921,400	1,008,000
Tehran–Saveh	550,004	582,099
Isfahan–Kashan	701,300	812,000
Isfahan–Saveh	1,689,000	1,940,300
Isfahan–Tehran	2,886,000	2,997,030
Yazd–Kashan	1,759,007	2,000,001
Yazd–Saveh	3,571,060	3,762,080
Yazd–Tehran	4,589,005	5,589,900
Damavand–Tehran	370,010	391,500
Damavand–Saveh	801,300	853,040
Damavand–Kashan	1,255,000	1,307,999
Abali–Tehran	340,033	363,501
Abali–Saveh	700,000	800,000
Abali–Kashan	1,677,000	1,899,304
Islamshahr–Tehran	180,901	190,512
Islamshahr–Saveh	500,102	560,088
Islamshahr–Kashan	900,030	1,000,012
Baqershahr–Tehran	160,961	170,662
Baqershahr–Saveh	540,203	575,067
Baqershahr–Kashan	910,000	1,030,010
Bumehen–Tehran	310,035	332,009
Bumehen–Saveh	680,200	730,400
Bumehen–Kashan	1,507,070	1,820,900
Robat Karim–Tehran	270,739	282,011
Robat Karim–Saveh	450,122	472,077
Robat Karim–Kashan	870,040	920,033
Pakdasht–Tehran	280,032	292,001
Pakdasht–Saveh	590,003	622,033
Pakdasht–Kashan	890,033	940,088
Rudehen–Tehran	310,901	335,888
Rudehen–Saveh	690,300	744,000
Rudehen–Kashan	1,600,200	1,705,009
Chahar Dangeh–Tehran	121,700	142,287
Chahar Dangeh–Saveh	570,601	592,111
Chahar Dangeh–Kashan	920,200	1,140,090
Kahrizak–Tehran	180,900	190,500
Kahrizak–Saveh	520,101	544,013
Kahrizak–Kashan	870,012	990,077
Lavasan–Tehran	220,999	239,980
Lavasan–Saveh	620,202	720,501
Lavasan–Kashan	1,500,330	1,605,440
Pardis–Tehran	270,999	289,918
Pardis–Saveh	650,100	702,100
Pardis–Kashan	1,300,060	1,770,010
Shahr-e Qods–Tehran	180,988	190,555
Shahr-e Qods–Saveh	580,999	619,187
Shahr-e Qods–Kashan	1,400,280	1,420,477
Varamin–Tehran	320,035	333,014
Varamin–Saveh	610,204	700,203
Varamin–Kashan	700,098	771,695
Fardis–Tehran	280,012	299,977
Fardis–Saveh	490,302	521,016
Fardis–Kashan	890,150	935,222
Shahr-e Rey–Tehran	141,821	165,220
Shahr-e Rey–Saveh	585,024	598,080
Shahr-e Rey–Kashan	990,400	1,170,056
Tehran–Km 17 Jade Makhsous	141,722	162,222
Damavand–Km 17 Jade Makhsous	470,144	490,011
Abali–Km 17 Jade Makhsous	390,212	405,200
Abali–Damavand	150,856	170,999
Islamshahr–Km 17 Jade Makhsous	180,902	190,514
Islamshahr–Damavand	453,941	467,254
Baqershahr–Damavand	400,314	419,100
Baqershahr–Km 17 Jade Makhsous	240,213	259,315
Bumehen–Damavand	150,888	170,944
Bumehen–Km 17 Jade Makhsous	361,220	391,020
Robat Karim–Damavand	555,009	580,070
Robat Karim–Km 17 Jade Makhsous	241,999	254,987
Pakdasht–Damavand	430,212	450,200
Pakdasht–Km 17 Jade Makhsous	330,033	343,802
Rudehen–Damavand	150,759	171,216
Rudehen–Km 17 Jade Makhsous	376,870	399,600
Chahar Dangeh–Damavand	390,999	417,765
Chahar Dangeh–Km 17 Jade Makhsous	270,013	289,222
Kahrizak–Damavand	441,947	457,200
Kahrizak–Km 17 Jade Makhsous	240,249	259,329
Lavasan–Damavand	350,044	372,901
Lavasan–Km 17 Jade Makhsous	366,822	389,110
Pardis–Damavand	210,300	220,040
Pardis–Km 17 Jade Makhsous	470,100	489,012
Shahr-e Qods–Damavand	469,199	488,510
Shahr-e Qods–Km 17 Jade Makhsous	230,210	240,322
Varamin–Damavand	540,001	570,010
Varamin–Km 17 Jade Makhsous	350,033	372,522
Fardis–Damavand	585,109	590,570
Fardis–Km 17 Jade Makhsous	151,788	172,217
Shahr-e Rey–Damavand	368,021	389,990
Shahr-e Rey–Km 17 Jade Makhsous	220,210	229,920
Tehran–Tehran	101,222	120,000
Damavand–Damavand	70,012	80,015
Shemiranat–Tehran	180,923	190,533
Shemiranat–Damavand	360,020	481,148
Shemiranat–Abali	330,034	353,281
Shemiranat–Islamshahr	190,934	210,521
Shemiranat–Baqershahr	170,231	185,600
Shemiranat–Bumehen	324,044	342,777
Shemiranat–Robat Karim	280,799	292,200
Shemiranat–Pakdasht	290,044	311,004
Shemiranat–Rudehen	320,888	346,877
Shemiranat–Chahar Dangeh	123,900	144,555
Shemiranat–Kahrizak	188,000	200,100
Shemiranat–Lavasan	220,000	229,080
Shemiranat–Pardis	270,000	280,000
Shemiranat–Shahr-e Qods	182,444	185,321
Shemiranat–Varamin	340,022	363,011
Shemiranat–Fardis	289,088	310,247
Shemiranat–Shahr-e Rey	144,679	170,000
Malard–Tehran	280,011	295,911
Malard–Damavand	585,222	591,364
Malard–Abali	470,238	490,666
Malard–Islamshahr	490,101	530,222
Malard–Baqershahr	230,944	348,960
Malard–Bumehen	470,208	490,019
Malard–Robat Karim	180,550	186,502
Malard–Pakdasht	390,127	417,744
Malard–Rudehen	470,121	492,023
Malard–Chahar Dangeh	271,711	283,019
Malard–Kahrizak	320,951	345,877
Malard–Lavasan	380,016	391,505
Malard–Pardis	430,122	442,000
Malard–Shahr-e Qods	170,700	180,201
Malard–Varamin	401,312	421,109
Malard–Fardis	80,200	88,201
Malard–Shahr-e Rey	310,022	320,800
Pishva–Tehran	340,248	369,711
Pishva–Damavand	480,120	502,011
Pishva–Abali	470,144	492,555
Pishva–Islamshahr	350,022	372,966
Pishva–Baqershahr	320,035	352,001
Pishva–Bumehen	450,140	480,015
Pishva–Robat Karim	390,280	411,255
Pishva–Pakdasht	210,990	229,911
Pishva–Rudehen	469,188	488,544
Pishva–Chahar Dangeh	331,031	351,211
Pishva–Kahrizak	320,901	355,800
Pishva–Lavasan	410,322	439,103
Pishva–Pardis	400,994	410,122
Pishva–Shahr-e Qods	430,814	419,101
Pishva–Varamin	50,824	60,813
Pishva–Fardis	440,814	479,101
Pishva–Shahr-e Rey	540,814	579,122

Table 12.

Capacity of facilities

Suppliers
Isfahan	500,000
Yazd	300,000
Tehran	600,000
Factories
Tehran	1,000,000
Saveh	800,000
Kashan	500,000
Recycling/landfilling
Damavand	300,000
Tehran	4,500,000
Km 17 Jade Makhsous	260,000

Table 13.

The capacity of facilities

Collection/Distribution
Damavand	320,000
Abali	100,000
Islamshahr	300,000
Baqershahr	500,000
Bumehen	400,000
Robat Karim	600,000
Pakdasht	660,400
Rudehen	370,000
Chahar Dangeh	200,000
Tehran	802,000
Kahrizak	530,000
Lavasan	570,000
Pardis	609,000
Shahr-e Qods	800,090
Varamin	302,000
Fardis	430,000
Shahr-e Rey	505,800
Damavand	779,000

Table 14.

Distance between facilities (suppliers–factories)

Km	f1: Kashan	f2: Saveh	f3: Tehran
S1: Tehran	246	135	14.8
S2: Isfahan	209	310	437
S3: Yazd	381	563	624

Table 15.

Distance between facilities (factories–CDCs)

Km	f1: Kashan	f2: Saveh	f3: Tehran
CDC1: Tehran	246	135	15.5
CDC2: Damavand	313	209	73
CDC3: Abali	302	200	64
CDC4: Islamshahr	229	111	27
CDC5: Baqershahr	230	130	24
CDC6: Bumehen	293	189	52
CDC7: Robat Karim	221	95	41
CDC8: Pakdasht	230	146	43
CDC9: Rudehen	295	191	54
CDC10: Chahar Dangeh	239	122	14
CDC11: Kahrizak	225	125	27
CDC12: Lavasan	276	172	37
CDC13: Pardis	288	183	46
CDC14: Shahr-e Qods	264	127	28
CDC15: Varamin	207	166	56
CDC16: Fardis	254	124	47
CDC17: Shahr-e Rey	243	139	17

Table 16.

Distance between facilities (CDCs–Customers)

Km	Customer 1, Tehran (Center)	Customer 2, Tehran (Center)	Customer 3, Tehran (Center)	Customer 4, Shemiranat (North)	Customer 5, Baqershahr (South)	Customer 6, Pardis (East)	Customer 7, Malard (West)	Customer 8, Pishva (Southeast)	Customer 9, Islamshahr (Southwest)	Customer 10, Lavasan (Northeast)
CDC1: Tehran	9.6	20	2.5	16	24	45	44	64	26	45
CDC2: Damavand	75	70.9	80	70	85	31.5	119	117	98	31
CDC3: Abali	64	60	69	61	74	20	106	107	84.6	20
CDC4: Islamshahr	32	41	26	41.5	25	73.6	37	68	6	73
CDC5: Baqershahr	30	40.2	27.4	40	4.5	60	59	49	27.1	60
CDC6: Bumehen	53.3	49	59	49	64	9.3	96	96	74	9.3
CDC7: Robat Karim	46	56	41	56	64	87	26	80	18	87
CDC8: Pakdasht	43	52	45	52	38	69.2	80	32	53	69
CDC9: Rudehen	57	53.2	62	53.4	68	13	103.4	100	78.7	13
CDC10: Chahar Dangeh	18	27.9	13	32	18.3	59	40	60	12	59
CDC11: Kahrizak	28	38	26	41	5.2	65	57	54	24	65
CDC12: Lavasan	36	26	41	26	50	41	79	82	60	41
CDC13: Pardis	45.2	41	50	40	55	5.1	87.2	87	66	3
CDC14: Shahr-e Qods	33	38	25	38.2	42	76	22	84	35	76
CDC15: Varamin	57	67.4	57	67	45	85	88	9.9	58	85
CDC16: Fardis	49	55.4	44	55	58	93	8.4	100	39	93
CDC17: Shahr-e Rey	22	31	20	31	10.7	52	51	47	25	52

We have selected ten customers as a sample, among too many customers

Table 17.

Distance between facilities (CDCs–RLCs)

Km	RLC1: Damavand	RLC2: Tehran	RLC3: Km 17 Jade Makhsous
CDC1: Tehran	71	10	17
CDC2: Damavand	6.8	71	103
CDC3: Abali	21	64	83
CDC4: Islamshahr	96	27	27
CDC5: Baqershahr	85	24	37
CDC6: Bumehen	21	52	73
CDC7: Robat Karim	111	41	39
CDC8: Pakdasht	94	43	61
CDC9: Rudehen	21	54	77
CDC10: Chahar Dangeh	84	14	44
CDC11: Kahrizak	91	27	38
CDC12: Lavasan	68	37	74
CDC13: Pardis	31	46	69
CDC14: Shahr-e Qods	101	28	35
CDC15: Varamin	110	56	68
CDC16: Fardis	119	47	21
CDC17: Shahr-e Rey	75	17	33

Table 18.

Minimum percentage of units of the returned product to be remanufactured, recycled, and landfilled

${\mathit{MN}}_{\mathit{dismantled}}$	0.3
$M{N}_{\text{disposed}}$	0.2

Table 19.

Demand of customers

Average demand of customers in a month

120

The software output of the case study is illustrated in Table 20 and Fig. 4.

Table 20.

Weighted sum method outputs

	Environment performance weight	Economic performance weight	Environment optimization value	Economic optimization value
1	0.1	0.9	11.27E + 13	1.08E + 13
2	0.2	0.8	9.44E + 13	2.17E + 13
3	0.3	0.7	8.50E + 13	3.25E + 13
4	0.4	0.6	7.20E + 13	4.33E + 13
5	0.5	0.5	7.11E + 13	5.41E + 13
6	0.6	0.4	6.02E + 13	6.49E + 13
7	0.7	0.3	4.09E + 13	7.58E + 13
8	0.8	0.2	3.17E + 13	8.66E + 13
9	0.9	0.1	2.08E + 13	9.74E + 13

Fig. 4.

Software output for economic and environment optimization values

Numerical Example

The efficiency of the mathematical model in small dimensions is demonstrated and analyzed through a numerical example. There are five types of facilities in the closed-loop network (CLN) in the numerical example, namely suppliers (S), factories (F), collection/distribution centers (CDC), recycling/landfill centers (RLC), and customers (C). There are three potential locations for supply chain facilities (F, CDC, RLC), and existing S and C are given. Tables 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34,and 35 show the required data for modeling and the results, as follows:

• S, suppliers (s = 1, 2, 3, 4, 5, 6, 7)

• F, potential factories (f = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10)

• I, potential CDCs (i = 1, 2, 3, 4, 5, 6, 7, 8)

• C, customers (c = 1, 2, 3, 4, 5)

• B, potential RLCs (b = 1, 2, 3, 4)

• TS, shipping alternatives from suppliers (ts = 1, 2, 3, 4, 5, 6)

• TF, shipping alternatives from factories (tf = 1, 2, 3, 4, 5, 6, 7, 8, 9)

• TI, shipping alternatives from CDCs (ti = 1, 2)

• TC, shipping alternatives from customers (tc = 1, 2, 3)

Table 21.

Data sources

Data	Sources
Demand of customers, fixed costs, variable costs, capacity data, shipping costs, hygiene costs	Kartina Puji Nurjanni [96] Sherafati et al. [83]. Billal and Hossain [84]. This study.
Distance	Google Maps [85].
CO2 information	Bera et al. [86]. HeidelbergCement Group [87]. This study

Table 22.

The computational process for optimization purposes is conducted through Lingo software

Lingo version	19.0
Operating system	Windows
Bit size	64
CPU	× 64
File size	40.3 MB

Table 23.

The demand of customers

d1	15
d2	18
d3	20
d4	25
d5	17

Table 24.

Fixed costs for opening facility

	In €
f1	60,000
f2	210,500
f3	100,000
f4	230,000
f5	190,000
f6	80,100
f7	200,400
f8	206,000
f9	50,500
f10	170,300
i1	15,000
i2	16,500
i3	17,000
i4	18,000
i5	20,000
i6	19,100
i7	14,400
i8	18,000
b1	10,000
b2	10,500
b3	12,000
b4	13,500

Table 25.

Variable  and hygienic costs

	Vs in €/ton	HVs in €/ton	Vf in €/ton	HVf in €/ton	Vrf in €/ton	HVrf in €/ton	Vi in €/ton	HVi in €/ton	Vri in €/ton	HVri in €/ton	Vb in €/ton	HVb in €/ton
s1	60.10	10.18
s2	75.12	12.18
s3	88.12	09.14
s4	47.98	06.18
s5	97.18	06.18
s6	42.98	14.17
s7	55.19	13.15
f1			60.18	12.04	40.18	17.18
f2			30.08	14.19	57.22	09.87
f3			36.00	09.18	58.13	08.13
f4			82.19	08.18	32.19	12.29
f5			23.12	11.10	45.20	10.03
f6			32.18	10.09	42.17	11.28
f7			37.19	14.13	38.18	17.17
f8			66.18	15.10	31.14	13.18
f9			32.18	16.12	32.10	19.13
f10			70.18	18.32	33.18	10.92
i1							24.13	17.25	30.14	03.186
i2							27.18	16.08	42.11	07.107
i3							50.17	10.11	52.16	09.08
4							10.45	09.22	31.12	09.99
i5							29.90	11.92	39.10	11.16
i6							30.00	08.18	40.10	13.88
i7							31.11	08.19	60.18	15.10
i8							23.72	10.00	29.78	16.10
b1											18.10	12.10
b2											20.55	13.73
b3											15.70	05.14
b4											42.99	08.08

Table 26.

Unit shipping cost with a hygiene protocol

	In €/ton
ts1	11.24
ts2	08.56
ts3	18.56
ts4	38.56
ts5	18.56
ts6	28.56
tf1	20.56
tf2	50.56
tf3	58.56
tf4	07.56
tf5	18.56
tf6	19.56
tf7	58.08
tf8	14.98
tf9	19.53
ti1	70.56
ti2	19.56
tc1	30.56
tc2	32.56
tc3	43.56

Table 27.

CO2 released due to the activities of facilities

	Emission in kg
s1	814,200
s2	900,005
s3	712,235
s4	700,205
s5	812,235
s6	700,205
s7	800,205
f1	794,185
f2	994,111
f3	854,182
f4	630,283
f5	752,889
f6	894,180
f7	794,185
f8	792,889
f9	994,185
f10	894,185
erf1	412,235
erf2	308,205
erf3	212,295
erf4	500,205
erf5	401,207
erf6	420,000
erf7	407,205
erf8	518,805
erf9	312,139
erf10	508,205
i1	612,235
i2	508,205
i3	712,295
i4	500,205
i5	401,207
i6	420,000
i7	607,205
i8	618,805
eri1	212,239
eri2	204,405
eri3	213,395
eri4	302,205
eri5	101,207
eri6	120,000
eri7	212,235
eri8	308,205
b1	712,235
b2	860,203
b3	612,212
b4	700,205

Table 28.

Shipping rates (Emission factors)

Transport mode	gCO2 (tonnes/km)
ts1	62.3
ts2	22.8
ts3	16.9
ts4	34.6
ts5	31.5
ts6	21.3
tf1	80.3
tf2	22.8
tf3	16.9
tf4	34.6
tf5	31.5
tf6	100.3
tf7	62.4
tf8	62.3
tf9	16.9
ti1	22.8
ti2	21.8
tc1	34.6
tc2	18.8
tc3	21.3

CO₂ emissions = CO₂ released by shipping alternative $\times$ distance $\times$ shipping rates

Table 29.

CO₂ released by a shipping alternative

Transport mode	Emission in tonnes
ts1	0.35
ts2	0.40
ts3	0.36
ts4	0.37
ts5	0.27
ts6	0.42
tf1	0.52
tf2	0.40
tf3	0.36
tf4	0.37
tf5	0.27
tf6	0.67
tf7	0.39
tf8	0.35
tf9	0.20
ti1	0.40
ti2	0.44
tc1	0.37
tc2	0.19
tc3	0.42

Table 30.

Minimum percent of the returned product to be remanufactured, recycled, and landfilled

$M{N}_{\text{dismantled}}$	0.4
$M{N}_{\text{disposed}}$	0.3

Table 31.

Maximum capacity limits of facilities

s1	700
s2	800
s3	720
s4	670
s5	700
s6	780
s7	900
Mf1	500
Mf2	450
Mf3	630
Mf4	700
Mf5	530
Mf6	550
Mf7	600
Mf8	610
Mf9	500
Mf10	400
i1	590
i2	550
i3	400
i4	620
i5	750
i6	890
i7	750
i8	480
b1	290
b2	355
b3	420
b4	320
Mrf1	400
Mrf2	420
Mrf3	620
Mrf4	680
Mrf5	410
Mrf6	540
Mrf7	520
Mrf8	390
Mrf9	400
Mrf10	260

Table 32.

Distance between facilities (Suppliers–Factories)

Km	s1	s2	s3	s4	s5	s6	s7
f1	100	210	350	500	620	650	700
f2	210	90	500	49	410	109	69
f3	380	420	320	120	400	59	870
f4	422	80	320	950	610	520	300
f5	30	700	870	532	273	100	501
f6	670	320	189	983	901	293	422
f7	220	100	540	623	600	187	610
f8	190	729	902	333	439	873	436
f9	550	503	900	289	287	672	780
f10	321	444	198	302	624	290	910

Table 33.

Distance between facilities (Factories–CDCs)

Km	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10
i1	327	629	102	320	211	155	114	320	210	765
i2	134	219	199	160	140	140	320	410	420	346
i3	325	382	134	560	610	167	605	204	211	211
i4	267	218	122	750	640	124	328	258	320	257
i5	378	346	989	420	860	108	888	932	406	315
i6	901	200	700	600	210	153	620	510	603	852
i7	108	130	166	128	180	120	413	120	130	210
i8	222	210	720	800	269	113	190	220	210	311

Table 34.

Distance between facilities (CDCs–Customers)

Km	i1	i2	i3	i4	i5	i6	i7	i8
c1	202	56	45	230	416	219	235	198
c2	199	68	110	519	255	132	120	120
c3	90	201	107	218	315	279	55	110
c4	180	90	114	140	240	300	80	85
c5	207	70	308	107	107	130	200	95

Table 35.

Distance between facilities (CDCs–RLCs)

Km	i1	i2	i3	i4	i5	i6	i7	i8
b1	102	55	45	230	319	219	325	98
b2	199	68	210	219	155	132	120	120
b3	90	201	107	218	115	279	55	110
b4	280	100	114	340	400	400	90	70

Table 36 shows the results of solving the model with LINGO for different objective weights.

Table 36.

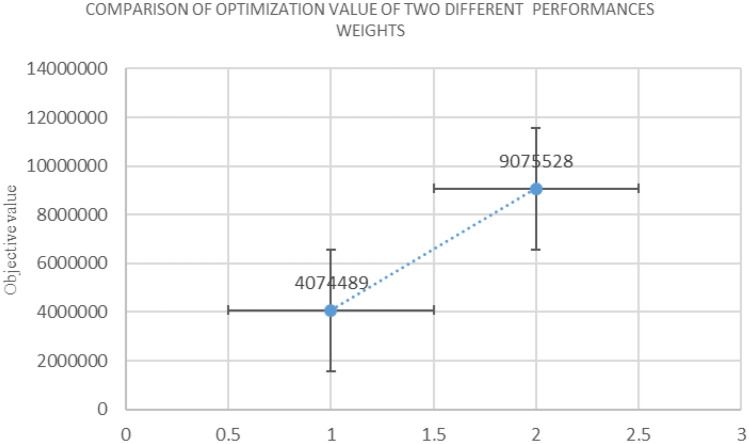
Results of solving the GSC model with Lingo during the COVID-19 pandemic (Different objective weights)

Objective	Σwi = 1	Σwi = 1
Economic performance	0.7030	0.2970
Environmental performance	0.2970	0.7030
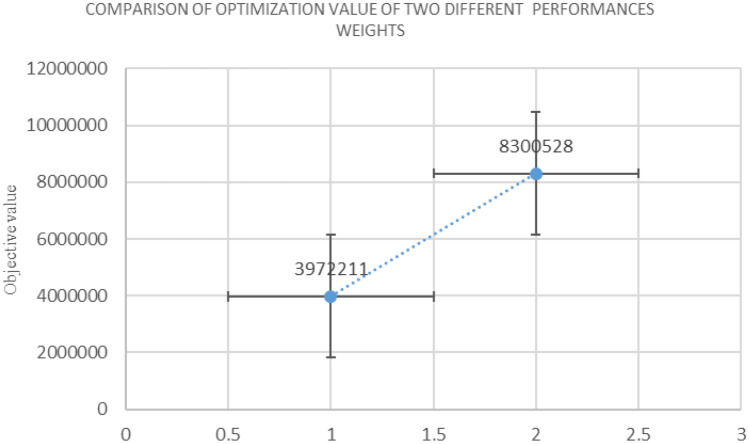
Objective value	Z*1 = 4,074,489, Z*2 = 9,075,528	Z*1 = 3,972,211, Z*2 = 8,300,528

w_i is generated randomly or determined by the DMs

In Fig. 5, you can see the problem in the small dimension.

Fig. 5.

A closed-loop network in small dimensions displayed

Optimization values of numerical examples are illustrated in Figs. 6 and 7.

Fig. 6.

The comparison between economic and environmental performances of numerical examples based on the importance of economic factors

Fig. 7.

The comparison between economic and environmental performances of numerical examples based on the importance of environmental factors

Discussion and Analysis

Sensitivity Analysis of w_i

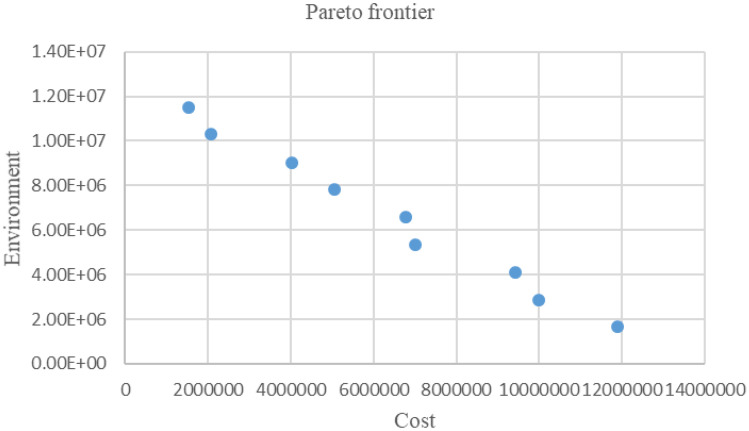
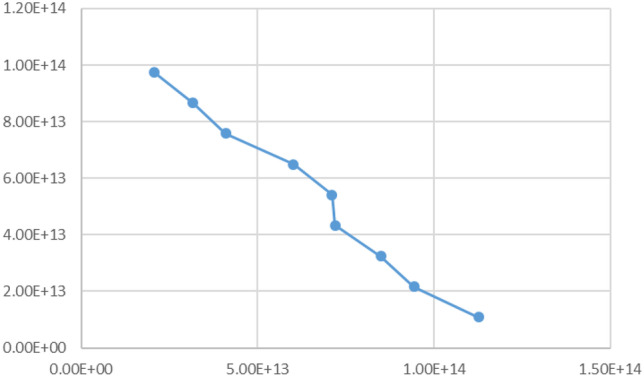
Lingo software is used to conduct the computation. The WSM determines different approximations of the POF. In this case, two weights (w₁ and w₂) exist because of two objective functions. It is noticeable that w₁ and w₂ are ≥ 0 and w₁ + w₂ is equal to 1. The performances with different weights are shown in Table 37, and the Pareto frontier is illustrated in Fig. 8.

Table 37.

Performances with different weights

Pareto point	Environment performance weights	Economic performance weights	Environment optimization value	Economic optimization value
1	0.1	0.9	1,522,877	1.15E + 07
2	0.2	0.8	2,079,644	1.03E + 07
3	0.3	0.7	4,018,883	9,038,574
4	0.4	0.6	5,043,115	7,806,791
5	0.5	0.5	6,775,999	6,575,008
6	0.6	0.4	7,006,990	5,343,225
7	0.7	0.3	9,432,224	4,111,443
8	0.8	0.2	1.00E + 07	2,879,660
9	0.9	0.1	1.19E + 07	1,647,877

Fig. 8.

Sensitivity analysis for different weights of environment and economic aspects

Comparison of Optimization Value

Economic and environmental aspects are compared separately for the optimization value (OV) of performance. Weights were assigned to other aspects in each step. The optimization value of the economic and environmental objectives is shown in Table 38.

$$\mathrm{Min}{w}_1{f}_1+w_2{f}_2$$

Table 38.

Economic and environmental aspects

Objective	w1 = 1	w2 = 1
Economic	1	0
Environmental	0	1
Optimization value	Z*1 = 416,094.0	Z*1 = 451,170.0
	Z*2 = 0.1273392E + 0	Z*2 = 0.1044302E + 0

s. t. Eqs. (3)–(18)

Where w₁ ≥ 0 and w₂ ≥ 0 are weights such that w₁ + w₂ = 1, and f₁ and f₂ are the OFs.

• The first assumption:

If w₁ = 1, then:

$$\mathrm{Min}{f}_1$$

s. t. Eqs. (3)–(18)

• The second assumption:

If w₂ = 1, then:

$$\mathrm{Min}{f}_2$$

s. t. Eqs. (3)–(18)

Sensitivity Analysis (Base Model/COVID-19 Model)

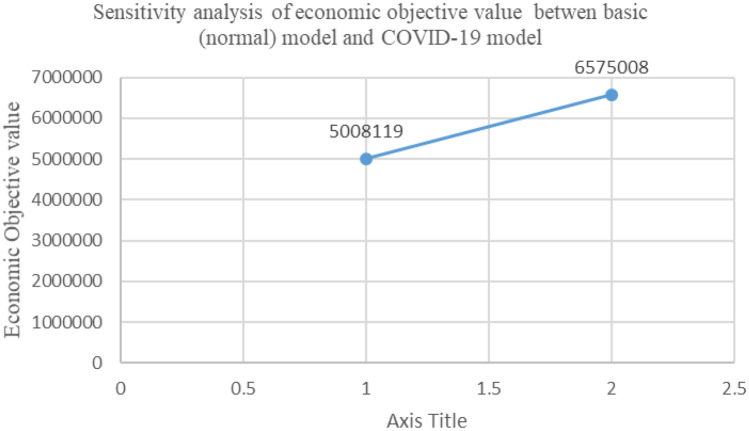
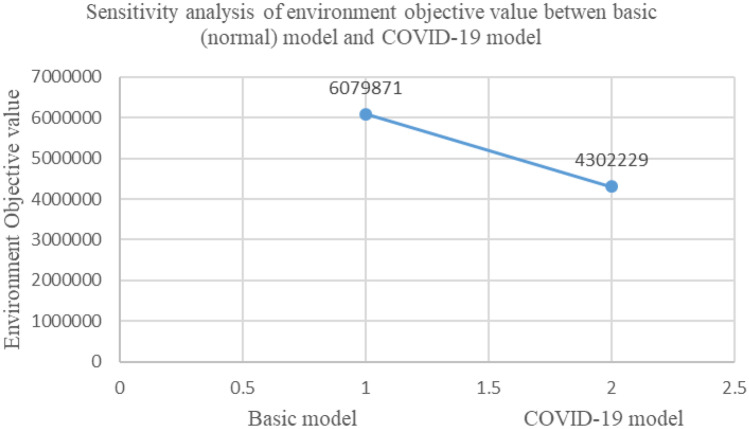
Optimal values have been compared between the COVID-19 condition model and the normal condition model. For more information, see Table 39. The mathematical model compared economic and environmental performances during the COVID-19 pandemic and under normal conditions. This paper presented a more realistic model. Figures 9, 10, 11, 12, and 13 show the relationships between COVID-19 and its environmental effects. The economic and environmental objective values are shown in Table 39 and Figs. 14 and 15.

Table 39.

Basic and COVID-19 condition model

Without considering COVID-19	Considering the COVID-19 (Current Research)
Normal fixed, variable, and shipping costs	Fixed, variable, shipping, and hygienic costs concerning prevention and control of COVID-19 (disinfection and sanitizer costs, PPE costs, COVID-19 test costs, costs of COVID-19 education, costs of COVID-19 medicines, vaccine, and vaccination)
Normal CO2 released	CO2 released concerning the lockdown days (reduction of CO2 emissions)
Economic objective value = 5,008,119	Economic objective value = 6,575,008
Environment objective value = 6,079,871	Environment objective value = 4,302,229

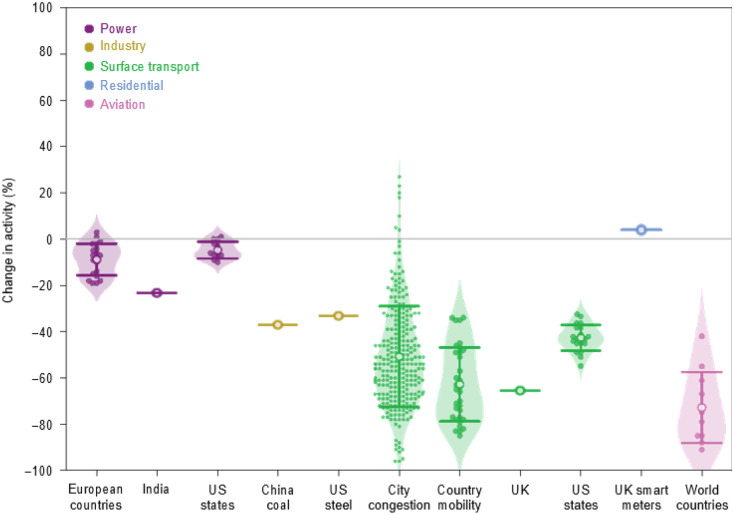
Fig. 9.

a-i Relationship between gas emissions and COVID-19 [88]

Fig. 10.

- Analysis of the relationship between total CO₂ emissions due to activities and COVID-19 [89]

Fig. 11.

CO₂ emission in India during the COVID-19 pandemic [90]

Fig. 12.

Change in activity during the COVID-19 pandemic [91, 92]

Fig. 13.

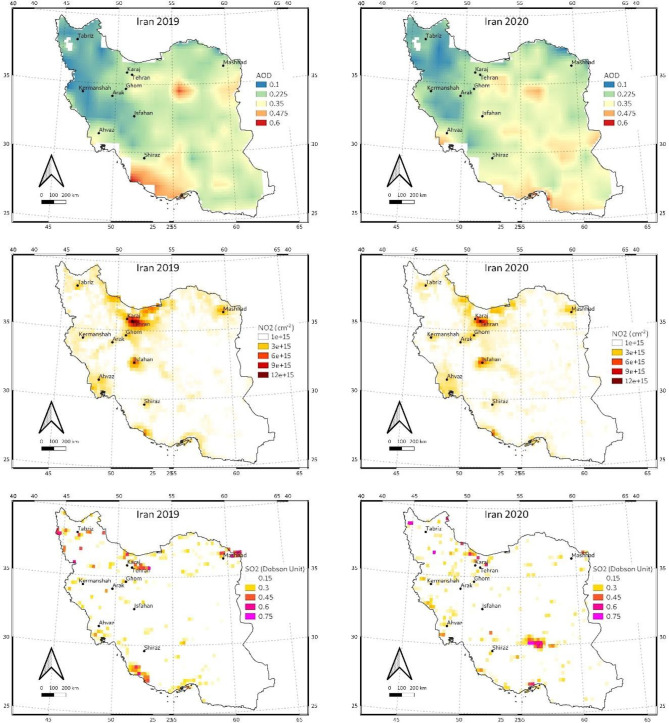
Iran's average GHG emissions between March 21 and April 21, 2019 and 2020 [93]

Fig. 14.

Sensitivity analysis of the economic objective value

Fig. 15.

Sensitivity analysis of the environment objective value

Findings

The summary of the paper’s findings is as follows:

• To determine the optimal trade-off between economic and environmental aspects during the COVID-19 pandemic and lockdowns, a mathematical model for GSC was designed.

• Incorporating hygiene into the SC design

• In this study, we examined two aspects of sustainability that are negatively and positively affected by COVID-19 and lockdowns.

Implications for Managers and Practical Suggestions

This research can lead to valuable policies for disaster management, particularly in COVID-19 conditions, such as:

• i.The proposed model allows managers to make informed decisions and determine the cost/CO₂ emission trade-off during the COVID-19 pandemic.
• ii.In making their COVID-19 cost estimates, SC managers should account for hygienic costs.
• iii.When disasters or emergencies like COVID-19 occur, managers should be able to replace tools and methods.

This study’s results contribute to SC management’s performance during the COVID-19 pandemic.

Conclusion and Outlook

COVID-19 is an exceptional and extraordinary event that impacts the SC. In this study, we proposed a GCLSCN during the COVID-19 pandemic. The MOMIP model can show the trade-offs between total cost and total CO₂ emissions during the pandemic and lockdowns. This model is sensitive to the cost structure. The cost includes two parts: normal cost without considering the coronavirus pandemic and the cost with considering coronavirus, including disinfection and sanitizer costs, PPE costs, COVID-19 test costs, costs of COVID-19 education, and costs of COVID-19 vaccine. A case study and numerical example have illustrated the validation of the presented model. The optimization value with different weight performances is calculated, and w_i (weight) sensitivity analysis is also measured. The proposed model is solved with Lingo 19.0 software. For the optimization value of performance, we compare the economic and environmental aspects separately. In each step, we allocated the weight of the function to other aspects. The findings of the proposed network illustrate the SC has become greener during the COVID-19 pandemic. The total cost of new SC was increased during the COVID-19 pandemic, but the lockdowns during the COVID-19 pandemic had direct positive effects on emissions and air quality. The findings of this paper included the following: designing the applied mathematical model of GSC to show better the trade-offs between economic and environmental aspects during the COVID-19 pandemic and lockdowns, designing the hygiene SC during the COVID-19 pandemic and lockdowns, and proposing the new indicators of economic aspects during the COVID-19 outbreak and lockdowns. At last, we find the impacts of COVID-19 and lockdowns on two aspects of sustainability. This paper presents a MOMIP model and COVID-19 pandemic issues in the CLSC framework. Therefore, this study designed a new and hygienic GSC model to fill this gap in the COVID-19 disaster. This is a mathematical article with a green approach aiming to propose guidelines for managers and scholars addressing SCM challenges during the COVID-19 disaster [12, 94, 95].

Limitations

We have some limitations in our work, which can be addressed by future research:

• Data from only one real company was available to us.

• Models are based on single-product networks.

• The network design is one-period.

Insights into Future Work

Perspectives for future work can be done:

1. In future research, consider supply chain agility concepts.

2. Add more environmental aspects to this model.

3. Add the social aspects to the model. It can lead to a sustainable supply chain.

4. For future research, upgrade the model to include the multi-products and multi-periods.

5. Add the stochastic parameters for this model.

Author Contribution

Sina Abbasi: conceptualization, software, methodology, formal analysis, writing of original draft, and visualization; Maryam Daneshmand-Mehr: methodology, supervision, data curation, and validation; Armin Ghane Kanafi: software, formulation, validation, and editing.

Availability of Data and Materials

Not applicable.

Code Availability

Custom code by Lingo software was written for this study. It is available on request.

Declarations

Ethical Approval and Consent to Participate.

Not applicable.

Consent for Publication

Not applicable.

Competing Interests

The authors declare no competing interests.