Skip to main content
NCBI home page
ACS Polymers Au logoLink to ACS Polymers Au
. 2022 Sep 8;2(6):467–477. doi: 10.1021/acspolymersau.2c00031

Computational Study of Mechanochemical Activation in Nanostructured Triblock Copolymers

Zijian Huo †, Stephen J Skala ‡, Lavinia R Falck †, Jennifer E Laaser †, Antonia Statt ‡,*
PMCID: PMC9756960  PMID: 36536889

Abstract

graphic file with name lg2c00031_0009.jpg

Force-driven chemical reactions have emerged as an attractive platform for diverse applications in polymeric materials. However, the microscopic chain conformations and topologies necessary for efficiently transducing macroscopic forces to the molecular scale are not well-understood. In this work, we use a coarse-grained model to investigate the impact of network-like topologies on mechanochemical activation in self-assembled triblock copolymers. We find that mechanochemical activation during tensile deformation depends strongly on both the polymer composition and chain conformation in these materials. Activation primarily occurs in the tie chains connecting different glassy domains and in loop chains that are hooked onto each other by physical entanglements. Activation also requires a higher stress in materials having a higher glassy block content. Overall, the lamellar samples show the highest percent activation at high stress. In contrast, at low stress, the spherical morphology, which has the lowest glassy fraction, shows the highest activation. Additionally, we observe a spatial pattern of activation, which appears to be tied to distortion of the self-assembled morphology. Higher activation is observed in the tips of the chevrons formed during deformation of lamellar samples as well as in the centers between the cylinders in the cylindrical morphology. Our work shows that changes in the network-like topology in different morphologies significantly impact mechanochemical activation efficiencies in these materials, suggesting that this area will be a fruitful avenue for further experimental research.

Keywords: mechanochemistry, triblock copolymers, molecular dynamics simulation, coarse-grained modeling, deformation

1. Introduction

The ability to drive chemical reactions by applying force across chemical bonds has received significant attention as a platform for strain sensing, chemical catalysis, and self-healing materials.1−7 A key requirement for these applications is the ability to efficiently transmit force to the force-responsive bond. To achieve this, polymer chains can be used as “handles” for pulling on the bonds both in solution8,9 and in cross-linked polymer materials.10−12 However, the polymer molecular weight and the network topology strongly impact whether chains experience high enough forces to activate the force-responsive bond before the material relaxes and the forces are evenly distributed across all chains, which in turn affects the overall activation efficiency.

Understanding what features of a network’s topology most favor activation is thus an essential question that must be addressed to facilitate development of useful mechanochemical materials. Block copolymers (BCPs) offer an attractive option for simultaneously controlling the network-like topology, and thus transmission of bulk forces to the molecular scale, and the overall mechanical properties of the material.13−16 ABA triblock copolymers with long enough chain lengths (N) and large enough interaction parameters (χ) microphase segregate into ordered morphologies ranging from spherical to cylindrical to lamellar, depending on the volume fractions of each block type.17,18 By choosing glassy A blocks and rubbery B blocks, the self-assembled A domains can serve as physical links that enable the B chains to behave like they are in a network.15,16,19 Importantly, the self-assembled structures not only have different overall symmetries but also different chain conformations.17 Although the influence of chain conformations (i.e., tie and loop chains) in the purely mechanical behavior of triblocks20−27 and cross-linked networks28,29 have been studied previously, it is not clear how those conformations influence the efficiency of mechanochemical activation in the material. Changing the morphology of the self-assembled structures is expected to drive substantial changes in the activation profile.

To date, however, testing the influence of morphology and chain conformations on activation has been difficult. In 2013, Jiang et al.30 synthesized triblock copolymers with a mechanochemically active spiropyran unit in the middle of the rubber block. While they did observe some dependence of activation on the weight fraction of the glassy blocks, the relatively low molecular weights of the polymers and the low segregation strength in their system precluded rigorous investigation of the role of morphology in mechanochemical activation. Ramirez et al. have also investigated mechanochemical activation in cast and electrospun triblock copolymers containing mechanophores in the midblock.31 They found that the triblock architecture promoted more activation than the midblock alone, but the inclusion of only a single polymer composition made drawing conclusions about the role of morphology impossible. While these studies are thus suggestive of the role of network-like connectivity in determining the efficiency of mechanochemical activation in triblock copolymers, significant work remains to elucidate the role of specific topological features of the network in promoting or hindering mechanochemical activation in these materials. Specifically, resolving the exact conformations and spatial locations of the activated molecules is critical for understanding how morphology affects mechanochemical activation.

Here, we address this problem by using coarse-grained molecular dynamics simulations to investigate mechanochemical activation in triblock copolymers, shown schematically in Figure 1. We use a parametrized bead–spring model for a triblockk copolymer and a double-well bond inspired by Silberstein et al.32,33 for the mechanophore, enabling force-driven activation. Taking a simulation-based approach enables investigation not only of the average response of the entire sample but also of how the conformations and spatial positions of individual chains drive differences in their activation across different self-assembled morphologies. While a number of groups have modeled either the deformation of homopolymers,32,34 purely rubbery,20−24 or rubbery-glassy26,27 triblock systems, they have not investigated the interplay of nanostructured morphology and mechanophore activation. Our work thus contributes to this gap in understanding force-driven activation in these materials. Using this computational approach, we find that activation is dependent on the sample morphology, chain conformations, and spatial location of the mechanophores within the morphology in triblock copolymers. In particular, we find that activation occurs primarily in the tie chains, and that the spherical morphology, which has the highest fraction of tie chains, exhibits the highest activation at low stress. More interestingly, however, we find that at high stress, the lamellar samples exhibit the highest overall activation despite having the lowest fraction of tie chains. This indicates that both chain orientation and the presence of glassy domains in the lamellar sample, which change the local force distribution, play an important role in mechanochemical activation in nanostructured polymeric materials, and it suggests that controlling network-like topology is a promising route toward materials with precisely tailored activation profiles.

Figure 1.

Figure 1

Open in a new tab

Schematic of the simulation system investigated in this work. A bead–spring model of a triblock copolymer, parametrized to match PMMA-b-PnBA-b-PMMA, is self-assembled into microphase-separated morphologies and then deformed under uniaxial strain. Transitions in the state of a mechanophore in the middle of each chain, represented by a double-well potential, are tracked throughout the deformation, allowing investigation of how activation depends on the morphology and local environment and conformation of the chains.

2. Results

2.1. Equilibrium Properties

Coarse-grained simulations were carried out on ABA triblock copolymers using a bead–spring model with the Kuhn segment molecular weights,35,36 average amorphous densities,36,37 and glass transition temperatures37,38 for both blocks parametrized to match poly(methyl methacrylate)-block-poly(n-butyl acrylate)-block-poly(methyl methacrylate) (PMMA-b-PnBA-b-PMMA) triblock copolymers, as described in the Methods Section and Supporting Information. The PMMA-b-PnBA-b-PMMA system was chosen for this work because it forms well-ordered morphologies and can be synthesized via controlled radical polymerizations that are compatible with the widely studied spiropyran mechanophore,30,39 which was modeled using a double-well bond potential. This double-well potential was chosen to represent the ring-opening reaction spiropyran undergoes. Experimentally, the associated activation energy barrier can be measured by single-molecule force spectroscopy.40 Alternatively, it can also be obtained from quantum-chemical calculations using the CoGEF method;41 while the exact shape of this potential may be complicated,41−45 for simplicity, we model this energy barrier with a double-well potential in our work. The effect of having an activation barrier in comparison to a single-well bond is illustrated in Figure S2 in the Supporting Information, and the influence of activation barrier height on overall activation-strain curves is shown in Figure S3 in the Supporting Information. In short, similar activation profiles are observed with different energy barriers and the relative trends between morphologies remain unchanged.

Each chain contained one mechanophore in the middle of the rubbery PnBA-block. Samples of three polymer compositions (summarized in Table 1) were generated, and 10 independent replicas were equilibrated for each composition. As shown in Figure 2, all systems self-assembled into the morphologies expected from the phase diagrams predicted by self-consistent field theory (SCFT) and showed the expected average domain spacings.17,18 Agreement with SCFT predictions was further assessed by determining the fraction of loop and tie chains in each sample,17 where loop chains are chains whose ends are both in the same A glassy domain, and tie chains are chains whose ends connect two different A domains, as illustrated in Figure 2d. The results were in good agreement with SCFT predictions,17,24 with tie-chain fractions of 0.73 ± 0.01, 0.62 ± 0.04, and 0.38 ± 0.03 in the spherical, cylindrical, and lamellar morphologies, respectively. Loop chains were further classified as “hooked” if they were entangled with (i.e., hooked onto) a loop chain originating from a different glassy domain. Details of the chain classification algorithm are provided in the Supporting Information. All morphologies were well phase-separated and had a negligible fraction of dangling/cilia ends in their initial equilibrated states, with approximately 1.5% dangling chains in the spherical sample as the highest observed quantity.

Table 1. Polymer Architectures and Configurations.

System Morphology fA V Tie chains Spacing
A8B50A8 spherical 0.16 72 σ × 72 σ × 72 σ 0.73 ± 0.01 18 σ
A15B50A15 cylindrical 0.26 80 σ × 69 σ × 40 σ 0.62 ± 0.04 20 σ
A43B50A43 lamellae 0.50 92 σ × 92 σ × 46 σ 0.38 ± 0.03 26 σ
Open in a new tab

Figure 2.

Figure 2

Open in a new tab

Snapshots of equilibrated morphologies and deformation axes for (a) spherical, (b) cylindrical, and (c) lamellar samples. Red beads are PMMA, transparent blue beads are PnBA, and SP beads are shown in yellow. (d) Schematic sketches of chain conformations studied in this paper.

This analysis indicates that the equilibration procedure described in Section 5.2 successfully generated correctly equilibrated triblock copolymer samples, with the expected network-like topologies. While some discrepancies in the domain spacings and loop and tie fractions were observed (see Supporting Information), such discrepancies are expected because the SCFT results are only valid for identical monomer sizes, whereas here the B beads are slightly bigger than the A beads.17 SCFT results also show a weak dependence of the tie fraction with degree of segregation and copolymer composition, which are neglected in this comparison.17 These effects are expected to be small, however, and the overall agreement between the simulation results and the SCFT predictions supports that the samples investigated here are fully equilibrated and accurately represent the morphologies of spherical, cylindrical, and lamellar triblock copolymers.

2.2. Stress Strain Behavior

To measure the stress–strain behavior as a function of morphology, the spherical, cylindrical, and lamellar samples were deformed perpendicular to their periodic microstructure at constant volume; while slight quantitative differences in the stress/strain curves and mechanochemical activation were observed with other deformation modes (e.g., deformation at constant pressure), the overall trends and conclusions reported in this work are not significantly influenced by the deformation method (see Supporting Information for a detailed discussion and comparison). Samples were deformed up to 400% elongation, corresponding to true strains between 0 and 1.63, and each stress–strain curve was averaged over 10 independent simulation runs. The resulting overall stress–strain curves are shown in Figure 3a. Overall, the stress–strain curves follow the expected behavior, with the stress increasing with the fraction of the glassy A component in the sample. Consistent with prior results from simulations25,46 and experiments,47,48 the absolute stress is highest for the lamellar morphology, followed by the cylindrical morphology, with the spherical morphology having the lowest stress.

Figure 3.

Figure 3

Open in a new tab

(a) Stress–strain curves for the spherical (sph), cylindrical (cyl), and lamellar (lam) morphologies and (b) contribution of each chain type to the overall stress–strain curve. The contributions are normalized such that the addition of all curves results in the total stress on the sample. Each stress–strain curve reflects an average over 10 independent simulation runs.

The stress–strain behavior exhibited a very short linear elastic regime at low strains, followed by a weak yield point for the lamellar sample, and a continuous increase of stress, indicating strain hardening at higher strain values. Generally, the behavior of the simulated BCP was somewhat more “ductile” than an experimental system would be. This effect is a known shortcoming of the Lennard-Jones (LJ) potential, which does not reproduce brittle failure modes under uniaxial deformation accurately.34,49 In addition to the pair-potential, periodic boundaries stabilize plastic flow49,50 and suppress crazing and shear banding. While we focus here mainly on the activation behavior of the embedded mechanophore in the rubbery block and do not investigate failure modes associated with the glassy domains directly, detailed investigation of mechanophore activation related to material failure may be an interesting direction for future work.

The stress–strain behavior as a function of chain type is shown in Figure 3b. The tie chains carried the majority of the total stress,25 especially for the cylindrical and spherical morphologies. In the lamellar sample, where tie chains make up 38% of the sample, loop chains transmit roughly half of the stress. When normalized by the absolute number of each type of chain (see Supporting Information), the average stress per chain is the same on all chains for low strain, up to a strain of roughly 1.2; for higher strains, the loop chains carry a lower than average stress, whereas the tie and entangled hooked chains carry higher than average stress. These results indicate that the contributions from the different types of chains obtained from the coarse-grained simulations are reasonable and provide a sound basis for analyzing mechanochemical activation across different types of chains.

Finally, we note that in the lamellar morphology, consistent with previous reports, some buckling46 and cavitation34 events were observed in the rubbery phase around a percent elongation of 200%. The cylindrical and spherical samples showed deformation of the microdomains but no large scale reorientation up to strains of approximately 170% for the cylindrical and 70% for the spherical samples. Cavitation was only observed in the cylindrical samples toward the very end of the deformation, at strains above approximately 350%. The main focus of this work was mechanophore activation at strains that correspond to low (affine) to higher nonaffine deformations. An in-depth analysis of activation related to mechanical failure mechanisms such as buckling and cavitation, which occur at even higher elongations, is left for future work.

2.3. Activation Behavior

The strain-induced mechanochemical activation of each sample was quantified over each deformation run by analyzing the lengths of the mechanophore bonds (represented by the double-well potentials) in the middle of each chain. The number of activated mechanophore units was defined as the number of double-well mechanophore bonds in the second minimum, which was calculated using a simple distance-based cutoff criterion (where the cutoff is located at the local maximum of the potential between the two minima). The total activation measured for each morphology is presented in Figure 4a. At low strains, all morphologies had a very similar low level of activation of about 5%, which is above the typically observed thermal activation of less than 2%. (sph: (1.4 ± 0.2) %; cyl: (1.8 ± 0.4) %; lam: (1.8 ± 0.3) %) At high strains, the fraction of mechanophore units activated increased with increasing glassy block content, consistent with the higher stress required to strain these materials. Overall, peak activations of approximately 20% (sph), 30% (cyl), and 45% (lam) were observed at the highest true strain value of 1.6.

Figure 4.

Figure 4

Open in a new tab

(a) Total activation of the mechanically active bond in different morphologies as function of strain, and (b) contribution of each chain type to the total activation for each morphology. Curves in (b) are normalized such that the sum of the activation for each individual chain type equals the total activation (black line).

As with the stress, the activation was also analyzed as a function of chain type. As seen in Figure 4b, across morphologies, the vast majority of the activation occurred in the tie chains—even in the lamellar morphology, where the tie chains make up only 38% of the sample and loop chains bear a comparable fraction of the total stress. Loop chains showed significantly lower activation, even when normalized by their relative fractions (see Supporting Information). This result suggests that control over the tie-chain fraction is critical for optimizing mechanochemical activation in block copolymers.

Because mechanophore activation rates depend on the force across the mechanochemically active bond rather than just the overall deformation, it is also useful to look at the activation as a function of stress rather than strain. As shown in Figure 5a, the spherical and cylindrical morphologies exhibit higher activation than the lamellar morphology at the same overall stress. This behavior reverses the strain-dependent trends observed in Figure 4, where the lamellar morphology had the highest activation at any given strain.

Figure 5.

Figure 5

Open in a new tab

(a) Total activation of the mechanically active bond in different morphologies as function of true stress. (b) Activation as function of average true stress on each chain type, for all three morphologies (spherical - dotted lines, cylindical - dashed lines, lamellar - solid lines) as indicated in the legend. True stress in (b) is calculated from the total true stress of each chain type for each morphology divided by the total number of chains of each chain type.

The same overall trends are observed when activation is plotted as function of average stress on each chain instead of total true strain, as shown in Figure 5b, but important differences emerge in the behavior of tie, loop, and entangled hooked chains. As seen in this figure, the loop chains that were not hooked onto other chains showed a consistently lower activation at the same average stress per chain than the tie chains or hooked loop chains, which was especially pronounced in the cylindrical and lamellar morphologies. The hooked loop chains, on the other hand, followed the tie-chain activation behavior quite closely, responding to stress in a similar way. From a geometric perspective, this is expected because two hooked chains should transmit forces very similarly to how a tie chain would.25 When normalized by number of chains, i.e, average activation per chain type (see Supporting Information), it becomes apparent that as the volume fraction of the A block (fA) decreases, the average activation of the hooked chains also decreases slightly: in the lamellar morphology, hooked chains had a slightly higher average activation than tie chains, in the cylindrical sample they were about the same, and in the spherical morphology, the hooked chains had a lower average activation than the tie chains. This trend was consistent with the amount of hooked chains in each morphology, with approximately 5% hooked chains in the lamellar samples, 1.7% in the cylindrical, and 1.3% in the spherical moprphology. From a material design standpoint, this result means that a large fraction of tie chains or hooked chains is desirable when a high overall activation is desired, especially at large strain. If a response at low absolute stress values is desired, spherical morphologies should give the highest activation at relatively low stress.

To gain more insight into the specific chain conformations in the rubbery B region and how they affect activation, primitive path analysis (PPA) was carried out on the entire deformation trajectory.51−54 In this analysis, the A beads were held fixed, and the PPA was applied only onto the B beads. The primitive path length Lc,B and the end-to-end distance Re,B of the rubbery midblock, as well as the number of kinks on the rubbery midblock, were then extracted from the primitive path structure. Details of the PPA analysis are provided in the Supporting Information.

Histograms of the primitive path contour lengths for all samples, separated by chain type and activation status, are shown in Figure 6. As seen in this figure, activated tie and hooked chains typically had a longer primitive path lengths than their nonactivated counterparts. The activated tie chains have Lc,B lengths around 55 σ, very close to maximum extension (σBBN ≈ 60 σ). The loop chains did not show such a trend, with roughly the same fraction activated regardless of their Lc,B. Interestingly, the activation depended somewhat on the number of kinks in the chains: at high strain rates, activated tie chains had a slightly lower average number of kinks than the nonactivated tie chains, and activated loop chains had a slightly higher average number kinks than the nonactivated loop chains. Details of this analysis are given in the Supporting Information. Analysis of the behavior of further subclasses of chains (e.g., loop chains entangled or hooked with tie chains, etc.) is beyond the scope of the present work but may be an interesting avenue for future analysis.

Figure 6.

Figure 6

Open in a new tab

Contour length Lc,B of the primitive path of the rubbery B block for different chain types (activated: red, blue, green or not activated: black, gray, dark gray), as indicated.

2.4. Orientation/Direction Dependence

The preceding results are all for deformation of each morphology perpendicular to its characteristic domain pattern. However, because experimental block copolymer samples are expected to contain a mixture of domain orientations, it is also important to understand how the morphology’s orientation relative to the applied force affects mechanochemical activation. To this end, additional uniaxial deformation tests were performed on each system, with force applied in the other perpendicular axes. The direction-dependent stress–strain and activation-strain behaviors are summarized in Figure 7. In the lamellar morphology, deformation in the x direction reflects deformation perpendicular to the lamellae, while deformations in the y and z directions are both deformations parallel to the lamellae, as shown in Figure 2. Because of this symmetry, the y and z responses were identical, and both the stress and activation were significantly lower for these deformations than for deformation perpendicular to the lamellae, where the chains are better aligned with the pulling direction. In the spherical case, all three directions are equivalent and exhibited identical stress and activation responses, as expected from the symmetry of this morphology. In the cylindrical case, on the other hand, all three directions behaved sightly differently; the x and z deformations are both perpendicular to the cylinder axes, but because the x axis is tilted 60° from the axis of hexagonal symmetry (see Figure 2), the deformation is not as well-aligned with the chains connecting the glassy domains. The lowest stress was observed for deformations parallel to the long axis of the cylinders, which is in agreement with prior experimental results.55,56 When the morphologies were deformed parallel to their characteristic domain directions, we did not observe any distinctive spatial patterns in activation, in contrast to the results shown on Figure 8.

Figure 7.

Figure 7

Open in a new tab

(a) Overall stress--strain and (b) overall activation curves of each morphology, deformed in different directions. See Table 1 for snapshots with indication of the directions. x is perpendicular to the lamellae, z is along the cylinder hexagonal axis, and y is parallel to the cylinder main axis.

Figure 8.

Figure 8

Open in a new tab

Spatial maps of the lamellar (top) and cylindrical samples (bottom) at approximately 1.2 true strain. For each sample, the top panel shows the density of B beads, the middle shows the local lateral stress, and the bottom shows the fraction of mechanophores activated, normalized by the local density of mechanophore beads. Note that the SP beads are located in the B-rich (blue) phase. The bin size for each 2D histogram was 1 σ.

Overall, the strain behavior is consistent with that observed in tensile experiments on aligned block copolymer samples,22,27,57 and the overall activation tracked the trend of the stress–strain curves. Importantly, the deformation axis most perpendicular to the glassy domain of each morphology always led to the largest activation; in a macroscopic sample with imperfectly aligned domains, one would observe some averaged overall activation and stress.

2.5. Spatial Localization of Activation/Stress

Finally, because the composition of self-assembled block copolymers varies spatially within the material, it is anticipated that mechanochemical activation may vary spatially within the B regions, as well. To investigate this hypothesis, each of the 10 independent runs for the lamellar and cylindrical morphologies were aligned and averaged to obtain spatial 2D maps of the fraction of B beads, the local lateral stress, and the local fraction of activated SP beads. Samples were aligned by shifting the closest center of mass of a domain to the origin and wrapping the shifted coordinates with respect to the periodic boundary conditions. The analysis was carried out at a true strain value of 1.2, or 300% elongation, to capture the effect of deformation while the morphology domain patterns were still relatively intact. The spherical system was omitted from this analysis because the spherical A regions became too distorted during elongation to allow robust alignment.

As shown in the top panel of Figure 8, the lamellar morphology underwent buckling and started to exhibit a chevron-like pattern at moderate to high strain. This behavior is consistent with prior observations in literature25,46 for similar triblock models. The buckling is caused by the Poisson effect due to the lateral stress mismatch in the glassy and rubbery phase.58 The exact modes of deformation and yield are expected to depend on strain rate and sample size, as shown in ref (58), although this effect was not investigated in this work. Negative lateral stresses emerged in the glassy domains, and positive lateral stresses emerged in the rubbery regions, indicating some compression of the glassy domains and expansion of the rubbery domains under tension. Additionally, some localization of extreme values of the stress near the interfaces was apparent in the rubbery regions.

Interestingly, activation in the lamellar samples was strongly correlated with the shape of the domains and not neccessarily with regions of high stress. Activation was localized toward the center and the tips of the chevron pattern in the lamellar phase, e.g., red areas in Figure 8. Note that the 2D activation map in this figure is normalized by the density of mechanophore beads, and regions with no mechanophore beads present are indicated in white. Therefore, the observed pattern is not an effect of increased density of mechanophore units, which is also higher toward the center of the rubbery regions. The mechanophore activation appears to not be correlated with extreme values in lateral stress but instead follows the pattern of spatial domain deformation.

Similarly, in the cylindrical morphology, a pronounced cross-hatch pattern appeared (lower panels in Figure 8), with the highest activation observed toward the middle of the rubbery regions, whereas the stress is highest at the interfaces between the rubbery and glassy phases. Similar to the lamellar morphology, the spatial pattern of activation followed the spatial domain deformation instead of regions of high stress. In general, in comparison to the lamellar morphology, the lateral stress in the cylindrical morphology was lower and had less pronounced positive or negative extremes.

The spherical morphology did not show any pronounced spatial activation features. We note, however, that a two-dimensional projection of the spherical morphology leads to averaging of both rubbery and glassy domains, which might hide spatial features. In addition, the spherical morphology preserved less of its spatial order when deformed, making aligning the 10 samples for averaging more challenging.

To conclude, it appears that the spatial deformation of the domains directly influences where mechanophores are activated, with the most pronounced activation occurring in the “tips” of the chevrons formed by the lamellar morphology. This illustrates that detailed understanding of each morphology and its deformation on the nanoscale is important for understanding the activation in these systems.

3. Discussion

In this work, we utilized coarse-grained molecular dynamics simulations with a simple model mechanophore to investigate mechanochemical activation in a series of well-ordered block copolymers. A key advantage of this approach, as illustrated in this work, is that it allows extraction of detailed information about how individual populations of chains do or do not participate in the activation process. As we show, modeling activation via molecular dynamics simulations allows the responses of tie, loop, and hooked chains to be analyzed separately, which is impossible in experimental systems. We find that tie and hooked chains activate much more efficiently than loop chains, which confirms our original hypothesis that activation strongly depends on chain conformations and highlights the critical importance of the network-like topology in determining the transmission of force to (and activation of) individual polymer chains.

These results suggest that block copolymer systems merit further experimental investigation as platforms for mechanochemical activation. As shown in this work, changing the composition of the block copolymer (and its self-assembled morphology) impacts both the modulus of the material and the efficiency with which it activates a mechanophore at the center of the rubbery midblock. We show that, unexpectedly, stress-activation curves and strain-activation curves show opposing trends, where spherical samples showed higher activation at low stress and lamellar morphologies showed higher activation at low strain. This means that for an application requiring activation at low stress and high strain, a spherical morphology may offer the best balance of low modulus and activation efficiency, while for an application requiring activation at high stress and low strain, a lamellar morphology will be more appropriate.

To enable application of these results to experimental systems, understanding the similarities and differences between the experimental and computational systems is critical. First, the strain rate used in the computational work is orders of magnitude higher than those typically used in experimental measurements. As a result, the computational model exhibits behaviors, such as cavitation, that likely do not play a significant role in low strain-rate experiments. As shown in the Supporting Information, we find that lowering the strain rate drives slightly earlier activation of the mechanophore units as the chains are able to relax and transmit force uniformly to the mechanically active bond. We also simplified the complex reactive molecular potential energy surface41−45 of mechanophore activation to a double-well potential, which is consistent with the level of detail in coarse-grained bead spring models. This level of resolution is known to lead to a loss of friction, more ductile behavior, and overall accelerated dynamics. While direct quantitative comparisons to experiments are challenging, and experimental systems may exhibit some differences in absolute activation profiles due to more efficient redistribution of force on the experimental time scale, this effect should not change any of the trends observed in terms of which chains activate and which do not.

Second, the morphologies used in this work were well-aligned relative to the stretching direction, while in experimental systems, the domain orientations are typically randomized, with grains on the order of hundreds of nm to a few μm.59,60 To a first approximation, measurements on experimental systems are thus expected to give a result that is essentially the average of the different orientations. In spherical systems, this effect should not change the overall activation profiles, because the spherical morphology is already symmetric along all three axes. In lamellar systems, on the other hand, this effect might significantly lower the average activation. This result may be further complicated by reorientation of domains under tensile deformation.57 Additionally, in experimental systems, the oriented grains have edges. As shown in Figure 8, activation in lamellar samples is localized near the tips of the buckled chevron pattern. This result suggests that activation may also be more pronounced at grain boundaries, where different orientations of the lamellar morphology join together. Understanding the effects of domain orientation and domain boundaries will be critical for understanding experimental mechanochemical activation profiles in these systems.

Finally, beyond the block copolymer system investigated in this work, we believe that explicit modeling of activation in coarse-grained simulations has the potential to expand understanding of a wide range of other mechanochemically active polymer systems as well. Loops, which our work shows are elastically and mechanochemically mostly inactive in the block copolymer systems, also play an important role in the mechanical properties of regularly cross-linked networks,61 and controlling loop defect content may offer new opportunities to improve activation in these types of networks. By directly modeling the mechanophore rather than inferring activation rates from a measured force, we also open the possibility of modeling mechanical responses of systems incorporating scissile mechanophores that cleave the polymer chains upon activation2,41 or mechanophores that change the length of the polymer chains as they are activated.9

4. Conclusions

In this work, we developed a simple model mechanophore that can be incorporated into coarse-grained bead–spring models of polymeric materials and used it to investigate mechanochemical activation in a series of well-ordered triblock copolymers. The equilibrated polymers generated from the coarse-grain model agree with SCFT predictions, and the incorporation of the mechanophore does not change the overall mechanical response of the material. We find that in triblock copolymers with higher fractions of the glassy end blocks, more stress is required to activate the mechanophore unit in the midblock than is required in triblocks with lower glassy block fractions. Additionally, we find that the chain topology is critical, with mechanophores located in tie chains activating at much higher rates than mechanophores located in loop chains. We also find that hooked loop chains behave very similarly to tie chains, showing similar stress-activation curves. Finally, we find that activation is not spatially uniform but instead depends strongly on where the mechanophore is located within the self-assembled morphology and how that morphology distorts during tensile deformation.

This work suggests that triblock copolymers may offer an attractive platform for controlling mechanochemical activation and should motivate further experimental work on these systems. This work also highlights the key role of network-like topology in determining mechanochemical activation, which may offer new opportunities to understand and optimize mechanochemical responses across a wide range of related systems.

5. Methods

5.1. Model

Molecular dynamics simulations of symmetric ABA triblock copolymers were carried out using a coarse-grained Kuhn segment level bead–spring model.62 Pair interactions were described by standard Lennard-Jones (LJ) potentials,63 and bonds were modeled with finite extensible nonlinear elastic (FENE) potentials.64−66 The model was parametrized to describe a poly(methyl methacrylate)-block-poly(n-butyl acrylate)-block-poly(methyl methacrylate) (PMMA-b-PnBA-b-PMMA) polymer system, with the mass mA = 1 m, diameter σAA = 1 σ, and interaction energy ϵAA = 1 ϵ of the A beads (each representing a PMMA Kuhn segment) chosen as the units of mass, length, and energy, respectively. The resulting derived units of temperature, pressure, and time were T* = kT/ϵ, p = ϵσ–3, and Inline graphic, and the parameters for the B beads were set as mB = 1.6 m, σBB = 1.2 σ, and ϵBB = 0.6 ϵ to parametrize the PnBA Kuhn segments (see Supporting Information). The cross-interaction parameters were chosen using Lorentz67 and Fender-Halsey68 mixing rules, yielding σAB = 1.1 σ and ϵAB = 0.75 ϵ, where ϵAB = 0.75 ϵ ensures that the polymer melt phase separates under the investigated conditions. For computational efficiency, all LJ pair interactions were cut at rcut = 3 σij, and a smoothing function69 was applied from ron = 2.5 σij to rcut to transition both energy and force smoothly to zero at rcut. Finally, the mechanophore unit was represented using a double-well potential, where the first minimum corresponds to the deactivated state and the second minimum represents the activated state, with an additional bead in the middle of the bond to prevent unphysical bond crossing in the activated state. Details of the double-well potential are provided in the Supporting Information.

All simulations were carried out in HOOMD-blue 2.9.270,71 using CUDA 10.1 on a single graphics processing unit (GPU) (NVIDIA GeForce GTX 1080Ti). The double-well potential was implemented in a custom plugin72 for HOOMD-blue.

5.2. Sample Generation/Equilibration

In all simulations, the degree of polymerization of the B midblock was set to NB = 50. The total number of A beads was then varied from 16 to 86 to achieve volume fractions fA of the A block from 0.16 to 0.50, targeting spherical, cylindrical, and lamellar phases. The polymer chains were placed randomly in a cuboid simulation box using standard periodic boundary conditions with the volume V = Lx × Ly × Lz at a number density of 0.55 σ3, as shown in Table 1. The randomly placed polymer chains were then annealed toward the target microphase-segregated structures using dissipative particle dynamics (DPD),73,74 which enables fast phase separation.75−77 Even with the fast equilibration typical for DPD, however, it took considerable time for the systems to phase separate and anneal into the ordered morphologies. Therefore, only a small number of test systems were directly equilibrated using DPD, resulting in the expected morphologies after ∼1 × 104 τ for lamellae, ∼5 × 104 τ for cylinders, and ∼6 × 104 τ for spherical morphologies. For the remaining samples, an external field with domain spacings matching those obtained from the test systems was applied to direct the self-assembly and speed up the equilibration, based on the method discussed in ref (78). Full details of the equilibration and directed self-assembly methods are provided in the Supporting Information.

After self-assembly, the soft potentials used for the equilibration runs were replaced with the LJ and FENE potentials described above, and the time step was consequently decreased to Δt = 0.005 τ to ensure numerical stability and energy conservation. The external field was removed, and further equilibration was performed in the NVT ensemble using a Langevin thermostat and a temperature T = 1.0 ϵ/kB for 2.5× 103 τ. After that, the equilibrated configuration was cooled down linearly within 4.5 × 103 τ to the desired temperature of T = 0.35 ϵ/kB using the NPT ensemble with the Martyna-Tobias-Klein (MTK) barostat-thermostat79 with coupling constants τ = 1.0 and τp = 1.2 at constant pressure p = 0. The system was then equilibrated at T = 0.35 ϵ/kB for another 500 τ. This temperature is well-below the glass transition temperature Tg ≈ 0.43 ϵ/kB of the A blocks80 and above Tg of the B blocks. The system was then further equilibrated at a constant temperature T = 0.35 ϵ/kB for another 500 τ to ensure an equilibrated morphology before the spiropyran units were incorporated into the center of the B beads. Full details of the equilibration procedure are provided in the Supporting Information.

5.3. Deformation

The tensile response of the equilibrated samples was simulated by deforming the equilibrated configurations at a strain rate of 4 × 10–4 τ–1 in an NVT ensemble using a Langevin thermostat with a constant temperature T = 0.35 ϵ/kB. The average stress was obtained from the simulation using the pressure tensor components, 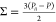Inline graphic where i is the direction of elongation and P is the pressure, Inline graphic.81 All uniaxial deformations were repeated 10 times with independently equilibrated samples. Samples were deformed to a maximum elongation of 400% to ensure that the entire range of sample responses was investigated.24

5.4. Analysis

In order to analyze the chain conformations, each chain was identified as either a tie, loop, or dangling or hooked chain. By clustering the different A-rich domains using DBSCAN,82 it was straightforward to identify which chain ends were either connecting different domains, in the same domain, or if one end was dangling free. To distinguish loop from hooked chains, the primitive path analysis algorithm51−54 was used on each rubbery B midblock. Using the reduced path, it is possible to determine which chain is entangled with which, and the hooked chains could be readily distinguished. Local stress was determined using the virial expression for stress on each particle and then binned in a two-dimensional histogram. More details about each of these analyses are provided in the Supporting Information.

Acknowledgments

This work was supported by grants from the National Science Foundation (DMR-1846665 and DMR- 2143864). This research was supported in part by the University of Pittsburgh Center for Research Computing through the resources provided.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acspolymersau.2c00031.

  • Details of coarse-grained model and simulation methods; supplemental results including histograms of primitive path quantities, results for the deformation rate dependence, disordered sample behavior, and additional stress–strain and strain-activation curves; supplemental discussion on effect of different deformation methods (PDF)

Author Contributions

The manuscript was prepared through contributions of all authors. J.L. and A.S. designed the research project. Z.H., S.S., and L.F. carried out and analyzed all simulations with guidance from A.S. Z.H., S.S., J.L, and A.S drafted and revised the manuscript. All authors have given approval of the final version of the manuscript. CRediT: Zijian Huo data curation (lead), formal analysis (lead), investigation (equal), software (equal), validation (equal), visualization (equal), writing-original draft (equal), writing-review & editing (equal); Stephen J Skala data curation (equal), formal analysis (equal), investigation (equal), software (equal), validation (equal), visualization (equal), writing-original draft (equal), writing-review & editing (equal); Lavinia R Falck data curation (supporting), formal analysis (supporting), visualization (supporting), writing-original draft (supporting); Jennifer E. Laaser conceptualization (equal), funding acquisition (equal), investigation (equal), project administration (equal), supervision (equal), writing-original draft (equal), writing-review & editing (equal); Antonia Statt data curation (equal), formal analysis (equal), funding acquisition (lead), investigation (equal), methodology (equal), project administration (equal), resources (equal), software (equal), supervision (equal), validation (equal), visualization (supporting), writing-original draft (equal), writing-review & editing (equal).

The authors declare no competing financial interest.

Supplementary Material

lg2c00031_si_001.pdf (877.4KB, pdf)

References

  1. Peterson G. I.; Larsen M. B.; Ganter M. A.; Storti D. W.; Boydston A. J. 3D-Printed Mechanochromic Materials. ACS Appl. Mater. Interfaces 2015, 7, 577–583. 10.1021/am506745m. [DOI] [PubMed] [Google Scholar]
  2. Li J.; Nagamani C.; Moore J. S. Polymer Mechanochemistry: From Destructive to Productive. Acc. Chem. Res. 2015, 48, 2181–2190. 10.1021/acs.accounts.5b00184. [DOI] [PubMed] [Google Scholar]
  3. Li Z.; Toivola R.; Ding F.; Yang J.; Lai P.-N.; Howie T.; Georgeson G.; Jang S.-H.; Li X.; Flinn B. D.; et al. Highly Sensitive Built-In Strain Sensors for Polymer Composites: Fluorescence Turn-On Response through Mechanochemical Activation. Adv. Mater. 2016, 28, 6592–6597. 10.1002/adma.201600589. [DOI] [PubMed] [Google Scholar]
  4. Piermattei A.; Karthikeyan S.; Sijbesma R. P. Activating catalysts with mechanical force. Nat. Chem. 2009, 1, 133–137. 10.1038/nchem.167. [DOI] [PubMed] [Google Scholar]
  5. Groote R.; Jakobs R. T. M.; Sijbesma R. P. Mechanocatalysis: Forcing Latent Catalysts into Action. Polym. Chem. 2013, 4, 4846. 10.1039/c3py00071k. [DOI] [Google Scholar]
  6. Diesendruck C. E.; Moore J. S. Mechanophores for Self-Healing Applications. Self-Healing Polymers 2013, 193–214. 10.1002/9783527670185.ch8. [DOI] [Google Scholar]
  7. Wang J.; Piskun I.; Craig S. L. Mechanochemical Strengthening of a Multi-mechanophore Benzocyclobutene Polymer. ACS Macro Lett. 2015, 4, 834–837. 10.1021/acsmacrolett.5b00440. [DOI] [PubMed] [Google Scholar]
  8. Potisek S. L.; Davis D. A.; Sottos N. R.; White S. R.; Moore J. S. Mechanophore-Linked Addition Polymers. J. Am. Chem. Soc. 2007, 129, 13808–13809. 10.1021/ja076189x. [DOI] [PubMed] [Google Scholar]
  9. Su J. K.; Feist J. D.; Yang J.; Mercer J. A. M.; Romaniuk J. A. H.; Chen Z.; Cegelski L.; Burns N. Z.; Xia Y. Synthesis and Mechanochemical Activation of Ladderene–Norbornene Block Copolymers. J. Am. Chem. Soc. 2018, 140, 12388–12391. 10.1021/jacs.8b08908. [DOI] [PubMed] [Google Scholar]
  10. Davis D. A.; Hamilton A.; Yang J.; Cremar L. D.; Van Gough D.; Potisek S. L.; Ong M. T.; Braun P. V.; Martinez T. J.; White S. R.; et al. Force-induced Activation of Covalent Bonds in Mechanoresponsive Polymeric Materials. Nature 2009, 459, 68–72. 10.1038/nature07970. [DOI] [PubMed] [Google Scholar]
  11. Versaw B. A.; Zeng T.; Hu X.; Robb M. J. Harnessing the Power of Force: Development of Mechanophores for Molecular Release. J. Am. Chem. Soc. 2021, 143, 21461–21473. 10.1021/jacs.1c11868. [DOI] [PubMed] [Google Scholar]
  12. Boulatov R. The Challenges and Opportunities of Contemporary Polymer Mechanochemistry. ChemPhysChem 2017, 18, 1419–1421. 10.1002/cphc.201700127. [DOI] [PubMed] [Google Scholar]
  13. Bates F. S.; Fredrickson G. H. Block Copolymers—Designer Soft Materials. Phys. Today 1999, 52, 32–38. 10.1063/1.882522. [DOI] [Google Scholar]
  14. Bates C. M.; Bates F. S. 50th Anniversary Perspective: Block Polymers—Pure Potential. Macromolecules 2017, 50, 3–22. 10.1021/acs.macromol.6b02355. [DOI] [Google Scholar]
  15. Inoue T.; Moritani M.; Hashimoto T.; Kawai H. Deformation Mechanism of Elastomeric Block Copolymers Having Spherical Domains of Hard Segments under Uniaxial Tensile Stress. Macromolecules 1971, 4, 500–507. 10.1021/ma60022a028. [DOI] [Google Scholar]
  16. Pakula T.; Saijo K.; Kawai H.; Hashimoto T. Deformation behavior of styrene-butadiene-styrene triblock copolymer with cylindrical morphology. Macromolecules 1985, 18, 1294–1302. 10.1021/ma00148a044. [DOI] [Google Scholar]
  17. Matsen M. W.; Thompson R. B. Equilibrium behavior of symmetric ABA triblock copolymer melts. J. Chem. Phys. 1999, 111, 7139–7146. 10.1063/1.480006. [DOI] [Google Scholar]
  18. Matsen M. W. Equilibrium behavior of asymmetric ABA triblock copolymer melts. J. Chem. Phys. 2000, 113, 5539–5544. 10.1063/1.1289889. [DOI] [Google Scholar]
  19. Tong J.-D.; Jerôme R. Dependence of the Ultimate Tensile Strength of Thermoplastic Elastomers of the Triblock Type on the Molecular Weight between Chain Entanglements of the Central Block. Macromolecules 2000, 33, 1479–1481. 10.1021/ma990404f. [DOI] [Google Scholar]
  20. Murat M.; Grest G. S.; Kremer K. Statics and dynamics of symmetric diblock copolymers: A molecular dynamics study. Macromolecules 1999, 32, 595–609. 10.1021/ma981512p. [DOI] [Google Scholar]
  21. Herschberg T.; Carrillo J.-M. Y.; Sumpter B. G.; Panagiotou E.; Kumar R. Topological Effects Near Order–Disorder Transitions in Symmetric Diblock Copolymer Melts. Macromolecules 2021, 54, 7492–7499. 10.1021/acs.macromol.1c00780. [DOI] [Google Scholar]
  22. Wang L.; Liu H.; Li F.; Shen J.; Zheng Z.; Gao Y.; Liu J.; Wu Y.; Zhang L. Stress–strain behavior of block-copolymers and their nanocomposites filled with uniform or Janus nanoparticles under shear: a molecular dynamics simulation. Phys. Chem. Chem. Phys. 2016, 18, 27232–27244. 10.1039/C6CP05853A. [DOI] [PubMed] [Google Scholar]
  23. Parker A. J.; Rottler J. Nonlinear Mechanics of Triblock Copolymer Elastomers: From Molecular Simulations to Network Models. ACS Macro Lett. 2017, 6, 786–790. 10.1021/acsmacrolett.7b00369. [DOI] [Google Scholar]
  24. Aoyagi T.; Honda T.; Doi M. Microstructural study of mechanical properties of the ABA triblock copolymer using self-consistent field and molecular dynamics. J. Chem. Phys. 2002, 117, 8153–8161. 10.1063/1.1510728. [DOI] [Google Scholar]
  25. Makke A.; Lame O.; Perez M.; Barrat J.-L. Influence of Tie and Loop Molecules on the Mechanical Properties of Lamellar Block Copolymers. Macromolecules 2012, 45, 8445–8452. 10.1021/ma301286y. [DOI] [Google Scholar]
  26. Makke A.; Perez M.; Lame O.; Barrat J.-L. Mechanical testing of glassy and rubbery polymers in numerical simulations: Role of boundary conditions in tensile stress experiments. J. Chem. Phys. 2009, 131, 014904. 10.1063/1.3148381. [DOI] [PubMed] [Google Scholar]
  27. Zheng Z.; Liu H.; Shen J.; Liu J.; Wu Y.; Zhang L. Tailoring the Static and Dynamic Mechanical Properties of Tri-Block Copolymers through Molecular Dynamics Simulation. Polymers 2016, 8, 335. 10.3390/polym8090335. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Arora A.; Lin T.-S.; Olsen B. D. Coarse-Grained Simulations for Fracture of Polymer Networks: Stress Versus Topological Inhomogeneities. Macromolecules 2022, 55, 4–14. 10.1021/acs.macromol.1c01689. [DOI] [Google Scholar]
  29. Wang J.; Lin T.-S.; Gu Y.; Wang R.; Olsen B. D.; Johnson J. A. Counting Secondary Loops Is Required for Accurate Prediction of End-Linked Polymer Network Elasticity. ACS Macro Lett. 2018, 7, 244–249. 10.1021/acsmacrolett.8b00008. [DOI] [PubMed] [Google Scholar]
  30. Jiang S.; Zhang L.; Xie T.; Lin Y.; Zhang H.; Xu Y.; Weng W.; Dai L. Mechanoresponsive PS-PnBA-PS Triblock Copolymers via Covalently Embedding Mechanophore. ACS Macro Lett. 2013, 2, 705–709. 10.1021/mz400198n. [DOI] [PubMed] [Google Scholar]
  31. Ramirez A. B.; Schmitt A.; Mahanthappa M.; Craig S. Enhancing covalent mechanochemistry in bulk polymers using electrospun ABA triblock copolymers. Faraday Discuss. 2014, 170, 337–344. 10.1039/C4FD00001C. [DOI] [PubMed] [Google Scholar]
  32. Silberstein M. N.; Min K.; Cremar L. D.; Degen C. M.; Martinez T. J.; Aluru N. R.; White S. R.; Sottos N. R. Modeling mechanophore activation within a crosslinked glassy matrix. J. Appl. Phys. 2013, 114, 023504. 10.1063/1.4812581. [DOI] [Google Scholar]
  33. Silberstein M. N.; Cremar L. D.; Beiermann B. A.; Kramer S. B.; Martinez T. J.; White S. R.; Sottos N. R. Modeling mechanophore activation within a viscous rubbery network. Journal of the Mechanics and Physics of Solids 2014, 63, 141–153. 10.1016/j.jmps.2013.09.014. [DOI] [Google Scholar]
  34. Makke A.; Perez M.; Rottler J.; Lame O.; Barrat J.-L. Predictors of Cavitation in Glassy Polymers under Tensile Strain: A Coarse-Grained Molecular Dynamics Investigation. Macromol. Theory Simul. 2011, 20, 826–836. 10.1002/mats.201100006. [DOI] [Google Scholar]
  35. Guo J.; André P.; Adam M.; Panyukov S.; Rubinstein M.; DeSimone J. M. Solution Properties of a Fluorinated Alkyl Methacrylate Polymer in Carbon Dioxide. Macromolecules 2006, 39, 3427–3434. 10.1021/ma052409k. [DOI] [Google Scholar]
  36. Fetters L.; Lohse D.; Colby R. Chain Dimensions and Entanglement Spacings. Physical properties of polymers handbook 2007, 447–454. 10.1007/978-0-387-69002-5_25. [DOI] [Google Scholar]
  37. Wypych G.Handbook of polymers, 2nd ed.; Elsevier, 2016. [Google Scholar]
  38. Zabet M.; Mishra S.; Boy R.; Walters K. B.; Naskar A. K.; Kundu S. Temperature-dependent self-assembly and rheological behavior of a thermoreversible pmma-Pn BA-PMMA triblock copolymer gel. J. Polym. Sci., Part B: Polym. Phys. 2017, 55, 877–887. 10.1002/polb.24336. [DOI] [Google Scholar]
  39. Ruzette A.-V.; Tencé-Girault S.; Leibler L.; Chauvin F.; Bertin D.; Guerret O.; Gérard P. Molecular Disorder and Mesoscopic Order in Polydisperse Acrylic Block Copolymers Prepared by Controlled Radical Polymerization. Macromolecules 2006, 39, 5804–5814. 10.1021/ma060541u. [DOI] [Google Scholar]
  40. Gossweiler G. R.; Kouznetsova T. B.; Craig S. L. Force-Rate Characterization of Two Spiropyran-Based Molecular Force Probes. J. Am. Chem. Soc. 2015, 137, 6148–6151. 10.1021/jacs.5b02492. [DOI] [PubMed] [Google Scholar]
  41. Klein I. M.; Husic C. C.; Kovács D. P.; Choquette N. J.; Robb M. J. Validation of the CoGEF Method as a Predictive Tool for Polymer Mechanochemistry. J. Am. Chem. Soc. 2020, 142, 16364–16381. 10.1021/jacs.0c06868. [DOI] [PubMed] [Google Scholar]
  42. Horst M.; Yang J.; Meisner J.; Kouznetsova T. B.; Martínez T. J.; Craig S. L.; Xia Y. Understanding the Mechanochemistry of Ladder-Type Cyclobutane Mechanophores by Single Molecule Force Spectroscopy. J. Am. Chem. Soc. 2021, 143, 12328–12334. 10.1021/jacs.1c05857. [DOI] [PubMed] [Google Scholar]
  43. Chen Y.; Mellot G.; van Luijk D.; Creton C.; Sijbesma R. P. Mechanochemical tools for polymer materials. Chem. Soc. Rev. 2021, 50, 4100–4140. 10.1039/D0CS00940G. [DOI] [PubMed] [Google Scholar]
  44. Kim T. A.; Beiermann B. A.; White S. R.; Sottos N. R. Effect of Mechanical Stress on Spiropyran-Merocyanine Reaction Kinetics in a Thermoplastic Polymer. ACS Macro Lett. 2016, 5, 1312–1316. 10.1021/acsmacrolett.6b00822. [DOI] [PubMed] [Google Scholar]
  45. Kim T. A.; Robb M. J.; Moore J. S.; White S. R.; Sottos N. R. Mechanical Reactivity of Two Different Spiropyran Mechanophores in Polydimethylsiloxane. Macromolecules 2018, 51, 9177–9183. 10.1021/acs.macromol.8b01919. [DOI] [Google Scholar]
  46. Makke A.; Lame O.; Perez M.; Barrat J.-L. Nanoscale Buckling in Lamellar Block Copolymers: A Molecular Dynamics Simulation Approach. Macromolecules 2013, 46, 7853–7864. 10.1021/ma400514h. [DOI] [Google Scholar]
  47. Adhikari R.; Michler G. H.; Huy T. A.; Ivan’kova E.; Godehardt R.; Lebek W.; Knoll K. Correlation between Molecular Architecture, Morphology, and Deformation Behaviour of Styrene/Butadiene Block Copolymers. Macromol. Chem. Phys. 2003, 204, 488–499. 10.1002/macp.200390022. [DOI] [Google Scholar]
  48. Tomita S.; Lei L.; Urushihara Y.; Kuwamoto S.; Matsushita T.; Sakamoto N.; Sasaki S.; Sakurai S. Strain-induced deformation of glassy spherical microdomains in elastomeric triblock copolymer films: Simultaneous measurements of a stress–strain curve with 2d-SAXS patterns. Macromolecules 2017, 50, 677–686. 10.1021/acs.macromol.6b02206. [DOI] [Google Scholar]
  49. Lin E. Y.; Riggleman R. A. Distinguishing failure modes in oligomeric polymer nanopillars. Soft Matter 2019, 15, 6589–6595. 10.1039/C9SM00699K. [DOI] [PubMed] [Google Scholar]
  50. Shi Y. Size-independent shear band formation in amorphous nanowires made from simulated casting. Appl. Phys. Lett. 2010, 96, 121909. 10.1063/1.3340908. [DOI] [Google Scholar]
  51. Karayiannis N. C.; Kröger M. Combined Molecular Algorithms for the Generation, Equilibration and Topological Analysis of Entangled Polymers: Methodology and Performance. International Journal of Molecular Sciences 2009, 10, 5054–5089. 10.3390/ijms10115054. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Shanbhag S.; Kröger M. Primitive path networks generated by annealing and geometrical methods: Insights into differences. Macromolecules 2007, 40, 2897–2903. 10.1021/ma062457k. [DOI] [Google Scholar]
  53. Kröger M. Shortest multiple disconnected path for the analysis of entanglements in two-and three-dimensional polymeric systems. Computer physics communications 2005, 168, 209–232. 10.1016/j.cpc.2005.01.020. [DOI] [Google Scholar]
  54. Foteinopoulou K.; Karayiannis N. C.; Mavrantzas V. G.; Kröger M. Primitive path identification and entanglement statistics in polymer melts: Results from direct topological analysis on atomistic polyethylene models. Macromolecules 2006, 39, 4207–4216. 10.1021/ma060306b. [DOI] [Google Scholar]
  55. Honeker C.; Thomas E.; Albalak R. J.; Hajduk D.; Gruner S.; Capel M. Perpendicular Deformation of a Near-Single-Crystal Triblock Copolymer with a Cylindrical Morphology. 1. Synchrotron SAXS. Macromolecules 2000, 33, 9395–9406. 10.1021/ma000593y. [DOI] [Google Scholar]
  56. Zhang H. J.; Luo F.; Ye Y.; Sun T. L.; Nonoyama T.; Kurokawa T.; Nakajima T. Tough Triblock Copolymer Hydrogels with Different Micromorphologies for Medical and Sensory Materials. ACS Applied Polymer Materials 2019, 1, 1948–1953. 10.1021/acsapm.9b00395. [DOI] [Google Scholar]
  57. Honeker C. C.; Thomas E. L. Impact of Morphological Orientation in Determining Mechanical Properties in Triblock Copolymer Systems. Chem. Mater. 1996, 8, 1702–1714. 10.1021/cm960146q. [DOI] [Google Scholar]
  58. Makke A.; Perez M.; Lame O.; Barrat J.-L. Nanoscale buckling deformation in layered copolymer materials. Proc. Natl. Acad. Sci. U. S. A. 2012, 109, 680–685. 10.1073/pnas.1111367109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Myers R. T.; Cohen R. E.; Bellare A. Use of Ultra-Small-Angle X-ray Scattering To Measure Grain Size of Lamellar Styrene-Butadiene Block Copolymers. Macromolecules 1999, 32, 2706–2711. 10.1021/ma9816618. [DOI] [Google Scholar]
  60. Rokhlenko Y.; Majewski P. W.; Larson S. R.; Gopalan P.; Yager K. G.; Osuji C. O. Implications of Grain Size Variation in Magnetic Field Alignment of Block Copolymer Blends. ACS Macro Lett. 2017, 6, 404–409. 10.1021/acsmacrolett.7b00036. [DOI] [PubMed] [Google Scholar]
  61. Zhong M.; Wang R.; Kawamoto K.; Olsen B. D.; Johnson J. A. Quantifying the impact of molecular defects on polymer network elasticity. Science 2016, 353, 1264–1268. 10.1126/science.aag0184. [DOI] [PubMed] [Google Scholar]
  62. Everaers R.; Karimi-Varzaneh H. A.; Fleck F.; Hojdis N.; Svaneborg C. Kremer–Grest Models for Commodity Polymer Melts: Linking Theory, Experiment, and Simulation at the Kuhn Scale. Macromolecules 2020, 53, 1901–1916. 10.1021/acs.macromol.9b02428. [DOI] [Google Scholar]
  63. Jones J. E. On the determination of molecular fields. II. From the equation of state of a gas. Proc. R. Soc. Lond. A 1924, 106, 463–477. 10.1098/rspa.1924.0082. [DOI] [Google Scholar]
  64. Grest G. S.; Kremer K. Statistical properties of random cross-linked rubbers. Macromolecules 1990, 23, 4994–5000. 10.1021/ma00225a020. [DOI] [Google Scholar]
  65. Grest G. S.; Kremer K. Molecular dynamics simulation for polymers in the presence of a heat bath. Phys. Rev. A 1986, 33, 3628–3631. 10.1103/PhysRevA.33.3628. [DOI] [PubMed] [Google Scholar]
  66. Kremer K.; Grest G. S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. 10.1063/1.458541. [DOI] [Google Scholar]
  67. Lorentz H. A. Ueber die Anwendung des Satzes vom Virial in der kinetischen Theorie der Gase. Annalen der Physik 1881, 248, 127–136. 10.1002/andp.18812480110. [DOI] [Google Scholar]
  68. Fender B. E. F.; Halsey G. D. Second Virial Coefficients of Argon, Krypton, and Argon-Krypton Mixtures at Low Temperatures. J. Chem. Phys. 1962, 36, 1881–1888. 10.1063/1.1701284. [DOI] [Google Scholar]
  69. Statt A.; Casademunt H.; Brangwynne C. P.; Panagiotopoulos A. Z. Model for disordered proteins with strongly sequence-dependent liquid phase behavior. J. Chem. Phys. 2020, 152, 075101. 10.1063/1.5141095. [DOI] [PubMed] [Google Scholar]
  70. Anderson J. A.; Glaser J.; Glotzer S. C. HOOMD-blue: A Python package for high-performance molecular dynamics and hard particle Monte Carlo simulations. Comput. Mater. Sci. 2020, 173, 109363. 10.1016/j.commatsci.2019.109363. [DOI] [Google Scholar]
  71. Phillips C. L.; Anderson J. A.; Glotzer S. C. Pseudo-random number generation for Brownian Dynamics and Dissipative Particle Dynamics simulations on GPU devices. J. Comput. Phys. 2011, 230, 7191–7201. 10.1016/j.jcp.2011.05.021. [DOI] [Google Scholar]
  72. Plugin for HOOMD-blue: azplugins, v0.10.0. https://github.com/mphowardlab/azplugins.
  73. Groot R. D.; Warren P. B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. 10.1063/1.474784. [DOI] [Google Scholar]
  74. Español P.; Warren P. B. Perspective: Dissipative particle dynamics. J. Chem. Phys. 2017, 146, 150901. 10.1063/1.4979514. [DOI] [PubMed] [Google Scholar]
  75. Ryu J. H.; Wee H. S.; Lee W. B. Molecular dynamics study on microstructures of diblock copolymer melts with soft potential and potential recovery. Phys. Rev. E 2016, 94, 032501. 10.1103/PhysRevE.94.032501. [DOI] [PubMed] [Google Scholar]
  76. Li Y.; Qian H.-J.; Lu Z.-Y.; Shi A.-C. Note: Effects of polydispersity on the phase behavior of AB diblock and BAB triblock copolymer melts: A dissipative particle dynamics simulation study. J. Chem. Phys. 2013, 139, 096101. 10.1063/1.4820235. [DOI] [PubMed] [Google Scholar]
  77. Parker A. J.; Rottler J. Using Soft Potentials for the Simulation of Block Copolymer Morphologies. Macromol. Theory Simul. 2014, 23, 401–409. 10.1002/mats.201400001. [DOI] [Google Scholar]
  78. Padmanabhan P.; Martinez-Veracoechea F.; Escobedo F. A. Computation of Free Energies of Cubic Bicontinuous Phases for Blends of Diblock Copolymer and Selective Homopolymer. Macromolecules 2016, 49, 5232–5243. 10.1021/acs.macromol.6b00123. [DOI] [Google Scholar]
  79. Martyna G. J.; Tobias D. J.; Klein M. L. Constant pressure molecular dynamics algorithms. J. Chem. Phys. 1994, 101, 4177–4189. 10.1063/1.467468. [DOI] [Google Scholar]
  80. Buchholz J.; Paul W.; Varnik F.; Binder K. Cooling rate dependence of the glass transition temperature of polymer melts: Molecular dynamics study. J. Chem. Phys. 2002, 117, 7364–7372. 10.1063/1.1508366. [DOI] [Google Scholar]
  81. Rottach D. R.; Curro J. G.; Grest G. S.; Thompson A. P. Effect of Strain History on Stress and Permanent Set in Cross-Linking Networks: A Molecular Dynamics Study. Macromolecules 2004, 37, 5468–5473. 10.1021/ma049723j. [DOI] [Google Scholar]
  82. Ester M.; Kriegel H. P.; Sander J.; Xiaowei X. A density-based algorithm for discovering clusters in large spatial databases with noise. Proceedings of the Second International Conference on Knowledge Discovery and Data Mining 1996, 226–231. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

lg2c00031_si_001.pdf (877.4KB, pdf)

Articles from ACS Polymers Au are provided here courtesy of American Chemical Society

RESOURCES